
 17.Охарактеризовать граф ˚
17.Охарактеризовать граф ˚|
1. Компетенции |
|
|
|
ПК- профессиональные компетенции ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетом документации, принимать участие в разработке проектной документации на модификацию информационной системы. ПК 2.1. Участвовать в разработке технического задания. ПК 2.3. Применять методики тестирования разрабатываемых приложений.
|
ОК- общие компетенции ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач профессионального и личностного развития. ОК5.Использовать информационно-коммуникационные технологии в профессиональной деятельности. ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями. ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. |
В результате освоения учебной дисциплины «Математика» обучающийся должен уметь:
- применять основные численные методы решения прикладных задач
В результате освоения учебной дисциплины обучающийся должен знать:
- роль и место математики в современном мире, а так же в решении профессиональных задач;
- основные понятия и методы математического анализа, дискретной математики, теории вероятностей и математической статистики;
Контрольная работа по теме « Графы»
1.Изобразить неориентированный граф , состоящий из
| вариант | вершин | ребер | вариант | вершин | ребер |
| 1 | 5 | 8 | 13 | 6 | 7 |
| 2 | 6 | 8 | 14 | 7 | 7 |
| 3 | 7 | 8 | 15 | 8 | 7 |
| 4 | 5 | 9 | 16 | 5 | 10 |
| 5 | 6 | 9 | 17 | 6 | 10 |
| 6 | 7 | 9 | 18 | 7 | 10 |
| 7 | 8 | 9 | 19 | 8 | 10 |
| 8 | 5 | 6 | 20 | 5 | 11 |
| 9 | 6 | 6 | 21 | 6 | 11 |
| 10 | 7 | 6 | 22 | 7 | 11 |
| 11 | 8 | 6 | 23 | 8 | 11 |
| 12 | 5 | 7 | 24 | 5 | 5 |
| 25 | 6 | 5 |
2.Выписать из данного графа две пары смежных и не смежных вершин
3. Выписать из данного графа две пары смежных и не смежных ребер
4.Выписать ребра , инцидентные вершине № 3.
5.Построить петлю в точке №2.
6. Достроить на графе изолированную точку.
7.Указать валентности всех вершин.
8. Изобразить любой подграф
9.Указать компоненту связанности данного графа.
10. Изобразить неориентированный, связанный граф по заданным условиям.
| вариант | Количество вершин | степень | степень | степень | вариант | Количество вершин | степень | степень | степень |
| 1 | 6 | 3(9) | 5(5) | 1(4) | 13 | 5 | 1(4) | 2(5) | 3(6) |
| 2 | 5 | 2(3) | 3(6) | 5(2) | 14 | 6 | 4(1) | 5(3) | 6(7) |
| 3 | 7 | 1(3) | 3(8) | 7(2) | 15 | 7 | 2(4) | 3(8) | 4(2) |
| 4 | 6 | 2(7) | 4(2) | 6(2) | 16 | 8 | 5(2) | 6(5) | 7(8) |
| 5 | 7 | 3(8) | 4(3) | 7(1) | 17 | 5 | 4(4) | 2(5) | 1(2) |
| 6 | 5 | 2(2) | 3(6) | 5(6) | 18 | 6 | 1(8) | 3(6) | 4(5) |
| 7 | 8 | 1(3) | 2(9) | 4(5) | 19 | 7 | 2(3) | 4(7) | 5(4) |
| 8 | 8 | 3(2) | 4(3) | 8(9) | 20 | 8 | 1(2) | 2(3) | 5(6) |
| 9 | 7 | 2(2) | 4(4) | 7(8) | 21 | 5 | 3(4) | 4(6) | 5(8) |
| 10 | 6 | 3(1) | 4(2) | 6(9) | 22 | 6 | 6(4) | 4(7) | 2(5) |
| 11 | 5 | 5(7) | 3(2) | 4(5) | 23 | 7 | 7(3) | 5(9) | 4(6) |
| 12 | 6 | 4(6) | 2(7) | 3(7) | 24 | 8 | 8(1) | 4(8) | 2(5) |
| 25 | 9 | 9(9) | 7(3) | 4(6) |
11. Описать данный граф.
12 . Изобразить ориентированный не связанный граф, состоящий из
| вариант | вершин | ребер | вариант | вершин | ребер |
| 1 | 6 | 8 | 14 | 6 | 7 |
| 2 | 7 | 8 | 15 | 7 | 7 |
| 3 | 5 | 9 | 16 | 8 | 7 |
| 4 | 6 | 9 | 17 | 5 | 10 |
| 5 | 7 | 9 | 18 | 6 | 10 |
| 6 | 8 | 9 | 19 | 7 | 10 |
| 7 | 5 | 6 | 20 | 8 | 10 |
| 8 | 6 | 6 | 21 | 5 | 11 |
| 9 | 7 | 6 | 22 | 6 | 11 |
| 10 | 8 | 6 | 23 | 7 | 11 |
| 11 | 5 | 7 | 24 | 8 | 11 |
| 12 | 5 | 8 | 25 | 5 | 5 |
| 13 | 6 | 5 |
13.Указать валентность исходящих дуг.
14 Выписать все пути из точки 2 в точку 5 и найти их длину (если пути не существует, то выбрать любой произвольный путь и найти его длину)
15. Дорисовать мост
16. Выделить точку сочленения.

 17.Охарактеризовать граф ˚
17.Охарактеризовать граф ˚








 1. 2. 3.
1. 2. 3.













4. 5 6
˚ ˚
7 8 9
10 11 12
˚ ˚
˚ ˚
˚
13 14 15
˚
˚ 17 18
16
˚ ˚
19
˚ 20 21
˚
23
22 ˚ ˚
˚ ˚ 24
˚ ˚
25 ˚ ˚
multiurok.ru
Графы
...
Дискретная математика
Семантическое дерево - это двоичное дерево, корень которого помечен двоичной функцией от m переменных, из каждого узла идут по два ребра, соответствующих двум значениям очередной переменной...
Орграфы, теория и применение
Орграф D состоит из конечного множества V вершин и набора упорядоченных пар различных вершин. В орграфе (ориентированным) маршрутом называется чередующаяся последовательность вершин и дуг v9, хг, uit...
Орграфы, теория и применение
Орграф D, обратный к данному орграфу D, имеет те же вершины, что и D, a дуга ии принадлежит D тогда и только тогда, когда дуга ии принадлежит D. Другими словами, орграф, обратный к орграфу D, получается изменением ориентации каждой дуги орграфа D...
Особенности применения теории графов при решении задач и в практической деятельности
Деревом называется связный граф, не содержащий циклов. В частности, дерево не имеет петель и кратных рёбер (поскольку кратные рёбра образуют цикл). Граф без циклов есть граф...
Представление бинарного дерева в виде массива
Хотя деревья общего вида достаточно важны, мы сосредоточимся на ограниченном классе деревьев, где каждый родитель имеет не более двух сыновей (Рис. 5). Такие бинарные деревья (binary trees) имеют унифицированную структуру...
Связность графов
Связный граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро; такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось 1 только один раз...
Связность графов
Рис 1 Рис. 2 Рис. 3 Рис. 4 граф связанность цепь дерево В предыдущем параграфе мы обсудили проблему существования замкнутой цепи, проходящей через каждое ребро заданного связного графа G...
Связность графов
В этом параграфе покажу, как можно обобщить некоторые определения, данные в предыдущих параграфах, на случай бесконечных графов. Напомним читателю, что бесконечным графом называется пара (V(G), Е(G))> где V(G)-- бесконечное множество элементов...
Связность графов
...
Спектр графа
Орграф G=(V,E) есть пара множеств, V- множество вершин, Е- множество дуг. Будем полагать, что А - матрица смежности, РG(л) (2.1) - характеристический многочлен, а - спектр графа G. С самого начала будем предполагать...
Спектр графа
Граф включает множество вершин и множество ребер, являющиеся подмножеством декартова квадрата множества вершин (т.е. каждое ребро соединяет ровно две вершины)...
Эйлеровы графы
Решение Эйлером задачи о Кёнигсбергских мостах привела к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данном графе G цикл...
Эйлеровы графы
№14 Можно ли нарисовать граф, изображённый а) на рисунке 2.10, а; б) на рисунке 2.10, б, не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз? Ответ. а) Можно. б) Нельзя. Рисуя граф в каждую вершину, за исключением начальной и конечной...
Элементы теории графов. Экономические приложения
Связный граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро; такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз...
math.bobrodobro.ru
Математические методы, применяемые в теории систем массового обслуживания
Первая работа по теории графов принадлежит Леонарду Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. Графами были названы схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых...
Метод Дейкстры нахождения кратчайшей цепи в связном графе
Пусть - граф. Конечная последовательность вершин и ребер графа , в которой каждое есть ребро, соединяющее вершины и , называется маршрутом на графе . Говорят, что маршрут (1.1) соединяет вершины и . Число называют длиной маршрута...
Орграфы, теория и применение
Граф G - совокупность двух множеств: вершин V и ребер E, между которыми определено отношение инцидентности. Каждое ребро e из E инцидентно ровно двум вершинам v, v, которые оно соединяет. При этом вершина v и ребро e называются инцидентными друг другу...
Орграфы, теория и применение
Матрица инцидентности A. По вертикали указываются вершины, по горизонтали - ребра. Aij=1 если вершина i инцидентна ребру j, в противном случае aij=0. Для орграфа aij=-1 если из вершины i исходит ребро j, aij=1 если в вершину i входит ребро j. Если ребро - петля...
Орграфы, теория и применение
Орграфы и матрицы. Матрицей сложностей A (D) орграфа D называется (рхр)-матрица аи> У которой ai}=, если vfl,-- дуга орграфа D, и atj~Q в противном случае. Сумма по столбцу легко проверить...
Особенности применения теории графов при решении задач и в практической деятельности
До сих пор мы задавали ориентированные и не ориентированные графы, изображая их с помощью рисунков. Можно задать граф как пару множеств, следуя определению, однако этот способ довольно громоздкий и представляет, скорее, теоретический интерес...
Особенности применения теории графов при решении задач и в практической деятельности
Вот мы рассмотрели все варианты графов, их элементы и теперь мы рассмотрим где и в каких сферах жизни используются графы. · В химии (для описания структур, путей сложных реакций...
Построение фигур без отрыва карандаша от бумаги
Почему же все попытки нарисовать "конверт", изображённый на рисунке 1а, одним росчерком, то есть, не отрывая руки от бумаги и не проводя дважды один и тот же отрезок. будут обречены на неудачу. А вот «распечатанный конверт»...
Построение фигур без отрыва карандаша от бумаги
Графы часто используются для решения логических проблем, связанных с перебором вариантов. Для примера рассмотрим такие задачи: Задача:Три брата - Ваня, Саша и Коля разного возраста. Ваня не старше Коли, а Саша не старше Вани...
Применение методов дискретной математики в экономике
...
Связность графов
В этом параграфе я расскажу об исследованиях некоторых важных типов графов. Вполне несвязные графы. Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом...
Связность графов
Одна из топологических характеристик графа. Граф называется связным, если для любых его вершин u и v существует цепь, соединяющая эти вершины. Числом вершинной связности графа G [обозначение а(G)] наз. наименьшее число вершин...
Эйлеровы графы
Вполне несвязные графы Определение.Граф, у которого множество рёбер пусто, называется вполне несвязным (или пустым) графом. Будем обозначать вполне несвязный граф с nвершинами через ; показан на рис. 1.5. Заметим...
Элементы теории графов. Экономические приложения
Граф - система, которая интуитивно может быть рассмотрена как множество кружков и множество соединяющих их линий (рис. 1). Кружки называются вершинами графа, линии со стрелками - дугами, без стрелок - ребрами. Граф...
Элементы теории графов. Экономические приложения
Вполне несвязные графы. Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Будем обозначать вполне несвязный граф с п вершинами через Nn; N4 показан на рис. 1. Заметим...
math.bobrodobro.ru
Графики и их функции
Рассмотрим основные алгебраические действия над функциями и их графиками, такие как сложение и вычитание (y = f(x) ±g(x)), умножение (y = f(x) ·g(x)), деление (y = f(x) / g(x)). При построении такого типа графиков следует учитывать...
Корни многочленов от одной переменной
Многочлены можно складывать, вычитать и умножать по обычным правилам раскрытия скобок и приведения подобных членов. При этом в результате снова получается многочлен. Указанные операции обладают известными свойствами: f (x) +g (x) =g (x) +f (x)...
Локальные формации с метаабелевыми группами
Определение 2.1. Всякое отображение множества всех классов групп в себя называется операцией на классах групп. Операции мы будем обозначать, как правило, прямыми большими латинскими буквами. Результат операции...
Математическое моделирование и численные методы в решении технических задач
Задача заключается в том, что бы изменить элементы исходной таблицы (массива) и вывести полученный результат в таком же виде. В данном случае мы каждый элемент таблицы умножили на 3. Текст задачи: const c=3; var t,p:text; a,b:array [1..10,1..10] of integer; i,j,n,m...
Практические приложения алгебры высказываний
...
Применение аппарата алгебры логики к решению содержательных задач
...
Разработка вычислительного устройства для выполнения операции умножения двоичных чисел
В ЭВМ операции умножения чисел с фиксированной запятой с помощью соответствующих алгоритмов сводиться к операциям сложения и сдвига. При умножении двух чисел произведение формируется суммированием частичных произведений...
Решение математических задач средствами Excel
Упражнение №5. Условие: Найдите матрицу, обратную данной:A=. Решение: 1) Вводим матрицуA в таблицу. 2) Выделяем область для обратной матрицы. 3) На панели инструментов выбираем "Вставить функцию", в диалоговом окне выбираем тип функции "МОБР"...
Теория вероятностей и математическая статистика
Часто возникает вопрос: насколько связаны два случайных события А и В друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого? В качестве примера связи между двумя событиями можно привести случаи...
Теория вероятностей на уроках математики
п.1. Отношения между событиями. Сравним следующие события: А - появление двух очков при бросании игральной кости., В-появление четного числа очков при бросании игральной кости. Замечаем следующие соотношения между событиями, если произошло А...
Теория вероятности
1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда...
Теория множеств
· Из двух множеств А и В можно образовать новое множество, объединяя все элементы множества А и все элементы множества. Объединением множеств А и В называется новое множество, состоящее из тех и только тех элементов...
Теория множеств
Введем операции над множествами и установим некоторую аналогию с операциями над другими математическими объектами, например, высказываниями. Операции над множествами и их свойства во многом аналогичны алгебре высказываний. Это...
Уравнения свертки. Обобщенные функции
...
Элементы высшей математики
Суммой матриц А и В будем называть такую матриц, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковые строение: или прямоугольные типа mn, или квадратные nn. Примеры: 1) Дано:...
math.bobrodobro.ru
| Самостоятельная работа «Графы» Вариант 1 1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
| A | B | C | D | E |
| A | 1 | ||||
| B | 1 | 2 | 2 | 7 | |
| C | 2 | 3 | |||
| D | 2 | 4 | |||
| E | 7 | 3 | 4 |
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5
2) 6
3) 7
4) 8
2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 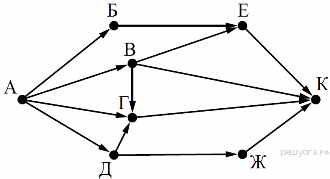
Самостоятельная работа «Графы»
Вариант 2
1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
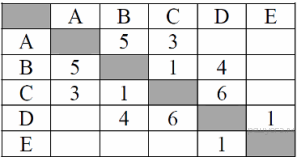
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 7
2) 8
3) 9
4) 10
2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 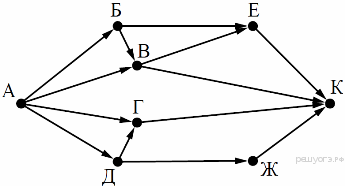
Самостоятельная работа «Графы»
Вариант 3
1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
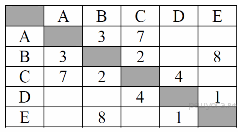
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 9
2) 10
3) 11
4) 12
2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 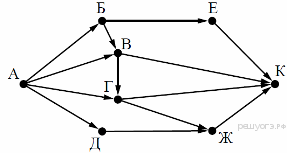
Самостоятельная работа «Графы»
Вариант 2
1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
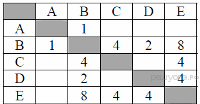
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5
2) 6
3) 7
4) 9
2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 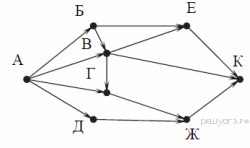
Самостоятельная работа «Графы»
Вариант 5
1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
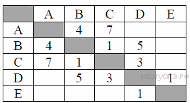
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 8
2) 9
3) 10
4) 11
2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 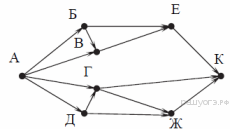
Самостоятельная работа «Графы»
Вариант 6
1. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
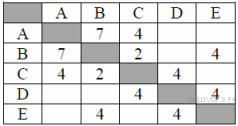
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
infourok.ru
|
1. Компетенции |
|
|
|
ПК- профессиональные компетенции ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетом документации, принимать участие в разработке проектной документации на модификацию информационной системы. ПК 2.1. Участвовать в разработке технического задания. ПК 2.3. Применять методики тестирования разрабатываемых приложений.
|
ОК- общие компетенции ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач профессионального и личностного развития. ОК5.Использовать информационно-коммуникационные технологии в профессиональной деятельности. ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями. ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. |
В результате освоения учебной дисциплины «Математика» обучающийся должен уметь:
- применять основные численные методы решения прикладных задач
В результате освоения учебной дисциплины обучающийся должен знать:
- роль и место математики в современном мире, а так же в решении профессиональных задач;
- основные понятия и методы математического анализа, дискретной математики, теории вероятностей и математической статистики;
Контрольная работа по теме « Графы»
1.Изобразить неориентированный граф , состоящий из
| вариант | вершин | ребер | вариант | вершин | ребер |
| 1 | 5 | 8 | 13 | 6 | 7 |
| 2 | 6 | 8 | 14 | 7 | 7 |
| 3 | 7 | 8 | 15 | 8 | 7 |
| 4 | 5 | 9 | 16 | 5 | 10 |
| 5 | 6 | 9 | 17 | 6 | 10 |
| 6 | 7 | 9 | 18 | 7 | 10 |
| 7 | 8 | 9 | 19 | 8 | 10 |
| 8 | 5 | 6 | 20 | 5 | 11 |
| 9 | 6 | 6 | 21 | 6 | 11 |
| 10 | 7 | 6 | 22 | 7 | 11 |
| 11 | 8 | 6 | 23 | 8 | 11 |
| 12 | 5 | 7 | 24 | 5 | 5 |
| 25 | 6 | 5 |
2.Выписать из данного графа две пары смежных и не смежных вершин
3. Выписать из данного графа две пары смежных и не смежных ребер
4.Выписать ребра , инцидентные вершине № 3.
5.Построить петлю в точке №2.
6. Достроить на графе изолированную точку.
7.Указать валентности всех вершин.
8. Изобразить любой подграф
9.Указать компоненту связанности данного графа.
10. Изобразить неориентированный, связанный граф по заданным условиям.
| вариант | Количество вершин | степень | степень | степень | вариант | Количество вершин | степень | степень | степень |
| 1 | 6 | 3(9) | 5(5) | 1(4) | 13 | 5 | 1(4) | 2(5) | 3(6) |
| 2 | 5 | 2(3) | 3(6) | 5(2) | 14 | 6 | 4(1) | 5(3) | 6(7) |
| 3 | 7 | 1(3) | 3(8) | 7(2) | 15 | 7 | 2(4) | 3(8) | 4(2) |
| 4 | 6 | 2(7) | 4(2) | 6(2) | 16 | 8 | 5(2) | 6(5) | 7(8) |
| 5 | 7 | 3(8) | 4(3) | 7(1) | 17 | 5 | 4(4) | 2(5) | 1(2) |
| 6 | 5 | 2(2) | 3(6) | 5(6) | 18 | 6 | 1(8) | 3(6) | 4(5) |
| 7 | 8 | 1(3) | 2(9) | 4(5) | 19 | 7 | 2(3) | 4(7) | 5(4) |
| 8 | 8 | 3(2) | 4(3) | 8(9) | 20 | 8 | 1(2) | 2(3) | 5(6) |
| 9 | 7 | 2(2) | 4(4) | 7(8) | 21 | 5 | 3(4) | 4(6) | 5(8) |
| 10 | 6 | 3(1) | 4(2) | 6(9) | 22 | 6 | 6(4) | 4(7) | 2(5) |
| 11 | 5 | 5(7) | 3(2) | 4(5) | 23 | 7 | 7(3) | 5(9) | 4(6) |
| 12 | 6 | 4(6) | 2(7) | 3(7) | 24 | 8 | 8(1) | 4(8) | 2(5) |
| 25 | 9 | 9(9) | 7(3) | 4(6) |
11. Описать данный граф.
12 . Изобразить ориентированный не связанный граф, состоящий из
| вариант | вершин | ребер | вариант | вершин | ребер |
| 1 | 6 | 8 | 14 | 6 | 7 |
| 2 | 7 | 8 | 15 | 7 | 7 |
| 3 | 5 | 9 | 16 | 8 | 7 |
| 4 | 6 | 9 | 17 | 5 | 10 |
| 5 | 7 | 9 | 18 | 6 | 10 |
| 6 | 8 | 9 | 19 | 7 | 10 |
| 7 | 5 | 6 | 20 | 8 | 10 |
| 8 | 6 | 6 | 21 | 5 | 11 |
| 9 | 7 | 6 | 22 | 6 | 11 |
| 10 | 8 | 6 | 23 | 7 | 11 |
| 11 | 5 | 7 | 24 | 8 | 11 |
| 12 | 5 | 8 | 25 | 5 | 5 |
| 13 | 6 | 5 |
13.Указать валентность исходящих дуг.
14 Выписать все пути из точки 2 в точку 5 и найти их длину (если пути не существует, то выбрать любой произвольный путь и найти его длину)
15. Дорисовать мост
16. Выделить точку сочленения.

 17.Охарактеризовать граф ˚
17.Охарактеризовать граф ˚








 1. 2. 3.
1. 2. 3.













4. 5 6
˚ ˚
7 8 9
10 11 12
˚ ˚
˚ ˚
˚
13 14 15
˚
˚ 17 18
16
˚ ˚
19
˚ 20 21
˚
23
22 ˚ ˚
˚ ˚ 24
˚ ˚
25 ˚ ˚
multiurok.ru
Содержание
Введение
Графы, орграфы, деревья
Операции над графами
Хранение графов в ЭВМ
Задача о максимальном потоке
Построение максимального потока. Примеры разбираемых задач
Литература
Введение
В коммерческой деятельности большинство возникающих задач удобно представлять для восприятия и анализа в виде сетей, которые позволяют ответить на два главных вопроса: до какого места необходимо дойти (цель) и какой путь следует избрать (как). Коммерческую деятельность можно рассматривать как совокупность задач, предназначенных для передвижения, складирования и распределения товаров, денег, документов, информации о поставках и покупателях воды, нефти, газа, электроэнергии, теле- и радиосистем. Наглядность и логическая обоснованность методов сетевого анализа позволяет выбрать довольно естественный подход к решению задач коммерческой деятельности. Сетевые модели для людей, не занимающихся научной работой, являются более понятными, чем другие модели, поскольку для них все же лучше один раз увидеть, чем сто раз услышать. В значительной степени методы сетевого анализа основаны на теории графов – области математики, началом развития которой явилась задача о кенигсбергских мостах, сформулированная швейцарским ученым Л. Эйлером в 1736 г. Через реку Прегель, на которой стоял город Кенигсберг, построено семь мостов (рис. 1), которые связывали с берегами и друг с другом два острова. Задача заключалась в том, чтобы пройти по всем мостам только один раз и вернуться обратно к началу маршрута. Эйлер доказал неразрешимость этой задачи.
Позже Д.К. Максвелл и Г.Р. Кирхгоф на основе исследования электрических цепей сформулировали некоторые принципы сетевого анализа. Были разработаны методы расчета наибольшей пропускной способности телефонных линий. В 40-х годах в результате развития теории исследования операций был разработан ряд математических методов, необходимых для анализа больших систем. В 50–60-х годах проводились работы по построению новых сетевых моделей и разработке алгоритмов их решения на основе элементов теории графов.
Графы, орграфы, деревья
Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии.
Основы теории графов разработал Л. Эйлер, решавший задачу о разработке замкнутого маршрута движения по мостам в г. Кенигсберге. При решении задачи он обозначил каждую часть суши точкой, а каждый мост – линией, их соединяющей. В результате был получен граф (рис. 1).
Эйлер доказал, что такая задача решения не имеет.
Эйлер Леонард (1707–1783) швейцарский математик, механик, физик, астроном. Автор более 800 работ по различным разделам математики и другим наукам.
Быстрое развитие теория графов получила с созданием электронно-вычислительной техники, которая позволяла решить многие задачи алгоритмизации.
Пусть на плоскости задано некоторое множество вершин X и множество U соединяющих их дуг. Графом называют бинарное отношение множества X и множеств U: G = = (X; U), или, иначе ƒ: X → К Здесь ƒ – отображение инциденций.
Граф называется ориентированным, если указано направление дуг и неориентированным, если такое направление не указано. Примером неориентированного графа является карта дорог.
Граф называется петлей, если его начало и конец совпадают.
Две вершины называются смежными, если существует соединяющая их дуга.
Ребро uj называется инцидентным вершине хj, если оно выходит или входит в вершину.
Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер или дуг.
Подграфом Ga графа G называется граф, в который входит лишь часть вершин графа G вместе с дугами их соединяющими.
Частным графом Gb графа называется граф, в который входит лишь часть дуг графа G вместе с вершинами их соединяющими. Карта шоссейных дорог это граф. Дороги Саратовской области это подграф, а главные дороги – это частный граф.
Путем в графе G называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным.
Контур – это конечный путь, у которого начальная и конечная вершины совпадают. Контур называется элементарным, если все его вершины различны (кроме начальной и конечной). Контур единичной дуги называется петлей.
В неориентированном графе понятие дуга, путь, контур заменяются соответственно на ребро, цепь, цикл.
Ребро – отрезок, соединяющий две вершины, цепь – последовательность ребер.
Цикл – конечная цепь, у которой начальная и конечная вершина совпадают.
Граф называется связанным, если любые его две вершины можно соединить цепью. Граф сильно связан, если для его двух любых вершин хi ≠хj существует путь, идущий из хi и хj.
Граф, который не является связанным, может быть разбит на конечное число связных графов, называемых компонентами, или частями.
Ребро графа G называется мостом, если граф, полученный из G путем удаления этого ребра, имеет больше компонент связности, чем граф G.
Точкой сочленения графа называется вершина, удаление которой приводит к увеличению числа его компонент связности.
На рисунке 3 ребро к – мост, а на рисунке 4 вершина 1 – точка сочленения.
www.coolreferat.com