, где
Разделы: Математика
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
, где
“
” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если 
, то 
, где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):
(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где 
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
(рис.3)
Обозначим буквой Е основное или универсальное множество, где 
A С Е (“”- любо число), т.е. А 
Е = Е; АЕ =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕ или Ā (рис.4)
Е
(рис.4)
Примерами для понимания этих понятий являются свойства:
_
А Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
АВ = А∩В
________ _ _
АВ = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (AB) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (АВ)
m (ABC) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).
А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
___________
m (АВС) = 3 => m (АВС) = 40 – 3 = 37
Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).
(рис.5)
К1 – множество учеников, решивших только одну задачу по алгебре;
К2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К3 – множество учеников, решивших только задачу по геометрии;
К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К5 – множество всех учеников, решивших все три задачи;
К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К7 – множество всех учеников, решивших только задачу по тригонометрии;
К8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
ВС) - m (А) - m (В) - m (С) + m (А∩В) + m (А∩С) + m (В∩С)Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
В) = 33С) = 31С) = 32Найти m (К1) + m (К3) + m (К7)
Ответ:
Только одну контрольную работу решили 18 учеников.
Решение задачи № 3
Найти m (К1) + m (К3) + m (К7)
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
xn--i1abbnckbmcl9fb.xn--p1ai
Вариант 17
1.Найти объединение и пересечение
А) множеств А=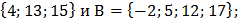
В) отрезков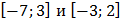 
.
2.Записать уравнение окружности с центром в точке С и радиусом r, если С(-2;3) и r=16.
3.На координатной плоскости штриховкой показать множество точек, удовлетворяющих неравенству 2х-у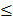
1.
4.На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств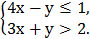 
5. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств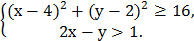 
6. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств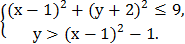 
Вариант 19
1.Найти объединение и пересечение
А) множеств А=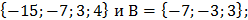
В) отрезков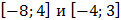 
.
2.Записать уравнение окружности с центром в точке С и радиусом r, если С(5;-1) и r=25.
3.На координатной плоскости штриховкой показать множество точек, удовлетворяющих неравенству 3х+у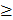
2.
4.На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств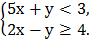 
5. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств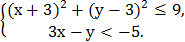 
6. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств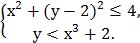 
Вариант 18
1.Найти объединение и пересечение
А) множеств А=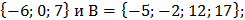
В) отрезков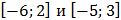 
.
2.Записать уравнение окружности с центром в точке С и радиусом r, если С(-3;2) и r=9.
3.На координатной плоскости штриховкой показать множество точек, удовлетворяющих неравенству 2х+у>1.
4.На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств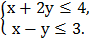 
5. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств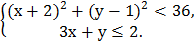 
6. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств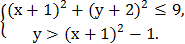 
Вариант 20
1.Найти объединение и пересечение
А) множеств А=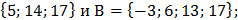
В) отрезков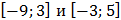 
.
2.Записать уравнение окружности с центром в точке С и радиусом r, если С(-3;4) и r=17.
3.На координатной плоскости штриховкой показать множество точек, удовлетворяющих неравенству 2х-у<2.
4.На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств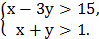 
5. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств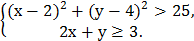 
6. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств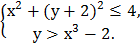 
infourok.ru
1. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
Задача 1. Представить множества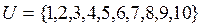 
, 
, 
, 
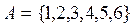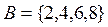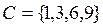на диаграмме Эйлера-Венна.
Решение. Поскольку множества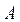 
, 
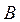и 
являются подмножествами множества 
, выберем в качестве универсального множества множество .
Диаграмма Эйлера-Венна выглядит следующим образом:
 |
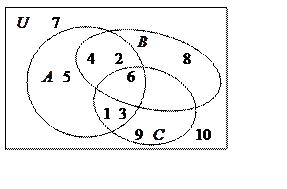Задача 2. Записать характеристические функции множеств 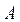, 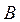и 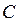(задача 1) в виде двоичных векторов. Пронумеровать каждую область диаграммы Эйлера-Венна двоичным номером.
Решение.
Так как универсальным множеством является множество 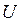, содержащее 10 элементов, характеристические функции его подмножеств могут быть представлены десятимерными двоичными векторами. Последовательность координат таких векторов соответствуют последовательности элементов множества 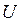.На каждом подмножестве координата вектора принимает значение 1, если элемент принадлежит подмножеству, и значение 0, если не принадлежит.
Следовательно,
.
 |
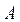: в нем ставится 1, если область содержит элементы множества 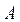, и 0 – если не содержит. Второй разряд соответствует множеству 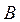и третий – множеству 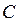. Задача 3. Составить булеан множества 
. Записать таблицу характеристических функций каждого множества.
Решение. Множество содержит четыре элемента, следовательно его булеан содержит 24=16 подмножеств.
Составим таблицу элементов булеана и их характеристических функций. При записи характеристических функций используем лексикографический метод записи последовательности двоичных векторов.
| Подмножества множества (элементы булеана) | Значения характеристических функций подмножеств | |||
| Элементы множества | ||||
| 2 | 4 | 6 | 8 | |
|
| 0 | 0 | 0 | 0 |
|
| 0 | 0 | 0 | 1 |
|
| 0 | 0 | 1 | 0 |
|
| 0 | 0 | 1 | 1 |
|
| 0 | 1 | 0 | 0 |
|
| 0 | 1 | 0 | 1 |
|
| 0 | 1 | 1 | 0 |
|
| 0 | 1 | 1 | 1 |
|
| 1 | 0 | 0 | 0 |
|
| 1 | 0 | 0 | 1 |
|
| 1 | 0 | 1 | 0 |
|
| 1 | 0 | 1 | 1 |
|
| 1 | 1 | 0 | 0 |
|
| 1 | 1 | 0 | 1 |
|
| 1 | 1 | 1 | 0 |
|
| 1 | 1 | 1 | 1 |
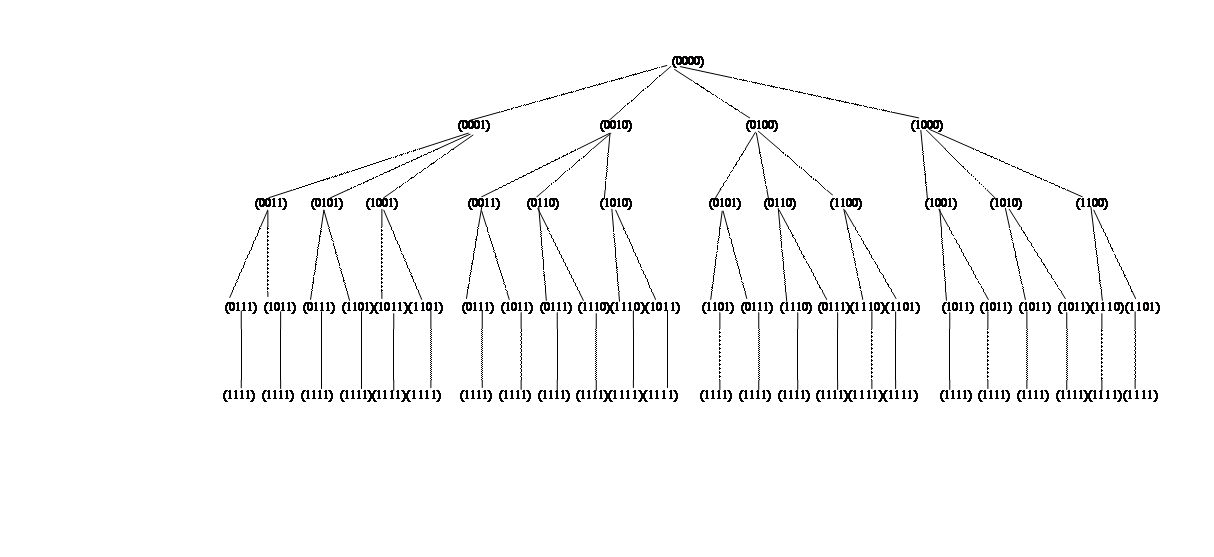
Задача 4. Составить диаграмму отношения включения на булеане множества и ее дерево путей. Записать все последовательности включений элементов булеана.
Решение. Диаграмма отношений включения между элементами булеана имеет 4 уровня: уровень 0 – пустое множество, характеристическая функция (0000), уровень 1 – множества, содержащие один элемент, уровень 2 – множества содержащие 2 элемента, уровень 3 – множества, содержащие 3 элемента, уровень 4 – множество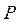 
, характеристическая функция (1111) (см. задачу 3).
Множества одного уровня несравнимы между собой по отношению включения, но двигаясь по любому пути диаграммы, получаем последовательную цепочку включений.
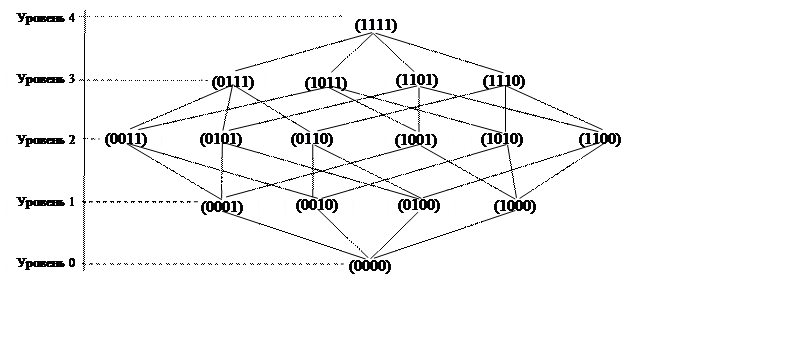Составим дерево путей по диаграмме включений (см. рис. стр.)
От нулевого уровня имеются четыре пути к множествам первого уровня. От каждого множества первого уровня имеется три пути к множествам второго уровня. От каждого множества второго уровня имеется два пути к множествам третьего уровня и от них по одному пути к множеству четвертого уровня.
Таким образом из 16 элементов булеана множества можно составить 24 различных последовательности множеств, упорядоченных отношением включения. Запишем эти последовательности.
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
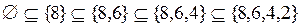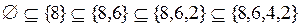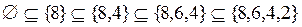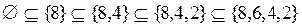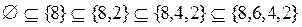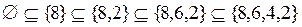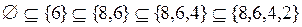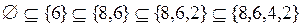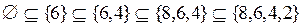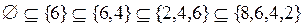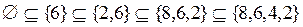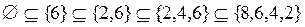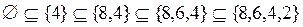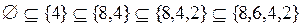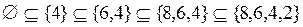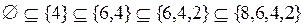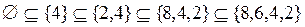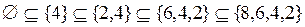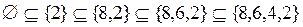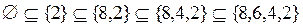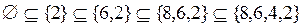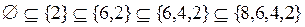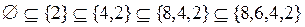Задача 5. Доказать равенства: 
, 
, где и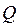 
– подмножества какого-либо универсального множества .
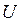Решение. Рассмотрим любой элемент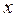 
универсального множества 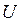. Используя определения операций над множествами, запишем в таблицу все возможные варианты принадлежности и непринадлежности 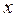каждому из множеств. При этом принадлежность элемента множеству будем обозначать единицей, непринадлежность – нулем.
Докажем равенство .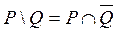
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Как видно из таблицы элемент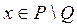 
тогда и только тогда, когда 
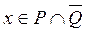. Следовательно, равенство 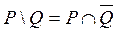справедливо для любых подмножеств множества .
Докажем равенство .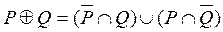
|
|
|
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Как видно из таблицы элемент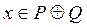 
тогда и только тогда, когда 
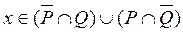. Следовательно, равенство 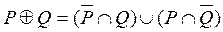справедливо для любых подмножеств множества .
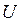Задача 6. Подмножества и 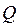множества 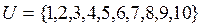заданы характеристическими функциями: 
, 
.
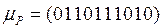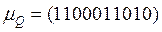Требуется:
1) Записать списки элементов множеств 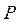и ;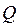
2) Выполнить над множествам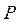и и 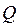операции: 
, 
, 
, 
, 
, 
, 
, 
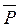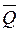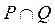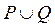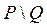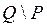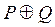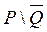, используя их характеристические функции.
3) Записать списки элементов всех полученных множеств.
Решение.
1) Запишем списки элементов множеств 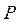и 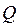, используя определение характеристической функции множества:
, 
.
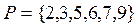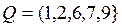2) Используя правила выполнения операций над множествами, выполним все указанные в задаче действия.
; 
.
; 
.
=
; 
.
=
; 
.
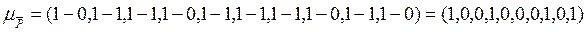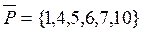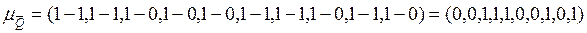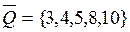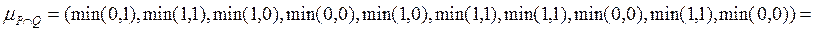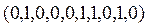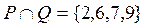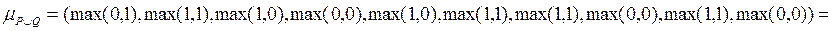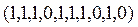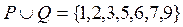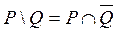(см. задачу 5).
=
; 
.
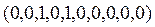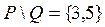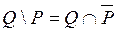(см. задачу 5).
=
; 
.
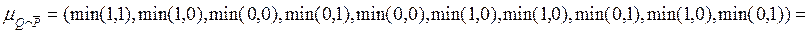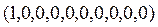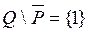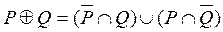(см. задачу 5).
=
=
; 
.
, 
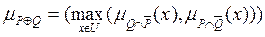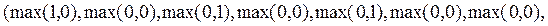
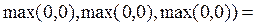
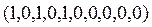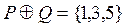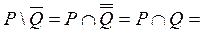
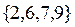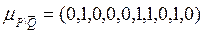. В равенстве 
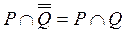использовано свойство дополнения 
.
Задача 7. Найти множество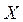 
через известные множества 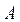, , 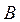если известно, что 
.
Решение. Построим таблицу принадлежности произвольного элемента 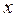универсального множества каждому из множеств, записанных в системе.
|
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
В таблице отмечены цветом те строки, которые соответствуют нарушению равенств системы. Выпишем строки, соответствующие системе:
| |
|
|
| Как видно из таблицы, элемент
| |
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 1 |
| |
| 1 | 0 | 1 | 1 |
| |
| 1 | 1 | 1 | 0 |
Задача 8. Решить уравнение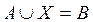 
.
Решение. Применим метод решения, использованный задаче 7.
|
|
|
|
| Из двух последних строк таблицы очевидно, что элемент, взятый из пересечения множеств Следовательно, данное уравнение не имеет решений. | |
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 |
| |
| 1 | 1 | 1 | 1 |
|
|
 |
vunivere.ru
тогда и только тогда, когда он принадлежит множеству 
или 
. Следовательно 
.
, 
