|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Реферат: Оптимизационные модели принятия решений. Задачи нелинейной оптимизации реферат
Пример задачи нелинейной оптимизации
Задача. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4,10), (10,40), (40,80). Нижняя граница доходности портфеля задана равной 15.
Экономико-математическая модель
Пусть xj, j= 1,2,3 – доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1)


Решение.
Приведенная ЭММ является моделью задачи нелинейного программирования. Специальный (рабочий) лист может быть подготовлен в виде:

формулы этого листа приведены в ячейках.

Диалоговое окно Поиск решения с введенными ограничениями, соответствующее приведенному выше рабочему листу:

Реализуя приведенную модель средствами MS Excel, будем иметь оптимальный портфель Марковица:
х1 = 0,5213, х2 = 0,2078, х3 = 0,2709,
т.е. доли ценных бумаг оказались равными 52,13%; 20,78% и 27,09%. При этом минимальный риск – 23,79, доходность портфеля оказалась равной заданной – 15.

Задачи для самостоятельного решения
1. Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем продукции равен 100= Х1 + Х2, где Х1 и Х2 – объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе зависят от объемов нелинейно:
 ,
,  .
.
Необходимо так распределить объем производства между технологическими способами, чтобы минимизировать общие затраты производства.
2. Найти максимальное значение функции  при ограничениях:
при ограничениях:

3. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (6,10), (10,50), (60,80). Нижняя граница доходности портфеля задана равной 20.
4. Найти минимум функции  при ограничениях:
при ограничениях:

Лабораторная работа №4. Метод кусочно-линейной аппроксимации
Пусть дана система неравенств вида 
 и целевая функция
и целевая функция , причем все функции
, причем все функции являются выпуклыми, а функцияz выпукла или вогнута на некотором выпуклом множестве М.
являются выпуклыми, а функцияz выпукла или вогнута на некотором выпуклом множестве М.
Рассмотрим приближенное решение задач выпуклого программирования с сепарабельными функциями методом кусочно-линейной аппроксимации.
Функция F(X)=F( ,…,xn) называется сепарабельной, если ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной, т. е. если
,…,xn) называется сепарабельной, если ее можно представить в виде суммы функций, каждая из которых зависит только от одной переменной, т. е. если
 или
или 
(не исключено, что  при некоторыхi).
при некоторыхi).
Пусть в задаче ВП и функция цели z, и все ограничения  являются сепарабельными. Тогда задача имеет вид: найти минимум выпуклой (максимум вогнутой) функции
являются сепарабельными. Тогда задача имеет вид: найти минимум выпуклой (максимум вогнутой) функции при ограничениях:
при ограничениях:

 .
.
Идея метода кусочно-линейной аппроксимации состоит в том, что все  и все
и все заменяются ломаными линиями, состоящими из прямолинейных отрезков. При этом исходная задача ВП заменяется новой, приближенной задачей, которая является задачей линейного программирования. Эта задача решается обычно симплексным методом, и ее решение является приближенным решением исходной задачи ВП.
заменяются ломаными линиями, состоящими из прямолинейных отрезков. При этом исходная задача ВП заменяется новой, приближенной задачей, которая является задачей линейного программирования. Эта задача решается обычно симплексным методом, и ее решение является приближенным решением исходной задачи ВП.
Для построения приближенной задачи рассмотрим кусочно-линейную аппроксимацию функции одной переменной h(x), заданной на отрезке [0,a]. Разобьем этот отрезок на r частей точками x <x
<x <…<x
<…<x так, чтобы x
так, чтобы x =0, x
=0, x =a. Вычислим значения функции h
=a. Вычислим значения функции h (x) (k=0,…,r) в этих точках. Соединим попарно точки (x
(x) (k=0,…,r) в этих точках. Соединим попарно точки (x ;h
;h ) и (x
) и (x ;h
;h ) отрезками прямых. Состоящая из этих отрезков ломаная
) отрезками прямых. Состоящая из этих отрезков ломаная аппроксимирует функциюh(x) на отрезке[0,a].
аппроксимирует функциюh(x) на отрезке[0,a].
Уравнение участка ломаной  между точками (x
между точками (x ;h
;h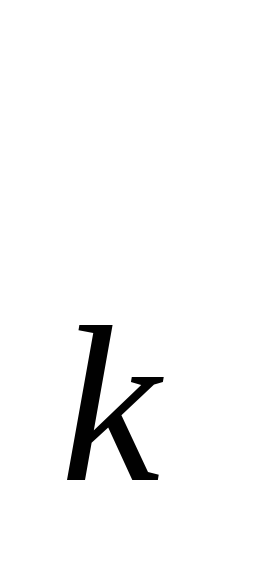 )и (x
)и (x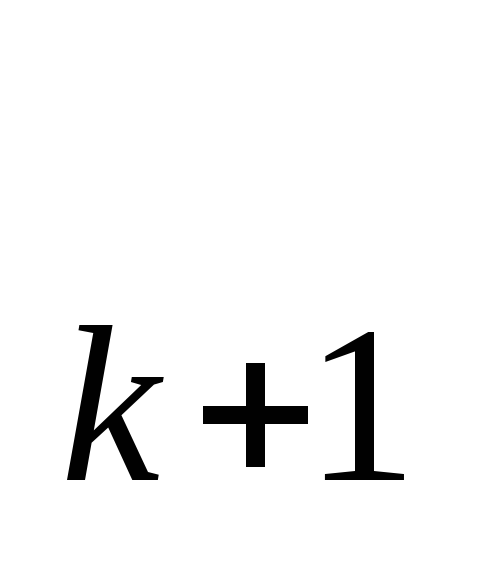 ;h
;h ) имеет вид
) имеет вид (уравнение прямой, построенной по двум заданным точкам).
(уравнение прямой, построенной по двум заданным точкам).
Если каждое из отношений в этом равенстве обозначить через  , то получим:
, то получим:
 и
и  , причем
, причем .
.
Обозначив  , можно переписать в виде:
, можно переписать в виде:

Таким образом, для любого x[0,a] уравнение ломаной можно записать в виде:
 ,
,
причем всегда отличны от нуля только для значения k (если x является внутренней точкой k-го отрезка разбиения), или одно, (если x совпадает с концом отрезка).
Возвращаясь к задаче ВП с сепарабельными функциями, отметим, что, прежде всего (в зависимости от системы ограничений) нужно определить интервал изменения каждой переменной x . Затем каждый этот интервал разбивается на части точкамиx
. Затем каждый этот интервал разбивается на части точкамиx и, с использованием полученных формул строится кусочно-линейная аппроксимация для функцийf
и, с использованием полученных формул строится кусочно-линейная аппроксимация для функцийf и
и . После этого можно для исходной задачи записать приближенную задачу: найти максимум функции
. После этого можно для исходной задачи записать приближенную задачу: найти максимум функции при ограничениях:
при ограничениях:


studfiles.net
Реферат - Оптимизационные модели принятия решений
--PAGE_BREAK--Нелинейные модели оптимизации в управленииВ настоящем разделе мы кратко рассмотрим задачи нелинейной оптимизации (называемые иначе оптимизационными задачами нелинейного программирования), математические модели которых содержат нелинейные зависимости от переменных. Источники нелинейности в задачах подобного типа могут относиться, в частности, к одной из двух категорий:
· Реально существующие и эмпирически наблюдаемые нелинейные соотношения, например непропорциональные зависимости между объемом производства и затратами, между количеством используемого в производстве компонента и некоторыми показателями качества готовой продукции, между затратами сырья и физическими параметрами (давление, температура и т.п.) соответствующего производственного процесса, между выручкой и объемом реализации и т.п.
· Установленные (постулируемые) руководством правила поведения или задаваемые зависимости, например, правила расчета с потребителями энергии или других видов услуг, правила определения страховых уровней запаса продукции, гипотезы о характере вероятностного распределения рассматриваемых в модели случайных величин, различного рода договорные условия взаимодействия между партнерами по бизнесу и др.
В качестве примера можно рассмотреть формирование оптимальной производственной программы предприятия. По критерию затрат учитывается себестоимость единицы продукции, которая уменьшается при увеличении объема выпускаемой продукции, что приводит к нелинейному критерию эффективности. Нелинейные зависимости возникают также в ограничениях задачи при точном учете норм расхода ресурсов на единицу производимой продукции.
Вообще говоря, решение нелинейных задач по сложности значительно превосходит решение рассмотренных ранее задач линейной оптимизации. В связи с этим долгое время в практике экономического управления модели линейной оптимизации успешно применялись даже при наличии нелинейности. В одних случаях нелинейность была несущественна и ею можно было пренебречь, в других – проводилась линеаризация нелинейных соотношений или применялись специальные приемы, например строились, так называемые, аппроксимационные модели, благодаря чему достигалась требуемая адекватность. Тем не менее, часто встречаются задачи, для которых нелинейность является существенной и упомянутые выше методы аппроксимации неэффективны, в связи с чем, нелинейность необходимо учитывать в явном виде.
В отличие от задачи линейной оптимизации (линейного программирования), не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может быть эффективен при решении задач одного типа и неприемлемым для задач другого типа. В связи с этим разработаны алгоритмы для решения каждого класса (типа) задач. Следует иметь в виду, что даже программы, ориентированные на решение определенного класса задач, не гарантируют правильность решения любых задач этого класса и оптимальность решения следует проверять в каждом конкретном случае.
Перечислим некоторые наиболее употребительные методы решения задач нелинейной оптимизации (нелинейного программирования):
· Оптимизация нелинейной функции с ограничениями на неотрицательность значений переменных (наиболее широко используемыми моделями данного класса являются модели квадратичного программирования, в которых целевая функция является квадратичной функцией переменных <img width=«83» height=«24» src=«ref-1_1645323556-158.coolpic» v:shapes="_x0000_i1098">).
· Модели выпуклого программирования; в моделях данного класса целевая функция является вогнутой (или выпуклой), а функции-ограничения являются выпуклыми функциями. При данных условиях локальный максимум (или минимум) функции является также глобальным. При решении таких задач используется метод множителей Лагранжа, а также теорема Куна-Таккера.
· Сепарабельное программирование. В задачах данного класса целевая функция и функции-ограничения могут быть представлены в виде сумм отдельных компонент. Данные задачи могут быть сведены к задачам линейного программирования.
· Дробно-нелинейное программирование. В этих задачах производится максимизация (минимизация) целевой функции вида <img width=«134» height=«24» src=«ref-1_1645323714-279.coolpic» v:shapes="_x0000_i1099"> · Если функции <img width=«40» height=«23» src=«ref-1_1645323993-135.coolpic» v:shapes="_x0000_i1100"> линейны (задача дробно-линейного программирования), то задача сводится к линейной.
· Невыпуклое программирование. Задачи данного типа принадлежат к наименее изученным и наиболее сложным задачам нелинейной оптимизации. В данном случае целевая функция и (или) функции-ограничения не выпуклы. Надежных методов решения таких задач в настоящее время не существует.
Мы ограничимся рассмотрением лишь наиболее простых задач нелинейной оптимизации, не требующих использования сложных аналитических выкладок и анализа, — задач, которые могут эффективно решаться на базе табличного процессора Excel.
Задача нелинейной оптимизации в общем случае состоит в отыскании такого вектора неизвестных
<img width=«162» height=«32» src=«ref-1_1645324128-525.coolpic» v:shapes="_x0000_i1101"> который обращал бы в максимум (минимум) функцию <img width=«183» height=«32» src=«ref-1_1645324653-592.coolpic» v:shapes="_x0000_i1102"> (2.6) и удовлетворял бы системе ограничений: <img width=«315» height=«61» src=«ref-1_1645325245-1453.coolpic» v:shapes="_x0000_i1103">, (2.7) где на некоторые или на все переменные налагается условие неотрицательности. продолжение --PAGE_BREAK--
www.ronl.ru
Нелинейная задача оптимизации производственной деятельности фирмы

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Пусть производственная фирма выпускает один продукт, либо несколько продуктов в заданной пропорции. Тогда ее выпуск за заданный плановый период – это количество единиц продукта одного вида, либо число многономенклатурных агрегатов.
Пусть для выпуска продукции фирмой используются два вида ресурсов. И величина выпуска описывается нелинейной двухфакторной производственной функцией Кобба-Дугласа:
 .
.
Здесь  - это количество используемых в течение планового периода единиц первого ресурса, а
- это количество используемых в течение планового периода единиц первого ресурса, а  - количество единиц второго ресурса. Обычно в качестве первого ресурса рассматривается капитал, а в качестве второго – труд. Положительный коэффициент
- количество единиц второго ресурса. Обычно в качестве первого ресурса рассматривается капитал, а в качестве второго – труд. Положительный коэффициент  равен объему выпуска продукции при единичных затратах ресурсов. Эластичность выпуска по первому ресурсу
равен объему выпуска продукции при единичных затратах ресурсов. Эластичность выпуска по первому ресурсу  удовлетворяет неравенствам
удовлетворяет неравенствам  . И эластичность выпуска по второму ресурсу
. И эластичность выпуска по второму ресурсу  удовлетворяет тем же неравенствам.
удовлетворяет тем же неравенствам.
По своему содержательному смыслу количества используемых ресурсов – неотрицательны. Это означает выполнение неравенств

Пусть известны цена единицы первого ресурса  и цена единицы второго ресурса
и цена единицы второго ресурса  . Тогда суммарные затраты на использование ресурсов в течение планового периода равны
. Тогда суммарные затраты на использование ресурсов в течение планового периода равны
 ,
,
где  и
и  – двумерные векторы, а
– двумерные векторы, а  – их скалярное произведение.
– их скалярное произведение.
Эти затраты не могут превышать максимально возможного за плановый период общего объема издержек  , что означает справедливость неравенства
, что означает справедливость неравенства
 .
.
Пусть известна цена единицы производимого продукта  . Тогда прибыль (чистый доход) фирмы за плановый период равна
. Тогда прибыль (чистый доход) фирмы за плановый период равна

Эту величину надо максимизировать.
Собирая все вместе, математическую постановку нелинейной задачи оптимизации производственной деятельности фирмы запишем в виде:
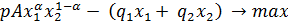
при ограничениях


Укажем способ решения этой задачи с помощью инструмента Поиск решения. Для примера рассмотрим задачу, исходные данные которой приведены в таблице 5.1.
Таблица 5.1
| q₁ | q₂ | Q | p | A | α | 1-α |
| 1,745 | 0,628 | 0,372 |
Математическая запись данного примера имеет вид:

при ограничениях


Рассмотрим три этапа решения данного примера с помощью инструмента Поиск решения.
Этап 1. Введем исходные данные нелинейной задачи оптимизации производственной деятельности фирмы. В соответствующие ячейки введем координаты начальной точки, формулы для вычисления суммарных затрат на использование ресурсов  , значения производственной функции Кобба-Дугласа
, значения производственной функции Кобба-Дугласа  и значения прибыли
и значения прибыли  . Для рассматриваемого примера это можно сделать, например, следующим образом.
. Для рассматриваемого примера это можно сделать, например, следующим образом.

Рисунок 5.1. Входные данные примера нелинейной задачи
оптимизации производственной деятельности фирмы
На рисунке 5.1 видно, что исходные данные примера расположены в горизонтальном массиве, элементы которого введены в ячейки диапазона B39:h49. Непосредственно над каждой ячейкой, расположенной в этом диапазоне, написано обозначение того входного параметра, который содержится в этой ячейке.
Для переменных компонент  и
и  вектора
вектора  , использован горизонтальный массив, состоящий из двух элементов, которые содержатся в ячейках диапазона B42:C42. Экспериментально замечено, что использовать в качестве начальных значений этих компонент нулевые значения нельзя. Инструмент Поиск решения принимает начальную точку (0,0) за оптимальное решение в тех задачах, в которых она не является даже точкой локального максимума. В качестве начальных точек рекомендуется выбирать точки с одинаковыми и положительными компонентами. В данном примере в качестве начальной точки выбрана точка (1,1).
, использован горизонтальный массив, состоящий из двух элементов, которые содержатся в ячейках диапазона B42:C42. Экспериментально замечено, что использовать в качестве начальных значений этих компонент нулевые значения нельзя. Инструмент Поиск решения принимает начальную точку (0,0) за оптимальное решение в тех задачах, в которых она не является даже точкой локального максимума. В качестве начальных точек рекомендуется выбирать точки с одинаковыми и положительными компонентами. В данном примере в качестве начальной точки выбрана точка (1,1).
В ячейку D42 введена формула для вычисления суммарных затрат на использование ресурсов  . В ней использована встроенная функция суммирования СУММПРОИЗВ из категории Математические функции. Эта функция возвращает сумму произведений соответствующих элементов массивов. Сама формула имеет запись =СУММПРОИЗВ(B39:C39;B42:C42).
. В ней использована встроенная функция суммирования СУММПРОИЗВ из категории Математические функции. Эта функция возвращает сумму произведений соответствующих элементов массивов. Сама формула имеет запись =СУММПРОИЗВ(B39:C39;B42:C42).
В ячейке E42 содержится формула для вычисления значения производственной функции Кобба-Дугласа  . Ее запись видна в верхней строке формул рисунка 5.1. Она имеет вид =F39*СТЕПЕНЬ(B42;G39)* СТЕПЕНЬ(C42;h49). В ней использована встроенная функция СТЕПЕНЬ (POWER) из категории Математические функции. Данная функция возвращает результат возведения числа в степень.
. Ее запись видна в верхней строке формул рисунка 5.1. Она имеет вид =F39*СТЕПЕНЬ(B42;G39)* СТЕПЕНЬ(C42;h49). В ней использована встроенная функция СТЕПЕНЬ (POWER) из категории Математические функции. Данная функция возвращает результат возведения числа в степень.
В ячейку F42 введена формула для вычисления значения прибыли  . Она имеет вид =E39*E42-D42. Ее запись видна в верхней строке формул рисунка 5.4.
. Она имеет вид =E39*E42-D42. Ее запись видна в верхней строке формул рисунка 5.4.
Этап 2. Вызовем инструмент Поиск решения и введем условия задачи.
После выполнения указанных выше действий появится диалоговое окно Поиск решения, показанное на рисунке 5.2.

Рисунок 5.2. Диалоговое окно Поиск решения для примера нелинейной
задачи оптимизации производственной деятельности фирмы
В пункте 3 подробно описано, как можно задать условия задачи в диалоговом окне Поиск решения.
Далее, после щелчка по кнопке Параметры, переходим в диалоговое окно Параметры поиска решения. Установим в нем значения параметров, показанные на рисунке 5.3.
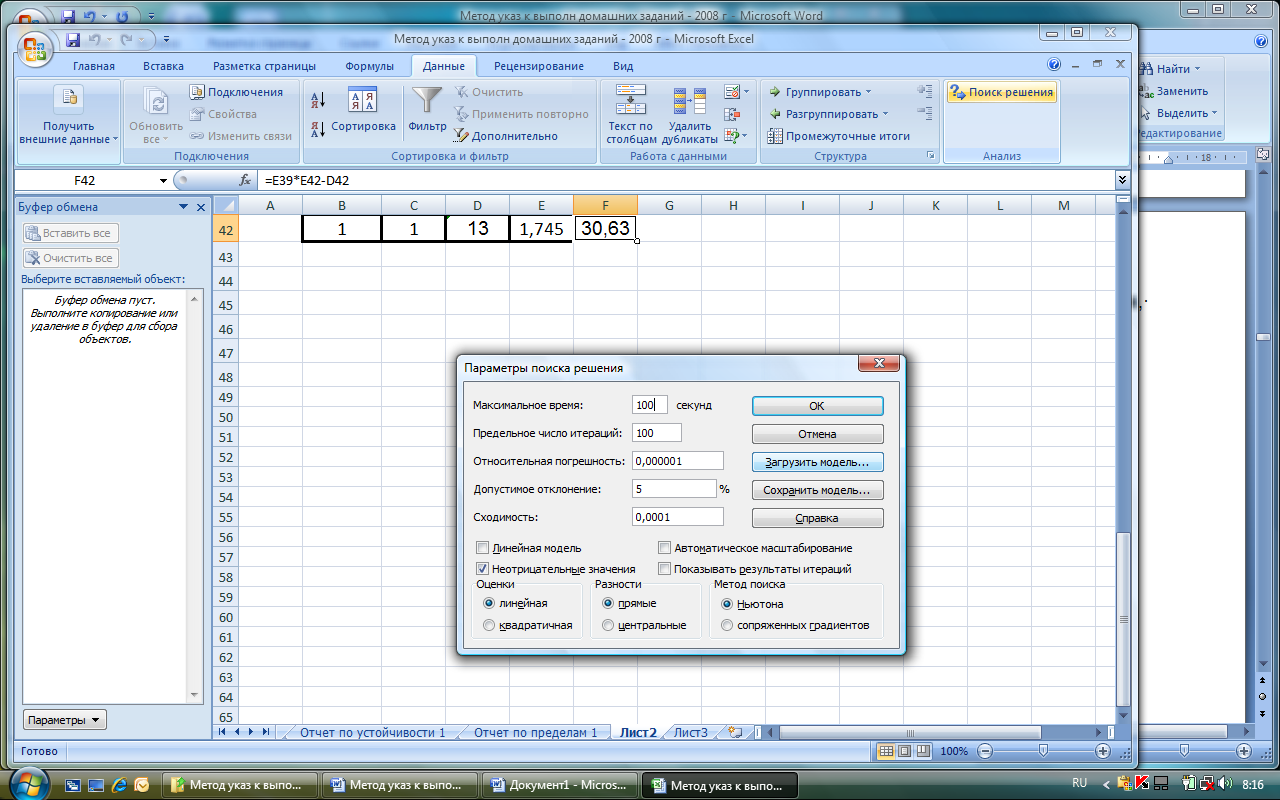
Рисунок 5.3. Диалоговое окно Параметры поиска решения для
примера нелинейной задачи оптимизации производственной
деятельности фирмы
На рисунке 5.3 видно, что флажок установлен только для параметра Неотрицательны значения. Флажок для параметра Линейная модель устанавливать нельзя, потому что решается нелинейная задача.
После окончания введения параметров щелкнем по кнопке OK и вернемся в диалоговое окно Поиск решения.
Этап 3. Решение задачи инструментом Поиск решения.
Для решения нашего примера инструментом Поиск решения, надо в диалоговом окне Поиск решения, показанном на рисунке 5.2, щелкнуть по кнопке Выполнить.
После завершения работы инструмента Поиск решения появится диалоговое окно Результаты поиска решения, изображенное на рисунке 3.5. В этом окне надо поставить флажок на опцию Сохранить найденное решениеи затем щелкнуть кнопку OK.
Результат решения нашего примера приведен на рисунке 5.4.

Рисунок 5.4. Результат решения примера нелинейной задачи
оптимизации производственной деятельности фирмы
Этап 4. Анализ полученного решения.
Сравнивая значения ячеек D39 и D42 видим, что суммарные затраты на использование ресурсов в течение планового периода в нашем примере являются максимально возможными.
megapredmet.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


