Вопрос о грамотном распределении инвестируемых средств в различные предприятия стоял всегда, но в последнее время он встал ещё жестче. Обилие фирм, предприятий, концернов и т. д., которые одновременно почти нереально про инвестировать, да и не все предприятия способны задействовать все вложенные в них средства. А ведь, несмотря на все сложности нужно инвестировать предприятия и развивать промышленность в целом и получать максимальный прирост прибыли предприятия от вложенных средств.

Тут и встаёт вопрос о том, как с наибольшей выгодой вложить средства, а также как с наименьшими затратами получить наибольший прирост прибыли предприятий в которые были вложены инвестиции. Для этого выдающимися учёными был разработан метод динамического программирования в сфере оптимизации и распределения средств между предприятиями.

Из всего вышесказанного легко понять актуальность данной темы в современном мире, особенно во времена мирового экономического кризиса, когда нужен четкий план развития предприятий и жесткий контроль за выполнением найденного оптимального плана распределения средств между предприятиями.

Целью курсовой работы является автоматизация процесса нахождения оптимального плана распределения инвестиций между несколькими предприятиями, который бы позволил предприятиям получать от вложенных в них инвестиций максимальный прирост прибыли, как на одном предприятии, так и в совокупности на всех предприятиях в целом.

Задачей данной курсовой работы стало изучение материала по данному математическому методу. Еще одной из основных задач курсовой работы явилась возможности овладеть данным методом нахождения оптимального плана распределения инвестиций между предприятиями, и получение углубленных знаний в данной сфере экономической оптимизации и математического планирования. Ещё одной задачей стало получение профессиональных навыков, а также опыта создания программного продукта, автоматизирующего достаточно сложный процесс в экономической сфере, разработанный в среде программирования Delphi

7 на языке программирования ObjectPascal(Delphi начиная с Delphi 7). А также закрепление материала по дисциплине «Математические методы» и закрепление полученных навыков программирования в среде программирования Delphi.

Разработанный программный продукт является эргономичным, что позволит использовать его даже на малопроизводительных персональных компьютерах. Так же интерфейс программного продукта является интуитивным, гармоничным и привлекательным, благодаря этому им может пользоваться даже начинающий пользователь. Ещё одой особенностью данного программного продукта является высокое быстродействие. Так же в программе имеется множество подсказок, которые позволят пользователю с легкостью пользоваться программным продуктом и легко его освоить.

Разработанный программный продукт на данном этапе жизненного цикла способен находить оптимальный план распределения инвестиций только между тремя предприятиями, но для количества условных единиц вкладываемых средств ограничений нет.

Сущность математического метода1.1 Характеристика математического метода, применимого для решения задачи

Данный математический метод изложен во многих литературных источниках, но наиболее подробно он описан в учебном материале “Математическое программирование в примерах и задачах” автор И.Л. Акулич. Весь дальнейший материал взят из указанного источника.

Динамическое программирование – это математический метод поиска оптимального управления, специально приспособленный к многошаговым процессам. Рассмотрим пример такого процесса.

Пусть планируется инвестирование Nпредприятий. Здесь шагом является инвестирование одного предприятия. На развитие предприятий выделяются средства, которые должны быть как-то распределены между этими предприятиями. В процессе их функционирования выделенные средства частично расходуются. Каждое предприятие приносит некоторый доход, зависящий от вложенных средств. Поэтому имеющиеся средства могут перераспределяться между предприятиями: каждому из них выделяется какая-то доля средств.

Ставится вопрос: как распределять имеющиеся средства между предприятиями, чтобы суммарный доход от всех предприятий был максимальным?

Перед нами типичная задача динамического программирования, в которой рассматривается управляемый процесс – функционирование группы предприятий. Управление процессом состоит в распределении (и перераспределении) средств. Управляющим воздействием (УВ) является выделение каких-то средств каждому из предприятий в начале года.

УВ на каждом шаге должно выбираться с учетом всех его последствий в дальнейшем. УВ должно быть дальновидным, с учетом перспективы. Нет смысла выбирать на рассматриваемом шаге наилучшее УВ, если в дальнейшем это помешает получить наилучшие результаты других шагов. УВ на каждом шаге надо выбирать “c

заглядыванием в будущее”, иначе возможны серьезные ошибки.

Действительно, предположим, что в рассмотренной группе предприятий одни заняты выпуском предметов потребления, а другие производят для этого машины. Причем целью является получение максимального объема выпуска предметов потребления. Пусть планируются капиталовложения первому предприятию. Исходя из их узких интересов данного шага, мы должны были бы все средства вложить в производство предметов потребления, пустить имеющиеся машины на полную мощность и добиться максимального объема прибыли. Но правильным ли будет такое решение в целом? Очевидно, нет. Имея в виду будущее, необходимо выделить какую-то долю средств и на производство машин. При этом объем продукции за первый год, естественно, снизится, зато будут созданы условия, позволяющие увеличивать ее производство в дальнейшем.

В формализме решения задач методом динамического программирования будут использоваться следующие обозначения:

N

– число шагов.

/>

– вектор, описывающий состояние системы на k-м шаге.

/>

– начальное состояние, т. е. состояние на 1-м шаге.

/>

– конечное состояние, т. е. состояние на последнем шаге.

Xk

– область допустимых состояний на k-ом шаге.

/>

– вектор УВ на k-ом шаге, обеспечивающий переход системы из состояния xk-1 в состояние xk.

Uk – область допустимых УВ на

k-ом шаге.

Wk

– величина выигрыша, полученного в результате реализации k-го шага.

S

– общий выигрыш за Nшагов.

/>– вектор оптимальной стратегии управления или ОУВ за

Nшагов.

Sk

+1(/>) – максимальный выигрыш, получаемый при переходе из любого состояния />/>в конечное состояние /> при оптимальной стратегии управления начиная с (k+1)-го шага.

S

1(/>) – максимальный выигрыш, получаемый за Nшагов при переходе системы из начального состояния /> в конечное /> при реализации оптимальной стратегии управления />. Очевидно, что S = S1(/>), если /> – фиксировано.

Метод динамического программирования опирается на условие отсутствия последействия и условие аддитивности целевой функции.

Условие отсутствия последействия. Состояние />, в которое перешла система за один k

-й шаг, зависит от состояния /> и выбранного УВ /> и не зависит от того, каким образом система пришла в состояние />, то есть

/>

Аналогично, величина выигрыша Wk

зависит от состояния /> и выбранного УВ />, то есть

/>

Условие аддитивности целевой функции.Общий выигрыш за N

шагов вычисляется по формуле

Определение. Оптимальной стратегией управления /> называется совокупность УВ />, то есть

/>, в результате реализации которых система за Nшагов переходит из начального состояния /> в конечное /> и при этом общий выигрыш S принимает наибольшее значение.

Условие отсутствия последствий позволяет сформулировать принцип оптимальности Беллмана.

Принцип оптимальности. Каково бы ни было допустимое состояние системы/>/>/> перед очередным i

-м шагом, надо выбрать допустимое УВ /> на этом шаге так, чтобы выигрыш Wi на i-м шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.

В качестве примера постановки задачи оптимального управления продолжим рассмотрение задачи управления финансированием группы предприятий. Пусть группе предприятий />

выделяются соответственно средства: />/>совокупность этих значений можно считать управлением на i-м шаге, то есть />. Управление /> процессом в целом представляет собой совокупность всех шаговых управлений, то есть />.

Управление может быть хорошим или плохим, эффективным или неэффективным. Эффективность управления />

оценивается показателем S. Возникает вопрос: как выбрать шаговые управления />, чтобы величина S обратилась в максимум?

Поставленная задача является задачей оптимального управления, а управление, при котором показатель S

достигает максимума, называется оптимальным. Оптимальное управление /> многошаговым процессом состоит из совокупности оптимальных шаговых управлений:

/>

Таким образом, перед нами стоит задача: определить оптимальное управление на каждом шаге />(i=1,2,...N) и, значит, оптимальное управление всем процессом />.

Мы отметили, что планируя многошаговый процесс, необходимо выбирать УВ на каждом шаге с учетом его дальнейших последствий на еще предстоящих шагах. Однако, из этого правила есть исключение. Среди всех шагов существует один, который может планироваться без «заглядывания в будущее». Какой это шаг? Очевидно, последний — после него других шагов нет. Этот шаг, единственный из всех, можно планировать так, чтобы он как таковой принес наибольшую выгоду. Спланировав оптимально этот последний шаг, можно к нему пристраивать предпоследний, к предпоследнему — предпредпоследний и т.д.

Поэтому процесс динамического программирования на 1-м этапе разворачивается от конца к началу, то есть раньше всех планируется последний, N-й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний? Очевидно, нужно сделать все возможные предположения о том, чем кончился предпоследний, (N — 1)-й шаг, и для каждого из них найти такое управление, при котором выигрыш (доход) на последнем шаге был бы максимален. Решив эту задачу, мы найдем условно оптимальное управление (УОУ) на N-м шаге, т.е. управление, которое надо применить, если (N — 1)-й шаг закончился определенным образом.

Предположим, что эта процедура выполнена, то есть для каждого исхода (N — 1)-го шага мы знаем УОУ на N-м шаге и соответствующий ему условно оптимальный выигрыш (УОВ). Теперь мы можем оптимизировать управление на предпоследнем, (N — 1)-м шаге. Сделаем все возможные предположения о том, чем кончился предпредпоследний, то есть (N — 2)-й шаг, и для каждого из этих предположений найдем такое управление на (N — 1)-м шаге, чтобы выигрыш за последние два шага (из которых последний уже оптимизирован) был максимален. Далее оптимизируется управление на (N — 2)-м шаге, и т.д.

Одним словом, на каждом шаге ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Этот принцип выбора управления, называется принципом оптимальности. Самоуправление, обеспечивающее оптимальное продолжение процесса относительно заданного состояния, называется УОУ на данном шаге.

Теперь предположим, что УОУ на каждом шаге нам известно: мы знаем, что делать дальше, в каком бы состоянии ни был процесс к началу каждого шага. Тогда мы можем найти уже не «условное», а действительно оптимальное управление на каждом шаге.

Действительно, пусть нам известно начальное состояние процесса. Теперь мы уже знаем, что делать на первом шаге: надо применить УОУ, найденное для первого шага и начального состояния. В результате этого управления после первого шага система перейдет в другое состояние; но для этого состояния мы знаем УОУ и г д. Таким образом, мы найдем оптимальное управление процессом, приводящее к максимально возможному выигрышу.

Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс «проходится» дважды: первый раз — от конца к началу, в результате чего находятся УОУ на каждом шаге и оптимальный выигрыш (тоже условный) на всех шагах, начиная с данного и до конца процесса; второй раз — от начала к концу, в результате чего находятся оптимальные управления на всех шагах процесса.

Можно сказать, что процедура построения оптимального управления методом динамического программирования распадается на две стадии: предварительную и окончательную. На предварительной стадии для каждого шага определяется УОУ зависящее от состояния системы (достигнутого в результате предыдущих шагов), и условно оптимальный выигрыш на всех оставшихся шагах, начиная с данного, также зависящий от состояния. На окончательной стадии определяется (безусловное) оптимальное управление для каждого шага. Предварительная (условная) оптимизация производится по шагам в обратном порядке: от последнего шага к первому; окончательная (безусловная) оптимизация — также по шагам, но в естественном порядке: от первого шага к последнему. Из двух стадий оптимизации несравненно более важной и трудоемкой является первая. После окончания первой стадии выполнение второй трудности не представляет: остается только «прочесть» рекомендации, уже заготовленные на первой стадии.

1.2 Аналитическое решение задачи

Рассмотрим задачу, когда инвестор выделяет средства в размере 5 условных единиц, которые должны быть распределены между тремя предприятиями.

Требуется, используя принцип оптимальности Беллмана, построить план распределения инвестиций между предприятиями, обеспечивающий наибольшую общую прибыль, если каждое предприятие при инвестировании в него средств X

у.е. приносит прибыль Pi (x) у.е. (i = l, 2 и 3) последующим данным, приведённым в таблице 1.

Таблица 1 – Исходные данные.

Инвестируемые средства (у.е.)

Общая прибыль (у.е.)

P1(x)

P2(x)

P3(x)

3,22

3,33

4,27

<span style=«font-size: 12

www.ronl.ru

Dinamicheskoe_programmirovanie

Динамическое программирование

Динамическое программирование (ДП) - метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы. Такие операции называются многошаговыми.

Задачи динамического программирования:

Задача распределения финансовых средств (капитальных вложений между направлениями их использования).
Замена технологического оборудования с учетом планирования текущих и капитальных затрат на его обслуживание.
Стратегическое планирование предприятия на несколько лет.
Разработка правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа.
Календарное планирование производства и др.

Общая постановка задачи ДП

Рассматривается управляемый процесс (например, экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования), который может быть разбит на несколько состояний (шагов). В качестве шага могут выступать временные периоды, предприятия и др.

Управляемый процесс в качестве объекта имеет систему S, которая в процессе управления переводится из начального состояния s0 в некоторое конечное состояние sn, где n – число состояний системы или шагов.

Управленческое решение принимается последовательно на каждом шаге. Управление, переводящее систему S из начального состояния в конечное, представляет собой совокупность n пошаговых управлений.

Особенности модели ДП:

- задача оптимизации интерпретируется как n - шаговый процесс управления;

- целевая функция модели является аддитивной (суммарной) функцией показателей эффективности каждого шага;

- выбор управления на k-ом шаге зависит только от состояния системы на этом шаге;

- каждое состояние системы послеk-го шага управления зависит только от предшествующего состояния и управления.

- на каждом шаге управление зависит от конечного числа управляющих переменных, а состояние- от конечного числа параметров.

Пусть - управление, переводящее систему из начального состояния в конечное. Состояние системы послеk-го шага управления - . Тогда последовательность состояний можно изобразить кружками.

Оценить каждое состояние системы можно при помощи показателя эффективности. Сумма всех показателей эффективности на каждом шаге будет представлять собой целевую функцию модели ДП.

Обозначим показатель эффективности k-го шага как :. Тогда целевая функциябудет представлять собой сумму оптимальных показателей эффективности всех шагов системы:.

Так как каждое состояние системы и показатель его эффективности зависит от предыдущего состояния и от управления, выбранного на данном шаге, то состояние системы в целом и суммарная эффективность на последующем шаге будут определяться начальным состоянием системы и вектором управления. Тогда целевую функцию можно представить в следующем виде:.

Каждое состояние системы может быть выражено:

Принцип оптимальности и уравнения Беллмана

Принцип оптимальности.

На каждом шаге управление выбирается так, чтобы оно в совокупности со всеми оптимальными управлениями на всех последующих шагах приводило к наилучшему суммарному показателю эффективности. Т.е. управление должно выбираться исходя из оптимальности управления в целом, а не только на каком-то конкретном шаге. В основу этого принципа положены особенности модели ДП. На основе данного принципа были сформулированы рекуррентные формулы Беллмана. Применение данных формул возможно на базе обратной или прямой схемы Беллмана. В обоих случаях является показателем эффективностиk-ого шага. На каждом шаге оптимальное управление выбирается из множества возможных управлений .

Обратная схема Беллмана.

При обратной схеме оптимизация осуществляется в результате обратного движения от последнего шага к первому. Сначала определяется оптимальная стратегия управления на n-ом шаге, затем на двух последних шагах, потом на трех последних шагах и т.д. до первого шага.

n-й шаг: состояние системы, зависящее от состояния,- управление наn-ом шаге, - целевая функцияn-го шага.

Оптимальный показатель эффективности n–го шага , равный суммарному показателю эффективности всех предыдущих шагов на множестве всевозможных управлений всевозможных состояний системы.

(n-1)-ый шаг

к-ый шаг

………………

1-ый шаг

Таким образом, в результате прохождения всех шагов от последнего к первому определяется оптимальное значение целевой функции. Чтобы найти оптимальную стратегию управления, т.е. определить решение задачи - , необходимо снова пройти всю последовательность шагов, только от начала к концу.

На первом шаге в качестве оптимального управления выбирается найденное условно оптимальное управление, характеризуемое показателем эффективности. Знаяи, на втором шаге находитсяи управлениеи т.д.

Процесс решения можно представить в виде схемы:

Прямая схема Беллмана

При прямой схеме процесс поиска решения выполняется в направлении от первого шага к последнему. Сначала определяют оптимальную стратегию управления на первом шаге, затем на двух первых шагах, затем на трех первых шагах и т.д. до последнего шага.

1 шаг

На данном шаге состояние системы - , предыдущее состояние -.- множество управлений на первом шаге. Показатель эффективности 1-го шага -.

2 шаг

……………..

k – ый шаг

……………..

n-ый шаг

В результате прохождения всех шагов от первого к последнему определяется оптимальное значение целевой функции, которое приравнивается оптимальному показателю эффективности n-го шага . Чтобы найти оптимальную стратегию управления, т.е. определить решение задачи -, необходимо снова пройти всю последовательность шагов - от последнего к первому.

Поиск оптимальной стратегии можно представить в виде схемы:

Общая схема применения метода ДП

Выбирается способ деления процесса управления на шаги.
Определяются параметры состояния и переменные управленияна каждом шаге.
Записываются уравнения состояний .
Вводится целевая функция.
Вводится в рассмотрение условные максимумы (минимумы) и условное оптимальное управление наk-м шаге: (в случае обратной схемы Беллмана),(при прямой схеме Беллмана).
Записываются основные уравнения для выбранной схемы Беллмана.
Последовательно решаются записанные уравнения Беллмана и получаются две последовательности функций: и.
После выполнения условной оптимизации определяется оптимальное решение поставленной задачи и.

Задача распределения средств между предприятиями

Задача распределения ресурсов между предприятиями является задачей динамического программирования.

Пусть имеется некоторая сумма средств, которую необходимо вложить в одно или несколько предприятий, чтобы получить максимальную прибыль от инвестирования. Предполагается, что в каждое из рассматриваемых предприятий может быть вложена как вся сумма инвестиций, так и частично, либо в предприятие может быть ничего не вложено, если инвестиции в него не эффективны. Для каждого предприятия должен быть рассчитан показатель эффективности инвестиций, который определяется в результате решения задачи ЛП о планировании производства.

Математическая модель для каждого вида предприятия имеет вид:

Целевая функция при ограничениях:

В модели использованы следующие обозначения:

- цена на j-ый вид товара для k-ого предприятия;

- оптимальный объем закупки i-ого вида ресурса k-ым предприятием;

- уровень запаса i-ого вида ресурса на k-ом предприятии;

- оптимальный план производства j-ого вида продукции на k-ом предприятии;

- норма расхода i-ого вида ресурса для производства единицы продукции j-ого вида на k-ом предприятии;

- рыночная цена i-ого вида ресурса для k-ого предприятия;

- объем финансовых средств, выделенных k-ому предприятию;

- минимальный объем заказов j-ого вида продукции на k-ом предприятии;

- предельная емкость рынка по j-ому виду продукции для k-ого предприятия.

В результате решения данной задачи будет получена величина дополнительного дохода от работы предприятия, которая представляет собой разницу прибыли при выделении инвестиций и прибыли, если инвестиции не производятся.

Вычисленные методами линейного программирования показатели эффективности деятельности каждого предприятия в зависимости от объема получаемых финансовых средств в дальнейшем используются для нахождения оптимального распределения средств между предприятиями методами динамического программирования.

Предполагается, что:

дополнительный доход каждого предприятия не зависит от объемов вложения средств в другие предприятия;
дополнительный доход каждого предприятия выражается в одних и тех же единицах;
совокупный дополнительный доход равен сумме дополнительных доходов, полученных каждым предприятием.

Для определения оптимальных средств инвестирования необходимо пройти следующие этапы:

интервал изменения выделяемых средств разбивается на элементарные отрезки;
для заданных значений выделяемых средств определяются показатели эффективности для всех предприятий;
по обратной (прямой) схеме используются уравнения Беллмана;
в обратной (прямой) последовательности, начиная от находятся оптимальные значения выделяемых средств.

Пример. Планируется деятельность 4 промышленных предприятий на очередной год. Необходимо между ними распределить 400 единиц ограниченного ресурса Q. Каждое предприятие i в зависимости от объема выделенных средств x получает дополнительный доход fi(x). Распределение ресурсов производится с точностью 80 единиц. Необходимо определить оптимальное распределение средств между предприятиями, обеспечивающее максимальную эффективность деятельности всех предприятий.

Объемы получаемых дополнительных доходов в зависимости от выделенных ресурсов x представлены в таблице 1.

Таблица 1

Объем выделенных ресурсов, x	Дополнительный доход предприятия в зависимости от объема выделенных средств, fi(x)
Объем выделенных ресурсов, x	f1(x)	f2(x)	f3(x)	f4(x)
0	0	0	0	0
80	30	28	35	27
160	57	62	67	73
240	120	122	130	125
320	150	146	144	152
400	180	175	180	178

Рассмотрим обратную схему Беллмана.

Согласно обратной схеме Беллмана начинаем с определения условно оптимальных капиталовложений, выделяемых для последнего четвертого (n-ого) предприятия. Для этого находим значения для каждогоx, принимающего значения 0, 80, 160, 240, 320, 400.

4 шаг.

Показатель эффективности 4-ого предприятия, равный суммарному показателю эффективности на всех шагах определяется как .

3 шаг

Находим - суммарный показатель эффективности деятельности 3 и 4 предприятий .

2 шаг

Вычислим объединённый показатель эффективности деятельности 2, 3 и 4 предприятий - .

1 шаг

Объединённый показатель эффективности деятельности 4-х предприятий - .

Таблица 2

Объем выделенных ресурсов, x	Показатели эффективности предприятий в зависимости от объема выделенных средств, Z i(x)
Объем выделенных ресурсов, x	Z4(x)	Z 3(x)	Z 2(x)	Z 1(x)
0	0	0	0	0
80	27	35	35	35
160	73	73	73	73
240	125	130	130	130
320	152	160	160	160
400	178	203	203	203

Чтобы найти оптимальную стратегию управления, необходимо рассмотреть всю последовательность шагов от последнего к первому.

В результате решения задачи распределения средств между предприятиями получили, что для обеспечения максимальной эффективности деятельности 4-х предприятий, равной 203 у.е., 1-ому и 2-ому предприятиям следует не выделять ресурсов, 3 предприятию необходимо выделить 240 единиц ресурса, 4-ому – 160 единиц.

№ вари-анта	Прирост выпуска продукции i - ого предприятия, fi(x)	Часть средств, выделяемых предприятиям, млн руб, x
№ вари-анта	Прирост выпуска продукции i - ого предприятия, fi(x)	0	20	40	60	80	100
	f1(x)	0	9	18	24	38	50
		0	9	17	29	38	47
		0	7	29	37	41	47
		0	9	20	35	44	48
		0	9	18	29	41	52
		0	11	21	40	54	63
		0	12	26	40	60	74
		0	14	24	37	45	47
		0	16	28	36	39	44
		0	18	28	39	47	55
		0	12	19	30	44	69
		0	11	34	46	53	68
		0	9	19	28	37	68
		0	12	25	34	46	58
		0	11	19	30	47	52
		0	9	20	42	45	59
		0	8	22	36	49	64
		0	8	24	42	58	67
		0	7	27	42	50	66
		0	5	30	40	52	65

№ вари-анта	Прирост выпуска продукции i - ого предприятия, fi(x)	Часть средств, выделяемых предприятиям, млн руб, x
№ вари-анта	Прирост выпуска продукции i - ого предприятия, fi(x)	0	20	40	60	80	100
1.	f2(x)	0	10	21	25	35	51
2.		0	11	21	29	36	56
3.		0	12	20	26	39	59
4.		0	11	22	25	29	47
5.		0	11	25	27	36	60
6.		0	10	19	23	40	57
7.		0	9	34	38	46	52
8.		0	8	22	29	37	52
9.		0	7	19	25	39	51
10.		0	14	18	24	39	59
11.		0	12	17	28	38	60
12.		0	10	12	20	29	47
13.		0	5	10	21	27	36
14.		0	7	10	21	32	41
15.		0	13	15	25	30	40
16.		0	12	20	31	39	47
17.		0	8	15	25	40	51
18.		0	7	16	24	41	51
19.		0	7	20	28	29	58
20.		0	9	21	25	29	57

studfiles.net

Дипломная работа - Задача о распределении средств между предприятиями

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

АЛТАЙСКИЙ ПРОМЫШЛЕННО-ЭКОНОМИЧЕСКИИ КОЛЛЕДЖ

Специальность программное обеспечение вычислительной техники и автоматизированных систем

Группа 11По071

КУРСОВАЯ РАБОТА

На тему

Задача о распределении средств между предприятиями

Студент:

Консультанты: Любицкая О.Н, Захарова О.А

“__” Мая 2009г.

БАРНАУЛ Оглавление

Введение. 3

Сущность математического метода… 5

1.1 Характеристика математического метода, применимого для решения задачи 5

1.2 Аналитическое решение задачи… 11

Решение задачи в среде визуального программирования Delphi15

2.1 Анализ процесса обработки информации и выбор структур данных для ее хранения… 15

2.2 Разработка основных алгоритмов решения задачи… 17

2.3 Построение графа состояний интерфейса… 19

2.3 Разработка форм ввода-вывода информации… 20

2.5 Контрольный пример. 23

Заключение. 30

Список использованных источников… 32

ПриложениеА… 33

Введение

Тема курсовой работы: задача о распределении средств между предприятиями.

Сущность математического метода1.1 Характеристика математического метода, применимого для решения задачи

заглядыванием в будущее”, иначе возможны серьезные ошибки.

N

– число шагов.

/>

– вектор, описывающий состояние системы на k-м шаге.

/>

– начальное состояние, т. е. состояние на 1-м шаге.

/>

– конечное состояние, т. е. состояние на последнем шаге.

Xk

– область допустимых состояний на k-ом шаге.

/>

– вектор УВ на k-ом шаге, обеспечивающий переход системы из состояния xk-1 в состояние xk.

Uk – область допустимых УВ на

k-ом шаге.

Wk

S

– общий выигрыш за Nшагов.

/>– вектор оптимальной стратегии управления или ОУВ за

Nшагов.

Sk

S

/>

Аналогично, величина выигрыша Wk

зависит от состояния /> и выбранного УВ />, то есть

/>

шагов вычисляется по формуле

Условие отсутствия последствий позволяет сформулировать принцип оптимальности Беллмана.

/>

1.2 Аналитическое решение задачи

у.е. приносит прибыль Pi (x) у.е. (i = l, 2 и 3) последующим данным, приведённым в таблице 1.

Таблица 1 – Исходные данные.

Инвестируемые средства (у.е.)

Общая прибыль (у.е.)

P1(x)

P2(x)

P3(x)

3,22

3,33

4,27

<span style=«font-size: 12

www.ronl.ru

Задача о распределении средств между предприятиями — КиберПедия

Рассмотрим схему решения задач динамического программирования с использованием уравнений Беллмана на примере задачи о распределении средств между предприятиями.

Постановка задачи.

Планируется деятельность трех предприятий на очередной год. Начальные средства s0, которые следует распределить, составляют 5 усл. ед. Размеры вложения в каждое предприятие кратны 1 усл. ед. Средства x, выделенные предприятию k, приносят в конце года прибыль 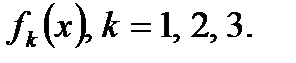Функции 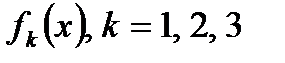заданы таблично (табл. 1). При решении подобных задач принято считать, что выполняются следующие предположения:

– прибыль 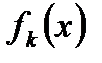предприятия k не зависит от вложения средств в другие предприятия;

– прибыль выражается в одних условных единицах;

– общая прибыль равна сумме прибылей, полученных от каждого предприятия.

Требуется определить, какое количество средств нужно выделить каждому предприятию, чтобы общая прибыль была наибольшей.

Таблица 1

Эффективность использования средств

Построим математическую модель задачи. Обозначим через xk количество средств, выделенных предприятию k. Общая прибыль равна сумме прибылей предприятий:

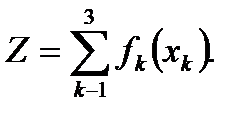(14)

Переменные xk удовлетворяют следующим ограничениям:

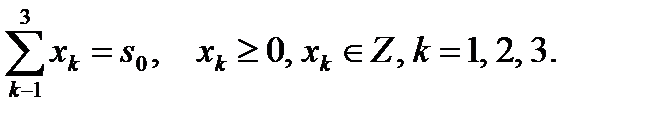(15)

Требуется найти переменные x1, x2, x3, удовлетворяющие системе ограничений (15), при которых функция (14) достигает максимума.

Особенность модели состоит в том, что хотя ограничения линейные и переменные целочисленные, методы целочисленного линейного программирования применять нельзя, так как функции fk(x) заданы таблично.

Процесс распределения средств 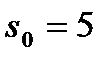можно рассматривать как трехшаговый, номер шага совпадает с номером предприятия. Выбор переменных x1, x2, x3 – это выбор управления 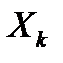соответственно на 1, 2 и 3 шаге. Конечное состояние процесса распределения 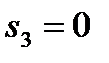, когда все средства вложены в производство.

Графически схема распределения показана на рис. 9.

Рис.9. Схема распределения средств

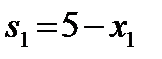
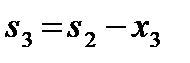
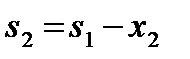
Уравнения состояний имеют вид:

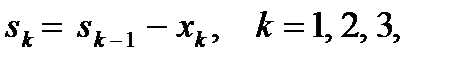(16)

где sk – параметр состояния, количество средств, оставшихся после k-го шага, т. е. эти средства остается распределить между (3 – k) оставшимися предприятиями.

Рассмотрим функцию 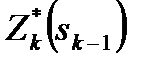– условную оптимальную прибыль, полученную от предприятий k, (k + 1), …, 3, если между ними оптимальным образом распределялись средства 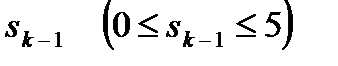. Допустимые управления на шаге k удовлетворяют условию: .

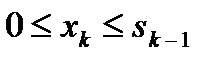Уравнения, связывающие оптимальную прибыль на каждом шаге, имеют вид:

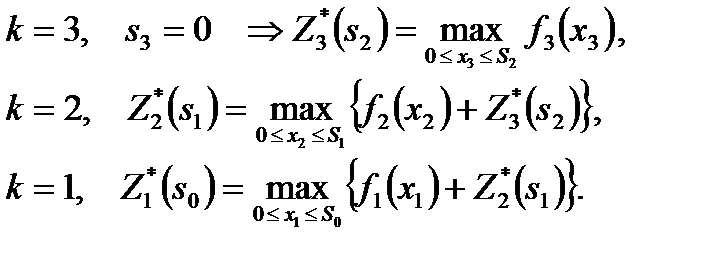(17)

Последовательно решаем уравнения, проводя условную оптимизацию каждого шага.

Решение задачи.

Шаг k=3. В табл. 1 прибыль 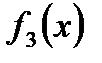монотонно возрастает, поэтому все средства, оставшиеся к третьему шагу, следует вложить в предприятие 3 (рис.10).

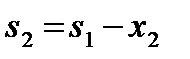
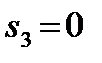
Рис.10. Распределение средств на шаге 3

При этом для возможных значений 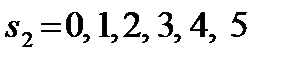получим:

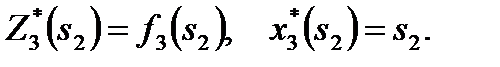(18)

Шаг k=2.Делаем все предположения относительно остатка средств 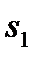ко второму шагу, т. е. после выбора значения 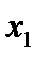величина 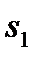может принимать значения 0, 1, 2, 3, 4, 5. В зависимости от этого выбираем 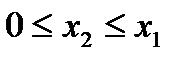, находим 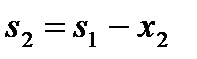и сравниваем для разных 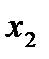при фиксированном 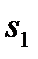значения суммы .

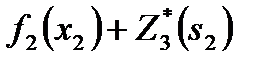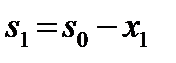
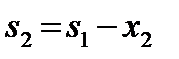
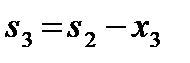
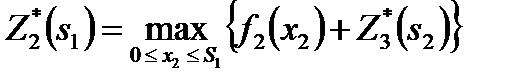
Рис.11. Распределение средств на шаге 2

Для каждого 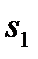наибольшее из этих значений 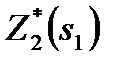– это условная оптимальная прибыль, получаемая при оптимальном распределении средств между 2-м и 3-м предприятиями (рис.11).

Вычисления записаны в таблице 2. Для каждого значения 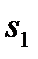оптимальные значения 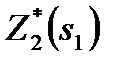и 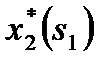записаны в графах 5 и 6.

Таблица 2

Оптимизация распределения средств при k=2

s1	x2	s2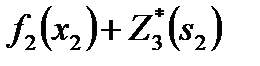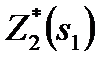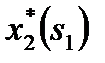

			0+4=4
		6+0=6
			0+8=8
		6+4=10
		9+0=9
			0+12=12
		6+8=14
		9+4=13
		12+0=12
			0+16=16
		6+12=18
		9+8=17
		12+4=16
		15+0=15
			0+20=20
		6+16=22
		9+12=21
		12+8=20
		15+4=19
		18+0=18

Шаг k=1.Графическое представление шага представлено на рисунке 12. Условная оптимизация проведена в таблице 3.

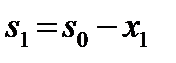
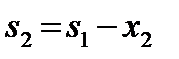
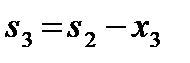
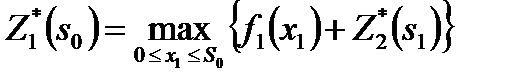
Рис.12. Распределение средств на шаге 1

Например, если 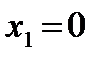, то 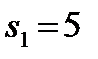. Прибыль, полученная от трех предприятий при условии, что 5 единиц средств будут распределены оптимально между оставшимися двумя предприятиями, равна 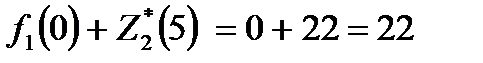. Значение 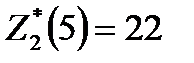взято из столбца 5 табл. 2 при 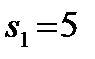. Если 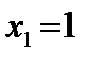, то 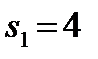. Суммарная прибыль при условии оптимального распределения средств равна 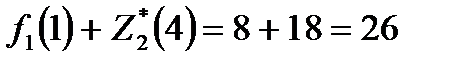. Значение 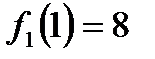взято из исходных данных (табл. 1), значение 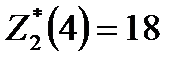– из столбца 5 табл. 2 при 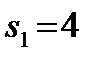. Аналогично вычислены остальные значения столбца 4 табл. 3.

Таблица 3

Оптимизация распределения средств при k=1

s0	x1	s1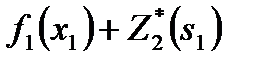
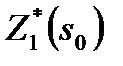
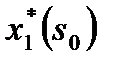
			0+22=22
		8+18=26
		10+14=24
		12+10=22
		14+6=20
		16+0=16

Оптимальное решение рассматриваемой задачи при 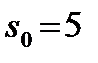выделено в таблице 3 жирным шрифтом. Максимум суммарной прибыли 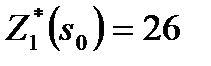получаем при условии, что первому предприятию выделяется 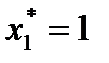усл. ед. и между 2 и 3 предприятиями распределяются 4 усл. ед. средств. Далее оптимальный вариант распределения находим из табл. 2 при 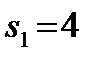: 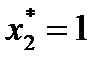усл. ед., 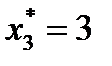усл. ед.

Достоинством метода является возможность изменения числа шагов (предприятий), проведение анализа решения на чувствительность к изменению 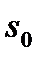, безразличие метода к способу задания функций .

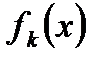cyberpedia.su

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..