
ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА (г. КАЗАНЬ)
Нижнекамский филиал
КОНТРОЛЬНАЯ РАБОТА
по неорганической химии .
за2 . семестр 2007/2008 уч. года
преподаватель: Давыдов Е.М. .
вариант.
Ткаченко .
фамилия
Семен .
имя
Ильич .
отчество
1 курса заочного отделения
1371з гр.
Содержание
Введение 3
1. Кинетическое уравнение химических реакций 4
2.Молекулярность реакций 13
Введение
Скорость любой химической реакции зависит от условий, в которых она протекает: от концентрации реагентов (или их давления, если это газы), температуры, наличия катализатора или излучения и т.д. Одни реакции протекают практически мгновенно (например, нейтрализация кислоты основанием), другие при обычных условиях идут настолько медленно, что заметные изменения концентраций реагентов наблюдаются лишь через несколько лет (например, взаимодействие водорода с кислородом с образованием воды в отсутствие катализатора). При этом существует множество реакций, протекающих с вполне измеримыми скоростями в обычных условиях. Химическая кинетика занимается определением скоростей химических реакций и изучением их механизма. Это относительно молодая наука, и в ней имеется много нерешенных проблем. Во всех кинетических исследованиях фигурируют время и промежуточные продукты (вещества, образующиеся на промежуточных стадиях реакции). Этим они отличаются от исследований систем в условиях химического равновесия, когда рассматриваются только начальное и конечное состояния реагентов.
Кинетическое уравнение химических реакций
В одном кинетическом эксперименте нередко участвуют одновременно две или несколько реакций, при этом их скорости могут зависеть от наличия загрязнений и следов катализаторов. В результате получаемые данные бывают плохо воспроизводимыми, что затрудняет их интерпретацию. Если с термодинамической точки зрения из одних и тех же исходных веществ возможно образование разных продуктов, следует подбором концентрации реагентов, температуры и специфического катализатора добиться, чтобы протекала именно та реакция, которая интересует исследователя. Скорость реакций обычно определяют при постоянной температуре, лучше при двух и более ее значениях, используя один или несколько высокоточных термостатов.
Измерение скоростей реакций. Скорости реакций измеряют разными способами. Можно отбирать пробы из термостатируемого реактора через строго определенные интервалы времени либо замедлять или полностью останавливать реакцию (быстрым охлаждением реактора или каким-либо иным способом) и анализировать пробы титрованием или другими аналитическими методами. Иногда одновременно запускают несколько идентичных реакций, а затем последовательно останавливают их быстрым охлаждением и анализируют продукты.
Если один из реагентов или продуктов реакции обладает оптической активностью, то следят за его концентрацией с помощью поляриметра. Аналогично, если изменение концентрации реагента или продукта реакции либо их обоих сопровождается изменением электропроводности, для кинетических измерений используют электрические методы. Иногда концентрацию одного из реагирующих веществ определяют, измеряя оптическую плотность раствора при определенной длине волны и используя закон Ламберта – Бера.
Скорость реакции можно рассчитать исходя из данных об изменении давления или объема в газофазной системе либо объема газа, выделяющегося в ходе реакции. В случае газофазных реакций, протекающих в потоке, в реактор иногда вводят катализатор или повышают температуру, чтобы ускорить процесс. Входные и выходные трубки в таких системах делают достаточно малыми, чтобы газы поступали в реактор и выходили из него как можно быстрее и в области с неконтролируемым градиентом температуры находились непродолжительное время. Время нахождения газов в реакторе (время протекания реакции) определяют исходя из объема газов, проходящих через реактор в 1 с, отнесенного к объему реактора. Если общее число молекул в ходе реакции изменяется, то оценить время становится довольно трудно. В проточных системах используются большие количества реагентов и получаются большие количества продуктов, что облегчает моделирование соответствующих химических процессов в промышленных масштабах.
Скорость реакции можно определить по уменьшению концентрации исходных веществ или по увеличению концентрации продуктов. Скорость уменьшения концентрации исходного вещества равна –dC/dt, а скорость увеличения концентрации продукта равна dC/dt, где С – концентрация, t – время. Концентрацию обычно измеряют в единицах молярности (моль/л), время – в секундах.
Порядок реакции. Порядок реакции – это эмпирическая величина, равная сумме показателей степеней, с которыми концентрации реагентов входят в выражение для скорости реакции. Так, для реакции
aA + bB ® mM + nN
скорость уменьшения концентрации С реагента А можно представить в виде

где СА и СВ – концентрации исходных веществ А и В соответственно. Порядок реакции в этом случае равен а + b. Коэффициент пропорциональности k, входящий в уравнение, называется константой скорости. Он равен скорости реакции при единичной концентрации реагентов.
Реакции первого порядка. Если скорость реакции зависит от концентрации только одного реагента в первой степени, то выражение для скорости принимает вид

О такой реакции говорят, что она является реакцией первого порядка.
Чтобы найти зависимость концентрации от времени, нужно проинтегрировать уравнение (1). Разделив переменные и проинтегрировав, получим
–ln C = kt + const
где ln – натуральный логарифм. Или, перейдя к десятичным логарифмам:

График зависимости lg C от t является прямой с тангенсом угла наклона –s, равным –k/2,303. Отсюда
k = 2,303Чs
Зная k и концентрацию С при данном t, можно найти константу интегрирования (const) и рассчитать концентрацию для любого момента времени. Константу интегрирования можно также определить из координат точки пересечения прямой с осью lg C при t = 0 (рис. 1).
Уравнение (1) можно проинтегрировать в пределах от С1 до С2, равных концентрациям реагента в моменты времени t1 и t2:

Отсюда

Размерность k равна размерности t –1.
Если в начальный момент времени (t1 = 0) C1 = C0, то концентрация C в любой момент времени t в соответствии с уравнением (2) будет равна

Уравнение (1) можно записать в другом виде, приняв, что а – это начальное количество реагента, x – его количество, прореагировавшее за время t. Тогда (а – x) равно количеству реагента, оставшемуся через время t, и уравнение реакции примет вид

Разделив переменные и проинтегрировав, получим
–ln(a – x) = kt + const
отсюда при t = 0, x = 0 и const = –ln a

Часто представляет интерес характеристическая величина t1/2 – время полупревращения реакции, т.е. время, за которое концентрация исходного вещества уменьшается вдвое. При x = (1/2)a и t = t1/2 из уравнения (3) получим

Это соотношение иллюстрирует важную особенность реакций первого порядка: время, за которое количество вещества уменьшается вдвое, не зависит от его количества в момент начала реакции и в любой данный момент реакции.
Если известна константа скорости k, можно рассчитать количество вещества, прореагировавшего к данному моменту времени, или определить, за какое время прореагирует данное количество вещества.
Уравнению первого порядка следуют многие химические реакции. Например, пентаоксид азота, растворенный в тетрахлориде углерода, разлагается при температуре 45° С в строгом соответствии с уравнением реакции первого порядка:

Реакции второго порядка. Когда скорость реакции пропорциональна квадрату концентрации отдельного реагента или концентрациям каждого из двух реагирующих веществ в первой степени, мы имеем дело с реакцией второго порядка. В дифференциальной форме выражения для скорости такой реакции имеют вид

и

Пусть a – начальная молярная концентрация реагента А, x – число его молей в 1 л, прореагировавшее за время t; тогда скорость реакции будет равна
dx/dt = k(a – x)2
или
dx/(a – x)2 = kdt
Проинтегрировав, получим
1/(a – x) = kt + C
Поскольку x = 0 при t = 0, константа С = 1/а. Отсюда

и

Если а и b – начальные молярные концентрации реагентов А и В соответственно и если за время t прореагировало x молей этих реагентов в 1 л, то, проинтегрировав соответствующее уравнение для скорости реакции, можно найти выражение для константы скорости:

Размерность k – л/(мольЧс). Численное значение k можно найти, подставив концентрации и время в уравнение (4) либо построив графики зависимости  или
или  от времени. Умножение наклона полученной таким образом прямой на 2,303/(a – b) дает k.
от времени. Умножение наклона полученной таким образом прямой на 2,303/(a – b) дает k.
Реакции третьего порядка. Скорость реакции третьего порядка может зависеть от концентрации одного реагента в третьей степени, либо концентрации одного реагента во второй степени и второго реагента в первой степени, либо от концентрации каждого из трех реагентов в первой степени. Так,

или
dx/dt = k(a – x)3
Разделение переменных и интегрирование дают

или

Здесь размерность k – л2 /(моль2 Чс).
Реакции нулевого порядка. Скорость реакций нулевого порядка не зависит от концентраций реагентов и определяется другими лимитирующими факторами, например площадью поверхности катализатора (в реакциях гетерогенного катализа) или поглощением света (в фотохимических реакциях). Уравнение для скорости такой реакции в дифференциальной форме имеет вид
–dC/dt = k
или, выраженное через концентрацию x продукта,
dx/dt = k
Проинтегрировав, получим
x = kt + C
Значению x = 0 соответствует t = 0, откуда константа С = 0 и
x = kt
В величину k могут входить различные константы, например интенсивность света, концентрация насыщенного раствора или пара. Размерность k – моль/(лЧс).
Реакции п-го порядка. В общем случае для реакции порядка п при п > 1 связь между концентрацией и временем для конечного времени наблюдения описывается уравнением

где С – концентрация реагента в момент времени t, C0– начальная концентрация. График зависимости 1/(Сn– 1 ) от t представляет собой прямую с наклоном (n–1) k. Размерность k – (моль/л)1 – n /c.
Реакции не всегда имеют целочисленный порядок. Показатели степени при концентрациях в выражении для скорости часто являются дробными. Однако и в этом случае порядок реакции равен сумме показателей степеней. Например, для реакции, скорость которой равна

порядок п = 0,7 + 1,8 = 2,5.
Часто порядок реакции, определяемый экспериментально, не соответствует порядку, который следует из стехиометрического уравнения. Большинство химических реакций включает две или несколько стадий, протекающих одновременно, что приводит к более сложным выражениям для скорости.
Определение порядка реакции. Подстановка в формулы. Если k остается постоянной при подстановке значений концентрации и времени в уравнение скорости реакции, значит, порядок реакции, задаваемый уравнением, верен. Если же расчеты не согласуются с экспериментальными данными, то реакция сложнее, чем предполагалось, и, вероятно, протекает в две или несколько стадий.
Графический метод. Для определения порядка реакции можно прибегнуть к графическому представлению функций, описывающих зависимость концентрации от времени. Если при построении зависимости С от t получается прямая, это означает, что реакция – нулевого порядка. Если линейна зависимость lg C от t, имеет место реакция первого порядка. При условии что начальная концентрация всех реагентов одинакова, реакция имеет второй порядок, если линейным является график зависимости 1/С от t, и третий – в случае линейности зависимости 1/С 2 от t.
Определение времени полупревращения. Для реакции первого порядка время, за которое прореагирует определенная часть реагента (например, половина), не зависит от начальной концентрации (см. выше),

Для реакции второго порядка при равенстве начальных концентраций обоих реагентов, а = b, время, за которое прореагирует половина вещества, обратно пропорционально начальной концентрации. Из приведенного выше выражения для константы скорости реакции второго порядка получаем

или
t1/2 = 1/ka
Изменение соотношения между реагентами. Если выражение для скорости представить как

где СА, СВ, СС… – концентрации участвующих в реакции веществ А, В и С ..., а а, b, с… – соответствующие показатели степени в уравнении для скорости, то порядок реакции п можно определить, увеличив вдвое значение СА без изменения СВ и СС и экспериментально определив величину Dx/Dt для СА и 2СА. Так, если  – скорость при концентрации 2СА, а
– скорость при концентрации 2СА, а  – скорость при концентрации СА, то, взяв отношение этих двух величин, получим
– скорость при концентрации СА, то, взяв отношение этих двух величин, получим

Предположим, что наблюдаемое отношение

равно 4; тогда а = 2 и реакция является реакцией второго порядка относительно реагента А. Если это отношение равно 2, то а = 1 и имеет место реакция первого порядка относительно того же реагента. Аналогичным образом определяют b, с и т.д.
Добавление избытка реагентов. Добавив в реакционную смесь в большом избытке все реагирующие вещества, кроме одного, можно определить порядок реакции по этому реагенту, т.е. показатель степени, с которым концентрация данного реагента входит в уравнение скорости. Таким же образом определяют порядок реакции по каждому реагенту.
Показатель степени для концентрации реагента А, не находящегося в избытке, устанавливают по графику зависимости dCA /dt от ln CA согласно уравнению

Наклон полученной прямой равен а. Константа kў является произведением константы скорости на концентрации реагентов, находящихся в избытке, взятые в соответствующих степенях.
Молекулярность реакции
Молекулярность реакции определяется числом молекул, участвующих в самой медленной, лимитирующей стадии. Реакции бывают моно-, би-, три- и т.д. молекулярными. Порядок реакции и ее молекулярность не всегда можно предсказать исходя из стехиометрии реакции; для этого нужно провести кинетические измерения. В некоторых случаях порядок и молекулярность реакции, определенные исходя из ее стехиометрии, совпадают.
Мономолекулярной называется такая реакция, в которой лимитирующей стадией является превращение одной молекулы, например распад ее на составляющие (диссоциация молекул иода I2 ® 2I) или превращение в другую молекулу в результате внутримолекулярной перестройки:

Бимолекулярная реакция – это взаимодействие двух молекул (например, молекулярного водорода с молекулярным иодом, h3 + I2 ® 2HI). Реакция, протекающая одновременно с участием трех молекул, называется тримолекулярной. Поскольку вероятность столкновения сразу трех молекул, да еще в правильной взаимной ориентации, очень мала, такие реакции происходят редко.
www.ronl.ru
По химии
Скорость химических реакций. Катализ и химическое равновесие
Цель работы
1) ознакомление с основными закономерностями протекания химических реакций и факторами, влияющими на скорость реакции;
2) ознакомление с катализаторами, химическим равновесием и факторами, влияющими на химическое равновесие.
Теоретическая часть
І. Скоростью реакции называется число актов химического взаимодействия, происходящих в единицу времени в единице объёма при гомогенных процессах или на единице поверхности при гетерогенных процессах.

О средней скорости химической реакции судят по изменению молярной концентрации реагирующих веществ за определённый интервал времени:
 ,
,
где  — средняя скорость химической реакции; c 1 – молярная концентрация вещества в момент τ 1, c 2 – молярная концентрация вещества в момент τ 2. Истинной скоростью химической реакции в данный момент называется первая производная концентрации по времени:
— средняя скорость химической реакции; c 1 – молярная концентрация вещества в момент τ 1, c 2 – молярная концентрация вещества в момент τ 2. Истинной скоростью химической реакции в данный момент называется первая производная концентрации по времени:
 .
.
В гомогенной системе скорость химической реакции зависит от природы реагирующих веществ, их концентрации, температуры, наличия катализатора, присутствия примесей и природы растворителя.
В гетерогенной системе взаимодействие осуществляется на поверхности раздела реагирующих веществ, поэтому зависит от диффузии вещества к поверхности (диффузионный режим), а если диффузия не влияет на скорость реакции (кинетический режим), то при прочих равных условиях увеличение поверхности раздела повышает скорость гетерогенной химической реакции.
Зависимость скорости реакции от концентрации определяется законом действующих масс (закон Гульдберга-Вааге):
если химическая реакция идёт в соответствии со стехиометрическим уравнением, то скорость реакции прямо пропорциональна произведению концентраций реагирующих веществ в степенях, равных стехиометрическим коэффициентам в уравнении реакции.
Для реакции записанной в общем виде, т.е.: nA+mB→qR+pD,
скорость реакции в соответствии с законом действующих масс выразится следующим образом:
(1):  .
.
Здесь [A] и [B] – молярные концентрации реагирующих веществ в данный момент времени;
n и m — стехиометрические коэффициенты при реагирующих веществах. Например, для реакции:

прямая и обратная скорости:
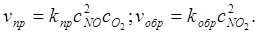
На практике приходится иметь дело со сложными процессами, состоящими не из одной, а из множества простых стадий, называемых элементарными актами, для каждой из которых можно записать своё выражение для скорости на основании закона действующих масс. В таком случае число молекул, участвующих в элементарном акте, определяет молекулярность взаимодействия. Для приведённого выше примера прямая реакция тримолекулярна, а обратная бимолекулярна.
В большинстве случаев показатели степени при концентрациях в уравнении закона действующих масс отличаются от числа молекул в уравнении реакции. Это происходит оттого, что уравнение реакции отражает лишь общий итог процесса. Показатели m и n в математическом уравнении (1) называют в таком случае порядком реакции по каждому из реагирующих веществ A или B, а их сумму (m+n) – общим порядком реакции. В каждом конкретном процессе в зависимости от условий может быть различный порядок реакции.
Коэффициент k называется константой скорости реакции и зависит от природы реагирующих веществ, температуры и катализатора. Численно константа скорости химической реакции равна скорости реакции при концентрациях реагирующих веществ, равных 1 моль/л. Однако реакции идут, как правило, по отдельным стадиям и общую скорость процесса определяет наиболее медленно развивающаяся стадия. Поэтому показатели степеней при концентрациях реагирующих веществ не совпадают с их стехиометрическими коэффициентами, а концентрации некоторых из реагирующих веществ вообще могут не входить в выражение скорости химических реакций.
Зависимость константы скорости реакции от температуры может быть выражена уравнением Аррениуса:
 ,
,
где Eакт – энергия активации;
k – константа скорости;
T – температура, К;
k0– константа;
R – газовая постоянная.
Энергией активации называется то количество энергии, которое надо сообщить молю реагирующих веществ для приведения его в реакционноспособное состояние. Энергия активации в реакции не исчезает и увеличивает тепловой эффект реакции.
При низких температурах можно считать, что скорость реакции возрастает при нагревании на 10˚ в 2…4 раза (правило Вант-Гоффа):
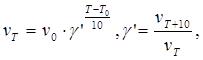
здесь γ΄ — температурный коэффициент Вант-Гоффа.
ІІ. Катализатором называется вещество, изменяющее скорость химической реакции, но в результате её само остающееся химически неизменным.
Каталитические процессы сводятся к двум типам: гомогенному и гетерогенному. При гомогенном катализе реагирующие вещества и катализатор составляют однофазную систему. При гетерогенном катализе реагирующие вещества и катализатор составляют систему из двух фаз, и каталитический процесс протекает на границах раздела. Скорость взаимодействия в этом случае пропорциональна поверхности раздела фаз.
Все химические реакции можно разделить на необратимые, направление которых не зависит от внешних условий, и обратимые, направление которых может изменяться в зависимости от температуры, концентрации и давления. Большинство реакций обратимо. Они протекают одновременно в двух направлениях, так как во всякой реакции по мере образования продуктов реакции возникает возможность взаимодействия между ними с образованием исходных веществ.
Рассмотрим обратимую реакцию в общем виде: aA+bB↔cC+dD.
Применив закон действующих масс к прямой и обратной реакциям, получим:
 (2)
(2)
где v 1 и v 2 – скорости прямой и обратной реакций.
По мере протекания реакции концентрация исходных веществ уменьшается, и скорость прямой реакции уменьшается, а скорость обратной увеличивается вследствие увеличения концентрации полученных веществ.
Через некоторое время наступает состояние, когда скорость обратного процесса становится равной скорости прямого: v 1 = v 2 .
Состояние, при котором скорость прямой реакции равна скорости обратной, называется химическим равновесием, а концентрации всех четырёх веществ – равновесными концентрациями. Тогда из соотношений (2) имеем:
Отсюда следует
 (3)
(3)
k 1 и k 2 для данной реакции при одной и той же температуре являются величинами постоянными, а значит, их отношение постоянно: Kc – величина постоянная и называется константой равновесия. Для реакций между газообразными веществами вместо концентраций можно использовать парциальные давления газов в смеси. При этом константу равновесия обозначают черезKp. Если концентрации выражены в мольных долях, то константа равновесия обозначается через KN. Между Kc ,Kp и KN существуют следующие зависимости:

где ∑n – алгебраическая сумма стехиометрических коэффициентов. Константа равновесия зависит от температуры и природы реагирующих веществ, но не зависит от катализатора, так как последний ускоряет и прямую, и обратную реакции.
Уравнение (3) вытекает из закона действующих масс для обратимых реакций. Его можно сформулировать так: Отношение произведения равновесных концентраций в степени их стехиометрических коэффициентов есть величина, постоянная при данной температуре.
Смещение равновесия в зависимости от изменения концентраций реагирующих веществ, температуры, давления (в случае газовых реакций) в общем случае определяется правилом Ле-Шателье: если в системе, находившейся в равновесии, изменить одно из условий ( t , p , c ), то происходит смещение равновесия в направлении той реакции, которая препятствует произведённому изменению .
Применяя принцип Ле-Шателье к разным случаям, можно сделать следующие выводы:
1) при увеличении равновесной концентрации одного из веществ система химического равновесия смещается в сторону той реакции, которая понижает концентрацию этого вещества;
2) при увеличении давления равновесие смещается в сторону образования меньшего числа молекул газа;
3) нагревание смещает равновесие в сторону эндотермической реакции, охлаждение – в сторону экзотермической реакции.
Практическая часть
Скорость химических реакций в гомогенной системе изучается на примере взаимодействия растворов серной кислоты и серноватистокислого натрия (тиосульфата):
Na2 S2 O3 + h3 SO4 → Na2 SO4 + S↓ + SO2 ↑ + h3 O
Сера, выделяющаяся в тонкораздробленном состоянии, даёт помутнение раствора. Момент исчезновения из поля зрения линеек или шрифта на бумаге, подложенной под стакан с реагирующим веществом, соответствует выделению определённого количества серы. Так как степень помутнения зависит от толщины слоя, то все опыты следует проводить в одном и том же стакане, чтобы объём жидкости и соответственно высота слоя были одинаковы.
Время, необходимое для выделения данного количества серы обратно пропорционально средней скорости процесса. Началом реакции считаем момент смешения растворов, условным концом реакции – выделение одного и того же количества серы.
Опыт 1. Зависимость скорости реакции от температуры
В ходе опыта смешали 20 мл раствора 0,5%-ного раствора серной кислоты и 20 мл 0,5%-ного раствора серноватистокислого натрия, предварительно измерив температуру растворов. Стаканчик со смесью был поставлен на лист линованной бумаги. В результате реакции: Na2 S2 O3 + h3 SO4 → Na2 SO4 + S↓ + SO2 ↑ + h3 O наблюдалось помутнение смеси. Был отмечен отрезок времени до условного окончания процесса.
Затем опыт был проделан ещё два раза, но температура растворов была поднята на 10˚C и 20˚C относительно первоначальной. Результаты измерений занесены в таблицу 1.
Табл. 1.
| № опыта | Температура растворов, ˚C | V(h3 SO4 ), мл | V(Na2 S2 O3 ), мл | Время, с | Условная скорость реакции  |
| 1 | 20 | 20 | 20 | 90 | 1,11 |
| 2 | 30 | 20 | 20 | 20 | 5 |
| 3 | 40 | 20 | 20 | 10 | 10 |
По данным таблицы можно рассчитать температурный коэффициент Вант-Гоффа для данных реакций:

 ;
;

Вывод: Температурный коэффициент Вант-Гоффа для реакции разложения пероксида водорода равен 3,25.
Опыт 2. Зависимость скорости химической реакции от концентрации реагирующих веществ при постоянной температуре
В один стаканчик налили 10 мл 0,5%-ного раствора серной кислоты. В другой налили 10 мл раствора серноватистокислого натрия и 20 мл дистиллированной воды. К раствору кислоты одновременно прилили воду и раствор соли и отметили по часам продолжительность опыта. Далее опыт был повторен с изменением концентрации соли: 20 мл раствора на 10 мл воды, 30 мл раствора соли.
Результаты измерений занесены в таблицу 2.
Табл. 2.
| № опыта | h3 SO4, мл | Na2 S2 O3, мл | h3 O, мл | Время, с | Усл. скорость реакции v |
| 1 | 10 | 10 | 20 | 110 | 0,909 |
| 2 | 10 | 20 | 10 | 50 | 2 |
| 3 | 10 | 30 | - | 35 | 2,857 |
По данным измерений можно определить порядок реакции n по скоростям, соответствующим двум различным концентрациям (метод Вант-Гоффа).

В результате вычислений получилось:
n 1 = 1,1375; n 2 = 0,8797; n ср = 1,008 ≈ 1.
Вывод: порядок реакции n по скоростям, соответствующим двум концентрациям близок к 1.
Опыт 3. Скорость химических реакций в гетерогенных системах
В две пробирки налили соляную кислоту. Затем в одну из них положили кусочек мрамора, а в другую – такой же кусочек, растёртый в порошок. В обеих пробирках проходила реакция:
CaCO3 + 2HCl → CaCl2 + h3 O + CO2 ↑.
Наблюдалось выделение газа. В пробирке, в которую был насыпан порошок, реакция проходила быстрее. Это объясняется тем, что площадь поверхности, на которой происходило взаимодействие веществ, была больше, чем в пробирке с цельным кусочком мрамора.
Вывод: в гетерогенных системах скорость реакции зависит от площади поверхности реагирующих веществ.
Опыт 4. Гетерогенный катализ.
а) Разложение пероксида водорода h3 O2 происходит и при комнатной температуре, но довольно медленно:
h3 O2 → h3 O + ½O2 .
Процесс разложения можно ускорить введением катализатора MnO2.
В 2 мл 3%-ного раствора h3 O2 всыпали щепотку оксида марганца (IV). Скорость реакции существенно возросла, наблюдалось бурное выделение пузырьков газа.
б) В пробирку налили серной кислоты, прилили раствор перманганата калия KMnO4. Полученную смесь разделили по трём пробиркам поровну. В каждую пробирку опустили по кусочку гранулированного цинка. В первую пробирку добавили несколько кристаллов KNO3, во вторую – в 2-3 раза большее количество нитрата калия, третью оставили для сравнения.
Наиболее быстро обесцвечивание раствора происходило во второй пробирке, в первой обесцвечивание проходило медленнее, в третьей – обесцвечивание было малозаметным. Аналогичным образом происходило и выделение пузырьков газа.
2KMnO4 + 3h3 SO4 + 2Zn → ZnSO4 + K2 SO4 + MnSO4 + 3h3 ↑

Вывод: MnO2 – катализатор в реакции разложения перекиси водорода. KNO3 – катализатор во взаимодействии цинка, серной кислоты и перманганата калия.
Опыт 5. Гомогенный катализ. В предыдущем опыте реакцию разложения пероксида водорода ускоряли гетерогенным катализатором – твёрдым оксидом марганца MnO2 .
h3 O2 → h3 O + ½O2 .
Эта реакция ускоряется также при помощи гомогенного катализатора – комплексного иона – тетра-аммиаката меди [Cu(Nh4 )4 ]2+. Этот катализатор является комплексным, поэтому необходимо исследовать влияние составляющих его компонентов – иона меди и аммиака. С этой целью в одну пробирку нужно налить 2 мл раствора CuSO4 и 0,5 мл h3 O2, во вторую – 2 мл водного раствора аммиака и 0,5 мл h3 O2. В обеих пробирках наблюдается образование мелких пузырьков кислорода в результате слабого каталитического действия составляющих комплексное соединение компонентов.
В третью пробирку необходимо прилить 2 мл раствора CuSO4 и добавить водного раствора аммиака до появления комплексного соединения темно-синего цвета:
CuSO4 + 4Nh4 ∙h3 O → 4h3 O + [Cu(Nh4 )4 ]SO4 .
К полученному раствору катализатора нужно прилить 2 мл 3%-ного h3 O2. Именно в третьей пробирке будет наблюдаться наиболее интенсивное выделение газа. При этом можно заметить, что катализатор во время реакции не расходуется, а лишь ускоряет течение процесса.
Вывод: [Cu(Nh4 )4 ]SO4 также является катализатором при разложении пероксида водорода.
Опыт 6. Сдвиг химического равновесия в гомогенной системе.
Влияние концентрации исходных веществ и продуктов реакции на химическое равновесие в гомогенной системе можно исследовать на примере реакции:
FeCl3 + 3Nh5 CNS ↔ Fe(CNS)3 + 3Nh5 Cl.
Смешаем в пробирке несколько миллилитров хлорида железа (III) и цианида аммония.
В результате содержимое пробирки окрашивается в тёмно-красный цвет. Полученную смесь разделили на 4 пробирки.
В первую добавили 2-3 капли роданистого аммония. Во вторую прилили немного концентрированного раствора хлорида железа (III). В третью всыпали немного кристаллического хлорида аммония и энергично встряхнули. Изменения цвета отмечены в таблице 3.
Табл. 3.
| Номер пробирки | Добавленное вещество | Изменение цвета раствора | Сдвиг равновесия |
| 1 | NH 4 CNS | темнеет | → |
| 2 | FeCl 3 | не меняется | - |
| 3 | NH 4 Cl (тв.) | светлеет | ← |
В первой пробирке v пр > v обр, во второй — v пр = v обр, в третьей — v пр < v обр .
По реакции с добавлением Nh5 CNS роданид железа образуется, что приводит к увеличению его концентрации и потемнению раствора, по реакции с добавлением Nh5 Cl (тв.) роданид железа расходуется, что приводит к уменьшению его концентрации и осветлению раствора.
Nh5 CNS сдвигает равновесие в сторону прямой реакции, а Nh5 Cl (тв.) в сторону обратной.
Выражение для константы химического равновесия:

Вывод: добавление цианида аммония сдвигает химическое равновесие в сторону прямой реакции, твёрдого хлорида аммония – в сторону обратной реакции, хлорида железа (III) не влияет на химическое равновесие.
Опыт 7. Влияние температуры на химическое равновесие
В пробирку налили 2 мл раствора аммиака и добавили 2 капли фенолфталеина. Пробирку нагрели. В результате изменения температуры раствор посветлел. Из-за повышения температуры часть раствора аммиака испарилась, следовательно, его концентрация уменьшилась. Нагревание сдвинуло равновесие в сторону обратной реакции.
Вывод: Нагревание сдвинуло химическое равновесие в сторону обратной реакции.
Основные выводы:
В результате проделанных опытов мы убедились в том, что на скорость химических реакций оказывают влияние множество факторов, таких как температура, давление, концентрация реагирующих веществ, наличие катализатора, площадь поверхности и т.д. Кроме того, вышеперечисленные факторы способны влиять на смещение химического равновесия в сторону прямой или обратной реакции.
Контрольные вопросы
1. Составить уравнения скоростей реакций:
2N2 O3 + O2 ↔ 2N2 O4 ;
v пр =k1 a2 b; v обр =k2 c2 .
2Me + O2 → 2MeO;
v =k·a2 b.
2. Как изменится скорость реакции CO +h3 O → CO2 + h3, протекающей в закрытом сосуде при T=313˚С, если давление увеличить в четыре раза.
Решение:
увеличение давления в 4 раза равносильно увеличению молярных концентраций веществ в 4 раза.
v 1 = k ·( 4a )( 4b )= 16v .
Скорость реакции возрастёт в 16 раз.
3. Реакция окисления NOвыражается следующим уравнением:
2NO + O2 → 2NO2 .
Начальная концентрация NO равна 0,3 моль/л, а кислорода – 0,15 моль/л. Как изменится скорость реакции, если увеличить концентрацию NO до 1,2 моль/л, а кислорода – до 0,6 моль/л.
Решение:
Скорость реакции до изменения параметров:
v 1 = k (0,3)2 (0,15) = 0,0135.
Скорость реакции после изменения параметров:
v 2 = k (1,2)2 (0,6) = 0,864.
v 2 / v 1 = 64.
Скорость реакции возрастёт в 64 раза.
4. При нагревании водорода и йода в закрытом сосуде до 444˚С обратимо протекает реакция по уравнению h3 + I2 ↔ 2 HI.
Равновесная смесь при этой температуре содержит 5,64 моль HI, 0,12 моль I2 и 5,28 моль h3. Вычислим константу равновесия реакции и исходные концентрации водорода и йода.
Решение:
Так как реакция проходит в закрытом сосуде, можно записать:
с1 : c 2 : c 3 = N 1 : N 2 : N 3 .

По закону сохранения массы:
0,12 моль·2 г/моль + 5,28 моль·254 г/моль +5,64 моль·2·128 г/моль = X·2 г/моль +Y·254 г/моль.
0,12/X=5,28/Y,
где X – количество водорода, Y – количество йода.
Решив систему уравнений, получим:
X=0,25 моль, Y=10,96 моль.
Концентрации соответственно равны 0,25 моль/л и 10,96 моль/л.
5. Константа равновесия реакции
Ch4 COOH + C2 H5 OH ↔ Ch4 COOC2 H5 + h3 O
при некоторой температуре равна 4. Определить состав смеси при равновесии, если в реакцию введены 1 моль кислоты и 2 моль спирта.
На основании закона сохранения массы:
60 г/моль·1 моль+ 34 г/моль·2 моль = 60 г/моль·A моль + 34 г/моль·2·B моль + 88 г/моль·C моль+18 г/моль·D моль, где А, В, С, D – количества веществ после реакции.
На основании данных задачи:
4 = AB/CD;B =2A;
88/C = 18/D.
Решив систему уравнений, получим:
A = 0,6 моль; B = 1,2 моль; C = 1,34 моль; D = 0,274 моль.
Ответ: 0,6 моль Ch4 COOH, 1,2 моль C2 H5 OH, 1,34 моль Ch4 COOC2 H5, 0,274 моль h3 O.
6. Константа равновесия Kp реакции синтеза аммиака
N2 + 3h3 ↔ 2Nh4
при 350˚С равна 2,32·1013. Вычислить Kc при этой температуре.
Решение:
T = 623 K;
Kc = Kp /(RT)6 = 2,32·1013 /(8,314·623)6 = 1,2·10-9 .
Ответ: Kc = 1,2·10-9 .
7. При 550˚С и 1,01325·105 Па степень диссоциации фосгена на оксид углерода и хлор равна 77%. Реакция протекает по уравнению
COCl2 ↔ CO +Cl2 .
Определить Kp и Kc, если исходная концентрация фосгена 1 кмоль/м3 .
Решение:
T = 823 K.
После реакции концентрация фосгена стала равной 0,23 кмоль/м3, а концентрации углекислого газа и хлора стали равными 0,77 кмоль/м3 .
Следовательно, Kp = (0,23 + 0,77 + 0,77)· 1,01325·105 = 1,79·105 ;
Kc = Kp /(8,314·823)3 = 5,59·10-7 .
Ответ: Kc = 5,59·10-7; Kp = 1,79·105 .
www.ronl.ru
Скорость химической реакции зависит не только от концентрации, но и от температуры. Как показывает опыт, скорость большинства реакций увеличивается при повышении температуры в 2 ÷ 4 раза на каждые 10 градусов.
Приближенной характеристикой зависимости скорости реакции от температуры является коэффициент реакции γ – отношение константы скорости при температуре Т+10 к константе скорости при температуре Т :
 . (5.1)
. (5.1)
Это соотношение, называемое правилом Вант–Гоффа, может быть применено лишь для приблизительных, ориентировочных расчетов. Это правило не выполняется при высоких температурах, когда температурный коэффициент скорости (γ) перестает быть постоянным, приближаясь к единице. Однако для узкого интервала температур правило Вант–Гоффа часто бывает полезным.
Расчеты показывают, что увеличение скорости реакции при повышении температуры не может быть объяснимо лишь возрастанием числа столкновений. Это происходит потому, что не каждое столкновение частиц приводит к химической реакции. Лишь тогда, когда сталкивающиеся молекулы обладают определенной энергией, столкновение может быть эффективным и привести к химической реакции. Эти предположения были впервые высказаны А. Аррениусом. Согласно ученому, к реакции приводит столкновение лишь тех молекул, энергия которых больше определенной величины Еа.
Таким образом, химическое взаимодействие осуществляется только между соударяющимися молекулами, которые достигли определенного энергетического уровня, характерного для данной реакции, ее энергетического барьера. Такие молекулы часто называют активными.
На основе взглядов Аррениуса была разработана теория активных соударений на базе молекулярно-кинетических представлений. Предложено считать активными столкновения, в которых суммарная энергия сталкивающихся возбужденных молекул А* и В* равна или больше Еа. При столкновении молекулы сближаются до расстояния, которое называется эффективным диаметром столкновений dэфф и при котором электроны и атомы одной молекулы попадают в поле действия электрических сил, возбуждаемых частицами другой молекулы. Только при таких условиях может произойти разрыв связей в исходных веществах и образование новых молекул. В первом приближении
 . (5.2)
. (5.2)
Все молекулы, запас энергии которых не ниже энергетического барьера реакции, находятся в особом состоянии, которое принято называть переходным, или состоянием активированного комплекса. Можно предположить, что система в состоянии активированного комплекса характеризуется тем, что в ней уже нет исходных веществ, но нет еще и продуктов реакций; исходные вещества переходят в продукты реакции.
Покажем схематически переход от исходных веществ А и В к продуктам реакции С и Д через состояние активированного комплекса А….В (рис. 5.1)

Рисунок 5.1 – Изменение энергии в ходе экзотермической реакции
Примем средний уровень энергии молекул исходных веществ в системе равным Е1, а среднюю энергию переходного состояния – Е|, то разность Е| — Е1 будет выражать энергию активации данной реакции – Еа. Энергия системы в переходном состоянии максимальна, а это значит, что активный комплекс крайне неустойчив. По ходу реакции он превращается в продукты взаимодействия С и D. В рассматриваемом примере средний уровень энергии молекул продуктов реакции Е2 ниже среднего уровня энергии молекул исходных веществ Е1. Это означает, что процесс протекает с выделением энергии (реакция экзотермическая).
Средний уровень энергии молекул продуктов реакции Е2 может быть выше среднего уровня энергии молекул исходных веществ Е1 (рис. 5.2).

Рисунок 5.2 – Изменение энергии в ходе эндотермической реакции
Процесс протекает с поглощением энергии (реакция эндотермическая). РазностьЕ2 – Е1 равна тепловому эффекту процесса ΔН .
Зависимость константы скорости реакции от температуры Аррениусом была представлена в виде:
 , (5.3)
, (5.3)
где А – предэкспотенциальный множитель, не зависящий от температур;
Т – температура, К;
R – газовая постоянная;
Eа – энергия активации (кал/моль, Дж/моль).
В химической кинетике часто пользуются уравнением Аррениуса в логарифмической форме:
 (5.4)
(5.4)
или
 . (5.5)
. (5.5)
Из уравнений (5.4) (5.5) следует, что зависимость  линейна (рис. 5.3)
линейна (рис. 5.3)

от температуры
Линейная зависимость ( lnk- 1/T) позволяет определить энергию активации Еа по тангенсу наклона прямой  и предэкспотенциальный множитель А по отрезку, отсекаемому прямой на оси ординат, когда 1/Т =0.
и предэкспотенциальный множитель А по отрезку, отсекаемому прямой на оси ординат, когда 1/Т =0.
Дифференцируя уравнение 5.4 по температуре, получим:
 . (5.6)
. (5.6)
Величина  , логарифм константы скорости, а следовательно, и сама константа с температурой возрастает.
, логарифм константы скорости, а следовательно, и сама константа с температурой возрастает.
Энергию активации можно также найти из уравнения (5.6), проинтегрировав его от Т1 до Т2 :

или
 . (5.7)
. (5.7)
Из уравнения 5.7 можно определить величину энергии активации, если известны значения констант скорости при двух температурах: Т1 и Т2 .
| Содержание | Начало |
5.2 Связь энергии активации с тепловым эффектом
Пусть протекает реакция:

Тогда для прямой реакции
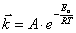 и
и  ;
;
для обратной реакции
 и
и  ,
,
вычитая из первого уравнения второе, получим:
 ,
,
но  ,
,
где К – константа равновесия,
тогда
 .
.
 ,
,
где ΔН – тепловой эффект реакции.
Сравнив два последние уравнения, получим:
 . (5.8)
. (5.8)
Из уравнения 5.8 следует, что разность между энергиями активации прямой и обратной реакции равна тепловому эффекту.
Контрольные вопросы:1. Правило Вант–Гоффа. Что такое температурный коэффициент реакции?
2. Изменение энергии активации в ходе экзотермической реакции.
3. Изменение энергии активации в ходе эндотермической реакции.
4. Дать определение энергии активации. Что такое активированный комплекс?
5. Уравнение Аррениуса. Как зависит константа химической реакции от температуры?
6. Вывести уравнения связи энергии активации с тепловым эффектом.
www.ronl.ru
Скорость химической реакции зависит не только от концентрации, но и от температуры. Как показывает опыт, скорость большинства реакций увеличивается при повышении температуры в 2 ÷ 4 раза на каждые 10 градусов.
Приближенной характеристикой зависимости скорости реакции от температуры является коэффициент реакции γ – отношение константы скорости при температуре Т+10 к константе скорости при температуре Т :
 . (5.1)
. (5.1)
Это соотношение, называемое правилом Вант–Гоффа, может быть применено лишь для приблизительных, ориентировочных расчетов. Это правило не выполняется при высоких температурах, когда температурный коэффициент скорости (γ) перестает быть постоянным, приближаясь к единице. Однако для узкого интервала температур правило Вант–Гоффа часто бывает полезным.
Расчеты показывают, что увеличение скорости реакции при повышении температуры не может быть объяснимо лишь возрастанием числа столкновений. Это происходит потому, что не каждое столкновение частиц приводит к химической реакции. Лишь тогда, когда сталкивающиеся молекулы обладают определенной энергией, столкновение может быть эффективным и привести к химической реакции. Эти предположения были впервые высказаны А. Аррениусом. Согласно ученому, к реакции приводит столкновение лишь тех молекул, энергия которых больше определенной величины Еа.
Таким образом, химическое взаимодействие осуществляется только между соударяющимися молекулами, которые достигли определенного энергетического уровня, характерного для данной реакции, ее энергетического барьера. Такие молекулы часто называют активными.
На основе взглядов Аррениуса была разработана теория активных соударений на базе молекулярно-кинетических представлений. Предложено считать активными столкновения, в которых суммарная энергия сталкивающихся возбужденных молекул А* и В* равна или больше Еа. При столкновении молекулы сближаются до расстояния, которое называется эффективным диаметром столкновений dэфф и при котором электроны и атомы одной молекулы попадают в поле действия электрических сил, возбуждаемых частицами другой молекулы. Только при таких условиях может произойти разрыв связей в исходных веществах и образование новых молекул. В первом приближении
 . (5.2)
. (5.2)
Все молекулы, запас энергии которых не ниже энергетического барьера реакции, находятся в особом состоянии, которое принято называть переходным, или состоянием активированного комплекса. Можно предположить, что система в состоянии активированного комплекса характеризуется тем, что в ней уже нет исходных веществ, но нет еще и продуктов реакций; исходные вещества переходят в продукты реакции.
Покажем схематически переход от исходных веществ А и В к продуктам реакции С и Д через состояние активированного комплекса А….В (рис. 5.1)

Рисунок 5.1 – Изменение энергии в ходе экзотермической реакции
Примем средний уровень энергии молекул исходных веществ в системе равным Е1, а среднюю энергию переходного состояния – Е|, то разность Е| — Е1 будет выражать энергию активации данной реакции – Еа. Энергия системы в переходном состоянии максимальна, а это значит, что активный комплекс крайне неустойчив. По ходу реакции он превращается в продукты взаимодействия С и D. В рассматриваемом примере средний уровень энергии молекул продуктов реакции Е2 ниже среднего уровня энергии молекул исходных веществ Е1. Это означает, что процесс протекает с выделением энергии (реакция экзотермическая).
Средний уровень энергии молекул продуктов реакции Е2 может быть выше среднего уровня энергии молекул исходных веществ Е1 (рис. 5.2).

Рисунок 5.2 – Изменение энергии в ходе эндотермической реакции
Процесс протекает с поглощением энергии (реакция эндотермическая). РазностьЕ2 – Е1 равна тепловому эффекту процесса ΔН .
Зависимость константы скорости реакции от температуры Аррениусом была представлена в виде:
 , (5.3)
, (5.3)
где А – предэкспотенциальный множитель, не зависящий от температур;
Т – температура, К;
R – газовая постоянная;
Eа – энергия активации (кал/моль, Дж/моль).
В химической кинетике часто пользуются уравнением Аррениуса в логарифмической форме:
 (5.4)
(5.4)
или
 . (5.5)
. (5.5)
Из уравнений (5.4) (5.5) следует, что зависимость  линейна (рис. 5.3)
линейна (рис. 5.3)

от температуры
Линейная зависимость ( lnk- 1/T) позволяет определить энергию активации Еа по тангенсу наклона прямой  и предэкспотенциальный множитель А по отрезку, отсекаемому прямой на оси ординат, когда 1/Т =0.
и предэкспотенциальный множитель А по отрезку, отсекаемому прямой на оси ординат, когда 1/Т =0.
Дифференцируя уравнение 5.4 по температуре, получим:
 . (5.6)
. (5.6)
Величина  , логарифм константы скорости, а следовательно, и сама константа с температурой возрастает.
, логарифм константы скорости, а следовательно, и сама константа с температурой возрастает.
Энергию активации можно также найти из уравнения (5.6), проинтегрировав его от Т1 до Т2 :

или
 . (5.7)
. (5.7)
Из уравнения 5.7 можно определить величину энергии активации, если известны значения констант скорости при двух температурах: Т1 и Т2 .
| Содержание | Начало |
5.2 Связь энергии активации с тепловым эффектом
Пусть протекает реакция:

Тогда для прямой реакции
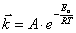 и
и  ;
;
для обратной реакции
 и
и  ,
,
вычитая из первого уравнения второе, получим:
 ,
,
но  ,
,
где К – константа равновесия,
тогда
 .
.
 ,
,
где ΔН – тепловой эффект реакции.
Сравнив два последние уравнения, получим:
 . (5.8)
. (5.8)
Из уравнения 5.8 следует, что разность между энергиями активации прямой и обратной реакции равна тепловому эффекту.
Контрольные вопросы:1. Правило Вант–Гоффа. Что такое температурный коэффициент реакции?
2. Изменение энергии активации в ходе экзотермической реакции.
3. Изменение энергии активации в ходе эндотермической реакции.
4. Дать определение энергии активации. Что такое активированный комплекс?
5. Уравнение Аррениуса. Как зависит константа химической реакции от температуры?
6. Вывести уравнения связи энергии активации с тепловым эффектом.
www.ronl.ru