 Рисунок 8.1 — Арбалет Леонардо да Винчи
Рисунок 8.1 — Арбалет Леонардо да ВинчиНаука, изучающая законы красоты и художественного творчества, применительно к предметам технической формы, называется технической эстетикой.
Одним из элементов технической эстетики можно считать техническое рисование.
Техническим рисунком люди пользовались давно и в самых разных его видах. Чаще всего технический рисунок используется при создании новых объектов.
Рождающаяся в сознании человека новая идея, возникший неожиданно новый образ объекта требуют немедленного закрепления, и наиболее простой, удобной и быстрой формой фиксации творческой мысли оказывается рисунок.
Инженеры — конструкторы чаще всего использовали реалистический рисунок (перспективный), примером могут служить многочисленные рисунки Леонардо да Винчи (Рисунок 8.1 и 8.2).
 Рисунок 8.1 — Арбалет Леонардо да Винчи
Рисунок 8.1 — Арбалет Леонардо да Винчи
 Рисунок 8.2 — Самоходная тележка Леонардо да Винч
Рисунок 8.2 — Самоходная тележка Леонардо да Винч
Активная творческая деятельность изобретателя, инженера всегда начинается с технического рисунка. Технический рисунок позволяет сразу увидеть преимущество новых конструкционных усовершенствований и дает основание приступить к переоборудованию или замене отдельных деталей машины. Решение задач по проектированию значительно облегчается при предварительном выполнении эскизов, технических рисунков.
Несколько таких предварительно выполненных изображений позволяют выбрать лучший вариант будущей формы, или конструкции предмета. Но главное достоинство технического рисунка состоит в том, что он заставляет автора идти дальше, вносить в свой рисунок добавления и исправления, активизирует и совершенствует его творческую мысль. А это в свою очередь принуждает конструктора переходить к новым рисункам до тех пор, пока автор не приблизится к идеалу.
Дизайнеры используют рисунки как перспективные, так и построенные в аксонометрических проекциях. Чаще деятельность дизайнера ограничивается изменением лишь внешнего вида объекта — нахождением более удобных для работы и эстетически красивых форм (Рисунок 8.2).

Рисунок 8.2 — Дизайн объектов технической формы
Значение технического рисунка в работе архитектора трудно переоценить. Его рисунки разнообразны и по характеру, и по манере исполнения. Технический рисунок у архитектора уже с первых шагов проектирования играет основополагающую роль. Какой бы объект мы не взяли, касается ли это планировки города, интерьера или комплекса зданий, техническому рисунку принадлежит главенствующая роль, а иногда и решающая (Рисунок 8.3). Рисунок 8.3 — Рисунок дизайнера интерьера
Рисунок 8.3 — Рисунок дизайнера интерьера
Модельеры мужской и женской одежды используют условный рисунок (Рисунок 8.4).
 Рисунок 8.4 — Рисунок модельера
Рисунок 8.4 — Рисунок модельера
Наравне со словом, рисунок служит средством выражения и передачи мысли. Иногда бывает трудно, а подчас и невозможно, выразить словами то, что легко представить наброском, схемой, чертежом или эскизом.
Даже в обыденной жизни мы часто прибегаем к помощи технического рисунка, объясняя друзьям свой адрес и расположение домов. Следовательно, раскрывая понятие термина «технический рисунок», нельзя узко и односторонне трактовать его содержание и назначение.
Итак, технический рисунок — это наглядное графическое изображение объекта, выполненное от руки в глазомерном масштабе, в котором ясно раскрыта техническая идея объекта, правильно переданы его конструктивная форма и верно найдены пропорциональные соотношения.
Курс «Техническое рисование» дает основные сведения, приемы, краткие методические указания и первоначальные навыки по выполнению технических рисунков.
Курс способствует развитию:
Работа построена по студийному принципу.
Рисунки оформляются рамкой и упрощенной надписью (Рисунок 8.5). Чертежи оформляют основной надписью по ГОСТ 2.104-68.

Рисунок 8.5 — Пример упрощенной основной надписи
Любой предмет можно представить как совокупность простейших геометрических объектов. В качестве геометрического объекта могут быть: точка, линия, поверхность, тело.
Изображение предмета на плоскость называется проекцией его на эту плоскость (плоскость проекций), а процесс получения проекций — проецированием (Рисунок 8.6).

Рисунок 8.6 — Методы проецирования
Перспективный рисунок — наглядное изображение предмета, выполненное от руки, на основе центральных (перспективных) проекций.
Параллельная проекция на одну аксонометрическую плоскость (плоскость проекций) координатных осей и объекта, фиксированного относительно этих осей называется аксонометрической проекцией объекта.
Объекты проецируются (за некоторым исключением) с искажением натуральной величины.
Отношение размеров изображения к действительным размерам, измеренным вдоль координатной оси, называется коэффициентом искажения по оси ( Кх, Ку, Kz ).
Для удобства пользованием коэффициентами применяют приведенные коэффициенты искажения (значения их приведены на Рисунке 8.7).

Рисунок 8.7 — Аксонометрические проекции
В аксонометрических проекциях отсутствуют перспективные искажения, вследствие чего изображение получается условным и простым.
Форму предмета можно строить точно по размерам (если нужно) и изображать ее «не как вижу, а как надо», с пониманием объективной сущности предмета. В этом заключается особенность технического рисунка и простота его выполнения, позволяющие сравнительно быстро приобрести необходимые навыки.
Для рисования используются мягкие карандаши, твердостью М, 2М, (НВ, В, 2В). Затачивают карандаш так, как показано на рисунке.

Умение выполнять технические рисунки не требует природных способностей, а приобретается упорными систематическими упражнениями.
Техника — совокупность приемов мастерства применяемых в каком-нибудь деле: музыкальная техника, техника шахматной игры и т.д. Следовательно, выполняющий рисунок должен обладать определенной техникой исполнения.
В проведении прямой линии должна участвовать не только кисть руки, а и вся рука: это дает возможность при прямолинейном движении кисти руки, выдержать прямолинейность отрезка.

Рисунок 8.8 — Вариант работы с карандашом
Карандаш при рисовании нужно держать свободно большим и указательным пальцами и поддерживать средним; мизинец может касаться бумаги. Остро заточенный конец карандаша должен быть расположен подальше от пальцев, что облегчает проведение плавных длинных линий (Рисунок 8.8). При уточнении и прорисовке отдельных деталей на рисунке предмета в работе уже принимают участие пальцы, что сказывается на движениях карандаша. Движения получаются ограниченными, но более точными; карандаш берут ближе к острию, что позволяет проводить более четкие линии.
Начинают рисовать тонкими, едва заметными линиями. Перед проведением прямой линии необходимо предварительно определить начальную и конечную точки ее, через которые легким движением
Почти невозможно одним движением руки проводить совершенно прямую и непрерывную линию. Следует рисовать ее по частям, длинными штрихами, не упуская из вида общего ее направления (Рисунок 8.9).

Рисунок 8.9 — Рисование длинных линий
Не следует ошибочно нанесенные первоначальные штрихи стирать резинкой, а нужно исправлять неудачно проведенную линию новыми штрихами только в местах, где она неправильна.
Горизонтальные и вертикальные направления необходимо чаще проверять относительно соответственных обрезов листа бумаги.
Все вертикальные линии удобнее проводить сверху вниз, а горизонтальные — слева направо (Рисунок 8.10).

Рисунок 8.10 — Рисование линий

Рисунок 8.11 — Деление отрезка на 2 части


Рисунок 8.12 — Деление отрезка на разное количество частей. Проведение линии под заданным углом
При недостаточном опыте рисования или эскизирования возникают затруднения при откладывании одинаковых отрезков. В таких случаях помогает использование так называемой «бумажной линейки». На небольшом кусочке бумажки намечают нужную длину отрезка и откладывают его необходимое число раз в каких-либо направлениях. Часто прибегать к этому методу не рекомендуется, так как это задерживает развитие глазомера.
Построение аксонометрических изображений плоских фигур является основой построения геометрических тел и технических предметов.
Многоугольник состоит из вершин (точек) и сторон (отрезков прямых линий), следовательно, построение его аксонометрии начинается с построения вершин с последующим соединением их прямыми линиями — сторонами многоугольника.
Построим рисунок квадрата АВСD в прямоугольной изометрии при условии, что сторона АD параллельна оси X, а сторона АВ параллельна оси Y. Квадрат изобразится в виде ромба АВСD.

Рисунок 8.13 — Построение аксонометрии квадрата

Рисунок 8.14 — Построение аксонометрии правильного шестиугольника
Окружность вначале следует рисовать вместе с квадратом, в который она вписывается. Это позволяет быстрее получить навык более правильного изображения окружностей в аксонометрических проекциях.

Рисунок 8.15 — Построение аксонометрии окружности
В реалистическом рисунке объемные предметы окружающей нас действительности изображаются такими, какими они существуют в природе и как их воспринимает глаз с данной точки зрения. В процессе рисования с натуры очень важно умение подмечать главное и характерное в окружающих нас вещах и явлениях.
Чтобы правильно передать форму предмета на плоскости листа, надо научиться определять его пропорции, необходимо уяснить его конструкцию, владеть техническими приемами рисования.
Пропорции — это соотношение величин частей предмета друг к другу и его частей к целому.
Чем точнее определены пропорции предметов на рисунке, тем больше сходства имеет изображение с натурой.
При определении пропорций изображаемого предмета пользуются взаимным сравнением размеров, то есть определяют визуально (на глаз), в каком отношении находится малый размер по отношению к большому (или наоборот). Сравнивать и проверять пропорции нужно не только в натуре, но и на рисунке.
Следует отличать истинные соотношения величин частей предмета от пропорций его изображения с определенной точки зрения.
Пропорции предмета при наблюдении с различных точек зрения будут восприниматься различно, но сам предмет в реалистическом изображении должен казаться нам тем же. Например, высота вазы будет казаться сильно сокращенной по отношению к ее ширине, если смотреть на нее со значительно более высокой точки зрения (Рисунок 8.16). Рисунок 8.16 — Пропорции. Рисунок вазы
Рисунок 8.16 — Пропорции. Рисунок вазы
Отмечая пропорции предмета на рисунке, надо учитывать его конструктивное строение. Так, например, ваза (на Рисунке 8.16) состоит из конусообразного горлышка, средней части яйцевидной формы и цилиндрического основания. Она представляет собой тело вращения, и поэтому в местах перехода форм четко видны окружности (с центрами на оси), которые нужно построить на рисунке.
Точность определения пропорций предмета зависит от глазомера рисующего. Глазомер развивается постепенно, благодаря систематическому рисованию с натуры.
Рассмотрим основные пропорции вазы, показанной на рисунке. Высота ее в 2 раза больше ширины. Если сравнить соотношение отдельных частей вазы по высоте, то высота горлышка составит 1/3 часть высоты вазы без подставки. Высота подставки нижней части вазы укладывается в высоте горлышка около 4 раз. Ширина подставки равна 1/2 ширины вазы в самом широком ее месте. Ширина узкой части горлышка несколько меньше 1/2 ширины верхнего края вазы и т. д.
При рисовании с натуры часто приходится решать более сложную задачу — находить пропорции предметов. Однако и в этом случае используется общий прием определения пропорций путем глазомерного сравнения величин. За единицу измерения можно взять один из предметов, входящих в группу.
Представление о масштабе следует из непосредственного глазомерного сравнения величин, что является условием правильного выполнения рисунка. Можно увеличивать и уменьшать предметы на рисунке, эскизе, чертеже — характер реальной действительности не меняется, если это увеличение тети уменьшение для всех элементов предмета делается пропорционально. Отношение размеров на рисунке должно быть равно отношению размеров в натуре.
Композиция — (compositio — (лат.)) в переводе означает составление, расположение, представляет собой средство придать единство различным частям художественного произведения.
Отдельные элементы композиции должны быть связаны между собой, а внимание зрителя сосредоточивается на главном предмете (композиционном центре), которому должно подчиняться все второстепенное (детали).
Основное требование, предъявляемое к композиции учебного рисунка, — уравновешенность расположения изображаемых предметов на листе.
Приступая к построению рисунка, нужно, прежде всего, изучить форму предмета, то есть провести внимательный анализ геометрических форм, составных элементов изображаемого предмета.
Общий путь анализа объектов сложной формы — расчленение их на более простые геометрические тела, или замена, на первых порах, построения элементов сложной формы элементами простой формы. Величину рисунка следует выбирать такой, чтобы мелкие элементы предмета были бы четко изображены. Для этого размер изображения увеличивают. Если нет необходимости детализировать мелкие элементы, или предмет имеет простую форму, то не нужно делать изображение большим. В грубом приближении рисунок должен занимать (50 — 75)% площади формата. Поэтому формат листа подбирают под планируемую величину изображения.
Деталь надо развернуть так, чтобы были видны три ее стороны (три измерения: длина, высота, ширина). Ориентация детали для различных аксонометрических проекций может меняться, принимая наиболее наглядное положение. Освещение детали, полагают, идет слева.
При компоновке рисунка, то есть расположении изображения на листе, нужно помнить, что наблюдатель, зритель, рассматривая изображение, подсознательно включает в поле изображения и некоторую часть пространства вокруг изображаемых предметов. Отсюда, если на деталь мы смотрели как бы сверху, то нужно в верхней части листа оставлять несколько больше места («больше неба»). При направлении взгляда на деталь как бы снизу изображение смещают вверх листа, оставляя больше «земли». Если главная часть детали (по содержанию) находится слева, то изображение на листе нужно сдвинуть чуть вправо, чтобы рамка не отвлекала внимание и не мешала восприятию изображения.
Композиция является одним из главных средств создания эстетических качеств изображения, она прямо связана с наглядностью и читаемостью рисунка. Поэтому, кроме названных особенностей для рисунка, очень важно выбрать такую аксонометрическую проекцию, которая наиболее полно раскрывает форму предмета.
Правильный выбор аксонометрической проекции обеспечивает большую наглядность изображения и простоту построения рисунка. Под наглядностью следует понимать наиболее отчетливую видимость на рисунке основных частей детали и наименьшее искажение ее форм.
Выбор аксонометрической проекции зависит также от формы детали. Главной задачей при этом является обеспечение видимости всех основных элементов изображаемой детали. Кроме того, отдельные части детали не должны закрывать друг друга.
Чтобы лучше представить, насколько важна наглядность изображения, сравним несколько рисунков таких предметов, как куб, цилиндр, деталь «фланец», выполненных в прямоугольных и косоугольных проекциях.
На Рисунке 8.17 эти предметы показаны в прямоугольной изометрической проекции. Грани куба получились мало выразительными, поскольку по всем трем направлениям координатных осей X, Y, Z они имеют одинаковые искажения.
 |  |
| Рисунок 8.17 — Прямоугольная изометрия | Рисунок 8.18 — Прямоугольная диметрия |
Прямоугольную изометрию применяют в тех случаях, когда три стороны предмета имеют одинаковое количество элементов, необходимых для характеристики изображаемого предмета, но куб получается мало выразительным.
Наибольшей наглядностью отличается изображение в прямоугольной диметрии как изображение, сходное с перспективным.
В прямоугольной диметрической проекции (Рисунок 8.18) благодаря большему сокращению размеров по одной из координатных осей рисунки куба и цилиндра получились более наглядными. Рисунок же детали «фланец» в прямоугольной диметрии менее выразителен, чем в прямоугольной изометрии.
На Рисунке 8.19 куб, цилиндр и фланец выполнены в косоугольной фронтальной изометрической проекции. Куб и цилиндр в этой проекции получились маловыразительными и с большим искажением формы. При изображении фланца потребовалось рисовать несколько окружностей, а нарисовать окружность сложнее, чем эллипс. Поэтому такой рисунок уступает в простоте построения. К тому же он нисколько не наглядней двух предшествующих рисунков.
 |  |
| Рисунок 8.19 — Косоугольная фронтальная изометрия | Рисунок 8.20 — Косоугольная горизонтальная изометрия |
Косоугольную фронтальную аксонометрию используют в случаях, когда обтекаемые формы предметов в виде кривых поверхностей можно расположить параллельно фронтальной плоскости проекций, тогда они изображаются в неискаженном виде и их проще рисовать.
В косоугольной горизонтальной изометрической проекции (Рисунок 8.20) все рисунки обладают меньшей наглядностью и строить их несколько сложнее.
Рисунки, выполненные в косоугольной фронтальной диметрической проекции, выглядят по-разному (Рисунок 8.21).
 |
| Рисунок 8.21 — Косоугольная фронтальная диметрия |
Цилиндр в косоугольной фронтальной диметрии получается мало выразительным и с большим искажением формы. Рисунки куба и фланца, наоборот, обладают хорошей наглядностью.
Таким образом, рисунок куба лучше всего выполнять в косоугольной фронтальной диметрии, рисунок цилиндра — в прямоугольной диметрии, а рисунок фланца — в прямоугольной изометрии.
В некоторых случаях сразу трудно определить, какой вид аксонометрии дает более наглядное изображение изделия (особенно, если у него имеются наклонные элементы — ребра, спицы, стенки…).
В таких случаях рекомендуется выполнять технические рисунки в различных аксонометрических проекциях и из них выбрать наиболее наглядный.
Плоскостное рисование (орнамент, фронтальные изображения фасадов зданий, планы сооружений) развивалось значительно быстрее рельефного изображения, хотя возникли они одновременно.
Зрительный подход к натуре может быть двоякий:
При плоскостном восприятии натура целиком, во всей своей пространственной сложности, изображается спроектированной на плоскости в ортогональной проекции.
Целью плоскостного рисования является развитие чувства пропорции и глазомера, восприятия и передачи на рисунке отношения размеров изображаемой фигуры; научиться «видеть» натуру. (Смотреть не значит видеть).
Чтобы «увидеть» надо внимательно рассмотреть, то есть изучить форму натуры. Разбивка контура предмета на более простые геометрические формы позволит легко и правильно его изобразить.
Даже дети дошкольного возраста с успехом нарисуют сидящего котенка после указания, что форма его составлена из двух эллипсов (овалов) разной величины и двух треугольников. Рисунок 8.22 — Плоскостной рисунок
Рисунок 8.22 — Плоскостной рисунок
Умению «видеть» при рисовании помогает знание законов математики, физики и других наук. Физиологи говорят: человек глядит не глазами, а мозгом. Убедимся в этом на примере рисунка чайника.
На Рисунке 8.22 чайник построен не правильно, так как учащийся недостаточно вдумчиво рисовал:
Итак, приступая к изучению изображаемого предмета, необходимо установить:
Переход от рисования плоскостных форм к рисованию объемных тел, в аксонометрической проекции осуществляется с помощью введения высотных размеров на основе построений аксонометрии плана (вида сверху) (Рисунок 8.23).

Рисунок 8.23 — Плоскостной рисунок и аксонометрия
Такой прием дает возможность непосредственно переходить от прямоугольного чертежа к наглядному изображению предмета.
а) Рисование детали с натуры
Прежде чем приступить к рисованию детали с натуры, рисующий должен проанализировать деталь, а именно:
б) Рисование детали по чертежу
Выполнение рисунка по чертежу требует от рисующего умения читать чертеж, то есть представлять форму детали в целом и отдельных ее частей. В процессе чтения необходимо тщательно изучить чертеж, сопоставить на глаз габаритные размеры предмета и соотношение его частей. Рисунок позволяет лучше понять конструктивную форму предмета.
При рисовании деталей по чертежу не следует делать никаких замеров при помощи циркуля или линейки. Все размеры надо брать в пропорциональном отношении на глаз. Рисунок можно выполнять либо увеличенным, либо уменьшенным в зависимости от его композиции. Так же как и при рисовании детали с натуры, вначале определяют на глаз отношения между крайними точками всей детали, а потом намечают размеры каждой отдельной ее части, сравнивая их величины. Таким образом, правила выполнения рисунка детали по чертежу точно такие же, как и при рисовании с натуры.
в) Рисование сборочной единицы с натуры
Сборочной единицей называется изделие, составные части которого подлежат соединению между собой на предприятии — изготовителе с помощью сборочных операций: свинчивания, пайки, опрессовки, развальцовки, склеивания и др.
Рисование сборочной единицы с натуры основано на тех же принципах, что и рисование с натуры отдельных деталей, а именно:
г) Рисование сборочной единицы по чертежу
Сборочный чертеж — документ, содержащий изображение сборочной единицы и другие данные, необходимые для ее сборки и контроля. Прежде чем приступить к построению рисунка сборочной единицы, надо ознакомиться со спецификацией и сборочным чертежом.
Спецификация — текстовый документ, определяющий состав изделия, состоящего из двух и более частей. По спецификации изучают последовательность соединения всех деталей между собой.
Выполнение рисунка сборочной единицы по чертежу требует от рисующего обязательного умения читать чертеж. Вначале надо изучить чертеж: выявить на глаз соотношение габаритных размеров и сопоставить отдельные части между собой и со всей сборкой в целом. Изучив характерные особенности формы каждой детали в механизме и расположение деталей относительно друг друга, приступают к построению рисунка, используя те же правила, что и при рисовании сборочной единицы с натуры.
В аксонометрических изображениях изделий разрезы, как правило, получают путем сечения плоскостями, параллельными плоскостям проекций, и условного удаления отсекаемой части. Разрезы следует применять в тех случаях, когда они действительно необходимы и при этом не теряется наглядность конструктивных форм.
Для отличия рассеченной части изделия от частей, не попавших в разрез, применяют штриховку. Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям с учетом коэффициента искажения по осям (Рисунок 8.24).

Рисунок 8.24 — Правила штриховки в аксонометрии
Характерно для рисования группы тел (когда натура состоит из нескольких геометрических элементов) то, что тела рисуются все сразу, а не каждый в отдельности.
«Художник должен работать как деревообделочник. Сначала он грубо обтесывает топором, потом строгает рубанком, и все дальше и дальше инструменты его тоньше, заканчивает он шкуркой, полировкой и лаком,» – слова известного художника И.Е.Репина.
В целях упрощения построения рисунка следует располагать изображение так, чтобы его основные измерения были параллельны аксонометрическим осям. Это позволяет строить изображение, откладывая размеры (или координаты) по направлениям соответствующих осей с учетом коэффициентов искажения. Изображая симметричные предметы, целесообразно одну из аксонометрических осей совмещать с осью симметрии предмета.
В процессе выполнения рисунка переводят объемную форму предмета в плоскостное изображение. При этом необходимо определить, как преобразуется видимая форма предмета при плоскостном изображении, какие части и элементы предмета изменяются, какие будут видимыми и т.д. Правильность решения этой задачи зависит от умения наблюдать и знания законов построения аксонометрии.
Необходимо разобраться в общей форме предмета и правильно понять ее. Для облегчения этой задачи можно применить способ обобщения (упрощения формы). Суть его заключается в том, что любую сложную форму рассматривают как простейшую геометрическую. Такой способ построения помогает правильно понять и изобразить трехмерный объемный предмет, развивает пространственное представление и облегчает работу.
Работу над рисунком необходимо начинать с больших обобщений, с решения общей задачи, постепенно переходя к решению частных второстепенных задач, которые в конечном результате не должны нарушать впечатления целого. Главному в предмете сначала нужно уделять больше внимания, чем второстепенному, являющемуся дополнением к целому.
Сначала определяют пропорции всей натуры, то есть отношение высоты к ширине всей группы тел, а затем определяют отношение отдельных тел друг к другу.
На следующем этапе на листе отмечают местоположение каждого элемента и его габариты, учитывая выявленные пропорции, тем самым строим как бы «скелет» натуры (Рисунок 8.25).

Рисунок 8.25 — Последовательность построения
Начинают рисунок легкими, едва заметными линиями, а затем, когда правильно решена композиция рисунка и найдены пропорции элементов и натуры в целом, постепенно уточняют линии и усиливают тон.
Все второстепенные, не характерные для изображаемого предмета детали не рисуют, а, прежде всего, устанавливают схематично, набросочными линиями общую форму натуры.
После этого начинают построение каждого элемента. Сложные элементы (тела вращения, многогранники) на первоначальном этапе можно заменять параллелепипедами, не вырисовывая мелкие особенности этих элементов.
Когда общая форма натуры будет найдена, можно приступить к размещению мелких элементов, также начиная с более крупных из них. Набросок натуры уточняется проверкой пропорционального соотношения геометрических элементов и симметрии.
Если линия проведена не правильно, то ее не стирают, а проводят рядом другую, более точную. Первоначальные неточные линии, проведенные при построении, зрительно на рисунке почти не воспринимаются. В стадии Завершения они поглощаются общим тоном рисунка.
Далее сотрем ненужные линии построения и проверим точность выполнения рисунка, после чего обведем рисунок более четким контуром.
Каждый предмет находится в конкретной световой среде и освещен не только основным источником света, но и светом, отраженным от окружающих его других предметов, которые, будучи сами также освещены, являются источником отраженного света. Светлые и хорошо освещенные предметы отражают много света, а темные и плохо освещенные — мало. Форма предметов ограничивается различными поверхностями, поэтому лучи света, падая на эти поверхности, распределяются на них неравномерно. Одни части поверхности получают больше света, другие меньше, а третьи почти совсем не получают световых лучей.
Для придания рисунку большей наглядности и выразительности в техническом рисовании применяются условные средства передачи объема с помощью светотеней — оттенения.
Светотенью называется распределение света на поверхности предмета. Она играет главную роль при восприятии объема предмета.
Освещенность предмета зависит от угла наклона световых лучей. В техническом рисовании условно принято считать, что источник света находится сверху и сзади рисующего, таким образом, свет всегда будет слева, а тень — справа.
Отображение выпуклости предмета достигается путем градации света и тени: наиболее освещенные поверхности оттеняются светлее, чем поверхности, удаленные от света.
Светотень состоит из следующих элементов: собственной тени, рефлекса, полутона, света и блика.
Освещенную часть поверхности предмета называют светом.
Собственная тень образуется на части поверхности тела, на которую не падают световые лучи основного источника света. Освещенная поверхность, отражая свет, ослабляет силу собственной тени.
Такое высветление собственной тени отраженным светом называется рефлексом. Рефлекс всегда бывает темнее поверхностей света и полутени.
Слабо освещенные места на поверхности предмета называются полутонами. При помощи полутонов осуществляется постепенный переход от тени к свету.
Блик — самое светлое пятно на предмете.
Для правильной передачи на изображении объема и формы предмета необходимо ясно представлять его конструкцию и расположение отдельных частей в пространстве по отношению к источнику света.
Самую большую освещенность получает поверхность в том случае, если лучи падают на нее перпендикулярно. Чем меньше угол наклона лучей по отношению к поверхности, тем меньше падает на нее лучей и тем слабее она освещена. Освещенность зависит также от расстояния поверхности до источника света.
Светотень на изображении выявляют тоном. Тон (tonos — греческое слово, означающее качество, оттенок) наносится различными способами и должен соответствовать отношению света и тени, наблюдаемому в натуре. Выдержать рисунок в тоне — значит передать на нем световую гамму от темного тона через оттенки серого к светлому, сведенные в гармонию тональных отношений. Самым светлым тоном на рисунке будет цвет бумаги, а самым темным — линия, проведенная графитом карандаша с полным нажимом.
Аксонометрические чертежи и технические рисунки, на которых использована светотень, бывают штриховые и тоновые. На штриховых рисунках тон передают условно — точками или штрихами, карандашом или тушью с помощью ручки с пером или рейсфедера (Рисунок 8.26, 8.27). На тоновых рисунках тон наносят карандашом, тушью, акварельными красками и пр. (Рисунок 8.28).

Рисунок 8.26 — Штриховка

Рисунок 8.27 — Шрафировка
Тон должен плавно переходить от белого до темного без заметных границ элементов светотени.
Технику работы карандашом при нанесении светотени на тоновом рисунке называют тушевкой.


Рисунок 8.28 — Тушевка
Явление освещенности лучше всего наблюдается на примере куба и цилиндра, помещенных рядом. Анализируя эти тела с точки зрения распределения элементов светотени, можно установить, что характер освещенности грани куба и поверхности цилиндра различен. Переход от света к тени на гранях куба резкий и определенный, тогда как переход освещенной поверхности цилиндра к теневой мягкий и постепенный.
Свет на поверхности предмета распределяется неодинаково: одни части поверхности освещаются больше, другие меньше. Существует два правила, которыми следует руководствоваться при нанесении светотеней на изображение:
Рассмотрим эти правила на примере куба (Рисунок 8.29).

Рисунок 8.29 — Распределение светотени на параллелепипеде
Горизонтальная грань куба освещена равномерно, но зона 6 вследствие того, что удалена от наблюдателя изображена более затемненной. Самым светлым местом на передней грани кажется зона 1. Однако зоны 1, 2, 3 освещены одинаково, но из — за контраста с находящейся рядом собственной тенью на правой грани куба зона 1 кажется более светлой, а зоны 2, 3 — менее светлыми. В зоне 4 освещение усиливается. Это рефлекс, полученный кубом от плоскости, на которой он находится. Из всех зон зоны 7 и 8 самые темные. Не следует опасаться перетемнить их. Эта ошибка вполне допустима, так как усиливается рельефность куба. В зоне 9 и особенно в зоне 10 наблюдается ярко выраженный рефлекс от горизонтальной плоскости проекций.
Штриховку наносят в зависимости от положения изображаемой многогранной поверхности. Вертикальные поверхности штрихуют в вертикальном направлении, горизонтальные — в горизонтальном (параллельно аксонометрическим осям), наклонные — в направлении, параллельном углу наклона плоскости.
Нанесение светотени на поверхности полого цилиндра показано на Рисунке 8.30.
Наружную и внутреннюю поверхности цилиндра можно разделить условно на семь равных зон. Эти зоны соответствуют следующим элементам светотени: 1 — полутень (полутон), 2 — свет, 3 — блик, 4 — свет, 5 — полутень (полутон), 6 — тень, 7 — рефлекс.

Рисунок 8.30 — Распределение светотени на цилиндре
Штриховку основания цилиндра наносят по тем же правилам, что и штриховку граней куба. На внешней и внутренней поверхностях цилиндра линии штриховки наносят параллельно образующим. Внутреннюю поверхность цилиндра Заштриховывают по такому же принципу, что и внешнюю, но блик, полутона, собственную тень и рефлекс соответственно перемещают на противолежащие зоны поверхности.
Нанесение тона на изображение рекомендуется выполнять от более темного к более светлому. Переходы от тени к свету должны быть незаметными. Необходимо сверять тональную взаимосвязь, сравнивая полученный тон с крайними тонами (темным и светлым).
Перед нанесением тушевки построенное изображение обводят с небольшим нажимом карандаша. Затем все стирают и на листе остаются «вмятины» от грифеля (они нам дают информацию о контуре изображения), после этого начинают затушевывать поверхности.
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Стоимость и возможные формы обучения (очно или дистанционно) смотрите разделе Цены. Подробнее о репетиторстве.cadinstructor.org
Рисование каркасов геометрических тел — это передача пространственного положения, предмета на плоскости листа бумаги. Пространственное положение предмета в натуре представляет собой определенно выраженный объем, поскольку тело заполняет часть пространства.
Вы уже знаете, что нарисовать подобие предмета или группы предметов, имеющих определенно выраженные объемы, на плоском листе бумаги невозможно без специальных знаний. Специальные знания приходят к тому, кто всерьез занялся изучением основ рисования, кто учится уметь видеть окружающий мир со всеми его предметами и явлениями.
Человека, не ознакомленного с принципами рисования, оставит равнодушным любая натурная постановка. Если ему предложить нарисовать уходящую в глубину прямую дорогу, он непременно набросает на бумаге пару сближающихся кверху, однообразных на всем протяжении от нижнего до верхнего края листа линий и не подумает даже, правильно или нет это сделано.
Итак, новое упражнение будет таким, где вам нужно передать какую-то протяженность предмета в глубину, показать его по высоте и длине (или ширине). Выходит, что предмет следует нарисовать так, чтобы в изображении он производил впечатление трехмерного (объемного). Добиться в рисунке впечатления трехмерности изображенного предмета как раз и является основной задачей рисования. Как среди всех геометрических фигур самую понятную по очертаниям форму имеет квадрат, так среди геометрических тел — куб, форма которого образуется квадратами граней, сходящимися под прямыми углами друг к другу. Ребра граней тоже сходятся у куба под прямыми углами. Если куб специально не расположить так, чтобы была видна только одна квадратная грань, все остальные его положения будут угловыми. Эти положения куба в пространстве обязательно выявят перспективные закономерности. Здесь вступает в свои права та трудность в рисовании, которую преодолевают с помощью специальных знаний о закономерностях перспективы.

Рис. 15
Чтобы проследить данные закономерности на примере самого понятного по форме геометрического тела, выполним рисунок каркаса куба (рис. 15).
Каркас куба изготовить легко, а польза от наблюдения и анализа его формы и тем более рисования несомненна. На примере каркаса практически знакомятся с понятием «конструкция предметной формы». Следовательно, видя куб «прозрачным», «насквозь», мы воочию убеждаемся в изменениях его объема под воздействием пространственных закономерностей, т.е. перспективных сокращений. С другой стороны, каркас куба показывает нам только границы его общей формы. Заключение любого объемного тела внутри определенных границ (очертаний) со всеми присущими ему характерными признаками составляет конструктивную основу формы предмета.
Геометрические тела настолько универсальны и логичны по своей структуре, что человеческая мысль соизмерила их с математическими категориями, выведя обоснование всех объемов в ранг уникальных. Все имеющиеся на свете живые и искусственные формы представляют собой разнообразные сочетания геометрических объемов.
Итак, конструкция куба означает действительное строение формы этого геометрического тела. Именно куб по праву является первым предметом, по которому вы учитесь передавать на бумаге определенно выраженный объем.
Изображая каркас куба, вы знакомитесь с принципом строения объемной формы. Этому помогает ясное представление конструкции куба, полученное благодаря каркасу, что позволяет точнее построить изображение.
Прежде чем приступить к работе по рисованию каркаса куба, необходимо подготовить рабочее место. Затем следует выбрать точку зрения на натуру. Лучшим расстоянием до каркаса куба от рисующего будет тройной размер высоты рисуемого предмета. Натура должна быть расположена ниже уровня глаз рисующих (ниже линии горизонта) и поставлена под углом к ним.
До проведения первой легкой вертикальной линии на бумаге постарайтесь найти пропорциональные отношения величины изображения к размерам формата. Для этого надо наметить общую форму каркаса куба. Здесь надо сделать некоторое усилие — увидеть в трехмерной натуре общий плоский силуэт и нанести его абрис на лист бумага.
После того как общая форма каркаса куба намечена, можно перейти к определению конструктивной основы предмета. Такое определение начните с построения нижнего основания куба, т.е. грани, соприкасающейся с плоскостью подставки. Разумеется, грани как таковой нет, она условна, но границы в виде четырех ребер из проволоки показывают ее место. Построение основания каркаса зависит от соблюдения правил перспективы.
Далее для построения каркаса куба проведите ближайшее вертикальное ребро, высоту которого определите на глаз. От этого ребра постройте перпендикулярные ему, но подчиняющиеся правилам перспективы остальные ребра, которые хорошо видны в натуре, и завершите рисунок каркаса куба.

Рис. 16

Рис. 17
Построение каркаса призмы, имеющей два основания треугольной формы, при условии, что проволочная модель расположена под углом и одна ее прямоугольная грань соприкасается с плоскостью подставки для натуры, связано с такими же способами изображения, как и в упражнении по рисованию каркаса куба. Нужно соблюсти пропорции и правила перспективы, получив, таким образом, представление о конструктивном строении еще одного геометрического тела.
Отличную возможность разобраться в принципах конструктивного построения формы дают проволочные модели еще двух геометрических тел иной формы — цилиндра и конуса. Если при рисовании куба и призмы вы встретились только с внешними границами — ребрами, образующими форму названных тел, то в новых упражнениях вы столкнетесь с принципиально новой конфигурацией натуры. Теперь в действие вступают дополнительные контуры построения — центральные оси, которые связываются с круглыми основаниями, а последние — друг с другом с помощью нескольких образующих (рис. 16, 17).
Но самым характерным в рисовании каркасов цилиндра и конуса будет изменение формы оснований, зрительно превращающихся из круглых в овальные (эллипсовидные). Проявите необходимое внимание к проволочным моделям, доведите каждый рисунок до полного сходства с натурой.
Контрольные вопросыhudozhnikam.ru
Муниципальное автономное учреждение дополнительного образования города Тулуна «Детская художественная школа»
План-конспект открытого урока
«Натюрморт из геометрических тел»
Преподаватель: Яворский А.Н.
Тулун, 2015 г.
Натюрморт из гипсовых геометрических тел.
Цель урока:
изобразить простым карандашом линейный рисунок натюрморта;
сформировать у учащихся конкретное представление о геометрическом теле;
развивать творческие способности и навыки в работе простым карандашом.
Задачи урока:
Познавательные:
Расширить представление о линейном рисунке и выразительной особенности.
Формировать умения и навыки владения графическим материалом. Дать представление о линии (напомнить).
Совершенствовать знания о композиционном решении изображения.
Развивающие:
Развивать умение анализировать форму предметов.
Осваивать законы изобразительной грамоты.
Формировать пространственное мышление.
Воспитывающие:
Развивать внимание, наблюдательность и усидчивость.
Методы обучения: по характеру познавательной деятельности – частично-поисковый методы; по способам организации и осуществления познавательной деятельности - объяснительно-иллюстративный.
Формы организации обучения: фронтальная и индивидуальная.
Форма урока: традиционная.
Тип урока: комбинированный
Средства обучения: диалог, живая натура .
План урока:
Организационный момент – 2 минуты.
Объяснение нового материала (презентация) – 10 минут.
Педагогический рисунок – 3 минуты.
Практическая работа учащихся – 20 минут.
Обсуждение работ, выставка – 5 минут.
ПЕРВЫЙ УРОК
Ход урока.
Организационная часть.
Приветствие. Проверка готовности учащихся к уроку. На столе – тетрадь в клеточку, формат А4, набор простых карандашей, ластик. На доске – экран, рисунки прошлых лет.
Объявление темы.
Ребята, посмотрите на постановку. Вы видите группу геометрических тел. Каких?

Куб, конус и цилиндр
Практическая работа.
На уроке вам нужно решить такие задачи:
расположение композиции рисунка;
перспективное построение каждой отдельной геометрической формы;
правильная передача взаимного расположения в пространстве;
правильное изображение пропорций геометрических тел.
1-й этап. Решение расположения листа вертикально или горизонтально.
Начинают рисунок группы геометрических тел с обобщённого наброска всей группы без выделения отдельных предметов.
Вначале короткими отрезками определяют конечные точки группы тел по горизонтали и по вертикали. 
Затем они соединяются в своеобразную геометрическую фигуру, очерчивающую основные границы всей группы. 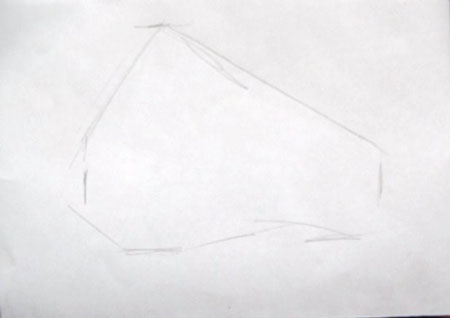
Первые карандашные засечки (линии) определяют и композиционное расположение рисунка всей группы, и её пространственное расположение, т. е. лист для рисования располагается горизонтально или вертикально.
2-й этап. Прорисовка линиями общих размеров и очертаний каждого геометрического тела. 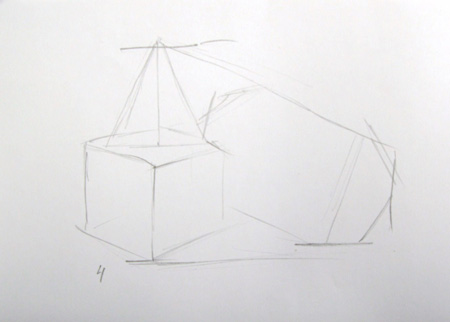
Сравнивать объёмные отношения одного тела по отношению к другому, уточняются пропорции тел по высоте, ширине.
Определить уровень горизонта (он находится на уровне глаз) и уровень перспективного сокращения плоскости, на которой расположена изображаемая группа предметов. Отсюда зависят пространственные отношения между предметами, степень перспективного сокращения их плоскостей (оснований, боковых граней), углы расположения ближайших задних граней.
Все предметы изображаются, как будто они прозрачны или сделаны из проволоки. Для этого прорисовываются и те грани и рёбра, которые невидны в натуре. Проверяем нижнее основание куба и нижнее основание описанной вокруг цилиндра призмы, чтобы не было проникновения куба в цилиндр.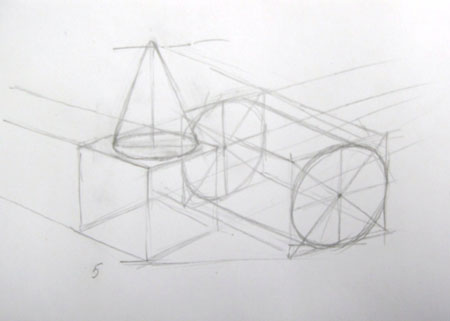
Всё построение ведётся тонкими линиями со слабым нажимом. Одновременно стираются вспомогательные линии, линии построения. Отделяем линией горизонтальную плоскость стола от вертикальной плоскости стены.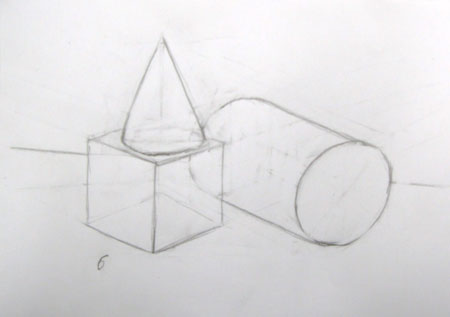
Следите за тем, чтобы формы и размеры предметов, а также их расположение относительно друг друга, были нанесены правильно. Особое внимание уделите овалам. Описывая изгибы, держите карандаш дальше от грифеля и проводите эти линии плавным движением руки от запястья. Нарисуйте контуры блика на конусе, если его увидите.
Мини-выставка и краткий анализ.
ВТОРОЙ УРОК
Цель: Решение в рисунке натюрморта светотени.
Задачи:
Передать в рисунке светотеневые отношения, соответствующие отношениям в натуре.
Обращать внимание на блик, свет, полутень тень, рефлекс, падающую тень.
План урока:
Организационный момент – 2 минуты.
Объяснение нового материала (презентация) – 10 минут.
Педагогический рисунок – 3 минуты.
Практическая работа учащихся – 20 минут.
Обсуждение работ, выставка – 5 минут.
Ход урока.
Организационная часть.
Приветствие. Проверка готовности к уроку.
Объявление темы.
Продолжаем рисование с натуры натюрморта из геометрических тел.
Практическая работа.
Тоновая проработка рисунка начинается с четкого определения и очерчивания на изображениях предметов границ собственной тени и падающих теней. При этом вначале создаются участки темного, затем среднего и, наконец, светлого тона.
Возьмите мягкий карандаш 3В и начните добавлять тон. Для этого широкими диагональными штрихами покрываются средним (не очень сильным) тоном затенённые стороны куба, цилиндра, конуса, независимо от того, собственная ли это тень или падающая.
Нажимая немного сильнее на тот же карандаш, заштрихуйте правую грань куба и основание цилиндра. Заштриховываем падающие тени от куба и цилиндра на горизонтальной плоскости и далее вокруг цилиндра. Усиливаем тон около границ света и тени, а это на грани куба и основании цилиндра. Легко наносим штриховку падающей тени от куба на цилиндре по форме.
Прорабатываем светлые и тёмные тона на конусе. Очень хорошо видно как усиливается тень к вершине и ослабляется к основанию конуса. Штрихи наносить нужно по форме.
В верхнем ближнем углу куба усиливаем нажим на карандаш при штриховке теневой грани. На ней хорошо виден рефлекс (отражение света или цвета от соседнего предмета) от освещённой поверхности цилиндра свет отражается в тени грани куба. Такое же отражение от драпировки видно и в тени основания цилиндра.
Усиливаем самые тёмные места в падающих тенях с соблюдением контрастов и рефлексов. Не забываем, что на границе освещённой поверхности с собственной тенью свет светлеет, а тень темнеет. Тень высветляется, если по соседству находится освещённый предмет.
Уточняем тона.  Продолжаем работу над фоном и усиливаем собственные и падающие тени. Определяем самые тёмные места в натюрморте. Мягким карандашом 4В, углубляя тон, показываем их.
Продолжаем работу над фоном и усиливаем собственные и падающие тени. Определяем самые тёмные места в натюрморте. Мягким карандашом 4В, углубляя тон, показываем их.
Заканчиваем работу над серой поверхностью.
Тени, отбрасываемые предметами на серую горизонтальную плоскость, малозаметны, поэтому их нужно обозначить лёгкой штриховкой. Эти тени помогут «привязать» предметы к поверхности стола.
Немного высветлим фон над цилиндром. Готовый рисунок. 
Выставка и оценка работ.
infourok.ru
2015-07-27T10:18:54+03:00
Автор:Тарасенко Снежана Анатольевна
27.07.2015
Рисование геометрических тел для начинающих – важный этап, который необходимо пройти. Данное занятие несложное и не занимает много времени, но навыки обязательно пригодятся в дальнейшем творчестве при изображении различных зданий, строений, предметов и объектов. Как правильно рисовать обычные геометрические тела вы сможете узнать из материалов нашей статьи.
Рисование простых геометрических фигур, в частности конуса, куба, призмы, шара, пирамиды и так далее, является необходимым этапом для живописцев, которые только начинают учиться данному виду искусства. Какой бы предмет вы не решили изобразить, без этих простых фигур вам никак не обойтись. В основе любого предмета быта, который легче всего нарисовать, лежат именно они. Приобретя эти навыки, вы без труда сможете нарисовать любое архитектурное строение, средство передвижения и другие объекты.
Попробуем научиться рисовать каждую из фигур.

Изображение цилиндра
Очень часто, при создании того или иного рисунка, нам необходимо, образно говоря, поместить объект в цилиндр. Для этого нужно знать правила его построения и умение использовать их в работе. Чтобы получить чертеж с этого геометрического тела, нужно, для начала, провести ось. Относительно ее будут намечаться основные элементы в виде овалов. Как можно увидеть на ниже представленном рисунке, изображение овалов, имеющих большой диаметр, рисуется всегда по отношению к оси изображаемой фигуры под прямым углом. После того, как были определены размеры оснований, длина самого тела, аккуратными линиями нужно нарисовать круги и провести к ним дополнительные линии. Данные наброски нужно делать легкими штрихами, слегка видными глазу. На нашем рисунке вы можете увидеть два варианта чертежей цилиндров, один из которых лежит, а второй расположен в вертикальном положении.

Если мы хотим построить цилиндр, нам обязательно необходимо использовать вспомогательные линии. Они являются средством для уточнения пропорций и положения фигуры в пространстве. Отдельные участки изображаемого геометрического тела следует заштриховать. Штриховка подчеркивает объем фигуры и показывает направление.
Рисование карандашом пирамид и призм
Чтобы прорисовка этих двух тел не вызывала никаких затруднений, особенно в том случае, если они имеют много граней, их нужно мысленно поместить в более простые фигуры. Если это пирамида, то мы впишем ее в конус. Если же речь идет о призме, то вписывать ее нужно в цилиндр. Во время работы над рисунком мы поступим таким образом. Наметив на листе общую композицию будущего изображения, приступим к прорисовке основания. Чтобы все получилось правильно, мы изначально нарисуем окружность (в перспективе), имеющую необходимые размеры. Затем, на нарисованной окружности отметим все шесть углов фигуры. Согласно натуры нам нужно проверить расположение углов в отношении друг друга. При правильности рисунка параллельные стороны должны сходиться в точках схода. Чтобы легче было выполнять в дальнейшем эти действия, сначала нужно научиться рисовать фигуры, находящиеся в вертикальном положении, и только после этого начинать прорисовывать лежащие пирамиды и призмы.
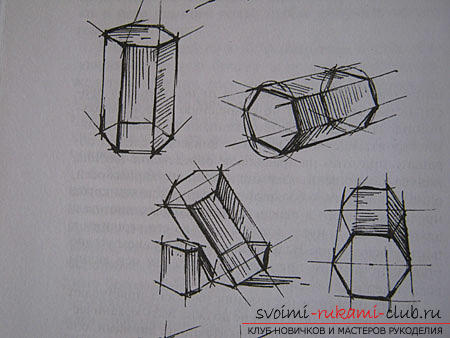
Процесс создания эскизов ящика
Чтобы сделать эскиз ящика, для начала нужно определить его положение в окружающем пространстве. После того, как линиями по краям контуров всего предмета сделаны необходимые отметки, требуется наметить в перспективе абсолютно все его стенки. Те линии, которые отсекают форму стенки, необходимо провести отрывисто, сразу. Такой подход дает возможность определить уровень горизонта, точку, в которой сходятся параллельные линии, проверки правильности передачи сокращения граней в перспективе. При прорисовке ящика важна тренировка. Чтобы добиться хорошего результата, рисовать объект нужно в разных положениях обязательно с натуры.
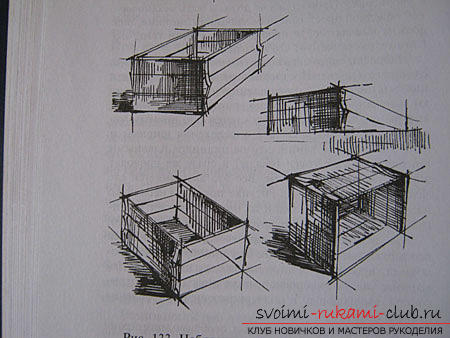
svoimi-rukami-club.ru
МБОУ «Средняя общеобразовательная школа №92 с углубленным изучением отдельных предметов»
X XII научно-практическая конференция школьников «Мы- будущее России»
Секция «Математика»
Тема: «Невозможные фигуры вокруг нас»
Автор работы:
Титов Илья,
ученик 6В класса
Научный руководитель:
Коваленко Ольга Алексеевна,
учитель математики
Кемерово 2015
ОглавлениеВведение 3
История возникновения невозможных фигур 3
Определение невозможных фигур 5
Виды невозможных фигур 6
Создание невозможных фигур 9
Применение невозможных фигур 10
Заключение. 15
Список литературы 16
ВведениеС древних времен люди пытались изображать животных, предметы быта, пейзажи на скале, глиняной дощечке, бересте, а позднее на бумаге и холсте. Понадобилось ни одно столетие, пока они научились объемные тела изображать на плоскости так, чтобы их сразу можно было отличить от плоских, чтобы чувствовалась глубина пространства.
Чтобы изображать на листе бумаги объемный предмет мы не задумываемся над тем, как же можно его, имеющего три измерения / длину, ширину и высоту / втиснуть в бумагу, которая имеет всего два измерения. Значит, нужны условности, которые позволяют поверить в трехмерность изображения. Меня заинтересовали фигуры, которые на первый взгляд кажутся обычными, а присмотревшись к которым создается впечатление, что существовать в реальном мире они не могут. Такие фигуры получили название невозможных фигур. Я захотел узнать о них.
Невозможные фигуры – это один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве.
Невозможные фигуры – это объекты, имеющие отношение к математике, изобразительному искусству и психологии. Невозможные фигуры уже несколько веков привлекают внимание людей.
Гипотеза: в нашей жизни нет ничего невозможного, главное знать под каким «углом» смотреть!
Целью работы является изучение невозможных фигур.
Задачи работы:
1. Рассмотреть виды невозможных фигур.
2. Найти области применения невозможных фигур.
3. Научится строить невозможные фигуры.
История возникновения невозможных фигурНевозможные фигуры достаточно часто встречаются на древних гравюрах, картинах и иконах — в одних случаях мы имеем с явными ошибками передачи перспективы, в других — с умышленными искажениями, обусловленными художественным замыслом.
В средневековой японской и персидской живописи невозможные объекты являются неотъемлемой частью восточного художественного стиля, дающего лишь общий набросок картины, детали которой «приходится» додумывать зрителю самостоятельно, в соответствии со своими предпочтениями.[1]
Картины с искаженной перспективой встречаются уже в начале первого тысячелетия. На миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована Мадонна с младенцем. [2] На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект нереальности.
Несмотря на это, систематическое их изучение началось лишь в середине XX века.
Основоположниками глубокого изучения невозможных фигур можно считать голландского художника Морица Корнилиса Эшера, шведского художника Оскара Реутерсварда и английского математика Роджера Пенроуза.
В 1934 году Оскар Реутерсвард случайно создал свою первую невозможную фигуру – треугольник, составленный из девяти кубиков. Оскар Реутерсвард родился в 1915 году в городе Стокгольме Швеция. Он обучался рисованию под руководством русского иммигранта профессора Академии Искусств в Санкт-Петербурге Михаила Каца и создал более 2500 различных невозможных фигур.
В 1954 году математик Роджер Пенроуз после лекции М.К. Эшера независимо от Реутерсварда заново открывает невозможный треугольник, но использует линейную, а не параллельную перспективу и соединяет вершины треугольника сплошными линиями, что усиливает эффект. Роджер Перноуз родился в Англии 8 августа 1931 года. [1] Он является выдающимся учёным современности, который активно работает в различных областях математики, общей теории относительности и квантовой теории и является членом Лондонского королевского общества. У него очень много наград, таких как премия Вольфа, медаль Дирака, премия Альберта Эйнштейна и медаль Королевского общества.
В 1958 году Пенроуз вместе со своим отцом Лайонелом Пенроузом публикует статью в Британском журнале по психологии, после которой невозможными фигурами заинтересовываются не только математики.
Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей[3].
В процессе своей работы он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии. Он был очарован всевозможными парадоксами и в том числе «невозможными фигурами». Парадоксальные идеи Роджера Пенроуза были использованы во многих работах Эшера. Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости и логика трехмерного пространства.
Эшер понимал, что геометрия определяет логику пространства, но и логика пространства определяет геометрию.
Эшер создал много работ, в которых изображал «невозможные фигуры», т.е. картины с нарушенной логикой пространства. Парадокс невозможных фигур основан на том, что наш мозг всегда пытается представить нарисованные на бумаге двухмерные рисунки как трехмерные. Наиболее интересная работа – литография «Водопад» – основана на фигуре невозможного треугольника, придуманного математиком Роджером Пенроузом. В этой работе два невозможных треугольника соединены в единую невозможную фигуру. Создается впечатление, что водопад является замкнутой системой, работающей по типу вечного двигателя, нарушая закон сохранения энергии. Обратите внимание на многогранники, установленные на башнях водопада.
Определение невозможных фигурДо сих пор не существует чёткого определения невозможных фигур. Мною было найдено несколько различных подходов к определению этого понятия.
Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры[2].
Невозможные фигуры – это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией.
Невозможные фигуры разделяются на два больших класса: одни имеют реальные трехмерные модели, а для других такие создать невозможно.
Как правило, чтобы трехмерная модель невозможной фигуры выглядела невозможной, она должна рассматриваться с какого-то определенного угла обзора, чтобы возникла иллюзия невозможности.
Необходимо прояснить различие между терминами «невозможная фигура», «невозможный объект» и «трехмерная модель». Трехмерная модель – это физически представимый объект, при рассмотрении которого в пространстве становятся видимыми все щели и изгибы, которые уничтожают иллюзию невозможности и данная модель теряет свое «волшебство». При проецировании данной модели на двухмерную плоскость получается невозможная фигура. Эта невозможная фигура (в отличие от трехмерной модели), создает впечатление невозможного объекта, который может существовать только в воображении человека, но не в пространстве.
Виды невозможных фигурУдивительный треугольник – трибар. Эта – фигура – возможно первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как «трехмерную прямоугольную структуру». Она также получила название «трибар». С первого взгляда трибар кажется просто изображением равностороннего треугольника. Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но, в общем, эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.
Геометрические фигуры – лучшие источник вдохновения для изобретения невозможных объектов. Например, возьмем простой куб. Каждый день мы видим их в огромном количестве в той или иной форме, как вы легко можете видеть из иллюстрации на соседней странице. Для построения этой фигуры мы взяли один из трибаров с предыдущей страницы и разбили его на кубы. При этом ничего не изменилось: новая фигура так же совершенно невозможна, как и предшествующая ей!
Эта фигура, состоящая из 12 кубов, была сконструирована на чертежной доске с помощью прямоугольного треугольника с углами в 30 и 60°. Чертежный треугольник использовали для того, чтобы вписать каждый куб в общую перспективу чертежа. Эффект невозможности, для создания которого использована эта перспектива, достигается неправильным расположением на переднем и заднем плане рядов кубов. Поэтому же принципу строится и трибар. Другими словами, рисунок основан на неправильном соединении правильных рядов кубов.
Следующую фигуру чаще всего называют «Бесконечной лестницей», «Вечной лестницей» или «Лестницей Пенроуза» – по имени ее создателей. Ее также называют «непрерывно восходящей и нисходящей тропой». «Бесконечная лестница» – одна из самых известных классических невозможностей. [1]
Впервые эта фигура была опубликована в 1958 году Лайонелом и Роджером Пенроузами вместе с трибаром и другими примерами зрительных иллюзий в British Journal of Psychology. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути. Если бы вам, в самом деле, пришлось пройти по этой лестнице, вы бы бесцельно поднимались и спускались по ней бесконечное число раз. Можно назвать это нескончаемым сизифовым трудом! С тех пор как Пенроузы опубликовали эту фигуру, она появлялась в печати чаще, чем какой-либо другой невозможный объект. «Бесконечную лестницу» можно встретить в книгах об играх, головоломках, иллюзиях, в учебниках по психологии и другим предметам.
«Бесконечной лестницей» с успехом воспользовался художник Мауриц К. Эшер, на этот раз в своей чарующей литографии «Восхождение и нисхождение», созданной в 1960 году. В этом рисунке, отражающем все возможности фигуры Пенроуза, вполне узнаваемая «Бесконечная лестница» аккуратно вписана в крышу монастыря. Монахи в капюшонах непрерывно движутся по лестнице в направлении по часовой стрелке и против нее. Они идут навстречу друг другу по невозможному пути. Им так и не удается ни подняться наверх, ни спуститься вниз. Соответственно, «Бесконечная лестница» стала чаще ассоциироваться с Эшером, перерисовавшим ее, чем с Пенроузами, которые ее придумали.
Несколько лет назад был снят фильм «Бесконечная лестница». В этом фильме мячик скачет на этой лестнице по кругу. Для усиления эффекта с каждым подпрыгиванием мячика звучит музыкальная нота, с каждым шагом вверх она поднимается на более высокий тон, но ноты не выходят за пределы октавы. После нескольких ступенек вверх наступает пауза, и следующий тон звучит октавой ниже, но наш мозг этого не воспринимает. Мячик и музыка в фильме «Бесконечная лестница» создают аудиовизуальную иллюзию» невозможную вдвойне.
Рассмотрим следующий пример – пространственную вилку.
Поскольку трудно одновременно рассматривать правую и левую стороны фигуры, то сразу сложно понять, что данный предмет – невозможен. Каждая из сторон, если рассматривать их отдельно, возможна в двухмерном изображении, но невозможна, если рассматривать объект в целом с одной точки.
Проблема возникает из-за двусмысленности в восприятии глубины. Мы не получаем достаточно информации о том, как расположены части фигуры, и, соответственно, непонятно, на что мы, собственно, смотрим. Проблема состоит в том, чтобы угадать положение среднего зубца. Если посмотреть на фигуру слева, то все три зубца располагаются на одном уровне, другими словами, у них одинаковые параметры пространства и глубины. А когда вы смотрите на фигуру справа, средний зубец как бы «проваливается» в сравнении с двумя внешними. Так где же именно расположен средний зубец? Очевидно, что он не может существовать в двух местах одновременно. Путаница происходит из-за того, что вы пытаетесь смотреть на эту фигуру как на трехмерный объект.
«Космическая вилка» основана на принципе неправильных соединений, которые возможны в двухмерной плоскости или на двухмерной поверхности, но никак не в трехмерном пространстве. В «Космической вилке» использовано то обстоятельство, что зубец с круглым сечением может быть нарисован с помощью пары параллельных линий. Перекладина же с квадратным сечением – с помощью трех линий. Иллюзия основана на том, что две параллельные линии образуют круглое сечение с одной стороны, прибавляя же к ним третью параллельную линию, мы получаем квадратное сечение – с другой. Для усиления противоречия все линии строго параллельны в пространстве. Если бы вы смогли сделать поперечное сечение в середине «Космической вилки» – вырезать из нее ломтик, как из батона, – как, по-вашему, он бы выглядел?
В иллюстрации представлены две разновидности «Космической вилки».
Еще один невозможный объект появился в 1966 году в Чикаго, штат Иллинойс, в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. [4]
«Волшебная» фотография этой фигуры была опубликована в июньском номере Scientific American magazine от 1966 года. Многие любители невозможных фигур проводили эксперименты с «Сумасшедшим ящиком», в результате чего эта фигура вошла в классическую «Большую Четверку» вместе с «Невозможным треугольником», «Бесконечной лестницей» и «Космической вилкой». Первоначально автор назвал ее «Свободным ящиком» и заявил, что она была «сконструирована для пересылки невозможных объектов в большом количестве». Многие также замечали, что ящик вполне подходит для помещения в него разных штуковин и других неопознанных объектов.
«Сумасшедший ящик» – это вывернутый наизнанку каркас куба. Фигуру можно воспринять двояко, но какого-либо последовательного решения нет. Как и многие другие невозможные объекты, «Сумасшедший ящик» основан на неправильных соединениях, допущенных при рисовании.
Непосредственным предшественником «Сумасшедшего ящика» была «невозможная коробка», которую держит сидящий мальчик в знаменитой гравюре Эшера «Бельведер» (1958). Предшественником; невозможной коробки Эшера был, в свою очередь, куб Неккера. Он не является невозможным объектом, однако представляет собой фигуру, в, которой параметр глубины может восприниматься неоднозначно.
Куб Неккера был впервые описан в 1832 году швейцарским кристаллографом Льюисом А. Неккером, который заметил, что кристаллы иногда зрительно меняют форму, когда на них смотришь[3]. На куб Неккера можно посмотреть как на плоскость, располагающуюся в двухмерном пространстве. Однако, из-за особенностей зрения, нам легче воспринимать трехмерные объекты, чем двухмерные. Когда мы вглядываемся в куб Неккера, то замечаем, что грань куба с точкой находится то на переднем, то на заднем плане, она перепрыгивает из одного положения в другое. Наше восприятие ищет этому подходящее объяснение. Но остается загадкой, насколько наш опыт и накопленные знания влияют на восприятие. Эти факторы очень важны при создании удивительных фигур, но как и в кубе Неккера, они «замедляют» восприятие.
Создание невозможных фигурКонечно, ни одну из невозможных фигур нельзя создать, действуя прямолинейно. Например, если вы возьмете три одинаковых деревянных бруска, вы не сможете совместить их так, чтобы получился невозможный треугольник. Однако при проецировании трехмерной фигуры на плоскость некоторые линии могут становиться невидимыми, перекрывать друг друга, стыковаться друг с другом и т.п. Исходя из этого, мы можем взять три различных бруска и составить треугольник, представленный на фотографии ниже.
Еще один способ создания невозможного треугольника был предложен русским художником и конструктором Вячеславом Колейчуком и опубликован в журнале «Техническая эстетика» №9 (1974). Все ребра данной конструкции являются прямыми линиями, а грани изогнуты, хотя на фронтальном виде фигуры этой изогнутости не видно. Он создал такую модель треугольника из дерева.
Существует и еще один способ, при помощи которого можно увидеть невозможную фигуру, причем двумя глазами сразу. Заключается он в следующем: необходимо создать огромную фигуру высотой с многоэтажный дом, расположить ее на обширном открытом пространстве и смотреть на нее с очень большого расстояния. В этом случае, даже смотря на фигуру двумя глазами, вы будете воспринимать ее как невозможную вследствие того, что оба ваших глаза будут получать изображения практически ничем не отличающиеся друг друга. Такая невозможная фигура была создана в австралийском городе Перт.
Применение невозможных фигурНевозможные фигуры в иконописи
Христианство очень редко использовало модели несуществующих фигур, но их изображения часто встречаются на иконах и фресках. До нашего времени сохранилось не так уж и много моделей невозможных фигур в храмах. Самым известным из них является изображение невозможного треугольника расположенного на экране перед алтарем. Он находится в церкви Святой Троицы, простроенной бенединскими монахами с 1150 по 1550 годы. Впоследствии она была разрушена, в 1869 году – восстановлена и перестроена. 

Изображения невозможных фигур встречается на иконах и фресках. Обычно это невозможная колоннада. Основание средней колонны удалено от зрителя. До сих пор исследователи не пришли к выводу о том, является такая конструкция замыслом художника или ошибкой. С моей точки зрения это было вызвано необходимостью вынести центральный образ на первый план и расширения пространства иконы. В качестве примера можно привести изображение «Мадонна с младенцем» с миниатюры из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене[1].
На иллюстрации изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект сюрреалистичности. К этой же группе можно отнести фреску из церкви Марии города Бреда (Голландия). Фреска была вскрыта под более поздними слоями в 1902 году и датируется концом XV века.
На иконе «Страшный суд» (ранний период) в верхнем регистре слева располагается изображение Небесного Иерусалима в виде города, обнесенного стенами с множеством башен и ворот. 
Внутри него, за восемью престолами, представлены святые по чинам: апостолы, мученики, преподобные, отшельники (юродивые), пророки, святители, мученицы и преподобные жены. Постепенно это изображение всё больше стилизировалось и упрощалось. К середине XV века в верхнем регистре иконы уже находилась арка с невозможными перекрытиями. [2]
Эти фрески были созданы Евгением Матько в Покровском храме в Воронежской области. На каждой из них можно видеть невозможные конструкции.
Оформление часовни Рождества Богородицы возле деревни Ижевцы в Черновецкой области (Украина). На фресках изображено большое количество невозможных фигур, что является характерным приемом художника. В большинстве других примеров использования невозможных конструкций в иконописи появление невозможных конструкций связано, скорее, с ошибками художников, нежели осознанными намерениями
Невозможные фигуры в архитектуре и скульптуре
За рубежом, на улицах городов, мы можем увидеть архитектурные воплощения невозможных фигур.
В последнее время было создано несколько мини скульптур и объемных моделей невозможных фигур. Им даже поставлен памятник.
Треугольник Пенроуза увековечен в городе Петре в Австралии. Он был установлен в 1999 году и теперь все, проходя мимо, могут увидеть невозможную фигуру.
Но стоит подойти с другой стороны, и тогда невозможная фигура станет совсем реальным сооружением.
В качестве примера невозможных фигур в архитектуре можно привести так называемые Кубические дома. Они были построены в 1984 году в Роттердаме (Нидерланды) архитектором Пиетом Бломом. Дома развернуты на угол в 45 градусов и расположены по шестиугольной сетке. Конструкция состоит из 32 кубов, соединенных друг с другом. Каждый кубический дом состоит из четырех этажей. На первом этаже – вход, на втором – кухня и гостиная, на третьем – спальня и ванная комната, на четвертом этаже часто устраивают оранжерею. Крыши домов, окрашенные в белый и серый цвета, при взгляде сбоку напоминают горные пики, покрытые снегом. Этот комплекс зданий обладает еще одним интересным свойством. С высоты птичьего полета здания образуют конструкцию, выглядящую как невозможная фигура.
Скульптура невозможного треугольника во дворе бельгийско отеля в деревне Ophoven. Скульптура выполнена из дерева и полиэстерола. Треугольник только кажется «невозможно» при просмотре с определенным углом. Фотография справа показывает, как это выглядит, если смотреть с других ракурсов. Эта скульптура была создана Матье Hamakers[3].
Невозможные фигуры в живописи
В живописи существует целое направление, которое называется импоссибилизм («невозможность») – изображение невозможных фигур, парадоксов. Интерес к импоссибилизму разгорелся к 1980 году. Этот термин был введен в обращение Тедди Бруниусом, профессором искусствоведения копенгагенского университета. Термин этот точно определяет то, что входит в это новое понятие: изображение предметов, которые кажутся реальными, но не могут существовать в физической реальности.
Оп-арт (англ. Op-art – сокращенный вариант optical art – оптическое искусство) – художественное течение второй половины 20 века, использующее различные зрительные иллюзии, основанные на особенностях восприятия плоских и пространственных фигур. Самостоятельным направлением в оп-арте является так называемый имп-арт (imp-art), использующее для достижения оптических иллюзий особенности отображения трёхмерных объектов на плоскости.
Наиболее известными представителями оп-арте являются Морис Эшер, венгерский художник Иштван Орос, фламандский художник Жос Де Мей, швейцарский художник Сандро дель Пре. Британский художник Джулиан Бивер – один из самых известных художников этого направления, который изображает свои шедевры не на бумаге, а на улицах города, стенах городских домов, где ими могут любоваться все.
Невозможные фигуры в филателистке
В 1982 году по заказу правительства Швеции Оскаром Реутерсвардом были выполнены марки с изображениями невозможных фигур. Марки выпускались ограниченным тиражом, сегодня они являются большой редкостью и пользуются большим спросом среди филателистов. В ближайшее время планируется очередной их тираж. Первая же из таких марок была посвящена математичскому конгрессу в Инсбруке (Австрия), проходившему в 1981 году. За основу взят невозможный ящик Эшера.
Шведские марки с изображениями знаменитых фигур Оскара Реутерсварда, выпущенные в 1982 году.
Невозможные фигуры в оформительском искусстве.
Не редко невозможные фигуры используются для оформления обложек журналов.

На обложке первого номера 2008 года журнала «Математика в школе» изображен коллаж из фрагментов картин бельгийского художника Жоса де Мея. Здесь можно увидеть двух частых персонажей картин художника – сову и человека с кубом. Сова для бельгийцев является символом теоретических знаний, и в то же время прозвищем глупого человека. Человек с невозможным кубом является в свою очередь одним из героев литографии М.К. Эшера «Бельведер», которого позаимствовал де Мей для своих картин. Именно де Мей окрасил одежду этого персонажа в характерные голландские цвета. Также можно увидеть другие фрагменты из картин бельгийского художника – большую невозможную конструкцию, расписанную математическими формулами, а также табличку с магическим квадратом Дюрера.
В оформлении обложек учебников по алгебре для 7 класса традиционно используются невозможные фигуры.
Невозможные фигуры в мультипликации
Интерес к невозможным фигурам отразился и в мультипликации и кинематографе.
В 1986 году на экраны выходит музыкальная сказка «Лабиринт», в которой юная девушка Сара попадает в крепость, которая представляет собой сооружение с искаженными измерениями и гравитацией, почти в точности повторяющим обстановку известной картины М.К. Эшера «Относительность».
Кто в детстве не смотрел мультфильм «В синем море, в белой пене...», снятом на студии «Арменфильм» в 1984 году. В фильме рассказывается сказка о том, как маленький мальчик освобождает из кувшина Короля Моря, после чего тот похищает мальчика и утаскивает его на дно моря.
В начале мультфильма есть сцена, в которой присутствуют нарушения перспективы. В них Король Моря оперирует с объектами, находящимися от него на большом расстоянии так, как будто просто маленького размера и находятся рядом с ним. Ниже представлены несколько скриншотов из этой сцены.

В современном популярном американском анимационном сериале Финес и Ферб, рассказывается о том, как проводят летние каникулы два сводных брата. Каждый день они затевают новый грандиозный проект
В 35 эпизоде второго сезона «Фуфельная сторона Луны» братья строят самое высокое здание в мире, которое достигает луны. Одна из комнат здания повторяет Относительность Эшера.
Невозможные фигуры в логотипах и символике
Известно использование невозможных фигур в массовой культуре.
Посмотрите на логотип французской автомобильной компании Renault. В 1972 году её символом стал невозможный четырёхугольник.


Позже в 1992 году невозможная фигура изменилась, она стала немного проще. Этот же символ был взят за основу мексиканским математическим сайтом. А 16 июня 2003 году поисковая система Google в честь дня рождения М.К. Эшера изменила свой логотип на один день, взяв за основу работу М. К. Эшера «Рисующие руки» 1948 года. Многие современные фирмы также берут за основу для своих логотипов невозможные фигуры. Особой популярностью пользуются невозможный треугольник и четырёхугольник.
Вот примеры логотипов реально существующих фирм, в начертании которых присутствуют невозможные фигуры.
Логотип мебельного магазина Мебельные галлюцинации.
Невозможное кольцо является логотипом компании Swirlyspace, занимающей разработкой приложений для iPhone.
Как правило, чтобы трехмерная модель невозможной фигуры выглядела невозможной, она должна рассматриваться с какого-то определенного угла обзора, чтобы возникла иллюзия невозможности. Это условие не позволяет нам видеть сцену с различных точек зрения, приблизиться к трехмерному объекту или рассмотреть его со всех сторон. Именно на это основан один из экспонатов познавательно-развлекательный центр «Галилео» в г. Новосибирск.
Невозможные фигуры заставляют наш разум сначала увидеть то, чего быть не должно, затем искать ответ — что же сделано не так. А ответ найти порой не так — то просто — он скрыт в оптическом, психологическом, логическом восприятии рисунков.
Изучив литературу по теме, я понял, что невозможное возможно и нереальные фигуры можно сделать своими руками. Рассмотрев способы построения невозможных фигур, я смог нарисовать свои невозможные фигуры.
Мне удалось показать, что все невозможные фигуры могут существовать в реальном мире.
Невозможные фигур широко используются в современной рекламе, промышленной графике, плакате, оформительском искусстве и логотипах различных фирм, найдется ещё много областей, в которых будут использоваться невозможные фигуры.
Таким образом, можно сказать, что мир невозможных фигур чрезвычайно интересен и многообразен. Работа может быть использована на занятиях по математике для развития пространственного мышления учащихся. Все это позволяет говорить об актуальности изучаемой темы.
Список литературыЛевитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26
Реутерсвард О. Невозможные фигуры. – М.: Стройиздат,1990, 206 с.
Ткачева М.В. Вращающиеся кубики. – М.: Дрофа, 2002. – 168 с.
kopilkaurokov.ru