Теорема Виета проект (разработка). Реферат теорема виета

1. Биография Франсуа Виета. Теорема Франсуа Виета и её значение в математике

Теорема Виета

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа» №13

Реферат:

«Теорема Виета»

Составили

учащиеся 9 в класса

Руководитель

Мартынова Е.Г.

Муром, 2010 г.

Содержание

Введение
Основная часть

Формулы Виета

Теорема Виета в школьном курсе
Теорема Виета в заочной физико – технической школе
Теорема Виета на централизованном тестировании

Заключение

Литература

«По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи постоянства такого:

Умножишь ты корни - и дробь уж готова;

В числителе с, в знаменателе a,

А сумма корней тоже дроби равна,

Хоть с минусом дробь эта, что за беда

В числителе b, в знаменателе а».

Введение

XV и XVI столетия были временем больших перемен в экономике, политической и культурной жизни европейских стран. Все перемены в жизни общества сопровождались широким обновлением культуры – расцветом естественных и точных наук, литературы на национальных языках и изобразительного искусства. К этому периоду относится творческая деятельность Франсуа Виета.

Виет Франсуа (1540 – 1603) родился в городе Фонтене ле-Конт провинции Пуату. Получив юридическое образование, он с девятнадцати лет успешно занимался адвокатской практикой в родном городе. Как адвокат Виет пользовался у населения авторитетом и уважением. Он был широко образованный человек. Знал астрономию и математику и всё свободное время уделял этим наукам.

Преподавая частным образом астрономию дочери одной знатной клиентки, Виет пришёл к мысли составить труд, посвящённый усовершенствованию птолемеевской системы. Затем он приступил к разработке тригонометрии и приложению её к решению алгебраических уравнений. В 1571 году Виет переехал в Париж и там познакомился с математиком Пьером Рамусом. Благодаря своему таланту и отчасти благодаря браку своей бывшей ученицы с принцем де Роганом, Виет сделал блестящую карьеру и стал советником Генриха III, а после его смерти Генриха IV.

Но главной страстью Виета была математика. Он глубоко изучил сочинения классиков Архимеда и Диофанта, ближайших предшественников Кардано, Бомбелли, Стевина и других. Виета они не только восхищали, в них он видел большой изъян, заключающийся в трудности понимания из-за словесной символики.

Почти все действия и знаки записывались словами, не было намёка на те удобные, почти автоматические правила, которыми мы сейчас пользуемся. Нельзя было записывать и, следовательно, начать в общем виде алгебраические сравнения или какие-нибудь другие алгебраические выражения. Каждый вид уравнения с числовыми коэффициентами решался по особому правилу. Так, например, у Кардано рассматривалось 66 видов алгебраических уравнений. Поэтому необходимо было доказать, что существуют такие общие действия над всеми числами, которые от этих самих чисел не зависят. Виет и его последователи установили, что не имеет значения, будет ли рассматриваемое число количеством предметов или длиной отрезка. Главное, что с этими числами можно производить алгебраические действия и в результате снова получать числа того же рода. Значит, их можно обозначить какими-либо отвлечёнными знаками. Виет это и сделал. Он не только ввел своё буквенное исчисление, но сделал принципиально новые открытия, поставив перед собой цель, изучать не числа, а действия над ними. Правда, у самого Виета алгебраические символы ещё были мало похожи на наши.

Такой способ записи позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Не случайно Виета называют «отцом» алгебры, основоположником буквенной символики. Особенно гордился Виет всем известной теперь теоремой о выражении коэффициентов уравнения через его корни, полученной им самостоятельно, хотя, как теперь стало известно, зависимость между коэффициентами и корнями уравнения (даже более общего вида, чем квадратного) была известна Кардано, а в таком виде, в каком мы пользуемся для квадратного уравнения, - древним вавилонянам.

I. Формулы Виета

Формулы Виета – формулы, выражающие коэффициенты многочлена через его корни. Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным его корням.

Формулировка

Если — корни многочлена

(каждый корень взят соответствующее его кратности число раз), то коэффициенты выражаются в виде симметрических многочленов от корней, а именно:

Иначе говоря, равно сумме всех возможных произведений из k корней.

Если старший коэффициент многочлена , то для применения формулы Виета необходимо предварительно разделить все коэффициенты на a0 (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

Доказательство

Доказательство осуществляется рассмотрением равенства

где правая часть представляет собой многочлен, разложенный на множители.

После перемножения элементов правой части, коэффициенты при одинаковых степенях x должны быть равными в обеих частях, из чего следуют формулы Виета.

Если бы многочлен не был приведённым, то есть имел бы старший коэффициент , то формулы, аналогичные полученным, давали бы выражения для отношений .

Формулы Виета, устанавливающие связь между корнями и коэффициентами произвольного многочлена, замечательны тем, что их правые части не меняются при любых перестановках корней

Примеры использования:

в квадратном уравнении

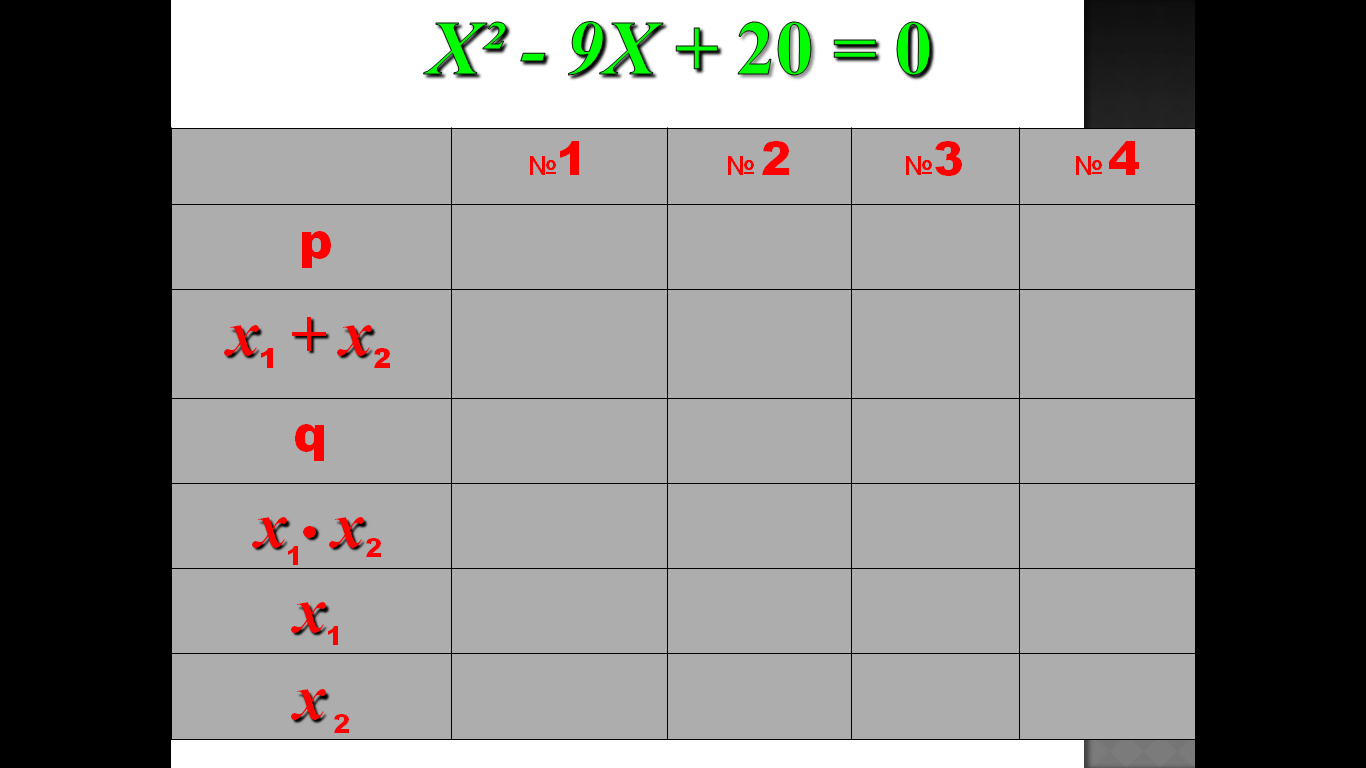
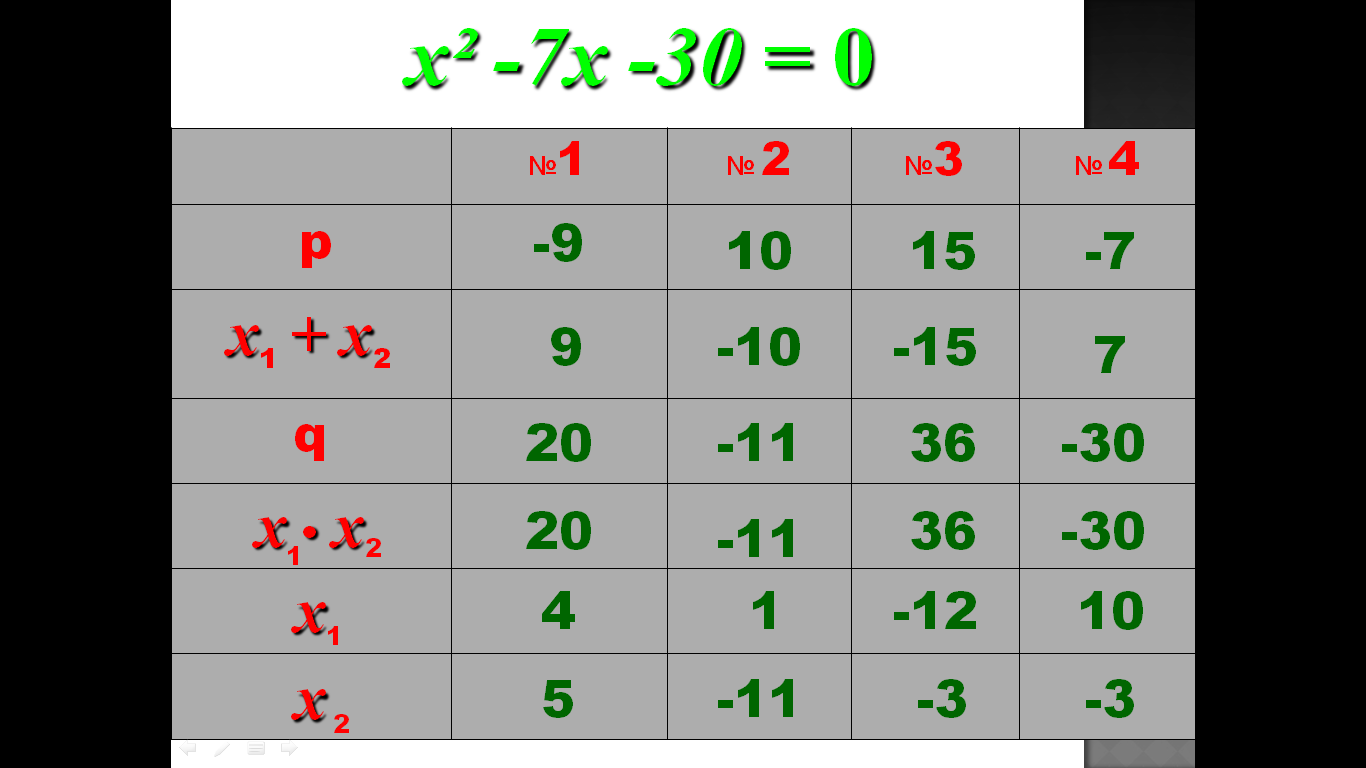
Сумма корней приведенного квадратного уравнения равна второму коэффициенту с обратным знаком, а произведение корней равно свободному члену.

Если x1 и x2 — корни квадратного уравнения ax2 + bx + c = 0 , то

и . (*)

В частном случае, если a = 1 (приведенная форма x2 + px + q = 0), то x1 + x2 = − p и x1x2 = q.

С помощью формул Виета можно получить разложение квадратного трёхчлена ax2+bx+c=0 на множители.

Из формул (*) следует, что , поэтому

Итак, если x1и x2- корни квадратного трёхчлена ax2 + bx + c, тогда для любого значения x будет верна формула .

в кубическом уравнении

Если x1,x2,x3 – корни кубического уравнения p(x) = ax3 + bx2 + cx + d = 0, то

II. Изучение теоремы Виета в школьном курсе

Соотношения между корнями и коэффициентами квадратного уравнения позволяют некоторых случаях находить его корни устно, не прибегая к формуле корней.

Попробуем, например, подобрать корни уравнения . Формулы Виета подсказывают решение: корнями должны быть числа, сумма которых равна 8 и произведение которых равно 15. Легко видеть, что этим условиям отвечают числа 5 и 3: 5 + 3 = 8 и 5 · 3 = 15. Подставив числа 5 и 3 в уравнение, убедимся, что они действительно являются его корнями: и

Решение квадратного уравнения путем подбора его корней основано на следующей теореме: если числа m и n таковы, что m + n = – p, a mn = q, то эти числа являются корнями уравнения .

Эта теорема обратна теореме Виета. Чтобы доказать ее, выразим коэффициенты уравнения через m и n: и q = mn. Значит, уравнения можно записать в таком виде: .

Подставим в уравнение вместо х поочередно числа m и n:

Таким образом, эти числа – корни уравнения.

1. Не решая уравнения, укажем, имеет ли оно корни и чему равны произведение и сумма корней.

2. Данное уравнение имеет корни. Объясним, почему уравнение имеет корни одинаковых знаков, и определим их.

3. Данное уравнение имеет корни. Объясним, почему уравнение имеет корни разных знаков. Определим, какой из корней больше по модулю – положительный или отрицательный.

4. Не применяя формулу корней, найдём второй корень уравнения, если известен первый .

5. для составления квадратного уравнения, имеющего корни 8 и 7, можно применить два способа:

1) составить произведение , откуда получаем уравнение .

2)использовать формулы Виета:

, откуда получаем то же уравнение .

Составим вторым способом квадратное уравнение, имеющие корни – 1 и 15.

6. Один из корней уравнения равен – 5.

Определим другой корень и коэффициент p.

Один из корней уравнения равен – 2.

Определим другой корень и коэффициент p.

7. Один из корней уравнения равен – 10.

Определим другой корень и коэффициент q.

Один из корней уравнения равен 3.

Определим другой корень и коэффициент q.

8. Найдём все целые значения p, при которых данное уравнение имеет целые корни.

Найдем все пары целых чисел, произведение которых равно 15.

Соответствующие значения p равны – 16, – 8, 16, 8.

9. Составим квадратное уравнение, корни которого на 2 меньше корней уравнения .

Пусть – корни уравнения, которое надо составить. Тогда

Получим уравнение

III. Изучение теоремы Виета в заочной физико – технической школе

Теореме Виета на всех этапах её изучения уделяется много внимания.

В федеральной заочной физико-технической школе при МФТИ также изучается теорема Виета. Рассмотрим некоторые упражнения из программы 9 класса.

Решите уравнение:

а) б)

в)

Решение: а) По теореме, обратной теореме Виета, и - корни данного уравнения.

Ответ:

б) Заметим, что является корнем данного уравнения. Значит, уравнение имеет корни, и, по теореме Виета, их произведение откуда

Ответ: – 1;

в) заметим, что является корнем. Из условия получем, что

Ответ: 1;

Пример. Пусть и – корни квадратного уравнения .

Выразить через коэффициенты уравнения.

По теореме Виета преобразуем выделив полный квадрат: Отсюда

Ответ:

Задача. Числа и являются корнями уравнения . Найдите а) ; б) .

Решение.

По теореме Виета .

а)

б)

Пример. Пусть и – корни квадратного уравнения .

Полагая, что и х2 0, составить квадратное уравнение, корнями которого являются числа и

Обозначим p= – и q=. По обратной теореме Виета числа и – корни уравнения . Выражаем, применяя к исходному уравнению прямую теорему Виета, числа p и q через a,b,c:

Итак, числа и - корни уравнения или

Заметим, что согласно условию задачи.

Ответ:

Пример 4. Найти все значения к, при которых уравнение

х2 + (2к - 5)х + к2 = 0 имеет только положительные корни.

Во – первых, нужно обеспечить, чтобы уравнение имело корни. Необходимое и достаточное условие этого - неотрицательность дискриминанта: (2к-5)2-4к2>0.

Во – вторых, уже с учетом этого нужно получить условие положительности корней. Простой способ дает теорема Виета. По этой теореме , и если оба корня положительны, то .

Это условие необходимо, но не достаточно, т.к. положительность произведения означает только то, что корни имеют одинаковые знаки (и могут оба казаться отрицательными). По теореме Виета . Если оба корня положительны, то и их сумма положительна, т.е. 5-2k>0.

stud24.ru

теорема Виета проект (разработка)

Муниципальное казенное образовательное учреждение

«Очкуровская средняя общеобразовательная школа»

Николаевского муниципального района Волгоградской области

Теорема Виета

Выполнила: Оноприенко Кристина,

обучающаяся 8 класса

МКОУ «Очкуровская СОШ»

Николаевского района

Руководитель: Е.А.Бульба

с. Очкуровка

2015

Оглавление

Введение……………………………………………………………………… ……3

Основная часть

1.Историческая справка……………………………………………………….4

2.Докозательство теоремы Виета……………………………………………..6

3.Состаление блока уравнений решаемых по теореме Виета……………….8

4.Составлеие тренажера………………………………………………………10

Заключение

Практическая значимость проекта……………………………………...12

Выводы…………………………………………………………………….13

Список источников информации…………………….………………………...14

Приложение……………………………………………………………………..15

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни - дробь уж готова! В числителе с, в знаменателе а. А сумма корней тоже дроби ровна. Хоть с минусом дробь, что за беда! В числителе b, в знаменателе а.

Введение

Актуальность темы проекта: Применение теоремы Виета является уникальным приемом для решения квадратных уравнений устно. В учебнике очень мало квадратных уравнений, решаемых по теореме Виета. Я и мои одноклассники допускаем ошибки.

Объектом исследования является теорема Виета , как неотъемлемая часть решения квадратных уравнений на уроках алгебры .

Предмет исследования – теорема Виета и составление блока уравнений для закрепления навыка решения квадратных уравнений.

Гипотеза: я предположила, что научиться безошибочно решать уравнения по теореме Виета можно, для этого нужен применяя тренажер.

Цель проекта: составить тренажер уравнений, решаемых по теореме Виета.

Задачи:

- узнать историю открытия теоремы Виета;
- провести исследование зависимости коэффициентов квадратного

уравнения и произведения и суммы его корней.

- научиться доказывать теорему Виета;
- самостоятельно составить уравнения, решаемые по теореме Виета
- оформить блок уравнений на бумажном носителе и составить тренажер в электронном виде
- предложить одноклассникам тренажер для решения уравнений по теореме Виета

Методы:

сравнение результатов самостоятельной работы до проекта и после тренировки решение квадратных уравнений применяя теорему Виета
изучение и анализ электронных источников и литературы
самостоятельная работа по составлению блока уравнений и тренажера

$C:\Users\User\Desktop\img2.jpg$

1.Исторические сведения

Франсуа Виет родился в 1540 году на юге Франции в небольшом городке Фантене-ле-Конт.

Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.

Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей и переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы. Он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вел дружескую переписку.

В 1571 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.

В 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.

В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Обретя покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи.

Виет изложил программу своих исследований и перечислил трактаты, объединенные общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом "Введение в аналитическое искусство". Основу своего подхода Виет называл видовой логистикой, он четко разграничивал числа, величины и отношения, собрав их в некую систему "видов". В эту систему входили, например, переменные, их корни, квадраты, кубы, квадрато-квадраты и т. д. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных - согласные.

Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.

Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: "Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D".

В трактате "Дополнения к геометрии" он стремился создать некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвертой степеней. Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.

Математиков столетиями интересовал вопрос решения треугольников, так как он диктовался нуждами астрономии, архитектуры, геодезии. Виет первым явно сформулировал в словесной форме теорему косинусов, хотя положения, эквивалентные ей, эпизодически применялись с первого века до нашей эры. Известный ранее своей трудностью случай решения треугольника по двум данным сторонам и одному из противолежащих им углов получил у Виета исчерпывающий разбор. Глубокое знание алгебры давало Виету большие преимущества. Причем интерес его к алгебре первоначально был вызван приложениями к тригонометрии и астрономии. Не только каждое новое применение алгебры давало импульс новым исследованиям по тригонометрии, но и полученные тригонометрические результаты являлись источником важных успехов алгебры. Виету, в частности, принадлежит вывод выражений для синусов (или хорд) и косинусов кратных дуг.

В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался сеньор де ла Биготье. В придворных новостях маркиз Летуаль писал: "...14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых ученых математиков века умер... в Париже. Ему было более шестидесяти лет".

2 .Доказательство теоремы Виета

3.Составление блока уравнений и электронного тренажера

х2 + 17х - 38 = 0,
х2 - 16х + 4 = 0,
3х2 + 8х - 15 = 0,
7х2 + 23х + 5 = 0,
х2 + 2х - 3 = 0,
х2 + 12х + 32 = 0,
х2 - 7х + 10 = 0,
х2 - 2х - 3= 0,
х2 + 12х + 32 = 0,
2х2 - 11х + 15 = 0,
3х2 + 3х - 18 = 0,
2х2 - 7х + 3 = 0,
х2 + 17х - 18 = 0,
х2 - 17х - 18 = 0,
х2 - 11х + 18 = 0,
х2 + 7х - 38 = 0,
х2 - 9х + 18 = 0,
х2 - 13х + 36 = 0,
х2 - 15х + 36 = 0,
х2 - 5х - 36 = 0.
х2 + х – 2 = 0
х2 + 2х – 3 =0
х2 - 3х + 2 =0
х2 - х – 2 = 0
х2 - 2х – 3 = 0
х2 - 3х – 4 = 0
x2 +17x -18=0
x2 + 23x – 24=0
x2 – 39x-40=0
x2 – 37x – 38=0
x2 – 3x – 10 = 0
x2 – 5x + 3 = 0
x2 + 8x – 11 = 0
x2 + 6х + 5 = 0
x2 – x – 12 = 0
x2 + 5x + 6 = 0
x2 + 3x – 10 = 0
x2 – 8x– 9 = 0
х 2 + х – 56 = 0
х 2 – 19х + 88 = 0
х 2 – 4х – 4 = 0
x 2 -15х+14=0
x 2 +8х+7=0
x2+9х+20=0
x2 +18х -11 = 0
x2 +27х – 24 = 0
5х2 +10х – 3 = 0
3х2 - 16х +9 = 0
x2 +18х -11 = 0
x2 +27х – 24 = 0
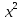-4х-21=0
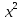-4х-21=0
x2-15х+56=0
x2-4х-60=0
x2+5х+6=0
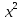+2х-3=0
x2+18х+81=0
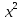-х-20=0
x2+4х+21=0
x2-10х-24=0
x2+х-56=0
x2-х-56=0
x2+3х+2=0
x2+5х-6=0
x2-18х+81=0
x2-9х+20=0
x2 -5х+6=0
x2-4х-21=0
-x2 -7х+6=0
x2-15х+56=0
х2 – 3х + 2 = 0
х2 – 4х + 3 = 0
х2 – 2х + 4 = 0
х2 – 2х + 5 = 0
х2 – 2х + 6 = 0
х2 – 11х + 24 = 0
х2 + 11х – 30 = 0
х2 + х – 12 = 0
x2 – 6х + 8 = 0
х2 – 15х + 14 = 0
x2 – 15x + 14 = 0
x2+ 4 х -21 =0
х2+ х – 42 =0
х2 – х – 20 =0
х2+ 4 х -32=0
х2- 2х – 35 =0
х2+ х - 20 =0
х2+ 7 х + 10 =0
х2- х - 6=0
х2+ 2 х +0=0
х2+ 6 х+0 =0
х2+ 3х - 18=0
х2+ 5 х -24=0
х2- 2 х - 24=0
х2 – 15х + 14 = 0
х2 + 8х + 7 =0
х2+ 9х – 20=0
х2 – 6х - 7 = 0
х2 + 3х - 10 = 0
х2 – х - 12 = 0

3.Тренажер

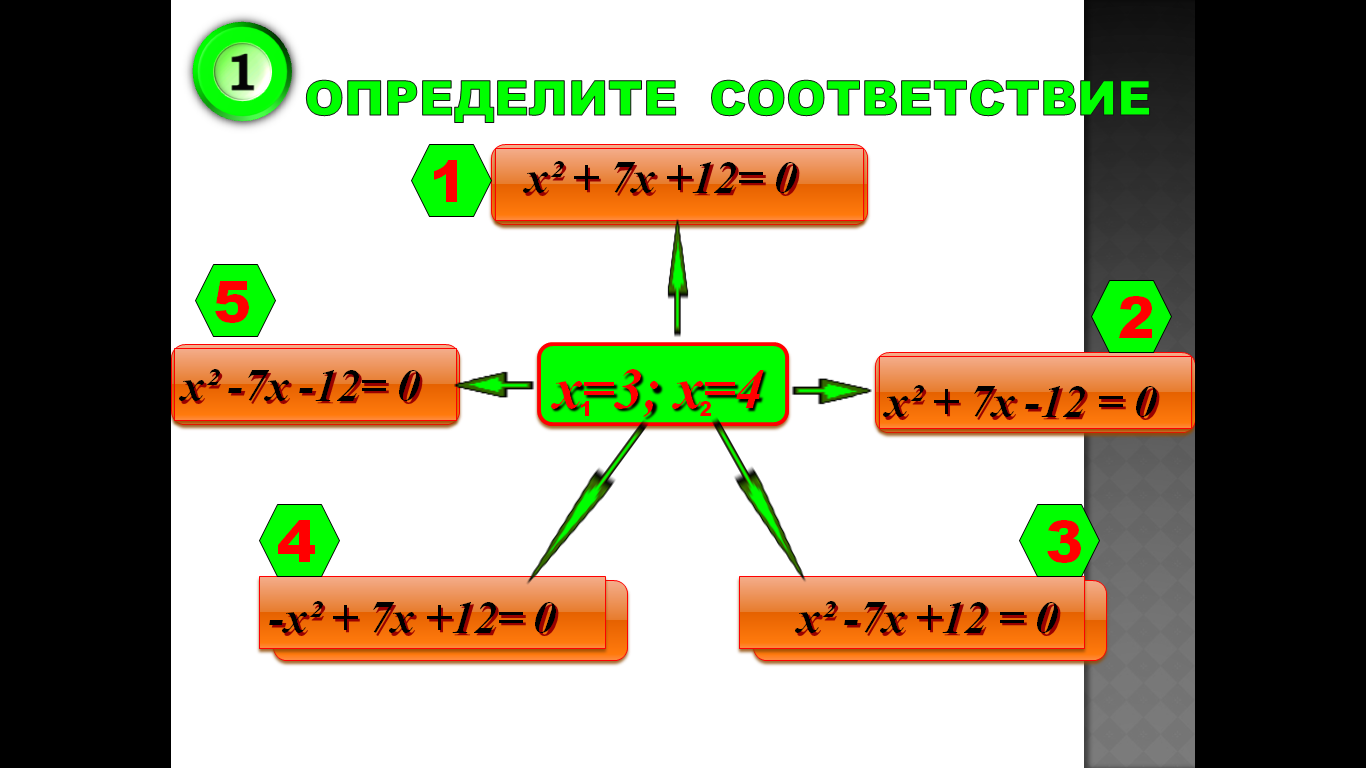
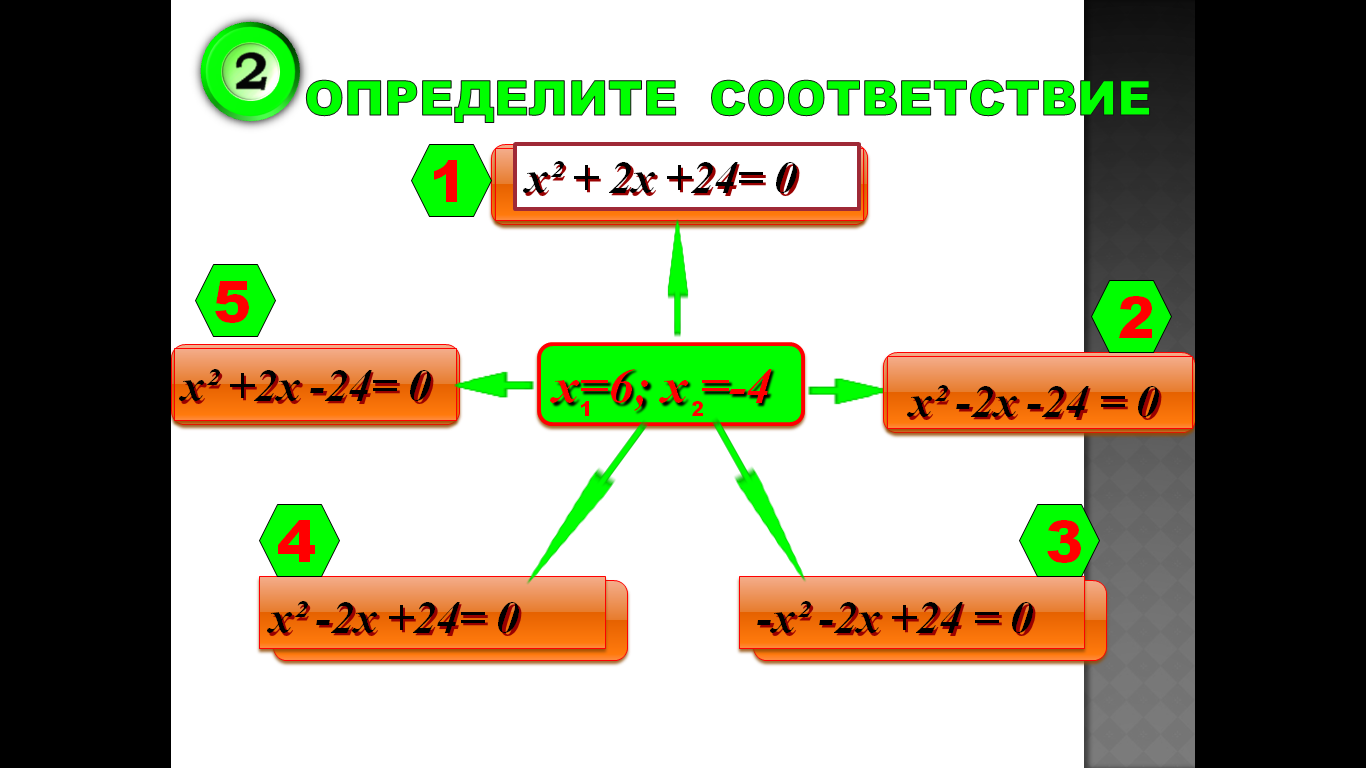
4.Практическая значимость проекта

Применение, а уроках алгебры 8 класса и при итоговом повторении ОГЭ

Выводы:

Результат моего труда – создан блок квадратных уравнений решаемых по теореме Виета.

Я увлеклась работой, проще всего было составить квадратные уравнения, в которых свободный член находится по таблице умножения. Теперь я не только безошибочно нахожу корни уравнения по теореме Виета, но и применяю ее при проверке решения любого квадратного уравнения.

Используя тренажер, я и мои одноклассники научилась решать квадратные уравнения, применяя теорему Виета.

Список источников информации:

Список литературы
1. Алгебра 8 класс: учебник для общеобразовательных учреждений. Г.В.Дорофеев, С.Б.Суворова
2. Дидактические материалы по алгебре для 8 класса. В.И.Жохов, Ю.Н.Макарычев, Н.Г.Миндюк. М.: Просвещение, 2000.
3. Математика. 8 класс: дидактические материалы к учебнику «Математика 8. Алгебра» / под ред. Г. В. Дорофеева. – М. : Дрофа, 2012г.\
4. Государственная итоговая аттестация. 9 класс. Математика. Тематические тестовые задания./Л.Д. Лаппо, М.А. Попов/-М.: Издательство « Экзамен », 2011

Интернет ресурсы

2.2 http://fcior.edu.ru/card/3726/kvadratnoe-uravnenie.html

2.3 http://kopilkaurokov.ru/matematika/uroki/107955

2.4 http://nsportal.ru/shkola/algebra/library/2012/12/10/razrabotki-urokov-po- teme-teorema-vieta

2.5 http://gigabaza.ru/doc/40685.html

Приложение

Этапы реализации проекта

Этапы

Методы исследования

Содержание работы

Планируемый результат

1.Информационный

Сбор информации, ее анализ

Изучение литературы

Материал для теоретической части проекта

2.Организационный

Анализ, обобщение

Разработка блока уравнений

Материал для работы

3. Технологический этап

Подбор уравнений

Составление тренажера

Тренажер

4. Заключительный

Обобщение опыта

Выводы о проделанной работе, оформление проекта

Проект. Оформление коллекции. Мастер-класс. Участие в конкурсе.

infourok.ru

"Теорема Франсуа Виета и её значение в математике"

Выдержка из работы

Департамент образования Владимирской области

Муниципальное образовательное учреждение средняя школа № 38

с углубленным изучением предметов художественно-эстетического профиля

Реферат

Теорема Франсуа Виета и её значение в математике

Выполнила: ученица 10 «А» класса

Коркина Анастасия

Научный руководитель: учитель математики

Тарханова Светлана Александровна

Владимир 2010

Содержание

1. Биография Франсуа Виета

2. История числа р

Список литературы

1. Биография Франсуа Виета

Франсуа Виет родился в 1540 г. во Франции в Фонтене-ле-Конт французской провинции Пуату -- Шарант. Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом. Учился сначала в местном францисканском монастыре, а затем -- в университете Пуатье, где получил степень бакалавра (1560). С 19 лет занимался адвокатской практикой в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике. Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей и переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы. Он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вел дружескую переписку.

Около 1570 года подготовил «Математический Канон» -- труд по тригонометрии, -- который издал в Париже в 1579 году.

В 1571 году переехал в Париж и вскоре перешёл на государственную службу, но увлечение его математикой продолжало расти.

Благодаря связям матери и браку своей ученицы с принцем де Роганом, Виет сделал блестящую карьеру и стал советником сначала короля Генриха III, который назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать выполнение распоряжений в стране и приостанавливать приказы крупных феодалов, а после его убийства -- Генриха IV. Во время когда Виет занимал этот пост голландский математик Андриан ван-Роумен, известный, пожалуй, тем, что вычислил число р; с восемнадцатью верными знаками, повторив тем самым через 150 лет результат среднеазиатского математика ал-Каши, в конце 16 столетия решил бросить вызов всем математикам мира. Он разослал во все европейские страны уравнение 45-й степени: x45 — 45×43 + 945×41 — 12 300×39 +… + 95 634×5 — 3795×3 + 45x = a, Французским математикам он решил это уравнение не посылать, считая, что там нет способных справиться с задачей: Декарт в то время еще не родился, Пьера Рамуса в 1572 убили в Варфоломеевскую ночь, о других математиках не было слышно. Так французские математики не смогли принять вызов. Больше всего было ущемлено самолюбие Генриха IV. — И все же у меня есть математик! — воскликнул король. — Позовите Виета!

В приемную короля вошел пятидесятитрехлетний седоволосый советник короля Франсуа Виет. Он тут же, в присутствие короля, министров и гостей, нашел один корень предложенного уравнения. Король ликовал, все поздравляли придворного советника. На следующий день Виет нашел еще 22 корня уравнения, описываемые выражением: при n=1,2,…, 22. Этим он и ограничился, так как остальные 22 корня — отрицательные, а Виет не признавал ни отрицательных, ни мнимых корней.

После такого успеха Виета составитель злополучного уравнения Роумен стал ревностным почитателем его. Нельзя сказать, что во Франции о Виете ничего не знали. Громкую славу он получил еще раньше, при Генрихе III во время франко-испанской войны. Испанские инквизиторы изобрели очень сложную тайнопись (шифр), которая все время изменялась и дополнялась. Благодаря этому шифру воинствующая и сильная в то время Испания могла свободно переписываться с противниками французского короля даже внутри Франции, и эта переписка оставалась неразгаданной. После бесплодных попыток найти ключ к шифру король обратился к Виету. Рассказывают, что Виет, две недели подряд дни и ночи просидев за работой, все же нашел ключ к испанскому шифру. После этого неожиданно для испанцев Франция стала выигрывать одно сражение за другим. Испанцы долго недоумевали. Наконец им стало известно, что шифр для французов уже не секрет и что виновник его расшифровки — Виет. Будучи уверенными, в невозможности разгадать способ тайнописи людьми, они обвинили Францию перед папой римским и инквизицией в кознях дьявола, а Виет был обвинен в союзе с дьяволом и приговорен к сожжению на костре. К счастью для науки, он не был выдан инквизиции.

Но все свое свободное время, весь свой досуг он отдавал занятиям математикой, а также астрономией. Особенно усиленно он начал работать в области математики с 1584 г. после отстранения от должности при королевском дворе. Виет детально изучил труды, как древних, так и современных ему математиков.

Франсуа Виет по существу создал новую алгебру. Он ввел в нее буквенную символику. Основные его идеи изложены в труде «Введение в аналитическое искусство». Он писал: «Все математики знали, что под их алгеброй и альмукабалой были скрыты несравненные сокровища, но не умели их найти: задачи, которые они считали наиболее трудными, совершенно легко решаются с помощью нашего искусства». Благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами и сами алгебраические выражения превратились в объекты, над которыми можно было производить те или иные действия. Ему принадлежит установление единообразного приема решения уравнений 2-й, 3-й 4-й степени, новый метод решения кубического уравнения, тригонометрическое решение в т.н. неприводимом случае, различные рациональные преобразования корней и пр. Среди этих открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений (формулы Виета).

Действительно, все мы знаем, как легко решать, например, квадратные уравнения. Для их решения имеются готовые формулы. До Ф. Виета решение каждого квадратного уравнения выполнялось по своим правилам в виде очень длинных словесных рассуждений и описаний, довольно громоздких действий. Даже само уравнение в современном виде не могли записать. Для этого тоже требовалось довольно длинное и сложное словесное описание. На овладение приемами решений уравнений требовались годы. Общих правил, подобных современным, а тем более формул решения уравнений не было. Постоянные коэффициенты буквами не обозначались. Рассматривались выражения только с конкретными числовыми коэффициентами.

Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: «Если В+D, умноженное на А, минус, А в квадрате равно ВD, то, А равно В и равно D».

В трактате «Дополнения к геометрии» он стремился создать некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвертой степеней. Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.

В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался сеньор де ла Биготье. В придворных новостях маркиз Летуаль писал: «… 14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых ученых математиков века умер… в Париже. Ему было более шестидесяти лет».

Отметим также, что Виет дал первое в Европе аналитическое (с помощью формулы) представление числа р.

Умер Виет в возрасте 63 лет в 1603 г.

Научная деятельность

Виет чётко представлял себе конечную цель -- разработку нового языка, своего рода обобщённой арифметики, которая даст возможность проводить математические исследования с недостижимыми ранее глубиной и общностью:

Все математики знали, что под их алгеброй… были скрыты несравненные сокровища, но не умели их найти; задачи, которые они считали наиболее трудными, совершенно легко решаются десятками с помощью нашего искусства, представляющего поэтому самый верный путь для математических изысканий.

Виет всюду делит изложение на две части: общие законы и их конкретно-числовые реализации. То есть он сначала решает задачи в общем виде, и только потом приводит числовые примеры. В общей части он обозначает буквами не только неизвестные, что уже встречалось ранее, но и все прочие параметры, для которых он придумал термин «коэффициенты» (буквально: содействующие). Виет использовал для этого только заглавные буквы -- гласные для неизвестных, согласные для коэффициентов.

Виет свободно применяет разнообразные алгебраические преобразование -- например, замену переменных или смену знака выражения при переносе его в другую часть уравнения. Это стоит отметить, принимая во внимание тогдашнее подозрительное отношение к отрицательным числам. Показатели степени у Виета ещё записываются словесно.

Новая система позволила просто, ясно и компактно описать общие законы арифметики и алгоритмы. Символика Виета была сразу же оценена учёными разных стран, которые приступили к её совершенствованию.

Другие заслуги Виета:

знаменитые «формулы Виета» для коэффициентов многочлена как функций его корней;

новый тригонометрический метод решения неприводимого кубического уравнения, применимый также для трисекции угла;

первый пример бесконечного произведения:

полное аналитическое изложение теории уравнений первых четырёх степеней;

идея применения трансцендентных функций к решению алгебраических уравнений;

оригинальный метод приближённого решения алгебраических уравнений с числовыми коэффициентами;

частичное решение задачи Аполлония о построении круга, касающегося трёх данных, в сочинении Apollonius Gallus (1600). Решение Виета не проходит для случая внешних касаний.

виет теорема алгебраический многочлен формула

История числа р

Многие полагают, что раз число р обозначается буквой греческого алфавита, то придумали его непременно древние греки. Конечно же, такой аргумент несостоятельный -- мало ли что сегодня обозначается буквами греческого алфавита: б-лучи (физика), у-орбитали (химия), в-рецепторы (биология)… Древние эллины оставили исключительно глубокий след в истории человеческой цивилизации, но приписывать все исключительно им было бы не в согласии с исторической правдой.

Мы сегодня прекрасно осведомлены о том, кто построил первый самолет, придумал радио и телевизор, оставил первый след подошвы на поверхности Луны. А вот кто первый догадался о замечательной связи длины окружности и ее диаметра -- увы, не знает никто. Возможно, об этом догадался какой-нибудь дотошный мастер, изготавливающий колесо для легкой колесницы, или землекоп, обустраивающий круглый колодец. А, может быть, гончар, лесоруб, строитель… -- кто бы это ни был, имя этого гения история нам не сберегла.

А вот когда появилось первое обозначение знаменитого числа буквой р мы можем сказать с большой степенью уверенности. Его мы находим в работе «Synopsis Palmoriorum Matheseos» («Обозрение достижений математики») английского преподавателя Уильяма Джонса (1675−1749), вышедшей в 1706 году. Несколько раньше, в 1647 году, английский математик Оутред (1574−1660) (кстати, автор знакомого нам знака умножения «х «) букву р применил для обозначения длины окружности. По-видимому, к этому обозначению его подвигла первая буква греческого слова жернрерш -- окружность (отсюда наше: периферия).

Обозначение р для отвлеченного числа 3,141 592… широко распространилось и, по сути, стало международным стандартом после того, как его стал применять выдающийся математик Леонард Эйлер (1707−1783) в своих получивших всемирную известность трудах. К этому обозначению Леонард Эйлер, скорее всего, пришел независимо от Джонса.

Представления о числе р претерпели удивительную эволюцию -- от смутных представлений древних, экспериментально -- буквально ощупью открывавших количественные закономерности окружающего мира до чрезвычайно глубоких математических теорий современности.

Натиск зыбучих песков забвения выдержали величественные «скалы-останцы» -- памятник древней шумеро-вавилонско-ассирийской культуры конца IV тысячелетия до нашей эры — начала нашей эры. Возможно, они уцелели под безжалостными ветрами истории лишь потому, что «сложены» были из обожженных на огне клинописных глиняных табличек. Из них мы узнаем о многогранных талантах и умениях древних жителей Междуречья.

Древние мастера уже делали многое из того, чем можем похвастаться мы. Делением года на 12 месяцев -- по числу знаков зодиака, а также суток -- на 24 часа мы обязаны древним халдеям. Прикладывая, школьный транспортир к углу, и определяя его величину в градусах, мы также отдаем дань памяти вавилонским ученым, впервые разделивших круг на 360 равных частей.

Как явствует из клинописных табличек, возраст которых -- ни много, ни мало -- несколько тысяч лет! -- жители Междуречья могли извлекать квадратные и кубические корни, решать квадратные уравнения, рассчитывать объемы плотин и осадных насыпей, имеющих довольно сложные геометрические очертания.

Но вот что удивительно: будучи искусными мастерами и инженерами, жители Междуречья применяли довольно грубое значение для числа р. Как следует из древних решений ряда задач, в своих расчетах они неявно пользовались значением р? 3.

Словесные рецепты древних вавилонян для вычисления площади круга можно выразить современной формулой

где S -- площадь круга, а С -- длина ограничивающей его окружности.

Способ, применявшийся для вывода этой формулы, неизвестен. Если в нее подставить знакомые современному школьнику выражения площади круга S =рr 2 и длины окружности С = 2рr, то из равенства

получим р=3.

Следующая задача содержится в одном из клинописных текстов, принадлежащих Британскому музею:

«60 длина окружности. 2, на сколько я спустился. Что есть хорда?» Речь в этой задаче идет о вычислении длины хорды АВ, стрелка которой CD равна 2, причем длина окружности равна 60.

Вот как нам предлагает решать эту задачу неизвестный вавилонский математик (числа записаны в удобной для нас десятичной системе счисления, которой в Междуречье не пользовались):

«Ты возведи 2 в квадрат, 4 ты видишь. 4 от 20, диаметра, отними, 16 ты видишь. 20, диаметр, возведи в квадрат, 400 ты видишь. 16 возведи в квадрат, 256 ты видишь. 256 от 400 отними, 144 ты видишь. Что есть квадратный корень из 144? 12, квадратный корень, это хорда. Таков способ».

Если не обращать внимания на одну вычислительную погрешность, то приведенный рецепт нахождения хорды соответствует формуле,

которую может вывести современный школьник (здесь, а = АВ, h -- CD, d -- диаметр окружности).

Примечательно, что в приведенном тексте при длине окружности С = 60 диаметр d получается равным 20 -- это соответствует значению р = 3. Тот факт, что радиус помещается в окружности в качестве хорды 6 раз, оставил неизгладимый отпечаток в мировоззрении жителей Междуречья. Они разделили год на 360 дней и сообразно этому круг (видимую орбиту Солнца) на 360 градусов.

В одной из глиняных табличек, найденных при раскопках 1936 года города Сузы, более чем в 200 милях к востоку от Вавилона, обнаружены расчеты, использующие более точное приближение для числа р: р? 3?. Известный историк науки профессор Отто Нейгебауэр полагает, что древним месопотамским вычислителям было известно лучшее приближение для р, применявшееся в тех случаях, когда грубое приближение р? 3 приводило к явно неправильным результатам. Однако не все специалисты разделяют его точку зрения. Например, Айзик Абрамович Вайман считает, что в «математических задачах значение р = 3?. — обнаружено лишь в одном случае, и то сомнительном».

Более точное значение для р использовали древние египтяне. В Лондоне и Нью-Йорке хранятся две части древнеегипетского папируса, который цитируют как «папирус Ринда (или Райнда)» -- по имени Henry Rhind мецената, приобретшего этот папирус в 1858 году. Гораздо логичнее было бы называть документ именем писца Ахмеса, составившего его в промежутке между 2000 и 1700 годами до нашей эры. Этот папирус был найден в 1858 году, расшифрован и опубликован А. Эйзенлором в 1877 году.

Стиль изложения Ахмеса близок к стилю древневавилонских табличек. В его записях мы также находим рецепты решения различных практических задач. В одной из таких задач папируса дается «наставление, как вычислить круглый хлебный амбар», имеющий форму круглого цилиндра с диаметром у основания 9 локтей. Для вычисления площади основания предлагается такой рецепт:

Из каких соображений получена эта формула? -- Неизвестно. Тем не менее, современные исследователи пытаются найти теоретические обоснования, которыми могли бы руководствоваться древние при ее выводе. Мы остановимся на двух современных реконструкциях вывода этой формулы, не лишенных изящества.

Находка профессора Глейзера

Одно из ранних приближений для числа р можно извлечь из канонического текста Библии, датируемого примерно X—V вв.еками до нашей эры. В третьей книге Царств подробно рассказывается о том, как мастер Хирам сооружал по заказу правителя Иудейского Израильского царства Соломона храм. Это культовое сооружение украшал большой бассейн для омовения священнослужителей под названием «медного моря»:

Нетрудно подсчитать, что в данном случае используется приближение для числа р=30/10 = 3.

Академик Российской академии образования профессор Г. Глейзер сравнительно недавно исследовал первоисточник процитированного выше текста. И вот к каким удивительным выводам пришел (поистине: удивительное рядом, только не нужно закрывать на него, глаза!)

В оригинальном тексте Ветхого завета слово линия (снурок) имеет два значения. Рядом с этим словом приписана буква ГЕЙ, про которую инструкция на полях указывает, что эта буква не произносится. Древним иудеям было свойственно придавать буквам ивритского алфавита определенные числовые значения. Если подсчитать сумму значений букв удлиненного слова (с буквой ГЕЙ), и укороченного (без этой буквы), то отношение двух полученных чисел оказывается равным 111 106=1,471 698 … Профессор Г. Глейзер предполагает, что упоминаемую в тексте длину снурка 30 локтей нужно умножить на этот коэффициент, тогда более точное значение длины окружности «литого моря» окажется равным 31,415 094… Соответственно этому новому значению длины снурка получаем р = 3,1 415 094…, что совпадает с точным значением р = 3,141 592… в первых четырех знаках. Это дало повод профессору Г. Глейзеру выдвинуть сенсационную гипотезу: еще в Древнем мире времен царя Соломона знали о числе р с точностью до 4−5 знаков.

В дошедших до нас с незапамятных времен математических текстах встречаются приближения для числа р различной точности. Все их можно охарактеризовать одной фразой: значение для р есть, но из каких соображений оно было получено -- неизвестно. Скорее всего, древние тщательно анализировали и сопоставляли результаты измерений окружающих их предметов. Любой здравомыслящий человек, столкнувшись с практической проблемой измерения длины окружности, может предложить множество способов, как это сделать: «померить» окружность ниточкой, «обкатать» ее линейкой или, наоборот, «прокатить» окружность вдоль линейки. В этой связи не вызывает удивления способ средневекового магистра Франкона из Льежа, который догадался сравнивать площади круга и квадрата взвешиванием фигур на весах. Опыт, практика, эмпирические данные играют важную роль в осмыслении закономерности окружающего мира и помогают выдвигать гипотезы, относящиеся к миру идей и абстракций -- миру математики. Ниже приводятся некоторые сведения о найденных древними математиками приближениях для числа р. Происхождение их неизвестно.

Любопытно, что живший в раннехристианскую эпоху римский архитектор Витрувий пользовался достаточно грубым приближением для числа р. Он проектировал внушительных размеров Римский театр и даже разрабатывал проекты городов. Но точность 3? для числа р его вполне удовлетворила!

В приведенной выше таблице обнаруживаются и удивительно точные значения. Результат китайского математика и астронома Цзу Чун-чжи отличается от точного значения р= 3,14 159 265… лишь в седьмом знаке после запятой! Очень долго (вплоть до реформ Петра-I) математическая мысль России находилась в глубоком летаргическом сне. В одной из берестяных грамот XVII века «Чта какое место по округе ведать вдоль и поперег» мы находим различные приближенные способы определения площадей круглых полей. Например, для решения задачи: «Было поле кругом 1 488 сажен. И ты скажи: что в том будет четвероугольном сажен и что вереди круга в дол и поперег до окольной меры мерою» предлагается такой рецепт: «…возьми меры, что кругом ево будет сажен и ту окружную меру раздели на четыре части; а четвертым паем таковожь число умножь: столько в том поле четвероугольных сажен будет, единую сажен не поте-ряешь.» В нашей символике этот рецепт можно записать в виде формулы:

Французскому математику Франсуа Виету (1540−1603) удалось выразить число р бесконечным произведением радикалов:

При выводе своей формулы Виет исходил из следующего свойства правильных вписанных в круг единичного радиуса многоугольников:

где Sk, S2k --площади правильных вписанных в круг единичного радиуса k -угольника и 2k -угольника; hk --апофема k-угольника. Отсюда

Между апофемами h3k и hk правильных вписанных в круг единичного радиуса 2k- и k-угольника существует следующая связь:

Ее можно получить из соотношения

между апофемой h и стороной a правильного вписанного в круг единичного радиуса многоугольника. Поскольку, то из предыдущего равенства получаем:

;

и т.д.

Список литературы

http: //www. hrono. ru/biograf/bio_we/viet. html

Показать Свернуть

inprofteh.com.ua

Теорема Виета проект (разработка). Реферат теорема виета

1. Биография Франсуа Виета. Теорема Франсуа Виета и её значение в математике

Похожие главы из других работ:

1.6 О теореме Виета

1. Биография

1. Биография Вейля

§1. Биография и творческий путь Б. В. Гнеденко

2.3 Теорема Виета

2.5 Формула Виета для многочленов (уравнений) высших степеней

Глава I. Краткая биография Н.И. Лобачевского

Глава I. Краткая биография Н.И. Лобачевского

Биография Исаака Ньютона

1.4 Тригонометрическая формула Виета

1. Биография А. Гурвица

1.3.8 Использование теоремы Виета

Теорема Виета

Доказательство

Примеры использования:

в квадратном уравнении

в кубическом уравнении

теорема Виета проект (разработка)

"Теорема Франсуа Виета и её значение в математике"

Выдержка из работы

Смотрите также