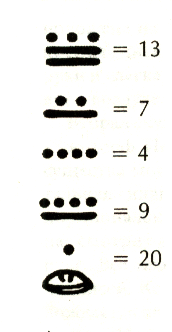Учебное пособие: ов : Календарь и система счисления майя. Реферат система счисления майя
Реферат - ов : Календарь и система счисления майя
Темы для рефератов :
- Календарь и система счисления майя.
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари.
- Египетские, вавилонские и греческие методы вычислений.
- Методы вычислений в «Альмагесте» Птолемея.
- Эволюция позиционных систем счисления (вавилоняне, майя, индо-арабская система).
- Метод исчерпывания Архимеда и его аксиомы для объемов и площадей.
- Суперэкспоненциальная система Архимеда для обозначения больших чисел.
- Методы вычислений в средние века.
- Доказательство Кузанского непротиворечивости догмата о триединстве Бога.
- Решение уравнений 3-ей и 4-той степеней. Появление мнимых чисел.
- Спиноза: попытка применения математических методов к этике.
- «Я стоял на плечах гигантов». Ньютон и его предшественники в создании анализа бесконечно малых.
- Лейбниц и идея calculus universalis.
- Ферма, Декарт и появление алгебраической символики.
- Проективная геометрия.
- Гаусс, Лобачевский, Бойяи, Риман: от классической геометрии к современной.
- История открытия Нептуна и Плутона.
- Кватернионы, р-адические числа и другие расширения числового поля.
- Группы и симметрии. Шубниковские группы.
- Нестандартный анализ и анализ бесконечно малых: сравнение.
- История и решение 10—той проблемы Гильберта.
- Примеры применения идеальных конструкций для перехода от одних практических результатов к другим.
- Теорема Оревкова и парадокс изобретателя.
- Неполнота теорий. Теоремы Геделя и Тарского.
- Классификация двумерных многообразий и разрешимость проблемы их эквивалентности.
- Яблоко Куратовского и другие парадоксальные следствия аксиомы выбора.
- Математика с аксиомой деретминированности.
- Появление первых механических вычислительных машин.
- Появление программного управления (Жаккард).
- Автоматы 18 века и их отличие от современных автоматов.
- Аналитическая машина Беббиджа.
- Августа Ада Лавлейс и появление программирования.
- Аналоговые машины.
- Первые машины Цузе.
- Марк-1 и ЭНИАК.
- Первые советские проекты вычислительных машин. МЭСМ.
- Первые серийные вычислительные машины (США, СССР и Европа).
- Проект пятого поколения (Япония). История его создания и причины неудачи.
- Алгоритм приближенного перебора Шеннона и его некорректность (Арлазаров, Адельсон-Вельский и др.)
- Проблема обучения для ЭВМ. Известные подходы к ее решению.
- ЭЛИЗА и проблема общения на естественном языке.
- Работы Т. Винограда и проблема понимания предложений естественного языка.
- Зарождение вычислительной лингвистики в США и в СССР.
- Общий решатель задач.
- Проблема машинного поиска доказательства теорем.
- Р. Луллий и появление идеи автоматического синтеза знания.
- Дж. Буль и появление алгебры логики.
- Появление теории алгоритмов (Карри, Тьюринг, Пост, Черч, Гильберт).
- Какие понятия программирование заимствовало из логики?
- Проблемы, связанные с представлением действительных чисел в машине.
- Понятия доказательных и гарантированно точных вычислений.
- Богданов и появление теории систем.
- Берталанффи и появление математической теории систем. Основные ее понятия.
- Понятие обратной связи. Примеры моделей с обратной связью.
- Дискуссии вокруг кибернетики на раннем этапе ее развития.
- Некорректные задачи и некоторые из методов их регуляризации.
Зачетные вопросы
- Определение понятия «Искусственный интеллект». Основные направления исследований.
- Основные понятия теории измерений.
- Задачи, решаемые методами Data Mining. Особенность этих задач.
- Задачи автоматической классификации (таксономии). Постановка и методы решения.
- Содержание и методы решения задач выбора информативных характеристик.
- Постановка и методы решения задачи распознавания образов.
- Обнаружение ошибок и заполнение пробелов в таблицах данных.
- Метрика в пространстве знаний. Задачи анализа знаний (Knowledge Mining).
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари. Роль астрономии в развитии математики.
- Египетские, вавилонские и средневековые методы вычислений. Влияние позиционной системы счисления.
- Разложение функции в ряд Фурье. Приближение произвольных периодических движений гармониками (принцип часовых механизмов).
- Зарождение идеи вычислительной машины и программирования.
- Первые вычислительные машины в Германии, США, Европе и СССР.
- БЭСМ-1, Стрела, М-2 и М-20.
- Понятие адресности системы команд. 0, 1, 2, 3, 4-адресные машины.
- Методы формального описания синтаксиса языков программирования. Первые языки и трансляторы.
- Понятие разделения времени. Первые операционные системы.
- Автомат и полугруппа. Поведение автомата без входа. Неразрешимость множества простых чисел автоматом.
- Отрицательная и положительная обратная связь. Устойчивость и неустойчивость. Предельные циклы. Простейшие катастрофы.
- Примеры некорректных задач. Простейшие методы регуляризации некорректных задач.
- Понятие схемы программ. Абстрактная интерпретация.
- Понятие аннотированной программы. Пред- и постусловия. Характеризация простейших операторов.
- Общая идея кибернетики. Примеры успешных кибернетических аналогий.
www.ronl.ru
Календарь и система счисления майя
Темы для рефератов : - Календарь и система счисления майя.
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари.
- Египетские, вавилонские и греческие методы вычислений.
- Методы вычислений в «Альмагесте» Птолемея.
- Эволюция позиционных систем счисления (вавилоняне, майя, индо-арабская система).
- Метод исчерпывания Архимеда и его аксиомы для объемов и площадей.
- Суперэкспоненциальная система Архимеда для обозначения больших чисел.
- Методы вычислений в средние века.
- Доказательство Кузанского непротиворечивости догмата о триединстве Бога.
- Решение уравнений 3-ей и 4-той степеней. Появление мнимых чисел.
- Спиноза: попытка применения математических методов к этике.
- «Я стоял на плечах гигантов». Ньютон и его предшественники в создании анализа бесконечно малых.
- Лейбниц и идея calculus universalis.
- Ферма, Декарт и появление алгебраической символики.
- Проективная геометрия.
- Гаусс, Лобачевский, Бойяи, Риман: от классической геометрии к современной.
- История открытия Нептуна и Плутона.
- Кватернионы, р-адические числа и другие расширения числового поля.
- Группы и симметрии. Шубниковские группы.
- Нестандартный анализ и анализ бесконечно малых: сравнение.
- История и решение 10—той проблемы Гильберта.
- Примеры применения идеальных конструкций для перехода от одних практических результатов к другим.
- Теорема Оревкова и парадокс изобретателя.
- Неполнота теорий. Теоремы Геделя и Тарского.
- Классификация двумерных многообразий и разрешимость проблемы их эквивалентности.
- Яблоко Куратовского и другие парадоксальные следствия аксиомы выбора.
- Математика с аксиомой деретминированности.
- Появление первых механических вычислительных машин.
- Появление программного управления (Жаккард).
- Автоматы 18 века и их отличие от современных автоматов.
- Аналитическая машина Беббиджа.
- Августа Ада Лавлейс и появление программирования.
- Аналоговые машины.
- Первые машины Цузе.
- Марк-1 и ЭНИАК.
- Первые советские проекты вычислительных машин. МЭСМ.
- Первые серийные вычислительные машины (США, СССР и Европа).
- Проект пятого поколения (Япония). История его создания и причины неудачи.
- Алгоритм приближенного перебора Шеннона и его некорректность (Арлазаров, Адельсон-Вельский и др.)
- Проблема обучения для ЭВМ. Известные подходы к ее решению.
- ЭЛИЗА и проблема общения на естественном языке.
- Работы Т. Винограда и проблема понимания предложений естественного языка.
- Зарождение вычислительной лингвистики в США и в СССР.
- Общий решатель задач.
- Проблема машинного поиска доказательства теорем.
- Р. Луллий и появление идеи автоматического синтеза знания.
- Дж. Буль и появление алгебры логики.
- Появление теории алгоритмов (Карри, Тьюринг, Пост, Черч, Гильберт).
- Какие понятия программирование заимствовало из логики?
- Проблемы, связанные с представлением действительных чисел в машине.
- Понятия доказательных и гарантированно точных вычислений.
- Богданов и появление теории систем.
- Берталанффи и появление математической теории систем. Основные ее понятия.
- Понятие обратной связи. Примеры моделей с обратной связью.
- Дискуссии вокруг кибернетики на раннем этапе ее развития.
- Некорректные задачи и некоторые из методов их регуляризации.
Зачетные вопросы - Определение понятия "Искусственный интеллект". Основные направления исследований.
- Основные понятия теории измерений.
- Задачи, решаемые методами Data Mining. Особенность этих задач.
- Задачи автоматической классификации (таксономии). Постановка и методы решения.
- Содержание и методы решения задач выбора информативных характеристик.
- Постановка и методы решения задачи распознавания образов.
- Обнаружение ошибок и заполнение пробелов в таблицах данных.
- Метрика в пространстве знаний. Задачи анализа знаний (Knowledge Mining).
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари. Роль астрономии в развитии математики.
- Египетские, вавилонские и средневековые методы вычислений. Влияние позиционной системы счисления.
- Разложение функции в ряд Фурье. Приближение произвольных периодических движений гармониками (принцип часовых механизмов).
- Зарождение идеи вычислительной машины и программирования.
- Первые вычислительные машины в Германии, США, Европе и СССР.
- БЭСМ-1, Стрела, М-2 и М-20.
- Понятие адресности системы команд. 0, 1, 2, 3, 4-адресные машины.
- Методы формального описания синтаксиса языков программирования. Первые языки и трансляторы.
- Понятие разделения времени. Первые операционные системы.
- Автомат и полугруппа. Поведение автомата без входа. Неразрешимость множества простых чисел автоматом.
- Отрицательная и положительная обратная связь. Устойчивость и неустойчивость. Предельные циклы. Простейшие катастрофы.
- Примеры некорректных задач. Простейшие методы регуляризации некорректных задач.
- Понятие схемы программ. Абстрактная интерпретация.
- Понятие аннотированной программы. Пред- и постусловия. Характеризация простейших операторов.
- Общая идея кибернетики. Примеры успешных кибернетических аналогий.
| www.yurii.ru
Рефератов : Календарь и система счисления майя
Календарь и система счисления майя.
Древние вычислительные машины. Стоунхедж и сибирские костяные календари.
Египетские, вавилонские и греческие методы вычислений.
Методы вычислений в «Альмагесте» Птолемея.
Эволюция позиционных систем счисления (вавилоняне, майя, индо-арабская система).
Метод исчерпывания Архимеда и его аксиомы для объемов и площадей.
Суперэкспоненциальная система Архимеда для обозначения больших чисел.
Методы вычислений в средние века.
Доказательство Кузанского непротиворечивости догмата о триединстве Бога.
Решение уравнений 3-ей и 4-той степеней. Появление мнимых чисел.
Спиноза: попытка применения математических методов к этике.
«Я стоял на плечах гигантов». Ньютон и его предшественники в создании анализа бесконечно малых.
Лейбниц и идея calculus universalis.
Ферма, Декарт и появление алгебраической символики.
Проективная геометрия.
Гаусс, Лобачевский, Бойяи, Риман: от классической геометрии к современной.
История открытия Нептуна и Плутона.
Кватернионы, р-адические числа и другие расширения числового поля.
Группы и симметрии. Шубниковские группы.
Нестандартный анализ и анализ бесконечно малых: сравнение.
История и решение 10—той проблемы Гильберта.
Примеры применения идеальных конструкций для перехода от одних практических результатов к другим.
Теорема Оревкова и парадокс изобретателя.
Неполнота теорий. Теоремы Геделя и Тарского.
Классификация двумерных многообразий и разрешимость проблемы их эквивалентности.
Яблоко Куратовского и другие парадоксальные следствия аксиомы выбора.
Математика с аксиомой деретминированности.
Появление первых механических вычислительных машин.
Появление программного управления (Жаккард).
Автоматы 18 века и их отличие от современных автоматов.
Аналитическая машина Беббиджа.
Августа Ада Лавлейс и появление программирования.
Аналоговые машины.
Первые машины Цузе.
Марк-1 и ЭНИАК.
Первые советские проекты вычислительных машин. МЭСМ.
Первые серийные вычислительные машины (США, СССР и Европа).
Проект пятого поколения (Япония). История его создания и причины неудачи.
Алгоритм приближенного перебора Шеннона и его некорректность (Арлазаров, Адельсон-Вельский и др.)
Проблема обучения для ЭВМ. Известные подходы к ее решению.
ЭЛИЗА и проблема общения на естественном языке.
Работы Т. Винограда и проблема понимания предложений естественного языка.
Зарождение вычислительной лингвистики в США и в СССР.
Общий решатель задач.
Проблема машинного поиска доказательства теорем.
Р. Луллий и появление идеи автоматического синтеза знания.
Дж. Буль и появление алгебры логики.
Появление теории алгоритмов (Карри, Тьюринг, Пост, Черч, Гильберт).
Какие понятия программирование заимствовало из логики?
Проблемы, связанные с представлением действительных чисел в машине.
Понятия доказательных и гарантированно точных вычислений.
Богданов и появление теории систем.
Берталанффи и появление математической теории систем. Основные ее понятия.
Понятие обратной связи. Примеры моделей с обратной связью.
Дискуссии вокруг кибернетики на раннем этапе ее развития.
Некорректные задачи и некоторые из методов их регуляризации.
Определение понятия "Искусственный интеллект". Основные направления исследований.
Основные понятия теории измерений.
Задачи, решаемые методами Data Mining. Особенность этих задач.
Задачи автоматической классификации (таксономии). Постановка и методы решения.
Содержание и методы решения задач выбора информативных характеристик.
Постановка и методы решения задачи распознавания образов.
Обнаружение ошибок и заполнение пробелов в таблицах данных.
Метрика в пространстве знаний. Задачи анализа знаний (Knowledge Mining).
Древние вычислительные машины. Стоунхедж и сибирские костяные календари. Роль астрономии в развитии математики.
Египетские, вавилонские и средневековые методы вычислений. Влияние позиционной системы счисления.
Разложение функции в ряд Фурье. Приближение произвольных периодических движений гармониками (принцип часовых механизмов).
Зарождение идеи вычислительной машины и программирования.
Первые вычислительные машины в Германии, США, Европе и СССР.
БЭСМ-1, Стрела, М-2 и М-20.
Понятие адресности системы команд. 0, 1, 2, 3, 4-адресные машины.
Методы формального описания синтаксиса языков программирования. Первые языки и трансляторы.
Понятие разделения времени. Первые операционные системы.
Автомат и полугруппа. Поведение автомата без входа. Неразрешимость множества простых чисел автоматом.
Отрицательная и положительная обратная связь. Устойчивость и неустойчивость. Предельные циклы. Простейшие катастрофы.
Примеры некорректных задач. Простейшие методы регуляризации некорректных задач.
Понятие схемы программ. Абстрактная интерпретация.
Понятие аннотированной программы. Пред- и постусловия. Характеризация простейших операторов.
Общая идея кибернетики. Примеры успешных кибернетических аналогий.
refdb.ru
Календарь и система счисления майя
Темы для рефератов:Календарь и система счисления майя.Древние вычислительные машины. Стоунхедж и сибирские костяные календари.Египетские, вавилонские и греческие методы вычислений.Методы вычислений в «Альмагесте» Птолемея.Эволюция позиционных систем счисления (вавилоняне, майя, индо-арабская система).Метод исчерпывания Архимеда и его аксиомы для объемов и площадей.Суперэкспоненциальная система Архимеда для обозначения больших чисел.Методы вычислений в средние века.Доказательство Кузанского непротиворечивости догмата о триединстве Бога.Решение уравнений 3-ей и 4-той степеней. Появление мнимых чисел.Спиноза: попытка применения математических методов к этике.«Я стоял на плечах гигантов». Ньютон и его предшественники в создании анализа бесконечно малых.Лейбниц и идея calculus universalis.Ферма, Декарт и появление алгебраической символики.Проективная геометрия.Гаусс, Лобачевский, Бойяи, Риман: от классической геометрии к современной.История открытия Нептуна и Плутона.Кватернионы, р-адические числа и другие расширения числового поля.Группы и симметрии. Шубниковские группы.Нестандартный анализ и анализ бесконечно малых: сравнение.История и решение 10—той проблемы Гильберта.Примеры применения идеальных конструкций для перехода от одних практических результатов к другим.Теорема Оревкова и парадокс изобретателя.Неполнота теорий. Теоремы Геделя и Тарского.Классификация двумерных многообразий и разрешимость проблемы их эквивалентности.Яблоко Куратовского и другие парадоксальные следствия аксиомы выбора.Математика с аксиомой деретминированности.Появление первых механических вычислительных машин.Появление программного управления (Жаккард).Автоматы 18 века и их отличие от современных автоматов.Аналитическая машина Беббиджа.Августа Ада Лавлейс и появление программирования.Аналоговые машины.Первые машины Цузе.Марк-1 и ЭНИАК.Первые советские проекты вычислительных машин. МЭСМ.Первые серийные вычислительные машины (США, СССР и Европа).Проект пятого поколения (Япония). История его создания и причины неудачи.Алгоритм приближенного перебора Шеннона и его некорректность (Арлазаров, Адельсон-Вельский и др.)Проблема обучения для ЭВМ. Известные подходы к ее решению.ЭЛИЗА и проблема общения на естественном языке.Работы Т. Винограда и проблема понимания предложений естественного языка.Зарождение вычислительной лингвистики в США и в СССР.Общий решатель задач.Проблема машинного поиска доказательства теорем.Р. Луллий и появление идеи автоматического синтеза знания.Дж. Буль и появление алгебры логики.Появление теории алгоритмов (Карри, Тьюринг, Пост, Черч, Гильберт).Какие понятия программирование заимствовало из логики?Проблемы, связанные с представлением действительных чисел в машине.Понятия доказательных и гарантированно точных вычислений.Богданов и появление теории систем.Берталанффи и появление математической теории систем. Основные ее понятия.Понятие обратной связи. Примеры моделей с обратной связью.Дискуссии вокруг кибернетики на раннем этапе ее развития.Некорректные задачи и некоторые из методов их регуляризации.Зачетные вопросыОпределение понятия "Искусственный интеллект". Основные направления исследований.Основные понятия теории измерений.Задачи, решаемые методами Data Mining. Особенность этих задач.Задачи автоматической классификации (таксономии). Постановка и методы решения.Содержание и методы решения задач выбора информативных характеристик.Постановка и методы решения задачи распознавания образов.Обнаружение ошибок и заполнение пробелов в таблицах данных.Метрика в пространстве знаний. Задачи анализа знаний (Knowledge Mining).Древние вычислительные машины. Стоунхедж и сибирские костяные календари. Роль астрономии в развитии математики.Египетские, вавилонские и средневековые методы вычислений. Влияние позиционной системы счисления.Разложение функции в ряд Фурье. Приближение произвольных периодических движений гармониками (принцип часовых механизмов).Зарождение идеи вычислительной машины и программирования.Первые вычислительные машины в Германии, США, Европе и СССР.БЭСМ-1, Стрела, М-2 и М-20. Понятие адресности системы команд. 0, 1, 2, 3, 4-адресные машины.Методы формального описания синтаксиса языков программирования. Первые языки и трансляторы.Понятие разделения времени. Первые операционные системы.Автомат и полугруппа. Поведение автомата без входа. Неразрешимость множества простых чисел автоматом. Другие файлы: Представление числовой информацииСистема счисления как способ записи информации с помощью заданного набора цифр. История развития различных систем счисления. Позиционные и непозиционн... История развития математикиВавилонская система счисления, таблицы обратных чисел и математика для исследования движений планет. Египетский календарь и введение символа для обозн... Цивилизация майя, причины крахаСоциальный строй древних майя, внешность индейцев. Религия майя и культы. Солнце Кинич-Ахау как один из главных богов. Ритуалы кровопускания у племени... Системы летоисчисления. КалендарьСущность летоисчисления как последовательности отсчета времени. Календарь как хронологическая система счисления, основанная на периодичности движения... Астрономия майя как земное отражение космосаОбщественная организация и религиозные верования. Астрономия и математика майя. Астрономы майя — на службе земледелия. Календарная система майя. Два к... |
www.tnu.in.ua
Учебное пособие - ов : Календарь и система счисления майя
Темы для рефератов :
- Календарь и система счисления майя.
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари.
- Египетские, вавилонские и греческие методы вычислений.
- Методы вычислений в «Альмагесте» Птолемея.
- Эволюция позиционных систем счисления (вавилоняне, майя, индо-арабская система).
- Метод исчерпывания Архимеда и его аксиомы для объемов и площадей.
- Суперэкспоненциальная система Архимеда для обозначения больших чисел.
- Методы вычислений в средние века.
- Доказательство Кузанского непротиворечивости догмата о триединстве Бога.
- Решение уравнений 3-ей и 4-той степеней. Появление мнимых чисел.
- Спиноза: попытка применения математических методов к этике.
- «Я стоял на плечах гигантов». Ньютон и его предшественники в создании анализа бесконечно малых.
- Лейбниц и идея calculus universalis.
- Ферма, Декарт и появление алгебраической символики.
- Проективная геометрия.
- Гаусс, Лобачевский, Бойяи, Риман: от классической геометрии к современной.
- История открытия Нептуна и Плутона.
- Кватернионы, р-адические числа и другие расширения числового поля.
- Группы и симметрии. Шубниковские группы.
- Нестандартный анализ и анализ бесконечно малых: сравнение.
- История и решение 10—той проблемы Гильберта.
- Примеры применения идеальных конструкций для перехода от одних практических результатов к другим.
- Теорема Оревкова и парадокс изобретателя.
- Неполнота теорий. Теоремы Геделя и Тарского.
- Классификация двумерных многообразий и разрешимость проблемы их эквивалентности.
- Яблоко Куратовского и другие парадоксальные следствия аксиомы выбора.
- Математика с аксиомой деретминированности.
- Появление первых механических вычислительных машин.
- Появление программного управления (Жаккард).
- Автоматы 18 века и их отличие от современных автоматов.
- Аналитическая машина Беббиджа.
- Августа Ада Лавлейс и появление программирования.
- Аналоговые машины.
- Первые машины Цузе.
- Марк-1 и ЭНИАК.
- Первые советские проекты вычислительных машин. МЭСМ.
- Первые серийные вычислительные машины (США, СССР и Европа).
- Проект пятого поколения (Япония). История его создания и причины неудачи.
- Алгоритм приближенного перебора Шеннона и его некорректность (Арлазаров, Адельсон-Вельский и др.)
- Проблема обучения для ЭВМ. Известные подходы к ее решению.
- ЭЛИЗА и проблема общения на естественном языке.
- Работы Т. Винограда и проблема понимания предложений естественного языка.
- Зарождение вычислительной лингвистики в США и в СССР.
- Общий решатель задач.
- Проблема машинного поиска доказательства теорем.
- Р. Луллий и появление идеи автоматического синтеза знания.
- Дж. Буль и появление алгебры логики.
- Появление теории алгоритмов (Карри, Тьюринг, Пост, Черч, Гильберт).
- Какие понятия программирование заимствовало из логики?
- Проблемы, связанные с представлением действительных чисел в машине.
- Понятия доказательных и гарантированно точных вычислений.
- Богданов и появление теории систем.
- Берталанффи и появление математической теории систем. Основные ее понятия.
- Понятие обратной связи. Примеры моделей с обратной связью.
- Дискуссии вокруг кибернетики на раннем этапе ее развития.
- Некорректные задачи и некоторые из методов их регуляризации.
Зачетные вопросы
- Определение понятия «Искусственный интеллект». Основные направления исследований.
- Основные понятия теории измерений.
- Задачи, решаемые методами Data Mining. Особенность этих задач.
- Задачи автоматической классификации (таксономии). Постановка и методы решения.
- Содержание и методы решения задач выбора информативных характеристик.
- Постановка и методы решения задачи распознавания образов.
- Обнаружение ошибок и заполнение пробелов в таблицах данных.
- Метрика в пространстве знаний. Задачи анализа знаний (Knowledge Mining).
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари. Роль астрономии в развитии математики.
- Египетские, вавилонские и средневековые методы вычислений. Влияние позиционной системы счисления.
- Разложение функции в ряд Фурье. Приближение произвольных периодических движений гармониками (принцип часовых механизмов).
- Зарождение идеи вычислительной машины и программирования.
- Первые вычислительные машины в Германии, США, Европе и СССР.
- БЭСМ-1, Стрела, М-2 и М-20.
- Понятие адресности системы команд. 0, 1, 2, 3, 4-адресные машины.
- Методы формального описания синтаксиса языков программирования. Первые языки и трансляторы.
- Понятие разделения времени. Первые операционные системы.
- Автомат и полугруппа. Поведение автомата без входа. Неразрешимость множества простых чисел автоматом.
- Отрицательная и положительная обратная связь. Устойчивость и неустойчивость. Предельные циклы. Простейшие катастрофы.
- Примеры некорректных задач. Простейшие методы регуляризации некорректных задач.
- Понятие схемы программ. Абстрактная интерпретация.
- Понятие аннотированной программы. Пред- и постусловия. Характеризация простейших операторов.
- Общая идея кибернетики. Примеры успешных кибернетических аналогий.
www.ronl.ru
Календарь и система счисления майя
Темы для рефератов: - Календарь и система счисления майя.
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари.
- Египетские, вавилонские и греческие методы вычислений.
- Методы вычислений в «Альмагесте» Птолемея.
- Эволюция позиционных систем счисления (вавилоняне, майя, индо-арабская система).
- Метод исчерпывания Архимеда и его аксиомы для объемов и площадей.
- Суперэкспоненциальная система Архимеда для обозначения больших чисел.
- Методы вычислений в средние века.
- Доказательство Кузанского непротиворечивости догмата о триединстве Бога.
- Решение уравнений 3-ей и 4-той степеней. Появление мнимых чисел.
- Спиноза: попытка применения математических методов к этике.
- «Я стоял на плечах гигантов». Ньютон и его предшественники в создании анализа бесконечно малых.
- Лейбниц и идея calculus universalis.
- Ферма, Декарт и появление алгебраической символики.
- Проективная геометрия.
- Гаусс, Лобачевский, Бойяи, Риман: от классической геометрии к современной.
- История открытия Нептуна и Плутона.
- Кватернионы, р-адические числа и другие расширения числового поля.
- Группы и симметрии. Шубниковские группы.
- Нестандартный анализ и анализ бесконечно малых: сравнение.
- История и решение 10—той проблемы Гильберта.
- Примеры применения идеальных конструкций для перехода от одних практических результатов к другим.
- Теорема Оревкова и парадокс изобретателя.
- Неполнота теорий. Теоремы Геделя и Тарского.
- Классификация двумерных многообразий и разрешимость проблемы их эквивалентности.
- Яблоко Куратовского и другие парадоксальные следствия аксиомы выбора.
- Математика с аксиомой деретминированности.
- Появление первых механических вычислительных машин.
- Появление программного управления (Жаккард).
- Автоматы 18 века и их отличие от современных автоматов.
- Аналитическая машина Беббиджа.
- Августа Ада Лавлейс и появление программирования.
- Аналоговые машины.
- Первые машины Цузе.
- Марк-1 и ЭНИАК.
- Первые советские проекты вычислительных машин. МЭСМ.
- Первые серийные вычислительные машины (США, СССР и Европа).
- Проект пятого поколения (Япония). История его создания и причины неудачи.
- Алгоритм приближенного перебора Шеннона и его некорректность (Арлазаров, Адельсон-Вельский и др.)
- Проблема обучения для ЭВМ. Известные подходы к ее решению.
- ЭЛИЗА и проблема общения на естественном языке.
- Работы Т. Винограда и проблема понимания предложений естественного языка.
- Зарождение вычислительной лингвистики в США и в СССР.
- Общий решатель задач.
- Проблема машинного поиска доказательства теорем.
- Р. Луллий и появление идеи автоматического синтеза знания.
- Дж. Буль и появление алгебры логики.
- Появление теории алгоритмов (Карри, Тьюринг, Пост, Черч, Гильберт).
- Какие понятия программирование заимствовало из логики?
- Проблемы, связанные с представлением действительных чисел в машине.
- Понятия доказательных и гарантированно точных вычислений.
- Богданов и появление теории систем.
- Берталанффи и появление математической теории систем. Основные ее понятия.
- Понятие обратной связи. Примеры моделей с обратной связью.
- Дискуссии вокруг кибернетики на раннем этапе ее развития.
- Некорректные задачи и некоторые из методов их регуляризации.
Зачетные вопросы - Определение понятия "Искусственный интеллект". Основные направления исследований.
- Основные понятия теории измерений.
- Задачи, решаемые методами Data Mining. Особенность этих задач.
- Задачи автоматической классификации (таксономии). Постановка и методы решения.
- Содержание и методы решения задач выбора информативных характеристик.
- Постановка и методы решения задачи распознавания образов.
- Обнаружение ошибок и заполнение пробелов в таблицах данных.
- Метрика в пространстве знаний. Задачи анализа знаний (Knowledge Mining).
- Древние вычислительные машины. Стоунхедж и сибирские костяные календари. Роль астрономии в развитии математики.
- Египетские, вавилонские и средневековые методы вычислений. Влияние позиционной системы счисления.
- Разложение функции в ряд Фурье. Приближение произвольных периодических движений гармониками (принцип часовых механизмов).
- Зарождение идеи вычислительной машины и программирования.
- Первые вычислительные машины в Германии, США, Европе и СССР.
- БЭСМ-1, Стрела, М-2 и М-20.
- Понятие адресности системы команд. 0, 1, 2, 3, 4-адресные машины.
- Методы формального описания синтаксиса языков программирования. Первые языки и трансляторы.
- Понятие разделения времени. Первые операционные системы.
- Автомат и полугруппа. Поведение автомата без входа. Неразрешимость множества простых чисел автоматом.
- Отрицательная и положительная обратная связь. Устойчивость и неустойчивость. Предельные циклы. Простейшие катастрофы.
- Примеры некорректных задач. Простейшие методы регуляризации некорректных задач.
- Понятие схемы программ. Абстрактная интерпретация.
- Понятие аннотированной программы. Пред- и постусловия. Характеризация простейших операторов.
- Общая идея кибернетики. Примеры успешных кибернетических аналогий.
| superbotanik.net
Возможности использования чисел в различных системах счисления с древности до наших дней
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕГОРОД ОКРУЖНОГО ЗНАЧЕНИЯ НИЖНЕВАРТОВСКМУНИЦИПАЛЬНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯСРЕДНЯЯ ШКОЛА №5
Научно-исследовательская работа по теме:
«ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ЧИСЕЛ В РАЗЛИЧНЫХ СИСТЕМАХ СЧИСЛЕНИЯ С ДРЕВНОСТИ ДО НАШИХ ДНЕЙ»
Автор: Бусова Евгения,
ученица 6 «В» класса
Руководитель: Губанова Светлана Владимировна,учитель математики
Нижневартовск
2015
Содержание.
Введение……………………………………………………………….3
Первобытная система счёта..................................................................7
Основание системы счисления……………………………………….6
Нумерация……………………………………………………………...7
Древнекитайская десятичная…………………………………………9
Календарь Майя……………………………………………………….11
Система счисления Майя ……………………………………………12
Заключение…………………………………………………………….15
Список используемых информационных ресурсов…………………16
Введение
На уроках математики я познакомилась с десятичной системой счисления. У меня возник вопрос: существовали или существуют другие системы счисления. Я решила найти в различных источниках информацию по этому вопросу.
Сейчас в мире очень актуальна тема – наука Майя, особенно их предсказание конца света в 2012 году.
Режиссеры уже сняли на эту тему фильм-катастрофу, в глянцевых журналах периодически появляются статьи на тему конца света, и так далее и тому подобное. Все эти предсказания строятся на том факте, что календарь майя заканчивается именно в 2012 году и завершает эру продолжительностью 5126 лет. И мне захотелось узнать, что представляет календарь Майя?
Цель моей работы
Ответить на вопрос действительно ли предсказание народа майя достоверно.
Задачи:
Познакомиться с первобытной, славянской, древнекитайской системой счисления.
Изучить систему счисления племени Майя.
Осуществить перевод чисел с календаря Майя в десятичную систему счисления.
Первобытная система счёта
У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.

Это самая простая система счисления. В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки , кружочка ○, или любой другой фигуры. Тогда числа будут записываться примерно так:
1
2
3
4
5
и т. д.
Такая система счисления использовалась, и до сих пор используется народами, не имеющими письменности.
Но иногда такой системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками в тетради количество проданных товаров.
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?
И люди начали изобретать системы счисления.
Основание системы счисления
Основание системы счисления – это число, на основе которого ведется счет. Например, если основание системы счисления равно десяти, то минимальная счетная группа этой системы счисления равна десяти, это значит, что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при этом запоминаем число десятков. В нашей «арабской» системе основанием является число десять. Есть системы счисления и с другим основанием. Это такие системы счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.
Десятеричная и пятеричная система возникла от того факта, что на одной руке человека пять пальцев, на обоих руках 10 пальцев.

Так проще считать. Если добавить пальцы и на ногах, то будет понятная и двадцатеричная система. Происхождение двенадцатеричной системы тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев.

Нумерация
Славянская кириллическая десятеричная алфавитная
нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:
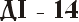
Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:
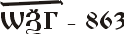 = 800+60+3
= 800+60+3
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
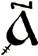
Тысяча
1000

Тьма
10 000

Легион
100 000

Леодр
1 000 000

Ворон
10 000 000

Колода
100 000 000
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
Древнекитайская десятичная
Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.

1

6

2

7
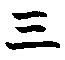
3

8

4

9

5
O
0
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.




10
100
1 000
10 000

 - 1*1 000 = 1000;
- 1*1 000 = 1000;




 - 5 * 100+4* 10+8 = 548
- 5 * 100+4* 10+8 = 548
Даже Пушкин предложил свой вариант формы арабских чисел. Он решил, что все десять арабских цифр, включая нуль, помещаются в магическом квадрате.
Календарь Майя
Один из самых интересных и загадочных подарков древних майянцев современной цивилизации - это календарь.

Мифы и легенды майянцев скрываются в их текстах, в которых главным действующим лицом оказываются числа. Числами наполнены мифы со времен сотворения мира, а числа 1, 4, 5, 7, 8, 9, 13 поистине кажутся священными. А свойства чисел, которыми пользовались Майя просто поражают воображение.
Трудно поверить, что всю историю человечества можно описать с помощью тринадцати чисел и двадцати символов. Но эти двадцать символов означают нечто большее, чем числа, скрывающиеся под особой формой, именуемой иероглифами. Эти иероглифы несут в себе смыслы и, таким образом, вся наука, мифология, мироздание оказывается вмешенным в матрицу размером 13 х 20. Первоначальное название этой матрицы из 260 элементов неизвестно, и археологи назвали ее «Цолькин» - «счет дней», или, буквально, «счет кинов» («кин» означает «Солнце», «день» и является основной единицей). Цолькин, который часто называют Священным Календарем, представляет собой одну из самых странных нумерологических систем. Священный календарь Майя кажется на первый взгляд архаичной реликвией, записанной на кодовом языке, дошедшей до нас из далекого прошлого.
Посмотрев на календарь Майя, я увидела непонятные значки и рисунки. И у меня появился вопрос, что это за непонятная система счисления? Стало интересно увидеть и понять, как в древности люди писали цифры, какие для этого они применяли значки? Как из этих цифр они составляли числа?
Система счисления Майя
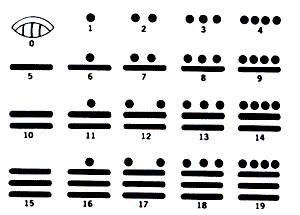
Система счисления Майя- это фантастически простая и гибкая система. Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы.
Единицы обозначаются точкой. Черта обозначает пятерку или число кратное произведению пяти и двадцати, а раковина означает нуль, завершение.
Из этих единиц строится позиционная система майя:
Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).
Число 20 изображалось из двух цифр, ноль и один наверху  и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками.
и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками.
Так, например, нетрудно перевести в десятичную систему счисления следующие символы
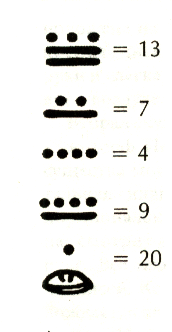
Получается чрезвычайно простая и гибкая система позиционного счисления.
В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу 359 только одну единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: 360 является начальным числом третьего порядка и его место уже не на второй, а на третьей полке.
Но тогда выходит, что начальное число третьего порядка больше начального числа второго не в двадцать раз (20x20=400, а не 360!), а только в восемнадцать! Значит, принцип двадцатеричности нарушен! Все верно. Это и есть исключение.
Дело в том, что у индейцев Майя 20 дней - кинов образовывали месяц или виналь. 18 месяцев - виналов образовывали год или туну (360 дней в году) и так далее:
Кин = 1 день. Виналь = 20 кин = 20 дней. Тун = 18 виналь = 360 дней = около 1 года. Катун = 20 тун = 7200 дней = около 20 лет. Бактун = 20 катун = 144000 дней = около 400 лет. Пиктун = 20 бактун = 2880000 дней = около 8000 лет. Калабтун = 20 пиктун = 57 600 000 дней = около 160000 лет. К'инчильтун = 20 калабтун = 1152000000 дней = около 3200000 лет. Алавтун = 20 кинчильтун = 23040000000 дней = около 64000000 лет.

Заключение
Я познакомилась с календарем индейцев Майя, изучила их систему счисления, узнала как возникли и развивались системы счисления разных народов мира.
Я убедилась, что система счисления индейцев Майя достаточно понятна, но еще раз посмотрев на их календарь, я смогла прочитать некоторые цифры, но не поняла его полное строение, т.к изображение нечеткое, стертое временем. Поэтому я считаю, что предсказание конца света в 2012 году не может быть точным.
В своей исследовательской работе хочется продолжить изучение систем счисления и ответь на вопрос, почему весь современный мир принял одну систему счисления?
Список используемых информационных ресурсов
1.Ван дер Ванден Б.Л. Пробуждающаяся наука М.,1959
2.Данн Дальмедино А.,Пейффер Ж., Пути и лабиринты. Очерки по истории математики М.,1986
3. Гельфман Э.Г., Вольфенгаут Ю.Ю., Демидова Л.Н., Жилина Е.И., Лобаненко Н.Б., Холодная М.А. Учебное пособие Десятичные дроби в Мум


infourok.ru





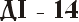
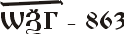 = 800+60+3
= 800+60+3









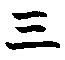









 - 1*1 000 = 1000;
- 1*1 000 = 1000;



 - 5 * 100+4* 10+8 = 548
- 5 * 100+4* 10+8 = 548


 и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками.
и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками.