Опорный план открытого урока
Преподаватель: Бажина А.С.
Дисциплина: «Математика»
Группа: А/ПСО(9)-15-01 (008)
Тема занятия: "Десятичный и натуральный логарифм. Формула перехода к другому
основанию"
Цели занятия:
Дидактическая повторить понятие логарифма числа, свойства логарифма; дать понятие десятичного и натурального логарифма.
Развивающая: овладеть знаниями и умениями для нахождения значений десятичного и натурального логарифма используя:
Воспитательная: развивать мышление обучающихся при выполнении упражнений; продолжить формировать умение правильно воспринимать и активно запоминать новую информацию.
Методическая цель: продолжить совершенствование методики проведения занятия с использованием современных технологий в процессе изложения нового материала, проверки знаний.
Формирование общих компетенций:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
Вид занятия: комбинированный урок.
Тип занятия: изучение нового материала.
Междисциплинарные связи: математический анализ, физика,
Учебно-методическое и материально-техническое оснащение занятия: мультимедиа-проектор, мультимедиа презентация, содержащая материал для повторения, изучения и закрепления теоретических знаний, для отработки навыков практического применения теории к решению упражнений, создания проблемной ситуации, учебник Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/[Ш.А. Алимов, Ю.М. Колягин], тетради.
План занятия
I.Организационно-мотивационный этап (5 мин)
1. Приветствие (осуществление первичного контакта со студентами).
2. Визуальный контроль готовности учащихся к проведению занятия.
3.Сообщение темы занятия.
4.Сообщение цели занятия и компетенций.
5.Ознакомление студентов с критериями оценки их работы на занятии:
Фронтальный опрос2 этап Проблемное задание
3 этап Работа у доски
Итого за занятие (балл)
Оценка уровня освоения темы (в баллах)
0,15
0,15
0,4
0,7
Оценка освоения компетенций (в баллах)
0,1
0,1
0,1
0,3
Оценка
0,25 балла – 5;
0,15 балла – 4;
0,1 балла – 3
0,25 балла – 5;
0,15 балла – 4;
0,1 балла – 3
0,5 балла – 5;
0,3 балла – 4;
0,1 балла – 3
[1-0,8) балла – 5;
[0,8-0,5) балла – 4;
[0,5-0,2] балла – 3
II.Актуализация знаний (6 – 10 мин)
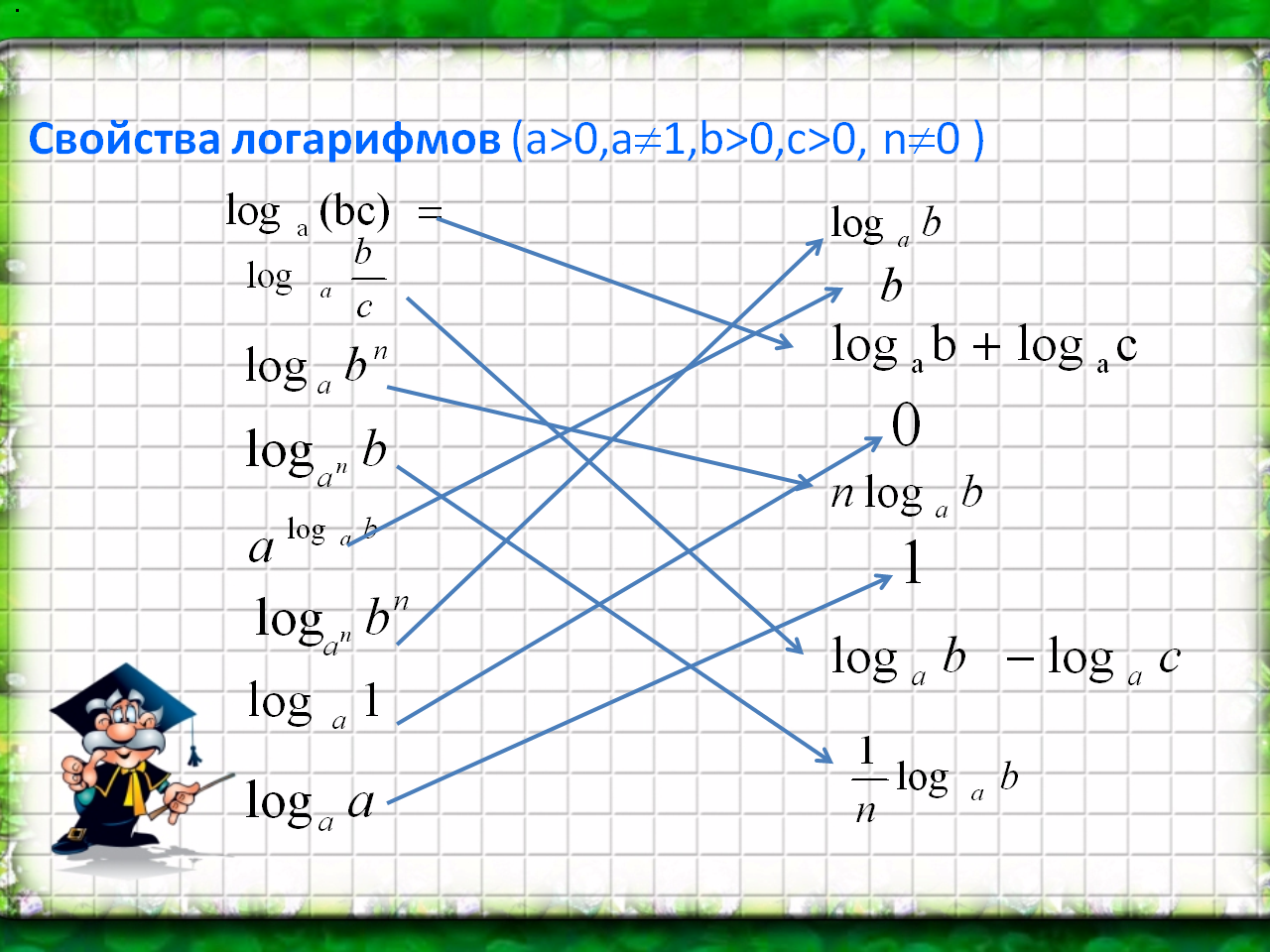
Повторение понятия и свойств логарифма (формулы на сопоставление)(слайд 6-7)
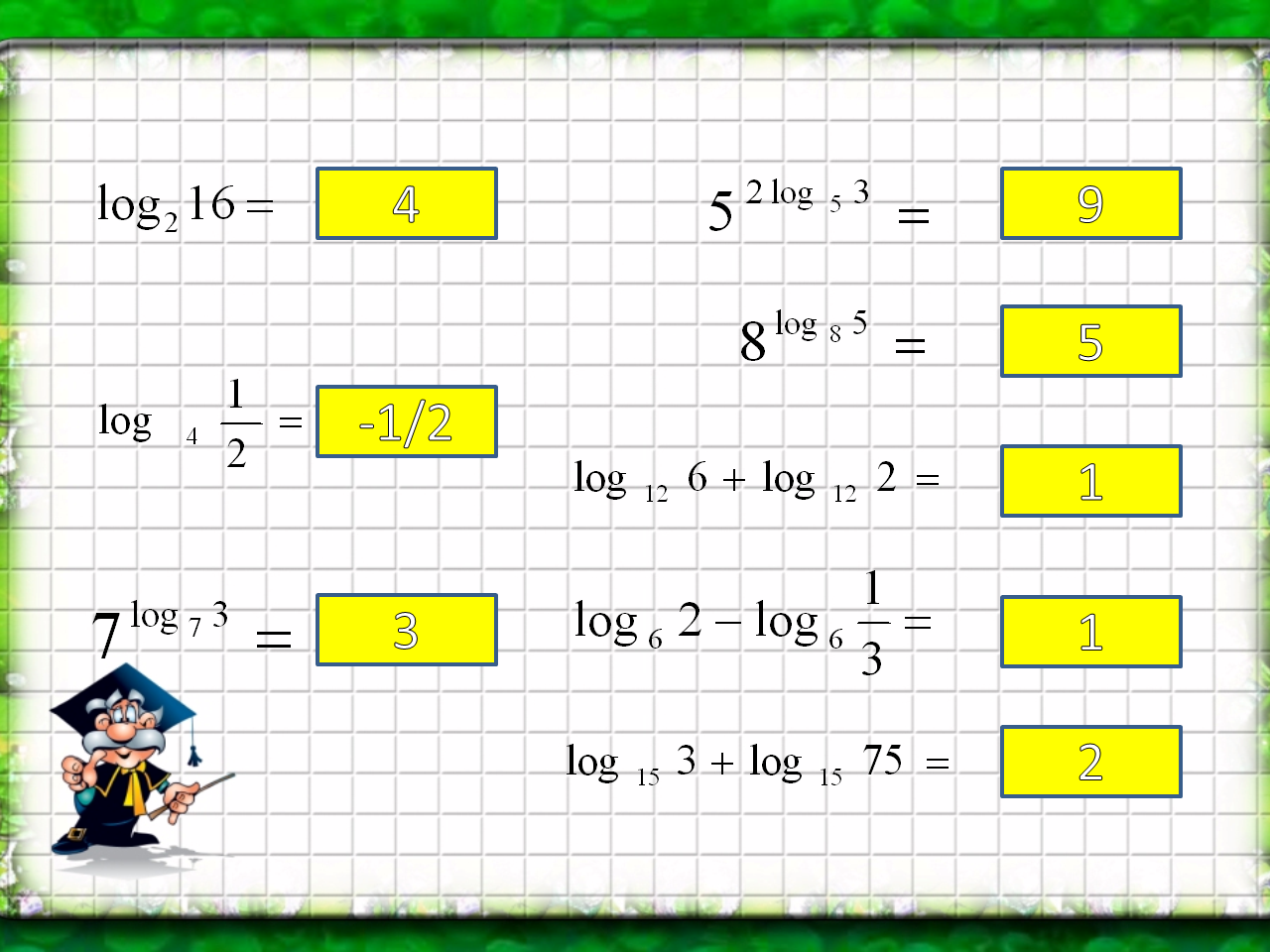
Нахождение логарифма числа по свойствам логарифма (устный опрос)(слайд 8)
III.Изучение нового учебного материала (20 мин)
План
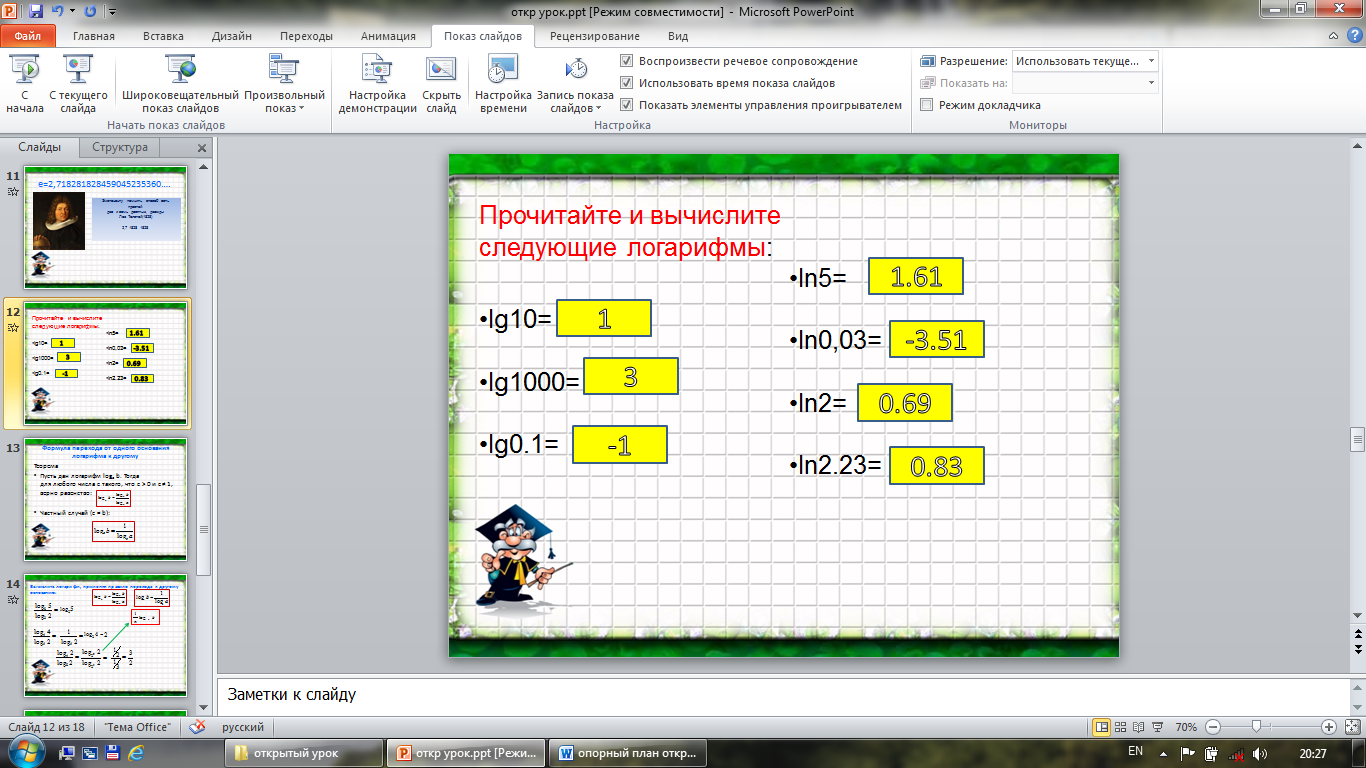
Определение десятичного логарифма. Обозначение. Правила вычисления (объяснение, конспект)(слайд 9-10)
Десятичным логарифмом называется логарифм по основанию 10.
Обозначение: lg (log 10 а = lg а)
Определение натурального логарифма. Обозначение. Правила вычисления (объяснение, конспект)(слайд 11)
Натуральным логарифмом называется логарифм по основанию е.
Обозначение: ln (log e а = ln а)
Историческая справка: Краткое сообщение из истории происхождения натурального логарифма.(слайд 12)
Практическое задание (устно) (слайд13)
Формулы перехода от одного основания логарифма к другому. Основные формулы объяснение, конспект)(слайд14)
Теорема
П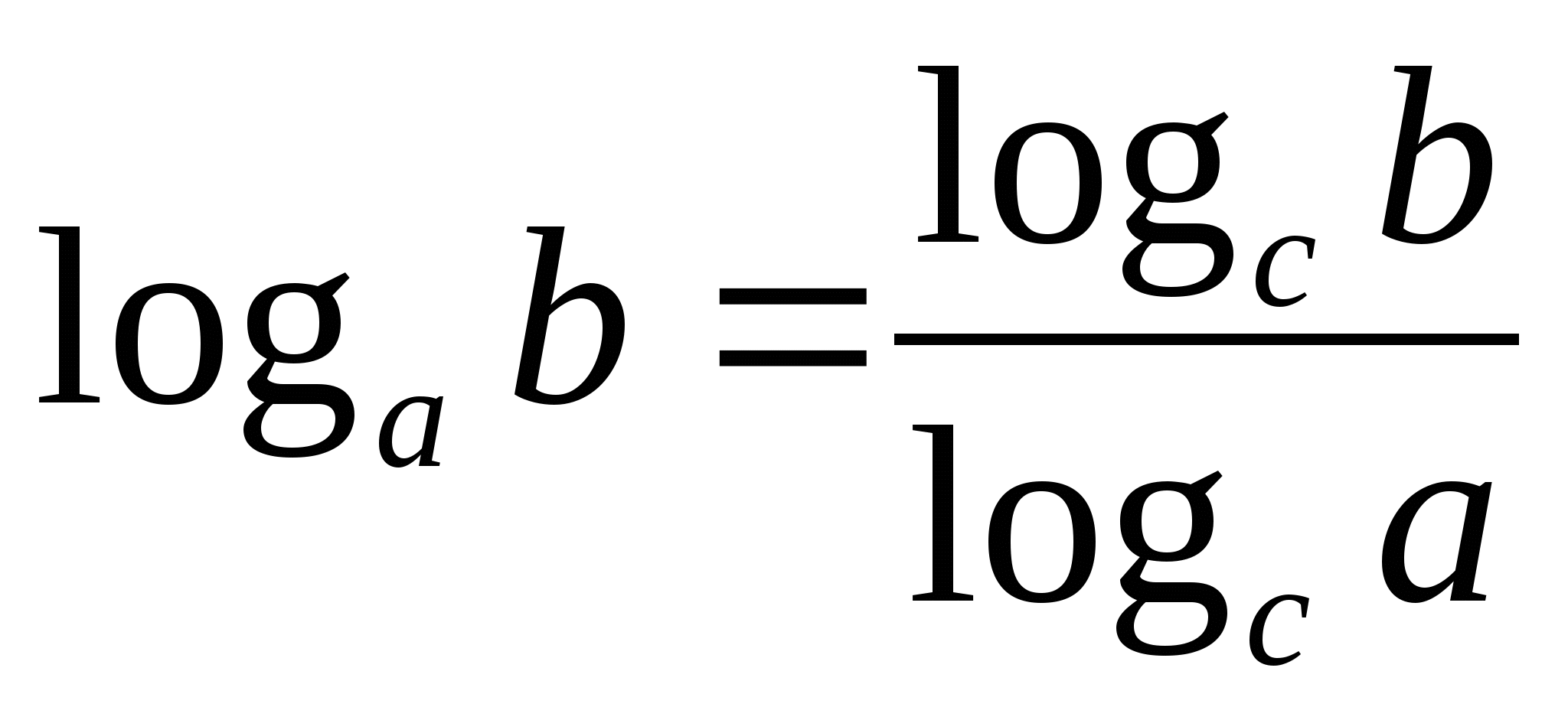
усть дан логарифм logab. Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:
Ч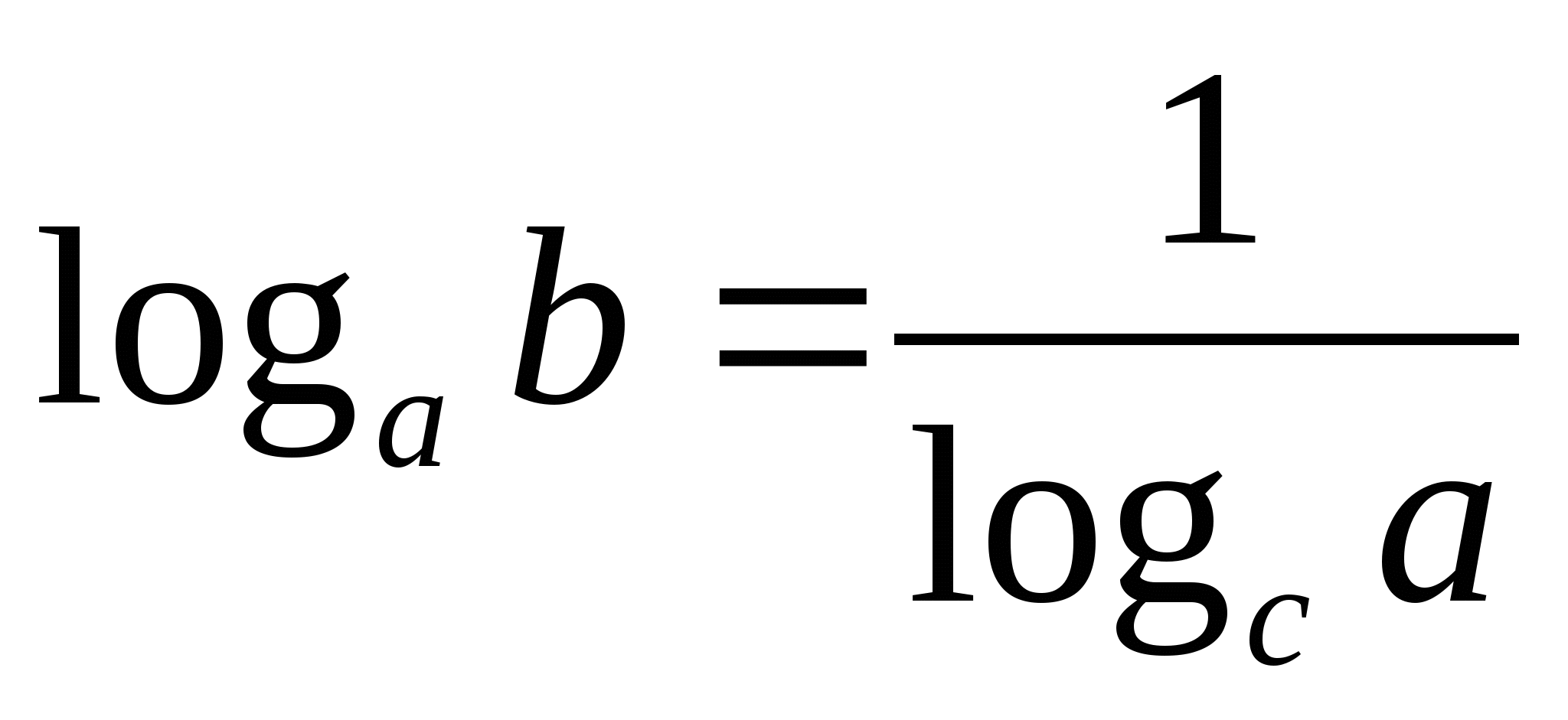
астный случай (c = b):
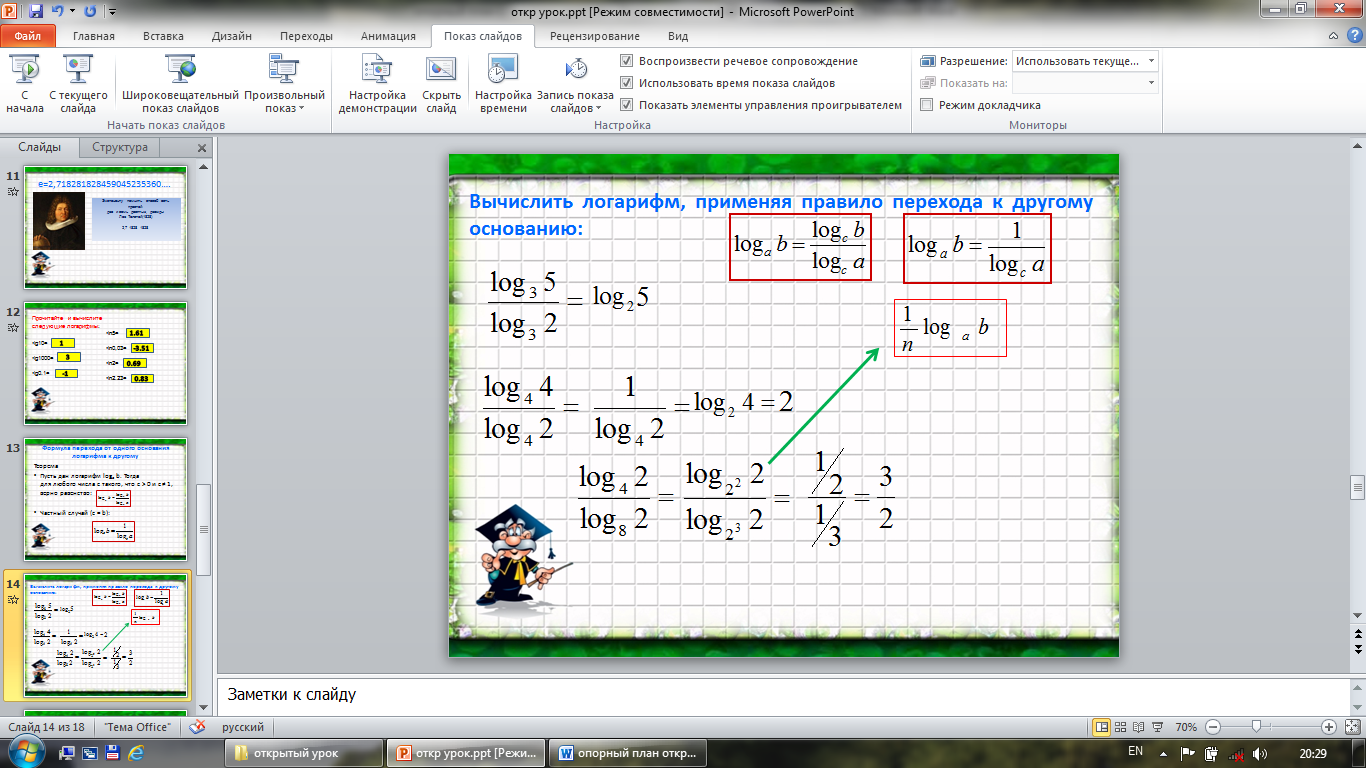
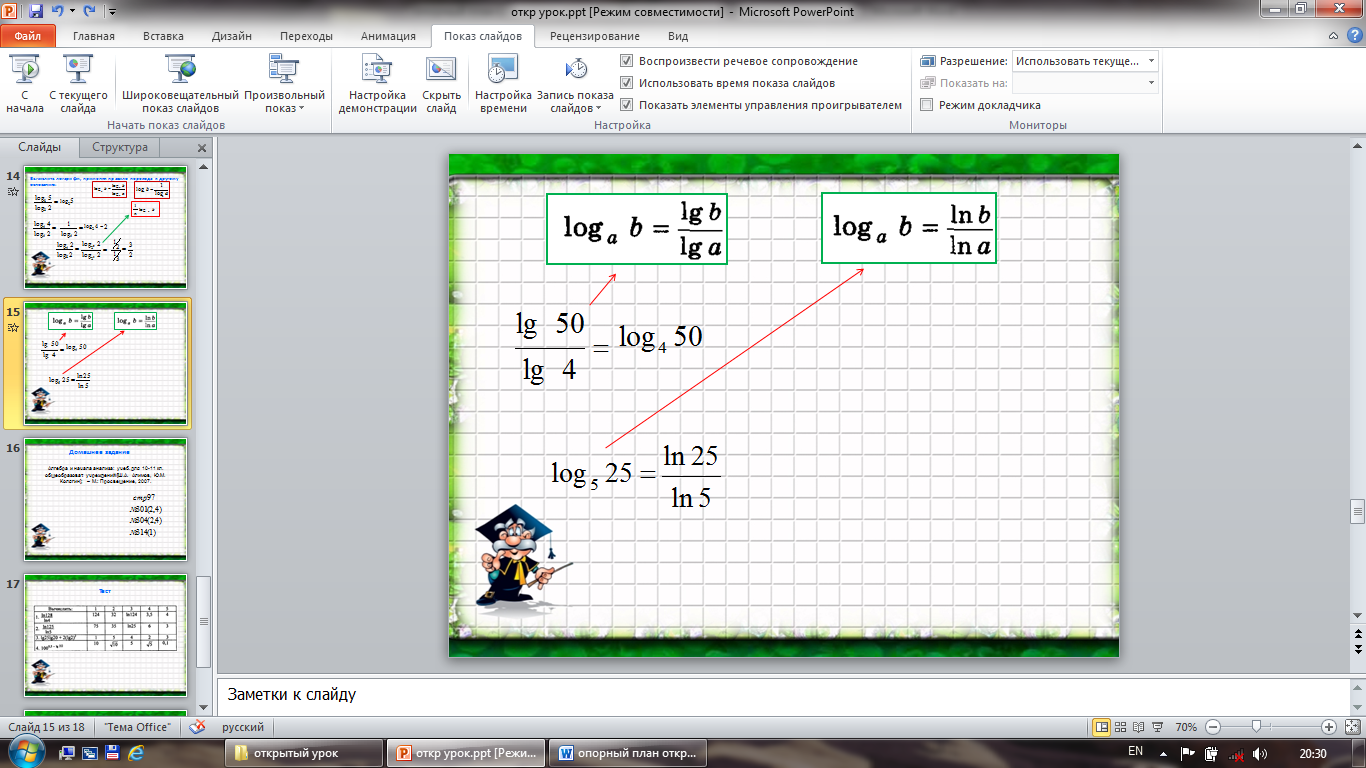
Практическое задание (устно) (слайд15-16)
Подведение итогов этапа.
Решение практических заданий: учебник Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/[Ш.А. Алимов, Ю.М. Колягин]; – М.: Просвещение, 2007.
№304(1,2), №306(1), №312(1)
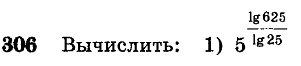
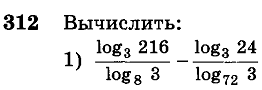
IV.Закрепление учебного материала (10 мин)
Тест (5 мин)(слайд 17)
Подведение итогов (проверка результатов теста)(слайд 18)
V.Домашнее задание (4 мин)
1.Подведение итогов занятия и анализ выставленных оценок.
2.Домашнее задание.(слайд 19)
Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/[Ш.А. Алимов, Ю.М. Колягин]; – М.: Просвещение, 2007.
№301(2,4), №304(2,4), №314(1)
infourok.ru
Новоазовская общеобразовательная школа I-III ступеней №2
Администрации Новоазовского района
Урок алгебры в 10-м классе по теме:
"Десятичные и натуральные логарифмы. Формула перехода"
Учитель математики, информатики
Специалист первой ктегории
Ноздренко Николай Николаевич
2016 г
Урок алгебры в 10-м классе по теме:
"Десятичные и натуральные логарифмы. Формула перехода"
Цели урока:
Образовательные:
повторить основные свойства логарифмов;
закрепить понятия десятичных и натуральных логарифмов;
формирование навыка работы с формулой перехода;
Развивающие:
развитие логического мышления (на основе усвоения учащимися причинно-следственных связей, сравнительного анализа), способности четко формулировать свои мысли.
Воспитывающие:
Тип урока: комбинированный.
Оборудование:
Учебник “Алгебра и начала анализа 10-11” Ш.А.Алимов и др.;
Компьютерная презентация;
Таблица свойств логарифмов;
Компьютеры;
Таблицы десятичных логарифмов.
Ход урока:
І. Организация класса
ІІ. Актуализация опорных знаний. Проверка домашнего задания
Фронтальный опрос
Учитель. Какую тему мы изучаем?
Ученик. Логарифмы.
Учитель. Для чего используется логарифм?
Ученик. Логарифм используется для нахождения показателя степени.
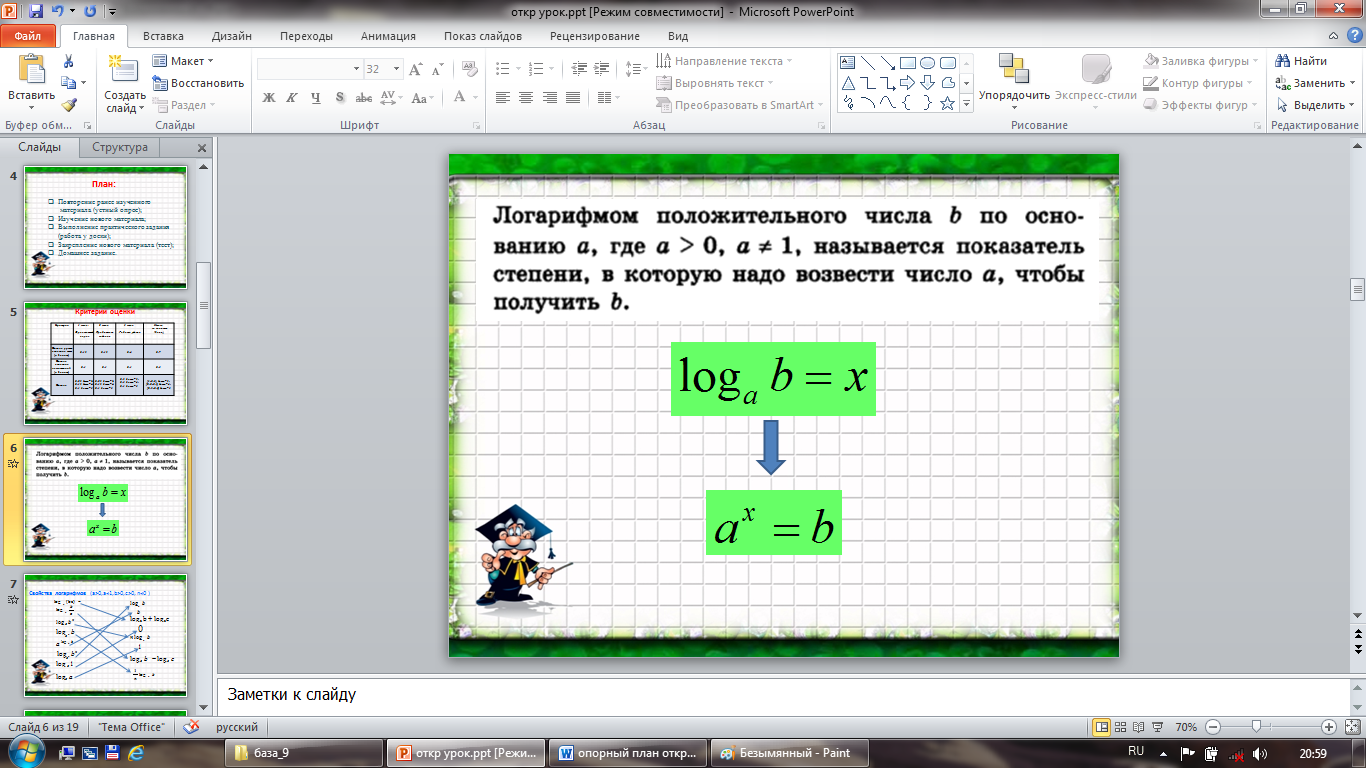
Учитель. Выразить через логарифм показатель степени х.
aх =b
Ученик: x=logab
Учитель. Что значит найти логарифм logab?
Ученик. Найти логарифм – значит найти показатель степени, в которую нужно возвести число а, чтобы получить число b.
Учитель. Приведите примеры логарифмов.
Учитель. Свойства логарифмов (дополнить запись)
Проверка домашнего задания. Вопросы у доски.
Устный счет (с использованием компьютера).
log3 = -3 log4 32 + log4 2 = 3
log0,3 1= 0 log10 25 + log10 4 = 2
log5 = log10 400 – log10 4 = 2
27 = -3 log2 44 – log2 11 = 2
log2 45 = 10 log4 8 + log4 2 = 2
log3 27 = 18 log4 8 – log4 2 = 1
log3 = log5 50 – log5 2 = 2
log8 64 5 = 10 log12 2 + log12 72 = 2
log2 = log8 32 – log8 4 = 1
log10 10 = 1 log4 2 + log4 2 = 1
1 = 0 log4 2 – log4 2 = 0
III. Мотивация учебной деятельности.
Презентация «Практическое применение логарифмов»
IV. Изучение нового материала
Десятичный логарифм
log10 a = lg a
Примеры десятичных логарифмов. Работа у доски.
Натуральный логарифм
loge a = ln a
Примеры натуральных логарифмов. Работа у доски.
Формулы перехода:
Проблема:
log2 8 = 3 log2 16 = 4
3 log2 14 4
Использование калькулятора? (только десятичный логарифм)
loga b = b / a
Воспользуемся этим свойством
log2 14 = 3,8
V. Физкультминутка.
VI. Закрепление изученного материала.
Работа за компьютером
Выполнить упр. № № 301, 302, 303, 304 (выразить у доски, рассчитать за компьютером)
Резерв (Самостоятельная работа№ 368, 369, 373)
VII. Домашнее задание.
Обработать § 17 стр. 96
Выполнить №301-304 (четные)
Найти ссылки на веб-ресурсы с примерами решения логарифмов.
VIII. Подведение итогов урока.
Что нового узнали на уроке? Для чего можно применить новые знания? Как вы оцениваете свою работу на уроке?
Оценивание учебной деятельности учащихся.
Приложение
Практическое применение логарифмов
Логарифмические функции распространены чрезвычайно широко как в математике, так и в естественных науках.
Ряд явлений природы помогает описать логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции.
Одним из наиболее наглядных примеров является логарифмическая спираль. Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.
Биология
Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины с её первоначальной формой. А такой рост может совершаться лишь по логарифмической спирали.
Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям.
Рога таких млекопитающих, как горные козлы, закручены по логарифмической спирали. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.
Астрономия
По логарифмическим спиралям закручены и многие Галактики, в частности Галактика, которой принадлежит Солнечная система.
Астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т. д. Легко понять, что «величина» звезды представляет собой не что иное, как логарифм ее физической яркости. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной при основании 2,5.
Музыка
«Ступени" темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношению к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. Отсюда видим, что номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков.
Психология
Время на принятие решения при наличии выбора можно оценить по закону Хикса. Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности раздражителя.
География
Рихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный логарифм перемещения (в микрометрах) иглы стандартного сейсмографа Вуда-Андерсона, расположенного на расстоянии не более 600 км от эпицентра.
Информатика
Применяется для вычисления основной единицы – бита. Бит — это двоичный логарифм вероятности равновероятных событий или сумма произведений вероятности на двоичный логарифм вероятности при равновероятных событиях.
Физика
Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень её хаотичности. Формула Циолковского применяется для расчёта скорости ракеты.
Единицей громкости звука служит «бел», практически - его десятая доля, «децибел». Разности громкостей в 1 бел отвечает отношение силы шумов 10. Значит, громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.
Химия
Водородный показатель, "pH ", — это мера активности ионов водорода в растворе, количественно выражающая его кислотность, вычисляется как отрицательный десятичный логарифм концентрации водородных ионов, выраженной в молях на литр
infourok.ru
Левенкова Оксана Юрьевна
Чебоксарский экономико-технологический колледж
Тема: Логарифмы и их свойства. Десятичные и натуральные логарифмы.
Цели и задачи занятия:
сформировать понятие логарифма числа, десятичного и натурального логарифма;
рассмотреть основные свойства логарифмов;
научить применять основное логарифмическое тождество и свойства логарифмов при нахождении значений выражений;
формирование умений и навыков применять основное логарифмическое тождество и свойства логарифмов для преобразования логарифмических выражений;
развитие математического мышления, умения логически мыслить и рационально работать;
воспитание познавательной активности, уверенности в себе.
Тип урока: усвоение новых знаний.
Методическое обеспечение: мультимедийное оборудование, презентация к уроку, учебники, индивидуальные карточки.
Ход занятия
1. Организационный момент
Приветствие учащихся, определение отсутствующих, заполнение группового журнала.
2. Актуализация знаний
Сообщается тема и цель занятия. (Слайды 1, 2)
Сегодня на занятии мы познакомимся с понятием логарифма числа, основным логарифмическим тождеством, изучим свойства логарифмов. В дальнейшем с их помощью мы будем решать логарифмические уравнения и неравенства.
Кроме математики, логарифмы также встречаются во многих разделах физики, находят широкое применение при обработке результатов тестирований в психологии и социологии, в составлении прогнозов погоды. С их помощью ученые научились определять точный возраст ископаемых пород и животных. Даже ряд явлений природы помогает описать именно логарифмическая зависимость. Одним из наиболее наглядных примеров является логарифмическая спираль. (Слайды 3, 4, 5)
3. Повторение ранее изученного материала
Экспресс-опрос
Понятие логарифма числа связано с решением показательных уравнений, поэтому вспомним:
Что называется степенью числа, основанием степени, показателем степени.
Вспомните свойства степеней.
Продолжите формулы: (Слайд 6)
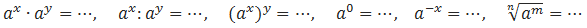
Решите устно следующие примеры:
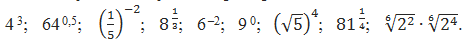
4. Изучение нового материала
План
Логарифм числа.
Основное логарифмическое тождество.
Основные свойства логарифмов.
Десятичные и натуральные логарифмы.
Логарифм числа
Остановимся на решении двух показательных уравнений. Решение уравнения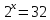 
не вызывает труда. Так как 32=
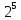, то данное уравнение примет вид 
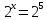. Поэтому уравнение имеет единственное решение x = 5.
А теперь рассмотрим уравнение 
. Обдумывая, ситуацию с таким показательным уравнением математики ввели новый символ – логарифм. С помощью этого символа корень уравнения записали так: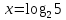 
(читается: логарифм числа 5 по основанию 2).
В общем виде: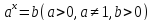 
, 
.
Дается определение логарифма (Слайд 7)
| Определение. Логарифмом положительного числа b по основанию a ( |
Например:
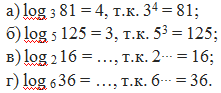
Основное логарифмическое тождество (Слайд 8)
Если корень подставить в уравнение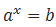
, то получим формулу 
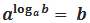(b 0, a 0 и a 1), которая называется основным логарифмическим тождеством.
Это равенство является краткой символической записью определения логарифмов.
Операцию нахождения логарифма числа называют ЛОГАРИФМИРОВАНИЕМ.
Решить примеры согласно тождеству:
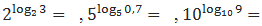
Сравните.
Основные свойства логарифмов (Слайд 9)
Основные свойства логарифмов вытекают из определения логарифма и свойств показательной функции. При любом a > 0, a ≠ 1 и любых положительных x и y выполнены равенства:
Десятичные и натуральные логарифмы (Слайд 10)
На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10.
Логарифм положительного числа b по основанию 10 называют десятичным логарифмом числа b и обозначают lg b, т.е. вместо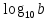 
пишут lg b.
Например,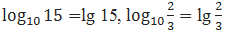 
Натуральным логарифмом (обозначается ln) называется логарифм по основанию e: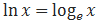 
Примеры вычисления десятичных логарифмов (Слайд 11)
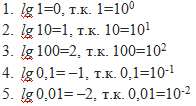
5. Закрепление изученного материала
№ 267 (устно), 268–271, 273, 274 (устно), 275–276, 290–294.
(Алимов Ш.А. Алгебра и начала математического анализа. 10–11 классы)
Индивидуальные карточки
6. Подведение итогов
1. Выставление и комментирование оценок на занятии.
2. Домашнее задание: Глава IV §15–§17, № 272, 281, 296.
7. Рефлексия
Преподаватель задает учащимся вопросы:
Какая тема была изучена на занятии?
Достигнута ли цель занятия?
Что больше всего запомнилось на занятии?
Учащиеся призваны воспроизвести в памяти то, что усвоили, и проанализировать выводы, которые были сделаны в течение всего занятия.
/data/files/o1487864235.pptx (логарифмы)
xn--j1ahfl.xn--p1ai
) называется показатель степени, в которую нужно возвести основание a, чтобы получить число b. 