
Реферат на тему:
Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению.
В своё время введение заучиваемой наизусть таблицы умножения революционизировало устный и письменный счёт. До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.
В российских школах значения традиционно доходят до 10×10. В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины (1 фут = 12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фунт стерлингов = 20 шиллингам, 1 шиллинг = 12 пенсам).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Возьмём таблицу умножения до 5×10:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
Чтобы узнать результат произведения 4×8 по таблице умножения, нужно взять 4 в левом столбце, 8 в верхней строке, провести от 4 горизонтальную линию, а от 8 вертикальную. Число, на которое попадают две линии является произведением.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 89 | 10 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 1618 | 20 |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 2427 | 30 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 4045 | 50 |
Точка совпадения чисел — 32. 32 — произведение чисел 4 и 8. Такой-же способ нахождения остальных чисел по таблице умножения.
Наряду с таблицей умножения, в некоторых случаях бывают удобны таблицы сложения.
Таблица Кэли — в абстрактной алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли. Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.
В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.
Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:
Таблица умножения в кольце вычетов по модулю 8
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 2 | 4 | 6 | 0 | 2 | 4 | 6 |
| 0 | 3 | 6 | 1 | 4 | 7 | 2 | 5 |
| 0 | 4 | 0 | 4 | 0 | 4 | 0 | 4 |
| 0 | 5 | 2 | 7 | 4 | 1 | 6 | 3 |
| 0 | 6 | 4 | 2 | 0 | 6 | 4 | 2 |
| 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Таблица умножения в поле вычетов по модулю 5
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 2 | 3 | 4 |
| 0 | 2 | 4 | 1 | 3 |
| 0 | 3 | 1 | 4 | 2 |
| 0 | 4 | 3 | 2 | 1 |
wreferat.baza-referat.ru
МОУ «Куровская средняя общеобразовательная школа №6»
РЕФЕРАТ ПО МАТЕМАТИКЕ НА ТЕМУ:
«НЕОБЫЧНЫЕ СПОСОБЫ УМНОЖЕНИЯ».
Выполнил ученик 6 «б» класса
Крестников Василий.
Руководитель:
Смирнова Татьяна Владимировна.
2011г.
Оглавление.
Вступление…………………………………………………………………………2
Основная часть. Необычные способы умножения…………………………3
2.1. Немного истории………………………………………………………………..3
2.2. Умножение на пальцах…………………………………………………………4
2.3. Умножение на 9…………………………………………………………………5
2.4. Индийский способ умножения……………………………………………….6
2.5. Умножение способом «Маленький замок»…………………………………7
2.6. Умножение способом «Ревность»……………………………………………8
2.7. Крестьянский способ умножения……………………………………………..9
2.8 Новый способ…………………………………………………………………..10
Заключение………………………………………………………………………11
Список литературы…………………………………………………………….12
1
I. Вступление.
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
Однажды мне случайно попалась книга С. Н. Олехника, Ю. В. Нестеренко и М. К. Потапова «Старинные занимательные задачи». Листая эту книгу, мое внимание привлекла страничка под названием «Умножение на пальцах». Оказалось, что можно умножать не только так как предлагают нам в учебниках математики. Мне стало интересно, а есть ли еще какие-нибудь способы вычислений. Ведь способность быстро производить вычисления вызывает откровенное удивление.
Постоянное применение современной вычислительной техники приводит к тому, что учащиеся затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или счетной машины. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического цикла.
Цель работы:
Показать необычные способы умножения.
Задачи:
Найти как можно больше необычных способов вычислений.
Научиться их применять.
Выбрать для себя самые интересные или более легкие, чем те которые предлагаются в школе, и использовать их при счете.
2
II. Основная часть. Необычные способы умножения.
2.1. Немного истории.
Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках».
И все эти приемы умножения — «шахматный или органчиком», «загибанием», «крестиком», «решеткой», «задом наперед», «алмазом» и прочие соперничали друг с другом и усваивались с большим трудом.
Давайте рассмотрим наиболее интересные и простые способы умножения.
3
2.2. Умножение на пальцах.
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.

4
2.3. Умножение на 9.
Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).

Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».

Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто.
7 клеток 2 клетки.
5
2.4. Индийский способ умножения.
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам.
Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:
537 6
(5 ∙ 6 =30) 30
537 6
(300 + 3 ∙ 6 = 318) 318
537 6
(3180 +7 ∙ 6 = 3222) 3222
6
2.5. Умножение способом «МАЛЕНЬКИЙ ЗАМОК».
Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.
За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.

7
2.6. Умножение чисел методом «ревность».
 Второй способ носит романтическое название «ревность», или «решётчатое умножение».
Второй способ носит романтическое название «ревность», или «решётчатое умножение».
Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.
В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063.
3 4 7
2
9
10 0 6 3
8
2.7. Крестьянский способ умножения.
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением
37……….32
74……….16
148……….8
296……….4
592……….2
1184……….1
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:
24 ∙ 17
24 ∙ 16 =
= 48 ∙ 8 =
= 96 ∙ 4 =
= 192 ∙ 2 =
=384 ∙ 1 = 384
24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408
9
2.8. Новый способ умножения.
Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35
Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.
В итоге получаем: 078235. Число 78235 и есть результат умножения.
Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

10
III. Заключение.
Научившись считать всеми представленными способами, я пришел к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.
Из всех найденных мною необычных способов счета более интересным показался способ «решетчатого умножения или ревность». Я показал его своим одноклассникам, и он им тоже очень понравился.
Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Заинтересовал меня новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.
Я думаю, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы.
11
Литература.
Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954. – 140 с.
Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/
Олехник С. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.
Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.
Перельман Я.И. Занимательная арифметика. М.Русанова,1994—205с.
Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004.
Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с.
12
sundekor.ru
Гончаров Геннадий Алексеевич (г.Воронеж)
Предлагаю ознакомиться с новым способом умножения чисел. Схожесть образующейся при вычислении матрицы из цифр, с треугольником относительна, но все же есть, особенно при умножении трехзначных чисел и выше. Для простого примера возьмем два целых двухзначных числа: 57 и 89, используя последовательное перемножение цифр одного множителя на другой, как классическим “столбиком”,
заполним по определенному алгоритму результатами каждого промежуточного произведения своеобразную треугольную матрицу, что приведет к получению конечного произведения 5073.
Далее пошагово:
Умножение ведется, в отличие от метода “столбиком”, слева направо. Для того чтобы было легче объяснят, пронумерую каждый разряд, куда будут заноситься промежуточные вычисления. ( синие цифры внизу каждой таблицы)
Умножаем первую цифру 5 первого множителя 57 последовательно слева направо на каждую цифру второго множителя 89.
1.1 5х8=40. Цифру 0 (числа 40) записываем в третий разряд таблицы 1.1 (С третьего разряда начинаем потому, что цифра 5, это основная цифра первого промежуточного этапа вычислений, и стоит она именно в столбце третьего разряда), а цифру 4(числа 40) переносим на один разряд таблицы влево и записываем в столбец четвертого разряда. Получаем следующий вид промежуточного вычисления:
Таблица 1.1
5х9=45. Цифру 5 ( числа 45) записываем в столбец второго разряда таблицы 1.2, т.е. смещаемся на один разряд вправо относительно разряда предыдущего шага вычислений (третьего разряда), а цифру 4 (числа 45) переносим на один разряд влево (в третий разряд таблицы), где уже стоит цифра 0, складываем их. В сумме получаем снова 4 и эту цифру записываем под цифрой 0 третьего разряда таблицы1.2. Получаем следующий вид промежуточного вычисления:
Таблица 1.2
Умножаем вторую цифру 7 первого множителя 57 последовательно слева направо на каждую цифру второго множителя 89.
7х8=56. Заполнение таблицы2.1 на этом этапе начинаем со второго разряда, т.к. цифра 7 (основная цифра этого этапа промежуточных вычислений) стоит именно в столбце второго разряда таблицы. Полученное число 56 складываем с цифрой 5, которая уже стоит в этом разряде (из предыдущих вычислений), в сумме получаем 61. Цифру 1 ( числа 61) записываем под цифрой 5 в столбец второго разряда таблицы, а цифру 6 (числа 61) переносим в третий разряд таблицы, где уже стоит цифра 4(нижняя в столбце третьего разряда) складываем их, в сумме получаем число 10. Цифру 0 (числа 10) записываем под цифрой 4 в столбец третьего разряда, а цифру 1 (числа 10)переносим в четвертый разряд и складываем её со стоящей в этом разряде цифрой 4, в сумме получаем число 5, которое записываем под цифрой 4 в столбец четвертого разряда. Получаем следующий вид промежуточного вычисления:
Таблица 2.1
| 8 | 9 | ||
| 5 | 7 | ||
| 4 | 5 | ||
| 5 | 4 | 1 | |
| 4 | 3 | 2 | 1 |
2.2 7х9=63 Цифру 3 (числа 63) записываем в столбец первого разряда таблицы2.2, т.е. смещаемся на один разряд вправо относительно предыдущего шага вычислений (в предыдущем шаге мы начинали заполнение таблицы со второго разряда т.к. во втором разряде стоит цифра 7 –основная цифра этого этапа вычислений), а цифру 6 (числа 63) переносим на один разряд влево относительно цифры 3 (во второй разряд таблицы), где нижней стоит цифра 1. Складываем их, в сумме получаем 7. Записываем цифру 7 под цифрой 1 в столбец второго разряда таблицы. Получаем следующий вид окончательного вычисления:
Таблица2.2
| 8 | 9 | ||
| 5 | 7 | ||
| 4 | 5 | 3 | |
| 5 | 4 | 1 | |
| 7 | |||
| 4 | 3 | 2 | 1 |
И теперь самое интересное:
Записав нижние цифры каждого разряда в одну строку, получаем итоговый результат.
(Выделен под нижней жирной чертой последней таблицы2.3.)
Таблица2.3
| 8 | 9 | ||
| 5 | 7 | ||
| 4 | 5 | 3 | |
| 5 | 4 | 1 | |
| 7 | |||
| 5 | 7 | 3 | |
| 4 | 3 | 2 | 1 |
Надеюсь, это было вам интересно.
www.ronl.ru
Урок математики в 3 классе,
Тема: УМНОЖЕНИЕ НА 1.
Цели урока:
1. исследовать правило умножения на 1;
2. отрабатывать навыки табличного умножения и деления;
3. учиться анализировать задачи и самостоятельно решать их;
4 развивать находчивость, сообразительность, логическое мышление, внимание, память, самостоятельность;
5. расширять кругозор учащихся;
6. способствовать развитию интереса учащихся и активизировать их познавательную деятельность;
7. воспитывать чувство взаимопомощи, трудолюбия, развивать интерес к предмету.
Оборудование: паровозик, «облачка» с цифрами и буквами, колоски с зёрнышками, Знайка (Н), цифры к компонентам, ребус к задаче, учебник «Математика - 3 кл., 1 часть / Моро, Бантова и др.
^ Ход урока:
а) Организационный момент
У.: Ну-ка, проверь дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Книжка, ручка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку «5».
б) Актуализация знаний.
У.: Сегодня нас ждет путешествие в страну, которой нет на карте. В этой стране мы повторим решение задач, выражений, проведем исследование одной очень важной темы. Эта страна - МАТЕМАТИКА. Математика приглашает в свое королевство тех, кто настойчив, кто часто говорит «почему?», кто не боится вычислений и цифр. Нашим девизом будут слова: «В математику тропинки одолеем без запинки». В пути вы должны помогать друг другу, если появятся трудности.
в) ^ Устный счет.
У.: Ну, что же, пора занимать места. Наш паровозик «Облачко» уже готов отправиться в путь. Но все вагончики разлетелись, их необходимо прицепить к паровозику.
У.: Ира собирает вагончики у доски, а остальные пишут в форме арифметического диктанта в тетради.
1) Коля старше Риты в 3 раза. Ему 9 лет. Сколько лет Рите? (3)
2) В семье 5 братьев. У каждого есть сестра. Сколько детей в семье?
(6)
3) Сбежала от Федоры посуда: 3 стакана, 3 чашки, 3 блюдца.
Кто сосчитать готов,
Сколько всего беглецов? (9)_
4) Сторона квадрата равна 3 см. Чему равен периметр? (12)
5) Дети окопали в саду 3 яблони, а груш в 5 раз больше. Сколько груш окапали дети? (15)
6) Длина прямоугольника 9 см., а ширина 2 см. Чему равна площадь прямоугольника? (18)
7) У деда Архипа большая семья.
Детей только семь -И все сыновья.
У каждого сына по трое ребят Внучата Архипа.
Их сколько внучат?(21)
8) Неизвестное число разделили на 4 и получили 6. Чему равно неизвестное число? (24)
9) Вдоль забора высажено 9 тополей на расстоянии 3 метров друг от друга. Какова длина забора? (27)
10) Сколько пальчиков на руках 3 мальчиков? (30)У.:
- Проверим. Какое напутствие получилось? (Желаю удачи).
• Какую закономерность заметили? (все числа делятся на 3).
• На какие группы можно разделить все числа? (однозначные и двузначные, чётные и нечётные)
• Составьте взаимообратные выражения.(9*3=27, 3*9=27, 27:3=9, 27:9=3) и т. д.
• Составьте неравенства.(9*3>18:6) и т. д.
• Все однозначные числа увеличьте в 9 раз.
• Мы отправились в путешествие на поезде.
• Как называется эта отрасль экономики?(транспорт)
• Какие профессии знаете? (пилот, шофер и т. д.)
- Вот и первая остановка «Новоселье». Здесь идет строительство. Нас тут встречает Миша. Он помог завершить постройку.
- Проверяем с использованием сигнальных карточек. Если правиль-ный ответ, то показываем красную карточку, а если неправильный, то по-казываем синюю.
- Как называется эта отрасль экономики?(строительство) Какиестроительные профессии вы знаете?(маляр, прораб и т. д. )
- В городе Сочи начинается строительство. Почему? (в связи с предстоящей Олимпиадой)
г) Физминутка.
д) Новая тема.
У.: Наша новая остановка «Колосок знаний». Однажды волшебник подарил мне маленькое зернышко. Из него вырос тоненький высокий стебелек, а вот зерен в колоске не было. Волшебник сказал, что это колосок знаний. Он заполнится зернами, если мы решим проблему нашего урока. Вы поможете заполнить колосок зернами, а я помогу вам.
Вырос в поле колосок,
Он и тонок, и высок,
Что-то новое узнаешь,
Полный колос получаешь.
7*1 89*1 1*27 1*14
1*12 83*1 10*1
У.:
- Какую закономерность вы заметили? (все числа умножали на 1)
- Попробуйте сформулировать правило! (при умножении любого числа на 1, получается то число, которое умножали.)
- Проверим по учебнику, правы ли мы? (с. 72)
- Молодцы! Вы помогли вырастить колосок. А к какой отрасли экономики можно отнести колосок? (сельское хозяйство) Какие с/х профессии вы знаете? (агроном, доярка и т. д.)
- Отгадайте загадку:
Хитрая плутовка,Рыжая головка,Пушистый хвост — краса,А зовут её (лиса)
- Как понимаете выражение «хитрая плутовка»?
- В какой, недавно прочитанной, сказке встречается хитрая плутовка?
- А она не только хитрая, но и хвастливая. Она хвастается, что все задания выполнила верно. Давайте проверим. (Задания записаны через ко-доскоп.)
52 * (48 - 47) = 1 (52) 28 : 4 * 1 = 7
(62 + 24) * 1 = 90 1 * 8 * 3 = 24
(70 - 69) * 14 = 15 (14) 32 - (1*32) = 1 (0)
- Верно ли лисичка решила примеры? (нет)
- Хорошо ли хвастаться?
е) Физминутка.
ж) Решение задач.
- Первое предлог, второе - летний дом, а целое - порой решается с трудом.
- На этой остановке нас встречает еще один известный герой.
Хоть ты смейся,
Хоть ты плачь,
Не могу решать задач.
Помогите мне, ребята,
Все расставить по местам.
Научусь решать задачи -
Буду благодарен вам.
Поможем?
№5, с.72 - устно.
- Что значит в 7 раз дешевле?
- Как узнать, сколько стоит блокнот? (/ )
- Как узнать, сколько стоят 4 блокнота? ( * )
- К какой отрасли экономики мы можем отнести эту зада-
чу?(торговля) Назовите профессии из отрасли «торгов-
ля».(продавец, менеджер и др.)
№3, с. 72.
- Давайте составим программу решения задачи.
- Подумайте, как записать задачу кратко.
- Какие главные слова выберете для краткой записи?
- Что сказано о яблоках, (грушах)?
- Что нужно узнать в задаче?
- Можем сразу ответить на вопрос задачи?
- Можем узнать сколько было груш?
-Как?
- Как узнать, на сколько одно число меньше другого?
- Запишите самостоятельно.
У.: А теперь поиграем в «пустяки». Посмотрите №2 на странице 72 и скажите, для кого сущий пустяк выполнить это задание. Докажите это и выполните. Запишите самостоятельно.
^ ГЕОМЕТРИЧЕСКИЙ МАТЕРИАЛ.
Вот мы добрались до дворца Короля Точки и принцессы Прямой. - Из каких геометрических фигур он состоит?
- Сколько треугольников? Квадратов? Прямоугольников?
- Чему равна площадь квадрата, если его сторона 5 см.?
^ ИТОГ УРОКА.
У.: Очень жаль, что путь не долог,
Возвращаться нам пора. Но на следующем уроке Вновь продолжится игра.
У. Мы преодолели все трудности, которые встретили в математическом путешествии и сделали еще один шаг на пути изучения математики. Наша общая победа сложилась из маленьких побед каждого из вас.
• Какие задания встретились в ходе игры?
• Какие задания показались самыми интересными?
• Какие наиболее трудными? Почему?
• Что вам удалось? Над чем надо еще поработать каждому из вас?
• Как бы вы оценили свою работу на уроке? Поднимите руки те, кто работал:
- в полную силу;
- работал хорошо, но мог бы работать лучше;
- Кто недоволен своей работой. Почему?
Д/з: в память о путешествии зарисуйте картинку.
www.ronl.ru
Гончаров Геннадий Алексеевич (г.Воронеж)
Предлагаю ознакомиться с новым способом умножения чисел. Схожесть образующейся при вычислении матрицы из цифр, с треугольником относительна, но все же есть, особенно при умножении трехзначных чисел и выше. Для простого примера возьмем два целых двухзначных числа: 57 и 89, используя последовательное перемножение цифр одного множителя на другой, как классическим “столбиком”,
заполним по определенному алгоритму результатами каждого промежуточного произведения своеобразную треугольную матрицу, что приведет к получению конечного произведения 5073.
Далее пошагово:
Умножение ведется, в отличие от метода “столбиком”, слева направо. Для того чтобы было легче объяснят, пронумерую каждый разряд, куда будут заноситься промежуточные вычисления. ( синие цифры внизу каждой таблицы)
Умножаем первую цифру 5 первого множителя 57 последовательно слева направо на каждую цифру второго множителя 89.
1.1 5х8=40. Цифру 0 (числа 40) записываем в третий разряд таблицы 1.1 (С третьего разряда начинаем потому, что цифра 5, это основная цифра первого промежуточного этапа вычислений, и стоит она именно в столбце третьего разряда), а цифру 4(числа 40) переносим на один разряд таблицы влево и записываем в столбец четвертого разряда. Получаем следующий вид промежуточного вычисления:
Таблица 1.1
5х9=45. Цифру 5 ( числа 45) записываем в столбец второго разряда таблицы 1.2, т.е. смещаемся на один разряд вправо относительно разряда предыдущего шага вычислений (третьего разряда), а цифру 4 (числа 45) переносим на один разряд влево (в третий разряд таблицы), где уже стоит цифра 0, складываем их. В сумме получаем снова 4 и эту цифру записываем под цифрой 0 третьего разряда таблицы1.2. Получаем следующий вид промежуточного вычисления:
Таблица 1.2
Умножаем вторую цифру 7 первого множителя 57 последовательно слева направо на каждую цифру второго множителя 89.
7х8=56. Заполнение таблицы2.1 на этом этапе начинаем со второго разряда, т.к. цифра 7 (основная цифра этого этапа промежуточных вычислений) стоит именно в столбце второго разряда таблицы. Полученное число 56 складываем с цифрой 5, которая уже стоит в этом разряде (из предыдущих вычислений), в сумме получаем 61. Цифру 1 ( числа 61) записываем под цифрой 5 в столбец второго разряда таблицы, а цифру 6 (числа 61) переносим в третий разряд таблицы, где уже стоит цифра 4(нижняя в столбце третьего разряда) складываем их, в сумме получаем число 10. Цифру 0 (числа 10) записываем под цифрой 4 в столбец третьего разряда, а цифру 1 (числа 10)переносим в четвертый разряд и складываем её со стоящей в этом разряде цифрой 4, в сумме получаем число 5, которое записываем под цифрой 4 в столбец четвертого разряда. Получаем следующий вид промежуточного вычисления:
Таблица 2.1
| 8 | 9 | ||
| 5 | 7 | ||
| 4 | 5 | ||
| 5 | 4 | 1 | |
| 4 | 3 | 2 | 1 |
2.2 7х9=63 Цифру 3 (числа 63) записываем в столбец первого разряда таблицы2.2, т.е. смещаемся на один разряд вправо относительно предыдущего шага вычислений (в предыдущем шаге мы начинали заполнение таблицы со второго разряда т.к. во втором разряде стоит цифра 7 –основная цифра этого этапа вычислений), а цифру 6 (числа 63) переносим на один разряд влево относительно цифры 3 (во второй разряд таблицы), где нижней стоит цифра 1. Складываем их, в сумме получаем 7. Записываем цифру 7 под цифрой 1 в столбец второго разряда таблицы. Получаем следующий вид окончательного вычисления:
Таблица2.2
| 8 | 9 | ||
| 5 | 7 | ||
| 4 | 5 | 3 | |
| 5 | 4 | 1 | |
| 7 | |||
| 4 | 3 | 2 | 1 |
И теперь самое интересное:
Записав нижние цифры каждого разряда в одну строку, получаем итоговый результат.
(Выделен под нижней жирной чертой последней таблицы2.3.)
Таблица2.3
| 8 | 9 | ||
| 5 | 7 | ||
| 4 | 5 | 3 | |
| 5 | 4 | 1 | |
| 7 | |||
| 5 | 7 | 3 | |
| 4 | 3 | 2 | 1 |
Надеюсь, это было вам интересно.
www.ronl.ru
Министерство образования и науки Удмуртской Республики
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 5 имени Б. А. Смирнова»
г. Воткинска
Реферат
Приемы активизации учащихся в процессе обучения внетабличному делению и умножению на уроках математики в 3 классе.
Учитель начальных классов:
Данилова Наталия Евгеньевна
г. Воткинск, 2013
Содержание:
Введение. с. 2 - 4
Глава 1. Общее понятие о познавательной деятельности. с. 5 - 9
1.1. Познавательная деятельность - продукт усвоения
социального опыта с. 5
1.2. Взаимосвязь практической и теоретической
деятельности человека с. 6
1.3. Специфические приёмы познавательной деятельности с. 7
1.4. Мастерство учителя в руководстве познавательной
деятельности учащихся с. 8
Вывод к главе 1. с. 9
Глава 2. Приёмы активизации учащихся в
процессе обучения математике в 3 классе
при изучении внетабличного деления и умножения с. 10 - 18
2.1. Сущность приёмов активизации с. 10
2.2 Приемы, способствующие активизации процесса
восприятия с. 11 - 12
2.3. Приемы, способствующие активизации процесса
запоминания с. 13
2.4. Активизация логического мышления с. 14 - 15
2.5. Активизация познавательной деятельности
учащихся в процессе формирования вычислительных навыков с. 16 - 19
Вывод к главе 2. с. 20
IV. Заключение по работе. с. 21 - 22
Литература. с. 23 - 24
Приложения.
1
Введение.
В настоящее время большое внимание в школе уделяется активизации познавательной деятельности учащихся. Многие учителя используют в своей практике различные приёмы, способствующие активности учащихся на уроке.
Так как познавательная деятельность формируется в процессе жизни человека, то педагог принимает в этом немалое участие. Ребёнок не рождается с готовым умом, готовой способностью к познанию. Учебная деятельность требует от ученика вполне определенных познавательных средств. И учитель должен знать, располагает ли этими средствами ученик. Ведь нередко, многие учащиеся не могут усвоить раздел или тему из-за их трудности.
Раздел “Внетабличное деление и умножение” в 3 классе представляет для школьников большую трудность в усвоении. Поэтому, чтобы повысить интерес к изучению данного раздела, необходимо использовать приёмы активизации познавательной деятельности. К таким приёмам относят: дидактические игры, логические задачи, самостоятельные работы и т.д.
В наши дни огромную роль играет развивающее обучение, одним из основателем которого, является Леонид Владимирович Занков. Приёмы активизации считаются средством, позволяющим организовать целенаправленную и систематическую работу над развитием учащихся в процессе обучения математике. Выполняя их, учащиеся овладевают новыми знаниями, приёмами умственной деятельности, закрепляют и совершенствуют умения и навыки.
Использование приёмов активизации учащихся в учебном процессе делает учение для учащихся интересным, ярким и увлекательным. Это способствует повышению успехов младших школьников.
Задача каждого учителя состоит в том, чтобы сформировать познавательную деятельность у всех учащихся. Каждый, кто берётся учить, должен уметь научить. Поэтому интенсивное развитие ребят достигается в процессе всей умело продуманной учебно-воспитательной работы: и приобретения знаний, и овладения навыками, и формирования побуждения к учению.
Возникновение интереса к математике у значительного числа учащихся в большинстве случаев зависит от работы учителей. Следовательно, каждый преподаватель должен знать требования, обеспечивающие эффективное управление процессом усвоения. В связи с этим следует отметить, что
2
учитель, планируя работу по формированию знаний, различных видов познавательной деятельности, должен брать за основу не урок, а цикл обучения, т. е. необходимую совокупность действий обучающего и учащегося.
В современной школе наблюдается увеличение умственной нагрузки на уроках математики. Поэтому нужно задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока.
Для этого необходимо разнообразить урок, т.е. включить в его структуру задания развивающего характера. Поскольку само развивающее обучение несёт в себе большие возможности, оно проявляет у учащихся активность и самостоятельность во всех видах учебной работы.
Кроме того, в практике многих учителей нестандартные уроки занимают не последнее место при активизации познавательной деятельности. Они помогают повысить интерес детей не только к какому-либо разделу, но и ко всему предмету в целом.
Однако следует помнить, что перенасыщать урок приёмами активизации не следует, так как в этом случае учебный процесс дети будут воспринимать лишь как игру. А это не принесёт никаких результатов. Школьники должны принимать учебный процесс в серьёзном виде, который способствует формированию знаний, умений, навыков.
Как уже говорилось выше, большую роль в усвоении знаний учащимися играет подготовка учителя к уроку. Поэтому преподавателям необходимо задумываться над разнообразием методов и приёмов, применяемых на уроке.
Почти всегда учащиеся активны лишь на тех уроках, где наблюдается хорошая подготовка учителя, быстрый темп его работы, а также использование приёмов активизации при актуализации ранее изученного.
Из исследований, проведённых среди учащихся 3 классов, изучавших внетабличное деление и умножение, было выявлено: дети, не усвоившие табличные случаи умножения и деления, испытывают трудности при изучении внетабличных случаев. В целях преодоления этих трудностей учитель должен сделать всё необходимое для усвоения учащимися трудного материала. А на помощь учителю для этого и придут логические задачи, дидактические игры, задания проблемного характера и т. д.
Целью данной работы считаю: исследовать влияние приёмов активизации познавательной деятельности учащихся при изучении внетабличных случаев деления и умножения.
3
Объект исследования: процесс активизации учащихся начальных классов.
Предмет исследования: приёмы активизации познавательной деятельности.
Проблема: каковы наиболее эффективные приёмы активизации учащихся при изучении внетабличных случаев деления и умножения.
Гипотеза исследования: эффективность приёмов активизации учащихся начальных классов может быть достигнута при следующих условиях: хорошая подготовка учителя к уроку; интерес учащихся к изучаемому материалу, а также соответствие приёмов активизации данной теме.
Задачи исследования:
1. Определить наиболее эффективные методы и приёмы активизации, отвечающие современным требованиям.
2. Проанализировать особенности обучения учащихся при изучении внетабличного деления и умножения.
3. Определить пути подготовки учителя к использованию приёмов активизации на уроках.
4. Провести экспериментальные исследования деятельности учителя и учащихся на уроках изучения внетабличного деления и умножения.
Методы исследования: теоретический анализ и синтез, классификация, обобщение, сравнение, наблюдение, эксперимент, изучение педагогического опыта.
4
Глава 1. Общее понятие о познавательной деятельности
1. 1. Познавательная деятельность - продукт усвоения социального опыта
О силе человеческого разума сложено немало легенд, написано много книг. Каждый день приносит всё новые и новые доказательства всемогущества человека.
А вот в первый период своей жизни человеческое дитя - самое беспомощное существо в мире.
Человеческое детство, в отличие от детства животных, длится десятилетия. Нередко подготовка к полезной для общества деятельности составляет четверть жизни человека.
Объясняется это тем, что у животных опыт предыдущих поколений закрепляется с помощью нервных механизмов, наследуется. Человек же, став социальным существом, перешёл на новый, социальный способ закрепления своего опыта - в предметах материальной и духовной культуры, в языке. Человек формируется только при наличии общественных условий жизни, без них человека не получается. Об этом говорят красноречиво случаи, когда дети вырастали среди тех или иных животных. Об одном из них ещё рассказывал французский философ Э. Кондильяк в своём “Трактате об ощущениях” (18 в.). Он писал о мальчике из Литвы, который жил среди медведей. Мальчик не умел говорить, не обнаруживал никакого разума, ходил на четвереньках, издавал звуки, совсем не похожие на человеческие.
Человек не приносит на свет никаких готовых форм поведения. Его развитие идёт путём усвоения (“присвоения”) опыта, накопленного предыдущими поколениями. Человек так могуч именно потому, что стоит на плечах предыдущих поколений, использует их многовековой опыт. Человек не рождается с готовыми, сформированными математическими способностями: он их может развить только путём приобщения к миру математики.
Конечно, индивид может внести, потом и свой личный вклад в социальный опыт, и стать, например, знаменитым математиком. Но происходит это не потому, что он родился от математика.
Когда опыт человечества был невелик, он усваивался в процессе практического общения ребёнка с миром при помощи родителей. Но постепенно в обществе появились специальные люди - учителя, общественная функция которых - передавать новому поколению опыт предыдущих.
5
1.2. Взаимосвязь практической и теоретической деятельности человека
Опыт, накопленный человечеством, можно классифицировать по-разному. Если в основу классификации положить содержание, то получим опыт интеллектуальный, этический, эстетический, физический, профессионально - практический и т. п. Можно поделить также весь опыт человечества на практический и теоретический. В каждом из них, в свою очередь, можно выделить опыт предметный и опыт операционный - опыт знаний и опыт способов действий с этими предметами и знаниями.
Человек должен овладеть различными видами как практической, так и теоретической деятельности.
Теоретические действия пронизывают всю человеческую практику. Без них практика была бы слепа, человек не смог бы выполнить даже самых простых практических действий.
Человек в своей жизни выполняет тысячи различных внешних, практических и внутренних, умственных действий, и все они приобретаются им при жизни. Человек не родится ни практиком, ни теоретиком, ни мыслителем. Всему этому он учится у старших.
Роль внешних действий в формировании умственных действий, связанных с изучением начальной математики, хорошо известна учителям. И ни один учитель не будет учить детей считать сразу устно или в уме. Но путь от внешнего к внутреннему проходят все новые умственные действия, и не только у детей младших классов, но и у учащихся старших классов и даже взрослых.
6
1.3. Специфические приёмы познавательной деятельности
Полноценное усвоение знаний предполагает формирование таких познавательных действий, которые составляют специфические приёмы, характерные для той или иной области знаний. Так, нельзя, например, сформировать приёмы математического мышления, минуя математические знания; нельзя сформировать лингвистическое мышление без работы над языковым материалом.
Приёмы познавательной деятельности не могут быть перенесены на любой предмет. Так, например, человек, великолепно владеющий специфическими приёмами мышления в области математики, может не уметь справиться с историческими задачами, и наоборот.
В школе открываются большие возможности для формирования различных приёмов мышления. Уже в начальных классах надо заботиться о математических приёмах мышления. Наибольшие затруднения у учащихся вызывает математика. Поэтому, если приёмы математического мышления не формируются у учащихся, то они, изучив весь курс математики, так и не научатся думать математически. А это означает, что математика изучена формально, что учащиеся не поняли её специфических особенностей.
Так, учащиеся 3 класса уверенно и быстро складывают многозначные числа столбиком, уверенно указывая, что писать под чертой, что “замечать” наверху. Но задайте вопрос: “А почему надо делать так?” Многие ученики теряются, не знают, что ответить. Это означает, что такие ученики выполняют арифметические действия успешно, но их математического смысла не понимают.
Таким образом, если учащимся раскрыть “секреты” математики, то они легко будут понимать и усваивать её. Если же этого не сделать, то учащиеся будут брать памятью, будут механически производить различные арифметические действия, не понимая их сути и, следовательно, не развивая своего математического мышления.
Обобщённые виды познавательной деятельности могут быть сформированы только при соответствующем построении учебных предметов. Их содержанием должны быть не частные явления, а их сущность.
Овладение общими методами познавательной деятельности позволяет учащимся не только самостоятельно анализировать новые частные явления, но и создавать их.
7
1.4. Мастерство учителя в руководстве познавательной деятельности учащихся
Мастерство управления познавательной деятельностью на уроке зависит от множества факторов. Одним из важнейших является умение учителя сделать свой предмет интересным для школьников. Ибо интерес, как отмечают учёные, положительно влияет на все психические процессы и функции: восприятие, внимание, память, мышление, волю. “В процессе обучения и воспитания школьника познавательный интерес выступает в многозначной роли: и как средство живого, увлекающего ученика обучения, и как сильный мотив отдельных учебных действий школьника и учения в целом, побуждающий к интенсивному и длительному протеканию познавательной деятельности школьника, в конечном итоге способствующая её направленности”
Трудно сказать, по каким путям поведёт школьника его естественный возрастной процесс активности, если он не будет направлен умственными интересами.
Каковы же условия становления учебно-познавательных интересов? Как учитель - мастер формирует их у учащихся на уроке? Что он делает, чтобы активизация учебной деятельности и интерес к учению постоянно развивались?
Учитель - мастер в становлении и развитии учащихся интересов к учению, как правило, постоянно руководствуется такими основными положениями:
1. Развитию познавательных интересов, любви к изучаемому предмету и к самому процессу обучения, способствует организация обучения, которая решает вопросы проблемного характера.
2. Обучение должно быть трудным, но посильным.
3. Яркость, эмоциональность учебного материала, взволнованность самого учителя с огромной силой воздействует на школьника, на его отношение к предмету.
Однообразная информация и однообразные способы действия очень быстро вызывают скуку.
8
Вывод к главе 1.
Большую роль в активизации познавательной деятельности учащихся играет учитель. Оттого, как будет построена его работа по изучению нового материала, от его мастерства зависит дальнейшее усвоение знаний детьми.
Но не следует всю ответственность за усвоение материала перекладывать на плечи учителя. Усвоение знаний, умений, навыков также зависит от самих учащихся, их психического состояния и настроя. Как отмечалось в пунктах выше, развитие одного ребёнка во многом отличается от развития другого. Поэтому учителю необходимо применять в обучении различные приёмы и методы, дифференцированный подход в обучении. Одним из ведущих методов, применяемых учителем для успешного усвоения знаний, являются развивающие методы обучения.
9
Глава 2. Приёмы активизации учащихся в процессе обучения математике в 3 классе при изучении внетабличного деления и умножения
2.1. Сущность приёмов активизации
Для того, чтобы добиться активности учащихся на уроке математике, нужно применять приёмы активизации познавательной деятельности.
Приём - составная часть или отдельная сторона метода. В процессе обучения приёмы играют важную роль, поскольку они побуждают учащихся к активному участию в освоении учебного материала: постановка вопросов при изложении учебной информации, включение в него отдельных практических упражнений, ситуационных задач, обращение к наглядным и техническим средствам, побуждение к ведению записей. Также с целью повышения активности учащихся на уроке используются различные методы: проблемные, объяснительно - иллюстративные, логические, метод самостоятельной работы, дидактическая игра, нестандартные виды уроков, тесты, а также различные формы учебной деятельности
Метод и приём могут меняться местами. Но независимо от этого, учитель обязан включить в структуру своего урока тот или иной приём, метод. В результате у учащихся будет формироваться интерес к учебному процессу, повышаться активность, что имеет немаловажное значение для учителя в его работе.
10
2.2 Приемы, способствующие активизации процесса восприятия
На уроке знакомства с внетабличным умножением и делением для развития самостоятельности предлагается учащимся такая последовательность упражнений.
1) Заменить числа суммой их разрядных слагаемых:
18=10+8 53=…+ 3 39 = …+…
24=20+… 61=…+… 72 = …+…
2) Прокомментировать решение и закончить его:
43+4=(40+3)+4=40+(3+4)=…
35-20=(30+5)-20=(30-…)+5= …
27-3=(20+7)-3=(7- …)+ …= …
38-5=(30+8)-5=(8-…)+…=…
32+7=(30+…)+7= (…+…)+…=…
3) На основе выполненных заданий предположить способ решения следующих примеров:
12 ∙ 5 = (10 + 2) ∙ 5 = (10 ∙ 5)+ (2 ∙ 5) =…+… =
24 ∙ 2 = …
26 : 2 = …
39 : 3 = …
Из приведенной записи видно, что примеры учащиеся решали самостоятельно. В качестве видов помощи было предложено повторение ранее изученного материала, готовое решение первого примера. Это позволило учащимся самостоятельно овладеть решением уже на первом уроке знакомства с внетабличным умножением и делением и приемами самоконтроля.
4) Полезно дать записи таких примеров с целью сравнения результатов:
20 ∙ 2 = 2 ∙ 2 =
90 : 3= 90 : 30=
и затем сравнить результаты в каждой строке.
11
Итоговым вопросом может быть такой: почему произведение (частное) в первом примере больше, чем во втором?
Таким образом, приведенные примеры свидетельствуют о том, что в развитии познавательной деятельности младших школьников многое зависит от умелого подбора заданий с учетом их разнообразия, творческого характера.
12
2.3. Приемы, способствующие активизации процесса запоминания.
В ходе учебной деятельности ученику приходится многое запоминать. Между тем память младшего школьника характеризуется преимущественно образностью, конкретностью, ограниченностью по объему. «Продуктивность памяти младших школьников зависит от понимания ими характера самой мнемической задачи и от владения соответствующими приемами и способами запоминания и воспроизведения», - замечает психолог В.С. Мухина в книге «Возрастная и педагогическая психология».
1) Установка на запоминание определенного материала на длительный срок и сосредоточения внимания на материале.
Например: урок знакомства с внетабличным случаем умножения вида
23 Х 5 . На уроке раскрывается важность изучаемого материала и показывается, что знание состава чисел будет способствовать быстрому и безошибочному счету в уме.
2) Обязательная проверка понимания учебного материала и сопоставление его с ранее изученным.
Например, задание для самостоятельной работы даже на этапе знакомства с новым материалом подбирается таким образом, чтобы учащиеся сами могли активно выполнять действия.
3) Выполни по аналогии:
22 ∙ 4 = (20 ∙ 4) + ( 2 ∙ 4) =
17 ∙ 3 = (10 ∙…) + ( 7 ∙…) =
19 ∙ 5 = ……………….
75 : 5 = ( 50 +….) : 5 = (…: 5) + ( 15 : …) = …+… =
38 : 2 = ( … + …) : 2 = ( 20 : …) + ( … + 2 ) = … + … =
4) Наглядный материал. Чем моложе учащиеся, тем большую роль в их познавательной деятельности играет чувственное восприятие. Поэтому и для запоминания материала важно опираться на наглядный материал (макеты, пособия, картины, таблицы, алгоритмы, ИКТ). ( Приложение 1)
13
3.4. Активизация логического мышления
Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся.
Прежде всего, нужно развивать у ребенка способность к анализу и синтезу. Острота аналитического ума позволяет разобраться в сложных вопросах. Способность к синтезу позволяет одновременно держать в поле зрения сложные ситуации, находить причинные связи между явлениями, овладевать длинной цепочкой умозаключений. Важно формировать у ребенка продуктивное мышление, то есть способность к созданию новых идей, умению устанавливать связи между фактами и группами фактов. Если ребенок выдвигает идею не новую для взрослых, но новую для коллектива или для самого себя, если он открывает что-то для себя, пусть известное для других, - это уже показатель продуктивности его мышления.
Уже в начальной школе при построении содержания обучения необходимо предусмотреть систему необходимых логических приемов мышления.
С учетом предметных связей используются следующие задания:
1) Установи аналогии и реши:
дерево + земля = 11
маргаритка • королева =
Ответ: 80 (Приложение 2)
2) Найди недостающее число. Рисунки с примерами каждого ряда составлены по определенному правилу, нужно догадаться, в чем состоит это правило, и дорисовать четвертый рисунок так, чтобы это правило сохранялось. (Приложение 3)
3) Блок – схема. Учащимся дается число, которое они вставляют в блок – схему и выполняют указанные действия. (Приложение 4).
4). Приём классификации. Учитель предлагает различные примеры на внетабличное деление и умножение, которые нужно сгруппировать по каким – либо признакам: по действиям, по результатам ( одинаковые) :
22 : 6 38 : 2 18 х 4
4 х 16 17 : 4 72 : 12
38 : 19 24 х 3 27 : 5
96 : 3 59 : 9 18 х 5
5) Прием анализа. Заменить числа суммой разрядных слагаемых:
69, 78, 68, 96, 39, 88, 54, 29, 47, 63.
14
6)Прием синтеза. Составить примеры на деление и умножение, используя только данные числа:
24, 3, 8, 12, 48, 4, 6, 2;
4, 3, 24, 6, 18, 72, 8;
42, 2, 21, 84, 4, 3, 7;
27, 3, 9, 54, 6, 18, 814
15
2.5. Активизация познавательной деятельности учащихся в процессе формирования вычислительных навыков
В практике обучения математике заметно больше влечение детей к текстовым задачам, нежели к вычислительным примерам. И это не удивительно: в задаче, как правило, интерпретируется некоторая реальная ситуация, близкая пониманию детей, явно выражена связь с практикой.
Вычислительные же примеры представляются детям весьма абстрактными, лишенными практической цели, а работа над ними – скучным занятием. Между тем именно вычислительные примеры являются основным средством формирования умений и навыков выполнять вычисления, без чего немыслимо овладеть основами наук, а также почти любым видом практической и профессиональной деятельности.
Сейчас в век компьютеризации отмечается формирование у всех школьников прочных умений выполнять устные и письменные вычисления. И это остается одной из важнейших целей обучения математике, составляет основу математического образования.
Детей следует научить не только вычислять, но и вырабатывать у них чувство числа, способность видения его через наблюдения. По словам выдающегося ученого Петербургской академии наук Л. Эйлера, свойства чисел, известных сегодня, по большей части были открыты путем наблюдений и задолго до того, как их истинность была подтверждена строгими доказательствами.
Говорят, что заставить учиться нельзя, учебой надо увлечь. И это совершенно справедливо. Настоящее сотрудничество учителя и ученика возможно лишь при условии: ученик будет хотеть делать то, что желает учитель.
Чтобы активизировать познавательную деятельность детей при выполнении ими вычислительных упражнений, надо внести элемент занимательности как в содержание, так и в форму такой работы.
Сознательное и прочное усвоение знаний учащимися проходит в процессе их активной умственной деятельности. Поэтому работу следует организовать на каждом уроке так, чтобы учебный материал становился предметом активных действий ученика.
Можно красочно оформить таблицы, сочинить стихи, зарифмовать задачи и придумать игры. И тогда в глазах учащихся засветится неподдельный интерес. Каждый день они будут делать для себя маленькие открытия и легко усваивать материал.
16
Упражнения в игровой и занимательной форме всегда вызывали интерес и способствовали прочному усвоению учебного материала.
Еще во втором классе при подготовительных упражнениях к табличному умножению и делению учащиеся считали:
Сколько ног у двух гусей? У двух цыплят? У двух петухов?
Сколько ножек у двух столов? А у двух журнальных столиков?
Я вижу 12 птичьих ног. Сколько воробьев прыгает?
По дороге бегут 16 собачьих лап. Сколько собак бежит?
В стойле стоят 28 лошадиных ног. Сколько лошадей в стойле?
У одного стола 4 ножки. А у 5 столов сколько?
Даже серьезный и большой по объему материал можно давать в игровой, увлекательной и доступной для детей форме. Урок должен не только увеличивать запас систематических знаний учащихся, но и воспитывать в них желание и умение учиться. Существует тесная связь между знаниями и познавательными интересами. Только учебная деятельность, построенная с преобладанием элементов, форм и правил игровой деятельности, с ее непосредственностью и эмоциональностью способствует желанию учиться с радостью и удовольствием.
Дидактическая игра – одно из эффективных средств развития интереса к учебному предмету. Она вызывает у детей живой интерес к процессу познания, активизирует их познавательную деятельность и помогает легче усвоить учебный материал.
В практике начальной школы дидактические игры могут выступать самостоятельно или взаимно дополнять друг друга. Использование каждого вида игры определяется целями, содержанием учебного материала, возрастными особенностями учащихся, умениями и навыками в проведении подобных игр.
Игра только внешне кажется развлечением, в действительности она требует серьезной предварительной подготовки со стороны учителя и учащихся. В процессе игры от детей требуется выдержка, большое умственное напряжение, проявление самостоятельности. Но игра всегда приносит удовлетворение и радость и не нужно бояться, что она нанесет ущерб научности. Сделав материал доступным, интересным, игра создает богатые возможности для выявления у учащихся общих знаний, понятий,
установлений межпредметных связей. Кроме того она способствует сплочению детского коллектива, формированию у учащихся взаимного уважения и понимания, влияет на отношения учителя и ученика, делая их
17
более доброжелательными. Но надо предостеречь начинающих учителей:
злоупотребление игрой в учебном процессе, несмотря на активность детей, может привести к пробелам в их знаниях.
Активизация деятельности учащихся на уроке – одно из основных направлений совершенствования учебно-воспитательного процесса в школе. Сознательное и прочное усвоение знаний учащихся проходит в процессе их активной умственной деятельности. Поэтому работу следует организовывать на каждом уроке так, чтобы учебный материал становился предметом активных действий ученика.
В процессе игры учащиеся незаметно для себя выполняют различные упражнения, где им приходится сравнивать числа и множества, выполнять арифметические действия, тренироваться в устном счете, решать задачи. Игра, ставит учащихся в условия поиска, пробуждает интерес к победе, а отсюда они стремятся быть быстрыми, собранными, ловкими, находчивыми, четко выполнять задания, соблюдая правила игры.
Ценность дидактической игры определяется не только потому, какую реакцию она вызовет со стороны детей, но и учитывается то, насколько она эффективно помогает решать учебную задачу. Подбирая какую-либо игру для урока, необходимо продумывать следующие вопросы:
цель игры;
какие умения и навыки будут формироваться в процессе ее проведения?
какие воспитательные цели преследуются в процессе игры?
понятна ли она для учащихся моего класса?
все ли учащиеся в одинаковой степени будут участвовать в игре?
подведение итогов игры.
Дидактические игры помогают в формировании ряда умений и навыков, обеспечивающих включение детей в учебную деятельность Трудное легко запоминается в игре. Поэтому при объяснении нового материала или закреплении пройденного игра помогает эффективно решать учебную, а иногда и воспитательную задачу.
(Приложения:
Игра «Да, нет»
Игра «Молчанка»
Игра «Кто быстрее?»
Игра «По порядку»
«Круговые примеры»
Игра «Какой ряд быстрее полетит на Луну?»
18
Игра «Какой ряд лучше?»
«Математическое домино»
Игра «Телефон»
Игра «Математическая эстафета»
Игра «Не ошибись»
Игра «Ладонь – кулак»
Игра «Числа – перебежки»
Игра «По какой тропинке ты пойдешь?»
Игра «Бабочки» )
19
Вывод к главе 2.
Это лишь некоторые виды работ на уроках математики, которые активизируют деятельность учащихся. При выполнении описанных выше заданий ребята думают, сравнивают, анализируют. И это способствует более прочному и осознанному усвоению знаний. Данные математические игры можно использовать на различных этапах урока: на этапе изучения нового материала, на этапе закрепления, на этапе проверки знаний, умений и навыков.
Использование игр на уроках математики позволяет более творчески подходить к оценке знаний учащихся, привлекать к работе всех учащихся класса, способствует формированию интереса к предмету, активизирует мыслительную деятельность учеников, развивает смекалку и наблюдательность.
20
Заключение.
В ходе анализа особенностей учащихся 3-го «и» класса при изучении темы «Внетабличное деление и умножение» выявлено, что в период с декабря 2012 г. по февраль 2013 г., благодаря следующим приемам активизации познавательной деятельности на уроках математики:
Комментирование - развивает коммуникативные, предметные, личностные умения.
2) Игровые приемы - развивают коммуникативные, предметные, личностные умения.
3) Работа по аналогии, работа по алгоритму - учащиеся развивают регулятивные умения;
у учащихся заметен рост в снижении ошибок при решении примеров по данной теме.
Внетабличное умножение:
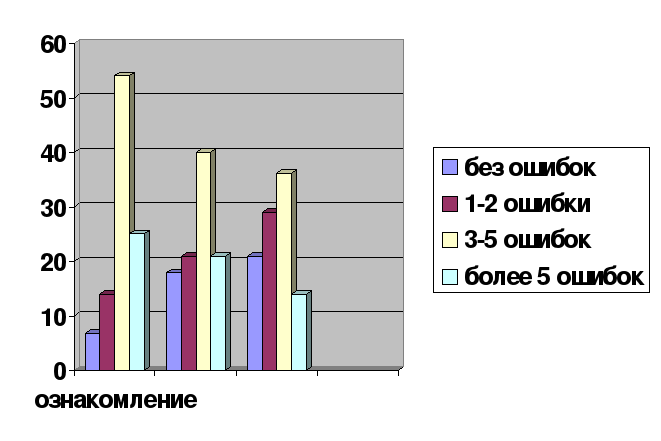
21
Внетабличное деление:
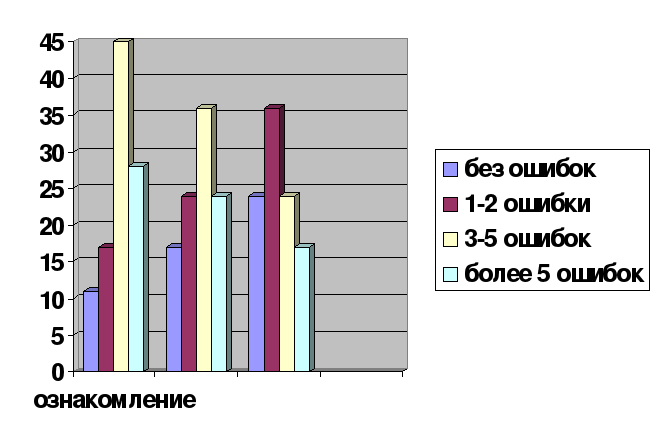
Тем самым, установлено, что приемы активизации познавательной деятельности на уроках математики важны для повышения качества знаний учащихся. (Приложение 20)
Следует учесть, что класс со средним и низким уровнем подготовленности. Есть четверо учащихся, которым тема очень сложна для понимания, и на всех уровнях проверки знаний по изучаемой теме эти учащиеся показали неудовлетворительный результат.
Как показало исследование, тема является актуальной и требует дальнейшего изучения методов и приемов.
Ребенок, который не научится управлять своими мыслями и своим вниманием, будет постоянно отвлекаться на уроках по пустякам. На его успеваемости это скажется самым негативным образом. Понятные мотивации и организованный процесс мышления детей очень быстро сделали свое дело – учиться им стало легче и интереснее.
Организация развивающего обучения предполагает создание условий для овладения школьниками приемами умственной деятельности. Овладение ими не только обеспечивает новый уровень усвоения, но и дает существенные сдвиги в умственном развитии. Овладев этими приемами, ученики становятся более самостоятельными в решении различных учебных заданий, могут рационально строить свою деятельность по усвоению новых знаний.
22
Литература:
1. Акимова С. Занимательная математика. - Санкт - Петербург, (Тритон), 1997 - 608 с.
2. Алиева С. К. «Грамматика русского языка и математика в таблицах и схемах» для начальных классов. Москва, Лист, 2001, 63 с.
3. Аргинская И. И., Дмитриева Н. Я., Полякова А. В., Романовская З. И. Обучаем по системе А. В. Занкова: 1-й год обучения: Кн. Для учителя. - М.: Просвещение, 1991. - 240 с.
4. Баженова И. Н. Педагогический поиск. - М.: Педагогика, 1989. - 560 с.
5. Балашов М.М. Дидактическая игра на уроке. Игру любят все! Школьные технологии. – 1998. – № 5 – С. 137 – 140.
6. Баранов С. П. Педагогика: Учеб. Пособие для педагогических училищ по специальности № 2001 (Преподавание в начальных классах общеобразовательной школы) - 2-е изд., переработанное - М.: Просвещение, 1987 - 368 с.
7. Данченко, Т. Игровые технологии в начальной школе. Учитель. – 2007. – № 6. – С. 44 – 46.
8. Жигалкина Т. К. Игровые и занимательные задания по математике: Пособие для учителя. - 2-е изд. - М.: Просвещение, 1989 - 47 с.
9. Козлова О. А. Роль современных дидактических игр в развитии познавательных интересов и способностей младших школьников. Начальная школа. – 2004. – № 11 – С. 49 – 52.
10. Лысенкова С. Н. Методом опережающего обучения: Книга для учителя: Из опыта работы. - М.: Просвещение, 1988. - 192 с.
11. Мокрушина О. А. Поурочные разработки по математике в 3 классе. В помощь школьному учителю. - М.: «ВАКО», 2005. – 205с.
12. Перова М. Н. Дидактические игры и упражнения по математике для работы с детьми дошкольного и младшего школьного возраста. М.: Просвещение, 1996. - 144 с.
13. Полякова А. В. Усвоение знаний и развитие младших школьников. - М.,1078.
14. Талызина Н. Ф. Формирование познавательной деятельности младших школьников: Книга для учителя. - М.: Просвещение, 1988. -175 с .
15. Тихомирова Л. Ф. «Математика в начальной школе» Развивающие игры, задания, упражнения. Москва, Сфера, 2001, 59 с.
16. Эрдниев П. М. Обучение математике в начальных классах (книга для учителя) 2 изд. Дополн. - М.: АО (Столетие), 1995. -272 с.
23
17. http://text.tr200.biz/referat_pedagogika/?referat=173957&page=1
18.http://nsportal.ru/nachalnaya-shkola/obshchepedagogicheskie-tekhnologii/diplomnaya-rabota
19. Р
20. sbornik_zadaniy.docx
infourok.ru

Разделы: Математика, Конкурс «Презентация к уроку»
Загрузить презентацию (410,9 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
“Счёт и вычисления – основа порядка в голове”. Песталоцци
Цель:
Содержание.
Ход занятия
Актуальность использования приемов быстрого счета.
В современной жизни каждому человеку часто приходится выполнять огромное количество расчётов и вычислений. Поэтому цель моей работы – показать лёгкие, быстрые и точные методы счёта, которые не только помогут вам во время каких-либо расчётах, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта. Основополагающим элементом вычислительной культуры являются сознательные и прочные вычислительные навыки. Проблема формирования вычислительной культуры актуальна для всего школьного курса математики, начиная с начальных классов, и требует не простого овладения вычислительными навыками, а использования их в различных ситуациях. Владение вычислительными умениями и навыками имеет большое значение для усвоения изучаемого материала, позволяет воспитывать ценные трудовые качества: ответственное отношение к своей работе, умение обнаруживать и исправлять допущенные в работе ошибки, аккуратное исполнение задания, творческое отношение к труду. Однако, в последнее время уровень вычислительных навыков, преобразований выражений имеет ярко выраженную тенденцию к снижению, учащиеся допускают массу ошибок при подсчетах, все чаще используют калькулятор, не мыслят рационально, что отрицательно сказывается на качестве обучения и уровне математических знаний учащихся в целом. Одной из составляющих вычислительной культуры является устный счёт, который имеет большое значение. Умение быстро и правильно произвести несложные вычисления “в уме” необходимо для каждого человека.
Старинные способы умножения чисел.
1. Старинный способ умножение на 9 на пальцах

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9 x 3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9 x 3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
2. Умножение методом Ферроля.
Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.
Например: 12х14=168
а) 2х4=8, пишем 8
б) 1х4+2х1=6, пишем 6
в) 1х1=1, пишем 1.
3. Японский способ умножения
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:
Этот рисунок состоит из 10 линий (количество может быть любым)
Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом:
(пересечения на рисунке указаны точками)

Количество пересечений:
1) Пересечения в верхнем левом крае (2) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа
3) Пересечения в нижнем правом крае (12) – третье число ответа.
Получается: 2; 10; 12.
Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.
3(2+1)1(0+1)2
Ответ: 312
4. Итальянский способ умножения (“Сеткой”)
В Италии, а также во многих странах Востока, этот способ приобрел большую известность.
Использование приема:
Например, умножим 6827 на 345.
1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.

2. Умножаем число каждого ряда последовательно на числа каждой колонки.

т.е.
Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.
(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)
3. Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.

Ответ: 2355315.
5. Русский способ умножения.
Этот прием умножения использовался русскими крестьянами примерно 2-4 века назад, а разработан был еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:
Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение
Однако как поступить, если при этом приходится делить пополам число нечетное? Народный способ легко выходит из этого затруднения. Надо, - гласит правило, - в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):
Сложив незачеркнутые числа, получаем вполне правильный результат:
Ответ: 323.
6. Индийский способ умножения.
Такой способ умножения использовали в Древней Индии.
Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.

Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 9х7, 9х9 и 9х3. Полученные произведения пишем в сетку (Б), имея в виду следующие правила:

Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).

Затем складываем цифры в колонках и получаем ответ: 72956.
Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это было возможно. Затем они складывали цифры в колонках и получали результат.
Заключение
Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, “экономическую - ситуацию” в стране, погоду на “завтра”, описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора - “Всё есть число!”.
Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.
Описывая старинные способы вычислений и современные приёмы быстрого счёта, я попытался показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.
“Кто с детских лет занимается математикой, тот развивает внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство в достижении цели”. (А.Маркушевич)
Литература.
xn--i1abbnckbmcl9fb.xn--p1ai