 называется множеством рациональных
чисел и обозначается : первой буквой
французского слова
называется множеством рациональных
чисел и обозначается : первой буквой
французского слова  : ("отношение".) Название этого
множества происходит также от латинского слова
: ("отношение".) Название этого
множества происходит также от латинского слова  : , что также
переводится как "отношение"
: , что также
переводится как "отношение"
Тема урока:
Цели урока:
систематизировать знания о
рациональных числах;
формирование навыка работы в парах;
развитие внимания и логического мышления.

Для счета предметов используются числа, которые называются натуральными . Для обозначения множества натуральных чисел употребляется буква N - первая буква латинского слова Naturalis - «естественный», «натуральный»
N - натуральные
1 , 2, 3, 4, 5, …

Числа,
им противоположные
Натуральные числа
5
3
6
4
2
1
-5
-4
-3
-2
-6
-1
Целые

Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z - первой буквой немецкого слова Zahl - «число».
Z - целые
… , -3, -2, - 1 , 0,
1 , 2, 3, …

Целые числа
Дробные числа
58
10
9
-4
0
1
7,1
0,1
2/7
3,2
0,(2)
Рациональные

Множество чисел, которое можно представить в виде , называется множеством рациональных чисел и обозначается буквой Q - первой буквой французского слова Quotient - «отношение». Есть также версия, что название рациональных чисел связано с латинским словом ratio – разум.
Q - рациональные
… , -3, -2, - 1 , 0, 1, 2, 3, …
+ дроби

Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера .
N Z Q

Математический символ ∈ называют знаком принадлежности ( элемент принадлежит множеству ) .
«n - натуральное число»
можно писать n ∈ N
«m - целое число»
можно писать m ∈ Z
«r - рациональное число»
можно писать r ∈ Q

Математический символ ⊂ называют знаком включения ( одно множество содержится в другом ).
«N - часть множества Z»
можно писать N ⊂ Z ,
«Z - часть множества Q»
можно писать Z ⊂ Q

Множества обозначают большими буквами,
элементы множества - маленькими буквами.
«x не принадлежит множеству X»
можно писать x ∉ X
«A не является частью (подмножеством) B»
можно писать A B .

N Z Q
Число 5 - ?
N, Z, Q
Число -7 - ?
Z, Q
Z, Q
Число -6,7 - ?
Число - ?
Q

1. нет
2. да
3. нет
4. да
5. да
6. нет
7. да
8. да
9. да
10. нет
11. нет
12. нет
13. да
14. да
15. нет

Переведите обыкновенные дроби в десятичные:
= 0,375 – конечная десятичная дробь
Если в знаменателе стоят 2, 5, их произведение или произведение комбинацийэтих чисел – всегда КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ!

Переведите обыкновенные дроби в десятичные:
= 0,272727272727272727… - бесконечная периодическая десятичная дробь
Для краткости написания – ПЕРИОД (круглые скобки)
0,272727272727272727…= 0,(27)

Прочитайте дроби:
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
чисто периодические
смешанные периодические


Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?
N Z Q
5 = 5,000… = 5,(0)
-8,37 = -8,37000… = -8,37(0)
Дроби - ?

Алгоритмы перевода рациональных чисел
в бесконечную десятичную периодическую дробь
= 0,375 = 0,375(0)
= 0,272727… = 0,(27)
Делим числитель
на знаменатель

Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?

Переведем б.п.д. дробь 0,(2)
в обыкновенную
Пусть х = 0,(2)
Это для
чисто периодической !!!
10х = 2,(2)
10х = 2,(2)
10 ( число цифр в периоде )
х = 0,(2)
10х – х = 2,(2) - 0,(2)
9х = 2
0,(2)

Переведем б.п.д. дробь 0,4(6)
в обыкновенную
Это для
смешанной периодической !!!
Пусть х = 0,4(6)
10х = 4,(6)
100х = 46,(6)
10 ( число цифр в периоде )
10х = 4,(6)
100х – 10х = 46,(6) - 4,(6)
90х = 42
0,4(6)
21


Чтобы обратить чисто периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, образованное из цифр, стоящих в периоде , а в знаменателе – написать цифру 9 столько раз, сколько цифр в периоде .
0,(2)=
2
0,(81)=
81
9
99
1 цифра
2 цифры

Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби
поставить число , равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода , и числа, образованного из цифр, стоящих после запятой до начала первого периода ; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде , и со столькими нулями , сколько цифр между запятой и началом периода .
6
4
4
0,4(6)=
9
0
1 цифра
1 цифра

- Знаю (умею, научился), как определить вид числа, его принадлежность к числовым множествам;
- Знаю (умею, научился) правильно пользоваться математической символикой в процессе выполнения заданий;
- Знаю (умею, научился) представлять рациональное число в виде конечной или бесконечной периодической дроби;
- Знаю (умею, научился) представлять бесконечную периодическую дробь в виде обыкновенной дроби;
.
![1. Дана фраза: «28 - рациональное число». Как можно записать иначе? а) 28 ∈ N б) 28 ∈ Q в) 28 ∈ Z 2. Вычисли значение дроби − d, если a = 13; b = 36; c = 0,9; d=1,76; 3. Утверждение «−17∈(−17;5]» является: а) ложным; б) истинным 4. Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым 5. Вычислить значение выражения:](/800/600/http/arhivurokov.ru//kopilka/uploads/user_file_548f1fe0e5611/img_user_file_548f1fe0e5611_25.jpg)
1. Дана фраза: «28 - рациональное число». Как можно записать иначе?
а) 28 ∈ N б) 28 ∈ Q в) 28 ∈ Z
2. Вычисли значение дроби − d, если a = 13; b = 36; c = 0,9; d=1,76;
3. Утверждение «−17∈(−17;5]» является:
а) ложным; б) истинным
4. Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым
5. Вычислить значение выражения:

Ресурсы интернета:
1 . http://www.librus.ru/childrens-corner/scientifically-
cognitive-literature/5676-mir-chisel.html
2. http://odur.let.rug.nl/magazijn/decennia/1745-1754_45.htm
3. http://project-gym6.narod.ru/1/62/euler.htm
4. http://sferica.by.ru/history/pi.html
5. http://www.peoples.ru/science/mathematics/simon_stevin/
6. http://www.proshkolu.ru/user/galrybo/file/455559/
7. http://www.free-lancers.net/users/vixen/
8. http://www.15a20.com.mx/images/sections/thumbs/
thumb_7312558.jpg
9. http://gr-matem.narod.ru/
10. http://www.i-u.ru/biblio/archive/depman_mir/01.aspx
11. Использованы материалы презентации Обуховой Н.С.
МОУ СОШ № 17 г. Заволжья Нижегородской области
kopilkaurokov.ru

Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области


Для счета предметов используются числа, которые называются натуральными . Для обозначения множества натуральных чисел употребляется буква N - первая буква латинского слова Naturalis - «естественный», «натуральный»
N - натуральные
1 , 2, 3, 4, 5, …

Числа,
им противоположные
Натуральные числа
5
3
6
4
2
1
-5
-4
-3
-2
-6
-1
Целые

Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z - первой буквой немецкого слова Zahl - «число».
Z - целые
… , -3, -2, - 1 , 0,
1 , 2, 3, …

Целые числа
Дробные числа
58
10
9
-4
0
1
7,1
0,1
2/7
3,2
0,(2)
Рациональные

Множество чисел, которое можно представить в виде , называется множеством рациональных чисел и обозначается буквой Q - первой буквой французского слова Quotient - «отношение». Есть также версия, что название рациональных чисел связано с латинским словом ratio – разум.
Q - рациональные
… , -3, -2, - 1 , 0, 1, 2, 3, …
+ дроби

Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера .
N Z Q

Математический символ ∈ называют знаком принадлежности ( элемент принадлежит множеству ) .
«n - натуральное число»
можно писать n ∈ N
«m - целое число»
можно писать m ∈ Z
«r - рациональное число»
можно писать r ∈ Q

Математический символ ⊂ называют знаком включения ( одно множество содержится в другом ).
«N - часть множества Z»
можно писать N ⊂ Z ,
«Z - часть множества Q»
можно писать Z ⊂ Q

Множества обозначают большими буквами,
элементы множества - маленькими буквами.
«x не принадлежит множеству X»
можно писать x ∉ X
«A не является частью (подмножеством) B»
можно писать A B .

N Z Q
Число 5 - ?
N, Z, Q
Число -7 - ?
Z, Q
Z, Q
Число -6,7 - ?
Число - ?
Q

Переведите обыкновенные дроби в десятичные:
= 0,375 – конечная десятичная дробь
Если в знаменателе стоят 2, 5, их произведение или произведение комбинацийэтих чисел – всегда КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ!

Переведите обыкновенные дроби в десятичные:
= 0,272727272727272727… - бесконечная периодическая десятичная дробь
Для краткости написания – ПЕРИОД (круглые скобки)
0,272727272727272727…= 0,(27)

Прочитайте дроби:
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
чисто периодические
смешанные периодические


Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?
N Z Q
5 = 5,000… = 5,(0)
-8,37 = -8,37000… = -8,37(0)
Дроби - ?

Алгоритмы перевода рациональных чисел
в бесконечную десятичную периодическую дробь
= 0,375 = 0,375(0)
= 0,272727… = 0,(27)
Делим числитель
на знаменатель

Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?

Переведем б.п.д. дробь 0,(2)
в обыкновенную
Пусть х = 0,(2)
Это для
чисто периодической !!!
10х = 2,(2)
10х = 2,(2)
10 ( число цифр в периоде )
х = 0,(2)
10х – х = 2,(2) - 0,(2)
9х = 2
0,(2)

Переведем б.п.д. дробь 0,4(6)
в обыкновенную
Это для
смешанной периодической !!!
Пусть х = 0,4(6)
10х = 4,(6)
100х = 46,(6)
10 ( число цифр в периоде )
10х = 4,(6)
100х – 10х = 46,(6) - 4,(6)
90х = 42
0,4(6)
21
multiurok.ru
Разделы: Математика
Цели урока:
Создать условия, при которых ученик:
В результате ученик:
Оборудование к уроку: проектор, компьютер, тетрадь с печатной основой (приложение1), презентация.
Ход урока
I. Мотивационно - ориентировочный этап.
-Проверим домашнее задание (слайд 2),которое поможет нам определить тему урока.
Заполните пропуски в тетради с печатной основой (приложение, слайд 3)
Для счета предметов используются числа,
которые называются натуральными. Для
обозначения множества натуральных чисел
употребляется буква : - первая буква латинского
слова 2 : , "естественный",
"натуральный". Натуральные числа, числа им
противоположные и число нуль, образуют множество
целых чисел, которое обозначается : - первой
буквой немецкого слова 0 : -
"число". Множество чисел, которые можно
представить в виде  называется множеством рациональных
чисел и обозначается : первой буквой
французского слова
называется множеством рациональных
чисел и обозначается : первой буквой
французского слова  : ("отношение".) Название этого
множества происходит также от латинского слова
: ("отношение".) Название этого
множества происходит также от латинского слова  : , что также
переводится как "отношение"
: , что также
переводится как "отношение"
-Спрогнозируйте тему урока. (Числовые множества)
- Известны ли вам те числовые множества, о которых идет речь в тексте. (Известны, их мы начали изучать в начальной школе, затем продолжили в 5,6 и 7 классах).
-Приведите примеры натуральных, целых и рациональных чисел.
-Вспомните отношения между множествами, назовите самое большое из них. (Множество рациональных чисел)
Уточним тему урока "Рациональные числа" (слайд 4) и запишем ее в тетрадь.
Спрогнозируйте цель урока: систематизировать знания о рациональных числах.
Краткая информация из истории развития числа сопровождается записями в тетради
:N - множество всех натуральных чисел, "
n - натуральное число" 
 ,
,
Z - множество всех целых чисел , " m - целое
число"  ,
,
Q - множество всех рациональных чисел, " r
- рациональное число". 


Историческая справка (слайды 5-18).
Натуральные числа возникли в силу необходимости вести счет любых предметов.
Натуральные числа несут ещё другую функцию: характеристику порядка предметов, расположенных в ряд.
О натуральном в смысле естественном ряде чисел говорится во "Введении в арифметику" греческого математика (неопифагорийца) Никомаха из Геразы.
В современном смысле понятие и термин "Натуральное число" встречается у французского философа и математика Ж.Даламбера(1717-1783)
Сумма и произведение натуральных чисел есть число натуральное.
Дроби естественно возникли при решении задач о разделе имущества, измерении земельных участков, исчислении времени.
Сумма, произведение и частное дробных чисел есть число дробное.
Доли или единичные дроби, у которых числитель единица, знаменателем же может быть любое целое число;
Дроби систематические, у которых числителями могут быть любые числа, знаменателями же - только числа некоторого частного вида, например, степени десяти или шестидесяти;
Дроби общего вида, у которых числители и знаменатели могут быть любыми числами.
Десятичные дроби в XV веке ввел самаркандский ученый ал - Каши. Ничего, не зная об открытии ал - Коши, десятичные дроби открыл второй раз, приблизительно через 150 лет, после него, фламандский ученый математик и инженер Симон Стевин в труде "Децималь" (1585 г).
Понятие отрицательных чисел возникло в практике решения алгебраических уравнений.
Отрицательные числа трактовались так же как долг при финансовых и бартерных расчетах.
Отрицательные числа ввели в математический обиход Михаэль Штифель (1487-1567) в книге "Полная арифметика" (1544), и Никола Шюке (1445-1500)- его работа была обнаружена в 1848 году.
Сумма, произведение и разность целых чисел есть число целое.
Отношения между множествами натуральных, целых и рациональных чисел наглядно демонстрирует геометрическая иллюстрация - круги Эйлера.
Леонард Эйлер жил в России в середине XVIII века и внес большой вклад в развитие математики.
Операционно-исполнительский этап.
Задание 1. (выполняется самостоятельно с последующей проверкой) (слайд 19 - проверка по щелчку)
Вычислите значения числовых выражений и изобразите их на кругах Эйлера числа а, в, с, d, m , если
| а в с d m |
1 : 5+0,8 =_________________________________ (1) 0,6: 0,2- 22 =________________________________ (-1) 17:3 -5 = __________________________________(1/3) (-1) 3 +( -1)2 =_______________________________ (0) 13 :2 +0,5 = _________________________________ (7) Оставшуюся на диаграмме точку обозначьте буквой "к". |
Задание 2 - интерактивный тест (слайд 20 - триггер) устная работа.
Используя диаграмму, определите, какие из высказываний истинные, а какие ложные.
Нам уже известно, что любое рациональное число
можно записать в виде отношения  , где
, где  .
.
Выполните следующее задание:
Задание3 (работа в парах " сильный - слабый")
Представьте в виде  , где
, где  числа:
числа:
- 3; 2; 0;  ;
;  ; 0,23; -3,14
; 0,23; -3,14
( ;
;  ;
;  ;
;  ;
;  ;
;  )
)
Вы также умеете записывать рациональные числа в виде десятичных дробей.
Задание 4 - интерактивный тест (слайд 21- триггер) устная работа.
Замените данные рациональные числа десятичными дробями.
 = (0,5) = (0,5) |
 = (0,2) = (0,2) |
 =(0,125) =(0,125) |
 =
(0,(3)) =
(0,(3)) |
 =
(0,25) =
(0,25) |
 = (0,4) = (0,4) |
 =
(0,375) =
(0,375) |
 =(0,6)) =(0,6)) |
 =(0,75) =(0,75) |
 = (0,6) = (0,6) |
 =(0,625) =(0,625) |
 =(0,1(6)) =(0,1(6)) |
Что замечаем? (Получились конечные и бесконечные десятичные дроби. В записи дробной части каждой бесконечной дроби повторяется одна и та же группа цифр).
Как называем мы такие бесконечные десятичные дроби? (Бесконечные десятичные периодические дроби).
Вспомните, как коротко мы записывали такие дроби. (Мы выделяли повторяющуюся группу цифр и записывали ее в круглые скобки).
Как называют повторяющуюся группу цифр? (Периодом).
Итак, различные рациональные числа представили их в виде десятичных дробей (конечных или бесконечных). Какой можно сделать вывод? (Любое рациональное число можно представить в виде десятичной дроби (конечной или бесконечной).
Вспомните, как записываются и читаются бесконечные десятичные дроби, выполнив следующее задание.
Задание 5 (работа в парах) (слайд 22)
Прочитайте дроби.
1) 0,(2) 2) 2,(21) 3) 1,(1) 4) -3,0(3) 5) -0,0(6) 6) 12,45(7)
Иногда периодические дроби разделяют на "чисто периодические", например. 0,(2) и "смешанные периодические"- 12,45(7).
Задание 6. Докажите, что равенства верны:
а) 0,222:= б)
0,8181:=
б)
0,8181:= в) 0,4666
:=
в) 0,4666
:= 
Каким способом мы это можем сделать?
Обыкновенную дробь представить в виде бесконечной десятичной периодической дроби, произведя деление числителя на знаменатель.
Сегодня мы рассмотрим два способа перевода десятичной периодической дроби в обыкновенную дробь (слайд 23, каждый шаг - по щелчку).
| Пусть х = 0,222:. 10 х = 2,222: 10х-х = 2,222:-0,222 9 х = 2 х = Значит, 0,222:= |
Сначала рассмотрим алгоритм перевода
чисто периодической дроби. Нужно умножить х на такое число, чтобы запятая передвинулась вправо ровно на один период. Каково это число? ( В периоде одна цифра, значит, надо умножить на 10). Вычтите из второго уравнение первое и найдите число х. |
По этому алгоритму проверьте второе равенство.
(Учащиеся записывают решение в тетради, один ученик выполняет задание у доски с комментариями)
Наводящий вопрос: на какое число нужно умножить бесконечную периодическую дробь, чтобы запятая передвинулась ровно на одну цифру.
В периоде две цифры, значит, надо умножить на 2.
х = 0,8181:
100 х = 81,8181:
100х-х = 81, 8181:-0,8181:
99 х = 81
х = 
х =  .
.
Значит, 0,8181:=
Запишем в виде обыкновенной дроби смешанную периодическую дробь 0,4666:
| х = 0,4666: 10х = 4,666: 100 х = 46,666: 100х -10 х = 46,666:-4,666.. 90 х = 42 х = |
Мы с вами изучили правило перевода
чистой периодической дроби в обыкновенную. Как
из смешанной периодической дроби получить
чистую периодическую дробь? Умножить на 10 k ,гдек - число цифр до периода. В нашем случае на 10. Далее ваши действия аналогичны примеру 1. (Выполняются самостоятельно с последующей проверкой) |
Существует еще одно правило перевода чисто периодических и смешанных дробей в обыкновенную дробь. Примем их без доказательства (слайд 25,26, каждый шаг - по щелчку).
Чтобы обратить чисто периодическую десятичную дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, образованное из цифр, стоящих в периоде, а в знаменатель - написать цифру 9 столько раз, сколько цифр в периоде.
Запишем дроби 0,222:и 0,8181: вторым способом
1) 0,222:= 2)
0,8181=
2)
0,8181=
Чтобы обратить смешанную периодическую десятичную дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованное из цифр, стоящих после запятой до начала первого периода. Полученную разность взять в качестве числителя дроби; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
1) 0,4(6) =
Какой способ позволяет быстрее достигнуть результата?
(Второй, но сформулировать правило достаточно сложно).
Задание 7 (взаимопроверка в парах) (слайд 27)
Представьте в виде обыкновенной дроби:
1) 1,(72) 2) 2,9(12) 3) 1,12(8)
Как представить данные десятичные дроби в виде обыкновенной дроби?
(Дробь нужно представить в виде суммы целого
числа и бесконечной периодической дроби,
бесконечную периодическую дробь перевести в
обыкновенную дробь по правилу, затем смешанную
дробь представить в виде  , где
, где .)
.)
Рефлексивно-оценочный этап.
Итак, подведем итог нашего урока. Какова цель стояла перед нами в начале урока?
(Систематизировать знания о числовых множествах. Научиться переводить бесконечные периодические десятичные дроби в обыкновенные.)
Достигли ли мы этой цели?
(Цель наша достигнута. Мы знаем, что все числа
объединены во множество рациональных чисел. На
этом множестве выполняются все известные нам
действия, кроме деления на ноль. Мы выделили
свойства рациональных чисел: любое число может
быть представлено в виде в виде дроби  , где
, где  или в виде
бесконечной периодической дроби. Научились
переводить бесконечные периодические дроби в
обыкновенные двумя способами, заметили, что
второй способ трудно формулировать, но его
применение ускорит получение результата).
или в виде
бесконечной периодической дроби. Научились
переводить бесконечные периодические дроби в
обыкновенные двумя способами, заметили, что
второй способ трудно формулировать, но его
применение ускорит получение результата).
Домашнее задание: по усмотрению учителя.
Графический диктант (проверка - слайд28).
1) 2011
2) 
3) любое целое является рациональным.
4) 
5) 
6) любое целое число является натуральным.
7) любое рациональное число можно записать в виде конечной или бесконечной периодической дроби.
8) сумма, разность, произведение и частное (если делитель не ноль) рациональных чисел есть число рациональное.
9) (- 37,4 - 26,6) : (0,1) - натуральное.
10) Q -обозначение множества рациональных чисел.
Оценка настроения (слайд 29).
xn--i1abbnckbmcl9fb.xn--p1ai
Урок алгебры в 8 классе А
Тема урока: Рациональные числа.
Тип урока: объяснение нового материала
Учебник: Алгебра – 8,Ю.Н.Макарычев,И.Е.Феоктистов,2011г.
Цели урока:
Образовательные. Дать ученикам понятие о множестве рациональных чисел.
Развивающие. Продолжать формирование элементов алгоритмической культуры, развивать логическое мышление, память, формировать грамотную математическую речь, способность к анализу и самооценке.
Воспитательные. Продолжить формирование коммуникабельности, толерантности, ответственности за свои суждения.
Ход урока:
1.Приветствие.
2.Устный счет:
а) 16,2+4,5=20,7
б) 27,8-12,3=15,5
в) 4,5· 6=27
г) 3,5 ÷ 0,7=5
3.Изучение нового материала.
Давайте вспомним, какие числа на сегодняшний день мы с вами знаем:
1.Натуральные числа – N
2.Для того чтобы вычитание натуральных чисел было выполнимо во всех случаях, множество натуральных чисел дополняют числом 0 и числами, противоположными натуральным и все вместе они составляют множество целых чисел – Z
3.Обыкновенной дробью называется число вида 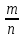 (где m – целое число, а n – натуральное число). Например:
(где m – целое число, а n – натуральное число). Например: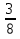 ,
,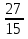 ,
,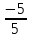 ,
,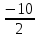 – обыкновенные дроби. Число m называют числителем дроби, а число n – знаменателем дроби.
– обыкновенные дроби. Число m называют числителем дроби, а число n – знаменателем дроби.
Всякое целое число можно также рассматривать как обыкновенную дробь со знаменателем 1. Например:-7,0,5
Напомню основное свойство дроби: если числитель и знаменатель данной дроби умножить или разделить на одно и тоже (не равное нулю) число, то получится дробь, равная данной дроби.
Пример 1.
Рассмотрим дробь 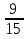 . Умножив ее числитель и знаменатель на число 2. Получаем дробь
. Умножив ее числитель и знаменатель на число 2. Получаем дробь 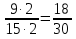 . Эта дробь равна данной.
. Эта дробь равна данной.
Разделим теперь числитель и знаменатель дроби 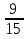 на число (-3). Получаем дробь
на число (-3). Получаем дробь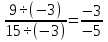 =
=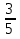 . Эта дробь также равна данной. Итак, имеем:
. Эта дробь также равна данной. Итак, имеем: 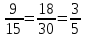 . Поэтому одну и ту же дробь можно представить в виде
. Поэтому одну и ту же дробь можно представить в виде 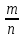 разными способами.
разными способами.
Обыкновенная дробь 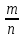 называется правильной, если
называется правильной, если 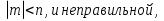
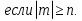
Пример 2.
а) дробь 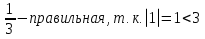
б) дробь 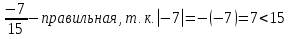
в) дробь 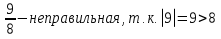
г) дробь 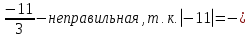 (-11)=11
(-11)=11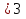 .
.
Неправильная дробь может быть записана в виде смешанной дроби, т.е. дроби, содержащей целую и дробную части. Например, 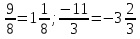 ,
,
4.Любую обыкновенную дробь можно записать в виде десятичной дроби, разделив «уголком» ее числитель на знаменатель.
Пример 3.
Обратить в десятичную дробь: а) 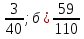 .
.
В случае а) была получена конечная десятичная дробь: 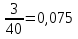 . В случае б) легко увидеть, что после выполненного деления вновь получается остаток 40, и процесс деления будет неограниченно продолжаться (отметь скобкой справа). Поэтому получаем:
. В случае б) легко увидеть, что после выполненного деления вновь получается остаток 40, и процесс деления будет неограниченно продолжаться (отметь скобкой справа). Поэтому получаем: 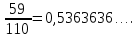 бесконечную периодическую десятичную дробь. При этом повторяющаяся группа цифр называется периодом. Принято период указывать в скобках:0,5 36 36 …=0,5(36). Читают: 0 целых 5 десятых и 36 в периоде.
бесконечную периодическую десятичную дробь. При этом повторяющаяся группа цифр называется периодом. Принято период указывать в скобках:0,5 36 36 …=0,5(36). Читают: 0 целых 5 десятых и 36 в периоде.
Учитывая, что конечная десятичная дробь не измениться, если после последней цифры записать любое количество нулей (например, 0,075=0,0750=0,07500 и т.д.), конечные десятичные дроби можно рассматривать как бесконечные периодические десятичные дроби с периодом нуль (например. 0,075=0,075(0)). Однако замечу, что период нуль никогда не указывается.
Таким образом, любая обыкновенная дробь 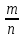 может быть представлена единственным образом в виде бесконечной периодической десятичной дроби.
может быть представлена единственным образом в виде бесконечной периодической десятичной дроби.
Справедливо также и обратное утверждение: любая бесконечная периодическая десятичная дробь может быть представлена единственным образом в виде обыкновенной дроби 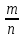 .
.
На примере рассмотрим, как производится такое обращение.
Пример 4.
Обратить в обыкновенную дробь: а)1,6; б)1,(15).
а) сразу запишем данную дробь в виде обыкновенной и выполним сокращение: 1,6=1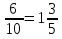 .
.
б) обозначим данное число буквой х=1,(15)=1,1515… т.к. период этой дроби содержит две цифры, то умножим число х на 10²=100 и получим 100х=115,1515…. Теперь найдем разность чисел 100х и х: 100х-х=99х=115,1515….-1,1515….=114. Для нахождения х получим уравнение: 99х=114,откуда х=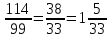 .
.
Проверить полученные результаты очень просто: надо опять обратить полученные обыкновенные дроби в десятичные:
а) 1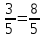 б) 1
б) 1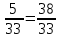
К сожалению, операции над бесконечными периодическими десятичными дробями выполнить намного сложнее. Самый простой способ решения таких задач: перевести эти дроби в обыкновенные и выполнить действия с ними.
Пример 5.
Вычислить (1,(3)-1,(6))÷0,(21)
а) х=1,(3)=1,3333….Умножим это число на 10 и получим:10х=13,3333….Тогда 10х-х=9х=13,3333….-1,3333….=12.Имеем 9х=12 и х=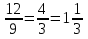 .
.
б)х=1,(6)=1,666…Умножим и это число на 10:10х=16,666….Получаем 10х-х=9х=16,666….-1,666…=15.Имеем 9х= 15 и х= 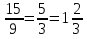 .
.
в) х=0,(21)=0,2121…Умножим это число на 100 и получим:100х=21,2121… Тогда 100х-х=99х=21,2121….-0,2121….=21,откуда 99х=21 и х=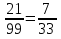 .
.
Теперь запишем этот пример для полученных обыкновенных дробей:
(1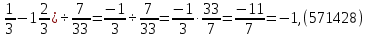 .
.
Таким образом, получаем дробь 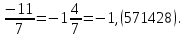
В заключение сделаем основной вывод: к рациональным числам относятся: целые числа, обыкновенные дроби, конечные десятичные дроби и бесконечные десятичные дроби. Все рациональные числа можно представить в виде 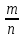 (где m- целое число, n – натуральное число).
(где m- целое число, n – натуральное число).
Множество рациональных чисел обозначают буквой Q.
Заметим, что разные бесконечные десятичные периодические дроби представляют разные рациональные числа. Исключением являются дроби с периодом 9, которые считают другой записью дробей с периодом 0.
Пример 6.
а) 2,(9)=2,99….=3,00…=3;
б) 2,37(9)=2,3799…=2,3800…=2,38.
Бесконечные десятичные дроби с периодом 9 заменяют дробями с периодом 0. При обращении обыкновенной дроби в десятичную не может получиться дробь с периодом 9.
Изобразите с помощью кругов Эйлера множество рациональных чисел.
4.Задание на уроке:
№360(устно),363,369,372,375.
5.Подведение итогов.
Контрольные вопросы:
1.Какие числа относятся к рациональным?
2.В каком виде записываются рациональные числа?
3.Как обозначают множество рациональных чисел?
Выставление оценок.
6.Домашнее задание:
П.16,вопр.1 на стр.132,№362,368,374.
Задание по карточкам:
а) 3,6 · 0,(3) + 6,(4) ÷ 2;
б) 2,8(3) – 1,2 · 1,(1) + 1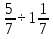 ;
;
в) 3,1(3) + 1,4÷0,(3) – 2,2;
г) 5,(2) ÷(3-1,(1)·2,4)+0,8;
д) 4,8(3) – 0,625- 2,25 · 0,1(6).
infourok.ru

« Числа не управляют миром, но они показывают, как управлять им».
( И. Гёте).

Проверка домашнего задания
Quotient
Ratio
Naturalis
Zahl
(-1) 7 +(-1) 8

Для счета предметов используются числа , которые называются натуральными . Для обозначения множества натуральных чисел употребляется буква N -первая буква латинского слова Naturalis , «естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z - первой буквой
немецкого слова Zahl - «число».
Множество чисел, которое можно представить в виде ,
называется множеством рациональных чисел и обозна-
чается- Q первой буквой французского слова Quotient
- «отношение».

Тема урока:
Цель урока:
систематизировать знания о
рациональных числах;
познакомиться с историей возникновения рациональных чисел;
выделить общее свойство рациональных чисел.

Натуральные числа возникли в силу необходимости вести счет любых предметов.
Натуральные числа несут ещё
другую функцию –
характеристика порядка предметов,
расположенных в ряд .
1 2 3 4 5 6 7 8 9 10 …

О натуральном, в смысле естественном,
ряде чисел говорится во «Введении в арифметику» греческого математика
( неопифагорийца) Никомаха из Геразы .
В современном смысле
понятие и термин
«Натуральное число»
встречается у французского
философа и математика Ж.Даламбера (1717-1783)

Натуральные числа
1, 2, 3, 4, 5, 6...
n - натуральное
Сумма и произведение натуральных
чисел есть число натуральное .

Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.

Дробные числа
Сумма, произведение и частное
дробных чисел есть число дробное.

1) доли или единичные дроби,
у которых числитель единица,
знаменателем же может быть
любое целое число;
2) дроби систематические , у которых
числителями могут быть любые числа,
знаменателями же – только числа некоторого
частного вида, например,
степени десяти или шестидесяти ;
3)дроби общего вида, у которых числители и знаменатели могут быть любыми числами.

Десятичные дроби в XV веке
ввел самаркандский ученый
ал - Каши .
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).

Понятие отрицательных чисел
возникло в практике решения алгебраических уравнений.
Отрицательные числа трактовались
так же как долг при финансовых и
бартерных расчетах.

Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500 )-
его работа была обнаружена в 1848 году.

Числа,
им противоположные
Натуральные числа
5
6
4
3
2
1
-4
-3
-2
-5
-1
-6
Целые

Целые числа
… -3;-2;-1;0,1, 2, 3,...
m - целое
Сумма, произведение и разность
целых чисел есть число целое .

Целые числа
Дробные числа
58
10
9
-4
0
1
3,2
7,1
0,1
2/7
0,(2)
Рациональные

Рациональные числа
r - рациональное
Сумма , произведение, разность и
частное рациональных чисел есть
число рациональное .

Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера .
Леонард Эйлер жил в России в
середине XY ΙΙΙ века и внес большой вклад
в развитие математики.

Задание 1.
Вычислите значения числовых выражений и изобразите их на диаграмме Эйлера.
Вместо недостающего числа впишите букву к .
а
в
с
d
k
m

Выясните, какие из высказываний
истинные:
ошибся
молодец
молодец
ошибся
ошибся
молодец
и
и
л
и
л
л
молодец
молодец
ошибся
ошибся
ошибся
молодец
л
и
и
и
л
л
ошибся
молодец
ошибся
молодец
молодец
ошибся
л
и
и
л
и
л

Замените данные рациональные числа
десятичными дробями.

Прочитайте дроби:
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
чисто периодические
смешанные периодические

Пусть х = 0,222…
10х = 2,222…
10х = 2,222…
х =0,222…
10х – х = 2,222…- 0,222
9х = 2
0,222…

Пусть х = 0,4666…
10х = 4,666…
100х = 46,666…
10х =4,666…
100х – 10х = 46,666…- 4,666
90х = 42
0,4666..

Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби поставить число,
образованное из цифр, стоящих в периоде ,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде .
0,(2)=
2
0,(81)=
81
99
9
1 цифра
2 цифры

Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число , равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода , и числа, образованного из цифр, стоящих после запятой до начала первого периода ;
а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде , и со столькими нулями , сколько цифр между запятой и началом периода .
4
6
4
0,4(6)=
9
0
1 цифра
1 цифра

Проверь соседа

да
нет
Проверь себя
МОЛОДЦЫ !


Ресурсы интернета:
http://www.librus.ru/childrens-corner/scientifically-cognitive-literature
/5676-mir-chisel.html
http://odur.let.rug.nl/magazijn/decennia/1745-1754_45.htm
http://project-gym6.narod.ru/1/62/ euler.htm
http://sferica.by.ru/history/pi.html
http://www.peoples.ru/science/mathematics/simon_stevin/
http://www.proshkolu.ru/user/galrybo/file/455559/
http://www.free-lancers.net/users/vixen/
http://www.15a20.com.mx/images/sections/thumbs/thumb_7312558.jpg
http://gr-matem.narod.ru/
http://www.i-u.ru/biblio/archive/depman_mir/01.aspx
kopilkaurokov.ru


Муниципальное бюджетное общеобразовательное учреждение «ОСОШ № 1»
Разработка урока по теме:
«РАЦИОНАЛЬНЫЕ ЧИСЛА»
8 класс
Учитель математики:
Корчагина Любовь Сергеевна
Город Очёр 2013 год
Голова, наполненная отрывочными,
бессвязными знаниями похожа на кладовую, в которой все в беспорядке и где сам хозяин ничего не отыщет; голова, где только система без знаний,
похожа на лавку, в которой на всех ящиках есть подписи, а в ящиках пусто
К.Д. Ушинский
Математика, как и всякая наука, представляет собой систему понятий и их отношений, имеет свою специфику. В предмете «математика» требуется громадная системность: если выпадает хотя бы одно звено, то делается непонятным все остальное. Для школьного курса математики характерным является также то, что многие понятия не вводятся сразу в полном объеме и содержании. Содержание и объем таких понятий расширяются и обогащаются постепенно, по мере развития курса. Например, развитие понятия рационального числа осуществляется постепенно – от натурального, целого, дробного.
Обобщение знаний осуществляется в следующей последовательности:
обобщение понятия
обобщение суждения
обобщение теорий
выделение содержательных линий, фундаментальных идей, методов.
При обобщении понятий устанавливаются метапредметные связи, благодаря чему знания становятся системными. Обобщение темы или раздела ставит школьника над изученным материалом, заставляет обозреть его сверху, выделить самое главное и важное, необходимое для дальнейшего продвижения. Одновременно идет активное повторение учебного материала, знания углубляются, расширяются и вырабатываются интеллектуальные умения и навыки. Параллельно формируются практические навыки (решение примеров, задач, уравнений, построение графиков и др.), т.е. теоретические знания применяются в прикладной, метапредметной деятельности. Практические знания расширяются и увеличивается степень их применения.
Осмысление учащимися учебного материала происходит в процессе углубленного раскрытия его содержания. Здесь участвуют все базовые сравнительные процессы: сравнение, сопоставление и различие, анализ и синтез, абстракция и обобщение.
Ученик должен хорошо понимать задачи и цели урока, сам формулировать их для себя. Он должен захотеть изучать материал, то есть иметь положительную мотивацию к изучению нового, понять какими способами он действует для достижения поставленных целей, уметь проконтролировать правильность своих достижений, соотнести результат с целью.
Урок по данной теме в 8 классе проводится перед введением понятия квадратного корня и иррациональных чисел. Урок обобщения и систематизации знаний про все числа, изученные с 1 по 7 класс. Он включает в себя повторение всех свойств с числами: натуральными, целыми, дробными. Это ступенька, без которой ученик не сможет подняться дальше, освоить новые понятия чисел.
Урок по теме «Рациональные числа» ( 8 класс)
Цель: 1. Обобщение и систематизация знаний о рациональных числах ( в пределах изученного в 5-7 классах)
2. Усвоение системы основных знаний и их углубление.
Ход урока.
Мотивация. Обобщение темы и целей урока. С первого класса вы изучаете числа и их свойства. Чисел так много, что невозможно назвать ни наибольшего, ни наименьшего из них. Однако все числа тесно связаны между собой и составляют целостную систему.
Какова эта система? Какова ее роль в развитии математической теории?
Об этом мы и узнаем на основе тех знаний, которые вы усвоили ранее.
(запись на доске)
Предлагаются учащимся следующие вопросы:
Схема каких чисел представлена? (натуральных)
Сколько математических знаков было введено для изображения всех чисел (10 знаков: 0,1,2,3…)
Почему это оказалось вполне достаточно? (На помощь пришли единицы счета 1,10,100.1000….)
Что вы умеете делать с натуральными числами? (выполнять сложение, вычитание, умножение, деление)
Все ли известные вам процессы с количественной стороны можно охарактеризовать с помощью натуральных чисел? (нет, например, изменение температуры воздуха так охарактеризовать нельзя)
Значит, необходимо было расширить систему натуральных чисел? (да)
Какие же еще числа пришлось ввести? (отрицательные целые числа)
Как же назвали совокупность чисел, состоящую из нуля, положительных и отрицательных чисел? (целые числа)
Числа с какими свойствами вам известны? (противоположные, простые, составные, взаимно простые)
( на доске запись)
В связи с понятием противоположных чисел в математику было введено еще одно важное понятие. Какое именно? ( Модуль числа)
Что такое модуль числа? (ІаІ = а, если а≥0
-а, если ≤0
Выполняем рисунок на доске
Мы вспомнили действия с натуральными числами. Давайте вспомним действия с целыми числами. Чем они отличаются?
Записываем на доске примеры, иллюстрирующие правила действий с целыми числами, и предлагаем учащимся устно выполнить необходимые действия:
-5 + 3= 3х(-2) =
-2 + (-3)= -3 х (-4)=
2- (-1)= -6 : 2=
-2 – (-4)= -8 : (-1)=
Попробуйте решить с помощью целых чисел пример первый (невозможно)
Решите с помощью целых чисел задачу:
Два слесаря должны выполнить срочный заказ. Один слесарь может его выполнить за 6 часов, а другой – за 10 часов. Успеют ли они, работая вместе, выполнить заказ за 5 часов? (невозможно)
Таким образом, возникает необходимость нового расширения числового множества. Какого?
(К целым числам прибавляются дробные)
И математики назвали эти числа рациональные.
Как же определяются рациональные числа? (Если число представим в виде дроби, то оно рационально.)
Давайте приведем примеры. (1/2, 3/7 …..)
А что можно сказать о числах 7 и 1/7, 8 и 1/8? (взаимно-обратные)
Обращаем внимание учащихся на то, что одно и то же рациональное число представлено в виде различных дробей: десятичных и простых.
Работа в парах: карточки на каждом столе
Задание по карточкам: перевести из обыкновенной дроби в десятичную: ½, ¾,5/2, 5/8. (правильные ответы показываются на карточке, идет взаимопроверка, подводятся итоги)
На доске задание: Прочитать дробь – 15/90, 200/1000, 300/300000 Вопрос: в чем неудобство чтения? (дробь большая, ее можно сократить) Да, именно поэтому пришла необходимость сокращения дробей.
Значит, для выполнения действий с дробями потребуется определенный пересмотр правил, давайте подумаем каких и проговорим.
С целью систематизации правил выполнения действий с дробями, предлагаем учащимся следующие упражнения:
2/5 · 3/7 = (6/35)
1/4 + 2/4 = (3/4)
1/3 + 1/2 = (5/6)
3/4 : 7/5 = ( 15/28)
3/5 – 1/5 = (2/5)
1/3 + 1/6 = (3/6)
1⅔ · 3⅔ = (55/9)
1/6 + 1/4 = (5/12)
Выполняя упражнения, нужно вспомнить и проговорить все правила с дробными числами.
Думаю, что мы все готовы к решению упражнений на все действия:
-3/5 : (1 – 7/10 · 2/7) =
– 1/6 – (1/3 · 1/12) =
-3⅔ · (- 3/4 - 1/6 =)
Решения проверяем с помощью доски. 3 человека работают у доски, остальные проверяют.
Задание. Упростить: 2 ·2·2 ·2·2·2·2·2·2 = 29 (возведение в степень)
Мы с вами подошли к пятому действию в математике – возведению в степень. С помощью этого действия удается решить широкий класс интересных задач.
Итак, приведем наши знаний в систему:
Мы знаем:
Слайд
Рациональное число, натуральное число, целое число
Противоположные числа
Простые
Составные
Взаимно простые
Числа, кратные числу а
Взаимно простые
Модуль числа
Слайд
Мы умеем:
- сравнивать рациональные числа
- складывать и вычитать
- умножать и делить
Умеем применять знания:
-вычислениям вида: -3/5 : (1 – 7/10 · 2/7) ; -3⅔ · (- 3/4 - 1/6)
-решению уравнений: -1/6 – (1/3 х +1/12 ) = 5/8
- решению задач, сводящихся к составлению пропорций: 120 : 100 = х : 15
- при изучении новых знаний.
4. Обобщение материала урока
На слайде
Рациональные числа.
Определение: числа, которые можно представить в виде дробей.
Основные понятия:
Рациональные числа; 2) натуральные числа 3) целое число; 4) противоположные числа 5) простые числа 6)составные числа 7) взаимно простые числа 8) числа, кратные некоторому числу а 9) взаимно обратные числа 10) модуль числа
Основные действия ( на уровне умений)
Сложение 2) вычитание 3) умножение 4) деление 5) возведение в степень
Основа вычислений – натуральные числа, с которыми связаны все остальные, а именно:
Отрицательные – через модуль
Десятичные дроби – через запятую
Дробные числа и дроби – через отношение целых чисел
Обращаем внимание учащихся на то, что изучение чисел еще далеко не закончено.
Во – первых, еще не закончено изучение рациональных чисел, во-вторых предстоит еще ввести иррациональные числа. Над чем вы подумаете дома.
Домашнее задание: 1. Подумать в чем отличие в названии чисел рациональное и иррациональное ( не в записи, а в понятии)2. Составить круги Эйлера по числовым множествам.
doc4web.ru
Автор публикации: Николаева Н.Ю.
Дата публикации: 24.11.2016
Краткое описание:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
botana.cc