Начальные условия 
Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.
Виды движений:
А) Равномерное прямолинейное движение материальной точки: Начальные условия
Б) Равноускоренное прямолинейное движение материальной точки:
. Начальные условия 
В) Движение тела по дуге окружности с постоянной по модулю скоростью: 
Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.
Описания движения. Существуют различные способы описания движения тел. При координатном способе задания положения тела в декартовой системе координат движение материальной точки определяется тремя функциями, выражающими зависимость координат от времени:
x=x(t), y=у(t) и z=z(t).
Эта зависимость координат от времени называется законом движения (или уравнением движения).
При векторном способе положение точки в пространстве определяется в любой момент времени радиус-вектором r=r(t), проведенным из начала координат до точки.
Существует еще один способ определения положения материальной точки в пространстве при заданной траектории ее движения: с помощью криволинейной координаты l(t).
Все три способа описания движения материальной точки эквивалентны, выбор любого из них определяется соображениями простоты получаемых уравнений движения и наглядности описания.
Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.
Линия, по которой движется некоторая точка тела, называется траекторией движения этой точки.
Длина участка траектории, пройденного точкой при ее движении, называется пройденным путем.
Изменение радиус- вектора с течением времени называют кинематическим законом: 
При этом координаты точек будут являться координатами по времени:x=x(t), y=y(t) и z=z(t).
При криволинейном движении путь больше модуля перемещения, так как длина дуги всегда больше длины стягивающей её хорды
Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени), называется перемещением. Результирующее перемещение равно векторной сумме последовательных перемещений.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории, и модуль перемещения равен пройденному пути.
Скорость - быстрота изменения координаты. При движении тела (материальной точки) нас интересует не только его положение в выбранной системе отсчета, но и закон движения, т. е. зависимость радиус-вектора от времени. Пусть моменту времени 
соответствует радиус-вектор
движущейся точки, а близкому моменту времени
— радиус-вектор
. Тогда за малый промежуток времени 
точка совершит малое перемещение, равное
Для характеристики движения тела вводится понятие средней скорости его движения:
Эта величина является векторной, совпадающей по направлению с вектором
. При неограниченном уменьшенииΔt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью 
:
Проекции скорости.
А) Равномерное прямолинейное движение материальной точки: 
Начальные условия 
Б) Равноускоренное прямолинейное движение материальной точки:
. Начальные условия 
В) Движение тела по дуге окружности с постоянной по модулю скоростью: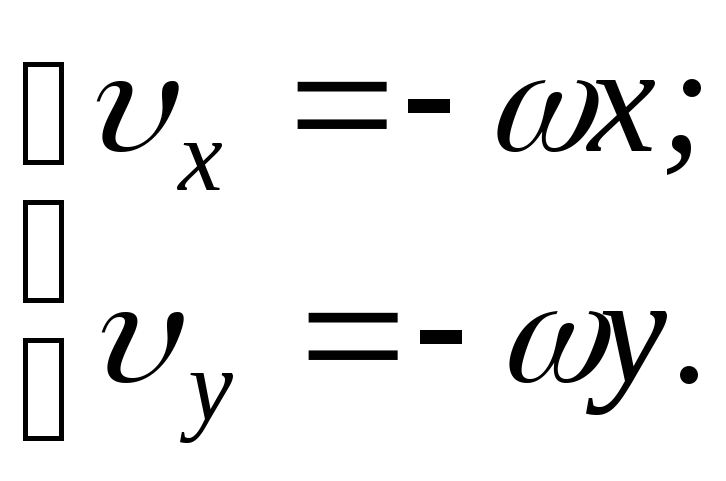 
studfiles.net
на тему: Виды движения
Выполнил: Мельников В.А.
Кемерово 2011г.
Содержание
Введение
Глава 1. Виды механического движения
Заключение
Список использованной литературы
Введение
Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.
Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Таким образом, механическое движение – это изменение положения тела в пространстве относительно других тел. Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. В данной работе мы рассмотрим основные виды механического движения
Механическое движение по форме траектории можно разделить на прямолинейное и криволинейное..
Движение называется прямолинейным, если за любые сколь угодно малые равные промежутки времени тело совершает одинаковые перемещения. То есть прямолинейное движение - это вид механического движения, при котором направление скорости не меняется. Но может меняться модуль скорости.
Криволинейное движение - это вид механического движения, при котором направление скорости изменяется. Модуль скорости может меняться.
А по закону движения виды механического движения делят на равномерные и неравномерные.
Если тело за равные промежутки времени проходит равные расстояния, то такое движение называется равномерным движением. При равномерном движении модуль скорости есть постоянная величина. А направление скорости может меняться.
Если тело за равные промежутки времени проходит различные расстояния, то такое движение называется неравномерным. При неравномерном движении модуль скорости есть переменная величина.
Направление скорости может меняться.
Если за равные промежутки времени модуль скорости изменяется на одну и ту же величину, то такое движение называется равнопеременным движением. Тангенциальное ускорение есть величина постоянная при равнопеременном движении. Если при этом направление скорости не меняется, то получим прямолинейное равнопеременное движение.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным движением. Для характеристики этого движения нужно знать скорость тела в данный момент времени или в данной точке траектории, т. е. мгновенную скорость, а также ускорение. Мгновенная скорость - это отношение достаточно малого перемещения на участке траектории, примыкающей к этой точке, к малому промежутку времени, в течение которого это перемещение совершается. Ускорение - величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Пусть при равнопеременном движении модуль скорости возрастает, такое движение называется равноускоренным движением.
Если при равнопеременном движении модуль скорости уменьшается, такое движение называется равнозамедленным движением.
Когда мы говорим о механическом движении тела, то можно рассмотреть понятие поступательного движения тела. Если при движении тела любая прямая, проведенная в этом теле, остается параллельной себе, то такое движение называется поступательным. Другими словами, поступательное движение – это движение тела, при котором все его точки движутся одинаково. Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение. При вращательном движении тела все точки этого тела движутся по концентрическим окружностям, при этом центры таких окружностей лежат на оси вращения. Ось вращения является прямой. Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось. Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное. Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях. Например, колебательное движение совершает маятник в часах.
Заключение
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. При рассмотрении вопросов, связанных с движением тел, можно не принимать во внимание размеры тела. Тело, размерами которого в данных условиях можно пренебречь, называют материальной точкой. Положение тела (точки) в пространстве можно определить относительно какого-либо другого тела, выбранного за тело отсчета A . Тело отсчета, связанная с ним система координат и часы составляют систему отсчета. Характеристики механического движения тела: траектория (линия, вдоль которой движется тело) , перемещение (направленный отрезок прямой, соединяющий начальное положение тела M 1 с его последующим положением M 2 ) , скорость (отношение перемещения ко времени движения - для равномерного движения). Характеристики механического движения относительны, т. е. они могут быть различными в разных системах отсчета
Во многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела.
Список использованной литературы
yaneuch.ru
Задача кинематики состоит в том, чтобы количественно (через уравнения) описать движение любых тел и установить взаимосвязи между величинами, характеризующими движение.
А как это сделать?
Каждое реальное тело в любой момент времени обладает некоторой геометрической формой, определенным образом ориентировано в пространстве и занимает в нем определенное место.
Но и форма, и ориентация в пространстве, и местоположение тела с течением времени могут изменяться.
Например, возьмем воздушный шарик. Шарик можно сжать (изменить его форму), можно повернуть (изменить его ориентацию в пространстве), можно перенести в другое место без изменения формы и ориентации. Изменение формы и (или) объема тела называется деформацией тела.
При деформации тела изменяются расстояния между его точками.
Изменение ориентации тела в пространстве называется поворотом, а происходящее при этом движение — вращательным движением тела.
Поворот тела наблюдается и при колебательном движении.
Если движение происходит без деформации и поворота тела, его называют поступательным.
Поступательное движение может быть, как прямолинейным, так и криволинейным. Траектории точек тела, движущегося поступательно, одинаковы между собой — каждая точка повторяет движение любой другой точки тела с некоторым постоянным сдвигом.
В общем случае движение тела представляет собой результат сложения трех движений: деформации, вращения и поступательного движения.
Описать движение тела в общем случае достаточно сложно, необходимы упрощения. Для этого в кинематике используют ряд физических моделей.
Если деформация тела незначительная, то ею можно пренебречь. В таких случаях можно использовать модель абсолютно твердого тела — воображаемого тела, которое никогда не деформируется.
В кинематике мы будем считать все тела абсолютно твердыми. Движение абсолютно твердых тел сводится уже только к двум видам: поступательному или вращению.
Если можно пренебречь вращением абсолютно твердого тела (или они нас в данной задаче не интересуют), то достаточно рассмотреть лишь поступательное движение тела. При таком движении все точки тела движутся одинаково, поэтому достаточно изучить движение любой одной точки тела. В таких случаях широко используют модель материальной точки.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Именно от поставленной задачи зависит, можно ли считать данное реальное тело материальной точкой. Так, если нас интересует движение крыльев бабочки, ее нельзя рассматривать как материальную точку. В то же время, земной шар можно считать материальной точкой, если интересоваться только движением Земли по орбите вокруг Солнца, а не вращением Земли вокруг своей оси.
Движение материальной точки полностью определено, если задана ее траектория и известно, в какой точке траектории она находится в каждый момент времени.
www.physbook.ru
(Назад)
(Cкачать работу)
Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!
Виды движения точки в зависимости от ускорения
Различают следующие виды движения точки в зависимости от ускорения:
Прямолинейное движение. В этом случае траектория движения точки – прямая, причем точка движется вдоль этой прямой в одном направлении. Радиус кривизны прямой R равен бесконечности (прямую можно считать окружностью бесконечно большого радиуса). Тогда
,поэтому может изменяться только алгебраическая величина скорости точки. Это изменение полностью характеризуется касательным ускорением.
Равномерное криволинейное движение. Так как при равномерном движении точки модуль скорости остается постоянным, то есть v = const, тогда
. Вектор полного ускорения а, следовательно, направлен по главной нормали в сторону вогнутости, модуль полного ускорения равен.
Равномерное прямолинейное движение. В этом случае
и ,а значит а = 0. Единственный вид движения, в котором ускорение точки все время остается равным нулю, - равномерное прямолинейное движение.
Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиной постоянной:
.Если при равномерном криволинейном движении точки модуль скорости возрастает, то движение называется равноускоренным, а если убывает – равнозамедленным.
При произвольном движении твердого тела отдельные его точки движутся по различным траекториям и имеют в каждый момент времени различные скорости и ускорения. Основными задачами кинематики твердого тела являются:
установление способа задания движения тела; изучение кинематических характеристик движения; определение траекторий, скоростей и ускорений всех точек движущегося тела.
Поступательным движением твердого тела называется такое движение, при котором отрезок прямой, соединяющий две произвольные точки тела, остается во время движения параллельным своему первоначальному положению.
Основная теорема поступательного движения. При поступательном движении твердого тела все его точки описывают конгруэнтные траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Доказательство:
Пусть твердое тело, совершающее движение относительно некоторой системы координат, занимает в момент времени t положение I, в момент t1 – положение II, в момент t2 – положение III и т. д. (рис. 1). Выберем в теле две произвольные точки А и В и построим вектор .
Рис. 1 Обозначим через А1, В1 и А2, В2 положения, которые занимают точки А и В в моменты времени t1 и t2 соответственно. Длина вектора как расстояние между точками абсолютно твердого тела, постоянна. Направление не изменяется в силу того, что тело движется поступательно. В этом случае траекторию точки В можно получить параллельным переносом на вектортраектории точки А. Следовательно, кривые ВВ1В2 и АА1А2 при наложении совпадают.
Так как векторы и равны, будут равны перемещения точек А и В, то есть =. Отнесем эти перемещения к отрезку времени , за который они произошли . Переходя в этом равенстве к пределу при t0, получим в соответствии с определением скорости точки,
, (1) гдеи– скорости точек А и В.
Точки А и В выбраны произвольно, следовательно при поступательном движении твердого тела векторы скоростей всех его точек в данный момент времени равны друг другу.
Так как равенство (1) имеет место в любой момент времени, то. Дифференцируя (1) по t получим, или . (2) В силу произвольности выбора точек А и В из равенства (2) следует, что векторы ускорения всех точек поступательно движущегося твердого тела равны между собой.
Следствия из теоремы:
поступательное движение твердого тела вполне определено движением одной из его точек; если скорость поступательного движения постоянна (v = const), то все точки тела совершают прямолинейное и равномерное движение.
5. Вращение твердого тела вокруг неподвижной оси
Вращательным движением твердого тела называется движение, при котором две его точки А и В остаются неподвижными. Так как тело абсолютно твердое, то вместе с точками А и В будут неподвижны все точки, лежащие на прямой АВ. Эта прямая называется осью вращения (рис. 2). Все точки тела при вращательном движении описывают дуги окружностей с центрами в основаниях перпендикуляров, опущенных из этих точек на ось вращения. Проведем через ось вращения две полуплоскости, одну из которых зафиксируем, а другую свяжем с телом. Двугранный угол , угол поворота, между этими полуплоскостями будет однозначно определять положение тела. Задавая значение угла в каждый момент времени t, можно тем самым определить положение тела для любого t. Уравнение (3) носит название закона вращательного движения тела. Функция (3) предполагается дважды дифференцируемой.
Главными кинематическими характеристиками вращательного движения тела будут угловая скорость (с-1) и угловое ускорение (с-2).
Пусть за некоторый промежуток времениугол получит приращение . Величинаназывается средней угловой скоростью тела. Предел, к которому стремится средняя угловая скорость при t0, называется угловой скоростью тела в данный момент времени t.
. (4) Если тело совершает вращательное движение по произвольному закону, то угловая скорость является функцией времени: .
Пусть за некоторый промежуток времениугловая скорость получила приращение . Величинаназывается средним угловым ускорением. Предел, к которому стремится среднее ускорение при t 0, называется угловым ускорением в данный момент времени t. . (5) Связь угловых характеристик вращающегося твердого тела с линейными кинематическими характеристиками вращающегося тела
Как уже отмечалось, траекторией любой точки М вращающегося тела является дуга окружности, лежащая в плоскости перпендикулярной оси вращения. Радиус этой окружности равен расстоянию от точки до оси. Рассмотрим траекторию движения некоторой точки М тела, вращающегося вокруг оси, перпендикулярной плоскости рисунка и проходящей через центр окружности (рис. 3).
Рис. 3
Если отсчитывать дуговую координату s точки М от ее начального положения М0 в направлении возрастания угла , то закон движения точки М по дуге окружности будет иметь вид . В этом случае алгебраическое значение скорости определяется по формуле: . (6) Найдем ускорение точки М: . Продифференцировав (6) по времени, определим алгебраическую величину касательного ускорения: . (7) Нормальное ускорение получим, подставляя (6) в выражение для нормального ускорения: . (8) Следовательно, для вектора ускорения имеем: . (9) Для модуля ускорения точки М имеем формулу: . (10) Из выражений (6) и (10) следует, что линейные кинематические характеристики точек зависят от угловых характеристик вращающегося твердого тела, а коэффициентом пропорциональности является радиус вращения.
До сих пор движение точки рассматривалось по отношению к неподвижной системе координат, но в ряде случаев целесообразно изучать движение точки одновременно в двух системах отсчёта, из которых одна является неподвижной, а другая - подвижной, совершающей определённым образом движение относительно первой. Движение точки, в этом случае, называют сложным. На рис. 4 изображены две системы координат: неподвижная Oxyz и подвижная O1x1y1z1. Движение, совершаемое точкой М по отношению к подвижной системе координат O1x1y1z1 называется относительным движением. Движение подвижной системы отсчёта O1x1y1z1 и всех точек пространства с ней связанных по отношению к неподвижной системе Oxyz называется переносным движением. Движение точки М относительно неподвижной системы координат Oxyz называется абсолютным.
Скорость точки М по отношению к неподвижной системе координат называется абсолютной скоростью точки.
Скорость точки М по отношению к подвижной системе координат называется относительной скоростью точки.
Переносной скоростью точки М называется скорость подвижной системы относительно неподвижной, в которой в данный момент времени находится движущаяся точка М.
Теорема о скорости точки в сложном движении.
Вектор абсолютной скорости точки в данный момент времени равен геометрической сумме векторов относительной и
referat.co
