Основной предпосылкой для всех математических знаний служит нумерация, которая у разных древних народов имела различный вид. По-видимому, все народы вначале обозначали числа зарубками на палочках, которые у русских назывались бирками. Такой способ записей долговых обязательств или налогов применялся малограмотным населением разных стран. На палочке делали нарезы, соответствующие сумме долга, или налога. Палочку раскалывали пополам: одну половину оставляли у должника или у плательщика, другую хранили у заимодавца или в казначействе. При расплате обе половинки проверяли складывание.

С появлением письменности, появились и цифры для записи чисел. Сначала эти цифры напоминали зарубки на палках, затем появились специальные знаки для некоторых чисел, таких, как 5 и 10.

В то время почти все нумерации были не позиционными, а похожими на римскую нумерацию. Однако, за несколько столетий до новой эры изобрели новый способ записи чисел, при котором цифрами служили буквы обычного алфавита.

В одной из русских рукописей XVII века читаем мы следующее: «...знай же то, что есть сто и что есть тысяща, и что есть тьма, и что есть легион, и что есть леодр...», «...сто есть десятью десять, а тысяща есть десять сот, а тьма есть десять тысящ, а легион есть десять тем, а леодр есть десять легионов...».

В то время, как в странах Западной Европы пользовались римской нумерацией, в древней России, находившейся подобно другим славянским странам в тесном культурном общении с Византией, получила распространение алфавитная нумерация, сходная с греческой.

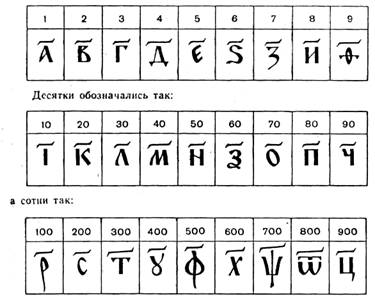
В древнерусской нумерации числа от 1 до 9, затем десятки и сотни изображались последовательными буквами славянского алфавита (именно, так называемой кириллицы, введенной в IX в.).

Из этого общего правила были некоторые исключения: 2 обозначалось не второй по счету буквой "буки", а третьей "веди", так как буква 3 (древняя бета, византийская вита) передавалась по-старорусски звуком "в". "Фита", стоящая на конце славянского алфавита, обозначала, как греческая 0 (древняя тэта, византийская фита), число 9, а 90 обозначалось буквой "червь" (у греков использовалась для этой цели буква "копиа", отсутствовавшая в живом греческом алфавите). Не использовались отдельные буквы. Для указания же того, что знак является не буквой, а цифрой, сверху над ним ставили специальный знак «~», называемый титло. Вот, например, как записывались первые девять чисел:

infourok.ru

Запись числа в Древней Руси

Государственное бюджетное профессиональное

образовательное учреждение Ростовской области

«Волгодонский педагогический колледж»

(ГБПОУ РО «ВПК»)

РЕФЕРАТ

Дисциплина: Математика

Тема: Запись числа в Древней Руси

Выполнил(а):

студентка

группы ПНК-2

Крецу Ю.Л.

Проверил(а):

Молотова Н.М.

Волгодонск

2016

Содержание:

1.Введение.....................................................................3

2.Появление письменности..........................................3

3.Исключения из правил..............................................5

4.Заключение................................................................6

Введение

Десятки тысяч назывались «тьмы», их обозначали, обводя знаки единиц кружками, например, числа 10 000, 20 000, 50 000 соответственно записывались следующим образом:

Отсюда и произошло название «Тьма народу», т. е. очень много народу. Сотни тысяч назывались «легионами», их обозначали, обводя знаки, единиц кружками из точек. Например, числа 100 000, 200 000 соответственно имели обозначение

Миллионы назывались «леодрами». Их обозначали, обводя знаки единиц кружками из лучей или запятых. Так, числа 106 и 2 • 106 обозначались соответственно

Сотни миллионов назывались «колодами». «Колода» имела специальное обозначение: над буквой и под буквой ставились квадратные скобки.

Числа от 11 до 19 обозначались так:

Остальные числа записывались буквами слева направо, например, числа 544 и 1135 имели соответственно обозначения

При записи больших чисел, чем тысячи, в практической деятельности (счете, торговле и т. д.) часто вместо «кружков» знак «≠ » ставили перед буквами, обозначавшими десятки и сотни, например, запись

означает числа соответственно 500 044 и 540 004.

Заключение

В приведенной системе обозначения чисел не шли дальше тысяч миллионов. Такой счет назывался «малый счет». В некоторых рукописях авторами рассматривался и «великий счет», доходивший до числа 1050. Далее говорилось: «И более сего несть человеческому уму разумети». Современная математика использует индийскую нумерацию. На Руси индийские цифры стали известны в начале XVIIв.

multiurok.ru

Математика в Древней Руси - Рефераты для всех

Опубликовано 18.04.2013 21:58

Предки русского народа — славяне — с незапамятных времён жили на землях Средней и Восточной Европы. Первые письменные упоминания о славянах встречаются в книгах древних римлян, написанных в самом начале нашей эры. Арабские книги говорят о том; что в середине первого тысячелетия славяне вели большую торговлю с греками, арабами и другими народами и храбро воевали с иноземцами, которые пытались их покорить. В X веке нашего летосчисления у славян появилась письменность. С этого времени начинается «писаная» история Древней Руси.

У славян, как и у всех других народов, первым учителем математики была жизнь, практика. Постепенно рождались и накапливались навыки счёта, правила измерения: ведь без этого нельзя было бы ни торговать, ни даже обмениваться продуктами. В первом тысячелетии у славян появилась денежная единица — рубль, название которой сохранилось до наших дней. Слово «рубль» происходит от глагола «рубить». Первые рубли, по всей вероятности, были просто кусочками металла, которые отрубали от полосы серебра или меди. Для того чтобы разрубить металлическую полосу на равные части, нужно было знать простейшие дроби, уметь складывать и вычитать числа. При измерении полей славяне употребляли и более сложные дроби. В раскопках славянских селений учёные находили изображения циркуля. Значит, древним славянам были известны некоторые свойства окружности. Основу своего алфавита славяне вместе с христианской религией позаимствовали от средневековых греков — византийцев. Способ записи цифр буквами со специальными значками —- «титлами» — они тоже взяли от греков (см. рисунок 1) . Крупные числа записывали с помощью специальных знаков, в названиях некоторых из них также видно византийское начало (см. рисунок 2) . С появлением письменности в Древней Руси стали появляться переводы греческих книг. Поначалу это были только «священные» книги, но и в них нет-нет да и встречались обрывки замечательной математики древних греков. Знания славян по математике постепенно росли.

Известно, что в Англии в VII веке чудом учёности считался монах, который умел выполнять деление чисел: долго считалось, что нет ничего труднее четырёх действий арифметики над целыми числами.

По-видимому, математические знания наших предков славян около 1000 года были не ниже, чем у западных народов.

Однако в XIII веке большая часть русских княжеств была захвачена ордами полудиких кочевников — монголов. Жизнь замерла; приостановилось и развитие древнерусской культуры.

Почти триста лет длилось монгольское иго. За это время наука Западной Европы сделала большой шаг вперёд: народы Европы ознакомились с замечательной математикой арабов и индийцев. А в отрезанной от всего культурного мира России математика стала отставать от науки Западной Европы. Для того чтобы потом, после свержения монгольского ига, снова выйти в ряды мировой науки, ей понадобилось несколько столетий.

В XVI веке при Иване Грозном на Руси появляются первые рукописные учебники по математике, а немного позже — печатные книги о применении математики для разных практических нужд, например «Книге сошного письма» и «Устав ратных, пушечных и иных дел, касающихся до воинской науки».

В 1134 году новгородский монах Кирик написал сочинение «. о том, как узнать человеку числа всех лет». Это самый древний дошедший до нас письменный памятник славянской математики. В своей рукописи Кирик подробно вычисляет, сколько лет, месяцев, недель и дней прошло от «сотворения мира» до года, в котором он, Кирик, писал свой труд. Главная «священная» книга христиан — Библия — дала церковникам основание утверждать, что мир был сотворён богом ровно за 5508 лет до начала нашего летосчисления. Кирик, по-видимому, где-то ошибся: число месяцев у него получилось больше, чем должно быть, но это, конечно, никому не повредило. Ведь вычисления Кирика никому, кроме него самого, не были нужны; они не могли принести никакой практической пользы людям. Видимо, Кирик был «числолюбцем», ему доставлял удовольствие сам процесс вычисления.

А вот для нас рукопись Кирика очень важна. Она ясно показывает, что славяне без малого тысячу лет назад отлично владели четырьмя действиями арифметики, свободно обращались с очень большими целыми числами и с очень маленькими дробями.

Что усвоение всего этого представляло большие трудности, доказывает хотя бы то, что в немецком языке есть поговорка: «Попал в дроби». Так говорят про человека, который оказался в трудном положении, или, по-нашему, «попал в переплёт».

Ещё в XVIII веке в одном английском учебнике арифметики было написано, что дроби приводят учащихся в уныние и к мысли: «В эти дебри мы не пойдём!».

Выходит, что в это время на Руси математика не только не отставала, но, пожалуй, шла даже немного впереди науки народов Западной Европы.

Трудно переоценить и значение рукописного труда, который, по мнению исследователей, можно назвать первым учебником геометрии - «Синодальная № 42» (см. рисунок 3) . Составителем рукописи, которая датируется 1625 годом, был Ивашка Елизарьев. “Сие предисловие собрал я, Ивашко, князь Елизарьев сын. от многих учителей и их книги у меня все”. В этом первом учебнике геометрии содержались не только способы решения задач, но и давались основы теоретических знаний по геометрии. Рукопись была богато иллюстрирована картинками, гравюрами, при этом, последние были вырезаны из неизвестной современникам книги по геометрии.

В 1682 году в Москве вышла книга: «Считание удобное, которым всякий человек, купующий и продающий, зело удобно изыскати может число всякой вещи». Это была первая в России не рукописная, а напечатанная в типографии книга по математике, которая должна была помогать решению разных практических задач. Была в ней таблица умножения (до 100х100), записанная славянскими цифрами.

Особенно важную роль в развитии русской науки сыграла книга «Арифметика, или наука числительная», написанная Леонтием Филипповичем Магницким (см. рисунок 4) . «Арифметика» Магницкого была издана при Петре I, в 1703 году и долгое время была настольной книгой всех образованных русских людей. Великий русский ученый Михаил Васильевич Ломоносов знал её наизусть и называл её вместе с учебником грамматики «вратами своей учености».

Книга Магницкого называлась «Арифметика», но кроме арифметики там были начала алгебры, геометрии, тригонометрии и даже немного мореходной астрономии. Это была настоящая энциклопедия по математике, в которой каждое правило, каждый приём подробно разъяснялся и подкреплялся решением примеров и практических задач.

Замечательной книгой Магницкого закончилась многовековая история древнерусской математики. Дальнейшее развитие отечественной математики происходило в тесной связи с наукой Западной Европы, а многие видные европейские ученые даже работали в России. Но это уже совершенно другая страница истории, узнать о которой Вы можете, прочитав «Развитие математики в России в середине XVIII века».

referat-4all.ru

Как на Руси считали, или Почему мы говорим «пятнадцать»? | Культура

В древности широко распространенными были системы, в которых числа обозначалась буквами алфавита. К таковым относилась и греческая алфавитная система, называемая также ионической. К славянским племенам она пришла вместе с христианством и письменностью. Первыми ей начали пользоваться южные славяне, затем — восточные.

Создана славянская нумерация была греческими монахами Кириллом и Мефодием в IX веке по образцу греческой. До сих пор такая форма записи чисел используется в православных церковных книгах.

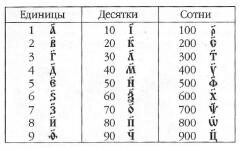Славянская кириллическая система Чтобы показать, что букву в данном контексте следует воспринимать как число, над ней писали специальный значок — титло, представляющий собой волнистую линию. Букве «аз» соответствовала, как вы, наверное, догадались, единица. Последней буквой в алфавите, имевшей числовое значение, была «цы». С ее помощью записывали число 900. Таким образом можно было легко записать любое целое число от 1 до 999.

Тысячи записывались теми же буквами с титлом, что и 1, 2, …, 9, но слева внизу изображался еще один знак — наклонная линия, которая пересекается двумя черточками. Десятки тысяч отмечались тоже первыми буквами алфавита, но без титла, а сами буквы брались в кружок. Для изображения сотен тысяч кружок составлялся из точек, а для миллионов — из черточек.

Записанные таким способом числа имели свои названия. Десять тысяч называли тьмой, сто тысяч — легионом, а миллион — леодром.

Описанная здесь нумерация называлась «малое число», или «малый счет». Кроме нее, существовал еще и «большой счет» («большое число», «великое число»).

Большой счет В этой системе миллион назывался тьмой. Тьма тем, или 10 в 12 степени, получает наименование легион. Легион легионов, или 10 в 24 степени, именовался леодр. За ним следовал ворон (вран) — леодр леодров, 10 в 48 степени. Воронов обозначали соответствующей буквой в кружке из крестиков. За вороном шла колода, «…и более сего несть человеческому уму разумевати». Интересно, что колода, на которой счет обрывался, была вовсе не вороном воронов, а десятью воронами. Ее показывала рамка из двух лежащих на боку квадратных скобок.

В славянской нумерации числа записывались так же, как и современные: запись шла слева направо, от старших разрядов к младшим. В ней ясно видны зачатки позиционной системы. Но числа от одиннадцати до девятнадцати записывались по-особенному: сначала писали букву, показывающую единицы, а затем ставили заглавную «и» с точкой, которой обозначалось число десять. Поэтому до сих пор мы говорим, например, «пятнадцать», то есть «пять на десять», произнося число так, как оно писалось много столетий назад.

Подобные системы счисления в прошлом не были чем-то необычным: кроме русских и греков, буквы алфавита подрабатывали цифрами у арабов, грузин, евреев, армян. Славянская кириллическая нумерация имела ранг официальной в России, Белоруссии, Украине, Болгарии, Венгрии, Сербии и Хорватии. Она просуществовала до XVII века, пока реформы Петра I не сделали ее историей.

shkolazhizni.ru

Математика Древней Руси — реферат

Пример: запишем число 365 на абаке и удвоим его.

Абак состоял из вертикальных колонок, в которых камешками и другими мелкими предметами можно было в нечетных колонках выразить единицы разрядов: от 1 до 4, а в четных – одним счетным предметом сразу пять разрядов.

В первой колонке нет косточек, во второй – положена одна косточка, что обозначает число 5. В третьей колонке лежит одна косточка, она обозначает один десяток; в четвертой также одна косточка, но она выражает сразу пять десятков, поскольку четвертая колонка – четная. Значит, этими двумя косточками в третьей и четвертой колонках обозначается число 60. В пятой колонке указаны три косточки, каждая из которых выражает 100, т.е. вместе 300. Т.о. на модели шестью косточками обозначено число 365.

Пусть требуется узнать, сколько будет стоить в гривнах 365 коров по цене в 2 гривны и 365 баранов по 10 резан.

Отложим число а = 365 на абаке. И разделим колонки схемы поперечной чертой. Удвоенный результат 2а = 730 расположим в верхней части модели. Это стоимость коров в гривнах. Для определения стоимости баранов в гривнах необходимо кроме удвоения сместить разрядные значения влево на одну пару колонок. Тогда получится, что 365 баранов стоят 73 гривны.

На этом примере видно, что вычисление стоимости коров по цене 2 гривны, отнесенное к 1-й группе сложности, и вычисление стоимости баранов по 10 рязан, отнесенное ко второй группе сложности, на модели абака выполняются аналогично: посредством операции удвоения. Разница состоит в различном прочтении результата. В первом случае результат читается в соответствии со способом записи числа а. Во втором случае разрядные значения смещаются на одну пару колонок: сотни читаются как десятки, а десятки как единицы.

Модель абака

Меры Древней Руси

С древности, мерой длины и веса всегда был человек: на сколько он протянет руку, сколько сможет поднять на плечи и т.д.

В Древней Руси была принята русская система мер (она использовалась до 1899 г.).

Меры длины:

1 миля (старорусская) = 7 вёрст = 7,4676 км. 1 верста = 500 саженей = 1066,8 м. 1 сажень = 3 аршина = 7 футов = 12 пядей = 48 вершков = 84 дюйма = 100 соток = 2,1336 м. 1 аршин = 4 четверти = 28 дюймов = 16 вершков = 71,12 см. 1 фут = 12 дюймам = 304,8 мм. 1 четверть (пядь) = 1/12 сажени = 1/4 аршина = 4 вершка = 7 дюймов = 177,8 мм. 1 вершок = 1,75 дюйма = 44,45 мм. 1 дюйм = 10 линиям = 25,4 мм. 1 сотка = 1/100 сажени = 84 точкам = 21,336 мм. 1 линия = 10 точкам = 2,54 мм. 1 точка = 1/100 дюйма = 1/10 линии = 0,254 мм.

Меры площади:

1 кв. верста = 250 000 кв. саженям = 1,1381 км². 1 десятина = 2400 кв. саженям = 10 925,4 м² = 1,0925 га. 1 четь = 1/2 десятины = 1200 кв. саженям = 5462,7 м² = 0,54627 га. 1 осьминник = 1/8 десятины = 300 кв. саженям = 1365,675 м² ≈ 0,137 га. 1 кв. сажень = 9 кв. аршинам = 49 кв. футам = 4,55225 м². 1 кв. аршин = 256 кв. вершкам = 0,505805 м². 1 кв. вершок = 19,758 см². 1 кв. фут = 144 кв. дюймам = 0,092903 м². 1 кв. дюйм = 100 кв. линиям = 0,00064516 м².

Меры объема:

1 куб. сажень = 27 куб. аршинам = 343 куб. футам = 9,7127 м³ 1 куб. аршин = 4096 куб. вершкам = 21 952 куб. дюймам = 359,7288 дм³ 1 куб. вершок = 5,3594 куб. дюймам = 87,8244 см³ 1 куб. фут = 1728 куб. дюймам = 28,3168 дм³ 1 куб. дюйм = 1000 куб. линий = 16,3871 см³ 1 куб. линия = 1/1000 куб. дюйма = 16,3871 мм³

Меры сыпучих тел:

1 цебр = 26—30 четвертям. 1 кадка (кадь, оков) = 2 половникам = 4 четвертям = 8 осьминам = 839,69 л (= 14 пудам ржи = 229,32 кг). 1 куль: ржи — 9 пудов + 10 фунтов = 151,52 кг; овса — 6 пудов + 5 фунтов = 100,33 кг 1 полокова, половник = 419,84 л (= 7 пудам ржи = 114,66 кг). 1 четверть, четь (для сыпучих тел) = 2 осьминам (получетвертям) = 4 полуосьминам = 8 четверикам = 64 гарнцам. (= 209,912 л (дм³) 1902 г.). (= 209,66 л 1835 г.). 1 осьмина = 4 четверикам = 104,95 л (=1¾ пуда ржи = 28,665 кг). 1 полосьмины = 52,48 л. 1 четверик = 1 мере[3] = 1⁄8 четверти = 8 гарнцам = 26,2387 л. (= 26,239 дм³ (л) (1902 г.)). (= 64 фунтам воды = 26,208 л (1835 г)). 1 получетверик = 13,12 л. 1 четвёрка = 6,56 л. 1 гарнец, малый четверик = ¼ ведра = 1⁄8 четверика = 12 стаканам = 3,2798 л. (= 3,28 дм³ (л) (1902 г.)). (=3,276 л (1835 г.)). 1 полугарнец (пол-малый четверик) = 1 штоф = 6 стаканам = 1,64 л. (Пол-пол-малый четверик = 0,82 л, Пол-пол-пол-малый четверик = 0,41 л). 1 стакан = 0,273 л.

Меры жидких тел:

1 бочка = 40 вёдрам = 491,976 л (491,96 л). 1 корчага = 2 ведра (около 25 л.). 1 ведро = 4 четвертям ведра = 10 штофам = 1/40 бочки = 12,29941 л (на 1902 г.). 1 четверть (ведра) = 1 гарнец = 2,5 штофа = 4 бутылкам для вина = 5 водочным бутылкам = 3,0748 л. 1 гарнец = 1/4 ведра = 12 стаканам. 1 штоф (кружка) = 3 фунтам чистой воды = 1/10 ведра = 2 водочным бутылкам = 10 чаркам = 20 шкаликам = 1,2299 л (1,2285 л). 1 винная бутылка = 1/16 ведра = 1/4 гарнца = 3 стаканам = 0,68; 0,77 л; 0,7687 л. 1 водочная (пивная) бутылка = 1/20 ведра = 5 чаркам = 0,615; 0,60 л. 1 бутылка = 3/40 ведра (Указ от 16 сентября 1744 года). 1 косушка = 1/40 ведра = 1/4 кружки = 1/4 штофа = 1/2 полуштофа = 1/2 водочной бутылки = 5 шкаликам = 0,307475 л. 1 стакан = 0,273 л. 1 четушка = 1/50 ведра = 245,98 мл. 1 чарка = 1/100 ведра = 2 шкаликам = 122,99 мл. 1 шкалик = 1/200 ведра = 61,5 мл.

Меры веса:

1 ласт = 6 четвертям = 72 пудам = 1179,36 кг. 1 четверть вощаная = 12 пудам = 196,56 кг. 1 берковец = 10 пудам = 400 гривнам (большим гривенкам, фунтам) = 800 гривенкам = 163,8 кг. 1 контарь = 40,95 кг. 1 пуд = 40 большим гривенкам или 40 фунтам = 80 малым гривенкам = 16 безменам = 1280 лотам = 16,380496 кг. 1 полпуда = 8,19 кг. 1 батман = 10 фунтам = 4,095 кг. 1 безмен = 5 малым гривенкам = 1/16 пуда = 1,022 кг. 1 полубезмен = 0,511 кг. 1 большая гривенка, гривна, (позднее — фунт) = 1/40 пуда = 2 малым гривенкам = 4 полугривенкам = 32 лотам = 96 золотникам = 9216 долям = 409,5 г (11—15 вв.). 1 фунт = 0,4095124 кг (с 1899 года). 1 гривенка малая = 2 полугривенкам = 48 золотникам = 1200 почкам = 4800 пирогам = 204,8 г. 1 полугривенка = 102,4 г.

Кирк Новгородец

Кирик Новгородец (1110 – не ранее 1156/1158) – средневековый новгородский мыслитель, диакон и доместник Антипова монастыря в Новгороде, автор «Учения о числах» (1136), математик, церковный писатель, летописец,музыкант.

Произведение Кирка начинается без авторского вступления. Материал разбит на небольшие разделы размером от 4 до 18 строк; они занумерованы, номера (в древнерусской нумерации) вынесены на поля листов.

В первых пяти параграфах идет речь о том, сколько прошло времени в различных единицах от «сотворения мира». До момента написания трактата, а именно: 1) в годах, 2) в месяцах, 3) в неделях, 4) в днях, 5) в часах. Каждый параграф содержит цифровой материал, связанный с числом 6644, как количество лет, которое прошло за указанный период. Это число точно датирует написание первых пяти пунктов 1136 годом. Пятый параграф завершается сентенцией, смысл которой таков: «ведь понемногу создается город и делается большим, так и знание понемногу растет».

В следующих пунктах говориться о теоретических основах календарных вычислений: об индикте, о солнечном и лунном «кругах», о тысячелетиях, о так называемых обновлениях неба, земли, моря, воды, о високосных годах, о «великом круге». В каждом параграфе материал так или иначе связан с датой 6644г.

В идущих далее пунктах говориться о числе месяцев, недель и дней в году с учетов високосных дней. Здесь материал не связан с 6644 г.

Затем говорится о количестве часов в году и дне. Следующие параграфы посвящены так называемым дробным делениям числа. Эти параграфы так же не связаны с датой 6644г.

К последнему параграфу примыкает, не имея самостоятельного номер, заключительный текст, в котором автор трактата указывает свое имя, год написания сочинения, ряд хронологических сведений и биографических данных о себе.

Таким образом, в этом «Учении» выделяются следующие разделы:

О единицах счета времени (§ 1 – 5)
О теоретических основах календаря (§ 6 – 18)
О дробных делениях числа (§ 19 – 27)

Заключительный текст (Заключение).

Сочинение Кирка – особого характера по форме, назначению и предмету изложения. Более всего соответствует жанру современной научно-популярной литературы.

Заключение

Итог изложения данных об облике древнерусской арифметической культуры X – первой половины XIII вв. в рамках данного доклада сводится к следующему.

Знания способов записи чисел в архаичной (кириллической) системе нумерации использовали многие слои общества: ремесленники, зодчие, переписчики книг, духовенство, чиновники, «профессиональные» вычислители и другие. Обучение цифровой символике велось параллельно с обучением письму, основными учебными пособиями служили особые «цифровые алфавиты», подобные буквенным.

Формирование древнерусской происходило как смешение византийской нумерации с кириллическим письмом с сохранением близости к греческому оригиналу. Цифровой византийский «язык» на русской почве изменился, но не настолько, чтобы не была понятна греческая математическая «речь». Это было важно для обеспечения поступления и усвоения математической информации из Византии.

На цифровом фундаменте основывались знания о производстве вычислительных операций с использованием наглядно-инструментального приспособления типа абака. Эти сведения были достоянием более узкого круга лиц – хронологов, чиновников административно-хозяйственного аппарата: волостей, тиунов и др.

Можно представить себе в следующем виде древнерусского вычислителя за работой. Его инструментами были: маленький мешочек с вишневыми и сливовыми косточками, дощечка для писания по воску («цера») и «писало» - металлическая или костяная палочка, имевшая с одной стороны заострение, а с другой – лопаточку.

На дальнейшее развитие математической культуры Древней Руси повлияло татаро-монгольское иго, которое отбросило славян на несколько столетий назад в развитии математической науки в частности.

Почти триста лет длилось монгольское иго. За это время наука Западной Европы сделала большой шаг вперёд: народы Европы ознакомились с замечательной математикой арабов и индийцев. А в задавленной захватчиками и отрезанной от всего культурного мира России математика стала отставать от науки Западной Европы.

Для того чтобы потом, после свержения монгольского ига, снова выйти в ряды мировой науки, ей понадобилось несколько столетий. В XVI веке, при Иоанне Грозном, на Руси появляются первые рукописные учебники по математике, а немного позже — печатные книги о применении математики для разных практических нужд; таковы, например, «Книга сошного письма» и «Устав ратных, пушечных и иных дел, касающихся до воинской науки».

В 1682 году в Москве вышла книга: «Считание удобное, которым всякий человек, купующий и продающий, зело удобно изыскати может число всякия вещи». Это была первая в России не рукописная, а напечатанная в типографии книга по математике, которая должна была помогать решению разных практических задач. Была в ней таблица умножения (до 100×100), записанная славянскими цифрами.

Особенно важную роль в развитии русской науки сыграла книга «Арифметика, или наука числительная», написанная Леонтием Филипповичем Магницким - hotcooltop.com. «Арифметика» Магницкого была издана при Петре I, в 1703 году, и долгое время была настольной книгой всех образованных русских людей. Великий русский учёный Михаил Васильевич Ломоносов знал её наизусть и называл её вместе с учебником грамматики «вратами своей учёности».

Книга Магницкого называлась «Арифметика», но, кроме арифметики, там были начала алгебры, геометрии, тригонометрии и даже немного мореходной астрономии. Это была настоящая энциклопедия по математике, в которой каждое правило, каждый приём подробно разъяснялся и подкреплялся решением примеров и практических задач - hotcooltop.com. Замечательной книгой Магницкого закончилась многовековая история древнерусской математики.

Список использованной литературы:

Р. А. Симонов – математическая мысль Древней Руси, М.: Наука, 1997г., 120с.
http://hotcooltop.com/article210.html
http://rus.ans4.com/27706153/kakaya-sistema-mer-byla-v-drevney-rusi/

referat911.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..