|
|
|
|
 Far |
| WinNavigator |
| Frigate |
| Norton
Commander |
| WinNC |
| Dos
Navigator |
| Servant
Salamander |
| Turbo
Browser |
|
|
| Winamp,
Skins, Plugins |
| Необходимые
Утилиты |
| Текстовые
редакторы |
| Юмор |
|
|
|
File managers and best utilites |
Лекция по дисциплине "Техническая механика" на тему "Основные понятия и аксиомы статики". Реферат на тему основные понятия и аксиомы статики
Лекция по дисциплине "Техническая механика" на тему "Основные понятия и аксиомы статики"
Тема: Основные понятия и аксиомы статики
Понятие о силе и системе сил
Сила — это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т.е. сила есть величина векторная,1 характеризующаяся точкой приложения (А), направлением (линией действия), величиной (модулем) (рис. 1). Силу измеряют в ньютонах,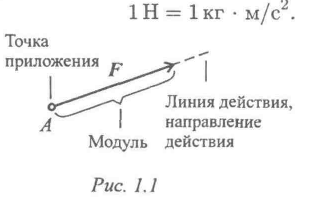
Рисунок 1
Силы, действующие на тело (или систему тел), делятся на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил.
Совокупность сил, действующих на какое-либо тело, называют системой сил.
Эквивалентная система сил — система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Аксиомы статики
В результате обобщения человеческого опыта были установлены общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики».
Первая аксиома
Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома
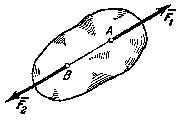
Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются (рис. 2).
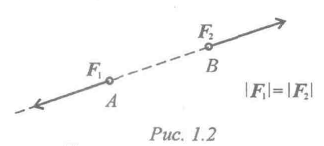
Рисунок 2
Третья аксиома
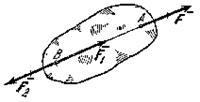
Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания системы сил, эквивалентной нулю) (рис. 3).
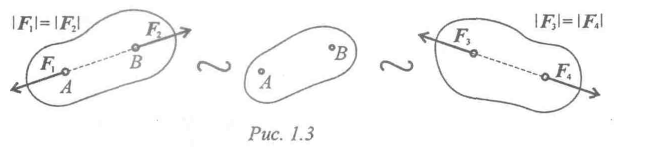
Рисунок 3
Четвертая аксиома (правило параллелограмма сил)
Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 4).
Вместо параллелограмма можно построить треугольник сил: силы вычерчивают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.
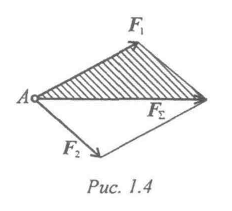
Рисунок 4
Пятая аксиома
При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 5).
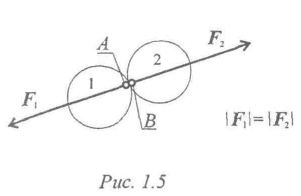
Рисунок.5
Следствие из второй и третьей аксиом
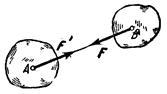
Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия (рис. 6).
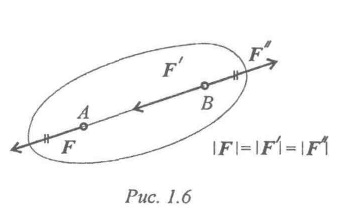
Рисунок 6
Сила F приложена в точке А. Требуется перенести ее в точку В. Используя третью аксиому, добавим в точке В уравновешенную систему сил (F';F"). Образуется уравновешенная по второй аксиоме система сил (F;F"). Убираем ее и получим в точке В силу F", равную заданной F.
Контрольные вопросы и задания
1. Какая из приведенных систем сил (рис. 5) уравновешена?
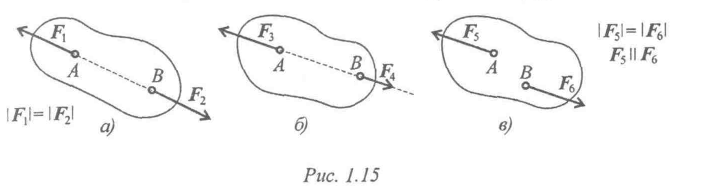
Рисунок 5
2. Какие силы системы (рис. 6 ) можно убрать, не нарушая механического состояния тела?
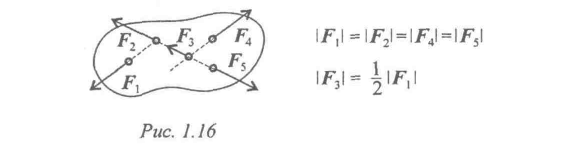
Рисунок 6
3. Тела 1 и 2 (рис. 7) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?
Рисунок 7
1 Векторные величины обозначаются полужирным шрифтом, скалярные величины — обычным.
infourok.ru
2.Предмет статики. Основные понятия и определения статики
Роль механики в подготовке будущего инженера-механика. Основные этапы развития механики.
Теоретическая механика не только позволяет объяснить ряд важных явлений в окружающем мире, но и служит научным фундаментом для многих технических дисциплин. Ее методами и приемами пользуются при всех технических расчетах, связанных с проектированием различных сооружений и машин и их эксплуатацией.
Помимо важного образовательного значения, изучение теоретической механики играет огромную роль в развитии профессионального мышления техника или будущего инженера. Чем лучше и глубже будут усвоены студентами основные положения теоретической механики, тем легче будет для них переход к продуктивному изучению специальных технических дисциплин, необходимых для инженерной деятельности.
Курс теоретической механики имеет давнюю историю, он формировался столетиями и традиционная методика его преподавания в большинстве вузов находится на достаточно высоком уровне. Вместе с тем для многих преподавателей высшей технической школы теоретическая механика - предмет традиционный, лишенный новизны и четкой практической значимости в подготовке будущего специалиста-инженера. Обучение строится по испытанной классической схеме изложения материала с последующим закреплением и контролем качества усвоения. Это не позволяет в полной мере рассматривать процесс преподавания теоретической механики как важный фактор профессиональной подготовки современного инженера.
Таким образом, учитывая, что фундаментом инженерного образования служат предметы физико-математического цикла, к числу которых относится теоретическая механика, очевидна необходимость выявления психолого-педагогических условий совершенствования преподавания теоретической механики будущим инженерам с целью улучшения их профессиональной подготовки и развития у них профессионально важных качеств.
Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.
Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.
Исследованием движения нетвердых тел – упругих, пластичных, жидких, газообразных, занимаются другие науки (сопротивление материалов, теория упругости, гидродинамика и т.д.).
Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.
Основные понятия:
1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.
В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН).
Сила является величиной векторной.
Основные понятия:
Про тело говорят, что оно находится в равновесии, если оно покоится или движется равномерно и прямолинейно относительно выбранной инерциальной системы отсчёта.
В статике материальные тела считают абсолютно твёрдыми, т.к. изменение размеров тел обычно мало по сравнению с начальными размерами.
Связи
На тело влияют внешние силы, а также другие материальные тела, ограничивающие перемещение данного тела в пространстве. Такие тела называют связями. Сила, с которой связь действует на тело, ограничивая его перемещение, называется реакцией связи. Для записи условия равновесия системы связи убирают, а реакции связей заменяют на равные им силы.
Например, если тело закреплено на шарнире, то шарнир является связью. Реакцией связи, при этом будет сила, проходящая через ось шарнира..
Системы сил
Если систему сил, действующих на твёрдое тело, можно заменить на другую систему сил, не изменяя механического состояния тела, то такие системы сил называются эквивалентными.
Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил. Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения.
Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил
Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.
Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.
Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю.
Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.
Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.
Вопрос№.3.Аксиомы статики
Аксиомы статики.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны
Аксиома1определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
Аксиома2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.
Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.
Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.
Аксиома4(принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.
Закон о равенстве действия и противодействия является одним из основных законов механики
Аксиома 5(принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.
Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).
Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.
Аксиома 1 Аксиома 2 Аксиома3 Аксиома 4
Вопрос№4. Связи и их реакции. Аксиома связей.
studfiles.net
1.1.1. Основные понятия и аксиомы статики
Материальной точкой называют тело, размерами которого можно пре-небречь. Она обладает массой и способностью взаимодействовать с другими материальными точками. Например, в небесной механике планеты, движущие-ся вокруг Солнца, часто рассматривают как материальные точки, поскольку их размеры малы по сравнению с размерами орбит. Пользоваться понятием мате-риальной точки целесообразно также и в том случае, когда все частицы движу-щегося физического тела перемещаются одинаково.Совокупность материальных точек, положения и движения которых взаимосвязаны между собой, называется системой материальных точек.
В теоретической механике пренебрегают малыми деформациями тел и считают эти тела абсолютно твердыми.
Абсолютно твердым телом называется такое тело, расстояние между дву-мя точками которого, во все время движения, остается величиной постоянной.
Силой называется количественная мера механического взаимодействия тел. Сила является векторной величиной, действие силы на тело определяется численным значением (модулем), направлением и точкой приложения силы (рис. 1.1).
Рис. 1.1.На схемах сила изображается направленным
отрезком. Основной едини-цей измерения силы является 1 Ньютон
(1Н). - Совокупность нескольких сил, действующих на тело,
называется систе-мой сил. - Эквивалентные системы сил - системы сил, оказывающие
одинаковое механическое действие на одно и то же тело. - Уравновешенная система сил - система сил, под действием
которой те-ло находится в равновесии. - Сила, эквивалентная некоторой
системе сил, называется равнодействующей. -
Сила, равная по модулю равнодействующей и направленная по линии ее действия в
противоположную сторону, называется уравновешивающей
силой. - Внешними силами называются
силы, действующие на тело со стороны других тел. - Внутренние силы - силы взаимодействия между частицами
одного и то-го же тела. В статике рассматриваются условия равновесия внешних
сил. Аксиомы статики.В основе статики лежат несколько не требующих до-казательства аксиом, из которых выводятся все теоремы и уравнения.
Аксиома 1. Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны (рис. 1.2).
Рис. 1.2 Рис. 1.3Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если
прибавить к ней или отнять от нее уравновешенную сис-тему сил 
(рис. 1.3).
Следствие из аксиомы 1 и
2. Действие силы на абсолютно твердое тело (АТТ) не изменится,
если точку приложения этой силы перенести по ли-нии ее действия. Пусть на тело в
точке А действует сила 
(рис. 1.4). Добавим в точке
В, выбранной произвольно на линии действия си-лы ,
уравновешенную систему сил 
и 
равных по абсолютной величине и направленных по линии ее действия. На основании
аксиомы 1 силы и будут
уравновешены и их можно отбросить (аксиома 2). В результате получим силу = , но приложенную не в
точке А, а в точке В. Отсюда следует, что сила, приложенная к АТТ, есть вектор
скользящий. 
, т.е. выражается по моду-лю и направлению диагональю
параллелограмма,построенного на этих силах (рис. 1.5).
Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине,
но противоположное по направлению противодействие. Действие и противодействие-это силы,
приложенные к двум раз-личным телам, поэтому они не уравновешиваются (рис. 1.6). Аксиома 5 Если деформируемое тело под действием системы сил находится в
равновесии, то при отвердевании его равновесие сохраняется.
Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем,
то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD
за-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится
(рис. 1.7).
Рис.1.7Связи и их
реакции. Твердое тело называется свободным, если оно мо-жет перемещаться в пространстве в
любом направлении (ВС в полете). Тело, ограничивающее свободу движения данного
твердого тела, является по отно-шению к нему связью. Твердое тело, свобода движения которого ограничена связями, называется
несвободным (движение самолета по ВПП). Сила, с
которой связь действует на тело, препятствуя его перемещению в том или ином
направлении, называется силой реакции этой связи.
Для нахождения реакции связей используют аксиому связей, на основании ко-торой
всякое несвободное тело можно рассматривать как свободное, если от-бросить
связи, заменив их действие на тело силами реакций этих связей. Направление силы
реакции связи противоположно тому направлению, в котором активные силы стремятся
переместить тело.
Различают три группы связей:
1. Гибкие связи (трос, цепь, ремень, канат). Реакции связей направлены по оси связей (рис. 1.8).
Рис. 1.8
Если нить отклоняется роликом, в котором не учитывается трение, то натя-жение нити не изменяется.
Например, натяжение тросов, идущих от штурвала к элеронам самолета, с обеих сторон равны по модулю
|Т1|= |Т3|, |Т2|= |Т4| (рис. 1.8б).
2. Твердые, идеально гладкие связи. Реакция направлена по общей нор-мали к поверхностям
соприкасающихся тел (рис. 1.9).
Рис. 1.9
3. Шарнирные связи. Шарниром в механике называется устройство, до-пускающее поворот одного тела
относительно другого, но ограничивающее при этом линейные перемещения этих тел. Шарнирами,
например, являются соеди-нения А, В, С элементов задней опоры самолета (рис. 1.10), узлы А,В,С,D
под-вески авиационного двигателя (рис. 1.11).
Реакция цилиндрического
шарнира 
может иметь любое
направление в плоскости, перпендикулярной оси шарнира. Направление реакции
зависит от ве-личины и направления действующих на тело сил. Реакция подвижного
шарнира всегда направлена по нормали к опорной поверхности шарнира (рис. 1.12б,
в). 
Рис. 1.12
Шаровой шарнир исключает любое перемещение тела во всех направле-ниях, кроме вращения, поэтому
реакция шарового шарнира может иметь любое направление в пространстве. Чаще всего эту реакцию
представляют в виде трех ее составляющих по осям координат x, y, z (рис. 1.13).
Рис. 1.13 Рис. 1.14
Разнообразные опорные устройства валов машин схематически представ-ляют подшипниками двух типов:
радиальным (цилиндрическим - А), не пре-пятствующим некоторым осевым смещениям вала и радиально-
упорным (В), исключающим осевые перемещения вала (рис. 1.14).
Неподвижная защемляющая опора или жесткая заделка. На заделанный конец балки со стороны опоры
действует система распределенных сил, кото-рую заменяем эквивалентной системой сосредоточенных сил
и моментом Ма, приложенных в точке А (рис. 1.15).
Рис. 1.15
www.mehanica-kvs.narod.ru
Темы заданий для самостоятельного изучения по теоретической механике с примерами освещения.
Тема № 1. СТАТИКА ТВЕРДОГО ТЕЛА
Основные понятия и аксиомы статики
Предмет статики. Статикой называется раздел механики, в котором изучаются законы сложения сил и условия равновесия материальных тел, находящихся под действием сил.
Под равновесием мы будем понимать состояние покоя тела по отношению к другим материальным телам. Если тело, по отношению к которому изучается равновесие, можно считать неподвижным, то равновесие условно называют абсолютным, а в противном случае -относительным. В статике мы будем изучать только так называемое абсолютное равновесие тел. Практически при инженерных расчетах абсолютным можно считать равновесие по отношению к Земле или к телам, жестко связанным с Землей. Справедливость этого утверждения будет обоснована в динамике, где понятие об абсолютном равновесии можно определить более строго. Там же будет рассмотрен и вопрос об относительном равновесии тел.
Условия равновесия тела существенно зависят от того, является ли это тело твердым, жидким или газообразным. Равновесие жидких и газообразных тел изучается в курсах гидростатики и аэростатики. В общем курсе механики рассматриваются обычно только задачи о равновесии твердых тел.
Все встречающиеся в природе твердые тела под влиянием внешних воздействий в той или иной мере изменяют свою форму (деформируются). Величины этих деформаций зависят от материала тел, их геометрической формы и размеров и от действующих нагрузок. Для обеспечения прочности различных инженерных сооружений и конструкций материал и размеры их частей подбирают так, чтобы деформации при действующих нагрузках были достаточно малы. Вследствие этого при изучении общих условий равновесия вполне допустимо пренебрегать малыми деформациями соответствующих твердых тел и рассматривать их как недеформируемые или абсолютно твердые.
Абсолютно твердым телом называется такое тело, расстояние между двумя любыми точками которого всегда остается постоянным.
Чтобы твердое тело под действием некоторой системы сил находилось в равновесии (в покое), необходимо чтобы эти силы удовлетворяли определенным условиям равновесия данной системы сил. Нахождение этих условий является одной из основных задач статики. Но для отыскания условий равновесия различных систем сил, а также для решения ряда других задач механики, оказывается необходимым уметь складывать силы, действующие на твердое тело, заменять действие одной системы сил другой системой и, в частности, приводить данную систему сил к простейшему виду. Поэтому в статике твердого тела рассматриваются следующие две основные задачи:
1) сложение сил и приведение систем сил, действующих на твердое тело, к простейшему виду;
2) определение условий равновесия действующих на твердое тело систем сил.
Сила. Состояние равновесия или движения данного тела зависит от характера его механических взаимодействий с другими телами, т.е. от тех давлений, притяжений или отталкиваний, которые данное тело испытывает в результате этих взаимодействий. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.
Рассматриваемые в механике величины, можно разделить на скалярные, т.е. такие, которые полностью характеризуются их численным значением, и векторные, т.е. такие, которые, помимо численного значения, характеризуются еще и направлением в пространстве.
Сила является величиной векторной. Ее действие на тело определяется: 1) численной величиной или модулем силы, 2) направлением силы, 3) точкой приложения силы.
Направление и точка приложения силы зависят от характера взаимодействия тел и их взаимного положения. Например, сила тяжести, действующая на какое-нибудь тело, направлена по вертикали вниз. Силы давления двух прижатых друг к другу гладких шаров направлены по нормали к поверхностям шаров в точках их касания и приложены в этих точках и т. д.
Графически сила изображается направленным отрезком (со стрелкой). Длина этого отрезка (АВ на рис. 1) выражает в выбранном масштабе модуль силы, направление отрезка соответствует направлению силы, его начало (точка А на рис. 1) обычно совпадает с точкой приложения силы. Иногда бывает удобно изображать силу так, что точкой приложения является ее конец - острие стрелки (как на рис. 4в). Прямая DE, вдоль которой направлена сила, называется линией действия силы. Силу обозначают буквой F. Модуль силы обозначается вертикальными черточками «по бокам» вектора. Системой сил называется совокупность сил, действующих на какое-нибудь абсолютно твердое тело.
Рис. 1.
Основные определения:
Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.
Если свободное твердое тело под действием данной системы сил может находиться в покое, то такая система сил называется уравновешенной.
Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.
Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Таким образом, равнодействующая - это сила, которая одна может заменить действие данной системы, сил на твердое тело.
Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.
Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.
Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, представляют собою по существу равнодействующие некоторых систем распределенных сил.
В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равнодействующую сил тяжестей его частиц. Линия действия этой равнодействующей проходит через точку, называемую центром тяжести тела.
Рис. 2
Аксиомы статики. Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики.Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1=F2 )и направлены вдоль одной прямой в противоположные стороны (рис. 2).
Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
А
ксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.
Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.
С
Рис. 3
ледствие из 1-й и 2-й аксиом.Точку приложения силы, действующей на абсолютно твердое тело, можно переносить вдоль ее линии действия в любую другую точку тела.В самом деле, пусть на твердое тело действует приложенная в точке А сила F (рис. 3). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы F1 и F2 ,такие, что Fl = F, F2 = - F. От этого действие силы F на тело не изменится. Но силы F и F2 согласно аксиоме 1 также образуют уравновешенную систему, которая может быть отброшена. В результате на тело будет действовать только одна сила Fl равная F, но приложенная в точке В.
Таким образом, вектор, изображающий силу F, можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).
Полученный результат справедлив только для сил, действующих на абсолютно твердое тело. При инженерных расчетах этим результатом можно пользоваться лишь тогда, когда исследуется внешнее действие сил на данную конструкцию, т.е. когда определяются общие условия равновесия конструкции.
Н
Рис. 4
апример, изображенный на (рис.4а) стержень АВ будет находиться в равновесии, если F1 = F2. При переносе обеих сил в какую-нибудь точкуС стержня (рис. 4, б), или при переносе силы F1 в точку В, а силы F2 в точку А (рис. 4, в), равновесие не нарушается. Однако внутреннее действие этих сил в каждом из рассмотренных случаев будет разным. В первом случае стержень под действием приложенных сил растягивается, во втором случае он не напряжен, а в третьем случае стержень будет сжиматься.А
Рис. 5
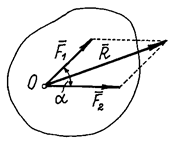
ксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, изображаемую диагональю параллелограмма, построенного на этих силах. Вектор К, равный диагонали параллелограмма, построенного на векторах F1 и F2 (рис. 5), называется геометрической суммой векторов F1 и F2:Следовательно, аксиому 3 можно еще формулировать так: равнодействующая двух сил, приложенных к телу в одной точке, равна геометрической (векторной) сумме этих сил и приложена в той же точке.
Аксиома 4. Два материальных тела всегда действуют друг на друга с силами, равными по модулю и направленными вдоль одной прямой в противоположные стороны (кратко: действие равно противодействию).
З
Рис. 6
акон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой F, то одновременно тело В действует на тело А с силой F = -F (рис. 6). Однако силы F и F' не образуют уравновешенной системы сил, так как они приложены к разным телам.Свойство внутренних сил. По аксиоме 4 любые две частицы твердого тела будут действовать друг на друга с равными по модулю и противоположно направленными силами. Так как при изучении общих условий равновесия тело можно рассматривать как абсолютно твердое, то (по аксиоме 1) все внутренние силы образуют при этом условии уравновешенную систему, которую (по аксиоме 2) можно отбросить. Следовательно, при изучении общих условий равновесия необходимо учитывать только внешние силы, действующие на данное твердое тело или данную конструкцию.
Аксиома 5 (принцип отвердевания). Если любое изменяемое (деформируемое) тело под действием данной системы сил находится в равновесии, то равновесие сохранится и тогда, когда тело отвердеет (станет абсолютно твердым).
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не должно нарушиться, если ее звенья сварить друг с другом; равновесие гибкой нити не нарушится, если она превратится в изогнутый жесткий стержень и т.д. Так как на покоящееся тело до и после отвердевания действует одна и та же система сил, то аксиому 5 можно еще выразить в другой форме: при равновесии силы, действующие на любое изменяемое (деформируемое) тело, удовлетворяют тем же условиям, что и для тела абсолютно твердого; однако для изменяемого тела эти условия, будучи необходимыми, могут не быть достаточными. Например, для равновесия гибкой нити под действием двух сил, приложенных к ее концам, необходимы те же условия, что и для жесткого стержня (силы должны быть равны по модулю и направлены вдоль нити в разные стороны). Но эти условия не будут достаточными. Для равновесия нити требуется еще, чтобы приложенные силы были растягивающими, т.е. направленными так, как на рис. 4а.
Принцип отвердевания широко используется в инженерных расчетах. Он позволяет при составлении условий равновесия рассматривать любое изменяемое тело (ремень, трос, цепь и т. п.) или любую изменяемую конструкцию как абсолютно жесткие и применять к ним методы статики твердого тела. Если полученных таким путем уравнений для решения задачи оказывается недостаточно, то дополнительно составляют уравнения, учитывающие или условия равновесия отдельных частей конструкции, или их деформации.
Тема № 2. ДИНАМИКА ТОЧКИ
studfiles.net
Основные аксиомы статики
Статика. Основные понятия и аксиомы
Основные понятия статики
Абсолютно твердое тело – это условно принятое тело, которое под действием внешних сил не деформируется.
Материальная точка – это условно принятое тело, размерами которого можно пренебречь в условиях данной задачи.
Сила — это мера механического взаимодействия материальных тел.
Сила есть величина векторная, характеризующаяся тремя факторами:
1) точкой приложения (А),
2) направлением (линией действия),
3) величиной (модулем) (рис. 1.1). Силу измеряют в Ньютонах,
1Н = 1кг·м/с2.
Силы, действующие на тело (или систему тел), делятся на внешние и внутренние.
Внешние силы бывают активные и реактивные.
Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил.
Совокупность сил, действующих на какое-либо тело, называют системой сил.
Эквивалентная система сил — система сил, действующая так же, как заданная.
Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей силой, действующей так же, как и система сил.
Равнодействующая сила– это сила, равная геометрической сумме всех сил действующих на тело.
Уравновешивающая сила – это сила, которая приводит тело в состояние покоя (равновесия).
Основные аксиомы статики
В результате обобщения человеческого опыта были установлены общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики.
Первая аксиома (принцип инерции) – материальная точка под действием внешних сил находится в равновесии, если равнодействующая равна нулю.
Вторая аксиома (принцип равенства двух сил) - две силы, являются взаимоуравновешивающими, если они равны по величине, лежат на одной прямой и противоположны по направлению (рис. 1.2).
Третья аксиома (принцип присоединения или исключения) – механическое состояние тела не изменится, если присоединить или исключить взаимоуравновешивающую систему сил (рис. 1.3).
Четвертая аксиома (принцип параллелограмма) -равнодействующая двух сил, приложенных к телу в одной точке, является диагональю параллелограмма, построенного на этих силах, как на сторонах (рис. 1.4).
Пятая аксиома (принцип действия и противодействия) - при взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 1.5).
Силы действующие и противодействующие всегда приложены к разным телам, поэтому они не уравновешиваются.
Силы, с которыми два тела действуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.
Тема 1.2. Плоская система сходящихся сил
ПССС - система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке(рис. 2.1).
Существует два способа определения равнодействующей ПССС: геометрический и аналитический.
Похожие статьи:
poznayka.org
Основные аксиомы статики
Поиск ЛекцийАксиомы статики выражают основные свойства сил, действующих на тело. Большинство аксиом статики является следствием основных законов механики, полученных как обобщение опыта. Так, закон инерции нашел свое отражение в условиях равновесия твердого тела. Их можно получить, решая вопрос о частном случае движения твердого тела – состоянии покоя.
Принцип независимости действия сил. Если на материальную точку (твердое тело) действуют одновременно несколько сил, то каждая из этих сил действует независимо от других. Иначе, эффект совместного действия нескольких сил, равен сумме эффектов действия каждой силы в отдельности. Следствием этого принципа механики является аксиома параллелограмма сил (аксиома III).
Рисунок 2 – Силы лежащие на одной прямой:
а - действие двух равных и противоположно направленных сил;
б – перенос силы по линии ее действия
Аксиома I. Если на абсолютно твердое тело действуют две равные и противоположные по направлению силы, лежащие на одной прямой, то они уравновешивают друг друга (рис. 2,а).
Аксиома II. Действие системы сил на абсолютно твердое тело не изменится, если к ней прибавить или отнять от нее любую уравновешенную систему сил.
Следствие из аксиом I и II.Действие силы на твердое тело не изменится, если эту силу перенести по линии ее действия в любую точку тела.
Пусть на тело в точке А действует сила F (рис. 2,б). Приложим к телу по линии действия силы F в точке В две уравновешенные силы F1 и F2, равные по модулю½F½. Система трех сил F, F1 и F2 будет эквивалентна либо силе F, либо силе F1 (так как сила F1=F и F2=-F, то систему уравновешенных сил F2, F можно не учитывать). В результате в точке В на тело будет действовать сила F1=F, что равносильно переносу силы F из точки А в точку В.
Аксиома III. Две силы, действующие на тело в одной точке, имеют равнодействующую в той же точке, изображаемую вектором, представляющим собой диагональ параллелограмма, построенного на векторах этих сил, как на сторонах.
Равнодействующую R (рис. 3) сил F1 и F2 называют геометрической суммой слагаемых векторов F1 + F2 = R. Следует отличать векторную сумму от скалярной суммы (алгебраической). Следовательно, аксиому III можно сформулировать так: равнодействующая двух сил, действующих на одно тело в одной точке, равна геометрической (векторной) сумме этих сил и приложена в той же точке тела. Данная аксиома выражает правило параллелограмма сил.
Рисунок 3 – Равнодействующая
двух сил, выходящих из одной точки
Рисунок 4 – Принцип противодействия
Аксиома IV (принцип противодействия). При всяком действии одного материального тела на другое возникает равное по величине и противоположное по направлению противодействие: F2 = - F1 (рис. 4). Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме IV рассматривается случай, когда силы приложены к разным телам, и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме II.
Этот принцип утверждает, что в природе не существует односторонних явлений. На рис. 5 изображена балка, опирающаяся на стены концами А и В. Для выявления сил действия и противодействия отделим балку от стен. Тогда силы действия балки на стену выражаются силами DA и DB, приложенными к стенам, а силы противодействия – силами RA и RB, приложенными к балке, которые в дальнейшем будем называть реакциями.
. 
Рисунок 5 – Опирание балки на опоры:
а – схема загружения балки; б – силы действия балки
на опоры и противодействия со стороны опор на балку
Аксиома V (принцип отвердения). Равновесие деформируемого тела, находящегося под действием системы сил, не нарушится, если под нагрузкой тело станет абсолютно твердым. Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.
Аксиома VI(аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме – в следующем параграфе).
Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.
Связи и реакции связей
Тело называется свободным, если оно может перемещаться в любом направлении, например воздушный шар в потоке воздуха. Обычно движение тел в пространстве ограничено. Такие тела называются несвободными.
Любое тело, ограничивающее свободу передвижения другого тела, называют связью. Используя аксиому связей, всякое несвободное тело можно рассматривать как свободное, если действие связей заменить силами – реакциями связей.
Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим, активным силам.
Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровая нагрузки и т. п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.
Одна из главных задач статики твердого тела – нахождение реакции связей. Для определения реакции связей необходимо найти величину этой реакции, линию и направление ее действия. Линия действия реакции обычно проходит через точку касания тела и связи. Численное значение реакции определяется расчетом, а направление реакции зависит от вида (конструкции) связи.
Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.
Рассмотрим основные типы связей, используемых в качестве опорных элементов или для соединения элементов сооружений в пространстве.
Свободное (незакрепленное) опирание тел на поверхность или точку опоры (рис. 6, а, б). Гладкая поверхность или точка опоры препятствуют перемещению тел только по направлению перпендикуляра, восстановленного из точек опоры к этой плоскости. Реакция в этих случаях направлена по нормали (перпендикуляру) к опирающейся поверхности.
Рисунок 6 – Свободное незакрепленное опирание тел:
а – на поверхность; б – на точки опорных элементов
Гибкие связи (рисунок 7, а, б). Под гибкими связями подразумевают тросы, нити, цепи, веревки и т. п. Перемещение тела от точки подвеса ограничено гибкой нерастяжимой нитью. Такая связь может воспринимать только растягивающие усилия. Реакции гибких связей направлены вдоль нити к точке ее прикрепления.
Рисунок 7 – Гибкие связи: а – подвеска груза с помощью троса;
б – фиксация груза с помощью двух тросов
Связь в виде жесткого стержня, шарнирно закрепленного по концам (рис. 8, а, б). Такая связь препятствует перемещению тела по оси стержня. Реакция направлена вдоль оси этого стержня. В отличие от гибкой нерастяжимой нити, шарнирный стержень строго фиксирует расстояние между двумя точками по концам стержня, которые не могут сблизиться (сжатие) или удалиться (растяжение).
. 
Рисунок 8 – Связи в виде жесткого стержня:
а – стержень препятствует перемещению бруса вниз;
б – стержень препятствует перемещению бруса вверх
Шарнирно - подвижные опоры (рис. 9, а, б). Под шарниром подразумевают связь, допускающую вращение одного тела по отношению к другому. Одним из распространенных видов шарнирно-подвижных опор являются катковые опоры (катки). Связь препятствует движению тела по нормали к опорной поверхности катков.
Таким образом, в подвижной (катковой) опоре возникает одна опорная реакция, направленная перпендикулярно плоскости опорной поверхности аналогично опорной реакции в шарнирном жестком стержне. Конструктивное решение шарнирно-подвижных опор может быть весьма разнообразным. В строительной механике такую опору изображают в виде шарнирного стержня (рис. 9, б).
Шарнирно-неподвижная опора (рис. 10, а, б). Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира. Такая опора не препятствует вращению вокруг оси, но препятствует движению тела в любом направлении в плоскости, перпендикулярной к оси шарнира.
Реакция R шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие Rx и Ry, соответствующие направлению выбранных осей (рис. 10, а).
| Рисунок 9 – Шарнирно подвижная опора: а – вид катковой опоры; б – расчетная схема шарнирно-подвижной опоры | Рисунок 10 – Шарнирно-неподвижная опора: а – вид шарнирно-неподвижной опоры; б, в – расчетные схемы шарнирно-неподвижных опор |
В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры (рис. 10, б) или шарнира (рис. 10, в).
Рисунок 11 – Жесткая заделка:
а – вид жесткой заделки; б – расчетная схема жесткой заделки
Жесткая заделка (рисунок 11, а, б). Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Балка, изображенная на рис.11, а, жестко заделана в стену в точке А. Перемещению ее в вертикальном направлении, препятствует реакция Ry, перемещению в горизонтальном направлении препятствует реакция Rx и повороту вокруг точки А – опорный момент МА. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Схематическое изображение такой опоры в строительной механике показано на рис. 11, б.
С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.
Проекция силы на ось
Ввиду особой важности для решения задач статики напомним известное из курса векторной алгебры определение проекции вектора на ось, в нашем случае - вектора F.
Проекцией вектора F = AB (рис. 12) на осьm называют отрезок АmВm оси m, заключенный между двумя плоскостями, перпендикулярными оси m и проходящими через начало и конец вектора F. Точка Аm – начало проекции, точка Вm – конец проекции.
| Рисунок 12 – Проекция силы на ось | Рисунок 13 – Правило силового треугольника |
Если направление от начала проекции Аm к концу проекции Вm совпадает с положительным направлением оси, то величину проекции берут со знаком плюс, а в противоположном случае – со знаком минус. Данное определение справедливо при любых расположениях вектора F и оси m в пространстве. На рис. 12 проекция силы F на ось m – Fm положительна.
Проведем ось m1, параллельную оси m. Так как отрезок ААm= СВm, а плоскости I и II перпендикулярны оси m, то АС=АmВm=Fm. Следовательно, при определении проекции силы на ось можно силу или ось переносить параллельно так, чтобы получились пересекающиеся прямые, а силу считать приложенной в точке пересечения.
Величину проекции силы на ось при всех возможных положениях силы можно определить по единой формуле Fm=Fcosa, где a - угол между направлением вектора силы и оси m. В практических расчетах удобнее умножать модуль силы на косинус ее острого угла с осью, а знак величины проекции определять из чертежа.
Равнодействующую двух сил можно получить из правила силового треугольника. Из правила параллелограмма отрезок АВ (рис. 13) равен и параллелен отрезку ОС. Поэтому, если мысленно отложить вектор силы F2 от конца вектора силы F1 (точка А), то равнодействующая R имеет начало в точке О, а конец - в точке В. Получили правило силового треугольника.
Аналогично, чтобы сложить систему сил, приложенных в одной точке, необходимо от конца первой силы отложить вектор второй силы, от конца второй силы отложить вектор третьей силы и т. д. Вектор равнодействующей R имеет начало в начале первой силы и конец в конце последней. Вектор R, замыкающий силовой многоугольник, называют векторной суммой сил.
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил. Система сходящихся сил, действующих на абсолютно твердое тело, всегда может быть заменена одной сосредоточенной силой – равнодействующей, проходящей через точку пересечения линий действия этих сил. Такая равнодействующая называется главным вектором системы сходящихся сил.
Момент силы. Пара сил
Действие силы на тело характеризуется ее численным значением (модулем), линией действия и направлением. Кроме того, в случае закрепленного тела (в одной или в нескольких точках) вводится понятие момента силы относительно точки.
Рисунок 14 –
Момент силы F относительно точки О
Момент силы относительно точки характеризует вращающее действие силы относительно этой точки. Его определяют как произведение силы F на длину перпендикуляра h, опущенного из этой точки на линию действия силы(рис. 14). Длину этого перпендикуляра называют плечом. Формулу для момента силы можно записать так: Moi = Fi hi , где индекс о обозначает точку, относительно которой определяют момент силы (центр момента), hi – плечо силы Fi .
Примем условно момент силы на рис. 15 положительным, если он стремится повернуть тело вокруг центра момента по ходу часовой стрелки, и отрицательным – против часовой стрелки. Тогда Mo1 = - F1h2, Mo2 =F2h3, Mo3 = 0. Момент силы F3 относительно точки о (Мо3) равен нулю, так как линия действия данной силы пересекает точку о.
Пара сил – это две равные по абсолютному значению параллельные силы, направленные в противоположные стороны и имеющие разные линии действия (рис. 16). Плоскость, в которой действует пара сил, называется плоскостью пары. Пара сил не имеет равнодействующей и может быть заменена только другой эквивалентной парой сил. Сумма проекций сил, образующих пару, на любую ось равна нулю. Момент пары равен произведению одной из ее сил на плечо.
Пара сил также сообщает телу вращательное движение, как и момент силы относительно точки.
| Рисунок 15 – Момент сил F1, F2, F3 относительно точки о | Рисунок 16 – Эквивалентные пары сил |
Часто пару сил изображают в виде изогнутой стрелки с обозначением момента (рис. 16). Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.
Например, внутренние силы будут различны для балок, изображенных на рис.17, а, б.
Рисунок 17 – Замена пары сил сосредоточенным моментом:
а) вид изогнутой оси балки при нагружении двумя сосредоточенными силами;
б) вид изогнутой оси балки при нагружении сосредоточенным моментом
poisk-ru.ru
Аксиомы статики, реферат — allRefers.ru
Аксиомы статики - раздел Механика, Теоретическая механика
Условия, при которых тело может находиться в равновесии, выводиться из нескольких основных положений, применяемых без доказательств, но подтвержденных опытом и называемых аксиомами статики. Основные аксиомы статики сформулированы выдающимся английским ученым Исааком Ньютоном и поэтому названы его именем.
Аксиома I(аксиома инерции, или первый закон Ньютона). Всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения до тех пор, пока какие – нибудь силы не выведут тело из этого состояния.
Способность материального тела сохранять движение при отсутствии действующих сил или постепенно изменять это движение, когда на тело начинают действовать силы, называется инерцией или инертностью. Инертность есть одно из основных свойств материи.
В соответствии с этой аксиомой состоянием равновесия считается такое состояние, когда тело находиться в покое или движется прямолинейно и равномерно, т.е. по инерции.
Аксиома II(аксиома взаимодействия, или третий закон Ньютона). Силы взаимодействия двух тел всегда равны по модулю ( |F1| = |F2| или
)и направлены по одной прямой и в противоположные стороны.
Рис. 1.2 Из третьего закона Ньютона вытекает, что одностороннего механического действия одного тела на другое не существует, т.е. силы взаимодействия – силы парные. Однако сила действия одного тела на другое и сила противодействия не представляет собой систему сил, т.к. они приложены к разным телам.
Аксиома III(закон равенства действия и противодействия). Для равновесия свободного твердого тела, находящегося под действием двух сил, необходимо и достаточно, чтобы эти силы были равны по модулю и действовали по одной прямой в противоположные стороны.
Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой 
, то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой 
= 
(рис. 1.3). Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам.
рис. 1.3.
Аксиома IV(принцип присоединения и отбрасывания систем сил, эквивалентной нулю). Всякую силу, действующую на абсолютно твердое тело, можно перенести вдоль линии ее действия в любую точку, не нарушив при этом его механического состояния.
Следствие из 2-й и 4-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис. 1.4). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы 
и 
, такие, что = , = . От этого действие силы на тело не изменится.
Но силы и согласно аксиоме 2 рис. 1.4.
также образуют уравновешенную систему, которая может быть отброшена. В результате на тело будет действовать только одна сила , равная , но приложенная в точке В.
Таким образом, вектор, изображающий силу , можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).
Аксиома V(правило параллелограмма). Равнодействующая двух сил, приложенных к телу в одной точке, приложена в той же точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на данных силах.
Вектор 
, равный диагонали параллелограмма, построенного на векторах и (рис.12), называется геометрической суммой векторов и : = + .
Величина равнодействующей
Рис. 1.3.
Конечно, 
Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, рис. 1.5
то
Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.
– Конец работы –
Эта тема принадлежит разделу:
Теоретическая механика
Теоретическая механика... Введение... Любое явление в ок ружающем нас макромире связано с движением следовательно не может не иметь того или иного...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Аксиомы статики
Все темы данного раздела:
Связи и реакции связей Все законы и теоремы статики справедливы для свободного твердого тела. Все тела делятся на свободные и
Определение равнодействующей геометрическим способом Знать геометрический способ определения равнодействующей системы сил, условия равновесия плоской систе
Равнодействующая сходящихся сил Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника си
Проекция силы на ось Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начал
Определение равнодействующей системы сил аналитическим способом Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равноде
Условия равновесия плоской системы сходящихся сил в аналитической форме Исходя из того, что равнодействующая равна нулю, получим:
Методика решения задач Решение каждой задачи можно условно разделить на три этапа. Первый этап: Отбрасываем внешние связи сис
Пара сил и момент силы относительно точки Знать обозначение, модуль и определение моментов пары сил и силы относительно точки, условия равновесия с
Эквивалентность пар Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическо
Опоры и опорные реакции балок Правило для определения направления реакций связей ( рис.1.22). Шарнирно-подвижная опора допускает п
Приведение силы к точке. Произвольная плоская система сил представляет собой систему сил, линии действия которых расположены в пло
Приведение плоской системы сил к данной точке Метод приведения одной силы к данной точке можно при
Влияние точки приведения Точка приведения выбрана произвольно. Произвольная плоская система сил представляет собой систему сил, ли
Теорема о моменте равнодействующей (теорема Вариньона) В общем случае произвольная плоская система сил приводится к главному вектору F'гл и к главному мо
Условие равновесия произвольно плоской системы сил 1)При равновесии главный вектор системы равен нулю (=0)
Балочные системы. Определение реакций опор и моментов защемления Иметь представление о видах опор и возникающих реакциях в опорах. Знать три формы уравнений равн
Виды нагрузок По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузк
Момент силы относительно точки Момент силы относительно оси характеризуется вращательным эффектом, создаваемым силой, стремящейся пове
Вектор в пространстве В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора
Приведение произвольной пространственной системы сил к центру О Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О. Силы необходимо параллельно пе
Некоторые определения теории механизмов и машин При дальнейшем изучении предмета теоретической механики, в особенности при решении задач, мы столкнемся с
Ускорение точки Векторная величина, характеризующая быстроту измене
Ускорение точки при криволинейном движении При движении точки по криволинейном траектории скорость меняет свое направление. Представим себе точку М
Равномерное движение Равномерное движение — это движение с постоянной скоростью: v = const. Для прямолинейного ра
Неравномерное движение При неравномерном движении численные значения скорости и ускорения меняются. Уравнение неравноме
Тема 2.2 Простейшие движения твердого тела Иметь представление о поступательном движении, его особенности и параметрах, о вращательном движении тел
Вращательное движение Движение, при котором по крайнем мере точки твердого тела или неизменяемой системы остаются неподвижными,
Частные случаи вращательного движения Равномерное вращение (угловая скорость постоянна): ω = const. Уравнение (закон) равн
Скорости и ускорения точек вращающегося тела Тело вращается вокруг точки О. Определим параметры движения точки Л, расположенной на расстоянии
Преобразование вращательного движения Преобразование вращательного движения осуществляется разнообразными механизмами, которые называются
Основные определения Сложным движением считают движение, которое можно разложить на несколько простых. Простыми движениям
Плоскопараллельное движение твердого тела Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тел
Метод определения мгновенного центра скоростей Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложно
Тема 3.2 Понятие трения Абсолютно гладких и абсолютно твердых тел в природе не существует, и поэтому при перемещении одного тела по
Трение скольжения Трением скольжения называется трение движения, при котором скорости тел в точке касания различ
Свободная и несвободная точки Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется сво
Принцип кинетостатики (принцип Даламбера) Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции
Работа постоянной силы на прямолинейном пути Работа силы в общем случае численно равна произведению модуля силы на длину пройденного мм пути и на косин
Работа постоянной силы на криволинейном пути Пусть точка М движется по дуге окружности и сила
Мощность Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Коэффициент полезного действия Способность тела при переходе из одного состояния в другое совершать работу называется энергией.
Закон изменения количества движения Количеством движения материальной точки называется векторная величина, равная произведению массы точк
Потенциальная и кинитецеская энергия Существуют две основные формы механической энергии: потенциальная энергия, или энергия положения,
Закон изменения кинетической энергии Пусть на материальную точку массой m действует постоянная сила
Основы динамики системы материальных точек Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической с
Основное уравнение динамики вращающегося тела Пусть твердое тело под действием внешних сил вращает
Моменты инерции некоторых тел Момент инерции сплошного цилиндра (рис. 3.19) Моме
Сопротивление материалов Иметь представление о видах расчетов в сопротивлении материалов, о классификации нагрузок, о внутренних
Тема 4.1 Основные положения. Гипотезы и допущения Практика показывает, что все части конструкций под действием нагрузок деформируются, т. е. изменяет сво
Внешние силы Всопротивлении материалов под внешними воздействиями подразумевается не только силовое взаимо
Деформации линейные и угловые. Упругость материалов В отличие от теоретической механики, где изучалось взаимодействие абсолютно жестких (недеформируемых) тел,
Допущения и ограничения, принятые в сопротивлении материалов Реальные строительные материалы, из которых возводятся различные здания и сооружения, представляют собой
Виды нагрузок и основных деформаций В процессе работы машин и сооружений их узлы и детали воспринимают и передают друг другу различные на
Формы элементов конструкции Все многообразие форм сводится к трем видам по одному признаку. 1. Брус — любое тело, у которого дл
Метод сечений. Напряжение Знать метод сечений, внутренние силовые факторы, составляющие напряжений. Уметь определять виды
Растяжение и сжатие Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает
Центральное растяжение прямого бруса. Напряжения Центральным растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечен
Напряжения при растяжении и сжатии При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения в поперечных се
Продольные и поперечные деформации. Закон Гука Иметь представление о продольных и поперечных деформациях и их связи. Знать закон Гука, зависимо
Закон Гука при растяжении и сжатии Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется зако
Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии. Используем известные формулы. Закон Гука σ=Еε. Откуда
Механические испытания. Статические испытания на растяжение и сжатие Это стандартные испытания: оборудование — стандартная разрывная машина, стан- дартный образец (кругл
Механические характеристики Механические характеристики материалов, т. е. величины, характеризующие их прочность, пластичность, упруго
allrefers.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|