Реферат: Кинетическая и потенциальная энергия. Реферат на тему кинетическая и потенциальная энергия

Реферат - Кинетическая и потенциальная энергия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ

ГУМАНИТАРНЫЙ ИНСТИТУТ

КАФЕДРА МАТЕМАТИКИ И МПМ

КОНСПЕКТ УРОКА ПО ФИЗИКЕ

(8 класс)

НА ТЕМУ:

«Кинетическая и потенциальная энергия»

Подготовила и провела

студент

физико-математического

факультета

группы 4М

Платошина Татьяна Сергеевна

методист по физике

Кузнецов Владислав Валентинович

Орехово-Зуево

2010г

Урок изучения нового материала и решения задач.

Кинетическая и потенциальная энергия.

Число: 8.11.2010

Класс: 8В

Тип урока: Комбинированный

Цели урока (триединые дидактические цели):

1. Обучающие: Повторить импульс, закон сохранения импульса. Решение задач на ЗСИ. Дать новые понятия кинетической и потенциальной энергии. Учиться применять полученные знания при решении задач.

2. Развивающие: учить выделять главное, строить аналогии, обобщать и систематизировать, развивать логическое мышление, умение анализировать данные и полученные результаты, развивать навыки самостоятельной работы, учится решать задачи по данной теме.

3. Воспитательные: воспитывать любовь к предмету, обогащать словарный запас, воспитывать взаимоуважение, дисциплину на уроке, наблюдательность; умение слушать своих одноклассников.

Ход урока:

1. Организационный момент: 2 мин

— взаимное приветствие учителя и учеников;

— проверка готовности кабинета;

— отметить отсутствующих (спросить у дежурного).

2. Проверка домашнего задания: 7мин

Учитель: Пожалуйста к доске, разбираем и проверяем домашнюю работу, задачи №

Учитель вызывает учеников к доске решать задачи, заданные на прошлом уроке на дом. Остальные ученики проверяют правильность решения при необходимости подсказывают и исправляют товарища. Если что-то непонятно, задают вопросы учителю.

3. Актуализация знаний. Фронтальный опрос.

· Дать понятие импульса.

· Прочитать ЗСИ.

· Какое движение называется реактивным, привести примеры?

· Какое топливо использовалось в первых ракетах?

· Под чьим руководством был запущен первый искусственный спутник Земли?

4. Изучение нового материала. 17-20 мин

Учитель: Сегодня на уроке мы будем изучать новую тему: Энергия.

План :

1. Ввести понятие механической энергии.

2. Ввести понятие потенциальной и кинетической энергии.

3. Вывод формул для кинетической энергии.

4. Вывод формул для потенциальной энергии.

Сегодня понятие энергии настолько вошло в наш обыденный лексикон, что мы, не задумываясь, применяем этот термин по поводу и без повода. Нам кажется, что это существует в реальности как отдельная вещь, или субстанция. Как, например, вода или воздух. Обычно мы часто говорим, чтобы поднять что-либо, или копать земли в саду, не хватает энергии. Если же нет света в доме, говорим, нет электрической энергии. Чтобы вскипятить чайник на газовой плите, «тратим» тепловую энергию, которая выделяется при сжигании природного газа. Также у всех на слуху механическая энергия, атомная энергия, ветровая энергия, и т.д

Так, что же это такое?

Термин «энергия» был введен в 1807 году английским ученым Т.Юнгом. В переводе с греческого это слово означает «Действие, деятельность».

Различные разделы физики изучают различные виды энергии. В ядерной физике- ядерную энергию, в молекулярной физике- внутреннюю и тепловую энергию, в механике- механическую энергию.

Говорят, что любое тело, способное совершить механическую работу, обладает механической энергией. Механическая энергия обозначается буквой Е и измеряется в тех же единицах что и работа, т. е. в джоулях

Например, если шар движется с некоторой скоростью в направлении неподвижного бруска, то при ударе брусок сместиться. Значит по отношению к бруску была совершена работа за счет энергии двигавшегося шара.

Следовательно, любое тело обладающее скоростью обладает энергией.

Этот вид механической энергии называется кинетической энергией Ек

Кинети́ческая эне́ргия — энергиямеханической системы, зависящая от скорости движения её тела.

Если тело некоторой массы поднимать на высоту h, то произведенная работа не будет зависит от того как мы поднимали тело( по вертикали, горизонтали или другому способу). Во всех этих случаях работа будет равна. Значит, поднимая тело, мы запасли работу, т. е. поднятое тело обладает энергией. Эта энергия не зависит от того, по какому пути происходил подъем, а определяется лишь положением тела (высотой, на которую оно поднято). Поэтому эту энергию называют энергией положения. Чаще ее называют потенциальной энергией.

Потенциальная энергия - энергия взаимодействия тел или частей тела. Потенциальная энергия (от латинского potentia — возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними.

Для расчета той и другой энергии существует общее правило. Чтобы определить энергию, которой обладает тело, надо найти работу, необходимую

для перевода этого тела из нулевого состояния в данное( нулевое состояние- состояние в котором в котором энергия тела считается равной нулю).Чем больше это работа, тем большей энергией обладает тело в данном состоянии… Воспользуемся этим правилом для расчета каждой из энергий.

Кинетическая энергия.

Предположим что тело массой mпод действием силы F начинает двигаться из состояния покоя и разгоняется до скорости v. тогда тело начнет двигаться с постоянным ускорением и совершит перемещение s.

Работа, необходимая для сообщения телу данной скорости находится:

A=Fs

По второму закону Ньютона: F=ma

A=mas

Путь, пройденный при равноускоренном движении из состояния покоя:

Формула для ускорения:

Подставляем эти значения в формулу работы:

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Потенциальная энергия.

Найдем потенциальную энергию тела, взаимодействующего с Землей.Пусте тело массой m поднято на высоту h. При равномерном подъеме, когда прикладываемая к телу сила равна по величине силе тяжести, эта работа может быть найдена так:

где

Потенциальна энергия тела, взаимодействующего с Землей, равна произведению массы этого тела, ускорению свободного падения и высоты на которой находиться тело.

За нулевое положение тела при расчете его потенциальной энергии необязательно выбирать то, которое расположено на поверхности Земли. Это может быть и уровень пола в помещении и поверхность стола. Нулевое положение, от которого отсчитывается высота тела, выбирают произвольно, руководствуясь соображениями удобства.

Мы рассчитали значения двух видов механической энергии. Совершенно очевидно что: чем больше энергия тела, тем большую работу оно может совершит.

5. Решение задачи: 10мин

№76 ( Громов, стр 135)

При равномерном подъеме, прикладываемая к телу сила совпадает по величине с силой тяжести, совершаемая работа рассчитывается так:

Дано СИ Решение

m=2,5т 2500кг

h=12м

А-? …(Дж)

№ 78 ( Громов, стр 135)

Дано СИ Решение

Кинетическая энергия:

m=400г 0,4кг

-? …(Дж)

6. Закрепление изученного.Подведение итогов: 3 мин

Учитель: Вспомним что мы сегодня изучили нового:

1. Какая энергия изучается в механике?

2. Чем обусловлены кинетическая и потенциальная энергии?

3. Как находятся кинетическая и потенциальная энергии?

7. Домашнее задание: 2мин

Выучить параграф 14, вопросы после параграфа,

задачи по учебнику № 77, 79

8. Выставление оценок в дневник за ответы на уроке.

Учитель: Урок окончен. До свидания.

www.ronl.ru

Доклад - Кинетическая и потенциальная энергия 2

Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Рассмотрим случай, когда на тело массой m действует постоянная сила (она может быть равнодействующей нескольких сил) и векторы силы и перемещения направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F∙s. Модуль силы по второму закону Ньютона равен F = m∙a, а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ1 и конечной υ2 скорости и ускорения а выражением

Отсюда для работы получаем

(1)

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .

Кинетическая энергия обозначается буквой Ek .

(2)

Тогда равенство (1) можно записать в таком виде:

A = Ek 2 – Ek 1. (3)

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

(4)

Физический смысл кинетической энергии:

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия — минимальная работа, которую необходимо совершить, чтобы перенести тело из некой точки отсчёта в данную точку в поле консервативных сил. Второе определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы. Третье определение: потенциальная энергия — это энергия взаимодействия. Единицы измерения [Дж]

Потенциальная энергия принимается равной нулю для некоторой точки пространства, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной точки называется нормировкой потенциальной энергии. Понятно также, что корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Силы, работа которых зависит от формы траектории, называются непотенциальными. При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.

Потенциальная энергия взаимодействия тела с Землей.

Найдем работу, совершаемую силой тяжести Fт при перемещении тела массой т вертикально вниз с высоты h2 над поверхностью Земли до высоты h3 (рис. 1).

Рис. 1.

Если разность h2 – h3 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести Fт во время движения тела можно считать постоянной и равной mg.

Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

A = F∙s = m∙g∙(hl – h3 ). (5)

Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести Fт = m∙g совершает работу

A = m∙g∙s∙cos a = m∙g∙h, (6)

где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

Рис. 2.

Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h', h" и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

(7)

где h2 и h3 – высоты от поверхности Земли, на которых расположены соответственно точки В и С.

Рис. 3.

Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.

При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.

Равенство (7) можно представить в таком виде:

A = – (m∙g∙h3 – m∙g∙hl ). (8)

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Работа силы тяжести при перемещении тела массой т из точки, расположенной на высоте h3, в точку, расположенную на высоте h2 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

А= – (Ер2 – Ер1 ). (9)

Потенциальная энергия обозначается буквой Ер.

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия Ер тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

Ep = m∙g∙h. (10)

Физический смысл потенциальной энергии взаимодействия тела с Землей:

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m, находящееся на высоте h, где h < h0(h0– нулевая высота), обладает отрицательной потенциальной энергией:

Еp = –m∙gh

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами т и М, находящихся на расстоянии r одна от другой, равна

(11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Еp = 0) принят при r = ∞. Потенциальная энергия гравитационного взаимодействия тела массой т с Землей, где h – высота тела над поверхностью Земли, М3 – масса Земли, R3 – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

(12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой т с Землей для малых высот h (h « R3 ) равна

Еp = m∙g∙h,

где – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x1 до конечного значения x2 (рис. 4, б, в).

Рис. 4.

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т. к. сила упругости линейно зависит от x) и умножить на модуль перемещения:

(13)

где Отсюда

или

(14)

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

(15)

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

А = –(Ер2 – Ер1 ). (16)

Если x2 = 0 и x1 = х, то, как видно из формул (14) и (15),

Ер = А.

Тогда физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

www.ronl.ru

Реферат: Кинетическая и потенциальная энергия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ

ГУМАНИТАРНЫЙ ИНСТИТУТ

КАФЕДРА МАТЕМАТИКИ И МПМ

КОНСПЕКТ УРОКА ПО ФИЗИКЕ

(8 класс)

НА ТЕМУ:

«Кинетическая и потенциальная энергия»

Подготовила и провела

студент

физико-математического

факультета

группы 4М

Платошина Татьяна Сергеевна

методист по физике

Кузнецов Владислав Валентинович

Орехово-Зуево

2010г

Урок изучения нового материала и решения задач.

Кинетическая и потенциальная энергия.

Число: 8.11.2010

Класс: 8В

Тип урока: Комбинированный

Цели урока (триединые дидактические цели):

Ход урока:

1. Организационный момент: 2 мин

- взаимное приветствие учителя и учеников;

- проверка готовности кабинета;

- отметить отсутствующих (спросить у дежурного).

2. Проверка домашнего задания: 7мин

Учитель: Пожалуйста к доске, разбираем и проверяем домашнюю работу, задачи №

3. Актуализация знаний. Фронтальный опрос.

· Дать понятие импульса.

· Прочитать ЗСИ.

· Какое движение называется реактивным, привести примеры?

· Какое топливо использовалось в первых ракетах?

· Под чьим руководством был запущен первый искусственный спутник Земли?

4. Изучение нового материала. 17-20 мин

Учитель: Сегодня на уроке мы будем изучать новую тему : Энергия.

План :

1. Ввести понятие механической энергии.

2. Ввести понятие потенциальной и кинетической энергии.

3. Вывод формул для кинетической энергии.

4. Вывод формул для потенциальной энергии.

Сегодня понятие энергии настолько вошло в наш обыденный лексикон, что мы, не задумываясь, применяем этот термин по поводу и без повода. Нам кажется, что это существует в реальности как отдельная вещь, или субстанция. Как, например, вода или воздух. Обычно мы часто говорим, чтобы поднять что-либо, или копать земли в саду, не хватает энергии. Если же нет света в доме, говорим, нет электрической энергии. Чтобы вскипятить чайник на газовой плите, "тратим" тепловую энергию, которая выделяется при сжигании природного газа. Также у всех на слуху механическая энергия, атомная энергия, ветровая энергия, и т.д

Так, что же это такое?

Говорят,что любое тело, способное совершить механическую работу, обладает механической энергией. Механическая энергия обозначается буквой Е и измеряется в тех же единицах что и работа, т. е. в джоулях

Например , если шар движется с некоторой скоростью в направлении неподвижного бруска, то при ударе брусок сместиться. Значит по отношению к бруску была совершена работа за счет энергии двигавшегося шара.

Следовательно, любое тело обладающее скоростью обладает энергией.

Этот вид механической энергии называется кинетической энергией Ек

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скорости движения её тела.

Потенциальная энергия - энергия взаимодействия тел или частей тела. Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними.

для перевода этого тела из нулевого состояния в данное( нулевое состояние- состояние в котором в котором энергия тела считается равной нулю).Чем больше это работа , тем большей энергией обладает тело в данном состоянии.. Воспользуемся этим правилом для расчета каждой из энергий.

Кинетическая энергия.

Предположим что тело массой m под действием силы F начинает двигаться из состояния покоя и разгоняется до скорости v. тогда тело начнет двигаться с постоянным ускорением и совершит перемещение s.

Работа, необходимая для сообщения телу данной скорости находится:

A=Fs

По второму закону Ньютона: F=ma

A=mas

Путь, пройденный при равноускоренном движении из состояния покоя:

Формула для ускорения :

Подставляем эти значения в формулу работы:

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Потенциальная энергия.

где

5. Решение задачи: 10мин

№76 ( Громов, стр 135)

Дано СИ Решение

m=2,5т 2500кг

h=12м

А-? …(Дж)

№ 78 ( Громов, стр 135)

Дано СИ Решение

Кинетическая энергия:

m=400г 0,4кг

-? …(Дж)

6. Закрепление изученного.Подведение итогов: 3 мин

Учитель: Вспомним что мы сегодня изучили нового:

1. Какая энергия изучается в механике?

2. Чем обусловлены кинетическая и потенциальная энергии?

3. Как находятся кинетическая и потенциальная энергии?

7. Домашнее задание: 2мин

Выучить параграф 14, вопросы после параграфа,

задачи по учебнику № 77, 79

8. Выставление оценок в дневник за ответы на уроке.

Учитель: Урок окончен. До свидания.

www.referatmix.ru

Реферат: Кинетическая и потенциальная энергия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ

ГУМАНИТАРНЫЙ ИНСТИТУТ

КАФЕДРА МАТЕМАТИКИ И МПМ

КОНСПЕКТ УРОКА ПО ФИЗИКЕ

(8 класс)

НА ТЕМУ:

«Кинетическая и потенциальная энергия»

Подготовила и провела

студент

физико-математического

факультета

группы 4М

Платошина Татьяна Сергеевна

методист по физике

Кузнецов Владислав Валентинович

Орехово-Зуево

2010г

Урок изучения нового материала и решения задач.

Кинетическая и потенциальная энергия.

Число:8.11.2010

Класс:8В

Тип урока:Комбинированный

Цели урока (триединые дидактические цели):

Ход урока:

1.Организационный момент:2 мин

- взаимное приветствие учителя и учеников;

- проверка готовности кабинета;

- отметить отсутствующих (спросить у дежурного).

2. Проверка домашнего задания: 7мин

Учитель:Пожалуйста к доске, разбираем и проверяем домашнюю работу, задачи №

3. Актуализация знаний. Фронтальный опрос.

· Дать понятие импульса.

· Прочитать ЗСИ.

· Какое движение называется реактивным, привести примеры?

· Какое топливо использовалось в первых ракетах?

· Под чьим руководством был запущен первый искусственный спутник Земли?

4. Изучение нового материала.17-20 мин

Учитель:Сегодня на уроке мы будем изучать новую тему : Энергия.

План :

1. Ввести понятие механической энергии.

2. Ввести понятие потенциальной и кинетической энергии.

3. Вывод формул для кинетической энергии.

4.Вывод формул для потенциальной энергии.

Сегодня понятие энергии настолько вошло в наш обыденный лексикон, что мы, не задумываясь, применяем этот термин по поводу и без повода. Нам кажется, что это существует в реальности как отдельная вещь, или субстанция. Как, например, вода или воздух.Обычно мы часто говорим, чтобы поднять что-либо, или копать земли в саду, не хватает энергии. Если же нет света в доме, говорим, нет электрической энергии. Чтобы вскипятить чайник на газовой плите, "тратим" тепловую энергию, которая выделяется при сжигании природного газа.Также у всех на слуху механическая энергия, атомная энергия, ветровая энергия, и т.д

Так, что же это такое?

Говорят,что любое тело, способное совершить механическую работу, обладает механической энергией. Механическая энергия обозначается буквой Е и измеряется в тех же единицах что и работа, т. е. в джоулях

Например , если шар движется с некоторой скоростью в направлении неподвижного бруска, то при ударе брусок сместиться. Значит по отношению к бруску была совершена работа за счет энергии двигавшегося шара.

Следовательно, любое тело обладающее скоростью обладает энергией.

Этот вид механической энергии называется кинетической энергией Ек

Кинети́ческая эне́ргия— энергиямеханической системы, зависящая от скорости движения её тела.

Потенциальная энергия -энергия взаимодействия тел или частей тела. Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними.

для перевода этого тела из нулевого состояния в данное( нулевое состояние- состояние в котором в котором энергия тела считается равной нулю).Чем больше это работа , тем большей энергией обладает тело в данном состоянии.. Воспользуемся этим правилом для расчета каждой из энергий.

Кинетическая энергия.

Работа, необходимая для сообщения телу данной скорости находится:

A=Fs

По второму закону Ньютона: F=ma

A=mas

Путь, пройденный при равноускоренном движении из состояния покоя:

Формула для ускорения :

Подставляем эти значения в формулу работы:

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Потенциальная энергия.

где

5. Решение задачи:10мин

№76 ( Громов, стр 135)

Дано СИ Решение

m=2,5т 2500кг

h=12м

А-? …(Дж)

№ 78 ( Громов, стр 135)

Дано СИ Решение

Кинетическая энергия:

m=400г 0,4кг

-? …(Дж)

6. Закрепление изученного.Подведение итогов:3 мин

Учитель:Вспомним что мы сегодня изучили нового:

1. Какая энергия изучается в механике?

2. Чем обусловлены кинетическая и потенциальная энергии?

3. Как находятся кинетическая и потенциальная энергии?

7. Домашнее задание:2мин

Выучить параграф 14, вопросы после параграфа,

задачи по учебнику № 77, 79

8. Выставление оценок в дневник за ответы на уроке.

Учитель:Урок окончен. До свидания.

superbotanik.net

Кинетическая и потенциальная энергии | Бесплатные курсовые, рефераты и дипломные работы

Кинетическая энергиямеханической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.

dA= dT.

Используя второй закон Ньютона F=mdv/dt

и умножая обе части равенства на перемещение dr, получим

Fdr =m(dv/dt)dr=dA

Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией

Т … = тv2/2. (12.1)

Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.

При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.

Потенциальная энергия —механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными,а силы, действующие в них,— консервативными.Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной;ее примером является сила трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией II. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

dA=-dП. (12.2)

Работа dА выражается как скалярное произведение силы F на перемещение drи выражение (12.2) можно записать в виде

Fdr=-dП. (12.3)

Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению.

Потенциальная энергия может быть определена исходя из (12.3) как

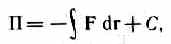
где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Для консервативных сил

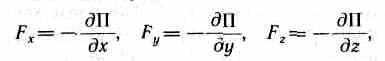
или в векторном виде

F=-gradП, (12.4) где

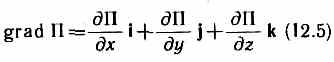
(i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П.

Для него наряду с обозначением grad П применяется также обозначение ÑП. Ñ («набла») означает символический вектор, называемый оператором Гамильтона или набла-оператором:

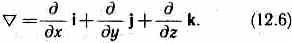
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна

П = mgh, (12.7)

где высота h отсчитывается от нулевого уровня, для которого П0 = 0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.

Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!}. Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h’), П=-mgh’.

Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

Fхупр= -kx,

где Fxупр — проекция силы упругости на ось х; k — коэффициент упругости(для пружины — жесткость),а знак минус указывает, что Fx упрнаправлена в сторону, противоположную деформации х.

По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.

Fx=-Fx упр=kx Элементарная работа dA, совершаемая силой Fxпри бесконечно малой деформации dx, равна

загрузка…

dA = Fx dx = kxdx,

а полная работа

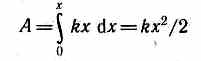
идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела

П=kx2/2.

Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.

Полная механическая энергия системы— энергия механического движения и взаимодействия:

Е = Е+П,

т. е. равна сумме кинетической и потенциальной энергий.

refac.ru

Реферат Кинетическая энергия

скачать

Реферат на тему:

План:

1 История
2 Физический смысл
3 Физический смысл работы
4 Релятивизм
5 Соотношение кинетической и внутренней энергии

Введение

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Единица измерения в системе СИ — Джоуль.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

1. История

Впервые теория кинетической энергии была изложена в трудах Г. Лейбница, посвященных понятию «живой силы»

2. Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

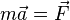
$m \vec a = \vec F$

$\vec{F}$ — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы ${\rm d} \vec s = \vec v {\rm d}t$ . Учитывая, что $\vec a = \frac{{\rm d}\vec{v}}{{\rm d}t}$ , Получим:

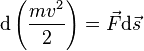
${\rm d} \left( {{m v^2} \over {2}} \right) = \vec F {\rm d} \vec s$

Если система замкнута, то есть $\vec F = 0$ , то $d \left( {{m v^2} \over {2}} \right) = 0$ , а величина

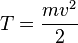
$T = {{m v^2} \over 2}$

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

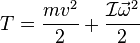
$T = \frac{m v^2}{2}+\frac{\mathcal{I} \vec \omega^2}{2}$

где:

$\ m$ — масса тела

$\ v$ — скорость центра масс тела

$\mathcal{I}$ — момент инерции тела

$\vec \omega$ — угловая скорость тела.

3. Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

$\ A_{12} = T_2 - T_1$

4. Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

$T = \frac{m c^2}{\sqrt{1- v^2/c^2 }}-m c^2$

где:

$\ m$ — масса объекта;

$\ v$ — скорость движения объекта в инерциальной системе отсчета;

$\ c$ — скорость света в вакууме ( $\ m c^2$ — энергия покоя).

Данную формулу можно переписать в следующем виде:

$T = \frac{m v^2}{1- v^2/c^2 + \sqrt{1- v^2/c^2 }}$

При малых скоростях ( $\ v \ll c$ ) последнее соотношение переходит в обычную формулу ${1 \over 2} m v^2$ .

5. Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и такие формы энергии, как тепло, рассматриваются как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое. То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов, молекул, и внутренняя тепловая энергия обусловлена движением атомов и молекул и рассматривается как следствие броуновского движения, а температура тела отличается от кинетической энергии такого движения лишь на постоянный коэффициент — постоянную Больцмана.

wreferat.baza-referat.ru

Доклад - Кинетическая и потенциальная энергия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ

ГУМАНИТАРНЫЙ ИНСТИТУТ

КАФЕДРА МАТЕМАТИКИ И МПМ

КОНСПЕКТ УРОКА ПО ФИЗИКЕ

(8 класс)

НА ТЕМУ:

«Кинетическая и потенциальная энергия»

Подготовила и провела

студент

физико-математического

факультета

группы 4М

Платошина Татьяна Сергеевна

методист по физике

Кузнецов Владислав Валентинович

Орехово-Зуево

2010г

Урок изучения нового материала и решения задач.

Кинетическая и потенциальная энергия.

Число: 8.11.2010

Класс: 8В

Тип урока: Комбинированный

Цели урока (триединые дидактические цели):

Ход урока:

1. Организационный момент: 2 мин

— взаимное приветствие учителя и учеников;

— проверка готовности кабинета;

— отметить отсутствующих (спросить у дежурного).

2. Проверка домашнего задания: 7мин

Учитель: Пожалуйста к доске, разбираем и проверяем домашнюю работу, задачи №

3. Актуализация знаний. Фронтальный опрос.

· Дать понятие импульса.

· Прочитать ЗСИ.

· Какое движение называется реактивным, привести примеры?

· Какое топливо использовалось в первых ракетах?

· Под чьим руководством был запущен первый искусственный спутник Земли?

4. Изучение нового материала. 17-20 мин

Учитель: Сегодня на уроке мы будем изучать новую тему: Энергия.

План :

1. Ввести понятие механической энергии.

2. Ввести понятие потенциальной и кинетической энергии.

3. Вывод формул для кинетической энергии.

4. Вывод формул для потенциальной энергии.

Так, что же это такое?

Следовательно, любое тело обладающее скоростью обладает энергией.

Этот вид механической энергии называется кинетической энергией Ек

Кинети́ческая эне́ргия — энергиямеханической системы, зависящая от скорости движения её тела.

Кинетическая энергия.

Работа, необходимая для сообщения телу данной скорости находится:

A=Fs

По второму закону Ньютона: F=ma

A=mas

Путь, пройденный при равноускоренном движении из состояния покоя:

Формула для ускорения:

Подставляем эти значения в формулу работы:

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Потенциальная энергия.

где

5. Решение задачи: 10мин

№76 ( Громов, стр 135)

Дано СИ Решение

m=2,5т 2500кг

h=12м

А-? …(Дж)

№ 78 ( Громов, стр 135)

Дано СИ Решение

Кинетическая энергия:

m=400г 0,4кг

-? …(Дж)

6. Закрепление изученного.Подведение итогов: 3 мин

Учитель: Вспомним что мы сегодня изучили нового:

1. Какая энергия изучается в механике?

2. Чем обусловлены кинетическая и потенциальная энергии?

3. Как находятся кинетическая и потенциальная энергии?

7. Домашнее задание: 2мин

Выучить параграф 14, вопросы после параграфа,

задачи по учебнику № 77, 79

8. Выставление оценок в дневник за ответы на уроке.

Учитель: Урок окончен. До свидания.

www.ronl.ru

Реферат: Кинетическая и потенциальная энергия. Реферат на тему кинетическая и потенциальная энергия

Реферат - Кинетическая и потенциальная энергия

Доклад - Кинетическая и потенциальная энергия 2

Реферат: Кинетическая и потенциальная энергия

Реферат: Кинетическая и потенциальная энергия

Кинетическая и потенциальная энергии | Бесплатные курсовые, рефераты и дипломные работы

Реферат Кинетическая энергия

План:

Введение

1. История

2. Физический смысл

3. Физический смысл работы

4. Релятивизм

5. Соотношение кинетической и внутренней энергии

Доклад - Кинетическая и потенциальная энергия

Смотрите также