 Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:
Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:Муниципальное общеобразовательное учреждение
средняя школа № 46.
КУРСОВАЯ РАБОТА
на тему: “Иррациональные уравнения”
Выполнил:
Ученик 8 “З” классаА.Волошук
Проверил:
Учитель математики Л.З.Фисенко
г. Ростов-на-Дону
2001г.
СОДЕРЖАНИЕ.
Введение 3 стр.
1.Из истории 4стр.
2.Определение иррациональных уравнений
2.1.Равносильные уравнения.
Следствия уравнений. 6 стр.
2.2.Опреднление иррациональных чисел. 9 стр.
3.Методы решения иррациональных уравнений.
3.1.Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень. 10стр. 3.2.Метод введения новых переменных. 12 стр.
3.3.Исскуственные приёмы решения иррациональных
уравнений 13 стр. Заключение 15 стр.
Список используемой литературы 16 стр.
ВВЕДЕНИЕ
В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, с параметрами, иррациональные и другие. Данная курсовая работа посвящена иррациональным уравнениям, методам их решения. Кроме того, в работе введены понятия уравнений следствий и равносильных уравнений, а также приведены примеры задач, математическими моделями которых служат иррациональные уравнения. В данной работе содержится небольшая историческая справка, посвященная введению иррациональных чисел
1. ИЗ ИСТОРИИ
Термин “рациональное” (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин “соизмеримый” (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.
Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих “Началах” Евклид излагает учение об иррациональностях чисто геометрически.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, “алогос” – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: “Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.”
Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя “Начала” Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в началеXII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.
Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли “арифметикой астрономов”. По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе “Ключ арифметики” ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих “приложениях к алгебре” (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление “Геометрии” Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.
В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.
2. ОПРЕДЕЛЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Равносильные уравнения. Следствия уравнений.
При решении уравнений выполняются различные тождественные преобразования над выражениями, входящими в уравнение. При этом исходное уравнение изменяется другими, имеющими те же корни. Такие уравнения называются равносильными.
Определение: Уравнение f(x)=g(x) равносильно уравнению f1(x)=g1(x), если каждый корень первого уравнения является корнем второго и обратно, каждый корень второго уравнения является корнем первого, т.е. их решения совпадают.
Например, уравнения 3x-6=0; 2х–1=3 равносильны, т.к. каждое из уравнений имеет один корень х=2.
Любые два уравнения, имеющие пустое множество корней, считают равносильными.
 Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:
Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:
 f(x)=g(x) f1(x)=g1(x)
f(x)=g(x) f1(x)=g1(x)
В процессе решения уравнений важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.
Теорема 1: Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.
Доказательство: Докажем, что уравнение f(x) = g(x)+q(x) (1) равносильно уравнению
f(x) – q(x) = g(x) (2)
Пусть х=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a).Но тогда по свойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее, что а – корень уравнения (2). Аналогично доказывается, что каждый корень уравнения (2) является и корнем уравнения (1).
Что и требовалось доказатью.
Теорема 2: Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.
Доказательство: докажем, что уравнение 6х–3=0 равносильно уравнению 2х–1=0
решим уравнение 6х–3=0 и уравнение 2х–1=0
6х=3 2х=1
х=0,5 х=0,5
так как корни уравнений равны, то уравнения равносильны.
Что и требовалось доказать.
Рассмотрим уравнение

ОДЗ этого уравнения {х ≠ 1, х ≠ -3}
Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находим корни х1=1, х2 = –2 . Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один корень х=-2.
 В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения
В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения
пусть даны два уравнения:
f1 (x) = g1 (x) (3)
f2 (x) = g2 (x)(4)
Если каждый корень уравнения (3) является корнем уравнения (4), то уравнение (4) называют следствием уравнения (3).
 Этот факт записывают так:
Этот факт записывают так:
В том случае, когда уравнение (3) - есть также следствие уравнения (4), эти уравнения равносильны.
 Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.
Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.
В приведенном выше примере уравнение – следствие х²+х–2=0, имеет два корня x1=1 и х2 =-2, а исходное уравнение имеет один корень х=-2. В этом случае корень х=1 называют посторонним для исходного уравнения

В общем случае корни уравнения-следствия, не являющиеся корнями исходного уравнения, называют посторонними.
 Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения
Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения
и потому отброшен.
 Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
ОДЗ которого {х ¹-2},

 получим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.
получим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.
В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней.
Например, уравнение (х+1)(х+3)= х+1 (5)
Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .
Если же обе части уравнения (5) разделить (“сократить”) на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля.
Для того, чтобы в процессе решения уравнения избежать потери корней, необходимо следить за тем, чтобы переход осуществлялся либо к равносильным уравнениям, либо к уравнениям-следствиям.
2.2. Определение иррациональных уравнений.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Например:

3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.
3.1. Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень.
Пример №1

 Решить уравнение
Решить уравнение
 Возведем обе части уравнения (1) в квадрат:
Возведем обе части уравнения (1) в квадрат:
далее последовательно имеем:
5х – 16 = х² - 4х + 4
х² - 4х + 4 – 5х + 16 = 0
х² - 9х + 20 = 0


 Проверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
Проверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
значения – корни уравнения.
Ответ: 4; 5.
Пример №2
Решить уравнение:

(2)
Решение:
Преобразуем уравнение к виду:
 и применим метод возведения в квадрат:
и применим метод возведения в квадрат:

далее последовательно получаем.

 Разделим обе части последнего уравнения почленно на 2:
Разделим обе части последнего уравнения почленно на 2:
 еще раз применим метод возведения в квадрат:
еще раз применим метод возведения в квадрат:
далее находим:
9(х+2)=4–4х+х²
9х+18–4+4х-х²=0
-х²+13х+14=0
х²-13х–14=0
х1+х2 =13 х1 =19
х1 х2 = -14 х2 = -1
по теореме, обратной теореме Виета, х1=14, х2 = -1
корни уравнения х²-13х–14 =0

Проверка: подставив значение х=-14 в уравнение (2), получим–
- не верное равенство. Поэтому х = -14 – не корень уравнения (2).
 Подставив значение x=-1 в уравнение (2), получим-
Подставив значение x=-1 в уравнение (2), получим-
- верное равенство. Поэтому x=-1- корень уравнения (2).
Ответ: -1
3.2 Метод введения новых переменных.

Решить уравнение
Решение:
Конечно, можно решить это уравнение методом возведения обеих частей уравнения в одну и ту же степень. Но можно решить и другим способом – методом введения новых переменных.

Введем новую переменную Тогда получим 2y²+y–3=0 – квадратное уравнение относительно переменной y. Найдем его корни:


Т.к. , то – не корень уравнения, т.к. не
может быть отрицательным числом . А - верное равенство, значит x=1- корень уравнения.
Ответ: 1.
Искусственные приёмы решения иррациональных уравнений.
Решить уравнение:
(1)
Решение:
Умножим обе части заданного уравнения на выражение
сопряжённое выражению
Так как
То уравнение (1) примет вид:
Или
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение:
(2)
Сложив уравнения (1) и (2), придём к уравнению
(3)
Решая уравнение (3) методом возведения в квадрат, получим:
Проверка:
x1=0, x2=4, x3= -4подставим в уравнение
1)
- не верное равенство, значит x1=0- не корень уравнения.
2)
- верное равенство, значит x2=4- корень уравнения.
3)
- не верное равенство, значит x3= -4- не корень уравнения.
Ответ: 4.
ЗАКЛЮЧЕНИЕ
Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат (или n-ую степень) или введением новой переменной. Кроме того, пользуются и искусственными приемами решения иррациональных уравнений.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.
1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений - Москва: Издательство “Мнемозина”, 1999.
2) М.Я.Выгодский. Справочник по элементарной математике - Москва: Издательство “Наука”, 1986.
3) А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство “Педагогика”, 1989.
4) А.И.Макушевич. Детская энциклопедия – Москва: Издательство “Педагогика”, 1972.
5) Н.Я.Виленкин. Алгебра для 9 класс. Учебное пособие для учащихся школ и классов с углубленным изучением изучением математики – Москва: Издательство “Просвещение”, 1998.
referat.store
Министерство образования и науки РФ.
МОУ “Ульканская средняя общеобразовательная школа №2”.
ТЕМА:
Решение иррациональных уравнений.
Реферат выполнен:
Верхошанской Светланой Александровной,
ученица 9”Г” класса.
Руководитель:
Высоцкая Лидия Степановна,
учитель математики.
Улькан
2005
СОДЕРЖАНИЕ:
Глава I. Историческая справка ………………………………….………………..2
Глава II §1. Решение иррациональных уравнений ………………………..……..3
§2. Преобразование иррациональных выражений ………………….….5
§3. Уравнения с радикалом третьей степени …………………………...6
§4. Введение нового неизвестного …………………………………...…7
Литература …………………………………………………………………………9
Историческая справка
об иррациональных уравнениях.
“Источником алгебраических иррациональностей является двузначность или многозначность задачи; ибо было бы невозможно выразить одним и тем же вычислением многие значения, удовлетворяющие одной и той же задаче, иначе, чем при помощи корней…; они же разве только в частных случаях могут быть сведены к рациональностям”.
(Лейбниц Г.)
Одной из конкретных причин появления математических теорий явилось открытие иррациональностей. Вначале это произошло в пределах геометрических изысканий в виде установления факта несоизмеримости двух отрезков прямой. Значение этого открытия в математике трудно переоценить. В математику, едва ли не впервые, вошла сложная теоретическая абстракция, не имеющая аналога в донаучном общечеловеческом опыте. Вероятно, самой первой иррациональностью, открытой древнегреческими математиками, было число  . Можно с определённой уверенностью считать, что исходным пунктом этого открытия были попытки найти общую меру с помощью алгоритма попеременного вычитания, известного сейчас как алгоритм Евклида. Возможно также, что некоторую роль сыграла задача математической теории музыки: деление октава, приводящее к пропорции 1:п=п:2. Не последнюю роль сыграл и характерный для пифагорейской школы общий интерес к теоретико-числовым проблемам.
. Можно с определённой уверенностью считать, что исходным пунктом этого открытия были попытки найти общую меру с помощью алгоритма попеременного вычитания, известного сейчас как алгоритм Евклида. Возможно также, что некоторую роль сыграла задача математической теории музыки: деление октава, приводящее к пропорции 1:п=п:2. Не последнюю роль сыграл и характерный для пифагорейской школы общий интерес к теоретико-числовым проблемам.
Древние математики нашли довольно быстро логически строгое доказательство иррациональности числа  путём сведения этого доказательства к формальному противоречию. Пусть
путём сведения этого доказательства к формальному противоречию. Пусть  , где m и n – взаимно простые числа. Тогда m2=2n2, откуда следует, что т2 чётное и, следовательно, п2 чётное. Чётно, следовательно и п. Получающееся противоречие (п не может быть одновременно и чётным и нечётным) указывает на неверность посылки, что число
, где m и n – взаимно простые числа. Тогда m2=2n2, откуда следует, что т2 чётное и, следовательно, п2 чётное. Чётно, следовательно и п. Получающееся противоречие (п не может быть одновременно и чётным и нечётным) указывает на неверность посылки, что число  рационально.
рационально.
Для исследования вновь открываемых квадратичных иррациональностей сразу же оказалось необходимым разрабатывать теорию делимости чисел. В самом деле, пусть  , где p и g - взаимно просты, а п является произведением только первых степеней сомножителей отсюда р2=пg2. Если t – простой делитель п, то р2 (а значит, и р) делится на t. Следовательно, р2 делится на t2. Но в п содержится только первая степень t. Значит g2 (равно как и g) делится на t. Но этот результат формально противоречит предположению, что р и g взаимно просты.
, где p и g - взаимно просты, а п является произведением только первых степеней сомножителей отсюда р2=пg2. Если t – простой делитель п, то р2 (а значит, и р) делится на t. Следовательно, р2 делится на t2. Но в п содержится только первая степень t. Значит g2 (равно как и g) делится на t. Но этот результат формально противоречит предположению, что р и g взаимно просты.
Вслед за иррациональностью числа  были открыты многие другие иррациональности. Так, Архит (около 428-365 до н.э.) доказал иррациональность чисел вида
были открыты многие другие иррациональности. Так, Архит (около 428-365 до н.э.) доказал иррациональность чисел вида  . Теодор из Кирены (V в. до н.э.) установил иррациональность квадратного корня из чисел 3,5,6,…,17, которые не являются полным квадратом. Теэтет (410-369 до н.э.) дал одну из первых классификаций иррациональностей.
. Теодор из Кирены (V в. до н.э.) установил иррациональность квадратного корня из чисел 3,5,6,…,17, которые не являются полным квадратом. Теэтет (410-369 до н.э.) дал одну из первых классификаций иррациональностей.
С появлением иррациональностей в древнегреческой математике возникли серьёзные трудности как в теоретико-числовом, так и в геометрическом плане.
Решение иррациональных уравнений.
Уравнения, в которых под знаком корня содержится переменная, называют иррациональными. Таково, например, уравнение  .
.
При решении иррациональных уравнений полученные решения требуют проверки, потому, например, что неверное равенство при возведении в квадрат может дать верное равенство. В самом деле, неверное равенство  при возведении в квадрат даёт верное равенство 12= (-1)2, 1=1.
при возведении в квадрат даёт верное равенство 12= (-1)2, 1=1.
Иногда удобнее решать иррациональные уравнения, используя равносильные переходы.
Пример 1. Решим уравнение  .
.
Возведём обе части этого уравнения в квадрат и получим  , откуда следует, что
, откуда следует, что  , т.е.
, т.е.  .
.
Проверим, что полученные числа являются решениями уравнения. Действительно, при подстановке их в данное уравнение получаются верные равенства:
 и
и 
Следовательно, x=3 или x=-3 – решение данного уравнения.
Пример 2. Решим уравнение  .
.
Возведя в квадрат обе части уравнения, получим  . После преобразований приходим к квадратному уравнению
. После преобразований приходим к квадратному уравнению  , корни которого
, корни которого  и
и  .
.
Проверим, являются ли найденные числа решениями данного уравнения. При подстановке в него числа 4 получим верное равенство  , т.е. 4 - решение данного уравнения. При подстановке же числа 1 получаем в правой части -1, а в левой части число 1. Следовательно, 1 не является решением уравнения; говорят, что это посторонний корень, полученный в результате принятого способа решения.
, т.е. 4 - решение данного уравнения. При подстановке же числа 1 получаем в правой части -1, а в левой части число 1. Следовательно, 1 не является решением уравнения; говорят, что это посторонний корень, полученный в результате принятого способа решения.
Ответ:  .
.
Пример 3. Решим уравнение  .
.
Возведём обе части этого уравнения в квадрат:  , откуда получаем уравнение
, откуда получаем уравнение  , корни которого
, корни которого  и
и  . Сразу ясно, что число -1 не является корнем данного уравнения, т.к. обе части его не определены при
. Сразу ясно, что число -1 не является корнем данного уравнения, т.к. обе части его не определены при  . При подстановке в уравнение числа 2 получаем верное равенство
. При подстановке в уравнение числа 2 получаем верное равенство  , следовательно, решением данного уравнения является только число 2.
, следовательно, решением данного уравнения является только число 2.
Пример 4. Решим уравнение  .
.
Возведя в квадрат обе части этого уравнения, получаем  ,
,  ,
,  . Подстановкой убеждаемся, что число 5 не является корнем данного уравнения. Поэтому уравнение не имеет решений.
. Подстановкой убеждаемся, что число 5 не является корнем данного уравнения. Поэтому уравнение не имеет решений.
Пример 5. Решим уравнение  .
.
По определению  - это такое неотрицательное число, квадрат которого равен подкоренному выражению. Другими словами, уравнение
- это такое неотрицательное число, квадрат которого равен подкоренному выражению. Другими словами, уравнение  равносильно системе:
равносильно системе:



Решая первое уравнение системы, равносильное уравнению  , получим корни 11 и 6, но условие
, получим корни 11 и 6, но условие  выполняется только для
выполняется только для  . Поэтому данное уравнение имеет один корень
. Поэтому данное уравнение имеет один корень  .
.
Пример 6. Решим уравнение  .
.
В отличие от рассмотренных ранее примеров данное иррациональное уравнение содержит не квадратный корень, а корень третьей степени. Поэтому для того, чтобы “избавиться от радикала”, надо возвести обе части уравнения не в квадрат, а в куб:  . После преобразований получаем:
. После преобразований получаем:

Итак,  ,
,  .
.
Пример 7. Решим систему уравнений:

П оложив
оложив  и
и  , приходим к системе
, приходим к системе

Р азложим левую часть второго уравнения на множители:
азложим левую часть второго уравнения на множители:  - и подставим в него из первого уравнения
- и подставим в него из первого уравнения  . Тогда получим систему, равносильную второй:
. Тогда получим систему, равносильную второй:

П одставляя во второе уравнение значение v, найденное из первого
одставляя во второе уравнение значение v, найденное из первого  , приходим к уравнению
, приходим к уравнению  , т.е.
, т.е.  .
.
Полученное квадратное уравнение имеет два корня:  и
и  .
.
Соответствующие значения v таковы:  и
и  . Переходя к переменным х и у, получаем:
. Переходя к переменным х и у, получаем:  , т.е.
, т.е.  ,
,  ,
,  ,
,  .
.
Преобразование иррациональных выражений.
Если знаменатель дроби содержит иррациональное выражение, то часто целесообразно избавиться от последнего.
Рассмотрим некоторые типичные случаи:

Пример:

При непосредственном возведении в квадрат обеих частей уравнения уравнение должно быть сначала преобразовано так, чтобы в одной части стояли только радикалы, а в другой – остальные члены исходного уравнения. Так поступают, если радикалов в уравнении два. Если же их три, то два из них оставляют в одной части уравнения, а третий переносят в другую. Затем обе части уравнения возводят в квадрат и проводятся необходимые преобразования (приведение подобных и т.п.). Далее все члены уравнения, не содержащие радикалов, снова переносятся в одну сторону уравнения, а оставшийся радикал (теперь он будет только один!) – в другую. Полученное уравнение вновь возводят в квадрат, и в итоге получается уравнение, не содержащее радикалов.
Пример. Введение новой переменной:
 .
.
Решение: Обозначим  , тогда
, тогда

Уравнение примет вид:

Возведём его в квадрат:

Это уравнение так же возводим в квадрат:



Проверка: полученные значения t мы должны проверить в уравнении (1), так как именно оно возводилось в квадрат. Проверка показывает, что  - посторонний корень, а
- посторонний корень, а  - действительно корень уравнения (1). Отсюда получим:
- действительно корень уравнения (1). Отсюда получим:



Ответ: 0;-1.
Уравнения с радикалом третьей степени.
При решении уравнений, содержащих радикалы 3-й степени, бывает полезно пользоваться сложением тождествами:

Пример 1.
 .
.
Возведём обе части этого уравнения в 3-ю степень и воспользуемся выше приведённым тождеством:

Заметим, что выражение стоящее в скобках равно 1, что следует из первоначального уравнения. Учитывая это и приводя подобные члены, получим:

Раскроем скобки, приведём подобные члены и решим квадратное уравнение. Его корни  и
и  . Если считать (по определению), что корень нечётной степени можно извлекать и из отрицательных чисел, то оба полученных числа являются решениями исходного уравнения.
. Если считать (по определению), что корень нечётной степени можно извлекать и из отрицательных чисел, то оба полученных числа являются решениями исходного уравнения.
Ответ:  .
.
Решение 2
Возведём две новые переменные  и
и  , тогда
, тогда  ,
,
 .
.
Заметим, что  .
.
В итоге получим систему уравнений:





Используя первоначальные уравнения системы, преобразуем вторые, заменив первую скобку единицей, а вторую подставим вместо неизвестного у выражение  , также полученное из первого
, также полученное из первого  .
.
Приведём подобные члены, раскрыв предварительно скобки и решив полученное квадратное уравнение. Его корни  и
и  . Вернёмся теперь к начальной подстановке и получим искомые решения:
. Вернёмся теперь к начальной подстановке и получим искомые решения:

Введение нового неизвестного.
Решив эти уравнения, найдём радикалы более высоких степеней, но наиболее часто использовавшийся способ их решения – введение нового(новых) неизвестного.
Пример 2.

Обозначим  , тогда
, тогда
а) 
Уравнение примет вид:

Корень  не удовлетворяет условию
не удовлетворяет условию 
Ответ: 76.
Методы решения иррациональных уравнений.
Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо является его следствием. Поэтому существуют два пути при решении иррациональных уравнений:
1) переход к выводным уравнениям (следствиям) с последующей проверкой корней;
2) переход к равносильным системам.
Второй подход избавляет от подстановки полученных корней в исходное уравнение (иногда такую проверку осуществить нелегко) и, вообще говоря, является более предпочтительным. Однако если в ходе решения оказалось, что проверка полученных корней не представляет труда, то можно не выяснять источники появления посторонних корней и не переходить к равносильным системам.
Пример 1.

Возведём в 6 степень:

Проверка:
 , т.е.
, т.е.  - верное равенство.
- верное равенство.
Ответ: 67.
Пример 2.

Преобразуем уравнение к виду:
 и возведём обе части в квадрат:
и возведём обе части в квадрат:

 , т.е.
, т.е.


Ещё раз возведём обе части в квадрат:
 , т.е.
, т.е.  ,
,  .
.
Проверка:
1) При 

2) 
Ответ:  .
.
Пример 3.

Положим  . Тогда
. Тогда  и мы получаем уравнение
и мы получаем уравнение  , откуда
, откуда  ,
,  .
.
Теперь задача свелась к решению двух уравнений:
 ;
;  . Возводя обе части уравнения
. Возводя обе части уравнения  в 5-ю степень, получим
в 5-ю степень, получим  , откуда
, откуда  .
.
Уравнение  - не имеет корней, поскольку под знаком возведения в дробную степень может содержаться неотрицательное число, а любая степень неотрицательного числа неотрицательна.
- не имеет корней, поскольку под знаком возведения в дробную степень может содержаться неотрицательное число, а любая степень неотрицательного числа неотрицательна.
Ответ: 34.
Список используемой литературы:
1) Справочник по математике.
В.А. Гусев, А.Г. Мордкович.: 1986г.
2) Углублённое изучение курса алгебры и математического анализа.
М.Л. Галицкий, М.М. Мошкович, С.И. Шварцабурд.: 1992г.
3) Возникновение и развитие математической науки.
К.А. Рыбников.: 1987г.
4) Ученикам о математике.
М.К. Гриненко.: 1993г.
topref.ru
Иррациональные уравнения
ВВЕДЕНИЕ
В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, с параметрами, иррациональные и другие. Данная курсовая работа посвящена иррациональным уравнениям, методам их решения. Кроме того, в работе введены понятия уравнений следствий и равносильных уравнений, а также приведены примеры задач, математическими моделями которых служат иррациональные уравнения. В данной работе содержится небольшая историческая справка, посвященная введению иррациональных чисел.
1. ИЗ ИСТОРИИ
Термин «рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.
Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих «Началах» Евклид излагает учение об иррациональностях чисто геометрически.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос» – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: «Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.»
Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.
Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли «арифметикой астрономов». По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе «Ключ арифметики» ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих «приложениях к алгебре» (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление «Геометрии» Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.
В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.
2. ОПРЕДЕЛЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Равносильные уравнения. Следствия уравнений.
При решении уравнений выполняются различные тождественные преобразования над выражениями, входящими в уравнение. При этом исходное уравнение изменяется другими, имеющими те же корни. Такие уравнения называются равносильными.
Определение: Уравнение f(x)=g(x) равносильно уравнению f1(x)=g1(x), если каждый корень первого уравнения является корнем второго и обратно, каждый корень второго уравнения является корнем первого, т.е. их решения совпадают.
Например, уравнения 3x-6=0; 2х–1=3 равносильны, т.к. каждое из уравнений имеет один корень х=2.
Любые два уравнения, имеющие пустое множество корней, считают равносильными.
 Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:
Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:
 |
В процессе решения уравнений важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.
Теорема 1: Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.
Доказательство: Докажем, что уравнение f(x) = g(x)+q(x) (1) равносильно уравнению
f(x) – q(x) = g(x) (2)
Пусть х=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a) . Но тогда по свойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее, что а – корень уравнения (2). Аналогично доказывается, что каждый корень уравнения (2) является и корнем уравнения (1).
Что и требовалось доказатью.
Теорема 2: Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.
Доказательство: докажем, что уравнение 6х–3=0 равносильно уравнению 2х–1=0
решим уравнение 6х–3=0 и уравнение 2х–1=0
6х=3 2х=1
х=0,5 х=0,5
так как корни уравнений равны, то уравнения равносильны.
Что и требовалось доказать.
Рассмотрим уравнение
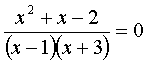 |
ОДЗ этого уравнения {х ≠ 1, х ≠ -3}
Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находим корни х1=1, х2 = –2 . Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один корень х=-2.
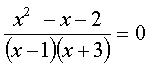 В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения
В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения
пусть даны два уравнения:
f1 (x) = g1 (x) (3)
f2 (x) = g2 (x) (4)
Если каждый корень уравнения (3) является корнем уравнения (4), то уравнение (4) называют следствием уравнения (3).
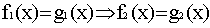 Этот факт записывают так:
Этот факт записывают так:
В том случае, когда уравнение (3) - есть также следствие уравнения (4), эти уравнения равносильны.
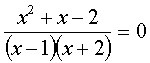 Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.
Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.
В приведенном выше примере уравнение – следствие х²+х–2=0, имеет два корня x1=1 и х2 =-2, а исходное уравнение имеет один корень х=-2. В этом случае корень х=1 называют посторонним для исходного уравнения
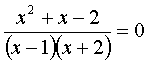
В общем случае корни уравнения-следствия, не являющиеся корнями исходного уравнения, называют посторонними.
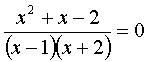 Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения и потому отброшен.
Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения и потому отброшен.
 Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
ОДЗ которого {х ¹-2},
 получим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.
получим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.
В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней.
Например, уравнение (х+1)(х+3)= х+1 (5)
Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .
Если же обе части уравнения (5) разделить («сократить») на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля.
Для того, чтобы в процессе решения уравнения избежать потери корней, необходимо следить за тем, чтобы переход осуществлялся либо к равносильным уравнениям, либо к уравнениям-следствиям.
2.2. Определение иррациональных уравнений.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Например:
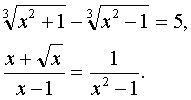 3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.
3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.
3.1. Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень.
Пример №1
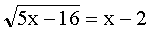
 |
 |
далее последовательно имеем:
5х – 16 = х² - 4х + 4
х² - 4х + 4 – 5х + 16 = 0
х² - 9х + 20 = 0
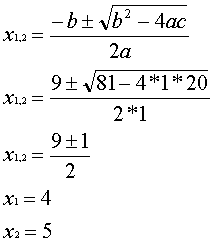
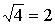
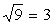 Проверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
Проверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
значения – корни уравнения.
Ответ: 4; 5.
Пример №2
Решить уравнение:
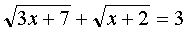
(2)
Решение:
Преобразуем уравнение к виду:
 и применим метод возведения в квадрат:
и применим метод возведения в квадрат:
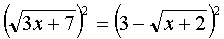
далее последовательно получаем.
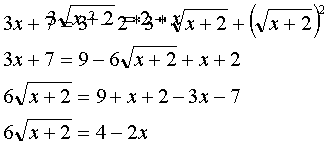
Разделим обе части последнего уравнения почленно на 2:
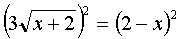 еще раз применим метод возведения в квадрат:
еще раз применим метод возведения в квадрат:
далее находим:
9(х+2)=4–4х+х²
9х+18–4+4х-х²=0
-х²+13х+14=0
х²-13х–14=0
х1+х2 =13 х1 =19
х1 х2 = -14 х2 = -1
по теореме, обратной теореме Виета, х1=14, х2 = -1
корни уравнения х²-13х–14 =0
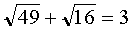
Проверка: подставив значение х=-14 в уравнение (2), получим–
- не верное равенство. Поэтому х = -14 – не корень уравнения (2).
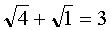 Подставив значение x=-1 в уравнение (2), получим-
Подставив значение x=-1 в уравнение (2), получим-
- верное равенство. Поэтому x=-1- корень уравнения (2).
Ответ: -1
3.2 Метод введения новых переменных.
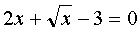
Решить уравнение
Решение:
Конечно, можно решить это уравнение методом возведения обеих частей уравнения в одну и ту же степень. Но можно решить и другим способом – методом введения новых переменных.
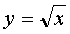
Введем новую переменную Тогда получим 2y²+y–3=0 – квадратное уравнение относительно переменной y. Найдем его корни:

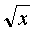
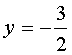
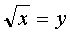
Т.к. , то – не корень уравнения, т.к. не
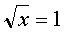
может быть отрицательным числом . А - верное равенство, значит x=1- корень уравнения.
Ответ: 1.
Искусственные приёмы решения иррациональных уравнений.
Решить уравнение:
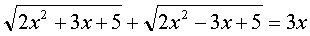
(1)
Решение:
Умножим обе части заданного уравнения на выражение

сопряжённое выражению

Так как
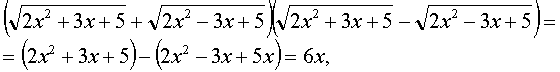
 То уравнение (1) примет вид:
То уравнение (1) примет вид:
Или
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение:
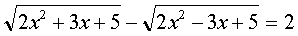
(2)
Сложив уравнения (1) и (2), придём к уравнению
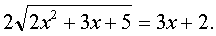
(3)
Решая уравнение (3) методом возведения в квадрат, получим:

Проверка:
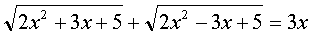
x1=0, x2=4, x3= -4 подставим в уравнение

1)
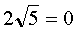
- не верное равенство, значит x1=0- не корень уравнения.
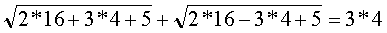 2)
2)
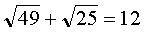
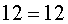 - верное равенство, значит x2=4- корень уравнения.
- верное равенство, значит x2=4- корень уравнения.
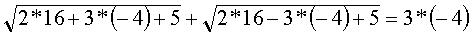
3)


- не верное равенство, значит x3= -4- не корень уравнения.
Ответ: 4.
ЗАКЛЮЧЕНИЕ
Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат (или n-ую степень) или введением новой переменной. Кроме того, пользуются и искусственными приемами решения иррациональных уравнений.
Список литературы
1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений - Москва: Издательство «Мнемозина», 1999.
2) М.Я.Выгодский. Справочник по элементарной математике - Москва: Издательство «Наука», 1986.
3) А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство «Педагогика», 1989.
4) А.И.Макушевич. Детская энциклопедия – Москва: Издательство «Педагогика», 1972.
5) Н.Я.Виленкин. Алгебра для 9 класс. Учебное пособие для учащихся школ и классов с углубленным изучением изучением математики – Москва: Издательство «Просвещение», 1998.
Для подготовки данной работы были использованы материалы с сайта http://www.ed.vseved.ru/
Дата добавления: 22.03.2003
www.km.ru
ВВЕДЕНИЕ
Вшкольном курсе алгебры рассматриваются различные виды уравнений – линейные,квадратные, биквадратные, кубические, рациональные, с параметрами,иррациональные и другие. Данная курсовая работа посвящена иррациональнымуравнениям, методам их решения. Кроме того, в работе введены понятия уравненийследствий и равносильных уравнений, а также приведены примеры задач,математическими моделями которых служат иррациональные уравнения. В данной работесодержится небольшая историческая справка, посвященная введению иррациональныхчисел.
1. ИЗ ИСТОРИИ
Термин«рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводомгреческого слова “логос”в отличие от рациональных чисел, числа, выражающиеотношение несоизмеримых величин, были названы еще в древности иррациональными,т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины“рациональный” и “иррациональный” относились не к числам, а к соизмеримым исоответственно не соизмеримым величинам, которые пифагорейцы называливыразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными.В V-VI вв.римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.
Древнегреческиематематики классической эпохи пользовались только рациональными числами(вернее целыми, дробными и положительными). В своих «Началах» Евклид излагаетучение об иррациональностях чисто геометрически.
МатематикиИндии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию иастрономию, не могли обойтись без иррациональных величин, которые, однако,длительное время не признавали за числа. Греки называли иррациональнуювеличину, например, корень из квадратного числа, «алогос» – невыразимоесловами, а позже европейские переводчики с арабского на латынь перевели этослово латинским словом surdus – глухой.В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известногопереводчика математических прозведений с арабского на латынь, затем уитальянского математика Леонардо Фабоначчи и других европейских математиков,вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математикРафаэль Бомбелли и нидерландский математик Симон Стевин считали понятиеиррационального числа равноправным с понятием рационального числа. Стевинписал: «Мы приходим к выводу, что не существует никаких абсурдных,иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чиселсуществует такое совершенство и согласие, что нам надо размышлять дни и ночинад их удивительной закономерностью.»
Ещедо Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудахупотребляли иррациональные числа как полноправные объекты алгебры. Более того,комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, ОмарХайям уже в начале XII в. теоретически расширяет понятие числа доположительного действительного числа. В том же направлении много было сделанокрупнейшим математиком XIII в. ат-Туси.
Математикии астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилонаи эллинистической эпохи широко пользовались шестидесятеричными дробями,арифметические действия с которыми они называли «арифметикой астрономов». Поаналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе «Ключ арифметики»ввел десятичные дроби которыми он пользовался для повышения точности извлечениякорней. Независимо от него по такому же пути шел открывший в 1585 г. десятичныедроби в Европе Симон Стевин, который в своих «приложениях к алгебре» (1594 г.)показал, что десятичные дроби можно использовать для бесконечно близкогоприближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррациональногочисла являются десятичные дроби. Появление «Геометрии» Декарта облегчилопонимание связи между измерением любых отрезков (и геометрических величинвообще) и необходимости расширения понятия рационального числа. На числовойоси иррациональные числа, как и рациональные, изображаются точками. Этогеометрическое толкование позволило лучше понять природу иррациональных чисел испособствовало их признанию.
В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и онеограниченном приближении к искомому числу с помощью бесконечных десятичныхдробей. Однако обоснованием свойств действительных чисел и полная теория ихбыла разработана лишь в XIX в.
2. ОПРЕДЕЛЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Равносильныеуравнения. Следствия уравнений.
Прирешении уравнений выполняются различные тождественные преобразования надвыражениями, входящими в уравнение. При этом исходное уравнение изменяетсядругими, имеющими те же корни. Такие уравнения называются равносильными.
Определение:Уравнение f(x)=g(x) равносильноуравнению f1(x)=g1(x), если каждый корень первого уравнения является корнем второго иобратно, каждый корень второго уравнения является корнем первого, т.е. ихрешения совпадают.
Например,уравнения 3x-6=0; 2х–1=3 равносильны, т.к. каждое изуравнений имеет один корень х=2.
Любыедва уравнения, имеющие пустое множество корней, считают равносильными.
/> Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны,обозначают так:
/> /> f(x)=g(x) f1(x)=g1(x)Впроцессе решения уравнений важно знать, при каких преобразованиях данноеуравнение переходит в равносильное ему уравнение.
Теорема1: Если какое-либо слагаемое перенести из одной части уравнения в другую,изменив его знак, то получим уравнение, равносильное данному.
Доказательство: Докажем, что уравнение f(x) = g(x)+q(x) (1) равносильно уравнению
f(x) – q(x) =g(x) (2)
Пустьх=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a). Но тогда посвойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее,что а – корень уравнения (2). Аналогично доказывается, что каждый кореньуравнения (2) является и корнем уравнения (1).
Чтои требовалось доказатью.
Теорема2: Если обе части уравнения умножить или разделить на отличное от нуля число,то получим уравнение, равносильное данному.
Доказательство:докажем, что уравнение 6х–3=0 равносильно уравнению 2х–1=0
решимуравнение 6х–3=0 и уравнение 2х–1=0
6х=3 2х=1
х=0,5 х=0,5
таккак корни уравнений равны, то уравнения равносильны.
Чтои требовалось доказать.
Рассмотримуравнение
/>
ОДЗэтого уравнения {х ≠ 1, х ≠ -3}
Мызнаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е.х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находимкорни х1=1, х2 = –2. Но число 1 не входит в ОДЗ данного уравнения и значит,исходное уравнение имеет один корень х=-2.
/> В этом случае говорят, чтоуравнение х²+х–2=0, есть следствие уравнения
пустьданы два уравнения:
f1 (x) = g1 (x) (3)
f2 (x) = g2 (x) (4)
Есликаждый корень уравнения (3) является корнем уравнения (4), то уравнение (4)называют следствием уравнения (3).
/> Этот факт записывают так:
Втом случае, когда уравнение (3) — есть также следствие уравнения (4), этиуравнения равносильны.
/> Два уравнения равносильны в том,и только в том случае, когда каждое из них является следствием другого.
Вприведенном выше примере уравнение – следствие х²+х–2=0, имеет два корня x1=1 и х2 =-2, аисходное уравнение имеет один корень х=-2. В этом случае корень х=1 называютпосторонним для исходного уравнения
/>
Вобщем случае корни уравнения-следствия, не являющиеся корнями исходногоуравнения, называют посторонними.
/> Итак, если при решении уравненияпроисходит переход к уравнению – следствию, то могли появиться посторонниекорни. В этом случае все корни уравнения-следствия нужно проверить, подставляяих в исходное уравнение. В некоторых случаях выявление посторонних корнейоблегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ,можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 невходит в ОДЗ уравнения и потому отброшен.
/> Иногда посторонние корни могутпоявиться и при тождественных преобразованиях, если они приводят к изменениюОДЗ уравнения. Например, после приведения подобных членов в левой частиуравнения
ОДЗкоторого {х ¹-2},
/> получим уравнение следствиех²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний,так как не входит в ОДЗ исходного уравнения.
Втех случаях, когда в результате преобразований произошел переход от исходногоуравнения к уравнению, не являющемуся его следствием, возможна потеря корней.
Например,уравнение (х+1)(х+3)= х+1 (5)
Имеетдва корня. Действительно, перенося все члены уравнения в левую часть и выносях+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .
Еслиже обе части уравнения (5) разделить («сократить») на х+1, то получим уравнениех+3=1, имеющее один корень х=-2. В результате такого преобразования кореньх=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащеепеременную, можно лишь в том случае, когда это выражение отлично от нуля.
Длятого, чтобы в процессе решения уравнения избежать потери корней, необходимоследить за тем, чтобы переход осуществлялся либо к равносильным уравнениям, либок уравнениям-следствиям.
2.2. Определение иррациональных уравнений.
Иррациональныминазываются уравнения, в которых переменная содержится под знаком корня или подзнаком операции возведения в дробную степень.
Например:
/>3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХУРАВНЕНИЙ.
3.1.Решение иррациональных уравнений методом возведения обеих частей уравнения водну и ту же степень.
Пример№1
/>
/> /> Решить уравнение /> /> Возведем обе части уравнения (1) вквадрат:далеепоследовательно имеем:
5х– 16 = х² — 4х + 4
х²- 4х + 4 – 5х + 16 = 0
х²- 9х + 20 = 0
/> />/>Проверка: Подставив х=5 в уравнение (1),получим – верное равенство. Подставив х= 4 в уравнение (1),получим – верное равенство. Значит оба найденных
значения– корни уравнения.
Ответ:4; 5.
Пример№2
Решитьуравнение:
/>
(2)
Решение:
Преобразуемуравнение к виду:
/> и применим метод возведения в квадрат:
/>
далеепоследовательно получаем.
/>
Разделимобе части последнего уравнения почленно на 2:
/> еще раз применим метод возведения вквадрат:
далеенаходим:
9(х+2)=4–4х+х²
9х+18–4+4х-х²=0
-х²+13х+14=0
х²-13х–14=0
х1+х2=13 х1 =19
х1х2 = -14 х2 = -1
потеореме, обратной теореме Виета, х1=14, х2 = -1
корниуравнения х²-13х–14 =0
/>
Проверка:подставив значение х=-14 в уравнение (2), получим–
— не верное равенство. Поэтому х = -14 – не корень уравнения (2).
/> Подставив значение x=-1 в уравнение (2), получим-
— верное равенство. Поэтому x=-1- кореньуравнения (2).
Ответ:-1
3.2 Метод введения новых переменных.
/>
Решитьуравнение
Решение:
Конечно,можно решить это уравнение методом возведения обеих частей уравнения в одну иту же степень. Но можно решить и другим способом – методом введения новыхпеременных.
/>
Введемновую переменную Тогда получим 2y²+y–3=0 – квадратное уравнение относительно переменной y. Найдем его корни:
/>
/>/>/>
Т.к. , то – не корень уравнения, т.к. не
/>
можетбыть отрицательным числом. А - верное равенство, значит x=1- корень уравнения.
Ответ:1.
Искусственныеприёмы решения иррациональных уравнений.
Решитьуравнение:
/>
(1)
Решение:
Умножим обе части заданного уравнения на выражение
/>
сопряжённоевыражению
/>
Таккак
/>
/>То уравнение (1) примет вид:
Или
Произведениеравно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, адругой при этом известен. Тогда x1=0.Остаётсярешить уравнение:
/>
(2)
Сложивуравнения (1) и (2), придём к уравнению
/>
(3)
Решаяуравнение (3) методом возведения в квадрат, получим:
/>
Проверка:
/>
x1=0, x2=4, x3= -4 подставимв уравнение
/>
1)
/>
- не верное равенство, значит x1=0- некорень уравнения.
/>2)
/>
/> — верное равенство, значит x2=4- корень уравнения.
/>
3)
/>
/>
- не верное равенство, значит x3= -4- некорень уравнения.
Ответ: 4.
ЗАКЛЮЧЕНИЕ
Итак,уравнения, которые содержат переменную под знаком корня, называютсяиррациональными. Иррациональные уравнения решаются в основном возведением обеихчастей уравнения в квадрат (или n-ую степень)или введением новой переменной. Кроме того, пользуются и искусственнымиприемами решения иррациональных уравнений.
Список литературы
1)А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений — Москва: Издательство «Мнемозина», 1999.
2)М.Я.Выгодский. Справочник по элементарной математике — Москва: Издательство«Наука», 1986.
3)А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство«Педагогика», 1989.
4)А.И.Макушевич. Детская энциклопедия – Москва: Издательство «Педагогика», 1972.
5)Н.Я.Виленкин. Алгебра для 9 класс. Учебное пособие для учащихся школ и классовс углубленным изучением изучением математики – Москва: Издательство «Просвещение»,1998.
Дляподготовки данной работы были использованы материалы с сайта www.ed.vseved.ru/
www.ronl.ru
.
Реферат выполнен Верхошанской Светланой Александровной, ученицей 9”Г” класса.
МОУ “Ульканская средняя общеобразовательная школа №2”.
Улькан
2005
Историческая справка об иррациональных уравнениях.
“Источником алгебраических иррациональностей является двузначность или многозначность задачи; ибо было бы невозможно выразить одним и тем же вычислением многие значения, удовлетворяющие одной и той же задаче, иначе, чем при помощи корней…; они же разве только в частных случаях могут быть сведены к рациональностям”.
(Лейбниц Г.)
Одной из конкретных причин появления математических теорий явилось открытие иррациональностей. Вначале это произошло в пределах геометрических изысканий в виде установления факта несоизмеримости двух отрезков прямой. Значение этого открытия в математике трудно переоценить. В математику, едва ли не впервые, вошла сложная теоретическая абстракция, не имеющая аналога в донаучном общечеловеческом опыте. Вероятно, самой первой иррациональностью, открытой древнегреческими математиками, было число . Можно с определённой уверенностью считать, что исходным пунктом этого открытия были попытки найти общую меру с помощью алгоритма попеременного вычитания, известного сейчас как алгоритм Евклида. Возможно также, что некоторую роль сыграла задача математической теории музыки: деление октава, приводящее к пропорции 1:п=п:2. Не последнюю роль сыграл и характерный для пифагорейской школы общий интерес к теоретико-числовым проблемам.
. Можно с определённой уверенностью считать, что исходным пунктом этого открытия были попытки найти общую меру с помощью алгоритма попеременного вычитания, известного сейчас как алгоритм Евклида. Возможно также, что некоторую роль сыграла задача математической теории музыки: деление октава, приводящее к пропорции 1:п=п:2. Не последнюю роль сыграл и характерный для пифагорейской школы общий интерес к теоретико-числовым проблемам.
Древние математики нашли довольно быстро логически строгое доказательство иррациональности числа путём сведения этого доказательства к формальному противоречию. Пусть
путём сведения этого доказательства к формальному противоречию. Пусть , где m и n – взаимно простые числа. Тогда m2=2n2, откуда следует, что т2 чётное и, следовательно, п2 чётное. Чётно, следовательно и п. Получающееся противоречие (п не может быть одновременно и чётным и нечётным) указывает на неверность посылки, что число
, где m и n – взаимно простые числа. Тогда m2=2n2, откуда следует, что т2 чётное и, следовательно, п2 чётное. Чётно, следовательно и п. Получающееся противоречие (п не может быть одновременно и чётным и нечётным) указывает на неверность посылки, что число рационально.
рационально.
Для исследования вновь открываемых квадратичных иррациональностей сразу же оказалось необходимым разрабатывать теорию делимости чисел. В самом деле, пусть , где p и g - взаимно просты, а п является произведением только первых степеней сомножителей отсюда р2=пg2. Если t – простой делитель п, то р2 (а значит, и р) делится на t. Следовательно, р2 делится на t2. Но в п содержится только первая степень t. Значит g2 (равно как и g) делится на t. Но этот результат формально противоречит предположению, что р и g взаимно просты.
, где p и g - взаимно просты, а п является произведением только первых степеней сомножителей отсюда р2=пg2. Если t – простой делитель п, то р2 (а значит, и р) делится на t. Следовательно, р2 делится на t2. Но в п содержится только первая степень t. Значит g2 (равно как и g) делится на t. Но этот результат формально противоречит предположению, что р и g взаимно просты.
Вслед за иррациональностью числа были открыты многие другие иррациональности. Так, Архит (около 428-365 до н.э.) доказал иррациональность чисел вида
были открыты многие другие иррациональности. Так, Архит (около 428-365 до н.э.) доказал иррациональность чисел вида . Теодор из Кирены (V в. до н.э.) установил иррациональность квадратного корня из чисел 3,5,6,…,17, которые не являются полным квадратом. Теэтет (410-369 до н.э.) дал одну из первых классификаций иррациональностей.
. Теодор из Кирены (V в. до н.э.) установил иррациональность квадратного корня из чисел 3,5,6,…,17, которые не являются полным квадратом. Теэтет (410-369 до н.э.) дал одну из первых классификаций иррациональностей.
С появлением иррациональностей в древнегреческой математике возникли серьёзные трудности как в теоретико-числовом, так и в геометрическом плане.
Решение иррациональных уравнений.
Уравнения, в которых под знаком корня содержится переменная, называют иррациональными. Таково, например, уравнение .
.
При решении иррациональных уравнений полученные решения требуют проверки, потому, например, что неверное равенство при возведении в квадрат может дать верное равенство. В самом деле, неверное равенство при возведении в квадрат даёт верное равенство 12= (-1)2, 1=1.
при возведении в квадрат даёт верное равенство 12= (-1)2, 1=1.
Иногда удобнее решать иррациональные уравнения, используя равносильные переходы.
Пример 1. Решим уравнение .
.
Возведём обе части этого уравнения в квадрат и получим , откуда следует, что
, откуда следует, что , т.е.
, т.е. .
.
Проверим, что полученные числа являются решениями уравнения. Действительно, при подстановке их в данное уравнение получаются верные равенства:
 и
и
Следовательно, x=3 или x=-3 – решение данного уравнения.
Пример 2. Решим уравнение .
.
Возведя в квадрат обе части уравнения, получим . После преобразований приходим к квадратному уравнению
. После преобразований приходим к квадратному уравнению , корни которого
, корни которого и
и .
.
Проверим, являются ли найденные числа решениями данного уравнения. При подстановке в него числа 4 получим верное равенство , т.е. 4 - решение данного уравнения. При подстановке же числа 1 получаем в правой части -1, а в левой части число 1. Следовательно, 1 не является решением уравнения; говорят, что это посторонний корень, полученный в результате принятого способа решения.
, т.е. 4 - решение данного уравнения. При подстановке же числа 1 получаем в правой части -1, а в левой части число 1. Следовательно, 1 не является решением уравнения; говорят, что это посторонний корень, полученный в результате принятого способа решения.
Ответ: .
.
Пример 3. Решим уравнение .
.
Возведём обе части этого уравнения в квадрат: , откуда получаем уравнение
, откуда получаем уравнение , корни которого
, корни которого и
и . Сразу ясно, что число -1 не является корнем данного уравнения, т.к. обе части его не определены при
. Сразу ясно, что число -1 не является корнем данного уравнения, т.к. обе части его не определены при . При подстановке в уравнение числа 2 получаем верное равенство
. При подстановке в уравнение числа 2 получаем верное равенство , следовательно, решением данного уравнения является только число 2.
, следовательно, решением данного уравнения является только число 2.
Пример 4. Решим уравнение .
.
Возведя в квадрат обе части этого уравнения, получаем ,
, ,
, . Подстановкой убеждаемся, что число 5 не является корнем данного уравнения. Поэтому уравнение не имеет решений.
. Подстановкой убеждаемся, что число 5 не является корнем данного уравнения. Поэтому уравнение не имеет решений.
Пример 5. Решим уравнение .
.
По определению - это такое неотрицательное число, квадрат которого равен подкоренному выражению. Другими словами, уравнение
- это такое неотрицательное число, квадрат которого равен подкоренному выражению. Другими словами, уравнение равносильно системе:
равносильно системе:



Решая первое уравнение системы, равносильное уравнению , получим корни 11 и 6, но условие
, получим корни 11 и 6, но условие выполняется только для
выполняется только для . Поэтому данное уравнение имеет один корень
. Поэтому данное уравнение имеет один корень .
.
Пример 6. Решим уравнение .
.
В отличие от рассмотренных ранее примеров данное иррациональное уравнение содержит не квадратный корень, а корень третьей степени. Поэтому для того, чтобы “избавиться от радикала”, надо возвести обе части уравнения не в квадрат, а в куб: . После преобразований получаем:
. После преобразований получаем:

Итак, ,
, .
.
Пример 7. Решим систему уравнений:

 Положив
Положив и
и , приходим к системе
, приходим к системе

 Разложим левую часть второго уравнения на множители:
Разложим левую часть второго уравнения на множители: - и подставим в него из первого уравнения
- и подставим в него из первого уравнения . Тогда получим систему, равносильную второй:
. Тогда получим систему, равносильную второй:

 Подставляя во второе уравнение значение v, найденное из первого
Подставляя во второе уравнение значение v, найденное из первого , приходим к уравнению
, приходим к уравнению , т.е.
, т.е. .
.
Полученное квадратное уравнение имеет два корня: и
и .
.
Соответствующие значения v таковы: и
и . Переходя к переменным х и у, получаем:
. Переходя к переменным х и у, получаем: , т.е.
, т.е. ,
, ,
, ,
, .
.
Преобразование иррациональных выражений.
Если знаменатель дроби содержит иррациональное выражение, то часто целесообразно избавиться от последнего.
Рассмотрим некоторые типичные случаи:

Пример:

При непосредственном возведении в квадрат обеих частей уравнения уравнение должно быть сначала преобразовано так, чтобы в одной части стояли только радикалы, а в другой – остальные члены исходного уравнения. Так поступают, если радикалов в уравнении два. Если же их три, то два из них оставляют в одной части уравнения, а третий переносят в другую. Затем обе части уравнения возводят в квадрат и проводятся необходимые преобразования (приведение подобных и т.п.). Далее все члены уравнения, не содержащие радикалов, снова переносятся в одну сторону уравнения, а оставшийся радикал (теперь он будет только один!) – в другую. Полученное уравнение вновь возводят в квадрат, и в итоге получается уравнение, не содержащее радикалов.
Пример. Введение новой переменной:
 .
.
Решение: Обозначим , тогда
, тогда

Уравнение примет вид:

Возведём его в квадрат:

Это уравнение так же возводим в квадрат:



Проверка: полученные значения t мы должны проверить в уравнении (1), так как именно оно возводилось в квадрат. Проверка показывает, что - посторонний корень, а
- посторонний корень, а - действительно корень уравнения (1). Отсюда получим:
- действительно корень уравнения (1). Отсюда получим:



Ответ: 0;-1.
Уравнения с радикалом третьей степени.
При решении уравнений, содержащих радикалы 3-й степени, бывает полезно пользоваться сложением тождествами:

Пример 1.
 .
.
Возведём обе части этого уравнения в 3-ю степень и воспользуемся выше приведённым тождеством:

Заметим, что выражение стоящее в скобках равно 1, что следует из первоначального уравнения. Учитывая это и приводя подобные члены, получим:

Раскроем скобки, приведём подобные члены и решим квадратное уравнение. Его корни и
и . Если считать (по определению), что корень нечётной степени можно извлекать и из отрицательных чисел, то оба полученных числа являются решениями исходного уравнения.
. Если считать (по определению), что корень нечётной степени можно извлекать и из отрицательных чисел, то оба полученных числа являются решениями исходного уравнения.
Ответ: .
.
Решение 2
Возведём две новые переменные и
и , тогда
, тогда ,
,
 .
.
Заметим, что .
.
В итоге получим систему уравнений:





Используя первоначальные уравнения системы, преобразуем вторые, заменив первую скобку единицей, а вторую подставим вместо неизвестного у выражение , также полученное из первого
, также полученное из первого .
.
Приведём подобные члены, раскрыв предварительно скобки и решив полученное квадратное уравнение. Его корни и
и . Вернёмся теперь к начальной подстановке и получим искомые решения:
. Вернёмся теперь к начальной подстановке и получим искомые решения:

Введение нового неизвестного.
Решив эти уравнения, найдём радикалы более высоких степеней, но наиболее часто использовавшийся способ их решения – введение нового(новых) неизвестного.
Пример 2.

Обозначим , тогда
, тогда
а)
Уравнение примет вид:

Корень не удовлетворяет условию
не удовлетворяет условию
Ответ: 76.
Методы решения иррациональных уравнений.
Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо является его следствием. Поэтому существуют два пути при решении иррациональных уравнений:
1) переход к выводным уравнениям (следствиям) с последующей проверкой корней;
2) переход к равносильным системам.
Второй подход избавляет от подстановки полученных корней в исходное уравнение (иногда такую проверку осуществить нелегко) и, вообще говоря, является более предпочтительным. Однако если в ходе решения оказалось, что проверка полученных корней не представляет труда, то можно не выяснять источники появления посторонних корней и не переходить к равносильным системам.
Пример 1.

Возведём в 6 степень:

Проверка:
 , т.е.
, т.е. - верное равенство.
- верное равенство.
Ответ: 67.
Пример 2.

Преобразуем уравнение к виду:
 и возведём обе части в квадрат:
и возведём обе части в квадрат:

 , т.е.
, т.е.


Ещё раз возведём обе части в квадрат:
 , т.е.
, т.е. ,
, .
.
Проверка:
1) При

2)
Ответ: .
.
Пример 3.

Положим . Тогда
. Тогда и мы получаем уравнение
и мы получаем уравнение , откуда
, откуда ,
, .
.
Теперь задача свелась к решению двух уравнений:
 ;
; . Возводя обе части уравнения
. Возводя обе части уравнения в 5-ю степень, получим
в 5-ю степень, получим , откуда
, откуда .
.
Уравнение - не имеет корней, поскольку под знаком возведения в дробную степень может содержаться неотрицательное число, а любая степень неотрицательного числа неотрицательна.
- не имеет корней, поскольку под знаком возведения в дробную степень может содержаться неотрицательное число, а любая степень неотрицательного числа неотрицательна.
Ответ: 34.
Список литературы
1) Справочник по математике. В.А. Гусев, А.Г. Мордкович.: 1986г.
2) Углублённое изучение курса алгебры и математического анализа. М.Л. Галицкий, М.М. Мошкович, С.И. Шварцабурд.: 1992г.
3) Возникновение и развитие математической науки. К.А. Рыбников.: 1987г.
4) Ученикам о математике. М.К. Гриненко.: 1993г.
superbotanik.net