Студента группы ИУ 3-32
Кондратова Николая
Рис. 1
(1)
где индекс F у знака интеграла указывает на то, что интегрирование ведется по всей площади сечения. Каждый из интегралов представляет собой сумму произведений, элементарных площадок dF на расстояние до соответствующей оси (х или у). Первый интеграл называется статическим моментом сечения относительно оси х, а второй — относительно оси у. Размерность статического момента см3. При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей, x1, y1 и x2, y2.Пусть расстояние между осями x1 и x2 равно b, а между осями y2 и y2 равно а (рис. 2). Положим, что площадь сечения F и статические моменты относительно осей x1 и y1, т. е. Sx1, и Sy1 заданы. Требуется определить Sx2 и Sy2.
Очевидно, х2 = x1 — а, y2 = y1 — b. Искомые статические моменты будут равны
или
Таким образом, при параллельном переносе осей статический момент меняется на величину, равную произведению площади F на расстояние между осями.
Рассмотрим более детально, например, первое из полученных выражений:
Величина b может быть любой: как положительной, так и отрицательной. Поэтому ее всегда можно подобрать (причем единственным образом) так, чтобы произведение bF было равно Sx1.Тогда статический момент Sx2, относительно оси x2 обращается в нуль.
Ось, относительно которой статический момент равен нулю, называется центральной. Среди семейства параллельных осей она является единственной, и расстояние до этой оси от некоторой, произвольно взятой, оси х1 равноРис. 2
Аналогично для другого семейства параллельных осей
Точка пересечения центральных осей называется центром тяжести сечения. Путем поворота осей можно показать, что статический момент относительно любой оси, проходящей через центр тяжести, равен нулю.
Нетрудно установить тождественность данного определения и обычного определения центра тяжести как точки приложения равнодействующих сил веса. Если уподобить рассмотренное сечение однородной пластинке, то сила веса пластинки во всех точках будет пропорциональна элементарной площади dF, а момент сил веса относительно некоторой оси — пропорционален статическому моменту. Этот момент сил веса относительно оси, проходящей через центр тяжести, равен нулю. В нуль обращается, следовательно, и статический момент относительно центральной оси.
В дополнение к статическим моментам рассмотрим еще три следующих интеграла:
(2)Через х и у обозначены текущие координаты элементарной площадки dF в произвольно взятой системе координат х, y. Первые два интеграла называются осевыми моментами инерции сечения относительно осей х и y соответственно. Третий интеграл называется центробежным моментом инерции сечения относительно осей х, у. Размерность моментов инерции см4.
Осевые моменты инерции всегда положительны, поскольку положительной считается площадь dF. Центробежный момент инерции может быть как положительным, так и отрицательным, в зависимости от расположения сечения относительно осей х, у.
Выведем формулы преобразования моментов инерции при параллельном переносе осей. Будем считать, что нам заданы моменты инерции и статические моменты относительно осей х1 и y1. Требуется определить моменты инерции относительно осей x2 и y2
(3)Подставляя сюда х2 = x1 — а и y2 = y1 — b и раскрывая скобки (согласно (1) и (2)) находим
Если оси x1 и y1 — центральные, то Sx1 = Sy1 = 0. Тогда
(4)
Следовательно, при параллельном переносе осей (если одна из осей — центральная) осевые моменты инерции меняются на величину, равную произведению площади на квадрат расстояния между осями.
Из первых двух формул (4) следует, что в семействе параллельных осей минимальный момент инерции получается относительно центральной оси (а = 0 или Ь = 0). Поэтому легко запомнить, что при переходе от центральных осей к нецентральным осевые моменты инерции увеличиваются и величины a2F и b2F следует к моментам инерции прибавлять, а при переходе от нецентральных осей к центральным — вычитать.
При определении центробежного момента инерции по формулам (4) следует учитывать знак величин а и b. Можно, однако, и сразу установить, в какую сторону меняется величина Jxy при параллельном переносе осей. Для этого следует иметь в виду, что часть площади, находящаяся в I и III квадрантах системы координат x1y1, дает положительное значение центробежного момента, а части, находящиеся в II и IV квадрантах, дают отрицательные значения. Поэтому при переносе осей проще всего устанавливать знак слагаемого abF в соответствии с тем, какие из четырех слагаемых площадей увеличиваются и какие — уменьшаются.
ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
Рис. 3
Посмотрим, как изменяются моменты инерции при повороте осей координат. Положим, даны моменты инерции некоторого сечения относительно осей х, у (не обязательно центральных). Требуется определить Ju, Jv, Juv — моменты инерции относительно осей и, v, повернутых относительно первой системы на угол (рис. 3).
Проектируем замкнутый четырехугольник ОАВСО на оси и и v. Так как проекция ломаной линии равна проекции замыкающей, находим:
u = y sin +x cos , v = y cos — x sin
В выражениях (3), подставив вместо x1 и y1 соответственно u и v, исключаем u и vоткуда
(5)
Рассмотрим два первых уравнения. Складывая их почленно, получим, что сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. При этомx2 + y2 = 2где — расстояние от начала координат до элементарной площадки (рис. 3). Таким образом,
Jx + Jy = Jpгде Jp— полярный момент инерции
величина которого, естественно, не зависит от поворота осей ху.
С изменением угла поворота осей каждая из величин Ju и Jv меняется, а сумма их остается неизменной. Следовательно, существует такое , при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение.
Дифференцируя выражение Ju (5) по и приравнивая производную нулю, находим
(6)
При этом значении угла один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции Juv при указанном угле обращается в нуль, что легко устанавливается из третьей формулы (5).
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Если они к тому же являются центральными, то тогда они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Для определения этого первые две формулы (5) перепишем в виде
Далее исключаем при помощи выражения (6) угол . Тогда
Верхний знак соответствует максимальному моменту инерции, а нижний — минимальному. После того как сечение вычерчено в масштабе и на чертеже показано положение главных осей, нетрудно установить, которой из двух осей соответствует максимальный и которой — минимальный момент инерции.
Если сечение имеет ось симметрии, то эта ось всегда будет главной .Центробежный момент инерции части сечения, расположенной по одну сторону от оси, будет равен моменту части, расположенной по другую сторону, но противоположен ему по знаку. Следовательно, Jху= 0 и оси х и у являются главными.
bukvasha.ru
Как уже отмечалось в главе 1, основным объектом, изучаемым в сопротивлении материалов, является стержень. Сопротивление стержня различным видам деформации зависит от материала и размеров – очертания и длины оси, формы поперечных сечений. При растяжении прямого бруса геометрической характеристикой поперечного сечения была его площадь (см. главу 2). В настоящей главе рассмотрим основные геометрические характеристики поперечных сечений стержня, определяющие сопротивление различным видам деформаций.
Определение положения центра тяжести
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями Oz и Oy (рис. 4.1). Выделим элемент площади dF с координатами z, y.
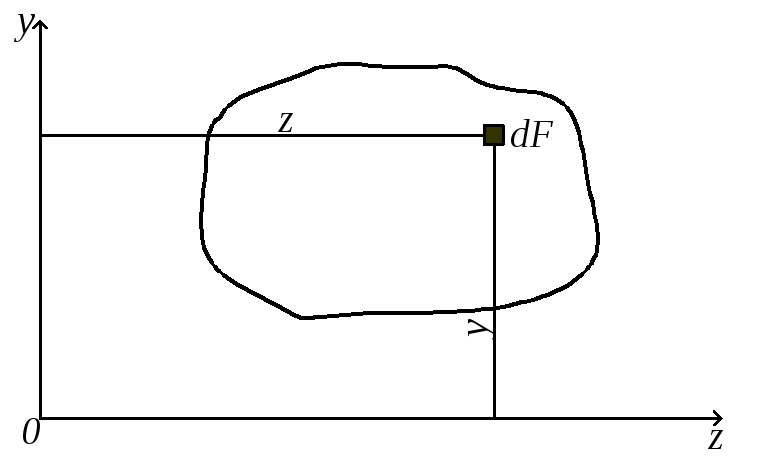
Рис. 4.1
По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражение для момента площади, которое называется статическим моментом. Так dSz = ydF и dSy = zdF – статические моменты элемента площади dF относительно осей Oz и Oy. Просуммировав по всей площади фигуры, получим статические моменты:
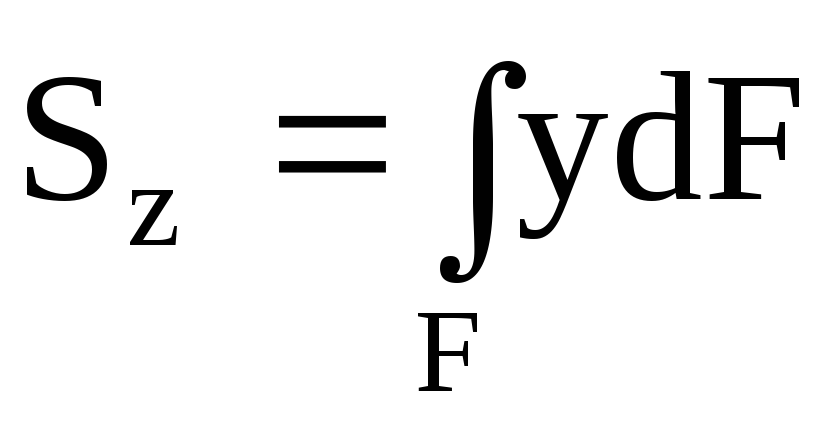 ,
, 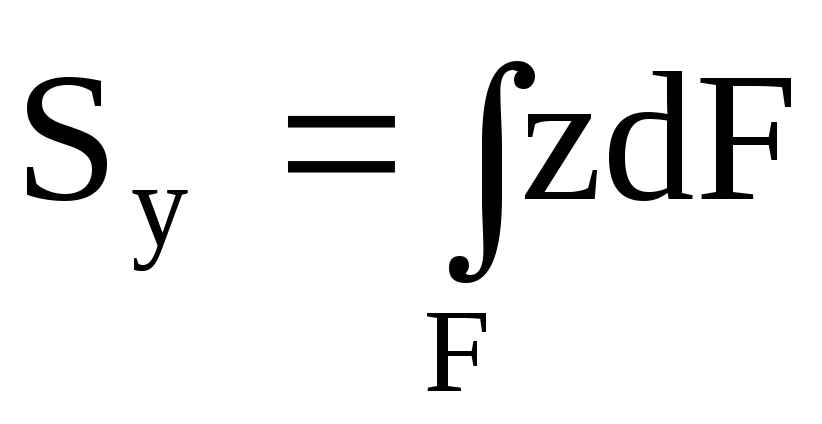 . (4.1)
. (4.1)
Статические моменты имеют размерность единицы длины в кубе (например, см3). Могут быть положительными и отрицательными, знак зависит от положения осей относительно фигуры. Ясно, что относительно каких-то осей статические моменты равны нулю – это оси, проходящие через центр тяжести фигуры.
Рассмотрим задачу о параллельном переносе осей (рис.4.2.).
| Рис. 4.2 | Дано: параллельные оси Oz, Oy и Cz1 Cy1, точка C – центр тяжести фигуры, a и b – расстояния между осями, Sz и Sy – известны. Определить: Sz1 и Sy1. Из рис.4.2. следует, что y1 = y – a и z1 = z – b. По определению |
 .
.
Подставим у1:
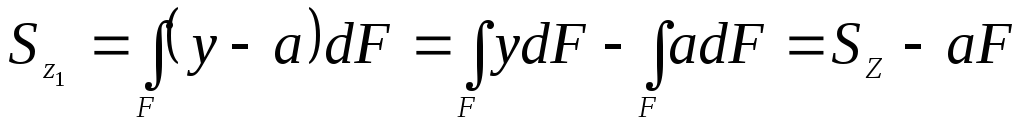 .
.
Получили формулы зависимостей между статическими моментами относительно параллельных осей.
 (4.2)
(4.2)
где F – площадь фигуры;
a и b – расстояния между осями.
Если оси Cz1 и Cy1 – центральные (проходят через центр тяжести), то Sz1 = Sy1 = 0. Тогда
0 = Sz – ycF, 0 = Sy - zcF.
Статический момент любой фигуры равен произведению площади на расстояние от центра тяжести фигуры до оси:
Sz = Fyc, Sy = Fzc. (4.3)
Отсюда координаты центра тяжести
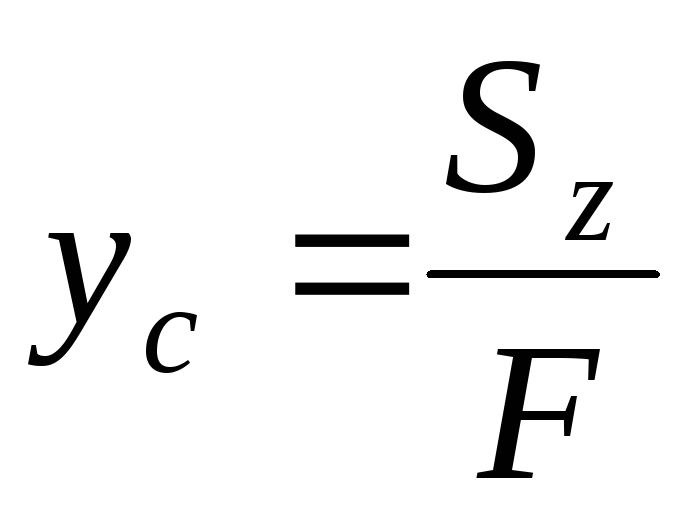 ,
, 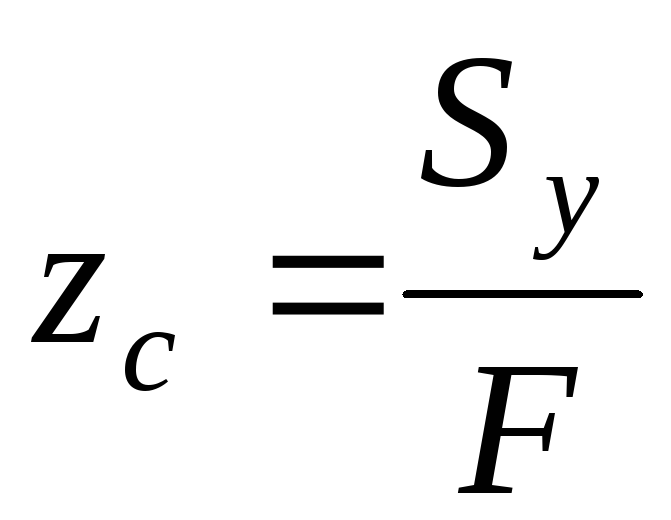 . (4.4)
. (4.4)
По формулам (4.4.) можно найти положение центра тяжести любой плоской фигуры. На рис.4.3. изображена криволинейная лопатка направляющего аппарата гидротурбины. Её необходимо разбить на простые фигуры – прямоугольники, для каждого из которых известна площадь (Fi) и положение центра тяжести (zi, yi) относительно заданных нами осей.
Статический момент площади фигуры относительно данной оси определится как сумма статических моментов каждой части. Координаты центра тяжести
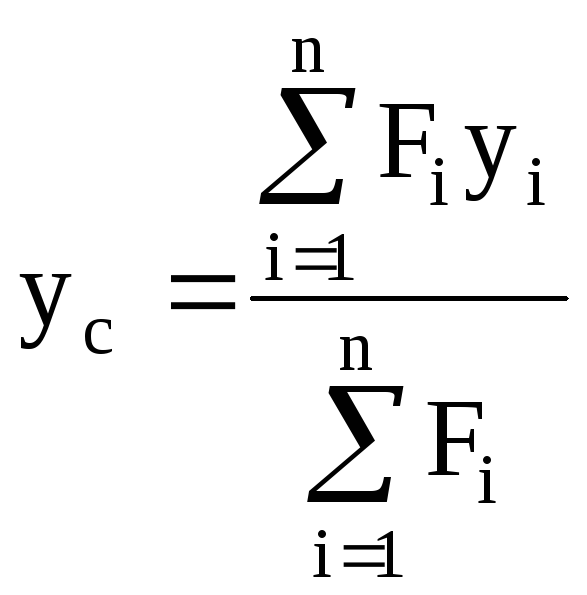 ,
, 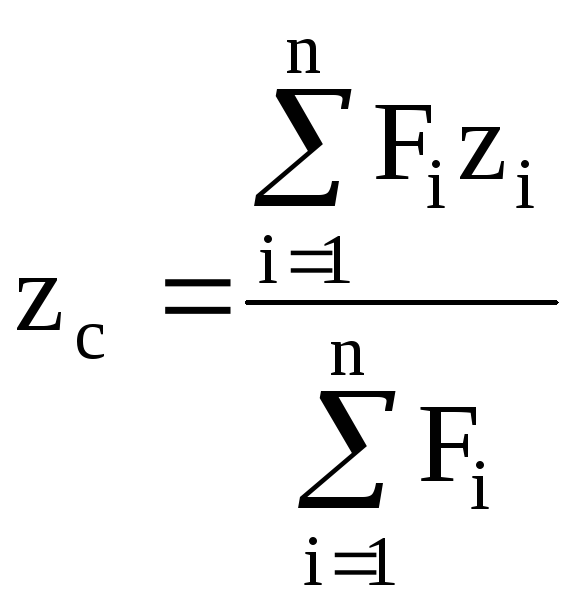 .(4.5)
.(4.5)
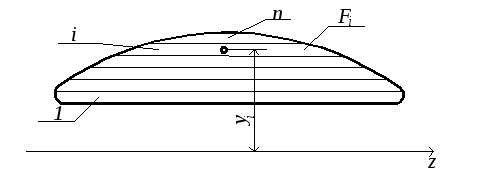
Рис.4.3
Моментом инерции называется характеристика, отличающаяся от статического момента тем, что координата входит в подынтегральное выражение в квадрате (рис.4.4). Моменты инерции бывают осевые или экваториальные – формула (4.6.), полярный – (4.7) и центробежный – (4.8).
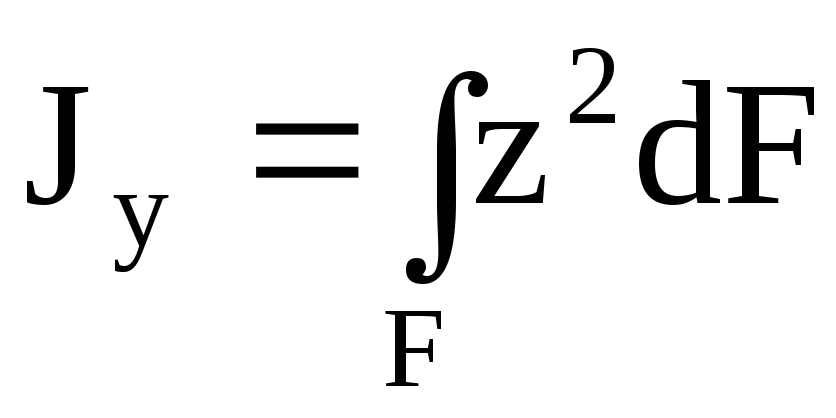 ,
, 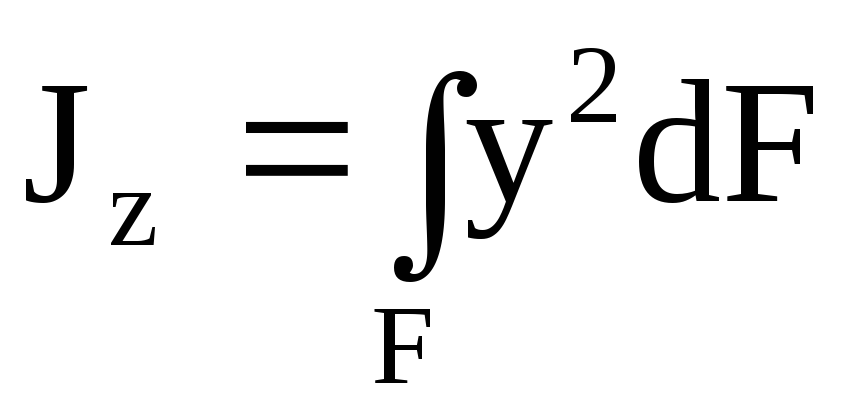 .(4.6)
.(4.6)
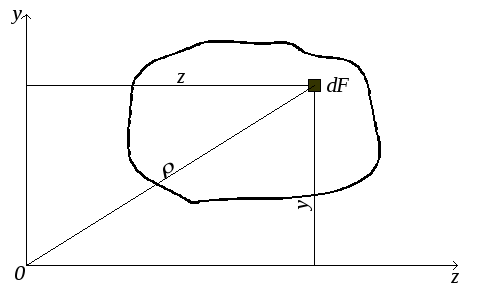
Рис.4.4
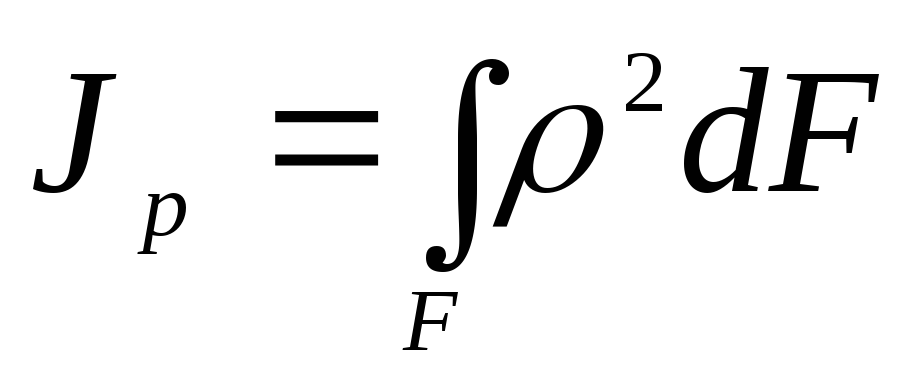 . (4.7)
. (4.7)
 . (4.8)
. (4.8)
Если начало координат совпадает с полюсом, то ρ2 = z2 + y2, следовательно
Jp = Jz + Jy. (4.9)
Размерность моментов инерции – единица длины в четвёртой степени (например, см4). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным
в зависимости от положения осей.
| Рис.4.5 | Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут её главными осями инерции, поскольку в этом случае |
каждой положительной величине zydF соответствует такая же отрицательная по другую сторону от оси симметрии (рис.4.5) и их сумма по всей площади фигуры равна нулю.
Главные оси, проходящие через центр тяжести, называются главными центральными осями.
Вычислим моменты инерции прямоугольника относительно главных центральных осей (рис.4.6,а). Оси z и y – главные, т.к. они являются осями симметрии, Jzy = 0.
а б
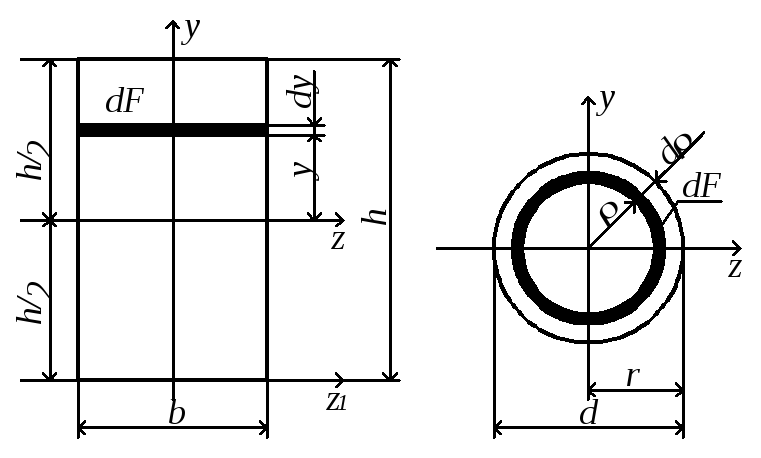
Рис.4.6
Для определения осевого момента инерции относительно оси z выделим элементарную площадку в виде полоски, параллельной оси z:
dF = bdy,
 .
.
Очевидно, что для определения Jy надо поменять местами стороны прямоугольника.
Главные осевые моменты инерции прямоугольника
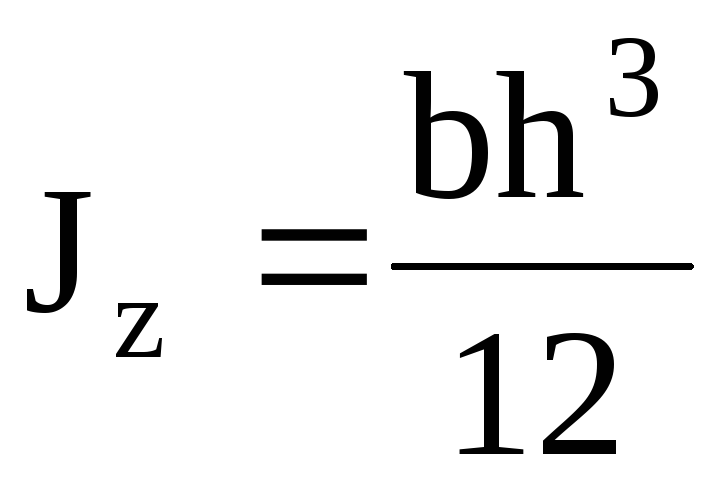 ,
,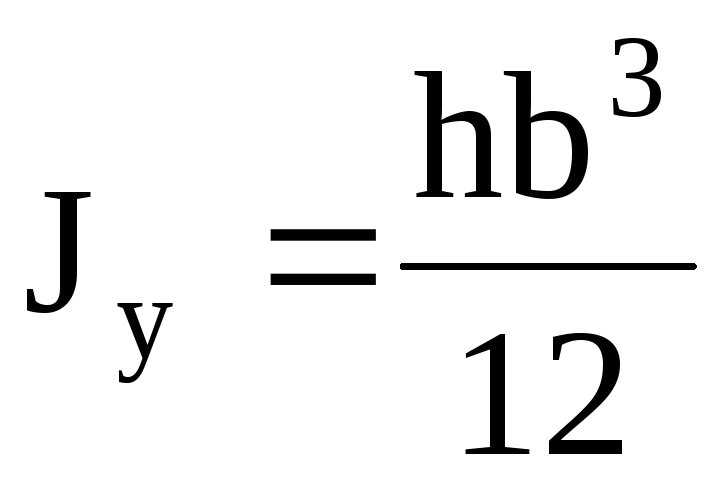 . (4.10)
. (4.10)
Вычислим полярный момент инерции круга относительно его центра, а также осевой момент инерции относительно центральной оси. При вычислении полярного момента инерции выделим элементарную площадку в виде тонкого кольца толщиной dρ (рис.4.6,б) и подсчитаем по формуле (4.7)
dF = 2πρdρ,
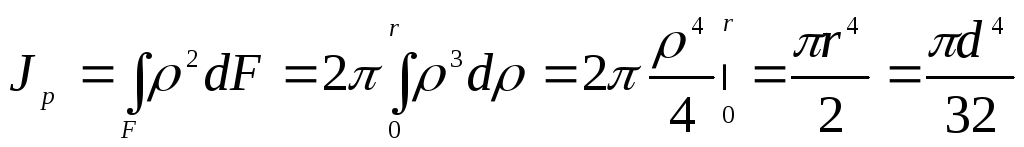 .
.
Полярный момент инерции круга
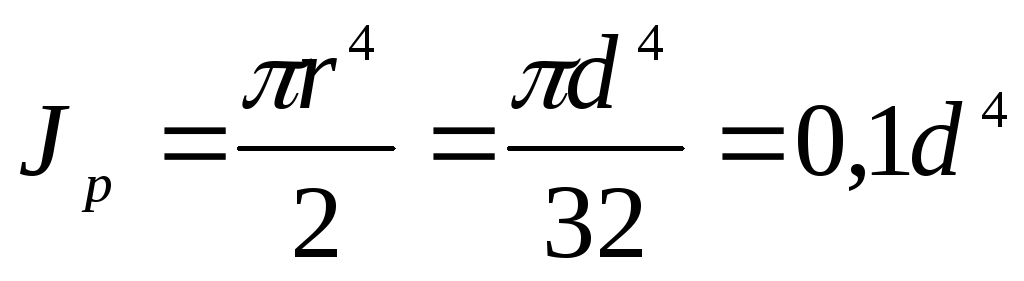 . (4.11)
. (4.11)
Осевой момент инерции круга легко найти из выражения (4.9), учитывая, что в силу симметрии Jz= Jy . Следовательно,
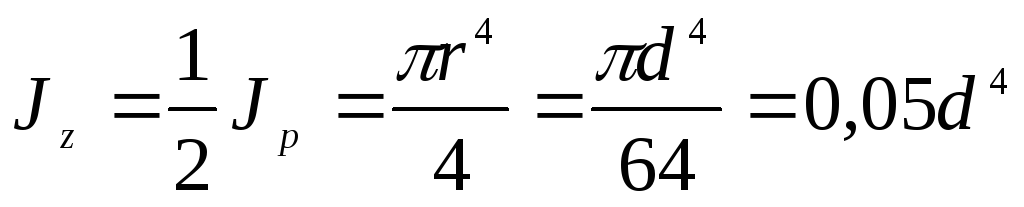 . (4.12)
. (4.12)
studfiles.net
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПОПЕРЕЧНЫХ СЕЧЕНИЙ
ГЕОМЕТРИЯ СЕЧЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ
П лощадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.
лощадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.
Рассмотрим поперечное сечение произвольной формы. Назначим декартову систему координат. Выделим элементарную площадку dA. Обозначим расстояние от центра тяжести элементарной площадки до оси z через y, до оси y через z, до начала координат через ρ. Тогда геометрические характеристики поперечного сечения можно представить в виде момента площади 
Площадь (А) – момент нулевого порядка  .
.
Статический момент площади (S) – момент первого порядка  , могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.
, могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.
Момент инерции (I) - момент второго порядка. Различают осевые (Iz, Iy), центробежный (Izy) и полярный (Iρ) моменты инерции:
 . Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].
. Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].
МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ ФИГУР
ПРЯМОУГОЛЬНИК ПОЛУКРУГ РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК







 КРУГ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
КРУГ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК









МОМЕНТЫ ИНЕРЦИИ СОСТАВНЫХ СЕЧЕНИЙ
Для определения геометрических характеристик составных сечений используется следующий подход. Сечение разбивают на несколько простых фигур, моменты инерции которых известны. В центре тяжести каждой фигуры назначают локальную систему координат. Выбирают систему координат относительно которой будет производится расчет. Затем все геометрические характеристики отдельных частей суммируются, а геометрические характеристики отверстий вычитаются. Пример приведен ниже.
С ечение сложной формы разбиваем на три прямоугольника,
ечение сложной формы разбиваем на три прямоугольника,
назначаем локальные системы координат с началом в
центре тяжести каждого прямоугольника. Расчет
будем производить в системе координат yz.
Ось y - проходит через левую, а ось z -
через нижнюю грань составного сечения.
При вычислении геометрических характеристик
необходимо помнить, что статический момент
площади фигуры относительно центральных
осей всегда равен нулю, также, как и центробежный момент инерции симметричного сечения.


ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
Аналогично формулам изменения нормальных и касательных напряжений при ПНС получены зависимости 
Моменты инерции относительно центральных осей, т.е. осей, проходящих через центр тяжести сечения, называют центральными. Оси, относительно которых центробежный момент инерции обращается в ноль, называют главными и относительно этих осей моменты инерции принимают экстремальное значение. Если главные оси проходят через центр тяжести сечения, то эти оси называют главными центральными, а моменты инерции относительно их – главными центральными моментами инерции.
Главные моменты инерции определяют, как  Положение главных осей инерции можно найти с помощью формулы
Положение главных осей инерции можно найти с помощью формулы
Используя приведенный выше материал, вычислим геометрические характеристики сечений, не имеющих осей симметрии и симметричных сечений.
ПРИМЕР 1
О пределить положение главных центральных осей инерции и вычислить моменты инерции относительно них. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.
пределить положение главных центральных осей инерции и вычислить моменты инерции относительно них. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.
Решение
П о сортаменту определим необходимые для расчета характеристики прокатного профиля. Необходимо обратить внимание на систему координат, принятую в сортаменте.
о сортаменту определим необходимые для расчета характеристики прокатного профиля. Необходимо обратить внимание на систему координат, принятую в сортаменте.
Двутавр №20: А=26,8см2, b=10см, Уголок 10/6,3: А=15,5см,
I x=1840см4, Iy=115см4, номер Ix=153см4, Iy=47,2см4, x0=1,58см,
x=1840см4, Iy=115см4, номер Ix=153см4, Iy=47,2см4, x0=1,58см,
двутавра соответствует его. y0=3,4см, Ixy=48,6см4.
высоте в см. В нашей Высота уголка составляет
системе координат 10см, а ширина полки 6,3см.
Iz1=Ix=1840см4, Iy1=Iy=115см4 Iy2=Ix=153см4, Iz2=Iy=47,2см4.
Пусть площадь двутавра будет А1, а площадь уголка А2, присвоим эти же индексы и остальным геометрическим характеристикам.
Назначим локальные системы координат, проходящие через центры тяжести двутавра и уголка. В строительстве принято направлять ось абсцисс вдоль стержня, тогда в поперечном сечении располагаются оси y и z.
Определим положение центра тяжести сечения (zс, yс)

Выберем за начало отсчета систему координат y1 и z1.

П осле нахождения координат нанесем с учетом знака на чертеж центр тяжести сечения. Если координаты были найдены верно, то центр тяжести должен находиться на прямой между центром тяжести двутавра и уголка. В данном случае эта проверка выполняется, поэтому можно приступить к следующим действиям. Проведем через центр тяжести центральные оси. Выставим расстояния от центральных осей сечения до осей, проходящих через центры тяжести уголка и двутавра. Все дальнейшие расчеты будут выполнены относительно центральных осей всего сечения.
осле нахождения координат нанесем с учетом знака на чертеж центр тяжести сечения. Если координаты были найдены верно, то центр тяжести должен находиться на прямой между центром тяжести двутавра и уголка. В данном случае эта проверка выполняется, поэтому можно приступить к следующим действиям. Проведем через центр тяжести центральные оси. Выставим расстояния от центральных осей сечения до осей, проходящих через центры тяжести уголка и двутавра. Все дальнейшие расчеты будут выполнены относительно центральных осей всего сечения.
2. Вычислим моменты инерции сечения

Т.к. центробежный момент инерции не равен нулю, значит, оси y и z не являются главными осями инерции.
4. Определим положение главных осей инерции


Нанесем главные оси инерции на чертеж, учитывая, что угол α0 получился отрицательный, поэтому поворот осей осуществляется по ходу часовой стрелки. Ближе к исходной оси, относительно которой момент инерции был больше (Iz), располагается ось umax, следовательно, рядом с осью, относительно которой момент инерции был меньше (Iy), будет находиться ось vmin.
5. Вычислим значения главных центральных моментов инерции сечения


4
studfiles.net
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПОПЕРЕЧНЫХ СЕЧЕНИЙ
ГЕОМЕТРИЯ СЕЧЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ
П лощадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.
лощадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.
Рассмотрим поперечное сечение произвольной формы. Назначим декартову систему координат. Выделим элементарную площадку dA. Обозначим расстояние от центра тяжести элементарной площадки до оси z через y, до оси y через z, до начала координат через ρ. Тогда геометрические характеристики поперечного сечения можно представить в виде момента площади 
Площадь (А) – момент нулевого порядка  .
.
Статический момент площади (S) – момент первого порядка  , могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.
, могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.
Момент инерции (I) - момент второго порядка. Различают осевые (Iz, Iy), центробежный (Izy) и полярный (Iρ) моменты инерции:
 . Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].
. Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].
МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ ФИГУР
ПРЯМОУГОЛЬНИК ПОЛУКРУГ РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК







 КРУГ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
КРУГ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК









МОМЕНТЫ ИНЕРЦИИ СОСТАВНЫХ СЕЧЕНИЙ
Для определения геометрических характеристик составных сечений используется следующий подход. Сечение разбивают на несколько простых фигур, моменты инерции которых известны. В центре тяжести каждой фигуры назначают локальную систему координат. Выбирают систему координат относительно которой будет производится расчет. Затем все геометрические характеристики отдельных частей суммируются, а геометрические характеристики отверстий вычитаются. Пример приведен ниже.
С ечение сложной формы разбиваем на три прямоугольника,
ечение сложной формы разбиваем на три прямоугольника,
назначаем локальные системы координат с началом в
центре тяжести каждого прямоугольника. Расчет
будем производить в системе координат yz.
Ось y - проходит через левую, а ось z -
через нижнюю грань составного сечения.
При вычислении геометрических характеристик
необходимо помнить, что статический момент
площади фигуры относительно центральных
осей всегда равен нулю, также, как и центробежный момент инерции симметричного сечения.


ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
Аналогично формулам изменения нормальных и касательных напряжений при ПНС получены зависимости 
Моменты инерции относительно центральных осей, т.е. осей, проходящих через центр тяжести сечения, называют центральными. Оси, относительно которых центробежный момент инерции обращается в ноль, называют главными и относительно этих осей моменты инерции принимают экстремальное значение. Если главные оси проходят через центр тяжести сечения, то эти оси называют главными центральными, а моменты инерции относительно их – главными центральными моментами инерции.
Главные моменты инерции определяют, как  Положение главных осей инерции можно найти с помощью формулы
Положение главных осей инерции можно найти с помощью формулы
Используя приведенный выше материал, вычислим геометрические характеристики сечений, не имеющих осей симметрии и симметричных сечений.
ПРИМЕР 1
О пределить положение главных центральных осей инерции и вычислить моменты инерции относительно них. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.
пределить положение главных центральных осей инерции и вычислить моменты инерции относительно них. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.
Решение
П о сортаменту определим необходимые для расчета характеристики прокатного профиля. Необходимо обратить внимание на систему координат, принятую в сортаменте.
о сортаменту определим необходимые для расчета характеристики прокатного профиля. Необходимо обратить внимание на систему координат, принятую в сортаменте.
Двутавр №20: А=26,8см2, b=10см, Уголок 10/6,3: А=15,5см,
I x=1840см4, Iy=115см4, номер Ix=153см4, Iy=47,2см4, x0=1,58см,
x=1840см4, Iy=115см4, номер Ix=153см4, Iy=47,2см4, x0=1,58см,
двутавра соответствует его. y0=3,4см, Ixy=48,6см4.
высоте в см. В нашей Высота уголка составляет
системе координат 10см, а ширина полки 6,3см.
Iz1=Ix=1840см4, Iy1=Iy=115см4 Iy2=Ix=153см4, Iz2=Iy=47,2см4.
Пусть площадь двутавра будет А1, а площадь уголка А2, присвоим эти же индексы и остальным геометрическим характеристикам.
Назначим локальные системы координат, проходящие через центры тяжести двутавра и уголка. В строительстве принято направлять ось абсцисс вдоль стержня, тогда в поперечном сечении располагаются оси y и z.
Определим положение центра тяжести сечения (zс, yс)

Выберем за начало отсчета систему координат y1 и z1.

П осле нахождения координат нанесем с учетом знака на чертеж центр тяжести сечения. Если координаты были найдены верно, то центр тяжести должен находиться на прямой между центром тяжести двутавра и уголка. В данном случае эта проверка выполняется, поэтому можно приступить к следующим действиям. Проведем через центр тяжести центральные оси. Выставим расстояния от центральных осей сечения до осей, проходящих через центры тяжести уголка и двутавра. Все дальнейшие расчеты будут выполнены относительно центральных осей всего сечения.
осле нахождения координат нанесем с учетом знака на чертеж центр тяжести сечения. Если координаты были найдены верно, то центр тяжести должен находиться на прямой между центром тяжести двутавра и уголка. В данном случае эта проверка выполняется, поэтому можно приступить к следующим действиям. Проведем через центр тяжести центральные оси. Выставим расстояния от центральных осей сечения до осей, проходящих через центры тяжести уголка и двутавра. Все дальнейшие расчеты будут выполнены относительно центральных осей всего сечения.
2. Вычислим моменты инерции сечения

Т.к. центробежный момент инерции не равен нулю, значит, оси y и z не являются главными осями инерции.
4. Определим положение главных осей инерции


Нанесем главные оси инерции на чертеж, учитывая, что угол α0 получился отрицательный, поэтому поворот осей осуществляется по ходу часовой стрелки. Ближе к исходной оси, относительно которой момент инерции был больше (Iz), располагается ось umax, следовательно, рядом с осью, относительно которой момент инерции был меньше (Iy), будет находиться ось vmin.
5. Вычислим значения главных центральных моментов инерции сечения


38
studfiles.net
БЕЛОРУССКИЙ ГОСУДРАСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра инженерной графики
РЕФЕРАТ
На тему:
«Деформация сдвига. Геометрические характеристики плоских сечений. Кручение стержней с круглым поперечным сечением»
МИНСК, 2008
ДЕФОРМАЦИЯ СДВИГА
Напряжения и деформации при сдвиге
При простом растяжении две части стержня, разделенные наклонным сечением, стремятся не только оторваться, но и сдвинуться одна относительно другой. Сдвигу противодействуют касательные напряжения, действующие в плоскости сечения.
На практике ряд деталей работает в таких условиях, когда причиной их разрушения является сдвиг одной части детали относительно другой. При расчете на прочность таких деталей учитываются касательные напряжения и расчет на прочность ведется по ним. Пусть к стержню приложены перпендикулярно его продольной оси две равные по модулю, но противоположно направленные силы, действующие очень близко друг от друга (рис1, а). При достаточной величине этих сил произойдетсрез– отделение правой части стержня относительно левой по сечению I – I. Деформации среза в зоне действия усилий предшествует перекашивание прямых углов элементарного объема – параллелепипеда с ребрамиabdс(1, б). На гранях параллелепипеда возникают касательные напряжения, направление которых определяется законом парности касательных напряжений. Если нормальные напряжения вызывают линейные деформации (удлинения и укорочения), токасательные напряжения вызывают угловые деформации γ,так называемыеуглы сдвига. При равенстве касательных напряжений по площадкам элементов деформированного тела (закон парности касательных напряжений) имеем одинаковые угловые деформации, углы сдвига.


Рис. 1
Чистым сдвигомназывают такое напряженное состояние, когда по граням элемента в виде бесконечно малого кубика действуют только касательные напряжения. Например, чистый сдвиг наблюдается во всех точках скручиваемого стержня с круглым поперечным сечением.
Пользуясь методом сечений, определим, что равнодействующая внутренних сил в плоскости I – I (плоскости сдвига) (рис. 1, а) равна внешней силе F, т.е. Q = F . Это усилие может вызвать лишь касательные напряжения, равномерно распределенные по плоскости сечения. Поэтому
τ = Q/A = F/A, (1)
гдеА– площадь поперечного сечения стержня.
Действительное распределение касательных напряжений по сечению I – I не является равномерным, в узких краевых зонах касательные напряжения приближаются к нулю. Но это обстоятельство при инженерных расчетах не принимается во внимание, так как область указанных отклонений мала по сравнению с размерами сечения.
Опыты показывают, что для большинства материалов до определенных величин нагружения имеется линейная зависимость между напряжениями и деформациями при сдвиге, которую выражает закон Гука:
τ = G·γ, (2)
гдеG– модуль упругости материала при сдвиге, или модуль упругости второго рода. Он связан с модулем упругости E при растяжении через коэффициент Пуассона μ следующей зависимостью:G = E/[2(1 + μ)]. Отметим, что для стали G ≈ 8·104МПа, для алюминия G ≈ 2,7·104МПа.
Так как разрушение детали при деформации сдвига называют срезом, расчет на прочность при данной деформации называют расчетом на сдвиг или на срез. Примером соединений, рассчитываемых на срез, являются заклепочные, болтовые, сварные, паяные, клеевые соединения.
Условие прочности при сдвиге имеет вид
τ =Q/A≤ τadm, (3)
гдеQ– равнодействующая внутренних сил в плоскости сдвига;А– площадь сдвига;τadm– допускаемое касательное напряжение материала детали.
Расчет на сдвиг заклепочных (болтовых) соединений
На рис. 2, а показано соединение двух листов заклепками. Под действием сил F листы стремятся сдвинуться один относительно другого, но этому препятствуют заклепки, на которые и передается действие сил. Картина возможного разрушения показана на рис. 2, б. Соединение может разрушиться за счет среза заклепок по плоскости соединения листов. Как показывают опыты, на каждую заклепку при статическом, т.е. практически неизменном, нагружении действует одинаковая сила, и заклепки разрушаются одновременно. Поэтому считают, что сила, приходящаяся на одну заклепку, будет равна Q = = F/k, гдеk– число заклепок.
Приняв равномерное распределение касательных напряжений по сечению заклепки, найдем их величину как τ = Q/A, где А = πd2/4 – площадь поперечного сечения заклепки диаметром d.

Рис. 2
Условие прочности заклепок на срез имеет вид
τ = F/(kA)= Q/A ≤ τadm, (4)
гдеτadm– допускаемое напряжение на срез материала заклепок, принимают τadm= (0,6…0,8) σadm. Если разрушение заклепок возможно по одной плоскости сдвига (рис. 2, а, б), то соединение называют односрезным, если по двум плоскостям (рис. 2, в) – двухсрезным. Из формулы можно определить необходимое число односрезных заклепок
k ≥ (4F)/(πd2·τadm). (5)
При двухсрезном и многосрезном заклепочном соединении нужно вместо числа k в формулу (4) подставлять общее число срезов заклепок, расположенных по одну сторону стыка соединяемых листов.
Если на конструкцию действуют динамические, т.е. изменяющиеся с большой скоростью, например, ударные и вибрационные нагрузки, при расчете заклепочных соединений на сдвиг необходимо учитывать неравномерность работы заклепок.
При соединении листов в конструкциях, представленных на рис. 5.14 не заклепками, а с помощью болтовых соединений, расчет болтов на сдвиг проводят аналогично приведенному расчету заклепок. Величиныdиτadmбудут соответственно обозначать диаметр болтов и допускаемое напряжение материала болтов на сдвиг (срез).
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций зависит только от величины поперечного сечения и свойств материала элементов.При деформациях кручения и изгиба, при расчетах сжатых стержней на устойчивость,прочность и жесткость элементов конструкции зависят также и от формы их поперечного сечения. К числу геометрических характеристик сечения, учитывающих его размеры, форму и влияющих на прочность и жесткость конструкций, относятся статические моменты, моменты инерции и моменты сопротивления сечения.
Статические моменты сечения. Центр масс сечения
Статическим моментом сеченияSотносительно любой оси называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на их расстояние до этой оси. Так, статический момент сечения (рис. 3) относительно осиz:
 , (6)
, (6)
гдеAi– площадь элементарной i– й площадки сечения, расположенной на расстоянииyiот осиz;n– число элементарных площадок сечения. При Ai→ 0 (dA) и n → ∞
 . (7)
. (7)
Размерность статических моментов – длина в кубе. Статические моменты могут быть положительными, отрицательными и равными нулю.
Считая, что поверхностная плотностьρ*сечения постоянна, координаты центра масс сеченияzc,ycможно выразить через статические моменты
 , (8)
, (8)
аналогично
 , (9)
, (9)
гдеmi– массы элементарных площадок сечения;М– масса сечения;А– площадь сечения;SzиSy– соответственно статические моменты сечения относительно координатных осейzиy.
Из выражений (8) и (9) видно, что при yc= 0; zc= 0, т.е.при прохождении координатных осей через центр масс С, статические моменты сечения относительно этих осей будут равны нулю, так как А ≠ 0.Такие координатные оси называют центральными. Это следствие можно выразить еще так:если статические моменты сечения относительно координатных осей равны нулю, т.е.Sz= 0,Sy= 0, то эти осиz,yпроходят через центр масс сеченияC.
Моменты инерции сечений
Полярным моментом инерции сеченияназывается взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до данного полюса (точки). Из рис. 3
 , (10)
, (10)
гдеρ– расстояние от площадкиdAдо полюса (точки 0).

Рис. 3 и 4
Осевым моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до оси. Так, моменты инерции сечения относительно координатных осейzиyбудут соответственно равны
 , (11)
, (11)
 . (12)
. (12)
Так как ρ2= z2+ y2, сравнив выражения (11), (12) и (13), получим
Iρ= Iz+ Iy, (13)
т.е. сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения рассматриваемых осей.Моменты инерции сечений – всегда положительные величины.
Моменты инерции прямоугольника, круга
Моменты инерции сечений вычисляются в следующей последовательности. Вначале находят момент инерции элементарной площадкиdAотносительно точки или оси. Считая, что число таких площадок стремится к бесконечности, далее вычисляют сумму моментов инерции площадок по всему сечению. Чаще всего детали типа стержней имеют форму поперечного сечения в виде круга или прямоугольника.
Вычислим момент инерции прямоугольника (рис. 4, а) с основаниемbи высотойhотносительно осиz, проходящей через центр масс параллельно основанию. За элементарную площадкуdAпримем площадь бесконечно тонкого слоя dA = bdy. Тогда
 . (15)
. (15)
Аналогично получим
Iy= hb3/12. (16)
Рассмотрим круг (рис. 5.16, б). Сначала определим полярный момент инерции круга относительно геометрического центра С: .
.
За элементарную площадкуdAпримем площадь бесконечно тонкого кольца толщинойdρ: dA = 2πρdρ. Тогда
 . (17)
. (17)
Найдем моменты инерции круга относительно координатных осейy,z, проходящих через центр массС. Так как оси являются диаметром круга, то Iy= Iz. Поэтому выражение (5.38) можно представить как Iρ=2 Iy= 2 Iz, откуда
Iy= Iz= Iρ/2 ≈ 0,05 d4. (18)
Для кольца моменты инерции равны разности моментов инерции внешнего и внутреннего кругов с диаметрами соответственноdиd1.
Тогда
Iρ≈ 0,1 (d4– d14), (19)
Iy≈ Iz≈ 0,05 (d4– d14). (20)
Понятие о крутящем моменте
Деформация кручения происходит при действии на стержень внешних пар сил, плоскости действия которых перпендикулярны оси стержня. При этом в поперечных сечениях стержня возникает только одна составляющая внутренних сил – крутящий моментТ. С явлением кручения встречаются при расчете валов, винтовых пружин и других элементов конструкций.
Если прямые незакрепленные стержни, подвергающиеся деформации кручения, равномерно вращаются или находятся в покое, алгебраическая сумма всехвнешних скручивающих (вращающих) моментовТеравна нулю.
Вращающиеся и испытывающие деформацию кручения стержни называютвалами. При расчете валов величины скручивающих моментов можно определить по передаваемой мощности и скорости вращения вала из выражения
Te= P/ω = 30P/πn = 9,55 P/n |Нм|, (21)
гдеР– мощность, передаваемая валом, Вт;n– угловая скорость вала в оборотах за минуту;ω– угловая скорость в рад/с.
На основании метода сеченийкрутящий момент Т в произвольном поперечном сечении стержня численно равен алгебраической сумме внешних Тескручивающих моментов, действующих на стержень по одну сторону от рассматриваемого сечения. Когда к валу приложено несколько внешнихТескручивающих моментов, крутящие моменты в сечениях различных участков будут разными. Для наглядности распределенияТпо длине скручиваемого стержня и для нахождения опасного сечения с наибольшим крутящим моментомТmaxстроятэпюры (графики) крутящих моментов.
При построении эпюрыТпроводят ось, параллельную оси стержня. Каждая ордината эпюры в принятом масштабе равна величине крутящего момента, действующего в том сечении, которому соответствует ордината. При расчетах на прочность и жесткость знакTне играет никакой роли, но для удобства построения эпюр будем считать крутящий моментТположительным, если при взгляде в торец отсеченной части стержня этот момент представляется направленным против хода часовой стрелки. Положительные по знаку крутящие моменты откладывают на эпюре выше оси, отрицательные – ниже.
На рис. 5, б представлена эпюра крутящих моментовТдля схемы нагружения вала тремя внешними моментамиТе(рис. 5, а). Отметим, что в сечениях, где приложен внешний скручивающий моментТе, ордината эпюрыТменяется скачком на величину, равную значению этого момента. Как видно из рис. 5, б, максимальный крутящий момент (Tmax= 10 Нм) не всегда равен наибольшему моменту внешних сил (Temax= 15 Нм).

Рис. 5
Рассмотрим стержень с круглым поперечным сечением (рис. 6, а), один конец которого закреплен, а другой нагружен парой сил с моментомТе. В результате действия момента внешних силТевозникает деформация кручения. Наблюдая при кручении характер искажения прямоугольников координатной сетки, нанесенной на боковой поверхности круглого стержня, обнаружили: прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных, а с учетом закона парности касательных напряжений и в продольных сечениях; контуры поперечных сечений в процессе деформации остаются плоскими, расстояния между ними не изменяются, а первоначальные прямолинейные образующие, нанесенные на боковую поверхность, превращаются в винтовые линии; диаметры торцового сечения повернутся на некоторый угол φ относительно своего начального положения, оставаясь прямой линией. Эти наблюдения позволили составить представление о механизме деформации кручения. Постоянство длины и диаметра деформируемого стержня свидетельствует об отсутствии нормальных напряжений в поперечных и продольных сечениях. Так как в поперечных и в продольных сечениях действуют только касательные напряжения, напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. Поперечные сечения, оставаясь плоскими, поворачиваются вокруг оси стержня относительно друг друга на некоторый угол, сохраняя длину и прямолинейность своих радиусов.
Выделим двумя поперечными сечениями элемент (рис. 6. б) скручиваемого стержня длинойdx. В результате деформации одно сечение повернется относительно другого на уголdφ. Будем считать левое сечение элементаdxнеподвижно закрепленным. Тогдаdφ– угол поворота правого торцового сечения вокруг продольной оси. Образующую АВОО1можно представить как параллелепипед длинойdxс бесконечно малыми основаниями АО1и ВО. В результате деформации этот параллелепипед займет положение АВ'ОО1. Величина ВВ' = γdx = ρdφ представляет собой абсолютный сдвиг граниВна поверхности стержня относительно граниАв направлении, перпендикулярном радиусу стержня. Величина абсолютного сдвига точек основанияОВпараллелепипеда зависит от их расстоянияρдо оси стержня. Сдвиг равен нулю на оси стержня и максимален, т.е. равен ВВ' на поверхности. Угол сдвига соответственно будет равен
γ = (dφ/dx)ρ, (22)
где dφ/dx – относительный угол закручивания. На основании закона Гука для сдвига можно записать
τρ= G·γ = G(dφ/dx)ρ, (23)
гдеG– модуль упругости материала стержня при сдвиге.


Рис. 6
Величина касательных напряжений в каждой точке сечения прямо пропорциональна расстояниюρот точки до центра масс сечения. На оси стержня при ρ = 0; напряжение τ = 0; в точках, расположенных в непосредственной близости от поверхности стержня напряжения максимальны. Эпюра измененияτρвдоль диаметра сечения показана на рис. 5.18, в. Так как величина относительного угла закручивания dφ/dx неизвестна, зависимостью (5.47) для определения касательных напряжений в сечении не пользуются.
Элементарная внутренняя сила, действующая в плоскости сечения на площадкуdAс напряжениемτρравна dQ = τρ·dA. Элементарный момент внутренних сил, действующий в плоскости сечения, т.е. элементарный крутящий момент, создаваемый силойdQотносительно центра сечения dT = ρdQ. Сумма этих моментов внутренних сил по всей площади поперечного сечения стержня равна крутящему моменту
 .
.
Так как G = const и dφ/dx = const, то
 , (24)
, (24)
гдеIp– полярный момент инерции сечения.
Выразим величину угла закручивания, отнесенного к единице длины стержня
dφ/dx= T/GIp. (25)
с учетом формулы (25) примет вид
τρ= (T/Ip) ·ρ. (26)
При инженерных расчетах интерес представляют наибольшие напряжения в сечении, т.е. напряжения на поверхности стержня при ρ = d/2,
 , (27)
, (27)
где Wp= 2Ip/d–полярный момент сопротивления – отношение полярного момента инерцииIpсечения к расстоянию от наиболее удаленной точки сечения до центра масс.
Полярный момент сопротивления для стержня круглого сечения диаметромdравен Wp≈ 0,2d3, а для стержня кольцевого сечения с внутренним диаметромd1– Wp≈ [0,2(d3– d14/d)].
Условие прочности стержня при кручении с постоянным по длине поперечным сечением имеет вид
τmax=Tmax/Wp≤τadm, (28)
гдеТmax– максимальный крутящий момент по длине деформируемого стержня;τadm– допускаемое напряжение при кручении, для стали обычно равно 0,5 … 0,6 допускаемого напряженияσadmпри растяжении. Предельный из условия прочности крутящий момент определяют по формуле
Tu≤ Wp·τadm, (29)
а минимальный диаметр скручиваемого стержня, учитывая что Wp= = 0,2d3≥ Tmax/τadmравен
d ≥ . (30)
. (30)
При сравнении стержней, выдерживающих одинаковый крутящий момент, т.е. имеющих поперечное сечение с равным полярным моментом сопротивленияWp, стержень с наименьшей площадьюАпоперечного сечения будет обладать меньшей массой. Для сравнения различных сечений применяют безразмерную величину, равную отношению Wp/ . Чем больше эта величина, тем рациональнее по затратам материала сечение. Так, для швеллера, двутавра она равна 0,04 … 0,07, а для круглого кольца с отношением внутреннего диаметра к внешнему равному 0,9 – она равна 1,16. При кручении рациональным является использование стержней с круглым кольцеобразным сечением.
. Чем больше эта величина, тем рациональнее по затратам материала сечение. Так, для швеллера, двутавра она равна 0,04 … 0,07, а для круглого кольца с отношением внутреннего диаметра к внешнему равному 0,9 – она равна 1,16. При кручении рациональным является использование стержней с круглым кольцеобразным сечением.
Определение деформаций при кручении стержней с круглым поперечным сечением
Деформация при кручении стержней определяется углом поворота поперечных сечений относительно начального положения. Воспользуемся формулой для выражения угла поворота сечения скручиваемого стержня на участке длиной dx
dφ = (Tdx)/GIp. (31)
Полный угол закручивания на участке длиной ℓ равен
 . (32)
. (32)
Если крутящий моментTи величинаGIp, называемая жесткостью при кручении, постоянны на всей длинеℓ, то полный угол закручивания в радианах будет равен
 . (33)
. (33)
Расчет стержней на прочность при кручении не исключает возможности возникновения недопустимых деформаций (углов поворота поперечных сечений) при целостности длинных стержней (деталей). Поэтому часто детали, испытывающие деформацию кручения, рассчитывают не только на прочность, но и на жесткость. Для обеспечения требуемой жесткости необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого, т.е.
(dφ/dx) = ≤ (dφ/dx)adm, (34)
≤ (dφ/dx)adm, (34)
где (dφ/dx)adm– допускаемый относительный угол закручивания в радианах на единицу длины стержня. Чаще (dφ/dx)'admзадают в градусах на метр длины, тогда выражение будет иметь вид
 (dφ/dx)'adm. (35)
(dφ/dx)'adm. (35)
Величину (dφ/dx)'admвыбирают в зависимости от назначения детали и ее размеров. В приборостроении (dφ/dx)'admпринимают в пределах 20 угловых минут на длине 1 м, т.е. (dφ/dx)'adm. =0,33 |º/м|. Из условия жесткости можно определить минимальный диаметр деформируемого стержня, учитывая, что Ip≈ 0,1d4
 (36)
(36)
или предельный по величине крутящий момент
Tu≤19 GIp. (37)
При совместных расчетах на прочность и жесткость при кручении диаметр стержня принимают равным наибольшему из найденных, а предельный крутящий моментТuограничивают наименьшим, полученным при проверке по зависимостям.
ЛИТЕРАТУРА
1. Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное пособие. М.: – Высш. шк., 2001. – 480 с.
2. Сурин В.М. Техническая механика: Учебное пособие. – Мн.: БГУИР, 2004. – 292 с.
3. Ванторин В.Д. Механизмы приборных и вычислительных систем: Учебное пособие. – М.: Высш. шк., 1999. – 415 с.
superbotanik.net
Основным объектом, изучаемым в курсе сопротивления материалов, является стержень. Сопротивление стержня различным видам деформации часто зависит не только от его материала и размеров, но и от очертаний оси, формы поперечных сечений и их расположения. Поэтому рассмотрим основные геометрические характеристики его поперечных сечений, определяющие сопротивление различным видам деформаций. К ним относятся площади поперечных сечений, статические моменты и моменты инерции.
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную
с координатными осями Ог и Оу (рис. 12).
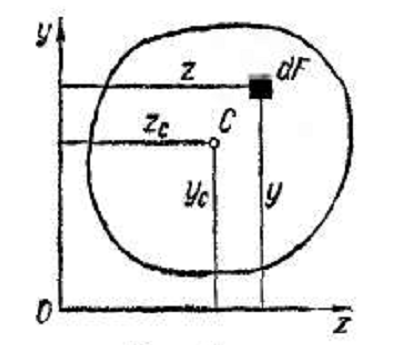
Рис 12
Выделим элемент площади dF с координатами z, у. По аналогии с выражением для момента силы относительно какой-либо оси составим выражение для момента площади, которое называется статическим моментом.
 ,
, 
статические моменты элемента площади относительно оси Оz и Оу.
Просуммировав такие произведения по всей площади фигуры, получим соответственно статические моменты относительно осей z и у:
 (2)
(2)
Статические моменты измеряются в единицах длины в кубе (например, см3).
Пусть zС, yс — координаты центра тяжести (ц.т.) фигуры. На основании теоремы о моменте равнодействующей можно написать следующие выражения:
 (3)
(3)
где F — площадь фигуры. Отсюда координаты центра тяжести
 (4)
(4)
Из формул (3) следует, что статические моменты площади относительно центральных осей (осей, проходящих через центр тяжести) равны нулю.
Пример. Вычислим статический момент треугольника (рис. 13) относительно оси, проходящей через основание.
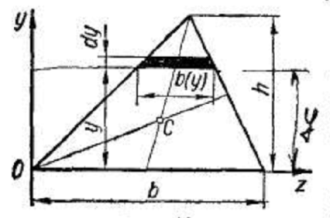
Рис 13
На расстоянии у от неё выделим элементарную площадку в виде полоски, параллельной оси z. Площадь полоски


или 
Для вычисления статических моментов сложной фигуры ее разбивают на простые части (рис. И), для каждой из которых известна площадь Fi и положение центра тяжести zt и yt. Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:

По формулам (2.3) и (2.4) находим координаты центра тяжести сложной фигуры:
 (5)
(5)
Осевым, или экваториальным, моментом инерции площади фигуры называют интеграл произведений элементарных площадей на квадраты их расстояний от рассматриваемой оси. Так, моменты относительно осей z и у:
 (7)
(7)
Величины осевых и полярных моментов инерции всегда положительны.
Центробежным моментом инерции называют интеграл произведений площадей элементарных площадок на их расстояния от координатных осей z и у:
 (8)
(8)
Размерность моментов инерции см4,  .
.
В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. В самом деле, центробежный момент инерции площади фигуры, показанной на рис. 14, а, относительно выбранной системы осей положителен, так как координаты г, у всех элементов положительны.
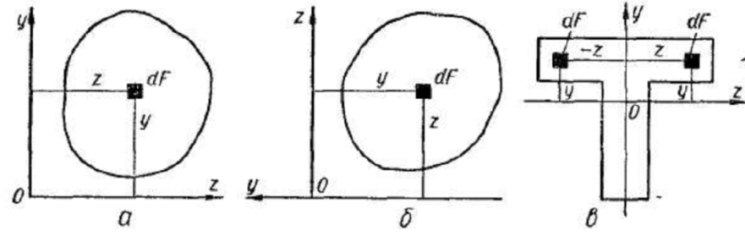
Рис 14
При повороте осей вокруг начала координат на 90° (рис. 14, б) знак центробежного момента инерции фигуры меняется на обратный, так как в этом положении координаты z всех элементов положительны, а координаты у — отрицательны. Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю.
studfiles.net
Как уже отмечалось в главе 1, основным объектом, изучаемым в сопротивлении материалов, является стержень. Сопротивление стержня различным видам деформации зависит от материала и размеров – очертания и длины оси, формы поперечных сечений. При растяжении прямого бруса геометрической характеристикой поперечного сечения была его площадь (см. главу 2). В настоящей главе рассмотрим основные геометрические характеристики поперечных сечений стержня, определяющие сопротивление различным видам деформаций.
Определение положения центра тяжести
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями Oz и Oy (рис. 4.1). Выделим элемент площади dF с координатами z, y.
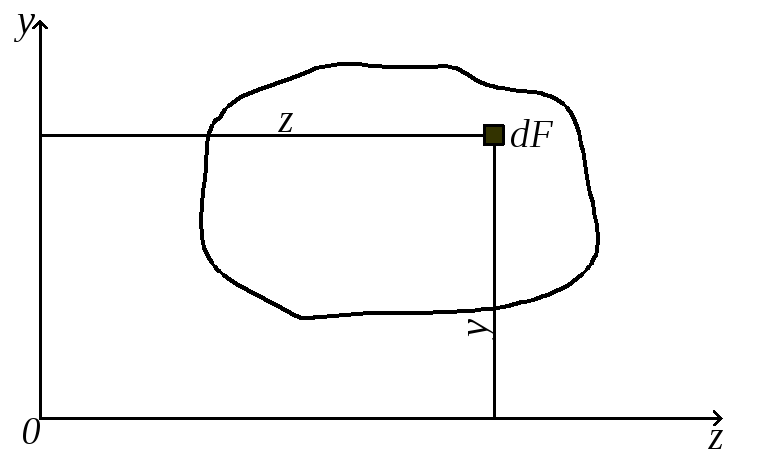
Рис. 4.1
По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражение для момента площади, которое называется статическим моментом. Так dSz = ydF и dSy = zdF – статические моменты элемента площади dF относительно осей Oz и Oy. Просуммировав по всей площади фигуры, получим статические моменты:
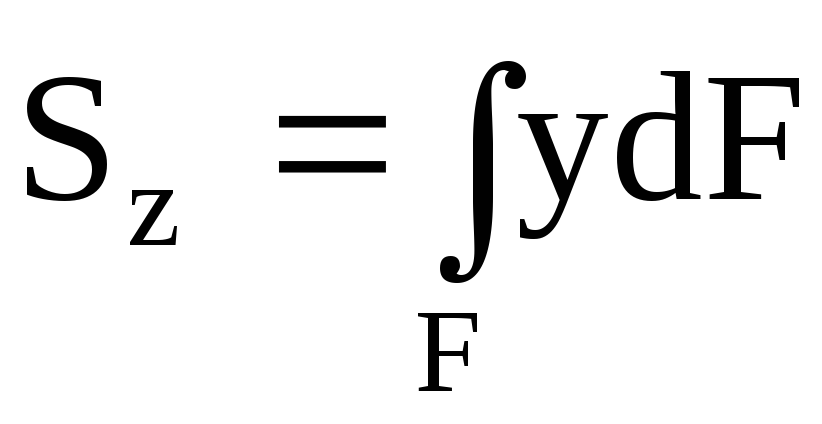 ,
, 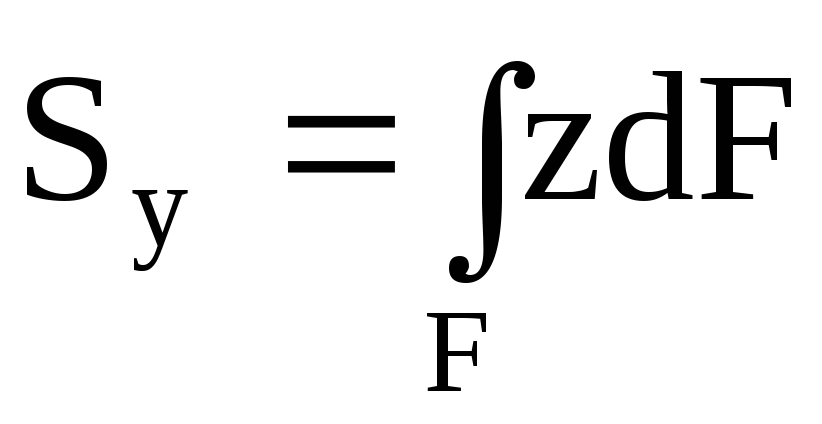 . (4.1)
. (4.1)
Статические моменты имеют размерность единицы длины в кубе (например, см3). Могут быть положительными и отрицательными, знак зависит от положения осей относительно фигуры. Ясно, что относительно каких-то осей статические моменты равны нулю – это оси, проходящие через центр тяжести фигуры.
Рассмотрим задачу о параллельном переносе осей (рис.4.2.).
| Рис. 4.2 | Дано: параллельные оси Oz, Oy и Cz1 Cy1, точка C – центр тяжести фигуры, a и b – расстояния между осями, Sz и Sy – известны. Определить: Sz1 и Sy1. Из рис.4.2. следует, что y1 = y – a и z1 = z – b. По определению |
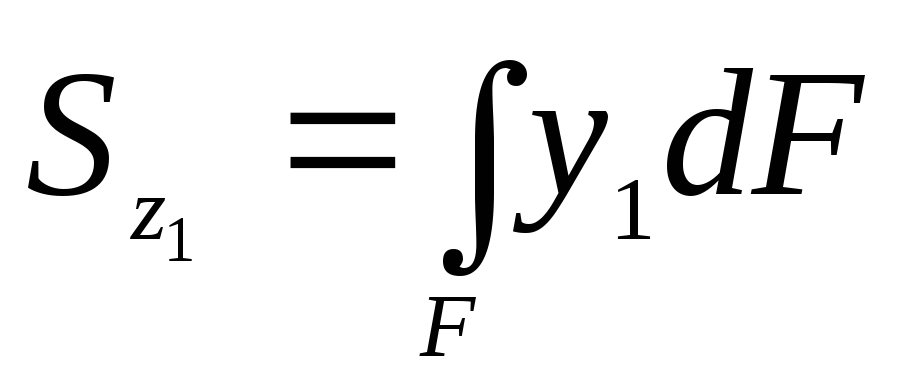 .
.
Подставим у1:
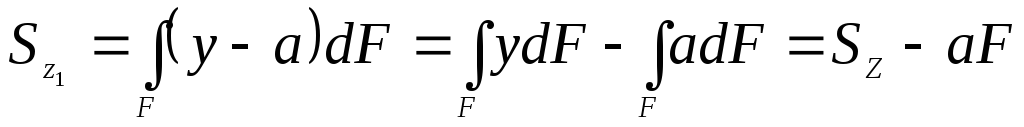 .
.
Получили формулы зависимостей между статическими моментами относительно параллельных осей.
 (4.2)
(4.2)
где F – площадь фигуры;
a и b – расстояния между осями.
Если оси Cz1 и Cy1 – центральные (проходят через центр тяжести), то Sz1 = Sy1 = 0. Тогда
0 = Sz – ycF, 0 = Sy - zcF.
Статический момент любой фигуры равен произведению площади на расстояние от центра тяжести фигуры до оси:
Sz = Fyc, Sy = Fzc. (4.3)
Отсюда координаты центра тяжести
 ,
, 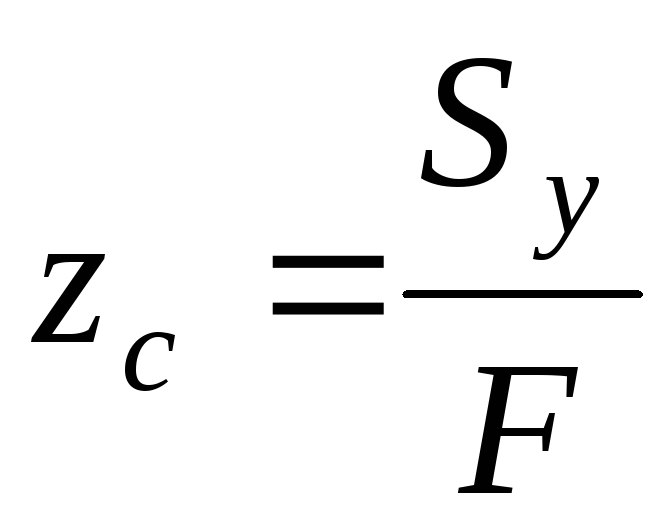 . (4.4)
. (4.4)
По формулам (4.4.) можно найти положение центра тяжести любой плоской фигуры. На рис.4.3. изображена криволинейная лопатка направляющего аппарата гидротурбины. Её необходимо разбить на простые фигуры – прямоугольники, для каждого из которых известна площадь (Fi) и положение центра тяжести (zi, yi) относительно заданных нами осей.
Статический момент площади фигуры относительно данной оси определится как сумма статических моментов каждой части. Координаты центра тяжести
 ,
, 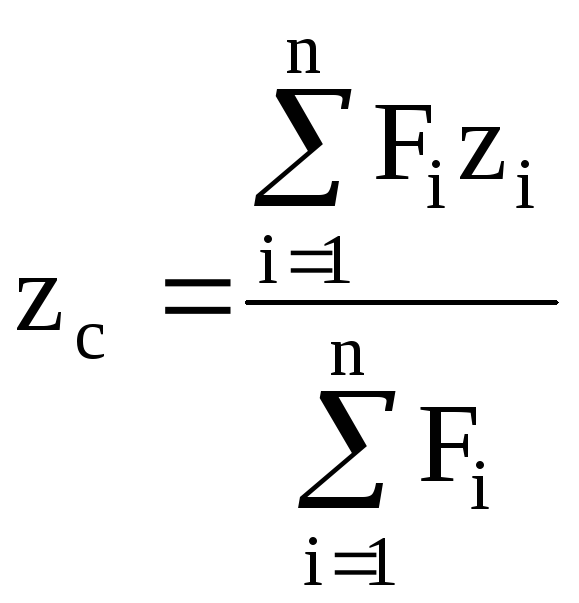 .(4.5)
.(4.5)
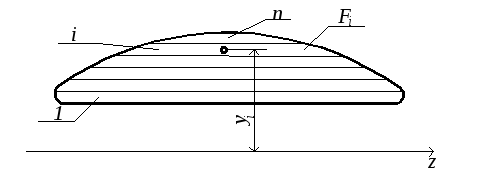
Рис.4.3
Моментом инерции называется характеристика, отличающаяся от статического момента тем, что координата входит в подынтегральное выражение в квадрате (рис.4.4). Моменты инерции бывают осевые или экваториальные – формула (4.6.), полярный – (4.7) и центробежный – (4.8).
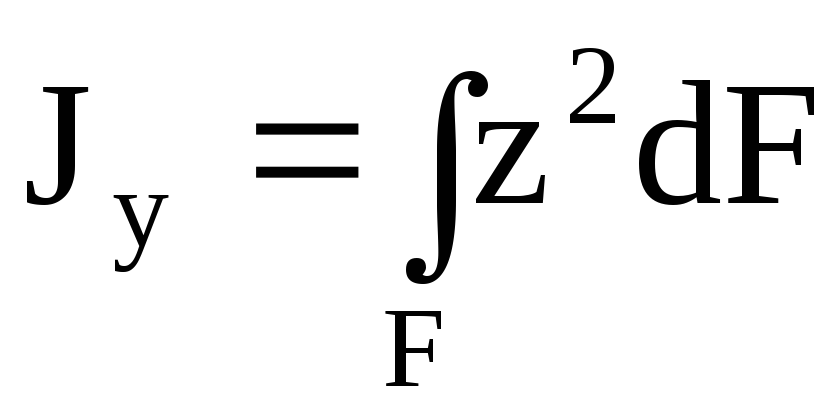 ,
, 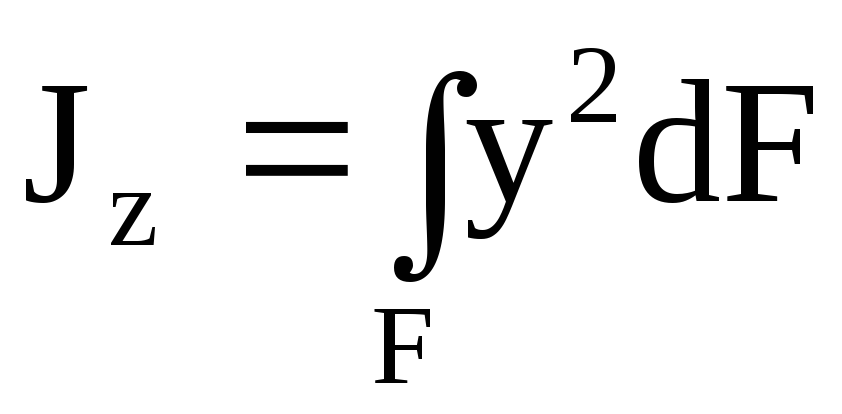 .(4.6)
.(4.6)
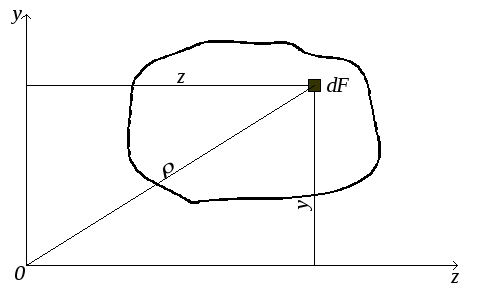
Рис.4.4
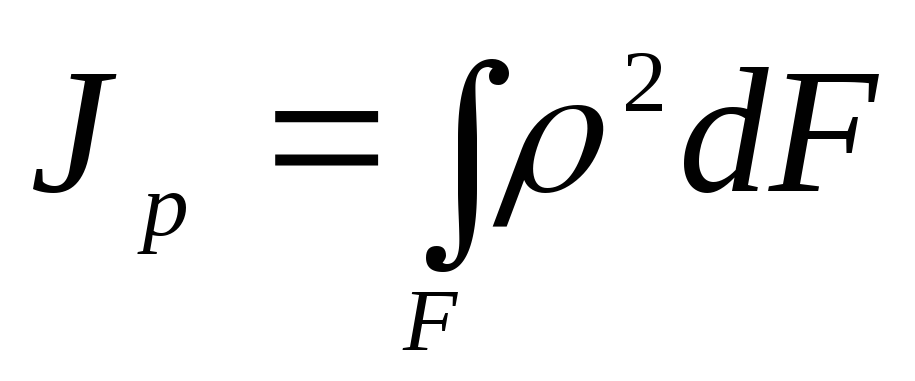 . (4.7)
. (4.7)
 . (4.8)
. (4.8)
Если начало координат совпадает с полюсом, то ρ2 = z2 + y2, следовательно
Jp = Jz + Jy. (4.9)
Размерность моментов инерции – единица длины в четвёртой степени (например, см4). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным
в зависимости от положения осей.
| Рис.4.5 | Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут её главными осями инерции, поскольку в этом случае |
каждой положительной величине zydF соответствует такая же отрицательная по другую сторону от оси симметрии (рис.4.5) и их сумма по всей площади фигуры равна нулю.
Главные оси, проходящие через центр тяжести, называются главными центральными осями.
Вычислим моменты инерции прямоугольника относительно главных центральных осей (рис.4.6,а). Оси z и y – главные, т.к. они являются осями симметрии, Jzy = 0.
а б
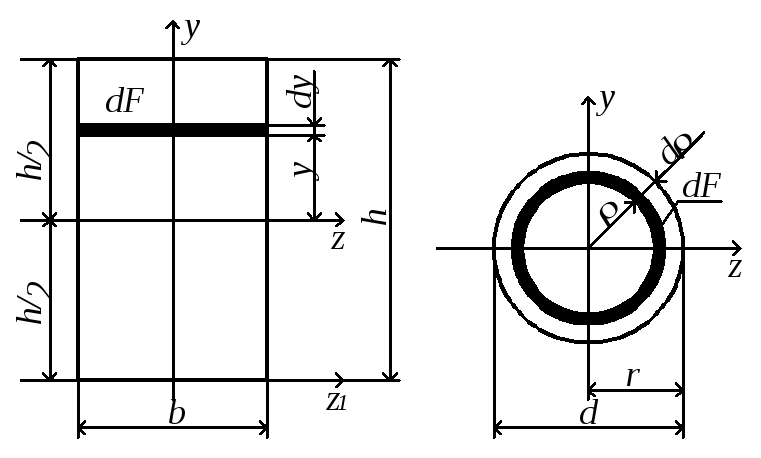
Рис.4.6
Для определения осевого момента инерции относительно оси z выделим элементарную площадку в виде полоски, параллельной оси z:
dF = bdy,
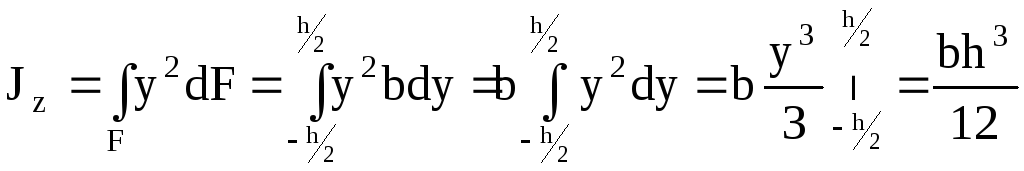 .
.
Очевидно, что для определения Jy надо поменять местами стороны прямоугольника.
Главные осевые моменты инерции прямоугольника
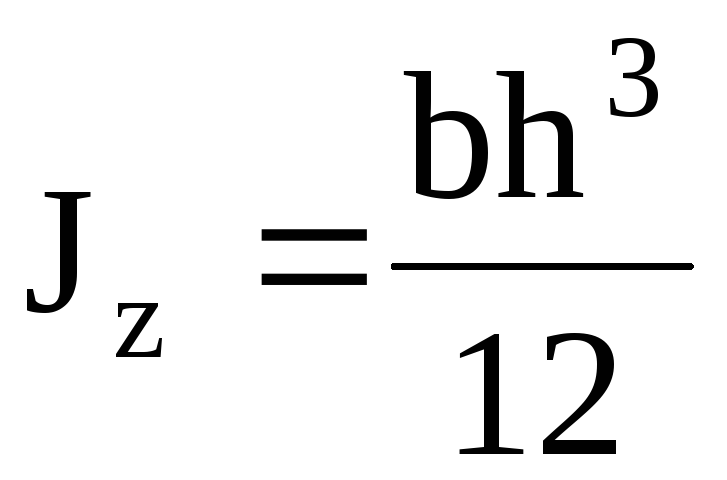 ,
,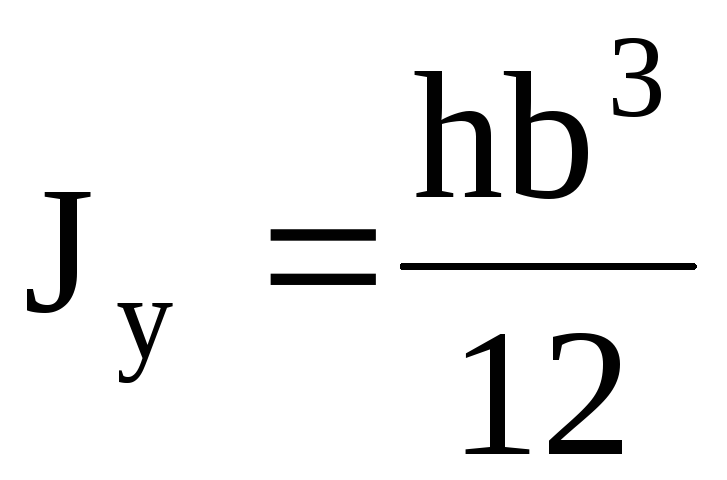 . (4.10)
. (4.10)
Вычислим полярный момент инерции круга относительно его центра, а также осевой момент инерции относительно центральной оси. При вычислении полярного момента инерции выделим элементарную площадку в виде тонкого кольца толщиной dρ (рис.4.6,б) и подсчитаем по формуле (4.7)
dF = 2πρdρ,
 .
.
Полярный момент инерции круга
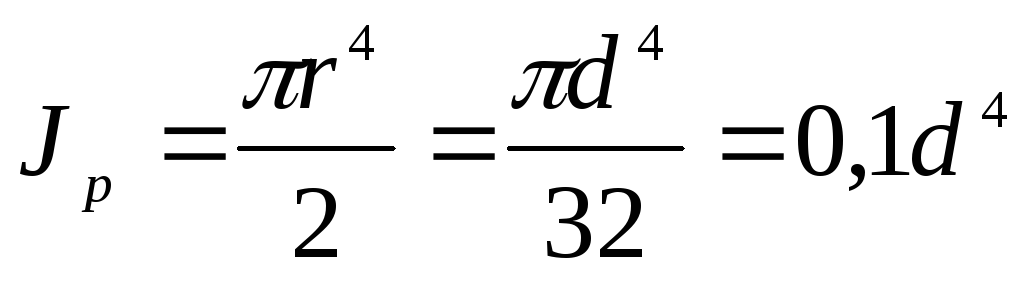 . (4.11)
. (4.11)
Осевой момент инерции круга легко найти из выражения (4.9), учитывая, что в силу симметрии Jz= Jy . Следовательно,
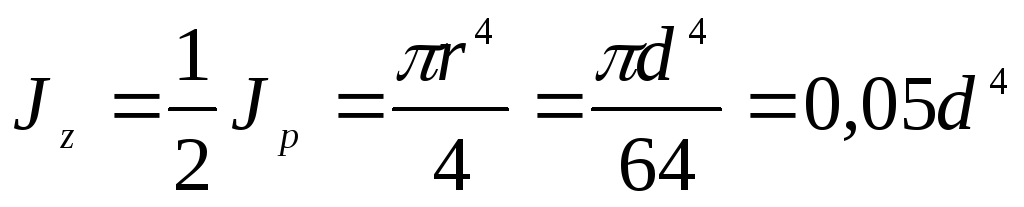 . (4.12)
. (4.12)
studfiles.net