или 
где 
Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.Проблема:
Нужны ли дроби в повседневной жизни людей?
Гипотеза:
В современном мире люди считают, что знание дробей необязательно для повседневной жизни.
Цель исследования:
Показать, что дроби играют важную роль не только в математике, но и в повседневной жизни.
Задачи исследования:
1. Изучить литературу по теме «Дроби».
2. Выяснить как пользовались дробями люди в разное время.
3. Изучить сферы деятельности людей, в которых используются дроби.
Методы исследования:
1. Опрос ( по результатам которого я увижу насколько современные люди видят пользу применения дробей в обычной жизни)
2. Анализ литературы
Обыкновенная дробь — запись рационального числа в виде
Рассмотрим чуть подробнее историю дробей.
Дроби в Древнем Египте
Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали 1/4, 1/8 …, затем 1/3 , 1/6 и т.д., то есть самые простые дроби, доли целого, называемые единичными или основными дробями. У них числитель всегда единица. Некоторые народы древности и, в первую очередь, египтяне выражали любую дробь в виде суммы только основных дробей. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами.
Вавилонские дроби
Происхождение шестидесятеричной системы счисления у вавилонян связано, как полагают ученые, с тем, что вавилонская денежная и весовая единицы измерения подразделялись в силу исторических условий на 60 равных частей:Шестидесятые доли были привычны в жизни вавилонян. Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602 = 3600, 603 = 216000 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями.
дроби в Древней Греции
В Древней Греции арифметику – учение об общих свойствах чисел – отделяли от логистики – искусства исчисления. Греки считали, что дроби можно использовать только в логистике. Здесь мы впервые встречаемся с общим понятием дроби вида m/n. Таким образом, можно считать, что впервые область натуральных чисел расширилась до области дополнительных рациональных чисел в Древней Греции не позднее V столетия до н. э. Греки свободно оперировали всеми арифметическими действиями с дробями, но числами их не признавали.
Таким образом мы видим, что зарождение дробей началось намного раньше, чем думаем.
Дроби играют важную роль, не только в математике, но и в обычной жизни и самых разнообразных профессиях. Повар, врач, портной, водитель- все эти профессии включают в себя знание дробей, рассмотрим подробнее в презентации.
Исходя из презентации, могу с уверенностью сказать о том, что дроби необходимы не только в математике. Несмотря на то, что в презентации были рассмотрены только сферы деятельности, я уверена, что многая деятельность встречается нам и в повседневной жизни, например, готовка, шитье и т.д.
Я провела несколько опросов, с помощью которых станет понятно подтверждается ли моя гипотеза или нет.1. Обладаете ли вы знаниями о дробях?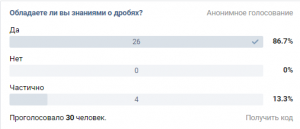
Как я и ожидала, огромная часть опрашиваемых обладает знаниями дробей. Всего 4 человека из 30 считают, что обладают лишь частичными знаниями.2.Приходилось ли вам в повседневной жизни пользоваться знаниями о дробях?
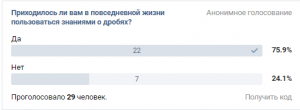Большинству из опрошенных приходилось пользоваться дробями в обычной жизни, однако, были те, кто полагает, что никогда не сталкивался с такой ситуацией.3. Необходимы ли знания о дробях в повседневной жизни?
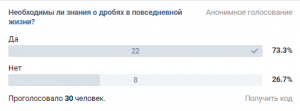Большая часть опрошенных считает, что знание дробей необходимо в повседневной жизни, с чем я полностью согласна, но были те, кто считает, что эти знания не нужны.4. В каких сферах чаще всего встречаются дроби?
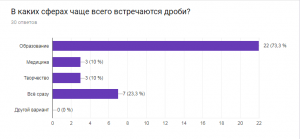Несомненно, самая большая часть ответивших, решила, что в сфере образования дроби встречаются чаще всего. Далее последовал ответ, что дроби чаще всего встречаются во ВСЕХ сферах, ну, а оставшиеся варианты были разделены поровну.5. Осознанно ли вы используете дроби в повседневной жизни?
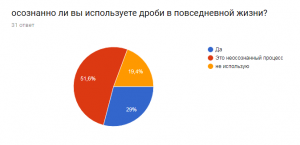Большая часть опрошенных использует дроби в повседневной жизни неосознанно, возможно, по этой причине, многие и выбрали 3 вариант, т.к. просто не могут вспомнить такое.Но были люди, которые осознанно используют дроби в обычной жизни.
Предлагаю вашему вниманию небольшой комикс по теме.Очень важно не только знать о дробях, но и разбираться в них.
Вывод: Изучая разнообразную литературу, проводя опросы, я пришла к выводу, что на сегодняшний день люди знают о дробях и используют их не только в математике, но и в повседневной жизни, причем процесс, когда мы используем дроби бессознателен. Таким образом моя гипотеза не подтвердилась, что очень хорошо.
Используемая литература:1. Возникновение дробейURL- http://www.webmath.ru/poleznoe/formules_12_0.php(дата обращения: 1.07.2017г.)2. Обыкновенные дроби в жизни людей URL-https://infourok.ru/obiknovennie-drobi-v-povsednevnoy-zhizni-376336.html( дата обращения: 2.07.2017)3. История дробей URL-http://schools.keldysh.ru/sch2905/drobi/history.htm(дата обращения: 4.07.2017)
iteach.vspu.ru
[link] и правильная дробь, называются смешанными. Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа. Например, для смешанной дроби [pic] [pic] число 3 - целая часть, [pic] а 2/5 - дробная.
Десятичная дробь, это дробь, которая записывается без знаменателя.Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
[pic] .
2.2 История возникновения дробей
История возникновения дробей, как ни странно ведется еще с ранней стадии развития человечества. Так, например, первобытным людям приходилось делить добычу между участниками охоты, когда число животных оказывалось не кратным числу охотников. Им приходилось делить 2 животных на трёх охотников. Вот и получал каждый 2/3 добычи. В результате стали появляться дробные числа. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась в целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага. Поэтому второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения. В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, четверть шага. Можно сделать вывод, что дробные числа возникли как результат измерения величин.
Таким образом, во всех цивилизациях понятие дроби возникло из процесса дробления целого на равные части. Русский термин «дробь», как и его аналоги в других языках, происходит от латинского «fractura», который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять, делить.
Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три – «треть», четыре – «четверть» и т. д.), для половины это не так – ее название во всех языках не имеет ничего общего со словом «два».
Система записи дробей, правила действий с ними заметно различались как у разных народов, так и в разные времена у одного и того же народа. Важную роль играли также многочисленные заимствования идей при культурных контактах различных цивилизаций. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
У римлян основной единицей измерения массы, а также и денежной единицей служил «асс». Асс делился на 12 равных частей - унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12. Со временем унции стали применяться для измерения любых величин. Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной. Данная система измерения до сих пор используется на мировом рынке драгоценных металлов.
У Египтян были основные, или единичные дроби. На протяжении многих веков египтяне именовали дроби “ломаным числом”, а первая дробь, с которой они познакомились, была 1/2. За ней последовали 1/4, 1/8, 1/16, …, затем 1/3, 1/6, …, т.е. самые простые дроби называемые единичными или основными дробями. У них числитель всегда единица.
Одним из первых известных упоминаний о египетских дробях является математический папирус Ринда. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 2/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф [pic] (ер, «[один] из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию (см. приложение № 1).
У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (больше чем 1/2) (см. приложение № 2).
У жителей Вавилона использовались шестидесятеричные дроби, то есть те, у которых в знаменателе всегда была цифра 60. Кстати, именно от этой системы мы получили в наследство деление часа и геометрические углы.
В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах можно найти следующие названия дробей на Руст: полтина, четь, треть, полтреть и т. д. (см приложение № 3).
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
А вот история возникновения десятичных дробей, которыми мы пользуемся сегодня, ведется из древнего Китая. Они обозначали дробь словами, используя меры длины чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки.
Более полную и систематическую трактовку получают десятичные дроби в трудах среднеазиатского ученного ал-Каши в 20-х годах XV века. Среднеазиатский город Самарканд был в XV веке большим научным центром. Там в знаменитой обсерватории, созданной видным астрономом Улугбеком, внуком Тамерлана, и работал в 20-х годах XV века крупный ученый того времени – Джемшид Гиясэддин ал-Каши. Это он впервые изложил учение о десятичных дробях в своей книге «Ключ арифметики», написанной в 1427 г. Он вводит специфическую для десятичных дробей запись: целая и дробная часть пишутся в одной строке. Для отделения первой части от дробной он не применяет запятую, а пишет целую часть черными чернилами, дробную же – красными или отделяет целую часть от дробной вертикальной чертой.
Но открытие десятичных дробей ал-Каши стало известно в Европе лишь спустя 300 лет после того, как эти дроби были в конце XVI века заново открыты фламандским инженером и ученом Симоном Стевиным (1548-1620). Его и считают создателем десятичных дробей. В своей книге «Десятая» он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании "изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов". Он писал цифры дробного числа в одну строку с цифрами целого числа, при этом нумеруя их.
В XVII века происходит активное внедрение дробей в науку, вследствие чего, вместо разделительной полоски, в дробь была введена точка. А в 1617 году шотландский математик Джон Непер предложил ввести в качестве разделителя дроби – запятую. Именно благодаря этому мы и получили те дроби, которыми пользуемся сегодня.
Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби, хотя по сути они повторяют их.
2.3 Дроби в повседневной жизни
В настоящее время в науке и во всех отраслях народного хозяйства десятичные дроби и частный их вид, проценты, применяется намного чаще, чем обыкновенные дроби. Невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел. Мы привыкли пользоваться благами цивилизации – автомобилем, телефоном, телевизором и прочей техникой, делающей нашу жизнь легче и интереснее. А сколько расчётов и вычислений делают конструкторы, инженеры, чтобы на свет всё время появлялись новинки, и везде в расчётах инженеров - конструкторов присутствуют дроби! Приведу такой пример. У нас в России стали выпускать новый современный пассажирский лайнер «Сухой Суперджет 100». Он имеет много положительных характеристик. Особенностью самолёта стал интерьер – 93 места с шагом кресел 86,36 см, что позволяет пассажирам чувствовать себя достаточно свободно: обычно у авиакомпаний этот шаг составляет 76,2 – 78,74 см. И это не является прихотью инженеров-конструкторов, а следствием точного расчета, основанного на полученных научных данных.
Еще в стародавние времена русские мастера-строители для того, чтобы получить качественный материал, например кирпич для строительства, использовали дроби, добавляя к определенным долям глины, определенные доли золы, извести и других компонентов. Именно поэтому храмы и церкви, возведённые в 9-11 веках, дошли до нас, что подтверждает высокое качества строительных материалов.
Десятичные дроби используются в различных отчётных документах в медицине, образовании, торговле, налоговой службе. А какая точность нужна в фармацевтике! При составлении лекарственных препаратов нужно предельное внимание при обращении с дробями.
А как близки дроби спортсменам! Возьмём для примера самый простой вид спорта – бег. В 1936 году легендарный Джесси Оуэнс в беге на 100 метров установил рекорд – 10,2 секунды. В течение двух десятков лет этот рекорд был пределом спортсменов-спринтеров. На Олимпиаде в Мехико в 1968 год этот рекорд был, наконец, побит – 9,9 секунды. В 2009 г. на данной дистанции установлен новый мировой рекорд – 9,58 секунды. Это время, показанное ямайским бегуном Усэйном Болтом, остается действующим мировым рекордом.
Интересна история золотой медали в конькобежном спорте на зимней Олимпиаде в Санкт-Мориц (Швейцария, 1948 г.). Оказывается, эту медаль не получил ни один конькобежец. На 2 месте пьедестала стояли 3 человека, на 3 месте – 2 человека, а 1 место осталось свободным. Вся причина опять же в десятичных дробях. В то время не учитывались сотые доли секунды, результаты у спортсменов оказались одинаковыми. Сейчас спортсмены борются даже не за десятые, а за сотые доли секунды! 0,01 доля секунды так мала, что за это время человек даже не успевает мигнуть. Судьбу призового места решает фотофиниш, который позволяет учитывать такие малые дробные числа. Сотые доли секунды позволили и мне завоевать золотую медаль в плавании вольным стилем на дистанции 50 метров.
Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дробные числа окружают нас и в быту, их можно отыскать и в комнате. Измеряя длину и ширину различных предметов, я ни разу не встретился с целым числом. В прошлом году перед ремонтом мы с папой решили две практические задачи с применением дробей, что помогло нам понять, сколько требуется обоев и краски для ремонта.
Моя мама бухгалтер, и она рассказала мне, что в бухгалтерии также используются дроби. Например, чтобы правильно рассчитать заработную плату и налоги, причитающиеся к уплате в бюджет, понадобятся десятичные дроби. Так ставка налога в Фонд медицинского страхования в 2015 году составляет 5,1%, а в Фонд социального страхования 2,9%.
И на кухне встречаются дроби. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда, расчета калорийности. Но сначала нужно купить определенное количество продуктов и рассчитать пропорции ингредиентов в составе блюда. Само блюдо нужно умело поделить на порции, в чем опять нам помогут дроби. В различных рецептах приготовления часто требуется взять 1/3 стакана сахара или 1/2 чайных ложки соды и т. д.
Дроби проникли даже в детскую художественную литературу! Например, в сказке Лии Гераскиной «В стране невыученных уроков» несчастный Витя Перестукин получил ответ своей задачи -1,5 землекопа. А в стихотворении Самуила Яковлевича Маршака «Про одного ученика и шесть единиц» одну из единиц ученик получил за неумение решать задачи на дроби.
Итак, делаем вывод, десятичные дроби и их частный вид «проценты» проникли во все сферы деятельности человека и успешно служат ему.
2.4 Мои наблюдения
Я провел анкетирование среди учащихся моего класса и их родителей. Результаты показали, что, к сожалению, не все одноклассники любят математику и не понимают, где в повседневной жизни можно встретить обыкновенные и десятичные дроби. Хорошо, что каждый из нас усвоил понятие математической дроби. Я рассказал, что выражение «попал в дроби» в переводе с немецкого языка означает попасть в трудное положение. Не так то и просты эти необыкновенные обыкновенные дроби! Результаты анкетирования см. в приложении № 4.
Отвечая на вопрос, где можно встретить по вашему мнению дроби в жизни, основная масса ребят и их родителей ответила - при оплате за коммунальные услуги, приготовление еды, строительство и ремонт (см. приложение № 5). Среди основных профессий, где применяются дроби были названы: бухгалтер, фармацевт, строитель, повар, продавец (см. приложение № 6)
2.5 Достижения науки и техники
Во второй половине 20 века возникла новая отрасль науки - промышленная электроника. Учёные исследуют строение вещества на клеточном, молекулярном и атомном уровнях. Трудно представить, насколько мала молекула. Все вещества на свете состоят из таких малых частиц – молекул. Если попросить всех жителей Земли дать по 1 000 000 000 молекул, то вы соберёте 0, 000 000 001 г вещества. Такую маленькую массу очень трудно ощутить на руке. Учёным приходится оперировать всё более мелкими единицами измерения. Эти сверхмалые величины: микро, нано («карлик»), пико и фемто обозначаются десятичными дробями со множеством нулей. Например, в 1 нанометре содержится 1 миллиардная часть метра: 1 нм =0,000000001 м. Эти величины можно увидеть только под электронным микроскопом. Применяя нанотехнологию, учёные выводят науку на совершенно новую ступень развития. Нет сомнения, что в новом веке, веке нанотехнологий, будут нужны ещё более точные дроби.
3. Заключение
В процессе познания действительности математика играет все возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось неразрешимыми, успешно решаются благодаря применению математики, тем самым расширяются возможности науки. Математика всегда была неотъемлемой и существенной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и развития личности. Сегодня можно с уверенностью сказать, что дроби – неотъемлемая часть нашей жизни.
В своей работе, я попытался показать, что практически во всех областях науки, техники, образования, медицины и т.д. применяются математические дроби. Знание понятия математическая дробь очень важно! Я считаю, что математика очень интересный и нужный предмет. Она позволяет развить умственные способности человека, тренирует память, усиливает быстроту мышления, умение прогнозировать, логически мыслить. Помните, математика жизненно необходима человечеству. Это ключ к прогрессу и процветанию.
4. Список используемой литературы
М.Я.Выгодский “Арифметика и алгебра в Древнем мире”(М. Наука,1967г)
Г.И.Глейзер “История математики в школе”(М. Просвещение,1964г)
И.Я.Депман “История арифметики” (М. Просвящение, 1959г)
Н.Я.Виленкин «За страницами учебника математики. Арифметика» (М. Просвещение, 2008)
5.Приложение № 1
Запись единичной дроби у древних египтян
[pic]
Приложение 2
Специальные символы для дробей в Древнем Египте
[pic]
Приложение № 3
Таблица № 1
Названия дробей на Руси
1/2 - половина, полтина1/3 – треть
1/4 – четь
1/6 – полтреть
1/8 - полчеть
1/12 –полполтреть
1/16 - полполчеть
1/24 – полполполтреть (малая треть)
1/32 – полполполчеть (малая четь)
1/5 – пятина
1/7 - седьмина
1/10 - десятина
Приложение №4
Таблица № 2
Приложение № 5
Д [pic] иаграмма № 1
[pic]
Приложение № 6
Диаграмма № 2
[pic] [pic]
Рецензия
на исследовательскую работу ученика 6 «А» класса МБОУ СОШ №64 города Самара Новикова Ивана .
Работа Новикова Ивана по теме «Дроби в жизни человека» посвящена исследованию истории развития обыкновенных и десятичных дробей , их необходимости и важности в повседневной жизни.
Тему «Дроби» начинают изучать с 5 класса. И , как показывает мне мой опыт ,это одна из наиболее сложных тем для усвоения детьми. При выполнении действий с дробями ученику требуется не только применить только что изученные правила ,но и вспомнить все, что было изучено ранее, в начальной школе. Степень сконцентрированности в этот момент максимальна и не удивительно, что появляется много вычислительных ошибок у детей. А если тема еще и не понятна или не интересна ,то вероятность не справиться с заданием возрастает многократно.
Как показывает практика работы в школе , когда ребенок более углубляется в изучение проходимого материала, то интерес к математике возрастает многократно. В своей работе Иван исследовал не только понятие дроби, но и проследил историю их возникновения, область применения дробей в повседневной жизни, их жизненную необходимость в некоторые моменты в нашей жизни.
Данная исследовательская работа содержит все необходимые структурные элементы для подобных работ – введение, основная часть, заключение, список источников информации, приложения. В работе чётко обозначены цель и задачи, которые были решены в процессе работы. Работа имеет большую практическую значимость и может быть использована и на уроках математики и во внеурочное время. Иваном проведена большая работа с литературой.
По мнению автора, эта тема является для него полезной, при выполнении работы Иван сделал для себя много важных открытий.
Работа Ивана показывает важность и актуальность математики в повседневной жизни.
Работа Новикова Ивана соответствует требованиям к исследовательским работам.
Учитель математики Ларионова М.М.
docbaza.ru
Слайд 1
МБОУ ООШ №31 г.к.Анапа ст.Гостагаевская Проект: «Дроби вокруг нас» Выполнили Ученицы 5 «Б» класса Бажанова Ирина Кононенко Кристина Хателишвили Александра Руководитель проекта Хателишвили Евгения Валентиновна 2012 – 2013 учебный годСлайд 2
Аннотация проекта Целью проекта является изучение понятия «дробь» как в окружающей нас жизни, так и в математике, подтверждение, или опровержение выдвинутой гипотезы о невозможности существования человека без дробей. В связи с поставленной целью необходимо решить следующие учебные задачи: Узнать историю возникновения дробей в математике; 2. Узнать, где человек встречается с понятием «дробь» в жизни; 3. Выяснить необходимость использования математических дробей как в профессиональной деятельности, так и в повседневной жизни.
Слайд 3
План проведения проекта 1 . Организационно-ознакомительный этап. Учитель выясняет имеющиеся знания по этой теме. Определяются темы для исследований, каждый из участников проекта будет исследовать свою тему 2. Исследовательский этап Проведение исследований. Сбор информации, а именно: ◆ самостоятельный поиск информации в Интернет, работа с печатными материалами; ◆ проведение опросов и их анализ; ◆ оформление работ; ◆ составление плана презентации ; ◆ создание презентации; ◆ подготовка к защите . 3. Защита проекта.
Слайд 4
Как возникли дроби в математике. Дроби на Руси Необходимость в дробях возникла на очень ранней ступени развития человека. В жизни человеку приходилось не только считать предметы, но и измерять величины. Люди измеряли длины, площади земельных участков, объемы, массы тел, время, вели расчеты за купленные или проданные товары. Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Так появились дроби . В русском языке слово дробь появилось в VIII веке, оно происходит от глагола «дробить » — разбивать, ломать на части. В первых учебниках математики (в VII веке) дроби так и назывались — « ломаные числа». У других народов название дроби также связано с глаголами « ломать», «разбивать», «раздроблять».
Слайд 5
- Половина, полтина - Треть -Четь - Пятина - Полтреть - Седьмина - Полчеть - Десятина - Пол-полтреть - Пол-полчеть Пол-пол-треть (малая) Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть. Дроби на Руси называли долями, то есть маленькими числами. В старых рукописях встречаются следующие названия дробей: половина, полчеть , полополочеть , треть, полтреть и т.д.
Слайд 6
Дроби в древнем Египте Изучение папирусов показало, что в Древнем Египте обозначали дроби не так, как обозначаем их мы: вверху –числитель , ниже черты – знаменатель. У них черты дроби не было, специального общего для всех дробей способа обозначения не было. Египтяне употребляли только дроби с числителем единица. Они все дроби старались записать как суммы долей. Например, вместо 8/15 они писали 1/3 + 1/5. Единственным исключением была дробь 2/3. Иногда это бывало удобно. В папирусе Ахмеса есть задача : " Разделить 7 хлебов между 8 людьми".
Слайд 7
" Разделить 7 хлебов между 8 людьми". Если резать каждый хлеб на 8 частей, придется провести 49 разрезов. А по-египетски эта задача решалась так. Дробь 7/8 записывали в виде долей: 1/2 + 1/4 + 1/8. Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба - на 4 части и один хлеб - на 8 долей, после чего каждому даем его часть . Но складывать такие дроби было неудобно. Поэтому папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде сумм долей. С помощью этой таблицы выполняли умножение и деление чисел.
Слайд 8
Эволюция записи дробей Народы прошли через многие варианты записи дробей, пока не пришли к современной записи. Вначале в записи дробей не использовалась дробная черта. Черта дроби появилась лишь только в 1202 году у итальянского математика Леонардо Пизанского. Он ввел слово дробь . Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик. Записывать дроби как сейчас стали арабы.
Слайд 9
Эволюция записи дробей Действия над дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби». Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в 1585 году голландский математик и инженер Симон Стевин. Посмотрите, как записывалась десятичная дробь – 0,1
Слайд 10
Вот , как изображалась дробь 14,382 Иоганн Гартман Бейер в 1603 году ввел запись Иоганн Кеплер в 1616 году - 14(382 Английский математик Вильям Оутред в 1631 году - Пьер Эригон в 1634 году - 14 382 ”’ Роберт Джагер в 1651 году -
Слайд 11
Дроби в построении изображения человека Голова составляет 1\8 часть туловище составляет 3\8 ноги составляют 4\8 части У взрослого человека размер головы укладывается в высоте фигуры 8 раз.
Слайд 12
Для построения изображения головы человека высоту головы делим на 7 частей. построение изображения головы человека 2\7 расстояние до глаз . Расстояние между глазами равно длине глаз Глаз Глаз 1\3 1\3 Ширина головы = 3\4 высоты головы От глаз до конца носа расстояние 2\7 + 1\14.
Слайд 14
Использование дробей в строительстве Без знаний дробей невозможно построить здания, возвести мосты, проложить асфальт и т.д. Чтобы сделать строительный раствор необходимо знать дроби.
Слайд 15
Из данной таблицы видно ,что в замесе раствора цементом марки 300 требуется на 1/10 меньше гравия , чем при использовании цемента марки 400, при этом воды понадобится на 1/10 больше. Марка бетона 200 300 400 цемент 1/8 1/10 1/10 песок 2/8 3/10 3/10 гравий 4/8 4/10 5/10 вода 1/8 2/10 1/10
Слайд 16
Дроби в музыке Шестнадцатая, восьмая, четвертная, половинная, целая нота. Названия длительностей служат одновременно и названиями чисел. Это равенство следует понимать в том смысле, что длительность слева равна суммарно длительности справа. С помощью чисел то же равенство можно записать в виде 1=1/4+1/4+1/2.
Слайд 17
В представленных произведениях просчитаем общую длительность всех нот входящих в каждый такт Третий такт : Первый такт : Второй такт : Нетрудно заметить, что в каждом такте любого произведения получили одни и те же числа. Это число называется размером музыкального произведения и записывается в начале нотного стана. Дроби в музыке
Слайд 18
Вывод Полученные результаты исследования подтверждают гипотезу, выдвинутую в начале исследования о том, что дроби учувствуют в нашей жизни повсеместно.
Слайд 19
Использованные материалы Балк М.Б. Математика после уроков. – М.: Просвещение,1997 http://www.1sentyabrya.ru/ http://www.petelin.ru/ http://www.bestreferat.ru/ http://www.letopisi.ru/ http://www.klassika.ru/ http://ru.wikiquote.org/ http://www.slideshare.net/ http://www.uroki.net/ http://www.dxdy.ru/
nsportal.ru
