|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
11. Формула Муавра. Извлечение корня из комплексного числа. Реферат формула муавра
Лекция 8. Формула Муавра. Корни из к.ч
Лекции по алгебре и геометрии. Семестр 1.
Лекция 8. Формула Муавра. Корни из комплексных чисел.
Краткое содержание: формула Муавра, деление к.ч. в тригонометрической форме записи, корни из к.ч. и их расположение на комплексной плоскости, группа корней из 1, многочлен деления круга и его разложение на неприводимые множители с действительными коэффициентами.
Глава 8. Формула Муавра. Корни из комплексных чисел.
п.1.Формула Муавра.
Теорема. (Формула Муавра, 1707 г.)
Для любого целого числа nи любого действительного числа имеет место следующее равенство:
имеет место следующее равенство:
 . (1)
. (1)
Доказательство. Разобьем доказательство на 3 этапа.
1) Пусть  – натуральное число. Так как комплексное число
– натуральное число. Так как комплексное число имеет модуль
имеет модуль , то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
, то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
2) Пусть теперь  . Тогда
. Тогда

 , ч.т.д.
, ч.т.д.
3) Пусть  , где
, где – натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и в поле комплексных чисел, имеем:
– натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и в поле комплексных чисел, имеем:


 .
.
Здесь мы использовали уже доказанные случаи формулы Муавра возведения в натуральную степень и в степень, равную (–1).
Теорема доказана.
Следствие. (О целых степенях комплексного числа.)
Пусть  . Тогда
. Тогда
 .
.
Доказательство предоставляется читателю.
п.2. Деление комплексных чисел в тригонометрической форме записи.
Теорема. (О делении комплексных чисел в тригонометрической форме)
Пусть  , где
, где и
и , где
, где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
 . (2)
. (2)
Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:


 , ч.т.д.
, ч.т.д.
Пример 1. Запишите комплексные числа  и
и в тригонометрической форме и найдите их произведение
в тригонометрической форме и найдите их произведение и частное
и частное .
.
Решение. 1) Комплексное число  на комплексной плоскости находится во второй четверти, поэтому
на комплексной плоскости находится во второй четверти, поэтому
 ,
,  .
.
2) Комплексное число  на комплексной плоскости находится во четвертой четверти, поэтому
на комплексной плоскости находится во четвертой четверти, поэтому
 ,
,  .
.
3) 
 .
.
 Ответ:
Ответ:  ,
, .
.
Пример 2. Вычислить  .
.
Решение. Комплексное число  на комплексной плоскости находится в третьей четверти, поэтому
на комплексной плоскости находится в третьей четверти, поэтому ,
,
Применим формулу Муавра:



 .
.
п.3. Корни из комплексных чисел.
Определение. Пусть  и
и . Корнемn-й степени из комплексного числаzназывается комплексное число
. Корнемn-й степени из комплексного числаzназывается комплексное число , такое, что
, такое, что .
.
Теорема. (Формула корней из комплексного числа.)
Для любого ненулевого комплексного числа
 , где
, где  , существует ровноnкорнейn-й степени из комплексного числаzи все они могут быть найдены по формуле
, существует ровноnкорнейn-й степени из комплексного числаzи все они могут быть найдены по формуле
 , (3)
, (3)
где  ,
, – арифметический кореньn-й степени из положительного числа
– арифметический кореньn-й степени из положительного числа .
.
Доказательство. Обозначим
 (4)
(4)
и докажем, что данное множество исчерпывает все множество корней n-й степени из комплексного числаz.
Доказательство проведем в 3 этапа. Сначала мы докажем, что все элементы множества (4) являются корнями n-й степени из комплексного числаz. Затем мы покажем, что среди корней множества (4) нет равных. И, наконец, мы покажем, что любой кореньn-й степени из комплексного числаzявляется элементом множества (4).
1) По следствию 2 формулы Муавра 

 , ч.т.д.
, ч.т.д.
2) Допустим, что  , где
, где и
и . Тогда по теореме о равенстве двух комплексных чисел в тригонометрической форме записи следует, что равны их аргументы.
. Тогда по теореме о равенстве двух комплексных чисел в тригонометрической форме записи следует, что равны их аргументы.
Но, аргумент числа  может отличаться от числа
может отличаться от числа на число кратное числу
на число кратное числу (т.е. на целое число оборотов) и аналогично для аргумента числа
(т.е. на целое число оборотов) и аналогично для аргумента числа . Отсюда следует, что
. Отсюда следует, что , где
, где . Умножим это равенство наn:
. Умножим это равенство наn: . Отсюда следует, что
. Отсюда следует, что и т.к. по нашему предположению
и т.к. по нашему предположению , то
, то , чего не может быть, т.к.
, чего не может быть, т.к. и
и . Получили противоречие. Следовательно, среди корней в множестве (10) нет равных, ч.т.д.
. Получили противоречие. Следовательно, среди корней в множестве (10) нет равных, ч.т.д.
3) Пусть теперь комплексное число  является корнемn-й степени из комплексного числаz, т.е.
является корнемn-й степени из комплексного числаz, т.е. . Так как
. Так как . Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства
. Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства и
и , где
, где . Из первого равенства получаем, что
. Из первого равенства получаем, что , а из второго следует
, а из второго следует .
.
Далее, разделим целое число tнаnс возможным остатком: , где
, где , а остатокrтакже является целым числом, но
, а остатокrтакже является целым числом, но . Отсюда
. Отсюда
 и
и
 . Таким образом, корень
. Таким образом, корень  является корнем из множества корней (4), ч.т.д.
является корнем из множества корней (4), ч.т.д.
Теорема доказана.
Пример. Вычислить  .
.
Решение. Запишем число  в тригонометрической форме записи:
в тригонометрической форме записи: . Тогда
. Тогда
 , где
, где

 ,
,  .
.
Ответ:  , где
, где
 ,
,
 ,
,
 .
.
п.4. Расположение корней на комплексной плоскости.
Перепишем формулу (3) в виде
 , где
, где  ,
, .
.
Заметим, что
 . (5)
. (5)
Из этой формулы мы видим, что аргументы корней образуют арифметическую прогрессию.
Так как модуль у всех корней одинаковый, то на комплексной плоскости они удалены от начала координат на одинаковое расстояние. Отсюда делаем вывод, что все корни на комплексной плоскости изображаются точками, лежащими на окружности радиуса  с центром в начале координат. Из формулы (5) мы видим, что угол между такими двумя соседними точками одинаковый. Отсюда делаем вывод, что все корни располагаются на окружности равномерно. Если соединить все соседние точки (корни) отрезками прямой, то получим правильныйn-угольник.
с центром в начале координат. Из формулы (5) мы видим, что угол между такими двумя соседними точками одинаковый. Отсюда делаем вывод, что все корни располагаются на окружности равномерно. Если соединить все соседние точки (корни) отрезками прямой, то получим правильныйn-угольник.

рис.1.
При изображении корней на комплексной плоскости около точки, с которой отождествляется корень проставляется только его аргумент, поскольку модули у всех корней одинаковые.
Пример. Изобразить все корни  на комплексной плоскости.
на комплексной плоскости.
Решение. Сами корни мы уже вычислили (см. предыдущий пример). Изображаем координатные оси, проводим окружность радиуса  с центром в начале координат и отмечаем на ней точки полярный угол которых равен:
с центром в начале координат и отмечаем на ней точки полярный угол которых равен:
 ,
,  ,
, .
.
Соединим построенные точки отрезками прямых и получаем правильный треугольник.


рис.2.
п.5*. Корни из единицы.
Пусть  – натуральное число. По формуле корней из комплексного числа, существует ровноnкорней из комплексного числа
– натуральное число. По формуле корней из комплексного числа, существует ровноnкорней из комплексного числа . Для вычисления этих корней запишем единицу в тригонометрической форме:
. Для вычисления этих корней запишем единицу в тригонометрической форме:
 , т.е.
, т.е.  ,
, .
.
Обозначим все множество корней через  . По формуле корней получаем:
. По формуле корней получаем:
 , (6)
, (6)
где
 ,
,  . (7)
. (7)
В частности,  ,
,
 . (8)
. (8)
Заметим, что  верна формула:
верна формула:
 . (9)
. (9)
Действительно, равенство (9) сразу же получается по формуле Муавра:
 .
.
Теперь мы все множество корней  из 1 можем записать так:
из 1 можем записать так:
 (10)
(10)
Теорема. Множество всех корней из 1 является коммутативной группой.
Доказательство. Сначала мы должны показать, что множество  замкнуто относительно умножения. Пусть
замкнуто относительно умножения. Пусть – два произвольных корня из 1, т.е.
– два произвольных корня из 1, т.е. . Найдем их произведение:
. Найдем их произведение:
 .
.
Замечаем, что
 . (11)
. (11)
Отсюда следует, что  , если
, если . В противном случае,
. В противном случае, . Обозначим через
. Обозначим через и
и . Тогда
. Тогда
 , ч.т.д.
, ч.т.д.
Таким образом, на множестве  определена операция умножения и т.к. она ассоциативна и коммутативна в поле комплексных чисел, то она ассоциативна и коммутативна и на множестве
определена операция умножения и т.к. она ассоциативна и коммутативна в поле комплексных чисел, то она ассоциативна и коммутативна и на множестве . Далее,
. Далее, . Покажем, что любой элемент из
. Покажем, что любой элемент из имеет обратный элемент также принадлежащий множеству
имеет обратный элемент также принадлежащий множеству :
:
 .
.
Действительно, по условию  . Тогда
. Тогда
 , т.е.
, т.е.  .
.
Теорема доказана.
Пример. Построить таблицу умножения для группы  .
.
Решение. Обозначим для простоты
 . Тогда
. Тогда , где
, где .
.
Заполняем таблицу Кэли (таблицу умножения):

Изобразим все корни третьей степени из 1 на комплексной плоскости. Т.к. их модуль равен 1, то все они лежат на тригонометрической (т.е. единичной) окружности:

рис.3.
Здесь,  ,
, .
.
п.6*. Многочлен деления круга.
Определение. Многочлен

называется многочленом деления круга.
Теорема. Все корни многочлена

являются корнями  -й степени из 1.
-й степени из 1.
Доказательство. Рассмотрим многочлен деления круга как сумму членов геометрической прогрессии со знаменателем х. Тогда
 .
.
Теорема доказана.
Так как корни из 1 делят единичную окружность на nравных дуг, то из теоремы следует, что все корни многочлена вместе с 1 делят окружность на равные дуги, откуда и произошло название этого многочлена.
вместе с 1 делят окружность на равные дуги, откуда и произошло название этого многочлена.
Поставим задачу разложить многочлен деления круга на неприводимые (неразложимые) множители с действительными коэффициентами.
Известно (см. Дополнение 6), что любой многочлен с действительными коэффициентами можно представить в виде:

 , (12)
, (12)
где  – все различные действительные корни многочлена
– все различные действительные корни многочлена ,m– их число,
,m– их число, – их кратности,t– число квадратных трехчленов с действительными коэффициентами
– их кратности,t– число квадратных трехчленов с действительными коэффициентами и отрицательными дискриминантами,
и отрицательными дискриминантами, – кратности соответствующих комплексных корней,
– кратности соответствующих комплексных корней, – старший коэффициент многочлена
– старший коэффициент многочлена ,n– его степень.
,n– его степень.
Замечание. Линейных множителей может и не быть. Тогда  и многочлен не имеет действительных корней. Аналогично, многочлен может не иметь комплексных корней, тогда
и многочлен не имеет действительных корней. Аналогично, многочлен может не иметь комплексных корней, тогда . Далее, очевидно, что степень многочлена
. Далее, очевидно, что степень многочлена
 . (13)
. (13)
Из последнего равенства вытекает следующее следствие.
Следствие. Любой многочлен нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень.
Легко получить разложение (12), если известны все корни многочлена f(x). Тогда многочлен раскладывается над полем комплексных чисел на линейные множители. Так как коэффициенты многочленаf(x) предполагаются действительными, то если многочлен имеет комплексный корень , то комплексно сопряженное ему число
, то комплексно сопряженное ему число также является корнем этого многочлена. Действительно, если
также является корнем этого многочлена. Действительно, если , то
, то .
.
Разложение многочлена f(x) на линейные множители будет иметь вид:

 , (14)
, (14)
где  – все различные действительные корни многочлена
– все различные действительные корни многочлена ,m– их число,
,m– их число, – их кратности,
– их кратности, – все различные комплексно сопряженные корни многочлена
– все различные комплексно сопряженные корни многочлена ,t– число пар всех различных комплексно сопряженных корней,
,t– число пар всех различных комплексно сопряженных корней, – их кратности,
– их кратности, – старший коэффициент многочлена
– старший коэффициент многочлена ,n– его степень.
,n– его степень.
Теперь, перемножим пару линейных множителей содержащие комплексно сопряженные корни. Пусть
 .
.
Тогда  , откуда и получаем:
, откуда и получаем:
 .
.
Проделав то же самое со всеми парами комплексно сопряженных корней, из разложения (14) получим разложение (12).
Осталось заметить, что все корни многочлена деления круга различны и их легко вычислить и, следовательно, получить разложение на линейные множители.
Пример. Разложить на неприводимые множители с действительными коэффициентами (т.е. на полем R) многочлен .
.
Решение. Решим уравнение  . Так как
. Так как
 , то найдя все корни уравнения
, то найдя все корни уравнения  , мы найдем тем самым все корни многочлена
, мы найдем тем самым все корни многочлена .
.
Имеем,  , где
, где
 .
.

рис.4.
Вычисляя остальные корни по формуле
 ,
,
 , получаем (см. рис.4):
, получаем (см. рис.4):
 ;
;  ;
;
 ;
;  .
.
Отсюда,  и
и



 , т.к.
, т.к.  ,
, ,
, ,
,
 .
.
Ответ:  .
.
п.7*. Исторический экскурс к вопросу о построении правильного многоугольника с помощью циркуля и линейки.
(Виленкин Н.Я. и др. За страницами учебника математики.)
Геометрические задачи на построение с помощью циркуля и линейки зародились еще в древней Греции во времена Евклида и Платона. Еще в те времена, математики умели строить с помощью циркуля и линейки правильные треугольники, пятиугольники и квадраты.
Более того, они умели с помощью циркуля и линейки делить угол пополам, поэтому они умели строить и правильные 6-ти, 10-ти и 15-ти угольники и все правильные n-угольники, где ,
, ,
, и
и ,
, . Очень важно, что с помощью линейки проводятся только отрезки прямых, а длины отрезков измеряются с помощью циркуля, а не делений на линейке. Так, используя эти инструменты можно построить отрезок, длина которого выражается числом, полученным из 1 с помощью четырех арифметических действий (сложения, вычитания, умножения, деления) и извлечением квадратного корня. Т.е. вначале есть только отрезок, длина которого принимается за 1. Тогда можно построить отрезок, длина которого равна рациональному числу или квадратному корню из рационального числа. Далее, если отрезок длины а уже построен с помощью циркуля и линейки, то можно построить с помощью этих инструментов отрезок длиныb, если числоbвыражается через а с помощью арифметических действий и квадратного корня. Говорят, что такое число выражается в квадратных радикалах.
. Очень важно, что с помощью линейки проводятся только отрезки прямых, а длины отрезков измеряются с помощью циркуля, а не делений на линейке. Так, используя эти инструменты можно построить отрезок, длина которого выражается числом, полученным из 1 с помощью четырех арифметических действий (сложения, вычитания, умножения, деления) и извлечением квадратного корня. Т.е. вначале есть только отрезок, длина которого принимается за 1. Тогда можно построить отрезок, длина которого равна рациональному числу или квадратному корню из рационального числа. Далее, если отрезок длины а уже построен с помощью циркуля и линейки, то можно построить с помощью этих инструментов отрезок длиныb, если числоbвыражается через а с помощью арифметических действий и квадратного корня. Говорят, что такое число выражается в квадратных радикалах.
Таким образом, с помощью циркуля и линейки можно построить отрезок, длина которого выражается в квадратных радикалах. Все это знали еще математики древней Греции. Задачу построения других правильных многоугольников (или доказательство невозможности таких построений) не могли решить в течение двух последующих тысячелетий, а решена она была немецким студентом филологического факультета Гёттингенского университета Карлом Фридрихом Гауссом в 1796 году. В то время Гауссу было 18 лет и он разрывался между занятиями филологией и математикой и не мог сделать окончательного выбора. Решение древней задачи помогло ему сделать окончательный выбор в пользу (и на пользу) математики. Страшно даже подумать на сколько бы затормозилось развитие математики останься Гаусс филологом! До сих пор математики всего мира называют Гаусса королем математики.
studfiles.net
формула Муавра — ПриМат
Любое комплексное число можно изобразить как точку на комплексной плоскости с координатами
и
, где ось абсцисс называется вещественной, а ось ординат — мнимой.
Определение 1:
Модулем комплексного числа называется корень суммы квадратов его действительной и мнимой частей. ,
,
Определение 2:
Величина угла, который образует вектор изображающий данное число на комплексной плоскости с вещественной осью называется аргументом этого комплексного числа Угол, отсчитываемый от оси против часовой стрелки — отрицательный, по — положительный.Углы, отличающиеся на
, соответствуют одному и тому же числу и записываются как:
,
.
Определение 3:
У комплексного числа существует тригонометрическая форма записи
Примеры:
Найти геометрическое место точек (ГМТ):
Формула Муавра:
Лемма 1:
Для любых двух комлексных чисел справедливо неравенство
Доказательство:
Пусть ,
(*)
(*)=
Литература:
Геометрическая интерпретация комплексных чисел
Лимит времени: 0
Информация
Тест на тему «Геометрическая интерпретация комплексных чисел»:
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается...
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
ib.mazurok.com
11. Формула Муавра. Извлечение корня из комплексного числа
Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую Формулой Муавра:
|
| (3.5) |
Из нее следует, что Для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.
Перейдем к процедуре извлечения корней. Известно, что во множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например,  не существует. В множестве комплексных чисел дело обстоит иначе.
не существует. В множестве комплексных чисел дело обстоит иначе.
Пусть  . Комплексное число
. Комплексное число  называется корнем
называется корнем  -й степени из
-й степени из  , если
, если  , т. е.:
, т. е.:
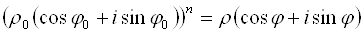
Или
 .
.
Модуль комплексного числа определяется однозначно, поэтому  или
или  (здесь имеется в виду арифметический корень).
(здесь имеется в виду арифметический корень).
Аргумент комплексного числа определяется с точностью до  . Следовательно,
. Следовательно,  , а
, а  .
.
Таким образом, комплексное число  , которое является корнем
, которое является корнем  -й степени из
-й степени из  имеет вид:
имеет вид:
|
| (3.6) |
Придавая  различные значения, мы не всегда будем получать различные корни. Действительно,
различные значения, мы не всегда будем получать различные корни. Действительно,  можно записать в виде
можно записать в виде  , где
, где  . Тогда:
. Тогда:
 ,
,
Т. е. значение аргумента при данном  отличается от значения аргумента при
отличается от значения аргумента при  на число, кратное
на число, кратное  . Следовательно, в формуле (2) можно ограничится лишь значениями
. Следовательно, в формуле (2) можно ограничится лишь значениями  . При таких значениях
. При таких значениях  получаются различные корни, так как разность между их аргументами по абсолютной величине меньше
получаются различные корни, так как разность между их аргументами по абсолютной величине меньше  .
.
Итак, для каждого ненулевого числа  существует ровно
существует ровно  корней
корней  -й степени из
-й степени из  .
.
Пример. Вычислить  .
.
Представим число, стоящее под знаком корня, в тригонометрической форме:


 .
.
Извлечем далее корень третьей степени из этого комплексного числа:
 .
.
Отсюда полагая, что  , получим:
, получим:
 ;
;
 ;
;
 .
.
Контрольные Вопросы к лекции №3
1. Счетные и несчетные числовые множества.
2. Ограниченные множества.
3. Границы и грани множеств.
4. Соединения элементов.
5. Вычисление числа размещений, перестановок и сочетаний.
6. Понятие комплексного числа.
7. Понятие мнимой единицы (числа  ).
).
8. Основные операции над комплексными числами.
9. Представление комплексного числа в тригонометрической форме.
10. Понятие модуля комплексного числа.
11. Понятие аргумента комплексного числа.
12. Охарактеризовать умножение и деление комплексных чисел в тригонометрической форме.
13. Формула Муавра.
| Следующая > |
matica.org.ua
Формула Муавра. Извлечение корня из комплексного числа.
Количество просмотров публикации Формула Муавра. Извлечение корня из комплексного числа. - 318
Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра.
| | (3.5) |
Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.
Перейдем к процедуре извлечения корней. Известно, что в множестве действительных чисел не из всякого действительного числа можно извлечь корень. К примеру, не существует. В множестве комплексных чисел дело обстоит иначе.
Пусть . Комплексное число
принято называть корнем
-й степени из
, в случае если
, ᴛ.ᴇ.
или
.
Модуль комплексного числа определяется однозначно, в связи с этим или
(здесь имеется в виду арифметический корень).
Аргумент комплексного числа определяется с точностью до . Следовательно,
, а
.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, комплексное число , ĸᴏᴛᴏᴩᴏᴇ является корнем
-й степени из
имеет вид:
| | (3.6) |
Придавая различные значения, мы не всегда будем получать различные корни. Действительно,
можно записать в виде
, где
. Тогда
,
Т.е. значение аргумента при данном отличается от значения аргумента при
на число, кратное
. Следовательно, в формуле (2) можно ограничится лишь значениями
. При таких значениях
получаются различные корни, так как разность между их аргументами по абсолютной величине меньше
.
Итак, для каждого ненулевого числа существует ровно
корней
-й степени из
.
Пример. Вычислить .
Представим число, стоящее под знаком корня в тригонометрической форме.
.
Извлечем далее корень третьей степени из этого комплексного числа
.
Отсюда полагая, что , получим
;
;
.
referatwork.ru
Реферат: Поле комплексных чисел
Вопросы поля комплексных чисел, описывается построение поля комплексных чисел, приводятся алгебраическая форма записи комплексных чисел, определение комплексного числа, действия над комплексными числами.
п.1. Построение поля комплексных чисел.
Рассмотрим множество . Определим на
. Определим на бинарные операции сложения
бинарные операции сложения , умножения
, умножения , унарную операцию
, унарную операцию и определим элементы
и определим элементы .
.
Для :
:
 ;
;
 ;
;
 .
.
Обозначим: .
.
Теорема 1. Алгебра является полем.
является полем.
Доказательство. Проверим, что алгебра есть абелева группа.
есть абелева группа.
Для
 .
.
Для
 .
.
Для
 .
.
Для
( .
.
Проверим, что операция - ассоциативна, то есть
- ассоциативна, то есть

 .
.
Действительно,



 .
.
Проверим левый закон дистрибутивности, то есть для

 .
.
Действительно,

 ,
,

 .
.
Аналогично проверяется справедливость правого закона дистрибутивности.
Из выше доказанного следует, что алгебра есть кольцо.
есть кольцо.
Проверим, что кольцо коммутативно, то есть для
коммутативно, то есть для
 .
.
Действительно,
 .
.
Проверим, что - кольцо с единицей 1, то есть
- кольцо с единицей 1, то есть
 .
.
Действительно,
 .
.
Так как , то
, то .
.
Докажем, что каждый ненулевой элемент кольца обратим. Пусть
обратим. Пусть , что равносильно
, что равносильно . Рассмотрим пару
. Рассмотрим пару и проверим, что эта пара является обратной к паре
и проверим, что эта пара является обратной к паре . Действительно,
. Действительно,
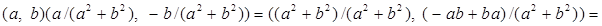
 .
.
Из выше доказанного следует, что алгебра - поле.
- поле.
Определение. Поле называется полем комплексных чисел, а его элементы - комплексными числами.
называется полем комплексных чисел, а его элементы - комплексными числами.
п.2. Алгебраическая форма записи комплексных чисел.
Обозначение. Множество комплексных чисел принято обозначать , то есть
, то есть . Приняты также следующие обозначения:
. Приняты также следующие обозначения:
 для
для .
.
Теорема 2. Каждое комплексное число может быть, и притом единственным образом, записано в виде:
может быть, и притом единственным образом, записано в виде:
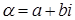 , где
, где . (Такая запись называется алгебраической формой записи комплексного числа
. (Такая запись называется алгебраической формой записи комплексного числа ).
).
Доказательство. Существуют такие, что
такие, что . Имеем
. Имеем
 .
.
Теорема 3. Число обладает свойством:
обладает свойством: .
.
Доказательство. .
.
Из равенства следует, что
следует, что .
.
Определение. Пусть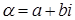 , где
, где . Число
. Число называется действительной частью,
называется действительной частью, - мнимой частью комплексного числа
- мнимой частью комплексного числа . Пишем
. Пишем .
.
Пусть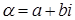 - алгебраическая форма записи комплексного числа
- алгебраическая форма записи комплексного числа . Тогда:
. Тогда:
если , то
, то ;
;
если , то
, то .
.
Определение. Если , то комплексное число
, то комплексное число называют чисто мнимым числом.
называют чисто мнимым числом.
Действия над комплексными числамив алгебраической форме
1) Для
 .
.
Другими словами: комплексное число равно нулю тогда и только тогда, когда у него действительная и мнимая части равны нулю.
Доказательство. .
.
2) Для
 .
.
Другими словами: два комплексных числа равны тогда и только тогда, когда у них, соответственно, равны действительная и мнимая части.
Доказательство. .
.
3) Для
 .
.
Другими словами: чтобы сложить два комплексных числа, нужно, соответственно, сложить их действительные и мнимые части.
Доказательство.
 .
.
4) Для
 .
.
Доказательство.
 .
.
5) Для
 .
.
Доказательство. .
.
6) Для , если
, если , то
, то
 .
.
Доказательство.
 .
.
п.3. Операция сопряжения.
Определение. Пусть комплексное число записано в алгебраической форме
записано в алгебраической форме . Числом сопряжённым с
. Числом сопряжённым с называется число
называется число .
.
Свойства операции сопряжения
Для , где
, где ,
, ,
, .
.
1).
Доказательство.
.
2) .
Доказательство. .
3) .
Доказательство.
.
.
4) Если a¹ 0, то .
.
Доказательство. .
.
5) .
.
Доказательство. .
.
6) .
.
Доказательство. .
.
С помощью операции сопряжения удобно производить деление комплексных чисел. Чтобы записать в алгебраической форме дробь с комплексными числителем и знаменателем нужно умножить числитель и знаменатель дроби на число, сопряжённое со знаменателем, и вычислить произведения в числителе и знаменателе.
п.4. Модуль комплексного числа.
Пусть записано в алгебраической форме
записано в алгебраической форме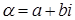 .
.
Определение. Модулем комплексного числа называется неотрицательное действительное число
называется неотрицательное действительное число .
.
Свойства модуля.
Для , где
, где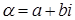 ,
, ,
, .
.
1) .
.
Доказательство.
 .
.
2) .
.
3) .
.
Доказательство. Свойство следует из свойства 6 операции сопряжения.
4) .
.
Доказательство. .
.
Отсюда следует нужное утверждение.
5) Если , то
, то .
.
Доказательство. .
.
6) Неравенство треугольника: .
.
Доказательство. Докажем сначала неравенство
 .
.
Имеем
(2) ,
,
так как
 .
.
Из (2) следует, что
 .
.
Из последнего неравенства следует неравенство (1).
Докажем теперь неравенство треугольника. Неравенство треугольника, очевидно, выполнено для . Докажем неравенство треугольника для
. Докажем неравенство треугольника для . Имеем
. Имеем
 .
.
7) .
.
Доказательство. . Отсюда следует нужное неравенство.
. Отсюда следует нужное неравенство.
8) .
.
Доказательство. Справедливы неравенства
 ,
, .
.
Одно из подчёркнутых чисел совпадает с .
.
п.5. Геометрическая интерпретация комплексных чисел.
Пусть записано в алгебраической форме
записано в алгебраической форме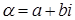 . Поставим в соответствие числу
. Поставим в соответствие числу точку плоскости с координатами
точку плоскости с координатами . Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
. Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
Числа и
и расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
Геометрический смысл модуля
Из Рис.1 видно, что расстояние от начала координат до числа равно
равно . Поэтому геометрический смысл
. Поэтому геометрический смысл - расстояние от
- расстояние от до начала координат.
до начала координат.
y


 bi a
bi a
i
 -1+i 1+i
-1+i 1+i
 - 1 0 1 a
- 1 0 1 a
x
- 1-i 1-i
- i
Рис.1.
 - bi `a
- bi `a
Пример. Изобразим на комплексной плоскости, на Рис.2, множества, заданные, соответственно, следующими условиями: ;
; ;
; .
.


 y | z | =1 y | z |£1 y | z |³1
y | z | =1 y | z |£1 y | z |³1
















 i i i
i i i






 - 1 1 - 1 1 - 1 1
- 1 1 - 1 1 - 1 1









 0 0 0
0 0 0












- i - i - i
Рис.2.
Пусть записано в алгебраической форме
записано в алгебраической форме . Имеем
. Имеем
 .
.
Из Рис.3 видно, что геометрический смысл модуля разности комплексных чисел - расстояние между этими числами.
 y
y

 b a
b a

d |b-d|



 b|a-c|
b|a-c|
Рис.3.
0 c a x
Пример. Изобразим на комплексной плоскости, на Рис.4, множества, заданные, соответственно, следующими условиями: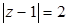 ;
; .
.

 y y
y y



 | z-1| =2 0
| z-1| =2 0
x
- i
- 1 0 1 3 x |z+i |> 1
- 2i
Рис.4.
Геометрическая интерпретация комплексных чиселвекторами плоскости
Поставим в соответствие числу связаный вектор плоскости с началом в начале координат и с концом в точке
связаный вектор плоскости с началом в начале координат и с концом в точке . Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
. Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
 y
y


 a+b
a+b
 b
b

 a
a
0 Рис.5
x
Геометрический смысл модуля комплексного числа , при интерпретации чисел векторами, - длина вектора
, при интерпретации чисел векторами, - длина вектора . Сумма комплексных чисел находится как сумма векторов.
. Сумма комплексных чисел находится как сумма векторов.
п.6. Тригонометрическая форма записикомплексного числа.
Определение. Аргументом комплексного числа называется число
называется число , равное величине угла между положительным направлением оси абсцисс и вектором
, равное величине угла между положительным направлением оси абсцисс и вектором ,
, определяется с точность до углов, кратных
определяется с точность до углов, кратных . Главным значением аргумента комплексного числа
. Главным значением аргумента комплексного числа называется то значение
называется то значение , которое принадлежит промежутку
, которое принадлежит промежутку , оно обозначается
, оно обозначается и
и .
.
Пусть записано в алгебраической форме
записано в алгебраической форме . Тогда из геометрической интерпретации
. Тогда из геометрической интерпретации следует, что:
следует, что:
 ;
;
 , если
, если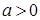 ;
;
 , если
, если ;
;
 , если
, если .
.
Заметим, что выражается только в радианах,
выражается только в радианах, не определён.
не определён.
Теорема 4. Каждое комплексное число может быть записано в виде
может быть записано в виде
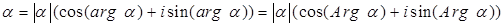 .
.
Доказательство. Изобразим вектором комплексной плоскости,
вектором комплексной плоскости,
см. Рис.6.





y
b a
Рис.6.
0 a x
Угол, образованный вектором и положительным направлением оси абсцисс, равен
и положительным направлением оси абсцисс, равен , следовательно,
, следовательно,
 . Поэтому
. Поэтому
 .
.
Определение. Если комплексное число записано в виде
записано в виде
 , то говорят, что
, то говорят, что записано в тригонометрической форме.
записано в тригонометрической форме.
Правила действий с комплексными числами,записанными в тригонометрической форме.
Пусть комплексные числа записаны в тригонометрической форме
записаны в тригонометрической форме
 .
.
1) ,
,
то есть при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Доказательство.

 .
.
2) Если , то
, то
 ,
,
то есть при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Доказательство. Обозначим . Так как
. Так как
 , то нужное утверждение доказано.
, то нужное утверждение доказано.
3) Если , то
, то
 .
.
4) Формула Муавра. Для ,
,
 .
.
Доказательство. Формула Муавра является следствием правила 1.
5) Обобщённая формула Муавра. Для ,
,
 .
.
Доказательство. Обобщённая формула Муавра является следствием формулы Муавра и свойства 3).
п.7. Показательная форма записи комплексного числа.
Обозначение. Для обозначим
обозначим
 . (1)
. (1)
Равенство (1) называют формулой Эйлера. При этом обозначении, запись комплексного числа в показательной форме принимает вид
в показательной форме принимает вид
 . (2)
. (2)
Из равенства (1) и правил действия с комплексными числами, записанными в тригонометрической форме, следует справедливость следующей теоремы .
Теорема 5. Для справедливы равенства:
справедливы равенства:
1) ;
;
2) ;
;
3) ;
;
4) ;
;
5) ;
;
6)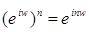 ;
;
7)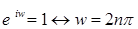
п.8. Связь между тригонометрическими и гиперболическими функциями.
Из формул Эйлера следует, что для
 .
.
Складывая и вычитая эти равенства находим, что для :
:
(1) ;
;
(2) .
.
Как известно, из курса математического анализа, гиперболические косинус, синус, тангенс, котангенс, соответственно,
 , для
, для , определяются равенствами:
, определяются равенствами:
 ;
; ;
;
 ;
; .
.
Если в формулах (1), (2), заменить на
на , то мы получим формулы для определения значений
, то мы получим формулы для определения значений . Эти формулы выражают гиперболические формулы через тригонометрические. Для
. Эти формулы выражают гиперболические формулы через тригонометрические. Для :
:
 ;
; ;
;
 ;
; .
.
п.9. Корни из комплексных чисел.
Определение. Пусть ,
, . Комплексное число
. Комплексное число называется корнем степени
называется корнем степени из
из , если
, если .
.
Теорема 6. Пусть ,
, - множество всех корней степени
- множество всех корней степени из 1. Тогда алгебра
из 1. Тогда алгебра - группа, (которая называется группой корней степени
- группа, (которая называется группой корней степени из 1).
из 1).
Доказательство. Пусть .
.
Проверим, что умножение – бинарная операция. Имеем - корень степени
- корень степени из 1.
из 1.
Проверим, что - унарная операция. Имеем
- унарная операция. Имеем - корень степени
- корень степени из 1.
из 1.
Очевидно, что 1 – корень степени из 1.
из 1.
Доказано, что - алгебра.
- алгебра.
То, что алгебра - группа, следует из свойств комплексных чисел.
- группа, следует из свойств комплексных чисел.
Теорема 7. Для существует точно
существует точно различных корней
различных корней степени
степени из 1,
из 1, ,
, . (1)
. (1)
Все корни расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0).
Доказательство. Проверим сначала, что числа , заданные равенством (1), являются корнями степени
, заданные равенством (1), являются корнями степени из 1. Действительно,
из 1. Действительно, .
.
Докажем, что любой корень степени
степени из 1 может быть вычислен по формуле (1). Т.к.
из 1 может быть вычислен по формуле (1). Т.к. , то
, то можно записать в показательой форме
можно записать в показательой форме .
.
Имеем . Поэтому
. Поэтому ,
, ,
, , где
, где . По теореме о делении с остатком, существуют такие
. По теореме о делении с остатком, существуют такие , что
, что , где
, где .
.
Значит, ,
, , т.е. вычисляется по формуле (1).
, т.е. вычисляется по формуле (1).
Изобразив числа, заданные формулой (1), на комплексной плоскости, мы увидим, что они расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0). В частности, числа, заданные формулой (1), попарно различны.
Теорема 8. Пусть ,
, ,
, ,
, . Тогда существует точно
. Тогда существует точно различных корней
различных корней степени
степени из
из ,
, ,
, . (2)
. (2)
Доказательство. Проверим сначала, что числа , заданные равенством (2), являются корнями степени
, заданные равенством (2), являются корнями степени из
из . Действительно,
. Действительно, .
.
Пусть - корень степени
- корень степени из
из . Докажем, что он вычисляется по формуле (2). Рассмотрим число
. Докажем, что он вычисляется по формуле (2). Рассмотрим число , где
, где определено формулой (2). Имеем
определено формулой (2). Имеем
Следовательно - корень степени
- корень степени из 1, т.е.
из 1, т.е. совпадает с одним из чисел
совпадает с одним из чисел . Имеем
. Имеем

Из вышедоказанного следует, что числа попарно различны.
попарно различны.
п.10. Мультисекция.
Теорема 1. (о мультисекции многочлена) Пусть
 - многочлен с числовыми коэффициентами,
- многочлен с числовыми коэффициентами, . Тогда
. Тогда
 , (1)
, (1)
где .
.
Доказательство. Для равенство (1) очевидно выполнено. Докажем (1) для
равенство (1) очевидно выполнено. Докажем (1) для . Имеем
. Имеем
 (2)
(2)
Если - целое, то и
и .
.
Если - не целое, то и по формуле суммы членов геометрической прогрессии
и по формуле суммы членов геометрической прогрессии
 .
.
Поэтому в (2) суммирование нужно вести только по тем , для которых
, для которых . Отсюда следует (1).
. Отсюда следует (1).
Заметим, что равенство (1) справедливо не только для многочленов, но и для рядов.
Следствие 1. Пусть . Тогда
. Тогда
. (3)
Доказательство. Рассмотрим многочлен
.
Применяя мультисекцию к многочлену , получим, что
,
где . Полагая в последнем равенстве получим, что
в последнем равенстве получим, что
 . (4)
. (4)
Имеем




 .
.
Приравнивая действительные части обеих частей равенства (4), получаем равенство (3).
п.11. Упорядоченные поля.
Определение. Упорядоченным полем называется алгебраическая система
 такая, что:
такая, что:
1) алгебра - поле;
- поле;
2) - линейный порядок на
- линейный порядок на ;
;
3) для
 ;
;
4) для
 .
.
Другими словами, упорядоченное поле - это поле, на множестве элементов которого определён линейный порядок , согласованный условиями 3), 4), с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел.
, согласованный условиями 3), 4), с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел.
Примерами упорядоченных полей являются поле рациональных и поле действительных чисел.
Теорема 9. Если - упорядоченное поле, то для
- упорядоченное поле, то для из условия
из условия , следует, что
, следует, что .
.
Доказательство. Так как - линейный порядок, то
- линейный порядок, то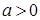 или
или . Если
. Если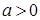 , то по условию 4)
, то по условию 4) . Если
. Если , то
, то и по условию 4),
и по условию 4), .
.
Теорема 10. Если - упорядоченное поле, то для
- упорядоченное поле, то для
 из условия
из условия следует, что
следует, что .
.
Доказательство. Из теоремы 9 следует, что и
и . Из условия 3 следует, что
. Из условия 3 следует, что .
.
Теорема 11. Поле комплексных чисел нельзя упорядочить.
нельзя упорядочить.
Доказательство. Предположим противное - поле комплексных чисел упорядоченно. Так как
упорядоченно. Так как , то по теореме 10
, то по теореме 10 - противоречие.
- противоречие.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
superbotanik.net
Формула Муавра. Извлечение корня из комплексного числа.
Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра.
 | (3.5) |
Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.
Перейдем к процедуре извлечения корней. Известно, что в множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например,  не существует. В множестве комплексных чисел дело обстоит иначе.
не существует. В множестве комплексных чисел дело обстоит иначе.
Пусть  . Комплексное число
. Комплексное число  называется корнем
называется корнем  -й степени из <img … src=»http://ok-t.ru/studopediaru/baza3/351586350881.files/image540.gif» />, если
-й степени из <img … src=»http://ok-t.ru/studopediaru/baza3/351586350881.files/image540.gif» />, если  , т.е.
, т.е.

или
 .
.
Модуль комплексного числа определяется однозначно, поэтому  или
или 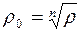 (здесь имеется в виду арифметический корень).
(здесь имеется в виду арифметический корень).
Аргумент комплексного числа определяется с точностью до  . Следовательно,
. Следовательно,  , а
, а  .
.
Таким образом, комплексное число  , которое является корнем
, которое является корнем  -й степени из
-й степени из  имеет вид:
имеет вид:
 | (3.6) |
Придавая  различные значения, мы не всегда будем получать различные корни. Действительно,
различные значения, мы не всегда будем получать различные корни. Действительно,  можно записать в виде
можно записать в виде  , где
, где  . Тогда
. Тогда  ,
,
Т.е. значение аргумента при данном  отличается от значения аргумента при
отличается от значения аргумента при  на число, кратное
на число, кратное  . Следовательно, в формуле (2) можно ограничится лишь значениями
. Следовательно, в формуле (2) можно ограничится лишь значениями  . При таких значениях
. При таких значениях  получаются различные корни, так как разность между их аргументами по абсолютной величине меньше
получаются различные корни, так как разность между их аргументами по абсолютной величине меньше  .
.
Итак, для каждого ненулевого числа  существует ровно
существует ровно  корней
корней  -й степени из
-й степени из  .
.
Пример. Вычислить  .
.
Представим число, стоящее под знаком корня в тригонометрической форме.


 .
.
Извлечем далее корень третьей степени из этого комплексного числа
 .
.
Отсюда полагая, что  , получим
, получим
 ;
;
 ;
;
 .
.
refac.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|




