Реферат на тему: "Из истории развития числа и счета". Реферат цифры

Реферат Цифры

скачать

Реферат на тему:

План:

1 История
2 Национальные варианты арабско-индийских десятичных цифр
3 Использование на монетах
4 Нумерация в книгах

Введение

Ци́фры — система знаков («буквы») для записи чисел («слов») (числовые знаки). Слово «цифра» без уточнения обычно означает один из следующих десяти («алфавит») знаков: 0 1 2 3 4 5 6 7 8 9 (т. н. «арабские цифры»). Сочетания этих цифр порождают дву-(и более)значные числа.

Существуют также много других вариантов («алфавитов»):

римские цифры (I V X L C D M)
шестнадцатеричные цифры (0 1 2 3 4 5 6 7 8 9 A B C D E F)
цифры майя (от 0 до 19)
в некоторых языках, например, в древнегреческом, в иврите, в церковнославянском, существует система записи чисел буквами и др.

Во множественном числе в обиходной речи слово «цифры» также может обозначать «числовые данные» (так как любое число записывается набором цифр). Например, «приведём такие цифры» (даже когда речь идёт об одном числовом данном, записанном одной цифрой, следует употреблять множественное число). Однако неверно говорить «здесь цифры больше», так как сравниваются не цифры, а числа.

Само слово «цифра» происходит от арабского «сыфр» («ноль») и в русском языке пишется через букву «и», в отличие от слов-исключений: цыган, цыплёнок, цыпочки и др..

1. История

В науке индийское происхождение так называемых арабских цифр было признано лишь в XIX веке. Первым учёным, высказавшим эту, для того времени новую, мысль, был русский востоковед Георг Яковлевич Кер (1692—1740). Кер с 1731 года служил в Москве переводчиком коллегии иностранных дел.

2. Национальные варианты арабско-индийских десятичных цифр

A B C D E F G H I J K L M N O P Q R S T

0	٠	۰	०	০	੦	૦	୦	௦	౦	೦	൦	๐	໐	༠	၀	០	᠐	᥆	᧐
1	١	۱	१	১	੧	૧	୧	௧	౧	೧	൧	๑	໑	༡	၁	១	᠑	᥇	᧑
2	٢	۲	२	২	੨	૨	୨	௨	౨	೨	൨	๒	໒	༢	၂	២	᠒	᥈	᧒
3	٣	۳	३	৩	੩	૩	୩	௩	౩	೩	൩	๓	໓	༣	၃	៣	᠓	᥉	᧓
4	٤	۴	४	৪	੪	૪	୪	௪	౪	೪	൪	๔	໔	༤	၄	៤	᠔	᥊	᧔
5	٥	۵	५	৫	੫	૫	୫	௫	౫	೫	൫	๕	໕	༥	၅	៥	᠕	᥋	᧕
6	٦	۶	६	৬	੬	૬	୬	௬	౬	೬	൬	๖	໖	༦	၆	៦	᠖	᥌	᧖
7	٧	۷	७	৭	੭	૭	୭	௭	౭	೭	൭	๗	໗	༧	၇	៧	᠗	᥍	᧗
8	٨	۸	८	৮	੮	૮	୮	௮	౮	೮	൮	๘	໘	༨	၈	៨	᠘	᥎	᧘
9	٩	۹	९	৯	੯	૯	୯	௯	౯	೯	൯	๙	໙	༩	၉	៩	᠙	᥏	᧙

A — стандартные европейские, B — арабские, C — восточно-арабские, D — деванагари, E — бенгальские, F — гурмукхи, G — гуджарати, H — ория, I — тамильские, J — телугу, K — каннада, L — малаяли, M — тайские, N — лаосские, O — тибетские, Р — бирманские, Q — кхмерские, R — монгольские, S — лимбу, T — new tai lue

3. Использование на монетах

На монетах индийские цифры впервые появляются в 976 году в Испании, где имелись непосредственные связи с арабами.

Наиболее ранняя русская монета с индийскими цифрами относится к 1654 году. Славянские цифры в последний раз появляются на медных монетах чеканки 1718 года[1].

4. Нумерация в книгах

Нумерация страниц большой книги (сочинения итальянского поэта Петрарки) дана впервые индийскими цифрами в 1471 году [1].

Примечания

↑ 12 Депман И. Я. История Арифметики. — изд. «Просвещение», Москва, 1965, стр.93

wreferat.baza-referat.ru

Реферат История возникновения цифр

Содержание 2

Для чего нужна математика 3

Пальцы и зарубки 3

Имя чисел 5

Новый способ записи чисел. 6

Новая, или арабская нумерация 6

Один, два, три… 7

Рисские, арабские и другие 12

Для чего нужна математика

Когда речь идёт о чём-нибудь очень простом, понятном мы часто говорим: «Дело ясно, как дважды два - четыре!»

А ведь прежде чем додуматься до того, что дважды два - четыре, людям пришлось учиться много-много тысяч лет.

Конечно, учение шло не за партой. Человек постепенно учился жить: строить жилища, находить дорогу в дальних походах, обрабатывать землю. И одновременно он учился считать. Потому что даже в самые далёкие времена, когда люди жили в пещерах и одевались в звериные шкуры, они не могли обойтись без счёта и меры.

Многие правила из ваших школьных учебников математики и геометрии были известны древним грекам две с лишним тысячи лет назад. Другие древние народы - египтяне, вавилоняне, китайцы, народы Индии - в третьем тысячелетии до нашего летосчисления имели знания по геометрии и арифметике, которых не хватает некоторым ученикам пятого или шестого класса.

Что было бы с людьми без математики даже представить трудно!!!

Пальцы и зарубки

Учиться считать люди начали в незапамятные времена, а учителем у них была сама жизнь.

Древние люди добывали себе пищу главным образом охотой. Чтобы добыча не ушла, её надо было окружить, ну вот хотя бы так: пять человек справа, семь сзади, четыре слева. Тут уж без счёта никак не обойдёшься! И вождь первобытного племени справлялся с этой задачей. Даже в те времена, когда человек не знал таких слов, как «пять» или «семь», он мог показать числа на пальцах рук.

Есть и сейчас на земле племена, которые при счёте не могут обойтись без помощи пальцев. Вместо числа пять они говорят «рука», десять – «две руки», а двадцать – «весь человек», - тут уж присчитываются и пальцы ног.

Пять — рука; Шесть — один на другой руке; Семь — два на другой руке; Десять — две руки, полчеловека; Пятнадцать — нога Шестнадцать — один на другой ноге Двадцать — один человек Двадцать два — два на руке другого человека Сорок — два человека Пятьдесят три — три на первой ноге у третьего человека.

Раньше люди чтобы пересчитать стадо из 128 оленей должны были взять семь человек.

Так люди начинали считать, пользуясь тем, что им дала сама природа – собственной пятернёй. Часто говорят: «Знаю, как свои пять пальцев». Не с того ли времени пошло это выражение, когда знать, что пальцев пять, значило то же, что уметь считать?

Несколько десятков лет назад учёные-археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой 30 тысяч лет тому назад какой-то древний охотник нанёс пятьдесят пять зарубок. Видно, что, делая эти зарубки, он считал по пальцам.

Узор на каждой кости состоял из одиннадцати групп, по пять зарубок в каждой. При этом первые пять групп он отделил от остальных длинной чертой. Позднее в Сибири и других местах были найдены сделанные в ту же далёкую эпоху каменные орудия и украшения, на которых тоже были чёрточки и точки, сгруппированные по 3. по 5 или по 7.

Много тысячелетий прошло с того времени. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварню, отмечают число фляг такими же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером или с надписью, которую привязывают к кулям с товарами, ящикам, тюкам и т. д. А ещё двести-триста лет тому назад это слово обозначало совсем иное. Так называли куски дерева, на которых зарубками отмечали сумму долга или подати. Бирку с зарубками раскалывали пополам, после чего одна половинка оставалась у должника, а другая – у заимодавца или сборщика податей. При расчёте половинки складывали вместе, и это позволяло определить сумму долга или податей без споров и сложных вычислений.

Чтобы с успехом заниматься сельским хозяйством, понадобились арифметические действия. Без подсчёта дней трудно было определить, когда надо засевать поля, когда надо начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары.

И вот более 8 тысяч лет тому назад древние пастухи стали делать из глины кружки – по одному на каждую овцу. Чтобы узнать, не пропала ли за день хоть одна овца, пастух откладывал по кружку каждый раз, когда очередное животное заходило в загон. И только убедившись, что овец вернулось столько же, сколько было кружков, он спокойно шёл спать. Но в его стаде были не только овцы – он пас и коров, и коз, и ослов. Поэтому пришлось делать из глины и другие фигурки. А земледельцы с помощью глиняных фигурок вели учёт собственного урожая, отмечая, сколько мешков зерна положено в амбар, сколько кувшинов масла выжато из оливок, сколько соткано кусков льняного полотна. Если овцы приносили приплод, пастух прибавлял к кружкам новые, а если часть овец шла на мясо, несколько кружков приходилось убирать. Иногда в большой мешок клали столько камешков, сколько было животных. Чем больше животных, тем больше камешков. Слово «калькулятор» произошло от латинского «калькулюс», что

означало «камень»! Так, ещё не умея считать, занимались древние люди арифметикой.

Имя чисел

Перекладывать каждый раз глиняные кружки с места на место было довольно утомительным занятием. Да и при обмене рыб на каменные ножи или антилоп на каменные топоры удобнее было сначала пересчитывать товары, а уж потом приступать к обмену. Но прошло много тысячелетий, прежде чем люди научились считать предметы. Для этого им пришлось придумать названия для чисел. Не даром ведь говорят: «Без названия нету знания».

О том, как появились имена у чисел, учёные узнают, изучая языки разных племён и народов. Например, оказалось, что у нивхов, живших в Сахалине и в низовьях Амура, числительные зависят от того, какие предметы считают. Важную роль играют форма предмета, так что по-нивсхи в сочетаниях «два яйца», «два камня», «два одеяла», «два глаза» и т. д. числительные различны. Одному русскому слову «два» соответствует несколько десятков различных слов. Много различных слов для одного и того же числительного применяют некоторые негритянские племена и племена, живущие на островах тихого океана.

И должно пройти много столетий, а может быть и тысячелетий, прежде чем одни и те же числительные стали применяться к предметам любого вида. Вот тогда и появились общие названия для чисел.

Учёные считают, что сначала названия получили только числа 1 и 2.

Когда древние римляне (в древности они говорили по латыни) придумывали имя числу 1, они исходили из того, что солнце на небе всегда одно. А название числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами и т. д. Но бывало, что числами 1 и 2 давали иные имена. Иногда их связывали с местоимениями «я» и «ты», были языки, где «один» звучало так же, как «мужчина», а «два» - как «женщина».

У некоторых ещё совсем недавно не было других числительных, кроме «один» и «два». А всё, что шло после двух называлось «много». Но потом понадобилось называть и другие числа. Ведь и собак у охотника, и стрел у него, и овец у пастуха может быть больше, чем две. И тут придумали замечательный выход: числа стали называть, повторяя несколько раз названия для единиц и двоек.

Например, некоторых папуасских племён (а живут папуасы на острове Новая Гвинея в Тихом океане) числительное «один» и сейчас звучит, «урапун», а числительное «два» - «окоза». Число 3 они называли «окоза-урапун», а число 4 – «окоза-окоза». Так они дошли до числа 6, которое получило имя «окоза-окоза-окоза». А дальше у них шло знакомое нам – «много» (конечно по - папуасски). И 10 у них «много», и 100 тоже «много».

Позднее другие племена дали особое имя числительному, которое мы называем «три». А так как до этого они считали «один», «два», «много», то это новое числительное стали применять вместо слова «много».

Новый способ записи чисел.

Мы с вами уже знаем, что первым способом «записи чисел» были зарубки на палке. Хорошо. Если число маленькое – десятки, Или, в крайнем случае, сотни. А если тысячи? Пока считаешь зарубки, чтобы «прочитать» число, пройдёт больше часа! Очень неудобная «запись»! И вот примерно пять тысяч лет назад почти одновременно в разных странах – Вавилоне, Египте, Китае – родился новый способ записи чисел.

Люди додумались до того, что числа можно записывать не просто зарубками-единицами. А по разрядам: отдельно единицы, отдельно десятки, отдельно сотни. Это было очень важным открытием. Считать и записывать числа теперь стало гораздо легче.

Новая, или арабская нумерация

Настоящая родина самой распространённой нумерации - Индия. В различных районах Индии существовали разнообразные системы нумерации, но в какой-то момент среди них выделилась одна. В ней цифры имели вид начальных букв соответствующих числительных на древнеиндийском языке - санскрите, использующем алфавит "Деванагари".

Первоначально этими знаками представлялись числа 1, 2, 3, … 9, 10, 20, 30, …, 90, 100, 1000; с их помощью записывались другие числа. Но в последствии был введен особый знак - жирная точка, или кружок, для указания пустующего разряда; и нумерация "Деванагари" превратилась в поместную десятичную систему. Как и когда совершился такой переход - до сих пор неизвестно. К середине VIII века позиционная система нумерации

получает широкое применение. В это же время она проникает в соседние страны: Индокитай, Китай, Тибет, Среднюю Азию.

Решающую роль в распространении индийской нумерации в арабских странах сыграло руководство, составленное в начале IX века Мухаммедом Аль Хорезми. Оно было переведено в Западной Европе на латинский язык в XII веке. В XIII веке индийская нумерация получает преобладание в Италии. В других странах она распространяется к XVI веку. Европейцы, заимствовав у арабов эту нумерацию, называли ее "арабской". Это исторически неправильное название удерживается и поныне.

Из арабского языка заимствовано и слово "цифра" (по-арабски "сыфр"), означающее буквально "пустое место" (перевод санскритского слова "сунья", имеющего тот же смысл). Это слово применялось для названия знака пустого разряда, и этот смысл сохраняло до XVIII века, хотя еще в XV веке появился латинский термин "нуль" (nullum - ничто). Форма индийских цифр претерпевала многообразные изменения.

Один, два, три…

Уже в три, четыре года, поднимаясь по лестнице, мы уверенно считаем ступеньки: «Раз. Два, три, четыре, пять…» А в первом классе пишем в тетради цифры:

Эти цифры называются арабскими, хотя арабы лишь передали в Европу индийскую десятеричную систему счисления с её цифрами.

«девять индусских знаков следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1.С помощью этих знаков и знака 0, который называется по-арабски «сифр», можно написать какое угодно число. («Книга об абаке» одного из первых математиков Эпохи Возрождения Леонардо Пизанского, получившего прозвище Фибоначчи)». Фибоначчи, издавший свою книгу в 1202 году, многое почерпнул из знакомства с математическими трудами арабов. Любопытно, что сам порядок цифр при их перечислении – 9, 8, 7, 6,… - отражает их заимствование у арабов, поскольку арабы пишут справа налево, а не слева направо.

Наверное, вы уже поняли, что слово «цифра», произошло от нуля у арабов, А в России ещё очень долго слово «цифра» означало значок нуля. Вот что говорится в «Арифметике» Магницкого 1703 год издания: «Нумерация есть счёт или способ представлять совершенно все числа с помощью десяти знаков, которые изображаются так: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Из них девять значащие, а

Последний же ноль (который цифрой или ничем именуется) сам по себе ничего не значит.

«Нумерация есть счет или способ представлять совершенно все числа с помощью десяти знаков, которые изображаются так: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Из них девять – значащие, а последний же 0 (который цифрой или ничем именуется) сам по себе ничего не значит».

«Нумерацiо есть счисление еже совершенно всz числа речию именовати, яже в десzту знаменованияхъ, или изwбражениz содержатсz, и изwбражаютсz сице: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, из нихже девzть назнаменователны суть, послёднее же 0 (еже цыфрою или ничемъ именуетсz) егда uбо (оно) едино стоитъ, тогда само w себе ничтоже значитъ».

Обратим внимание, что буквы в старинном тексте еще сильно отличаются от современных, а цифры – те же, что и в ваших учебниках. Но, конечно же, они не сразу стали такими. Вот как они выглядели в Индии в 200 году:

Тогда не было еще нуля и позиционной записи чисел, но со временем написание цифр совершенствовалось, причем по–разному и в разных местностях Индии. Появился нуль – и возникла позиционная система записи чисел. Арабы выбрали из этих различных видов цифр наиболее удачные. От них цифры продолжили свой путь по земле. Вот в каком виде они публикуются у римского писателя Боэтия (600 год):

В 1350 году в сочинениях греческого монаха Максима Плануда мы видим их такими:

В 1480 году в книге «Зеркало вселенной» англичанина Какстона они изображаются следующим образом:

И лишь в 1522 году в книге итальянца Тонсталля приобретают более–менее современный вид:

Любопытно, что в самой Индии цифры тоже видоизменялись и к началу ХХ века стали выглядеть так:

Хотя в XVI веке в Европе уже было развито книгопечатание, цифры в книгах того времени, как мы видим, очень похожи на рукописные. Многие художники работали над созданием разнообразных типографских шрифтов – формой букв и цифр, стараясь придать им красивый вид (при этом каждый

знак должен был достаточно сильно отличаться от другого). Вот один из цифровых шрифтов:

1 2 3 4 5 6 7 8 9 0

Но история цифр на этом не кончается. Недавно в ряде стран стали использовать следующую запись:

5 6 7 8 9

Чем эти цифры лучше обычных? А тем, что у четных цифр «хвостики» идут вверх, а у нечетных – вниз. Теперь уже труднее спутать, скажем, цифры 2 и 5. Правда, это нововведение широко не привилось, но приведенное ниже начертание цифр знакомо каждому из нас:

Подобные цифры мы видим на микрокалькуляторах и ручных электронных часах. С помощью набора семи отрезков удается изобразить каждую из десяти цифр.

Еще одно изображение цифр, связанное с потребностями техники, мы находим на обороте почтового конверта:

Здесь в написании цифры участвуют уже девять отрезков. Эти цифры предназначены для электронной машины, сортирующей корреспонденцию. Жирные черточки над индексом на конверте нужны для того, чтобы машина смогла точно настроиться на написанный нами индекс:

Если мы заговорили об электронных машинах, отметим, что хотя они получают числа в десятичной записи и в том же виде выдают нам результаты вычислений, но для «внутренних нужд» пользуются двоичной системой счисления. На перфоленте, используемой в ЭВМ для хранения информации, первые девять цифр выглядят так:

Цифре 0 соответствует пробел. Маленькие пробитые точки посредине перфоленты служат для ее перемещения и фиксации.

Двоичная система счисления, как и десятичная, является позиционной системой: значение величины числа зависит от входящих цифр и их мест в написании числа. И если в десятичной системе десять единиц предыдущего разряда составляют единицу следующего разряда, то в двоичной системе единицу следующего разряда составляют две единицы предыдущего.

Поэтому для записи чисел в двоичной системе достаточно всего двух цифр – 0 и 1:

1=12, 2=102, 3=112,

4=1002, 5=1012, 6=1102,…

(Маленькая цифра 2 около числа означает, что запись произведена в двоичной системе счисления.)

Сравнив эти записи с перфолентой, мы увидим, что пробой на перфоленте соответствует цифре 1, а его отсутствие – цифре 0.

Машина читает запись на перфоленте с помощью фотоэлементов: они отмечают пробитые отверстия, регистрируя свет, проникающий через отверстия, а в непробитых участках лента загораживает фотоэлемент от источника света.

Похожий принцип заложен и в основу так называемого полосного кода.

Мы часто видим полосатый прямоугольник, встречающийся на разнообразных товарах:

Что означают эти полоски? Оказывается, с их помощью записано расположенное внизу число – код товара. Компьютер, находящийся в кассовом аппарате, с помощью фотоэлементов считывает код. Для этого било проводят табличку с кодом в специальном месте кассового аппарата, либо по коду проводят «считывающим карандашом», соединенным с кассовым аппаратом. Таким образом, компьютер получает информацию о продаваемом товаре. В соответствии с ней он выдает из своей памяти цену, а сам запоминает, что данный экземпляр куплен. В результате всегда известно, сколько какого товара куплено и на какую сумму, какой товар нужно еще доставить в торговый зал.

Но как устроен полосатый код?

С помощью полосок можно записывать число так, как на перфоленте: тонкая черная полоска – 0. Но представлять число можно по–разному. Можно просто записать его в двоичной системе счисления (например, число 5 762 752 950 запишется в двоичной системе так: 110101110111010010001101102).

А можно каждую цифру числа записать в двоичной системе – тогда на одну цифру будет достаточно четырёх полосок, а затем представить число набором получившихся полосок.

В таблице, приведённой чуть ниже, каждая цифра записывается так же отдельно, но не в двоичной системе, а по–другому. Каждой цифре соответствует семь значков 0 и 1. Код состоит из двух частей – левой и правой, – и цифры в левой и правой частях записываются в соответствии со следующей таблицей:

Левая часть кода

Правая часть кода

0001101

0011001

0010011

0111101

0100011

0110001

0101111

0111011

0110111

0001011

1110010

1100110

1101100

1000010

1011100

1001110

1010000

1000100

1001000

1110100

Посмотрим сначала на левую часть таблицы. Запись каждого числа начинается с 0 и заканчивается 1. Эти знаки не характеризуют числа, а служат для отделения одного числа от другого. На само число приходится пять знаков, и они выбраны так, чтобы любые два числа различались не менее чем в двух местах. Запись чисел в правой части таблицы симметрична записи слева, а именно: вместо цифры 0 на соответствующем месте стоит цифра 1, а вместо 1 стоит 0.

На рисунке каждой цифре соответствует описанная комбинация из семи полосок, расположенная над ней. Все что мы говорили, относится к коротким полоскам. Первые три длинные полоски, средние и последние полоски (им соответствует набор 101) являются указателями начала, середины и конца шифра. Длинные полоски, следующие за тремя первыми, соответствуют цифре, расположенной сбоку слева, например цифре 0. Аналогично длинные полоски перед последними тремя полосками соответствуют цифре, расположенной сбоку справа, например цифре 6.

Эти боковые числа служат для защиты считывания от ошибок. Их значения таковы, чтобы утроенная сумма чисел, стоящих на четных местах, сложенная вместе с суммой чисел, стоящих на нечетных местах, делилась на 10. Суммирование производится слева направо: считается, что цифра, стоящая сбоку слева, находится на нулевой (значит, четном) месте. В нашем случае 3(0+7+2+5+9+0)+(5+6+7+2+5+6)=100.

Если компьютер неправильно прочтет одну из цифр, то сразу обнаружит ошибку. Он не сможет обнаружить ошибку лишь в том случае, если прочтет, по крайней мере, две цифры ошибочно, причем так, чтобы ошибки «скомпенсировались» и полученная сумма снова делилась на десять. Но вероятность этого чрезвычайно мала.

Такая защищенность от ошибок очень важна, иначе за батон хлеба компьютер мог бы потребовать от покупателя стоимость, скажем, большой коробки шоколадных конфет.

Защита от ошибок заложена и в стандартной форме написания почтового индекса. Любые две цифры отличаются не меньше, чем в пяти местах.

Надо сказать, что программисты ЭВМ в последнее время пишут ноль вот так:

Дело в том, что в программе ЭВМ буквы и цифры могут произвольно перемежаться. Чтобы отличить нуль от буквы О, была введена эта запись. Так сняты возможные ошибки при использовании латинского шрифта. А при использовании русского шрифта возникает возможность спутать букву З с цифрой 3, а букву Ч с цифрой 4. Может быть, и эти цифры будут изменяться? Посмотрим. Время покажет.

Рисские, арабские и другие

Выше мы говорили о записи чисел цифрами, вернее, об истории самих цифр, которые принято называть арабскими. Но часто мы пользуемся и другими цифрами. Записи «ХХ век», «Глава IV» не ставят нас в затруднительное положение. Здесь числа представлены римскими цифрами. Почему же до сих пор мы пользуемся этой системой записи чисел? Наверное, потому, что с ее помощью можно отделять одни числа от других. Так, запись 25.XI.1990 сразу говорит о том, что это – дата: 25 ноября 1990 года.

Итак, римские цифры. Что они означают?

I – Один

V – Пять

X – Десять

L – Пятьдесят

C – Сто

D – Пятьсот

M – Тысяча

Поэтому, увидев на фронтоне старого особняка запись MDCCLXXXIX, мы без труда прочтем дату его постройки – 1789 год.

Следует отметить, что существует и второй способ записи чисел римскими цифрами, при котором меньшая цифра не ставится впереди большей, и поэтому число 4 записывается как IIII, число 9 как VIIII, а число 99 как LXXXXVIIII.

Но как быть с очень большими числами в десятки и сотни тысяч? Например, как записать число 275748? Римляне поступали просто: CCLXXVmDCCXLVIII.

Буква m показывает, что число, стоящее впереди нее, выражает количество тысяч в данном числе. Но вернемся к арабским цифрам. Как уже говорилось, арабы, заимствовав индийскую десятичную систему счисления с ее цифрами, несколько изменили сами цифры. Дальнейшее изменение цифр происходило в Европы. В результате цифры стали не похожими на те, которыми пользовались индусы. Но самое интересное в том, что цифры, которыми пользуются арабы сейчас, также не похожи на «международные» арабские цифры. Сравним с записью арабских чисел. Разница велика.

1 2 3 4 5 6 7 8 9 0

Помимо «международной», собственную систему записи чисел используют не только арабы. Так, в Китае издавна существовала система записи чисел с помощью иероглифов.

Числа традиционно записывались вертикально, сверху вниз. При этом числа 20, 30, 40, … записывались столбиком из двух символов. Нижний символ означал, что речь идет о десятках, а верхний указывал их число. Такие числа, как 47, записывались столбиком из трех символов: к числу 40 снизу добавлялся иероглиф, обозначающий цифру 7. Аналогичная система использовалась для обозначения сотен, тысяч и т.д. Вот, например, как выглядит число 503 в этой записи:

Существовали и другие варианты вертикальной записи чисел, больших 20. Попробуем разгадать секреты двух таких записей, рассматривая два представления числа 28.

В начале XX столетия в Китае была введена обычная форма записи – слева направо. В этой записи число 47 выглядит так:

Иероглифы используются для записи цифр, например, в Китае, Японии и Корее. Однако традиционная вертикальная система записи сохранилась лишь на острове Тайвань.

На почтовых марках, монетах, бумажных денежных знаках многих стран национальные цифры часто располагаются радом с «международными». Такое соседство можно увидеть, к примеру, на почтовых марках Ливии.

Посмотрим на рисунок. Перед нами изображение двух сторон японской монеты в одну иену. Первый иероглиф правого изображения означает цифру 1, а второй означает слово «иена».

А вот банкнота, выпущенная в Камбодже. На ней мы видим цифры, принятые в этой стране:

Список использованной литературы

За страницами учебника математики. (И.Я.Депман, Н.Я.Виленкин)
Математические миниатюры. (А.П.Савин)
С математикой в путь. (Н.Лэнгдон, Ч.Снейп).
В мире чисел. (И.Я. Депман, составитель Ю.И. Смирнов)
Энциклопедия.

bukvasha.ru

Реферат по математике История чисел курсанта Гусева

Государственное бюджетное профессиональное образовательное учреждение

города Москвы

"Колледж полиции"

Реферат по дисциплине Математика

на тему:

«История чисел»

Выполнил

курсант 15 взвода

Гусев М.А.

Преподаватель

Зайцева О.Н.

Москва

2015

Содержание

Введение………………………………………………………………..……3 стр.

Число, как основное понятие математики..…..……………………..…….4 стр.

Из истории возникновения счета и чисел…..……………………..………4 стр.

Цифры древних цивилизаций …………………………………….………..8 стр.

• Цифры в Древнем Египте ………………………………………..…….....9 стр.

• Цифры племени майя …………………………………………….……...10 стр.

• Цифры Древнего Китая ………………………………………………….11 стр.

• Цифры древней Греции …………………………………………….……12 стр.

• Славянская кириллическая нумерация ……………………..…………..12 стр.

• Римские цифры...........................................................................................13 стр.

• Цифровые знаки Индии.............................................................................13 стр.

•Вклад мусульман в развитие системы счисления....................................13 стр.

Полезное открытие нуль……………………..............................................14 стр.

Заключение………………………………………………………………...16 стр.

Литература…………………………………………………………………17 стр.

Введение.

«Все есть число» - говорили пифагорейцы. На протяжении всей своей жизни мы сталкиваемся с числами и выполняем над ними арифметические действия. Числа составляются из цифр. Как возникли цифры, каковы были варианты написания цифр у разных народов, что общего в их написании, каковы правила составления чисел и цифр? Эти вопросы заинтересовали меня. Поэтому целью данной работы является исследование истории возникновения чисел, связанной с необходимостью выражения всех чисел знаками.

Цель:

- доказать, что числа появились в древнее время;

- изучить историю возникновения цифр;

- сравнить записи цифр разных народов.

Проблема: почему мы обозначаем цифры именно так (0,1,2,3,4,5,6,7,8,9), а не по-другому (римскими или китайскими).

Задача: установить, где и кем были придуманы первые числа.

Основные методы исследования: анализ литературы, сравнение, анализ и обобщение полученных в ходе исследования данных.

Число, как основное понятие математики.

Еще в глубокой древности числа относились к области тайного. Они зашифровывались символами, и считались символами гармонии мира. Существует много теорий о происхождении чисел.

Число является одним из основных понятий математики. Понятие числа развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами.

Существует большое количество определений понятию «число». Первое научное определение числа дал Эвклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 – около 355 гг. до н. э.): «Единица есть то, в соответствии, с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Магницкий в своей «Арифметике» (1703 г.).

Еще раньше Эвклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц».

Со слов греческого философа Ямвлиха, еще Фалес Милетский – родоначальник греческой стихийно-материалистической философии – учил, что «число есть система единиц». Это определение было известно и Пифагору.

Согласно учению Пифагора, числа являются мистической сущностью вещей, математические абстракции таинственно руководят миром, устанавливая в нем определенный порядок. Пифагорейцы высказывали предположение о том, что все закономерности мира можно выразить с помощью чисел. Числа признавались не просто выражениями закономерного порядка, но и основой материального мира. Пифагор говорил: «Все вещи можно представить в виде чисел».

Древние египтяне были убеждены, что постижение священной науки чисел составляет одну из высших ступеней герметического действия, без него не может быть посвящения.

У китайцев нечетные числа – это Ян (небо – благоприятность), четные числа – инь (земля, изменчивость и неблагоприятность). Нечетность символизирует незавершенность, непрекращающийся процесс, постоянное продолжение, то есть все то, что не имеет конца, относятся к области вечного. Поэтому в орнаментах, в укрощениях архитектурных или скульптурных сооружений используется обычно нечетное число черт или элементов. Числа – символ порядка. Реки, деревья и горы представляют собой материализованные числа.

Из истории возникновения счета и чисел.

Учиться считать люди начали в незапамятные времена, а учителем у них была сама жизнь.

Первобытные люди не знали ни скотоводства, ни земледелия. Они охотились на диких зверей, ловили рыбу, собирали ягоды, грибы и орехи, выкапывали из земли съедобные корни. Больше всего мяса давала им охота на мамонтов. Но, когда они истребили всех мамонтов, а стада зубров и бизонов, оленей и буйволов в результате охоты сильно сократились, пришлось задумываться над тем, чем же теперь питаться. Тогда люди стали возделывать землю и приручили некоторых животных. Чтобы с успехом заниматься сельским хозяйством, понадобились арифметические знания. Без подсчета дней трудно было определить, когда надо засевать поля, когда начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары. Так, еще не умея считать, занимались древние люди арифметикой.

Люди научились считать еще в каменном веке. На первых этапах существования человеческого общества числа, открытые в процессе практической деятельности, служили для примитивного счета предметов, дней, шагов и т.п. Предметы считать просто; один, два, три, четыре.… Измерить небольшое расстояние тоже несложно. Надо только иметь какую нибудь мерку. Даже теперь мы нередко меряем расстояние по способу первобытных людей — считаем шаги. В первобытном обществе человек нуждался лишь в нескольких первых числах. Но с развитием цивилизации ему потребовалось изобретать все большие и большие числа. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда.

С зарождением обмена продуктами труда у людей появилась необходимость сравнивать число предметов одного вида с числом предмета другого вида. На этом этапе возникли понятия «больше», «меньше», «столько же» или «равно». Знания постепенно росли, и чем дальше, тем больше увеличилась потребность в умении считать и мерить.

Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. Любой предмет можно было увидеть и потрогать. Число потрогать нельзя, и вместе с тем числа реально существуют, поскольку все предметы можно посчитать. Эта странность заставила людей приписывать числам сверхъестественные свойства.

Жизнь заставляла племена учиться быстрее, поэтому у земледельческих народов математика из наборов отдельных простейших правил постепенно стала превращаться в науку.

О том, как появились имена у чисел, ученые узнают, изучая языки разных племен и народов. Ученые считают, что названия получили только числа 1 и 2. У некоторых племен еще совсем недавно не было других числительных кроме "один" и "два". А все, что шло после двух, называлось "много". То, что первобытные люди сначала знали только «один», «два» и «много», подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов. Но потом понадобилось называть и другие числа. У некоторых племен Австралии и Полинезии до самого последнего времени было только два числительных: «один» и «два», а все числа больше двух, получали названия в виде сочетаний этих двух числительных: число 3 – это «два и один», 4 – «два и два», 5 – «два, два, один».

Позднее другие племена дали особое имя числительному, которое мы называем "три". А так как до того они считали "один", "два", "много", то это новое числительное стали применять вместо слова "много". И сейчас мать, рассердившись на непослушного сына, говорит ему: " Что я, три раза должна повторять одно и тоже!" Русская пословица говорит: "Обещанного три года ждут". Иногда числом 3 весь окружающий человека мир - его делили на земное, подземное и небесное царства. Поэтому число 3 стало у многих народов священным. Когда они придумывали легенды о богах, то выделяли из них трех самых главных. Например, египтяне особо чтили Осириса, Гора и Исиду. В русских сказках особую роль играет число три. Во многих из них участвует три брата. Во многих сказках герой сражается с трехглавым змеем, в других сказках злой царь посылает героя "за тридевять земель, в тридесятое царство".

Другие народы делили мир не по вертикали, а по горизонтали. Они знали четыре стороны света - восток, запад, север, юг, знали четыре главных ветра. У этих народов главную роль играло не число 3, а число 4.

То, что число семь особое, люди считали очень давно. Ведь еще древние охотники, а потом и древние земледельцы, и скотоводы наблюдали за небом. Их внимание издавна привлекало созвездие Большой Медведицы - изображение семи звезд этого созвездия часто встречаются на древнейших изделиях. И может быть, один из первых результатов арифметики " три да четыре дает семь" люди получили, заметив, ковш Большой Медведицы складывается из трех звезд ручки и четырех остальных звезд. От шумеров почитание семерки перешло к другим народам. Древние греки насчитывали, например, семь чудес света. Да и сейчас мы пользуемся семидневной неделей. И если сама эта неделя возникла из наблюдений за фазами Луны, то названия ее дней у многих современных народов идут от шумеров. Они называли эти дни в честь богов, которые, как они считали, были связаны с небесными светилами. В честь своих богов дни недели назвали и римляне.

Древние люди добывали себе пищу главным образом охотой. На крупного зверя — бизона или лося — приходилось охотиться всем племенем: в одиночку ведь с ним и не справишься. Чтобы добыча не ушла, ее надо было окружить, ну хотя бы так: пять человек справа, семь сзади, четыре слева. Тут уж без счёта никак не обойдешься! И вождь первобытного племени справлялся с этой задачей. Даже в те времена, когда человек не знал таких слов, как «пять» или «семь», он мог показать числа на пальцах рук.

И старые методы счета вытеснил новый - счет по пальцам. Так люди начинали учиться считать, пользуясь тем, что дала им сама природа, — собственной пятернёй.

Пальцы оказались прекрасной вычислительной машиной. С их помощью можно было считать до 5, а если взять две руки, то и до 10. А, научившись считать по пальцам до десяти, люди сделали следующий шаг вперед и стали считать десятками. А в странах, где люди ходили босиком, по пальцам легко было досчитать до 20. И если одни папуасские племена умели считать лишь до шести, то другие доходили в счете до нескольких десятков. Только для этого приходилось приглашать сразу много счетчиков. Есть и сейчас на земле племена, которые при счёте не могут обойтись без помощи пальцев. Вместо числа пять они говорят «рука», десять — «две руки», а двадцать — «весь человек», — тут уж пересчитываются и пальцы ног.

А в Англии и сейчас первые десять чисел называют общим именем "пальцы". Значит, и англичане когда-то считали по пальцам. Похоже на то, что скачок от десятка к сотне был сделан не сразу. Сначала следующим за десятью узловым числом стало у одних народов 40, а у других 60.

Число 40 играло важную роль и в старой русской системе мер: в пуде считалось 40 фунтов, в бочке - 40 ведер и т.д. То, что это число играло столь важную роль у русских и их предков, можно объяснить тем, что раньше в их жизни особую роль играло число 4. Поэтому, когда начинали считать десятками, то именно четыре десятка считалось самым большим числом.

Но были народы, у которых в самой глубокой древности шел счет до шести. Когда они перешли на счет десятками, то особое имя у них получили не четыре, а шесть десятков.

Гораздо труднее найти мерку для времени. Тут ни пальцы, ни шаги не помогут: время можно измерять только временем. А мерка? Мерку надо было искать в природе.

Самыми древними «часами», которые к тому же никогда останавливались и не ломались, оказалось солнце. Утро, день, вечер, ночь. Не очень уж точные мерки, но поначалу первобытному человеку этого было достаточно. Потом люди научились определять время более точно: днём — по солнцу, а ночью — по звёздам. Звёзды были для людей не только первыми часами, но и первым компасом.

Но самое удивительное то, что следы счета шестидесятками сохранились до наших дней. Ведь до сих пор мы делим час на 60 минут, а минуту - на 60 секунд. Счет шестидесятками сохранился не только в измерении времени. Еще несколько десятилетий тому назад на Украине, в Польше и Прибалтике и Германии яйца, яблоки, груши продавали на копы - кучи по 60 штук в каждой.

Но потребности людей росли и росли. Наступил момент, когда уже и 40, и 60, и даже 100 перестали казаться слишком большими числами. Тогда для того, чтобы сказать "очень много" стали говорить " сорок сороков" или " шестьдесят шестидесятков".

У народов, пользующихся сотней, идею невообразимого множества воплощала сотня сотен. В русском языке она получила название "тьма". Но применяли это слово вместо "очень много": " У сильного всегда бессильный виноват: Тому в Истории мы тьму примеров слышим... ( И.А. Крылов. "Волк и Ягненок"). И сейчас, увидев большую толпу, мы восклицаем: "Народу - тьма" или даже "Тьма-тьмущая!" В этих словах воскресает язык далеких предков.

Для того чтобы считать дни, нужны большие числа: десятки, сотни и даже тысячи. Тут, конечно, никаких пальцев для счёта хватить не могло! Да и считая предметы, их можно было перекладывать, пересчитывать несколько раз. А в счёте времени ошибаться нельзя. Прошедший день исчез, его не вернёшь, не присоединишь к другим.

А как разделить год? Весь год — это целых 365 дней, очень большая и не всегда удобная мера времени. На помощь пришла луна. Люди заметили, что от полнолуния до полнолуния проходит почти ровно тридцать суток. Так появилась ещё одна мера времени — месяц. Понятно, почему и по-русски и на многих других языках слово «месяц» означает и луну, и отрезок времени. Потом месяц стали делить ещё на четыре части. Из этих четвертушек месяца родились наши недели.

Продвижение людей в "числовом море" напоминало настоящее морское путешествие. Как моряки в древности вели корабль от одного острова к другому, так и в "числовом море" выделялись "острова", то есть узловые числа - 10,40,60,100. Они служили ориентирами, а про другие числа говорили, что они настолько больше или меньше узлового числа. Сейчас десятичная система счисления применяется почти у всех народов.

Цифры древних цивилизаций

В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счете возникла так же естественно, как и потребность в добывании огня.

Додумались. Ведь можно было каждый день делать зарубку на палке и потом зарубки эти сосчитать. Так началась первая на земле запись прожитых дней. Только делали её не пером, а топором. Именно таким деревянным календарём пользовался на необитаемом острове Робинзон Крузо. Через каждые тридцать дней, то есть каждое новолуние, он делал на своём календаре зарубку длиннее. Получалась отметка месяца. Из месяцев складывался год.

Единичная система счисления первобытных людей, рисовавших палочки на стенах пещеры или делавших зарубки на костях животных и ветках деревьев, не забыта и в наши дни. Как узнать, на каком курсе учится курсант колледжа полиции? Сосчитайте, сколько полосок нашито на рукаве его формы. О количестве самолетов противника. Сбитых асом в воздушных боях, говорит число звездочек, нарисованных на фюзеляже его самолета. Поштучно считать предметы удобно тогда, когда их не очень много. Пересчитывать же таким образом большие совокупности скучно и утомительно, поэтому возникла идея объединения единицы в группы. Появился счет пятерками, десятками, двадцатками – по количеству пальцев рук и ног «счетовода».

Некоторые народы — например индейцы в Северной Америке — вместо зарубок на палке завязывали узлы на шнуре или верёвке.

Так люди постепенно учились считать до сотен и тысяч и даже «записывать» эти числа с помощью палки или верёвки.

Постепенно росли знания людей, и чем дальше, тем больше увеличивалась потребность в умении считать и мерить. Скотоводам приходилось пересчитывать свои стада, а при этом счёт мог идти уже сотнями и тысячами. Земледельцу надо было знать, сколько земли засеять, чтобы прокормить себя до следующего урожая, А время посева? Ведь, если посеять не во время, урожая не получишь!

Счёт времени по лунным месяцам уже не годился. Нужен был более точный календарь. К тому же людям всё чаще приходилось сталкиваться с большими числами, запомнить которые трудно или даже невозможно. Нужно было придумать, как их записывать.

• Цифры в Древнем Египте

Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находились очень далеко одна от другой, их числовые системы очень похожи: использование засечек на дереве или камне для записи прошедших дней.

Египетские жрецы писали на свитках папируса, изготовленных из стеблей определенных сортов тростника, а в Месопотамии на мягкой глине.

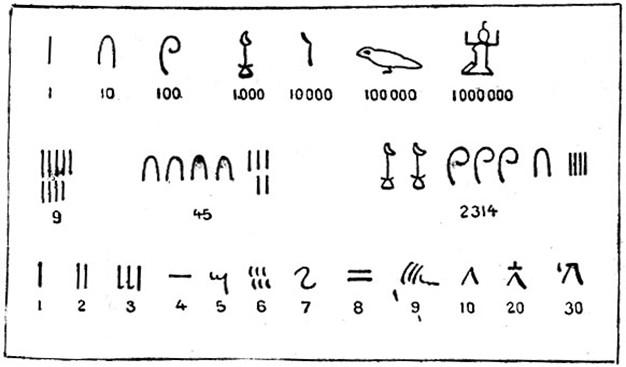
В египетской системе цифрами являлись иероглифические символы; они обозначали числа 1, 10, 100, и т.д. до миллиона.

Числа можно записывать не просто зарубками-единицами, а по разрядам: отдельно единицы, отдельно десятки, отдельно сотни. Это было очень важным открытием. Считать и записывать числа теперь стало гораздо легче.

Несколько тысяч лет, что разделяют эти первые цифры от современных, на Земле жило очень много самых разных народов. И у многих из них были свои цифры. И все эти цифры были столь же непохожи на наши нынешние.

В древнем Вавилоне считали не десятками, а шестидесятками. Число шестьдесят играло у них такую же роль, как у нас десять. Вавилоняне пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек — десять. Эти чёрточки у них получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали.

Вавилонская запись чисел была не очень удобной. Скучное занятие — рисовать много клинышков или уголков подряд, чтобы записать число двумя знаками. А если число было большое, то нередко происходила путаница, потому что специального значка для обозначения разряда 60 не было. И, например, число 3600 изображалось, как и единица, вертикальным клином. Вот тут и разберись!

• Цифры племени майя

Очень интересная система счёта была у народа майя, который жил в Центральной Америке, там, где сейчас государство Мексика. Чванливая Европа еще считала по пальцам, когда математики древних майя ввели понятие нуля и оперировали бесконечно большими величинами. Древние майя самостоятельно пришли к использованию позиционного принципа. Они сами додумались до него, причем почти на целое тысячелетие раньше старого Света. Запись цифровых знаков, образующих число. Майя вели вертикально, снизу вверх, как бы возводя некую этажерку цифр.

Цифры майя:

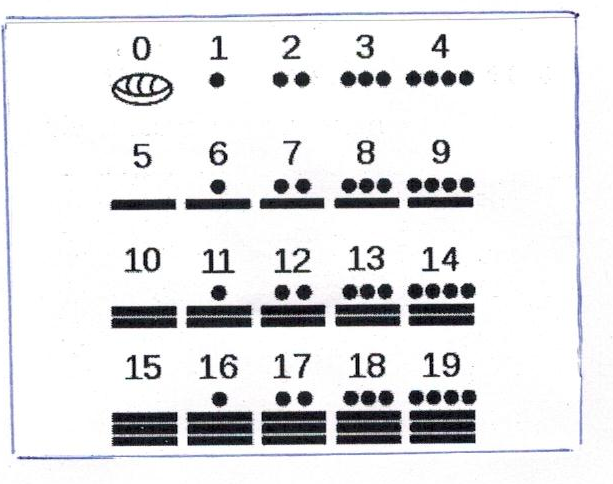
Майя считали двадцатками — у них была двадцатеричная система счёта. Числа от 1 до 20 обозначались точками и чёрточками. Если под числом был нарисован особый значок в виде глаза, это значило, что число надо увеличить в двадцать раз. Получались уже не единицы, а двадцатки, второй разряд. Если глаз был нарисован дважды, то число надо было дважды умножить на двадцать. Это был третий разряд — четырёхсотки. Выходит, что изображение глаза играло у майя ту же роль, что у нас цифра нуль. Только они рисовали глаз не рядом с числом, а под ним.

• Цифры Древнего Китая

Эта нумерация одна из старейших и самых прогрессивных. Возникла эта нумерация около 4000 тысяч лет тому назад в Китае. Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда – кружок – аналог нашего нуля). Кроме цифр от 1 до 9 там есть ещё значки для 10, 100 и 1000. Если справа от цифры стоит значок «10», — значит, цифру надо умножить на 10. Получаются десятки, второй разряд.

Цифры древнего Китая:

• Цифры Древней Греции

В Древней Греции имели хождение две основные системы счисления – аттическая и ионическая (она же алфавитная).

Аттическая система счисления использовалась греками уже к 5 веку на нашей эры. По существу это была десятичная система, а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначающая единицу, повторенная нужное число раз, означала числа до четырех. После четырех греки вместо пяти черт введи новый символ Г, первую букву слова «пента» (пять). Дойдя до десяти, они введи еще один новый символ D, первую букву слова «дека» (десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ Н означал 100 (гекатон), Х – 1000 (хилион), М – 10000 (мирион или мириада). Числа 6, 7, 8, 9, обозначались сочетаниями этих знаков: ГI, ГII, ГIII, ГIIII.

Вторая принятая в Древней Греции ионическая система счисления – алфавитная – получила широкое распространение в начале Александрийской эпохи. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную ту. Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим, чем случайное совпадение. Запись алфавитными символами могла делаться в любом порядке, так как число получалось как сумма значений отдельных букв.

Греческий алфавит

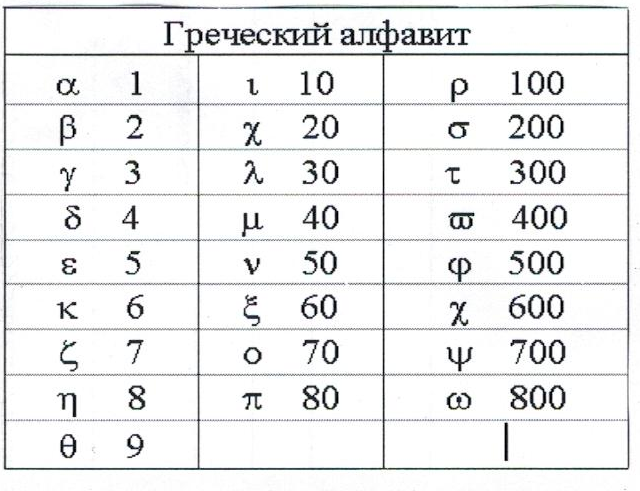
• Славянская кириллическая нумерация

Записи чисел, основанные на кириллице, эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. Отдельная буква в ней соответствовала каждой цифре (от 1 до 9), каждому десятку (от 10 до 90) и каждой сотне (от 100 до 900). Чтобы отличать буквы от цифр, над буквами с числовым значением ставили специальный знак – титло. Большие числа выражались словами. Например, 10 000 – тьма, 100 000 – легион, 1 000 000 – леодр. Эта система чисел использовалась в России до тех пор, пока Петр I не заменил её арабскими цифрами. Сейчас подобная числовая запись используется в некоторых церковных книгах, которые написаны на старославянском языке.

• Римские цифры

Среди множества иероглифических систем счисления, которые существовали в разные времена у разных народов, только одна используется до сих пор. Её цифры знакомы всем, хотя им уже около 2,5 тысячелетий. Эти цифры встречаются на циферблатах часов, фронтонах старинных и современных зданий, страницах книг. Ну конечно же, речь идет о римской системе счисления. Нельзя сказать, что время совсем не коснулось облика римских цифр. Древние римляне изобрели систему исчисления, основанную на использовании букв для отображения цифр. Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы.

Как читать римские цифры? Одно из правил записи римских чисел гласит: «Если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае меньшая цифра не может повторяться), то меньшая вычитается из большей». К примеру,

VII = 5 + 1 + 1 = 7; или IX = 10 – 1 = 9.

В наши дни любую из римских цифр запрещается записывать в одном числе более трёх раз подряд. В связи с этим выражения VIIII, XXXX считаются не корректными.

Горизонтальная линия над буквой увеличивает её значение в 1000 раз.

__ ___

Например, V означает 5000, СШ 103000.

• Цифровые знаки Индии

Мы называем изобретенные индийцами цифры 1, 2, 3, ……, 9 и ноль арабскими, так как заимствовали их у арабов, но сами арабы называли эти цифры индийскими, а арифметику, основанную на десятичной системе – «индийским счетом». На основе цифр брахми выработались современные индийские цифры, применяющиеся в десятичной позиционной системе. В то время как у других народов для записи чисел употреблялось несколько десятков различных знаков, у индийцев их число снизилось до 10, включая и обозначение ноля. Писали индийцы на белой доске, засыпанной красным песком. Орудием для записи служила палочка.

•Вклад мусульман в развитие системы счисления

У народов, входивших в состав арабского государства, первым крупным математиком был ученый аль-Хорезми. Его сочинение по арифметике дошло до нашего времени только в переводе на латинский язык. Оно сыграло значительную роль в развитии европейской математики, так как именно в нём европейцы познакомились с индийскими методами записи чисел. Вследствие того, что эти сведения были получены европейцами из книги, автор которой жил в арабском государстве и писал на арабском языке, индийские цифры стали именоваться «арабскими». Этими цифрами пользуется сейчас весь мир.

Существует интересная версия, что вид арабских цифр связан с количеством углов в их написании. Со временем углы сгладились, и цифры приобрели привычный для нас вид.

Полезное открытие - нуль

Любопытны были различные методы обозначения чисел, придуманные египтянами и вавилонянами, греками и римлянами. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были всё новые и новые знаки. И когда один из величайших древнегреческих математиков Архимед научился называть громадные числа, никто из купцов, чиновников или военачальников не обратил на это внимания. А метод Архимеда был и впрямь замечателен. Он просто называл обычную единицу единицей чисел первых, а мириаду мириад, то есть 100000000, — единицей чисел вторых. Мириаду мириад чисел вторых он назвал единицей чисел третьих и так вел счёт до мириады мириад чисел мириадо-мириадных.

Чтобы представить себе, каким громадным было это число, достаточно сказать, что по-нашему оно записывается в виде единицы с 800000000 нулями. Но и здесь не остановился великий ученый. Мириаду мириад чисел мириадо-мириадных он назвал единицей чисел второго периода и, продолжая идти вперёд, дошёл до чисел мириадо-мириадного периода. Насколько велико это число, сказать почти невозможно. Если записать его обычным почерком на бумажной ленте, то эта лента окажется во много тысяч раз длиннее, чем расстояние от Земли до Солнца! Чтобы записать, сколько нулей в числе Архимеда, надо написать цифру 8 и поставить после неё 16 нулей.

Но хотя названия громадных чисел у Архимеда уже были, обозначать их он ещё толком не умел. Не хватало ему самой малости. Архимед, один из гениальнейших математиков, не додумался до…нуля!

Впервые нуль был придуман вавилонянами примерно две тысячи лет назад. Но они применяли его лишь для обозначения пропущенных разрядов. Писать нули в конце записи числа они не догадались. Да к тому же их система счисления была, как мы знаем, шестидесятичной, и поэтому их открытие оказалось незамеченным народами, считавшими в десятичной системе счисления. Может быть, к идее о нуле для десятичной системы счёта пришли счётчики на абаке, знавшие, что иногда не приходится не класть камешки в какую-нибудь канавку на доске? Может быть, это сделали александрийские купцы? Но обычно считают, что это замечательное достижение было сделано в Индии полторы тысячи лет тому назад.

Нуль был присоединён к девяти цифрам, и появилась возможность обозначать этими девятью цифрами любое число как бы велико оно не было.

И самое главное, запись таких гигантских чисел стала довольно короткой. Ведь если бы живший тридцать тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок на волчьих костях ему пришлось бы истребить 20 тысяч волков. А для записи миллиарда не хватило бы волков во всех европейских лесах. Теперь же вся запись умещалась в одной строке!

Надо сказать, что хотя введение обозначения нуля оказалось чрезвычайно полезным для математики, первоначально некоторые «учёные» встретили это нововведение враждебно. «Зачем обозначать то, чего нет!» Но полезность нового открытия скоро стала ясна всем.

Заключение.

Изучая данный вопрос, я пришел к выводу, что:

Числа появились в древние времена (около 5000 лет назад).

Изучив историю возникновения цифр, я узнал, что арабские цифры были заимствованы арабами в Индии. Они передали данный способ записи в Европу. Современные цифры отличаются от индийских, т.к. арабы их видоизменили, приспосабливая к своему письму.

Способы записи чисел в древнеегипетской нумерации, древнегреческой, славянской кириллической и римской нумерации похожи, различны только сами знаки. Способы записи чисел у древних майя и арабов так же схожи. А вот в древнем Китае использовался свой способ записи, который называется мультипликативным (т.е. умножение). Таким образом, моя гипотеза, что способы записи чисел у разных народов схожи, частично подтвердилась.

Самым ценным вкладом в сокровищницу математических знаний человечества является употребляемый нами арабский способ записи при помощи десяти знаков чисел: 1,2,3,4,5,6,7,8,9,0 она удобна и проста, в отличие, например, от древнекитайской или римской.

На сегодняшний день параллельно с арабскими цифрами используются и римские (для обозначения размеров одежды, веков и др.).

Работать над темой мне понравилось, так как я еще узнал какой магический смысл, помимо математического, вкладывался в каждую из цифр.

Литература.

1. «Я познаю мир». Детская энциклопедия. Москва, «Астрель», 2004г.

2. «Школьникам о математике и математиках». Составитель Лиман М.М., Москва, «Просвещение», 1989г.

3. «Энциклопедия для детей», том 11 математика, Москва, «Аванта+», 2000г.

4. Иллюстрированный энциклопедический словарь, Москва, Научное

издательство «Большая Российская энциклопедия», 1998г.

5. URL http://doc4web.ru/matematika/referat-na-temu-iz-istorii-razvitiya-chisla-i-scheta.html

дата обращения к источнику (10.10.2015)

6. URL http://ppt4web.ru/matematika/istorija-chisel.html дата обращения к источнику (11.10.2015)

infourok.ru

Реферат - Цифры - Литература и русский язык

Автор: Бунин Иван .

«Мой дорогой, когда ты вырастешь, вспомнишь ли ты, как однажды зимним вечером ты вышел из детской в столовую, — это было после одной из наших ссор, — и, опустив глаза, сделал такое грустное личико? Ты большой шалун, и когда что-нибудь увлечет тебя, ты не знаешь удержу. Но я не знаю никого трогательнее тебя, когда ты притихнешь, подойдешь и прижмешься к моему плечу! Если же это происходит после ссоры, и я говорю тебе ласковое слово, как порывисто ты целуешь меня, в избытке преданности и нежности, на которую способно только детство! Но это была слишком крупная ссора…»

В тот вечер ты даже не решился подойти ко мне: «Покойной ночи, дядечка» — сказал ты и, поклонившись, шаркнул ножкой (после ссоры ты хотел быть особенно благовоспитанным мальчиком). Я ответил так, будто между нами ничего не было: «Покойной ночи». Но мог ли ты удовлетвориться этим? Забыв обиду, ты опять вернулся к заветной мечте, что пленяла тебя весь день: «Дядечка, прости меня… Я больше не буду… И пожалуйста, покажи мне цифры!» Можно ли было после этого медлить с ответом? Я помедлил, ведь я очень умный дядя…

В тот день ты проснулся с новой мечтой, которая захватила всю твою душу: иметь свои книжки с картинками, пенал, цветные карандаши и выучиться читать и писать цифры! И все это сразу, в один день! Едва проснувшись, ты позвал меня в детскую и засыпал просьбами: купить книг и карандашей и немедленно приняться за цифры. «Сегодня царский день, все заперто» — соврал я, уж очень не хотелось мне идти в город. «Нет, не царский!» — закричал было ты, но я пригрозил, и ты вздохнул: «Ну, а цифры? Ведь можно же?». «Завтра» — отрезал я, понимая, что тем лишаю тебя счастья, но не полагается баловать детей…

«Ну хорошо же!» — пригрозил ты и, как только оделся, пробормотал молитву и выпил чашку молока, принялся шалить, и весь день нельзя было унять тебя. Радость, смешанная с нетерпением, волновала тебя все больше, и вечером ты нашел им выход. Ты начал подпрыгивать, бить изо всей силы ногами в пол и громко кричать. И мамино замечание ты проигнорировал, и бабушкино, а мне в ответ особенно пронзительно крикнул и ещё сильнее ударил в пол. И вот тут начинается история…

Я сделал вид, что не замечаю тебя, но внутри весь похолодел от внезапной ненависти. И ты крикнул снова, весь отдавшись своей радости так, что сам господь улыбнулся бы при этом крике. Но я в бешенстве вскочил со стула. Каким ужасом исказилось твое лицо! Ты растерянно крикнул ещё раз, для того, чтобы показать, что не испугался. А я кинулся к тебе, дернул за руку, крепко и с наслаждением шлепнул и, вытолкнув из комнаты, захлопнул дверь. Вот тебе и цифры!

От боли и жестокой обиды ты закатился страшным и пронзительным криком. Ещё раз, ещё… Затем вопли потекли без умолку. К ним прибавились рыдания, потом крики о помощи: «Ой больно! Ой умираю!» «Небось не умрешь, — холодно сказал я. — Покричишь и смолкнешь». Но мне было стыдно, я не поднимал глаз на бабушку, у которой вдруг задрожали губы. «Ой, бабушка!» — взывал ты к последнему прибежищу. А бабушка в угоду мне и маме крепилась, но едва сидела на месте.

Ты понял, что мы решили не сдаваться, что никто не придет утешить тебя. Но прекратить вопли сразу было невозможно, хотя бы из-за самолюбия. Ты охрип, но все кричал и кричал… И мне хотелось встать, войти в детскую большим слоном и пресечь твои страдания. Но разве это согласуется с правилами воспитания и с достоинством справедливого, но строгого дяди? Наконец ты затих…

Только через полчаса я заглянул будто по постороннему делу в детскую. Ты сидел на полу весь в слезах, судорожно вздыхал и забавлялся своими незатейливыми игрушками — пустыми коробками спичек. Как сжалось мое сердце! Но я едва взглянул на тебя. «Теперь я никогда больше не буду любить тебя, — сказал ты, глядя на меня злыми, полными презрения глазами. — И никогда ничего не куплю тебе! И даже японскую копеечку, какую тогда подарил, отберу!»

Потом заходили мама и бабушка, и так же делая вид, что зашли случайно. Заводили речь, о нехороших и непослушных детях, и советовали попросить прощения. «А то я умру» — говорила бабушка печально и жестоко. «И умирай» — отвечал ты сумрачным шепотом. И мы оставили тебя, и сделали вид, что совсем забыли о тебе.

Опустился вечер, ты все так же сидел на полу и передвигал коробки. Мне стало мучительно, и я решил выйти и побродить по городу. «Бесстыдник! — зашептала тогда бабушка. — Дядя любит тебя! Кто же купит тебе пенал, книжку? А цифры?» И твое самолюбие было сломлено.

Я знаю, чем дороже мне моя мечта, тем меньше надежд на её достижение. И тогда я лукавлю: делаю вид, что равнодушен. Но что мог сделать ты? Ты проснулся, исполненный жаждой счастья. Но жизнь ответила: «Потерпи!» В ответ ты буйствовал, не в силах смирить эту жажду. Тогда жизнь ударила обидой, и ты закричал о боли. Но и тут жизнь не дрогнула: «Смирись!» И ты смирился.

Как робко ты вышел из детской: «Прости меня, и дай хоть каплю счастья, что так сладко мучит меня». И жизнь смилостивилась: «Ну ладно, давай карандаши и бумагу». Какой радостью засияли твои глаза! Как ты боялся рассердить меня, как жадно ты ловил каждое мое слово! С каким старанием ты выводил полные таинственного значения черточки! Теперь уже и я наслаждался твоей радостью. «Один… Два… Пять…» — говорил ты, с трудом водя по бумаге. «Да нет, не так. Один, два, три, четыре». — «Да, три! Я знаю», — радостно отвечал ты и выводил три, как большую прописную букву Е.

www.ronl.ru

Доклад - Цифры - Литература и русский язык

Автор: Бунин Иван .

www.ronl.ru

Реферат - Цифры 2 - Литература и русский язык

Цифры

Автор: Бунин И.А.

Иван Алексеевич Бунин

ЦИФРЫ

Мой дорогой, когда ты вырастешь, вспомнишь ли ты, как однажды зимним вечером ты вышел из детской в столовую, остановился на пороге, — это было после одной из наших ссор с тобой, — и, опустив глаза, сделал такое грустное личико?

Должен сказать тебе: ты большой шалун. Когда что-нибудь увлечет тебя, ты не знаешь удержу. Ты часто с раннего утра до поздней ночи не даешь покоя всему дому своим криком и беготней. Зато я и не знаю ничего трогательнее тебя, когда ты, насладившись своим буйством, притихнешь, побродишь по комнатам и, наконец, подойдешь и сиротливо прижмешься к моему плечу! Если же дело происходит после ссоры и если я в эту минуту скажу тебе хоть одно ласковое слово, то нельзя выразить, что ты тогда делаешь с моим сердцем! Как порывисто кидаешься ты целовать меня, как крепко обвиваешь руками мою шею, в избытке той беззаветной преданности, той страстной нежности, на которую способно только детство!

Но это была слишком крупная ссора.

Помнишь ли, что в этот вечер ты даже не решился близко подойти ко мне?

— Покойной ночи, дядечка, — тихо сказал ты мне и, поклонившись, шаркнул ножкой.

Конечно, ты хотел, после всех своих преступлений, показаться особенно деликатным, особенно приличным и кротким мальчиком. Нянька, передавая тебе единственный известный ей признак благовоспитанности, когда-то учила тебя: «Шаркни ножкой!» И вот ты, чтобы задобрить меня, вспомнил, что у тебя есть в запасе хорошие манеры. И я понял это — и поспешил ответить так, как будто между нами ничего не произошло, но все-таки очень сдержанно:

— Покойной ночи.

Но мог ли ты удовлетвориться таким миром? Да и лукавить ты не горазд еще. Перестрадав свое горе, твое сердце с новой страстью вернулось к той заветной мечте, которая так пленяла тебя весь этот день. И вечером, как только эта мечта опять овладела тобою, ты забыл и свою обиду, и свое самолюбие, и свое твердое решение всю жизнь ненавидеть меня. Ты помолчал, собрал силы и вдруг, торопясь и волнуясь, сказал мне:

— Дядечка, прости меня… Я больше не буду… И, пожалуйста, все-таки покажи мне цифры! Пожалуйста!

Можно ли было после этого медлить ответом? А я все-таки помедлил. Я, видишь ли, очень, очень умный дядя…

Ты в этот день проснулся с новой мыслью, с новой мечтой, которая захватила всю твою душу.

Только что открылись для тебя еще не изведанные радости: иметь свои собственные книжки с картинками, пенал, цветные карандаши — непременно цветные! — и выучиться читать, рисовать и писать цифры. И все это сразу, в один день, как можно скорее. Открыв утром глаза, ты тотчас же позвал меня в детскую и засыпал горячими просьбами: как можно скорее выписать тебе детский журнал, купить книг, карандашей, бумаги и немедленно приняться за цифры.

— Но сегодня царский день, все заперто, — соврал я, чтобы оттянуть дело до завтра или хоть до вечера: уж очень не хотелось мне идти в город.

Но ты замотал головою.

— Нет, нет, не царский! — закричал ты слишком тонким голоском, поднимая брови. — Вовсе не царский — я знаю.

— Да уверяю тебя, царский! — сказал я.

— А я знаю, что не царский! Ну, пожа-алуйста!

— Если ты будешь приставать, — сказал я строго и твердо то, что говорят в таких случаях все дяди, — если ты будешь приставать, так и совсем не куплю ничего.

Ты задумался.

— Ну, что ж делать! — сказал ты со вздохом. — Ну, царский, так царский. Ну, а цифры? Ведь можно же, — сказал ты, опять поднимая брови, но уже басом, рассудительно, ведь можно же в царский день показывать цифры?

— Нет, нельзя, — поспешно сказала бабушка. — Придет полицейский и арестует… И не приставай к дяде.

— Ну, это-то уж лишнее, — ответил я бабушке, — А просто мне не хочется сейчас. Вот завтра или вечером покажу.

— Нет, ты сейчас покажи!

— Сейчас не хочу. Сказал — завтра.

— Ну, во-от, — протянул ты. — Теперь говоришь — завтра, а потом скажешь — еще завтра. Нет, покажи сейчас!

Сердце тихо говорило мне, что я совершаю в эту минуту великий грех — лишаю тебя счастья, радости… Но тут пришло в голову мудрое правило: вредно, не полагается баловать детей.

И я твердо отрезал:

— Завтра. Раз сказано — завтра, значит, так и надо сделать,

— Ну, хорошо же, дядька! — пригрозил ты дерзко и весело. — Помни ты это себе!

И стал поспешно одеваться.

И как только оделся, как только пробормотал вслед за бабушкой: «Отче наш, иже еси на небеси...» — и проглотил чашку молока, — вихрем понесся в зал. А через минуту оттуда уже слышались грохот опрокидываемых стульев и удалые крики…

И весь день нельзя было унять тебя. И обедал ты наспех, рассеянно, болтая ногами, и все смотрел на меня блестящими странными глазами.

— Покажешь? — спрашивал ты иногда. — Непременно покажешь?

— Завтра непременно покажу, — отвечал я.

— Ах, как хорошо! — вскрикивал ты. — Дай бог поскорее, поскорее завтра!

Но радость, смешанная с нетерпением, волновала тебя все больше и больше. И вот, когда мы — бабушка, мама и я — сидели перед вечером за чаем, ты нашел еще один исход своему волнению.

III

Ты придумал отличную игру: подпрыгивать, бить изо всей силы ногами в пол и при этом так звонко вскрикивать, что у нас чуть не лопались барабанные перепонки.

— Перестань, Женя, — сказала мама. В ответ на это ты — трах ногами в пол!

— Перестань же, деточка, когда мама просит, сказала бабушка.

Но бабушки-то ты уж и совсем не боишься. Трах ногами в пол!

— Да перестань, — сказал я, досадливо морщась и пытаясь продолжать разговор.

— Сам перестань! — звонко крикнул ты мне в ответ, с дерзким блеском в глазах и, подпрыгнув, еще сильнее ударил в пол и еще пронзительнее крикнул в такт.

Я пожал плечом и сделал вид, что больше не замечаю тебя.

Но вот тут-то и начинается история.

Я, говорю, сделал вид, что не замечаю тебя. Но сказать ли правду? Я не только не забыл о тебе после твоего дерзкого крика, но весь похолодел от внезапной ненависти к тебе. И уже должен был употребить усилия, чтобы делать вид, что не замечаю тебя, и продолжать разыгрывать роль спокойного и рассудительного.

Но и этим дело не кончилось.

Ты крикнул снова. Крикнул, совершенно позабыв о нас и весь отдавшись тому, что происходило в твоей переполненной жизнью душе, — крикнул таким звонким криком беспричинной, божественной радости, что сам господь бог улыбнулся бы при этом крике. Я же в бешенстве вскочил со стула.

— Перестань! — рявкнул я вдруг, неожиданно для самого себя, во все горло.

Какой черт окатил меня в эту минуту целым ушатом злобы? У меня помутилось сознание. И надо было видеть, как дрогнуло, как исказилось на мгновение твое лицо молнией ужаса!

— А! — звонко и растерянно крикнул ты еще раз.

И уже без всякой радости, а только для того, чтобы показать, что ты не испугался, криво и жалко ударил в пол каблуками.

А я — я кинулся к тебе, дернул тебя за руку, да так, что ты волчком перевернулся передо мною, крепко и с наслаждением шлепнул тебя и, вытолкнув из комнаты, захлопнул дверь.

Вот тебе и цифры!

От боли, от острого и внезапного оскорбления, так грубо ударившего тебя в сердце в один из самых радостных моментов твоего детства, ты, вылетевши за дверь, закатился таким страшным, таким пронзительным альтом, на какой не способен ни один певец в мире. И надолго, надолго замер… Затем набрал в легкие воздуху еще больше и поднял альт уже до невероятной высоты…

Затем паузы между верхней и нижней нотами стали сокращаться, — вопли потекли без умолку. К воплям прибавились рыдания, к рыданиям — крики о помощи. Сознание твое стало проясняться, и ты начал играть, с мучительным наслаждением играть роль умирающего.

— О-ой, больно! Ой, мамочка, умираю!

— Небось не умрешь, — холодно сказал я. — Покричишь, покричишь, да и смолкнешь.

Но ты не смолкал.

Разговор, конечно, оборвался. Мне было уже стыдно, и я зажигал папиросу, не поднимая глаз на бабушку. А у бабушки вдруг задрожали губы, брови, и, отвернувшись к окну, она стала быстро, быстро колотить чайной ложкой по столу.

— Ужасно испорченный ребенок! — сказала, нахмуриваясь и стараясь быть беспристрастной, мама и снова взялась за свое вязанье. — Ужасно избалован!

— Ой, бабушка! Ой, милая моя бабушка! — вопил ты диким голосом, взывая теперь к последнему прибежищу — к бабушке.

И бабушка едва сидела на месте.

Ее сердце рвалось в детскую, но, в угоду мне и маме, она крепилась, смотрела из-под дрожащих бровей на темневшую улицу и быстро стучала ложечкой по столу.

Понял тогда и ты, что мы решили не сдаваться, что никто не утолит твоей боли и обиды поцелуями, мольбами о прощении. Да и слез уже не хватало. Ты до изнеможения упился своими рыданиями, своим детским горем, с которым не сравнится, может быть, ни одно человеческое горе, по прекратить вопли сразу было невозможно, хотя бы из-за одного самолюбия.

Ясно было слышно: кричать тебе уже не хочется, голос охрип и срывается, слез нет. Но ты все кричал и кричал!

Было невмоготу и мне. Хотелось встать с места, распахнуть дверь в детскую и сразу, каким-нибудь одним горячим слоном, пресечь твои страдания. Но разве это согласуется с правилами разумного воспитания и с достоинством справедливого, хотя и строго дяди? Наконец ты затих…

— И мы тотчас помирились? — спрашиваешь ты.

Нет, я таки выдержал характер. Я по крайней мере через полчаса после того, как ты затих, заглянул в детскую. И то так? Подошел к дверям, сделал серьезное лицо и растворил их с таким видом, точно у меня было какое-то дело. А ты в это время уже возвращался мало-помалу к обыденной жизни.

Ты сидел на полу, изредка подергивался от глубоких прерывистых вздохов, обычных у детей после долгого плача, и с потемневшим от размазанных слез личиком забавлялся своими незатейливыми игрушками — пустыми коробочками от спичек, — расставляя их по полу, между раздвинутых ног, в каком-то, только тебе одному известном порядке.

Как сжалось мое сердце при виде этих коробочек!

Но, делая вид, что отношения наши прерваны, что я оскорблен тобою, я едва взглянул на тебя. Я внимательно и строго осмотрел подоконники, столы… Где это мой портсигар?.. И уже хотел выйти, как вдруг ты поднял голову и, глядя на меня злыми, полными презрения глазами, хрипло сказал:

— Теперь я никогда больше не буду любить тебя.

Потом подумал, хотел сказать еще что-то очень обидное, но запнулся, не нашелся и сказал первое, что пришло в голову:

— И никогда ничего не куплю тебе.

— Пожалуйста! — небрежно ответил я, пожимая плечом. — Пожалуйста! Я от такого дурного мальчика и не взял бы ничего.

— Даже и японскую копеечку, какую тогда подарил, назад возьму! — крикнул ты тонким, дрогнувшим голосом, делая последнюю попытку уязвить меня.

— А вот это уж и совсем нехорошо! — ответил я. — Дарить и потом отнимать! Впрочем, это твое дело.

Потом заходили к тебе мама и бабушка. И так же, как я, делали сначала вид, что вошли случайно… по делу… Затем качали головами и, стараясь не придавать своим словам значения, заводили речь о том, как это нехорошо, когда дети растут непослушными, дерзкими и добиваются того, что их никто не любит. А кончили тем, что советовали тебе пойти ко мне и попросить у меня прощения.

— А то дядя рассердится и уедет в Москву, — говорили бабушка грустным тоном, — И никогда больше не приедет к нам.

— И пускай не приедет! — отвечал ты едва слышно, все ниже опуская голову.

— Ну, я умру, — говорила бабушка еще печальнее, совсем не думая о том, к какому жестокому средству прибегает она, чтобы заставить тебя переломить свою гордость.

— И умирай, — отвечал ты сумрачным шепотом.

— Хорош! — сказал я, снова чувствуя приступ раздражения. — Хорош! — повторил я, дымя папиросой и поглядывая в окно на темную пустую улицу.

И, переждав, пока пожилая худая горничная, всегда молчаливая и печальная от сознания, что она — вдова машиниста, зажгла в столовой лампу, прибавил:

— Вот так мальчик!

— Да не обращай на него внимания, — сказала мама, заглядывая под матовый колпак лампы, не коптит ли. — Охота тебе разговаривать с такой злючкой!

И мы сделали вид, что совсем забыли о тебе.

В детской огня еще не зажигали, и стекла ее окон казались теперь синими-синими. Зимний вечер стоял за ними, и в детской было сумрачно и грустно. Ты сидел на полу и передвигал коробочки. И эти коробочки мучили меня. Я встал и решил побродить по городу.

Но тут послышался шепот бабушки.

— Бесстыдник, бесстыдник! — зашептала она укоризненно. — Дядя тебя любит, возит тебе игрушки, гостинцы…

Я громко прервал:

— Бабушка, этого говорить не следует. Это лишнее. Тут дело не в гостинцах.

Но бабушка знала, что делает.

— Как же не в гостинцах? — ответила она. — Не дорог гостинец, а дорога память.

И, помолчав, ударила по самой чувствительной струне твоего сердца:

— А кто же купит ему теперь пенал, бумаги, книжку с картинками? Да что пенал! Пенал — туда-сюда. А цифры? Ведь уж этого не купишь ни за какие деньги. Впрочем, прибавила она, — делай, как знаешь. Сиди тут один в темноте.

И вышла из детской.

Кончено — самолюбие твое было сломлено! Ты был побежден.

Чем неосуществимее мечта, тем пленительнее, чем пленительнее, тем неосуществимее. Я уже знаю это.

С самых ранних дней моих я у нее во власти. Но я знаю и то, что, чем дороже мне моя мечта, тем менее надежд на достижение ее. И я уже давно в борьбе с нею. Я лукавлю: делаю вид, что я равнодушен. Но что мог сделать ты?

Счастье, счастье!

Ты открыл утром глаза, переполненный жаждою счастья. И с детской доверчивостью, с открытым сердцем кинулся к жизни: скорее, скорее!

Но жизнь ответила:

— Потерпи.

— Ну пожалуйста! — воскликнул ты страстно.

— Замолчи, иначе ничего не получишь!

— Ну погоди же! — крикнул ты злобно. И на время смолк.

Но сердце твое буйствовало. Ты бесновался, с грохотом валял стулья, бил ногами в пол, звонко вскрикивал от переполнявшей твое сердце радостной жажды… Тогда жизнь со всего размаха ударила тебя в сердце тупым ножом обиды. И ты закатился бешеным криком боли, призывом на помощь.

Но и тут не дрогнул ни один мускул на лице жизни… Смирись, смирись!

И ты смирился.

VII

Помнишь ли, как робко вышел ты из детской и что ты сказал мне?

— Дядечка! — сказал ты мне, обессиленный борьбой за счастье и все еще алкая его. — Дядечка, прости меня. И дай мне хоть каплю того счастья, жажда которого так сладко мучит меня.

Ни жизнь обидчива.

Она сделала притворно печальное лицо.

— Цифры! Я понимаю, что это счастье… Но ты не любишь дядю, огорчаешь его…

— Да нет, неправда, — люблю, очень люблю! — горячо воскликнул ты.

И жизнь наконец смилостивилась.

— Ну уж бог с тобою! Неси сюда к столу стул, давай карандаши, бумагу…

И какой радостью засияли твои глаза!

Как хлопотал ты! Как боялся рассердить меня, каким покорным, деликатным, осторожным в каждом своем движении старался ты быть! И как жадно ловил ты каждое мое слово!

Глубоко дыша от волнения, поминутно слюнявя огрызок карандаша, с каким старанием налегал ты на стол грудью и крутил головой, выводя таинственные, полные какого-то божественного значения черточки!

Теперь уже и я наслаждался твоею радостью, с нежностью обоняя запах твоих волос: детские волосы хорошо пахнут, — совсем как маленькие птички.

— Один… Два… Пять… — говорил ты, с трудом водя по бумаге.

— Да нет, не так. Один, два, три, четыре.

— Сейчас, сейчас, — говорил ты поспешно. — Я сначала: один, два…

И смущенно глядел на меня.

— Ну, три…

— Да, да, три! — подхватил ты радостно. — Я знаю. И выводил три, как большую прописную букву Е.

1906

www.ronl.ru

"Из истории развития числа и счета"

Министерство образования Российской Федерации

Пермский государственный гуманитарно-педагогический университет

Из истории развития числа и счета.

Выполнила:

Черемных Светлана

Анатольевна.

2013г

Введение.

Можно ли представить себе мир без чисел? На протяжении всей своей жизни мы сталкиваемся с числами и выполняем над ними арифметические действия. Нас это не удивляет. Мы воспринимаем это, как факт, как само собой разумеющееся и даже не задумываясь об их происхождении. Без знания прошлого нельзя понять настоящее. Поэтому целью данной работы является исследование истории возникновения чисел, связанной с необходимостью выражения всех чисел знаками.

Пересчитывая предметы, мы даем этому множеству количественную характеристику, даже не задумываясь о том, что и в далекие времена наши предки могли считать или, во всяком случае, могли определить количество предметов. Мы живем среди чисел. Само возникновение понятия числа - одно из гениальных проявлений человеческого разума. При помощи чисел производятся измерения, сравнения, вычисления, рисование, проектирование, даже можно делать умозаключения, выводы.

Число - важнейшее понятие математики. Потребовалось несколько тысячелетий, чтобы это понятие приобрело форму, которая в настоящий момент признается удовлетворительной подавляющим большинством математиков.

Так, первые области применения математики были связаны с созерцанием звезд и земледелием. Изучение звездного неба позволило проложить торговые морские пути, караванные дороги в новые районы и резко увеличить эффект торговли между государствами. Обмен товарами приводил к обмену культурными ценностями, к развитию толерантности как явления, лежащего в основе мирного сосуществования различных рас и народов.

Практически ежедневно мы сталкиваемся с необходимостью обработки числовой информации, что влечет за собой необходимость создания и усовершенствования вычислительных устройств, благодаря которым обрабатывается огромное количество данных за наименьшее время. Так, для электронного хранения данных в памяти компьютера удобны две цифры, поскольку они требуют только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0). Такое представление информации называется двоичным или цифровым кодированием. Способы цифрового кодирования текстов, звуков, изображений, а также трехмерных объектов были придуманы в 80-х годах прошлого века.

Цифры, знаки обозначения арифметических действий и другие математические символы вырабатывались людьми постепенно на протяжении веков. Большинство их образовалось из рисунков, чертежей, букв и сокращённых слов.

1. Развитие представления о понятии "число".

Пифагорейцы считали, что числа принадлежат к миру принципов, лежащих в основе мира вещей. Пифагор говорил: «Все вещи можно представить в виде чисел».

Аристотель называл число «началом и сущностью вещей, их взаимодействием и состоянием».

Люди научились считать еще в каменном веке. На первых этапах существования человеческого общества числа, открытые в процессе практической деятельности, служили для примитивного счета предметов, дней, шагов и т.п. В первобытном обществе человек нуждался лишь в нескольких первых числах. Но с развитием цивилизации ему потребовалось изобретать все большие и большие числа. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда.

То, что первобытные люди сначала знали только «один», «два» и «много», подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов. У некоторых племен Австралии и Полинезии до самого последнего времени было только два числительных: «один» и «два», а все числа больше двух, получали названия в виде сочетаний этих двух числительных: число 3 – это «два и один», 4 – «два и два», 5 – «два, два, один».

Из истории возникновения счета и чисел.

Учиться считать люди начали в незапамятные времена, а учителем у них была сама жизнь.

Древние люди добывали себе пищу главным образом охотой. На крупного зверя — бизона или лося — приходилось охотиться всем племенем: в одиночку ведь с ним и не справишься. Чтобы добыча не ушла, ее надо было окружить, ну хотя бы так: пять человек справа, семь сзади, четыре слева. Тут уж без счёта никак не обойдешься! И вождь первобытного племени справлялся с этой задачей, Даже в те времена, когда человек не знал таких слов, как «пять» или «семь», он мог показать числа на пальцах рук.

Есть и сейчас на земле племена, которые при счёте не могут обойтись без помощи пальцев. Вместо числа пять они говорят «рука», десять — «две руки», а двадцать — «весь человек», — тут уж присчитываются числа на пальцах рук. В Африке есть племя, где и в наше время люди считают «один», «два», «три», а дальше «много».

Так люди начинали учиться считать, пользуясь тем, что дала им сама природа, — собственной пятернёй.

Предметы считать просто; один, два, три, четыре.… Измерить небольшое расстояние тоже несложно. Надо только иметь какую – нибудь мерку. Даже теперь мы нередко меряем расстояние по способу первобытных людей — считаем шаги.

Звёзды были для людей не только первыми часами, но и первым компасом.

Для того чтобы считать дни нужны большие числа: десятки, сотни и даже тысячи. Тут, конечно, никаких пальцев для счёта хватить не могло! Да и считая предметы, их можно было перекладывать, пересчитывать несколько раз. А в счёте времени ошибаться нельзя. Прошедший день исчез, его не вернёшь, не присоединишь к другим.

Как же считали дни люди в те времена, когда они и писать не умели?

Додумались. Ведь можно было каждый день делать зарубку на палке и потом зарубки эти сосчитать. Так началась первая на земле запись прожитых дней. Только делали её не пером, а топором. Именно таким деревянным календарём пользовался на необитаемом острове Робинзон Крузо. Через каждые тридцать дней, то есть каждое новолуние, он делал на своём календаре зарубку подлиннее. Получалась отметка месяца. Из месяцев складывался год.

Около пяти тысяч лет назад люди додумались до того, что числа можно записывать не просто зарубками-единицами, а по разрядам: отдельно единицы, отдельно десятки, отдельно сотни. Это было очень важным открытием. Считать и записывать числа теперь стало гораздо легче.

Вавилонская запись чисел была не очень удобной. Скучное занятие — рисовать много клинышков или уголков подряд, чтобы записать число двумя знаками. А если число было большое, то нередко происходила путаница, потому что специального значка для обозначения разряда 60 не было. И например, число 3600 изображалось, как и единица, вертикальным клином. Вот тут и разберись!

Очень интересная система счёта была у народа майя, который жил в Центральной Америке (там, где сейчас государство Мексика). Около двух тысяч лет назад индейцы майя были гораздо культурнее, чем народы, жившие в то время в Европе.

Китайцы, как и египтяне, пользовались десятичной системой счёта. Кроме цифр от 1 до 9 там есть ещё значки для 10, 100 и 1000. Если справа от цифры стоит значок «10», — значит, цифру надо умножить на 10, Получаются десятки, второй разряд.

Индийцы очень обрадовались этой возможности, и в их легендах есть повествования о битвах, в которых участвовало такое количество обезьян, что для его обозначения надо было написать после единицы ещё 23 нуля! Столько обезьян не поместится во всей Солнечной системе.

Как же в древности пользовались люди своим умением считать? Для чего им была нужна математика?

Народам-земледельцам, для того чтобы прожить и прокормиться, нужно было знать гораздо больше, чем кочевникам-скотоводам. Жизнь заставляла их учиться быстрее. Поэтому у земледельческих народов математика из набора отдельных простейших правил постепенно стала превращаться в науку.

Развитие представления о понятии "число".

Аристотель называл число «началом и сущностью вещей, их взаимодействием и состоянием».

Люди научились считать еще в каменном веке. На первых этапах существования человеческого общества числа, открытые в процессе практической деятельности, служили для примитивного счета предметов, дней, шагов и т.п. В первобытном обществе человек нуждался лишь в нескольких первых числах. Но с развитием цивилизации ему потребовалось изобретать все большие и большие числа. Этот процесс продолжался на протяжении многих столетий и потребовал напряженного интеллектуального труда.

Число, как основное понятие математики.

Существует большое количество определений понятию «число». Первое научное определение числа дал Эвклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 – около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Магницкий в своей «Арифметике» (1703 г.).

Исследование множеств чисел с применением кругов Эйлера

Натуральные числа

Считается, что термин «натуральное число» впервые применил римский государственный деятель, философ, автор трудов по математике и теории музыки Боэций (480 – 524 гг.), но еще греческий математик Никомах из Геразы говорил о натуральном, то есть природном ряде чисел.

Понятием «натуральное число» в современном его понимании последовательно пользовался выдающийся французский математик, философ-просветитель Даламбер (1717-1783 гг.).

Итак, изучение математики начиналось с натуральных чисел, недаром они и называются натуральными, то есть «природными», естественными, обыкновенными. Это числа 1, 2, 3, 4, …

С появлением натурального ряда был сделан первый шаг к созданию математики. Сейчас все понимают, что натуральный ряд чисел бесконечен. В древности люди этого не знали. Сначала они умели считать до трех, потом до десяти, до сорока, до ста, а дальше была «тьма», «легион» «леодр» «ворон», «колода», после чего добавляли, что большего числа не существует.

Натуральный ряд был очень коротким. Расширить его удалось великому механику и математику древности Архимеду (III в. до н.э.). Архимед написал знаменитый труд Псаммит, или Исчисление песчинок». В нем он подсчитал число песчинок, которые могли бы заполнить шар радиусом 15.000.000.000.000 километров. До Архимеда в Древней Греции самым большим числом считалось 10.000.000 мириад. Мириадой называлось число 10000, от греческого слова «мирос» - «неисчислимо большое». Архимед начал считать мириадами мириад и в результате вывел свою систему счисления. Наибольшее число его системы содержит 80.000.000.000.000.000 нулей. Это число так велико, что если напечатать его обыкновенным шрифтом на машинке, то этой лентой можно опоясать Земной шар по экватору более 2 миллионов раз. Даже ракете с первой космической скоростью (8км/с) пришлось бы лететь вдоль этой ленты более 300 лет. Вот до какого огромного числа простирается натуральный ряд. Но и это число не последнее. За ним еще числа, числа, числа, числа… до бесконечности. Если натуральный ряд чисел кажется вам скучным и однообразным, всмотритесь в него повнимательнее, и вы найдете много удивительного и неожиданного.

Натуральные числа понадобились человеку прежде всего для счёта предметов, и мы, наверное, ничего тут пояснять не будем, ведь каждый знает смысл вопроса «сколько?», каждый умеет считать. Есть ещё одно назначение натуральных чисел — отвечать на вопрос «который?».

Таким образом, натуральные числа имеют две основные функции:

- характеристика количества предметов;

- характеристика порядка предметов, размещенных в ряд.

Развитие числовой записи.

Самая ранняя запись чисел производилась еще в отдаленные эпохи жизни человечества – это узелки, зарубки, нанизанные на шнур раковины или орехи.

Числовая запись в Древнем Вавилоне производилась на глиняных табличках. Орудием служил трехгранный брусок, которым на глине выдавливались клиновидные фигуры. Меняя положение клинка, можно было обозначать разные числа. Например, знак ▼ означал единицу, ◄ – десяток. При помощи этих знаков, применяя метод сложения, можно было выражать и многозначные числа .

Египетская запись чисел совершалась с помощью отдельных рисунков. Египтяне придумали особые знаки для единиц, десятков, сотен и других больших чисел. Записи производились преимущественно красками на папирусе. Иногда же материалом для записи служили камень, дерево, кожа, холст.

Индейцы племени майя писали любое число, используя только точку, линию и кружочек.

Римляне заимствовали метод записи чисел у одного из племен Древней Италии. Числа выражались при помощи букв. А именно числа 1, 5, 10, 50, 100, 500 и 1000 обозначались буквами I, V, X, L, C, D и M. Римская запись чисел широко используется и в наше время. Для запоминания обозначений цифр в порядке убывания существует такая шуточная фраза: «Мы Дарим Сочные Лимоны, Хватит Всем И еще останется».

Цифровые знаки Индии не совпадают по очертаниям с современными, но имеют с ними сходство. В то время как у других народов для записи чисел употреблялось несколько десятков различных знаков, у индийцев их число снизилось до 10, включая и обозначение ноля. Писали индийцы на белой доске, засыпанной красным песком. Орудием для записи служила палочка.

Славянская система записи чисел основана на кириллице. Отдельная буква в ней соответствовала каждой цифре (от 1 до 9), каждому десятку (от 10 до 90) и каждой сотне (от 100 до 900). Чтобы отличать буквы от цифр, над буквами с числовым значением ставили специальный знак – титло. Большие числа выражались словами. Например, 10 000 – тьма, 100 000 – легион, 1 000 000 – леодр. Эта система чисел использовалась в России до тех пор, пока Петр I не заменил её арабскими цифрами. Сейчас подобная числовая запись используется в некоторых церковных книгах, которые написаны на старославянском языке.

Четыре действия арифметики.

Сложение и вычитание.

Числа были придуманы людьми, чтобы обозначать количество предметов: стрел в колчане, мешков зерна в амбаре, овец в стаде. Но эти величины непостоянны – количество предметов то увеличивалось, то уменьшалось, поэтому важно было складывать и вычитать.

Когда числа были небольшими, это делалось просто: рисовали черточки на дереве, завязывали узелки на веревке. Пасет пастух стадо овец, на поясе у него веревка, а на веревке столько узелков, сколько овец в стаде. Родился ягнёнок – пастух завязал ещё один узелок. Утащили волки ещё двух овец - развязал два узелка. Вместо верёвки часто использовали живой «вычислительный прибор» - пальцы. Обычно так считают малыши. Большого труда стоит преподавателям отучить первоклассников от такого счёта и приучить к устному счёту в «уме». Однако наиболее стойкие продолжают считать на пальцах, держа руки в карманах, чтобы не видел учитель. А один первоклассник складывал числа, глядя на циферблат часов.

С развитием цивилизации появились различные приёмы счёта. Они были необходимы и купцам, и ремесленникам, и тогдашним «банкирам» - ростовщикам. Однако искусством счёта владели не многие. Для расчётов привлекали специально обученных людей – счетчиков.

Умножение.

Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.

За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Один из них носит название «ревность», или «решётчатое умножение». Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, - пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».

В России среди крестьян некоторых губерний был распространён способ, который не требовал знания всей таблицы умножения. Он получил название «русский крестьянский способ умножения». Здесь необходимо было лишь умение умножать и делить числа на 2. Перемножим ещё раз числа 1998 и 987 этим способом. Напишем одно из чисел слева, а второе – справа на одной строчке. Левое число будем делить на 2, а правое – умножать на 2 и результаты записывать в столбик.

Если при делении возникнет остаток (т. е. делимое окажется нечётным числом), то он отбрасывается. Умножение и деление на 2 продолжаем до тех пор, пока слева не останется 1. Затем вычеркнем те строчки столбиков, в которых слева стоят чётные числа. Теперь сложим оставшиеся числа в правом столбце – получим 1 972 026. Это и есть произведение перемножаемых чисел.

Деление.

Хотя умножение в старину и считалось нелёгким делом, однако деление было ещё сложнее. В Италии до сих пор сохранилась поговорка «Трудное дело деление». Так обычно говорят, когда оказываются перед почти неразрешимой проблемой.

В Средние века людей, умевших производить деление, можно было пересчитать по пальцам. Их уважительно называли «магистрами деления». Они переезжали из города в город по приглашениям купцов, желавших привести в порядок свои счета.

Методов деления придумано немало. Монах-математик Герберт, будущий Папа Римский Сильвестр II., привёл в своих сочинениях несколько способов деления на абаке. При этом он придерживался таких принципов: - как можно меньше применять таблицу умножения, в частности не использовать умножение в уме двузначных чисел на однозначные; - избегать вычитаний, заменяя их сложениями; - работа должна выполняться автоматически, без проверок, при которых тоже могут появиться ошибки. Такие строгие ограничения он ввёл, учитывая, сколь неграмотны были монахи, производившие таблицы умножения. Но в итоге, правила Герберта оказались настолько сложными, что не были понятны даже самым прилежным счётчикам-абацистам.

Когда в Европе появился арабский способ деления, основанный на принятой сейчас позиционной десятиной системе счисления, он получил название «золотое деление». Им мы пользуемся и по сей день. А метод Герберта стали называть «железным делением».

Кроме этих способов были и другие. Например, раскладывали делитель на множители, а затем последовательно делили делимое на эти числа. При этом для деления на однозначные числа существовал специальный метод.

Долгое время в Европе конкурировали два способа деления: «золотое деление» и «галера». Прежде всего, напомним правила «золотого деления». Разделим 987 654 на 346

Заключение.

Потребность в счете, измерениях, и желании проследить за изменением количественной характеристики, послужило толчком в зарождении математики и основными математическими действиями над числами. История показывает, как тяжел был путь выбора наиболее удобного варианта действий над числами. И не в последнюю очередь от этого зависит дальнейшее распространение и развитие математики как науки. Изучая исторические процессы развития общества и математики, видно, что понятие числа прошло длинный исторический путь развития и наука о числах и действиях над ними необходима для прогрессивного развития человеческого общества. Числа составляют часть человеческого мышления и мы порой не отдаем себе отчета, насколько важны они в нашей жизни.

При исследовании истории возникновения чисел была установлена зависимость между возникновением чисел и необходимостью выражения всех чисел знаками. Эта зависимость повлияла на появление знаков-цифр, которые заменили другие не совсем удобные способы обозначения. Самым ценным вкладом в сокровищницу математических знаний человечества является употребляемый нами способ записи при помощи десяти знаков чисел: 1,2,3,4,5,6,7,8,9,0.

Литература.

1. Выгодский М.Л. Арифметика и алгебра в древнем мире М. 1967г.

2. Депман И. Истории Арифметики М. 1965г.

3. Депман И. Мир чисел М.1966г.

globuss24.ru

0	٠	۰	०	০	੦	૦	୦	௦	౦	೦	൦	๐	໐	༠	၀	០	᠐	᥆	᧐
1	١	۱	१	১	੧	૧	୧	௧	౧	೧	൧	๑	໑	༡	၁	១	᠑	᥇	᧑
2	٢	۲	२	২	੨	૨	୨	௨	౨	೨	൨	๒	໒	༢	၂	២	᠒	᥈	᧒
3	٣	۳	३	৩	੩	૩	୩	௩	౩	೩	൩	๓	໓	༣	၃	៣	᠓	᥉	᧓
4	٤	۴	४	৪	੪	૪	୪	௪	౪	೪	൪	๔	໔	༤	၄	៤	᠔	᥊	᧔
5	٥	۵	५	৫	੫	૫	୫	௫	౫	೫	൫	๕	໕	༥	၅	៥	᠕	᥋	᧕
6	٦	۶	६	৬	੬	૬	୬	௬	౬	೬	൬	๖	໖	༦	၆	៦	᠖	᥌	᧖
7	٧	۷	७	৭	੭	૭	୭	௭	౭	೭	൭	๗	໗	༧	၇	៧	᠗	᥍	᧗
8	٨	۸	८	৮	੮	૮	୮	௮	౮	೮	൮	๘	໘	༨	၈	៨	᠘	᥎	᧘
9	٩	۹	९	৯	੯	૯	୯	௯	౯	೯	൯	๙	໙	༩	၉	៩	᠙	᥏	᧙

0	٠	۰	०	০	੦	૦	୦	௦	౦	೦	൦	๐	໐	༠	၀	០	᠐	᥆	᧐
1	١	۱	१	১	੧	૧	୧	௧	౧	೧	൧	๑	໑	༡	၁	១	᠑	᥇	᧑
2	٢	۲	२	২	੨	૨	୨	௨	౨	೨	൨	๒	໒	༢	၂	២	᠒	᥈	᧒
3	٣	۳	३	৩	੩	૩	୩	௩	౩	೩	൩	๓	໓	༣	၃	៣	᠓	᥉	᧓
4	٤	۴	४	৪	੪	૪	୪	௪	౪	೪	൪	๔	໔	༤	၄	៤	᠔	᥊	᧔
5	٥	۵	५	৫	੫	૫	୫	௫	౫	೫	൫	๕	໕	༥	၅	៥	᠕	᥋	᧕
6	٦	۶	६	৬	੬	૬	୬	௬	౬	೬	൬	๖	໖	༦	၆	៦	᠖	᥌	᧖
7	٧	۷	७	৭	੭	૭	୭	௭	౭	೭	൭	๗	໗	༧	၇	៧	᠗	᥍	᧗
8	٨	۸	८	৮	੮	૮	୮	௮	౮	೮	൮	๘	໘	༨	၈	៨	᠘	᥎	᧘
9	٩	۹	९	৯	੯	૯	୯	௯	౯	೯	൯	๙	໙	༩	၉	៩	᠙	᥏	᧙

Реферат на тему: "Из истории развития числа и счета". Реферат цифры

Реферат Цифры

План:

Введение

1. История

2. Национальные варианты арабско-индийских десятичных цифр

3. Использование на монетах

4. Нумерация в книгах

Примечания

Реферат История возникновения цифр

Для чего нужна математика

Пальцы и зарубки

Имя чисел

Новый способ записи чисел.

Новая, или арабская нумерация

Один, два, три…

Рисские, арабские и другие

Реферат по математике История чисел курсанта Гусева

Реферат - Цифры - Литература и русский язык

Доклад - Цифры - Литература и русский язык

Реферат - Цифры 2 - Литература и русский язык

Цифры

"Из истории развития числа и счета"

Смотрите также

0	٠	۰	०	০	੦	૦	୦	௦	౦	೦	൦	๐	໐	༠	၀	០	᠐	᥆	᧐
1	١	۱	१	১	੧	૧	୧	௧	౧	೧	൧	๑	໑	༡	၁	១	᠑	᥇	᧑
2	٢	۲	२	২	੨	૨	୨	௨	౨	೨	൨	๒	໒	༢	၂	២	᠒	᥈	᧒
3	٣	۳	३	৩	੩	૩	୩	௩	౩	೩	൩	๓	໓	༣	၃	៣	᠓	᥉	᧓
4	٤	۴	४	৪	੪	૪	୪	௪	౪	೪	൪	๔	໔	༤	၄	៤	᠔	᥊	᧔
5	٥	۵	५	৫	੫	૫	୫	௫	౫	೫	൫	๕	໕	༥	၅	៥	᠕	᥋	᧕
6	٦	۶	६	৬	੬	૬	୬	௬	౬	೬	൬	๖	໖	༦	၆	៦	᠖	᥌	᧖
7	٧	۷	७	৭	੭	૭	୭	௭	౭	೭	൭	๗	໗	༧	၇	៧	᠗	᥍	᧗
8	٨	۸	८	৮	੮	૮	୮	௮	౮	೮	൮	๘	໘	༨	၈	៨	᠘	᥎	᧘
9	٩	۹	९	৯	੯	૯	୯	௯	౯	೯	൯	๙	໙	༩	၉	៩	᠙	᥏	᧙