Назовём этот урок "Концепция числовой окружности". В этом случае по моему мнению, слово "концепция" замечательно укладывается в название того, что нам с вами предстоит разобрать. Одно из пояснений слова "концепция" в Википедии это ведущий замысел. Не смотря на кажущуюся сложность концепция нашей окружности проста и логична, и что важно, её понимание открывает двери к легкому восприятию последующих материалов по тригонометрии. Концепцию числовой окружности я решил передать так, как я это делаю на своих индивидуальных занятиях. Однажды на занятии, когда я преподавал эту тему, моя ученица воскликнула: "Это так просто! Почему нам это не рассказывают в школе?!" Надеюсь в большинстве случаев всё таки рассказывают, но для тех кто пропустил или не успел за текущим учебным процессом, предоставляю возможность прочитать об этом.
Вы заметили, что сайт на котором мы занимаемся называется "Тетрадка в клеточку"? Это не просто так 🙂 Вооружимся тетрадкой в клеточку, циркулем, линейкой, ластиком, простым карандашом и ручкой. Это необходимый и достаточный набор для участия в нашем мастер классе. Мозг человека не сохраняет информацию, которую не считает важной, иначе переполнение памяти было бы неминуемым. Надо передать мозгу сигнал, что эта информация важна. С этой целью обязательно проделайте самостоятельные упражнения.
Начнём! Числовая окружность это. Как вы думаете, что это? Правильно, это прежде всего окружность 🙂 Но это ведь не просто окружность, она ещё и числовая 🙂 По аналогии с числовой прямой, она должна иметь начальную точку отсчёта, то есть ноль. И действительно за начало отсчёта на числовой окружности принята её крайняя правая точка. На рисунке 1 эта точка обозначена буквой A0. Но опять же по аналогии с числовой прямой, наша окружность должна иметь положительное и отрицательное направление. И действительно для числовой окружности принято, что направление против часовой стрелки будет положительным, а по часовой соответственно - отрицательным.
Подытожим: на числовой окружности ноль соответствует крайней правой точке, положительным направлением принято направление против часовой стрелки и отрицательным - по часовой.
B можно добраться по различным траекториям. Как отмечалось ранее, если двигаться против часовой стрелки, то значение будет положительным, а если по часовой, то - отрицательным. Каждая траектория представляет собой дугу, которой ставится в соответствие угол поворота. Величина угла поворота измеряется в градусной или радианной мере.
Например: 360° - полный оборот, 180° - половина оборота, 90° - четверть оборота, 270° - три четверти оборота, и т.д. На рисунке 3 показаны некоторые значения в градусах, которые соответствуют точке B. Обратите внимание, как отличаются значения углов соответствующие точке B. Различия в значениях углов кратны 360. Что вполне логично, все траектории от начала отсчета A0 к точке B отличаются на целое количество оборотов, а значит на целое количество углов в 360°.
Если радиус изогнуть вдоль окружности, получим дугу размером 1 радиан. Это проиллюстрировано на рисунке 4. Проблема состоит в том, что количество радиан в половине окружности является не целым числом, более того это число нельзя записать в виде десятичной дроби с конечным количеством дробных разрядов. Количество радиан в половине окружности примерно равно 3,141592653. Это число, как вы уже наверное догадались, обозначают буквой π. Называют это число константой пи или просто числом π. Таким образом, величина угла равная 180°, в радианной мере равна π радиан. Все значения в радианах удобно привязывать к числу пи.
Как выразить в радианы величину угла, градусная мера которого известна? Изучите примеры, поупражняйтесь с заданиями и проверьте свои знания выполнив тест.
Длина одного оборота окружности, очевидно равна 2π радиан, а значит значения соответствующие точке на окружности будут отличаться на целое количество длин равных 2π радиан, смотрим рисунок 5.
Ниже приведены ссылки на примеры нахождения точки на числовой окружности по значению угла в радианах. Поупражняйтесь в решении заданий и протестируйте себя.
Что касается числовой окружности, то её концепция нами разобрана, но это ещё не всё. Для тригонометрии нужна не просто числовая окружность, нужна единичная числовая окружность. Добавив прилагательное "единичная" мы добавляем к нашей числовой окружности ещё одно условие - её радиус должен быть равен единице. Это свойство единичной числовой окружности пригодится в дальнейшем.
Для превращения единичной числовой окружности в тригонометрическую добавим координатную плоскость с началом координат в её центре, как показано на рисунке 6. Обратите внимание, что единичные отрезки осей координатной плоскости, являются радиусами окружности, поскольку ее радиус так же равен единице. Ещё один важный момент: начало отсчёта числовой окружности, в котором находится А0 попадает на пересечение с осью x. В тригонометрической окружности ось y принято называть осью синусов, а ось x - осью косинусов.
Отметим на числовой окружности точку B и найдём её координаты, построив проекции на ось косинусов и ось синусов. Пусть точке B соответствует одно из значений углов равное α, тогда координата x точки B будет равна cosα (косинусу альфа), а координата y - sinα (синусу альфа). Построения проиллюстрированы на рисунке 7. В этом случае значение α называется аргументом тригонометрической функции а координаты точки Bα(x, y), которой соответствует угол α, значением тригонометрической функции: значение косинуса альфа cosα = x , значение синуса альфа sinα = y.
К числовой окружности через её крайнюю правую точку проведем касательную, задав ей направление аналогичное направлению оси синусов. Отметим на полученной новой оси начало отсчета в точке пересечения с осью косинусов и единичный отрезок размером в один радиус окружности. Такую ось принято называть осью тангенсов. Построим ещё одну ось. Эта ось будет касаться верхней точки окружности и будет со направлена с осью косинусов. Начало её отсчета отметим в точке пересечения с осью синусов, а единичный отрезок традиционно будет равен радиусу окружности. Такую ось принято называть осью котангенсов. Через начало координат и точку Bα, которой соответствует значение угла α, проведем прямую. Построенная прямая пересекает ось тангенсов и ось котангенсов в определенных точках. Так как оси тангенса и котангенса являются числовыми, то точкам пересечений можно поставить в соответствие числовые значения. Они и есть значения тангенса и котангенса исходного угла альфа. Построения проиллюстрированы на рисунке 8.
Координатную плоскость условно можно разделить на четыре части. Все точки координатной плоскости, находящиеся выше оси x и правее оси y называют первой четвертью. Дальше против часовой стрелки: выше оси x и левее оси y - второй четвертью, ниже оси x и левее оси y - третей четвертью, ниже оси x и правее оси y - четвертой четвертью.
Рассмотрим знаки тригонометрических функций значений углов для точек окружности находящихся в I четверти. Из рисунка 9 видно, что для точки Bα, находящейся в I четверти: cosα > 0, sinα > 0, tgα > 0, ctgα > 0. Из чего делаем вывод, что синус, косинус, тангенс и котангенс аргументов соответствующих точкам I четверти положительны.
Для II четверти. Из рисунка 10 видно, что для точки Bα, находящейся во II четверти: cosα < 0, sinα > 0, tgα < 0, ctgα < 0. Из чего делаем вывод, что синус аргументов соответствующих точкам II четверти положителен, а вот косинус, тангенс и котангенс - отрицательны.
Для III четверти. Из рисунка 11 видно, что для точки Bα, находящейся в III четверти: cosα < 0, sinα < 0, tgα > 0, ctgα > 0. Из чего делаем вывод, что синус и косинус аргументов соответствующих точкам III четверти отрицательны, а тангенс и котангенс - положительны.
Для IV четверти. Из рисунка 12 видно, что для точки Bα, находящейся в IV четверти: cosα > 0, sinα < 0, tgα < 0, ctgα < 0. Из чего делаем вывод, что косинус аргументов соответствующих точкам IV четверти положителен, а синус, тангенс и котангенс - отрицательны.
На рисунке 13 показаны знаки синуса в четвертях координатной плоскости.
На рисунке 14 показаны знаки косинуса в четвертях координатной плоскости.
На рисунке 15 показаны знаки тангенса и контангенса в четвертях координатной плоскости.
referat-4all.ru
На этом уроке мы вспомним определение числовой прямой и дадим новое определение числовой окружности. Также подробно рассмотрим важное свойство числовой окружности и важные точки на ней. Дадим определение прямой и обратной задачи для числовой окружности и решим несколько примеров подобных задач.
Тема: Тригонометрические функции
Урок: Числовая окружность
Для любой функции независимый аргумент откладывается либо на числовой прямой, либо на окружности. Охарактеризуем и числовую прямую, и числовую окружность.
Прямая становится числовой (координатной) прямой, если отмечено начало координат, выбраны направление и масштаб (рис. 1).
Числовая прямая устанавливает взаимно-однозначное соответствие между всеми точками прямой и всеми действительными числами.
Например, берем число 
откладываем на координатной оси, получаем точку 
Возьмем число 
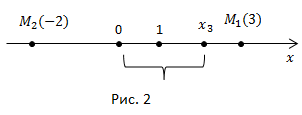
откладываем на оси, получаем точку 
(рис. 2).
И наоборот, если мы взяли любую точку 
на координатной прямой, то найдется единственное соответствующее ей действительное число (рис. 2).
К такому соответствию люди пришли не сразу. Чтобы понять это, вспомним основные числовые множества.
Сначала ввели множество натуральных чисел 
Затем множество целых чисел 
Множество рациональных чисел 
Предполагалось, что этих множеств будет достаточно, и существует взаимно-однозначное соответствие между всеми рациональными числами и точками прямой. Но оказалось, что на числовой прямой есть бесчисленное множество точек, которые нельзя описать числами вида 
Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1. Она равна 
(рис. 3).
Найдется ли среди множества рациональных чисел число, в точности равное 
Нет, не найдется. Докажем этот факт.
Докажем методом от противного. Предположим, что существует дробь, равная 
т.е. 
Тогда 
Возведем обе части в квадрат, 
Очевидно, что правая часть равенства делится на 2, 
. Значит и 
Тогда 
Но тогда и 
А значит, 
Тогда получается, что дробь 
сократимая. Это противоречит условию, значит 
Число 
иррациональное. Множество рациональных и иррациональных чисел образуют множество действительных чисел 
Если мы возьмем любую точку на прямой, ей будет соответствовать какое-либо действительное число. И если мы возьмем любое действительное число, ему будет соответствовать единственная точка на координатной прямой.
Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.
Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное. Масштаб – длина окружности 
(рис. 4).
Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу 
поставить в соответствие точку окружности и наоборот.
Задав число 
получаем точку на окружности 
(рис. 4).
Каждому действительному числу соответствует точка на окружности. А наоборот?
Точка 
соответствует числу . А если взять числа 
Все эти числа своим образом на окружности имеют только одну точку
Например, 
соответствует точке B (рис. 4).
Возьмем все числа 
Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.
Если есть фиксированное число то ему соответствует только одна точка окружности
Если есть точка окружности, то ей соответствует множество чисел
В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.
Рассмотрим основные точки на окружности.
Задано число 
Найти, какой точке оно соответствует.
Разделив дугу 
пополам, получаем точку 
(рис. 5).
Обратная задача – дана точка 
середина дуги 
Найти все действительные числа, которые ей соответствуют.
Отметим на числовой окружности все дуги, кратные 
(рис. 6).
Важны также дуги, кратные 
Дано число 
Нужно найти соответствующую точку.
Обратная задача – дана точка, нужно найти каким числам она соответствует.
(рис. 7).
Мы рассмотрели две стандартные задачи на двух важнейших точках.
Пример 1.
a) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A
это два целых оборота и еще половина, и 
Получаем точку M – это середина третьей четверти (рис. 8).
Ответ. Точка M – середина третьей четверти.
b) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A полный оборот и еще 
получаем точку N (рис. 9).
Ответ: Точка N находится в первой четверти.
Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаимно-однозначное соответствие между точками этой прямой и множеством действительных чисел. Такого взаимно-однозначного соответствия нет на окружности. Каждому действительному числу на окружности соответствует единственная точка, но каждой точке числовой окружности соответствует бесчисленное множество действительных чисел.
На следующем уроке мы рассмотрим числовую окружность в координатной плоскости.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 11.6 – 11.12, 11.15 – 11.17.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
mirror.vsibiri.info
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка. Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.Отсчет от точки А против часовой стрелки называется положительным направлением.Отсчет от точки А по часовой стрелке называется отрицательным направлением.
Числовая окружность на координатной плоскости.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
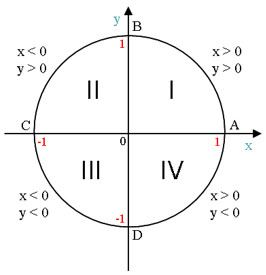
Значения x и y в четвертях числовой окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
x > 0, y > 0 | x < 0, y > 0 | x < 0, y < 0 | x > 0, y < 0 |
Значение любой точки числовой окружности:
Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: –1 ≤ x ≤ 1; –1 ≤ y ≤ 1 |
Основные величины числовой окружности:
| Величинав радианах | Величина в радиусах |
Окружность | 2π | 360º |
Полуокружность | π | 180º |
Четверть окружности | π—2 | 90º |
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
- Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
- Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
- Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:(1)π, 3π, 5π, 7π. Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение: t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число: M(t) = M(t + 2πk), где k ∈ Z. Число k называется параметром. |
Уравнение числовой окружности (второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
raal100.narod.ru
Для любой функции независимый аргумент откладывается либо на числовой прямой, либо на окружности. Охарактеризуем и числовую прямую, и числовую окружность.
Прямая становится числовой (координатной) прямой, если отмечено начало координат, выбраны направление и масштаб (рис. 1).
Числовая прямая устанавливает взаимно-однозначное соответствие между всеми точками прямой и всеми действительными числами.
Например, берем число 
откладываем на координатной оси, получаем точку 
Возьмем число 
откладываем на оси, получаем точку 
(рис. 2).
И наоборот, если мы взяли любую точку 
на координатной прямой, то найдется единственное соответствующее ей действительное число (рис. 2).
К такому соответствию люди пришли не сразу. Чтобы понять это, вспомним основные числовые множества.
Сначала ввели множество натуральных чисел 
Затем множество целых чисел 
Множество рациональных чисел 
Предполагалось, что этих множеств будет достаточно, и существует взаимно-однозначное соответствие между всеми рациональными числами и точками прямой. Но оказалось, что на числовой прямой есть бесчисленное множество точек, которые нельзя описать числами вида 
Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1. Она равна 
(рис. 3).
Найдется ли среди множества рациональных чисел число, в точности равное 
Нет, не найдется. Докажем этот факт.
Докажем методом от противного. Предположим, что существует дробь, равная 
т.е. 
Тогда 
Возведем обе части в квадрат, 
Очевидно, что правая часть равенства делится на 2, 
. Значит и 
Тогда 
Но тогда и 
А значит, 
Тогда получается, что дробь 
сократимая. Это противоречит условию, значит 
Число 
иррациональное. Множество рациональных и иррациональных чисел образуют множество действительных чисел 
Если мы возьмем любую точку на прямой, ей будет соответствовать какое-либо действительное число. И если мы возьмем любое действительное число, ему будет соответствовать единственная точка на координатной прямой.
Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.
Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное. Масштаб – длина окружности 
(рис. 4).
Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу 
поставить в соответствие точку на окружности и наоборот.
Задав число 
получаем точку на окружности 
(рис. 4).
Каждому действительному числу соответствует точка на окружности. А наоборот?
Точка 
соответствует числу . А если взять числа 
Все эти числа своим образом на окружности имеют только одну точку
Например, 
соответствует точке B (рис. 4).
Возьмем все числа 
Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.
Если есть фиксированное число то ему соответствует только одна точка окружности
Если есть точка окружности, то ей соответствует множество чисел
В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.
Рассмотрим основные точки на окружности.
Задано число 
Найти, какой точке на окружности оно соответствует.
Разделив дугу 
пополам, получаем точку 
(рис. 5).
Обратная задача – дана точка 
середина дуги 
Найти все действительные числа, которые ей соответствуют.
Отметим на числовой окружности все дуги, кратные 
(рис. 6).
Важны также дуги, кратные 
Дано число 
Нужно найти соответствующую точку.
Обратная задача – дана точка, нужно найти каким числам она соответствует.
(рис. 7).
Мы рассмотрели две стандартные задачи на двух важнейших точках.
Пример 1.
a) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A
это два целых оборота и еще половина, и 
Получаем точку M – это середина третьей четверти (рис. 8).
Ответ. Точка M – середина третьей четверти.
b) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A полный оборот и еще 
получаем точку N (рис. 9).
Ответ: Точка N находится в первой четверти.
Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаимно-однозначное соответствие между точками этой прямой и множеством действительных чисел. Такого взаимно-однозначного соответствия нет на окружности. Каждому действительному числу на окружности соответствует единственная точка, но каждой точке числовой окружности соответствует бесчисленное множество действительных чисел.
Ранее мы изучили числовую окружность и выяснили её свойства (рис. 1).
Рис. 1
Каждому действительному числу 
соответствует единственная точка 
на окружности.
Каждой точке 
на числовой окружности соответствует не только число 
но и все числа вида 
Поместим окружность в координатную плоскость. По прежнему, каждому числу соответствует точка на окружности. Теперь этой точке на окружности соответствуют две координаты, как и любой точке координатной плоскости.
(рис. 2).
Рис. 2
Наша задача – по данному числу найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.
Пример 1.Дана точка 
– середина дуги 
Точке соответствуют числа вида 
Найти координаты точки (рис. 3).
Рис. 3
Решение:
Координаты можно найти двумя разными способами, рассмотрим их по очереди.
1. Точка лежит на окружности, R=1, значит, она удовлетворяет уравнению окружности 
по условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол 
Это значит также, что прямая 
делит первую четверть ровно пополам, значит, это прямая 
Точка лежит на прямой 
поэтому удовлетворяет уравнению этой прямой.
Составим систему из двух уравнений.
Решив систему, получим искомые координаты.
2. Рассмотрим 
прямоугольный (рис. 4).
Рис. 4
Итак, мы задали число нашли точку и её координаты. Определим также координаты симметричных ей точек (рис. 5).
Рис. 5
Следующая задача – таким же образом определить координаты точек, кратных 
Окружность радиуса R=1 помещена в координатную плоскость, 
Найти точку на окружности и её координаты (рис. 6).
Рис. 6
Решение:
Рассмотрим 
– прямоугольный.
т. е. угол 
Найдем координаты симметричных точек (рис. 7).
Рис. 7
Мы задали число 
нашли точку на окружности, эта точка единственная, и нашли её координаты.
Самостоятельно рекомендуется найти координаты точки, соответствующей числу 
Пример 1. Дана точка 
Найти её прямоугольные координаты.
Решение:
Точка 
середина третьей четверти (рис. 8).
Рис. 8
Мы поместили числовую окружность в координатную плоскость, научились находить по числу точку на окружности и её координаты. Эта техника лежит в основе определения синуса и косинуса, которые будут рассмотрены далее.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/chislovaya-okruzhnost-2
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/chislovaya-okruzhnost-na-koordinatnoy-ploskosti
https://www.youtube.com/watch?v=NTqNXLwAaKo
https://www.youtube.com/watch?v=k6UPDd--yGo
https://www.youtube.com/watch?v=8aUlWR5zNis
http://mathematics-tests.com/10-klass-chislovaya-okruzhnost
http://www.kmrz.ru/catimg/40/400239.jpg
http://shkolnie.ru/pars_docs/refs/18/17881/17881_html_m73662372.jpg
www.kursoteka.ru
Для любой функции независимый аргумент откладывается либо на числовой прямой, либо на окружности. Охарактеризуем и числовую прямую, и числовую окружность.
Прямая становится числовой (координатной) прямой, если отмечено начало координат, выбраны направление и масштаб (рис. 1).
Числовая прямая устанавливает взаимно-однозначное соответствие между всеми точками прямой и всеми действительными числами.
Например, берем число откладываем на координатной оси, получаем точку Возьмем число откладываем на оси, получаем точку (рис. 2).
И наоборот, если мы взяли любую точку на координатной прямой, то найдется единственное соответствующее ей действительное число (рис. 2).
К такому соответствию люди пришли не сразу. Чтобы понять это, вспомним основные числовые множества.
Сначала ввели множество натуральных чисел
Затем множество целых чисел
Множество рациональных чисел
Предполагалось, что этих множеств будет достаточно, и существует взаимно-однозначное соответствие между всеми рациональными числами и точками прямой. Но оказалось, что на числовой прямой есть бесчисленное множество точек, которые нельзя описать числами вида
Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1. Она равна (рис. 3).
Найдется ли среди множества рациональных чисел число, в точности равное Нет, не найдется. Докажем этот факт.
Докажем методом от противного. Предположим, что существует дробь, равная т.е.
Тогда Возведем обе части в квадрат, Очевидно, что правая часть равенства делится на 2, . Значит и Тогда Но тогда и А значит, Тогда получается, что дробь сократимая. Это противоречит условию, значит
Число иррациональное. Множество рациональных и иррациональных чисел образуют множество действительных чисел Если мы возьмем любую точку на прямой, ей будет соответствовать какое-либо действительное число. И если мы возьмем любое действительное число, ему будет соответствовать единственная точка на координатной прямой.
Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.
Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное. Масштаб – длина окружности (рис. 4).
Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу поставить в соответствие точку на окружности и наоборот.
Задав число получаем точку на окружности
(рис. 4).
Каждому действительному числу соответствует точка на окружности. А наоборот?
Точка соответствует числу . А если взять числа Все эти числа своим образом на окружности имеют только одну точку
Например, соответствует точке B (рис. 4).
Возьмем все числа Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.
Если есть фиксированное число то ему соответствует только одна точка окружности
Если есть точка окружности, то ей соответствует множество чисел
В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.
Рассмотрим основные точки на окружности.
Задано число Найти, какой точке на окружности оно соответствует.
Разделив дугу пополам, получаем точку (рис. 5).
Обратная задача – дана точка середина дуги Найти все действительные числа, которые ей соответствуют.
Отметим на числовой окружности все дуги, кратные (рис. 6).
Важны также дуги, кратные
Дано число Нужно найти соответствующую точку.
Обратная задача – дана точка, нужно найти каким числам она соответствует.
(рис. 7).
Мы рассмотрели две стандартные задачи на двух важнейших точках.
Пример 1.
a) Найти на числовой окружности точку с координатой
Решение:
Откладываем от точки Aэто два целых оборота и еще половина, и Получаем точку M – это середина третьей четверти (рис. 8).
Ответ. Точка M – середина третьей четверти.
b) Найти на числовой окружности точку с координатой
Решение:
Откладываем от точки A полный оборот и еще получаем точку N (рис. 9).
Ответ: Точка N находится в первой четверти.
Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаимно-однозначное соответствие между точками этой прямой и множеством действительных чисел. Такого взаимно-однозначного соответствия нет на окружности. Каждому действительному числу на окружности соответствует единственная точка, но каждой точке числовой окружности соответствует бесчисленное множество действительных чисел.
Ранее мы изучили числовую окружность и выяснили её свойства (рис. 1).
Рис. 1
Каждому действительному числу соответствует единственная точка на окружности.
Каждой точке на числовой окружности соответствует не только число но и все числа вида
Поместим окружность в координатную плоскость. По прежнему, каждому числу соответствует точка на окружности. Теперь этой точке на окружности соответствуют две координаты, как и любой точке координатной плоскости.
(рис. 2).
Рис. 2
Наша задача – по данному числу найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.
Пример 1.Дана точка – середина дуги Точке соответствуют числа вида
Найти координаты точки (рис. 3).
Рис. 3
Решение:
Координаты можно найти двумя разными способами, рассмотрим их по очереди.
1. Точка лежит на окружности, R=1, значит, она удовлетворяет уравнению окружности
по условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол Это значит также, что прямая делит первую четверть ровно пополам, значит, это прямая
Точка лежит на прямой поэтому удовлетворяет уравнению этой прямой.
Составим систему из двух уравнений.
Решив систему, получим искомые координаты.
2. Рассмотрим прямоугольный (рис. 4).
Рис. 4
Итак, мы задали число нашли точку и её координаты. Определим также координаты симметричных ей точек (рис. 5).
Рис. 5
Следующая задача – таким же образом определить координаты точек, кратных
Окружность радиуса R=1 помещена в координатную плоскость, Найти точку на окружности и её координаты (рис. 6).
Рис. 6
Решение:
Рассмотрим – прямоугольный.
т. е. угол
Найдем координаты симметричных точек (рис. 7).
Рис. 7
Мы задали число нашли точку на окружности, эта точка единственная, и нашли её координаты.
Самостоятельно рекомендуется найти координаты точки, соответствующей числу
Пример 1. Дана точка Найти её прямоугольные координаты.
Решение:
Точка середина третьей четверти (рис. 8).
Рис. 8
Мы поместили числовую окружность в координатную плоскость, научились находить по числу точку на окружности и её координаты. Эта техника лежит в основе определения синуса и косинуса, которые будут рассмотрены далее.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/chislovaya-okruzhnost-2
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/chislovaya-okruzhnost-na-koordinatnoy-ploskosti
https://www.youtube.com/watch?v=NTqNXLwAaKo
https://www.youtube.com/watch?v=k6UPDd--yGo
https://www.youtube.com/watch?v=8aUlWR5zNis
http://mathematics-tests.com/10-klass-chislovaya-okruzhnost
http://www.kmrz.ru/catimg/40/400239.jpg
http://shkolnie.ru/pars_docs/refs/18/17881/17881_html_m73662372.jpg
www.kursoteka.ru
В реальной жизни часто встречается движение по окружности. Например, соревнования велосипедистов, которые проезжают определенный круг на время или соревнования гоночных автомобилей, которым надо проехать наибольшее количество кругов за отведенное время.
Рассмотрим конкретный пример…Бегун бежит по кругу длиной 400 метров. Спортсмен стартует в точке А (рис. 1) и движется против часовой стрелки. Где он будет находится через 200 м, 800 м, 1500 м? А где провести финишную черту, если бегуну необходимо пробежать 4195 м?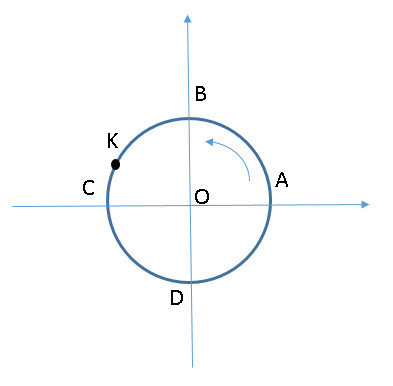 
Решение: Через 200 м бегун будет находиться в точке С. Так как он пробежит ровно половину дистанции.
Пробежав 800 м, бегун сделает ровно два круга и окажется в точке А.
1500м – это 3 круга по 400 м (1200 м) и еще 300 м , то есть $\frac{3}{4}$ от беговой дорожки, финиш этой дистанции в точке D.
Где будет находиться наш бегун пробежав 4195 м? 10 кругов – это 4000 м, останется пробежать 195 м, это на 5 м меньше, чем половина дистанции. Значит финиш будет в точки K, расположенной около точки С.
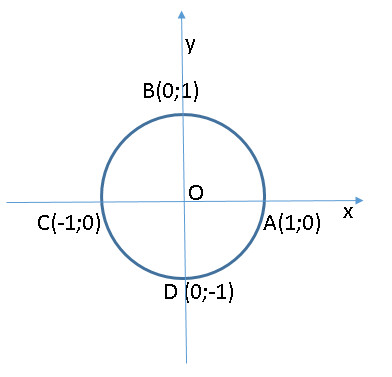
2) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка. Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.Диаметры АС и BD делят окружность на четыре четверти: первая четверть – это дуга AB.вторая четверть – дуга BC.третья четверть – дуга CD.четвертая четверть – дуга DA.
3) Начальная точка числовой окружности – точка А.Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.
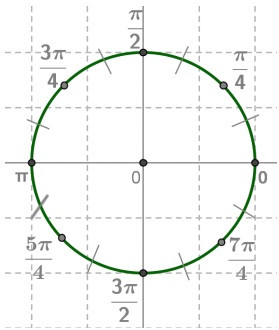
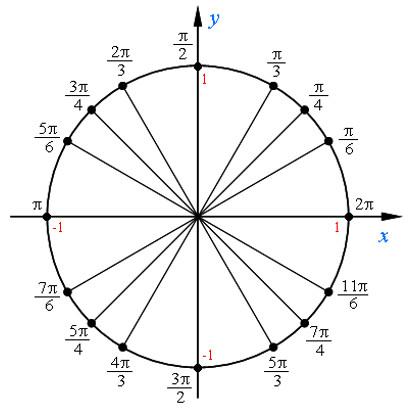
Каждая из четырёх четвертей числовой окружности разделена на три равные части. Около каждой из полученных двенадцати точек записано число, которому она соответствует.
Для числовой окружности верно следующее утверждение:Если точка $М$ числовой окружности соответствует числу $t$ , то она соответствует и числу вида $t+2π *k$, где $k$ – целое число. $М(t) = M(t+2π*k)$.
Рассмотрим пример. В единичной окружности дуга АВ разделена точкой М на две равные части, а точками К и Р — на три равные части. Чему равна длина дуги: AM, МВ, АК, КР, РB, АР, КМ?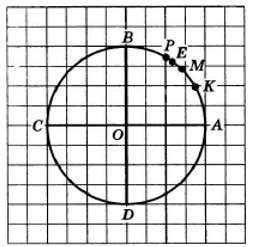
Длина дуги $АВ =\frac{π}{2}$. Разделив ее на две равные части точкой М, получим две дуги, длиной $\frac{π}{4}$ каждая. Значит, $AM =МВ=\frac{π}{4}$.
Дуга АВ разбита на три равные части точками К и Р. Длина каждой полученной части равна $\frac{1}{3}* \frac{π}{2}$, т. е. $\frac{π}{6}$. Значит, $АК = КР = РВ =\frac{π}{6}$.
Дуга АР состоит из двух дуг АК и КР длиной — $\frac{π}{6}$. Значит, $АР = 2 *\frac{π}{6} =\frac{π}{3}$.
Осталось вычислить длину дуги КМ. Эта дуга получается из дуги AM исключением дуги АК. Таким образом, $КМ = AM – АК =\frac{π}{4} - \frac{π}{6} = \frac{π}{12}$.
Задача:Найти на числовой окружности точку, которая соответствует заданному числу:$2π$, $\frac{7π}{2}$, $\frac{π}{4}$, $-\frac{3π}{2}$.
Решение: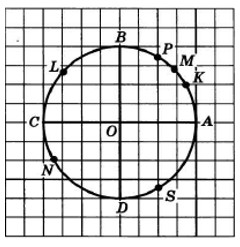
Числу $2π$ соответствует точка А, т.к. пройдя по окружности путь длиной $2π$, т.е. ровно одну окружность, мы опять попадем в точку А.
Числу $\frac{7π}{2}$ соответствует точка D, т.к. $\frac{7π}{2}=2π+\frac{3π}{2}$, т.е. двигаясь в положительном направлении, нужно пройти целую окружность и дополнительно путь длиной $\frac{3π}{2}$, который закончится в точке D.
Числу $\frac{π}{4}$ соответствует точка М, т.к. двигаясь в положительном направлении, нужно пройти путь в половину дуги АВ длиной $\frac{π}{2}$, который закончится в точке M.
Числу $-\frac{3π}{2}$ соответствует точка В, т.к. двигаясь в отрицательном направлении из точки А, нужно пройти путь длиной $\frac{3π}{2}$, который закончится в точке В.
Пример.Найти на числовой окружности точки: а) $21\frac{π}{4}$;б) $-37\frac{π}{6}$.
Решение: Воспользуемся формулой: $М(t) = M(t+2π*k)$ (8 слайд) получим:а) $\frac{21π}{4} = (4+\frac{5}{4})*π = 4π +\frac{5π}{4} = 2*2π +\frac{5π}{4}$, значит числу $\frac{21π}{4}$ соответствует такое же число, что и числу $\frac{5}{4π}$ – середина третьей четверти.
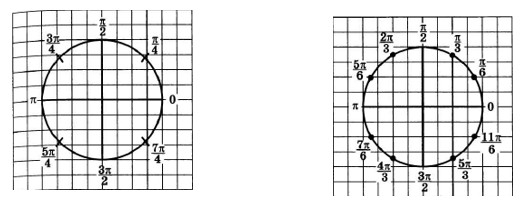
б) $-\frac{37π}{6}=-(6+\frac{1}{6})*π =-(6π +\frac{π}{6}) = -3*2π - \frac{π }{6}$. Значит, числу $-\frac{37π}{6}$ соответствует такое же число, что и числу $-\frac{1}{6π}$. Тоже самое, что и $\frac{11π}{6}$.
Пример.Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие заданной дуге: а) ВА;б) МK.
Решение:а) Дуга ВА – это дуга с началом в точке В и концом в точке А, при движении по окружности против часовой стрелки. Точка В соответственно равна $\frac{π}{2}$, а точка А равна $2π$. Значит, для точек t имеем: $\frac{π}{2} ≤ t ≤ 2π$. Но согласно формуле на слайде 8, числам $\frac{π}{2}$ и $2π$ соответствуют числа вида $\frac{π}{2}+2π*k$ и $2π+2π*k$ соответственно. Тогда наше число t принимает значения:$\frac{π}{2} +2π*k ≤ t ≤ 2π +2π*k$, где $к$ – целое число.
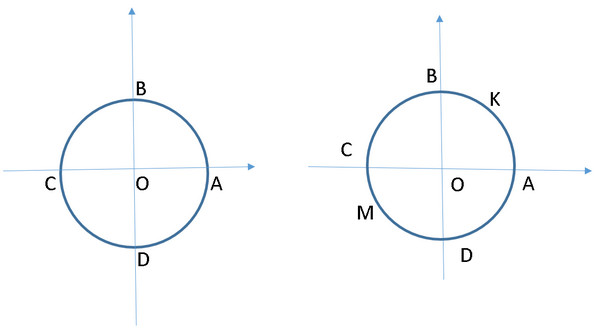
б) Дуга МK – это дуга с началом в точке М и концом в точке К. Точка М соответственно равна $-\frac{3π}{4}$, а точка К равна $\frac{π}{4}$.Значит для точек t имеем:$\frac{-3π}{4} ≤ t ≤\frac{π}{4}$.Согласно формуле на слайде 8 числам $-\frac{3π}{4}$ и $\frac{π}{4}$ соответствуют числа вида: $-\frac{3π}{4}+2π*k$ и $\frac{π}{4}+2π*k$ соответственно.Тогда наше число t принимает значения:$-\frac{3π}{4}+2π*k ≤ t ≤ \frac{π}{4} +2π*k$, где $к$ – целое число.
1) На единичной окружности дуга ВС разделена точкой Т на две равные части, а точками К и Р на три равные части. Чему равна длина дуги: ВТ, ТС, ВК, КР, РС, ВР, КТ?
2) Найти на числовой окружности точку, которая соответствует заданному числу: $π$, $\frac{11π}{2}$, $\frac{21π}{4}$, $-\frac{7π}{2}$, $\frac{17π}{6}$.
3) Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие заданной дуге:а) АВ;б) АС;в) PM, где P – середина дуги АВ, а точка М – середина DA.
mathematics-tests.com
Тема: Тригонометрические функции
Урок: Числовая окружность
Для любой функции независимый аргумент откладывается либо на числовой прямой, либо на окружности. Охарактеризуем и числовую прямую, и числовую окружность.
Прямая становится числовой (координатной) прямой, если отмечено начало координат, выбраны направление и масштаб (рис. 1).
Числовая прямая устанавливает взаимно-однозначное соответствие между всеми точками прямой и всеми действительными числами.
Например, берем число 
откладываем на координатной оси, получаем точку 
Возьмем число 
откладываем на оси, получаем точку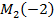 
(рис. 2).
И наоборот, если мы взяли любую точку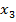 
на координатной прямой, то найдется единственное соответствующее ей действительное число (рис. 2).
К такому соответствию люди пришли не сразу. Чтобы понять это, вспомним основные числовые множества.
Сначала ввели множество натуральных чисел 
Затем множество целых чисел 
Множество рациональных чисел 
Предполагалось, что этих множеств будет достаточно, и существует взаимно-однозначное соответствие между всеми рациональными числами и точками прямой. Но оказалось, что на числовой прямой есть бесчисленное множество точек, которые нельзя описать числами вида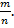 
Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1. Она равна 
(рис. 3).
Найдется ли среди множества рациональных чисел число, в точности равное 
Нет, не найдется. Докажем этот факт.
Докажем методом от противного. Предположим, что существует дробь, равная 
т.е.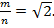 
Тогда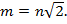 
Возведем обе части в квадрат, 
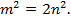Очевидно, что правая часть равенства делится на 2, 
. Значит и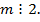 
Тогда 
Но тогда и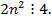 
А значит, 
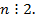Тогда получается, что дробь 
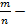сократимая. Это противоречит условию, значит 
Число 
иррациональное. Множество рациональных и иррациональных чисел образуют множество действительных чисел 
Если мы возьмем любую точку на прямой, ей будет соответствовать какое-либо действительное число. И если мы возьмем любое действительное число, ему будет соответствовать единственная точка на координатной прямой.
Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.
Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное. Масштаб – длина окружности 
(рис. 4).
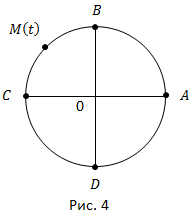
Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу 
поставить в соответствие точку на окружности и наоборот.
Задав число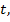 
получаем точку на окружности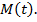 
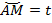(рис. 4).
Каждому действительному числу соответствует точка на окружности. А наоборот?
Точка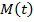 
соответствует числу . А если взять числа 
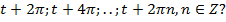Все эти числа своим образом на окружности имеют только одну точку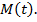
Например, 
соответствует точке B (рис. 4).
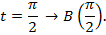
Возьмем все числа 
Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.
Если есть фиксированное число 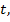то ему соответствует только одна точка окружности
Если есть точка окружности, то ей соответствует множество чисел
В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.
Рассмотрим основные точки на окружности.
Задано число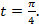 
Найти, какой точке на окружности оно соответствует.
Разделив дугу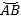 
пополам, получаем точку 
(рис. 5).
Обратная задача – дана точка 
середина дуги 
Найти все действительные числа, которые ей соответствуют.
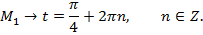
Отметим на числовой окружности все дуги, кратные 
(рис. 6).
Важны также дуги, кратные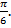 
Дано число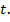 
Нужно найти соответствующую точку.
Обратная задача – дана точка, нужно найти каким числам она соответствует.
(рис. 7).
Мы рассмотрели две стандартные задачи на двух важнейших точках.
Пример 1.
a) Найти на числовой окружности точку с координатой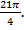 
Решение:
Откладываем от точки A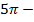
это два целых оборота и еще половина, и 
Получаем точку M – это середина третьей четверти (рис. 8).
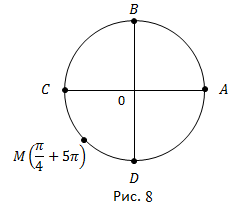
Ответ. Точка M – середина третьей четверти.
b) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A полный оборот и еще 
получаем точку N (рис. 9).
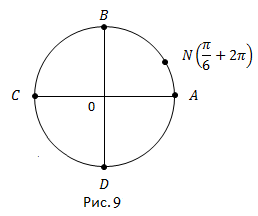
Ответ: Точка N находится в первой четверти.
Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаимно-однозначное соответствие между точками этой прямой и множеством действительных чисел. Такого взаимно-однозначного соответствия нет на окружности. Каждому действительному числу на окружности соответствует единственная точка, но каждой точке числовой окружности соответствует бесчисленное множество действительных чисел.
На следующем уроке мы рассмотрим числовую окружность в координатной плоскости.
Список литературы по теме "Числовая окружность", "Точка на окружности"
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 11.6 – 11.12, 11.15 – 11.17.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
interneturok.ru
