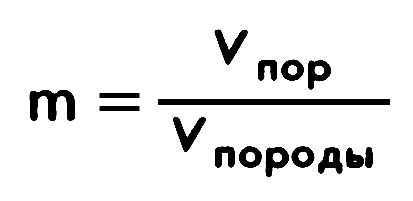WinNavigator

Frigate

Norton Commander

WinNC

Dos Navigator

Servant Salamander

Turbo Browser

Winamp, Skins, Plugins

Необходимые Утилиты

Текстовые редакторы

Юмор

File managers and best utilites

Реферат: Лекция №25. Биоинформатика. Реферат биоинформатика

Реферат - Лекция №25. Биоинформатика

Лекцию читает Андрей Александрович Миронов, профессор факультета биоинженерии и биоинформатики МГУ.

В настоящее время слово биоинформатика стало очень модным, оно употребляется в трех разных смыслах. Первый смысл связывают с телепатией, экстрасенсорикой и т.д., об этом мы говорить не будем. Второй смысл связан с применением компьютеров для изучения любого биологического объекта, но эту тему мы тоже не будем затрагивать. Речь пойдет о биоинформатике в узком смысле слова, а именно о применении компьютерных методов для решения задач молекулярной биологии, в основном анализа разных последовательностей (аминокислотных, нуклеотидных). Эта наука возникла в 1976-1978 годах, окончательно оформилась в 1980 году со специальным выпуском журнала «Nucleic Acid Research» (NAR). Биоинформатика включает в себя:

базы данных, в которых хранится биологическая информация
набор инструментов для анализа тех данных, которые лежат в таких базах
правильное применение компьютерных методов для правильного решения биологических задач

На рисунке показаны соотношение этапов развития биоинформатики (справа) с возникновением разных экспериментальных методик и полученных результатов экспериментальных исследований.

В 1962 году была придумана концепция «молекулярных часов», в 1965 была секвенирована тРНК, определена ее вторичная структура, в это же время были созданы базы данных PIR для хранения информации об аминокислотных последовательностях. В 1972 году было придумано клонирование. В 1978 году были разработаны методы секвенирования, была создана база данных пространственных структур белков. В 1980 был выпущен спецвыпуск журнала NAR, посвященный биоинформатике, затем были придуманы некоторые алгоритмы выравнивания последовательностей, о которых речь пойдет дальше. Дальше был придуман метод ПЦР (полимеразная цепная реакция), а в биоинформатике — алгоритмы поиска похожих фрагментов последовательностей в базах данных. В 1987 году оформился GeneBank (коллекция нуклеотидных последовательностей) и т.д.

Биолог в биоинформатике обычно имеет дело с базами данных и инструментами их анализа. Теперь разберемся, какие базы данных бывают в зависимости от того, что в них помещают. Первый тип – архивные базы данных, это большая свалка, куда любой может поместить все, что захочет. К таким базам относятся

GeneBank & EMBL – здесь хранятся первичные последовательности
PDB – пространственные структуры белков,

и многое другое.

В качестве курьеза могу привести пример: в архивной базе данных указано, что в геноме археи (архебактерии) есть ген, кодирующий белок главного комплекса гистосовместимости, что является полной чепухой.

Второй тип – курируемые базы данных, за достоверность которых отвечает хозяева базы данных. Туда информацию никто не присылает, ее из архивных баз данных отбирают эксперты, проверяя достоверность информации – что записано в этих последовательностях, какие есть экпериментальные основания для того, чтобы считать, что эти последовательности выполняют ту или иную функцию.

К базам данных такого типа относятся:

Swiss- Prot – наиболее качественная база данных, содержащая аминокислотные последовательности белков
KEGG – информация о метаболизме (такая, которая представлена на карте метаболических путей, которую те, кто ходит на лекции, видели на лекции № 2)
FlyBase – информация о Drosophila
COG – информация об ортологичных генах.

Поддержание базы требует работы кураторов или аннотаторов.Тем не менее, даже в курируемых базах данных могут встречаться курьезные надписи, например такая забавная надпись:

CAUTION: AN ORF CALLED DSDC WAS ORIGINALLY (REF.3) ASSIGNED TO THE WRONG DNA STRAND AND THOUGHT TO BE A D- SERINE DEAMINASE ACTIVATOR, IT WAS THEN RESEQUENCED BY REF.2 AND STILL THOUGHT TO BE «DSDC», BUT THIS TIME TO FUNCTION AS A D-SERINE PERMEASE. IT IS REF.1 THAT SHOWED THAT DSDC IS ANOTHER GENE AND THAT THIS SEQUENCE SHOULD BE CALLED DSDX. IT SHOULD ALSO BE NOTED THAT THE C-TERMINAL PART OF DSDX (FROM 338 ONWARD) WAS ALSO SEQUENCED (REF.6 AND REF.7) AND WAS THOUGHT TO BE A SEPARATE ORF (YES, DON'T WORRY, WE ALSO HAD PROBLEMS UNDERSTANDING WHAT HAPPENED!).

По крайне мере здесь кураторы базы данных честно признаются, что не знают, как это случилось.

Третий тип – производные базы данных. Такие базы получаются в результате обработки данных из архивных и курируемых баз данных. Сюда входит:

SCOP – База данных структурной классификации белков (описывается структура белков)
PFAM – База данных по семействам белков
GO (Gene Ontology) – Классификация генов (попытка создания набора терминов, упорядочивания терминологии, чтобы один ген не назывался по разному, и чтобы разным генам не давали одинаковые названия)
ProDom – белковые домены
AsMamDB – альтернативный сплайсинг у млекопитающих

И интегрированные базы данных, в которых вся информация (курируемая, не курируемая) свалена в кучу, и введя имя гена, можно найти всю связанную с ним информацию – в каких организмах встречается, в каком месте генома локализован, какие функции выполняет и т.д.

NCBI Entrez – доступ к информации о нуклеотидных и аминокислотных последовательностях и структурах
Ecocyc – все о E. coli – гены, белки, метаболизм и пр.

Теперь перейдем к рассмотрению инструментов биоинформатике. Инструменты определяются задачами, которые мы хотим решать.

Основу биоинформатики составляют сравнения. Если у нас есть, например, аминокислотная последовательность, о которой у нас есть экспериментальные данные, и известны ее функции, и другая, похожая на нее последовательность, мы можем предположить, что эти последовательности выполняют сходные функции. Это задача поиска сходства последовательностей

Другая задача связана с анализом генома. Недавно было объявлено, что полностью просеквенирован геном человека, но так же просеквенировали геномы и других организмов: три генома растений, мыши, крысы, кошки, собаки, курицы, рыбы, лягушки завершается, шимпанзе завершается, две дрозофилы сделаны, малярийный комар, червяки, дрожжи и т.д. – всего около 30 видов эукариотических геномов. Также просеквенированы сотни бактериальных геномов. Один бактериальный геном можно просеквенировать в хорошо оборудованной лаборатории за неделю. При этом получают длинную нуклеотидную последовательность нуклеотидов. Там есть гены – белок-кодирующие участки, и участки, кодирующие тРНК и рРНК. Возникает задача найти эти гены. Другая задача – поиск сигналов в ДНК, то есть тех участков ДНК, которые отвечают за регуляцию — сайты связывания регуляторных белков, элементы вторичной структуры мРНК, которая транскрибируется с этого гена и др.

Есть задача предсказания вторичной структуры РНК. А также есть большой класс задач анализа белков. Для решения этих задач надо создавать методы анализа, то есть алгоритмов (протоколов) и программ для анализа. При создании метода надо иметь критерий того, что метод адекватен, соответствует реальности.

Как оценить «правильность» метода? Геном типичной бактерии содержит около 1000 генов. Как уже упоминалось, секвенировать геном можно за неделю. Экспериментальная характеристика одного белка требует как минимум 2 месяца работы современной лаборатории.

Для того, чтобы определить, насколько предложенный метод анализа хорош и правилен, существует так называемый «золотой стандарт». Например, у нас есть метод определения генов. Если после его применения на какой-либо последовательности, в которой известно месторасположение генов, наши результаты совпадают с тем, что есть на самом деле на 80-90%, значит наш метод правильный и эффективный. В этом и заключается суть «золотого стандарта».

Или предсказание вторичной структуры РНК. Экспериментально ее определить очень трудно, но есть РНК, структура которых хорошо известна – это рРНК и тРНК. И если наш метод хорошо предсказывает структуру этих известных РНК, то можно ожидать, что и для других РНК он будет давать хорошие предсказания.

Вернемся к первой задаче – сравнению последовательностей. Запишем одну последовательность под другой.

attgtACcTCgTgG-AA----

-----AC-TCaTaGcAAccag

Нам надо при сравнении найти наилучший вариант, так выровнять эту пару последовательностей, чтобы количество совпадений будет максимальным (парное выравнивание). Качество выравнивания оценивают, назначая штрафы за несовпадение букв и за наличие пробелов (когда приходится раздвигать одну последовательность для того, чтобы получить наибольшее число совпадающих позиций).

Таким образом, первым делом после секвенирования последовательности ищут в базах данных похожие последовательности, чтобы после сравнения судить о том, какие функции несет эта последовательность. Если две буквы совпали, значит они находятся под давлением отбора, они функционально важны. Известно, что аминокислоты различаются по своим свойствам, поэтому если произошла аминокислотная замена, это может почти никак не повлиять на работу белка, а может сильно его изменить.

Например, если лизин (положительно заряженная аминокислота заменится на лейцин (похожий по созвучию, но совершенно несходный по свойствам), то для пространственной структуры и функций белка это может оказаться катастрофой. А вот замена лизина на аргинин (также положительно заряженный) может не сказаться на структуре белка.

Поэтому при сравнении аминокислотных последовательностей учитывают также матрицу сопоставления аминокислотных остатков (похожих, менее похожих и совсем непохожих).

Как осуществляется выравнивание? Пишем одну последовательность под другой.

Сколько есть способов написать одну последовательность S1 длиной m под другой – S2 длиной n (со вставками)? Об этом можно доказать теорему – попробуйте.

Построим выборочную последовательность S длиной m+ n следующим образом: возьмем несколько символов из последовательности S1, потом несколько символов из последовательности S2 потом опять несколько символов из S1, потом опять несколько из S2.

– Каждой выборочной последовательности S соответствует выравнивание и по каждому выравниванию можно построить выборочную последовательность. (Доказать!)

– Количество выборочных последовательностей равно

(Доказать!)

Таким образом количество выравниваний можно определить по формуле:

А как же найти оптимальное среди такого большого количества? Можно, конечно, попробовать разные способы, но оказывается, что этот поиск сводится к задаче поиска оптимального пути на графе. Задача поиска оптимального пути на графе решается методами динамического программирования следующим образом. Мы пишем одну последовательность над другой. И у нас есть некая ячейка, в которой мы будем хранить вес наилучшего выравнивания префиксов (то фрагментов последовательности от начала до данного места). И если у нас известен вес наилучшего выравнивания в 3 ячейках (см. слайд ниже), то мы можем определить вес наилучшего выравнивания в четвертой ячейке. То есть, для того, чтобы найти вес оптимального выравнивания, нам надо просмотреть m*n ячеек (количество ячеек в прямоугольной матрице MxN). Как принято говорить в информатике, это – квадратичный алгоритм. Он занимает время и объем памяти, пропорциональный квадрату длины последовательности. И вместо случайного перебора большого числа вариантов, мы решаем задачу довольно быстро.

Откуда берутся матрицы замен? Мы берем некоторое количество выравниваний, в которое по тем или иным причинам верим, и смотрим, как часто у нас происходят такие замены. Тогда матрица замен является логарифмом отношения некоторых вероятностей, которые можно оценить как частоты.

Итак, у нас имеется замечательный квадратичный алгоритм поиска сходства. Время решения задачи выравнивания пропорционально L1*L2. Мы сравниваем имеющуюся у нас последовательность с последовательностями в банке. L1 = размер банка = 108, а для генома человека 3х109. Сравниваемая последовательность обычно имеет размер L2=103, количество операций примерно равно 100*1011=1013.) Обычный компьютер имеет быстродействие около 109 операций в сек. На каждый шаг надо ≈102 операций. Тогда время работы равно T≈106 сек ≈ 11 дней. То есть, просеквенировав бактериальный геном из 3000 генов (приблизительно за неделю), на то, чтобы его охарактеризовать, мы потратим 11*3000 дней, то есть проанализировать дольше чем секвенировать, что, конечно, не очень хорошо.

Решением является то, что мы до применения методов динамического программирования сначала выбираем правильных кандидатов для сравнения. Есть такая программа BLAST (basic local alignment search tool), которую все биологи очень любят, она почти правильная. То есть она почти всегда работает так, как требует «золотой стандарт».

Основная идея ее работы заключается в хешировании. В самом начале мы один раз проходим по всему банку и для каждого короткого слова с заранее зафиксированной длиной мы запишем список позиций, где оно встречается в банках.

Здесь показано для слов длиной 4, в реальности слова берут не длиной 4, как показано на рис., а длиной 7 или 10 или 13, но принцип тот же. В каких-то случаях «слову» соответствует три позициями, в других – 100 позиций.

Дальше мы идем вдоль последовательности «Query» (та последовательность, которую мы хотим прогнать по банку) и выбираем очередные слова. Смотрим в таблице, где встречается это слово, вытягиваем найденные последовательности из банка и строим выравнивание их с нашей исходной последовательности. Это делается быстро, так как мы сравниваем нашу последовательность не со всеми последовательностями из банка, а только те, которые соответствуют нашему «слову» (tttgc в показанном случае). И выравнивание строим тоже не так аккуратно, как это делает алгоритм динамического программирования, а используем упрощенную схему.

Затем мы оцениваем статистическую значимость этого выравнивания – так называемую e-value. Вообще, есть два понятия, которые очень часто встречаются в биоинформатике: e-value и р-value. Е-value – это сколько мы ожидаем увидеть совпадений с таким весом (то есть такого качества), если бы у нас наши последовательность и банк были случайными. Если они случайные, то мы ожидали бы увидеть e-12 совпадений.

e-value – это ожидаемое число событий, может быть больше единицы. Если e-value маленькое, то, значит, совпадение значимое, и оно несет большую биологическую информацию. Р-value – это вероятность встречи такого соответствия (не может быть больше единицы). При оценке e-value, да и вообще при любых статистических оценках, важно, какая модель лежит в основе всего этого дела. Модель, которая лежит в основе e-value, конечно же, неправильная, потому что мы не знаем правильность статистических характеристик биологических последовательностей. Е-value просто дает нам ориентир, и реально, если мы имеем e-value порядка 10-2, то это, как правило, мусор, незначимое соответствие. Правда, есть некоторые специалисты с такой интуицией о структуре белков, которые могут работать с выравниваниями с e-value даже порядка 1. А обычно если исследователи видят e-value > 10-3, они с этим не работают.

Есть разные модификации BLAST: BLASTp (выравнивание аминокислотных последовательностей), BLASTn (выравнивание нуклеотидных последовательностей), BLASTx (выравнивание всех возможных транслятов нашей нуклеотидной последовательности против банка аминокислотных последовательностей), TBLASTx (выравнивание всех возможных транслятов нашей нуклеотидной последовательности против всех транслятов банка нуклеотидных последовательностей). Еще нужно знать, что Nr Data Base – (non redundant) — это база, против которой обычно прогоняют BLAST, в которой нет повторяющихся последовательностей, из которой убраны дубли для того, чтобы не гонять BLAST по одним и тем же последовательностям. И score – это вес выравнивания.

А если на нашу последовательность при поиске налипло, например, не одна, а двадцать последовательностей. При этом возникает задача написать все эти последовательности друг под другом, чтобы увидеть, в какой мере они совпадают, что консервативно (устойчиво повторяется), а что нет, и как устроена наша аминокислотная последовательность. Эта задача называется

www.ronl.ru

Читать реферат по всему другому: "«Биоинформатика: современное состояние и перспективы»"

(Назад) (Cкачать работу)

Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Выпускная работа по

«Основам информационных технологий»

Магистранта

кафедры генетики

биологического факультета

Панкратова Василия

Руководители:

член-кор. НАН Беларуси, профессор, д.б.н. Давыденко О. Г.,

старший преподаватель Шешко С.М.

Минск – 2010 г.

Оглавление

Выпускная работа по 8 Минск – 2010 г. 9 Оглавление 10 Список обозначений ко всей выпускной работе 11 Реферат на тему «Биоинформатика: современное состояние и перспективы» 12 Введение 12 Глава 1. Обзор литературы 13 Работа с геномными и протеомными базами данных 14 Выравнивание последовательностей 15 Поиск генов и регуляторных элементов 17 Моделирование пространственной структуры биомолекул 19 Поиск лекарственных средств 21 Молекулярная фиолгения 22 Обработка цифровых изображений 23 Системная биология 24 Глава 2 Методика исследования 26 Глава 3 Результаты и их обсуждение 28 Поиск нуклеотидной последовательности гена ND6 28 Подбор праймеров для амплификации гена ND6 30 Сравнение полученной последовательности со стандартной 31 Выявление функциональной значимости найденных замен 32 Заключение 35 Список литературы к реферату 35 Предметный указатель к реферату 36 Интернет ресурсы в биологии 37 Ресурсы для поиска биологической информации 37 http://www.ncbi.nlm.nih.gov/pubmed 37 http://blast.ncbi.nlm.nih.gov/Blast.cgi 37 http://www.ncbi.nlm.nih.gov/sites/gquery 38 http://www.mitomap.org/MITOMAP 39 Ресурсы для работы с нуклеотидными и аминокислотными последовательностями 39 http://www.bioinformatics.org/sms2/ 39 http://expasy.org/tools/ 40 http://biotools.umassmed.edu/bioapps/primer3_www.cgi 41 Действующий личный сайт в WWW 42 Граф научных интересов. 43 Вопросы по основам информационных технологий 44 Вопрос по специальности 44 Вопрос по общему курсу 45 Презентация магистерской диссертации 46 Список литературы к выпускной работе 47 Приложение 49

Список обозначений ко всей выпускной работе

БИ	Биоинформатика
ДНК	Дезоксирибонуклеиновая кислота
ПО	Программное обеспечение
ПЦР	Полимеразная цепная реакция
РНК	Рибонуклеиновая кислота
СБ	Системная биология

Реферат на тему «Биоинформатика: современное состояние и перспективы» Введение

Бурное развитие молекулярной биологии и генетики в конце 20го – начале 21го веков привело к накоплению огромного массива экспериментальных данных, в первую очередь последовательностей ДНК, РНК и белков, цифровых биологических изображений и структур сигнальных сетей, хранение и анализ которых не возможен без применения соответствующего ПО. Хотя и раньше информационные технологии использовались биологами, например, для статистической обработки полученных данных, именно бум молекулярной биологии вызвал у специалистов-биологов потребность в специализированных инструментах для решения конкретных задач по обработке биологической информации. Как раз с этим связано возникновение БИ как самостоятельной области науки [6]. Уже сейчас большинство исследователей в области молекулярной биологии и генетики пользуются биоинформационными инструментами на этапе планирования эксперимента и обработки полученных экспериментальных данных. Более того, имеется большое количество опубликованных работ, полностью основанных на применении БИ для решения конкретных биологических проблем [7]. Вполне вероятно, что в перспективе будет возможным компьютерное моделирование биологических систем различной сложности, что позволит вывести биологию на принципиально иной уровень.

Кроме рассмотрения основных направлений развития, достижений и перспектив БИ, данной работе будет представлен конкретный пример использования биоинформатических средств в молекулярно-генетической работе. В рамках данной работы необходимо проверить, имеет ли больной Х мутацию в гене ND2, приводящую к нарушению его функции. Для достижения этой цели необходимо

Подобрать праймеры для амлификации и секвенирования гена ND2Провести его амплификацию и секвенированиеСравнить полученную последовательность со стандартной последовательностью гена ND2 человека и выявить отличияПроверить, являются ли эти отличия уже описанными мутациями или полиморфизмамиЕсли найденная мутация окажется ранее не описанной, то необходимо проверить, скажется ли она на функционировании белка

На этапах 1,3,4,5 использовались те или иные биоинформатические инструменты.

Глава 1. Обзор литературы

Несмотря на непродолжительное время существования БИ, в этой сфере уже выявились конкретные направления и во многих из них уже имеются ощутимые достижения. Далее кратко будут рассмотрены основные задачи, которые могут быть решены с использованием биоинформатического подхода. К их числу относятся следующие [1,5]:

Работа с геномными и протеомными базами данныхВыравнивание (alighnment) нуклеотидных или аминокислотных последовательностейПоиск генов и различных регуляторных последовательностей в данном геномеМоделирование вторичной, третичной и четвертичной структур белков на основании их аминокислотной последовательностейПоиск функциональных доменов в молекулах белков (реакционных центров, трансмембранных доменов, сигнальных последовательностей и т.д.)Предсказание внутриклеточной локализации белка и характера его взаимодействия с другими белкамиПоиск лекарствМолекулярная филогенияОбработка цифровых изображенийСистемная биология и моделирование биологических систем

Работа с геномными и протеомными базами данных

Первый геном бактерии был полностью секвенирован в 1995 году. С тех пор, благодаря развитию методов секвенирования ДНК, определены нуклеотидные последовательности геном многих видов живых организмов, в том числе человека, шимпанзе, нескольких видов растений, дрозофилы, пекарских дрожжей и многих бактерий.

С точки зрения БИ геном любого живого организма представляет собой последовательность длиной от 106 (бактерии) до 1011 (некоторые растения) символов (нуклеотидов), состоящую из четырех различных нуклеотидов (А, Т, Г и Ц). Очевидно, что само по себе создание геномных баз данных, в которых пользователи могли бы легко найти интересующий их участок генома конкретного организма, – это уже довольно непростая задача [6]. Тем не менее, в настоящее время существует довольно много баз данных, доступных в интернете, позволяющих работать с нуклеотидными последовательностями различных геномов. В зависимости от типа информации, хранящихся в них, все базы данных делятся на архивные, курируемые и интегрированные. В первые из них любой пользователь может добавить определенные им последовательности без какой-либо проверки их достоверности. Соответственно, такая база будет более полной, но менее достоверной. При подаче новой последовательности в курируемую базу происходит оценка достоверности как самой последовательности, так и найденных в ее составе генов и регуляторных последовательностей. Следовательно, такая база будет более надежной. Третий тип, интегрированные базы данных, такие как NCBI Entrez, предоставляют возможности поиска по многим как архивным, так и курируемым базам. Кроме того, базы можно разделить на специализированные, в которых хранятся последовательности генома только одного вида, но по этому геному представлена более подробная информация (например, есть специализированные базы данных по геномам дрозофилы, дрожжей, кишечной палочки и других организмов), и общие – в таких базах можно получить информацию о геномах многих организмов. Работа с геномными базами данных осуществляется через программы, называемыми геномными браузерами, многие из которых доступны он-лайн (например, Ensemble, UCSC Genome Browser и другие). С помощью геномного браузера можно найти участок генома с заданными координатами, ген по его названию или нуклеотидной последовательности, узнать предполагаемую или подтвержденную функцию данного участка ДНК и т.д.

Кроме геномных, существуют еще и протеомные базы данных, хотя иногда два этих типа баз могут быть объединены в один. В протеомных базах данных (наиболее известная и качественная из них – Swiss-Prot) можно найти аминокислотную последовательность белка по

referat.co

Сущность биоинформатики — реферат

Как оценить "правильность" метода? Геном типичной бактерии содержит около 1000 генов. Как уже упоминалось, секвенировать геном можно за неделю. Экспериментальная характеристика одного белка требует как минимум 2 месяца работы современной лаборатории.

Вернемся к первой задаче – сравнению последовательностей. Запишем одну последовательность под другой.

attgtACcTCgTgG-AA----

-----AC-TCaTaGcAAccag

Итак, как осуществляется выравнивание?

Пишем одну последовательность под другой.

Найдем, сколько есть способов написать одну последовательность S1 длиной m под другой – S2 длиной n (со вставками).

–Каждой выборочной последовательности S соответствует выравнивание и по каждому выравниванию можно построить выборочную последовательность.

–Количество выборочных последовательностей равно

Таким образом количество выравниваний можно определить по формуле:

Решением является то, что до применения методов динамического программирования сначала выбираем правильных кандидатов для сравнения. Есть такая программа BLAST (basic local alignment search tool), которую все биологи очень любят, она почти правильная. То есть она почти всегда работает так, как требует "золотой стандарт".

Здесь показано для слов длиной 4, в реальности слова берут не длиной 4, как показано на рис., а длиной 7 или 10 или 13, но принцип тот же. В каких-то случаях "слову" соответствует три позициями, в других – 100 позиций.

Дальше мы идем вдоль последовательности "Query" (та последовательность, которую мы хотим прогнать по банку) и выбираем очередные слова. Смотрим в таблице, где встречается это слово, вытягиваем найденные последовательности из банка и строим выравнивание их с нашей исходной последовательности. Это делается быстро, так как мы сравниваем нашу последовательность не со всеми последовательностями из банка, а только те, которые соответствуют нашему "слову" (tttgc в показанном случае). И выравнивание строим тоже не так аккуратно, как это делает алгоритм динамического программирования, а используем упрощенную схему.

Есть разные модификации BLAST: BLASTp (выравнивание аминокислотных последовательностей), BLASTn (выравнивание нуклеотидных последовательностей), BLASTx (выравнивание всех возможных транслятов нашей нуклеотидной последовательности против банка аминокислотных последовательностей), TBLASTx (выравнивание всех возможных транслятов нашей нуклеотидной последовательности против всех транслятов банка нуклеотидных последовательностей). Еще нужно знать, что Nr Data Base – (non redundant) - это база, против которой обычно прогоняют BLAST, в которой нет повторяющихся последовательностей, из которой убраны дубли для того, чтобы не гонять BLAST по одним и тем же последовательностям. И score – это вес выравнивания.

Множественное выравнивание

Множественное выравнивание – это такой способ написания нескольких последовательностей друг под другом (может быть, с пропусками в каких-то позициях в разных последовательностях) , чтобы в каждом столбце стояли гомологичные позиции.

Для этой задачи тоже есть «золотой стандарт». Это выравнивание, которое бы получилось, если бы мы выровняли друг под другом последовательности, которые имеют одинаковую пространственную структуру. То есть две экспериментально установленные пространственные структуры белка сопоставляем и отмечаем, какие аминокислотные остатки друг под другом встали (эти остатки соответствуют гомологичным позициям). Это – биологически обоснованное выравнивание. Возникает задача - найти способ (построить алгоритм и определить параметры), который выравнивает последовательности "золотого стандарта" (то есть последовательности, для которых пространственная структура известно) правильно. Если такой алгоритм построен, то есть надежда, что он выровняет последовательности с неизвестной пространственной структурой тоже правильно.

Для решения задачи множественного выравнивания можно попробовать написать многомерную матрицу и построить методом динамического программирования с просмотром многомерной матрицы. Тогда количество вершин будет порядка Ln , где L – длина, а n – количество последовательностей. Так как типичное количество последовательностей в семействе белков сотни, то 300 аминокислот дадут 300100 – это очень много, этот алгоритм для множественного выравнивания не подходит.

Тогда придумали метод прогрессивного выравнивания. Зная расстояния между любой парой последовательностей, можно построить выравнивание, определить вес выравнивания, и построить какое-то бинарное дерево. Затем, обходя это дерево, последовательно проводятся парные выравнивания наиболее близких последовательностей. Объединяются, получаем выравнивание. Соединяются суперпоследовательности, получают следующее выравнивание. В конце концов получают выравнивание в корне.

Такое постепенное построение выравнивание решает задачу, которую мы не можем сформулировать математически. В биоинформатике очень часто нельзя построить математическую формулировку задачи, которую мы решаем. Поэтому формулировка задачи, которую решает алгоритм BLAST, выглядит так: мы находим то, что находит программа BLAST. Также мы не можем сказать, что мы оптимизируем при множественном выравнивании.

Одна и та же биологическая задача может приводить к разным математическим постановкам одной и той же задачи. Есть примеры, когда одна и та же задача может быть построена так, что она будет математически решаемой или математически не решаемой. Есть класс задач, для которых не существует хороших алгоритмов. Но при построении множественных выравниваний мы решаем с помощью данного алгоритма, без формулировки математической задачи.

Вывод:

Конечно, в данной работе представлен лишь один из многочисленных примеров применения биоинформатики и применения динамического программирования в алгоритмах. В действительности подобных реализаций намного больше.

Биоинформатика плотно внедряется в современную науку. Она уже помогла достичь многого людям, которые работают в исследовательских областях медицины. Возможно, алгоритмы, которые используются в этой сфере являются одними из самых сложных. Но это наука молода, ей есть куда двигаться, еще многое можно постичь используя информатику. Думаю, открытия в медицине теперь вплотную связаны с развитием информатики, новыми алгоритмами и компьютерными технологиями. Как выяснилось, динамическое программирование стало неотъемлемой частью биоинформатики. Алгоритмы динамического программирования наилучшим способом подходят для описания структур, геномов, и я думаю биоинформатику можно использовать не только в генетике, но непосредственно в фармацевтике (т.к. физико-химический состав известных элементов может быть описан машинными алгоритмами), что может привести к более быстрому развитию этой отрасли и нахождению новых препаратов для лечения пока неизлечимых болезней, а так же сопоставлению структур растительных препаратов, которые могут влиять на структуру вирусов (например связывать некоторые компоненты, и выводить их из организма, тем самым обеспечивая излечение), что поможет снизить потребление химических веществ (в данном случае в виде медицинских препаратов).

student.zoomru.ru