|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Глава 2. Плоская система сходящихся сил. Плоская система сил реферат
ПЛОСКАЯ СИСТЕМА СИЛ | Бесплатные курсовые, рефераты и дипломные работы
Однородная балка длины  и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если
и веса Р удерживается в равновесии нитью ВС и шарниром А. Найти натяжение нити и реакцию шарнира А, если  (рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной … фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.
(рис. 7). Реакция нити ВС направлена по нити, а реакция шарнира А определяется в соответствии с теоремой о трех силах: если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Заменив действие связей их реакциями, мы можем перейти от реальной схемы нагружения к расчетной (рис. 7, а). Учитывая, что сила Р приложена в середине балки и следовательно точка К (точка пересечения сил), делит отрезок ВС пополам, определим углы в полученной … фигуре. Решение данной задачи может быть проведено двумя методами: геометрическим и аналитическим.


Рис. 7 Рис. 7, а
Геометрический метод.
Из сил, действующих на тело, строим силовой треугольник, который должен быть замкнутым, т.к. под действием этих сил тело находится в равновесии
(рис. 7, б). Для этого откладываем силы по известным направлениям, в любом выбранном масштабе.
 Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:
Таким образом, задача определения опорных реакций сводится к задаче решения полученного силового треугольника. Для решения воспользуемся теоремой синусов и составляем следующее соотношение:

откуда получаем 
Рис. 7, б
Аналитический метод.
Для решения задачи составляются уравнения равновесия в виде суммы проекций всех сил на оси координат. Направления осей показаны на рис.7, а.
 (1)
(1)
 (2)
(2)
Из первого уравнения получаем RC =RA. Из второго находим  .
.
Плоской называется такая система сил, линии действий которых расположены в одной плоскости. При рассмотрении плоской системы сил введем определения для нагрузок. Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело
(рис. 8).
 Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
Плоскость, в которой расположена данная пара, называется плоскостью действия этой пары. Перпендикуляр, опущенный из точки приложения одной из сил на линию
действия другой называется плечом пары (d). Действие пары сил определяется моментом пары. Численное значение момента пары определяется как произведение модуля одной из сил на плечо этой пары.

Приведем следующие два свойства пар сил:
1. Данную пару, не изменяя её действия на тело, можно переносить как угодно в плоскости её действия.
2. Не изменяя действия данной пары на тело, можно изменять модуль сил и плечо этой пары, сохраняя неизменным модуль и направление вращения пары.
 Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т.е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Другим важным понятием является момент силы относительно данной точки (рис. 9). Момент силы относительно данной точки равен произведению модуля силы на плечо, т.е. длину перпендикуляра, опущенного из этой точки на линию действия силы. Следовательно, будем иметь
Mo(F)=±F∙h.
Момент силы считается положительным, если тело под действием данной силы стремится вращаться относительно точки О против часовой стрелки.
Отметим следующие свойства момента силы:
1. Момент силы относительно данной точки не изменяется при переносе точки приложения силы вдоль линии действия силы.
2. Момент силы относительно данной точки обращается в нуль в том случае, когда линия действия силы проходит через эту точку.
При решении задач на плоскую систему сил пользуются уравнениями равновесия. Для равновесия плоской системы сил необходимо и достаточно, чтобы сумма проекций этих сил на две координатные оси и сумма моментов относительно произвольно выбранной точки равнялись нулю

Существуют и две другие формы условий равновесия, но они используются гораздо реже.
Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось, не перпендикулярную к прямой АВ, были равны нулю.
Третья форма: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительной любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю.
 ;
;
 .
.
| | | следующая страница ==> | |
| СИСТЕМА СХОДЯЩИХСЯ СИЛ | | | Система связанных тел |
Дата добавления: 2014-02-26; просмотров: 2.
Поделиться с ДРУЗЬЯМИ:refac.ru
Глава 2. Плоская система сходящихся сил
2.1. Сложение плоской системы сходящихся сил. Геометрическое условие равновесия
Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке, называется плоской системой сходящихся сил. Если силы сходящейся системы приложены к разным точкам тела, то по первому следствию из аксиом статики каждую силу можно перенести в точку пересечения линий действия и получить эквивалентную систему сил, приложенных к одной точке (рис. 2.1).

Рис. 2.1. Плоская система сходящихся сил
Две силы, приложенные к одной точке тела, образуют простейшую плоскую систему сходящихся сил (две пересекающиеся прямые всегда лежат в одной плоскости).
Рассмотрим систему сил  , приложенных в точкеА. Требуется найти их равнодействующую (рис. 2.2).
, приложенных в точкеА. Требуется найти их равнодействующую (рис. 2.2).
Применив правило силового треугольника, сложим силы  и
и  . Для этого из конца вектора
. Для этого из конца вектора  отложим вектор
отложим вектор  и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил
и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил  и
и  :
:


Рис. 2.2. Многоугольник сил
Теперь сложим силу  с силой
с силой  . Для этого из конца вектора ВС =
. Для этого из конца вектора ВС =  отложим вектор
отложим вектор  и, соединив точки А и D, получим равнодействующую трех сил:
и, соединив точки А и D, получим равнодействующую трех сил:

где  – искомая равнодействующая.
– искомая равнодействующая.
Порядок построения сторон силового многоугольника не влияет на окончательный результат.
Чтобы уравновесить систему сил, достаточно к ней добавить еще одну силу, численно равную равнодействующей, но направленную в противоположную сторону (рис. 2.3).

Рис. 2.3. Равнодействующая системы сил
Необходимое и достаточное условие равновесия системы сходящихся сил в геометрической форме: система сходящихся сил уравновешена тогда и только тогда, когда силовой многоугольник замкнут.
2.2. Определение равнодействующей системы сходящихся сил методом проекций. Аналитическое условие равновесия
Вместо построения силового многоугольника равнодействующую системы сходящихся сил более точно и значительно быстрее находят вычислением с помощью метода проекций, который обычно называется аналитическим.
Проекцией вектора  на ось называется длина направленного отрезка оси, заключенного между двумя перпендикулярами, опущенными из начала и конца вектора
на ось называется длина направленного отрезка оси, заключенного между двумя перпендикулярами, опущенными из начала и конца вектора  . Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси (рис. 2.4):
. Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси (рис. 2.4):

Рис. 2.4. Проекции векторов сил на оси
Рассмотрим определение равнодействующей системы сходящихся сил методом проекций.
Допустим, что для заданной системы сходящихся сил построен многоугольник ABCDE, в котором вектор  – искомая равнодействующая данной системы.
– искомая равнодействующая данной системы.

Рис. 2.5. Многоугольник сил
Выбрав систему координатных осей X и Y в плоскости силового многоугольника, спроецируем его на эти оси:

В краткой форме эти равенства записываются так:

где  – знак суммы, а индекс k последовательно принимает значения от 1 до n, по числу сходящихся сил, равнодействующая которых определяется.
– знак суммы, а индекс k последовательно принимает значения от 1 до n, по числу сходящихся сил, равнодействующая которых определяется.
Таким образом, проекция равнодействующей системы сходящихся сил на каждую из осей координат равна алгебраической сумме проекций составляющих сил на ту же ось:
 .
.
Условие равновесия плоской системы сходящихся сил в аналитической форме: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на каждую из двух осей координат были равны нулю.
studfiles.net
1.5.Плоская сходящаяся система сил.
Рассмотрим систему сил, лежащих в одной плоскости, линии действия которых пересекаются в точке А (рис.1.16). После переноса точек приложения сил в точку А можно последовательно сложить все силы, строя силовой многоугольник, таким образом, заменяя все силы одной равнодействующей. Следовательно, плоская система сходящихся сил имеет равнодействующую, приложенную в точке пересечения сил и равную геометрической сумме всех сил данной системы.
|
|
Вторая задача статики - разработка условий равновесия. Они могут быть получены в двух видах:
1. Геометрическое условие. Очевидно, что система сходящихся сил будет эквивалентна нулю, если силовой многоугольник, построенный из сил системы, будет замкнут. В этом случае 
2. Аналитическое условие. Из формулы (1.3) следует, что величина равнодействующей  будет равно нулю, если выполняются условия:
будет равно нулю, если выполняются условия:
Fкx=0;
(1.4)
Fкy=0.
Выражения (1.4) являются уравнениями равновесия плоской сходящейся системы сил: система сил находится в равновесии, когда алгебраическая сумма проекций всех сил системы на оси Х и У равна нулю.
1.6.Решение задач
Для решения задач статики можно воспользоваться следующим планом.
1. Выбрать объект, равновесие которого следует рассмотреть. Таким объектом может быть точка, тело либо система тел.
2. Приложить действующие на этот объект силы.
3. Отбросить связи, заменив их действие реакциями .
4. Определить тип полученной системы сил. Убедиться, что число неизвестных в задаче равно числу уравнений равновесия, то есть выяснить статическую определимость задачи.
5. Выбрать оси координат. При выборе осей следует помнить, что уравнение будет проще, если в него входит меньшее количество неизвестных, то есть необходимо, по возможности, оси координат брать перпендикулярно одной из неизвестных реакций.
6. Составить уравнения равновесия, соответствующие данному виду системы сил, и решить их относительно неизвестных.
| Пример (рис.1.17) Два стержня связаны между собой и со стеной шарнирами. К шарниру В на нити подвешен груз весом 100 Н. Определить усилия в стержнях. Решение. Поскольку стержни соединены в точке В, она будет служить объектом равновесия. Hа нее будет действовать сила натяжения нити, равная весу груза Р. |
|
Связями для точки В служат стержни АВ и ВС. Отбрасывая связи заменим их реакциями - и
и , которые направлены вдоль стержня. Направляя усилия в от точки В предполагаем, что оба стержня растянуты. На точку В действуют три силы, лежащие в одной плоскости и пересекающиеся в одной точке, то есть плоская сходящаяся система сил, для которой можно составить два уравнения равновесия:
, которые направлены вдоль стержня. Направляя усилия в от точки В предполагаем, что оба стержня растянуты. На точку В действуют три силы, лежащие в одной плоскости и пересекающиеся в одной точке, то есть плоская сходящаяся система сил, для которой можно составить два уравнения равновесия:
Fкx=0 , Fкy=0.
В этих уравнениях находится 2 неизвестных - усилия S1 и S2. Оси координат направим вдоль стержней. Составляем уравнения равновесия.
Fkx=S1-Pcos(60)=0;
Fky=S2+Pcos(30)=0.
Из первого уравнения находим:
S1=P cos(60)=1000,5=50 H,
из второго: S2= - Pcos(30)= - 1000,867= - 86,7 H.
Усилие S2 получилось отрицательным, то есть стержень ВС будет не растягиваться, а сжиматься.

В данном решении использовался аналитический метод. Для примера приведем геометрическое решение задачи. Для этого нужно построить из сил, действующих на точку В векторный треугольник. Вначале в масштабе построим силу Р (рис.1.18). Из начала и конца этой силы проводим прямые, параллельные усилиям
 и
и  , получая, таким образом, замкнутый силовой треугольник. При этом для замыкания треугольника мы были вынуждены сменить направление усилия
, получая, таким образом, замкнутый силовой треугольник. При этом для замыкания треугольника мы были вынуждены сменить направление усилия . Из треугольника, в котором усилие Р является гипотенузой, а S1 и S2 - катетами, находим:
. Из треугольника, в котором усилие Р является гипотенузой, а S1 и S2 - катетами, находим:
S1=Pcos(60)=50 H,
S2=Pcos(30)=86,7 H.
studfiles.net
Плоская система сходящихся сил.
Плоская система сходящихся сил – это система сил линии действия которых сходятся в одной точке, называются сходящимися.
Пусть дана система сходящихся сил F1, F2, F3, линии, действия которых сходятся в точке О. для того, чтобы заменить эту систему сил равнодействующей силой необходимо:
1. Перенести силы в точку 0 (на основании следствия из аксиом).
2. Почленно сложить вектора сил (на основании аксиомы 4). Равнодействующая всегда направлена из начала первого вектора в конец последнего вектора силы. В результате векторного сложения образуется силовой многоугольник.
Плоская система сходящихся сил имеет два условия равновесия:
1. Геометрическое условие: плоская система сходящихся сил находится в равновесии, если силовой многоугольник замкнут, т. е. равнодействующая равна нулю.
2. Аналитическое условие: плоская система сходящихся сил находится в равновесии, если алгебраические суммы проекций всех сил системы на оси х и у равны нулю.
∑Fix = 0
∑Fiy = 0
\Пара сил.
Пара сил – это система двух равных сил, лежащих на параллельных прямых и направленных в противоположные стороны.
Действие пары на тело определяется моментом на пару.
Момент – это произведение модуля силы на плечо.
Плечо – кратчайшее расстояние между линиями действия силы.
Если пара поворачивает плечо по ходу часовой стрелки, то момент считается положительным, а если против хода, то отрицательным.
Пара сил обладает свойствами:
1. не нарушая действия пары на тело можно её переносить в любую точку плоскости.
2. Две пары сил являются эквивалентными, если их моменты равны.
Система пар сил находится в равновесии, если сумма моментов всех пар системы равно нулю.
∑Mi (F) = 0
Произвольная плоская система сил.
Момент силы относительно точки.
Плечо – это кратчайшее расстояние от выбранной точки до линии действия силы.
Момент силы относительно точки может быть равен нулю, если сила проходит через выбранную точку.
Между моментом пары и моментом силы есть разница: момент пары есть величина постоянная, а момент силы относительно точки по знаку зависит от выбора точки.
Три формы равновесия произвольной плоской системы сил.
1. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси х и у равны нулю, а также равна нулю сумма моментов всех сил относительно любой точки.
∑Fix = 0
∑Fiy = 0
∑Mi(Fi) = 0
2. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на одну из осей х или у равна нулю, а также, если равны нулю алгебраические суммы моментов всех сил относительно любых двух точек.
∑Fix = 0
∑MА(Fi) = 0
∑MВ(Fi) = 0
3. Произвольная плоская система сил находится в равновесии, если алгебраические суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой.
∑MА(Fi) = 0
∑MВ(Fi) = 0
∑Mi(Fi) = 0
Пространственная система сил.
Пространственная система сил – это система сил, как угодно расположенных в пространстве.
Суммой трех сил, сходящихся в одной точке, является сила по величине и направлению, совпадающая с диагональю параллелепипеда, построенного на заданных силах.
Момент силы относительно оси равен произведению модуля силы на кратчайшее расстояние от выбранной оси до линии действия силы.
Момент может равняться нулю, если:
1. Сила лежит на выбранной оси.
2. Сила пересекает выбранную ось.
3. Сила параллельна оси.
При приведении пространственной системы сил к точке, её можно заменить на эквивалентную систему с главным вектором и главным моментом.
Главный вектор – это геометрическая сумма всех сил системы.
Главный момент – это сумма моментов, компенсирующих пар.
Пространственная система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси x, y, z равны нулю, а также равны нулю моменты всех сил относительно этих же осей.
КИНЕМАТИКА.
Кинематика изучает виды движения.
Формулы связи:
S=φr
υ=ωr
αt=εr
αn=ω2r
infopedia.su
1.5. Плоская система произвольно расположенных сил
Задача приведения системы произвольно расположенных сил к простейшему виду связана с необходимостью их переноса по плоскости параллельно самим себе. Рассмотрим предварительно теорему о возможности такого переноса.
Теорема о параллельном переносе силы (теорема Пуансо).
Пусть в точке А тела приложена сила  , которую требуется перенести самой себе в точкуВ (рис. 16,а). Приложим в точке В уравновешенную систему из двух сил
, которую требуется перенести самой себе в точкуВ (рис. 16,а). Приложим в точке В уравновешенную систему из двух сил  и
и , равных и параллельных
, равных и параллельных (рис. 16,б). Тогда силу
(рис. 16,б). Тогда силу можно считать силой
можно считать силой , перенесенной в точкуВ, а силы
, перенесенной в точкуВ, а силы  и
и , образуют пару с моментомM=Fh. Таким образом, состояние, изображенное на рис. 16,в, соответствует первоначальному состоянию тела.
, образуют пару с моментомM=Fh. Таким образом, состояние, изображенное на рис. 16,в, соответствует первоначальному состоянию тела.

а) б) в)
Рис. 16
Итак, не изменяя действия силы на тело, ее можно перенести в любую точку параллельно самой себе, добавив пару сил, момент которой равен моменту заданной силы относительно новой точки приложения (рис. 16,в).
1. Приведение плоской системы сил к данной точке.
Пусть на твердое тело действует произвольная плоская система  ,
, ,
, (рис. 17,а).
(рис. 17,а).

а) б) в) г)
Рис. 17
Выберем произвольную точку О – центр приведения. Перенесем все силы в точку О, добавляя при этом соответствующие пары. В результате приведения получим систему сил  ,
, ,…
,… и систему парM1=F1h2, M2=F2h3, …, Mn=Fnhn (рис. 17,б).
и систему парM1=F1h2, M2=F2h3, …, Mn=Fnhn (рис. 17,б).
Силы, приложенные в точке, можно заменить одной силой, равной их векторной сумме, – главным вектором Fp (рис. 17,в)
 (8)
(8)
Моменты, действующие на тело, можно заменить одним моментом, равным их алгебраической сумме, – главным моментом:
 (9)
(9)
Таким образом, произвольную плоскую систему сил всегда можно заменить главным вектором и главным моментом (рис. 17,г).
2. Условия равновесия произвольной плоской системы сил.
Произвольная плоская система сил находится в равновесии, если главный вектор и главный момент этой системы относительно любой точки равны нулю, т.е.
 ,
,  (10)
(10)
Первое равенство эквивалентно двум равенствам:
 ;
; 
Итак, для равновесия тела, находящегося под действием произвольной плоской системы сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра равнялась нулю. Уравнения равновесия произвольной плоской системы сил:
 ;
; ;
; (11)
(11)
Возможны и другие формы записи уравнений равновесия:
 ;
;  ;
; (12)
(12)
где ось X не должна быть перпендикулярна линии АВ. Или
 ;
; 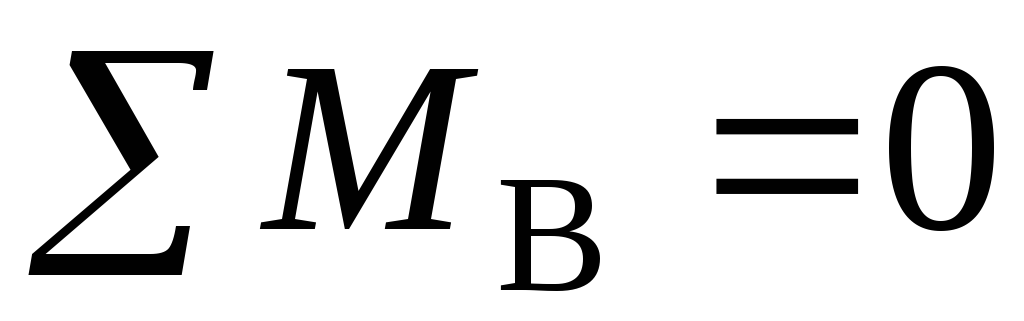 ;
; (13)
(13)
где точки А, В и С не должны лежать на одной прямой.
1.6. Примеры решения задач
В рассмотренных ниже примерах необходимо найти реакции связей. Решения приводятся в общем виде (без численных значений).
Задача 1.
Определить реакции стержней кронштейна, приведенного на рис. 18,а. Дано: F, , .

а) б)
Рис. 18
Объект равновесия – узел А. Отбрасываем стержни и заменяем их действие соответствующими реакциями R1 и R2 (рис. 18,б). Записываем два уравнения равновесия:
 ;
;  (14)
(14)
 ;
;  (15)
(15)
Решая эту систему уравнений, находим реакциями R1 и R2.
Задача 2.
Найти полную реакцию неподвижного цилиндрического шарнира А и реакцию в стержне ВС, удерживающих в равновесии тело прямоугольной формы (рис. 19,а). Дано: F, а, b.

а) б)
Рис. 19
Объект равновесия – тело прямоугольной формы. Отбрасываем связи (шарнир А и стержень ВС) и заменяем их действие соответствующими реакциями RAX, RAY и RBC (рис.19,б). Первые два уравнения равновесия будут иметь вид:
 ;
; (16)
(16)
 ;
; ; (17)
; (17)
В качестве третьего уравнения равновесия запишем сумму моментов всех сил относительно точки А:
 ;
;  (18)
(18)
Необходимые для решения этих уравнений величины находятся следующим образом:
 ;
;  ;
;  (19)
(19)
Решая эту систему уравнений находим RAX, RAY и RBC. Тогда
 (20)
(20)
Для проверки решения задачи можно использовать уравнение суммы моментов всех сил относительно любой другой точки тела, например, В:
 (21)
(21)
Если задача решена верно, то это уравнение будет равно нулю.
Задача 3.
Невесомая балка опирается на две опоры – цилиндрический неподвижный шарнир в точке А и подвижный шарнир в точке В (рис. 20,а). Необходимо найти реакции в этих опорах, если даны: F, q, М , а, b, с.

а) б)
Рис. 20
Объект равновесия – балка. Отбрасываем связи (шарниры в точках А и В) и заменяем их соответствующими реакциями RAX, RAY и RBC (рис.20, б).
Первые два уравнения равновесия будут иметь вид:
 ;
;  (22)
(22)
 ;
; 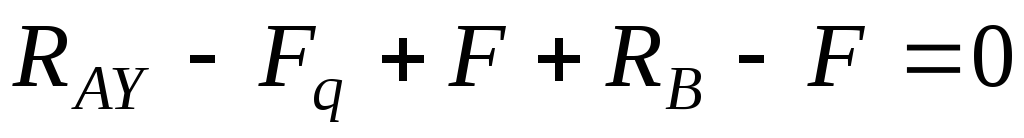 ,где
,где  .(23)
.(23)
В качестве третьего уравнения равновесия запишем сумму моментов всех сил относительно точки А:
 ;
;  (24)
(24)
Решая эту систему уравнений, находим RAX, RAY и RBC. Для проверки решения задачи можно использовать уравнение суммы моментов всех сил относительно точки В:
 . (25)
. (25)
Если задача решена верно, то это уравнение будет равно нулю.
Задача 4.
Горизонтальный стержень жестко защемлен одним концом в точке А (рис.21,а). Найти реакции в этой точке, если дано: F, М, q, а, b, .

а) б)
Рис. 21
Объект равновесия – горизонтальный стержень. Отбрасываем связь (жесткая заделка в точке А) и заменяем ее соответствующими реакциями RAX, RAY и MА (рис 21,б). Составляем три уравнения равновесия:
 ;
;  , (26)
, (26)
 ;
;  , (27)
, (27)
где Fq1=qa; Fq2=qb;
 ;
;  , (28)
, (28)
где h=asin.
Решая эту систему уравнений, находим RAX, RAY и MА. Тогда  .
.
Для проверки решения задачи составляем уравнение суммы моментов всех сил относительно точки В:
 (29)
(29)
Если задача решена верно, то уравнение (29) будет равно нулю.
studfiles.net
Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил.
Математика  Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил.
Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил.
Количество просмотров публикации Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил. - 1115
| Наименование параметра | Значение |
| Тема статьи: | Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил. |
| Рубрика (тематическая категория) | Математика |
Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости, в которой лежат силы. В плоских системах нет крайне важно сти использовать векторное представление момента. Теорема Вариньона – если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (ᴛ.ᴇ. с учетом знака) сумме моментов всех сил относит. той же точки.
Теорема Вариньона ( теорема о моменте равнодействующей силы): момент равнодействующей относительно любой точки = геометрической сумме моментов составляющих сил относительно той же точки. Условия равновесия пространств. сист.сил:
åFkx=0; åFky=0; åFkz=0; åMx(Fk)=0; åMy(Fk)=0; åMz(Fk)=0. Условия равновесия для системы параллельных сил (||z): åFkz=0; åMx(Fk)=0; åMy(Fk)=0. Центр параллельных сил – точка, через которую проходит линия действия равнодействующей системы ||-ых сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол. Координаты центра ||-ых сил: и т.д.
Условия равновесия пл. сист. сил: векторное: . аналитич:
, или
где А,В,С – точки, не лежащие на одной прямой, или , ось "х" не перпендикулярна отрезку АВ.
Равновесие тел при наличии трения. Закон Кулона (закон Амонта – Кулона): максимальная сила сцепления пропорциональна нормальному давлению тела на плоскость
, fсц – коэффициент сцепления (зависит от материала, состояния поверхностей, определяется экспер-но). Направление силы сцепления противоположно направлению того движения, ĸᴏᴛᴏᴩᴏᴇ возникло бы при отсутствии сцепления. При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Ее направление противоположно скорости тела
, f –коэффициент трения скольжения (определяется опытным путем). f<fсц. Реакция шероховатой (реальной) поверхности в отличии от идеально гладкой имеет две составляющие: нормальную реакцию и силу сцепления (или силу трения при движении). Угол jсц–угол сцепления (jтр – угол трения) tgjсц=fсц (tgjтр=f). Конус с вершиной в точке касания тел, образующая которого составляет угол сцепления (угол трения) с нормалью к поверхностям тела назыв. конусом сцепления (конус трения). Для того чтобы тело начало движение, крайне важно (и достаточно), чтобы равнодействующая активных сил находилась вне конуса трения. Трение качения – сопротивление, возникающее при качении одного тела по поверхности другого. Причина его появления в деформации катка и плоскости в точке их соприкосновения и смещения нормальной реакции в сторону возможного движения. Мтр= fkN – момент трения качения, fk – коэффициент трения качения; имеет размерность длины.
Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил. - понятие и виды. Классификация и особенности категории "Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил." 2014, 2015.
referatwork.ru
Плоская система сил — реферат
Далее перейдем к рассмотрению основных деформаций. Из практики известно, что в процессе эксплуатации элементы конструкций испытывают следующие основные деформации:
- растяжение; эту деформацию испытывают, например, канаты, тросы, цепи, шток протяжного станка;
- сжатие; на сжатие работают, например, колонны, кирпичная кладка, пуансоны штампов;
- сдвиг; деформацию сдвига испытывают заклепки, болты, шпонки, швы сварных соединений. Деформацию сдвига, до- веденную до разрушения материала, называют срезом. Срез возникает, например, при резке ножницами или штамповке деталей из листового материала;
- кручение; на кручение работают валы, передающие мощность при вращательном движении. Обычно деформация кручения сопровождается другими деформациями, например изгибом;
- изгиб; на изгиб работают балки, оси, зубья зубчатых колес и другие элементы конструкций.
Очень часто элементы конструкций подвергаются действию нагрузок, вызывающих одновременно несколько основных деформаций. Так, например, в теоретической механике мы рассмотрели усилия, действующие на колесо червячной передачи. Очевидно, что в этом случае возникают следующие деформации вала червячного колеса:
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635 — 1703).
Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Коэффициент пропорциональности Е характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.
Модуль упругости и напряжение выражаются в одинаковых единицах:
[£] = [а]/[8] = Па.
Значения Е, МПа, для некоторых материалов:
Чугун (1,5...1,6) 105
Сталь (1,96...2,16) 105
Медь (1,0...1,3)105
Сплавы алюминия (0,69...0,71) 105
Дерево (вдоль волокон) (0,1...0,16) 105
Текстолит (0,06...0,1)105
Капрон (0,01... 0,02) 105
Если в формулу закона Гука подставим выражения a = N/A, 8 = А///, то получим
M=Nl/(EA).
Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства материала и геометрические размеры поперечного сечения бруса.
Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса.
Отношение называется жесткостью бруса при растяжении или сжатии.
Приведенные выше формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовленных из одного материала и при постоянной продольной силе.
Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков.
Диаграмма растяжения низкоуглеродистой стали представлена на рис. 19.6. Эта диаграмма имеет следующие характерные точки.
Точка А практически соответствует и другому пределу, который называется пределом упругости.
Пределом упругости ауп называется то наибольшее напряжение, до которого деформации практически остаются упругими.
Точка С соответствует пределу текучести.
Пределом текучести ат называется такое напряжение, при котором в образце появляется заметное удлинение без увеличения нагрузки.
При достижении предела текучести поверхность образца становится матовой, так как на ней появляется сетка линий Людерса-Чернова, наклоненных к оси под углом 45°.
Эти линии впервые были описаны в 1859 г. немецким металлургом Людерсом и независимо от него в 1884 г. русским металлургом Д.К. Черновым (1839—1921), предложившим использовать их при экспериментальном изучении напряжений в сложных деталях.
Предел текучести является основной механической характеристикой при оценке прочности пластичных материалов. Точка В соответствует временному сопротивлению или пределу прочности.
Временным сопротивлением ав называется условное напряжение, равное отношению максимальной силы, которую выдерживает образец, к первоначальной площади его поперечного сечения (для стали СтЗ ав400 МПа).
При достижении временного сопротивления на растягиваемом образце образуется местное сужение — шейка, т. е. начинается разрушение образца.
В определении временного сопротивления говорится об условном напряжении, так как в сечениях шейки напряжения будут больше.
Пределом прочности апч называется временное сопротивление образца, разрушающегося без образования шейки. Предел прочности является основной механической характеристикой при оценке прочности хрупких материалов.
Точка И соответствует напряжению, возникающему в образце в момент разрыва во всех поперечных сечениях, кроме сечений шейки.
Точка М соответствует напряжению, возникающему в наименьшем поперечном сечении шейки в момент разрыва. Это напряжение можно назвать напряжением разрыва.
6. Расчетная формула при растяжении и сжатии
Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности. Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных.
Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой я:
Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Сечение, для которого коэффициент запаса прочности наименьший, называется опасным.
Минимально необходимый коэффициент запаса прочности называют допускаемым и обозначают [д]. Допускаемый коэффициент запаса прочности зависит от свойств, качества и однородности материала, точности представления о нагрузках, действующих на конструкцию, ответственности конструкции и многих других причин. Для пластичных материалов [л] = 1,2...2,5, для хрупких [я] = 2...5, для древесины [я] = 8...12.
Отношение предельного напряжения к допускаемому коэффициенту запаса прочности называют допускаемым напряжением и обозначают [ст].
Расчетная формула при растяжении и сжатии имеет вид: и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле а = Лт/А, не должно превышать допускаемое.
Список литературы:
- Бать М.И и др. Теоретическая механика в примерах и задачах. Учеб.пособ. для вузов. В 2-х т./М.И.Бать, Г.Ю.Джанелидзе, А.С. Кельзон.-9-е изд., перераб.-М.:Наука,1990.-670 с.
- Бутенин Н.В. и др. Курс теоретической механики: Учеб.пособие для студ-ов вузов по техн.спец.:В 2-х т./Н.В.Бутенин, Я.Л.Лунц, Д.Р.Меркин. СПб.: Лань.-5-е изд., испр.-1998.-729 с.
- Курс теоретической механики: Учебник для вузов по направлению подгот.дипломир.специалистов в области техники и технологии/ [ В.И.Дронг, В.В.Дубинин,М.М., Ильин и др.];Под ред.К.С.Колесникова.-3-е изд.,стер. М. : Изд- во МГТУ им. Н.Э.Баумана,2005.-735 с.- (Механика в техническом университете:В 8 т.;Т.1)
- Мещерский И.В. Задачи по теоретической механике: Учеб. пособие для студ.вузов,обуч.по техн.спец./И.В.Мещерский; Под ред. В.А.Пальмова, Д.Д.Меркина.-45-е изд.,стер.-СПб.и др.: Лань,2006.-447 с. 2. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов/С.М.Тарг.-15-е изд.,стер.-М.:Высш.шк.,2005.-415 с.
- Павловский М.А. и др. Теоретическая механика. Динамика:Учеб. для втузов/М.А.Павловский, Л.Ю.Акинфиева, О.Ф.Бойчук; Под общ.ред.М.А.Павловского.- Киев:Выща.шк.,1990.-479 c.
- Сборник заданий для курсовых работ по теоретической механике: Учеб. пособие для студ.втузов/[А.А. Яблонский, С. С.Норейко,С.А.Вольфсон и др.];Под общ. ред. А. А. Яблонского.- 11-е изд.,стер.-М.:Интеграл- Пресс,2004.-382 с.
referat911.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|




