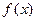 задана в отрезке [0,1] в точках
задана в отрезке [0,1] в точках 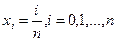 , при некотором фиксированном n. В этом случае можно построить многочлен Бернштейна:
, при некотором фиксированном n. В этом случае можно построить многочлен Бернштейна: 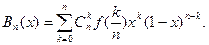
Предположим, что функция 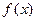 задана в отрезке [0,1] в точках
задана в отрезке [0,1] в точках 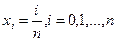 , при некотором фиксированном n. В этом случае можно построить многочлен Бернштейна:
, при некотором фиксированном n. В этом случае можно построить многочлен Бернштейна: 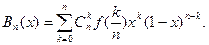
Можно доказать, что при 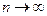 многочлены
многочлены 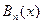 стремятся к функции
стремятся к функции 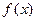 равномерно по x; кроме того, для любого конкретного целого
равномерно по x; кроме того, для любого конкретного целого 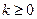 имеет место предельное соотношение для производных:
имеет место предельное соотношение для производных: 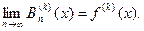
Наконец, известно, что если число 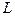 удовлетворяет неравенству
удовлетворяет неравенству 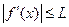 на всем отрезке [0,1], то для любого
на всем отрезке [0,1], то для любого 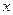 из этого отрезка выполняется неравенство:
из этого отрезка выполняется неравенство: 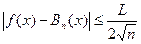 .
.
Это, конечно, позволяет оценивать ошибку, которая возникает при соответствующей … интерполяционной замене.
Сказанное выше для случая функции 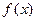 одной переменной можно обобщить на случай двух и более переменных. Мы ограничимся обобщением только на случай двух переменных.
одной переменной можно обобщить на случай двух и более переменных. Мы ограничимся обобщением только на случай двух переменных.
Итак, пусть имеется функция 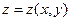 на квадрате
на квадрате
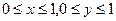 ,
,
причем реально она задана в узлах решетки
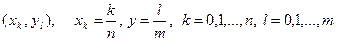 ,
,
при заранее фиксированных натуральных числах 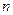 и
и 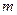 . Построим по этой информации следующий многочлен от двух переменных:
. Построим по этой информации следующий многочлен от двух переменных:
 ,
,
где 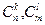 — биномиальные коэффициенты. Это — многочлен Бернштейна для заданной функции на заданной решетке. С его помощью так же можно осуществлять интерполяцию, принимая его значение в той или иной точке квадрата за значение самой функции. Можно доказать, что для любой точки квадрата имеет место неравенство:
— биномиальные коэффициенты. Это — многочлен Бернштейна для заданной функции на заданной решетке. С его помощью так же можно осуществлять интерполяцию, принимая его значение в той или иной точке квадрата за значение самой функции. Можно доказать, что для любой точки квадрата имеет место неравенство:
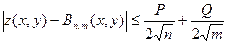 ,
,
которое позволяет оценить погрешность интерполяции. (Здесь константы 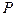 и
и 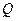 удовлетворяют в рассматриваемом квадрате неравенствам).
удовлетворяют в рассматриваемом квадрате неравенствам).
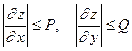 .
.
Замечание.Случай одной переменной рассматривался выше на отрезке [0, 1], а случай двух переменных — в единичном квадрате. В действительности, рассмотрения возможны на любом отрезке [a,b] и на любом прямоугольнике [a,b;c,d]. Для этого в исходной ситуации (т.е. на произвольном отрезке или на произвольном прямоугольнике нужно сделать линейную замену переменных).
Подробнее: пусть функция 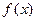 задана в точках
задана в точках 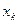 отрезка
отрезка 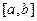 , где при некотором фиксированном
, где при некотором фиксированном 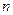
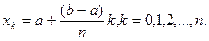
Положим
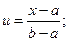 тогда
тогда 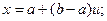
если теперь в 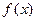 положить
положить 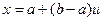 , то возникнет ситуация функции
, то возникнет ситуация функции 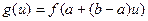 , заданной уже на отрезке [0, 1]. Аналогично, в случае двух переменных надо сделать замену:
, заданной уже на отрезке [0, 1]. Аналогично, в случае двух переменных надо сделать замену:
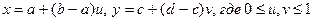 ,
,
после чего возникнет ситуация единичного квадрата.
refac.ru
В вычислительной математике многочлены Бернштейна — это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна. [1][2]
Устойчивым алгоритмом вычисления многочленов в форме Бернштейна является алгоритм де Кастелье.
Многочлены в форме Бернштейна были описаны Сергеем Натановичем Бернштейном в 1912 году и использованы им в конструктивном доказательстве аппроксимационной теоремы Вейерштрасса. С развитием компьютерной графики, полиномы Бернштейна, заключённые в промежуток x ∈ [0, 1], стали играть важную роль при построении кривых Безье.
(n + 1) базисных многочленов Бернштейна степени n находятся по формуле

где 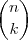 — биномиальный коэффициент.
— биномиальный коэффициент.
Базисные многочлены Бернштейна степени n образуют базис для линейного пространства 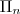 многочленов степени n.
многочленов степени n.
Линейная комбинация базисных полиномов Бернштейна
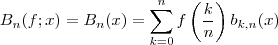
называется многочленом (полиномом) Бернштейна или многочленом в форме Бернштейна степени n.Коэффициенты 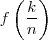 называются коэффициентами Бернштейна или коэффициентами Безье.
называются коэффициентами Бернштейна или коэффициентами Безье.
Вот некоторые базисные полиномы Бернштейна:
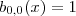
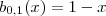
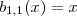
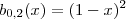
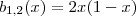
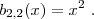
| Этот раздел не завершён.Вы поможете проекту, исправив и дополнив его. |
Леммы о моментах
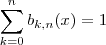 для любых n и x, так как
для любых n и x, так как 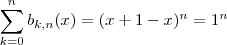
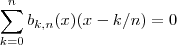 для любых n и x
для любых n и x
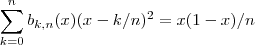 для любых n и x
для любых n и x
| Этот раздел не завершён.Вы поможете проекту, исправив и дополнив его. |
dictionary.sensagent.com
(n + 1) базисных многочленов Бернштейна степени n находятся по формуле
bk,n(x)=(nk)xk(1−x)n−k,k=0,…,n.{\displaystyle b_{k,n}(x)={\binom {n}{k}}x^{k}(1-x)^{n-k},\qquad k=0,\ldots ,n.}где (nk){\displaystyle {\binom {n}{k}}} — биномиальный коэффициент.
Базисные многочлены Бернштейна степени n образуют базис для линейного пространства Πn{\displaystyle \Pi _{n}} многочленов степени n.
Линейная комбинация базисных полиномов Бернштейна
Bn(f;x)=Bn(x)=∑k=0nf(kn)bk,n(x){\displaystyle B_{n}(f;x)=B_{n}(x)=\sum _{k=0}^{n}f\left({\frac {k}{n}}\right)b_{k,n}(x)}называется многочленом Бернштейна или точнее многочленом в форме Бернштейна степени n. Коэффициенты f(kn){\displaystyle f\left({\frac {k}{n}}\right)} называются коэффициентами Бернштейна или коэффициентами Безье.
Вот некоторые базисные полиномы Бернштейна:
b0,0(x)=1{\displaystyle b_{0,0}(x)=1} b0,1(x)=1−x{\displaystyle b_{0,1}(x)=1-x} b1,1(x)=x{\displaystyle b_{1,1}(x)=x} b0,2(x)=(1−x)2{\displaystyle b_{0,2}(x)=(1-x)^{2}} b1,2(x)=2x(1−x){\displaystyle b_{1,2}(x)=2x(1-x)} b2,2(x)=x2 .{\displaystyle b_{2,2}(x)=x^{2}\ .}Дифференцирование
bk,n′(x)=nbk,n−1(x)+nbk−1,n−1(x){\displaystyle b'_{k,n}(x)=n\,b_{k,n-1}(x)+n\,b_{k-1,n-1}(x)}
bk,n(l)(x)=n!(n−l)!∑j=0l(lj)bk−j,n−l(x){\displaystyle b_{k,n}^{(l)}(x)={\frac {n!}{(n-l)!}}\sum _{j=0}^{l}{\binom {l}{j}}b_{k-j,n-l}(x)}
Леммы о моментах
∑k=0nbk,n(x)=1{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)=1} для любых n и x, так как ∑k=0nbk,n(x)=(x+1−x)n=1n{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)=(x+1-x)^{n}=1^{n}}
∑k=0nbk,n(x)(x−k/n)=0{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)(x-k/n)=0} для любых n и x
∑k=0nbk,n(x)(x−k/n)2=x(1−x)/n{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)(x-k/n)^{2}=x(1-x)/n} для любых n и x
www-wikipediya.ru
(n + 1) базисных многочленов Бернштейна степени n находятся по формуле
bk,n(x)=(nk)xk(1−x)n−k,k=0,…,n.{\displaystyle b_{k,n}(x)={\binom {n}{k}}x^{k}(1-x)^{n-k},\qquad k=0,\ldots ,n.}где (nk){\displaystyle {\binom {n}{k}}} — биномиальный коэффициент.
Базисные многочлены Бернштейна степени n образуют базис для линейного пространства Πn{\displaystyle \Pi _{n}} многочленов степени n.
Линейная комбинация базисных полиномов Бернштейна
Bn(f;x)=Bn(x)=∑k=0nf(kn)bk,n(x){\displaystyle B_{n}(f;x)=B_{n}(x)=\sum _{k=0}^{n}f\left({\frac {k}{n}}\right)b_{k,n}(x)}называется многочленом Бернштейна или точнее многочленом в форме Бернштейна степени n. Коэффициенты f(kn){\displaystyle f\left({\frac {k}{n}}\right)} называются коэффициентами Бернштейна или коэффициентами Безье.
Вот некоторые базисные полиномы Бернштейна:
b0,0(x)=1{\displaystyle b_{0,0}(x)=1} b0,1(x)=1−x{\displaystyle b_{0,1}(x)=1-x} b1,1(x)=x{\displaystyle b_{1,1}(x)=x} b0,2(x)=(1−x)2{\displaystyle b_{0,2}(x)=(1-x)^{2}} b1,2(x)=2x(1−x){\displaystyle b_{1,2}(x)=2x(1-x)} b2,2(x)=x2 .{\displaystyle b_{2,2}(x)=x^{2}\ .}Дифференцирование
bk,n′(x)=nbk,n−1(x)+nbk−1,n−1(x){\displaystyle b'_{k,n}(x)=n\,b_{k,n-1}(x)+n\,b_{k-1,n-1}(x)}
bk,n(l)(x)=n!(n−l)!∑j=0l(lj)bk−j,n−l(x){\displaystyle b_{k,n}^{(l)}(x)={\frac {n!}{(n-l)!}}\sum _{j=0}^{l}{\binom {l}{j}}b_{k-j,n-l}(x)}
Леммы о моментах
∑k=0nbk,n(x)=1{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)=1} для любых n и x, так как ∑k=0nbk,n(x)=(x+1−x)n=1n{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)=(x+1-x)^{n}=1^{n}}
∑k=0nbk,n(x)(x−k/n)=0{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)(x-k/n)=0} для любых n и x
∑k=0nbk,n(x)(x−k/n)2=x(1−x)/n{\displaystyle \sum _{k=0}^{n}b_{k,n}(x)(x-k/n)^{2}=x(1-x)/n} для любых n и x
ru-wiki.org
Реферат на тему:
В математике, многочлены или полиномы от одной переменной — функции вида
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.
Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.
Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (см. аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.
Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.
Многочлен (или полином) от n переменных — есть конечная формальная сумма вида
где есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается
.
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен x4 − 2, неприводимый в поле рациональных чисел, разлагается на три множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.
Пусть A есть алгебра над кольцом R. Произвольный многочлен определяет полиномиальную функцию
Чаще всего рассматривают случай A = R.
В случае, если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов), функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены
и
из
определяют тождественно равные функции
.
wreferat.baza-referat.ru
В вычислительной математике многочлены Бернштейна — это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна. [1][2]
Устойчивым алгоритмом вычисления многочленов в форме Бернштейна является алгоритм де Кастельжо.
Многочлены в форме Бернштейна были описаны Сергеем Натановичем Бернштейном в 1912 году и использованы им в конструктивном доказательстве аппроксимационной теоремы Вейерштрасса. С развитием компьютерной графики, полиномы Бернштейна, заключённые в промежуток x ∈ [0, 1], стали играть важную роль при построении кривых Безье.
(n + 1) базисных многочленов Бернштейна степени n находятся по формуле

где  — биномиальный коэффициент.
— биномиальный коэффициент.
Базисные многочлены Бернштейна степени n образуют базис для линейного пространства  многочленов степени n.
многочленов степени n.
Линейная комбинация базисных полиномов Бернштейна

называется многочленом (полиномом) Бернштейна или многочленом в форме Бернштейна степени n. Коэффициенты  называются коэффициентами Бернштейна или коэффициентами Безье.
называются коэффициентами Бернштейна или коэффициентами Безье.
Вот некоторые базисные полиномы Бернштейна:






 | Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
Леммы о моментах
 для любых n и x, так как
для любых n и x, так как 
 для любых n и x
для любых n и x
 для любых n и x
для любых n и x
 | Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
dikc.academic.ru
Реферат на тему:
В математике, многочлены или полиномы от одной переменной — функции вида
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.
Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.
Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (см. аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.
Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.
Многочлен (или полином) от n переменных — есть конечная формальная сумма вида
где есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается
.
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен x4 − 2, неприводимый в поле рациональных чисел, разлагается на три множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.
Пусть A есть алгебра над кольцом R. Произвольный многочлен определяет полиномиальную функцию
Чаще всего рассматривают случай A = R.
В случае, если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов), функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены
и
из
определяют тождественно равные функции
.
wreferat.baza-referat.ru