
Порой кажется, что наш мир прост и понятен. На самом деле это великая загадка Вселенной, сотворившей такую совершенную планету. А может, её создал тот, кто наверняка знает, что делает? Над этим вопросом трудятся величайшие умы современности.

Они каждый раз приходят к выводу, что невозможно сотворить все то, что мы имеем, без Высшего разума. Какая необыкновенная, сложная и в то же время простая и непосредственная наша планета Земля! Окружающий мир удивителен своими правилами, формами, красками.
Первое, на что можно обратить внимание на нашей огромной и удивительной планете, - это осевая симметрия. Она обнаруживается во всех формах окружающего мира, а также является основным принципом красоты, идеальности и пропорциональности. Это не что иное, как математика в природе.
Понятие "симметрия" означает гармонию, правильность. Это свойство окружающей действительности, систематизирующее фрагменты и превращающее их в единое целое. Ещё в древней Греции начали впервые замечать признаки этого закона. Например, Платон считал, что красота появляется исключительно вследствие симметрии и соразмерности. В действительности, если посмотреть на предметы пропорциональные, правильные и завершённые, то наше внутреннее состояние будет прекрасным.
Давайте взглянем на любое существо, например самое совершенное - человека. Мы увидим строение тела, которое с обеих сторон выглядит одинаково. Ещё можно перечислять множество образцов, таких как насекомые, животные, морские обитатели, птицы. Каждый вид имеет свой окрас. 
Если присутствует какой-нибудь узор или рисунок, он, как известно, отражается зеркально относительно центровой линии. Все организмы созданы благодаря правилам мироздания. Такие математические закономерности прослеживаются и в неживой природе.
Если обращать внимание на все явления, такие как смерч, радуга, растения, снежинки, то можно обнаружить в них много общего. Относительно оси симметрии листок дерева делится пополам, и каждая часть будет отражением предыдущей. 
Еще если взять в качестве примера смерч, который возвышается вертикально и имеет вид воронки, то его тоже можно условно разделить на две абсолютно одинаковые половинки. Можно встретить явление симметрии в смене дня и ночи, времён года. Законы окружающего мира - это математика в природе, которая имеет свою совершенную систему. На неё опирается вся концепция создания Вселенной.
Мы нечасто задумываемся над явлениями природы. Пошёл снег или дождь, выглянуло солнышко или грянул гром - привычное состояние меняющейся погоды. Рассмотрим разноцветную дугу, которую обычно можно обнаружить после выпадения осадков. Радуга в небе - удивительное явление природы, сопровождающееся видимым только человеческому глазу спектром всех цветов. Это случается за счёт прохождения лучей солнца через уходящую тучу. Каждая дождинка служит призмой, которая обладает оптическими свойствами. Можно сказать, что любая капля является маленькой радугой.

Проходя через водную преграду, лучи меняют свой изначальный цвет. Всякий поток света имеет определённую длину и оттенок. Поэтому наш глаз воспринимает радугу именно такой разноцветной. Заметим интересный факт, что это явление может лицезреть исключительно только человек. Потому что это всего лишь иллюзия.
Идеальную соразмерность чаще всего можно встретить в мире животных. Они награждены такой пропорцией, которая равна корню от соответствия числа PHI к единице. Это соотношение является связующим фактом всех животных на планете. Великие умы древности называли это число божественной пропорцией. Её ещё можно назвать золотым сечением. 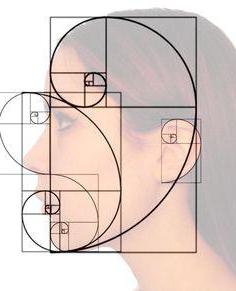
Этому правилу полностью соответствует гармоничность строения человека. Например, если определить расстояние между глазами и бровями, то оно будет равно божественной постоянной.
Золотое сечение - это пример того, сколь важна математика в природе, закону которой начали следовать дизайнеры, художники, архитекторы, создатели красивых и совершенных вещей. Они создают с помощью божественной постоянной свои творения, которые имеют сбалансированность, гармонию и на них приятно смотреть. Наш ум способен считать красивым те вещи, предметы, явления, где есть неравное соотношение частей. Пропорциональностью наш мозг называет именно золотое сечение.
Как справедливо отметил немецкий учёный Гуго Вейль, корни симметрии пришли через математику. Многие отмечали совершенность геометрических фигур и обращали на них внимание. Например, пчелиные соты - это не что иное, как шестиугольник, сотворённый самой природой. Ещё можно обратить внимание на шишки ели, которые имеют цилиндрическую форму. Также в окружающем мире часто встречается спираль: рога крупного и мелкого скота, раковины моллюсков, молекулы ДНК.

Спираль ДНК сотворена по принципу золотого сечения. Она является связующим звеном между схемой материального тела и её реальным образом. А если рассмотреть мозг, то он представляет собой не что иное, как проводник между телом и разумом. Интеллект связывает жизнь и форму её проявления и позволяет жизни, заключённой в форме, познавать саму себя. С помощью этого человечеству достижимо понять окружающую планету, искать в ней закономерности, которые затем применять к изучению внутреннего мира.
Митоз клетки состоит из четырёх фаз:

За счёт уникального способа деления, каждая последующая после размножения клетка имеет такой же состав генов, как её материнская. Состав хромосом обе клетки получают одинаковый. Здесь не обошлось без такой науки, как геометрия. Прогрессия в митозе имеет важное значение, так как по этому принципу размножаются все клетки.
Этот процесс служит гарантией постоянного набора хромосом и генетических материалов в каждой клетке. За счёт митоза происходит развитие организма, размножение, регенерация. В случае нарушения деления клетки из-за действия каких-то ядов хромосомы могут не разойтись по своим половинкам, или в них, возможно, будут наблюдаться нарушения в строении. Это станет явным показателем начинающихся мутаций.
Что общего в математике и природе? На этот вопрос вы найдёте ответ в нашей статье. А если копнуть глубже, то нужно сказать, что с помощью изучения окружающего мира человек познаёт самого себя. Без Высшего разума, породившего все живое, не могло бы ничего быть. Природа находится исключительно в гармонии, в строгой последовательности своих законов. А возможно ли все это без разума?
Приведём высказывание учёного, философа, математика и физика Анри Пуанкаре, который, как никто другой, сможет дать ответ на вопрос о том, действительно ли математика в природе является основополагающей. Некоторым материалистам могут не понравиться такие рассуждения, но навряд ли они смогли бы их опровергнуть. Пуанкаре говорит, что гармония, которую человеческий разум хочет открыть в природе, не может существовать вне его. Объективная реальность, которая присутствует в умах хотя бы нескольких индивидов, может быть доступна всему человечеству. Связь, которая собирает воедино мыслительную деятельность, и называется гармонией мира. В последнее время на пути к такому процессу есть колоссальные продвижения, но они очень малы. Эти звенья, связывающие Вселенную и индивида, должны быть ценны любым человеческим умом, который чувствителен к этим процессам.
fb.ru
Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете назвал спираль «кривой жизни».
Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляют себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках «упакованы» по логарифмическим («золотым») спиралям, завивающимся навстречу друг другу, причем числа «правых» и «левых» спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.

Приглядимся внимательно к побегу цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.
Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

Рассматривая расположение листьев на стебле растений можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (В).
У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза так же создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста. 


В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62/38.

Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.
Золотое сечение можно найти и в анатомии. Закон золотого сечения просматривается в количественном членении человеческого тела, соответствующем числам ряда Фибоначчи. Примером может быть число костей туловища, черепа и конечностей. Так, в скелете туловища различают три костных системы: позвоночник, реберный его отдел, грудину. Грудина включает 3 кости (рукоятку, тело и мечевидный отросток). Позвоночник состоит из 33 (34) позвонков; от них отходят 12-13 пар ребер. Мозговой череп состоит из 8 костей. В верхней и нижней челюстях с каждой стороны имеется по 8 альвеол и соответственно - корни 8 зубов.
Скелет верхней конечности состоит из 3 частей (плечевой, костей предплечья и костей кисти). Кисть включает 8 костей запястья, 5 пястных костей и кости 5 пальцев. Каждый палец, кроме большого, имеет по 3 фаланги. Таким образом, морфогенез кисти, включающей 2 соседних члена числового ряда Фибоначчи – в частности, 8 костей запястья, 5 костей пясти – приближается к золотому сечению 1,618=8/5. 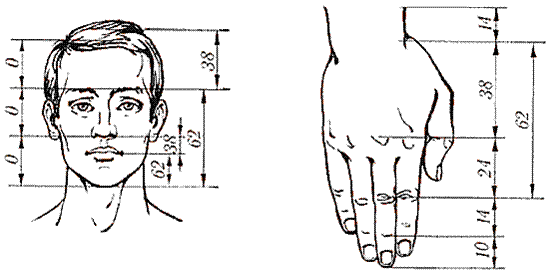
infourok.ru

Разделы: Математика, Внеклассная работа
Клуб объединяет школьников 8-11-х классов, увлекающихся математикой и информатикой. На его заседаниях они выступают и с исследовательскими работами, показывающими связь математики с другими школьными предметами и окружающим миром.
На данном заседании школьники выступали с сообщениями о великих математиках, которые увлекались поэзией и драматургией, с исследовательскими работами “Симметрия в природе” и “Золотое сечение в геометрии и природе” и конкурсными работами “Лучший урок письма”.
ПУСКАЙ МЫ ПИФАГОРАМИ НЕ СТАНЕМ. А ВДРУГ?
Цели заседания: воспитание интереса к математике; развитие творческих способностей, устной и письменной речи школьников; сконцентрировать их внимание на ценностях родного языка.
План проведения
1. Математики и поэзия.
2. Математика в природе.
3. “Лучший урок письма”.
1. Математики и поэзия.1. Математика и поэзия. Что роднит их, казалось, на первой взгляд разные… Но женщина-математик Софья Васильевна Ковалевская говорит о математике так: “Это наука, требующая наиболее фантазии, нельзя быть математиком, не будучи в то же время поэтом в душе”.
Она – великий математик, она – признанный писатель и поэт. Вот одно из ее стихотворений.
“ЕСЛИ ТЫ В ЖИЗНИ…”
Если ты в жизни, хотя на мгновенье Истину в сердце своем ощутил, Если луч правды сквозь мрак и сомненье Ярким сияньем твой путь озарил: Чтобы в решеньи своем неизменном Рок ни назначил тебе впереди – Память об этом мгновеньи священном Вечно храни, как святыню, в груди. Тучи сберутся громадой нестройной, Небо покроется черною мглой, С ясной решимостью, с верой спокойной Бурю ты встреть и померься с грозой.
В “Воспоминаниях детства” Софья Васильевна Ковалевская пишет: “Хотелось бы мне знать, может ли кто-нибудь определить точно тот момент своего существования, кода в первый раз возникло в нем отчетливое представление о своем собственном я, - первый проблеск сознательной жизни”.
(Звучат отрывки из ее произведения “Воспоминания детства” и повести “Нигилистка”.)
2. Великий русский ученый М. В. Ломоносов говорил о математике так: “Математику уже затем учить надо, что она ум в порядок приводит”. И вот отрывок из его стихотворения:
О вы, которых ожидает Отечество от недр своих И видеть таковых желает, Каких зовет от стран чужих, О, ваши дни благословенны! Дерзайте ныне ободрены Раченьем вашим показать, Что может собственных Платонов И быстрых разумом Невтонов Российская земля рожать.
3. Как видите, ученым не чужда поэзия. Как показывает история науки, еще со времен пифагорейцев выдающиеся математики увлекались поэзией и даже сами пробовали писать.
Но разве писал стихи великий русский геометр Лобачевский? Ректор Казанского университета и известный математик вдруг в 1834 году “рискнул” опубликовать свое стихотворение “Разлив Волги при Казани”. Вот отрывок его:
“Ты поражаешь ли поля опустошеньем? Ты похищаешь ли надежды поселян? Нет! На водах твоих всегда благословенье Почиет благодарных стран, Тобой, питаемых, тобой обогащенных! Ты и земли безвредная краса, И светлые в струях твоих невозмущенных, Как в чистой совести, сияют небеса. Вот образ мирного могущества России! Ее разлив не страшен никому. Великодушие обуздывает силы, всегда, везде покорные ему.
Эта публикация, по-видимому, связана с приездом Пушкина в Казань в сентябре 1833 года, где он собирал материалы о восстании Пугачева. Жена Лобачевского – сестра Великопольского, давнишнего приятеля Пушкина, на вечерах которого бывали Пушкин и Лобачевский. Встретились два гения. Может быть, после встречи с Лобачевским Пушкин сказал: “Вдохновение нужно в поэзии, как в геометрии”.
Вопрос о предпосылках прекрасного, о роли математики в искусстве волновал еще древних греков, причем свой интерес они унаследовали от предшествующих цивилизаций. В наше время геометрия – необходимый элемент общего образования и культуры, представляет большой исторический интерес, имеет серьезное практическое применение и обладает внутренней красотой.
Выступления школьников, демонстрация практических работ
(представлены тезисы исследовательских работ)
1. “Золотое сечение в геометрии и природе”
Пристальное, глубокое изучение природы есть источник самых плодотворных открытий математики
Ш. Фурье
Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением и если первое можно сравнить с мерой золота, то второе – с драгоценным камнем.
Золотым сечением (делением) и даже “божественной пропорцией” называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. Это отношение приближенно равно 0,618 или 5/8.
В геометрии “золотым сечением” называется также деление отрезка в среднем и крайнем отношениях, при котором длина большего отрезка есть среднее геометрическое, или, как часто говорят, среднее пропорциональное длин всего отрезка и его меньшей части. “Золотое сечение” отрезка можно определить, достроив его до прямоугольного треугольника, в котором данный отрезок будет гипотенузой. Доказательство можно провести с помощью теоремы Пифагора. Эта задача очень древняя, она присутствует в “Началах” Евклида, который решил ее геометрически.
Замечательный пример “золотого сечения” представляет собой правильный пятиугольник – выпуклый и звездчатый, который называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и опознавательным знаком. Пентаграмма была хорошо известна в Древнем Египте. Но непосредственно как эмблема здоровья она была принята в Древней Греции. Существует гипотеза, что пентаграмма – первичное понятие, а “золотое сечение” вторично. Пентаграмму никто не изобретал, ее лишь скопировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. (В своей работе я рассматривала цветки картофеля, шиповника, яблони). Те и другие создания природы. Человек наблюдает тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем “золотая” пропорция.
Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя из листьев третье расположено в месте золотого сечения. Я это исследовала на традесканции и разновидностях плюща.
Расположение листьев на деревьях не случайно, а подчиняется определенным математическим законам. Если рассмотреть веточку с листьями, то можно заметить, что основания черешков располагаются по винтовой линии, каждый следующий лист прикреплен выше и в сторону от предыдущего. Если соединить последовательно основания листьев ниткой, то она обовьется вокруг стебля по правильной винтовой линии. Проследив за расположением листьев по этой спирали, можно заметить, что листья расположены одни над другими. Часть спирали, заключенная между двумя такими листьями, называется в ботанике “циклом”. Листорасположение обозначают в виде дроби, в числителе которой число оборотов одного цикла спирали, а в знаменателе – число листьев в одном цикле. Наиболее распространенные типы листорасположений: ?, 1/3, 2/5, 3/8,5/13 и т.д.
Ботаники давно заметили, что этот ряд отличается одной любопытной и довольно неожиданной особенностью: каждая из этих дробей, начиная с третьей, получается из предыдущих путем сложения их числителей и знаменателей. Числители и знаменатели дают ряд Фибоначчи: 1, 2, 3, 5, 8… и 2, 3, 5, 8, 13…. Все эти дроби дают точные приближения к числу 0,62.
Закон золотого деления действует, значит, и в растительном мире.
Знаменитый зодчий Ле Корбюзье нашел золотое сечение во многих пропорциях человеческой фигуры. Если высоту хорошо сложенной фигуры разделить в крайнем и среднем отношении, то линия раздела окажется на высоте талии. Особенно хорошо удовлетворяет этой пропорции мужская фигура, и художники давно знают, что вопреки общему мнению, мужчины сложены красивее, чем женщины.
Каждую отдельно взятую часть тела (голову, руку, кисть) также можно разделить на естественные части по закону золотого сечения.
Рука, например, при рассмотрении согласно принципу золотого деления распадется на “свои анатомические части – плечо, предплечье, кисть. Разделение кисти руки также отвечает этому принципу.
В эпоху Возрождения математическое понятие – золотая пропорция было возведено в ранг главного эстетического принципа. Леонардо да Винчи именовал ее Sectio aurea, откуда и получил начало термин “золотое сечение”.
Пропорциональность в природе, искусстве означает соблюдение соотношений между размерами отдельных частей растения, скульптуры и является непременным условием правильного и красивого изображения предмета.
Эти удивительные и даже неожиданные сведения о математических законах в природе вызывают интерес к изучению математики в школе.
Симметрия в природе
Математика… выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного.
Аристотель
Трудно найти человека, который не имел бы какого-то представления о симметрии. “Симметрия” - слово греческого происхождения. Оно, как и слово “гармония”, означает соразмерность, наличие определенного порядка, закономерности в расположении частей. Известный немецкий математик Герман Вейль дал определение симметрии таким образом: “Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство”
В математике рассматриваются различные виды симметрии. Каждый из них имеет свое название: осевая симметрия (симметрия относительно прямой), центральная симметрия (симметрия относительно точки) и зеркальная симметрия (симметрия относительно плоскости).
Природа – удивительный творец и мастер. Все живое в природе обладает свойством симметрии.
Если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать. Свойство симметричности, присущее живой природе, человек использовал в своих достижениях: изобрел самолет, создал уникальные здания архитектуры. Да и сам человек является фигурой симметричной.
Симметрию можно увидеть среди цветов. Осевой симметрией обладают цветки семейства розоцветных, а центральной симметрией – семейство крестоцветных. Симметрию можно увидеть и на листьях деревьев.
Симметрия, характерная для представителей животного мира, называется билатеральной симметрией.
Однако симметрия существует и там, где ее не видно на первый взгляд. Физик скажет, что всякое твердое тело – кристалл. Знаменитый кристаллограф Евграф Степанович Федоров сказал: “Кристаллы блещут симметрией”. Химик скажет, что все тела состоят из молекул, а молекулы состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии.
Таким образом, данное преобразование фигур (симметрия) вошло в математику в результате наблюдения человека за окружающим миром. Оно встречается часто и повсеместно. Поэтому даже не искушенный человек обычно легко усматривает симметрию в относительно простых ее проявлениях.
Симметрии посвящены такие строчки:
О, симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза!
В своей работе я представляю гербарий растений, модели фигур, поделки, обладающие симметрией.
Данная тема исследования помогает понимать связь математики с другими науками и окружающим миром.
3. “Лучший урок письма”.Педагог:
Дорогие друзья! А сейчас перед вами выступит ученица 11 класса Иванова Юлия. С ее работами по математике вы уже знакомы. Это – “Применение функции для решения задач сельскохозяйственной практики”, “Геометрия на туристической тропе”, с которыми Юля успешно выступала на Всероссийских конкурсах. Сегодня она представляет работу совсем иного характера – “Письмо другу”, которое стало победителем Всероссийского конкурса “Лучший урок письма”.
“Письмо другу”
Здравствуй, дорогой друг!
Пишет тебе ученица Шимановской средней школы, Вяземского района, Смоленской области Иванова Юлия.
Очень хочу рассказать тебе о своей родной школе, об учителях, которые работают у нас, ведь я считаю их самыми лучшими учителями.
Школе нашей 44 года. Сейчас в ней 124 ученика, ее посещают и воспитанники приюта “Дом милосердия”, находящегося на территории нашего села. Мы очень дружны с этими детьми, которые лишены семейного тепла и домашнего уюта…
…Уже несколько лет в школе работает клуб Пифагор” - это добровольное объединение старшеклассников, увлекающихся математикой и имеющих способности к исследовательской и творческой деятельности. На заседаниях клуба рассматриваются вопросы применения математики в окружающем мире. Особенно мне понравились такие клубные занятия, как “Математика. Поэзия. Искусство”, “Применение производной в физике и технике”, “Симметрия в природе”.
На базе клуба работают и кружки “Юный программист” и “За страницами учебника математики”.
Руководит работой клуба “Пифагор” Заслуженный учитель России, учитель математики Харитонова Людмила Георгиевна.
Я тоже являюсь членом клуба “Пифагор”, и уже четыре года занимаюсь исследовательской работой. Наша школа с агротехнической направленностью, поэтому тема моей работы связана с сельским хозяйством: “Применение линейной функции, прямой и обратной пропорциональности при решении задач сельскохозяйственной практики”. В работе я предлагаю сельскохозяйственные задачи для учащихся 7-9классов. Их можно решать как на уроках математики, так и использовать как дополнительный материал к домашним заданиям. Данные в этих задачах взяты из справочников по сельскому хозяйству для средней полосы России. Для тех, кто живет в сельской местности, я считаю, очень важно уметь решать практические задачи, задачи сельскохозяйственной практики. Они помогают рационально и экономично вести хозяйство, основываясь на научные достижения.
Мне бы хотелось еще рассказать про свою любимую школу, про интересные мероприятия, которые проводятся у нас, про свой класс. Я продолжу свой рассказ в следующем письме.
Дорогой друг, напиши мне про свою школу, чем вы занимаетесь в свободное время, про своих учителей и одноклассников…
Педагог:
Занимаетесь ли вы исследовательской работой по предмету, поэзией или просто пишете письма другу другу – вы занимаетесь творчеством, Вы – готовите себя к жизни, ведь вам строить наше будущее, лучшее будущее. Удачи вам! И до новых встреч в нашем клубе.
xn--i1abbnckbmcl9fb.xn--p1ai
Золотое сечение в природе и искусстве
Автор: Седлинский Игорь Николаевич
Гимназия № 1 г. Апатиты, Мурманская обл.
Четвертая региональная научная и инженерная выставка «Будущее Севера»
Мурманск
2002 год
Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое- деление отрезка в среднем и крайнем отношении.
И. Кеплер
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Самым известным из всех иррациональных чисел, то есть чисел, десятичные разложения которых бесконечны и непериодичны, следует считать число p – отношение длины окружности к ее диаметру. Иррациональное число j («фи») известно не столь широко, но оно выражает фундаментальное отношение, имеющее почти такой же универсальный характер, как и число p. Сходство между числами p и j этим не исчерпывается: подобно p, j обладает свойством возникать в самых неожиданных местах .
Что такое золотая пропорция.
Пусть длина некоторого отрезка равна А (рис.1), длина его большей части равна Х, тогда (А – Х) – длина меньшей части отрезка. Пусть отношение всего отрезка к большей его части равно отношению большей части к меньшей. Составим отношение согласно допущению: . (1)
Такое деление отрезка и называется со времен древних греков делением отрезка в крайнем и среднем отношении.
От пропорции (1) перейдем к равенству A(A-X)=X2. Получаем квадратное уравнение . Длина отрезка X выражается положительным числом, поэтому из двух корней выбираем положительный: .
Число обозначается буквой j или буквой t («тау») в серьезной математике. Не менее важное значение имеет число, обратное j, которое обозначается Ф. Число j — единственное положительное число, которое обращается в обратное себе при прибавлении единицы.
=1/j
Обратим внимание на удивительную инвариантность золотой пропорции:
Такие значительные преобразования, как возведение в степень, не смогли уничтожить сущность этой уникальной пропорции, ее «душу». Следующие соотношения еще раз демонстрируют инвариантность золотой пропорции:
-2-
и т.д.
Подобно числу p, Ф можно представить в виде суммы бесконечного ряда многими способами. Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер Ф :
Ф =lim 1+
Ф = lim
С золотой пропорцией тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. В этом ряду каждое последующее число является суммой двух предыдущих чисел. Спустя четыре столетия после открытия Фибоначчи ряда чисел И.Кеплер установил, что отношение рядом стоящих чисел в пределе стремится к золотой пропорции Ф. Это свойство присуще не только числам Фибоначчи. Начав с любых двух чисел и построив аддитивный ряд, в котором каждый член равен сумме двух предыдущих (например, ряд 7, 2, 9, 11, 20, …), мы обнаружили, что отношение двух последовательных членов такого ряда также стремится к числу j: чем дальше мы будем продвигаться от начала ряда, тем лучше будет приближение.
В дальнейшем увидим, что числа Фибоначчи часто появляются в самых неожиданных местах, при этом неотступно сопровождая золотую пропорцию.
Золотые фигуры.
В геометрии существуют различные способы построения золотой пропорции, причем характерно, что для построения достаточно взять самые простые геометрические фигуры – квадрат или прямоугольный треугольник с соотношением катетов 1:2. Если с середины стороны квадрата провести окружность радиусом, равным диагонали полуквадрата, то на ее пересечении с продолженной стороной квадрата получим отрезок, который меньше стороны квадрата в соответствии с золотой пропорцией. Еще проще построение золотой пропорции в прямоугольном треугольнике 1:2:. Достаточно провести две дуги окружности, пересекающиеся в одной точке на гипотенузе (рис.2), и большой катет будет разделен в соответствии с золотой пропорцией.
Золотое сечение можно увидеть и в пентаграмме — так называли греки звездчатый многоугольник (рис.3). Он служит символом Пифагорейского союза – религиозной секты и научной школы по главе с Пифагором, которая проповедовала братскую любовь к друг другу, отречение от внешнего мира, общность имущества и т.д. На подобных устоях основывались очень многие секты. Но Пифагорийский союз отличало от других то, что пифагорейцы считали возможным добиться очищения духа при помощи математики. По их теории, в основу мирового порядка положены числа. Мир, считали они, состоит из противоположностей, а гармония приводит противоположности к единству. Гармония же заключается в числовых отношениях. Пифагорейцы приписывали числам различные свойства. Так, четные числа они называли женскими, нечетные (кроме 1) – мужскими. Число 5 – как сумма первого женского числа (2) и первого мужского (3) – считалось символом любви. Отсюда такое внимание к пентаграмме, имеющей 5 углов.
Благоговейное отношение к пентаграмме было характерно и для средневековых мистиков, которые многое заимствовали у пифагорейцев. В средние века считалось, что пентаграмма служит охранным знаком от сатаны. Вспомним, например, как описывает Гете проникновение дьявола Мефистофеля в келью доктора Фауста, на которой была начертана пентаграмма. Мефистофель сначала послал черного пуделя отгрызть кончик двери с частью пентаграммы. Только после этого он смог предстать перед Фаустом.
Интересно, что стороны пентаграммы, пресекаясь, образуют правильный пятиугольник, в котором пресечение диагоналей дает нам новую пентаграмму, а в пересечении ее сторон мы снова видим правильный пятиугольник, открывающий возможность построения новой пентаграммы. И так далее до бесконечности.
Пентаграмма представляет собой вместилище золотых пропорций. На рис.3 среди отрезков HJ, EH, EJ, EB отношение каждого последующего к предыдущему равно золотой пропорции. Пентаграмма также содержит золотые треугольники –остроугольные с углами ,,и тупоугольные с углами ,и .Из рис. 4 видно, что остроугольный треугольник АВС разбивается на три треугольника золотой пропорции. В них стороны равны:AD=1, DB=Ф,BC=AB=Ф+1=Ф2,AC=AE=Ф.
Интересен еще один замечательный треугольник, в котором проявляется золотая пропорция. В этом треугольнике углы равны, и , а их отношение составляет 5:3:2. В нем отношение большого катета к гипотенузе равно половине золотой пропорции Ф/2. Это отношение отвечает равенству Ф/2 = cos. Отсюда вытекает формула, связывающая золотую пропорцию с числом p:
Ф=.
Эта простая и по-своему красивая формула связывает число «пи» с золотой пропорцией. Не свидетельствует ли это о фундаментальности золотой пропорции, о ее родстве с таким универсальным числом, как «пи»? Характерно, что в рассмотренном треугольнике отношение углов отвечает отношению небольших целых чисел 5, 3 и 2, а отношения сторон несоизмеримы.
Множество «золотых» фигур дополняет золотой прямоугольник, отношение сторон которого равно числу Ф.
Золотой прямоугольник обладает многими необычными свойствами. Отрезав от него квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники (рис.5)
Тем самым будет построен пример совершенного квадрируемого прямоугольника бесконечного порядка. Точки, делящие стороны прямоугольников в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь. Полюс спирали лежит на пересечении пунктирных диагоналей (рис.6). Разумеется, «вращающиеся квадраты», как их принято называть, могут не только закручивать, но и раскручивать спираль. Для этого лишь требуется строить не уменьшающиеся, а все увеличивающиеся квадраты. Логарифмическая спираль – единственный тип спирали, не меняющей своей формы при увеличении размеров. Если в логарифмической спирали из центра О провести прямую, то образующиеся отрезки ОА, ОВ, ОС, ОD и т. д., полученные при пересечении прямой с витками спирали, образуют геометрическую прогрессию, то есть ОА/ОВ=ОВ/ОС=ОС/OD=…= m, где m – постоянное число.
Отрезки радиуса, заключенного между последовательными витками спирали, также образуют прогрессию с отношением АВ/ВС=ВС/СD=…=n. Частным случаем спирали является такая, которая отвечает значению n, равному Ф, т. е. золотой пропорции. Такая спираль называется «кривой гармонического возрастания».
Вездесущий филлотаксис.
Характерной чертой строения растений и их развития является спиральность. Еще Гете, который был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений, по спирали происходит рост ткани в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровнях.
Исследования показали, что движение протоплазмы в клетке часто спиральное. Рост клеток также может быть спиральным, как показал ученый Кастл. В жидкой среде клетки встречаются спиральные нити волокон – цитонем. И, наконец, носители информации – молекулы ДНК – также скручены в спираль. Следует отметить, что термин «спираль» не отражает точно строение молекул ДНК; более правильно говорить о винтовом расположении полипептидных цепей в этой молекуле. Во многих других случаях, рассмотренных в ботанике, речь также идет, по существу, не о спирали, а о винтовом расположении элементов структуры; к сожалению, термины часто смешивают.
Нет сомнений, что наследственная спиральность является одним из основных свойств организмов, она отражает один из существенных признаков живого. На первый взгляд кажется, что в кристаллах неорганических веществ спиральность или винтовая структура отсутствуют. Однако более глубокие исследования показали, что винтовое расположение атомов наблюдается и в некоторых кристаллах и выражается в образовании так называемых винтовых дислокаций. Такие кристаллы состоят из единственной винтообразной изогнутой атомной плоскости. При каждом обороте вокруг оси эта плоскость поднимается на один шаг винта, равный межатомному расстоянию. Следует добавить, что кристаллы с такой винтовой структурой обладают сверхпрочностью. От винтовой структуры молекул ДНК до закручивания усиков растений – таковы формы проявления спиральности на различных уровнях организации растений. Отчетливо проявляется эта особенность организации растений в закономерностях листорасположения.
Существует несколько способов листорасположения. В первом листья побега располагаются строго один под другим, образуя вертикальные ряды – ортостихи. Условная спираль, соединяющая места расположения листьев на побеге, называется генетической, или основной спиралью, точнее, винтовой линией и делится на ряд листовых циклов. Генетическим этот винт называется потому, что расположение листьев в нем отвечает порядку появления в нем листьев. Проекция на плоскость листорасположения позволяет в долях окружности выразить угол расхождения листьев.
Винтовое расположение листьев выражают дробью, числитель которой равен числу оборотов по стеблю воображаемого винта одного листового цикла, а знаменатель- числу листьев в данном цикле, совпадающему с числом ортостих на стебле. Эта дробь позволяет рассчитать и угол расхождения листьев.
Оказалось, что каждое растение характеризуется своим листорасположением. Так, у липы, вяза, бука, злаков листорасположение описывается формулой 1/2, у дуба и вишни – 2/5, у малины, груши, тополя, барбариса – 3/8, у миндаля, облепихи – 5/13 и т.д. Нетрудно видеть, что в формулах листорасположения встречаются числа Фибоначчи, расположенные через одно.
Посмотрим на сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно — по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13 или 13 и 21. Такие же спирали видны в поперечных разрезах почек; здесь числа спиралей относятся
как числа 3/5, 5/8, 8/13. В корзинках подсолнечника семена также расположены по
-5-
двум спиралям, их число составляет обычно 34 и 55, 55 и 89. Здесь вновь мы видим закономерное сочетание чисел Фибоначчи, расположенных рядом: 2/3, 3/5, 5/8, 13/21 и т.д. Их отношение в пределе стремится к числу j = 0,61803…
Рассмотренную закономерность расположения листьев, чешуек, семян называют филлотаксисом.
При изменении формулы листорасположения изменяется и угол расхождения листьев. Формула 1/2 характеризует двурядное расположение листьев под углом друг от друга. При формуле 1/3 угол между листьями будет , а при формуле 2/5 — и т.д. В предельном случае, когда отношение чисел в формуле будет отвечать золотой пропорции — 0,38196… угол расхождения листьев станет равным , который был назван «идеальным» углом, или углом золотой пропорции (=Ф2). Установлено, что при расположении листьев под идеальным углом ни один лист не будет располагаться точно над другим, чем создаются лучшие условия для фотосинтеза.
Загадки египетских пирамид.
Все на свете страшится времени. А время страшится пирамид.
Арабская пословица
О египетских пирамидах с восхищением писал греческий историк Геродот. Первым европейцем, спустившимся в глубь пирамиды, был римский ученый Плиний Старший. Согласно многим описаниям, эти гигантские монолиты имели совсем иной вид, чем в наше время. Они сияли на солнце белой глазурью отполированных известняковых плит на фоне многоколонных прилегающих храмов. Рядом с царскими пирамидами стояли малые пирамиды жен и членов семьи фараонов.
Среди грандиозных пирамид Египта особое место занимает великая пирамида фараона Хеопса. Она самая крупная и наиболее хорошо изученная. Чего только не находили в ее пропорциях! Число «пи» и золотую пропорцию, число дней в году, расстояние до Солнца, диаметр Земли и т.п. Однако при расчете этих величин получались неточности, возникали недоразумения, в результате чего подвергались сомнению даже простейшие пропорции в размерах пирамиды и все сообщения о скрытых в геометрии пирамиды математических сведениях объявлялись выдумкой.
Правильная четырехгранная пирамида является одной из хорошо изученных геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление вверх.
Очевидно, размеры пирамиды: площадь ее основания и высота — не были выбраны случайно, а должны нести какие-то геометрические, математические идеи, информацию об уровне знаний египетских жрецов. Причем следует напомнить, что эти знания составляли тайну и были доступны лишь ограниченному числу лиц, поэтому и в геометрии пирамиды они должны быть воплощены не в явной, а в скрытой форме.
Методической ошибкой многих исследователей является то, что они использовали размеры пирамид, выраженные в метрической системе мер. Но ведь египтяне пользовались другой системой мер! Из этой системы и следует исходить при анализе размерных отношений в пирамидах.
Прежде чем приступить к анализу формы и размеров пирамиды Хеопса, следует учесть уровень знаний тех времен, психологию создателей пирамиды. У египтян было три единицы длины: локоть (466 мм), равнявшийся семи ладоням (66,5 мм), которая, в свою очередь, равнялась четырем пальцам (16,6 мм).
Трудно допустить, что строители пирамиды пользовались исходными размерами, выраженными в долях локтя; более очевидно, что основные исходные размеры были определены в целых единицах длины – локтях.
Рассмотрим размеры пирамиды Хеопса (рис.7). Длина стороны основания пирамиды (L) принята равной 233,16 м. Эта величина отвечает почти точно 500 локтям. Очевидно, размер основания пирамиды при ее строительстве и был определен в 500 локтей.
Высота пирамиды (H) оценивается исследователями различно от 146,6 до 148,2 м. И в зависимости от принятой высоты пирамиды изменяются и все отношения ее геометрических элементов. Поэтому на этой величине следует остановиться особо. Одним из чудес великой пирамиды является очень точная подгонка ее каменных блоков и плит; между ними буквально нигде не просунешь лезвия бритвы (0,1 мм). Но никакого чуда здесь не оказалось. В процессе строительства каменные блоки не могли быть изготовлены столь точно: для этого у древних египтян просто не было средств – ни обрабатывающих, ни измерительных. Но за длительное время под воздействием колоссального давления (достигающего 500 тонн на 1 м2 нижней поверхности) произошла «усадка» конструкции, пластическая деформация строительных блоков, вследствие чего они и оказались так тесно подогнанными. В результате усадки высота пирамиды стала меньше, чем она была в период завершения строительства. Какой же она была первоначально? Ее можно воссоздать, если найти основную «геометрическую идею», положенную в основу сооружения.
Угол наклона граней пирамиды еще в 1837 году определил английский полковник Г.Вайз: он равен . Указанному значению угла отвечает тангенс, равный 1,272. Эта величина, отвечающая отношению высот пирамиды к половине ее основания, очень близка к корню квадратному из золотой пропорции = 1,27202 и является иррациональной величиной. Поэтому, скорее всего, в основу треугольника OMN пирамиды Хеопса и было заложено отношение OM/MN, равное .
Итак, примем отношение катетов, т.е. высоты пирамиды H к половине ее основания, равным 1,272. При этом высота пирамиды Хеопса будет равна точно 318 локтей, или 148,28 м. Такую высоту, очевидно, имела пирамида Хеопса при завершении ее сооружения ( или должна была иметь по проекту).
Таким образом, основные элементы конструкции пирамиды имели следующие размеры: сторона основания – 500 локтей, высота – 318 локтей. Отсюда следует, что апофема боковой грани ON равна 404,5 локтя.
А теперь посмотрим, какие интересные соотношения следуют из этих геометрических размеров. Отношения сторон в треугольнике OMN пирамиды равно: OM/MN=ON/OM=1,272=; ON/MN=Ф.
Рассмотрим теперь поверхность пирамиды. Она состоит из четырех треугольников и квадрата основания. Основание треугольника BOC равно 500 локтям, высота его равна 404,5 локтя. По теореме Пифагора можно рассчитать длину боковых ребер OB и OC. Они равны 475,5 локтя.
Площадь основания пирамиды равна 250000 кв. локтей, площадь боковой грани 101125 кв. локтей, а площадь четырех граней пирамиды равна 404500 кв. локтей. Отношение поверхности граней к площади основания также равно золотой пропорции.
Еще Геродот, основываясь на рассказах египетских жрецов, писал, что площадь квадрата, построенного на высоте пирамиды, равна площади каждой из его боковых граней. По нашим расчетам, квадрат высоты равен 3182 = 101127 кв. локтей, что почти точно отвечает площади боковой грани (101125 кв. локтей).
Многие исследователи указывают, что отношение удвоенной стороны основания 2L к высоте пирамиды H отвечает числу «пи». Однако в связи с тем, что высота пирамиды принималась равной современной и не всегда однозначной, число «пи» получалось разным: 3,16-3,18. На почве этого возникали сомнения, предпринимались различные подгонки, стали говорить даже о некоем «египетском p», равном 3,16. Если принять высоту пирамиды равной 318 локтям, то отношение 2L/H=1000/318 будет равно 3,144. Эта величина очень близка к современному значению числа «пи» (3,14159…).
Интересно сравнить два основных отношения, установленных нами при изучении геометрических пропорций пирамиды: 2H/L=и 2L/H=p. Отсюда получаем простую и красивую формулу, связывающую число «пи» и золотую пропорцию: 4/p=.
Гениальные создатели пирамиды Хеопса стремились поразить далеких потомков глубиной своих знаний, и они достигли этого. Следует лишь удивляться высокому знанию и искусству древних математиков и архитекторов Египта, которые смогли воплотить в пирамиде две иррациональные (т.е. неизмеримые) величины – p и Ф со столь поразительной точностью, оперируя исходными отношениями целых чисел – стороной основания и высотой пирамиды, выраженных в локтях.
Золотая пропорция в искусстве Древней Греции.
Великолепные памятники архитектуры оставили нам зодчие Древней Греции. И среди них первое место по праву принадлежит Парфенону.
Всю вторую половину V в. до н.э. на Акрополе шло строительство храмов, пропилей (преддверий), алтаря и статуи Афины Воительницы. В 447 году начались работы над храмом Афины – Парфеноном и продолжались до 434 года до н.э. Для создания гармонической композиции на холме его строители даже увеличили холм в южной части, соорудив для этого мощную насыпь.
Как указывает исследователь Г. И. Соколов, протяженность холма перед Парфеноном, длины храма Афины и участка Акрополя за Парфеноном относятся как отрезки золотой пропорции. При взгляде на Парфенон от места расположения пропилей отношения массива скалы и храма также соответствуют золотой пропорции. Таким образом, золотая пропорция была использована уже при создании композиции храмов на священном холме.
Размеры Парфенона хорошо изучены, но приводимые замеры не всегда однозначны. Следует учесть, о чем сказано ниже, что геометрия архитектуры храма очень непростая – в ней почти отсутствуют прямые линии, поэтому определение размеров затруднено. Известно, что фасад Парфенона вписан в прямоугольник со сторонами 1: 2, а план образует прямоугольник со сторонами 1 и . Известно, что диагональ прямоугольника 1:2 имеет размер , следовательно, прямоугольник фасада и является исходным в построении геометрии Парфенона.
Ширина Парфенона оценена в 100 греческих футов (3089 см), а размер высоты несколько варьирует у различных авторов. Так, по данным Н. Бруно, высота Парфенона 61,8, высота трех ступеней основания и колонны – 38,2, высота перекрытия и фронтона – 23,6 футов. Указанные размеры образуют ряд золотой пропорции: 100: 61,8 = 61,8: 38,2 = 38,2 :23,6 = Ф.
Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали и находили в соотношениях его частей золотую пропорцию. В работе В.Смоляка, посвященной изучению пропорций Парфенона, установлен закономерный ряд золотых пропорций. Приняв за единицу ширину торцового фасада храма, Смоляк получил прогрессию, состоящую из 8 членов ряда: 1: j: j2: j3: j4: j5: j6. Указанным членам ряда отвечают основные пропорции фасада Парфенона (рис.8).
В некоторых сооружениях древнего мира золотая пропорция выражена не в пропорциях формы зданий, а в деталях внутренней композиции, даже в числе мест для зрителей. Интересные данные приводит Э.Сороко. Построенный Поликлетом-младшим театр был рассчитан на 15 тысяч зрителей. Места для зрителей (театроп) имели 2 яруса: первый- 34 ряда мест, а второй – 21 ряд (числа Фибоначчи). Раствор угла, охватывающего пространство между театропом и скемой (пристройка для переодевания актеров и хранения реквизита), делит окружность основания амфитеатра в отношении : , что равно 1: 1,618…. Это соотношение углов реализовано практически во всех античных театрах. Театр Диониса в Афинах трехъярусный. Первый ярус имеет 13 секторов, второй – 21 сектор.
Древние скульпторы знали и использовали золотую пропорцию как критерий гармонии, канон красоты, корни которой лежат в пропорциях человеческого тела. “Человеческое тело – лучшая красота на земле”, — утверждал Н.Чернышевский. Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов: Фидия, Поликлета, Мирона, Праксителя. В создании своих творений греческие мастера использовали принцип золотой пропорции. Центр золотой пропорции строения человеческого тела располагался точно на месте пупка. И не случайно величину золотой пропорции принято обозначать буквой Ф; это сделано в честь Фидия – творца бессмертных скульптурных произведений.
Одним из высших достижений классического греческого искусства может служить статуя “Дорифор”, изваянная Поликлетом. Фигура юноши выражает единство прекрасного и доблестного, лежащих в основе греческих принципов искусства. Широкие плечи почти равны высоте туловища, высота головы восемь раз укладывается в высоте тела, а золотой пропорции отвечает положение пупка на теле атлета.
Но проанализируем другие пропорции знаменитой статуи. Расстояние от подошвы копьеносца до его колена равна j3, высота шеи вместе с головой — j4, длина шеи до уха — j5, а расстояние от уха до макушки — j6. Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9).
Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции.
Ритмы сердца и мозга.
Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает, а затем выталкивает кровь и гонит ее по телу. Предсердия выполняют роль резервуара, принимающего кровь из вен, а желудочки — насоса, ритмически перекачивающего кровь в артерии. Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке в момент его сжатия (систолы). В артериях во время систолы желудочков кровяное давление достигает максимальной величины, равной 115-125 мм рт.ст. у здорового молодого человека. В момент расслабления сердечной мышцы (диастолы) давление снижается до 70-80 мм рт.ст. Отношение максимального (систолического ) к минимальному (диастолическому) давлению равно в среднем 1,6, т.е. близко к золотой пропорции.
Сердце бьется непрерывно – от рождения человека до его смерти. Его работа должна быть оптимальной, обусловленной законами самоорганизации биологических систем. Отклонения от оптимального режима вызывают различные заболевания. А так как золотая пропорция является одним из критериев самоорганизации в живой природе, естественно предположить, что и в работе сердца возможно проявление этого критерия. Нужны были глубокие исследования, и они были проведены советским ученым В.Д.Цветковым.
При работе сердца возникает электрический ток, который можно уловить специальным прибором и получить кривую – электрокардиограмму (ЭКГ) с характерными зубцами, отражающими различные циклы работы сердца. На ЭКГ человека выделяются два участка различной длительности, соответствующие систолической и диастолической деятельности сердца. В.Цветков установил, что у человека и у других млекопитающих имеется оптимальная («золотая») частота сердцебиения, при которой длительности систолы, диастолы и полного сердечного цикла соотносятся между собой в пропорции 0,382: 0,618: 1, т.е. в полном соответствии с золотой пропорцией. Так, например, для человека эта частота равна 63 ударам в минуту, для собак – 94, что отвечает реальной частоте сердцебиения в состоянии покоя.
Далее В.Цветков обнаружил, что систолическое давление крови в аорте равно 0,382, а диастолическое – 0,618 от среднего давления крови в аорте. Доля объема левого желудочка при ударном выбросе крови по отношению к конечнодиастолическому объему у десяти видов млекопитающих в состоянии покоя составляет 0,37-0,4, что в среднем также отвечает золотой пропорции. Таким образом, работа сердца в отношении временных циклов, изменения давления крови и объемов желудочков оптимизировано по одному и тому же принципу – по правилу золотой пропорции.
Мозг человека представляет собой сложнейшую самонастраивающуюся систему, основным назначение которой является регуляция деятельности различных органов человеческого тела, осуществление связи человека с окружающей средой. В составе мозга различают серое и белое вещества. Серое вещество представляет собой скопление нервных клеток, белое – нервных волокон, отростков этих клеток. Нервная клетка с отростком называется нейроном. Нейроны мозга образуют разнообразные сети, взаимодействующие с помощью электрических сигналов.
Конфигурации нейронных сетей представляют собой колебательные электрические цепи. Различным состояниям мозга соответствуют электрические колебания с разными частотами.
Многочисленные исследования показали, что в мозгу взрослого человека при различных его состояниях преобладают электрические колебания определенных частот. Изменение активации мозга происходит не непрерывно, а только дискретно, скачками от одного уровня к другому. Каждому состоянию мозга соответствуют свои специфические волны электрических колебаний.
Состоянию спокойного бодрствования отвечает наиболее устойчивый a- ритм с частотами колебаний преимущественно от 8 до 13 герц. Это основной ритм электрических колебаний мозга, он появляется в детском возрасте и постепенно с возрастом увеличивается с 2-3 до 8-13 гц в возрасте 8-16 лет. Наиболее медленные колебания с частотой 0,5 –4 гц у D- ритма, характерно для состояния глубокого сна. Для D- ритма верхняя граничная частота достаточно стабильна и равна 3-4 гц, а пределы нижней граничной частоты изменяются от 0,2 до 1,5 гц.
При появлении неприятности или опасности в мозгу доминирует q — ритм с частотами от 4-7 до 6-8 (по данным различных авторов). Советские ученые-братья Я.и А. Соколовы считают, что наиболее устойчивы для q- ритма граничные частоты колебаний 4 — 7 гц. Умственной работе отвечает b- ритм с граничными частотами 14-35гц. (по другим данным, диапазон частот этого ритма более широк – от 14 до 100гц). Эмоциональному возбуждению мозга соответствует g- ритм с граничными частотами 35-55 гц. Нетрудно заметить, что граничные частоты ритмов почти точно отвечают числам Фибоначчи. Отклонения граничных частот от чисел Фибоначчи находятся в пределах точности эксперимента. Соколовы считают, что существуют еще не обнаруженные опытами r- ритм и s- ритм. Расчеты показали, что у s- ритма пограничные частоты 118 и 225 гц, а у r- ритма — 55 и 118 гц. И здесь очевидна близость чисел Фибоначчи.
Исследования в этой области только начинаются, впереди — открытие самых сокровенных тайн организации и работы мозга человека, закономерности его эволюции.
Алгебра музыки.
В композиции многих музыкальных произведений отмечается наличие некоторого «кульминационного взлета», высшей точки, причем такое построение характерно не только для произведения в целом, но и для его отдельных частей. Такая высшая точка крайне редко расположена в центре произведения или его композиционной части, обычно она смещена, асимметрична. Изучая восьмитактные мелодии Бетховена, Шопена, Скрябина, советский музыковед Л.Мазель установил, что во многих из них вершина, или высшая точка, приходится на сильную долю шестого такта или на последнюю мелкую долю пятого такта, т.е. находится в точке золотого сечения. По мнению Л.Мазеля, число подобных восьмитактов, где подъем мелодии занимает пять тактов, а последующий спуск – три, необычайно велико. Их можно без труда найти почти у каждого автора, сочинявшего музыку в гармоническом стиле.
Очевидно, такое расположение кульминационных моментов музыкальной мелодии является важным элементом ее гармонической композиции, придающим художественную выразительность и эстетическую эмоциональность мелодии.
Характерно, что в некоторых случаях авторы музыкальных произведений смещали их вершину от точки золотого сечения, что придавало мелодиям неустойчивый характер. По мнению Л.Мазеля, это входило в намерения авторов, например, при сочинении скерцо, рондообразных финалов.
Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято Л.Сабанеевым. Им было изучено две тысячи произведений различных композиторов. По его мнению, временное протяжение музыкального произведения делится «некоторыми вехами», которые выделяются при восприятии музыки и облегчают созерцание формы целого. Все эти музыкальные вехи делят целое на части, как правило, по закону золотого сечения.
По наблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. Количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Наиболее детально были изучены все 27 этюдов Шопена. В них обнаружено 154 золотых сечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаях строение музыкального произведения сочетало в себе симметричность и золотое сечение одновременно; в этих случаях оно делилось на несколько симметричных частей, в каждой из которых проявляется золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а внутри каждой из них наблюдаются проявления золотой пропорции.
Характерно, что наиболее часто золотое сечение обнаруживается в произведениях высокохудожественных, принадлежащих гениальным авторам. Может быть, частота проявлений золотой пропорции является одним из объективных критериев оценки гениальности музыкальных произведений и их авторов?
Итак, можно признать, что золотая пропорция является критерием гармонии композиции музыкального произведения.
Музыка стихов.
Многое в структуре произведений поэзии роднит этот вид искусства с музыкой. Каждый стих обладает своей музыкальной формой – своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся некоторые черты музыкальных композиций, закономерности музыкальной гармонии, а следовательно, и золотая пропорция, и числа Фибоначчи.
Исследования поэтических произведений с этих позиций только начинаются. И начинать нужно с поэзии А.С.Пушкина. Ведь его произведения — образец наиболее выдающихся творений русской культуры, образец высочайшего уровня гармонии. С поэзии А.С.Пушкина мы и начнем поиски золотой пропорции – мерила гармонии и красоты.
Для анализа метрики стихотворений А.С.Пушкина рассмотрены его произведения периода 1829-1836 г.г., периода создания наиболее совершенных стихов. Сюда вошло 109 стихов. Число строк в стихотворениях этого периода изменялось от 4 до 116. Однако большие стихотворные формы встречаются редко; число стихотворений с количеством строк более 60 составило всего 9 штук. Средний размер этих стихотворений составил 88 строк.
Казалось бы, величина стихотворения, определяемая числом строк, может изменяться произвольно и непрерывно от самой малой в четыре строки до самых больших. Однако оказалось, что это не так. Размеры стихов распределены совсем не равномерно; выделяются предпочтительные и редко встречающиеся размеры. На графике распределения стихотворений А.С.Пушкина по числу строк в них отчетливо выделяется несколько максимумов — наиболее встречающихся размеров (рис.10). Они явно тяготеют к числам 5, 8, 13, 21, 34. Проявляется вполне закономерная тенденция в творческой манере поэта – он явно предпочитает стихотворения, размер которых близок к числам ряда Фибоначчи.
Только ли стихотворения А.С. Пушкина тяготеют в своих размерах к числам Фибоначчи?
Конечно, нет. И у других поэтов проявляется тяготение размера стихов к 8,13,21 строчкам, но ни у одного из русских поэтов эта тенденция не выражена так отчетливо, как у А.С.Пушкина. Стихотворения В.Брюсова отличаются совершенством своих форм. И неудивительно, что в их размерности также проявляются числа Фибоначчи. Было проанализировано 360 стихотворений поэта из его двухтомника; эти стихи охватывали период от 1882 до 1912 года. Только в трех стихотворениях число строк составило 70, 85, 90 (что в среднем близко к числу Фибоначчи 89). Остальные стихотворения содержали значительно меньше строк – от 8 до 36 и крайне редко несколько больше.
Среди рассмотренных стихотворений В.Брюсова явно преобладают те, в которых число строчек равно или близко к числам Фибоначчи. Они распределены следующим образом:
стихотворения с числом строк 8 25 шт. 7%
— * — 131 77 шт. 21,5% — * — 211 70 шт. 19,6% — * — 342 36 шт. 10,0%
Общее число этих стихотворений составило 208 шт. или 58%. К остальным относятся стихотворения с числом строчек 10, 14, 16, 18, 24, 26, 28, 31, 32 и т.д. Поэт явно предпочитал стихотворения с числом строк 8, 131, 211 как наиболее оптимальные для выражения мыслей и чувств.
Обратимся вновь к произведениям А.С.Пушкина. Рассмотрим композицию «Пиковой дамы». В этой повести кульминационным моментом является сцена в спальне графини, куда проник Германн в надежде узнать тайну трех карт, сцена, которая оканчивается смертью графини в повести 853 строки. Кульминационный момент повести – это смерть графини. Ему отвечает 535 –я строка. Эта строка расположена в повести почти точно в месте золотого сечения, т.к. 853:535=1,6 .
Повесть «Пиковая дама» состоит из шести глав. Посмотрим, не проявляется ли в композиции глав золотая пропорция? В первой главе золотому сечению отвечает 68 строчка (всего в главе 110 строк). Но ведь это же узловая точка повествования, в ней переломный момент всей главы: откроет ли Сен — Жермен свою тайну графине!
Вторая глава повести содержит 219 строк. Золотое сечение здесь приходится на 135 строку. Но ведь это кульминационный момент главы, Лиза увидела в окне стоящего на улице Германна! Отсюда начался для нее новый отсчет времени, начались события, определившие всю ее дальнейшую судьбу. А.С.Пушкин совершенно точно определил это место во второй главе: ведь 219:135 = 1,62.
Третья глава повести описывает усилия Германна попасть в дом старой графини, выведать у нее тайну трех карт. Это место начинает новый отсчет времени для Германна. Эта ситуация приходится на 131 строку третьей главы, а всего в ней 212 строк. Разделив 212 на 131, мы получим точно золотую пропорцию 1,618!
В четвертой главе размером 113 строк золотая пропорция приходится на 70 строку. Это также переломный, трагический момент в жизни Лизы.
В пятой главе описано посещение Германна похорон графини. 46 строка пятой главы разделила повествование на две части: первая — похороны графини и вторая – сон Германна. Эта 46 строка также отвечает золотой пропорции, ведь всего в этой главе 75 строк (75:46=1,63).
В последней главе повести золотая пропорция приходится на 77 строчку, которая завершает описание первого дня игры Германна в карты и первого его выигрыша. Как видим, и в композиции последней главы повести присутствует золотая пропорция.
Золотая пропорция присутствует и в композиции других произведений Пушкина. В рассказе «Станционный смотритель» 377 строк. Кульминационный момент рассказа – это известие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строкой. Здесь почти точное соответствие золотой пропорции.
В маленьком рассказе «Гробовщик» всего 229 строк. Со 139 строки начинается описание страшного сна гробовщика. И здесь переломный момент рассказа приходится почти точно на золотую пропорцию (229:1,618=141 строка).
Совпадение кульминационных моментов в произведениях А.С.Пушкина с золотой пропорцией удивительно близкое, в пределах 1-3 строк. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.
Заключение.
Рациональные и иррациональные числа являются своеобразными противоположностями. Но природа едина, и ее противоположности не только находятся в противодействии, борьбе, но и в единстве. И не удивительно, что многие иррациональные числа выражаются через совокупность целых чисел. Все три числа:p, e и Ф – связаны между собой простыми отношениями и могут быть выражены в виде пределов бесконечных дробей. Кроме того, на примере золотой пропорции показано, что целые числа натурального ряда: 1, 2, 3, … могут быть выражены через иррациональное число Ф. Кроме того, число Ф с любой степенью точности может быть выражено через отношение целых чисел. Разве эти примеры не свидетельствуют о единстве рационального и иррационального в природе?!
Мы так часто говорим о единстве и борьбе противоположностей, что это понятие стало тривиальным, само собой разумеющимся и не требующим исследования. Может быть, поэтому этот фундаментальный закон природы так мало исследован и углублен и, что характерно, почти совершенно не математизирован. А между тем он достоин самого пристального изучения и развития – ведь это один из основных, наиболее общих законов мироздания.
Список литературы
Н. Васютинский “Золотая пропорция” –М.,”Молодая гвардия”, 1990
А. Азевич “Двадцать уроков гармонии” –М., “Школа-Пресс”, 1998
М. Гарднер “Математические головоломки и развлечения” –М., “Мир”, 1971
Д. Пидоу “Геометрия и искусство” – М., “Мир”, 1989
Энциклопедический словарь юного математика –М.,1989
Журнал “Квант”, 1973, № 8
Журнал “Математика в школе”, 1994, № 2, № 3
www.ronl.ru
Реферат выполнил Филитов Василий Сергеевич
Московский Государственный Институт Управления Правительства Москвы
Кафедра Математики
Москва
2003 год
Абстрагирование как мыслительный процесс
Для более или менее подробного обсуждения предмета математики необходимо предварительно выяснить генезис и особенности ее важнейших исходных понятий, т.к. математика отличается от других наук, прежде всего, используемыми ею абстракциями. Стержневым вопросом философских проблем математики является отношение ее понятий к реальности, вопрос об объективном содержании математического знания. Чтобы лучше понять характер этих взаимоотношений, необходимо рассмотреть ключевой вопрос – процесс образования математических абстракций.
Процесс абстрагирования есть существенный и необходимый прием познания окружающей нас действительности. Если на чувственной ступени познания человек с помощью ощущений отображает явления природы, то путем мышления (в обобщенной форме и опосредованно) он проникает в сущность этих явлений. Однако было бы ошибкой полагать, что здесь происходит просто логическая переработка чувственных данных, что в мышлении нет ничего, чего не было бы в ощущениях.
Процесс абстрагирования и вытекающий из него процесс анализа являет собой отвлечение от несущественных сторон изучаемого объекта, выделение и рассмотрение только существенных свойств. Цель абстрагирования – получение более глубокого и «чистого» знания об объекте, чем на чувственной ступени познания. Таким образом, процесс абстрагирования завершается образованием исходных абстракций, однако они являют собой нечто неконкретное и одностороннее, поэтому для получения более глубоких и правильных знаний об изучаемом объекте, необходимо учитывать и вторую, чувственную ступень познания. Необходимо провести движение теперь уже от общего к частному путем синтеза.
Путем созерцания возможно познать лишь внешнюю сторону предмета, в то время как абстрагирование позволяет познать его сущность. Это объясняет то, почему современная математика зачастую способна глубже и адекватнее описать сложные процессы действительности, хотя по мере своего развития ее понятия имеют все меньше сходства с реальными явлениями окружающего нас мира, утрачивают свою наглядность.
Таковы характерные черты и возможности приема абстрагирования в его органическом единстве с методами восхождения от абстрактного к конкретному, анализа и синтеза. Но в чем же заключается своеобразие математических абстракций?
Специфика математических абстракций
Как уже отмечалось, процесс абстрагирования в обычных науках заключается в мысленном отвлечении от несуществующих сторон изучаемого предмета. Однако в математике все оказывается более сложным. Имеются ли такие исходные понятия, которые отображали бы реально существующие свойства и стороны предмета, явления, процесса? Подавляющее большинство ученых дает на этот вопрос отрицательный ответ.
И вот почему. Возьмем, к примеру, такую область математики, как геометрию. В материальной действительности мы, строго говоря, не найдем квадрата, треугольника, прямой линии и тому подобных объектов. Иначе говоря, формирование этих объектов нельзя понимать как результат выделения человеком каких-то математических свойств в явлениях внешнего мира. Они – результат творческого воображения, логического конструирования, идеализации.
Среди ученых бытуют противоположные взгляды, в частности, утверждение о том, что математические свойства и фигуры есть не что иное, как плод чистой фантазии, который ничего общего не имеет с объективной реальностью. Голландский ученый А. Гейтинг писал, что математика «не выражает истину о внешнем мире, а связана исключительно с умственными построениями». Это утверждение ставит исследователя на ошибочные позиции наивного реализма, идеализма, априоризма и конвенционализма. А Энгельс писал: «Понятия и фигуры взяты не откуда-нибудь, а из действительного мира. Десять пальцев, на которых люди научились считать, т.е. производить первую арифметическую операцию, представляют собой все, что угодно, только не продукт свободного творчества разума». Позже он дополнил свою мысль: «мы доходим до продуктов свободного творчества и воображения самого разума», т.е. до таких понятий, связь которых с окружающим миром непосредственно не просматривается.
Как же исторически и логически происходил процесс образования исходных понятий натурального числа в арифметике и фигуры в геометрии?
Как показывают исследователи древней культуры, в ранний период развития общества люди не имели понятия числа, хотя своеобразный счет ими, конечно, осуществлялся: скажем, величину стада овец они выражали с помощью пальцев рук. Со временем количество объектов стали определять путем отождествления их совокупности с равночисленным множеством других предметов. Например, одна из гипотез об изготовлении гигантских статуй на острове Пасхи звучит так: туземцы вытесывали туловища из серого камня и «парики» из красного в разных каньонах и, не умея считать, они были вынуждены употреблять камешки, сопоставляя их сначала с телами, а потом с головами.
Как мы видим, первоначально человек не отделял количество вещей от них самих, используя так называемые «именованные числа» — две руки, три пальца т т.п. Человек не абстрагировал понятие числа от понятия вещи. Этому он научился значительно позже. Человек начал пользоваться рядом натуральных, порядковых и количественных чисел.
Абстракция отождествления и понятие числа
Это был гигантский скачок в совершенствовании представлений человека о мире, как писал Д. Гильберт. При этом в сложном процессе становления понятия натурального числа первостепенное значение имела фундаментальная для науки абстракция отождествления. Кстати, использование ее далеко не ограничивается областью математики, как писала С.А. Янковская. Существенно, что выявление тождества не только не исключает, но, наоборот, предполагает различия между сопоставляемыми объектами. Без единства этих противоположностей сравнение как таковое теряет всякий смысл.
Эта абстракция использовалась Карлом Марксом в научной теории стоимости.
Итак, практические потребности в счете и измерениях, связанные с развитием общественного производства и совершенствованием экономики, явились причиной такого революционного акта, как возникновение понятия натурального числа, что, в свою очередь, послужило исторически исходным пунктом дальнейшего развития математики. А поскольку решающую роль сыграла абстракция отождествления, то логическое определение понятия числа осуществляется с обязательным ее использованием.
По мнению известного ученого Г.Фрёге, число есть не что иное, как общее свойство класса эквивалентных множеств – совокупностей предметов независимо от их качественной определенности и природы. Важно, что сравниваемые множества обладали изоморфизмом, когда каждому члену одного соответствует единственный член другого.
Наряду с использованием абстракции отождествления, в период зарождения математического знания применялась операция сравнения, которая допускает оценку в суждениях типа «больше», «меньше», «равно». В дальнейшем большую роль сыграла также операция косвенного измерения, когда фокус человеческого внимания смещался в сторону отношений между числами, в которых отражались реальные взаимосвязи между объектами, что свидетельствовало о возрастании активности познающего субъекта. Благодаря косвенному измерению возникли три другие простейшие арифметические операции – вычитание, умножение и деление. В.Вундт писал, что без косвенного измерения величин «никогда бы не развилось математическое мышление».
Понятие фигуры
Метод соотнесенности, который выявляет схожие черты в сравниваемых предметах, лежит в основе формирования понятия фигуры, поскольку при этом используется принцип подобия, выражающий важнейшее общее свойство различных геометрических тел. Понятие фигуры, в отличие от понятия числа, складывалось без его точного прообраза в действительности, поэтому человек вынужден был пользоваться не только абстракцией отождествления, но и приемом идеализации в чистом виде.
Сущность данного приема заключается в образовании таких абстракций, которые отражают не только реально существующие свойства объекта, а, как писал Н.А. Шанин, значительно отклоняющиеся или даже воображаемые. Как уже отмечалось, в природе не существует линий, точек, правильных треугольников, квадратов и других геометрических фигур. Но, тем не менее, без этих исходных, первоначальных понятий в математике не обойтись. И ученые вынуждены были логически конструировать такие объекты, имея лишь в какой-то мере сходную внешнюю форму предметов в окружающей нас действительности. Для примера лучше всего взять астрономию. Земля и другие планеты Солнечной системы, включай само Солнце, человеку давно представлялись в виде шара, но мы сегодня хорошо знаем, что это не совсем верные, а точнее – совершенно неверные представления. Так, наша планета как бы сплюснута в районе полюсов и поэтому является эллипсоидом вращения. Кроме того, на ней присутствуют неровности.
Исходные первоначальные понятия арифметики и геометрии не могут быть определены классическим способом (т.е. подведены под более широкое родовое понятие с указанием на видовое отличие), потому что не существует более широких фундаментальных категорий математического характера. По этой причине определения точки, прямой и других исходных понятий даны Евклидом на интуитивном уровне и при дальнейшем доказательстве теорем фактически не использовались. Геометрическая точка (по Евклиду) это то, что не имеет частей; у линии нет толщины, она является следом движущейся точки; плоскость – результат движения прямой линии и т.д. Впрочем, и значительно позже многие ученые вынуждены были давать определение исходных математических понятий на интуитивном уровне.
Количество и качество в математике
Итак, объекты действительности представляют собой единство дискретного и непрерывного (недизъюнктивность). Если в натуральном числе фиксируется дискретность и в связи с этим устойчивость внешней стороны явлений действительности, то в понятии фигуры – непрерывность и тоже устойчивость.
Примечательно, что натуральные числа и фигуры оказываются сходными с чувственными образами в том отношении, что в данных понятиях отображается внешняя сторона предметов действительности. Именно это имел в виду Платон, когда сближал математические абстракции с чувственностью. Но он не учитывал, что отмеченный феномен касается лишь исходных понятий математики.
Абстракции математики многоступенчаты, имеют разную степень общности. На первых этапах ее развития в понятии числа отвлекались от качественных особенностей реальных объектов, позже – от конкретных чисел и величин в результате создания алгебры и введения буквенной символики. Наконец, на современном этапе отвлекаются даже от конкретного содержания зависимостей, так что, например, обычные арифметические действия (сложение, вычитание, умножение и деление), осуществляемые с абстрактными объектами математических структур, предстают уже в виде абстрактных операций.
Абстракции современной математики в значительной степени отличаются от исходных понятий. Они выражают не только количественную сторону реальных процессов объективной действительности. В противном случае трудно объяснить удивительную, непостижимую «эффективность математики в естествознании», как писал Ю. Вигнер, т.е. тот факт, что ее нынешние модели зачастую описывают довольно неплохо сложные процессы материальной действительности.
Кстати, позиция сторонников количественной концепции, т.е. тех, кто предполагает, что математика исследует лишь количественную сторону процессов действительности и убеждены в том, что определения количества (и качества, соответственно) в математике должны быть отличны от философских, выглядит искусственной, неправомерной. Понятие количества и качества должны быть одинаковы для всех наук.
Количество – это и внешнее, и внутреннее, и различное в сходных по качеству объектах, и, вместе с тем, сходное в различных по своему качеству вещах. Это такая определенность предметов, явлений, которая характеризует их величину, форму, интенсивность свойств, темпы развития и т.п.
Попытки в прошлом дать два понятия материи (философское и естественнонаучное) были признаны ошибочными.
Математика в какой-то мере описывает и качественную сторону явлений материальной действительности (правда, частично, косвенно, опосредованно и своеобразно, с помощью особого искусственного языка), тем более, что существует неразрывная связь количества и качества.
Уже исходные категории математики количественную сторону явлений действительности отображают дизъюнктивно и в этом смысле неадекватно, огрублено. В дальнейшем используются понятия более высоких уровней общности (абстракции от абстракций), зачастую не имеющие никакого референта в окружающем мире (например, любой тройке действительных чисел соответствует точка в реальном пространстве трех измерений, а для четверки, пятерки и т.п. чисел адекватны уже так называемые многомерные, параметрические пространства). Тем не менее, современная математика точнее, полнее описывает реальные явления, чем раньше. Это происходит, очевидно, благодаря потенциальным возможностям аксиоматического метода и способностям развитой математики выражать в какой-то мере и качественную сторону процесса действительности. При этом количество не сводится к величинам или выражающим их числам, как это было до второй половины XIX в.
Заключение
Рассматриваемые абстракции обладают спецификой. Их характерной особенностью является следующее: отвлечение исходных категорий от качественной стороны объектов действительности, наличие элементов идеализации, значительная относительная самостоятельность этих понятий, ведущая к необходимости создания «идеальных элементов», не имеющих прообраза в объективном мире (например, квадратный корень из -1), иерархия математических абстракций.
Важное в методологическом отношении обстоятельство – исходные понятия фиксируют момент устойчивости явлений окружающего мира, которые на самом деле представляют собой, как известно, единство устойчивости и изменяемости, так что каждый объект есть и результат, и процесс, и то и не то, движущееся тело и находится в данном месте, и вместе с тем его там нет. Если натуральное число можно рассматривать как инвариант класса эквивалентных множеств, то фигуру – как инвариант внешней формы подобных тел.
Итак, в исходных понятиях элементарной математики отображаются либо дискретность и устойчивость внешней количественной стороны явлений действительности, либо (в случае понятия фигуры) непрерывность и опять-таки устойчивость внешней природы предметов материального мира.
И в заключение привожу определение математики с точки зрения рассматриваемой темы. Математика – своеобразный, формальный способ теоретического описания действительности, область знания, имеющая особый статус в системе наук; с ее помощью можно, в принципе, описать любой процесс объективной действительности. Для математики более характерен метод, чем предмет, в качестве же своих объектов она рассматривает пространственные формы и количественные отношения действительности, точнее, идеализированные объекты, начиная с натурального числа и фигуры и кончая своеобразными структурами.
Список литературы
Жуков «Специфика математических абстракций», Минск, 1986.
Бурбаки Н. «Очерки по истории математики», Москва, изд. Наука, 1963.
Энциклопедия юного математика
www.ronl.ru
Автор: Седлинский Игорь Николаевич
Гимназия № 1 г. Апатиты, Мурманская обл.
Четвертаярегиональная научная и инженерная выставка «Будущее Севера»
Мурманск
2002 год
Геометриявладеет двумя сокровищами: одно из них – теорема Пифагора, другое- делениеотрезка в среднем и крайнем отношении.
И.Кеплер
Человекразличает окружающие его предметы по форме. Интерес к форме какого-либопредмета может быть продиктован жизненной необходимостью, а может быть вызванкрасотой формы. Форма, в основе построения которой лежат сочетание симметрии изолотого сечения, способствует наилучшему зрительному восприятию и появлениюощущения красоты и гармонии. Целое всегда состоит из частей, части разнойвеличины находятся в определенном отношении друг к другу и к целому. Принципзолотого сечения – высшее проявление структурного и функциональногосовершенства целого и его частей в искусстве, науке, технике и природе.
Самымизвестным из всех иррациональных чисел, то есть чисел, десятичные разложениякоторых бесконечны и непериодичны, следует считать число p – отношение длины окружности к еедиаметру. Иррациональное число j («фи»)известно не столь широко, но оно выражает фундаментальное отношение, имеющеепочти такой же универсальный характер, как и число p. Сходство между числами p и j этим не исчерпывается: подобно p, j обладаетсвойством возникать в самых неожиданных местах .
Что такое золотая пропорция.
Пустьдлина некоторого отрезка равна А (рис.1), длина его большей части равна Х,тогда (А – Х) – длина меньшей части отрезка. Пусть отношение всего отрезка кбольшей его части равно отношению большей части к меньшей. Составим отношениесогласно допущению: />. (1)
Такоеделение отрезка и называется со времен древних греков делением отрезка вкрайнем и среднем отношении.
Отпропорции (1) перейдем к равенству A(A-X)=X2. Получаем квадратное уравнение />. Длина отрезка X выражается положительным числом, поэтому из двух корнейвыбираем положительный: />.
Число/> обозначаетсябуквой j или буквой t («тау») в серьезной математике. Не менее важное значение имеетчисло, обратное j, котороеобозначается Ф. Число j — единственноеположительное число, которое обращается в обратное себе при прибавленииединицы.
/>=1/j
Обратимвнимание на удивительную инвариантность золотой пропорции:
/>
Такиезначительные преобразования, как возведение в степень, не смогли уничтожитьсущность этой уникальной пропорции, ее «душу». Следующие соотношения еще раздемонстрируют инвариантность золотой пропорции:
/>
/>
-2-
/>
/> и т.д.
Подобночислу p, Ф можнопредставить в виде суммы бесконечного ряда многими способами. Предельная простотаследующих двух примеров еще раз подчеркивает фундаментальный характер Ф :
Ф =lim 1+/>/>
Ф = lim />
С золотойпропорцией тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. Вэтом ряду каждое последующее число является суммой двух предыдущих чисел.Спустя четыре столетия после открытия Фибоначчи ряда чисел И.Кеплер установил,что отношение рядом стоящих чисел в пределе стремится к золотой пропорции Ф.Это свойство присуще не только числам Фибоначчи. Начав с любых двух чисел ипостроив аддитивный ряд, в котором каждый член равен сумме двух предыдущих(например, ряд 7, 2, 9, 11, 20, …), мы обнаружили, что отношение двухпоследовательных членов такого ряда также стремится к числу j: чем дальше мы будем продвигаться отначала ряда, тем лучше будет приближение.
Вдальнейшем увидим, что числа Фибоначчи часто появляются в самых неожиданныхместах, при этом неотступно сопровождая золотую пропорцию.
Золотые фигуры.
Вгеометрии существуют различные способы построения золотой пропорции, причемхарактерно, что для построения достаточно взять самые простые геометрическиефигуры – квадрат или прямоугольный треугольник с соотношением катетов 1:2. Еслис середины стороны квадрата провести окружность радиусом, равным диагонали полуквадрата, то на ее пересечении с продолженной стороной квадрата получимотрезок, который меньше стороны квадрата в соответствии с золотой пропорцией.Еще проще построение золотой пропорции в прямоугольном треугольнике 1:2:/>. Достаточнопровести две дуги окружности, пересекающиеся в одной точке на гипотенузе(рис.2), и большой катет будет разделен в соответствии с золотой пропорцией.
Золотоесечение можно увидеть и в пентаграмме — так называли греки звездчатыймногоугольник (рис.3). Он служит символом Пифагорейского союза – религиознойсекты и научной школы по главе с Пифагором, которая проповедовала братскуюлюбовь к друг другу, отречение от внешнего мира, общность имущества и т.д. Наподобных устоях основывались очень многие секты. Но Пифагорийский союз отличалоот других то, что пифагорейцы считали возможным добиться очищения духа припомощи математики. По их теории, в основу мирового порядка положены числа. Мир,считали они, состоит из противоположностей, а гармония приводитпротивоположности к единству. Гармония же заключается в числовых отношениях.Пифагорейцы приписывали числам различные свойства. Так, четные числа ониназывали женскими, нечетные (кроме 1) – мужскими. Число 5 – как сумма первого женскогочисла (2) и первого мужского (3) – считалось символом любви. Отсюда такоевнимание к пентаграмме, имеющей 5 углов.
Благоговейноеотношение к пентаграмме было характерно и для средневековых мистиков, которыемногое заимствовали у пифагорейцев. В средние века считалось, что пентаграммаслужит охранным знаком от сатаны. Вспомним, например, как описывает Гетепроникновение дьявола Мефистофеля в келью доктора Фауста, на которой быланачертана пентаграмма. Мефистофель сначала послал черного пуделя отгрызтькончик двери с частью пентаграммы. Только после этого он смог предстать передФаустом.
Интересно,что стороны пентаграммы, пресекаясь, образуют правильный пятиугольник, вкотором пресечение диагоналей дает нам новую пентаграмму, а в пересечении ее сторонмы снова видим правильный пятиугольник, открывающий возможность построенияновой пентаграммы. И так далее до бесконечности.
Пентаграммапредставляет собой вместилище золотых пропорций. На рис.3 среди отрезков HJ, EH, EJ, EB отношение каждого последующего к предыдущему равно золотойпропорции. Пентаграмма также содержит золотые треугольники–остроугольные с углами />,/>,/>и тупоугольные с углами />,/>и />.Из рис. 4 видно, что остроугольный треугольник АВС разбивается натри треугольника золотой пропорции. В них стороны равны:AD=1, DB=Ф,BC=AB=Ф+1=Ф2,AC=AE=Ф.
Интересенеще один замечательный треугольник, в котором проявляется золотая пропорция. Вэтом треугольнике углы равны/>, /> и />, а их отношение составляет 5:3:2.В нем отношение большого катета к гипотенузе равно половине золотой пропорцииФ/2. Это отношение отвечает равенству Ф/2 = cos />/>.Отсюда вытекает формула, связывающая золотую пропорцию с числом p:
Ф=/>.
Этапростая и по-своему красивая формула связывает число «пи» с золотой пропорцией.Не свидетельствует ли это о фундаментальности золотой пропорции, о ее родстве стаким универсальным числом, как «пи»? Характерно, что в рассмотренномтреугольнике отношение углов отвечает отношению небольших целых чисел 5, 3 и2, а отношения сторон несоизмеримы.
Множество«золотых» фигур дополняет золотой прямоугольник, отношение сторон которогоравно числу Ф.
Золотойпрямоугольник обладает многими необычными свойствами. Отрезав от него квадрат,сторона которого равна меньшей стороне прямоугольника, мы снова получим золотойпрямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получатьвсе меньшие и меньшие золотые прямоугольники (рис.5)
Темсамым будет построен пример совершенного квадрируемого прямоугольникабесконечного порядка. Точки, делящие стороны прямоугольников в среднем икрайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь.Полюс спирали лежит на пересечении пунктирных диагоналей (рис.6). Разумеется,«вращающиеся квадраты», как их принято называть, могут не только закручивать,но и раскручивать спираль. Для этого лишь требуется строить не уменьшающиеся, авсе увеличивающиеся квадраты. Логарифмическая спираль – единственный типспирали, не меняющей своей формы при увеличении размеров. Если влогарифмической спирали из центра О провести прямую, то образующиеся отрезкиОА, ОВ, ОС, ОD и т. д., полученные при пересечении прямой с витками спирали,образуют геометрическую прогрессию, то есть ОА/ОВ=ОВ/ОС=ОС/OD=…= m, где m –постоянное число.
Отрезкирадиуса, заключенного между последовательными витками спирали, также образуютпрогрессию с отношением АВ/ВС=ВС/СD=…=n. Частным случаем спирали являетсятакая, которая отвечает значению n, равному Ф, т. е. золотой пропорции. Такаяспираль называется «кривой гармонического возрастания».
Вездесущий филлотаксис.
Характернойчертой строения растений и их развития является спиральность. Еще Гете, которыйбыл не только великим поэтом, но и естествоиспытателем, считал спиральностьодним из характерных признаков всех организмов, проявлением самой сокровеннойсущности жизни. Спирально закручиваются усики растений, по спирали происходитрост ткани в стволах деревьев, по спирали расположены семечки в подсолнечнике,спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно,в этом проявляется наследственность организации растений, а ее корни следуетискать на клеточном и молекулярном уровнях.
Исследованияпоказали, что движение протоплазмы в клетке часто спиральное. Рост клеток такжеможет быть спиральным, как показал ученый Кастл. В жидкой среде клеткивстречаются спиральные нити волокон – цитонем. И, наконец, носители информации– молекулы ДНК – также скручены в спираль. Следует отметить, что термин«спираль» не отражает точно строение молекул ДНК; более правильно говорить овинтовом расположении полипептидных цепей в этой молекуле. Во многих другихслучаях, рассмотренных в ботанике, речь также идет, по существу, не о спирали,а о винтовом расположении элементов структуры; к сожалению, термины частосмешивают.
Нетсомнений, что наследственная спиральность является одним из основных свойстворганизмов, она отражает один из существенных признаков живого. На первыйвзгляд кажется, что в кристаллах неорганических веществ спиральность иливинтовая структура отсутствуют. Однако более глубокие исследования показали,что винтовое расположение атомов наблюдается и в некоторых кристаллах ивыражается в образовании так называемых винтовых дислокаций. Такие кристаллысостоят из единственной винтообразной изогнутой атомной плоскости. При каждомобороте вокруг оси эта плоскость поднимается на один шаг винта, равныймежатомному расстоянию. Следует добавить, что кристаллы с такой винтовойструктурой обладают сверхпрочностью. От винтовой структуры молекул ДНК дозакручивания усиков растений – таковы формы проявления спиральности на различныхуровнях организации растений. Отчетливо проявляется эта особенность организациирастений в закономерностях листорасположения.
Существуетнесколько способов листорасположения. В первом листья побега располагаютсястрого один под другим, образуя вертикальные ряды – ортостихи. Условнаяспираль, соединяющая места расположения листьев на побеге, называетсягенетической, или основной спиралью, точнее, винтовой линией и делится на рядлистовых циклов. Генетическим этот винт называется потому, что расположениелистьев в нем отвечает порядку появления в нем листьев. Проекция на плоскостьлисторасположения позволяет в долях окружности выразить угол расхождениялистьев.
Винтовоерасположение листьев выражают дробью, числитель которой равен числу оборотов постеблю воображаемого винта одного листового цикла, а знаменатель- числулистьев в данном цикле, совпадающему с числом ортостих на стебле. Эта дробьпозволяет рассчитать и угол расхождения листьев.
Оказалось,что каждое растение характеризуется своим листорасположением. Так, у липы,вяза, бука, злаков листорасположение описывается формулой 1/2, у дуба и вишни –2/5, у малины, груши, тополя, барбариса – 3/8, у миндаля, облепихи – 5/13 ит.д. Нетрудно видеть, что в формулах листорасположения встречаются числаФибоначчи, расположенные через одно.
Посмотримна сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно - по двум спиралям, которые пересекаются приблизительно под прямым углом. Числотаких спиралей у сосновых шишек равно 8 и 13 или 13 и 21. Такие же спираливидны в поперечных разрезах почек; здесь числа спиралей относятся
как числа 3/5, 5/8, 8/13. В корзинках подсолнечника семена также расположены по
-5-
двумспиралям, их число составляет обычно 34 и 55, 55 и 89. Здесь вновь мы видимзакономерное сочетание чисел Фибоначчи, расположенных рядом: 2/3, 3/5, 5/8,13/21 и т.д. Их отношение в пределе стремится к числу j = 0,61803…
Рассмотреннуюзакономерность расположения листьев, чешуек, семян называют филлотаксисом.
Приизменении формулы листорасположения изменяется и угол расхождения листьев.Формула 1/2 характеризует двурядное расположение листьев под углом />друг от друга.При формуле 1/3 угол между листьями будет />, а при формуле 2/5 — /> и т.д. Впредельном случае, когда отношение чисел в формуле будет отвечать золотойпропорции - 0,38196… угол расхождения листьев станет равным />, который был назван«идеальным» углом, или углом золотой пропорции (/>=Ф2). Установлено, что прирасположении листьев под идеальным углом ни один лист не будет располагатьсяточно над другим, чем создаются лучшие условия для фотосинтеза.
Загадки египетских пирамид.
Всена свете страшится времени. А время страшится пирамид.
Арабскаяпословица
Оегипетских пирамидах с восхищением писал греческий историк Геродот. Первымевропейцем, спустившимся в глубь пирамиды, был римский ученый Плиний Старший.Согласно многим описаниям, эти гигантские монолиты имели совсем иной вид, чем внаше время. Они сияли на солнце белой глазурью отполированных известняковыхплит на фоне многоколонных прилегающих храмов. Рядом с царскими пирамидамистояли малые пирамиды жен и членов семьи фараонов.
Средиграндиозных пирамид Египта особое место занимает великая пирамида фараонаХеопса. Она самая крупная и наиболее хорошо изученная. Чего только не находилив ее пропорциях! Число «пи» и золотую пропорцию, число дней в году, расстояниедо Солнца, диаметр Земли и т.п. Однако при расчете этих величин получалисьнеточности, возникали недоразумения, в результате чего подвергались сомнениюдаже простейшие пропорции в размерах пирамиды и все сообщения о скрытых вгеометрии пирамиды математических сведениях объявлялись выдумкой.
Правильнаячетырехгранная пирамида является одной из хорошо изученных геометрическихфигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость,надежность, устремление вверх.
Очевидно,размеры пирамиды: площадь ее основания и высота — не были выбраны случайно, адолжны нести какие-то геометрические, математические идеи, информацию об уровнезнаний египетских жрецов. Причем следует напомнить, что эти знания составлялитайну и были доступны лишь ограниченному числу лиц, поэтому и в геометриипирамиды они должны быть воплощены не в явной, а в скрытой форме.
Методическойошибкой многих исследователей является то, что они использовали размерыпирамид, выраженные в метрической системе мер. Но ведь египтяне пользовалисьдругой системой мер! Из этой системы и следует исходить при анализе размерныхотношений в пирамидах.
Преждечем приступить к анализу формы и размеров пирамиды Хеопса, следует учестьуровень знаний тех времен, психологию создателей пирамиды. У египтян было триединицы длины: локоть (466 мм), равнявшийся семи ладоням (66,5 мм), которая, всвою очередь, равнялась четырем пальцам (16,6 мм).
Труднодопустить, что строители пирамиды пользовались исходными размерами, выраженнымив долях локтя; более очевидно, что основные исходные размеры были определены вцелых единицах длины – локтях.
Рассмотримразмеры пирамиды Хеопса (рис.7). Длина стороны основания пирамиды (L) принята равной 233,16 м. Эта величина отвечает почтиточно 500 локтям. Очевидно, размер основания пирамиды при ее строительстве ибыл определен в 500 локтей.
Высота пирамиды (H) оценивается исследователями различноот 146,6 до 148,2 м. И в зависимости от принятой высоты пирамиды изменяются ивсе отношения ее геометрических элементов. Поэтому на этой величине следуетостановиться особо. Одним из чудес великой пирамиды является оченьточная подгонка ее каменных блоков и плит; между ними буквально нигде непросунешь лезвия бритвы (0,1 мм). Но никакого чуда здесь не оказалось. Впроцессе строительства каменные блоки не могли быть изготовлены столь точно:для этого у древних египтян просто не было средств – ни обрабатывающих, ниизмерительных. Но за длительное время под воздействием колоссального давления(достигающего 500 тонн на 1 м2 нижней поверхности) произошла «усадка»конструкции, пластическая деформация строительных блоков, вследствие чего они иоказались так тесно подогнанными. В результате усадки высота пирамиды сталаменьше, чем она была в период завершения строительства. Какой же она былапервоначально? Ее можно воссоздать, если найти основную «геометрическую идею»,положенную в основу сооружения.
Уголнаклона граней пирамиды еще в 1837 году определил английский полковник Г.Вайз:он равен />.Указанному значению угла отвечает тангенс, равный 1,272. Эта величина,отвечающая отношению высот пирамиды к половине ее основания, очень близка ккорню квадратному из золотой пропорции />= 1,27202 и является иррациональнойвеличиной. Поэтому, скорее всего, в основу треугольника OMN пирамиды Хеопса и было заложено отношениеOM/MN,равное />.
Итак,примем отношение катетов, т.е. высоты пирамиды H к половине ее основания, равным 1,272. При этом высота пирамидыХеопса будет равна точно 318 локтей, или 148,28 м. Такую высоту, очевидно,имела пирамида Хеопса при завершении ее сооружения ( или должна была иметь попроекту).
Такимобразом, основные элементы конструкции пирамиды имели следующие размеры:сторона основания – 500 локтей, высота – 318 локтей. Отсюда следует, чтоапофема боковой грани ON равна 404,5локтя.
Атеперь посмотрим, какие интересные соотношения следуют из этих геометрическихразмеров. Отношения сторон в треугольнике OMN пирамиды равно: OM/MN=ON/OM=1,272=/>; ON/MN=Ф.
Рассмотримтеперь поверхность пирамиды. Она состоит из четырех треугольников и квадратаоснования. Основание треугольника BOC равно500 локтям, высота его равна 404,5 локтя. По теореме Пифагора можно рассчитатьдлину боковых ребер OB и OC. Они равны 475,5 локтя.
Площадьоснования пирамиды равна 250000 кв. локтей, площадь боковой грани 101125 кв.локтей, а площадь четырех граней пирамиды равна 404500 кв. локтей. Отношениеповерхности граней к площади основания также равно золотой пропорции.
ЕщеГеродот, основываясь на рассказах египетских жрецов, писал, что площадьквадрата, построенного на высоте пирамиды, равна площади каждой из его боковыхграней. По нашим расчетам, квадрат высоты равен 3182 = 101127 кв. локтей, чтопочти точно отвечает площади боковой грани (101125 кв. локтей).
Многиеисследователи указывают, что отношение удвоенной стороны основания 2L к высоте пирамиды H отвечает числу «пи». Однако в связи с тем, что высота пирамидыпринималась равной современной и не всегда однозначной, число «пи» получалосьразным: 3,16-3,18. На почве этого возникали сомнения, предпринимались различныеподгонки, стали говорить даже о некоем «египетском p», равном 3,16. Если принять высотупирамиды равной 318 локтям, то отношение 2L/H=1000/318 будет равно 3,144. Эта величинаочень близка к современному значению числа «пи» (3,14159…).
Интересносравнить два основных отношения, установленных нами при изучении геометрическихпропорций пирамиды: 2H/L=/>и 2L/H=p. Отсюда получаем простую и красивую формулу, связывающую число«пи» и золотую пропорцию: 4/p=/>.
Гениальныесоздатели пирамиды Хеопса стремились поразить далеких потомков глубиной своихзнаний, и они достигли этого. Следует лишь удивляться высокому знанию иискусству древних математиков и архитекторов Египта, которые смогли воплотить впирамиде две иррациональные (т.е. неизмеримые) величины – p и Ф со столь поразительной точностью,оперируя исходными отношениями целых чисел – стороной основания и высотойпирамиды, выраженных в локтях.
Золотая пропорция в искусстве ДревнейГреции.
Великолепныепамятники архитектуры оставили нам зодчие Древней Греции. И среди них первоеместо по праву принадлежит Парфенону.
Всювторую половину V в. до н.э. на Акрополе шло строительствохрамов, пропилей (преддверий), алтаря и статуи Афины Воительницы. В 447 годуначались работы над храмом Афины – Парфеноном и продолжались до 434 года дон.э. Для создания гармонической композиции на холме его строители дажеувеличили холм в южной части, соорудив для этого мощную насыпь.
Какуказывает исследователь Г. И. Соколов, протяженность холма перед Парфеноном,длины храма Афины и участка Акрополя за Парфеноном относятся как отрезкизолотой пропорции. При взгляде на Парфенон от места расположения пропилейотношения массива скалы и храма также соответствуют золотой пропорции. Такимобразом, золотая пропорция была использована уже при создании композиции храмовна священном холме.
РазмерыПарфенона хорошо изучены, но приводимые замеры не всегда однозначны. Следуетучесть, о чем сказано ниже, что геометрия архитектуры храма очень непростая – вней почти отсутствуют прямые линии, поэтому определение размеров затруднено.Известно, что фасад Парфенона вписан в прямоугольник со сторонами 1: 2, аплан образует прямоугольник со сторонами 1 и />. Известно, что диагональпрямоугольника 1:2 имеет размер />, следовательно, прямоугольникфасада и является исходным в построении геометрии Парфенона.
ШиринаПарфенона оценена в 100 греческих футов (3089 см), а размер высоты нескольковарьирует у различных авторов. Так, по данным Н. Бруно, высота Парфенона 61,8 , высота трех ступеней основания и колонны – 38,2 , высота перекрытия ифронтона – 23,6 футов. Указанные размеры образуют ряд золотой пропорции: 100:61,8 = 61,8: 38,2 = 38,2 :23,6 = Ф.
Многиеисследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали инаходили в соотношениях его частей золотую пропорцию. В работе В.Смоляка,посвященной изучению пропорций Парфенона, установлен закономерный ряд золотыхпропорций. Приняв за единицу ширину торцового фасада храма, Смоляк получилпрогрессию, состоящую из 8 членов ряда: 1: j: j2: j3: j4: j5: j6. Указанным членам ряда отвечают основныепропорции фасада Парфенона (рис.8).
Внекоторых сооружениях древнего мира золотая пропорция выражена не в пропорцияхформы зданий, а в деталях внутренней композиции, даже в числе мест длязрителей. Интересные данные приводит Э.Сороко. Построенный Поликлетом-младшимтеатр был рассчитан на 15 тысяч зрителей. Места для зрителей (театроп) имели 2яруса: первый- 34 ряда мест, а второй – 21 ряд (числа Фибоначчи). Раствор угла, охватывающего пространство между театропом и скемой (пристройка дляпереодевания актеров и хранения реквизита), делит окружность основанияамфитеатра в отношении />: />, что равно 1: 1,618…. Это соотношение углов реализованопрактически во всех античных театрах. Театр Диониса в Афинах трехъярусный.Первый ярус имеет 13 секторов, второй – 21 сектор.
Древниескульпторы знали и использовали золотую пропорцию как критерий гармонии, канонкрасоты, корни которой лежат в пропорциях человеческого тела. “Человеческоетело – лучшая красота на земле”, — утверждал Н.Чернышевский. Эталонами красотычеловеческого тела, образцами гармонического телосложения издавна и по правусчитаются великие творения греческих скульпторов: Фидия, Поликлета, Мирона,Праксителя. В создании своих творений греческие мастера использовали принципзолотой пропорции. Центр золотой пропорции строения человеческого теларасполагался точно на месте пупка. И не случайно величину золотой пропорциипринято обозначать буквой Ф; это сделано в честь Фидия – творца бессмертныхскульптурных произведений.
Однимиз высших достижений классического греческого искусства может служить статуя“Дорифор”, изваянная Поликлетом. Фигура юноши выражает единство прекрасного идоблестного, лежащих в основе греческих принципов искусства. Широкие плечипочти равны высоте туловища, высота головы восемь раз укладывается в высотетела, а золотой пропорции отвечает положение пупка на теле атлета.
Нопроанализируем другие пропорции знаменитой статуи. Расстояние от подошвыкопьеносца до его колена равна j3, высота шеи вместе с головой — j4, длина шеи до уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мывидим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9).
Такимобразом, золотое сечение – один из основополагающих принципов в искусствеантичной Греции.
Ритмы сердца и мозга.
Равномернобьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце какпоршень сжимает, а затем выталкивает кровь и гонит ее по телу. Предсердиявыполняют роль резервуара, принимающего кровь из вен, а желудочки - насоса,ритмически перекачивающего кровь в артерии. Давление крови изменяется впроцессе работы сердца. Наибольшей величины оно достигает в левом желудочке вмомент его сжатия (систолы). В артериях во время систолы желудочков кровяноедавление достигает максимальной величины, равной 115-125 мм рт.ст. у здоровогомолодого человека. В момент расслабления сердечной мышцы (диастолы) давлениеснижается до 70-80 мм рт.ст. Отношение максимального (систолического ) к минимальному(диастолическому) давлению равно в среднем 1,6, т.е. близко к золотойпропорции.
Сердцебьется непрерывно – от рождения человека до его смерти. Его работа должна бытьоптимальной, обусловленной законами самоорганизации биологических систем.Отклонения от оптимального режима вызывают различные заболевания. А так какзолотая пропорция является одним из критериев самоорганизации в живой природе,естественно предположить, что и в работе сердца возможно проявление этогокритерия. Нужны были глубокие исследования, и они были проведены советскимученым В.Д.Цветковым.
Приработе сердца возникает электрический ток, который можно уловить специальнымприбором и получить кривую – электрокардиограмму (ЭКГ) с характерными зубцами,отражающими различные циклы работы сердца. На ЭКГ человека выделяются дваучастка различной длительности, соответствующие систолической и диастолическойдеятельности сердца. В.Цветков установил, что у человека и у другихмлекопитающих имеется оптимальная («золотая») частота сердцебиения, при которойдлительности систолы, диастолы и полного сердечного цикла соотносятся междусобой в пропорции 0,382: 0,618: 1, т.е. в полном соответствии с золотойпропорцией. Так, например, для человека эта частота равна 63 ударам в минуту,для собак – 94, что отвечает реальной частоте сердцебиения в состоянии покоя.
ДалееВ.Цветков обнаружил, что систолическое давление крови в аорте равно 0,382 , адиастолическое – 0,618 от среднего давления крови в аорте. Доля объема левогожелудочка при ударном выбросе крови по отношению к конечнодиастолическомуобъему у десяти видов млекопитающих в состоянии покоя составляет 0,37-0,4 ,что в среднем также отвечает золотой пропорции. Таким образом, работа сердца вотношении временных циклов, изменения давления крови и объемов желудочковоптимизировано по одному и тому же принципу – по правилу золотой пропорции.
Мозгчеловека представляет собой сложнейшую самонастраивающуюся систему, основнымназначение которой является регуляция деятельности различных органов человеческоготела, осуществление связи человека с окружающей средой. В составе мозга различают серое и белое вещества. Серое вещество представляет собой скоплениенервных клеток, белое – нервных волокон, отростков этих клеток. Нервная клеткас отростком называется нейроном. Нейроны мозга образуют разнообразные сети,взаимодействующие с помощью электрических сигналов.
Конфигурациинейронных сетей представляют собой колебательные электрические цепи. Различнымсостояниям мозга соответствуют электрические колебания с разными частотами.
Многочисленныеисследования показали, что в мозгу взрослого человека при различных егосостояниях преобладают электрические колебания определенных частот. Изменение активации мозга происходит не непрерывно, а только дискретно, скачками отодного уровня к другому. Каждому состоянию мозга соответствуют своиспецифические волны электрических колебаний.
Состояниюспокойного бодрствования отвечает наиболее устойчивый a- ритм с частотами колебаний преимущественноот 8 до 13 герц. Это основной ритм электрических колебаний мозга, он появляетсяв детском возрасте и постепенно с возрастом увеличивается с 2-3 до 8-13 гц ввозрасте 8-16 лет. Наиболее медленные колебания с частотой 0,5 –4 гц у D- ритма, характерно для состоянияглубокого сна. Для D- ритма верхняяграничная частота достаточно стабильна и равна 3-4 гц, а пределы нижнейграничной частоты изменяются от 0,2 до 1,5 гц.
Припоявлении неприятности или опасности в мозгу доминирует q — ритм с частотами от 4-7 до 6-8 (поданным различных авторов). Советские ученые-братья Я.и А. Соколовы считают,что наиболее устойчивы для q- ритмаграничные частоты колебаний 4 — 7 гц. Умственной работе отвечает b- ритм с граничными частотами 14-35гц.(по другим данным, диапазон частот этого ритма более широк – от 14 до 100гц).Эмоциональному возбуждению мозга соответствует g- ритм с граничными частотами 35-55 гц. Нетрудно заметить, чтограничные частоты ритмов почти точно отвечают числам Фибоначчи. Отклоненияграничных частот от чисел Фибоначчи находятся в пределах точности эксперимента.Соколовы считают, что существуют еще не обнаруженные опытами r- ритм и s- ритм. Расчеты показали, что у s- ритма пограничные частоты 118 и 225 гц, а у r- ритма - 55 и 118 гц. И здесь очевиднаблизость чисел Фибоначчи.
Исследованияв этой области только начинаются, впереди - открытие самых сокровенных тайнорганизации и работы мозга человека, закономерности его эволюции.
Алгебра музыки.
Вкомпозиции многих музыкальных произведений отмечается наличие некоторого«кульминационного взлета», высшей точки, причем такое построение характерно нетолько для произведения в целом, но и для его отдельных частей. Такая высшаяточка крайне редко расположена в центре произведения или его композиционнойчасти, обычно она смещена, асимметрична. Изучая восьмитактные мелодииБетховена, Шопена, Скрябина, советский музыковед Л.Мазель установил, что вомногих из них вершина, или высшая точка, приходится на сильную долю шестоготакта или на последнюю мелкую долю пятого такта, т.е. находится в точкезолотого сечения. По мнению Л.Мазеля, число подобных восьмитактов, где подъеммелодии занимает пять тактов, а последующий спуск – три, необычайно велико. Ихможно без труда найти почти у каждого автора, сочинявшего музыку вгармоническом стиле.
Очевидно,такое расположение кульминационных моментов музыкальной мелодии является важнымэлементом ее гармонической композиции, придающим художественную выразительностьи эстетическую эмоциональность мелодии.
Характерно,что в некоторых случаях авторы музыкальных произведений смещали их вершину отточки золотого сечения, что придавало мелодиям неустойчивый характер. По мнениюЛ.Мазеля, это входило в намерения авторов, например, при сочинении скерцо,рондообразных финалов.
Наиболееобширное исследование проявлений золотого сечения в музыке было предпринятоЛ.Сабанеевым. Им было изучено две тысячи произведений различных композиторов.По его мнению, временное протяжение музыкального произведения делится«некоторыми вехами», которые выделяются при восприятии музыки и облегчаютсозерцание формы целого. Все эти музыкальные вехи делят целое на части, какправило, по закону золотого сечения.
Понаблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторовобычно констатируется не одно золотое сечение, а целая серия подобных сечений.Каждое такое сечение отражает свое музыкальное событие, качественный скачок вразвитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторовнаблюдалось 3275 золотых сечений. Количество произведений, в которыхнаблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количествомузыкальных произведений, в которых имеется золотое сечение, у Аренского (95%),Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%),Шуберта (91%).
Наиболеедетально были изучены все 27 этюдов Шопена. В них обнаружено 154 золотыхсечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаяхстроение музыкального произведения сочетало в себе симметричность и золотоесечение одновременно; в этих случаях оно делилось на несколько симметричныхчастей, в каждой из которых проявляется золотое сечение. У Бетховена такжесочинения делятся на две симметричные части, а внутри каждой из них наблюдаютсяпроявления золотой пропорции.
Характерно,что наиболее часто золотое сечение обнаруживается в произведенияхвысокохудожественных, принадлежащих гениальным авторам. Может быть, частотапроявлений золотой пропорции является одним из объективных критериев оценкигениальности музыкальных произведений и их авторов?
Итак,можно признать, что золотая пропорция является критерием гармонии композициимузыкального произведения.
Музыка стихов.
Многоев структуре произведений поэзии роднит этот вид искусства с музыкой. Каждыйстих обладает своей музыкальной формой – своей ритмикой и мелодией. Можноожидать, что в строении стихотворений проявятся некоторые черты музыкальныхкомпозиций, закономерности музыкальной гармонии, а следовательно, и золотаяпропорция, и числа Фибоначчи.
Исследованияпоэтических произведений с этих позиций только начинаются. И начинать нужно споэзии А.С.Пушкина. Ведь его произведения - образец наиболее выдающихсятворений русской культуры, образец высочайшего уровня гармонии. С поэзииА.С.Пушкина мы и начнем поиски золотой пропорции – мерила гармонии и красоты.
Дляанализа метрики стихотворений А.С.Пушкина рассмотрены его произведения периода1829-1836 г.г., периода создания наиболее совершенных стихов. Сюда вошло 109стихов. Число строк в стихотворениях этого периода изменялось от 4 до 116.Однако большие стихотворные формы встречаются редко; число стихотворений сколичеством строк более 60 составило всего 9 штук. Средний размер этихстихотворений составил 88 строк.
Казалосьбы, величина стихотворения, определяемая числом строк, может изменятьсяпроизвольно и непрерывно от самой малой в четыре строки до самых больших.Однако оказалось, что это не так. Размеры стихов распределены совсем неравномерно; выделяются предпочтительные и редко встречающиеся размеры. Награфике распределения стихотворений А.С.Пушкина по числу строк в них отчетливовыделяется несколько максимумов — наиболее встречающихся размеров (рис.10).Они явно тяготеют к числам 5, 8, 13, 21, 34. Проявляется вполне закономернаятенденция в творческой манере поэта – он явно предпочитает стихотворения,размер которых близок к числам ряда Фибоначчи.
Тольколи стихотворения А.С. Пушкина тяготеют в своих размерах к числам Фибоначчи?
Конечно,нет. И у других поэтов проявляется тяготение размера стихов к 8,13,21 строчкам,но ни у одного из русских поэтов эта тенденция не выражена так отчетливо, как уА.С.Пушкина. Стихотворения В.Брюсова отличаются совершенством своих форм. Инеудивительно, что в их размерности также проявляются числа Фибоначчи. Былопроанализировано 360 стихотворений поэта из его двухтомника; эти стихиохватывали период от 1882 до 1912 года. Только в трех стихотворениях числострок составило 70, 85, 90 (что в среднем близко к числу Фибоначчи 89).Остальные стихотворения содержали значительно меньше строк – от 8 до 36 икрайне редко несколько больше.
Средирассмотренных стихотворений В.Брюсова явно преобладают те, в которых числострочек равно или близко к числам Фибоначчи. Они распределены следующимобразом:
стихотворенияс числом строк 8 25 шт. 7%
- * - 13/>1 77 шт. 21,5% - * - 21/>1 70 шт.19,6% - * - 34/>2 36шт. 10,0%
Общеечисло этих стихотворений составило 208 шт. или 58%. К остальным относятсястихотворения с числом строчек 10, 14, 16, 18, 24, 26, 28, 31, 32 и т.д. Поэтявно предпочитал стихотворения с числом строк 8, 13/>1, 21/>1 как наиболее оптимальные длявыражения мыслей и чувств.
Обратимсявновь к произведениям А.С.Пушкина. Рассмотрим композицию «Пиковой дамы». Вэтой повести кульминационным моментом является сцена в спальне графини, кудапроник Германн в надежде узнать тайну трех карт, сцена, которая оканчиваетсясмертью графини в повести 853 строки. Кульминационный момент повести – этосмерть графини. Ему отвечает 535 –я строка. Эта строка расположена в повестипочти точно в месте золотого сечения, т.к. 853:535=1,6 .
Повесть«Пиковая дама» состоит из шести глав. Посмотрим, не проявляется ли в композицииглав золотая пропорция? В первой главе золотому сечению отвечает 68 строчка(всего в главе 110 строк). Но ведь это же узловая точка повествования, в нейпереломный момент всей главы: откроет ли Сен — Жермен свою тайну графине!
Втораяглава повести содержит 219 строк. Золотое сечение здесь приходится на 135строку. Но ведь это кульминационный момент главы, Лиза увидела в окне стоящегона улице Германна! Отсюда начался для нее новый отсчет времени, началисьсобытия, определившие всю ее дальнейшую судьбу. А.С.Пушкин совершенно точноопределил это место во второй главе: ведь 219:135 = 1,62.
Третьяглава повести описывает усилия Германна попасть в дом старой графини, выведатьу нее тайну трех карт. Это место начинает новый отсчет времени для Германна.Эта ситуация приходится на 131 строку третьей главы, а всего в ней 212 строк. Разделив212 на 131, мы получим точно золотую пропорцию 1,618!
Вчетвертой главе размером 113 строк золотая пропорция приходится на 70 строку.Это также переломный, трагический момент в жизни Лизы.
Впятой главе описано посещение Германна похорон графини. 46 строка пятой главыразделила повествование на две части: первая — похороны графини и вторая – сонГерманна. Эта 46 строка также отвечает золотой пропорции, ведь всего в этойглаве 75 строк (75:46=1,63).
Впоследней главе повести золотая пропорция приходится на 77 строчку, котораязавершает описание первого дня игры Германна в карты и первого его выигрыша.Как видим, и в композиции последней главы повести присутствует золотаяпропорция.
Золотаяпропорция присутствует и в композиции других произведений Пушкина. В рассказе«Станционный смотритель» 377 строк. Кульминационный момент рассказа – этоизвестие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен вофразе, которая является 214 строкой. Здесь почти точное соответствие золотойпропорции.
Вмаленьком рассказе «Гробовщик» всего 229 строк. Со 139 строки начинаетсяописание страшного сна гробовщика. И здесь переломный момент рассказаприходится почти точно на золотую пропорцию (229:1,618=141 строка).
Совпадениекульминационных моментов в произведениях А.С.Пушкина с золотой пропорциейудивительно близкое, в пределах 1-3 строк. Чувство гармонии у него было развитонеобыкновенно, что объективно подтверждает гениальность великого поэта иписателя.
Заключение.
Рациональные и иррациональные числа являются своеобразными противоположностями. Но природаедина, и ее противоположности не только находятся в противодействии, борьбе, нои в единстве. И не удивительно, что многие иррациональные числа выражаютсячерез совокупность целых чисел. Все три числа:p, e и Ф – связаны между собой простымиотношениями и могут быть выражены в виде пределов бесконечных дробей. Крометого, на примере золотой пропорции показано, что целые числа натурального ряда: 1, 2, 3, … могут быть выражены через иррациональное число Ф. Кроме того,число Ф с любой степенью точности может быть выражено через отношение целыхчисел. Разве эти примеры не свидетельствуют о единстве рационального ииррационального в природе?!
Мытак часто говорим о единстве и борьбе противоположностей, что это понятие сталотривиальным, само собой разумеющимся и не требующим исследования. Может быть,поэтому этот фундаментальный закон природы так мало исследован и углублен и,что характерно, почти совершенно не математизирован. А между тем он достоинсамого пристального изучения и развития – ведь это один из основных, наиболееобщих законов мироздания.
Список литературы
Н.Васютинский “Золотая пропорция” –М.,”Молодая гвардия”, 1990
А.Азевич “Двадцать уроков гармонии” –М., “Школа-Пресс”, 1998
М.Гарднер “Математические головоломки и развлечения” –М., “Мир”, 1971
Д. Пидоу “Геометрия и искусство” – М., “Мир”, 1989
Энциклопедическийсловарь юного математика –М.,1989
Журнал“Квант”, 1973, № 8
Журнал“Математика в школе”, 1994, № 2, № 3
Дляподготовки данной работы были использованы материалы с сайта www.ed.vseved.ru/
www.ronl.ru
Реферат выполнил Филитов Василий Сергеевич
Московский Государственный Институт Управления Правительства Москвы
Кафедра Математики
Москва
2003 год
Абстрагирование как мыслительный процесс
Для более или менее подробного обсуждения предмета математики необходимо предварительно выяснить генезис и особенности ее важнейших исходных понятий, т.к. математика отличается от других наук, прежде всего, используемыми ею абстракциями. Стержневым вопросом философских проблем математики является отношение ее понятий к реальности, вопрос об объективном содержании математического знания. Чтобы лучше понять характер этих взаимоотношений, необходимо рассмотреть ключевой вопрос – процесс образования математических абстракций.
Процесс абстрагирования есть существенный и необходимый прием познания окружающей нас действительности. Если на чувственной ступени познания человек с помощью ощущений отображает явления природы, то путем мышления (в обобщенной форме и опосредованно) он проникает в сущность этих явлений. Однако было бы ошибкой полагать, что здесь происходит просто логическая переработка чувственных данных, что в мышлении нет ничего, чего не было бы в ощущениях.
Процесс абстрагирования и вытекающий из него процесс анализа являет собой отвлечение от несущественных сторон изучаемого объекта, выделение и рассмотрение только существенных свойств. Цель абстрагирования – получение более глубокого и «чистого» знания об объекте, чем на чувственной ступени познания. Таким образом, процесс абстрагирования завершается образованием исходных абстракций, однако они являют собой нечто неконкретное и одностороннее, поэтому для получения более глубоких и правильных знаний об изучаемом объекте, необходимо учитывать и вторую, чувственную ступень познания. Необходимо провести движение теперь уже от общего к частному путем синтеза.
Путем созерцания возможно познать лишь внешнюю сторону предмета, в то время как абстрагирование позволяет познать его сущность. Это объясняет то, почему современная математика зачастую способна глубже и адекватнее описать сложные процессы действительности, хотя по мере своего развития ее понятия имеют все меньше сходства с реальными явлениями окружающего нас мира, утрачивают свою наглядность.
Таковы характерные черты и возможности приема абстрагирования в его органическом единстве с методами восхождения от абстрактного к конкретному, анализа и синтеза. Но в чем же заключается своеобразие математических абстракций?
Специфика математических абстракций
Как уже отмечалось, процесс абстрагирования в обычных науках заключается в мысленном отвлечении от несуществующих сторон изучаемого предмета. Однако в математике все оказывается более сложным. Имеются ли такие исходные понятия, которые отображали бы реально существующие свойства и стороны предмета, явления, процесса? Подавляющее большинство ученых дает на этот вопрос отрицательный ответ.
И вот почему. Возьмем, к примеру, такую область математики, как геометрию. В материальной действительности мы, строго говоря, не найдем квадрата, треугольника, прямой линии и тому подобных объектов. Иначе говоря, формирование этих объектов нельзя понимать как результат выделения человеком каких-то математических свойств в явлениях внешнего мира. Они – результат творческого воображения, логического конструирования, идеализации.
Среди ученых бытуют противоположные взгляды, в частности, утверждение о том, что математические свойства и фигуры есть не что иное, как плод чистой фантазии, который ничего общего не имеет с объективной реальностью. Голландский ученый А. Гейтинг писал, что математика «не выражает истину о внешнем мире, а связана исключительно с умственными построениями». Это утверждение ставит исследователя на ошибочные позиции наивного реализма, идеализма, априоризма и конвенционализма. А Энгельс писал: «Понятия и фигуры взяты не откуда-нибудь, а из действительного мира. Десять пальцев, на которых люди научились считать, т.е. производить первую арифметическую операцию, представляют собой все, что угодно, только не продукт свободного творчества разума». Позже он дополнил свою мысль: «мы доходим до продуктов свободного творчества и воображения самого разума», т.е. до таких понятий, связь которых с окружающим миром непосредственно не просматривается.
Как же исторически и логически происходил процесс образования исходных понятий натурального числа в арифметике и фигуры в геометрии?
Как показывают исследователи древней культуры, в ранний период развития общества люди не имели понятия числа, хотя своеобразный счет ими, конечно, осуществлялся: скажем, величину стада овец они выражали с помощью пальцев рук. Со временем количество объектов стали определять путем отождествления их совокупности с равночисленным множеством других предметов. Например, одна из гипотез об изготовлении гигантских статуй на острове Пасхи звучит так: туземцы вытесывали туловища из серого камня и «парики» из красного в разных каньонах и, не умея считать, они были вынуждены употреблять камешки, сопоставляя их сначала с телами, а потом с головами.
Как мы видим, первоначально человек не отделял количество вещей от них самих, используя так называемые «именованные числа» — две руки, три пальца т т.п. Человек не абстрагировал понятие числа от понятия вещи. Этому он научился значительно позже. Человек начал пользоваться рядом натуральных, порядковых и количественных чисел.
Абстракция отождествления и понятие числа
Это был гигантский скачок в совершенствовании представлений человека о мире, как писал Д. Гильберт. При этом в сложном процессе становления понятия натурального числа первостепенное значение имела фундаментальная для науки абстракция отождествления. Кстати, использование ее далеко не ограничивается областью математики, как писала С.А. Янковская. Существенно, что выявление тождества не только не исключает, но, наоборот, предполагает различия между сопоставляемыми объектами. Без единства этих противоположностей сравнение как таковое теряет всякий смысл.
Эта абстракция использовалась Карлом Марксом в научной теории стоимости.
Итак, практические потребности в счете и измерениях, связанные с развитием общественного производства и совершенствованием экономики, явились причиной такого революционного акта, как возникновение понятия натурального числа, что, в свою очередь, послужило исторически исходным пунктом дальнейшего развития математики. А поскольку решающую роль сыграла абстракция отождествления, то логическое определение понятия числа осуществляется с обязательным ее использованием.
По мнению известного ученого Г.Фрёге, число есть не что иное, как общее свойство класса эквивалентных множеств – совокупностей предметов независимо от их качественной определенности и природы. Важно, что сравниваемые множества обладали изоморфизмом, когда каждому члену одного соответствует единственный член другого.
Наряду с использованием абстракции отождествления, в период зарождения математического знания применялась операция сравнения, которая допускает оценку в суждениях типа «больше», «меньше», «равно». В дальнейшем большую роль сыграла также операция косвенного измерения, когда фокус человеческого внимания смещался в сторону отношений между числами, в которых отражались реальные взаимосвязи между объектами, что свидетельствовало о возрастании активности познающего субъекта. Благодаря косвенному измерению возникли три другие простейшие арифметические операции – вычитание, умножение и деление. В.Вундт писал, что без косвенного измерения величин «никогда бы не развилось математическое мышление».
Понятие фигуры
Метод соотнесенности, который выявляет схожие черты в сравниваемых предметах, лежит в основе формирования понятия фигуры, поскольку при этом используется принцип подобия, выражающий важнейшее общее свойство различных геометрических тел. Понятие фигуры, в отличие от понятия числа, складывалось без его точного прообраза в действительности, поэтому человек вынужден был пользоваться не только абстракцией отождествления, но и приемом идеализации в чистом виде.
Сущность данного приема заключается в образовании таких абстракций, которые отражают не только реально существующие свойства объекта, а, как писал Н.А. Шанин, значительно отклоняющиеся или даже воображаемые. Как уже отмечалось, в природе не существует линий, точек, правильных треугольников, квадратов и других геометрических фигур. Но, тем не менее, без этих исходных, первоначальных понятий в математике не обойтись. И ученые вынуждены были логически конструировать такие объекты, имея лишь в какой-то мере сходную внешнюю форму предметов в окружающей нас действительности. Для примера лучше всего взять астрономию. Земля и другие планеты Солнечной системы, включай само Солнце, человеку давно представлялись в виде шара, но мы сегодня хорошо знаем, что это не совсем верные, а точнее – совершенно неверные представления. Так, наша планета как бы сплюснута в районе полюсов и поэтому является эллипсоидом вращения. Кроме того, на ней присутствуют неровности.
Исходные первоначальные понятия арифметики и геометрии не могут быть определены классическим способом (т.е. подведены под более широкое родовое понятие с указанием на видовое отличие), потому что не существует более широких фундаментальных категорий математического характера. По этой причине определения точки, прямой и других исходных понятий даны Евклидом на интуитивном уровне и при дальнейшем доказательстве теорем фактически не использовались. Геометрическая точка (по Евклиду) это то, что не имеет частей; у линии нет толщины, она является следом движущейся точки; плоскость – результат движения прямой линии и т.д. Впрочем, и значительно позже многие ученые вынуждены были давать определение исходных математических понятий на интуитивном уровне.
Количество и качество в математике
Итак, объекты действительности представляют собой единство дискретного и непрерывного (недизъюнктивность). Если в натуральном числе фиксируется дискретность и в связи с этим устойчивость внешней стороны явлений действительности, то в понятии фигуры – непрерывность и тоже устойчивость.
Примечательно, что натуральные числа и фигуры оказываются сходными с чувственными образами в том отношении, что в данных понятиях отображается внешняя сторона предметов действительности. Именно это имел в виду Платон, когда сближал математические абстракции с чувственностью. Но он не учитывал, что отмеченный феномен касается лишь исходных понятий математики.
Абстракции математики многоступенчаты, имеют разную степень общности. На первых этапах ее развития в понятии числа отвлекались от качественных особенностей реальных объектов, позже – от конкретных чисел и величин в результате создания алгебры и введения буквенной символики. Наконец, на современном этапе отвлекаются даже от конкретного содержания зависимостей, так что, например, обычные арифметические действия (сложение, вычитание, умножение и деление), осуществляемые с абстрактными объектами математических структур, предстают уже в виде абстрактных операций.
Абстракции современной математики в значительной степени отличаются от исходных понятий. Они выражают не только количественную сторону реальных процессов объективной действительности. В противном случае трудно объяснить удивительную, непостижимую «эффективность математики в естествознании», как писал Ю. Вигнер, т.е. тот факт, что ее нынешние модели зачастую описывают довольно неплохо сложные процессы материальной действительности.
Кстати, позиция сторонников количественной концепции, т.е. тех, кто предполагает, что математика исследует лишь количественную сторону процессов действительности и убеждены в том, что определения количества (и качества, соответственно) в математике должны быть отличны от философских, выглядит искусственной, неправомерной. Понятие количества и качества должны быть одинаковы для всех наук.
Количество – это и внешнее, и внутреннее, и различное в сходных по качеству объектах, и, вместе с тем, сходное в различных по своему качеству вещах. Это такая определенность предметов, явлений, которая характеризует их величину, форму, интенсивность свойств, темпы развития и т.п.
Попытки в прошлом дать два понятия материи (философское и естественнонаучное) были признаны ошибочными.
Математика в какой-то мере описывает и качественную сторону явлений материальной действительности (правда, частично, косвенно, опосредованно и своеобразно, с помощью особого искусственного языка), тем более, что существует неразрывная связь количества и качества.
Уже исходные категории математики количественную сторону явлений действительности отображают дизъюнктивно и в этом смысле неадекватно, огрублено. В дальнейшем используются понятия более высоких уровней общности (абстракции от абстракций), зачастую не имеющие никакого референта в окружающем мире (например, любой тройке действительных чисел соответствует точка в реальном пространстве трех измерений, а для четверки, пятерки и т.п. чисел адекватны уже так называемые многомерные, параметрические пространства). Тем не менее, современная математика точнее, полнее описывает реальные явления, чем раньше. Это происходит, очевидно, благодаря потенциальным возможностям аксиоматического метода и способностям развитой математики выражать в какой-то мере и качественную сторону процесса действительности. При этом количество не сводится к величинам или выражающим их числам, как это было до второй половины XIX в.
Заключение
Рассматриваемые абстракции обладают спецификой. Их характерной особенностью является следующее: отвлечение исходных категорий от качественной стороны объектов действительности, наличие элементов идеализации, значительная относительная самостоятельность этих понятий, ведущая к необходимости создания «идеальных элементов», не имеющих прообраза в объективном мире (например, квадратный корень из -1), иерархия математических абстракций.
Важное в методологическом отношении обстоятельство – исходные понятия фиксируют момент устойчивости явлений окружающего мира, которые на самом деле представляют собой, как известно, единство устойчивости и изменяемости, так что каждый объект есть и результат, и процесс, и то и не то, движущееся тело и находится в данном месте, и вместе с тем его там нет. Если натуральное число можно рассматривать как инвариант класса эквивалентных множеств, то фигуру – как инвариант внешней формы подобных тел.
Итак, в исходных понятиях элементарной математики отображаются либо дискретность и устойчивость внешней количественной стороны явлений действительности, либо (в случае понятия фигуры) непрерывность и опять-таки устойчивость внешней природы предметов материального мира.
И в заключение привожу определение математики с точки зрения рассматриваемой темы. Математика – своеобразный, формальный способ теоретического описания действительности, область знания, имеющая особый статус в системе наук; с ее помощью можно, в принципе, описать любой процесс объективной действительности. Для математики более характерен метод, чем предмет, в качестве же своих объектов она рассматривает пространственные формы и количественные отношения действительности, точнее, идеализированные объекты, начиная с натурального числа и фигуры и кончая своеобразными структурами.
Список литературы
Жуков «Специфика математических абстракций», Минск, 1986.
Бурбаки Н. «Очерки по истории математики», Москва, изд. Наука, 1963.
Энциклопедия юного математика
www.ronl.ru