





















 Министерство общего и профессионального образования
Министерство общего и профессионального образования





















 Министерство общего и профессионального образования
Министерство общего и профессионального образования
Ростовской области
муниципальное общеобразовательное учреждение
средняя общеобразовательная школы № 8
Музыка и математика
Выполнила: Лебедь Диана,
ученица 5 а класса.
Руководитель: Голубова
Наталья Валерьевна,
учитель математики.
Волгодонск, 2015
Содержание
Введение 3
Связь между музыкой и математикой 3
Практическая часть
3.1Создание математической модели музыкального фрагмента 5
3.2Транспонирование мелодии с помощью математической модели. 7
3.3Исследование дат рождения 8
Заключение 11
Список литературы 12
ВВЕДЕНИЕ
«Музыка есть таинственная арифметика души;
Она вычисляет, сама того не подозревая»
Г.Лейбниц.
Актуальность: На одном из занятий кружка, когда я сказала, что у меня не очень хорошие способности по математике, моя учительница спросила о моих успехах по сольфеджио. Услышав мой ответ, что по сольфеджио у меня хорошие успехи, Наталья Валерьевна сказала, что и по математике должно быть хорошо. Я задумалась над тем, что услышала. Действительно, мне нравятся уроки математики, люблю решать задачи. Нравится музыка и игра на фортепиано, пение. Неужели такие две совершенно разные области как математика и музыка взаимосвязаны? В своей работе я выдвинула следующую гипотезу: любое музыкальное произведение можно представить, как некую математическую модель.
Цель: на примере музыкальных произведений выявить взаимосвязь между музыкой и математикой.
Задачи:
1.Выяснить, были ли в истории попытки связать музыку с математикой.
2. Провести свое исследование по установлению связи между музыкой и цифрами, рассмотрев музыкальные произведения как математическую модель.
3. Переложить числа (даты рождения одноклассников) на музыку. Установить связь между звуками и способностями личности.
Объект исследования: музыка и математика.
Методы исследования:
1.Изучение, обработка и анализ документов.
2.Метод исследования музыкального произведения.
3.Метод проблемно-поисковой ситуации.
СВЯЗЬ МЕЖДУ МУЗЫКОЙ И МАТЕМАТИКОЙ
Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.
В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.
Свое отношение к математике и музыки ученые высказывались в своих личных переписках. Так, к примеру, Лейбниц в письме Гольдбаху пишет: “Музыка есть скрытое арифметическое упражнение души, не умеющей считать”. На что Гольдбах ему отвечает: “Музыка – это проявление скрытой математики”.
История знает массу людей, талант которых многогранен и способности к одному роду занятий как бы дополняют способности к другому. Леонардо да Винчи был скульптором, художником, архитектором, инженером; пел, преподавал пение и был первым, кто изучил природу вокального искусства.
Александр Сергеевич Грибоедов, русский писатель и дипломат, был еще композитором, пианистом и органистом. Михаил Иванович Глинка прекрасно рисовал. Эйнштейн играл на скрипке... Дети, обучающиеся музыке, обычно обнаруживают способности и тягу к другим видам искусства, потому что, помимо когнитивных способностей, музыка развивает эмоции, улучшает личностные качества.
Однако, одним из первых, кто попытался выразить красоту музыки с помощью чисел, был Пифагор. Он создал свою школу мудрости, положив в ее основу два предмета – музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.
Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Родился Пифагор около 570 года до нашей эры на острове Самосее. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева. Они проводили занятия математикой под музыку, так как заметили, что она благотворно влияет на интеллект. Он учился музыки в Египте и сделал ее предметом науки в Италии. Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Одним из достижений Пифагора и его последователей в математической теории музыки был разработанный ими «Пифагоров строй». Новая технология использовалась для настройки популярного в то время инструмента – лиры. Тем не менее, «Пифагоров строй» был несовершенен, как и древнегреческая арифметика. Расстояние между соседними звуками «Пифагорова строя» неодинаковые. Он – неравномерный. Чтобы сыграть мелодию, от какой- либо другой ноты, лиру каждый раз нужно перенастраивать. Исследованию музыки посвящали свои работы многие величайшие математики, такие как: Рене Декарт ( его первый труд - “Compendium Musicae” в переводе “Трактат о музыке” ) , Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли и другие.
Вывод. «Раздумывая об искусстве и науке, об их взаимосвязях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая и духовная деятельность человека. Что между ними размещается все, что человечество создало в области наук и искусства» – писал Г. Нейгауз. Изучив работы ученых, мною было установлено, что в прошлом были неоднократные попытки рассматривать музыку, как один из объектов изучения математики. Таким образом, многие учёные в древности считали, что гармония чисел является сродни гармонии звуков и дополняет друг друга, музыку и математику.
ПРАКТИЧЕСКАЯ ЧАСТЬ.
Создание математической модели музыкального фрагмента.
Рассмотрим фрагмент польки А. Спадавеккиа «Добрый хук» из кинофильма «Золушка». Попробуем сделать математическую модель этого произведения: каждой ноте соответствует номер ступени. Цифра 1 – I ступень, 2 – II ,3 – III, 4 – IV, 5 – V ,6 – VI ,7 – VII, 8 – I, 9 – II ,10 – III. Переложили ноты на числа и получили при этом такой ряд чисел:
Правая рука: 3553 l 455 l 466 l 531 l 3553 l 455 l 3653 l 1 II
Левая рука 1535 l 2545 l 2545 l 1535 l 1535 l 2545 l 2545 l 351 II
Черта между цифрами служит тактовой четой, то есть делит их на такты, так как сделано в произведении. 
В музыке есть понятие – устойчивые ступени, на которых строится тоническое трезвучие (Т5/3): 1, 3, 5 ступени.
Если в каждом полном такте сложить номера устойчивых ступеней, то мы заметим следующую закономерность:
Правая рука
Левая рука
1 такт
3+5+3+5=16
1+5+3+5=14
2 такт
4+5+5=14
2+5+4+5=16
3 такт
4+6+6=16
2+5+4+5=16
4 такт
5+3+1=9
1+5+3+5=14
5 такт
3+5+3+5=16
1+5+3+5=14
6 такт
4+5+5=14
2+5+4+5=16
7 такт
3+6+5+3=17
2+5+4+5=16
8 такт
1
3+5+1=9
Наблюдаем, что в произведении есть повторяющиеся группы чисел и для левой руки: 16,14,16,9,16,14,17,1 и для правой руки 14,16,16,14,14,16,16,9 – это 14,16.
Ритм – один из важнейших элементов музыки. Ритм – чередование длительностей. Рассмотрим ритм 3/4, музыканты называют его размером. В такте могут встречаться такие чередования длительностей:
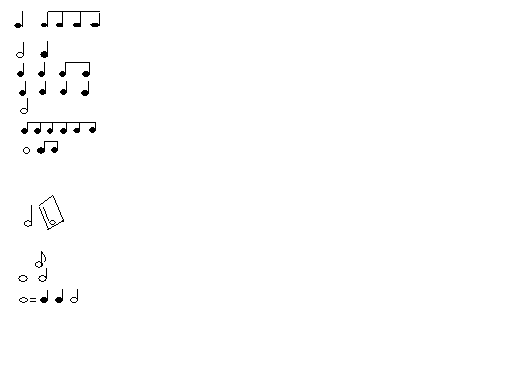
1.
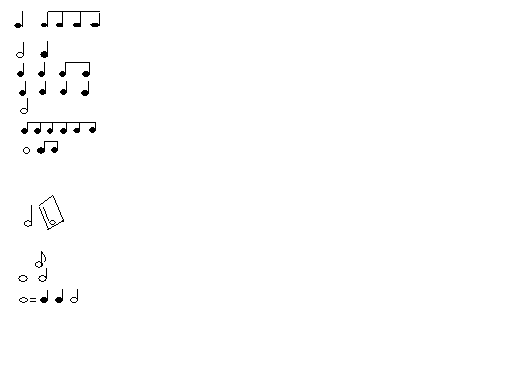
3.
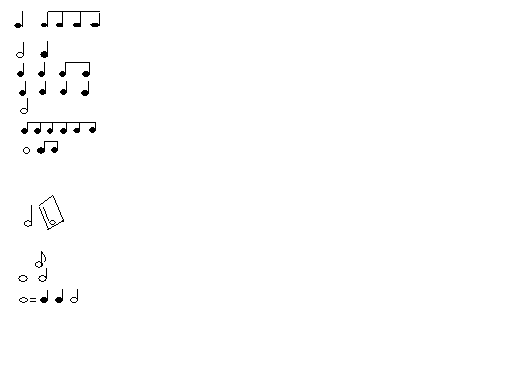
2.
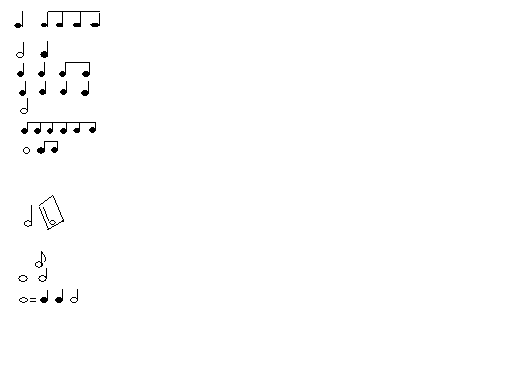
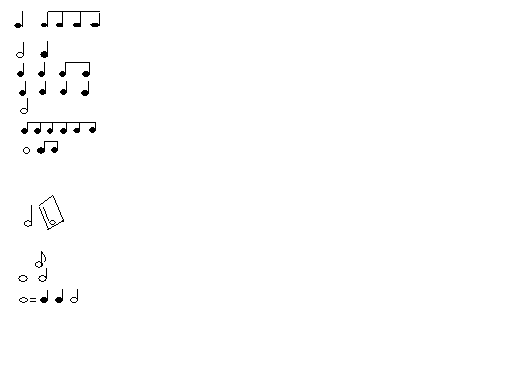
7.
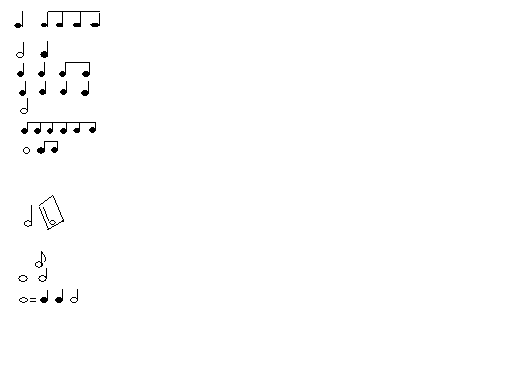
6.
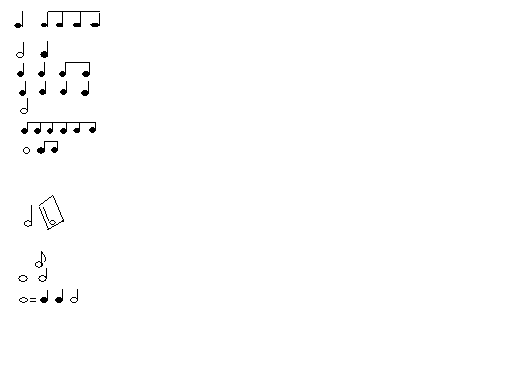
5. 
4.
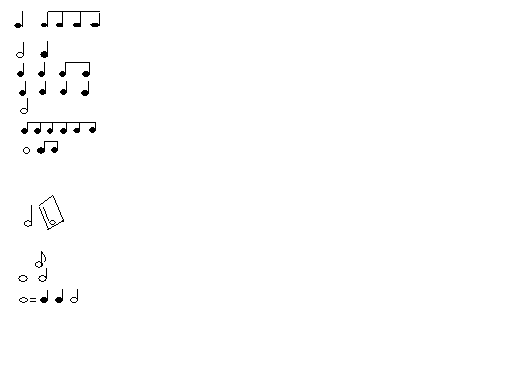
В музыке существуют и другие размеры 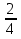 ,
, 
Рассмотрим ритм, размер  чередования длительностей: 1/2 I 1/4 1/4 I 1/8 1/8 1/ 8 1/8 II
чередования длительностей: 1/2 I 1/4 1/4 I 1/8 1/8 1/ 8 1/8 II
Правая рука
Левая рука
1 такт
1/8+1/8+1/8+1/8=4/8
1/8+1/8+1/8+1/8=4/8
2 такт
1/8+1/8+1/4=2/8+1/4=4/8
1/8+1/8+1/8+1/8=4/8
3 такт
1/8+1/8+1/4=2/8+1/4=4/8
1/8+1/8+1/8+1/8=4/8
4 такт
1/8+1/8+1/4=2/8+1/4=4/8
1/8+1/8+1/8+1/8=4/8
5 такт
1/8+1/8+1/8+1/8=4/8
1/8+1/8+1/8+1/8=4/8
6 такт
1/8+1/8+1/4=2/8+1/4=4/8
1/8+1/8+1/8+1/8=4/8
7 такт
1/8+1/8+1/8+1/8=4/8
1/8+1/8+1/8+1/8=4/8
8 такт
1/2
1/8+1/8+1/4=2/8+1/4=4/8
Сумма длительностей в каждом такте равна размеру 2/4=1/2=4/8.
Найдем сумму длительностей всех нот музыкальной фразы: 4/8+4/8+4/8+4/8+4/8+4/8+4/8+1/2=28/8+1/2=7/2+1/2=8/2=4
Сумма всех длительностей в музыкальной фразе равна целому числу.
Значит, зная ступени, длительности нот, размер я могу записать эту пьесу в любой другой тональности или от другой ноты, т. е. транспонировать.
Транспонировние. «Плясовая».
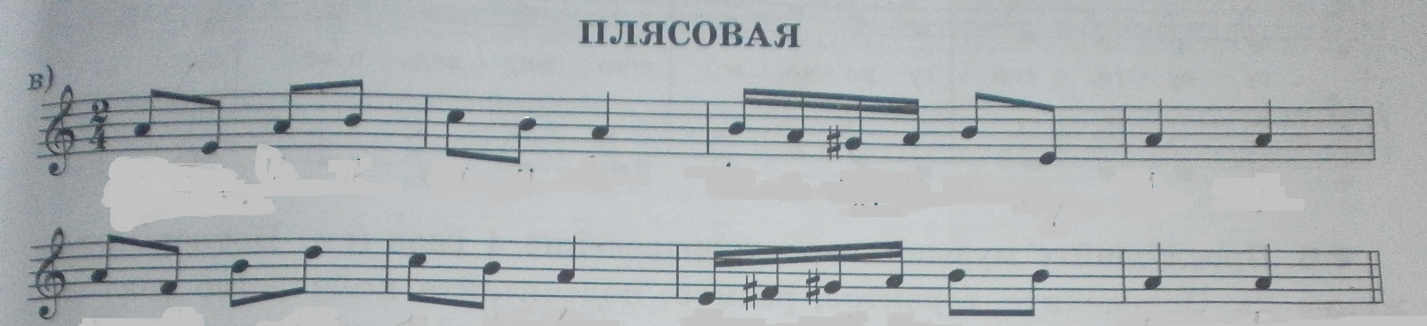
Проставив ступени и записав длительности нот, я получила математическую модель пьесы, чтобы не перепутать октавы я поставила стрелочки, но можно было у каждой ступени указать номер октавы.
1.Последовательность ступеней 1512 321 21# 7 1 2 5 11 1624 321 5#6#7122 11
2.Размер 2/4 и длительности: 1/8 1/8 1/8 1/8 1/8 1/8 1/4 1/16 1/16 1/16 1/16 1/8 1/8 1/4 1/4 1/8 1/8 1/8 1/8 1/8 1/8 1/4 I /16 1/16 1/16 1/16 1/8 1/8 1/4 1/4
3. Сложила устойчивые ступени, получила последовательность 8,4,7,2,1,4,6,2. Повторение чисел есть , 4 повторяется через 3 цифры и 2 повторяется через 3 цифры.
Правая рука
1 такт
1+5+2=8
2 такт
3+1=4
3 такт
1+1+5=7
4 такт
1+1=2
5 такт
1
6 такт
3+1=4
7 такт
5+1=6
8 такт
1+1=2
Затем записала гамму от ноты фа и проставила номера ступеней:

Проставила ступени в каждом такте и записала мелодию.
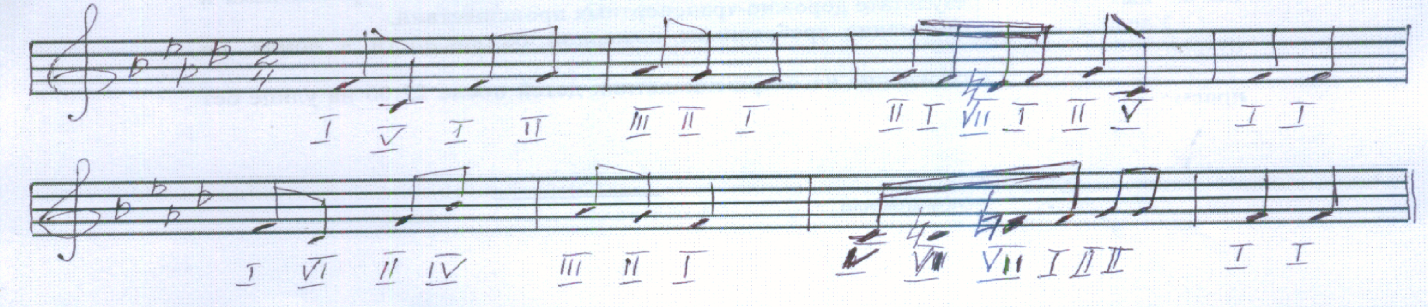
В своей исследовательской работе я выдвинула гипотезу о том, что любое музыкальное произведение можно представить как математическую модель.
По изложенному в работе способу перевода из нот в числовой ряд следует, что моя гипотеза верна, так как способов перевода может быть несколько. В работе я рассмотрела два способа: запись мелодии по ступеням и сложение устойчивых ступеней, запись ритмического рисунка с помощью дробей. Данная модель помогла транспонировать мелодию в другую тональность.
Исследование дат рождения
Следуя теории Пифагора, числа обладают абсолютной властью над всеми событиями, над всеми живыми существами, а значит, числа правят музыкой. В своих работах он утверждал, что музыка подчиняется высшему закону (математике) и вследствие этого восстанавливает в организме человека гармонию.
Нумерология – паранаука о числах. Нумерология имеет еще одно распространенная название – магия чисел. В нумерологии все слова, имена, числа можно свести к единичным разрядам (однозначным человеком), которые соответствует оккультным характеристикам, влияющим на жизнь человека. Это значит, что каждому числу, согласно нумерологии, соответствует определенные свойства, образы и понятия. Нумерологию используют для определенного характера человека, его природных способностей для выявления сильных и слабых сторон его личности, а также для определения характера человека, его природных способностей, для выявления сильных и слабых сторон его личностей, а также для определения подходящих профессии, места проживания и многих других факторов.
Даты рождений – это ряд чисел. Попробуем установить связь между числами и музыкой.
Мною были исследованы даты рождений 12 учащихся 5а класса, в котором я обучаюсь. Как известно дата – набор цифр. Мы предложим даты на ноты. В таблице, где знак «– », мелодия звучала негармонично, а значит, диссонанс. А если мелодично, то знак « + » – это консонанс. Каждой ноте мы присвоили номер ступени. До – 0, ре -1, ми – 2, фа – 3, соль – 4, ля – 5, си – 6, до– 7, ре – 8, ми – 9.

У каждого человека получилось по мелодическому ряду:
№
ФИ
Дата
Нотная последовательность
увлечения
1
Борцов Евгений
18.06.2003

_
акробатика
2
Горяинова Надежда
26.09.2003

_
литература, биология
4
Калачева Дарья
04.01.2003

_
особых увлечений нет, успехи в точных науках
5
Кирман Алина
05.09.2003

_
спорт, точные науки, танцы
10
Макарова Марина
26.12.2002

_
точные науки, танцы
6
Козлова Татьяна
08.03.2003

+
спорт, танцы
7
Лебедь Диана
11.10.2003

+
музыка
8
Малашенко Виктор
08.09.2003

+
конструирование, хорошо поет
9
Плотников Петр
07.08.2003

+
Хорошо поет, конструирование, точные науки
3
Жукова Арина
21.09.2003

+
художественная школа
После того, как мы переложили даты рождения на мелодию, попробуем установить связь между звучанием даты рождения и способностями человека.
I Группа (дети, у которых мелодии благозвучные):
№
ФИ
Дата
Нотная последовательность
увлечения
6
Козлова Татьяна
08.03.2003

+
спорт, танцы
7
Лебедь Диана
11.10.2003

+
музыка
8
Малашенко Виктор
08.09.2003

+
конструирование, хорошо поет
9
Плотников Петр
07.08.2003

+
Хорошо поет, конструирование, точные науки
3
Жукова Арина
21.09.2003

+
художественная школа
II группа (дети, у которых мелодии звучали «резко»):
№
ФИ
Дата
Нотная последовательность
увлечения
1
Борцов Евгений
18.06.2003

_
акробатика
2
Горяинова Надежда
26.09.2003

_
литература, биология
4
Калачева Дарья
04.01.2003

_
особых увлечений нет, успехи в точных науках
5
Кирман Алина
05.09.2003

_
спорт, точные науки, танцы
10
Макарова Марина
26.12.2002

_
точные науки, танцы
Методом опроса я выяснила, чем каждый ученик увлекается.
Дети класса творческие люди на это влияют их даты рождения. В первой группе, музыкальный ряд звучал мелодичнее, большинство детей с творческими наклонностями: некоторые из них занимаются в художественной школе или танцами. Данная группа детей обладает творческими способностями, косвенно или напрямую связана с музыкой.
Во второй группе, где музыкальный звучал «резко», надо отметить, что очень «резко, даже безобразно» звучащих не было, большинство детей занимаются изучением точных наук, техническим моделированием, предпочитают занятия спортом.
Следует отметить, что в исследуемой группе оказались те, кто по тем или иным причинам ничем не увлекаются и не занимаются в каких либо секциях. Предполагаю, что возможно, они имеют эти склонности, но они ещё не реализовали их.
Вывод: большее количества учащихся класса имеют творческие способности. Возможно, именно с этим связанно активное участие класса во всех школьных мероприятиях, свободно организуем классные вечера, концерты для родителей.
Мои исследования оказались интересны не только мне, но и одноклассникам.
ЗАКЛЮЧЕНИЕ.
В результате проделанной работы мною были выполнены поставленные задачи. Рассмотрела связь ритмов и чисел, дробей и длительностей нот. Работа над этой темой позволила выявить много интересной информации о закономерностях, которые встречаются в музыке и математике. Построила математическую модель музыкального произведения полька «Добрый жук» из к/ф « Золушка». Установила связь между датами и ступенями, переложила даты рождений одноклассников на музыку. Но для утверждения того, что звучание даты рождения определяет определенный тип особенностей человека, необходимо большее количество исследуемых.
Возможность перевода нот в числовой ряд подтверждает мою гипотезу. Математика – царица наук, тесным образом перекликается с музыкой. Несомненно, математика пронизывает музыку.
Выполняя работу, я отметила, что в мелодии постоянно происходит чередование сильных и слабых долей, чередование тактов, где сильных долей больше с тактами, где меньше или только одна сильная доля, что музыкальная фраза заканчивается 1 ступенью. Если проанализировать больше произведений и более сложные музыкальные формы, то вероятно можно выявить еще закономерности. Также мне пришла идея попробовать одну и ту же последовательность нот записать в разных ритмических рисунках, а может и придумать свою композицию, например, по «красивой» числовой последовательности.
Список литературы:
1. Деплан И. Я. Мир чисел. М.: «Просвещение», 2005
2.Дэвид Филипс. Нумерология и открытие внутреннего “Я”. Полное практическое руководство. СПб: София, 2007, 256с.
3. Жмудь Л. Я. Пифагор и его школа М.: Наука, 1990, 192с.
4. Холопов Ю. Н. Консонанс и диссонанс // Музыкальный энциклопедический словарь. М.: Советская энциклопедия, 1990.
5. Сольфеджио 2 класс
6. Энциклопедия для детей. Т. 7. Искусство. Ч. 1. – Э68-е изд., испр./Глав. Ред. М.Д. Аксенова. – М..6 Аванта +, 2006 – 688 с.: ил.
7. Энциклопедический словарь юного математика. М.; «Педагогика» 1985г
12. Я познаю мир: Детская энциклопедия: Музыка /авт. А.С. Кленов. Под общей ред. О.Г. Хинн. – М.: ООО Фирма «Издательство АСТ», 2010. – 46
Интернет ресурсы:
1.http://www.stonot.ru/
2.http://www.krugosvet.ru/
3.http://www.wikipedia.org/
4. http://ru.wikibooks.org/wiki
5.http://www.piano-notes.net/
infourok.ru
Пифагорова гамма.
Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.
Плутарх.
Введение
Известно, что при восприятии музыкального произведения в сознании слушателя нередко возникают различного рода представления (зрительные, двигательные, осязательные, слуховые и прочие). Другие виды искусства например: рисунок или картина, мы воспринимаем как изображение того или иного определенного объекта, рассказ или стихотворение при помощи конкретных слов, сообщают нам о том или ином событии, явлении, предмете. В музыке же отражаются существенные стороны жизни, главным образом через раскрытие внутреннего мира человека, человеческих переживаний, его идей, чувств и др. Некоторые считают, что дети, играющие на музыкальных инструментах грамотнее других. К сожалению, об этом факте сейчас забыли. И родители, и учителя. Нотные тетради сегодня явно проигрывают компьютерам, иностранным языкам и точным наукам. Уроки музыки в наше время непопулярны. Ни в форме целенаправленного специального музыкального образования, ни в виде частных занятий для общего развития. В то время как еще до нашей эры Пифагор создал свою «школу мудрости» положив в ее основу два «искусства» – музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. В развитии пространственного мышления – верный помощник – музыка, т.к. из-за плохого пространственного мышления учащиеся часто не могут подписать в столбик цифры при арифметических действиях, правильно понять условия задач (особенно на тему времени, скорости и расстояния), ошибаются в устном арифметическом счете. Музыка учит не только видеть, но и воспроизводить увиденное; не только слышать, но и предоставлять то, что слышишь.
Гаммой или звукорядом, называется последовательность звуков (ступеней) некоторой музыкальной системы (лада), расположенных, начиная от основного звука (основного тона), в восходящем порядке.
Название «гамма» происходит от греческой буквы Г γ (гамма), которой в средние века обозначали крайний тон звукоряда, а затем и весь звукоряд. Важнейшей характеристикой музыкального строя является его высота, представляющая отражение в сознании частоты колебания звучащего тела, например, струны. Чем больше частота колебаний струны, тем «выше» представляется нам звук. Каждый отдельно взятый звук не образует музыкальной системы и, если он не слишком громкий, не вызывает у нас особой реакции. Однако уже сочетание двух звуков в иных случаях получается приятным и благозвучным, а в других, наоборот, «режет» ухо. Согласованное сочетание двух звуков называется консонансом, а несогласованное – диссонансом. Ясно, что консонанс или диссонанс двух тонов определяется высотным расстоянием между этими тонами или интервалом.
Интервалом между двумя тональностями мы назовем порядковый номер ступени верхнего тона относительно нижнего в данном звукоряде.
Если нажать на фортепиано последовательно несколько клавиш, то получится бессвязный набор звуков. Конечно, эти звуки вроде бы подходят друг к другу, но их совокупность покажется оборванной, незаконченной. Есть наиболее устойчивая, основная ступень, которая называется тоникой. Итак, звуки как-то связаны между собой, одни из них являются неустойчивыми и тяготеют к другим – устойчивым. Но не только от этого зависит характер музыкальной системы. Например можно нажать восемь клавиш от ноты до (до мажор), и от ноты ля (ля минор), и услышать то, что эти гаммы звучат по-разному: первая – мажор – грустно и пасмурно. Следовательно, существует и другая характеристика системы звуков – наклонение: мажорное или минорное.
Ладом называется приятная для слуха взаимосвязь музыкальных звуков, определяемых зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука – тоники, и имеющая определенный характер звучания – наклонение.
| Порядок интервалов (снизу вверх) | Древнегреческое название лада | Средневековое название лада |
Наклонение |
| 1 1 ½ 1 1 1 ½ | Лидийский | Ионийский | Натур. мажор |
| 1 ½ 1 1 1 ½ 1 | Фригийский | Дорийский | Минорное |
| ½ 1 1 1 ½ 1 1 | Дорийский | Фригийский | Минорное |
| ½ 1 1 ½ 1 1 1 | Гипердорийский | Гипофригийский | Минорное |
| 1 1 1 ½ 1 1 ½ | Гиполидийский | Лидийский | Мажорное |
| 1 1 ½ 1 1 ½ 1 | Гипофригийский (ионийский) | Миксолидийский | Мажорное |
| 1 ½ 1 1 ½ 1 1 | Гиподорийский (эолийский) | Эолийский | Натур. мажор |
История музыкальной культуры знает множество ладов, свойственных разным народам и разным временам. Древние греки знали с десяток ладов, а лады некоторых восточных стран и Индии чрезвычайно сложны, своеобразны и непривычны для европейского слуха.
Наиболее распространенные современные лады состоят из семи основных ступеней, каждая из которых может повышаться или понижаться, что дает еще пять дополнительных звуков. Таким образом, диатоническая (7-ступенчатая) гамма лада превращается в хроматическую (12-звуковую). Первой ступенью лада является тоника. Законы строения лада – это целая наука, краеугольный камень музыкознания, а изучению этих законов многие ученые и композиторы посвятили всю жизнь.
Нам известен пифагоров строй, т.е. математическое выражение интервальных коэффициентов, лидийской гаммы, или, в современной терминологии, строй натурального мажора:
1 9 81 4 3 27 243 2
8 64 3 2 16 128
до ре ми фа соль ля си до
9 9 256 9 9 9 256
8 8 243 8 8 8 243
Здесь цифры внизу обозначают интервальные коэффициенты соседних ступеней гаммы; напомним, что 9/8 есть тон, а 256/243 – полутон. Основные консонансные (консонанс – согласованное сочетание двух звуков) интервалы в пределах октавы – квинта и кварта – являются соответственно средним арифметическим и средним гармоническим частот основного тона и октавы. Кроме того, октава, квинта, кварта и тон образуют геометрическую пропорцию:
октава / квинта = кварта / тон.
Таким образом, музыкальная гамма разделена на пропорциональные части: она буквально пронизана пропорциями, а пропорциональность, как мы знаем является одним из объективных критериев красоты. Однако на этом математика музыкальной гаммы не кончается, а, скорее, только начинается.
Итак, для того, чтобы иметь возможность переходить из лада в лад, строй должен быть равномерным.
Каждый лад греки наполняли определенным этико-эстетичетким содержанием, его «этосом», устанавливая ясную связь между музыкальными образами и состоянием души. Музыке приписывали магические и даже врачебные функции, но особенное значение придавалось музыке как средству воспитания.
В общем мы разобрали Пифагоров строй. И увидели, насколько тонко древние греки чувствовал
Заключение
Музыка приучает к ежедневному труду, воспитывает терпение, силу води и усидчивость. Совершенствует эмоции, дает особое видение окружающего мира, что так необходимы для изучения математики.
Прослушивание музыки Моцарта способствует развитию умственных математических способностей. Музыка Брамса избавляет от усталости, а музыка Чайковского помогает бороться с раздражительностью. В общем музыка организовывает работу мозга. Развить слух, нужный для того чтобы правильно понять произведение, очень не просто. Развитие слуха достигается активным слушанием музыки, игрой на музыкальных инструментах, а также специальными занятиями сольфеджио. Реже встречающийся абсолютный слух правильнее было бы назвать абсолютной памятью на высоту звука: люди, обладающие таким слухом, точно узнают высоту каждого отдельно взятого звука, не сравнивая его с каким-либо другим. Для развития музыканта большое значение имеет и внутренний слух, т.е. способность внутренне слышать музыку, а также умение мысленно воспроизвести ее, читая ноты. Пифагор, знаменитый философ и математик, положил начало особой науке – музыкальной акустике. Альберт Эйнштейн тоже изучал музыку, даже играл на скрипке. Он говорил: "Настоящая наука и настоящая музыка требуют однородного мыслительного процесса.” Благодаря этому он открыл закон относительности. Михаил Иванович Глинка – гениальный русский композитор – благодаря хорошей игре на скрипке, прекрасно рисовал.
Итак, музыка дает нам возможность воспринимать не только эмоции, идею произведения, но она еще помогает нам научиться слышать, мыслить и запоминать.
и музыку.
sar18021977.ucoz.ru
Алиса Самбурская, к.п.н.
«Взаимосвязью между музыкой и математикой интересовались еще в древности. И это неудивительно, поскольку присутствие в музыке математического компонента очевидно. Самые важные характеристики звука – его высота и длительность – определяются количеством колебаний и продолжительностью звучания, которые в свою очередь выражаются посредством конкретного числа.
Как известно, пифагорейцы предположили, что в основе мира лежит некая абстракция – число. Более того, число в различных ипостасях: «бог-число», «вещь-число», «искусство-число» и т.д. стало у них сущностью мира. Эта числовая конструкция бытия мыслилась ими как конкретный «музыкально-числовой космос» или «строй мира», действующий гармонично во всех проявлениях. Таким образом, Пифагор и его последователи попытались объединить математику, гармонию и музыку в единую сущность не только космоса, но и человеческой души и конкретной вещи. Музыкальная гармония мыслилась древними как некая логически построенная система, которая имеет много общего с математикой. В глубокой древности было подмечено определенное соответствие между высотой звука и конкретным числом, определяющим длину струны. Именно по этому принципу был создан широко популярный в античности музыкальный инструмент – лира, который впоследствии стал эмблемой музыкальной искусства.
Рассмотрим взаимосвязи между математикой и музыкой с точки зрения ее теоретического построения. Основой математических знаний является арифметический счет. Счет, как числовой ряд, состоит из определенной последовательности чисел, в которой каждое последующее число больше предыдущего на одну единицу – и это уже само по себе является определенной ритмической закономерностью. Арифметические действия с числами происходят путем перемещения по этому числовому ряду либо в сторону увеличения, либо наоборот. Чтобы, например, к двум прибавить пять, нужно от 2 переместиться на 5 единиц в сторону увеличения чисел – получаем 7. По аналогии, музыкальный звукоряд – это последовательность музыкальных звуков, в которой каждый последующий звук выше предыдущего также на одну единицу, (в музыке ей соответствует полутон), если звукоряд восходящий. Cоответственно, если звукоряд нисходящий, то каждый последующий звук ниже предыдущего на пол-тона. Аналогично арифметическому действию мы можем вычислить музыкальный звук путем перемещения по музыкальному ряду.
Ученые, изучавшие взаимосвязь между восприятием музыки и мыслительными процессами (Генрих Гетце 1994, Мария Спайхигер 2000) утверждают, что оперируя математическим рядом чисел и выполняя любые арифметические действия «в уме», будь то сложение, вычитание, умножение, деление или даже извлечение корня и возведение в степень, человек достигает результата весьма похожими пространственными мыслительными операциями, что и при дифференциации звуковысотности и длительности. Нам также кажется весьма логичным утверждение, что существует определенная связь между арифметическими и музыкальными мыслительными операциями. При написании музыкального диктанта человек, не обладающий абсолютным музыкальным слухом вполне в состоянии записать точно и правильно прослушанную им мелодию, если он хорошо дифференцирует сравнительную звуковысотность (выше-ниже), темп (быстрее-медленнее), музыкальные длительности (дольше, короче, длиннее). Способность дифференцировать эти сравнительные соотношения тренируется и развивается музыкальными занятиями. Те же соотношения используются и в математике.
Определение интервала в музыке есть не что иное как вычисление разности между двумя звуками. Интересно и то, что когда музыканты воспринимают музыкальные интервалы, то в их воображении автоматически возникает числовой ряд, отрезок которого равен определенному интервальному отрезку, т.е. представляется отрезок чисел от 1 до 4 - если слышат кварту, от 1 до 7, если септиму и т.д. Наверное, возможно также представление септимы как отрезок чисел от 2 до 9 или от 3 до 10 – он также равен 7.
Построение музыкального произведения имеет свою логику и числовые характеристики. Соотношение частей музыкального произведения образуют музыкальную форму. Составные элементы музыкальных форм – мотивы, фразы, предложения, периоды – в совокупности образуют мелодию. Обычно мотив умещается в 1-2 такта, отрезок из 2-3 мотивов образует относительно законченное музыкальное построение, называемое фразой; 2фразы образуют предложение, 2 предложения составляют законченный раздел, завершающийся кадансом и который называется периодом, который состоит в свою очередь из 8 или 16 тактов. Разные способы развития и сопоставления элементов мелодии образуют различные типы музыкальных форм. Так, последование 2 периодов образуют простую двухчастную форму, 3 раздела образуют сложную трехчастную форму. Существуют и другие музыкальные формы: тема с вариациями, куплетная форма, рондо, сонатная форма, фуга, смешанные формы. Но все они представляют собой определенную формулу музыкального построения, как, например, известная 12-тактовая формула классического блюза или формула построения джазовой пьесы.
Изучив определенные законы построения музыкального произведения, можно научиться сочинять музыку – по формуле, точно также как и формально сочинять стихи. (Правда, нет гарантии, что эти произведения будут представлять из себя какую-либо художественную ценность). И хотя композиторами становятся далеко не все студенты музыкальных отделений, тем не менее на занятиях по музыкальной гармонии фуги сочиняют все.
Что же касается нотной записи, то здесь без математических знаний не обойтись! То, с чего собственно и начинается музыка, один из основных элементов выразительности мелодии (наряду с различной высотой, интервальными соотношениями звуков, составляющих мелодию) – это ритм. Мелодия образуется только в том случае, если звуки организованы ритмически, т.е. определяются определенными длительностями. Чередование звуков вне ритма не воспринимается как мелодия; ритм же подчас настолько ярко характеризует мелодию, что ее можно узнать только по обозначению длительностей звуков без указания их высоты.
Основные ритмические измерения, применяемые в музыке - это относительные длительности: целая нота, половинная, четвертная, восьмая, шестнадцатая, тридцать вторая.
Относительной длительностью называется продолжительность данного звука по сравнению с другими. Абсолютная же длительность звуков в музыке устанавливается темпом, т.е. скоростью звучания, а именно показателем скорости по метроному. Доля такта – это единица метра музыкального размера. Доли такта представляют собой малые отрезки одинаковой длительности, из которых складывается данный текст. Величина доли такта указывается в знаменателе дроби, обозначающей размер: например, в размере 3/4 – долей такта является четвертная нота, в размере 2/2 – половинная, в размере 3/8 – восьмая. Числитель дроби указывает количество долей в такте. Показатель по метроному определяет, сколько долей (половинных, четвертных или восьмых) должно прозвучать в течение минуты.
Так, обозначение четвертная нота = 80 указывает, что в минуту должны прозвучать 80 четвертных долей (и соответственно – 40 половинных или 160 восьмых и т.д.). Причем абсолютная длительность звуков является важнейшим условием музыкальной выразительности, от которого зависит замысел музыкального произведения.
Таким образом, общность и единообразие математических и музыкально-теоретических процессов очевидно, и это служит свидетельством того, что занятия математикой могут значительно облегчить изучение музыкальной гармонии и сольфеджио, и наоборот – решение музыкальных задач и упражнений или даже просто активное восприятие музыки может способствовать улучшению арифметических навыков.
В связи с этим нам представляется весьма интересным использование музыкальных видов деятельности при обучении детей математике.
____
ГЛОССАРИЙ
Полутон – наименьшее расстояние между двумя различными по высоте звуками, «единица измерения» в музыкальной системе.
Диктант музыкальный – специальное упражнение по сольфеджио, небольшой музыкальный отрывок, предназначенный для прослушиваний, запоминания и записи нотными знаками.
Абсолютный слух – абсолютная память на высоту любого звука.
Музыкальный интервал – расстояние между двумя звуками. Если звуки взяты последовательно, то такой интервал называется мелодический, если звуки взяты одновременно – гармонический.» [сайт "Музыка интеллекта" http://alicepush.ucoz.ru/]
***
Впрочем… ?
Великий немецкий композитор Людвиг Ван Бетховен так и не смог освоить все арифметические операции. Умножение и деление были для него нераскрытой тайной. Например, чтобы умножить 12 на 60, гениальный композитор 60 раз складывал по 12. Правда и математики не оставались "в долгу" перед музыкальным искусством. Так, великому австрийскому математику Георгу Вега музыка была настолько чужда, что он говорил: "Не существует ни хорошей музыки, ни плохой. Существует лишь большой шум и малый шум". [Математический юмор. //Виртуальная школа юного математика. - http://www.math.md/school/zanimat/iumor/iumor.html]
***
И тем не менее !
studfiles.net
Настоящая наука и настоящая музыка требуют однородного мыслительного процесса. А. Эйнштейн
Нам известен пифагоров строй, т.е. математическое выражение интервальных коэффициентов, лидийской гаммы, или, в современной терминологии, строй натурального мажора:
1 9 81 4 3 27 243 2
8 64 3 2 16 128
до ре ми фа соль ля си до
9 9 256 9 9 9 256
8 8 243 8 8 8 243
Здесь цифры внизу обозначают интервальные коэффициенты соседних ступеней гаммы; напомним, что 9/8 есть тон, а 256/243- полутон. Основные консонансные (консонанс — согласованное сочетание двух звуков ) интервалы в пределах октавы — квинта и кварта — являются соответственно средним арифметическим и средним гармоническим частот основного тона и октавы. Кроме того, октава, квинта, кварта и тон образуют геометрическую пропорцию:
октава / квинта = кварта / тон.
Таким образом, музыкальная гамма разделена на пропорциональные части: она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты. Однако на этом математика музыкальной гаммы не кончается, а, скорее, только начинается.
Прежде всего, из соотношения видно, что расстояния между соседними ступенями пифагорова строя неодинаковы. Поэтому, во-первых, от ноты до можно было играть только в лидийском ладу, а чтобы сыграть от этой ноты, скажем, в дорийском ладу, необходимо было перестраивать почти все струны лиры. Во-вторых, от ноты ре получался уже не лидийский, а фригийский лад и, вообще, от каждой новой ноты начинался новый лад ( 7 ладов — по одному на каждую из 7 нот октавы). Поэтому, чтобы сыграть мелодию в лидийском ладу от другой ноты (чего, безусловно, требовали ограниченные возможности человеческого голоса: один поет выше, другой — ниже), лиру, также следовало перестраивать. (Конечно, если всю жизнь играть в одном ладу и одной тональности, то семи нот в октаве будет вполне достаточно. До сих пор прекрасно обходятся семью звуками некоторые гармошки и другие инструменты).
Итак, для того, чтобы иметь возможность переходить из лада в лад и из тональности в тональность, строй должен быть равномерным, т.е. иметь одинаково высотные расстояния (интервальные коэффициенты) между звуками. Казалось бы, что проще: нужно разделить каждый тон — интервал пополам на два полутона, т.е. получить еще пять дополнительных звуков, и шкала пифагорова строя станет равномерной. Но вот тут то и таилась основная трудность.
Дело в том, что половина тона (V9/8~1,0607) в точности не равна полутону (256/243~1,0545). Поэтому если в качестве единого масштаба строя взять полутон V9/8, т.е. заменить на него имеющиеся два полутона 256/243, то эти 12 новых полутонов приведут нас не точно в октаву, а чуточку выше: (V9/8) 12=(9/8)6=2,0273. Интервал между октавой, полученной шагами по 12-равномерным полутонам V9/8, и чистой октавой равен и называется пифагоровой коммой (коммой в музыкальной акустике называется интервал, не превышающий 1/9 целого тона. Пифагорова комма приблизительно равна 1/9 тона).
Представляя пифагорову комму в виде
мы получим ещё один важный результат: 12 квинт с точностью до пифагоровой коммы равны 7 октавам.
Но , т.е. новый полутон содержал иррациональное число V2, которого пифагорейцы боялись, как огня. Взять столь “некрасивое” число в качестве единицы измерения музыкальной гаммы было немыслимым для пифагорейцев: это противоречило всей философии целочисленных отношений. Поэтому пифагорейцы пошли другим путём: в качестве основы музыкальной гаммы они взяли квинту, красивое число 3/2.
Рассмотрим ряд, составленный из степеней числа 3/2:
......
Оказывается, с помощью этого красивого симметричного ряда можно получить все интервальные коэффициенты пифагорова строя. Начнем с середины ряда и все получаемые звуки будем сводить в одну октаву, умножая или деля их интервальные коэффициенты на нужные степени числа 2 (интервальный коэффициент октавы)ю Новые звуки будем обозначать либо ближайшим снизу основным звуком с добавлением слова “диез ” () при движении по квинтам вверх, либо ближайшим сверху основным звуком с добавлением слова “бемоль ” () при движении по квинтам вниз. Это означает соответственно повышение или понижение основного звука. Итак,
соль
ре
ля
Как видим, двигаясь по квинтам вверх и вниз от основного тона, мы получили все ступени пифагорова строя, каждая из которых в свою очередь может быть повышена, понижена, дважды повышена или понижена и т.д. Процесс этот, к сожалению, бесконечен. Точного октавного повторения основного тона (до) мы так и не получим. (Легко видеть, что си-диез и ре-бемоль-бемоль совпадают с основным тоном (до) опять же с точностью до пифагоровой коммы.) Следовательно, и точно разделить октаву на целое число частей этим методом мы не сможем.
Таким образом, желая разделить пять тонов на полутона, мы получили, по крайней мере, 10 промежуточных звуков.
Какие из этих дополнительных звуков взять: с бемолями или с диезами”? Для музыкантов, играющих на инструментах с нефиксированной высотой звуков (скрипачей, например), эта проблема не стоит. Они берут и те, и другие. В результате звучание скрипки становится более выразительным и контрастным, так как в ладе обостряются тяготения неустойчивых звуков к устойчивым. Этим во многом объясняется то “волшебное пение” скрипки, которое доступно ей одной.
Что касается инструментов с фиксированной высотой звуков, то введение 10 дополнительных звуков на 7 основных слишком бы усложнило и инструменты, и игру на них. Тем более, что и это не решщало окончательно проблему и более тонкие построения требовали всё новых и новых звуков. На сегодня в теории музыки известна масса строев с числом ступеней от 17 до 84! Но все они так и остались в кабинетах теоретиков. Практика же, руководствуясь мудрым критерием простоты (и красоты ), оставила только пять дополнительных звуков: по одному в каждом из целых тонов. Они и стали чёрными клавишами (дополнительными) фортепиано.
Так в октаве стало 12 звуков. Поскольку каждая пара дополнительных звуков отличалась лишь на пифагорову комму (это легко проверить), то их попросту приравнивали между собой (до-диез стал равен ре-бемолю и т.д.). Такое приравнивание звуков с одинаковой высотой, но разными названиями в теории музыки называется энгармонизмом. Тонкости ладового звучания были принесены в жертву простоте. Инструменты же с числом звуков в октаве, превышающим 12, можно увидеть только в музеях. В московском Музее музыкальной культуры имени М. И. Глинки хранится рояль русского писателя, музыканта и музыковеда В. Ф. Одоевского (1804-1869), в каждой октаве которого 17 клавиш.
Квинтовая цепь пифагорова строя дала простой способ настройки инструментов с фиксированной высотой звуков: органов, клавесинов, фортепиано. От основного тона (сегодня по общему признанию им является звук ля первой октавы) откладывалось? октав — скелет музыкальной шкалы. Эти октавы заполнялись 12 звуками вверх и вниз. Какие из звуков взять за дополнительные — повышенные или пониженные, — особого значения не имело. Важно было другое: пифагорова комма оставалась внутри октавы. Её можно было переместить в любое место октавы, но нельзя было сделать только одного: нельзя было от неё избавиться! И она продолжала портить кровь музыкантам на протяжении столетий. Почему?
Если взять пифагоров строй с пониженными дополнительными звуками:
си до ре ми фа соль ля си до1
.243 1 256 9 32 81 4 1024 3 128 27 16 243 2 512
256 243 8 27 64 3 729 2 81 16 9 128 243...
то в таком строе все квинты будут звучать чисто (иметь интервальный коэффициент 3/2), кроме одной. Квинта си — соль-бемоль будет иметь интервальный коэффициент 1024 / 729: 243 / 256 ~ 1,4798, а не 1,5! От чистой квинты она отличается на пифагорову комму: 1,5 / 1,4798 ~ 10136. Такая квинта на органе издавала пронзительный, неприятный звук, похожий на завывание волка, за что и была прозвана “волчьей квинтой” или просто “волком”. Обращением “волчьей квинты ” является “волчья кварта” соль-бемоль — си, которая тоже отличается от чистой кварты (4/3 = 1,333...) на пифагорову комму: 243 / 127: 1024 / 729 ~ 1,3515;
1,3515 / 1,3333 ~ 1,0136. Можно сказать, что вся история развития музыкальных строев была историей борьбы с “волками”. Но об этом — чуть позже.
А сейчас обратим внимание на второй существенный недостаток пифагорова строя. Его заметил ещё во II веке древнегреческий ученый пифагореец Дидим. Дело в том, что пифагорова терция (81 / 64) при гармоническом, т.е. одновременном, исполнении обоих тонов, образующих терцию, звучит слишком напряжённо. Дидим предложил заменить пифагорову терцию (81 / 64) так называемой “чистой терцией” (5 /4 = 80 / 64), которая гармонически звучит значительно приятнее, хотя, как видим, лишь чуть — чуть отличается от пифагоровой терции. Разность пифагоровой и чистой терций (81 / 64: 80 / 64 = 81 / 80 ~ 1,0125) называется дидимовой коммой и приблизительно равна1 / 10 целого тона.
Однако идеи Дидима, как это не раз случалось сучёными Древней Греции, опередили историю почти на полторы тысячи лет. Они не нашли подходящей почвы для развития, увяли, умерли и были воскрешены только в конце XV века...
… В XIV веке в Европе получает широкое распространение орган, ставший официальным инструментом католической церкви. С развитием органа развивается и многоголосие, которого не знала ни Древняя Греция, ни раннее средневековье. В течение столетий орган настраивался в пифагоровом строе. Никакого другого строя средневековье не знало. Но пифагоровы терции звучали на органе особенно жёстко и не давали покоя музыкантам.
В XVI веке выдающийся итальянский композитор и музыкальный теоретик Джозеффе Царлино (1517-1590) воскресил идеи Дидима. Так родился новый квинтово — терцовый строй, названный чистым строем. Новое всегда с трудом пробивает себе дорогу. Учение Царлино подверглось резким нападкам. Любопытно, что среди тех, кто не признавал учения Царлино и вёл с ним непримиримую борьбу, был Винченцо Галилей — выдающийся итальянский лютнист и отец великого революционера Галилео Галилея.
Чистая терция (5 /4), ставшая наравне с квинтой полноправной хозяйкой нового строя, звучит приятнее пифагоровой. Отметим одну поразительную закономерность: интервальный коэффициент чистой терции (её называют также большой терцией) есть среднее арифметическое интервальных коэффициентов основного тона (1) и квинты (3 /2):
А дополнение большой терции (5 /4) до квинты (3 /2) — малая терция (3 /2: 5 /4 = 6 /5) — является средним гармоническим основного тона и квинты:
Оба этих интервала дают приятное звучание; таким образом, закон целочисленных отношений Пифагора расширяется, а внутри музыкальной гаммы появляются ещё две пропорции!
Предполагают, что ещё Архит умел выражать большую и малую терции как среднее арифметическое и гармоническое тона и квинты. Однако письменное свидетельство этому мы находим лишь в объёмном труде “Универсальная гармония” Марена Мерсенна (1588-1648) — монаха францисканского ордена, французского математика, теоретика музыки и философа, учившегося в иезуитском колледже Ла Флеш вместе с Рене Декартом. Труд Мерсенна — нескончаемое исследование об интервалах, полное всеобъемлющих умозрений. На десяти страницах огромного формата автор глубокомысленно обсуждает, например, “является ли унисон консонансом”, и попутно решает вопрос, “как бы человек мог поднять землю”, и т.д. Однако, несмотря на чрезвычайную напыщенность, которая, впрочем, была неотъемлемой чертой всех сочинений того времени, работа Мерсенна содержала интересные идеи и прозрения. В частности, это касалось консонантности и пропорций большой и малой терций. Сегодня большую и малую терции относят к группе несовершенных консонансов.
Но вернёмся к работам Царлино. Выдающейся заслугой его было не только выявление консонантности большой терции (5 /4), но и построение “совершенной гармонии” — объединение большой терции и квинты в гармоническое трезвучие. Это был первый в истории музыки аккорд, а само трезвучие
ныне именуется мажорным и является основой всего гармонического языка музыки. Кроме того, Царлино обнаружил, что если отложить те же большую терцию и квинту вниз от основного тона, то окраска звучания аккорда существенно изменится. Светлые тона мажора подёргиваются пасмурной дымкой иного звучания — минора. Приводя аккорд 2/3: 4/5: 1 к основному тону (умножая на 3/2, т.е. сдвигая вверх на квинту), получаем минорное трезвучие
Так был открыт закон, известный сегодня каждому юному музыканту: смена большой терции на малую переводит мажорное трезвучие в минорное.
Мажорное трезвучие было взято за основу чистого строя. Обрамляя мажорное трезвучие 1: 5/4: 3/2 такими же трезвучиями сверху и снизу и сводя умножением и делением на 2 построенные звуки в одну октаву, получаем чистый строй лидийской гаммы (натурального мажора)
до ре ми фа соль ля си до1
1 9 5 4 3 5 15 2
8 4 3 2 3 8
9 10 16 9 10 9 16
8 9 15 8 9 8 15
Отмечены тоны, изменившиеся по сравнению с пифагоровым строем, цифры внизу обозначают интервалы между ступенями.
Как видим, числовые характеристики чистого строя более простые. Однако сам строй стал менее равномерным: в нём, кроме полутона 15 /16, появились две разновидности целых тонов 9/8 и 10/9. Знакомые с музыкальной грамотой, конечно, увидели, что мажорные трезвучия (4:5:6) чистого строя построены на тонике (до ), субдоминанте (фа), и доминанте (соль ).
С помощью целых тонов 9/8 и 10/9 и полутона 16/15 легко построить чистый строй фригийской гаммы:
9 6 4 3 5 16
1 8 5 3 2 3 9 2
Теперь стало два деления целых тонов чистого строя. Чистый строй в истории музыки сыграл короткую, но заметную роль. Его звучание стало намного ярче и богаче по сравнению с пифагоровым строем. Чистый строй способствовал формированию мажорного и минорного ладов, развитию музыкальной гармонии. Но...
Вместе с достоинствами пришли и недостатки. Всё те же ненавистные музыкантам “волки” поселились теперь уже не на дополнительных, а на основных ступенях чистого строя! Легко проверить, что квинта между II и VI ступенями (ре — ля) является самым настоящим “волком”: 5/3:9/8 = 27/20 = 1,35:
до ре ми фа соль ля си до1 ре1
..1 9 5 4 3 5 15 2 9 ...
8 4 3 2 3 8 4
|
|
Следовательно, настроив орган в чистом строе ноты до, например, органист не мог уже перейти в тональности ре мажор ире минор, т.е. в те тональности, где “волчья квинта” входит в тоническое трезвучие и встречается наиболее часто. Разумеется, приходилось исключать и те тональности, где эта квинта входила в доминанту и субдоминанту, которые также являются основными ступенями лада. Таким образом, органист оказывался что называется связанным по рукам: модуляции, т.е. переходы, в другие тональности были крайне ограничены и опасны, и это лишало музыку значительной части её выразительных средств.
“Волки” продолжали донимать органистов. На фоне “совершенной гармонии” чистого строя это было особенно невыносимо. Забавный случай рассказывают о французском композиторе и теоретике музыки, страстном приверженце чистого строя, Жане Рамо (1683-1764). Однажды Рамо, желая отказаться от предлагаемой ему должности церковного органиста, выпустил из органа столько “волков”, что привёл в ужас святых отцов и убедил их в своей “бесталанности”. Святые отцы поспешили удалиться вместе со своими лестными предложениями.
Однако проблема оставалась. Выгнать “волков” из органа, т.е. найти закон построения нового музыкального строя, а значит, и рецепт новой настройки органа, наряду с музыкантами безрезультатно пытались и математики: Кеплер, Декарт, Лейбниц, Эйлер. О теории гармонии Эйлера шутливо говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов.
Но то, что не смог сделать изощрённый ум математика, сделала обыкновенная смекалка простого органиста...
www.ronl.ru
МКУ «УПРАВЛЕНИЕ ОБРАЗОВАНИЯ ИСПОЛНИТЕЛЬНОГО КОМИТЕТА ЧИСТОПОЛЬСКОГО МУНИЦИПАЛЬНОГО РАЙОНА РЕСПУБЛИКИ ТАТАРСТАН»
МБОУ «Гимназия №3»
Математика и музыка
Секция: Математика Выполнила: ученица 6В класса Чехонина Екатерина Научный руководитель: Назарова М. А. учитель математики, II квалификационная категория по должности «учитель» |
г. Чистополь, 2013
Содержание
Введение……………………………………………………………………… 3
Цели, задачи………………………………………………………………… 4
I этап: Знакомство с математикой и её историей………… …………...... 5-6
II этап: Знакомство с музыкой и её историей………………………….… 7-8
III этап: Размышления древних математиков и музыкантов..…………..... 9
IV этап: Сходства и различия математики и музыки…..…………...….. 10-11
Заключение …………………………………………………………………... 12
Список используемой литературы ………………………………………… 13.
Введение.
«Музыку я разъял как труп,Проверив алгеброй гармонию»
От этих слов, вложенных А.С. Пушкиным в уста Сальери, веет мертвящей пропастью между музыкой и математикой. Отравлен Моцарт - живое воплощение музыки, и сама музыка мертва под математическим скальпелем убийцы гения. Разве не отражают эти пушкинские строки мнение большинства людей, что между математикой и музыкой нет, и не может быть ничего общего?
Между тем именно исследованию музыки посвящали свои работы многие величайшие математики: например крупная работа Леонарда Эйлера - "Диссертация о звуке" начиналась словами: "Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков". А. Лейбниц в письме Гольдбаху пишет: "Музыка есть скрытое арифметическое упражнение души, не умеющей считать". И.Гольдбах ему отвечает: "Музыка - это проявление скрытой математики".
Почему же скрытой? Ведь в Древней Греции музыка прямо считалась частью математики, а еще точнее, разделом теории чисел. Первым, кто попытался выразить красоту музыки с помощью чисел, был Пифагор.
Тогда получается, что математика и музыка – сёстры? Или нет? Почему бы в этом не разобраться?
Цель моей работы:
узнать новое о математике и музыке, и выяснить, родственны ли они между собой?
Для достижения поставленной цели я определила ряд задач:
Основными источниками информации являются учебники по сольфеджио, сочинения философов, научные статьи.
Первый этап исследования
Знакомство с математикой и её историей
Для начала давайте разберемся, что такое математика. Это слово нам очень хорошо знакомо, но если посмотреть в словарях, то мы узнаем много нового. С этого я и начала свою исследовательскую работу. И вот что у меня получилось:
Слово «математика» произошло от древнегреческого, что означает изучение, знание, наука.
А вот как В. Даль объясняет значение этого слова:
«МАТЕМАТИКА ж. наука о величинах и количествах; все, что можно выразить цифрою, принадлежит математике - чистая, занимается величинами отвлеченно; - прикладная, прилагает первую к делу, к предметам. Математика делится на арифметику и геометрию, первая располагает цифрами, вторая протяжениями и пространствами. Алгебра заменяет цифры более общими знаками, буквами; аналитика (включающая в себе и алгебру) добивается выразить все общими формулами, уравнениями, без помощи чертежа. Прикладная математика, по предмету зовется: механикою, оптикою, геодезиею и пр.»
В современных словарях даётся такое пояснение:
«Математика – наука, изучающая величины, количественные отношения и пространственные формы».
Значит, основу математики составляют величины, количественные отношения, формулы, которые в свою очередь состоят из чисел.
Также я познакомилась с историей математики. Оказывается, её развитие началось вместе с тем, как человек стал использовать абстракции. Простая абстракция — число; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Второй этап исследования
Знакомство с музыкой и её историей
А теперь давайте разберёмся, что же такое музыка и из чего она состоит:
Музыка (образовано от греческого слова муза) — искусство, средством воплощения художественных образов для которого являются звук и тишина, особым образом организованные во времени.
Пояснение В. Даля:
«МУЗЫКА и музыка ж. искусство стройного и согласного сочетания звуков, как последовательных (мелодия, напев, голос), так и совместных (гармония, созвучие)».
Проследив происхождение, я узнала, что развитие музыки неотделимо от деятельного развития чувственных способностей человека — ход слухового освоения человеком музыкального материала в изменяющихся культурных условиях составляет наиболее фундаментальный уровень истории музыки.
В раннем фольклоре различных народов музыкальный звук неустойчив по высоте. Мелодия зачастую представляет собой совокупность подъёмов и спадов, объединяющих контрастные высотные зоны в ритмическом порядке, зависящем от ритмики словесного текста и танца. Однако этот первичный звук высотный контраст уже наделён эмоциональной выразительностью благодаря включенности музицирования в быт, в трудовые процессы, в ритуалы. Постоянство этих связей, формирующее первичные музыкальные жанры, приводит к стабилизации высот (и, как следствие, к их закреплению в определённом строе).
Тем самым, в общественном музыкальном сознании высота звука отделяется от тембра голоса и речевой артикуляции; появляется категория лада. Возникают звукоряды и основанные на них мелодии. Звуковысотность, зафиксированная в музыкальном строе, предполагает развитие слуховых навыков особой музыкальной памяти, удерживающей положение. Обретая точную высоту, интонация становится способной воплотить более широкий образный смысл. Он, с одной стороны, выступает как сохранившийся в интонационных формулах след их прошлого значения, связанного с контекстом музицирования, с первичным жанром; с другой стороны — продолжается процесс «вбирания» смысла в интонацию «извне», из образующихся новых связей музыки и слова, музицирования и его социокультурного контекста.
А из чего же состоит музыка?
В наше время музыкой могут быть названы и чарующие переливы арфы, и скрип открываемой двери, и шум заводского цеха. Все это - искусство организации звуковых последовательностей. "Сырьем" для большинства сонат, песен, опер служат музыкальные звуки (нотами), которые отличаются от шумов. Чтобы прояснить суть этого отличия, уточним, что же такое звук.
Всякий звук - это колебания обычного воздуха. Когда человек поет, у него происходит колебание голосовых связок. Когда звучит музыкальный инструмент, колеблются струны. Одна из основных характеристик колебательного процесса - частота колебаний. Музыкальные звуки имеют ту особенность, что им присуща вполне определенная частота колебаний. А вот про шумы нельзя сказать, что им соответствует какая-либо конкретная частота - они представляют собой беспорядочную смесь.
Третий этап исследования
Размышления древних математиков и музыкантов.
Так в чем же сходство математики и музыки? Обратимся к трудам человека, которого знают и математики, и музыканты. Как вы могли догадаться это Пифагор. Все знают его теорему и таблицу. А вот музыкантам он известен как создатель теории музыки.
Гармония, по мнению Пифагора, есть система трех созвучий — кварты, квинты и октавы. На базе тетрахорда (четырех струн, четырех звуков, четырех нот, четырех чисел) 6, 8, 9 и 12 можно построить и полный звукоряд, двенадцати нотный или какой-нибудь еще. Полный строй получался, если откладывать от какой-либо ноты чистую квинту вверх (или вниз). Таким образом, можно получить все ноты, примерно соответствующие нашему двенадцати нотному звукоряду. Опуская (или поднимая) ноты на октаву вниз, сводя их в одну октаву, можно получить звуковысотные соотношения для всех нот.
Пифагор считал математику и музыку неразрывными по отношению друг к другу. Такого же мнения были его ученики - пифагорейцы. Они считали, что музыка является частным проявлением математики. Они создали учение о Космосе, как о музыкально звучащем теле. По их мнению, Космос – это ряд небесных тел, каждое из которых при вращении издает свой музыкальный звук; расстояния между сферами и издаваемые ими звуки соответствуют гармоничным музыкальным интервалам.
Четвёртый этап исследования
Сходства и различия математики и музыки
Но неужели сходство есть только в утверждениях древних философов? Конечно, нет! Сходства можно увидеть в знакомом всем инструменте – фортепьяно. Расположение октав на этом инструменте можно сравнить с координатной прямой. Все мы знаем, что координатная прямая не имеет конца и начала, но имеет точку О(0), которая делит её на равные части, Справа от точки О находятся положительные числа по порядку (1,2, 3, 4,), а слева отрицательные в обратном порядке (-1, -2, -3, -4). На фортепьяно примерно так же: оно условно делится на равные части. Справа от середины октавы идут по порядку (1,2,3,),а слева в обратном порядке (малая, большая, контроктава, субконтроктава). Но фортепьяно в отличие от прямой имеет начало и конец.
Сходства музыки и математики можно увидеть и в системе координат. Для начала давайте познакомимся и с её историей. Такая простая и привычная вещь, как система координат, была введена в математический инструментарий не так давно: ее изобрел Декарт в XVII веке. Это изобретение по праву называют гениальным - трудно себе представить развитие алгебры и геометрии без системы координат. Но вот что интересно: в том, что математика лишь с XVII века пользуется этой замечательной системой, виноваты только сами математики - они в течение шести веков не замечали ту же систему координат буквально у себя под боком - в музыке, а точнее, в системе записи музыки, разработанной Гвидо Аретинским еще в XI веке. Действительно, посмотрев на ноты, мы увидим не что иное, как самый настоящий график музыки: по вертикальной оси определяется высота звука, по горизонтальной - момент его появления, т.е. время.
А что же насчет звуков? Неужели главная составляющая музыки не связана с математикой? Сегодня вряд ли кто-нибудь решится сводить музыку к определенным числовым действиям. Очевидно, надо начать с другого. Окружающий нас мир кроме звуков наполнен еще и ритмами. О чем говорит это слово? Посмотрите вокруг: ритмично звучат шаги, ритмичен ход часов, ритмично биение пульса человека, ритмично наше дыхание и т.д. И стоит нам услышать слово «ритм», как наши мысли невольно обращаются к музыке. И это понятно: ведь ритм – один из важнейших элементов музыки. Оказывается, и среди чисел можно обнаружить ритмы. Возьмем натуральный ряд чисел: 0,|1,2,3|4,5,6|7,8,9|и т.д. Увеличивая каждое число на «1», будем обращать внимание на все числа, кратные 3. И вот что у нас получится (см. пример). Мы пришли к красивому, равномерному ритму, звучащему как музыкальный размер 3/4. Смысл у этой дроби тот же что используется в математике: мы разделили целую на четыре части и три из них включили в такт. Конечно, не всякий человек может понять это, а только тот, кто имеет музыкальное образование и что бы объяснить человеку, не знающему законов музыки надо обратиться к математике. В музыке мы имеем дело с короткими и длинными длительностями, они составляют основу любого ритма: целая нота (), половинная (
), одна четверная (
), одна восьмая (
), одна шестнадцатая (
). Каждая образуется делением целой ноты на два, четыре, восемь шестнадцать. Названия длительности служат одновременно и названиями чисел. Здесь же проявляется геометрическая прогрессия и если записать длительности от «целой» (которая принята в музыке за единицу) по степени убывания, то получим:
Заключение
Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства. Эту связь не раз подчеркивали и математики, и музыканты. Вот что говорил далекий от математики человек – известный пианист Генрих Нейгауз: «Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и что между ними размещается все, что человечество создало в области науки и искусства».
Таким образом, о взаимосвязях математики и музыки можно говорить бесконечно долго, открывая все новые и новые, неожиданные и часто странные, одинаковые определения, понятия и смыслы.
9. Список литературы
« В тональности ми мажор», Азевич Алексей.
«Рациональность и аффект», Хельга де ля Мотт-Хабер.
«Язык, музыка, математика», Б. Варга. Ю. Дюмень, Э. Лопариц.
« Элективные курсы». Издательство «Учитель», 2006 год, г. Волгоград, Л. Сагателова, В. Студенецка.
file://localhost/Математика%20. и %20 Музыка.html.
file://localhost/Математика%20. и %50 Музыка.html.
1. Н.Я. Виленкин, А.С. Чесноков и др. Математика. Учебник для 6 класса средней школы. – М., Просвещение, 1993.- С. 153, №926
2. Н. Васюткин. „Золотая пропорция”.
3. Математический энциклопедический словарь. – М., 1988.
4.Журнал «Начальная школа»
5. Энциклопедический словарь юного математика. – М., 1985.
6. Н.Д. Изместьева, Н.Л. Терский.
7. http://www.yandex.ru
8. http://www.google.ru
(Материал из Викицитатника )
В.П. Ковалев "Математика в музыке". Выступление на семинаре в Московском физико-техническом институте в секции математических основ жизнеустройства.
О.Н.Макеева Научно-исследовательская работа по теме: «Математическое представление музыки».
Интернет ресурс: http://ru.wikibooks.org/wiki
Интернет ресурс: Letopisi.ru Проект «Музыкальная математика»
А. Устинов «Музыка и математика»
nsportal.ru
Муниципальное бюджетное образовательное учреждение
дополнительного образования детей
«Центр дополнительного образования детей» пгт. Нижний Одес
Выполнил:
Поливанов Клим
объединение «Волшебные клавиши»
Руководитель:
Ширишорина И.И.
педагог дополнительного образования
пгт. Нижний Одес
2013 год
Оглавление
1. Введение стр. 3
2. Обзор литературы стр. 3
3. Исследование
3.1. Связь музыки и математики стр. 4
3.2. Связь цифр и музыки стр. 6
4. Заключение стр. 8
5. Список использованной литературы стр. 10
6. Приложение
1.ВВЕДЕНИЕ
Однажды, слушая весёлую песенку «Дважды два четыре», меня посетила мысль: «Если с помощью этой песенки можно легко запомнить некоторую часть таблицы умножения, то наверняка существует связь музыки с математикой»
Я задал себе вопрос: «Какая связь может быть между математикой, мудрой царицей всех наук, и музыкой? Как могут взаимодействовать такие совершенно разные предметы?» Я решил найти ответы на эти вопросы и доказать, что связь между музыкой и математикой существует.
Гипотеза: Если связь между музыкой и математикой существует, то занятия музыкой помогают изучению математики.
Я поставил перед собой цель: доказать, что связь между музыкой и математикой существует.
Для достижения цели определил задачи:
Сроки работы: сентябрь-октябрь 2013 года
Этапы работы:
1 этап – подготовительный: изучение литературы, сбор информации;
2 этап – практический: исследование связи музыки и математики;
исследование связи цифр и музыки.
Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел.
Подбирая информацию и интересные факты по этому вопросу, я узнал, что оказывается, люди уже очень давно задумывались о связи музыки и математики.
Древнегреческий математик-философ Пифагор (Приложение1), живший в VI веке до н. э., был первым, кто изучил и установил связь между музыкой и математикой:
Музыка для Пифагора стала даже не средством вдохновения, а предметом научных изысканий, и именно в музыке Пифагор нашел прямое доказательство своему знаменитому тезису: «Все есть число».
Пифагор утверждал, что весь мир есть распределенная по числам гармония. А числа эти образуют соотношения, что и интервалы между различными ступенями гаммы. Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени: октава – 8 , квинта – 5, кварта – 4 и т. д.
Необходимую, существенную связь музыки и числа обнаружили ученые – философы пифагорейцы, которые открыли числовые соотношения, лежащие в основе музыкальных созвучий, и сформулировали ряд акустических законов музыки.
Уже тогда, в древнем мире, они считали, что музыка без математики не существует. Путем долгих, сложных исследований, с помощью математических правил и законов древним ученым все-таки удалось доказать связь музыки с математикой.
Прошло почти две с половиной тысячи лет со дня смерти Пифагора, но и сейчас время от времени в газетах и журналах появляются сообщения об открытии новых числовых чудес и их связи с музыкой.
Из изученной литературы, я убедился, что мир звуков и пространство чисел издавна соседствуют друг с другом. Исходя из этого, я попытался найти общие точки соприкосновения (совпадения) точной науки математики и прекрасного, изящного искусства – музыки.
3. ИССЛЕДОВАНИЕ
3.1. Связь музыки и математики
Математика (греч. - знание, наука). Математика – царица всех наук, символ мудрости. Красота математики является одним из связующих звеньев науки и искусства.
Музыка (греч. – искусство муз), значит искусство, отражающее действительность в звуковых, художественных образах.
Из знаний, полученных на уроках по математике и занятий по музыке, я выявил следующие совпадения:
Первое - это цифровые обозначения. Как и в математике, в музыке встречаются цифры: звукоряд – 7 нот, нотный стан – 5 линеек. Интервалы: прима – 1, секунда – 2, терция – 3, кварта – 4, квинта – 5, секста – 6, септима – 7, октава – 8. Обозначения аппликатуры и размер произведения записывается тоже при помощи цифр.
Второе совпадение – это ритм. Ритм важнейший элемент в музыке. У каждого музыкального произведения свой ритмический рисунок (чередование нот разной длительности). Числа, оказывается, тоже обладают ритмом.
Например, числа кратные 3(трём) обладают следующим ритмом: Начнем с 0 и, увеличивая каждый раз на 1, будем акцентировать все числа, кратные 3. Получается 0 1 2 3 4 5 6 7 8…. и т.д. Получается красивый, правильный, равномерный ритм, звучащий как музыкальный размер 3/4, который соответствует вальсу.
Если посчитать числа, кратные двум 0 1 2 3 4 5 6 7 8 9 и т.д. то увидим, что мы пришли к ритму, звучащему, как музыкальный размер 2/4. Таким образом, числа обладают ритмом.
Третье совпадение – наличие в музыке и математике противоположностей.
Музыка | Математика |
Мажор - минор Быстро - медленно Тихо - громко Низкий звук - высокий звук Бемоль (понижение) – диез (повышение) | Плюс-минус Больше – меньше Сложение – вычитание Умножение – деление Четное число – нечетное число |
Четвертое совпадение я обнаружил при изучении темы по математике «Дроби». Я занимаюсь музыкой с 7 лет и знаю, что в целой ноте - две половинных, четыре четвертных, восемь восьмых, 16 шестнадцатых. Оказывается, что длительности получаются так же, как и дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать так же как дробные числа: 1/2, ¼, 1/8, 1/16. Следовательно, названия длительностей служат одновременно и названиями чисел. (Приложение 3)
Пятое совпадение - в музыке, как и в математике, есть понятие параллельности. Это - параллельные тональности (например, до мажор – ля минор), а ещё линии нотного стана всегда параллельны, то есть, никогда не пересекаются.
Таким образом, я установил 5 совпадений музыки с математикой, из чего можно сделать вывод, что занимаясь музыкой, человек развивает и тренирует свои математические способности.
3.2. Связь цифр и музыки
Следуя теории Пифагора, числа обладают абсолютной властью над всеми событиями, а значит, числа правят музыкой. Он считал, что гармония чисел сродни гармонии звуков. Даты рождений – это ряд чисел. Я попробовал установить связь между числами и музыкой.
Мною были исследованы даты рождений учащихся 4а класса, в котором я обучаюсь. Как известно дата – набор цифр. Я переложил даты на ноты. Цифра 1 – I ступень (до), 2 – ре, 3 – ми, 4 – фа, 5 – соль, 6 – ля, 7 – си, 8 –до, 9 – ре.
После чего я нашёл среднее арифметическое число - дня, месяца и года рождения каждого ученика. Если получается двузначное число, то необходимо сложить первую и вторую цифру (например, двузначное число 29 – это 2+9 = 11, 11 – это 1+1=2). У каждого человека получилось по три ноты, которые соответствуют дате рождения (Приложение 4) Если сыграть эти ноты одновременно, получаются аккорды.
По звучанию аккордов, ученики разделились на две группы: аккорды, звучавшие гармонично (в музыке их называют консонансом) и аккорды с неприятным резким звучанием (в музыке резкое звучание называется диссонансом).
После того, как я переложил даты рождения на аккорды, попробовал установить связь между звучанием даты рождения и способностями человека. Методом опроса я выяснил, чем каждый ученик увлекается. (Приложение 5). Таким образом, получилось две группы:
I группа (дети, у которых аккорды благозвучные):
В первой группе (самой многочисленной – 23 человека), где аккорды звучат мелодично, оказалось большинство детей с творческими наклонностями: некоторые из них занимаются в художественной или музыкальной школе, занимаются танцами, любят рисовать и читать книги. Данная группа детей обладает творческими способностями, которые косвенно или напрямую связаны с музыкой.
II группа (дети, у которых аккорды не благозвучные):Доненко Ариана – играть в настольные и компьютерные игры Косьяненко Артём – любит решать задачи, головоломки Огородников Даниил – играет в футбол
Во второй группе оказалось всего 3 человека. Им нравится заниматься спортом, решать задачи и головоломки, играть в компьютерные и настольные игры.
Получилось, что большинство учеников класса имеют творческие способности. Меня это очень порадовало. Возможно, именно с этим связанно активное участие нашего класса во всех школьных мероприятиях, концертах. Мои исследования оказались интересны не только мне, но и классному руководителю. Они помогут ему планировать работу, как со всем классом, так и с отдельным учеником.
Таким образом, я установил, что цифры (даты рождения) можно переложить на ноты и установить их связь со способностями людей.
Из изученной литературы я убедился, что мир звуков и пространство чисел издавна соседствуют друг с другом.
В ходе проведения исследования, я выявил общие точки соприкосновения (совпадения) точной науки математики и прекрасного, изящного искусства – музыки.
В подтверждении теории Пифагора, что числа правят музыкой, установил связь между цифрами и музыкой, и их влиянием на творческие способности людей.
Таким образом, данное исследование доказывает, что такие разные предметы имеют общие точки соприкосновения и взаимосвязаны друг с другом. Ребята, которые занимаются музыкой, развивают и тренируют свои математические способности. Из чего можно сделать вывод, что музыка помогает изучать математику. Моя гипотеза подтвердилась.
1.Деплан И. Я. Мир чисел. М.: «Просвещение», 20052. Жмудь Л. Я. Пифагор и его школа М.: Наука, 1990, 192с.3. Энциклопедия для детей. Т. 7. Искусство. Ч. 1. – Э68-е изд., испр./Глав. Ред. М.Д. Аксенова. – М..6 Аванта +, 2006 – 688 с.: ил.4. Энциклопедический словарь юного музыканта Э68/сост. В.В. Медушевский, О.О. Очаковская. – М.: Педагогика, 2007. – 352с., ил.5. Энциклопедический словарь юного математика. М.; «Педагогика» 1985г6. Я познаю мир: Детская энциклопедия: Музыка /авт. А.С. Кленов. Под общей ред. О.Г. Хинн. – М.: ООО Фирма «Издательство АСТ», 2010. – 46
Интернет ресурсы:1. http://www.stonot.ru/2. http://www.krugosvet.ru/3. http://www.wikipedia.org/4. http://ru.wikibooks.org/wiki5. http://www.piano-notes.net/6. Интернет ресурс: http://Letopisi.ru Проект «Музыкальная математика»
Приложение 1
Пифагор Самосский
(лат. Pythagoras; 570 – 490 гг. до н. э.) – древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев.
Приложение 2
Монохорд ПифагораПервым музыкальным инструментом Пифагора был монохорд. Инструмент под названием монохорд в переводе означает «однострун». Монохорд – один из первых шагов на пути к рождению фортепиано. Ему было суждено сыграть в истории музыки огромную роль. Именно он является предком нынешнего фортепиано.
Сначала к его единственной струне добавили еще одну, а затем стали натягивать все большее число струн. Позднее играли на нескольких струнах. Появился инструмент цилибалы, на Руси – гусли. В средние века (XIV в.) знали и пользовались органом. Вот и пришла к кому-то в голову замечательная мысль: приспособить клавиатуру к многострунному монохорду.
Так появились клавикорд, клавесин, а затем фортепиано.
Приложение 3
Схема деления целой ноты
Приложение 4
Исследование дат рождения
Приложение 5
Анкета по изучению интересов учеников моего класса
Фамилия, имя:__________________________________________________________________
ПОДЧЕРКНИ ЛЮБИМЫЕ ЗАНЯТИЯ:
- заниматься спортом
- читать книги
- ходить в спортивные секции
- решать разные задачи, головоломки
- заниматься танцами
- заниматься пением, музыкой
- рисовать
- играть в настольные игры
- играть в компьютерные игры
Resource id #3968nsportal.ru
Муниципальное общеобразовательное бюджетное учреждение
Лицей № 8 г.Тынды Амурской области
Научно-исследовательская работа
тема:
«Математика в МузыкеиМузыка в Математике»
Подготовил ученик 7А класса
Астапович Виктор
Научный руководитель:
Плеханова М.В. учитель музыки
Содержание
Введение 3
Глава 1. Общие элементы в математике и музыке 5
1.1. Ритм 5
1.2. Отражение 6
1.3. Противоположности 7
1.4. Упорядочение 8
1.5. Пропорции 8
1.6. Интервалы и математика 9
Глава 2. Логарифмы в музыке 10
Глава 3. Математический анализ гармонии в музыке 12
Глава 4. Алгебра – сестра гармонии, а композиторы –
первые программисты 16
Заключение 18
Список литературы 19
Введение
Звуки умертвив,
Музыку я разъял как труп,
Поверил я алгеброй гармонию…
А.С. Пушкин
Математика и музыка – два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
Давно уже ученые занимались вопросом: почему в музыкальной октаве семь основных звуков – столько же, сколько цветов в спектре солнечного света. Еще, ничего не зная о природе звуков, человек интуитивно подстраивал струны так, чтобы они создавали благозвучие.
Пифагору принадлежит математическое объяснение основ гармонии; по его определению, наиболее естественно воспринимаются человеком частоты, которые находятся между собой в простых числовых отношениях. Вот откуда в отношении частот в октаве 1:2, и благозвучное трезвучие с отношением частот 4:5:6. Уменьшая последовательно длины струн, мы получим природный звукоряд из 16 звуков, но почему же древние музыканты приняли звукоряд, состоящий из семи основных звуков, и лишь позже добавили еще пять дополнительных (так появились черные клавиши в пианино).
По свидетельству историков древнейшая греческая лира (Орорея) имела четыре струны. Первая струна – основа, у второй струны число колебаний относится к числу колебаний первой струны 4:3 (как у катетов «священного» египетского треугольника). Это кварта основного тона. Число колебаний третьей струны по отношению к основному типу равно 3:2, это – квинта основного тона. Четвертая струна – октава, число колебаний у нее в два раза больше, чем у основы (как отношение катетов в треугольнике 1:2: 5)
Значительно позже появилась семиструнная греческая гамма, которая является развитием четырехструнного строя. В семиструнной гамме отношение частот рядом расположенных звуков 1, 12 (например, ре/до=294/262; соль/фа=392/349). Но очень близкое отношение имеют стороны треугольника 1:2:, оно равно 5/2=1,118 =1,12.
Естественно возникает вопрос, не явились ли закономерности в геометрическом прямоугольном треугольнике со сторонами 1:2: основой для разработки музыкальной гаммы? Если же связь сторон треугольника и отношения частот звуков в семиструнной гамме не случайна, то в таком случае построение музыкальной гаммы связано с золотой пропорцией. Однако трудно допустить, что музыкальная гамма явилась итогом «научной разработки», более вероятно, что она была найдена эмпирическим путем, на основании интуиции музыкантов.
Взаимосвязь математики и музыки является одной из самых актуальных тем. Она до сих пор полностью не раскрыта и не изучена, чем и привлекает к себе внимание многих ученых и математиков. Поверхностно рассмотрев значение этих двух наук, нам кажется, что они совершенно несопоставимы, ведь разве может быть сходство между математикой- царицей всех наук, символом мудрости и музыки - наиболее отвлеченным видом искусства. Но если всмотреться вглубь, то нетрудно заметить, что мир звуков и пространство чисел издавна соседствуют друг с другом.
В своей работе я попытаюсь установить связь между математикой и музыкой и найти их общие элементы.
Глава 1. Общие элементы в математике и музыке
1.1. Ритм
Во всем царит гармонии закон
И в мире все суть ритм, аккорд и тон.
Джон Драйден
Ритм в музыке
Ритм – один из важнейших элементов музыки. Ритм – чередование длительностей. Рассмотрим ритм 3/4 . В такте могут встречаться такие чередования длительностей:
От правильно подобранного ритма зависит звучание мелодии.
Ритм в математике.
Ритмы можно обнаружить и среди чисел. Взять хотя бы дробь 2/82. Ее можно записать в виде 2/82=0,0243902439…или кратно 2/82= 0,(02439)
Здесь мы обнаруживаем ритм. Дробь 2/82 записывается в виде бесконечной периодической дроби, да и период ее также отличается необыкновенной правильностью:02439. Нам известно, что 0,(02439)=2439/99999=271/1111
Итак, мы проследили, что ритм встречается как в музыке, так и в математике.
1.2. Отражение
В повседневной жизни слово «Отражение» мы воспринимаем, как отражение в зеркале каких-либо предметов. Но мало кто задумывается, что отражаться также могут ноты и цифры.
Отражение в математике
Числа, состоящие из цифр 8 и 0, не изменяются при отражении в зеркале. Если зеркало ставить не сбоку от числа, а сверху или снизу, то при отражении в таком зеркале остается неизменной только цифра 3.
Умножение чисел на -1 очень похоже на отражение в зеркале.
Рассмотрим числовую прямую
____________________________________________________
-5 -4 -3 -2 -1 0 1 2 3 4 5
0 – делит прямую на две части.
Правая и левая части очень похожи, и каждая полупрямая почти совпадает с зеркальным отражением другой. Почти, но не совсем. Найдем различие между полупрямыми.
______________________________
0 1 2 3 4 5
Если поставить зеркало в нуле так, чтобы оно было перпендикулярно прямой, полупрямая вместе со своим отражением образует прямую, которая выглядит так:
____________________________________________________
0 1 2 3 4 5
Назовем ее зеркальной числовой прямой. Сравним зеркальную числовую прямую с настоящей. Зеркало заменяет -1 числом 1, -2 –числом 2, -3 – числом 3 и т.д., т.е. превращает отрицательные числа в положительные.
Этого же результата можно достичь и не прибегая к помощи зеркала, если отрицательные числа умножить на (-1).
Например: (-1)*(-1)=+1,
(-2)*(-1)=+2.
Отражение в музыке
Также как и цифры 8 и 0 длительности / и П при отражении совпадают с оригиналом.
Симметричные ритмы не содержат половинных нот.
- половинная нота.
Начертим ее отражение.
Получили - полностью противоречит симметрии.
Совершенно симметричный ритм может состоять из нот следующих трех длительностей: четвертных /, пар восьмых П и целых .
/ П П /, П // П - ритмы не «переворачивающиеся» при отражении в зеркале.
1.3. Противоположности.
Очень часто встречаются противоположности в характерах людей: злой - добрый, агрессивный - спокойный и т. д.
Но мы рассмотрим противоположности в музыке и математике.
Противоположности в музыке
Медленно - быстро.
Характер музыки во многом определяется ее темпом. Музыкальные произведения, будь то народная песня или полифония, нельзя исполнять в произвольном темпе. Неправильно выбранный темп до неузнаваемости исказит характер музыки.
Короткое – длинное (произведение).
Высокое – низкое.
Высота звука зависит от частоты колебаний: при большой частоте колебаний звук выше, при меньшей – ниже.
Противоположности в математике
Отрицательное число – положительное.
Сложение – вычитание.
Четное – нечетное.
Делитель – кратное.
Простое число – составное число.
Плюс – минус.
Умножение – деление.
Прямая – кривая.
1.4. Упорядочение
Упорядочение в математике
Рассмотрим набор вещественных чисел:
12 48 9 1
3 6 10 125 300
Входящие в него числа не упорядочены. Их можно упорядочить, например, по возрастанию: 1 3 6 9 10 12 48 125 300;
или по убыванию: 300 125 48 12 10 9 6 1.
Упорядочение в музыке
Упорядочить означает расположить в ряд. Иногда под упорядочением
понимают классификацию, или разбиение на группы, по определенным признакам. Например: классификация народных песен по месту, где они были записаны собирателями, по времени проведения этнографической экспедиции, тональности, ладу, содержанию.
1.5. Пропорции
Шестнадцатая, восьмая, четвертная, половинная, целая нота … Названия длительностей служат одновременно и названиями чисел. В самом деле, длительность соответствует
и дробь 1/16, называются одинаково. Перечень совпадений можно продолжить.
соответствует 1/8
соответствует 1/1
соответствует 1/4
Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробей. Половинная нота потому и называется половинной или ½, что звучит вдвое короче целой ноты. Ее длительность составляет ½ длительности целой ноты и т.д.
Мы видим, что длительности получаются так же, как дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать так же как дробные числа, например
Это равенство следует понимать в том смысле, что длительность слева равна суммарно длительности справа. С помощью чисел то же равенство можно записать в виде 1=1/4+1/4+1/2.
1.6. Интервалы и математика
Интервал (от греческого – расстояние) – это сочетание двух звуков.
Названия интервалов в переводе на русский язык означают число.
Прима – один
Секунда – два
Терция – три
Кварта – четыре
Квинта – пять
Секста – шесть
Септима – семь
Октава – восемь
Нона – девять
Децима – десять
Ундецима – одиннадцать
Терцдецима – двенадцать
Квартдецима – четырнадцать
Квинтдецима – пятнадцать
Глава 2. Логарифмы в музыке
Музыканты редко увлекаются математикой, большинство из них уважают эту науку, однако стараются держаться от нее подальше. Но все же музыканты соприкасаются с математикой гораздо чаще, чем сами подозревают, и притом с такими страшными вещами, как логарифмы.
А.Эйхенвальд в своей статье писал так: «Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом ничего не имеют общего. Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприменимой».
Но все же Эйхенвальду удалось доказать своему товарищу, что играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах. И действительно, так называемые «ступени» темперированной
хроматической гаммы не расставлены на равных расстояниях ни по
отношению к числам, ни по отношению к длинам волн соответствующих
звуков, а представляют собой логарифмы этих величин. Только основание
этих логарифмов равно 2, а не 10, как принято в других случаях.
Оказывается, что номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков. Можно даже сказать, что номер октавы представляет собой характеристику, а номер звука в данной октаве – мантиссу этого логарифма.
ХVII век ознаменовался новыми открытиями в области математики. В 1614 году опубликованы таблицы логарифмов. Их автор – шотландец Д.Непер. Он не был математиком по профессии. Получив хорошее образование у себя на родине, Д. Непер занимался астрономией и математикой как любитель и добился некоторых важных открытий. Теперь его именем называют ряд правил и формул сферической геометрии. Впоследствии в предисловии к своему сочинению, посвященному таблицам, он писал: «Я всегда старался, насколько позволяли мои силы и способности, отделаться от скуки и трудности вычислений, докучность которых обыкновенно отпугивает многих от изучения математики».
ХVIII век открыл новые страницы в истории музыки. Около 1700 года немецкий органист А. Веркмайстер осуществил гениальное решение: отказался от совершенных и несовершенных консонансов пифагорейской гаммы. Сохранив октаву, он разделил ее на 12 равных частей. Пифагорова комма исчезла. Новый музыкальный строй позволил выполнять транспонирование мелодии. С введением этого строя в музыке восторжествовала темперация (от латинского - соразмерность).
Органы, настроенные А .Веркмайстером, зазвучали в равномерно – темперированном строе. Преимущества нового строя были бесспорны. Строй носил замкнутый характер и состоял из интервалов, вполне приемлемых для музыкального слуха как в мелодическом, так и в гармоническом отношении. В нем совершенно спокойно можно было осуществлять переходы от тональности в тональность. И.С. Бах доказал жизнеспособность новой музыкальной системы, написав «Хорошо темперированный клавир», состоящий из 12 мажорных и 12 минорных произведений. Авторитет великого композитора примирил споры математиков и музыкантов, выступавших «за» или «против» нового музыкального строя.
История создания равномерной темперации еще раз свидетельствует о том, как тесно переплетаются судьбы математики и музыки. Рождение нового музыкального строя не могло произойти без изобретения логарифмов и развития алгебры иррациональных величин. Без знания логарифмов провести расчеты равномерно-темперированного строя было бы невозможно. Логарифмы стали своеобразной «алгеброй гармонии», на которой выросла темперация.
Глава 3. Математический анализ гармонии в музыке
Анализ гармонии в музыке не исчерпывается установлением закономерностей звучания в гамме, изучение природы благозвучных аккордов. Интересно было определить природу прекрасного в произведениях великих композиторов, определить, в чем причина их привлекательности, эстетической ценности.
Более 30 лет отдал изучению закономерностей гармонии в музыке и природе композитор М. Марутаев. Он разработал концепцию универсальной гармонии, определяющим элементом которой является выявление единых числовых характеристик – общих как для природы, так и для музыки. М. Марутаев ввел понятие о нарушенной симметрии и получил «основные числа нарушенной симметрии (Sн)»: 0,713; 0,718; 0,729 и т.д. до 0,992. Мерой нарушения симметрии композитор считает величину 2 в степ.5/11 равную 1,37035…, которая, по его мнению, выражает сущность гармонии.
Оказалось, что во многих музыкальных произведениях, изученных М. Марутаевым, соотношения частей отвечают числам нарушенной симметрии (Sн), а после их математического преобразования получается величина 1,37 – мера гармонии природы.
Теорию «нарушенной симметрии» М. Марутаев использовал для анализа музыкального темперированного звукоряда, в котором интервал между двумя до разбит на 12 частей. Центром симметрии здесь является корень квадратный из 2. После исключения из ряда числа 2 была получена усредненная величина нарушенной симметрии, равная 1,37. Таким образом, считает М.Марутаев, установлена связь звукоряда с мировой физической константой. Путем математических преобразований композитор установил также связь золотой пропорции со значением малой секунды, равной 2 в степени 1/12 =1,059.
Таким образом, можно предполагать, что природа формулирует свои законы (если не все, то некоторые), на языке музыки.
В композиции многих музыкальных произведений отмечается наличие некоторого «кульминационного взлета», высшей точки, причем такое построение характерно не только для произведения в целом, но и для его отдельных частей
Такая высшая точка крайне редко расположена в центре произведения или его композиционной части, обычно она смещена, ассиметрична. Изучая восьмитактные мелодии Бетховена, Шопена, Скрябина русский музыковед Л. Мазель установил, что во многих из них вершина, или высшая точка, приходится на сильную долю шестого такта или на последнюю мелкую долю пятого такта, то есть находится в точке золотого сечения. По мнению Л. Мазеля, число подобных восьми тактов, где подъем мелодии занимает пять тактов, а последующий спуск – три, необычайно велико; их можно без труда найти почти у каждого автора, сочинявшего музыку в гармоническом стиле.
Очевидно, такое расположение кульминационных моментов музыкальной мелодии является важным элементом ее гармонической композиции, придающим художественную выразительность и эстетическую эмоциональность мелодии. Рисунок мелодии строится по схеме: длительный период нарастания эмоционального напряжения, затем остановка и после – более краткий период спада. Может быть, ощущение гармонии такой композиции имеет психофизиологическую основу. Ведь и сердечная деятельность (а ведь сердце считается «вместилищем» чувств), и пульсация крови в сосудах тела подчинены такой же ассиметричной ритмике, основанной на золотой пропорции. В конечном итоге музыка только тогда доставляет эстетическое, эмоциональное удовлетворение, когда гармония музыки входит в резонанс с внутренней гармонией человека.
Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято Л. Сабанеевым. Им было изучено 2000 произведений различных произведений композиторов. По его мнению, временное протяжение музыкального произведения делится «некоторыми вехами», которые выделяются при восприятии музыки и облегчают формы целого. Такими вехами могут быть границы изменения структуры мелодии, интонационные кульминационные пункты (как положительные, так и отрицательные), изменения тональности и т.д. Все эти музыкальные события делят целое на части, как правило, по закону золотого сечения.
По наблюдениям Л. Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, сопряженное с происходящим возле него «эстетическим событием», а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачек в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений; количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Наиболее детально были изучены Л. Сабанеевым все 27 этюдов Шопена. В них обнаружено 154 золотых сечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаях строение музыкального произведения сочетало в себе симметричность и золотое сечение одновременно; в этих случаях оно делилось на несколько симметричных частей, в каждой из которых проявляется золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а внутри каждой из них наблюдаются проявления золотой пропорции.
Интересно, что в этюдах Шопена проявляется не одно выражение золотой пропорции, а целый ряд величин, связанных этим отношением: 0,618; 0,382; 0,236; 0,146; 0,090; и 0,058; реже встречались 0,854; 0,764 и 0,472. Первый ряд из шести чисел образует геометрическую прогрессию с показателем, равным 1,618, а три других числа являются произведениями золотой пропорции (0,764:0,472=1,618). Мелодия как бы растет и развивается, подчиняясь закону золотой пропорции.
Характерно, отмечает Л. Сабанеев, что наиболее часто золотое сечение обнаруживается в произведениях высокохудожественных, принадлежащих гениальным авторам. Может быть, частота проявлений золотой пропорции является одним из объективных критериев оценки гениальности музыкальных произведений и их авторы? И тогда вместо споров о достоинствах той или иной музыки достаточно произвести математический подсчет? И уже не представляется случайным тот факт, что в произведениях композиторов ХХ века золотая пропорция встречается значительно реже, чем у их коллег прошлых веков.
Итак, можно признать, что золотая пропорция является критерием гармонии композиции музыкального произведения. Тогда можно предположить, что чем точнее соответствие произведения музыки золотой пропорции, тем выше степень гармонии, а отклонение от золотой пропорции – свидетельство несовершенства музыки.
Но не будем спешить с таким заключением. В искусстве часто отклонения от правила не менее ценны, чем само правило. Не следует забывать, что золотое сечение – иррациональная величина и ее невозможно выразить отношением целых чисел. А ведь мы замеряем размер частей в целом по числу тактов и выражаем их в целых числах.
Л. Сабанеев считает, что это противоречие снимается, если учесть, что «живое музыкальное произведение никогда не идет точно метрически, его метрическая координата никогда не «пропорциональна» реальному времени. И темп музыки не является постоянной величиной, а переменной функцией метрического времени». Варьируя нюансами темпа, композитор может добиться точного соответствия структуры музыкального произведения золотой пропорции.
Не в этом ли заключен секрет исполнительского мастерства музыкантов, достижения лишь немногими из них наибольшей выразительности, наибольшей силы эмоционального воздействия при использовании одной и той же нотной записи? Деформируя темп исполнения произведения в его различных частях, исполнитель реализует особенности своего исполнительского мастерства и добивается наивысшего успеха, приближаясь при этом и, в частности, к точному соответствию золотой пропорции.
Глава 4. Алгебра – сестра гармонии, а композиторы - первые программисты
«Он алгеброй гармонию разъял», - обвиняли знаменитого Сальери поклонники Моцарта. Придворный сочинитель честно пытался просчитать, какие аккорды более других могут усладить слух Его Величества. Композиторские упражнения Сальери ушли в небытие, а музыка Моцарта пережила века. В самом деле: можно ли в такую тонкую эмоциональную структуру, как музыка, вмешиваться сухим и точным математическим скальпелем? И вообще – что может быть общего у гармонии и алгебры?
На самом деле, математики в музыке гораздо больше, чем можно было бы предположить. И те, кто просто знаком с нотной грамотой, и профессиональные музыканты не всегда знают о строгой математической основе музыкального произведения. Оказывается, что частотный звукоряд гаммы представляет собой ни что иное, как геометрическую прогрессию с коэффициентом 1,059463. И вообще, любую пьесу или сонату можно рассматривать как программу: строгое чередование музыкальных мотивов, фраз, предложений и периодов, определенная протяженность во времени – все это очень похоже на модули компьютерной задачи.
Алексей Устинов утверждает: «Можно рискнуть назвать композиторов самыми первыми программистами. Как в партитурах, так и в текстах компьютерных программ есть блоки, условия, циклы, переходы, метки и прочие «программистские» атрибуты. Фактически, инженеры, разрабатывающие первые программы для компьютеров, пришли к тем же или очень схожим с ними приемам в организации текста, которые уже давно применялись в записях музыки нотами».
Первые опыты по активному применению математики в сфере искусства начались в семидесятые годы двадцатого века, на заре развития компьютерных технологий и на фоне успехов математики. Поясняет доктор искусствоведения Николай Бажанов: «Тогда казалось, что компьютер может практически все, стоит лишь приложить небольшие усилия к написанию соответствующей программы. Возникли опыты с компьютерным моделированием – музыки, прозаического и поэтического текста, других образно – художественных сфер культуры. Важно, что именно работы в области математического моделирования парадоксальным, но естественным образом показали, насколько сложно на самом деле устроена образная часть человеческой культуры, насколько сложны законы, по которым она существует»
Заключение
Итак, стало очевидным, что многие вопросы, связанные с природой музыки и ее воздействием на человека могут быть описаны языком математики. Так, музыкальные интервалы натурального звукоряда определяются отношениями частот близких натуральных чисел, а образование звука в музыкальных инструментах описывается математическими задачами. В построении музыкального строя чувствуются математическая точность и гармония. А золотое сечение может быть применено к анализу построения музыкальных фрагментов. Искусствоведы создали подробные схемы, в которых содержится геометрический анализ великой музыки. Наиболее удачным в этом отношении примером является Хроматическая фантазия и Фуга ре минор И.С. Баха. Слушая это замечательное произведение, не только восторгаешься красотой музыки, но и чувствуешь ее скрытую музыкальную гармонию. А математика открывает еще одну грань гениальности великого композитора.
Исследуя связь между математикой и музыкой, я пришла к выводу, что чем глубже поддается музыкальное произведение математическому анализу, исследованию и подчиняется каким – либо математическим законам, тем более гармонично и прекрасно его звучание, тем больше оно волнует человеческую душу. Кроме того, я убедилась, что в этой области еще очень много важного, интересного и занимательного не раскрыто и можно смело вести исследования этой темы.
Список литературы
1. Б. Варга, Ю. Димень, Э. Лопариц. „Язык, музыка, математика”.
2. Н. Васюткин. „Золотая пропорция”.
3. Математический энциклопедический словарь. – М., 1988.
4. Я. И. Перельман. „Занимательная алгебра. Занимательная геометрия”. –
М., 2002.
5. Энциклопедический словарь юного математика. – М., 1985.
6. htth://wwww.1gb/ru/show_artikle.php?upd=126
7. htth://www.vn.ru/09.01/2003/socicty/23466/
nsportal.ru