Реферат на тему:
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения значений одной или нескольких из этих величин приводят к систематическому изменению значений другой или других величин.[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение [2], либо коэффициент корреляции
(или
)[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]
В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Более тонкий инструмент для изучения связи между двумя случайными величинами является понятие взаимной информации.
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где — математическое ожидание.
Свойства ковариации:
Доказательство
Доказательство
Введём в рассмотрение случайную величину (где
— среднеквадратическое отклонение) и найдём её дисперсию
. Выполнив выкладки получим:
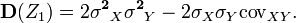
Любая дисперсия неотрицательна, поэтому

Отсюда
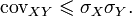
Введя случайную величину , аналогично
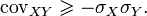
Объединив полученные неравенства имеем

Или
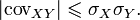
Итак,
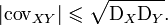
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
Коэффициент корреляции изменяется в пределах от минус единицы до единицы[11].
Доказательство
Разделив обе части двойного неравенства на
получим
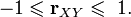
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где
— коэффициент регрессии,
— среднеквадратическое отклонение соответствующего факторного признака[12].
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где S = P − Q.
P — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
t — число связанных рангов в ряду X и Y соответственно.
Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности d и вычисляется коэффициент корреляции Спирмена:
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
m — число групп, которые ранжируются.
n — число переменных.
Rij — ранг i-фактора у j-единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Доказательство
Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, и
. Подсчитаем дисперсию случайной величины ξ = aX + bY:

Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде

Поскольку всегда можно выбрать числа a и b так, чтобы (например, если
, то берём произвольное a и
), то при этих a и b дисперсия
, и значит ξ = aX + bY = 0 почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на
, и Y — на
.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как изменчивость y равна нулю.
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
wreferat.baza-referat.ru
Реферат на тему:
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения значений одной или нескольких из этих величин приводят к систематическому изменению значений другой или других величин.[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение [2], либо коэффициент корреляции
(или
)[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]
В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Более тонкий инструмент для изучения связи между двумя случайными величинами является понятие взаимной информации.
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где — математическое ожидание.
Свойства ковариации:
Доказательство
Доказательство
Введём в рассмотрение случайную величину (где
— среднеквадратическое отклонение) и найдём её дисперсию
. Выполнив выкладки получим:
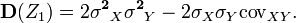
Любая дисперсия неотрицательна, поэтому

Отсюда
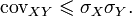
Введя случайную величину , аналогично
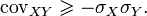
Объединив полученные неравенства имеем

Или
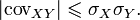
Итак,
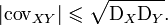
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
Коэффициент корреляции изменяется в пределах от минус единицы до единицы[11].
Доказательство
Разделив обе части двойного неравенства на
получим
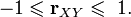
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где
— коэффициент регрессии,
— среднеквадратическое отклонение соответствующего факторного признака[12].
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где S = P − Q.
P — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
t — число связанных рангов в ряду X и Y соответственно.
Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности d и вычисляется коэффициент корреляции Спирмена:
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
m — число групп, которые ранжируются.
n — число переменных.
Rij — ранг i-фактора у j-единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Доказательство
Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, и
. Подсчитаем дисперсию случайной величины ξ = aX + bY:

Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде

Поскольку всегда можно выбрать числа a и b так, чтобы (например, если
, то берём произвольное a и
), то при этих a и b дисперсия
, и значит ξ = aX + bY = 0 почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на
, и Y — на
.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как изменчивость y равна нулю.
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
wreferat.baza-referat.ru
Реферат на тему:
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения значений одной или нескольких из этих величин приводят к систематическому изменению значений другой или других величин.[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение [2], либо коэффициент корреляции
(или
)[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]
В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Более тонкий инструмент для изучения связи между двумя случайными величинами является понятие взаимной информации.
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где — математическое ожидание.
Свойства ковариации:
Доказательство
Доказательство
Введём в рассмотрение случайную величину (где
— среднеквадратическое отклонение) и найдём её дисперсию
. Выполнив выкладки получим:
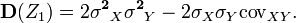
Любая дисперсия неотрицательна, поэтому

Отсюда
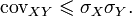
Введя случайную величину , аналогично
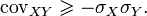
Объединив полученные неравенства имеем

Или
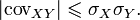
Итак,
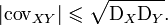
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
Коэффициент корреляции изменяется в пределах от минус единицы до единицы[11].
Доказательство
Разделив обе части двойного неравенства на
получим
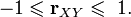
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где
— коэффициент регрессии,
— среднеквадратическое отклонение соответствующего факторного признака[12].
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где S = P − Q.
P — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
t — число связанных рангов в ряду X и Y соответственно.
Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности d и вычисляется коэффициент корреляции Спирмена:
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
m — число групп, которые ранжируются.
n — число переменных.
Rij — ранг i-фактора у j-единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Доказательство
Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, и
. Подсчитаем дисперсию случайной величины ξ = aX + bY:

Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде

Поскольку всегда можно выбрать числа a и b так, чтобы (например, если
, то берём произвольное a и
), то при этих a и b дисперсия
, и значит ξ = aX + bY = 0 почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на
, и Y — на
.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как изменчивость y равна нулю.
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
wreferat.baza-referat.ru
Реферат на тему:
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения значений одной или нескольких из этих величин приводят к систематическому изменению значений другой или других величин.[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение [2], либо коэффициент корреляции
(или
)[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]
В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Более тонкий инструмент для изучения связи между двумя случайными величинами является понятие взаимной информации.
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где — математическое ожидание.
Свойства ковариации:
Доказательство
Доказательство
Введём в рассмотрение случайную величину (где
— среднеквадратическое отклонение) и найдём её дисперсию
. Выполнив выкладки получим:
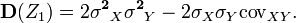
Любая дисперсия неотрицательна, поэтому

Отсюда
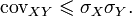
Введя случайную величину , аналогично
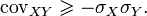
Объединив полученные неравенства имеем

Или
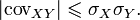
Итак,
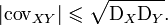
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
Коэффициент корреляции изменяется в пределах от минус единицы до единицы[11].
Доказательство
Разделив обе части двойного неравенства на
получим
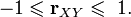
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где
— коэффициент регрессии,
— среднеквадратическое отклонение соответствующего факторного признака[12].
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где S = P − Q.
P — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
t — число связанных рангов в ряду X и Y соответственно.
Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности d и вычисляется коэффициент корреляции Спирмена:
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
m — число групп, которые ранжируются.
n — число переменных.
Rij — ранг i-фактора у j-единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Доказательство
Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, и
. Подсчитаем дисперсию случайной величины ξ = aX + bY:

Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде

Поскольку всегда можно выбрать числа a и b так, чтобы (например, если
, то берём произвольное a и
), то при этих a и b дисперсия
, и значит ξ = aX + bY = 0 почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на
, и Y — на
.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как изменчивость y равна нулю.
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
wreferat.baza-referat.ru
Содержание
1 Определение формы связи
2 Выбор формы связи
3 Аналитическое выражение связи
4 Измерение тесноты связи
5 Множественная корреляция
6 Методы измерения тесноты связи
Список использованной литературы
1 Определение формы связи
Корреляционный анализ решает две основные задачи:
Первая задача заключается в определении формы связи, т.е. в установлении математической формы, в которой выражается данная связь.
Это очень важно, так как от правильного выбора формы связи зависит конечный результат изучения взаимосвязи между признаками.
Вторая задача состоит в измерении тесноты, т.е. меры связи между признаками с целью установить степень влияния данного фактора на результат.
Она решается математически путем определения параметров корреляционного уравнения.
Затем проводятся оценка и анализ полученных результатов при помощи специальных показателей корреляционного метода (коэффициентов детерминации, линейной и множественной корреляции и т.д.), а также проверка существенности связи между изучаемыми признаками.
2 Выбор формы связи
Определяющая роль в выборе формы связи между явлениями принадлежит теоретическому анализу. Так, например, чем больше размер основного капитала предприятия (факторный признак), тем больше при прочих равных условиях оно выпускает продукции (результативный признак).
С ростом факторного признака здесь, как правило, равномерно растет и результативный, поэтому зависимость между ними может быть выражена уравнением прямой Y=a+b*x, которое называется линейным уравнением регрессии.
Параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу. При x = 0 a = Y. Увеличение количества внесенных удобрений приводит, при прочих равных условиях, к росту урожайности, но чрезмерное внесение их без изменения других элементов к дальнейшему повышению урожайности не приводит, а, наоборот, снижает ее.
Такая зависимость может быть выражена уравнением параболы Y=a+b*x+c*x2 .
Параметр c характеризует степень ускорения или замедления кривизны параболы, и при c>0 парабола имеет минимум, а при c<0 — максимум. Параметр b, характеризует угол наклона кривой, а параметр a — начало кривой.
Однако с помощью теоретического анализа не всегда удается установить форму связи. В таких случаях приходится только предполагать о наличии определенной формы связи. Проверить эти предположения можно при помощи графического анализа, который используется для выбора формы связи между явлениями, хотя графический метод изучения связи применяется и самостоятельно.
3 Аналитическое выражение связи
Применение методов корреляционного анализа дает возможность выражать связь между признаками аналитически — в виде уравнения — и придавать ей количественное выражение. Рассмотрим применение приемов корреляционного анализа на конкретном примере.
Допустим, что между стоимостью основного капитала и выпуском продукции существует прямолинейная связь, которая выражается уравнением прямой Y=a+b*x.
Необходимо найти параметры a и b, что позволит определить теоретические значения Y для разных значений x. Причем a и b должны быть такими, чтобы было достигнуто максимальное приближение к первоначальным (эмпирическим) значениям теоретических значений Y. Эта задача решается при помощи способа наименьших квадратов, основное условие которого сводится к определению параметров a и b, таким образом, чтобы
.
Математически доказано, что условие минимума обеспечивается, если параметры a и b, определяются при помощи системы двух нормальных уравнений, отвечающих требованию метода наименьших квадратов:
Первое уравнение есть сумма всех первоначальных уравнений. Второе получается умножением обеих частей уравнения прямой на один и тот же множитель.
Математически доказано, что условие соблюдается, если в качестве такого множителя принять значение факторного признака, т.е. если уравнение прямой умножить на х. Кроме рассмотренных функций связи в экономическом анализе часто применяются степенная, показательная и гиперболическая функции. Степенная функция имеет вид Y=axb .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1 %. При х = 1 a = Y.
Для определения параметров степенной функции вначале ее приводят к линейному виду путем логарифмирования: lg y=lg a+ blg x, а затем строят систему нормальных уравнений:
Решив систему двух нормальных уравнений, находят логарифмы параметров логарифмической функции a и b, а затем и сами параметры a и b. При помощи степенной функции определяют, например, зависимость между фондом заработной платы и выпуском продукции, затратами труда и выпуском продукции и т.д.
Если факторный признака x растет в арифметической прогрессии, а результативный у — в геометрической, то такая зависимость выражается показательной функцией Y=a+bx. Для определения параметров показательной функции ее также вначале приводят к линейному виду путем логарифмирования: lg y=lg a+ xlg b, а затем строят систему нормальных уравнений:
Вычислив соответствующие данные и решив систему двух нормальных уравнений, находят параметры показательной функции a и b.
В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы:
Y=a+b/x.
И здесь задача заключается в нахождении параметров a и b при помощи системы двух нормальных уравнений:
При помощи гиперболической функции изучают, например, связь между выпуском продукции и себестоимостью, уровнем издержек обращения (в процентах к товарооборот и товарооборотом в торговле, сроками уборки и урожайностью и т.д.).
Таким образом, применение различных функций в качестве уравнения связи сводится к определению параметров уравнения по способу наименьших квадратов при помощи системы нормальных уравнений.
В малых совокупностях значение коэффициента регрессии подвержено случайным колебаниям. Поэтому возникает необходимость в определении достоверности коэффициента регрессии. Достоверность коэффициента регрессии определяется так же, как и в выборочном наблюдении, т.е. устанавливаются средняя и предельная ошибки для выборочной средней и доли.
Средняя ошибка коэффициента регрессии определяется по формуле:
где σ20 — случайная дисперсия;
σ2 — общая дисперсия,
n — число коррелируемых пар.
4 Измерение тесноты связи
Чтобы измерить тесноту прямолинейной связи между двумя признаками, пользуются парным коэффициентом корреляции, который обозначается r.
Так как при корреляционной связи имеют дело не с приращением функции в связи с изменением аргумента, а с сопряженной вариацией результативных и факторных признаков, то определение тесноты связи, по существу, сводится к изучению этой сопряженности, т.е. того, в какой мере отклонение от среднего уровня одного признака сопряжено с отклонением другого. Это значит, что при наличии полной прямой связи все значения (х-X) и (у-Y) должны иметь одинаковые знаки, при полной обратной — разные, при частичной связи знаки в преобладающем числе случаев будут совпадать, а при отсутствии связи — совпадать примерно в равном числе случаев.
Для оценки существенности коэффициента корреляции пользуются специально разработанной таблицей критических значений r.
Коэффициент корреляции r применяется только в тех случаях, когда между явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по формуле:
где у — первоначальные значения;
— среднее значение;
Y — теоретические (выровненные) значения переменной величины.
Показатель остаточной, случайной дисперсии определяется по формуле:
Она характеризует размер отклонений эмпирических значений результативного признака у от теоретических Y, т.е. случайную вариацию.
Общая дисперсия:
характеризует размер отклонений эмпирических значений результативного признака у от , т.е. общую вариацию.
Отношение случайной дисперсии к общей характеризует долю случайной вариации в общей вариации, а
есть не что иное, как доля факторной вариации в общей, потому что по правилу сложения дисперсий общая дисперсия равна сумме факторной и случайной дисперсий:
σ2 =σ2Y +σ20.
Подставим в формулу индекса корреляции соответствующие обозначения случайной, общей и факторной дисперсий и получим:
Таким образом, индекс корреляции характеризует долю факторной вариации в общей:
однако с той лишь разницей, что вместо групповых средних берутся теоретические значения Y.
Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1.
При функциональной зависимости случайная вариация , индекс корреляции равен 1. При отсутствии связи R = 0, потому что Y=y.
Коэффициент корреляции является мерой тесноты связи только для линейной формы связи, а индекс корреляции — и для линейной, и для криволинейной. При прямолинейной связи коэффициент корреляции по своей абсолютной величине равен индексу корреляции:
|r|=R.
Если индекс корреляции возвести в квадрат, то получим коэффициент детерминации
R2 =σ2Y /σ2 .
Он характеризует роль факторной вариации в общей вариации и по построению аналогичен корреляционному отношению η2.
Как и корреляционное отношение, коэффициент детерминации R2 может быть исчислен при помощи дисперсионного анализа, так как дисперсионный анализ позволяет расчленить общую дисперсию на факторную и случайную.
Однако при дисперсионном анализе для разложения дисперсии пользуются методом группировок, а при корреляционном анализе — корреляционными уравнениями.
Коэффициент детерминации является наиболее конкретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основание группировки.
При прямолинейной парной связи факторную дисперсию можно определить без вычисления теоретических значений Y по следующей формуле:
5 Множественная корреляция
До сих пор мы рассматривали корреляционные связи между двумя признаками: результативным (у) и факторным (х). Например, выпуск продукции зависит не только от размера основного капитала, но и от уровня квалификации рабочих, состояния оборудования, обеспеченности и качества сырья и материалов, организации труда и т.д. В связи с этим возникает необходимость в изучении, измерении связи между результативным признаком, двумя и более факторными. Этим занимается множественная корреляция.
Множественная корреляция решает три задачи. Она определяет:
— форму связи;
— тесноту связи;
— влияние отдельных факторов на общий результат.
Определение формы связи.
Определение формы связи сводится обычно к отысканию уравнения связно с факторами x,z,w,...v. Так, линейное уравнение зависимости результативного признака от двух факторных определяется по формуле
=a0+a1 x+a2 z
Для определения параметров а0, a1 и а2, по способу наименьших квадратов необходимо решить следующую систему трех нормальных уравнений:
Измерение тесноты связи.
При определении тесноты связи для множественной зависимости пользуются коэффициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреляции. Так, при изучении связи между результативным признаком y и двумя факторными признаками — х и z, нужно предварительно определить тесноту связи между у и х, между у и z, т.е. вычислить коэффициенты парной корреляции, а затем для определения тесноты связи результативного признака от двух факторных исчислить коэффициент множественной корреляции по следующей формуле:
где rxy, rzy, rzx — парные коэффициенты корреляции.
Коэффициент множественной корреляции колеблется в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный результат.
Если коэффициент множественной корреляции возвести в квадрат, то получим совокупный коэффициент детерминации, который характеризует долю вариации результативного признака у под воздействием всех изучаемых факторных признаков.
Совокупный коэффициент детерминации, как и при парной корреляции, можно исчислить по следующей формуле:
R2 =σ2y /σ2y
где σ2Y — дисперсия факторных признаков,
σ2y — дисперсия результативного признака.
Однако вычисление теоретических значений Y при множественной корреляции и сложно, и громоздко. Поэтому факторную дисперсию σ2Y исчисляют по следующей формуле:
Проверка существенности связи при множественной корреляции по сути ничем не отличается от проверки при парной корреляции.
Поскольку факторные признаки действуют не изолированно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между х и у при постоянном z рассчитывается по следующей формуле:
В настоящее время на практике широкое распространение получил многофакторный корреляционный анализ;
6 Методы измерения тесноты связи
Измерение тесноты связи при помощи дисперсионного и корреляционного анализа связано с определенными сложностями и требует громоздких вычислений. Для ориентировочной оценки тесноты связи пользуются приближенными показателями, не требующими сложных, трудоемких расчетов. К ним относятся: коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов, коэффициент ассоциации и коэффициент взаимной сопряженности.
Коэффициент корреляции знаков основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней
(x- ) и (y- ):
i=(u-v)/(u+v),
где u — число пар с одинаковыми знаками отклонений х и у от и ;
v — число пар с разными знаками отклонений х и у оти .
Коэффициент корреляции знаков колеблется в пределах от -1 до +1. Чем ближе коэффициент к 1, тем теснее связь. Если и<v, то i>0, так как число согласованных знаков больше, чем несогласованных, и связь прямая. При и< v имеем i<0, потому что число несогласованных знаков больше, чем согласованных, и связь обратная.
Если и = v, то i =0, и связи нет.
Коэффициент корреляции рангов исчисляется не по первичным данным, а по рангам (порядковым номерам), которые присваиваются всем значениям изучаемых признаков, расположенным в порядке их возрастания.
Если значения признака совпадают, то определяется средний ранг путем деления суммы рангов на число значений. Коэффициент корреляции рангов определяется по формуле
где d2 — квадрат разности рангов для каждой единицы, d=x-y;
n — число рангов;
s — средний ранг.
Коэффициент корреляции рангов также колеблется в пределах от -1 до +1. Если ранги по обоим признакам совпадают, то ηd2 =0, значит, ρ=1 и, следовательно, связь полная прямая. Если ρ= -1, связь полная обратная, при ρ=0 связь между признаками отсутствует.
Коэффициент ассоциации применяется для установления меры связи между двумя качественными альтернативными признаками.
Для его вычисления строится комбинационная четырехклеточная таблица, которая выражает связь между двумя альтернативными явлениями.
Коэффициент ассоциации рассчитывается по формуле:
Коэффициент ассоциации также изменяется от -1 до +1. Чем А ближе к единице, тем сильнее связаны между собой изучаемые признаки. При ad>bc связь прямая, а при ad<bc связь обратная, при ad = bc A = 0 и связь отсутствует.
Коэффициент взаимной сопряженности применяется в тех случаях, когда требуется установить связь между качественными признаками, каждый из которых состоит из трех и более групп.
Различия между условным и безусловным распределением свидетельствуют о влиянии факторного признака на распределение совокупности по результативному признаку, т.е. о наличии связи между факторным и результативным признаками, а чем больше эти различия, тем в большей мере признаки связаны между собой, тем теснее связь между ними.
Для определения степени тесноты связи вычисляется специальный показатель, который называется коэффициентом взаимной сопряженности. Он определяется по следующей формуле:
где n — число единиц совокупности;
m1 и m2 — число групп по первому и второму признакам;
X2 — показатель абсолютной квадратической сопряженности Пирсона.
Показатель абсолютной квадратической сопряженности Пирсона характеризует близость условных распределений к безусловным.
Этот показатель, как и критерий X2, исчисляется по формуле:
где ωij — частости условного распределения в i-й строке;
ωj — частости безусловного распределения;
j — номер столбца.
Если признаки независимы, то ωij =ωj, откуда X2 =0 и, значит, С = 0. Если же связь функциональная, то коэффициент взаимной сопряженности будет равен единице.
www.ronl.ru
Реферат на тему:
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения значений одной или нескольких из этих величин приводят к систематическому изменению значений другой или других величин.[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение [2], либо коэффициент корреляции
(или
)[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.[5]
В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Более тонкий инструмент для изучения связи между двумя случайными величинами является понятие взаимной информации.
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин[7]:
где — математическое ожидание.
Свойства ковариации:
Доказательство
Доказательство
Введём в рассмотрение случайную величину (где
— среднеквадратическое отклонение) и найдём её дисперсию
. Выполнив выкладки получим:
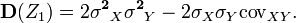
Любая дисперсия неотрицательна, поэтому

Отсюда
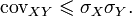
Введя случайную величину , аналогично
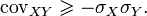
Объединив полученные неравенства имеем

Или
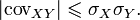
Итак,
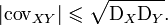
Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон (англ.)русск. в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле[10][8]:
Коэффициент корреляции изменяется в пределах от минус единицы до единицы[11].
Доказательство
Разделив обе части двойного неравенства на
получим
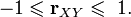
Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: где
— коэффициент регрессии,
— среднеквадратическое отклонение соответствующего факторного признака[12].
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где S = P − Q.
P — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
t — число связанных рангов в ряду X и Y соответственно.
Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности d и вычисляется коэффициент корреляции Спирмена:
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
m — число групп, которые ранжируются.
n — число переменных.
Rij — ранг i-фактора у j-единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Доказательство
Рассмотрим случайные величины X и Y c нулевыми средними, и дисперсиями, равными, соответственно, и
. Подсчитаем дисперсию случайной величины ξ = aX + bY:

Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде

Поскольку всегда можно выбрать числа a и b так, чтобы (например, если
, то берём произвольное a и
), то при этих a и b дисперсия
, и значит ξ = aX + bY = 0 почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на
, и Y — на
.
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как изменчивость y равна нулю.
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
www.wreferat.baza-referat.ru
Корреляции
Определение корреляции
Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал.
Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.
Наиболее часто используемый коэффициент корреляции Пирсона r называется также линейной корреляцией, т.к. измеряет степень линейных связей между переменными.
Простая линейная корреляция (Пирсона r)
Корреляция Пирсона (далее называемая просто корреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале. Она определяет степень, с которой значения двух переменных "пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения.
Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).
Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.
Как интерпретировать значения корреляций
Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации r2) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как "величину" корреляции, так и ее значимость.
Значимость корреляций
Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной y является нормальным (с постоянной дисперсией для всех значений независимой переменной x).
Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие. Тем не менее, имеется несколько серьезных опасностей, о которых следует знать, для этого см. следующие разделы.
По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.
Некоторые исследователи применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2 стандартных отклонений (и даже ±1.5 стандартных отклонений) вокруг выборочного среднего.
Другим возможным источником трудностей, связанным с линейной корреляцией Пирсона r, является форма зависимости. Корреляция Пирсона r хорошо подходит для описания линейной зависимости. Отклонения от линейности увеличивают общую сумму квадратов расстояний от регрессионной прямой, даже если она представляет "истинные" и очень тесные связи между переменными. Итак, еще одной причиной, вызывающей необходимость рассмотрения диаграммы рассеяния для каждого коэффициента корреляции, является нелинейность.
Что делать, если корреляция сильная, однако зависимость явно нелинейная? К сожалению, не существует простого ответа на данный вопрос, так как не имеется естественного обобщения коэффициента корреляции Пирсона r на случай нелинейных зависимостей.
Если попарное исключение пропущенных данных не приводит к какому-либо систематическому сдвигу в оценках, то все эти статистики будут похожи на аналогичные статистики, вычисленные при построчном способе удаления пропусков. Если наблюдается значительное различие, то есть основание предполагать наличие сдвига в оценках.
yaneuch.ru