и 
, где — радиус (расстояние от центра вращения до точки), — полярный угол (угол поворота).
Поступательное движение твердого тела
При поступательном движении твердого тела все его точки тела имеют одинаковые (совпадающие при наложении) траектории, одинаковые по численному значению и направлению скорости и ускорения. Поэтому рассмотренные выше кинематические характеристики материальной точки целиком и полностью применимы к поступательному движению твердого тела.
При описании вращательного движения удобно пользоваться полярными координатами и , где — радиус (расстояние от центра вращения до точки), — полярный угол (угол поворота).
Угловое перемещение – аксиальный скользящий вектор, модуль которого равен углу поворота, направление определяется правилом правого винта, а модуль равен углу поворота. При малых … углах поворота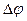  (1.1.18) Угловая скорость:  , (1.1.19) |  Рис.1.5 |
Угловое ускорение: 
(1.1.20)
Единицы углового перемещения, угловой скорости и углового ускорения —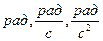 
.
Векторы 
и 
лежат на оси вращения. Направление вектора совпадает с направлением вектора 
. Вектор направлен в сторону вектора при ускоренном движении и противоположен ему при замедленном (рис.1.5).
В случае равнопеременного вращения тела (
) из (1.1.20) 
получаем закон скорости: 
(1.1.21)
Подставив (1.1.21) в (1.1.19), получим: 
(1.1.22)
Установим связь между линейными и угловыми кинематическими характеристиками точки. Если за время 
точка 
описала дугу 
(рис.1.6), то модуль ее линейной скорости (с учетом (1.1.3) и (1.1.18)) равен: 
(1.1.23)
или 
. (1.1.26)
В табл. 1.2 приведены кинематические характеристики тела при поступательном и вращательном движениях.
Таблица 1.2
refac.ru
Пусть некоторая точка движется по окружности радиуса r. Изменение положения точки в пространстве за промежуток времени t определяется углом поворота 
(рис. 3). Элементарный поворот на угол
можно рассматривать как вектор
. Модуль вектора 
равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.
Рис. 3
Угловой скоростью 
называется векторная величина, равная пределу отношения угла поворота
к промежутку времениt, за который этот поворот произошел, при стремлении t к нулю:
,
где 
– первая производная от функции угла поворота 
радиус-вектора 
по времени t. Эту производную принято обозначать, как 
.
Вектор 
направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым ускорением 
называется векторная величина, равная пределу отношения изменения угловой скорости
к промежутку времениt, за который это изменение произошло, при стремлении t к нулю:
,
где 
– первая производная от функции
по времени t,
–вторая производная от функции 
по времени t.
Эти производные принято обозначать соответственно в виде: 
и
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора 
совпадает с направлением вектора угловой скорости
, а при замедленном – противоположно ему.
Кинематические параметры поступательного и вращательного движения связаны между собой. Связь скорости 
и угловой скорости
(см. рис. 3) определяется следующим образом:
.
В векторном виде эту связь для векторов 
и
можно записать с помощью векторного произведения:
.
Ускорение а также можно выразить через угловые параметры, разложив ускорение а на две составляющие 
и
, то есть:
.
Тангенциальная составляющая 
выражается через угловое ускорение
:
,
а нормальная составляющая 
– через угловую скорость
:
.
Тогда ускорение: 
.
При равномерном вращении угловая скорость 
не изменяется. В этом случае вращение можно характеризоватьпериодом вращения T , то есть временем, за которое точка совершает один полный оборот.
Угловая скорость равномерного вращения связана с периодом вращения:
.
Частотой вращения n называется число полных оборотов, совершаемых телом в единицу времени. При равномерном вращении:
, откуда 
.
Первый закон Ньютона: существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Такие системы отсчета называются инерциальными.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение тела под действием приложенной к нему силы: если на тело действует сила, то это тело приобретает ускорение, прямо пропорциональное действующей силе и обратно пропорциональное массе данного тела:
.
В том случае, если на тела действует не одна, а несколько сил, то приведенная в этой формуле сила 
является равнодействующей всех действующих на это тело сил и определяется их векторной суммой.
Из уравнения второго закона Ньютона следует:
.
В случае неизменности массы тела можно записать:
, где 
.
Вектор 
называетсяимпульсом (или количеством движения) тела.
Отсюда следует иная формулировка второго закона Ньютона, называемая формулировкой в дифференциальном виде, а именно: скорость изменения импульса тела равна силе, действующей на этр тело, то есть
.
В том случае, если на тела действует не одна, а несколько сил, то приведенная в этой формуле сила 
является равнодействующей всех действующих на это тело сил и определяется их векторной суммой.
Третий закон Ньютона определяет взаимодействие между материальными точками: если первая материальной точка действует на вторую с силой 
, то вторая точка действует на первую с силой 
, по модулю равной, а по направлению противоположной силе 
(силы
и 
направлены по прямой, соединяющей взаимодействующие точки).
Импульс системы тел. Если принять, что импульс системы, состоящей из n тел, можно определить, как векторную сумму импульсов всех n тел, то есть 
, то из третьего закона Ньютона при условии отсутствия внешних сил (то есть, для замкнутой системы) следует:
, т.е. 
.
Таким образом, импульс замкнутой системы тел не изменяется с течением времени, что является законом сохранения импульса.
studfiles.net
Пусть некоторая точка движется по окружности радиуса r. Изменение положения точки в пространстве за промежуток времени Dt определяется углом поворота 
(рис. 3). Элементарный поворот на угол
можно рассматривать как вектор
. Модуль вектора 
равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.
Рис. 3
Угловой скоростью 
называется векторная величина, равная пределу отношения угла поворота
к промежутку времениDt, за который этот поворот произошел, при стремлении Dt к нулю:
,
где 
– первая производная от функции угла поворота
радиус-вектора
по времени t. Эту производную принято обозначать, как 
.
Вектор 
направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым ускорением 
называется векторная величина, равная пределу отношения изменения угловой скорости
к промежутку времениDt, за который это изменение произошло, при стремлении Dt к нулю:
,
где 
– первая производная от функции
по времени t,
–вторая производная от функции 
по времени t.
Эти производные принято обозначать соответственно в виде: 
и
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора 
совпадает с направлением вектора угловой скорости
, а при замедленном – противоположно ему.
Кинематические параметры поступательного и вращательного движения связаны между собой. Связь скорости 
и угловой скорости
(см. рис. 3) определяется следующим образом:
.
В векторном виде эту связь для векторов 
и
можно записать с помощью векторного произведения:
.
Ускорение а также можно выразить через угловые параметры, разложив ускорение а на две составляющие 
и
, то есть:
.
Тангенциальная составляющая 
выражается через угловое ускорение
:
,
а нормальная составляющая 
– через угловую скорость
:
.
Тогда ускорение: 
.
При равномерном вращении угловая скорость 
не изменяется. В этом случае вращение можно характеризоватьпериодом вращения T , то есть временем, за которое точка совершает один полный оборот.
Угловая скорость равномерного вращения связана с периодом вращения:
.
Частотой вращения n называется число полных оборотов, совершаемых телом в единицу времени. При равномерном вращении:
, откуда 
.
Первый закон Ньютона: существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Такие системы отсчета называются инерциальными.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение тела под действием приложенной к нему силы: если на тело действует сила, то это тело приобретает ускорение, прямо пропорциональное действующей силе и обратно пропорциональное массе данного тела:
.
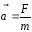В том случае, если на тела действует не одна, а несколько сил, то приведенная в этой формуле сила 
является равнодействующей всех действующих на это тело сил и определяется их векторной суммой.
Из уравнения второго закона Ньютона следует:
.
В случае неизменности массы тела можно записать:
, где 
.
Вектор 
называетсяимпульсом (или количеством движения) тела.
Отсюда следует иная формулировка второго закона Ньютона, называемая формулировкой в дифференциальном виде, а именно: скорость изменения импульса тела равна силе, действующей на этр тело, то есть
.
В том случае, если на тела действует не одна, а несколько сил, то приведенная в этой формуле сила 
является равнодействующей всех действующих на это тело сил и определяется их векторной суммой.
Третий закон Ньютона определяет взаимодействие между материальными точками: если первая материальной точка действует на вторую с силой 
, то вторая точка действует на первую с силой
, по модулю равной, а по направлению противоположной силе 
(силы
и 
направлены по прямой, соединяющей взаимодействующие точки).
Импульс системы тел. Если принять, что импульс системы, состоящей из n тел, можно определить, как векторную сумму импульсов всех n тел, то есть 
, то из третьего закона Ньютона при условии отсутствия внешних сил (то есть, для замкнутой системы) следует:
, т.е.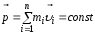 
.
Таким образом, импульс замкнутой системы тел не изменяется с течением времени, что является законом сохранения импульса.
studfiles.net
Произвольное движение абсолютно твердого тела можно представить в виде суммы двух движений: поступательного и вращательного.
Поступательное движение — движение, при котором все точки тела движутся по одинаковым траекториям. В этом случае движение тела можно рассматривать как движение материальной точки.
Вращательное движение — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения тела.
Изменение положения тела в пространстве при вращательном движении определяется углом поворота 
тела относительно некоторого начального положения.
Угловая скорость 
равна первой производной от угла поворота 
тела по времениt:
Угловое ускорение εравно первой производной от угловой скорости 
тела по времениt:
Если материальная точка движется по окружности радиуса 
с постоянной угловой скоростью 
, то ее угловые и линейные характеристики движения связаны соотношениями:
Частные случаи вращательного движения.
угловая скорость 
;
угловое ускорение ε = 0;
угол поворота изменяется по закону: 
.
угловое ускорение 
;
угловая скорость и угол поворота изменяются по законам:
.
Знак + соответствует равноускоренному, а знак ─ — равнозамедленному вращению; 
—угловая скорость тела в момент времени 
= 0.
Период вращения 
— время, в течение которого тело совершает один полный оборот.
Частота вращения 
— число оборотов, совершаемых телом за единицу времени.
Связь между периодом, частотой и угловой скоростью:
,
Основное уравнение динамики материальной точки (второй закон Ньютона):
где 
— равнодействующая сила, действующая на материальную точку;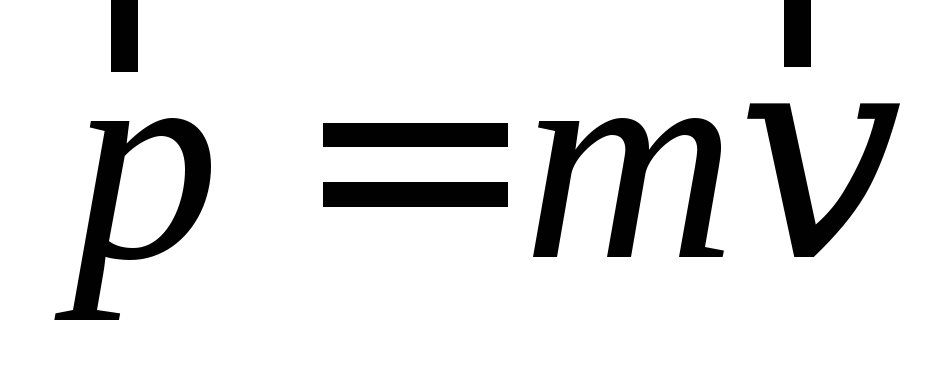
— импульс,
— масса,
— скорость материальной точки.
Если масса тела постоянна, то
,
где 
— ускорение, приобретаемое телом массой
под действием силы
.
Закон Гука:
Fупр = ─ kx,
где Fупр — сила упругости;k— коэффициент упругости или жесткость пружины;x— изменение длины пружины. Знак─означает, что сила упругости направлена против изменения длины пружины.
Закон трения скольжения:
где Fтр— сила трения скольжения;
– сила реакции опоры;
– коэффициент трения скольжения.
Сила тяжести:
где m— масса тела;
– ускорение свободного падения.
Изменение импульса тела равно импульсу приложенных к нему сил:
Закон сохранения импульса: в изолированной системе векторная сумма импульсов входящих в нее тел остается постоянной:
Координата материальной точки меняется по закону: 
Найти перемещение, путь и среднюю скорость движения материальной точки за времяt= 2cпосле начала движения. Построить график зависимости координаты от времени.A = 1 м; ω = π рад/с.
Решение:
График зависимости координаты 
от времениtимеет вид:
Рис. 1
Величина перемещения материальной точки вдоль оси 
равна:
.
где 
— координата точки в начальный момент времени
, а
— в момент времениt= 2c. Отсюда находим величину перемещения:
.
Траекторией движения точки является отрезок прямой от –1 м до +1 м. Этот отрезок точка, как видно из графика (рис. 1), за время t= 2cпроходит дважды. Следовательно, путь
равен:
Средняя скорость движения по определению равна:
Здесь ΔS = SΔt = t.
Поэтому: 
Ответ: 
2. Камень брошен горизонтально с начальной скоростью 
относительно поверхности земли. Найти уравнение траектории движения камня и радиус кривизны траектории в момент времениt.
Р
ешение:
Движение камня рассматриваем в системе отсчета, связанной с землей. Вдоль оси 
камень по условию задачи движется равномерно со скоростью
. Поэтому координата меняется по закону:
(1)
Вдоль оси 
камень падает с постоянным ускорением, равным ускорению свободного паденияg. Поэтому скорость камня вдоль оси
равна
gt, а координата
меняется по закону:
(2)
Рис. 2
Из уравнения (1) получаем: 
.
Подставив 
формулу (2), получим уравнение траектории движения камня:
Радиус кривизны Rтраектории находим из определения нормального ускорения:
,
где 
— полная скорость камня, равная
Отсюда получаем радиус кривизны траектории:
. (3)
Нормальное ускорение направлено к центру кривизны траектории перпендикулярно вектору полной скорости 
камня. С другой стороны, нормальное ускорение является составляющей полного ускорения, которое в данной задаче равноg. Из рис. 2 следует, что
, а
. (4)
Поэтому 
.
Подставив (4) в (3), получаем:
,
или
.
Ответ: 
,
.
Пушка стреляет под углом 
к горизонту. Начальная скорость снаряда равна
. Найти максимальную высоту и дальность полета снаряда. Сопротивление воздуха не учитывать.
Решение
Разложим вектор скорости 
на составляющие вдоль осей координат
и
(см. рис. 3):
(1)
Рис.3
Движение снаряда вдоль оси 
является равнопеременным, поэтому:
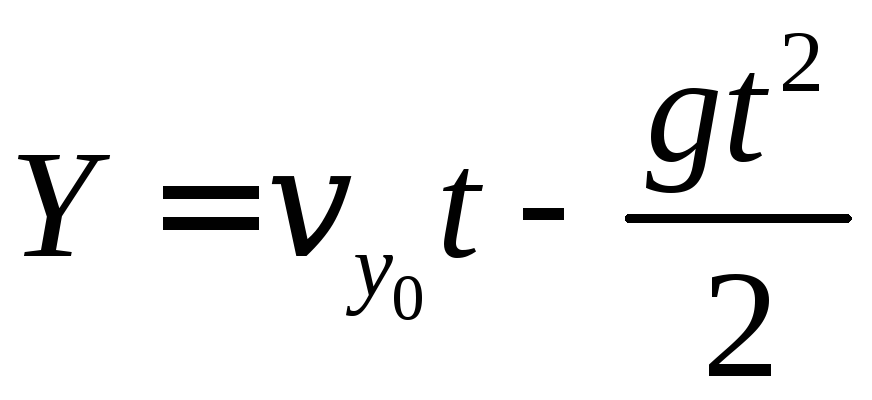, (2)
(3)
Снаряд поднимается вверх, пока вертикальная составляющая его скорости 
не станет равна нулю. Из уравнения (3) находим время подъема:
(4)
Подставив (4) в (2), находим максимальную высоту подъема 
:
(5)
Снаряд, достигнув максимальной высоты подъема, опускается с ускорением свободного падения. Очевидно, что в этом случае:
,
где 
— время падения снаряда.
Учитывая (4) и (5), получаем, что время падения снаряда равно времени его подъема. Полное время полета снаряда равно:
(6)
За это время снаряд пролетит по горизонтали расстояние:
. (7)
Подставив (1) в формулы (5), (6), (7), находим высоту и дальность полета снаряда: 
Ответ: 
4. Вал токарного станка за 2 с приобретает угловую скорость ω = 628 рад/с. Считая вращение тела равноускоренным, найти угловое ускорение и число оборотов вала за это время.
Решение:
Дано:
При равнопеременном вращении угол поворота тела и его угловая скорость меняются по закону:
Из последнего соотношения: находим угловое ускорение:
studfiles.net
Количество просмотров публикации Кинематика вращательного движения - 188
Пусть некоторая точка движется по окружности радиуса r. Изменение положения точки в пространстве за промежуток времени Dt определяется углом поворота (рис. 3). Элементарный поворот на угол
можно рассматривать как вектор
. Модуль вектора
равен углу поворота͵ а его направление совпадает с направлением поступательного движения острия правого винта͵ головка которого вращается в направлении движения точки по окружн
ости, ᴛ.ᴇ. подчиняетсяправилу правого винта.
Рис. 3
Угловой скоростью принято называть векторная величина, равная пределу отношения угла поворота
к промежутку времени Dt, за который данный поворот произошел, при стремлении Dt к нулю:
,
где – первая производная от функции угла поворота
радиус-вектора
по времениt. Эту производную принято обозначать, как
.
Вектор направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым ускорением принято называть векторная величина, равная пределу отношения изменения угловой скорости
к промежутку времени Dt, за который это изменение произошло, при стремлении Dt к нулю:
,
где – первая производная от функции
по времениt,
– вторая производная от функции
по времениt.
Эти производные принято обозначать соответственно в виде: и
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора совпадает с направлением вектора угловой скорости
, а при замедленном – противоположно ему.
Кинематические параметры поступательного и вращательного движения связаны между собой. Связь скорости и угловой скорости
(см. рис. 3) определяется следующим образом:
.
В векторном виде эту связь для векторов и
можно записать с помощью векторного произведения:
.
Ускорение а также можно выразить через угловые параметры, разложив ускорение а на две составляющие и
, то есть:
.
Тангенциальная составляющая выражается через угловое ускорение
:
,
а нормальная составляющая – через угловую скорость
:
.
Тогда ускорение: .
Поступательное движение твердого тела При поступательном движении твердого тела все его точки тела имеют одинаковые (совпадающие при наложении) траектории, одинаковые по численному значению и направлению скорости и ускорения. Поэтому рассмотренные выше... [читать подробнее].
Тело, деформациями которого в данных условиях движения, можно пренебречь называют абсолютно твердым телом. При вращательном движении радиус-вектор каждой точки поворачивается за одно и то время на один и тот же угол . называют углом поворота тела. Угловой... [читать подробнее].
Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы... [читать подробнее].
Рассмотрим материальную точку, движущуюся по окружности. Введем в рассмотрение основные характеристики ее движения. , где - угловая скорость , где - угловое ускорение Данные формулы определяют по величине &... [читать подробнее].
При описании вращат. движения используют полярные координаты r и j, где r— радиус (расстояние от центра вращения до MT), а j ¾ полярный угол (угол поворота). Элементарные повороты обозначают или и рассматривают как псевдовекторы. Угловое перемещение векторная величина,... [читать подробнее].
Пусть м. т. движется со скоростью по окружности радиуса rвокруг неподвижной оси вращения (рис.1.4а). Положение точки на окружности определяет радиус-вектор , а вектор его элементарного приращения направлен по касательной к окружности. Введем понятие вектора элементарного... [читать подробнее].
Если точка вращается вокруг неподвижной оси , то она описывает окружность с центром на оси вращения, а плоскость этой окружности перпендикулярна оси вращения. Быстроту и направление вращения характеризуют угловой скоростью , равной первой производной от углового... [читать подробнее].
referatwork.ru
Илья Сухарев
Москва, 2002г.
Дорогие читатели, очень прошу Вас относиться ко всему изложенному в данной статье, как к моему личному мнению, совсем не окончательному. Мне и самому трудно представить, что описанное реально. Буду рад если кому-то из Вас моя статья добавит интереса к наукам. Для тех же из Вас, кто считает, что необычных, описанных в статье ситуаций не может быть – потому что этого не может быть никогда. Для тех я адресую следующие слова: “ Нелепость – ненаучный термин. Размерность физических величин –не догма, а искусственное средство для описания реальных процессов. И что бы Вы делали без некоторых учебников, что бы доказать правоту законов?”
Принято считать (официальной – академической наукой), что в макромире не существует иных способов движения, кроме опорных (в узком смысле реактивных). Т. е. нет движения без отталкивания (притяжения) от чего (к чему) либо, отбрасывания массы (в смысле причины – начала) и т.д. Далее утверждается, что в любой замкнутой системе (сумма внешних сил = 0), содержащей в себе источник (причину) движения (т. е. силу, энергию), координаты центра массы системы относительно инерциальной системы отсчета, остаются неизменными. Так центры масс всех замкнутых систем, включающих в себя любые известные движущиеся летательные аппараты и землю, остаются на земле (точнее внутри земного шара). Согласно с этими же общепринятыми представлениями устроены все двигательные и соответственно транспортные системы (КПД которых, как известно далек от 100%).
Главные законы физики (механики): три Закона Ньютона и следствия из них – законы сохранения энергии, импульсов, моментов импульсов. Из этих законов (при аккуратном, корректном их применении) не вытекает необходимость сохранения координат центра массы замкнутой системы, включающей движущиеся объекты и причины их движения (опоры - силы).
Рассмотрим в качестве примера альтернативного без опорного (в смысле без наличия внешней силы) механического движения, следующую задачу:
К цилиндру с радиусом основания R и массой m прикреплена жесткая невесомая платформа (центр шарика и центр цилиндра находятся в плоскости zy), на которой находится шарик, радиус которого r и масса m. После взрыва (тонкий красный слой) часть энергии перешла в кинетическую энергию цилиндра и шара E.
Как будут соотноситься количества прямолинейных, поступательных движений шара и цилиндра после взрыва?
Решаем задачу с помощью второго и третьего законов Ньютона, законов сохранения импульса, момента импульса и энергии.
Второй закон Ньютона гласит – Изменению движения быть пропорциональным действующей силе и происходить вдоль прямой, по которой эта сила прилагается.
Современная трактовка второго закона - Скорость изменения импульса тела равна векторной сумме действующих на него сил: dp/dt = Fi..
(Под импульсом, в соответствии с оригиналом закона, следует понимать сумму количеств всех движений (импульсов и моментов импульсов), как вращательных – так и поступательных. Автор)
Третий закон Ньютона гласит – Любая пара частиц (тел) системы действует друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти частицы (центры масс тел).
В природе нет односторонних действий, есть только взаимодействия. Действующая и противодействующая силы имеют следующие особенности: обе эти силы имеют одинаковую природу; силы равны по величине при любых движениях взаимодействующих тел друг относительно друга; эти силы приложены к разным телам.
Решение:
В используемом для решения задачи втором законе Ньютона, не различаются вращательное и поступательное движения. Поэтому нет необходимости делать такие различия и в следствиях из этого закона – законах сохранения … Тогда направления вращательного, поступательного движения цилиндра и действия приложенной к цилиндру силы, следует считать одинаковыми. Такое решение является законным и не лишено физического смысла (по меньшей мере, применительно к нашей задаче), так как в действительности (экспериментально), вращающееся тело может передать энергию другому телу, обусловив его поступательное, прямолинейное движение. Направление такого поступательного движения совпадает с направлением действия силы, вызвавшей вращение первого тела. Иными словами, существенная характеристика любого, в том числе и вращательного движения - это направление действия силы, являющейся причиной такого движения.
И действительно, если предположить обратное вышесказанному, то тогда в случае разлета двух тел под действием общей пары сил, в замкнутой системе, (как в нашей задаче), согласно теории абсолютно упругого удара, возникает следующая ситуация: Второе тело движется не только поступательно, но и вращается. Энергия этого вращения, вместе с энергией поступательного движения может быть полностью передана третьему телу, которое будет двигаться только поступательно и прямолинейно. Тогда значение нового импульса третьего (ударяемого) тела превысит значение импульса второго (ударяющего) тела, в котором не учитывалось количество его вращательного движения. Но согласно допущенному предположению, величина импульса первого, не вращающегося тела = величине импульса второго тела, в котором не учитывается количество его собственного вращения. Такая ситуация неизбежно приводит к противоречию с законом сохранения импульса. Противоречие с законом в описанном случае, тем более очевидно, что возможна и обратная ситуация, когда первое (не вращающееся) тело передаст всю свою энергию другому телу, сообщив ему вращение. Не учитывание такого вращения в импульсе последнего (ударяемого) тела, делает значение его импульса меньше значения импульса ударяющего тела, что опять же приведет к противоречию с законом.
Допустим:
Масса цилиндра > массы шара. Момент инерции цилиндра относительно его центра имеет значение, обуславливающее такую скорость движения шара, какую он имел бы при условии равенства масс шара и цилиндра, но в случае, когда сила, приложенная к цилиндру, была направлена к центру цилиндра и не привела бы к его вращению. Очевидно, что такие значения массы и момента инерции цилиндра могут реально существовать.
Цилиндру, посредством приложенной к нему силы, передается количество поступательного движения, равное количеству поступательного движения шара.
Примем массу шара, ускорение и скорость его поступательного движения равными 1, тогда количество поступательного движения цилиндра, тоже должно быть равно 1, а ускорение и скорость его поступательного движения = w2 = v2 = m1/m2. Тогда в соответствии с вышеуказанными допущениями, количество поступательного движения цилиндра в данной задаче = количеству поступательного движения предполагаемого цилиндра (m3), у которого (при всех равных с условиями задачи внешних условиях) масса = 1 и сила приложена к его центру. Опишем это равенство импульсов двух цилиндров уравнением m2 v2 = m3 v3 = 1.
Согласно третьему закону Ньютона, сила, приложенная к цилиндру численно равна силе приложенной к шару. Из равенства сил приложенных к обоим цилиндрам, в соответствии со вторым допущением, вытекает другое равенство F = m2 w2 = m3 w3 = 1
Из обоих уравнений следует, что выполнение допущения 2., для цилиндра в данной задаче, возможно только при условии приложения силы к центру цилиндра, так как в противном случае часть силы уйдет на работу по вращению и тогда скорости поступательного движения окажется недостаточно для равенства импульсов (не включающих вращение) шара и цилиндра. Что не соответствует исходным условиям. В действительности, “импульс” - количество прямолинейного движения цилиндра будет равен разности импульса шара и “момента импульса” - количества вращательного движения цилиндра.
Отсюда вывод – закон сохранения импульса не нарушается, если под импульсом понимать сумму количеств всех движений (и вращательного), происходящих от одной (общей) силы. Как и завещал великий Ньютон.
Закон сохранения импульса: импульс системы до взрыва равен нулю, так как система замкнута он будет равен нулю и после взрыва.
P = const = 0 = m1v1 + m2v2 + Iw => m1v1 > m2v2
W - угловая скорость вращения цилиндра. I – момент инерции цилиндра.
Количество вращательного движения цилиндра относительно независимой инерциальной системы отсчета = 0, а точнее говоря - не имеет физического смысла. Внутри же описанной в задаче замкнутой системы, количество вращательного движения цилиндра тождественно импульсу, имеющему общую с вращением причину – силу, имеет одинаковое с таким импульсом направление и учитывается наравне (вместе) с ним. Так как момент импульса – это мера вращательного движения тела, то в отсутствии реального вращения шара, наделять его каким бы то ни было моментом импульса (кроме = 0), не имеет физического смысла. Таким образом, в задаче, момент импульса замкнутой системы до и после взрыва, следует понимать = 0.
Закон сохранения энергии: энергия Е складывается из кинетической энергии не вращающегося шарика, кинетической энергии поступательного движения цилиндра и кинетической энергии вращательного движения цилиндра:
Количество поступательного движения цилиндра, в нашей задаче будет заведомо меньше чем у шара. Следовательно, центр массы замкнутой системы неизбежно сместится, что служит примером “без опорного” или “само” движения.
И так центр массы замкнутой системы (шар – цилиндр) после разлета начинает двигаться в направлении движения шара. Теперь с помощью несложного технического решения (по типу соединительной штанги), мы обеспечиваем неупругий удар шара с цилиндром - и в результате получаем поступательное движение всей системы. Что и надеялись доказать.
Современная техника и технологии дают достаточный выбор вариантов (возможностей) сделать этот процесс замкнутым, цикличным (расталкивание + стягивание центров масс) с минимальными потерями на трение и вредный разогрев и для перевода энергии вращения “цилиндра” через снятие ЭДС индукции в часть энергии для расталкивания и или стягивания. У меня есть несколько интересных решений.
Движитель, работающий на таком “без опорном” принципе может использоваться на любом транспорте, включая летающие тарелки, вилки и т.д. Экономический эффект от таких “самодвижущихся” систем, по моему личному мнению, может быть сопоставим с переходом от древнего волока к магнитной подушке или от паровых к электродвигателям. Короче говоря, перспективы внедрения данного принципа могут теряться далеко в звездных туманностях.
Достаточно сказать, что при установке нового двигателя на автомобиль (независимо от источника питания, вида топлива), отпадает необходимость во всех узлах и агрегатах обеспечивающих передачу вращения с ведущего вала двигателя на колесную пару (ось). В том числе коленвалах, распредвалах, коробке передач, сцеплении, тормозах (на колесах) и т. д. А это до 50 % веса авто и куча вредного трения и нагрева. Кроме этого протектор на шинах не нужен, как и у самолетов.
Кроме этого, если данное предположение подтвердится на практике, то все науки получат грандиозный импульс к развитию и новым открытиям. Но это уже тема другой статьи.
За работу товарищи!
www.neuch.ru
Илья Сухарев
Москва, 2002г.
Дорогие читатели, очень прошу Вас относиться ко всему изложенному в данной статье, как к моему личному мнению, совсем не окончательному. Мне и самому трудно представить, что описанное реально. Буду рад если кому-то из Вас моя статья добавит интереса к наукам. Для тех же из Вас, кто считает, что необычных, описанных в статье ситуаций не может быть – потому что этого не может быть никогда. Для тех я адресую следующие слова: “ Нелепость – ненаучный термин. Размерность физических величин –не догма, а искусственное средство для описания реальных процессов. И что бы Вы делали без некоторых учебников, что бы доказать правоту законов?”
Секрет летающей тарелки или противоречия в некоторых умах.
Принято считать (официальной – академической наукой), что в макромире не существует иных способов движения, кроме опорных (в узком смысле реактивных). Т. е. нет движения без отталкивания (притяжения) от чего (к чему) либо, отбрасывания массы (в смысле причины – начала) и т.д. Далее утверждается, что в любой замкнутой системе (сумма внешних сил = 0), содержащей в себе источник (причину) движения (т. е. силу, энергию), координаты центра массы системы относительно инерциальной системы отсчета, остаются неизменными. Так центры масс всех замкнутых систем, включающих в себя любые известные движущиеся летательные аппараты и землю, остаются на земле (точнее внутри земного шара). Согласно с этими же общепринятыми представлениями устроены все двигательные и соответственно транспортные системы (КПД которых, как известно далек от 100%).
Главные законы физики (механики): три Закона Ньютона и следствия из них – законы сохранения энергии, импульсов, моментов импульсов. Из этих законов (при аккуратном, корректном их применении) не вытекает необходимость сохранения координат центра массы замкнутой системы, включающей движущиеся объекты и причины их движения (опоры - силы).
Рассмотрим в качестве примера альтернативного без опорного (в смысле без наличия внешней силы) механического движения, следующую задачу:
Условие задачи:
К цилиндру с радиусом основания R и массой m прикреплена жесткая невесомая платформа (центр шарика и центр цилиндра находятся в плоскости zy), на которой находится шарик, радиус которого r и масса m. После взрыва (тонкий красный слой) часть энергии перешла в кинетическую энергию цилиндра и шара E.
Как будут соотноситься количества прямолинейных, поступательных движений шара и цилиндра после взрыва?
Решаем задачу с помощью второго и третьего законов Ньютона, законов сохранения импульса, момента импульса и энергии.
Второй закон Ньютона гласит – Изменению движения быть пропорциональным действующей силе и происходить вдоль прямой, по которой эта сила прилагается.
Современная трактовка второго закона - Скорость изменения импульса тела равна векторной сумме действующих на него сил: dp/dt = Fi..
(Под импульсом, в соответствии с оригиналом закона, следует понимать сумму количеств всех движений (импульсов и моментов импульсов), как вращательных – так и поступательных. Автор)
Третий закон Ньютона гласит – Любая пара частиц (тел) системы действует друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти частицы (центры масс тел).
В природе нет односторонних действий, есть только взаимодействия. Действующая и противодействующая силы имеют следующие особенности: обе эти силы имеют одинаковую природу; силы равны по величине при любых движениях взаимодействующих тел друг относительно друга; эти силы приложены к разным телам.
Решение:
В используемом для решения задачи втором законе Ньютона, не различаются вращательное и поступательное движения. Поэтому нет необходимости делать такие различия и в следствиях из этого закона – законах сохранения … Тогда направления вращательного, поступательного движения цилиндра и действия приложенной к цилиндру силы, следует считать одинаковыми. Такое решение является законным и не лишено физического смысла (по меньшей мере, применительно к нашей задаче), так как в действительности (экспериментально), вращающееся тело может передать энергию другому телу, обусловив его поступательное, прямолинейное движение. Направление такого поступательного движения совпадает с направлением действия силы, вызвавшей вращение первого тела. Иными словами, существенная характеристика любого, в том числе и вращательного движения - это направление действия силы, являющейся причиной такого движения.
И действительно, если предположить обратное вышесказанному, то тогда в случае разлета двух тел под действием общей пары сил, в замкнутой системе, (как в нашей задаче), согласно теории абсолютно упругого удара, возникает следующая ситуация: Второе тело движется не только поступательно, но и вращается. Энергия этого вращения, вместе с энергией поступательного движения может быть полностью передана третьему телу, которое будет двигаться только поступательно и прямолинейно. Тогда значение нового импульса третьего (ударяемого) тела превысит значение импульса второго (ударяющего) тела, в котором не учитывалось количество его вращательного движения. Но согласно допущенному предположению, величина импульса первого, не вращающегося тела = величине импульса второго тела, в котором не учитывается количество его собственного вращения. Такая ситуация неизбежно приводит к противоречию с законом сохранения импульса. Противоречие с законом в описанном случае, тем более очевидно, что возможна и обратная ситуация, когда первое (не вращающееся) тело передаст всю свою энергию другому телу, сообщив ему вращение. Не учитывание такого вращения в импульсе последнего (ударяемого) тела, делает значение его импульса меньше значения импульса ударяющего тела, что опять же приведет к противоречию с законом.
Допустим:
Масса цилиндра > массы шара. Момент инерции цилиндра относительно его центра имеет значение, обуславливающее такую скорость движения шара, какую он имел бы при условии равенства масс шара и цилиндра, но в случае, когда сила, приложенная к цилиндру, была направлена к центру цилиндра и не привела бы к его вращению. Очевидно, что такие значения массы и момента инерции цилиндра могут реально существовать.
Цилиндру, посредством приложенной к нему силы, передается количество поступательного движения, равное количеству поступательного движения шара.
Примем массу шара, ускорение и скорость его поступательного движения равными 1, тогда количество поступательного движения цилиндра, тоже должно быть равно 1, а ускорение и скорость его поступательного движения = w2 = v2 = m1/m2. Тогда в соответствии с вышеуказанными допущениями, количество поступательного движения цилиндра в данной задаче = количеству поступательного движения предполагаемого цилиндра (m3), у которого (при всех равных с условиями задачи внешних условиях) масса = 1 и сила приложена к его центру. Опишем это равенство импульсов двух цилиндров уравнением m2 v2 = m3 v3 = 1.
Согласно третьему закону Ньютона, сила, приложенная к цилиндру численно равна силе приложенной к шару. Из равенства сил приложенных к обоим цилиндрам, в соответствии со вторым допущением, вытекает другое равенство F = m2 w2 = m3 w3 = 1
Из обоих уравнений следует, что выполнение допущения 2., для цилиндра в данной задаче, возможно только при условии приложения силы к центру цилиндра, так как в противном случае часть силы уйдет на работу по вращению и тогда скорости поступательного движения окажется недостаточно для равенства импульсов (не включающих вращение) шара и цилиндра. Что не соответствует исходным условиям. В действительности, “импульс” - количество прямолинейного движения цилиндра будет равен разности импульса шара и “момента импульса” - количества вращательного движения цилиндра.
Отсюда вывод – закон сохранения импульса не нарушается, если под импульсом понимать сумму количеств всех движений (и вращательного), происходящих от одной (общей) силы. Как и завещал великий Ньютон.
Закон сохранения импульса: импульс системы до взрыва равен нулю, так как система замкнута он будет равен нулю и после взрыва.
P = const = 0 = m1v1 + m2v2 + Iw => m1v1 > m2v2
W - угловая скорость вращения цилиндра. I – момент инерции цилиндра.
Количество вращательного движения цилиндра относительно независимой инерциальной системы отсчета = 0, а точнее говоря - не имеет физического смысла. Внутри же описанной в задаче замкнутой системы, количество вращательного движения цилиндра тождественно импульсу, имеющему общую с вращением причину – силу, имеет одинаковое с таким импульсом направление и учитывается наравне (вместе) с ним. Так как момент импульса – это мера вращательного движения тела, то в отсутствии реального вращения шара, наделять его каким бы то ни было моментом импульса (кроме = 0), не имеет физического смысла. Таким образом, в задаче, момент импульса замкнутой системы до и после взрыва, следует понимать = 0.
Закон сохранения энергии: энергия Е складывается из кинетической энергии не вращающегося шарика, кинетической энергии поступательного движения цилиндра и кинетической энергии вращательного движения цилиндра:
Количество поступательного движения цилиндра, в нашей задаче будет заведомо меньше чем у шара. Следовательно, центр массы замкнутой системы неизбежно сместится, что служит примером “без опорного” или “само” движения.
И так центр массы замкнутой системы (шар – цилиндр) после разлета начинает двигаться в направлении движения шара. Теперь с помощью несложного технического решения (по типу соединительной штанги), мы обеспечиваем неупругий удар шара с цилиндром - и в результате получаем поступательное движение всей системы. Что и надеялись доказать.
Современная техника и технологии дают достаточный выбор вариантов (возможностей) сделать этот процесс замкнутым, цикличным (расталкивание + стягивание центров масс) с минимальными потерями на трение и вредный разогрев и для перевода энергии вращения “цилиндра” через снятие ЭДС индукции в часть энергии для расталкивания и или стягивания. У меня есть несколько интересных решений.
Движитель, работающий на таком “без опорном” принципе может использоваться на любом транспорте, включая летающие тарелки, вилки и т.д. Экономический эффект от таких “самодвижущихся” систем, по моему личному мнению, может быть сопоставим с переходом от древнего волока к магнитной подушке или от паровых к электродвигателям. Короче говоря, перспективы внедрения данного принципа могут теряться далеко в звездных туманностях.
Достаточно сказать, что при установке нового двигателя на автомобиль (независимо от источника питания, вида топлива), отпадает необходимость во всех узлах и агрегатах обеспечивающих передачу вращения с ведущего вала двигателя на колесную пару (ось). В том числе коленвалах, распредвалах, коробке передач, сцеплении, тормозах (на колесах) и т. д. А это до 50 % веса авто и куча вредного трения и нагрева. Кроме этого протектор на шинах не нужен, как и у самолетов.
Кроме этого, если данное предположение подтвердится на практике, то все науки получат грандиозный импульс к развитию и новым открытиям. Но это уже тема другой статьи.
За работу товарищи!
superbotanik.net
