Реферат на тему:
Юлиа́нский день (JD) — астрономический способ измерения времени, при котором считается число дней, прошедших начиная с полудня 1 января 4713 до н. э. юлианского календаря или, что то же самое, 24 ноября 4714 г. до н. э. григорианского календаря (соответственно, −4712 г. и −4713 г. по астрономическому счёту лет[1]). Первый день имел номер 0. С тех пор по настоящее время прошло немногим менее 2,5 миллионов дней. Даты сменяются в полдень UT или TT. Для точного обозначения времени применяют дробную часть, например, JD = 2451545,25 соответствует 18 часам 1 января 2000 г., 3 часа дня 2 августа 1942 г. — JD 2430574,125, 13,5 июня 1944 г. — JD 2431255,0.
Текущий юлианский день JD=2455749.192222
Юлианский период был предложен Скалигером для целей истории и хронологии. Поскольку историкам постоянно требуется работать с различными календарными системами и различными эпохами, Скалигер предложил простую погодную хронологическую шкалу, к которой можно было бы приводить все исторические даты — юлианский период. Каждый год нумеровался тремя числами — Индиктом (от 1 до 15), Золотым числом (от 1 до 19) и Солнечным числом (от 1 до 28). На начало цикла 1 января 4713 до н. э. все числа были равны 1. Длительность цикла равняется 15*19*28, то есть 7980 годам, через это время все цифры повторяются. Конец первого юлианского периода придётся на 23 января 3268 года по григорианскому календарю.
В 1849 году для удобства астрономических расчетов Гершель предложил все даты выражать через число дней, прошедших от начала цикла Скалигера. Началом дня Гершель выбрал полдень по меридиану Александрии, так как именно так отсчитывались дни в классическом Альмагесте Клавдия Птолемея. Использование полдня как границы суток удобно для датирования астрономических наблюдений, так как вся ночь попадает в один и тот же юлианский день.
К концу XIX века юлианский день постепенно начал использоваться в астрономической литературе. За начало дня обычно брали полдень по Гринвическому меридиану, который в 1884 года получил статус международного.
Юлианский день можно применять для определения дня недели, для перевода дат одного календаря в даты другого, для определения промежутка времени между двумя датами и т. п.
В формулах:
year — год, если вы хотите использовать его для дат до нашей эры, необходимо перевести год до н. э. в отрицательный год (например, 10 г. до н. э. = −9).
month — номер месяца, январь — 1, февраль — 2 и т. д.
day — день месяца.
hour — часы от 0 до 23.
minute — минуты от 0 до 59.
second — секунды от 0 до 59, могут содержать дробную часть.
JDN — это номер юлианского дня (Julian Day Number), который начинается в полдень числа, для которого производятся вычисления.
JD — юлианская дата, содержащая дробную часть.
Вначале нужно вычислить промежуточные коэффициенты:
После этого можно вычислить номер юлианского дня:
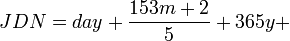
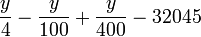
Все деления целочисленные, то есть остатки деления отбрасываются.
Формула справедлива для дат после 23 ноября −4713 г.
Вначале нужно вычислить промежуточные коэффициенты (они те же, что и для григорианского календаря):
После этого можно вычислить номер юлианского дня:
Для дат юлианского календаря существует также формула:

Все операции деления — целочисленные, то есть, остатки деления отбрасываются. Формулы справедливы начиная с −4712 года (то есть, для положительных значений JDN).
Для перехода к «полной» юлианской дате, содержащей дробную часть, можно воспользоваться формулой:
При делении в этой формуле дробная часть не отбрасывается. Сутки не должны содержать високосной секунды (23:59:60).
Например, полдень (12 ч, 0 минут, 0 секунд) 1 января 2000 г. соответствует JD = 2451545,0.
День недели может быть вычислен как остаток от деления JDN на 7. При этом 0 соответствует понедельнику, 1 — вторнику и т. д..
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
Сначала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по юлианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
С начала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по григорианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
Большое количество цифр в юлианском дне и смена дат в полдень во многих случаях неудобны, поэтому разработано большое количество систем счёта дней, аналогичных юлианскому дню
| Юлианский день (JD) | 12:00 1 января, 4713 до н. э., Пн | 2455749.192222 | ||
| Номер юлианского дня (JDN) | 12:00 1 января, 4713 до н. э., Пн (день № 0) | JDN = floor (JD) | 2455749 | |
| Reduced Julian Day (RJD) | 12:00 16 ноября, 1858, Вт | RJD = JD − 2400000 | 55749.19222 | Иногда используется астрономами |
| Модифицированный юлианский день (MJD) | 00:00 17 ноября, 1858, Ср | MJD = JD − 2400000,5 | 55748.69222 | Введен SAO в 1957, сменяется в полночь. |
| Truncated Julian Day (TJD) | 00:00 24 мая, 1968, Пт00:00 10 ноября, 1995, Вт. | TJD = JD − 2440000,5TJD = (JD − 0,5) mod 10000 | 15748.692225748.69222 | - Определение, введённое NASA[2] — определение NIST |
| Дублинский юлианский день (DJD) | 12:00 31 декабря, 1899, Вс. | DJD = JD − 2415020 | 40729.19222 | Введен IAU в 1955 |
| Хронологический юлианский день (CJD) | 00:00 1 января, 4713 до н. э., Пн | CJD = JD + 0,5 + часовой пояс | 2455749.6922222 (UT) | Свой для каждого часового пояса; Дата меняется в полночь по местному времени |
| Лилианский день (англ.) (LDN) | 00:00 15 октября 1582, Friday (день № 1) | floor (JD − 2299160,5) | 156588 | |
| ANSI Дата | 00:00 1 января 1601, Пн (день № 1) | floor (JD − 2305812,5) | 149936 | По нему считаются даты COBOL |
| Rata Die | 1 января, 1, Пн (день № 1) | floor (JD − 1721424,5) | 734324 | Счёт дней нашей эры по григорианскому календарю |
| Время Юникс | 1 января, 1970, Вт. | (JD − 2440587,5) × 86400 | 1309970208 | Считается посекундно |
Там, где требуются вычисления с точностью до минут и более, указывается, относительно какой системы приводится значение юлианского дня. Если это UTC, соответствующий юлианский день обозначают JDUTC, если это часто использующееся в астрономии эфемеридное время, юлианский день обозначают JED.
www.wreferat.baza-referat.ru
Реферат на тему:
Юлиа́нский день (JD) — астрономический способ измерения времени, при котором считается число дней, прошедших начиная с полудня 1 января 4713 до н. э. юлианского календаря или, что то же самое, 24 ноября 4714 г. до н. э. григорианского календаря (соответственно, −4712 г. и −4713 г. по астрономическому счёту лет[1]). Первый день имел номер 0. С тех пор по настоящее время прошло немногим менее 2,5 миллионов дней. Даты сменяются в полдень UT или TT. Для точного обозначения времени применяют дробную часть, например, JD = 2451545,25 соответствует 18 часам 1 января 2000 г., 3 часа дня 2 августа 1942 г. — JD 2430574,125, 13,5 июня 1944 г. — JD 2431255,0.
Текущий юлианский день JD=2455749.192222
Юлианский период был предложен Скалигером для целей истории и хронологии. Поскольку историкам постоянно требуется работать с различными календарными системами и различными эпохами, Скалигер предложил простую погодную хронологическую шкалу, к которой можно было бы приводить все исторические даты — юлианский период. Каждый год нумеровался тремя числами — Индиктом (от 1 до 15), Золотым числом (от 1 до 19) и Солнечным числом (от 1 до 28). На начало цикла 1 января 4713 до н. э. все числа были равны 1. Длительность цикла равняется 15*19*28, то есть 7980 годам, через это время все цифры повторяются. Конец первого юлианского периода придётся на 23 января 3268 года по григорианскому календарю.
В 1849 году для удобства астрономических расчетов Гершель предложил все даты выражать через число дней, прошедших от начала цикла Скалигера. Началом дня Гершель выбрал полдень по меридиану Александрии, так как именно так отсчитывались дни в классическом Альмагесте Клавдия Птолемея. Использование полдня как границы суток удобно для датирования астрономических наблюдений, так как вся ночь попадает в один и тот же юлианский день.
К концу XIX века юлианский день постепенно начал использоваться в астрономической литературе. За начало дня обычно брали полдень по Гринвическому меридиану, который в 1884 года получил статус международного.
Юлианский день можно применять для определения дня недели, для перевода дат одного календаря в даты другого, для определения промежутка времени между двумя датами и т. п.
В формулах:
year — год, если вы хотите использовать его для дат до нашей эры, необходимо перевести год до н. э. в отрицательный год (например, 10 г. до н. э. = −9).
month — номер месяца, январь — 1, февраль — 2 и т. д.
day — день месяца.
hour — часы от 0 до 23.
minute — минуты от 0 до 59.
second — секунды от 0 до 59, могут содержать дробную часть.
JDN — это номер юлианского дня (Julian Day Number), который начинается в полдень числа, для которого производятся вычисления.
JD — юлианская дата, содержащая дробную часть.
Вначале нужно вычислить промежуточные коэффициенты:
После этого можно вычислить номер юлианского дня:
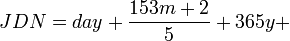
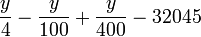
Все деления целочисленные, то есть остатки деления отбрасываются.
Формула справедлива для дат после 23 ноября −4713 г.
Вначале нужно вычислить промежуточные коэффициенты (они те же, что и для григорианского календаря):
После этого можно вычислить номер юлианского дня:
Для дат юлианского календаря существует также формула:

Все операции деления — целочисленные, то есть, остатки деления отбрасываются. Формулы справедливы начиная с −4712 года (то есть, для положительных значений JDN).
Для перехода к «полной» юлианской дате, содержащей дробную часть, можно воспользоваться формулой:
При делении в этой формуле дробная часть не отбрасывается. Сутки не должны содержать високосной секунды (23:59:60).
Например, полдень (12 ч, 0 минут, 0 секунд) 1 января 2000 г. соответствует JD = 2451545,0.
День недели может быть вычислен как остаток от деления JDN на 7. При этом 0 соответствует понедельнику, 1 — вторнику и т. д..
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
Сначала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по юлианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
С начала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по григорианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
Большое количество цифр в юлианском дне и смена дат в полдень во многих случаях неудобны, поэтому разработано большое количество систем счёта дней, аналогичных юлианскому дню
| Юлианский день (JD) | 12:00 1 января, 4713 до н. э., Пн | 2455749.192222 | ||
| Номер юлианского дня (JDN) | 12:00 1 января, 4713 до н. э., Пн (день № 0) | JDN = floor (JD) | 2455749 | |
| Reduced Julian Day (RJD) | 12:00 16 ноября, 1858, Вт | RJD = JD − 2400000 | 55749.19222 | Иногда используется астрономами |
| Модифицированный юлианский день (MJD) | 00:00 17 ноября, 1858, Ср | MJD = JD − 2400000,5 | 55748.69222 | Введен SAO в 1957, сменяется в полночь. |
| Truncated Julian Day (TJD) | 00:00 24 мая, 1968, Пт00:00 10 ноября, 1995, Вт. | TJD = JD − 2440000,5TJD = (JD − 0,5) mod 10000 | 15748.692225748.69222 | - Определение, введённое NASA[2] — определение NIST |
| Дублинский юлианский день (DJD) | 12:00 31 декабря, 1899, Вс. | DJD = JD − 2415020 | 40729.19222 | Введен IAU в 1955 |
| Хронологический юлианский день (CJD) | 00:00 1 января, 4713 до н. э., Пн | CJD = JD + 0,5 + часовой пояс | 2455749.6922222 (UT) | Свой для каждого часового пояса; Дата меняется в полночь по местному времени |
| Лилианский день (англ.) (LDN) | 00:00 15 октября 1582, Friday (день № 1) | floor (JD − 2299160,5) | 156588 | |
| ANSI Дата | 00:00 1 января 1601, Пн (день № 1) | floor (JD − 2305812,5) | 149936 | По нему считаются даты COBOL |
| Rata Die | 1 января, 1, Пн (день № 1) | floor (JD − 1721424,5) | 734324 | Счёт дней нашей эры по григорианскому календарю |
| Время Юникс | 1 января, 1970, Вт. | (JD − 2440587,5) × 86400 | 1309970208 | Считается посекундно |
Там, где требуются вычисления с точностью до минут и более, указывается, относительно какой системы приводится значение юлианского дня. Если это UTC, соответствующий юлианский день обозначают JDUTC, если это часто использующееся в астрономии эфемеридное время, юлианский день обозначают JED.
wreferat.baza-referat.ru
Реферат на тему:
Юлиа́нский день (JD) — астрономический способ измерения времени, при котором считается число дней, прошедших начиная с полудня 1 января 4713 до н. э. юлианского календаря или, что то же самое, 24 ноября 4714 г. до н. э. григорианского календаря (соответственно, −4712 г. и −4713 г. по астрономическому счёту лет[1]). Первый день имел номер 0. С тех пор по настоящее время прошло немногим менее 2,5 миллионов дней. Даты сменяются в полдень UT или TT. Для точного обозначения времени применяют дробную часть, например, JD = 2451545,25 соответствует 18 часам 1 января 2000 г., 3 часа дня 2 августа 1942 г. — JD 2430574,125, 13,5 июня 1944 г. — JD 2431255,0.
Текущий юлианский день JD=2455749.192222
Юлианский период был предложен Скалигером для целей истории и хронологии. Поскольку историкам постоянно требуется работать с различными календарными системами и различными эпохами, Скалигер предложил простую погодную хронологическую шкалу, к которой можно было бы приводить все исторические даты — юлианский период. Каждый год нумеровался тремя числами — Индиктом (от 1 до 15), Золотым числом (от 1 до 19) и Солнечным числом (от 1 до 28). На начало цикла 1 января 4713 до н. э. все числа были равны 1. Длительность цикла равняется 15*19*28, то есть 7980 годам, через это время все цифры повторяются. Конец первого юлианского периода придётся на 23 января 3268 года по григорианскому календарю.
В 1849 году для удобства астрономических расчетов Гершель предложил все даты выражать через число дней, прошедших от начала цикла Скалигера. Началом дня Гершель выбрал полдень по меридиану Александрии, так как именно так отсчитывались дни в классическом Альмагесте Клавдия Птолемея. Использование полдня как границы суток удобно для датирования астрономических наблюдений, так как вся ночь попадает в один и тот же юлианский день.
К концу XIX века юлианский день постепенно начал использоваться в астрономической литературе. За начало дня обычно брали полдень по Гринвическому меридиану, который в 1884 года получил статус международного.
Юлианский день можно применять для определения дня недели, для перевода дат одного календаря в даты другого, для определения промежутка времени между двумя датами и т. п.
В формулах:
year — год, если вы хотите использовать его для дат до нашей эры, необходимо перевести год до н. э. в отрицательный год (например, 10 г. до н. э. = −9).
month — номер месяца, январь — 1, февраль — 2 и т. д.
day — день месяца.
hour — часы от 0 до 23.
minute — минуты от 0 до 59.
second — секунды от 0 до 59, могут содержать дробную часть.
JDN — это номер юлианского дня (Julian Day Number), который начинается в полдень числа, для которого производятся вычисления.
JD — юлианская дата, содержащая дробную часть.
Вначале нужно вычислить промежуточные коэффициенты:
После этого можно вычислить номер юлианского дня:
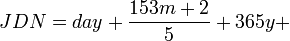
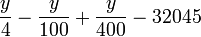
Все деления целочисленные, то есть остатки деления отбрасываются.
Формула справедлива для дат после 23 ноября −4713 г.
Вначале нужно вычислить промежуточные коэффициенты (они те же, что и для григорианского календаря):
После этого можно вычислить номер юлианского дня:
Для дат юлианского календаря существует также формула:

Все операции деления — целочисленные, то есть, остатки деления отбрасываются. Формулы справедливы начиная с −4712 года (то есть, для положительных значений JDN).
Для перехода к «полной» юлианской дате, содержащей дробную часть, можно воспользоваться формулой:
При делении в этой формуле дробная часть не отбрасывается. Сутки не должны содержать високосной секунды (23:59:60).
Например, полдень (12 ч, 0 минут, 0 секунд) 1 января 2000 г. соответствует JD = 2451545,0.
День недели может быть вычислен как остаток от деления JDN на 7. При этом 0 соответствует понедельнику, 1 — вторнику и т. д..
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
Сначала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по юлианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
С начала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по григорианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
Большое количество цифр в юлианском дне и смена дат в полдень во многих случаях неудобны, поэтому разработано большое количество систем счёта дней, аналогичных юлианскому дню
| Юлианский день (JD) | 12:00 1 января, 4713 до н. э., Пн | 2455749.192222 | ||
| Номер юлианского дня (JDN) | 12:00 1 января, 4713 до н. э., Пн (день № 0) | JDN = floor (JD) | 2455749 | |
| Reduced Julian Day (RJD) | 12:00 16 ноября, 1858, Вт | RJD = JD − 2400000 | 55749.19222 | Иногда используется астрономами |
| Модифицированный юлианский день (MJD) | 00:00 17 ноября, 1858, Ср | MJD = JD − 2400000,5 | 55748.69222 | Введен SAO в 1957, сменяется в полночь. |
| Truncated Julian Day (TJD) | 00:00 24 мая, 1968, Пт00:00 10 ноября, 1995, Вт. | TJD = JD − 2440000,5TJD = (JD − 0,5) mod 10000 | 15748.692225748.69222 | - Определение, введённое NASA[2] — определение NIST |
| Дублинский юлианский день (DJD) | 12:00 31 декабря, 1899, Вс. | DJD = JD − 2415020 | 40729.19222 | Введен IAU в 1955 |
| Хронологический юлианский день (CJD) | 00:00 1 января, 4713 до н. э., Пн | CJD = JD + 0,5 + часовой пояс | 2455749.6922222 (UT) | Свой для каждого часового пояса; Дата меняется в полночь по местному времени |
| Лилианский день (англ.) (LDN) | 00:00 15 октября 1582, Friday (день № 1) | floor (JD − 2299160,5) | 156588 | |
| ANSI Дата | 00:00 1 января 1601, Пн (день № 1) | floor (JD − 2305812,5) | 149936 | По нему считаются даты COBOL |
| Rata Die | 1 января, 1, Пн (день № 1) | floor (JD − 1721424,5) | 734324 | Счёт дней нашей эры по григорианскому календарю |
| Время Юникс | 1 января, 1970, Вт. | (JD − 2440587,5) × 86400 | 1309970208 | Считается посекундно |
Там, где требуются вычисления с точностью до минут и более, указывается, относительно какой системы приводится значение юлианского дня. Если это UTC, соответствующий юлианский день обозначают JDUTC, если это часто использующееся в астрономии эфемеридное время, юлианский день обозначают JED.
wreferat.baza-referat.ru
Реферат на тему:
Юлиа́нский день (JD) — астрономический способ измерения времени, при котором считается число дней, прошедших начиная с полудня 1 января 4713 до н. э. юлианского календаря или, что то же самое, 24 ноября 4714 г. до н. э. григорианского календаря (соответственно, −4712 г. и −4713 г. по астрономическому счёту лет[1]). Первый день имел номер 0. С тех пор по настоящее время прошло немногим менее 2,5 миллионов дней. Даты сменяются в полдень UT или TT. Для точного обозначения времени применяют дробную часть, например, JD = 2451545,25 соответствует 18 часам 1 января 2000 г., 3 часа дня 2 августа 1942 г. — JD 2430574,125, 13,5 июня 1944 г. — JD 2431255,0.
Текущий юлианский день JD=2455749.192222
Юлианский период был предложен Скалигером для целей истории и хронологии. Поскольку историкам постоянно требуется работать с различными календарными системами и различными эпохами, Скалигер предложил простую погодную хронологическую шкалу, к которой можно было бы приводить все исторические даты — юлианский период. Каждый год нумеровался тремя числами — Индиктом (от 1 до 15), Золотым числом (от 1 до 19) и Солнечным числом (от 1 до 28). На начало цикла 1 января 4713 до н. э. все числа были равны 1. Длительность цикла равняется 15*19*28, то есть 7980 годам, через это время все цифры повторяются. Конец первого юлианского периода придётся на 23 января 3268 года по григорианскому календарю.
В 1849 году для удобства астрономических расчетов Гершель предложил все даты выражать через число дней, прошедших от начала цикла Скалигера. Началом дня Гершель выбрал полдень по меридиану Александрии, так как именно так отсчитывались дни в классическом Альмагесте Клавдия Птолемея. Использование полдня как границы суток удобно для датирования астрономических наблюдений, так как вся ночь попадает в один и тот же юлианский день.
К концу XIX века юлианский день постепенно начал использоваться в астрономической литературе. За начало дня обычно брали полдень по Гринвическому меридиану, который в 1884 года получил статус международного.
Юлианский день можно применять для определения дня недели, для перевода дат одного календаря в даты другого, для определения промежутка времени между двумя датами и т. п.
В формулах:
year — год, если вы хотите использовать его для дат до нашей эры, необходимо перевести год до н. э. в отрицательный год (например, 10 г. до н. э. = −9).
month — номер месяца, январь — 1, февраль — 2 и т. д.
day — день месяца.
hour — часы от 0 до 23.
minute — минуты от 0 до 59.
second — секунды от 0 до 59, могут содержать дробную часть.
JDN — это номер юлианского дня (Julian Day Number), который начинается в полдень числа, для которого производятся вычисления.
JD — юлианская дата, содержащая дробную часть.
Вначале нужно вычислить промежуточные коэффициенты:
После этого можно вычислить номер юлианского дня:
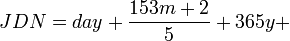
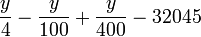
Все деления целочисленные, то есть остатки деления отбрасываются.
Формула справедлива для дат после 23 ноября −4713 г.
Вначале нужно вычислить промежуточные коэффициенты (они те же, что и для григорианского календаря):
После этого можно вычислить номер юлианского дня:
Для дат юлианского календаря существует также формула:

Все операции деления — целочисленные, то есть, остатки деления отбрасываются. Формулы справедливы начиная с −4712 года (то есть, для положительных значений JDN).
Для перехода к «полной» юлианской дате, содержащей дробную часть, можно воспользоваться формулой:
При делении в этой формуле дробная часть не отбрасывается. Сутки не должны содержать високосной секунды (23:59:60).
Например, полдень (12 ч, 0 минут, 0 секунд) 1 января 2000 г. соответствует JD = 2451545,0.
День недели может быть вычислен как остаток от деления JDN на 7. При этом 0 соответствует понедельнику, 1 — вторнику и т. д..
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
Сначала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по юлианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
С начала нужно вычислить промежуточные коэффициенты:
После этого можно вычислить день, месяц и год по григорианскому календарю:
Все деления целочисленные, дробная часть отбрасывается. Поэтому 12*(m/10) в формуле для месяца не следует вычислять как (12*m)/10.
Большое количество цифр в юлианском дне и смена дат в полдень во многих случаях неудобны, поэтому разработано большое количество систем счёта дней, аналогичных юлианскому дню
| Юлианский день (JD) | 12:00 1 января, 4713 до н. э., Пн | 2455749.192222 | ||
| Номер юлианского дня (JDN) | 12:00 1 января, 4713 до н. э., Пн (день № 0) | JDN = floor (JD) | 2455749 | |
| Reduced Julian Day (RJD) | 12:00 16 ноября, 1858, Вт | RJD = JD − 2400000 | 55749.19222 | Иногда используется астрономами |
| Модифицированный юлианский день (MJD) | 00:00 17 ноября, 1858, Ср | MJD = JD − 2400000,5 | 55748.69222 | Введен SAO в 1957, сменяется в полночь. |
| Truncated Julian Day (TJD) | 00:00 24 мая, 1968, Пт00:00 10 ноября, 1995, Вт. | TJD = JD − 2440000,5TJD = (JD − 0,5) mod 10000 | 15748.692225748.69222 | - Определение, введённое NASA[2] — определение NIST |
| Дублинский юлианский день (DJD) | 12:00 31 декабря, 1899, Вс. | DJD = JD − 2415020 | 40729.19222 | Введен IAU в 1955 |
| Хронологический юлианский день (CJD) | 00:00 1 января, 4713 до н. э., Пн | CJD = JD + 0,5 + часовой пояс | 2455749.6922222 (UT) | Свой для каждого часового пояса; Дата меняется в полночь по местному времени |
| Лилианский день (англ.) (LDN) | 00:00 15 октября 1582, Friday (день № 1) | floor (JD − 2299160,5) | 156588 | |
| ANSI Дата | 00:00 1 января 1601, Пн (день № 1) | floor (JD − 2305812,5) | 149936 | По нему считаются даты COBOL |
| Rata Die | 1 января, 1, Пн (день № 1) | floor (JD − 1721424,5) | 734324 | Счёт дней нашей эры по григорианскому календарю |
| Время Юникс | 1 января, 1970, Вт. | (JD − 2440587,5) × 86400 | 1309970208 | Считается посекундно |
Там, где требуются вычисления с точностью до минут и более, указывается, относительно какой системы приводится значение юлианского дня. Если это UTC, соответствующий юлианский день обозначают JDUTC, если это часто использующееся в астрономии эфемеридное время, юлианский день обозначают JED.
www.wreferat.baza-referat.ru