Количество просмотров публикации Индексы Миллера - 502
В кристалле
Образование плоскостей и направлений
Для обозначения кристаллографических плоскостей в настоящее время общепринятой является система индексов Миллера. Поясним ее сущность.
Далее поступают по следующей схеме;
1) берут отрезки, отсекаемые плоскостью на осях координат: 1:2:3;
2) берут величины, обратные этим отрезкам: ;
3) приводят к общему знаменателю: ;
4) отбрасывают знаменатель: 6:3:2 – индексы Миллера для плоскости.
Миллеровские индексы плоскостей заключаются в круглые скобки – (632), знак отношения между индексами не ставится.
В случае если плоскость параллельна какой-либо оси, ее проекция на эту ось равна бесконечности. Для такой плоскости соответствующий индекс Миллера равен нулю. В случае если плоскость отсекает некоторый отрезок с отрицательным знаком, то соответствующий индекс Миллера будет также отрицательным, и черточка ставится сверху над индексами.
Рассмотрим пример кубической решетки. Нас интересует плоскость abcd (рисунок 2.6). Пусть ребро куба равно 1. Плоскость abcd имеет индексы Миллера (100). В случае если мы хотим обозначить не одну плоскость, а семейство плоскостей, то индексы Миллера берутся в фигурные скобки {100}.
Плоскость cdeq имеет индексы Миллера (101). Плоскость deg имеет индексы Миллера (111). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, мы описали три основные плоскости для кубической решетки (рисунок 2.7).
Рассмотрим тот же пример кубической решетки (рисунок 2.6):
Направление ОХ: [100].
Направление ОА: [101].
Направление перпендикулярное плоскости (111): [111].
2.3.2
Смоделируем частицы в узлах кристаллической решетки в виде идеальных (не деформированных) соприкасающихся шаров. Тогда плотность упаковки (коэффициент упаковки или компактность данной решетки) представляет собой отношение объёма, занимаемого шарами в элементарной ячейке, ко всему объёму самой элементарной ячейки. В качестве примера рассмотрим примитивную кубическую ячейку (рисунок 2.8).
Пусть радиус шара r. Тогда длина ребра куба 2r. Объем одного шара . Внутрь попадает часть шара
. Таких шаров 8, и каждый принадлежит ячейке на 1/8. Тогда объём, занимаемый шарами внутри ячейки,
. Объем ячейки:
. И плотность упаковки: f =
=
= 0,52.
referatwork.ru
Д
ля обозначения плоскостей и направлений кристалла используются так называемые кристаллографические индексы Миллера. Для их получения проведем оси координатX,Y,Z вдоль базисных векторов 
. Пусть некоторая плоскость пересекает такую координатную систему в точках с координатами: 
; 
;
. 
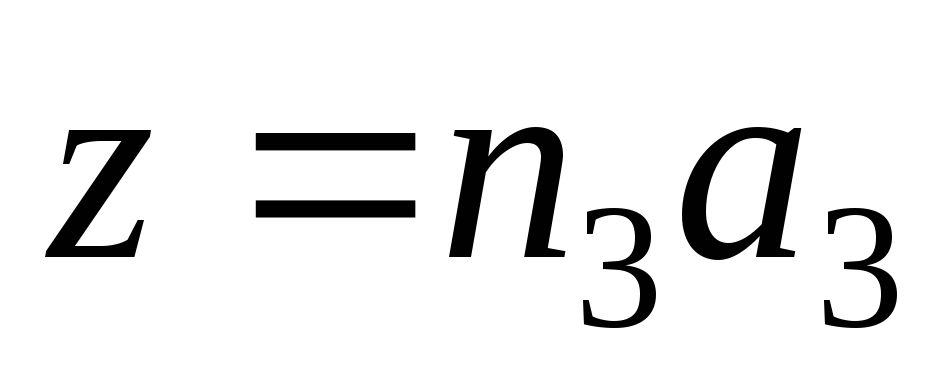- целые или дробные числа, выражают наклон плоскостей по отношению к осям координатной системы. Теперь составим отношение обратных чисел
и приведем это отношение к отношению наименьших целых чисел: 
; R - наименьшее кратное, а h, k, l и есть индексы Миллера для указанной плоскости. При обозначении плоскостей индексы Миллера заключаются в круглые скобки, без каких либо знаков между ними.
Предположим 
; 
; 
. Такие же индексы будут иметь остальные плоскости параллельные ей. Если плоскость параллельна одной из координатных осей, то соответствующий индекс равен нулю, если плоскость отсекает координату при отрицательных значениях, то над соответствующим индексом Миллера сверху ставится знак“-”. Направления перпендикулярные плоскости (hkl) обозначаются теми же индексами заключенными в квадратные скобки [hkl]. Система плоскостей одного кристаллографического типа обозначаются {hkl}, направления обозначаются <hkl>. Для примера найдем обозначения характерных плоскостей и направлений в кристаллах кубической системы (а1 = а2 = а3 = а; α = β= γ= 900). Для этого вырежем кристалл в форме куба с ребрами вдоль базисных векторов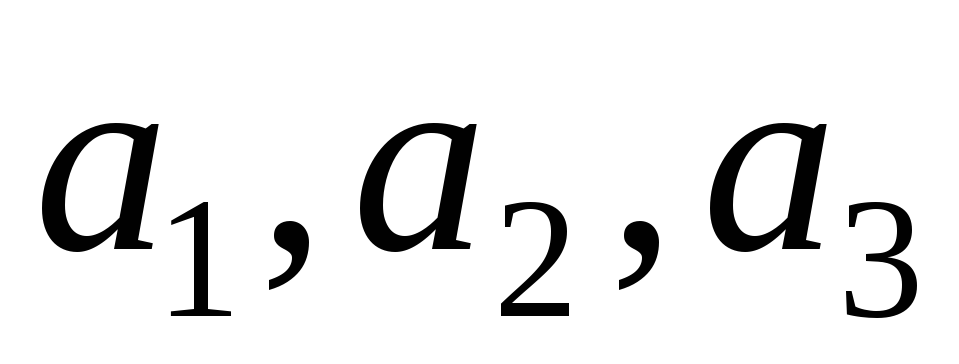 
. Осиx, ,y, z н
аправлены вдоль базисных векторов. Найдем индексы Миллера для заштрихованной плоскости 1. Она пересекает координатные оси в точках с координатами: 
; 
; 
. Тогда индексы Миллера для плоскости 2: (010), для 3: (001). x1[100], y1[010], z1[001]. Плоскость противоположную (100), обозначают 
и так д
алее. В
се плоскости (100), (010), (001),
,
,
кристаллографически одинаковые и их обозначают {100}. На рисунке заштрихована плоскость (110), для этой плоскости одинаковыми являются плоскости (011), (101). На следующем рисунке заштрихована плоскость (111). Для обозначения плоскостей в кристаллах гексагональной системы используют 4 индекса Миллера, для этого проводят чет
ыре координатные осиx, y, u, z,. Ось z параллельна ребру а3. 
; 
.
Плоскость перпендикулярная оси 
называется базисной плоскостью. Осиx, y, u располагают в базисной плоскости под углом 1200 друг к другу. Для тог чтобы найти (hkil), находят координаты точек пересечения с кристаллографическими осями.
Д
ля примера найдем индексы Миллера для плоскости АВ, которая перпендикулярна плоскости рисунка. Координаты точек пересечения этой плоскостью координатных осей: 
,
; 
; 
. Следовательно, направления вдоль осиz есть [0001], i = - (h+k). Возникает вопрос, почему используем четыре а не три индекса Миллера при обозначении плоскостей и направлений в кристаллах гексагональной системы. Оказывается, что при обозначении тремя индексами Миллера однотипные плоскости кристаллов гексагональной системы имели бы разное число единиц и нулей, и их нельзя было бы обозначить как {hkl}. Для примера уберем ось u, тогда плоскости СВ=(010), 
,
. Обозначение этих плоскостей имеют вид: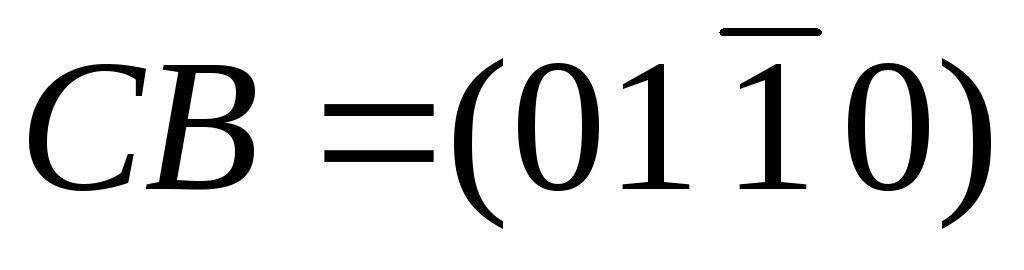 
,
, видно что все однотипные плоскостиCB, DB, DF, FL имеют две единицы и два нуля, и тогда их можно обозначить {1100}.
studfiles.net
Пусть плоскость отсекает на осях координат отрезки ОА, ОВ и ОС (в единицах периода решетки). Рассчитаем обратные им величины H = 1/ОА, K = 1/ОВ, L = 1/ОС и определим наименьшие целые числа с таким же соотношением, как H : K : L = h : k : l. Целочисленные (hkl) называются индексами Миллера плоскости.
В кубических кристаллах индексы (100) относятся к плоскости, параллельной осям У и Z; индексы (010) — к плоскости, параллельной осям X и Z, а (001) — к плоскости, параллельной осям X и Y. В кристаллах с ортогональными осями эти плоскости вместе с тем перпендикулярны соответственно осям X, Y и Z.
Для обозначения направлений в кристалле применяют индексы в виде наименьших целых чисел, относящихся между собой как компоненты вектора, параллельного данному направлению. В отличие от обозначения плоскостей их пишут в квадратных скобках. В кубических кристаллах эти направления перпендикулярны плоскости с теми же индексами. Положительное направление оси X обозначают [100], положительное направление оси Y — [010], отрицательное направление оси Z — [001], диагональ куба — [111] и т.д. Обозначения кристаллографических плоскостей и направлений приведены, на рис. 2.2.
Плоскости, отсекающие равные отрезки, но расположенные в других октантах, эквивалентны в кристаллографическом и физико-химическом отношениях. Они образуют совокупность эквивалентных плоскостей – {hkl} или систему плоскостей, у которых h, k, l могут быть записаны в любом порядке и с любым числом минусов перед индексами. Минус записывается над индексом.
Положение направления в пространственной решетке может быть легко определено координатами атома, ближайшего к началу координат и лежащего на данном направлении.
Совокупность эквивалентных направлений или система направлений обозначается <hkl>, где h, k, l могут быть записаны в любом порядке и с любым числом минусов: <100> ‑ совокупность направлений, параллельных всем ребрам куба; {100} ‑ совокупность плоскостей, параллельных всем граням куба.
Рис. 2.2. Примеры обозначения кристаллографических
плоскостей и направлений в кубических кристаллах
с помощью индексов Миллера
Пример 1. Определить индексы плоскости, отсекающей на осях решетки отрезки А = 1, В = 2, С = - 4.
Отношения величин, обратных отрезкам, 1/А : 1/В : 1/С = 1/1 : 1/2 : 1/(-4). Доводим это отношение до отношения трех целых чисел, умножая на общий знаменатель 4, дополнительными множителями будут 4 и 2. 1/А : 1/В : 1/С = 4 : 2 :(- 1). Это и будут искомые h, k, l. Индексы плоскости (42
).
Пример 2. Определить отрезки, которые отсекает на осях решетки плоскость (023).
Записываем величины, обратные индексам плоскости: 1/0, 1/2, 1/3. Умножаем на общий знаменатель, равный 6 (доводим отрезки до целых чисел). Отрезки, отсекаемые плоскостью на осях, будут равны А = 
, В = 3, С = 2. Эта плоскость будет параллельна оси х, так как А =
.
Некоторые твердые вещества обладают способностью образовывать не одну, а две и более кристаллические структуры, устойчивые при различных температурах и давлениях. Такое свойство материалов называют полиморфизмом, а отвечающие им кристаллические структуры называют полиморфными формами или аллотропными модификациями вещества.
Модификацию, устойчивую при нормальной и более низкой температуре, принято обозначать буквой α; модификации, устойчивые при более высоких температурах, обозначают соответственно буквами β, γ и т.д.
Полиморфизм широко распространен среди технических материалов и имеет важное значение для их обработки и эксплуатации.
Классическим примером полиморфизма является низкотемпературное превращение белого олова (β-Sn) в серое (α-Sn), известное в технике как «оловянная чума».
Практический интерес представляет полиморфизм углерода — существование его в виде алмаза или графита. В обычных условиях графит является более устойчивой модификацией, чем алмаз. Однако при повышении давления устойчивость алмаза растет, а графита падает, и при достаточно высоких давлениях алмаз становится более устойчивым. Если при этом повысить температуру, чтобы увеличить подвижность атомов, то графит можно перевести в алмаз. На этом принципе основано получение искусственных алмазов. В Советском Союзе их промышленное производство началось в 1961 г. Синтез проводят под давлением порядка 1010 Па при температуре на уровне 2000 °С. Получаемые таким образом искусственные алмазы имеют более высокую прочность и твердость, нежели природные кристаллы.
studfiles.net
В кристалле
Образование плоскостей и направлений
Для обозначения кристаллографических плоскостей в настоящее время общепринятой является система индексов Миллера. Поясним ее сущность.
 |
Далее поступают по следующей схеме;
1) берут отрезки, отсекаемые плоскостью на осях координат: 1:2:3;
2) берут величины, обратные этим отрезкам: 
;
3) приводят к общему знаменателю: 
;
4) отбрасывают знаменатель: 6:3:2 – индексы Миллера для плоскости.
Миллеровские индексы плоскостей заключаются в круглые скобки – (632), знак отношения между индексами не ставится.
Если плоскость параллельна какой-либо оси, ее проекция на эту ось равна бесконечности. Для такой плоскости соответствующий индекс Миллера равен нулю. Если плоскость отсекает некоторый отрезок с отрицательным знаком, то соответствующий индекс Миллера будет также отрицательным, и черточка ставится сверху над индексами
.
Рассмотрим пример кубической решетки. Нас интересует плоскость abcd (рисунок 2.6). Пусть ребро куба равно 1. Плоскость abcd имеет индексы Миллера (100). Если мы хотим обозначить не одну плоскость, а семейство плоскостей, то индексы Миллера берутся в фигурные скобки {100}.
Плоскость cdeq имеет индексы Миллера (101). Плоскость deg имеет индексы Миллера (111). Таким образом, мы описали три основные плоскости для кубической решетки (рисунок 2.7).
 |
Рассмотрим тот же пример кубической решетки (рисунок 2.6):
Направление ОХ: [100].
Направление ОА: [101].
Направление перпендикулярное плоскости (111): [111].
2.3.2
 |
Смоделируем частицы в узлах кристаллической решетки в виде идеальных (не деформированных) соприкасающихся шаров. Тогда плотность упаковки (коэффициент упаковки или компактность данной решетки) представляет собой отношение объема, занимаемого шарами в элементарной ячейке, ко всему объему самой элементарной ячейки. В качестве примера рассмотрим примитивную кубическую ячейку (рисунок 2.8).
Пусть радиус шара r. Тогда длина ребра куба 2r. Объем одного шара 
. Внутрь попадает часть шара 
. Таких шаров 8, и каждый принадлежит ячейке на 1/8. Тогда объем, занимаемый шарами внутри ячейки, 
. Объем ячейки: 
. И плотность упаковки: f = 
= 
= 0,52.
 |
3-net.ru
(Назад)
(Cкачать работу)
Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!
ЛАБОРАТОРНАЯ РАБОТА КРИСТАЛЛОГРАФИЧЕСКИЕ СИМВОЛЫЦель работы: 1) Знакомство с системой обозначения граней и направлений;
2) Определение индексов граней и ребер кристаллов;
3) Решение некоторых типичных кристаллографических задач с использованием условия зональности.
Важнейшее значение в кристаллографии имеет вопрос об аналитической записи взаимного расположения граней и ребер кристалла в пространстве. С этой целью применяют кристаллографические символы, определяющие положение любой грани и ребра кристалла относительно принятых координатных осей.
Символы гранейПоложение грани кристалла можно описать с помощью трех отрезков, отсекаемых этой гранью на координатных осях. Кристаллографическую систему характеризуют геометрические константы кристалл: осевые углы (, , ) и осевые единицы (a0, b0, c0). Осевыми единицами называют отрезки a0, b0, c0 , отсекаемые единичной гранью на координатных осях x,y,z соответственно. В соответствии с симметрией кристалла масштаб измерения отрезков, отсекаемых гранью на осях, определяется для каждой сингонии соотношением между осевыми единицами (табл. 1).
Таблица 1.
| Сингония | Угловыесоотношения | Осевыеединицы |
Кубическая | ===90 | a0=b0=c0 |
Тетрагональная | ===90 | a0=b0c0 |
Ромбическая | ===90 | a0b0c0 |
Моноклинная | ==90 | a0b0c0 |
Триклинная | 90 | a0b0c0 |
Гексагональная | ==90,=120 | a0=b0c0 |
В методе параметров (метод Вейса) для определения грани используется тройка безразмерных векторов a, b, c, соответствующих отрезкам, отсекаемым гранью на координатных осях и измеренных с помощью осевых единиц a0, b0, c0 (рис. 1) a=OA/a0, b=OB/b0, c=OC/c0.
Для выбора масштаба измерения, после установки кристалла, среди его наиболее развитых граней находят такую, которая пересекает все три оси. Отрезки, отсекаемые такой гранью кристалла, принимают за единичные, а саму грань - за единичную. Её параметры: (1:1:1). Чтобы определить параметры любой другой грани кристалла, необходимо найти соотношение отрезков, отсекаемых ею на координатных осях и отнесенных к соответствующим единичным отрезкам a0, b0, c0.
Такое обозначение граней с помощью параметров имеет один существенный недостаток: неудобство обозначения граней, параллельных координатным осям. Например, грань, параллельная плоскости XOY, запишется как (::1), поскольку такая грань пересекает лишь ось Z. Между тем, грани параллельные координатным осям, представляют для кристаллографии особый интерес.
В методе индексов (метод Миллера) положение любой грани кристаллов в трехосной системе координат определяется тройкой целых, как правило, небольших, взаимно-простых чисел – индексов h, k, l, представляющих собой отношение обратных величин параметров. Тогда грань, параллельная плоскости XOY будет иметь индексы h:k:l=1/:1/:1/1=0:0:1. Индексы грани заключают в круглые скобки, не разделяя их друг от друга никакими знаками. Следовательно, рассмотренная выше грань имеет символ (001).
В кристаллографической практике метод индексов Миллера получил широкое распространение. Следует иметь в виду, что параллельные грани имеют один и тот же символ, соответствующий грани ближайшей к началу координат.
Благодаря высокой симметрии кубических кристаллов, их индицирование (определение индексов всех граней) осуществляется достаточно просто. Единичная грань кубического кристалла должна составлять с координатными осями равные углы и отсекать на них равные отрезки. Легко видеть, что такой гранью может быть выбрана грань октаэдра или тетраэдра, через которую проходит поворотная ось третьего порядка.
z
y
x
A
B
C
a0
b0
c0
Рис. 1. Грань кристалла, отсекающая на координатных осях отрезки ОА=аа0, ОВ=bb0, OC=cc0 .
Символы реберЛюбое направление (ребро кристалла) в данной системе координат может быть задано: 1) двумя точками, лежащими на заданном направлении, не проходящим через начало координат; 2) одной точкой, если направление проходит через эту точку и начало координат.
Если осевые единицы единичной грани равны a0, b0, c0 , а точки А (x1, y1, z1) и В (x2, y2, z2) лежат на заданном направлении, то проекции отрезка АВ будут равны:
(AB)x=x2-x1,(AB)y=y2-y1,(AB)z=z2-z1.
Тогда символ направления [r s t] определится как
.
Таким образом, заданное направление определяется отношением трех проекций отрезка, лежащем на этом направлении, к соответствующим осевым единицам и выражается с помощью целых взаимно простых чисел r, s, t, записываемых в квадратных скобках [r s t]. В случае, когда заданное направление проходит через точку А [[000]] начала координат и точку В [[x y z]] можно записать.Из приведенного выше правила определения символов ребер следует, что если данный отрезок АВ или данное направление перемещать в пространстве параллельно самому себе, то его символ не изменится.
Заданное направление может быть определено и с помощью углов , , , которые оно образует с координатными осями x, y, z. Для отрезка АВ, лежащего на заданном направлении, можно записать:
.
В кубических кристаллах:
.
Несложные геометрические рассмотрения показывают, что для кубических кристаллов отношение направляющих косинусов нормали к грани (h k l) пропорционально отношению индексов:
,
отсюда:
.
Таким образом, при индицировании направлений в кубических кристаллах следует помнить, что символы направления и перпендикулярной ему грани обозначаются одинаковыми индексами. Например, направление [111] перпендикулярно грани (111), а направление [110] – грани (110).
Основные кристаллографические соотношенияУгол между двумя направлениями.
Чтобы найти угол между двумя направлениями [r1, s1, t1], [r2, s2, t2] необходимо вспомнить одно из правил аналитической геометрии о нахождении скалярного произведения двух векторов .
.
Если .
(Здесь - тройка единичных векторов координатной системы), то для прямоугольной системы координат имеем:
,
.
Откуда
.
2) Угол между направлением и плоскостью
Учитывая, что для кубических кристаллов перпендикуляры к плоскостям (h k l) изображаются как [h k l], легко найти угол между таким перпендикуляром и заданным направлением [r s t].
Исходный угол будет дополнительным к 90, т.е. =(90-) и определится как
.
3) Условие зональности.
Кристаллографической зоной называется совокупность граней кристалла, параллельных одному направлению, называемому осью зоны. Чтобы какая-либо плоскость (h k l) принадлежала зоне, ось которой [r s t] , необходимо, чтобы направление, параллельное оси зоны, лежало в этой плоскости. Следовательно, косинус угла между перпендикуляром к заданной плоскости (h k l) и осью зоны [r s t] должен быть равен нулю. При этом условие зональности для кубических кристаллов может быть записано как
.
Используя условие зональности, легко определить символ ребра [r s t] , образованного двумя гранями (h2 k1 l1) и (h3 k2 l2) из совместного решения уравнений:
.
Решение данной системы уравнений можно представить в виде:Рассмотренную задачу можно назвать нахождением символа зоны по символам граней кристалла.
Аналогичным образом решается задача о нахождении символа грани (h k l), в которой лежат два заданных направления [r1 s1 t1] и [r2 s2 t2]. В этом случае решение системы уравнений
Дает индексы искомой грани (h k l).
4) Межплоскостное расстояние и индексы плоскости.
При расчете рентгенограмм необходимо знать связь межплоскостного расстояния d с индексами (h k l) , отражающего семейства плоскостей. геометрическое рассмотрение для ортогональной системы координат дает следующие зависимости:
- для ромбической сингонии;
- для тетрагональной сингонии;
- для кубической сингонии.
План работыПроизвести индицирование всех граней и ребер заданных кристаллов.Найти угол между двумя заданными направлениями в кристаллах кубической,. тетрагональной и ромбической сингоний при известных параметрах решетки.Определить угол между двумя заданными плоскостями, направлением и плоскостью в кубических кристаллах.Найти символ зоны по известным символам граней. Найти
referat.co
| Рис. 121. Индексы Миллера граней кубического и октаэдрического кристаллов |  |
Мысленно построим в кристалле прямоугольную систему координат, оси которой расположены параллельно поверхностям, на которых лежат узлы решетки. Тогда каждая такая узловая плоскость отсекает на осях координат отрезки, которые можно использовать в качестве характеристики строения кристалла. При этом используют обратные величины отношений этих отрезков к постоянной решетки , выражаемые как наименьшие целые числа. Эти числа называют индексами Миллера. Например, плоскость (123) отсекает на осях координат отрезки 1, и 7з длины ребра элементарной ячейки. Узловая плоскость (100) параллельна плоскости г/2и смещена в направлении оси х на расстояние постоянной решетки. Плоскость (110) проходит [c.109]
Обычно грани кристаллов описывают обратными величинами кратных отношений стандартных отрезков отсюда возникает другое название-закон рациональных индексов. На рис. 9-7 три линии, выбранные в качестве осей, могут быть также ребрами кристалла. Рассматриваемая грань ЛВС отсекает на этих осях отрезки а, Ь, с. Какая-то другая грань кристалла, нанример DE , может быть описана через эти отрезки как ajh. Ь/к, с/1. Здесь h, к, / простые целые числа или нуль. Их называют индексами Миллера. Отрезок бесконечен, если грань параллельна какой-то оси, тогда h, к или / соответственно будут равны нулю. Для ортогональных осей индексы граней куба (100), (010) и (001). Индексы грани DE на рис. 9-7 равны (231). [c.407]
VI-1-2. Для того чтобы определить индекс Миллера, берут обратную величину индекса Вайса. В данном случае получим 7 > /21 О- Чтобы исключить дроби, умножим эти величины на 2 и получим 4, 3, 0. [c.259]
Разумеется, частицы, из которых состоят кристаллы,— атомы, ионы или молекулы, не являются кубиками или параллелепипедами. Однако, как мы увидим ниже, они располагаются в кристаллах в правильном порядке, образуя кристаллическую решетку, которая состоит из элементарных ячеек, имеющих форму параллелепипедов. На законе целых чисел основана система обозначений граней кристаллов. Для каждой грани пишут набор обратных значений длин отрезков, отсекаемых ею на осях х, у и г. Длины выражают относительными величинами, соответствующими отрезками, отсекаемыми на соответствующих осях одной из граней (единичной гранью). Такие обозначения называют индексами Миллера. На р 1С. 1.74 показаны индексы Миллера для граней кубических и [c.138]
Миллера. На рис. 121 показаны индексы Миллера для граней кубических и октаэдрических кристаллов (знак минус здесь пишут над цифрой). [c.245]
Направления и плоскости в кристаллах обозначаются индексами Миллера. Индексы, определяющие положение поверхностей, заключаются в круглые скобки, а индексы, определяющие направления, - в квадратные скобки. Например, на рисунке 1.3.7, а - [100] - направление легкого намагничивания [ПО]-среднего [111] -трудного. [c.27]
Трехмерную решетку кристалла можно представить себе как совокупность параллельных равноудаленных друг от друга атомных плоскостей, образованных расположенными в них атомами. На рис. 36 показаны некоторые возможные атомные плоскости в различных типах кубической решетки. Все плоскости, одинаково ориентированные в пространстве, составляют семейство плоскостей, которые характеризуются так называемыми кристаллографическими индексами (или индексами Миллера). Под этими индексами, [c.71]
Индексами грани (индексами Миллера) на-3 ы в а ю-т три взаимно простых числа, взятые [c.120]
Индексы Миллера кЫ используются для описания как внешних граней, так и внутренних плоскостей решетки кристалла. [c.394]
Реальная решетка имеет индексы Миллера (О, к, [), (1, к, /), (2, к, I) и т. д. Вместо того чтобы брать в качестве начала координат точку на ребре реальной решетки, как мы это делали на рис. 17.12, поместим ее в центр. Выберем точку А в реальной решетке на оси а. Существует целый набор возможных плоскостей, параллельных линии ОА с к, равным нулю [т.е. набор плоскостей (О, к, /)]. Перпендикуляры, опущенные из О на плоскости этого набора, напоминают спицы колеса, центром которого является точка О. Все обратные решетки, построенные на основе нормалей к этим плоскостям, будут лежать в плоскости О, к, I обратной решетки, показанной на рис. 17.13. Все плоскости [c.377]
Индексы Вайса некоторой кристаллической гран имеют значения /2, 7з, [c.55]
Какие индексы Вайса и индексы Миллера имеет кри сталлическая грань, показанная на рисунке. [c.55]
Для получения индексов Миллера берут обратные индексы Вайса, т. е. в данном случае /2. А. 7з> и умножают их на 6 для уничтожения дробей. В результате получим 3, б, 2. [c.259]
При холодной вытяжке происходит ориентация в направлении вытяжки плоскости с индексами Миллера [100], а затем других плоскостей. Существуют преимущественные плоскости скольжения, причем в процессе вытяжки кристаллит стремится оказаться в наиболее выгодном энергетическом положении по отношению к приложенному напряжению. [c.146]
Рис. 11.2-4. а —развитие грани (210) кристалла, показанное в двумерном виде б — индексы Миллера (кк1) для грани кристалла. [c.395]
Как определяют индексы Миллера hkl для плоскости кристаллической решетки Нарисуйте первые от начала координат плоскости решетки 110, 120 и 010 для двумерной проекции ромбической элементарной ячейки с параметрами а = 10 A, [c.414]
В квадратных скобках указаны индексы Миллера, характеризующие направление диффузионного потока. [c.530]
Вся установка для рентгеносруктурного анализа автоматизирована и связана с ЭВМ. Вычйсляют распределение электронных плотностей р(х, у, г) в элементарной ячейке. Каждый рефлекс характеризуется с помощью индексов Миллера к, к и I. К—объем элементарной ячейки, ДА, к, I) — структурный фактор и а(А, к, [c.383]
Поведение других металлов различно. Платина и никель проявляют специфическое взаимодействие некоторых плоскостей своих кристаллов с серой, повышая тем самым как селективность, так и активность (см. разд. 6.2). Подтверждено [16], что это происходит вследствие как реконструкции поверхности катализатора, так и разницы в поверхностной энергии различных кристаллографических плоскостей металла, обладающих низкими индексами Миллера. Считают, что адсорбция небольших количеств НгЗ изменяет энергетический баланс поверхности и приводит к новому равновесному распределению плоскостей с различной каталитической активностью. Такое объяснение имеет важные последствия для тех типов реакций, на которые влияют отравление катализаторов сероводородом или реконструкция поверхности под его действием. Таким образом, этот вид отравления должен влиять в значительно большей степени на такие структурно-чувствительные реакции как гидрогенолиз и изомеризация, чем на такие структурно-нечувствительные реакции как гидрогенизация. [c.150]
В пространственной решетке через отдельные группы атомов можно провести бесчисленное количество параллельных плоскостей. Совокупность параллельных атомных плоскостей называется семейством атомных плоскостей, а расстояние между ними — межплоскостным расстоянием й (рис. 55). Количество атомов, входящих в ту или иную плоскость, различно и тем меньше, чем меньше межнлоскостное расстояние. Положение любой атомной плоскости в пространственной решетке определяется при помощи трех простых целых чисел. Эти числа называются индексами плоскости (индексы Миллера) и представляют собой величины, обратные величинам отрезков, отсекаемых плоскостью на осях координат. Р1ндексы плоскости обозначаются буквами Н, к, I и заключаются в скобки. [c.112]
Атомная структура К. описывается как совокупность повторяющихся в пространстве одинаковых элементарных ячеек, имеющих форму параллелепипедов с ребрами а, Ь, с (периоды кристаллич. решетки). Расположение атомных плоскостей кристаллнч. решетки (к-рым могут соответствовать и грани К.) характеризуется кристаллография, индексами (или индексами М и л л ера). Они связаны с отсекаемыми соответствующей плоскостью на трех осях кристаллографич. системы координат отрезками, длины к-рых p , и Рз выражены в постоянных решетки а, Ь, с. Если величины, обратные p , р и р , привести к общему знаменателю, а затем отбросить его, то полученные трн целых числа А = Р2Р3, к = p p , I = p p и есть индексы Миллера. Они записываются в круглых скобках (кк1). Как правило, К. имеет грани с малыми значениями индексов, напр. (100), (ПО), (311). Равенство нулю одного или двух индексов означает, что плоскости параллельны одной нз кристаллографич. осей (осей координат). Если грань пересекает отрицат. направление оси, то над индексом ставится знак минус, напр. (121). Периоды ячеек а, с и утлы между ребрами а, 0, у измеряют рентгенографически. [c.537]
Эти обозначения часто называют индексами Миллера, поскольку они были предложены Витвеллом (1825 г.) и Гроссманом (1829 г.) и изложены в книге Миллера ио кристаллографии (1829 г.). Таким образом, грани кристаллов стали изображать тремя целыми числами, хотя о внутренней структуре кристаллов ничего не было известно. [c.571]
Рассмотрим рис. А7.2. Пусть одна и та же точка X будет центром решетки как в реальном, так и обратном пространстве. Пусть также ось х кристаллической решетки вертикальна, Никаки г предположений относительно величины параметра а элементарной ячейки делать нет необходимости. Показаны таюке две плоскости (/ и 2) одного семейства плоскостей hkl. Плоскость / про.ходит через начало координат. Плоскость 2 пересскает ось л- в точке 5. По определению индексов Миллера имеем [c.297]
Общая химия (1979) -- [ c.171 ]Начала органической химии Книга первая (1969) -- [ c.355 ]
Химия твердого тела Теория и приложения Ч.2 (1988) -- [ c.20 , c.171 , c.173 , c.175 , c.179 , c.188 , c.191 , c.199 , c.202 , c.223 ]
Физическая механика реальных кристаллов (1981) -- [ c.20 ]
Нестехиометрические соединения (1971) -- [ c.22 ]
Кристаллография (1976) -- [ c.17 , c.18 , c.20 , c.133 ]
Начала органической химии Кн 1 Издание 2 (1975) -- [ c.332 ]
Физическая химия (1967) -- [ c.651 , c.663 ]
chem21.info
Количество просмотров публикации Геометрия кристаллической решетки. Индексы Миллера. Обратная решетка. - 291
В идеальном кристалле центры атомов образуют периодическую структуру, называемую кристаллической решеткой. Точки, в которых расположены центры атомов, называются узлами кристаллической решетки. Кристаллы обладают свойством симметрии, ᴛ.ᴇ. свойством совмещаться с собой при поворотах, отражениях, параллельных переносах. Наиболее важным свойством монокристаллов является их периодическая структура.
Наименьшая часть кристалла, пространственным повторением которой образуется весь кристалл, принято называть элементарной ячейкой. Элементарная ячейка может содержать один или несколько ионов, атомов или молекул. В целом ячейка электрически нейтральна. Выбранную элементарную ячейку характеризуют тремя векторами базовых трансляций
совпадающими с ее тремя ребрами, сходящимися в одной точке. Объем элементарной ячейки определяется по формуле:
. (1)
Пространственную решетку характеризуют этими же тремя векторами , задав их длины
, которые называются периодами кристаллической решетки и углами α12, α13, α23 между ними; именно эти параметры содержатся во всех справочниках по структуре веществ. В случае если бесконечный монокристалл сместить на вектор
n1, n2, n3 – целые числа (2)
то он совместится с самим собой. Это свойство принято называть трансляционной симметрией. Система точек, даваемая формулой (2) принято называть решеткой Браве. Любое преобразование, совмещающее решетку с собой, принято называть преобразованием симметрии.
Различают следующие основные типы элементарных ячеек:
а) б) в) г)
а) простая, в которой узлы расположены в вершинах параллелепипеда;
б) объёмно-центрированная – узлы расположены в вершинах и в центре параллелепипеда;
в) гранецентрированная – узлы в вершинах и центрах граней;
г) базоцентрированная – узлы в вершинах и в центрах двух противоположных граней.
В общем случае элементарная ячейка, имеющая форму параллелепипеда, не обладает симметрией кристаллической решетки. Вигнер и Зейтц показали, как можно выбрать элементарную ячейку, чтобы она обладала такой симметрией. Для этого нужно выбрать некоторый атом и провести от него отрезки к ближайшим атомам. Построить через середины этих отрезков плоскости, перпендикулярные к ним. Пересечение этих плоскостей определит минимальный многогранник, содержащий внутри данный атом. Такой многогранник принято называть ячейкой Вигнера-Зейтца.
Узлы, направления и плоскости в кристалле обозначают с помощью индексов Миллера.
Индексы узлов. Как видно из (1), положение узла определяется заданием его координат . Индексы узла записывают [n1 n2 n3]. Для отрицательного числа знак "–" ставится над индексом, к примеру
.
Индексы направления. Для описания направления выбирается прямая, проходящая через начало координат и узел. Индекс узла одновременно является индексом направления.
Индексы плоскости (h k l) – набор трех целых чисел, заключенных в круглые скобки. Положение плоскости определяется заданием трех отрезков А, В, С, которые она отсекает на осях решетки:
(4)
На рисунке, приведенном ниже, указаны индексы Миллера для некоторых плоскостей в кристалле с простой кубической решеткой.
Рассмотрим множество точек , составляющих решетку Браве, и плоскую волну
. При произвольном векторе
такая волна не будет обладать периодичностью решетки Браве, ᴛ.ᴇ. :
. (5)
Но при определенном выборе вектора будет выполняться условие
. (6)
Множество волновых векторов называют обратной решеткой, если плоская волна
имеет периодичность данной решетки Браве. Обратная решетка всегда определяется по отношению к некоторой конкретной решетке Браве.
Как следует из (6), эти векторы удовлетворяют условию
. (7)
Вектор можно записать в виде линейной комбинации некоторых векторов
. (8)
Векторы называют основными векторами трансляции обратной решетки. Οʜᴎ связаны с основными векторами трансляции решетки Браве следующим образом:
, (9)
где V0 – объём элементарной ячейки решетки Браве, определяемый по формуле (1).Векторы прямой и обратной решетки связаны соотношением:
(10)
Для кристалла с простой кубической решеткой достаточно рассматривать изменение компонент k1, k2, k3 вектора обратной решетки в пределах:
, (11)
где а – длина ребра кубической элементарной ячейки.
Область значений (11) называют зоной Бриллюэна. Зона Бриллюэна в обратном пространстве строится аналогично тому, как ячейка Вигнера-Зейтца в прямом пространстве.
referatwork.ru
