|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
/ Реферат на тему. Газовые законы реферат
Газовые законы., реферат — allRefers.ru
Газовые законы. - Лекция, раздел Философия, Часть 1. МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Если разрешить уравнение состояния идеального газа

относительно какого-либо из параметров, например, p, то уравнение состояния примет вид
 .
.
И известные из школьного курса физики законы Бойля-Мариотта и Гей-Люссака дают уравнения состояния для случаев, когда один параметров остается постоянным.
Известные газовые законы (Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро) были открыты опытным путем задолго до появления молекулярно-кинетической теории. Эти законы были установлены на опытах с газами, находящимися в условиях, не очень сильно отличающихся от нормальных атмосферных условий, т.е. при не очень низких температурах и не очень высоких давлениях. При иных условиях экспериментальные газовые законы уже не точно отражают свойства газов, т.е. все эти законы являются приближенными.
Рассмотрим некоторые из этих законов:
1) Закон Бойля-Мариотта (m = const, T = const).
Изучая изотермические процессы, английский ученый Бойль (1662г.) и французский ученый Мариотт (1667г.) независимо друг от друга установили следующий закон:
ОПРЕДЕЛЕНИЕ: Для данной массы газа при постоянной температуре (T = const) давление газа изменяется обратно пропорционально объему.
 Аналитически это можно записать в виде: P·V = const (T = const). Совокупность состояний, отвечающих одной и той же температуре, изобразится на диаграмме (P, V) кривой, определяемой уравнением гиперболы. Каждому значению температуры соответствует своя кривая, называемая изотермой. А переход газа из одного состояния в другой, совершающийся при постоянной температуре, называется изотермическим процессом.
Аналитически это можно записать в виде: P·V = const (T = const). Совокупность состояний, отвечающих одной и той же температуре, изобразится на диаграмме (P, V) кривой, определяемой уравнением гиперболы. Каждому значению температуры соответствует своя кривая, называемая изотермой. А переход газа из одного состояния в другой, совершающийся при постоянной температуре, называется изотермическим процессом.
2) Закон Гей-Люссака (m = const, P = const).
Изучая изобарические газовые процессы, французский физик Гей-Люссак в 1802г. установил следующий закон:
ОПРЕДЕЛЕНИЕ: Для данной массы газа при постоянном давлении объем газа меняется линейно с ростом температуры: ,где V – объем газа при температуре t°;V0 – объем газа при 0°C;a – термический коэффициент объемного расширения (
,где V – объем газа при температуре t°;V0 – объем газа при 0°C;a – термический коэффициент объемного расширения ( ).
).
 Термический коэффициент объемного расширения показывает, на какую часть относительно первоначального объема изменится объем газа при его нагреве на 1°. Для большинства газов
Термический коэффициент объемного расширения показывает, на какую часть относительно первоначального объема изменится объем газа при его нагреве на 1°. Для большинства газов  .
.
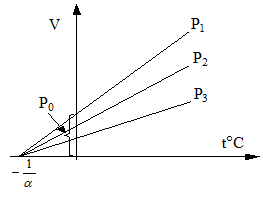
Процесс, протекающий при постоянном давлении, называется изобарическим. Для газа такой процесс отобразится на диаграмме (V, t°) прямой; здесь различные прямые отвечают разным давлениям и называются изобарами.
3) Закон Шарля (m = const, V = const).
ОПРЕДЕЛЕНИЕ: Для данной массы газа при постоянном объеме давление газа изменяется линейно с ростом температуры: ,где P – давление газа при температуре t°;P0 – давление газа при 0°C;g – термический коэффициент давления газа (
,где P – давление газа при температуре t°;P0 – давление газа при 0°C;g – термический коэффициент давления газа ( ).
).
Аналогично сказанному ранее относительно коэффициента “a”, термический коэффициент давления газа показывает, на какую часть относительно первоначального давления изменится давление газа при его нагревании на 1°С.
 Для идеального газа также
Для идеального газа также  . Для идеального газа
. Для идеального газа  .
.
Изохорический процесс, т.е. процесс, протекающий при постоянном объеме на диаграмме (P, t°) изобразится прямой линией. Различные прямые соответствую различным объемам и называются изохорами.
Заметим теперь, что все изобары и изохоры пересекают ось t° в одной и той же точке, определяемой из условия 1+a×t°=0. Откуда  .
.
Если за начало отсчета температуры взять нуль (как это и было), то получим шкалу температур по Цельсию. Если сместить начало отсчета в точку -273.15, то перейдем к другой температурной шкале, которая называется абсолютной (или шкалой Кельвина).
В соответствии с определением абсолютной шкалы между абсолютной температурой (Т) и температурой по Цельсию (t) существует следующее соотношение:
 . (9.1)
. (9.1)
Температура равная 0°К называется абсолютным нулем.
Для установления абсолютной шкалы температур и абсолютного нуля мы воспользовались законами Гей-Люссака и Шарля и поступили сугубо формально. Однако Кельвин в 1852г., исходя из иных физических соображений установил такую же абсолютную шкалу температур с тем же значением абсолютного нуля, какие ранее были получены формально. Поэтому понятия абсолютной температуры и абсолютного нуля не следует рассматривать как формальные, не имеющие физического смысла. Кельвин показал, что абсолютный нуль – это самая низкая из возможных температур вещества. При абсолютном нуле прекращается хаотическое движение молекул в веществе. Однако это не означает, что в нем прекращается всякое движение. Сохраняется, например, движение электронов в атоме. В настоящее время удается охлаждать малые объемы вещества до температуры очень близкой к абсолютному нулю, не достигая последнего лишь на несколько тысячных долей градуса.
Перейдем теперь в уравнениях, описывающих законы Гей-Люссака и Шарля от температуры по Цельсию к абсолютной температуре, подставив вместо t величину  .
.
Тогда
 . (9.2)
. (9.2)
и аналогично
 (при условии g=a).
(при условии g=a).
Из этих уравнений следует, что
 | (P = const) | (9.3) |
 | (V = const) | (9.4) |
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной и той же изобаре (для уравнения (9.3)), или одной и той же изохоре (для уравнения (9.4)).
Итак, при постоянном давлении объем газа пропорционален абсолютной температуре; и при постоянном объеме давление газа пропорционально абсолютной температуре.
Всякий реальный газ тем точнее следует уравнениям PV = const,  ,
,  , чем меньше его плотность, т.е., чем больший объем он занимает.
, чем меньше его плотность, т.е., чем больший объем он занимает.
В соответствии с уравнением PV = const, объем растет с уменьшением давления, а согласно с  объем возрастает с температурой. Следовательно, рассмотренные газовые законы справедливы при не слишком низких температурах и невысоких давлениях.
объем возрастает с температурой. Следовательно, рассмотренные газовые законы справедливы при не слишком низких температурах и невысоких давлениях.
Газ, который точно следует этим уравнениям, называется идеальным. Всякий реальный газ по мере убывания его плотности приближается к идеальному.
Замечание:
1. Закон Дальтона.
ОПРЕДЕЛЕНИЕ: Парциальным давлением газа, входящего в газовую смесь, называется то давление, которое имел бы этот газ, если бы все остальные газы были удалены из объема.
В 1801гю английский физик и химик Дальтон установил соотношение между давлением газовой смеси и парциальными давлениями входящих в нее газов.
ОПРЕДЕЛЕНИЕ: Давление газовой смеси равно сумме парциальных давлений входящих в нее газов.
P=P1+P2+P3+…
– Конец работы –
Эта тема принадлежит разделу:
Часть 1. МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Часть МЕХАНИКА... МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА ЛЕКЦИЯ Несколько вводных замечаний о предмете физики Материей в...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Газовые законы.
Все темы данного раздела:
Несколько вводных замечаний о предмете физики. Мир, окружающий нас материален: он состоит из вечно существующей и непрерывно движущейся материи. Мате
Механика Простейшим видом движения материи является механическое движение. ОПРЕДЕЛЕНИЕ: механическое движени
Кинематика движения материальной точки. Характеристики движения. Положение материальной точки M в пространстве в данный момент времени может быть задано радиус-вектором
Вектор скорости. Средняя и мгновенная скорость. Движения различных тел различаются тем, что тела за одинаков
Путь при неравномерном движении. За малый промежуток времени Dt перемещение графически изобра
Ускорение при криволинейном движении (тангенциальное и нормальное ускорение). Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем на
Угловая скорость. ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно тве
Угловое ускорение. Вектор угловой скорости может изменяться как за счет изменен
Связь между линейной и угловой скоростью. Пусть за малый промежуток времени Dt тело повернулось на угол Dj (рис. 2.17). Точка, находящаяся на рассто
Динамика Раздел механики, исследующий законы и причины, вызывающие движение тел, т.е. изучает движение материальных
II закон Ньютона. ОПРЕДЕЛЕНИЕ: Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционал
III закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия: если тело M1 действует на тело M2
Импульс. Закон сохранения импульса. В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами систе
Работа и энергия. Пусть тело, на которое действует сила , проходит, двигаясь по
Мощность. На практике имеет значение не только величина совершенной работы, но и время, в течение которого она соверш
Энергия. Из опыта известно, что тела часто оказываются в состоянии совершать работу над другими телами. ОПРЕДЕЛ
Кинетическая энергия тела. Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки). Напишем уравнение дви
Потенциальное поле сил. Силы консервативные и неконсервативные. Если частица (тело) в каждой точке пространства подвержена воздействию других тел, то говорят, что эта части
Потенциальная энергия тела в поле сил тяжести (в поле тяготения Земли). Поле тяготения Земли есть силовое поле, поэтому любое движение тела в силовом поле сопровождается совершен
Потенциальная энергия в гравитационном поле (в поле всемирного тяготения). Установленный Ньютоном закон всемирного тяготения гласит: ОПРЕДЕЛЕНИЕ: Гравитационная сила или
Потенциальная энергия упруго деформированного тела. Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруг
Закон сохранения энергии. Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частиц
Поступательное движение твердого тела. ОПРЕДЕЛЕНИЕ: Абсолютно твердым телом будем называть такое тело, деформациями которого в условиях рассм
Вращательное движение твердого тела. ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки
Момент импульса тела. Для описания вращательного движения потребуется ещё одна величина
Основное уравнение динамики вращательного движения. Рассмотрим систему материальных точек, каждая из которых может перемещаться, оставаясь в одной из плоскост
Кинетическая энергия вращающегося твердого тела. 1. Рассмотрим вращение тела вокруг неподвижной оси Z. Разо
Работа внешних сил при вращательном движении твердого тела. Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z. Пусть на массу
Линии и трубки тока. Гидродинамика изучает движение жидкостей, однако ее законы п
Уравнение Бернулли. Будем рассматривать идеальную несжимаемую жидкость, в котор
Силы внутреннего трения. Реальной жидкости присуща вязкость, которая проявляется в то
Ламинарное и турбулентное течения. При достаточно малой скорости движения жидкости наблюдается слоистое или ламинарное течение, ког
Течение жидкости в круглой трубе. При движении жидкости в круглой трубе ее скорость равна нулю
Движение тел в жидкостях и газах. При движении симметричных тел в жидкостях и газах возникает сила лобового сопротивления, направл
Законы Кеплера. К началу 17 столетия большинство ученых окончательно убедилось в справедливости гелиоцентрической системы
Опыт Кавендиша. Первой успешной попыткой определения «g» были измерения, осу
Напряженность гравитационного поля. Потенциал гравитационного поля. Гравитационное взаимодействие осуществляется через гравитационное поле. Это поле проявляет себя в том, по
Принцип относительности. В разд. 2.1. для механических систем был сформулирован следующий принцип относительности: во всех
Постулаты специальной (частной) теории относительности. Преобразования Лоренца Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности: 1. Физиче
Следствия из преобразований Лоренца. Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.
Интервал между событиями. В теории относительности вводят понятие события, которое определяется местом, где оно произошло, и врем
Уравнение гармонического колебательного движения. Пусть на некоторое тело массы “m” действует квазиупругая сила
Графическое изображение гармонических колебаний. Векторная диаграмма. Сложение нескольких колебаний одинакового направления (или, что то же самое, сложение нескольких гармониче
Скорость, ускорение и энергия колеблющегося тела. Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного проце
Гармонический осциллятор. Систему, описываемую уравнением , где
Физический маятник. ОПРЕДЕЛЕНИЕ: Физическим маятником будем называть твердо
Затухающие колебания. При выводе уравнения гармонических колебаний считалось, что колеблющаяся точка находится под действием то
Вынужденные колебания. Резонанс. Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колеб
Предмет и методы молекулярной физики. Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя и так
Термодинамическая система. Параметры состояния системы. Равновесное и неравновесное состояние. ОПРЕДЕЛЕНИЕ: Термодинамической системой называется совокупность тел, обменивающихся энергией, как дру
Идеальный газ. Параметры состояния идеального газа. ОПРЕДЕЛЕНИЕ: Идеальным газом называется газ, при рассмотрении свойств которого соблюдаются следующие усло
Физический смысл универсальной газовой постоянной. Универсальная газовая постоянная имеет размерность работы,
Основное уравнение кинетической теории газов Если в предыдущем разделе применялся термодинамический метод исследования, то в этом разделе будет исполь
Барометрическая формула. Распределение Больцмана Давно известно, что давление газа над поверхностью Земли уме
Максвелловское распределение молекул по скоростям В результате столкновений молекулы обмениваются скоростями, а в случае тройных и более сложных столкновен
Явления переноса. Длина свободного пробега молекул В предыдущих разделах мы рассматривали свойства тел, находящихся в тепловом равновесии. Данный раздел посв
Явление диффузии Диффузией называют процесс взаимного проникновения молекул соприкасающихся веществ, обусловле
Явление теплопроводности и вязкости Явление теплопроводности вещества определяет многие очень важные технические процессы и широко применяет
Внутренняя энергия идеального газа Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии
Работа и теплота. Первое начало термодинамики Внутренняя энергия газа (и другой термодинамической системы) может изменяться в основном за счет двух проц
Работа газовых изопроцессов Пусть газ заключен в цилиндрический сосуд, закрытый плотно п
Молекулярно-кинетическая теория теплоемкостей Теплоемкостью тела C называют физическую величину, численно равную количеству тепла, которое
Адиабатический процесс Наряду с изопроцессами существует адиабатический процесс, широко распространенный в природе. Адиабат
Круговые обратимые процессы. Цикл Карно Механические процессы обладают замечательным свойством обратимости. Например, брошенный камень, описав не
Понятие об энтропии. Энтропия идеального газа Для цикла Карно из формул (10.17) и (10.21) легко получить соотношение Q1 /T1 - Q2 /T2 = 0.
Второе начало термодинамики Понятие энтропии помогло строго математически сформулировать закономерности, позволяющие определить нап
Статистическое толкование второго начала термодинамики Состояние макроскопического тела (т.е. тела, образованного огромным числом молекул) может быть задано с пом
Уравнение Ван-дер-Ваальса Поведение реальных газов при их малых плотностях хорошо описывается уравнением Клапейрона:
Критическое состояние вещества Важное значение уравнения Ван-дер-Ваальса заклю
Эффект Джоуля-Томсона В реальном газе между молекулами действуют силы притяжения и отталкивания. Силы притяжения обусловлены ди
allrefers.ru
Реферат на тему
Реферат на тему: Газовые законы. Изопроцессы. ученицы 11 «А» класса Щегловой Анны
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров - давление, объем или температура - остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа. Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа. Изотермический процесс - процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля - Мариотта. Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой - термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы. Изохорный процесс - процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов. Изобарный процесс - процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака, как и закон Шарля, не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов. Законы Бойля - Мариотта, Гей-Люссака и Шарля называют частными газовыми законами. Они являются частными случаями объединенного газового закона: Отношение произведения давления газа и объема к температуре для данной массы газа - величина постоянная: PV/T=const.
|
|
|
|
|
|
Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление - это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

studfiles.net
Газовые законы
Радио  Газовые законы
Газовые законы
Количество просмотров публикации Газовые законы - 379
| Наименование параметра | Значение |
| Тема статьи: | Газовые законы |
| Рубрика (тематическая категория) | Радио |
§ Уравнение состояния идеального газа Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) связывает давление (р), объём (V) и температуру (T) идеального газа произвольной массы (m), в данном состоянии идеального газа. , где M – молярная масса, R – универсальная газовая постоянная.
§ Уравнение Клапейрона Переход данной массы идеального газа из одного состояния в другое подчиняется соотношению
§ Закон Бойля-Мариотта (изотермический процесс) Для газа данной массы при переходе из одного состояния в другое при постоянной температуре (T) произведение давления (р) газа на его объём (V) не меняется. , (при T=const)
§ Закон Гей-Люссака (изобарный процесс) Для газа данной массы при переходе из одного состояния в другое при постоянном давлении (р) отношение объёма (V) к абсолютной температуре (T) есть величина постоянная для всех газовых состояний. , (при p=const)
§ Закон Шарля (изохорный процесс) Для газа данной массы при переходе из одного состояния в другое при постоянном объёме (V) отношение давления (р) к абсолютной температуре (T) есть величина постоянная для всех газовых состояний. , (при p=const)
§ Закон Дальтона Для разреженных (идеальных) газов давление (р) смеси равно сумме парциальных давлений (р1, р2,… рn) компонентов смеси. СИ: Па
Газовые законы - понятие и виды. Классификация и особенности категории "Газовые законы" 2014, 2015.
Читайте также
Основные физические свойства жидкостей и газов. Под жидкостью в гидравлике принимают сплошную среду, обладающую свойством текучести. Текучесть жидкости обусловлена тем, что жидкость способна оказывать достаточно сильное противодействие сжимающим усилиям и... [читать подробнее].
Многие вещества (кислород, водород, азот, углекислый газ, аммиак и др.) существуют в газообразном состоянии. Состояние газа описывается определенными законами. Экспериментально установлено, что все газы (при постоянной температуре) одинаково сжимаются (закон... [читать подробнее].
Многие вещества (кислород, водород, азот, углекислый газ, аммиак и др.) существуют в газообразном состоянии. Состояние газа описывается определенными законами. Экспериментально установлено, что все газы (при постоянной температуре) одинаково сжимаются (закон... [читать подробнее].
Газовые законы установлены в 17 веке экспериментально. Однако, их можно получить, используя уравнение Менделеева - Клапейрона. Закон Бойля-Мариотта.Для данногоколичества вещества рассмотрим изотермический процесс, то есть процесс, протекающий без изменения температуры... [читать подробнее].
Если разрешить уравнение состояния идеального газа относительно какого-либо из параметров, например, p, то уравнение состояния примет вид . И известные из школьного курса физики законы Бойля-Мариотта и Гей-Люссака дают уравнения состояния для случаев, когда один... [читать подробнее].
Лекция №3: Газовые законы. Основные газовые процессы. Под парциальным давлением газа Рп понимают давление этого газа в предположении, что при температуре смеси в объёме, занимаемом смесью, находится только рассматриваемый газ. В соответствии с законом Дальтона,... [читать подробнее].
Под парциальным давлением газа Рп понимают давление этого газа в предположении, что при температуре смеси в объёме, занимаемом смесью, находится только рассматриваемый газ. В соответствии с законом Дальтона, давление смеси идеальных газов равно сумме парциальных... [читать подробнее].
Фундаментальные законы химии. Атомно–молекулярная теория. Создал атомно-молекулярное учение и открыл закон сохранения массы веществ М.В. Ломоносов. Он четко различал две ступени в строении вещества: элементы (в нашем понимании – атомы) и корпускулы (молекулы).... [читать подробнее].
Закон Бойля-Мариотта (изотермический процесс, T=const) При постоянной Т давление изменяется обратно пропорционально объему (рис.22). Рисунок 22. Закон Гей-Люссака (изобарический процесс, P=const) – При увеличении температуры, скорость молекул увеличивается и они... [читать подробнее].
referatwork.ru
Газовые законы, все формулы и примеры решений
Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.
Рассмотрим каждый из них.
Закон Бойля-Мариотта (изотермический процесс)
Изотермическим процессомназывают изменение состояния газа, при котором его температура остаётся постоянной.
Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:
![Rendered by QuickLaTeX.com \[pV=const\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-b6a0e1c9907e66394f21f66b0ad83546_l3.png)
Этот же закон можно переписать в другом виде (для двух состояний идеального газа):
![Rendered by QuickLaTeX.com \[p_1V_1=p_2V_2\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-6d24df79d38a4661577b20787800f0fd_l3.png)
Этот закон следует из уравнения Менделеева – Клапейрона:
![Rendered by QuickLaTeX.com \[pV=const=\frac{m}{\mu}RT\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-265b7b1889a9e336feda278ae9ea0a10_l3.png)
Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.
Графики зависимости параметров газа при постоянной температуре называются изотермами.
Обозначив константу буквой 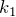 , запишем функциональную зависимость давления от объема при изотермическом процессе:
, запишем функциональную зависимость давления от объема при изотермическом процессе:
![Rendered by QuickLaTeX.com \[p=\frac{k_1}{V}\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-d3f71353d9335a47b4ae7554dee80629_l3.png)
Видно, что давление газа обратно пропорционально его объему. Графиком обратной пропорциональности, а, следовательно, и графиком изотермы в координатах  является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах
является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах 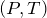 и
и  соответственно.
соответственно.

Рис.1. Графики изотермических процессов в различных координатах
Закон Гей-Люссака (изобарный процесс)
Изобарным процессомназывают изменение состояния газа, при котором его давление остаётся постоянным.
Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:
![Rendered by QuickLaTeX.com \[\frac{V}{T}=const\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-747fda05986389c0174cb5bfb2000ac6_l3.png)
Для двух состояний газа этот закон запишется в виде:
![Rendered by QuickLaTeX.com \[\frac{V_1}{T_1}=\frac{V_2}{T_2}\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-8713464adb4b286072d14af754e99e68_l3.png)
Этот закон также следует из уравнения Менделеева – Клапейрона:
![Rendered by QuickLaTeX.com \[\frac{V}{T}=const=\frac{mR}{\mu}\cdot \frac{1}{p}\ \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-b7afef091fec656ede72ba39777639f6_l3.png)
Графики зависимости параметров газа при постоянном давлении называются изобарами.
Рассмотрим два изобарных процесса с давлениями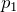 и
и 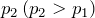 . В координатах
. В координатах  и
и 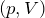 изобары будут иметь вид прямых линий, перпендикулярных оси
изобары будут иметь вид прямых линий, перпендикулярных оси 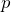 (рис.2 а,б).
(рис.2 а,б).
Определим вид графика в координатах  .Обозначив константу буквой
.Обозначив константу буквой  , запишем функциональную зависимость объема от температуры при изобарном процессе:
, запишем функциональную зависимость объема от температуры при изобарном процессе:
![Rendered by QuickLaTeX.com \[V=k_2T\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-a0b6ac5824117f55045655807f491aba_l3.png)
Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах 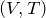 является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.
является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.

Рис.2. Графики изобарных процессов в различных координатах
Закон Шарля (изохорный процесс)
Изохорным процессомназывают изменение состояния газа, при котором его объем остаётся постоянным.
Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:
![Rendered by QuickLaTeX.com \[\frac{p}{T}=const\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-cc89e3387f7fb9d68b467f8894a784cd_l3.png)
Для двух состояний газа этот закон запишется в виде:
![Rendered by QuickLaTeX.com \[\frac{p_1}{T_1}=\frac{p_2}{T_2}\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-d9892b5d937b12a7f0aac7ab20f4c9fc_l3.png)
Этот закон также можно получить из уравнения Менделеева – Клапейрона:
![Rendered by QuickLaTeX.com \[\frac{p}{T}=const=\frac{mR}{\mu}\cdot \frac{1}{V}\ \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-4ef25951ad717ad111d622ace79ddc83_l3.png)
Графики зависимости параметров газа при постоянном давлении называются изохорами.
Рассмотрим два изохорных процесса с объемами  и
и 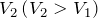 . В координатах
. В координатах  и
и 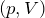 графиками изохор будут прямые, перпендикулярные оси
графиками изохор будут прямые, перпендикулярные оси 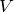 (рис.3 а, б).
(рис.3 а, б).
Для определения вида графика изохорного процесса в координатах  обозначим константу в законе Шарля буквой
обозначим константу в законе Шарля буквой 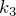 , получим:
, получим:
![Rendered by QuickLaTeX.com \[p=k_3T\]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-b343aafdae4816354e70d510bf502acd_l3.png)
Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (рис.3, в).
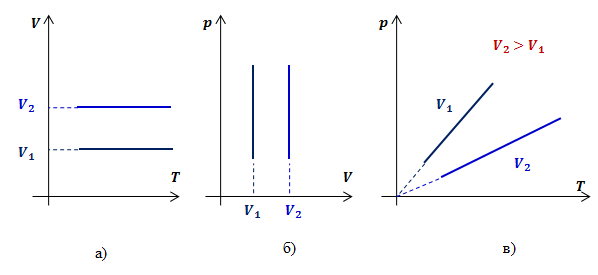
Рис.3. Графики изохорных процессов в различных координатах
Примеры решения задач
ru.solverbook.com
Газовые законы — реферат
Министерство Образования Российской Федерации
Краевое государственное бюджетное образовательное учреждение среднего профессионального образования (среднее специальное учебное заведение) «АЧИНСКИЙ ПРОФЕССИОНАЛЬНО-ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ»
Реферат
по предмету "Основы гидравлики"
на тему: "Газовые законы"
Выполнил: Хайруллина А.А.
Проверил: Бурмистрова А.И.
Ачинск, 2013
Газовые законы
Газ всегда заполняет объём, ограниченный непроницаемыми для него стенками. Так, например, газовый баллон или камера автомобильной шины практически равномерно заполнены газом.
Итак , установим, от чего зависит давление газа? Во-первых, от степени сжатия газа, т.е. от того от того, сколько молекул газа находится в определённом объёме. Например, накачивая шину или сжимая её, мы заставляем газ сильнее давить на стенки камеры.
Во-вторых, от того, какова температура газа.Обычно изменение давления вызывается обеими причинами сразу: и изменением объёма, и изменением температуры. Но можно осуществить явление так, что при изменении объёма температура будет меняться ничтожно мало или при изменении температуры объём практически останется неизменным. Этими случаями мы сперва и займёмся, сделав предварительно ещё следующее замечание.
Формула, выражающая закон Шарля.
Закон Шарля позволяет рассчитать давление газа при любой температуре, если известно его давление при 0°С. Пусть давление при 0°С данной массы газа в данном объеме есть p0, а давление того же газа при температуре t есть p. Приращение температуры есть t, следовательно, приращение давления равно ap0t и искомое давление равноP =p0+ap0t=p0 (1+at)= p0(1+t/273) Этой формулой можно пользоваться также и в том случае, если газ охлажден ниже 0°С; при этом t будет иметь отрицательные значения. При очень низких температурах, когда газ приближается к состоянию сжижения, а также в случае сильно сжатых газов закон Шарля неприложим и формула перестает быть годной.
Закон Шарля с точки зрения молекулярной теории
Что происходит в микромире молекул, когда температура газа меняется, например когда температура газа повышается и давление его увеличивается? С точки зрения молекулярной теории возможны две причины увеличения давления, данного газа: во-первых, могло увеличиться число ударов молекул на 1 см2 в течение 1 сек; во-вторых, могло увеличиться количество движения, передаваемое при ударе в стенку одной молекулой. И та и другая причина требует увеличения скорости молекул. Отсюда становится ясным, что повышение температуры газа (в макромире) есть увеличение средней скорости беспорядочного движения молекул (в микромире). Опыты по определению скоростей газовых молекул, о которых буду говорить немного далее, подтверждают этот вывод. Когда мы имеем дело не с газом, а с твердым иди жидким телом, в нашем распоряжении нет таких непосредственных методов определения скорости молекул тела. Однако и в этих случаях несомненно, что с повышением температуры скорость движения молекул возрастает.
Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы.
Мы установили, как зависит давление газа от температуры, если объем остается неизменным. Теперь посмотрим, как меняется давление некоторой массы газа в зависимости от занимаемого ею объема, если температура остается неизменной. Однако, прежде чем перейти к этому вопросу, надо выяснить, как поддерживать температуру газа неизменной. Для этого надо изучить, что происходит, с температурой газа, если объем его меняется настолько быстро, что теплообмен газа с окружающими телами практически отсутствует. Произведем такой опыт. В закрытую с одного конца толстостенную трубку из прозрачного материала поместим ватку, слегка смоченную эфиром, и этим создадим внутри трубки смесь паров эфира с воздухом, взрывающуюся при нагревании. Затем быстро вдвинем в трубку плотно входящий поршень. Мы увидим, что внутри трубки произойдет маленький взрыв. Это значит, что при сжатии смеси паров эфира с воздухом температура смеси резко повысилась. Это явление вполне понятно. Сжимая газ внешней силой, мы производим работу, в результате которой внутренняя энергия газа должна была увеличиться; это и произошло—газ нагрелся. Теперь предоставим газу расширяться и производить при этом работу против сил внешнего давления. Это можно осуществить. Пусть в большой бутыли находится сжатый воздух, имеющий комнатную температуру. Сообщив бутыль с внешним воздухом, дадим воздуху в бутыли возможность расширяться, выходя из небольшого. отверстия наружу, и поместим в струе расширяющегося воздуха термометр или колбу с трубкой. Термометр покажет температуру, заметно более низкую, чем комнатная, а капля в трубке, присоединенной к колбе, побежит в сторону колбы, что также будет указывать на понижение температуры воздуха в струе. Значит, когда газ расширяется и при этом совершает работу, он охлаждается и внутренняя энергия его убывает. Ясно, что нагревание газа при сжатии и охлаждение при расширении являются выражением закона сохранения энергии. Если мы обратимся к микромиру, то явления нагревания газа при сжатии и охлаждения при расширении станут вполне ясными. Когда молекула ударяется о неподвижную стенку и отскакивает от нее, скорость, а следовательно, и кинетическая энергия молекулы, в среднем такова же, как и до удара о стенку. Но если молекула ударяется и отскакивает от надвигающегося на нее поршня, ее скорость и кинетическая энергия больше, чем до удара о поршень (подобно тому как скорость теннисного мяча увеличивается, если его ударить во встречном направлении ракеткой). Надвигающийся поршень передает отражающейся от него молекуле дополнительную энергию. Поэтому внутренняя энергий газа при сжатии возрастает. При отскакивании от удаляющегося поршня скорость молекулы уменьшается, ибо молекула совершает работу, толкая отходящий поршень. Поэтому расширение газа, связанное с отодвиганием поршня или слоев окружающего газа, сопровождается совершением работы и приводит к уменьшению внутренней энергии газа. Итак, сжатие газа внешней силой вызывает его нагревание, а расширение газа сопровождается его охлаждением. Это явление в некоторой мере имеет место всегда, но особенно резко заметаю тогда, когда обмен теплотой с окружающими телами сведен к минимуму, ибо такой обмен может в большей или меньшей степени компенсировать изменение температуры. Процессы, при которых передача теплоты настолько ничтожна, что ею можно пренебречь, называют адиабатическими. Возвратимся к вопросу, поставленному в начале главы. Как обеспечить постоянство температуры газа, несмотря на изменения его объема? Очевидно, для этого надо непрерывно передавать газу теплоту извне, если он расширяется, и непрерывно отбирать от него теплоту, передавая ее окружающим телам, если газ сжимается. В частности, температура газа остается достаточно постоянной, если расширение или сжатие газа производится очень медленно, а передача теплоты извне или вовне может происходить с достаточной быстротой. При медленном расширении теплота от окружающих тел передается газу и его температура снижается так мало, что этим снижением можно пренебречь. При медленном сжатии теплота, наоборот, передается от газа к окружающим телам, и вследствие этого температура его повышается лишь ничтожно мало. Процессы, при которых температура поддерживается неизменной, называют изотермическими.
Закон Бойля — Мариотта
Перейдем теперь к более подробному изучению вопроса, как меняется давление некоторой массы газа, если температура его остается неизменной и меняется только объем газа. Мы уже выяснили, что такой изотермический процесс осуществляется при условии постоянства температуры тел, окружающих газ, и настолько медленного изменения объема газа, что температура газа в любой момент процесса не отличается от температуры окружающих тел.
Мы ставим, таким образом, вопрос: как связаны между собой объем и давление при изотермическом изменении состояния газа? Ежедневный опыт учит нас, что при уменьшении объема некоторой массы газа давление его увеличивается. В качестве примера можно указать повышение упругости при накачивании футбольного мяча, велосипедной или автомобильной шины. Возникает вопрос: как именно увеличивается давление газа при уменьшении объема, если температура газа остается неизменной?Ответ на этот вопрос дали исследования, произведенные в XVII столетии английским физиком и химиком Робертом Бойлем (1627—1691) и французским физиком Эдемом Мариоттом (1620—1684).
Опыты, устанавливающие зависимость между объемом и давлением газа, можно воспроизвести: на вертикальной стойке, снабжённой делениями, находятся стеклянные трубки А и В, соединенные резиновой трубкой С. В трубки налита ртуть. Трубка В сверху открыта, на трубке А имеется кран. Закроем этот кран, заперев таким образом некоторую массу воздуха в трубке А. Пока мы не сдвигаем трубок, уровень ртути в обеих трубках одинаков. Это значит, что давление воздуха, запертого в трубке А, такое же, как и давление окружающего воздуха.
Будем теперь медленно поднимать трубку В. Мы увидим, что ртуть в обеих трубках будет подниматься, но не одинаково: в трубке В уровень ртути будет все время выше, чем в А. Если же опустить трубку В, то уровень ртути в обоих коленах понижается, но в трубке В понижение больше, чем в А. Объем воздуха, запертого в трубке А, можно отсчитать по делениям трубки А. Давление этого воздуха будет отличаться от атмосферного на величину давления столба ртути, высота которого равна разности уровней ртути в трубках А и В. При. поднятии трубки В давление столба ртути прибавляется к атмосферному давлению. Объем воздуха в А при этом уменьшается. При опускании трубки В уровень ртути в ней оказывается ниже, чем в А, и давление столба ртути вычитается из атмосферного давления; объем воздуха в А соответственно увеличивается. Сопоставляя полученные таким образом значения давления и объема воздуха, запертого в трубке А, убедимся, что при увеличении объема некоторой массы воздуха в определенное число раз давление его во столько же раз уменьшается, и наоборот. Температуру воздуха в трубке при наших опытах можно считать неизменной. Подобные же опыты можно" произвести и с другими газами. Результаты получаются такие же. Итак, давление некоторой массы газа при неизменной температуре обратно пропорционально объему газа (закон Бойля—Мариотта). Для разреженных газов закон Бойля — Мариотта выполняется с высокой степенью точности. Для газов же сильно сжатых или охлажденных обнаруживаются заметные отступления от этого закона.
Формула, выражающая закон Бойля — Мариотта.
Зависимость между плотностью газа и его давлением.
Вспомним, что плотностью вещества называется масса, заключенная в единице объема. Если мы как-нибудь изменим объем данной массы газа, то изменится и плотность газа. Если, например, мы уменьшим объем газа в пять раз, то плотность газа увеличится в пять раз. При этом увеличится и давление газа; если температура не изменилась, то, как показывает закон Бойля — Мариотта, давление увеличится тоже в пять раз. Из этого примера видно, что при изотермическом процессе давление газа изменяется прямо пропорционально его плотности. Обозначив плотности газа при давлениях P1 и P2 буквами d1 иd2, можем написать:
Этот важный результат можно считать другим и более существенным выражением закона Бойля — Мариотта. Дело в том, что вместо объема газа, который зависит от случайного обстоятельства — оттого, какая выбрана масса газа,— в формулу (3) входит плотность газа, которая, также как и давление, характеризует состояние газа и вовсе не зависит от случайного выбора его массы.
Молекулярное толкование закона Бойля — Мариотта.
В предыдущей главе мы выяснили на основании закона Бойля — Мариотта, что при неизменной температуре давление газа пропорционально его плотности. Если плотность газа меняется, то во столько же раз меняется и число молекул в 1 см3. Если газ не слишком сжат и движение газовых молекул можно считать совершенно независимым друг от друга, то число ударов за 1 сек на 1 см2 стенки сосуда пропорционально числу молекул в 1 см3. Следовательно, если средняя скорость молекул не меняется с течением времени (мы уже видели, что в макромире это означает постоянство температуры), то давление газа должно быть пропорционально числу молекул в 1 см3, т.е. плотности газа. Таким образом, закон Бойля — Мариотта является прекрасным подтверждением наших представлений о строении газа.
Однако, закон Бойля — Мариотта перестает оправдываться, если перейти к большим давлениям. И это обстоятельство может быть прояснено, как считал еще М. В. Ломоносов, на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объем газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях. более существенным является второе обстоятельство и произведение PV немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение PV увеличивается. Итак, и сам закон Бойля — Мариотта и отступления от него подтверждают молекулярную теорию.
Изменение объема газа при изменении температуры
Мы изучали, как зависит давление некоторой массы газа от температуры, если объём остается неизменным, и от объема, занимаемого газом, если температура остается неизменной. Теперь установим, как ведет себя газ, если меняются его температура и объем, а давление остается постоянным.
Рассмотрим такой опыт. Коснемся Ладонью сосуда, изображенного на рис., в котором горизонтальный столбик ртути запирает некоторую массу воздуха. Газ в сосуде нагреется, его давление повысится, и ртутный столбик начнет перемещаться вправо. Движение столбика прекратится, когда благодаря увеличению объема воздуха в сосуде давление его сделается равным наружному. Таким образом, в конечном результате этого опыта объем воздуха при нагревании увеличился, а давление осталось неизменным. Если бы мы знали, как изменилась в нашем опыте температура воздуха в сосуде, и точно измерили, как меняется объем Газа, мы могли бы изучить это явление с количественной стороны. Очевидно, что для этого надо заключить сосуд в оболочку, заботясь о том, чтобы все части прибора имели одну и ту же температуру, точно измерить объем запертой массы газа, затем изменить эту температуру и измерить приращение объема газа.
Закон Гей-Люссака.
Количественное Исследование зависимости объема газа от температуры при неизменном давлении было произведено французским физиком и химиком Гей-Люссаком (1778—1850) в 1802 г. Опыты показали, что увеличение объема газа пропорционально приращению температуры. Поэтому тепловое расширение газа можно, так же, как и для других тел, охарактеризовать при помощи коэффициента объемного расширения b. Оказалось, что для газов этот закон соблюдается гораздо лучше, чем для твердых и жидких тел, так что коэффициент объемного расширения газов есть величина, практически постоянная даже при очень значительных повышениях Температуры, тогда как для жидких и твердых тел это; постоянство соблюдается лишь приблизительно.
Отсюда найдем:
Опыты Гей-Люссака и других обнаружили замечательный результат. Оказалось, что коэффициент объемного расширения у всех газов одинаков (точнее, почти одинаков) и равняется (1/273)град-1= =0,00366град-1. Таким образом, при нагревании при постоянном давлении на1° объем некоторой массы газа увеличивается на 1/273 того объема, который эта масса газа занимала при 0°С (закон Гей-Люссака). Как видно, коэффициент расширения газов совпадает с их термическим коэффициентом давления.
Закон Дальтона
До сих пор мы говорили о давлении какого-нибудь одного газа — кислорода, водорода и т. п. Но в природе и в технике мы очень часто имеем дело со смесью нескольких газов. Самый важный пример этого — воздух, являющийся смесью азота, кислорода, аргона, углекислого газа и других газов. От чего зависит давление смеси газов?
freepapers.ru
Газовые законы.
Количество просмотров публикации Газовые законы. - 107
Газовые законы установлены в 17 веке экспериментально. При этом, их можно получить, используя уравнение Менделеева - Клапейрона.
Закон Бойля-Мариотта.Для данногоколичества вещества рассмотрим изотермический процесс, то есть процесс, протекающий без изменения температуры (Т= const). Используя уравнение (2.6) или (2.7), получим уравнение изотермы, выраженное через давление и объём газа:
(2.7)
или (2.7’)
Для данного количества вещества при изотермическом процессе произведение давления на объём есть величина постоянная.
Для построения диаграммы Р(V) выразим давление через объём
.
Зависимость между давлением и объёмом – обратно пропорциональная, графически представлена гиперболой на рис.2.3 а. Температурные зависимости давления и объёма представлены на рис.2.3 б и в, соответственно.
Закон Гей-Люссака. Для данного количества вещества
рассмотрим изобарический процесс, то есть процесс, протекающий без изменения давления
(Р = const). Используя уравнение (2.6) или (2.7), получим уравнение изобары, выраженное через температуру и объём:
, (2.8)
через параметры начального и конечного состояния или
.
Для данного количества вещества при изобарическом процессе отношение объёма к температуре (или наоборот) есть постоянная величина.
Изобарический закон можно записать и в виде: . Здесь V0 - объём газа при t=00C, t- температура в 0С, a - термический коэффициент объёмного расширения;
. Для идеального газа
,
, но
, тогда
- термический коэффициент объёмного расширения идеального газа равен величине, обратной температуры. Изображение этого процесса приведено на рис. 2.4.
Закон Шарля. Для данного количества вещества рассмотрим изохорический процесс, то есть процесс, протекающий без изменения объёма (V = const). Используя уравнение (2.6) или (2.7), получим уравнение изохоры, выраженное через температуру и давление газа:
, (2.9)
Читайте также
Основные физические свойства жидкостей и газов. Под жидкостью в гидравлике принимают сплошную среду, обладающую свойством текучести. Текучесть жидкости обусловлена тем, что жидкость способна оказывать достаточно сильное противодействие сжимающим усилиям и... [читать подробнее].
Многие вещества (кислород, водород, азот, углекислый газ, аммиак и др.) существуют в газообразном состоянии. Состояние газа описывается определенными законами. Экспериментально установлено, что все газы (при постоянной температуре) одинаково сжимаются (закон... [читать подробнее].
Многие вещества (кислород, водород, азот, углекислый газ, аммиак и др.) существуют в газообразном состоянии. Состояние газа описывается определенными законами. Экспериментально установлено, что все газы (при постоянной температуре) одинаково сжимаются (закон... [читать подробнее].
Если разрешить уравнение состояния идеального газа относительно какого-либо из параметров, например, p, то уравнение состояния примет вид . И известные из школьного курса физики законы Бойля-Мариотта и Гей-Люссака дают уравнения состояния для случаев, когда один... [читать подробнее].
Лекция №3: Газовые законы. Основные газовые процессы. Под парциальным давлением газа Рп понимают давление этого газа в предположении, что при температуре смеси в объёме, занимаемом смесью, находится только рассматриваемый газ. В соответствии с законом Дальтона,... [читать подробнее].
Под парциальным давлением газа Рп понимают давление этого газа в предположении, что при температуре смеси в объёме, занимаемом смесью, находится только рассматриваемый газ. В соответствии с законом Дальтона, давление смеси идеальных газов равно сумме парциальных... [читать подробнее].
Фундаментальные законы химии. Атомно–молекулярная теория. Создал атомно-молекулярное учение и открыл закон сохранения массы веществ М.В. Ломоносов. Он четко различал две ступени в строении вещества: элементы (в нашем понимании – атомы) и корпускулы (молекулы).... [читать подробнее].
§ Уравнение состояния идеального газа Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) связывает давление (р), объём (V) и температуру (T) идеального газа произвольной массы (m), в данном состоянии идеального газа. , где M – молярная масса, R –... [читать подробнее].
Закон Бойля-Мариотта (изотермический процесс, T=const) При постоянной Т давление изменяется обратно пропорционально объему (рис.22). Рисунок 22. Закон Гей-Люссака (изобарический процесс, P=const) – При увеличении температуры, скорость молекул увеличивается и они... [читать подробнее].
referatwork.ru
Газовые законы в живой природе и медицине
Л.В.Логинов, многопрофильный комплекс (гимназия-лицей) N 109, г. Москва
Наверное, у каждого учителя есть желание объяснить материал по-своему или рассмотреть его с позиций, отличных от традиционных. Тем более что начавшееся профилирование обучения вынуждает это делать. Возьмем, к примеру, тему, которую проходят в школе и в 8-м, и в 10-м классах, – «Газы». Свойства газов упоминаются (или изучаются) уже в курсе природоведения в 5-м классе (!). Позже ребят знакомят с использованием сжатого воздуха, с приборами для измерения атмосферного давления, учат решать задачи на изменение давления воздуха при изменении других параметров, как правило, в автомобильной шине, шаре, резиновой лодке. Налицо определенный технический уклон, хотя изредка встречаются и другие задачи, например, как отпить воды из бутылки при плотно прижатых к горлышку губах, так что воздух в бутылку не пропускается, или, как пауку серебрянке построить воздушный домик в воде. Тот факт, что газовые законы активно работают в живой природе, широко применяются в медицине, как правило, не акцентируется, ни слова не говорится о том, зачем паук серебрянка строит себе тот самый воздушный домик, как он может сидеть в таком домике до получаса, а в состоянии анабиоза (спячки) – и дольше... Ведь при дыхании кислород-то непрерывно расходуется! Вдох и выдох, газообмен в легких у животных и у человека происходят тоже в соответствии с газовыми законами. Так что эта тема не только очень живая, но и актуальная. И остановиться на ней стоит.
Начнем с того, что закон Бойля–Мариотта начинает «работать на человека» (как, впрочем, и на любое млекопитающее) с момента его рождения, с первого самостоятельного вздоха. При дыхании межреберные мышцы и диафрагма периодически изменяют объем грудной клетки. Когда грудная клетка расширяется, давление воздуха в легких падает ниже атмосферного, т.е. «срабатывает» изотермический закон (р0V0 = р1V1), и вследствие образовавшегося перепада давлений происходит вдох. Другими словами, воздух идет из окружающей среды в легкие самотеком до тех пор, пока величины давления в легких и в окружающей среде не выравняются.
Выдох происходит аналогично: вследствие уменьшения объема легких давление воздуха в них становится больше, чем внешнее атмосферное, и за счет обратного перепада давлений он выходит наружу. Схематическое изображение процесса дыхания дано на рис. 1.
Важную роль в этом процессе играет плевральная полость, в которой при дыхании возникают разрежения. Если хирургическим путем открыть наружному воздуху (под нормальным атмосферным давлением) доступ в плевральное пространство, то атмосферное давление сожмет легкое, выключив его из процесса дыхания. Именно так делают при лечении легочного туберкулеза (метод пневмоторакса).
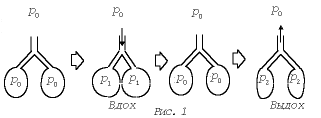
Теперь рассмотрим процесс «переработки» воздуха, поступившего в легкие. Давление воздуха складывается из парциальных давлений входящих в него газов (по закону Дальтона: рсмеси= р1+ р2+ р3+...+ рn). Как известно, свежий воздух состоит из кислорода (20,94%), углекислого газа (0,03%), азота и инертных газов (79,03%). Состав же выдыхаемого воздуха иной: кислорода — 16,3%, углекислого газа — 4%, азота и инертных газов — 79,7%. Видно, что кислорода становится меньше, а углекислого газа — больше (количество остальных газов почти не меняется). Это означает, что и парциальное давление кислорода уменьшается, а углекислого газа — растет. Стенки легочных пузырьков (альвеол) способны пропускать сквозь себя в кровь и обратно молекулы газов при наличии разности давлений газов в альвеолах и в крови. В результате после вдоха кислород из области с бо'льшим парциальным давлением движется в область с меньшим парциальным давлением, т.е. из альвеол в кровь. Углекислый же газ выводится из крови в альвеолы, после чего «переработанный» воздух выдыхается. Так работают «обычные» или, как их еще называют, биологические легкие.
Но существует еще и понятие физических легких. Это не биологический орган, а физическая система, которая функционирует подобно биологическим легким. Благодаря физическим легким дышит водяной паук серебрянка. Его тело покрыто мелким несмачиваемым пушком. Когда паук погружается в воду, к телу пристают мельчайшие пузырьки воздуха, покрывая его сплошной воздушной оболочкой. В воде эта оболочка блестит, делая паука похожим на шарик ртути. Выставляя из воды кончик брюшка, паук забирает крупный пузырек воздуха и, придерживая его задними ножками, отправляется в глубину.
Среди водных растений он натягивает нити своей паутины, «клетку» для воздушного шарика, который все больше и больше наполняется воздухом по мере совершения пауком очередных «рейсов» на поверхность. Когда воздушный домик становится достаточно просторным, паук переходит к отдыху. Он дышит воздухом своего же домика, хотя принесенного запаса кислорода в нем даже отдыхающему пауку должно было хватить всего на несколько минут. Но возможность отдыхать дает сама природа. Вернее, физические законы.
Дело в том, что в воде вокруг домика-пузырька также имеется воздух. Правда, в растворенном виде. По мере расходования кислорода в пузырьке уменьшается его парциальное давление по сравнению с давлением в воде, и растворенный в воде кислород диффундирует в пузырек. Углекислый же газ, наоборот, диффундирует из домика в воду, где его парциальное давление меньше. Конечно, этот газообмен не позволяет полностью компенсировать затраты кислорода на дыхание, но тем не менее паук получает возможность обновлять атмосферу значительно реже, минут через 30, а то и более. Если паук находится в состоянии анабиоза, то воздуха от одной ходки наверх хватает на очень длительное время.
Таким образом, физические легкие — это «приспособление природы», в котором «дышит» сам пузырек, а не паук. А последний дышит уже своими биологическими легкими, т.е. воздухом, имеющимся в пузырьке.
Перейдем к проблеме измерения рабочего объема легких, т.е. объема воздуха, вдыхаемого (или выдыхаемого) при глубоком вдохе (выдохе). Известно, что он меньше полного объема легких. Следовательно, при каждом вдохе-выдохе в легких обновляется не весь воздух. По рабочему объему легких (вернее, по отношению рабочего объема к полному) можно сделать вывод о состоянии дыхательной системы человека. Различные заболевания (например астма), курение, а также малоподвижный образ жизни приводят к уменьшению рабочего объема.
Для начала необходимо знать полный объем легких. Это задача не из простых, т.к. экспериментальным путем на живом человеке этого делать не стоит. Да и как? Реально просматривается только один способ: произвести вскрытие, извлечь легкие, наполнить водой «под завязку», после чего эту воду вылить в мензурку (или большую мерную кружку). Да и то нет гарантии, что к моменту наполнения водой легкие будут расправленными и смогут вместить воды «по максимуму».
В настоящее время полный объем легких обычно определяют расчетным путем, по формуле Дюбуа, которая устанавливает зависимость площади поверхности тела человека от его массы и роста:
S = 0,167•
где m — масса тела в [кг], L — длина тела, рост в [м]. (Разумеется, для получения в свое время этой эмпирической формулы потребовались и вскрытия.) Следует сразу обратить внимание учащихся, что эта формула — только для чисел, т.е. единицы физических величин в ней не сходятся. Далее пользуются известной зависимостью, согласно которой на 1 м2 поверхности приходится у мужчин — 2,5 л, у женщин — 2 л полного объема легких.
В качестве примера можно рассчитать полный объем легких кого-нибудь из присутствующих. Кстати, ученики обычно предлагают кандидатуру... учителя! Этим стоит воспользоваться для того, чтобы затем кто-либо из учеников рассчитал и свой объем, если вспомнит массу и рост. Это в дальнейшем, по ходу урока, пригодится. Например, при массе 75 кг и росте 176 см площадь поверхности тела юноши составляет 1,92 м2. Следовательно, полный объем легких 4,8 л.
Теперь об измерении рабочего объема легких. С ним дела обстоят проще, поэтому можно организовать достаточно интересную дискуссию о том, какой должна быть конструкция прибора для таких измерений. К настоящему времени разработано достаточно много подходящих конструкций, но, несмотря даже на принципиальные различия, все эти приборы носят общее название спирометры. Разумеется, дискуссию надо направлять в нужное русло. Диалог с учениками может получиться, к примеру, следующим.
Учитель. Итак, давайте подумаем, как измерить объем воздуха, который выдыхает человек за один раз. Причем имейте в виду, что нужно получить значение объема воздуха при нормальном атмосферном давлении.
Ученик. Выдохнуть его в полиэтиленовый пакет и измерить объем.
Учитель. Как?
Ученик. Хотя бы опустить в воду и измерить объем вытесняемой жидкости. Оболочка — тонкая, так что объем пакета с воздухом примерно равен объему одного воздуха.
Учитель. Но ведь пакет, погруженный в жидкость, будет испытывать давление жидкости. Кстати, как оно называется?
Ученик. ...Гидростатическое... Ну тогда... не погружать, а измерить как-нибудь. Линейкой...
Учитель. А что, надутый полиэтиленовый пакет имеет форму параллелепипеда или шара? Только в этих случаях достаточно было бы линейки и соответствующих формул.
Ученик. Ну тогда выдохнуть в воздушный шарик. Он-то круглый!
Учитель. Да, но только при надувании резина...
Ученик. ...натягивается...
Учитель. ...и оказывает давление на воздух. И давление воздуха будет больше атмосферного, а объем соответственно меньше. (Ученики задумываются.)
Учитель. Воздух будет испытывать давление жидкости, если только воздушный пузырь будет погружен в нее. А если не погружать?.. Просто придержать выдохнутый воздух у поверхности воды...
Ученик. Чем?
Учитель. А вот чем? Думайте.
Ученик. Каким-нибудь поплавком или перевернутым стаканчиком.
Учитель. Идея неплохая, но поясните, что дальше-то... Каков объем воздуха в поплавке?
Ученик. Чем больше воздуха, тем сильнее поплавок всплывает.
Учитель. В общем, верно. И как в этот поплавок выдохнуть воздух?
Ученик. Подвести трубочку снизу, и через нее...
Учитель. Но ведь поплавок своей надводной частью тоже будет давить на воздух...
Ученик. Надо сделать поплавок из тонкого и легкого материала, чтобы он почти совсем не давил. Хотя бы тот же полиэтилен.
Учитель. Хорошо. А как по высоте всплытия будем определять объем?
Ученик. Нанесем шкалу на поплавок.
Учитель. Верно, но показания будут правильными, если поплавок будет сохранять строго вертикальное положение. Как обеспечить вертикальность?
Ученик. Пусть поднимается внутри какой-нибудь трубки, по диаметру такой же.
Учитель. А еще лучше, если этой трубкой будет сам сосуд с водой. А поплавок — его невесомой и поднимающейся крышкой. Осталось только сделать так, чтобы между сосудом и поплавком-крышкой не было...
Ученик. Трения!
Учитель. Прекрасно! Итак, мы с вами сформулировали основные принципы построения спирометра. Давайте сделаем рисунок.

Учащиеся зарисовывают схему, показанную на рис. 2, в тетрадь. Затем говорим, что первые медицинские спирометры были именно такой конструкции. Но она громоздкая, хрупкая, неудобная: при резком перемещении прибора вода может вылиться. Поэтому сейчас чаще всего можно встретить так называемые турбинные спирометры типа ССП. Наверняка, многие имели дело с ними на диспансеризации. Лучше всего, если удастся такой спирометр попросить на время в каком-нибудь медицинском учреждении для демонстрации. С ним легко работать, он маленький, легкий, а главное — принцип работы предельно прост: поток выдыхаемого воздуха давит на лопасти турбинки, вал которой соединен через передаточный механизм со стрелкой, скользящей вдоль шкалы. Чем больше воздуха прошло через турбинку, тем больше оборотов она сделает, тем выше показания прибора.
Если удалось где-то взять напрокат спирометр ССП, то после объяснения принципа работы его можно продемонстрировать. Сначала — сам учитель, затем (разумеется, после смены трубочки) ученик, желательно такого же роста и телосложения, еще лучше — курящий. Сразу станет видно, что при одинаковом полном объеме легких рабочий объем у курящего меньше, чем у некурящего. (И это в пятнадцать-то лет! А что будет дальше?!) Конечно, не факт, что после этого учащийся сразу бросит курить, но где-то «под коркой» у него это отложится. Глядишь, кто-то из собиравшихся начать курить не сделает этого или начнет в более позднем возрасте. Так что ненавязчивая антиникотиновая пропаганда тоже, дай Бог, пойдет на пользу.
Обычно после звонка с урока учащиеся еще долго (с разрешения учителя, конечно же) измеряют объем своих легких и «уличают» друг друга в курении. Короче, получается и познавательно, и весело. Только учитель ОБЯЗАН СЛЕДИТЬ, чтобы учащиеся каждый раз меняли трубочки, в которые дуют.
superbotanik.net
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|






