|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Урок-игра для 6 класса "Длина окружности и площадь круга". Длина окружности и площадь круга 6 класс реферат
Площадь круга
В этом докладе рассказывается о таком важном математическом понятии, как площадь круга. В работе приводятся исторические выкладки и рассматривается очень интересный и наглядный метод расчета площади круга. Наш доклад написан на языке понятном для шестиклассников.
А вот в статье, приведенной ниже, мы решили углубиться в исследование этой интересной темы.
Возможно к этой статье ребенок сможет вернуться, будучи в старших классах, а возможно, многое поймет уже и сейчас. Многие интересные, красивые, но и трудные теоремы связаны с окружностью. Тот, кто не изучил ее свойства или не умеет их применять, еще не знает геометрии. Так что окружность можно назвать своего рода «колесом геометрии». К тому же одно из свойств колеса – его ось остается все время на неизменном расстоянии от поверхности, по которой оно катиться, - в математической формулировке превращается в определение окружности.


Окружность – это множество точек плоскости, удаленных от некоторой точки, ее центра, на одно и то же расстояние, или радиус (от лат. Radius– «спица колеса», «луч»). Радиус окружности - это отрезок, соединяющий центр с точками окружности. Два свойства окружности выделяют ее среди других замкнутых линий. Прежде всего она ограничивает наибольшую площадь по сравнению со всеми замкнутыми кривыми той же длины (т.е. периметра). Это так называемое изопериметрическое свойство окружности.
Далее окружность может скользить по самой себе, причем ее произвольная точка может совместиться с любой другой. Кроме окружности это свойство присуще только одной линии – прямой, но она не замкнута. А потому, для того чтобы кривая сабля точно входила в ножны, она должна быть изогнута по окружности. Часть плоскости, заключенная внутри окружности (т.е. состоящая из точек, удаленных от центра окружности на расстояние, не большее радиуса) называется кругом.
Хорда – это отрезок, соединяющий любые две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Он вдвое длиннее радиуса и является наибольшим возможным расстоянием между точками окружности. Любая хорда, а значит и любой отрезок между точками круга, целиком принадлежит кругу; другими словами, круг – выпуклая фигура. Прямая имеет не более двух общих точек с окружностью. Если таких точек две, прямая называется секущей, а если одна – касательной. Две окружности не могут иметь более двух общих точек. Если таких точек две – говорят, что окружности пересекаются, если же одна, -что они касаются друг друга. Причем касание бывает внешним, когда окружности расположены одна вне другой, или внутренним, когда одна лежит внутри другой. Если у окружностей нет общих точек, но есть общий центр, то они называются концентрическими.
Длина окружности и площадь круга.
Формулы 2πR для величины окружности радиуса R и, πR² для вычисления площади ограниченного ею круга, известны многим. Они пользовались особым вниманием математиков и вычислителей на протяжении тысячелетий. Интерес к все более точному определению постоянной π долгое время поддерживался надеждами осуществить квадратуру круга – построить циркулем и линейкой квадрат, равновеликий данному кругу, а еще более – стремлением опровергнуть ложные «решения» этой задачи. В дальнейшем уточнение значения числа π стало своего рода математическим спортом, а в наше время – еще и способом продемонстрировать достоинства компьютерных программ и самих компьютеров.
Собственно, же формулы просто выражают тот факт, что длина окружности пропорциональна ее радиусу, а площадь круга – квадрату радиуса, причем первый коэффициент пропорциональности вдвое больше второго. Указанные свойства следуют из определений длины окружности и площади круга. Но сами эти определения не столь просты, как в случае длины отрезка или площади многоугольника. Ведь здесь нам приходиться иметь дело с «кривыми» фигурами. Площади криволинейных фигур определяют, строя все более близкие к ним по форме многоугольники. Детали определений могут отличаться, но в любом случае их суть сводиться к следующему предложению. Если последовательность многоугольников mₓ, содержащихся в данной фигуре Ф, и последовательность многоугольников Мₓ, содержащих ее таковы, что разность площадей Мₓ и mₓ становиться сколь угодно малой с ростом x, то площади многоугольников обеих последовательностей стремятся к одному и тому же предельному значению, которое и принимается за площадь Ф.
| 86 Скачивания |
Другие интересные презентации по этому предмету:
school-present.ru
Урок-игра для 6 класса "Длина окружности и площадь круга"
МОУ «Осташевская средняя общеобразовательная школа»
Урок «Длина окружности. Площадь круга»
Класс: 6
Учитель: Шорникова Светлана Павловна
2007-2008 учебный год
Урок
«Длина окружности. Площадь круга»
У учеников 6-го класса преобладает образно-наглядное мышление. Поэтому материал, предлагаемый на уроке, должен быть не только доступен, но и наглядно представлять изучаемое понятие. Мало просто дать формулу для вычисления длины окружности, желательно, чтобы ученики сами смогли ее вывести путем логических рассуждений, применяя ранее изученный материал.
Для включения в работу необходима разминка или устный счет. Задания разминки должны способствовать хорошему восприятию нового материала. Хорошо, если ребята вспомнят умножение числа на десятичную дробь, округление чисел и возведение в квадрат. На этом фоне новый материал преподносится как что-то уже знакомое, просто забытое. А углубление в изучение материала происходит в результате вывода формулы. Это достигается проблемно-поисковым методом. Словесный и наглядный методы обучения позволяют воспринять материал учеником в удобной для него форме. А то, что он сам догадался и вывел формулу, позволит надолго ее запомнить.
Немаловажным моментом является предварительная подготовка к «мини-спектаклю». Наглядная демонстрация круга и окружности дает возможность усвоить различие между понятиями и услышать их определение из уст одноклассников в стихотворной форме.
Цели:
Обучающая: выведение формулы длины окружности и площади круга, знакомство с числом р, обучение применению формулы при решении задач.
Развивающая: развитие кругозора, мышления, внимания, культуры математической речи, привитие интереса к изучению математики.
Воспитательная: воспитание ответственности, аккуратности и самостоятельности.
Оборудование
Предметы круглой формы (стаканы различной величины, крышки, баночки и т.п.), нитки, линейки, калькуляторы; демонстрационный круг, разделенный на 16 долей.
ХОД УРОКА
1. Организационный момент
2. Устный счет
1) Округлите число 3,1415926:
а) до десятичных; б) до тысячных;
в) до сотых.
2) Вычислите:
2 ∙ 3,1; 4 ∙ 3,12; 6 ∙ 6,24.
3) Вычислите:
22; 42; 72; 3 ∙ 22; 3 ∙ 42; 3 ∙ 72.
3. Новый материал
Назовите единицы измерения длины.
Назовите предметы, имеющие круглую форму.
Можно ли линейкой измерить длину окружности предмета круглой формы?
Как можно это сделать?
Учитель предлагает нитью измерить длину окружности лежащих на парте предметов, измерить их диаметр и разделить (можно с помощью калькулятора) длину окружности на диаметр.
Работа ведется парами, результаты записываются в тетрадях и на доске. Затем учитель предлагает сравнить результаты, полученные каждой парой учащихся, объясняет, что называется числом π = 3,1415926… Это отношение известно со времен Архимеда, его считают равным 22/7; с его помощью можно найти длину окружности без нитки, измерив только диаметр или радиус. Это делают по формуле С = πd = 2πr.
К

 ак измерить площадь круга?
ак измерить площадь круга?













Если мы начертим окружность на бумаге в клетку, то внутри образовавшегося круга окажутся не только целые квадраты. Таким образом найти площадь круга очень трудно (рис.1.) .
Рис. 1



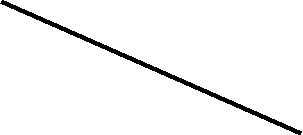

Рис. 2

Попробуем круг разделить на 16 долей (рис.2).
Составим из секторов фигуру (рис. 3).
С = πr
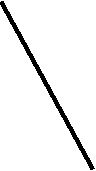
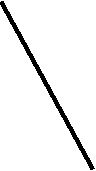
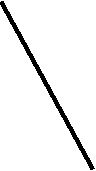

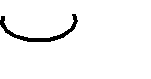
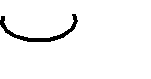
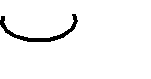







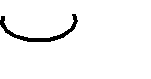
Рис. 3
На какую известную фигуру она похожа ?
Какие измерения необходимо знать для нахождения площади этого прямоугольника ?
Что является шириной и длиной прямоугольника ?
Как найти его площадь ?
Учащиеся выводя формулу площади круга через площадь прямоугольника, у которого ширина равна радиусу круга, а длина равна половине длины окружности.
S = πr ∙ r2 = πr2.
4. Закрепление
Найдите длину окружности и площадь круга, если :
а) r = 4; б) r = 2; в) r = 3.
Результаты проверяются.
5. Театрализованное повторение
(Выступают двое ребят, изображающие круг и окруужность)
Окружность. Меня зовут окружностью,
Горжусь своей я нужностью.
Все до единой точки мои
От центра равноудалены.
У меня есть друг…
Часть плоскости я заключаю в круг.
Круг. Нас радиус с окружностью роднит,
Друг к другу тянет, как магнит.
Окружность. Про радиус запомните скорей –
Это отрезок от центра до точки
моей.
Круг. Всегда диаметр с ней и с мной.
Знай, это радиус двойной.
Окружность. Но что всего важней: диаметр мой
Почти в три раза с одной
седьмой
Меня короче. Это отношение
Окружности к диаметру
за двести лет
До нашей эры вывел Архимед.
Что справедливо это заключение,
Ни в ком не может вызвать
сомнения.
Круг. Вы мне должны на слово верить:
Площадь круга можно мерить.
Скажу собравшимся гостям:
«Дели окружность пополам
И множь на радиус. Тогда, как говорится,
Ты площадь выразишь в квадратных
единицах.»
Вместе. Хоть для вас мы и друзья,
Путать нас никак нельзя.
6. Подведение итогов и задание на дом.
infourok.ru
Длина окружности и площадь круга 6 класс

Длина окружности и площадь круга.
Урок математики в 6 классе.

Ну-ка, проверь дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Толька лишь оценку пять.

Назовите: а) окружность, б) круг.
2)
3)
4)
1)
5)
6)
7)

Определения
Окружность –
фигура, состоящая из множества
точек плоскости, равноудаленных от
центра.
Радиус окружности –
отрезок, соединяющий центр
окружности с любой точкой
окружности

Хорда –
отрезок, соединяющий любые две
точки окружности
Диаметр –
отрезок, соединяющий любые две
точки окружности и проходящий
через центр окружности

- Дайте названия линиям и точкам
Какой формулой
связаны радиус и диаметр?

Факты
- Радиусы одной окружности . . .
- Число π равно. . .
- Если известен диаметр, то длина
окружности вычисляется по
формуле. . .
- Если известен радиус, то длина
окружности вычисляется по
формуле. . .

Площадь круга
Применим переместительный и сочетательный законы:
h
a
S мн-ка = · ( a · h )· n =
· ( a · n ) · h
S круга = · 2 π R · R =
πR 2
R
S круга = πR 2
2πR

С=2πD
S=πR²

Задача
Окружность арены цирка имеет
длину 40,8 метра. Найдите диаметр и
площадь арены.

Одолела нас дремота,
Шевельнуться неохота
Ну-ка делайте со мною
Упражнение такое:
Раз – поднялись, потянулись,
Два – нагнулись, разогнулись,
Три – в ладоши три хлопка
Головою три кивка.

Задача
Длина окружности равна 47,1 см.
Найдите длину другой окружности,
радиус которой составляет 60%
радиуса первой.

Задача
Найдите площадь ¼ круга, радиус
которого 4,4дм.
Число π округлите до десятых

- Работа в парах
1) Постройте окружность с диаметром, равным :
а.) 8 см; б) 4 см.
а)найдите длину каждой окружности
б) во сколько раз длина одной окружности больше длины другой?
в) в каком отношении находится радиус меньшей окружности
к радиусу большей?
2) Заполните таблицу, считая ≈ 3,14.
r
d
0,1 м
С
20 см
12 дм
Герберт Спенсер, английский философ, говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».

Ребята с какими понятиями мы сегодня на уроке познакомились?
Круг
Площадь круга находится по формуле
Как называется число, приближенно равное 3,14
Часть плоскости, ограниченная окружностью
π
S=πR²
С=2π D
Фигура, состоящая из множества
точек плоскости, равноудаленных
от центра
D

Домашнее задание: п. 5.7 , № 1031(в) , № 1032 (в), № 1038(***)
multiurok.ru
"Длина окружности. Площадь круга". 6-й класс

Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (840,7 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательные:
- Обобщить и систематизировать умения и навыки по теме «Длина окружности. Площадь круга».
Развивающие:
- Развивать логическое мышление, способствовать расширению кругозора, развитию математической речи.
Воспитательные:
- Развивать творческое и умственное мышление, побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу, воспитанию эстетических качеств.
Оборудование: мультимедийный проектор и компьютер, презентация «Длина окружности. Площадь круга».
Ход урока
1. Организационный момент.
Приветствие, сообщение темы и цели урока.
2. Актуализация знаний и умений.
Устно:
1) Назовите: 1) радиус; 2) диаметр окружности (слайд 2). 2) Назовите формулу для вычисления: а) длины окружности; б) площади круга (слайд 3). 2) Вычислите длину окружности: а) радиуса 2 см; б) диаметра 2см (слайд 4 - 5). 3) Вычислите площадь круга: а) радиуса 2 см; б) диаметра 2см (слайд 6 - 7). 4) Как изменится длина окружности, если ее радиус: а) увеличили в 4 раза; б) уменьшили в 4 раза (слайд 8 - 9).Вывод: Длина окружности прямо – пропорциональна её радиусу. 7) Сравните длины голубой и черной линий (слайд 10).Ответ: Длина черной и голубой линий одинаковы. (2πR/2=πR – длина синей линии. (2π(r1+r2))/2=πR – длина черной линии).
3. Выполнение учащимися индивидуально письменных заданий с последующей проверкой.
№1 Вычислите длину окружности: а) радиуса 1,54см; б) диаметра 2,12см, π≈3,14.№2 Вычислите площадь круга, длину окружности: а) радиуса 1,2см; б) диаметра 2,2см, π≈3,14.№3 Вычислите площадь круга, если длина окружности 12,56см, π≈3,14.№4 Вычислите диаметр окружности, если ее длина равна: а) 56,52дм; б) 37,68см; π≈3,14.№5 Вычислите площадь круга, если диаметр 6см, π≈3,14.
4. Задания по готовым рисункам.
Устно: (Обсуждение с детьми хода решения задач; на слайдах показан ход решения.)
№1 Найдите площадь кольца, если радиусы 3см и 4 см, π≈3 (слайд 11 - 12). 1)42*3=48(см2) – площадь большого круга. 2)32*3=27(см2) – площадь маленького круга. 3)48-27=21(см2) – площадь кольца.
№2 Из круга r=4см вырезали квадрата, со стороной 2см. Найдите площадь закрашенной фигуры π≈3 (слайд 13 - 14). 1)42*3=48(см2) – площадь круга. 2)22 =4(см2) – площадь квадрата. 3)48-4=44(см2) – площадь закрашенной фигуры.
№3 Из квадрата со стороной 6см вырезали круг, наибольшей площади. Найдите площадь закрашенной фигуры, π≈3 (слайд 15 - 16). 1)62 =36(см2) площадь квадрата. 2)6/2=3(см) – длина радиуса. 2)32*3=27(см2) – площадь круга 3)36-27=9(см2) – площадь закрашенной фигуры.
№4 Сторона квадрата 6см. Найдите площадь закрашенной фигуры (слайд 17 - 18). 1)62 =36(см2) площадь квадрата. 2)6/2=3(см) – длина радиуса. 2)32*3=27(см2) – площадь круга. 3)27/2=13,5(см2) – площадь полукруга. 3)36-13,5=22,5(см2) – площадь закрашенной фигуры.
№5 Найдите площадь закрашенной фигуры, если сторона квадрата равна 4 см, π≈3 (слайд 19 - 23). 1)42 =16(см2) площадь квадрата. 2)4/2=2(см) – длина радиуса. 2)22*3=12(см2) – площадь круга. (Кругов получается два) 3)12*2=24(см2) – площадь всех полукругов. 3)16+24=40(см2) – площадь закрашенной фигуры.
№6 На сторонах квадрата, как на диаметрах, построили полукруги внутри квадрата. Найдите площадь закрашенной фигуры. Сторона квадрата 4 см, π≈3 (слайд 24 - 26). 1)4/2=2(см) – длина радиуса. 2)22*3=12(см2) – площадь круга. (Кругов получается два) 3)12*2=24(см2) – площадь всех полукругов. 4)42 =16(см2) площадь квадрата. 5)24-16=8(см2) – площадь закрашенной фигуры.
Письменно:
№1 Диаметр колеса телеги равен 80 см, колесо сделало 500 оборотов, π≈3,14. Найдите путь лошади? (слайд 27).
№2 Найдите длину окружности и площадь круглого стола, диаметр которого равен 100 см, π≈3,14. (слайд 28).
№3 Какую толщину имеет дерево на высоте 0,5м, если длина тесьмы, которой опоясано дерево на этой высоте, равна 157см? π≈3,14. (слайд 29).
5. Подведение итогов (характеристика работы учащихся, определение типичных ошибок и пробелов в знаниях и умениях, а также путей их устранения и совершенствования).
6.Постановка задания на дом.
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
"Длина окружности и площадь круга" урок математики, 6 класс
КОММУНАЛЬНОЕ ГОСУДАРСТВЕННОЕ 
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ "ГИМНАЗИЯ №24"
ОТДЕЛА ОБРАЗОВАНИЯ АКИМАТА
ГОРОДА ТАРАЗ ЖАМБЫЛСКОЙ ОБЛАСТИ
Методическая разработка открытого урока
по математике в 6-м классе
«Длина окружности и площадь круга»
(решение задач)
декада кафедры ПСС "Радуга"
урок подготовлен учителем математики
высшей категории Бахаревой О.А
Тараз-2017 год
класс: 6"б"
дата: 12.10.2017
Тема: Длина окружности и площадь круга (решение задач)
Цель урока: Создать условия для закрепления знаний учащихся по данной теме. Способствовать развитию математической речи; оперативной памяти, произвольного внимания, наглядно-действенного мышления; воспитывать культуру поведения при фронтальной, индивидуальной и групповой работе.
Тип урока: урок обобщения и систематизации знаний
Технологии: критического мышления, проблемного обучения, самодиагностики и самокоррекции результатов.
Виды деятельности: работа в группах , в парах , индивидуальная работа в картах урока с взаимо- и самопроверкой, фронтальная работа с классом .
Планируемые образовательные результаты:
Предметные: учащиеся должны знать определения окружности и круга, элементов окружности; формулы позволяющие находить радиус, диаметр , длину окружности и площадь круга; уметь решать задачи с применением формул, выражать одну величину через другую и находить площадь комбинированной фигуры ; развитие умений учащихся проводить несложные доказательные рассуждения в ходе решения ; развитие умений учащихся организовывать сотрудничество и совместную деятельность с учителем и сверстниками, работать индивидуально, в группах, аргументировать и отстаивать свое мнение.
Личностные: способность к самооценке на основе критерия успешной учебной деятельности.
Регулятивные: умения определять и формулировать цель на уроке с помощью учителя; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение.
Коммуникативные: умения оформлять свои мысли в устной и письменной форме; слушать и понимать речь других; совместно договариваться о правилах работе в группе.
Познавательные: умения ориентироваться в своей системе знаний; преобразовывать информацию из одной формы в другую.
Оборудование: раздаточный материал, карты урока, телевизор, линейка, циркуль.
Ход урока
1.Организационный этап.
Добрый день дорогие ребята, гости.
С добрым утром. Начат день,Первым делом гоним лень.На уроке не зевать,А работать и читать.
На уроке будь старательным,
Будь спокойным и внимательным.Всё пиши, не отставая,Слушай, не перебивая.Говорите чётко, внятно,Чтобы было всё понятно.
Я хочу начать наш урок со слов французского писателя Анатоля Франса: «Учиться можно только весело. Чтобы переваривать знания, надо поглощать их с аппетитом». На уроке ребята будем следовать этому совету писателя, будем активными, внимательными, будем поглощать, знания с большим желанием ведь они пригодятся вам в вашей дальнейшей жизни. Сегодня у нас заключительный урок и наша задача показать свои знания, умения, навыки.
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Прежде , чем приступить к работе мы должны выяснить какая тема урока и чем мы с вами будем заниматься на уроке, для этого проведем инвентаризацию наших знаний, то есть вспомним, чем мы занимались на прошлых уроках "Инвентаризация знаний" (ответы на вопросы учителя)
C
P


 1) назовите центр окружности
1) назовите центр окружности
2) радиус окружности ( если их несколько, то перечислить все)
3) какой из радиусов имеет наибольшую длину?
N
 4) в окружности площадь находится по формуле S=
4) в окружности площадь находится по формуле S= r2
r2
5) если отрезок ВN = 7 см, то может ли отрезок BС быть равным 10 см?
6) назовите диаметры окружности
K
B
M
7) если отрезок NP = 8 cm, то может ли отрезок МР быть равным 16 см?
8) Отрезок FO является радиусом ?
Подведение итога: О чем шла речь? Какова тема урока? Какая цель урока?
3.Актуализация опорных знаний
Учащиеся по группам заполняют кластер "Окружность"(Отгадайте загадку, ответ запишите и покажите на рисунке)
1.Вроде круг, но дело в том,Что иначе мы зовемНарисованный кружок.В чем секрет? Скажи, дружок!Эта странная наружностьНазывается…. (окружность)
2.Он точку окружности соединяет
С центром ее — это каждый ведь знает.
Он буквою «г» обозначается.
А вы мне скажите, как он называется? (радиус)
3. Точка внутри круга, от которой равноудалены все точки окружности, называется .....(центр)
4. Две точки, взятые на окружности, разобьют эту окружность на две части, которые называются.....(дуга)
5.Это величина.
И только она одна
Размер поверхностей измеряет,
В квадрате определяет. (площадь)
6. Отрезок, соединяющий две точки окружности и не проходящий через центр, называется ... (хорда)
7. Есть отрезок длинный, есть короче,
По линейке его чертим, между прочим.
Сантиметров пять — величина,
Называется она... (длина)
8. Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? (круг)
9. Отрезок, соединяющий две точки на окружности и проходящий через центр, называется....(диаметр)
Определение критериев оценивания работы групп
-правильность выполнения работы
-полнота выполнения задания
-аккуратность выполнения чертежей
Познакомимся с происхождением некоторых терминов и понятий.
Циркуль - от латинского слова - круг
Радиус - от латинского слова - луч, спица в колесе
Диаметр - от латинского слова - поперечник, насквозь измеряющий
Центр - от латинского слова - колющее орудие, которым в древности подгоняли животных в упряжке, а также остриё ножки циркуля.
4.Закрепление знаний учащихся по данной теме
а)"Найди пару"
б)Заполнить таблицу
| R=5 | d = 10 | C= 31,4 | S=78,5 |
| d=11 | r = 5,5 | C =34,54 | S= 94,985 |
| C=56,52 | r = 9 | d =18 | S=254,34 |
| S=28,26 | r =3 | d =6 | C =18,84 |
| S=0,785 | r = 0,5 | d =1 | C=3,14 |
| C=5,024 | r = 0,8 | d =1,6 | S= 2,0096 |
| d = 15 | r = 7,5 | C=23,55 | S=176,625 |
| r = 3,5 | d =7 | C =21,98 | S=38,465 |
в) "Проблемное поле"



Определение критериев оценивания работы групп
оформление решения
правильность решения
-комментирование решения
5.Подведение итогов урока
Заслушать синквейны учащихся (примерные ответы учащихся)
| 1. Хорда 2. Небольшая, отрезок 3. Рисуем, измеряем, ищем 4. Находится в окружности 5. Отрезок | 1. Радиус 2. Часть, отрезок 3. Рисуем, измеряем, проводим 4. Радиус соединяет центр с любой точкой, лежащей на окружности 5. Отрезок | Круг 2. Круглый 3. Чертим, измеряем, доказываем 4. Равноудаленный от центральной точки 5. Простая фигура |
Окончен урок, и выполнен план.
Спасибо, ребята, огромное вам.
За то, что упорно и дружно трудились,
И знания точно уж вам пригодились
1 вариант.
"Найди пару"
| Окружность – замкнутая линия без самопересечений… | …ограниченная окружностью. | |
| Радиус – это отрезок, соединяющий… | …две точки окружности и проходящий через центр. | |
| Круг – это часть плоскости,… | …две точки окружности. | |
| Диаметр – это отрезок, соединяющий… | …все точки которой находятся на одинаковом расстоянии от центра. | |
| Хорда - это отрезок, соединяющий… | …соединяющий центр окружности с любой точкой на окружности. | |
| Формула длины окружности через радиус | r = d : 2 | |
| Формула нахождения радиуса окружности через диаметр | C=2 | |
| Формула нахождения площади круга через диаметр | S= | |
| Формула нахождения диаметра через длину окружности | d = 2r | |
| Формула нахождения площади круга через радиус | C= | |
| Формула нахождения радиуса окружности через длину окружности | S= | |
| Формула нахождения диаметра через радиус | d= C: | |
| Формула нахождения длины окружности через диаметр | r =C:2 |
2 вариант.
"Найди пару"
| Диаметр – это отрезок, соединяющий… | …ограниченная окружностью. | |
| Хорда - это отрезок, соединяющий… | …две точки окружности и проходящий через центр. | |
| Круг – это часть плоскости,… | …две точки окружности. | |
| Окружность – замкнутая линия без самопересечений… | …все точки которой находятся на одинаковом расстоянии от центра. | |
| Радиус – это отрезок, соединяющий… | …соединяющий центр окружности с любой точкой на окружности. | |
| Формула нахождения радиуса окружности через длину окружности | r = d : 2 | |
| Формула нахождения радиуса окружности через диаметр | C=2 | |
| Формула нахождения длины окружности через диаметр | S= | |
| Формула нахождения диаметра через длину окружности | d = 2r | |
| Формула нахождения площади круга через радиус | C= | |
| Формула нахождения площади круга через диаметр | S= | |
| Формула нахождения диаметра через радиус | d= C: | |
| Формула длины окружности через радиус | r =C:2 |
| План урока | ||||
| № | Этап урока | Деятельность учителя | Деятельность ученика | Форма оценивания |
| 1. | Организационный момент | Эмоциональный настрой. Задача: создать коллаборативную среду способствующую повышению эффективности восприятия нового. Проверка готовности к учебному занятию, организация внимания детей. | Эмоциональный настрой в результате начинается формирование коллаборативной среды на основе установление субъект – субъектных отношений. Приветствуют учителя. Включаются в деловой ритм. | |
| 2 | Постановка цели и задач урока. Мотивация учеб-ной деятельности учащихся | Мотивирует учащихся, вместе с ними определяет цель урока; акцентирует внимание учащихся на значимость темы "Инвентаризация знаний" | Заполняют карту урока (подписывают фамилию имя, номер группы) Участвуют в беседе с учителем, отвечают на поставленные вопросы, приводят примеры Определяют тему и цель урока. Осмысление цели урока. | формативное |
| 3 | Актуализация опорных знаний | Определение критериев оценивания работы групп -полнота выполнения задания -аккуратность выполнения чертежей -правильность выполнения работы Инструктаж по выполнению задания | Составление кластера Работа учащихся в группе | Взаимооценивание смайлики |
| 4 | Закрепление знаний учащихся по данной теме | Организация деятельности учащихся по закреплению изученного материала "Найди пару" Заполнить таблицу "Проблемное поле" Определение критериев оценивания работы групп -оформление решения -правильность решения -комментирование решения | Выполнение учащимися различных видов работы на отработку применения формул Индивидуальная работа учащихся по вариантам. Найти начало и конец определения, установить соответствие названием и формулой Учащиеся заполняют таблицу по нахождению неизвестного элемента окружности Работа учащихся в группе по нахождению площади комбинированной фигуры. | Взаимопроверка в парах Индивидуальная работа , проверка по образцу Демонстрационное решение представителя группы у доски |
| 5 | Подведение итогов урока | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. На первой строчке записывается одно слово – существительное. Это и есть тема синквейна. На второй строчке пишутся два прилагательных, раскрывающих тему синквейна. На третьей строчке записываются три глагола, описывающих действия, относящиеся к теме синквейна. На четвертой строчке размещается целая фраза, предложение, состоящее из нескольких слов, передающее отношение к теме. Таким предложением может быть крылатое выражение, цитата, пословица или составленная самим учащимся фраза в контексте с темой. Пятая строчка – это слово-резюме, которое выражает личное отношение учащегося к теме. | Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач. | Формативное |
| 6 | Рефлексия | На этом мы заканчиваем наш урок, и я бы хотела что бы вы его оценили. | Учащиеся в графе рефлексия анализируют свою деятельность мне все понятно на уроке испытывал(а) затруднения Тему я не понял(а). Осталось много вопросов | |
| 7. | Домашнее задание. | Инструктаж о выполнении домашнего задания | Учащиеся записывают домашнее задание | |
intolimp.org
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|



 d2
d2


