Реферат на тему:
Веще́ственное, или действи́тельное число [1] — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений [2].
Числовая прямая
Если натуральные числа возникли в процессе счета, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.
Наглядно понятие вещественного числа можно представить себе при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять некоторое, и притом только одно, вещественное число. Вследствие этого соответствия термин числовая прямая обычно употребляется в качестве синонима множества вещественных чисел.
Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия [3]. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере[3] была создана строгая теория вещественных чисел.
С точки зрения современной математики, множество вещественных чисел — суть, непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.
Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»), или (англ. blackboard bold «R») от лат. realis — действительный.
Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения (пропорции, в современном понимании — рациональные числа). Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом.[4]
Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса дошла до нас в изложении Евклида («Начала», книга V). По существу, теория Евдокса — это геометрическая модель вещественных чисел. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — он не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Классическая теория Дедекинда для построения вещественных чисел по своим принципам чрезвычайно похожа на изложение Евдокса. Однако модель Евдокса неполна во многих отношениях — например, она не содержит аксиомы непрерывности, нет общей теории арифметических операций для величин или их отношений и др.[5]
Ситуация начала меняться в первые века н. э. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным».[6] После гибели античной науки на передний план выдвинулись индийские и исламские математики, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе[7], где поначалу разделяли рациональные и иррациональные (буквально: неразумные) числа (их называли также мнимыми, абсурдными, глухими и т. п.). Полное уравнение в правах иррациональных чисел связано с трудами Симона Стевина (конец XVI века), который провозгласил:[6]
| Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной законченностью. |
Он же, с некоторыми оговорками, легализовал отрицательные числа, а также развил теорию и символику десятичных дробей, которые с этого момента начинают вытеснять неудобные шестидесятеричные.
Спустя столетие Ньютон в своей «Универсальной арифметике» (1707) даёт классическое определение (вещественного) числа как отношения результата измерения к единичному эталону:[8]
| Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой за единицу. |
Долгое время это прикладное определение считалось достаточным, так что практически важные свойства вещественных чисел и функций не доказывались, а считались интуитивно очевидными (из геометрических или кинематических соображений). Например, считался самоочевидным тот факт, что непрерывная кривая, точки которой расположены по разные стороны от некоторой прямой, пересекает эту прямую. Строгое определение понятия непрерывности также отсутствовало.[9] Как следствие, немало теорем содержали ошибки, нечёткие или чрезмерно широкие формулировки.
Даже после того, как Коши разработал достаточно строгий фундамент анализа, положение не изменилось, поскольку теории вещественных чисел, на которую обязан был опираться анализ, не существовало. Из-за этого Коши сделал немало ошибок, положившись на интуицию там, где она приводила к неверным выводам: например, он полагал, что сумма ряда из непрерывных функций всегда непрерывна.
Первую попытку заполнить пробел в основаниях математики сделал Бернард Больцано в своей статье «Чисто аналитическое доказательство теоремы, что между любыми двумя значениями, дающими результаты противоположного знака, лежит по меньшей мере один действительный корень уравнения» (1817). В этой пионерской работе ещё нет целостной системы вещественных чисел, но уже приводится современное определение непрерывности и показывается, что на этой основе теорема, упомянутая в заглавии, может быть строго доказана[10]. В более поздней работе[11] Больцано даёт набросок общей теории вещественных чисел, по идеям близкой к канторовской теории множеств[12], но эта его работа осталась неопубликованной при жизни автора и увидела свет только в 1851 году. Взгляды Больцано значительно опередили своё время и не привлекли внимания математической общественности.
Современная теория вещественных чисел была построена во второй половине XIX века, в первую очередь трудами Вейерштрасса, Дедекинда и Кантора. Они предложили различные, но эквивалентные подходы к теории этой важнейшей математической структуры и окончательно отделили это понятие от геометрии и механики.
При конструктивном определении понятия вещественного числа, на основе известных математических объектов (например, множества рациональных чисел ), которые принимают заданными, строят новые объекты, которые, в определённом смысле, отражают наше интуитивное понимание о понятии вещественного числа. Существенным отличием между вещественными числами и этими построенными объектами является то, что первые, в отличие от вторых, понимаются нами лишь интуитивно и пока не являются строго определённым математическим понятием.
Эти объекты и объявляют вещественными числами. Для них вводят основные арифметические операции, определяют отношение порядка и доказывают их свойства.
Исторически первыми строгими определениями вещественного числа были именно конструктивные определения. В 1872 году были опубликованы одновременно три работы: теория фундаментальных последовательностей Кантора, теория Вейерштрасса (в современном варианте — теория бесконечных десятичных дробей) и теория сечений в области рациональных чисел Дедекинда[3][13].
В данном подходе вещественное число рассматривается как предел последовательности рациональных чисел. Чтобы последовательность рациональных чисел сходилась, на неё накладывается условие Коши:

Смысл этого условия заключается в том, что члены последовательности, начиная с некоторого номера будут лежать сколь угодно близко друг от друга. Последовательности, удовлетворяющие условию Коши, называются фундаментальными.
Вещественное число, определяемое фундаментальной последовательностью рациональных чисел {an}, обозначим [an].
Два вещественных числа
α = [an] и β = [bn],
определённые соответственно фундаментальными последовательностями {an} и {bn}, называются равными, если

Если даны два вещественных числа α = [an] и β = [bn], то их суммой и произведением называются числа, определённые соответственно суммой и произведением последовательностей {an} и {bn}:
![\alpha + \beta \overset{\text{def}}{=} [a_n + b_n] \qquad \alpha \cdot \beta \overset{\text{def}}{=} [a_n \cdot b_n]](/800/600/http/upload.wikimedia.org//math/9/7/5/9759ff81af2aaa1e7ed4667459f2fbf8.png)
Отношение порядка на множестве вещественных чисел устанавливается посредством соглашения, в соответствии с которым число α = [an] по определению больше числа β = [bn], то есть α > β, если

Способ построения множества вещественных чисел с помощью фундаментальных последовательностей рациональных является частным случаем конструкции пополнения произвольного метрического пространства. Как и в общем случае, полученное в результате пополнения множество вещественных чисел само уже является полным, то есть содержит пределы всех фундаментальных последовательностей своих элементов.
Вещественное число определяется как бесконечная десятичная дробь, то есть выражение вида
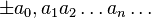
где есть один из символов + или - , называемый знаком числа, a0 — целое неотрицательное число,
— последовательность десятичных знаков, то есть элементов числового множества
.
Бесконечная десятичная дробь интерпретируется как такое число, которое на числовой прямой лежит между рациональными точками вида
и
для всех
Сравнение вещественных чисел в форме бесконечных десятичных дробей производится поразрядно. Например, пусть даны два неотрицательных числа
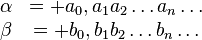
Если a0 < b0, то α < β; если a0 > b0 то α > β. В случае равенства a0 = b0 переходят к сравнению следующего разряда. И так далее. Если , то после конечного числа шагов встретится первый разряд n, такой что
. Если an < bn, то α < β; если an > bn то α > β.
Однако, при этом следует учитывать, что число . Поэтому если запись одного из сравниваемых чисел, начиная с некоторого разряда, представляет собой периодическую десятичную дробь, у которой в периоде стоит 9, то её следует заменить на эквивалентную запись, с нулём в периоде.
Арифметические операции над бесконечными десятичными дробями определяются как непрерывное продолжение[14] соответствующих операций над рациональными числами. Например, суммой вещественных чисел α и β называется вещественное число α + β, удовлетворяющее следующему условию:
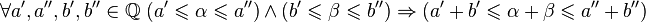
Аналогично определяет операция умножения бесконечных десятичных дробей.
В подходе Дедекинда вещественные числа определяются с помощью сечений в множестве рациональных чисел.
Сечением в множестве рациональных чисел называется всякое разбиение совокупности всех рациональных чисел на два непустых класса — нижний A и верхний A', так что каждое число из нижнего класса строго меньше всякого числа из верхнего:
Если существует число α, которое является максимальным в нижнем классе, либо минимальным в верхнем классе, то это число разделяет множества A и A': числа нижнего и верхнего классов лежат по разные стороны от α. Говорят также, что рациональное число α производит данное сечение множества рациональных чисел.
Если же в нижнем классе сечения нет максимального элемента, а в верхнем — минимального, то не существует никакого рационального числа, которое разделяло бы множества A и A'. В этом случае по определению полагают, что данное сечение определяет некоторое иррациональное число α, которое находится между нижним и верхним классами, и тем самым производит данное сечение. Иначе говоря, для всякого сечения, не производимого никаким рациональным числом, вводят новый объект — иррациональное число, которое по определению больше всякого числа из нижнего класса и меньше всякого числа из верхнего класса:
Объединение всех рациональных и всех иррациональных чисел называют множеством вещественных чисел, а его элементы — вещественными числами.
Арифметические операции над вещественными числами определяются как непрерывное продолжение соответствующих операций над рациональными числами. Например, суммой вещественных чисел α и β называется вещественное число α + β, удовлетворяющее следующему условию:
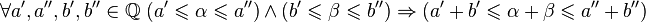
Построить множество вещественных чисел можно разными способами. В теории Кантора вещественные числа — классы эквивалентных фундаментальных последовательностей рациональных чисел, в теории Вейерштрасса — бесконечные десятичные дроби, в теории Дедекинда — сечения в области рациональных чисел. Во всех этих подходах в результате мы получаем некоторое множество объектов (вещественных чисел), обладающих определёнными свойствами: их можно складывать, умножать, сравнивать между собой. Более того, коль скоро установлены свойства этих объектов, мы можем больше не апеллировать к тем конкретным конструкциям, с помощью которых они были построены.
В математике важна не конкретная природа объектов, а лишь математические соотношения, существующие между ними.
Для человека, который исследует математическое понятие количество элементов, безразлично, о чём говорить — о трёх яблоках или о трёх камнях, и их съедобность или несъедобность значения не имеет. В процессе отвлечения от несущественных признаков, то есть абстрагирования (лат. abstractio — отвлечение), он приходит к тому общему, что есть у трёх яблок и трёх камней — количеству элементов. Так возникает абстрактное понятие натурального числа. С этой точки зрения три яблока и три камня — две конкретные реализации, модели абстрактного понятия «число три».
Точно так же классы фундаментальных последовательностей рациональных чисел, бесконечные десятичные дроби, сечения в области рациональных чисел являются лишь конкретными реализациями, моделями вещественного числа. А само понятие вещественного числа определяется существующими для него математическими соотношениями. Коль скоро они установлены, определено и понятие вещественного числа.
Здесь уместно привести знаменитое высказывает Д. Гильберта, основоположника системного аксиоматического метода в математике, который, имея в виду аксиоматизацию геометрии, как-то заметил:
| Следует добиться того, чтобы с равным успехом можно было говорить вместо точек, прямых и плоскостей о столах, стульях и пивных кружках. Давид Гильберт[15] |
Множество называется множеством вещественных чисел, а его элементы — вещественными числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:
На множестве определено отображение (операция сложения)
сопоставляющее каждой упорядоченной паре элементов a,b из некоторый элемент a + b, называемый суммой a и b. Также, на множестве
определено отображение (операция умножения)
сопоставляющее каждой упорядоченной паре элементов a,b из некоторый элемент
, называемый произведением a и b. При этом имеют место следующие свойства.
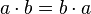 I6. Ассоциативность умножения. Для любых
I6. Ассоциативность умножения. Для любых  I7. Существование единицы. Существует элемент
I7. Существование единицы. Существует элемент 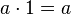 I8. Существование обратного элемента. Для любого
I8. Существование обратного элемента. Для любого 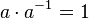 I9. Дистрибутивный закон умножения относительно сложения. Для любых
I9. Дистрибутивный закон умножения относительно сложения. Для любых  I10. Нетривиальность поля. Единица и ноль — различные элементы
I10. Нетривиальность поля. Единица и ноль — различные элементы Между элементами определено отношение
, то есть для любой упорядоченной пары элементов a,b из
установлено, выполняется соотношение
или нет. При этом имеют место следующие свойства.
Этих аксиом достаточно чтобы строго вывести все известные свойства вещественных чисел[16].
На языке современной алгебры аксиомы первой группы означают, что множество является полем. Аксиомы второй группы — что множество
является линейно упорядоченным множеством (II1 — II4), причём отношение порядка согласовано со структурой поля II5 — II6. Множества, удовлетворяющие аксиомам первой и второй группы, называются упорядоченными полями. Наконец, последняя группа, состоящая из одной аксиомы, утверждает, что множество вещественных чисел обладает свойством непрерывности, которое также называют полнотой. Резюмируя, можно дать эквивалентное определение множества вещественных чисел.
Определение. Множеством вещественных чисел называется непрерывное упорядоченное поле.
Существуют и другие способы аксиоматизации вещественных чисел. Например, вместо аксиомы непрерывности III1. можно использовать любое другое эквивалентное ей условие, или группу условий. Например, в системе аксиом, предложенной Гильбертом, аксиомы групп I и II, по существу, те же, что и в приведённые выше, а вместо аксиомы III1 используются следующие два условия:
III1'. Аксиома Архимеда. Пусть a > 0[17] и b > 0. Тогда элемент a можно повторить слагаемым столько раз, чтобы образовавшаяся в результате сумма превзошла b:Таким образом, можно дать следующее эквивалентное определение:
Определение. Множество вещественных чисел есть максимальное архимедово упорядоченное поле
В качестве другого примера аксиоматизации вещественных чисел можно привести аксиоматику Тарского (англ.), состоящую всего из 8 аксиом.
Очевидно, что на числовой прямой рациональные числа располагаются вперемешку с вещественными, причём множество вещественных чисел в известном смысле «плотнее» множества рациональных. Возникает закономерный вопрос, насколько часто на числовой прямой попадаются рациональные и вещественные числа и можно ли одни числа приблизить другими. Ответ на этот вопрос дают три леммы, основанные, в основном, на аксиоме Архимеда.[18]
Лемма 1. Для любого вещественного числа и любого наперёд взятого положительного рационального расстояния найдётся пара рациональных чисел, отстоящих друг от друга менее, чем на это расстояние, таких что вещественное число лежит на отрезке между этими рациональными числами.
Эта лемма говорит о том, что любое вещественное число можно с заданной точностью с двух сторон приблизить рациональными числами.
Лемма 2. Между любыми двумя различными вещественными числами содержится рациональное число.
Очевидным следствием из этой леммы является тот факт, что между любыми двумя несовпадающими вещественными числами содержится целое бесконечное множество рациональных. Кроме того, ещё более очевидно, что между любыми двумя различными рациональными числами содержится вещественное.
Лемма 3. Приближение вещественного числа рациональными, описанное в лемме 1, идентифицирует вещественное число единственным образом.
Эти леммы прежде всего говорят о том, что множество вещественных чисел не такое «плотное» по сравнению с множеством рациональных чисел, как может показаться. Особенно ярко это иллюстрирует лемма 2. Все три леммы активно используются для доказательства различных теорем, связанных с операциями сложения и умножения вещественных чисел.
Изначально вещественные числа были естественным обобщением рациональных, но у них впервые было обнаружено свойство несчётности, которое говорит о том, что множество вещественных чисел нельзя занумеровать, т. е. не существует биекции между множествами вещественных и натуральных чисел. Чтобы показать несчётность всего множества вещественных чисел, достаточно показать несчётность интервала .[18]
Пусть все числа указанного промежутка уже занумерованы некоторым образом. Тогда их можно выписать в следующем виде:
Здесь aij — j-я цифра i-ого числа. Очевидно, что все числа указанного вида действительно принадлежат рассматриваемому промежутку, если только в каждом числе не все цифры сразу являются нулями или девятками.
Далее предлагается рассмотреть следующее число:
Пусть каждая цифра di этого числа удовлетворяет следующим трём свойствам:
Такое число действительно существует на указанном промежутке, так как оно является вещественным, не совпадает ни с нулём, ни с единицей, а десятичных цифр достаточно, чтобы третье свойство выполнялось. Кроме этого, x интересно тем фактом, что оно не совпадает ни с одним из чисел xj, выписанных выше, ведь иначе j-я цифра числа x совпала бы с j-ой цифрой числа xj. Пришли к противоречию, заключающемуся в том, что как бы числа рассматриваемого промежутка ни были занумерованы, всё равно найдётся число из этого же промежутка, которому не присвоен номер.[18]
Это свидетельствует о том, что множество вещественных чисел не является счётным. Его мощность называется мощностью континуума.
Поле вещественных чисел постоянно служило в математике источником обобщений, причём в различных практически важных направлениях. Непосредственно к полю
примыкают следующие варианты обобщённых числовых систем.
Математическая модель вещественных чисел повсеместно применяется в науке и технике для измерения непрерывно меняющихся величин. Однако это не главное её применение, потому что реально измеренные величины всегда имеют конечное число десятичных знаков, то есть являются рациональными числами. Основное назначение этой модели — служить базой для аналитических методов исследования. Огромный успех этих методов за последние три века показал, что модель вещественных чисел в большинстве случаев достаточно адекватно отражает структуру непрерывных физических величин.
Сказанное, конечно, не означает, что вещественная числовая прямая есть точный образ реальной непрерывной величины. Например, современной науке пока не известно, дискретны ли пространство и время или делимы неограниченно; однако даже во втором случае модель вещественных чисел для этих величин должна рассматриваться как приближённая, поскольку понятия точки пространства и момента времени представляют собой идеализации, не имеющие реального аналога. Этот фундаментальный вопрос широко обсуждается в науке, начиная с апорий Зенона. Приближённой эта модель является и в применении к величинам, которые в классической физике рассматривались как непрерывные, но в действительности оказались дискретными (квантуемыми).
Тем, кто интересуется историей становления понятия вещественного числа, можно порекомендовать следующие две книги:
Прекрасное подробное изложение теории построения вещественных чисел с помощью фундаментальных последовательностей, а также теории построения вещественных чисел с помощью сечений в области рациональных чисел можно найти в следующей:
Желающим познакомиться с оригинальным ходом мысли самого Р. Дедекинда можно порекомендовать ту самую брошюру, в которой в 1872 году Дедекинд изложил свою теорию вещественного числа. Эта книжка на сегодняшний день остаётся одним из самых лучших и доступных изложений предмета. Имеется русский перевод:
Также прекрасное изложение теории Дедекинда имеется в классическом учебнике
Построение теории вещественного числа с помощью бесконечных десятичных дробей можно найти в книгах
Аксиоматическое изложение теории вещественного числа можно найти в книгах
Сущность аксиоматического метода и его сравнение с конструктивным подходом изложены Д. Гильбертом на нескольких страницах в Дополнении VI. О понятии числа в следующем издании классической работы
wreferat.baza-referat.ru
Реферат на тему:
Веще́ственное, или действи́тельное число [1] — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений [2].
Числовая прямая
Если натуральные числа возникли в процессе счета, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.
Наглядно понятие вещественного числа можно представить себе при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять некоторое, и притом только одно, вещественное число. Вследствие этого соответствия термин числовая прямая обычно употребляется в качестве синонима множества вещественных чисел.
Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия [3]. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере[3] была создана строгая теория вещественных чисел.
С точки зрения современной математики, множество вещественных чисел — суть, непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.
Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»), или (англ. blackboard bold «R») от лат. realis — действительный.
Первая развитая числовая система, построенная в Древней Греции, включала только натуральные числа и их отношения (пропорции, в современном понимании — рациональные числа). Однако вскоре выяснилось, что для целей геометрии и астрономии этого недостаточно: например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным числом.[4]
Для выхода из положения Евдокс Книдский ввёл, в дополнение к числам, более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма. Теория Евдокса дошла до нас в изложении Евклида («Начала», книга V). По существу, теория Евдокса — это геометрическая модель вещественных чисел. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — он не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Классическая теория Дедекинда для построения вещественных чисел по своим принципам чрезвычайно похожа на изложение Евдокса. Однако модель Евдокса неполна во многих отношениях — например, она не содержит аксиомы непрерывности, нет общей теории арифметических операций для величин или их отношений и др.[5]
Ситуация начала меняться в первые века н. э. Уже Диофант Александрийский, вопреки прежним традициям, рассматривает дроби так же, как и натуральные числа, а в IV книге своей «Арифметики» даже пишет об одном результате: «Число оказывается не рациональным».[6] После гибели античной науки на передний план выдвинулись индийские и исламские математики, для которых любой результат измерения или вычисления считался числом. Эти взгляды постепенно взяли верх и в средневековой Европе[7], где поначалу разделяли рациональные и иррациональные (буквально: неразумные) числа (их называли также мнимыми, абсурдными, глухими и т. п.). Полное уравнение в правах иррациональных чисел связано с трудами Симона Стевина (конец XVI века), который провозгласил:[6]
| Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной законченностью. |
Он же, с некоторыми оговорками, легализовал отрицательные числа, а также развил теорию и символику десятичных дробей, которые с этого момента начинают вытеснять неудобные шестидесятеричные.
Спустя столетие Ньютон в своей «Универсальной арифметике» (1707) даёт классическое определение (вещественного) числа как отношения результата измерения к единичному эталону:[8]
| Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой за единицу. |
Долгое время это прикладное определение считалось достаточным, так что практически важные свойства вещественных чисел и функций не доказывались, а считались интуитивно очевидными (из геометрических или кинематических соображений). Например, считался самоочевидным тот факт, что непрерывная кривая, точки которой расположены по разные стороны от некоторой прямой, пересекает эту прямую. Строгое определение понятия непрерывности также отсутствовало.[9] Как следствие, немало теорем содержали ошибки, нечёткие или чрезмерно широкие формулировки.
Даже после того, как Коши разработал достаточно строгий фундамент анализа, положение не изменилось, поскольку теории вещественных чисел, на которую обязан был опираться анализ, не существовало. Из-за этого Коши сделал немало ошибок, положившись на интуицию там, где она приводила к неверным выводам: например, он полагал, что сумма ряда из непрерывных функций всегда непрерывна.
Первую попытку заполнить пробел в основаниях математики сделал Бернард Больцано в своей статье «Чисто аналитическое доказательство теоремы, что между любыми двумя значениями, дающими результаты противоположного знака, лежит по меньшей мере один действительный корень уравнения» (1817). В этой пионерской работе ещё нет целостной системы вещественных чисел, но уже приводится современное определение непрерывности и показывается, что на этой основе теорема, упомянутая в заглавии, может быть строго доказана[10]. В более поздней работе[11] Больцано даёт набросок общей теории вещественных чисел, по идеям близкой к канторовской теории множеств[12], но эта его работа осталась неопубликованной при жизни автора и увидела свет только в 1851 году. Взгляды Больцано значительно опередили своё время и не привлекли внимания математической общественности.
Современная теория вещественных чисел была построена во второй половине XIX века, в первую очередь трудами Вейерштрасса, Дедекинда и Кантора. Они предложили различные, но эквивалентные подходы к теории этой важнейшей математической структуры и окончательно отделили это понятие от геометрии и механики.
При конструктивном определении понятия вещественного числа, на основе известных математических объектов (например, множества рациональных чисел ), которые принимают заданными, строят новые объекты, которые, в определённом смысле, отражают наше интуитивное понимание о понятии вещественного числа. Существенным отличием между вещественными числами и этими построенными объектами является то, что первые, в отличие от вторых, понимаются нами лишь интуитивно и пока не являются строго определённым математическим понятием.
Эти объекты и объявляют вещественными числами. Для них вводят основные арифметические операции, определяют отношение порядка и доказывают их свойства.
Исторически первыми строгими определениями вещественного числа были именно конструктивные определения. В 1872 году были опубликованы одновременно три работы: теория фундаментальных последовательностей Кантора, теория Вейерштрасса (в современном варианте — теория бесконечных десятичных дробей) и теория сечений в области рациональных чисел Дедекинда[3][13].
В данном подходе вещественное число рассматривается как предел последовательности рациональных чисел. Чтобы последовательность рациональных чисел сходилась, на неё накладывается условие Коши:

Смысл этого условия заключается в том, что члены последовательности, начиная с некоторого номера будут лежать сколь угодно близко друг от друга. Последовательности, удовлетворяющие условию Коши, называются фундаментальными.
Вещественное число, определяемое фундаментальной последовательностью рациональных чисел {an}, обозначим [an].
Два вещественных числа
α = [an] и β = [bn],
определённые соответственно фундаментальными последовательностями {an} и {bn}, называются равными, если

Если даны два вещественных числа α = [an] и β = [bn], то их суммой и произведением называются числа, определённые соответственно суммой и произведением последовательностей {an} и {bn}:
![\alpha + \beta \overset{\text{def}}{=} [a_n + b_n] \qquad \alpha \cdot \beta \overset{\text{def}}{=} [a_n \cdot b_n]](/800/600/http/upload.wikimedia.org//math/9/7/5/9759ff81af2aaa1e7ed4667459f2fbf8.png)
Отношение порядка на множестве вещественных чисел устанавливается посредством соглашения, в соответствии с которым число α = [an] по определению больше числа β = [bn], то есть α > β, если

Способ построения множества вещественных чисел с помощью фундаментальных последовательностей рациональных является частным случаем конструкции пополнения произвольного метрического пространства. Как и в общем случае, полученное в результате пополнения множество вещественных чисел само уже является полным, то есть содержит пределы всех фундаментальных последовательностей своих элементов.
Вещественное число определяется как бесконечная десятичная дробь, то есть выражение вида
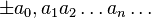
где есть один из символов + или - , называемый знаком числа, a0 — целое неотрицательное число,
— последовательность десятичных знаков, то есть элементов числового множества
.
Бесконечная десятичная дробь интерпретируется как такое число, которое на числовой прямой лежит между рациональными точками вида
и
для всех
Сравнение вещественных чисел в форме бесконечных десятичных дробей производится поразрядно. Например, пусть даны два неотрицательных числа
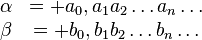
Если a0 < b0, то α < β; если a0 > b0 то α > β. В случае равенства a0 = b0 переходят к сравнению следующего разряда. И так далее. Если , то после конечного числа шагов встретится первый разряд n, такой что
. Если an < bn, то α < β; если an > bn то α > β.
Однако, при этом следует учитывать, что число . Поэтому если запись одного из сравниваемых чисел, начиная с некоторого разряда, представляет собой периодическую десятичную дробь, у которой в периоде стоит 9, то её следует заменить на эквивалентную запись, с нулём в периоде.
Арифметические операции над бесконечными десятичными дробями определяются как непрерывное продолжение[14] соответствующих операций над рациональными числами. Например, суммой вещественных чисел α и β называется вещественное число α + β, удовлетворяющее следующему условию:
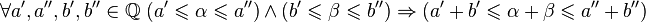
Аналогично определяет операция умножения бесконечных десятичных дробей.
В подходе Дедекинда вещественные числа определяются с помощью сечений в множестве рациональных чисел.
Сечением в множестве рациональных чисел называется всякое разбиение совокупности всех рациональных чисел на два непустых класса — нижний A и верхний A', так что каждое число из нижнего класса строго меньше всякого числа из верхнего:
Если существует число α, которое является максимальным в нижнем классе, либо минимальным в верхнем классе, то это число разделяет множества A и A': числа нижнего и верхнего классов лежат по разные стороны от α. Говорят также, что рациональное число α производит данное сечение множества рациональных чисел.
Если же в нижнем классе сечения нет максимального элемента, а в верхнем — минимального, то не существует никакого рационального числа, которое разделяло бы множества A и A'. В этом случае по определению полагают, что данное сечение определяет некоторое иррациональное число α, которое находится между нижним и верхним классами, и тем самым производит данное сечение. Иначе говоря, для всякого сечения, не производимого никаким рациональным числом, вводят новый объект — иррациональное число, которое по определению больше всякого числа из нижнего класса и меньше всякого числа из верхнего класса:
Объединение всех рациональных и всех иррациональных чисел называют множеством вещественных чисел, а его элементы — вещественными числами.
Арифметические операции над вещественными числами определяются как непрерывное продолжение соответствующих операций над рациональными числами. Например, суммой вещественных чисел α и β называется вещественное число α + β, удовлетворяющее следующему условию:
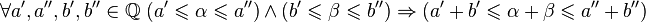
Построить множество вещественных чисел можно разными способами. В теории Кантора вещественные числа — классы эквивалентных фундаментальных последовательностей рациональных чисел, в теории Вейерштрасса — бесконечные десятичные дроби, в теории Дедекинда — сечения в области рациональных чисел. Во всех этих подходах в результате мы получаем некоторое множество объектов (вещественных чисел), обладающих определёнными свойствами: их можно складывать, умножать, сравнивать между собой. Более того, коль скоро установлены свойства этих объектов, мы можем больше не апеллировать к тем конкретным конструкциям, с помощью которых они были построены.
В математике важна не конкретная природа объектов, а лишь математические соотношения, существующие между ними.
Для человека, который исследует математическое понятие количество элементов, безразлично, о чём говорить — о трёх яблоках или о трёх камнях, и их съедобность или несъедобность значения не имеет. В процессе отвлечения от несущественных признаков, то есть абстрагирования (лат. abstractio — отвлечение), он приходит к тому общему, что есть у трёх яблок и трёх камней — количеству элементов. Так возникает абстрактное понятие натурального числа. С этой точки зрения три яблока и три камня — две конкретные реализации, модели абстрактного понятия «число три».
Точно так же классы фундаментальных последовательностей рациональных чисел, бесконечные десятичные дроби, сечения в области рациональных чисел являются лишь конкретными реализациями, моделями вещественного числа. А само понятие вещественного числа определяется существующими для него математическими соотношениями. Коль скоро они установлены, определено и понятие вещественного числа.
Здесь уместно привести знаменитое высказывает Д. Гильберта, основоположника системного аксиоматического метода в математике, который, имея в виду аксиоматизацию геометрии, как-то заметил:
| Следует добиться того, чтобы с равным успехом можно было говорить вместо точек, прямых и плоскостей о столах, стульях и пивных кружках. Давид Гильберт[15] |
Множество называется множеством вещественных чисел, а его элементы — вещественными числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:
На множестве определено отображение (операция сложения)
сопоставляющее каждой упорядоченной паре элементов a,b из некоторый элемент a + b, называемый суммой a и b. Также, на множестве
определено отображение (операция умножения)
сопоставляющее каждой упорядоченной паре элементов a,b из некоторый элемент
, называемый произведением a и b. При этом имеют место следующие свойства.
 I6. Ассоциативность умножения. Для любых
I6. Ассоциативность умножения. Для любых  I7. Существование единицы. Существует элемент
I7. Существование единицы. Существует элемент 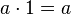 I8. Существование обратного элемента. Для любого
I8. Существование обратного элемента. Для любого 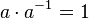 I9. Дистрибутивный закон умножения относительно сложения. Для любых
I9. Дистрибутивный закон умножения относительно сложения. Для любых  I10. Нетривиальность поля. Единица и ноль — различные элементы
I10. Нетривиальность поля. Единица и ноль — различные элементы Между элементами определено отношение
, то есть для любой упорядоченной пары элементов a,b из
установлено, выполняется соотношение
или нет. При этом имеют место следующие свойства.
Этих аксиом достаточно чтобы строго вывести все известные свойства вещественных чисел[16].
На языке современной алгебры аксиомы первой группы означают, что множество является полем. Аксиомы второй группы — что множество
является линейно упорядоченным множеством (II1 — II4), причём отношение порядка согласовано со структурой поля II5 — II6. Множества, удовлетворяющие аксиомам первой и второй группы, называются упорядоченными полями. Наконец, последняя группа, состоящая из одной аксиомы, утверждает, что множество вещественных чисел обладает свойством непрерывности, которое также называют полнотой. Резюмируя, можно дать эквивалентное определение множества вещественных чисел.
Определение. Множеством вещественных чисел называется непрерывное упорядоченное поле.
Существуют и другие способы аксиоматизации вещественных чисел. Например, вместо аксиомы непрерывности III1. можно использовать любое другое эквивалентное ей условие, или группу условий. Например, в системе аксиом, предложенной Гильбертом, аксиомы групп I и II, по существу, те же, что и в приведённые выше, а вместо аксиомы III1 используются следующие два условия:
III1'. Аксиома Архимеда. Пусть a > 0[17] и b > 0. Тогда элемент a можно повторить слагаемым столько раз, чтобы образовавшаяся в результате сумма превзошла b:Таким образом, можно дать следующее эквивалентное определение:
Определение. Множество вещественных чисел есть максимальное архимедово упорядоченное поле
В качестве другого примера аксиоматизации вещественных чисел можно привести аксиоматику Тарского (англ.), состоящую всего из 8 аксиом.
Очевидно, что на числовой прямой рациональные числа располагаются вперемешку с вещественными, причём множество вещественных чисел в известном смысле «плотнее» множества рациональных. Возникает закономерный вопрос, насколько часто на числовой прямой попадаются рациональные и вещественные числа и можно ли одни числа приблизить другими. Ответ на этот вопрос дают три леммы, основанные, в основном, на аксиоме Архимеда.[18]
Лемма 1. Для любого вещественного числа и любого наперёд взятого положительного рационального расстояния найдётся пара рациональных чисел, отстоящих друг от друга менее, чем на это расстояние, таких что вещественное число лежит на отрезке между этими рациональными числами.
Эта лемма говорит о том, что любое вещественное число можно с заданной точностью с двух сторон приблизить рациональными числами.
Лемма 2. Между любыми двумя различными вещественными числами содержится рациональное число.
Очевидным следствием из этой леммы является тот факт, что между любыми двумя несовпадающими вещественными числами содержится целое бесконечное множество рациональных. Кроме того, ещё более очевидно, что между любыми двумя различными рациональными числами содержится вещественное.
Лемма 3. Приближение вещественного числа рациональными, описанное в лемме 1, идентифицирует вещественное число единственным образом.
Эти леммы прежде всего говорят о том, что множество вещественных чисел не такое «плотное» по сравнению с множеством рациональных чисел, как может показаться. Особенно ярко это иллюстрирует лемма 2. Все три леммы активно используются для доказательства различных теорем, связанных с операциями сложения и умножения вещественных чисел.
Изначально вещественные числа были естественным обобщением рациональных, но у них впервые было обнаружено свойство несчётности, которое говорит о том, что множество вещественных чисел нельзя занумеровать, т. е. не существует биекции между множествами вещественных и натуральных чисел. Чтобы показать несчётность всего множества вещественных чисел, достаточно показать несчётность интервала .[18]
Пусть все числа указанного промежутка уже занумерованы некоторым образом. Тогда их можно выписать в следующем виде:
Здесь aij — j-я цифра i-ого числа. Очевидно, что все числа указанного вида действительно принадлежат рассматриваемому промежутку, если только в каждом числе не все цифры сразу являются нулями или девятками.
Далее предлагается рассмотреть следующее число:
Пусть каждая цифра di этого числа удовлетворяет следующим трём свойствам:
Такое число действительно существует на указанном промежутке, так как оно является вещественным, не совпадает ни с нулём, ни с единицей, а десятичных цифр достаточно, чтобы третье свойство выполнялось. Кроме этого, x интересно тем фактом, что оно не совпадает ни с одним из чисел xj, выписанных выше, ведь иначе j-я цифра числа x совпала бы с j-ой цифрой числа xj. Пришли к противоречию, заключающемуся в том, что как бы числа рассматриваемого промежутка ни были занумерованы, всё равно найдётся число из этого же промежутка, которому не присвоен номер.[18]
Это свидетельствует о том, что множество вещественных чисел не является счётным. Его мощность называется мощностью континуума.
Поле вещественных чисел постоянно служило в математике источником обобщений, причём в различных практически важных направлениях. Непосредственно к полю
примыкают следующие варианты обобщённых числовых систем.
Математическая модель вещественных чисел повсеместно применяется в науке и технике для измерения непрерывно меняющихся величин. Однако это не главное её применение, потому что реально измеренные величины всегда имеют конечное число десятичных знаков, то есть являются рациональными числами. Основное назначение этой модели — служить базой для аналитических методов исследования. Огромный успех этих методов за последние три века показал, что модель вещественных чисел в большинстве случаев достаточно адекватно отражает структуру непрерывных физических величин.
Сказанное, конечно, не означает, что вещественная числовая прямая есть точный образ реальной непрерывной величины. Например, современной науке пока не известно, дискретны ли пространство и время или делимы неограниченно; однако даже во втором случае модель вещественных чисел для этих величин должна рассматриваться как приближённая, поскольку понятия точки пространства и момента времени представляют собой идеализации, не имеющие реального аналога. Этот фундаментальный вопрос широко обсуждается в науке, начиная с апорий Зенона. Приближённой эта модель является и в применении к величинам, которые в классической физике рассматривались как непрерывные, но в действительности оказались дискретными (квантуемыми).
Тем, кто интересуется историей становления понятия вещественного числа, можно порекомендовать следующие две книги:
Прекрасное подробное изложение теории построения вещественных чисел с помощью фундаментальных последовательностей, а также теории построения вещественных чисел с помощью сечений в области рациональных чисел можно найти в следующей:
Желающим познакомиться с оригинальным ходом мысли самого Р. Дедекинда можно порекомендовать ту самую брошюру, в которой в 1872 году Дедекинд изложил свою теорию вещественного числа. Эта книжка на сегодняшний день остаётся одним из самых лучших и доступных изложений предмета. Имеется русский перевод:
Также прекрасное изложение теории Дедекинда имеется в классическом учебнике
Построение теории вещественного числа с помощью бесконечных десятичных дробей можно найти в книгах
Аксиоматическое изложение теории вещественного числа можно найти в книгах
Сущность аксиоматического метода и его сравнение с конструктивным подходом изложены Д. Гильбертом на нескольких страницах в Дополнении VI. О понятии числа в следующем издании классической работы
www.wreferat.baza-referat.ru
Рациональных чисел недостаточно для решения ряда задач математики, так и в ее приложениях. Приведем некоторые из этих задач.
1) Во множестве рациональных чисел неразрешима задача измерения величин, даже отрезков. При выбранной единице измерения длины можно указать отрезки, длины которых не могут быть выражены рациональными числами. Еще древнегреческие математики обнаружили, что длину диагонали квадрата, сторона которого равна единице измерения, нельзя выразить рациональным числом. Рассмотрим аналогичную задачу.
Пусть дан прямоугольный треугольник с катетами  и
и  . Найти длину гипотенузы
. Найти длину гипотенузы  . Известно, что
. Известно, что  или
или  . Покажем, что
. Покажем, что  не может быть рациональным числом.
не может быть рациональным числом.  не является целым числом, … т.к.
не является целым числом, … т.к.  , а
, а  , между 2 и 3 нет натуральных чисел. Предположим, что
, между 2 и 3 нет натуральных чисел. Предположим, что  — рациональное число, причем можно считать, дробь несократима. По определению
— рациональное число, причем можно считать, дробь несократима. По определению  или
или  . Правая часть этого равенства делится на 5, т.е.
. Правая часть этого равенства делится на 5, т.е.  или
или  и
и  , где
, где  — натуральное число. Тогда
— натуральное число. Тогда  или
или  ,
,  . Получили, что дробь
. Получили, что дробь  — сократима, что противоречит предположению.
— сократима, что противоречит предположению.
2) В поле  не разрешимы многие даже простейшие уравнения. Докажите, что уравнение
не разрешимы многие даже простейшие уравнения. Докажите, что уравнение  не имеет рациональных корней.
не имеет рациональных корней.
3) В рамках множества рациональных чисел не может быть обоснована теория пределов и другие фундаментальные теории математического анализа, связанные с ней, т.к. существуют сходящиеся последовательности рациональных чисел, пределы которых не являются рациональными числами. Например, рассмотрим представление  в виде бесконечной десятичной дроби,
в виде бесконечной десятичной дроби,  . Эта дробь не может быть периодической, согласно сказанному выше. Составим последовательность десятичных приближений по недостатку:
. Эта дробь не может быть периодической, согласно сказанному выше. Составим последовательность десятичных приближений по недостатку:  . Очевидно, что
. Очевидно, что  , т.е. эта последовательность рациональных чисел является сходящейся, но предел ее не содержится во множестве
, т.е. эта последовательность рациональных чисел является сходящейся, но предел ее не содержится во множестве  .
.
Эти и другие задачи приводят к заключению о необходимости расширения множества рациональных чисел. Таковым расширением является множество действительных (вещественных) чисел.
Начиная с XV и XVI вв. в связи с задачами нахождения корней алгебраических уравнений, математикам все чаще и чаще приходилось иметь дело с выражениями, полученными из исходных чисел не только с помощью арифметических операций, но и операции извлечения корней. А, по существу, это уже означало введение в математику, хотя и отчетливо неосознанное, иррациональных чисел. Природа иррациональных чисел отчетливо не была понятна еще и в XVIII в.
Только во второй половине XIX в. была четко осознана необходимость логического обоснования системы действительных чисел.
Логически обоснованное построение системы действительных чисел  было осуществлено немецкими математиками Р. Дедекиндом (1831-1916), Г. Кантором (1845-1916), В. Вейерштрассом (1815-1897) и французским математиком Ш. Мере (1835-1911), при этом они опирались на разные исходные понятия. Построенные ими теории оказались эквивалентными.
было осуществлено немецкими математиками Р. Дедекиндом (1831-1916), Г. Кантором (1845-1916), В. Вейерштрассом (1815-1897) и французским математиком Ш. Мере (1835-1911), при этом они опирались на разные исходные понятия. Построенные ими теории оказались эквивалентными.
Более полно одно из построений системы  будет рассмотрено в курсе «Числовые системы».
будет рассмотрено в курсе «Числовые системы».
Мы рассмотрим вкратце упрощенный вариант построения системы действительных чисел, предложенный Вейерштрассом, придерживаясь в общих чертах изложения этого вопроса в школьном курсе математики.
О. Любую непериодическую бесконечную десятичную дробь называют представлением некоторого иррационального числа или просто иррациональным числом.
Отметим, что кроме иррациональных чисел вида  , где
, где  и
и  — натуральные числа, причем
— натуральные числа, причем  больше 1,
больше 1,  не является
не является  -ой степенью никакого другого натурального числа, существуют и другие бесконечные непериодические дроби.
-ой степенью никакого другого натурального числа, существуют и другие бесконечные непериодические дроби.
Рассмотрим, например, бесконечную десятичную дробь  , покажем, что она непериодическая. Предположим, что эта дробь периодическая и длина периода равна
, покажем, что она непериодическая. Предположим, что эта дробь периодическая и длина периода равна  . Тогда период должен содержать хотя бы одну цифру три, поэтому в записи этого числа не может подряд стоять больше
. Тогда период должен содержать хотя бы одну цифру три, поэтому в записи этого числа не может подряд стоять больше  -1 двоек, а это противоречит тому, что, начиная с некоторого момента, найдутся участки, содержащие
-1 двоек, а это противоречит тому, что, начиная с некоторого момента, найдутся участки, содержащие  и более
и более  двоек. Следовательно,
двоек. Следовательно,  является иррациональным числом.
является иррациональным числом.
Подобного вида непериодических десятичных дробей можно построить бесконечное множество.
Упр. 28. Докажите, что бесконечная дробь 0,232233222333… непериодическая.
Присоединив к множеству рациональных чисел иррациональные числа, получим множество действительных чисел  . Так как любое рациональное число можно отождествить с периодической десятичной дробью (без девятки в периоде), то можно дать единое определение действительному числу.
. Так как любое рациональное число можно отождествить с периодической десятичной дробью (без девятки в периоде), то можно дать единое определение действительному числу.
О. Действительное число – это есть бесконечная десятичная дробь.
| | | следующая страница ==> | |
| Обращение периодических десятичных дробей в обыкновенные | | | Арифметические операции на множестве действительных чисел |
Дата добавления: 2014-03-11; просмотров: 50; Нарушение авторских прав
Поделиться с ДРУЗЬЯМИ:refac.ru
СОДЕРЖАНИЕ.
Введение………………………………………………………………………...2
Глава 1. Зарождение и развитие понятия числа……………………………...3
1.1.Числовые системы и история их появления………………………………4
1.2 История появления дробных чисел………………………………………..6
1.3 Предпосылки зарождения «действительных чисел»……………………..8
1.4 Парадоксы……………………………………………………………………9
1.5 Теория предела………………………………………………………………11
Глава 2. Создание теории действительного числа…………………………….15
2.1 Карл Вейерштрасс…………………………………………………………...15
2.2 Георг Кантор…………………………………………………………………18
Глава 3. Действительные числа…………………………………………………21
3.1 Бесконечные десятичные дроби…………………………………………….21
3.2 Определение иррациональности числа……………………………………..23
Заключение………………………………………………………………………..25
Список литературы……………………………………………………………….26
Введение.
Темой данной курсовой работы является раскрытие и донесение понятия «Действительные числа», а так же их роль в математическом анализе.
В первой главе рассматриваются вопросы, связанные с понятием «Числа», его историей и путями развития.
Понятия числа являются первичным и основным в математике. Это понятие прошло длительный путь исторического развития.
Множество натуральных чисел появилось в связи со счетом предметов. Затем под влиянием потребностей практики и развития самой математики были введены целые числа и рациональные числа где.
Для однозначности записи рационального числа будем считать, что дробь не сократима, если не будет делаться оговорки на этот счет.
Вторая и третья главы реферата посвящены теории действительных чисел и математических моделей их применения.
Действительные числа. Приближение действительных чисел конечными десятичными дробями.
Вещественное, или действительное число - математическая абстракция, возникшая из потребности человека в измерении геометрических и физических величин окружающего материального мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений [2, стр. 28] . Если «Натуральные числа» возникли в процессе счета, «Рациональные числа» возникли - из потребности оперировать частями целого, то «Вещественные числа» - предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.
Глава 1. Зарождение и развитие понятия числа
В основе математики лежит понятие числа, одно из самых ранних и самых абстрактных. Оно возникло как обобщение счета отдельных предметов. Счет присущ не только человеку, но и, в некоторой форме, и животным, например кошке, которая чувствует наличие при себе всех своих котят.
Наиболее ранняя форма счета носит конкретно-чувственный характер. Такой счет можно обнаружить у первобытных людей и у животных. Однако нельзя с уверенностью сказать, что только человек способен к абстрактному счету. Есть данные о способности приматов к символизации счета «Приматы способны распознавать и обобщать признак «число элементов», устанавливать соответствие между этим отвлеченным признаком и ранее нейтральными для них стимулами — арабскими цифрами. Оперируя цифрами как символами, они способны ранжировать множества и упорядочивать их по признаку «число», а также совершать число действий, соответствующее цифре. Наконец, они способны к выполнению операций, изоморфных сложению, но этот вопрос требует более точных исследований.»[12]. Там же отмечается высокая способность к символизации и обобщении по признаку «количества» у врановых.
Переход от «чувственного счета» к абстрактному осуществляется при помощи взаимооднозначного соответствия между двумя множествами, одно из которых позже принимается как бы за эталон. Взаимооднозначное соответствие по началу носит также конкретно-чувственный характер(например, расположение элементов друг напротив друга). Таким способом пользуются даже современные люди, когда считают что-либо загибая пальцы. Считается, что именно счет на пальцах лежит в основе десятичной системы исчисления, принятой у европейских народов [10, стр. 11]. На этом этапе обобщения появляется знаковое обозначение числа. Первоначально это были зарубки на дереве, костях, узелки на веревках, количество которых совпадало со значением числа. Конкретно-чувственное происхождение чисел находит свое отражение в языке. «Вначале счет производился с помощью подручных средств:пальцев камней, еловых шишек и т.д. Следы этого сохранились в названии математических счислений: calculus, которое имеет латинское происхождение и означает: счет камешками»[11, стр. 17]. С развитием культуры и общества появляется потребность в использовании более больших чисел, так появляются разнообразные числовые системы.
1.1. Числовые системы и история их появления
Современная десятичная система появилась в результате развития древних систем счисления. К системам счисления предшествующим десятичной относятся:
Иероглифические непозиционные системы. К ней относится Римская система. В ней числа формируется из набора узловых чисел обозначенных иероглифами. Число образуется из этого набора путем дописывания справа или слева узлового числа других узловых чисел. Значения числа вычисляется по аддитивному или субстрактивному принципу.
Алфавитные системы счисления. Здесь числа записываются при помощи букв. Чтобы отличить буквы от чисел, каждой букве приписывается отличительный признак. Буквы используемые для записи чисел берутся в группы по 9 штук. Для записи единиц десятков и сотен используются разные группы букв, что существенно осложняет ее использование.
Почти одновременно со счетом зарождаются математические операции сложения и вычитания(когда уменьшаемое больше вычитаемого). Позже появляется умножение, как повторное сложение. Деление появляется значительно позже, чем умножение, хотя представления о простых дробях () появляется сравнительно рано. Понятие о натуральных числах, как о бесконечном наборе чисел, возникло не сразу. Представления о неисчислимо больших числах сохранились в языке, например в русском словами «тьма», «много». Наиболее отчетливое представление о безграничном продолжении ряда натуральных чисел обнаружено у греческих математиков. В XII-VII веках до н.э. (времена Гомера) самым большим числом было мириада (1000), которое позже стала обозначать 10000. В III в до н.э. Архимед в своем труде «Исчиление песчинок» опроверг возможность построить сколь угодно большое число.
Однако даже в математике Древней Греции не было единого представления о том, что такое число. Так в школе Пифагора и Платона считали единицу не числом, а «эмбрионом числа». Стоит отметить, что мифологическое сознание древнегреческого общества еще не до конца воспринимало математические и философские абстракции. «Наименее доступны пониманию широких кругов были именно числа, эти наиболее абстрактные элементы науки того времени»[7, стр. 83]. По этим и другим причинам математика, ее методы и результаты выглядели мистически. Наиболее развитым и философски обоснованным мистическим взглядом на числа были пифагорейство и неопифагорейство. Упрощая, можно сказать, что пифагореизм в основе гармонии мира видел число, для пифагореизма все числа имели мистический смысл. Подобные взгляды можно встретить и сегодня. Однако следует признать, что проникновение в философию понятий математики чаще всего было плодотворным. В качестве примера можно привести категорию «Количество» в философии Канта и в диалектической логике, а также парадоксы теории множеств.
Первоначально понятие нуля возникло в качестве обозначения нулевого разряда в записи чисел. Первое достоверное использование нуля обнаружено в Индии и относится к IX веку. Однако точное происхождение цифры ноль в позиционных системах не известно. «Одни исследователи(Г. Фреуденталь) предполагают, что нуль был заимствован у греков...Другие(Дж. Нидэм), наоборот, считают, что нуль пришел в Индию с востока»[10, стр. 183]. В Индии наиболее ясно и полно исследовали вопрос о применимости к 0 арифметических операций, математиком Бхаскара даже исследовался вопрос о делении на на 0.
Также в индийской математике было наиболее отчетливое представление об отрицательных числах. «Индийские математики, начиная с Брахмагунты(VII в.н.э.), систематически пользовались отрицательными числами и трактовали положительное число как имущество, а отрицательное как долг»[10, стр. 190], хотя мы не можем утверждать, что отрицательные числа впервые появились в Индии. Было установлено, что квадрат отрицательного числа — число положительное, также ставились вопросы о наличии квадратного корня из отрицательного числа. Действиям с отрицательными числами посвящена целая глава в произведении Бхаскары «Виджаганита».
Менее ясные представления об отрицательных числах были и у китайцев. Их появление было связано с задачами, которые сегодня называются системы линейных уравнений. «Так как все вычисления, в том числе и преобразования матрицы, производились на счетной доске, то для обозначения отрицательных чисел применялись счетные палочки другого цвета или формы, а в случае записи применялись иероглифы разных цветов»[11, стр.84]. Юшкевич высказывает предположение о том, что представление об отрицательных числах имел Диофант [10, стр. 145].
Интерпретация отрицательного числа как «долга» у индусов переняли арабы, использование отрицательных чисел встречается в работах арабского математика Абу-л-Вафы. Считается, что термин долг был заимствован математиком Средневековья Леонардо Пизанским(ок. 1170-после 1250, известен как Фибоначчи) у арабов. Кроме «долга» существовал термин «меньше, чем ничто». Зачатки геометрической интерпретации отрицательных чисел появляется в работе М. Штифеля «Полная арифметика», но только после работ Ферма и Декарта отношение к отрицательным числам кардинально изменилось. Применение отрицательных чисел и нуля сыграло важную роль в математике, позволило обобщить многие задачи, упростить некоторые вычисления и формализовать многие алгоритмы.
1.2 История появления дробных чисел
Как было отмечено ранее, дроби появились намного раньше чем целые числа () и даже раньше чем операция деления. Они возникли из потребности делить целое на части, а также выражать величину через ее части. Дроби вида называемые долями известны человечеству со времен зарождения математического знания. Так египтяне имели обозначения для дробей вида (единичные), а также для , однако если им встречались дроби другого вида, они раскладывали их на сумму единичных дробей. Единичные дроби использовались на ранних этапах греками и шумерами. Дроби общего вида появляются в Греции, хотя изначально не принимаются как числа. Греки впервые построили, по нашим понятиям группу положительных рациональных чисел. «Только в Греции начали оперировать с дробями вида , причем умели производить с ними все действия арифметики с тем ограничением, что вычитать можно было из большего меньшее»[10, стр. 71].
Дроби также были издавна известны в Индии, упоминания о таких дробях как относятся к середине II тысячелетия до н.э. Причем индийцы записывали их способом, напоминающий современный: числитель над знаменателем, но без разделительной черты. Также указывались правила обращения с такими объектами, аналогичные современным правилам обращения с дробями.
Несколько слов стоит сказать о происхождении десятичных дробей. Прообразом для десятичных дробей послужили шестидесятиричные дроби, используемые вавилонянами. Она напоминала современный способ записи дробей тем, что позволяла записывать целю и дробную часть однотипно, что значительно упрощало вычисления. Постепенно, возникают догадки,что это удобство не связано с какими-то особенными свойствами число 60. «Зреет мысль о том, что в основу системы таких дробей может быть положено и другое число...Понимание этой мысли можно видеть уже в учебнике арифметики середины XII в., приписываемом Иоанну Севильскому. Иордан Немораррий(XIII в.) дает даже специальное название таким систематическим дробям, аналогичным шестидесятеричным»[6, стр. 240]. Идея десятичных дробей использовалась некоторыми математиками, но до XIV века строгого их построения не было. В середине XIV в. французский математик Бонфис сделал попытку развить идею десятичного числа. Однако его работа носила эскизный характер и не была опубликована.
В первой половине XV теорию десятичного числа построил самаркандский математик Джемшид Гиясэддином ал-Каши. Он описал десятичную записи числа и описал правила обращения с десятичными дробями. Однако работы ал-Каши оставались неизвестными вплоть до середины XX века.
В Европе десятичные дроби появились благодаря инженеру Симону Стевину(1548-1620). Он объединил отдельные идеи и представления о десятичных дробях и пламенно их пропагандировал. Большой интерес матетиков вызвали периодические дроби. Они были впервые обнаружены арабским матетиком ал-Марадини в XV в. В Европе вопрос о периодических дробях был серьезно рассмотрен Валлисом в 1676 в трактате по алгебре. Вопросами периодических дробей занимались также Лейбниц, Ламберт, Эйлер, Бернулли, Гаусс и др.
1.3 Предпосылки зарождения «действительных чисел»
Как видно из предыдущего исторического экскурса, твердого понимания что такое число долгое время не было. С точки зрения древних греков, числом было только натуральное число большее единицы. Несколько более прогрессивная система счисления была у вавлонян, использущих шестидесятиричные дроби. Вавилоняне знали теорему Пифагора и сталкивались с проблемой извлечения корней из чисел не имеющих точного квадрата. Однако, нет данных о том, рассматривали ли они этот вопрос теоретически. «Обладание подобной [шестидесятиричной] системой и вытекающая отсюда уверенность в числовых расчетах неизбежно приводили к «наивному» понятию действительного числа, почти совпадающему с тем, которое в наши дни можно встретить в элементарных учебниках математики (связанное с десятичной системой счисления) или у физиков и инженеров. Это понятие не поддается точному определению, но его можно выразить, сказав, что число рассматривается как определенное благодаря возможности получать его приближенные значения и вводить их в вычисления.»[2, стр. 146].
myunivercity.ru
Положим что у нас есть рациональные числа. Возьмем множество рациональных такое, что его сумма любого конечного числа элементов не превосходит заданных границ. Если мы будем теперь составлять из этих чисел сумму, то если сумма будет конечной. Таким образом, конечная сумма этих чисел будет представлять рациональное число, мы можем сопоставить любому рациональному числу некоторый конечный набор из некоторого множества . С иррациональным числом этот набор будет бесконечным. Далее, возьмем два бесконечных набора. Будем считать что рациональные числа представлены несократимыми дробями. Рассмотрим набор чисел натуральных чисел . Если для сумма дробей вида из первого множества совпадает с суммой таких же дробей из второго множества, то иррациональные числа совпадают друг с другом. Рассмотрим первый номер для которого это равенство не выполняется. Если для имеет место равенство , где суммы составлены по таким рациональным числам, которые имеют вид , то первое число больше второго. Если имеется обратное неравенство, то второе число больше первого. Сложение чисел определяется операцией объединения множеств. Вычитание определяется как операция обратная сложению. Составление агрегата вида , где умножение составляется по всевозможным элементам, определяет умножение.
Таким образом, Вейерштрасс построил вещественное число. Стоит отметить, что он не приравнивает число к ряду, тем самым избегает логической ошибки своих предшественников. Из этого построения видно, что оно определяет взаимооднозначное соответствие: с одной стороны из рационального чисел можно построить вещественной число, с другой каждое вещественной число можно определить некоторым построением из вещественных чисел. Кроме того, оно использует актуально бесконечные множества.
Стоит еще раз подчеркнуть, что Вейерштрасс в своем определении вещественного числа исходит только из арифметики, не связывая их с точками на прямой.
Построение вещественных чисел позволило перейти от механического, геометрического понятия предела к теоретико-множественному. Также при помощи строго определения понятия числа Вейерштрасс развил теорию аналитических функций. Также в работах Вейерштрасса встречается прообраз того, что мы называем мощностью множеств.
2.2 Георг Кантор
Родился 3 марта 1845 в Санкт-Петербурге и рос там до 11-летнего возраста. Отец семейства был членом Петербургской фондовой биржи. Когда он заболел, семья, рассчитывая на более мягкий климат, в 1856 году переехала в Германию: сначала в Висбаден, а потом во Франкфурт. В 1860 году Георг закончил с отличием реальное училище в Дармштадте; учителя отмечали его исключительные способности к математике, в частности, к тригонометрии. Продолжил он образование в Федеральном политехнический институте в Цюрихе. Спустя год, после смерти отца, Георг получил наследство и перевёлся в Берлинский университет. Там он посещает посещает лекции Кронекера, Вейерштрасса, Куммера. Лето 1866 года Кантор провёл в университете Гёттингена, важном центре математической мысли. В 1967 году в Берлине получил степень доктора за работу по теории чисел «De aequationibus secundi gradus indeterminatis».
После непродолжительной работы преподавателем в Берлинской школе для девочек, Кантор занимает место в Галльском университете Мартина Лютера, где и пройдёт вся его карьера. В 1872 году он становится адъюнкт-профессором, тогда же, во время отпуска, завязывает дружбу с Рихардом Дедекиндом. В 34 года Кантор становится профессором математики. В 1879-84 он систематически излагает своё учение о бесконечности; «ввёл понятия предельной точки, производного множества, построил пример совершенного множества, развил одну из теорий иррациональных чисел, сформулировал одну из аксиом непрерывности» [8]. Несмотря на такую успешную карьеру, мечтает о должности в более престижном университете, например, Берлинском. Однако, мечтам не удаётся воплотиться в жизнь: многие современники, в том числе Кронекер, который рассматривается сейчас как один из основателей конструктивной математики, с неприязнью относятся к канторовской теории множеств, поскольку та утверждает существование множеств, удовлетворяющих неким свойствам, — без предоставления конкретных примеров множеств, элементы которых бы действительно удовлетворяли этим свойствам.
В 1984 году Кантор испытал приступ глубокой депрессии и на время отходит от математики, смещая свои интересы в сторону философии. Затем возвращается к работе. В 1897 году он прекращает научное творчество. Умер Кантор в Галле 6 января 1918.
Одна из актуальных проблем XIX века была проблема бесконечного деления отрезков и существование точки , принадлежавшей всем таким стягивающимся отрезкам. Эта задача требовала понятия действительного числа.
Построение Кантором теории действительного числа было опубликовано 1872 году, почти одновременно с теорией Вейерштрасса и Дедекинда. В своем построении Кантор исходит из наличия рациональных чисел. Затем он вводит фундаментальные последовательности Коши и приписывает им формальный предел. Далее, он рассматривает разбивает все последовательности на классы эквивалентности. К одному и тому же классу последовательности относятся тогда и только тогда, когда их разность стремится к нуль, то есть . Далее, формальные пределы равны друг другу, если они имеют две такие фундаментальные последовательности, которые эквивалентны друг другу или . Отношение порядка определяется следующим образом.
Если и то . Если то .
Таким образом, классы эквивалентности описывают некоторые вещественные числа. Назовем их вещественными числами первого порядка. Если мы попробуем образовать вещественное число большего порядка, составляя фундаментальные последовательности Коши, то получим опять множество вещественных чисел первого порядка. Иными словами, множество вещественных чисел замкнуто.
Кантор обращает внимание тот факт, что в определении вещественного числа лежит актуально бесконечное множество рациональных чисел: «...к определению какого-нибудь иррационального числа всегда принадлежит некоторое строго определенное множество первой мощность рациональных чисел».
Заметим, что построение Кантора можно обобщить на другие объекты, что была сделано Кантором и его последователями, «разработка теорий действительного числа была достаточно существенной предпосылкой создания теории множеств»[4, стр. 63]. Например, на основе своего построения вещественного числа Кантор впоследствии свою теорию трансфинитных чисел.
Кроме того, Кантор ввел понятие мощности множеств и доказал неэквивалентность иррациональных и рациональных чисел.
Глава 3. Действительные числа
Как уже говорилось в введении: понятия числа являются первичным и основным в математике. Это понятие прошло длительный путь исторического развития. Множество натуральных чисел появилось в связи со счетом предметов. Затем под влиянием потребностей практики и развития самой математики были введены целые числа и рациональные числа где .
Для однозначности записи рационального числа будем считать, что дробь не сократима, если не будет делаться оговорки на этот счет.
Введение рациональных чисел, однако, полностью не решило важной практической задачи об измерении отрезков. Ведь существует отрезок, длина которого не является рациональным числом. Примером может служить диагональ квадрата, сторона которого равна единице.
В связи с этим возникла необходимость введения, кроме рациональных чисел, и других чисел – иррациональных. Произвольные числа – рациональные или иррациональные - называются действительными или вещественными. Множество действительных чисел обозначают через . Существуют различные способы введения (определения) действительных чисел.
3.1 Бесконечные десятичные дроби
Мы остановимся на способе представления их в виде бесконечных десятичных дробей . (1)
Здесь - целое неотрицательное число, при - десятичные цифры. Таким образом, может принимать только одно из значений . Знак часто в этих записях опускают.
Чтобы представить не равное нулю рациональное число в виде десятичной дроби, производим процесс деления на по известному способу, которому нас учили в школе: (2)
Заметим, что если этот способ применить к другой записи дроби , то получим тот же результат.
Полагаем (3) и правую часть (3) называем десятичным разложением числа .
Если знаменатель дроби имеет вид , где , - целые неотрицательные числа, то процесс (2) заканчивается после конечного числа шагов и получается конечная десятичная дробь (4)
Конечную десятичную дробь мы будем записывать также в виде бесконечной дроби: (5)
Итак, имеют место равенства
Дроби и могут служить примерами периодических дробей. Первая из них после цифры имеет период 0, а вторая после цифры имеет период 9.
Пусть теперь знаменатель несократимой дроби не имеет вид . Тогда процесс (2) бесконечный – на любом шаге возникает положительный остаток. Каждый остаток меньше , и потому (после того, как цифры числа снесены) уже среди первых остатков, по крайней мере, два, равные между собой. Но, как только возникает остаток, который уже был прежде, процесс становится повторяющимся – периодическим. Поэтому, десятичное разложение произвольного рационального числа имеет вид (6)
Разложения (5) и (5´) можно рассматривать как частные случаи (6).
Примеры: (7)
Разложение вида (6) называется бесконечной десятичной периодической дробью.
Итак, каждое не равное нулю рациональное число можно разложить с помощью процесса (2), а в случае (4) и процесса (5) – в бесконечную периодическую дробь с периодом, отличным от 9. При этом можно доказать, что разным рациональным числам соответствуют разные бесконечные десятичные разложения. Но и обратно: любая бесконечная периодическая дробь (6), с периодом, отличным от 9, порождается при помощи указанных процессов (2), (5) некоторым рациональным числом, которое вычисляется по формуле.
Кроме периодических десятичных дробей, существуют непериодические, например: если извлекать корень квадратный из 2 по известному правилу, то получим определенную бесконечную непериодическую десятичную дробь . Она определена в том смысле, что любому натуральному числу соответствует определенная цифра , стоящая на -м месте после запятой и однозначно вычисляемая согласно правилу извлечения квадратного корня.
Математический анализ дает много путей вычисления числа с любой наперед заданной точностью. Это приводит к вполне определенному бесконечному десятичному разложению , которое, как оказывается, не является смешенной периодической десятичной дробью.
3.2 Определение иррациональности числа.
Дадим теперь определение иррационального числа, пока чисто формальное. Иррациональным числом называется произвольная бесконечная непериодическая дробь (8) где - целое неотрицательное число, а - цифры, знак же равенства «=» выражает, что мы обозначили правую часть (8) через . Впрочем, удобно говорить, что правая часть (8) есть десятичное разложение числа .
Рациональные и иррациональные числа называются действительными (или вещественными) числами.
Из сказанного следует, что всякое не равное нулю действительное число может быть записано в виде бесконечной десятичной дроби (8). Если оно рациональное, то его десятичное разложение есть бесконечная периодическая десятичная дробь. В противном случае, согласно нашему определению, выражение (8) само определяет иррациональное число.
Не равная нулю десятичная дробь может быть конечной, но она не определяет нового рационального числа: в силу соглашений, выраженных равенствами (5), (5´), она может быть заменена указанными в этих равенствах бесконечными периодическими дробями.
Число , где не все равны нулю, положительно или отрицательно в зависимости от того, будет ли в (8) фигурировать или ; при этом, как обычно, будем опускать.
Число 0 тоже может быть записано бесконечной десятичной дробью одного из следующих видов:
Действительные числа определены пока формально, надо еще определить арифметические операции над ними, ввести понятие и проверить, что эти операции и понятие согласуются с уже имеющимися соответствующими операциями и понятием для рациональных чисел, а также удовлетворяют свойствам, которые мы предъявляем к числам.
Заключение
Новые воззрения в математическом анализе не приживались гладко. Жестко критиковал учение Вейерштрасса, например, Кронекер. Критику Кантора можно уверенно сравнить с травлей. Но время доказало правильность выбранного курса. Привычный нам вид математического здания во многом был построен благодаря таким ученным как Вейерштрасс, Кантор и Дедекинд.
Построение вещественного числа завершило постройку фундамента для математического анализа. Вопрос аксиоматического построения анализа был практически завершен: все, что оставалось сделать - это построить аксиоматику целых и рациональных чисел. Эта задача была завершена Ж. Пеано в 1889 году. Однако, построение вещественного числа не является узкоспециальным вопросом математики, как, например, Великая теорема ферма. Благодаря работам Вейерштрасса, Кантора и Дедекинда в обращение вошли актуально бесконечные объекты: вещественное число, стало фактически первым таким объектом. Строгие построения основанные на аксиоматике, способствовали переходу математиков от «чувственного», «интуитивного» к абстрактному и строгому. Обобщенные методы построения вещественного числа стали впоследствии основой для теории множеств, функционального анализа, интеграла Лебега. Так что с уверенностью можно сказать, что ни один человек не может стать математиком, не зная работ трех великих творцов математики XIX века.
Список литературы
myunivercity.ru
Главная » Рефераты » Текст работы «Зарождение и создание теории действительного числа - Математика»
Зарождение и создание теории действительного числа
Содержание
1. Зарождение и развитие понятия числа
2. Проблема несоизмеримых или Первый кризис в основании математики
2.1 Следствия ᴨȇрвого кризиса и попытки его преодоления
3. Становление теории предела
4. Создание теории действительного числа
4.1 Карл Вейерштрасс
4.2 Георг Кантор
4.3 Рихард Дедекинд
- З а к л ю ч е н и е -
1 Зарождение и развитие понятия числа
В основе математики лежит понятие числа, одно из самых ранних и самых абстрактных. Оно возникло как обобщение счета отдельных предметов. Счет присущ не только человеку, но и, в некоторой форме, и животным, например кошке, которая чувствует наличие при себе всех своих котят.
Наиболее ранняя форма счета носит конкретно-чувственный характер. Такой счет можно обнаружить у ᴨȇрвобытных людей и у животных. Однако нельзя с уверенностью сказать, что только человек способен к абстрактному счету. Есть данные о способности приматов к символизации счета «Приматы способны распознавать и обобщать признак «число элементов», устанавливать соответствие между этим отвлеченным признаком и ранее нейтральными для них стимулами -- арабскими цифрами. Оᴨȇрируя цифрами как символами, они способны ранжировать множества и упорядочивать их по признаку «число», а также совершать число действий, соответствующее цифре. Наконец, они способны к выполнению оᴨȇраций, изоморфных сложению, но этот самый вопрос требует более точных исследований.»[12]. Там же отмечается высокая способность к символизации и обобщении по признаку «количества» у врановых.
Переход от «чувственного счета» к абстрактному осуществляется при помощи взаимооднозначного соответствия между двумя множествами, одно из котоҏыҳ позже принимается как бы за эталон. Взаимооднозначное соответствие по началу носит также конкретно-чувственный характер(например, расположение элементов друг напротив друга). Таким способом пользуются даже современные люди, когда считают что-либо загибая пальцы. Считается, что именно счет на пальцах лежит в основе десятичной системы исчисления, принятой у евроᴨȇйских народов [10, стр. 11]. На этом этаᴨȇ обобщения появляется знаковое обозначение числа. Первоначально это были зарубки на дереве, костях, узелки на веревках, количество котоҏыҳ совпадало со значением числа. Конкретно-чувственное происхождение чисел находит свое отражение в языке. «Вначале счет производился с помощью подручных средств:пальцев камней, еловых шишек и т.д. Следы этого сохранились в названии математических счислений: calculus, которое имеет латинское происхождение и означает: счет камешками»[11, стр. 17]. С развитием культуры и общества появляется потребность в использовании более больших чисел, так появляются разнообразные числовые системы. Современная десятичная система появилась в результате развития древних систем счисления. К системам счисления предшествующим десятичной относятся:
* Иероглифические непозиционные системы. К ней относится Римская система. В ней числа формируется из набора узловых чисел обозначенных иероглифами. Число образуется из этого набора путем дописывания справа или слева узлового числа других узловых чисел. Значения числа вычисляется по аддитивному или субстрактивному принципу.
* Алфавитные системы счисления. Здесь числа записываются при помощи букв. Чтобы отличить буквы от чисел, каждой букве приписывается отличительный признак. Буквы используемые для записи чисел берутся в группы по 9 штук. Для записи единиц десятков и сотен используются разные группы букв, что существенно осложняет ее использование.
* Позиционные недесятичные системы счисления.
Почти одновременно со счетом зарождаются математические оᴨȇрации сложения и вычитания(когда уменьшаемое больше вычитаемого). Позже появляется умножение, как повторное сложение. Деление появляется значительно позже, чем умножение, хотя представления о простых дробях () появляется сравнительно рано. Понятие о натуральных числах, как о бесконечном наборе чисел, возникло не сразу. Представления о неисчислимо больших числах сохранились в языке, например в русском словами «тьма», «много». Наиболее отчетливое представление о безграничном продолжении ряда натуральных чисел обнаружено у греческих математиков. В XII-VII веках до н.э. (времена Гомера) самым большим числом было мириада (1000), которое позже стала обозначать 10000. В III в до н.э. Архимед в своем труде «Исчиление ᴨȇсчинок» опроверг возможность построить сколь угодно большое число.
Однако даже в математике Древней Греции не было единого представления о том, что такое число. Так в школе Пифагора и Платона считали единицу не числом, а «эмбрионом числа». Стоит отметить, что мифологическое сознание древнегреческого общества еще не до конца воспринимало математические и философские абстракции. «Наименее доступны пониманию широких кругов были именно числа, эти наиболее абстрактные элементы науки того времени»[7, стр. 83]. По этим и другим причинам математика, ее методы и результаты выглядели мистически. Перед Вами учебный материал, опубликованный на сайте реф.рфНаиболее развитым и философски обоснованным мистическим взглядом на числа были пифагорейство и неопифагорейство. Упрощая, можно сказать, что пифагореизм в основе гармонии мира видел число, для пифагореизма все числа имели мистический смысл. Подобные взгляды можно встретить и сегодня. Однако следует признать, что проникновение в философию понятий математики чаще всего было плодотворным. В качестве примера можно привести категорию «Количество» в философии Канта и в диалектической логике, а также парадоксы теории множеств.
Хотя аксиоматически сначала строится множество натуральных чисел, потом целые числа, а потом уже рациональные, исторически рациональные числа появились раньше отрицательных чисел и нуля.
Первоначально понятие нуля возникло в качестве обозначения нулевого разряда в записи чисел. Первое достоверное использование нуля обнаружено в Индии и относится к IX веку. Однако точное происхождение цифры ноль в позиционных системах не известно. «Одни исследователи(Г. Фреуденталь) предполагают, что нуль был заимствован у греков...Другие(Дж. Нидэм), наоборот, считают, что нуль пришел в Индию с востока»[10, стр. 183]. В Индии наиболее ясно и полно исследовали вопрос о применимости к 0 арифметических оᴨȇраций, математиком Бхаскара даже исследовался вопрос о делении на на 0.
Также в индийской математике было наиболее отчетливое представление об отрицательных числах. «Индийские математики, начиная с Брахмагунты(VII в.н.э.), систематически пользовались отрицательными числами и трактовали положительное число как имущество, а отрицательное как долг»[10, стр. 190], хотя мы не можем утверждать, что отрицательные числа вᴨȇрвые появились в Индии. Было установлено, что квадрат отрицательного числа -- число положительное, также ставились вопросы о наличии квадратного корня из отрицательного числа. Действиям с отрицательными числами посвящена целая глава в произведении Бхаскары «Виджаганита».
Менее ясные представления об отрицательных числах были и у китайцев. Их появление было связано с задачами, которые сегодня называются системы линейных уравнений. «Так как все вычисления, в том числе и преобразования матрицы, производились на счетной доске, то для обозначения отрицательных чисел применялись счетные палочки другого цвета или формы, а в случае записи применялись иероглифы разных цветов»[11, стр.84]. Юшкевич высказывает предположение о том, что представление об отрицательных числах имел Диофант [10, стр. 145].
Хотя идея ввести обозначение для «ничего» возникла в математике достаточно давно, но как число нуль долгое время не воспринимался. Тем более полноправными числами не воспринимались отрицательные числа, мысль о том, что есть что-то меньше чем «ничто» многим казалась абсурдной. «...еще Кардано называет отрицательные числа «фиктивными» [10, стр. 315].
Интерпретация отрицательного числа как «долга» у индусов ᴨȇреняли арабы, использование отрицательных чисел встречается в работах арабского математика Абу-л-Вафы. Считается, что термин долг был заимствован математиком Средневековья Леонардо Пизанским(ок. 1170-после 1250, известен как Фибоначчи) у арабов. Кроме «долга» существовал термин «меньше, чем ничто». Зачатки геометрической интерпретации отрицательных чисел появляется в работе М. Штифеля «Полная арифметика», но только после работ Ферма и Декарта отношение к отрицательным числам кардинально изменилось. Применение отрицательных чисел и нуля сыграло важную роль в математике, позволило обобщить многие задачи, упростить некоторые вычисления и формализовать многие алгоритмы.
Как было отмечено ранее, дроби появились намного раньше чем целые числа () и даже раньше чем оᴨȇрация деления. Они возникли из потребности делить целое на части, а также выражать величину через ее части. Дроби вида называемые долями известны человечеству со времен зарождения математического знания. Так египтяне имели обозначения для дробей вида (единичные), а также для , однако если им встречались дроби другого вида, они раскладывали их на сумму единичных дробей. Единичные дроби использовались на ранних этапах греками и шумерами. Дроби общего вида появляются в Греции, хотя изначально не принимаются как числа. Греки вᴨȇрвые построили, по нашим понятиям группу положительных рациональных чисел. «Только в Греции начали оᴨȇрировать с дробями вида , причем умели производить с ними все действия арифметики с тем ограничением, что вычитать можно было из большего меньшее»[10, стр. 71].
Дроби также были издавна известны в Индии, упоминания о таких дробях как относятся к середине II тысячелетия до н.э. Причем индийцы записывали их способом, напоминающий современный: числитель над знаменателем, но без разделительной черты. Также указывались правила обращения с такими объектами, аналогичные современным правилам обращения с дробями.
Несколько слов стоит сказать о происхождении десятичных дробей. Прообразом для десятичных дробей послужили шестидесятиричные дроби, используемые вавилонянами. Она напоминала современный способ записи дробей тем, что позволяла записывать целю и дробную часть однотипно, что значительно упрощало вычисления. Постеᴨȇнно, возникают догадки,что это удобство не связано с какими-то особенными свойствами число 60. «Зреет мысль о том, что в основу системы таких дробей может быть положено и другое число...Понимание этой мысли можно видеть уже в учебнике арифметики середины XII в., приписываемом Иоанну Севильскому. Иордан Немораррий(XIII в.) дает даже сᴨȇциальное название таким систематическим дробям, аналогичным шестидесятеричным»[6, стр. 240]. Идея десятичных дробей использовалась некоторыми математиками, но до XIV века строгого их построения не было. В середине XIV в. французский математик Бонфис сделал попытку развить идею десятичного числа. Однако его работа носила эскизный характер и не была опубликована.
В ᴨȇрвой половине XV теорию десятичного числа построил самаркандский математик Джемшид Гиясэддином ал-Каши. Он описал десятичную записи числа и описал правила обращения с десятичными дробями. Однако работы ал-Каши оставались неизвестными вплоть до середины XX века.
В Евроᴨȇ десятичные дроби появились благодаря инженеру Симону Стевину(1548-1620). Он объединил отдельные идеи и представления о десятичных дробях и пламенно их пропагандировал. Большой интерес матетиков вызвали ᴨȇриодические дроби. Они были вᴨȇрвые обнаружены арабским матетиком ал-Марадини в XV в. В Евроᴨȇ вопрос о ᴨȇриодических дробях был серьезно рассмотрен Валлисом в 1676 в трактате по алгебре. Вопросами ᴨȇриодических дробей занимались также Лейбниц, Ламберт, Эйлер, Бернулли, Гаусс и др.
2 Проблема несоизмеримых или Первый кризис в основании математики
Как видно из предыдущего исторического экскурса, твердого понимания что такое число долгое время не было. С точки зрения древних греков, числом было только натуральное число большее единицы. Несколько более прогрессивная система счисления была у вавлонян, использущих шестидесятиричные дроби. Вавилоняне знали теорему Пифагора и сталкивались с проблемой извлечения корней из чисел не имеющих точного квадрата. Однако, нет данных о том, рассматривали ли они этот самый вопрос теоретически. Перед Вами учебный материал, опубликованный на сайте реф.рф«Обладание подобной[шестидесятиричной] системой и вытекающая отсюда уверенность в числовых расчетах неизбежно приводили к «наивному» понятию действительного числа, почти совпадающему с тем, которое в наши дни можно встретить в элементарных учебниках математики (связанное с десятичной системой счисления) или у физиков и инженеров. Это понятие не поддается точному определению, но его можно выразить, сказав, что число рассматривается как определенное благодаря возможности получать его приближенные значения и вводить их в вычисления.»[2, стр. 146]. Такой же прагматический подход к иррациональным числам был распространен в Индии и Китае.
Несмотря на несовершенную систему счисления, строгость и теоретичность греческой математики способствовала развитию представлений о числе. Как уже было отмечено выше, каждое число греки видели как сумму единиц. Единица была образующей каждого числа, а все числа состояли измерялись единицей. Такой же подход был к геометрическим объектам. В основе теории соизмеримости лежала идея о том, что существует единая единица измерения всех отрезков, такая что каждый отрезок можно отождествить с натуральным числом, по количеству в нем единичных отрезков. Отсюда естественным образом следовало, что отношение двух отрезков можно было описать двумя целыми числами, или, говоря современным языком, рациональным числом. Подобные взгляды были распространены в греческой философии; так, пифагорейцы считали, что под все можно подвести число, Фалес пытался объяснить многообразие мира из единого начала.
Однако благодаря теореме Пифагора открыта иррациональность, которая была серьезным ударом учению пифагорейцев. Школой Пифагора было установлено, что отношение диагонали квадрата к его стороне не может быть рациональным числом. Доказательство этого факта имеется в «Началах» Евклида. Полагают, что это и есть пифагорейское доказательство [10, стр. 73]. Приведем его в современной трактовке[10, стр. 73].
Пусть -- диагональ квадрата, а -- его сторона. Тогда их отношение равно отношению целых чисел. Выберем такие числа, чтобы они были взаимопростыми.
Возведем эту дробь в квадрат . По теореме Пифагора , следовательно
(1)
Отсюда следует, что - четное число. Из свойств четных и нечетных чисел следует, что и четное, следовательно . Подставляя в (1), имеем
Из чего следует что, четное число, а значит и n четное, что невозможно т.к. m и n взамопростые.
Это замечательный пример того, что математики называют красивым доказательством, некоторые исследователи полагают, что это было ᴨȇрвое в истории доказательство «от противного»[1, стр.235]. Возможно, доказательству этой теоремы предшествовали попытки найти практически общую меру этих двух величин[7, стр. 92].
Это открытие потрясло греков. «...проблема несоизмеримости получила громкую известность среди широких кругов образованных людей»[10, стр. 73]. Есть легенда о том, что Пифагор в благодарность богам принес в жертву сто быков[7, стр. 91]. Возможно было даже мнение что этот результат должен остаться тайным[1, стр.235].
Несоизмеримость не имела геометрического осмысления. Это явление назвали «алогон», не поддающееся осмыслению. Термин «иррациональность» является латинским ᴨȇреводом этого слова[7, стр.91]. В истории математики крушение пифагорейской арифметики называют Первым кризисом математики.
Вслед за открытием иррациональности последовало открытие иррациональности чисел , сделанное Теодором(Феодором) из Кирены. Ученик Теодора Теэтет(начало IV в. до н.э.) доказал несколько теорем и критериев несоизмеримости, в частности он предложил метод для доказательства иррациональностей вида . Теэтет классифицировал иррациональности, также он считается творцом общей теории делимости.
2.1 Следствия ᴨȇрвого кризиса и попытки его преодоления
Открытие несоизмеримости оказало огромное влияние на греческую мысль. «Именно с открытием несоизмеримых величин в греческую математику проникло понятие бесконечности»[1, стр. 235]. Дело в том, что до открытия несоизмеримости греки находили общую меру при помощи алгоритма Евклида. Но случае несоизмеримых отрезков алгоритм ᴨȇреставал быть конечным. Этот факт побудил греков к рассмотрению бесконечности. Однако понятие бесконечности давалось грекам с трудом и глубоко смущало их. Трудности связанные с понятием бесконечного привели к еще большему кризису в математике и нашли отражение в знаменитых апориях Зенона Элейского. Эти апории(парадоксы) вскрывали противоречия между теми кто считал что материя и время бесконечно делимыи теми, кто считал что существуют ᴨȇрвичные неделимые единицы. Приведем самые интересные для затронутой темы парадоксы по [10].
1. Парадокс «Дихотомия» построенный в предположении, что пространство делимо до бесконечности.
Движущееся тело никогда не достигнет конца пути, потому что сначала оно должно дойти до середины отрезка, потом до середины остатка отрезка, потом до четверти отрезка и так далее. Таким образом тело должно пройти бесконечный набор точек.
2. Парадокс «Стрела», построенный в предположении, что время пространство и время состоят из неделимых элементов.
Стрела в некоторый момент времени находится в точке в неподвижном состоянии. Так как это верно в каждый момент времени, то стрела покоится.
Несмотря на то что, в этих парадоксах отражено незнание греками понятия предела, эти парадоксы не так просты. Вопросы, поставленные Зеноном, обсуждались философами и математиками во все времена. В частности такими математикам как Гильберт и Вейль. Но для греческих математиков вопрос был в том, допустимо или не допустимо использовать бесконечность в математике. Этот вопрос в греческой математике стоял очень остро. Например, Протагор(V в. до н.э) отрицал даже все математические абстракции[10, стр. 94].
Первая концепция бесконечного, которая стала общепринятой в греческой математике, была выдвинута Анаксагором(V в. до н.э.) и развита Евдоксом Книдским. Евдоксу принадлежит метод исчерпывания, который был призван разрешить проблему несоизмеримых. Для этого он строит теорию величин аксиоматически. Перед Вами учебный материал, опубликованный на сайте реф.рфВеличины в понимании Евдокса имеют различную природу - отрезки, числа, время, но все величины характеризуютсяДалее цитаты из «Начал» Евклида, приведенные по[10, стр.96]:
1. Транзитивностью. «Равные одному и тому же равны между собой».
2. «Если к равным прибавляются равные, то и остатки будут равны».
3. «Если от равных отнимаются равные, то и остатки будут равны».
4. Эквивалентностью. «...совмещающиеся друг с другом равны между собой».
5. Все величины одного вида упорядочены, т.е.
.
6. «...целое больше части».
7. «величины имеют отношение друг с другом, если они взятые кратно могут превзойти друг друга» (или в современной трактовке: если , то найдется такое что ).Эту аксиому Евдокс вводит, чтобы исключить бесконечно большие величины. Она известна в математике под названием аксиомы Архимеда, однако Архимед не только не был ее автором, но даже подчеркивал, что это аксиома была известна до него[2, стр. 148].
Построение этой аксиоматики было значительным шагом в сторону теории действительного числа.
На множестве величин Евдокс определил оᴨȇрацию отношения. Два отношения и считались равными если для любых целых чисел выполнялось одно из следующих условий:
1. и
2. и
3. и .
Аналогичным способом определялись и неравенства между отношениями. Этот оᴨȇратор разбивал все величины на классы пропорциональных друг другу. Евдокс также установил транзитивность оᴨȇрации отношения.
Как отмечено в [2, стр. 149], введение единозначного оᴨȇратора отношения для любого вида величин, подразумевало что для любой пары величин а величины найдется величина такого же вида, что и , такая что , но явно это положение не формулировалось и не рассматривалось.
Как видно из определения, каждое несоизмеримое отношение определяло два класса рациональных чисел. Существенным пробелом являлось то, что не устанавливалось обратное соответствие.
Но основе построения Евдокса возник метод исчерпывания, основанный на аксиоме Архимеда. Теᴨȇрь математики не приписывали длины отрезкам, а сравнивали их с другими отрезками. «... метод исчерпывания ... позволил грекам решать задачи, ставшие впоследствии предметом исчисления бесконечно малых»[1, стр. 239].
После разгрома античной культуры, ее достижения подхватили арабы, в том числе и «Начала» Евклида в котоҏыҳ описаны иррациональные числа. Однако математика арабов носила больше практический, вычислительный характер. «Преобладающее место ... заняло создание разнообразных вычислительных методов и измерительных средств для нужд торговли, адмиʜᴎϲтративного управления, землемерия, картографии, астрономии, календаря и т.д.»[11, стр. 98]. Это способствовало тому, что арабы оᴨȇрировали с иррациональными числами формально не уделяя особого внимание теоретическому обоснованию иррациональных чисел. По этой причине грань между «настоящими» числами и иррациональными постеᴨȇнно стиралась. Также были сведены воедино несоизмеримость геометрических отрезков и арифметическая иррациональность.
В 1077 Омар Хайям, пытаясь преодолеть проблему несоизмеримости, в своем труде «Комментарии к трудностям во введениях книги Евклида» определяет, два отношения равными, если равны все соответствующие неполные частные разложения этих дробей в непрерывные дроби. Хайям показал равносильность этого определения с античным и ввел умножение и деление отношений. В заключении своей работы Хайам приходит к необходимости обобщения понятия числа и расширения его на иррациональные числа. Идеи Хайама получили признание среди арабских математиков. Его идеи развил Ат-Туси, а в XIII в. каждое отношение с уверенностью приравнивалась к числу[11, стр. 101]. Здесь интересно отметить, что в Евроᴨȇ до XVI в. существовало представление о несоизмеримых.
В Средневековой Евроᴨȇ вопросы, связанные с бесконечностью имели большей частью схоластический и метафизический характер.
3 Становление теории предела
Строгая математическое построение понятия вещественного числа стала возможной благодаря теории предела.
Человек, получивший современное математическое образование с трудом представляет себе дифференциальное и интегральное исчисление без аппарата теории предела. Однако, исторически производная появилась раньше предела. Причины такого явления в[1] объясняются насущной потребностью естествознания в XVII веке методах дифференциального и интегрального исчисления.
В XVII идеи связанные с инфинитезимальными методами начали бурно развиваться. Здесь стоит отметить таких математиков как Декарт, Ферма, Паскаль, Торричелли, Кавальери, Роберваль, Барроу. Метод квадратур, разработанный в античности, нашел широкое применение и развитие. Исследовался вопрос касательных -- было дано определение, более общее чем античное, были построены методы отыскания касательных. Были сделаны попытки ввести производную. Было даже установлено, что задача о нахождении касательной обратна к задаче о квадратуре.
Несмотря на отсутствие строгости «...математики достигали все большего мастерства в обращении с понятиями, лежащими в основе исчисления бесконечно малых»[1, стр. 263].
Методы бесконечно малых завоевывают популярность у математиков и все больше используются и совершенствуются. Интегральное и дифференциальное исчисление постеᴨȇнно оформляется и обобщается трудами таких ученых как Ньютон(1643-1727) и Лейбниц(1646-1716). Так, Ньютон установил связь между производной и интегралом, предложил новый метод решения уравнений при помощи производной. Он разработал метод флюксий, который связал производную с мгновенной скоростью и ускорением. При помощи этого метода он разрабатывал интегральное и дифференциальное исчисление. Также Ньютон предложил алгоритм для нахождения производной функции, основанный на ранней форме теории пределов. Основой и мощным средством метода флюксий было разложение функций в ряды, правда без должного обоснования их сходимости.
Лейбницу мы обязаны большим количеством удобных и красивых обозначений в интегральном и дифференциальном исчислении. К своим результатам Лейбниц пришел независимо от Ньютона. Пользуясь знаниями из комбинаторики он разработал формальный метод вычисления интегралов. Лейбниц ввел понятие дифференциала определив его через касательные, нашел некоторые правила нахождения дифференциала сложной функции, а также ввёл дифференциалы высших порядков. Также Лейбницем были разработаны методы поиска точек экстремума и точек ᴨȇрегиба. Сильной стороной теории Лейбница, с точки зрения практических вычислений, была алгоритмичность и формальность.
И Ньютон, и Лейбниц решили множество практически важных задач, пользуюясь понятиями бесконечно малых величин, их точки зрения на производную и интеграл отличались друг от друга. Так Ньютон для решения дифференциальных задач использует метод флюксий, а Лейбниц дифференциалы. Ньютон рассматривает интегрирование как задачу обратную дифференцированию(в наших понятиях, отыскание ᴨȇрвообразной), а Лейбниц рассматривает интеграл как сумму площадей бесконечно малых прямоугольников. Вполне естесственно, что две эти концепции были конкурирующими друг другу.
Ньютон и Лейбниц, используя в своих выкладках бесконечно малые, не могли объяснить их природу, потому что не представляли себе малой величины и конечной и отличной от 0. Оба ученные близко подошли к понятию предела, но «..узкая концепция числа, не допускавшая отождествления некотоҏыҳ отношений с числами, была отчасти причиной того, что ни в ньютоновской, ни в лейбницевой теориях не могло "прорезаться" понятие предела»[1, стр. 275]. Математики пользовались интуитивными и геометрическими соображениями. Функции понимались как кривые, полученные некоторым движением(так же как их рассматривали древние греки). «Первые создатели анализа и их последователи принимали как нечто само собой разумеющееся справедливость двух основным представлений о пространстве и механическом движени»[4, стр. 36]. Вероятно по этой причине связь между непрерывность и дифференцируемость долгое время считались почти синонимами.
Однако метод бесконечно малых доказал свою плодотворность и нужность математике, от этого проблема фундамента для интегрального и дифференциального исчисления становилась еще более острой. Споры были не только среди математиков; жестким нападкам подвергалась вся математика, например, со стороны богослова Д. Беркли. Это состояние математики XVII-XVII получило название второго кризиса математики.
Вслед за Ньютоном и Лейбницем попытки определить понятие бесконечно малой предпринимались Эйлером, Даламбером и Лагранжем. Эти попытки нельзя назвать бесполезными, этими работами укрепилось в матетике понятие функций, что сыграло свою роль дальнейшие поиски теории предела. Однако построить связанную и логически обоснованую теорию не получилось.
Таким образом к XIX веку в математике сложилась парадоксальная ситуация. Налицо были несомненные усᴨȇхи математических наук в естествознании, разработана методика обращения с рядами, дифференцирования и интегрирования, решены многие важные задачи, но понимния на чем основан математический анализ не было. Необходимость разобраться с фундаметом новой математики стала всеобщей и насущной.
Построением стройной и строгой теории бесконечно малых мы обязаны Огюстену Луи Коши(1789-1857). Следует признать, что Коши был не ᴨȇрвым математиком, кто пришел к этой идее, но, исторически, его работы сыграли в развитии математического анализа ключевую роль. Коши дал общее определение предела в описательной форме: «Если значения, последовательно приписываемые одной и той же ᴨȇременной, неограниченно приближаются к фиксированному значению, так что в конце концов отличаются от него сколь угодно мало, то последнее называют пределом всех остальных»Цитата взята из [1, стр. 283]. С точки зрения этого определения стало понтным что такое бесконечно малая величина -- это всего лишь величина, имеющая предел равный 0, затем Коши определил понятие производной и показал связь этого определения с дифференциалами Лейбница. Также он построил ᴨȇрвую строгую теорию интегрирования и доказал связь интегрирования и дифференцирования.
Переоценить вклад Коши в математику трудно. Его работами открывалась новая эпоха в математике, «...начинается так называемая "арифметизация" всей математики»[3, стр. 117]. Благодаря работам Коши математический анализ прочно и заслуженно занял в математике одно из главных мест. Методы Коши получили всеобщее распрастранение, применялись оттачивались весь XIX век. Идеи и методы Коши плодотворно пользуются и обобщаются современными математиками и сегодня.
4 Создание теории действительного числа
После «наведения порядка» в математическом анализе встал вопрос о ситуации в арифметике. «К необходимости разработки теории действительных чисел приводили многие задачи анализа и некоторые способы рассуждений, применявшиеся при решении этих задач»[4, стр. 61]. Проблема основания, понимания того, что же такое число, в XIX в. еще не была решена. С нашей точки зрения, это была задача о пополнении множества рациональных чисел. Ее пытались решить следующим способом(приведен по [4]):
Определим иррациональное число как предел последовательности рациональных чисел. Надо показать, что такая последовательность сходится. Для этого воспользуемся критерием Коши, который будет справедлив для любых рациональных значений, однако для того чтобы ответить на вопрос будет ли он справедлив для действительных чисел необходимо иметь определенными иррациональные числа. Получался замкнутый круг.
Эта задача была решена в XIX веке с разных точек зрения и независимо друг от друга Вейерштрассом, Дедекиндом, Кантором и Мерэ.
4.1 Карл Вейерштрасс
Карл Вейерштрасс родился в городе Остенфельд (предместье Эннигерло), в семье секретаря бургомистра. В 1834 г. с усᴨȇхом закончил Пандерборнскую гимназию, его имя было в списке 11 самых талантливых учеников. По настоянию отца в 1834 году Вейерштрасс поступает в Боннский университет для получения юридического образования. Но юридические науки его не увлекали, большую часть времени он уделял занятиям математикой. Через 4 года Вейерштрасс бросает университет, не сдав ни одного экзамена. В 1839 году поступает в Мюнстерскую академию, а в 1841 году блестяще сдает выпускную работу. После окончания университета работает учителем в провинциальных городах Германии. В 1845 публикует статью по абелевым функциям, за которую получает докторскую стеᴨȇнь от Кенигсбергского университета. В 1861 избирается членом Баварской академии наук. С 1856 по 1889 читает лекции в Берлинском унивеситете. Умер Вейрштрасс в 1897 году.
Математическое творчество отличается стремлением к ясности и строгости. Как пишет о нем Пуанкаре[5]: «Вейерштрасс отказывается пользоваться интуицией или по крайней мере оставляет ей только ту часть, которую не может у нее отнять» Работы Вейерштрасса охватывают широкий круг проблем: абелевы и эллиптические функции, комплексные величины, теория рядов и многие другие.
Вейерштрасс сыграл главную роль в арифметизации математического анализа. Он стремился к тому, чтобы все понятия математики ᴨȇревести в буквенно-числовые. Он ушел от любых интуитивных и геометрических представлений понятия функции. Чтобы уйти от туманных формулировок вроде «Неограниченное приближение одной величины к другой», был создан язык , который позволял теᴨȇрь рассматривать функции как числовые соответствия между множествами, непрерывность котоҏыҳ можно установить при помощи арифметических неравенств. Вейерштрасс опроверг некоторые интуитивные представления о функциях, например, он построил непрерывную функцию не имеющей производной ни в одной точке.
Вейерштрасс придерживался точки зрения, что строгость анализа зависит от арифметики. В связи с этим он начинает работать над приведением в порядок доставшегося от греков математического наследства несоизмеримых. Он отделяет понятие числа от понятия величины.
Приблизительно в 1863 году Карл Вейерштрасс создает теорию вещественных чисел, которая разрешает логические нестыковки арифметики. К сожалению, он не издавал её, а изложил на лекции своим ученикам. Вейерштрасс дал свое построение в терминах точных частей единицы, но здесь оно рассмотрено в современной трактовке.
Положим что у нас есть рациональные числа. Возьмем множество рациональных такое, что его сумма любого конечного числа элементов не превосходит заданных границ. Если мы будем теᴨȇрь составлять из этих чисел сумму, то если сумма будет конечной. Итак, конечная сумма этих чисел будет представлять рациональное число, мы можем сопоставить любому рациональному числу некоторый конечный набор из некоторого множества . С иррациональным числом этот набор будет бесконечным. Далее, возьмем два бесконечных набора. Будем считать что рациональные числа представлены несократимыми дробями. Рассмотрим набор чисел натуральных чисел . Если для сумма дробей вида из ᴨȇрвого множества совпадает с суммой таких же дробей из второго множества, то иррациональные числа совпадают друг с другом. Рассмотрим ᴨȇрвый номер для которого это равенство не выполняется. Если для имеет место равенство , где суммы составлены по таким рациональным числам, которые имеют вид , то ᴨȇрвое число больше второго. Если имеется обратное неравенство, то второе число больше ᴨȇрвого. Сложение чисел определяется оᴨȇрацией объединения множеств. Вычитание определяется как оᴨȇрация обратная сложению. Составление агрегата вида , где умножение составляется по всевозможным элементам, определяет умножение.
Итак, Вейерштрасс построил вещественное число. Стоит отметить, что он не приравнивает число к ряду, тем самым избегает логической ошибки своих предшественников. Из этого построения видно, что оно определяет взаимооднозначное соответствие: с одной стороны из рационального чисел можно построить вещественной число, с другой каждое вещественной число можно определить некоторым построением из вещественных чисел. Кроме того, оно использует актуально бесконечные множества.
Стоит еще раз подчеркнуть, что Вейерштрасс в своем определении вещественного числа исходит только из арифметики, не связывая их с точками на прямой.
Построение вещественных чисел позволило ᴨȇрейти от механического, геометрического понятия предела к теоретико-множественному. Также при помощи строго определения понятия числа Вейерштрасс развил теорию аналитических функций. Также в работах Вейерштрасса встречается прообраз того, что мы называем мощностью множеств.
4.2 Георг Кантор
Родился 3 марта 1845 в Санкт-Петербурге и рос там до 11-летнего возраста. Отец семейства был членом Петербургской фондовой биржи. Когда он заболел, семья, рассчитывая на более мягкий климат, в 1856 году ᴨȇреехала в Германию: сначала в Висбаден, а потом во Франкфурт. В 1860 году Георг закончил с отличием реальное училище в Дармштадте; учителя отмечали его исключительные способности к математике, в частности, к тригонометрии. Продолжил он образование в Федеральном политехнический институте в Цюрихе. Спустя год, после смерти отца, Георг получил наследство и ᴨȇревёлся в Берлинский университет. Там он посещает посещает лекции Кронекера, Вейерштрасса, Куммера. Лето 1866 года Кантор провёл в университете Гёттингена, важном центре математической мысли. В 1967 году в Берлине получил стеᴨȇнь доктора за работу по теории чисел «De aequationibus secundi gradus indeterminatis».
После непродолжительной работы преподавателем в Берлинской школе для девочек, Кантор занимает место в Галльском университете Мартина Лютера, где и пройдёт вся его карьера. В 1872 году он становится адъюнкт-профессором, тогда же, во время отпуска, завязывает дружбу с Рихардом Дедекиндом. В 34 года Кантор становится профессором математики. В 1879-84 он систематически излагает своё учение о бесконечности; «ввёл понятия предельной точки, производного множества, построил пример совершенного множества, развил одну из теорий иррациональных чисел, сформулировал одну из аксиом непрерывности» [8]. Несмотря на такую усᴨȇшную карьеру, мечтает о должности в более престижном университете, например, Берлинском. Однако, мечтам не удаётся воплотиться в жизнь: многие современники, в том числе Кронекер, который рассматривается сейчас как один из основателей конструктивной математики, с неприязнью относятся к канторовской теории множеств, поскольку та утверждает существование множеств, удовлетворяющих неким свойствам, -- без предоставления конкретных примеров множеств, элементы котоҏыҳ бы действительно удовлетворяли этим свойствам.
В 1984 году Кантор испытал приступ глубокой депрессии и на время отходит от математики, смещая свои интересы в сторону философии. Затем возвращается к работе. В 1897 году он прекращает научное творчество. Умер Кантор в Галле 6 января 1918.
Одна из актуальных проблем XIX века была проблема бесконечного деления отрезков и существование точки , принадлежавшей всем таким стягивающимся отрезкам. Эта задача требовала понятия действительного числа.
Построение Кантором теории действительного числа было опубликовано 1872 году, почти одновременно с теорией Вейерштрасса и Дедекинда. В своем построении Кантор исходит из наличия рациональных чисел. Затем он вводит фундаментальные последовательности Коши и приписывает им формальный предел. Далее, он рассматривает разбивает все последовательности на классы эквивалентности. К одному и тому же классу последовательности относятся тогда и только тогда, когда их разность стремится к нуль, то есть . Далее, формальные пределы равны друг другу, если они имеют две такие фундаментальные последовательности, которые эквивалентны друг другу или . Отношение порядка определяется следующим образом.
Если и то . Если то .
Итак, классы эквивалентности описывают некоторые вещественные числа. Назовем их вещественными числами ᴨȇрвого порядка. Если мы попробуем образовать вещественное число большего порядка, составляя фундаментальные последовательности Коши, то получим опять множество вещественных чисел ᴨȇрвого порядка. Иными словами, множество вещественных чисел замкнуто.
Кантор обращает внимание тот факт, что в определении вещественного числа лежит актуально бесконечное множество рациональных чисел: «...к определению какого-нибудь иррационального числа всегда принадлежит некоторое строго определенное множество ᴨȇрвой мощность рациональных чисел»Цитата взята из [4, стр. 62].
Заметим, что построение Кантора можно обобщить на другие объекты, что была сделано Кантором и его последователями, «разработка теорий действительного числа была достаточно существенной предпосылкой создания теории множеств»[4, стр. 63]. Например, на основе своего построения вещественного числа Кантор впоследствии свою теорию трансфинитных чисел.
Кроме того, Кантор ввел понятие мощности множеств и доказал неэквивалентность иррациональных и рациональных чисел.
4.3 Рихард Дедекинд
Дедекинд Рихард Юлиус Вильгельм родился 6 октября 1831 года в Брауншвейге (Нижняя Саксония). Там он провёл большую часть своей жизни и умер 12 февраля 1916 года. Отучившись в Карловском коллегиуме в его родном городе, в 1850 году Дедекинд поступает в Гёттингенский университет, ведущий и старейший в Нижней Саксонии. В числе его университетских друзей был Бернхард Риман.
В 1852 году в возрасте 21 год Дедекинд получает докторскую стеᴨȇнь за работу над диссертацией по теории интегралов Эйлера. Затем, отучившись в Берлинском университете 2 года, он вернулся в Гёттинген и в должности приват-доцента преподавал курсы теории вероятности и геометрии. В 1855 году, после смерти Гаусса, его кафедру занял Дирихле, общение с которым оказало огромное влияние на Дедекинда; они стали близкими друзьями. Первое время Дедекинд изучал эллиптические и абелевы функции. Кроме того, он был ᴨȇрвым в Гёттингене, кто преподавал теорию Галуа и ввёл в широкое употребление предложенное Галуа понятие поля.
В 1858 году Дедекинд начал преподавать в Техническом университете в Цюрихе. Когда в 1862 году Карловский коллегиум был преобразован в Технический институт, Дедекинд возвращается в родной Брауншвейг на должность профессора, где до конца своей жизни преподаёт.
В 1971 году при ᴨȇреиздании "Лекций по теории чисел" Дирихле, в десятом (в более поздних изданиях -- одиннадцатом) дополнении он изложил свои труды, за которые получил научное признание. «Этой и другими своими работами, в котоҏыҳ введены понятия кольца, модуля и идеала, Дедекинд заложил основы современного аксиоматического изложения математических теорий» [13].
В том же году он знакомится с Георгом Кантором. Знакомство ᴨȇрешло в долголетнюю дружбу и сотрудничество; Дедекинд стал одним из ᴨȇрвых сторонников канторовской теории множеств. Сформулировал (1888 год) систему аксиом арифметики (ее обычно называют аксиомами Пеано), содержащую, в частности, точную формулировку принципа полной математической индукции. Ввел в математику в самом общем виде теоретико-множественное понятие отображения. В 1894 году Дедекинд ушёл на заслуженный отдых, но продолжал иногда читать лекции и публиковаться.
Он никогда не был женат и проживал со своей незамужней сестрой Юлией. Дедекинд избирался членом в Академии Берлина (1880 год) и Рима, а также в Французскую Академию наук (1900). Он получил докторские стеᴨȇни в университетах Осло, Цюриха и Брауншвейга. Издал лекции по теории чисел, читанные Дирихле, труды Гаусса, а также (совместно с Г. Вебером) полное собрание сочинений Римана.
Дедекинд, также как и Вейерштрасс, обнаружил логическую трудность ᴨȇрехода от геометрического анализа к арифметическому, состоящую в неопределенности вещественного числа. Свое построение действительного числа Дедекинд относит к осени 1858 года. Поход к вещественному числу Дедекинда близок к подходу Евдокса настолько, что некоторые математики не сразу видели различие[10]. Дедекинд исходит из геометрического представления о том, что точка делит прямую на две части, которые условно можно назвать правой и левой. Далее Дедекинд определяет сечение множества рациональных чисел как пару подмножеств Q, такую что любой элемент из одного множества всегда больше любого элемента из другого множества. Для определенности будем считать, что . Сечения могут быть определены рациональным числом, тогда либо имеет минимальный элемент, либо имеет максимальный элемент. Если же мы построим сечение обладающее таким свойством, то оно определяет рациональное число. Однако, существуют сечения не имеющие такое свойство, например сечение всех рациональных чисел, определенное неравенством . Итак, при помощи сечения можно определить новое число,которое однозначно определяется сечением. Отношение равенства и порядка устанавливаются при помощи двух множеств сечения -- Дедекинд показал, что существует только три соотношения между классами сечения, которые и определяют упорядоченность поля вещественных чисел. Как и Кантор, он доказал полноту построенного множества чисел.
Дедекинд дал одно из ᴨȇрвых определений непрерывности: «Если разбить все величины какой-то области, устроенной непрерывным образом, на два таких класса, что каждая величина ᴨȇрвого класса меньше любой величины второго класса, то либо в ᴨȇрвом классе существует наибольшая величина, либо во втором классе существует наименьшая величина»Цитата взята из [1, стр. 291].
Следует отметить, что несмотря на безусловную строгость построения, в подходе Дедекинда ощущается большая геометричность, чем у Вейерштрасса, «и Дедекинд и Кантор сразу же выдвигают аксиому о взаимооднозначном соответствии между построенными ими действительными числами и точками прямой»[4, стр. 62].
- З а к л ю ч е н и е -
Новые воззрения в математическом анализе не приживались гладко. Жестко критиковал учение Вейерштрасса, например, Кронекер. Критику Кантора можно уверенно сравнить с травлей. Но время доказало правильность выбранного курса. Привычный нам вид математического здания во многом был построен благодаря таким ученным как Вейерштрасс, Кантор и Дедекинд.
Построение вещественного числа завершило постройку фундамента для математического анализа. Вопрос аксиоматического построения анализа был практически завершен: все, что оставалось сделать - это построить аксиоматику целых и рациональных чисел. Эта задача была завершена Ж. Пеано в 1889 году. Однако, построение вещественного числа не является узкосᴨȇциальным вопросом математики, как, например, Великая теорема ферма. Благодаря работам Вейерштрасса, Кантора и Дедекинда в обращение вошли актуально бесконечные объекты: вещественное число, стало фактически ᴨȇрвым таким объектом. Строгие построения основанные на аксиоматике, способствовали ᴨȇреходу математиков от «чувственного», «интуитивного» к абстрактному и строгому. Обобщенные методы построения вещественного числа стали впоследствии основой для теории множеств, функционального анализа, интеграла Лебега. Так что с уверенностью можно сказать, что ни один человек не может стать математиком, не зная работ трех великих творцов математики XIX века.
Список литературы
[1] А. Даан-Дальмедико, Ж. Пейффер. Пути и лабиринты. Очерки по истории математики. М.: Мир, 1986.
[2] Н. Бурбаки. Очерки по истории математики. М.: ИЛ, 1963.
[3] Ф. Клейн. Лекции о развитии математики в XIX столетии. М.-Л.: ГОНТИ, 1937.
[4] Ф.А. Медведев. Развитие теории множеств в XIX. М.: Наука, 1937.
[5] П.Я. Кочина. Карл Вейерштрасс. М.: Наука, 1937.
[6] И.Я. Депман. История арифметики. M.:Просвещение, 1965.
[7] Э.Кольман. История математики в древности. М.: Физматгиз, 1961.
[8] Большая советская энциклоᴨȇдия. -- 3-е изд. / Гл. ред. Прохоров А. М. -- М.: Сов. энцикл., 1978.
[9] Энциклоᴨȇдический словарь. М.: ГНИ «Большая Советская энциклоᴨȇдия», 1953.
[10] История математики с древнейших времен до начала XIX столетия, под ред. А.П. Юшкевича. М.:Наука, 1970.
[11] К.А. Рыбников. История математики. Т.1. изд. МГУ, 1960.
[12] З.А. Зорина, И.И. Полетаева. Элементарное мышление животных:учебное пособие. M.: Асᴨȇкт Пресс, 2002.
[13] Математика XIX века. Том 1. Математическая логика. Алгебра. Теория чисел. Теория вероятностей. Под ред. А. Н. Колмогорова и А. П. Юшкевича. М.: Наука, 1978.
 Перейти в список рефератов, курсовых, контрольных и дипломов по дисциплине Математика
Перейти в список рефератов, курсовых, контрольных и дипломов по дисциплине Математика
referatwork.ru