WinNavigator

Frigate

Norton Commander

WinNC

Dos Navigator

Servant Salamander

Turbo Browser

Winamp, Skins, Plugins

Необходимые Утилиты

Текстовые редакторы

Юмор

File managers and best utilites

Доклад: Числовые характеристики случайных величин и случайных функций. Числовые характеристики случайной величины реферат

Реферат - Числовые характеристики случайных величин и случайных функций.

Случайной величиной называется такая величина, которая в результате опыта может принимать различные заранее не известные численные значения при сохранении определенной совокупности условий, сопровождающий данный опыт. Одни случайные величины могут принимать отдельные друг от друга изолированные числовые значения. Такие случайные величины называются дискретными или прерывными.

Числовые характеристики случайных величин. 1)Математическое ожидание (среднее значение).Определение:

Математическим ожиданием называется- для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания) — для непрерывной случайной величины: Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания).Свойства математического ожидания:a. Если С — постоянная величина, то МС = С, b. МСх = СМх, c. Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy, d. Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj) при разных условиях Hj, то условное математическое ожидание определяется как

или Если известны вероятности событий Hj, может быть найдено полное математическое ожидание:

Если f(x) — есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины: — для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.

-для непрерывной случайной величины: Интеграл должен быть абсолютно сходящимся. 2. Дисперсия случайной величины. Определение:

Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания: Dx = M(x-Mx)2 — для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)- для непрерывной случайной величины:

Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии).Свойства дисперсии:a. Если С — постоянная величина, то DС = 0, b. DСх = С2Dх, c. Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин), d. Для вычисления дисперсии удобно использовать формулу: Dx = Mx2 — (Mx)2

28)Измерения и наблюдения. Классификация измерения.Дискретные – это такие измерения которые выполняются через определённый интервал времени.Непрерывные – это те измерения которые ведутся всегда автоматизированными аппаратами.Необходимые – это измерения минимальное количество которых обеспечивает.Избыточные – это такие которые выполнены сверх необходимых.Равноточные – это такие СКП результат измерения которых будет одинаковый.По степени взаимо связи: взаимонезависимы – измерение погрешности которой формируется различными факторами.корреляционновзаимозависимы – это измерения в состав погрешности которых входит одна и та же общая погрешность сформирована одним и тем же фактором.Функциональнозависимы – это измерения все погрешности которых формируются одним и тем же фактором..

29)Классификация погрешности и их свойства. Методы учёта систематических погрешностей.Погрешность измерения называется разница между измеренным и истинным значением величины.Непосредственно источник погрешности является: несовершенство приборов и инструментов, несовершенство органов чувств и не стабильность психического состояния, незакономерные колебания параметров внешней среды, нестабильность метода измерений, несовершенство метода измерений.По характеру действия на величину погрешности подразделяются на: случайные, Систематические.

систематические на: Постоянные, Переменные, периодические, прогрессивные, грубые (промахи).

www.ronl.ru

Основные числовые характеристики случайных величин.

1.Математическое ожидание и его свойства.

Математическим ожиданием случайной величины Х называется число, равное сумме произведений всех возможных значений случайной величины на их вероятности.

Свойства математического ожидания:

1) , где;

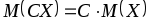
5) М (М (Х)) = М (Х) ‒ следует из первого свойства и определения математического ожидания.

2.Дисперсия и её свойства

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

D(X)=M(X ‒ M(

Дисперсия показывает степень разброса случайной величины относительно её математического ожидания.

Преобразовав формулу D(X)=M(X ‒ M(

D(X)= ‒ формула для вычисления дисперсии.

Свойства дисперсии:

3.Среднее квадратическое отклонение случайной величины.

Средним квадратическим отклонением случайной величины X называется корень квадратный из дисперсии этой величины:

4.Мода случайной величины.

Модой (х) случайной величины называется наиболее вероятное ее значение, то есть значение, вероятность которого максимальна.

Если максимальные вероятности принимают несколько значений случайных величин, то такое распределение называется полимодальным.

Пример.

Дискретная случайная величина X задана законом распределения:

	‒1	0	1	2
	0,1	0,2	0,1	0,6

Найти: числовые характеристики случайной величины: M(X), D(X), Ϭ(X), (х).

Решение:

Построим многоугольник распределения данной случайной величины.

1. Математическое ожидание:

2. Дисперсия:

3. Средне квадратическое откланение:

4. так как максимальная вероятность этого значения равна 0,6.

5. Моменты случайных величин

Начальным моментом k ‒ го порядка называется математическое ожидание k ‒ й степени случайной величины:

при k=1;

Центральным моментом случайной величины (X) называется математические ожидание k‒й степени отклонения случайной величины (Х) от ее математического ожидания:

при k=2,=D(Х).

Функция распределения случайной величины.

Функцией распределения случайной величины (F(x)) – называется вероятность того, что случайная величина X примет значения меньше x. Следовательно,

т.е. геометрически значения X будут левее x:

Так как F(x) – вероятность события X < x, то

Пример

xi	1	4	5	7
pi	0,4	0,1	0,3	0,2

Найти функцию распределения F(x) и построить график.

Решение:

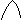
1 4 5 7

1. Если x ≤ 1,то F(x) = 0.

2. Если 1< x ≤ 4, например, x=2, то F(2) = P(X < 2 ) = 0,4

3. Если 4 < x ≤ 5, например, x = 4,5, то F(4,5) = P(X<4,5) = P(X=1)+P(X=4)=0,4+0,1=0,5

4.Если 5 < x ≤ 7, например x=6, то F(6)=P(X<6)=P(X=1)+P(X=4)+P(X=5)=0,4+0,1+0,3=0,8

5. Если x > 7, например x =8, то F(8)=P(X<8)=P(X=1)+P(X=4)+P(X=5)+P(X=7)= 0,4+0,1+0,3+0,2=1

0; если x ≤ 1

0,4; если 1< x ≤ 4

F(x) = 0,5 если 4 < x ≤ 5

0,8; если 5 < x≤ 7

1; если x > 7

studfiles.net

Реферат Случайные величины

скачать

Реферат на тему:

План:

1 Определение
- 1.1 Пространство элементарных событий
- 1.2 Алгебра событий
- 1.3 Вероятность
- 1.4 Определение случайной величины
2 Классификация
3 Методы описания
4 Простейшие обобщения

Введение

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причем появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Формальное математическое определение следующее: пусть $(\Omega,\mathcal{F}, \mathbb{P})$ — вероятностное пространство, тогда случайной величиной называется функция $X\colon\Omega \to \mathbb{R}$ , измеримая относительно $\mathcal{F}$ и борелевской σ-алгебры на $\mathbb{R}$ . Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением.

1. Определение

1.1. Пространство элементарных событий

Пространство элементарных событий Ω в случае бросания игральной кости

Если бросается игральная кость, то в результате верхней гранью может оказаться одна из шести граней с количеством точек от одной до шести. Выпадение какой-либо грани в данном случае в теории вероятностей называется элементарным событием $~\omega_k$ [1], то есть

$~\omega_1$ — грань с одной точкой;
$~\omega_2$ — грань с двумя точками;
...
$~\omega_6$ — грань с шестью точками.

Множество всех граней $~\{\omega_1, \ldots, \omega_6\}$ образует пространство элементарных событий $~\Omega$ , подмножества которого называются случайными событиями ~A_n [1]. В случае однократного подбрасывания игровой кости примерами событий являются

выпадение грани с нечётным количеством точек, то есть событие — это выпадение грани с одной точкой или грани с тремя точками, или грани с пятью точками). Математически событие записывается как множество, содержащее элементарные события: $~\omega_1$ , $~\omega_3$ и $~\omega_5$ . Таким образом, $~A=\{~\omega_1, ~\omega_3, ~\omega_5\}$ ;
выпадение грани с чётным количеством точек, то есть событие — это выпадение грани с двумя точками или грани с четырьмя точками, или грани с шестью точками. Математически событие записывается как множество, содержащее элементарные события: $~\omega_2$ , $~\omega_4$ и $~\omega_6$ . Таким образом, $~A=\{~\omega_2, ~\omega_4, ~\omega_6\}$ ;

1.2. Алгебра событий

Множество случайных событий образует алгебру событий $\mathfrak{A}$ [2], если выполняются следующие условия:

$\mathfrak{A}$ содержит пустое множество $~\varnothing$ .
Если событие A принадлежит $\mathfrak{A}$ , то и его дополнение принадлежит $\mathfrak{A}$ . С помощью кванторов это записывает так: $\forall A\in \mathfrak{A}$ : $\Omega\setminus A\in\mathfrak{A}$ .
Если A1 и A2 принадлежат $\mathfrak{A}$ , то их объединение также принадлежит $~\mathfrak{A}$ . С помощью кванторов это записывается следующим образом ( $\forall A_1, A_2\in \mathfrak{A}$ ) ( $A_1 \cup A_2$ ) $\in \mathfrak{A}$ .

Если вместо третьего условия $\mathfrak{A}$ удовлетворяет другому условию: объединение счётного подсемейства из $\mathfrak{A}$ также принадлежит $~\mathfrak{A}$ , то множество случайных событий $\mathfrak{A}$ образует σ-алгебру событий.

σ-алгебра событий является частным случаем σ-алгебры множеств.

Самая маленькая среди всех возможных σ-алгебр, элементами которой являются все интервалы на вещественной прямой, называется борелевской σ-алгеброй $~\mathcal{B}$ на множестве вещественных чисел $~\mathbb{R}$ .

1.3. Вероятность

Если каждому элементарному событию поставить в соответствие число $p_i\in[0,1]$ , для которого выполняется условие:

$~\Sigma p_i=1$ ,

то считается, что заданы вероятности элементарных событий $p_i\in[0,1]$ . Вероятность события, как счётного подмножества пространства элементарных событий, определяется как сумма вероятностей тех элементарных событий, которые принадлежат этому событию. Требование счётности важно, так как, иначе сумма будет не определена.

Рассмотрим пример определения вероятности различных случайных событий. Например, если событие является пустым множеством, то его вероятность равна нулю[3]:

$P(~\varnothing)=0$ .

Если событием является пространство элементарных событий, то его вероятность равна единице:

$P(~\Omega)=1$ .

Вероятность события (подмножества пространства элементарных событий) равна сумме вероятностей тех элементарных событий, которые включает в себя рассматриваемое событие.

1.4. Определение случайной величины

Случайной величиной называется функция $~\xi\colon\Omega \to \mathbb{R}$ , измеримая относительно $\mathcal{F}$ и борелевской σ-алгебры на $\mathbb{R}$ [4].

Случайную величину можно определить и другим эквивалентным способом[4]. Функция $~\xi\colon\Omega \to \mathbb{R}$ называется случайной величиной, если для любых вещественных чисел a и b множество событий $~\omega$ , таких что $~\xi(\omega)\in(a,b)$ , принадлежит $\mathcal{F}$ .

2. Классификация

Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).

На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).

Пример смешанной случайной величины — время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.
В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.
Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.

С одной стороны, с одной схемой испытаний и с отдельными событиями в ней одновременно может быть связано сразу несколько числовых величин, которые требуется анализировать совместно.

Например, координаты (абсцисса, ордината) какого-то разрыва снаряда при стрельбе по наземной цели; метрические размеры (длина, ширина и т. д.) детали при контроле качества; результаты медобследования (температура, давление, пульс и пр.) при диагностике больного; данные переписи населения (по возрасту, полу, достатку и пр.).

Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.

3. Методы описания

Частично задать случайную величину, описав этим все её вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна F(b)-F(a). Преимущество использования функции распределения заключается в том, что с её помощью удаётся достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения.

Если случайная величина дискретная, то полное и однозначное математическое описание её распределения определяется указанием вероятностей pk = P(ξ = xk) всех возможных значений этой случайной величины. В качестве примера рассмотрим биномиальный и пуассоновский законы распределения.

Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта N раз. В каждом опыте «успех» может наступить с вероятностью p, «неудача» — с вероятностью q=1-p. Закон распределения в этом случае определяется формулой Бернулли:

$P_{k,n}=C_n^k\cdot p^k \cdot q^{n-k}$ .

При стремлении n к бесконечности произведение np остаётся равной константе λ, а закон распределения сходится к закону Пуассона, который описывается следующей формулой:

$p(k) \equiv \mathbb{P}(Y=k) = \frac{\lambda^k}{k!}\, e^{-\lambda}$ ,

где

символ "!" обозначает факториал,
$e = 2.718281828\ldots$ — основание натурального логарифма.

4. Простейшие обобщения

Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,

Измеримая функция $X\colon\Omega \to \mathbb{R}^n$ называется n-мерным случайным вектором (относительно борелевской σ-алгебры на $\mathbb{R}^n$ ).
Измеримая функция $X\colon\Omega \to \mathbb{C}^n$ называется n-мерным комплексным случайным вектором (также относительно соответствующей борелевской σ-алгебры).
Измеримая функция, отображающая вероятностное пространство в пространство подмножеств некоторого (конечного) множества, называется (конечным) случайным множеством.

Примечания

↑ 12Чернова Н. И. Глава 1. § 2. Элементарная теория вероятностей // Теория вероятностей - www.nsu.ru/mmf/tvims/chernova/tv/lec/node4.html#SECTION000222. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.
Чернова Н. И. Глава 3. § 1. Алгебра и сигма-алгебра событий // Теория вероятностей - www.nsu.ru/mmf/tvims/chernova/tv/lec/node9.html#SECTION000410. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.
Чернова Н. И. ГЛАВА 1 § 2. Элементарная теория вероятностей // Теория вероятностей - www.nsu.ru/mmf/tvims/chernova/tv/lec/node4.html#SECTION000225. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.
↑ 12Чернова Н. И. Глава 6. Случайные величины и их распределения § 1. Случайные величины // Теория вероятностей - www.nsu.ru/mmf/tvims/chernova/tv/lec/node23.html#SECTION000710. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.

Литература

Гнеденко Б. В. Курс теории вероятности. — 8-е изд. доп. и испр.. — М.: Едиториал УРСС, 2005. — 448 с.
Математический энциклопедический словарь / Гл. ред. Прохоров Ю. В.. — 2-е изд. — М.: «Советская энциклопедия», 1998. — 847 с.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. — Учебное пособие для ВУЗов. — М.: Радио и связь, 1991. — 608 с. — ISBN 5-256-00789-0
Чернова Н. И. Теория вероятностей - www.nsu.ru/mmf/tvims/chernova/tv/lec/lec.html. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.

wreferat.baza-referat.ru

Реферат - Основные числовые характеристики случайных величин

Результаты, изложенные в параграфах 2.2 и 2.3, показывают, что полную характеристикудискретной и непрерывной случайных величин можно получить, зная законы их распределения. Однако во многих практически значимых ситуациях пользуются так называемымичисловыми характеристиками случайных величин, главное назначение этих характеристик – выразить в сжатой форме наиболее существенные особенности распределения случайных величин. Важно, что данные параметры представляют собой конкретные (постоянные) значения, которые можно оценивать с помощью полученных в опытах данных. Этими оценками занимается «Описательная статистика».

В теории вероятностей и математической статистике используется достаточно много различных характеристик, но мы рассмотрим только наиболее употребляемые. Причем лишь для части из них приведем формулы, по которым рассчитываются их значения, в остальных случаях вычисления оставим компьютеру.

Рассмотримхарактеристики положения – математическое ожидание, моду, медиану.

Онихарактеризуют положение случайной величины на числовой оси, т.е.указывают некоторое ориентировочное значение, около которого группируются все возможные значения случайной величины. Среди них важнейшую роль играет математическое ожидание М(Х).

Математическое ожидание М(Х) случайной величины Х является вероятностным аналогом ее среднего арифметического (М(Х)= илиМ(Х)»).

Для дискретной случайной величины М(Х) вычисляется по формуле:

М(Х)= х1р1 + х2р2 +…+ хnрn =. (18)

Для непрерывной случайной величины М(Х) определяют по формулам:

М(Х)= или М(Х)= (19)

где f(x) – плотность вероятности, dP = f(x)dx – элемент вероятности (аналог pi для малого интервала Dx (dx)).

Пример: Вычислите среднее значение непрерывной случайной величины, имеющей на отрезке (a, b) равномерное распределение.

Решение: при равномерном распределении плотность вероятности на интервале (a, b) постоянна, т.е. f(х) = fo = const, а вне (a, b) равна нулю; из условия нормировки (15) найдем значение f0:

= f0 = f0× x = (b-a)f0, откуда

Поэтому:

M(X)= = = (a + b).

Следовательно, математическое ожидание М(Х) совпадает с серединой интервала (a, b), определяющей, т.е. = M(X) = .

Модой Мо(Х) дискретной случайной величины называют ее наиболее вероятное значение (рис.4а), а непрерывной – значение Х, при котором плотность вероятности максимальна (рис.4б).

Медианой (Ме) случайной величины обычно пользуются только для непрерывных случайных величин, хотя формально ее можно определить и для дискретных Х. МедианойМе(Х)случайной величины называют такое значение Х, которое делит все распределение на две равновероятные части, т.е. вероятности Р(Х < Ме) и Р(Х > Ме) оказываются равными между собой:

Р(Х < Ме)= Р(Х > Ме)= .

Поэтому медиану можно вычислить из соотношения:

= .

Графически медиана – это значение случайной величины, ордината которой делит площадь, ограниченную кривой распределения, пополам: S1= S2 (рис. 4в).

Если М(Х), Мо(Х)и Ме(Х) совпадают, то распределение случайной величины называют симметричным, в противном случае – асимметричным.

Характеристики рассеяния – это дисперсия и стандартное отклонение (среднее квадратическое отклонение)

Дисперсия D(X)случайной величины Х определяется как математическое ожидание квадрата отклонения случайной Х от ее математического ожидания М(Х):

D(X) = M[X – M(X)]2 , (20)

или D(X) = M(X2 ) – [M(X)]2. (21)

При конкретных расчетах для дискретной случайной величины эти формулы записываются так:

D(X) = [хi–М(Х)]2 × рi, илиD(X) = хi2 рi – [M(X)]2 (22)

Для непрерывной случайной величины, распределенной в интервале (a,b), они имеют вид:

D(X)= [x–M(X)]2 f(x)dx, илиD(X) = х2 f(x)dx – [M(X)]2, (23)

а для интервала (-∞,+∞):

D(X)= [x–M(X)]2 f(x)dx, илиD(X)= х2 f(x)dx– [M(X)]2. (24)

Дисперсия характеризует рассеяние, разбросанность, значений случайной величины Х относительно ее математического ожидания. Само слово «дисперсия» означает «рассеяние».

Однако дисперсия D(Х) имеет размерность квадрата случайной величины, что весьма неудобно при оценке разброса в физических, биологических, медицинских и других приложениях. Поэтому обычно пользуются параметром, размерность которого совпадает с размерностью Х. Это – среднее квадратическое (иначе – стандартное) отклонение случайной величины Х, которое обозначают s (Х):

s (Х) =. (25)

Итак, математическое ожидание, мода, медиана, дисперсия и среднее квадратическое отклонение являются наиболее употребляемыми числовыми характеристиками случайных величин, каждая из которых выражает какое-нибудь характерное свойство их распределения.

www.ronl.ru