/ Реферат алгоритмы. Алгоритмы реферат
Реферат алгоритмы
Реферат на тему:
Реферат по теме Понятие алгоритма, его свойства. Описание алгоритмов с помощью блок схем на языке Turbo Pascal.
Выполнял ученик 11 Э группы
Баженов Юрий.
Введение. Процессор электронно-вычислительной машины, это чудо техники, умеет, тем не менее, выполнять лишь простейшие команды. Каким же образом компьютер решает сложнейшие задачи обработки информации? Для решения этих задач программист должен составить подробное описание последовательности действий, которые необходимо выполнить центральному процессору компьютера. Составление такого пошагового описания процесса решения задачи называется алгоритмизацией, а алгоритмом называется конечный набор правил, расположенных в определённом логическом порядке, позволяющий исполнителюрешать любую конкретную задачу из некоторого класса однотипных задач. В разных ситуациях в роли исполнителя может выступать электронное или какое-либо иное устройство или человек (например, военнослужащий, охраняющий склад боеприпасов и действующий согласно алгоритмам, записанным в устав караульной службы). ^ Алгоритм. Свойства алгоритма. Само слово «алгоритм» возникло из названия латинского перевода книги арабского математика IX века Аль-Хорезми «Algoritmi de numero Indoru», что можно перевести как «Трактат Аль-Хорезми об арифметическом искусстве индусов». Составление алгоритмов и вопросы их существования являются предметом серьёзных математических исследований. ^ Свойства алгоритма. При составлении и записи алгоритма необходимо обеспечить, чтобы он обладал рядом свойств. Однозначность алгоритма, под которой понимается единственность толкования исполнителем правила построения действий и порядок их выполнения. Чтобы алгоритм обладал этим свойством, он должен быть записан командами из системы команд исполнителя. ^ Конечность алгоритма – обязательность завершения каждого из действий, составляющих алгоритм, и завершимость выполнения алгоритма в целом. Результативность алгоритма, предполагающая, что выполнение алгоритма должно завершиться получением определённых результатов. Массовость, т. е. возможность применения данного алгоритма для решения целого класса задач, отвечающих общей постановке задачи. Для того чтобы алгоритм обладал свойством массовости, следует составлять алгоритм, используя обозначения величин и избегая конкретных значений. ^ Правильность алгоритма, под которой понимается способность алгоритма давать правильные результаты решения поставленных задач. Эффективность – для решения задачи должны использоваться ограниченные ресурсы компьютера (процессорное время, объём оперативной памяти и т. д.). ^ Описание алгоритмов на естественном языке. Если речь идёт о составлении алгоритмов для процессора ЭВМ (электронно-вычислительной машины), исполнителем является процессор. Упрощённая модель процессора содержит устройство считывания данных, стёк (специальную оперативную память небольшого объёма, предназначенную для временного хранения данных) и арифметическое устройство, которое может выполнять арифметические действия. Предположим, что программа, составленная для такого процессора, содержит числовые данные и символы арифметических действий над этими данными. Вот пример такой программы, предназначенной для вычисления сумм двух чисел 2 и 3: 2, 3, + Проследим выполнение этой программы. Первая операция - считывание в стёк значения 2. Затем в стёк считывается второе значение (3). Первое значение при этом сдвигается во вторую ячейку памяти. Третий шаг выполнения программы – вычисление суммы двух считанных значений (они называются операндами). Результат этой операции – значение 5 – записывается в первую ячейку стёка. Был рассмотрен пример простейшей программы. Она является записью алгоритма решения некоторого класса задач – задач вычисления суммы двух чисел. Обозначим эти числа a и b. Тогда алгоритм можно записать следующим образом:
Считать число a.
Считать число b.
Выполнить суммирование c := a + b.
Вывести число c.
Это пример записи алгоритма на естественном языке, то есть на языке человеческого общения. Видно, что формулировка алгоритма не зависит от конкретных значений переменных a и b, поэтому его можно применять для решения достаточно большого числа сходных задач, вместе составляющих целый классзадач суммирования. Алгоритм описывает действия не над конкретными значениями, а над абстрактными объектами. Основными объектами программирования являются переменные. Переменные в программе отличаются от переменных, используемых в записи математических формул. Несмотря на сходство терминов, правила использования переменных в программах для компьютера отличаются от правил работы с математическими переменными. Это различие необходимо уяснить. В программировании переменную можно трактовать как одну или несколько ячеек оперативной памяти компьютера, которым присвоено определённое имя. Содержимое этих ячеек может меняться, но имя переменной остаётся неизменным. В математике значение переменной в рамках определённой задачи неизменно, но меняется в других задачах из данного класса. Именно поэтому конструкция а := а + 1 воспринимается программистом совершенно естественно, а уравнение a = a + 1 математик сочтёт неверным. В первом случае имеется в виду вычисление суммы содержимого ячейки а и числовой константы 1 и занесение полученного результата в ту же ячейку а. Второй случай равносилен неверному тождеству 0 = 1. Оставим алгоритм решения следующей задачи. Пусть заданы два значения x и y. Необходимо сравнить эти значения и напечатать имя большей переменной. Для этой задачи достаточно сравнить оба значения и в зависимости от результата сравнения вывести на печать символ «х» и символ «у»:
Ввести значение x.
Ввести значение y.
Если x < y, то напечатать «у», иначе напечатать «х».
В этом алгоритме используются алгоритмические структуры - линейная последовательность операций иветвление (шаг 3, условный оператор). Последняя структура называется так потому, что после передачи в неё управления выполнение алгоритма может пойти по одному из двух возможных ветвлений. То, какая ветвь будет выбрана, зависит от выполнения условия. Линейная последовательность в данном примере состоит из блоков ввода/вывода данных. Для записи алгоритмов использовался естественный язык. Иногда используют полуформальный язык с ограниченным словарём (часто на основе английского языка), промежуточный между естественным языком и языком программирования. Такой язык называется псевдокодом. Запись алгоритма на псевдокоде называется структурным планом. Псевдокод удобен тем, что позволяет программисту сосредоточиться на формулировке алгоритма, не задумываясь над синтаксическими особенностями конкретного языка программирования. ^ Описание алгоритмов с помощью блок-схем. Для разработки структуры программы удобнее пользоваться записью алгоритма в виде блок-схемы (в англоязычной литературе используется термин flow-chart). Для изображения основных алгоритмических структур и блоков на блок-схемах используют специальные графические символы. Они приведены на рисунке Начало/конец алгоритма Передача управления Ввод данных Блок вычислений Начало (заголовок) цикла Конец цикла Ветвление Вывод данных Составим алгоритм вычисления квадратного корня из произвольного положительного вещественного числа х методом Герона и запишем его на естественном языке, а также в виде блок-схемы. Метод основан на многократном применении формулы: 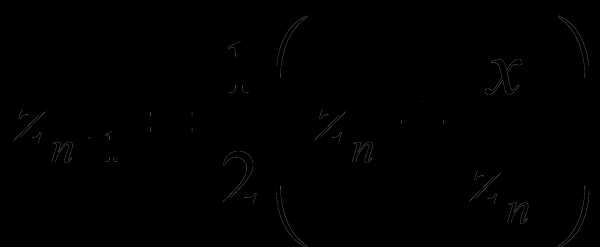 при
при 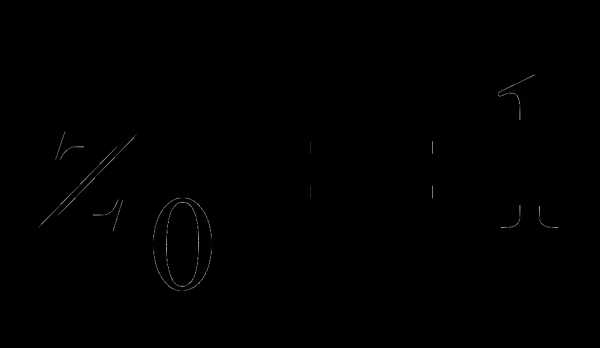 . Числовая последовательность
. Числовая последовательность  в пределе при сходится к искомому значению. Выполним только 5 итераций метода, считая, что при этом будет достигнута достаточно хорошая точность. Обычно десяти итераций метода Герона более чем достаточно для достижения хорошей точность расчёта. Оба варианта записи алгоритма:
в пределе при сходится к искомому значению. Выполним только 5 итераций метода, считая, что при этом будет достигнута достаточно хорошая точность. Обычно десяти итераций метода Герона более чем достаточно для достижения хорошей точность расчёта. Оба варианта записи алгоритма:
| | Ввести х. Присвоить  . . Присвоить  . . Присвоить . Присвоить  . . Если  , то перейти к шагу 4, иначе напечатать значение , то перейти к шагу 4, иначе напечатать значение 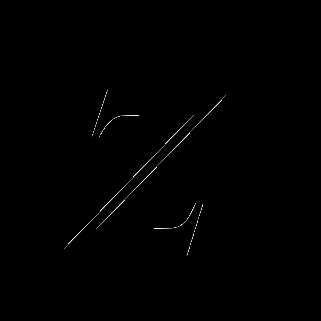 . .
|
А теперь займёмся самым любимым занятием школьников всех времён и народов – решением квадратного уравнения: . Будем полагать, что коэффициенты этого уравнения  ,
, 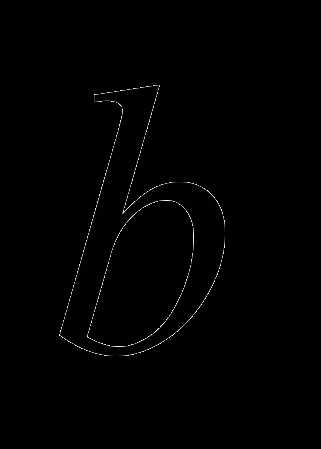 и
и  представляют собой вещественные числа. Простейший случай предполагает, что все коэффициенты отличны от нуля. В зависимости от знака дискриминанта квадратного уравнения возможны три случая:
представляют собой вещественные числа. Простейший случай предполагает, что все коэффициенты отличны от нуля. В зависимости от знака дискриминанта квадратного уравнения возможны три случая:
Если 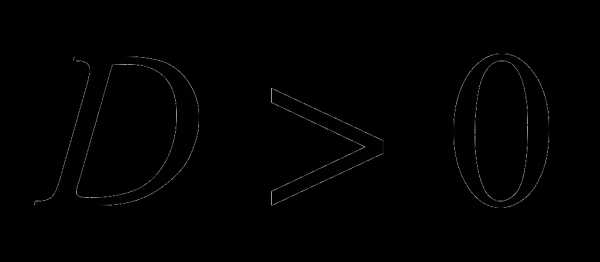 , то имеются два различных вещественных корня, которые можно вычислить по следующим формулам:
, то имеются два различных вещественных корня, которые можно вычислить по следующим формулам:
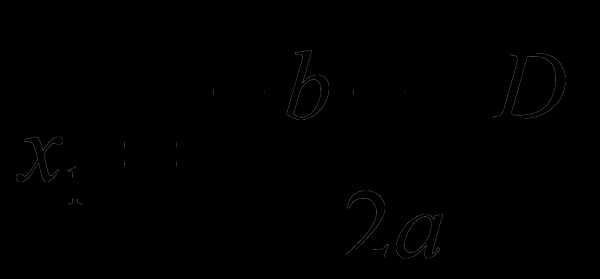 ,
, 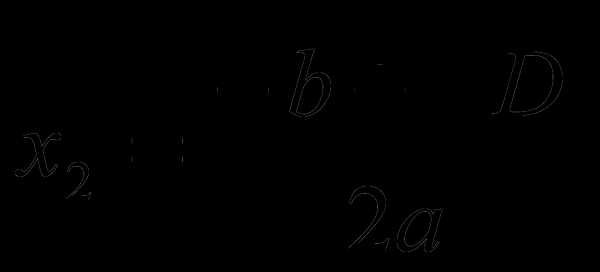 .
.
Если , то имеется единственный корень (точнее, двукратный корень):
 .
.
Если  , то вещественных корней нет.
, то вещественных корней нет.
Блок схема алгоритма приведена на рисунке: 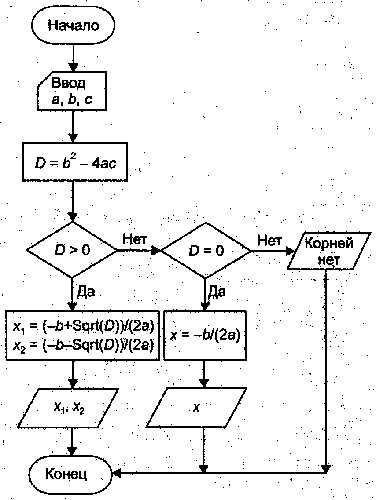 Следует заметить, что приведённый алгоритм предназначен для решения узкого класса задач – квадратных уравнений с «хорошими» коэффициентами. Если допустить, что коэффициенты могут принимать произвольные вещественные значения, есть опасность, что при определённых значениях коэффициента (например,
Следует заметить, что приведённый алгоритм предназначен для решения узкого класса задач – квадратных уравнений с «хорошими» коэффициентами. Если допустить, что коэффициенты могут принимать произвольные вещественные значения, есть опасность, что при определённых значениях коэффициента (например,  ) возникает аварийная ситуация (деление на ноль). Качественный алгоритм и качественная программа должны быть устойчивыми, то есть при любых входных параметрах завершение работы программы должно быть нормальным, хотя, возможно, и сопровождаться предупреждающим сообщением о некорректности входных данных. Свойством устойчивости обладает алгоритм решения квадратного уравнения, приведённый на рисунке: Ра
) возникает аварийная ситуация (деление на ноль). Качественный алгоритм и качественная программа должны быть устойчивыми, то есть при любых входных параметрах завершение работы программы должно быть нормальным, хотя, возможно, и сопровождаться предупреждающим сообщением о некорректности входных данных. Свойством устойчивости обладает алгоритм решения квадратного уравнения, приведённый на рисунке: Ра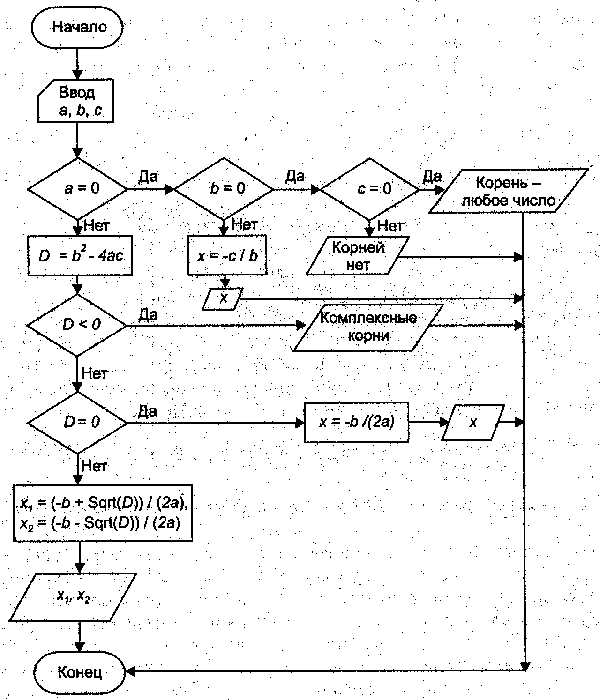 зработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнениятрассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
зработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнениятрассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
| i | z |
| 0 | 1,00000 |
| 1 | 1,50000 |
| 2 | 1,41666 |
| 3 | 1,41421 |
| 4 | 1,41421 |
| 5 | 1,41421 |
Как видно из таблицы, уже после третьей итерации приближенное значение квадратного корня отличается от точного 1,414213 лишь в шестом знаке после запятой. Заключение. Создание алгоритма для решения задач какого-либо типа, его представление исполнителю в удобной для него форме – это творческий акт. Алгоритм может быть представлен различными способами: на разговорном естественном язык; на языке блок-схем; на языке программирования. Выбор и разработка алгоритма и численного метода решения задачи имеют важнейшее значение для успешной работы над программой. Тщательно проработанный алгоритм решения задачи – необходимое условие эффективной работы по составлению алгоритму.
studfiles.net
Реферат Алгоритм
скачатьРеферат на тему:
План:
Введение- 1 Определения алгоритма
- 2 Формальные свойства алгоритмов
- 3 История термина
- 4 Виды алгоритмов
- 5 Наличие исходных данных и некоторого результата
- 6 Форма алгоритмов
- 7 Эффективность алгоритмов
Литература
Введение
Алгори́тм, от имени учёного аль-Хорезми (перс. خوارزمی [al-Khwārazmī]) — точный набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное время. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система.
Ранее часто писали «алгорифм», сейчас такое написание используется редко, но, тем не менее, имеет место (например, Нормальный алгорифм Маркова).
Часто в качестве исполнителя выступает некоторый механизм (компьютер, токарный станок, швейная машина), но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек.
1. Определения алгоритма
Единого «истинного» определения понятия «алгоритм» нет.
«Алгоритм — это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность». (Д. Э. Кнут)
«Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи». (А. Колмогоров)
«Алгоритм — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату». (А. Марков)
«Алгоритм — точное предписание о выполнении в определённом порядке некоторой системы операций, ведущих к решению всех задач данного типа». (Философский словарь / Под ред. М. М. Розенталя)
«Алгоритм — строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд». (Николай Дмитриевич Угринович, учебник «Информатика и информ. технологии»)
«Алгоритм — это последовательность действий, направленных на получение определённого результата за конечное число шагов».
«Алгоритм — однозначно, доступно и кратко (условные понятия — названия этапа) описанная последовательность процедур для воспроизводства процесса с обусловленным задачей алгоритма результатом при заданных начальных условиях. Универсальность (или специализация) алгоритма определяется применимостью и надёжностью данного алгоритма для решения нестандартных задач».
«Алгоритм — это понятные и точные предписания исполнителю совершить конечное число шагов, направленных на решение поставленной задачи».
«Алгоритм — это некоторый конечный набор рассчитанных на определённого исполнителя операций в результате выполнения которых через определённое число шагов может быть достигнута поставленная цель или решена задача определённого типа».
«Алгоритм — это последовательность действий, либо приводящая к решению задачи, либо поясняющая почему это решение получить нельзя».
«Алгоритм — это точная, однозначная, конечная последовательность действий, которую должен выполнить пользователь для достижения конкретной цели либо для решения конкретной задачи или группы задач».
«Алгоритм — это точное предписание, которое задаёт вычислительный (алгоритмический) процесс, начинающийся с произвольного исходного данного и направленный на получение полностью определяемым этим исходным данным результата».
«Алгоритм — это описание последовательности действий, которое ведёт к конечному результату».[]
2. Формальные свойства алгоритмов
Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:
- Дискретность — алгоритм должен представлять процесс решения задачи как последовательное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно.
- Детерминированность (определённость). В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа. Однако при включении метода генерации случайных чисел в список «исходных данных», вероятностный алгоритм становится подвидом обычного.
- Понятность — алгоритм для исполнителя должен включать только те команды, которые ему (исполнителю) доступны, которые входят в его систему команд.
- Завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов.[источник не указан 199 дней] С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.
- Массовость (универсальность). Алгоритм должен быть применим к разным наборам исходных данных.
- Результативность — завершение алгоритма определёнными результатами.
- Алгоритм содержит ошибки, если приводит к получению неправильных результатов либо не даёт результатов вовсе.
- Алгоритм не содержит ошибок, если он даёт правильные результаты для любых допустимых исходных данных.
3. История термина
Современное формальное определение алгоритма было дано в 30—50-х годы XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча — Тьюринга), Н. Винера, А. А. Маркова.
Само слово «алгоритм» происходит от имени учёного Абу Абдуллах Мухаммеда ибн Муса аль-Хорезми (алгоритм — аль-Хорезми). Около 825 года он написал сочинение, в котором впервые дал описание придуманной в Индии позиционной десятичной системы счисления. К сожалению, арабский оригинал книги не сохранился. Аль-Хорезми сформулировал правила вычислений в новой системе и, вероятно, впервые использовал цифру 0 для обозначения пропущенной позиции в записи числа (её индийское название арабы перевели как as-sifr или просто sifr, отсюда такие слова, как «цифра» и «шифр»). Приблизительно в это же время индийские цифры начали применять и другие арабские учёные. В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритмы о счёте индийском»). По-арабски же книга именовалась Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»). Из оригинального названия книги происходит слово Алгебра (алгебра — аль-джебр).
Таким образом, мы видим, что латинизированное имя среднеазиатского учёного было вынесено в заглавие книги, и сегодня ни у кого нет сомнений, что слово «алгоритм» попало в европейские языки именно благодаря этому сочинению. Однако вопрос о его смысле длительное время вызывал ожесточённые споры. На протяжении многих веков происхождению слова давались самые разные объяснения.
Одни выводили algorism из греческих algiros (больной) и arithmos (число). Из такого объяснения не очень ясно, почему числа именно «больные». Или же лингвистам больными казались люди, имеющие несчастье заниматься вычислениями? Своё объяснение предлагал и энциклопедический словарь Брокгауза и Ефрона. В нём алгорифм (кстати, до революции использовалось написание алгориѳм, через фиту) производится «от арабского слова Аль-Горетм, то есть корень». Разумеется, эти объяснения вряд ли можно счесть убедительными.
Упомянутый выше перевод сочинения аль-Хорезми стал первой ласточкой, и в течение нескольких следующих столетий появилось множество других трудов, посвящённых всё тому же вопросу — обучению искусству счёта с помощью цифр. И все они в названии имели слово algoritmi или algorismi.
Про аль-Хорезми позднейшие авторы ничего не знали, но поскольку первый перевод книги начинается словами: «Dixit algorizmi: …» («Аль-Хорезми говорил: …»), всё ещё связывали это слово с именем конкретного человека. Очень распространённой была версия о греческом происхождении книги. В англо-норманнской рукописи XIII века, написанной в стихах, читаем:
"Алгоризм был придуман в Греции. Это часть арифметики. Придуман он был мастером по имени Алгоризм, который дал ему своё имя. И поскольку его звали Алгоризм, Он назвал свою книгу «Алгоризм».
Около 1250 года английский астроном и математик Иоанн Сакробоско написал труд по арифметике Algorismus vulgaris, на столетия ставший основным учебником по вычислениям в десятичной позиционной системе счисления во многих европейских университетах. Во введении Сакробоско назвал автором науки о счёте мудреца по имени Алгус (Algus). А в популярной средневековой поэме «Роман о Розе» (1275—1280) Жана де Мена «греческий философ Алгус» ставится в один ряд с Платоном, Аристотелем, Евклидом и Птолемеем! Встречался также вариант написания имени Аргус (Argus). И хотя, согласно древнегреческой мифологии, корабль «Арго» был построен Ясоном, именно этому Арго приписывалось строительство корабля.
«Мастер Алгус» (или Аргус) стал в средневековой литературе олицетворением счётного искусства. И в уже упоминавшейся «Романе о розе», и в известной итальянской поэме «Цветок», написанной Дуранте, имеются фрагменты, в которых говорится, что даже «mestre Argus» не сумеет подсчитать, сколько раз ссорятся и мирятся влюблённые. Английский поэт Джефри Чосер в поэме «Книга герцогини» (1369 г.) пишет, что даже «славный счётчик Аргус» (noble countour Argu) не сможет счесть чудовищ, явившихся в кошмарных видениях герою.
Впрочем, греческая версия была не единственной. Мифический Алгор (Algor) именовался то королём Кастилии (Rex quodam Castelliae), то индийским королём, то арабским мудрецом (philosophus Algus nomine Arabicus).
Однако со временем такие объяснения всё менее занимали математиков, и слово algorism (или algorismus), неизменно присутствовавшее в названиях математических сочинений, обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многие европейские языки. Например, с пометкой «устар.» оно присутствует в представительном словаре английского языка Webster’s New World Dictionary, изданном в 1957 г.
Алгоритм — это искусство счёта с помощью цифр, но поначалу слово «цифра» относилось только к нулю. Знаменитый французский трувер Готье де Куанси (Gautier de Coincy, 1177—1236) в одном из стихотворений использовал слова algorismus-cipher (которые означали цифру 0) как метафору для характеристики абсолютно никчёмного человека. Очевидно, понимание такого образа требовало соответствующей подготовки слушателей, а это означает, что новая система счисления уже была им достаточно хорошо известна.
Многие века абак был фактически единственным средством для практичных вычислений, им пользовались и купцы, и менялы, и учёные. Достоинства вычислений на счётной доске разъяснял в своих сочинениях такой выдающийся мыслитель, как Герберт Аврилакский (938—1003), ставший в 999 г. папой римским под именем Сильвестра II. Новое с огромным трудом пробивало себе дорогу, и в историю математики вошло упорное противостояние лагерей алгорисмиков и абацистов (иногда называемых гербекистами), которые пропагандировали использование для вычислений абака вместо арабских цифр. Интересно, что известный французский математик Николя Шюке (Nicolas Chuquet, 1445—1488) в реестр налогоплательщиков города Лиона был вписан как алгорисмик (algoriste). Но прошло не одно столетие, прежде чем новый способ счёта окончательно утвердился, столько времени потребовалось, чтобы выработать общепризнанные обозначения, усовершенствовать и приспособить к записи на бумаге методы вычислений. В Западной Европе учителей арифметики вплоть до XVII века продолжали называть «магистрами абака», как, например, математика Никколо Тарталью (1500—1557).
Итак, сочинения по искусству счёта назывались Алгоритмами. Из многих сотен можно выделить и такие необычные, как написанный в стихах трактат Carmen de Algorismo (латинское carmen и означает стихи) Александра де Вилла Деи (Alexander de Villa Dei, ум. 1240) или учебник венского астронома и математика Георга Пурбаха (Georg Peurbach, 1423—1461) Opus algorismi jocundissimi («Веселейшее сочинение по алгоритму»).
Постепенно значение слова расширялось. Учёные начинали применять его не только к сугубо вычислительным, но и к другим математическим процедурам. Например, около 1360 г. французский философ Николай Орем (Nicolaus Oresme, 1323/25-1382) написал математический трактат Algorismus proportionum («Вычисление пропорций»), в котором впервые использовал степени с дробными показателями и фактически вплотную подошёл к идее логарифмов. Когда же на смену абаку пришёл так называемый счёт на линиях, многочисленные руководства по нему стали называть Algorithmus linealis, то есть правила счёта на линиях.
Можно обратить внимание на то, что первоначальная форма algorismi спустя какое-то время потеряла последнюю букву, и слово приобрело более удобное для европейского произношения вид algorism. Позднее и оно, в свою очередь, подверглось искажению, скорее всего, связанному со словом arithmetic.
В 1684 году Готфрид Лейбниц в сочинении Nova Methodvs pro maximis et minimis, itemque tangentibus… впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.
В XVIII веке в одном из германских математических словарей, Vollstandiges mathematisches Lexicon (изданном в Лейпциге в 1747 г.), термин algorithmus всё ещё объясняется как понятие о четырёх арифметических операциях. Но такое значение не было единственным, ведь терминология математической науки в те времена ещё только формировалась. В частности, выражение algorithmus infinitesimalis применялось к способам выполнения действий с бесконечно малыми величинами. Пользовался словом алгоритм и Леонард Эйлер, одна из работ которого так и называется — «Использование нового алгоритма для решения проблемы Пелля» (De usu novi algorithmi in problemate Pelliano solvendo). Мы видим, что понимание Эйлером алгоритма как синонима способа решения задачи уже очень близко к современному.
Однако потребовалось ещё почти два столетия, чтобы все старинные значения слова вышли из употребления. Этот процесс можно проследить на примере проникновения слова «алгоритм» в русский язык.
Историки датируют 1691 годом один из списков древнерусского учебника арифметики, известного как «Счётная мудрость». Это сочинение известно во многих вариантах (самые ранние из них почти на сто лет старше) и восходит к ещё более древним рукописям XVI в. По ним можно проследить, как знание арабских цифр и правил действий с ними постепенно распространялось на Руси. Полное название этого учебника — «Сия книга, глаголемая по еллински и по гречески арифметика, а по немецки алгоризма, а по русски цифирная счётная мудрость».
Таким образом, слово «алгоритм» понималось первыми русскими математиками так же, как и в Западной Европе. Однако его не было ни в знаменитом словаре В. И. Даля, ни спустя сто лет в «Толковом словаре русского языка» под редакцией Д. Н. Ушакова (1935 г.). Зато слово «алгорифм» можно найти и в популярном дореволюционном Энциклопедическом словаре братьев Гранат, и в первом издании Большой советской энциклопедии (БСЭ), изданном в 1926 г. И там, и там оно трактуется одинаково: как правило, по которому выполняется то или иное из четырёх арифметических действий в десятичной системе счисления. Однако к началу XX в. для математиков слово «алгоритм» уже означало любой арифметический или алгебраический процесс, выполняемый по строго определённым правилам, и это объяснение также даётся в следующих изданиях БСЭ.
Алгоритмы становились предметом всё более пристального внимания учёных, и постепенно это понятие заняло одно из центральных мест в современной математике. Что же касается людей, от математики далёких, то к началу сороковых годов это слово они могли услышать разве что во время учёбы в школе, в сочетании «алгоритм Евклида». Несмотря на это, алгоритм всё ещё воспринимался как термин сугубо специальный, что подтверждается отсутствием соответствующих статей в менее объёмных изданиях. В частности, его нет даже в десятитомной Малой советской энциклопедии (1957 г.), не говоря уже об однотомных энциклопедических словарях. Но зато спустя десять лет, в третьем издании Большой советской энциклопедии (1969 г.) алгоритм уже характеризуется как одна из основных категорий математики, «не обладающих формальным определением в терминах более простых понятий, и абстрагируемых непосредственно из опыта». Как мы видим, отличие даже от трактовки первым изданием БСЭ разительное! За сорок лет алгоритм превратился в одно из ключевых понятий математики, и признанием этого стало включение слова уже не в энциклопедии, а в словари. Например, оно присутствует в академическом «Словаре русского языка» (1981 г.) именно как термин из области математики.
Одновременно с развитием понятия алгоритма постепенно происходила и его экспансия из чистой математики в другие сферы. И начало ей положило появление компьютеров, благодаря которому слово «алгоритм» вошло в 1985 г. во все школьные учебники информатики и обрело новую жизнь. Вообще можно сказать, что его сегодняшняя известность напрямую связана со степенью распространения компьютеров. Например, в третьем томе «Детской энциклопедии» (1959 г.) о вычислительных машинах говорится немало, но они ещё не стали чем-то привычным и воспринимаются скорее как некий атрибут светлого, но достаточно далёкого будущего. Соответственно и алгоритмы ни разу не упоминаются на её страницах. Но уже в начале 70-х гг. прошлого столетия, когда компьютеры перестали быть экзотической диковинкой, слово «алгоритм» стремительно входит в обиход. Это чутко фиксируют энциклопедические издания. В «Энциклопедии кибернетики» (1974 г.) в статье «Алгоритм» он уже связывается с реализацией на вычислительных машинах, а в «Советской военной энциклопедии» (1976 г.) даже появляется отдельная статья «Алгоритм решения задачи на ЭВМ». За последние полтора-два десятилетия компьютер стал неотъемлемым атрибутом нашей жизни, компьютерная лексика становится всё более привычной. Слово «алгоритм» в наши дни известно, вероятно, каждому. Оно уверенно шагнуло даже в разговорную речь, и сегодня мы нередко встречаем в газетах и слышим в выступлениях политиков выражения вроде «алгоритм поведения», «алгоритм успеха» или даже «алгоритм предательства». Академик Н. Н. Моисеев назвал свою книгу «Алгоритмы развития», а известный врач Н. М. Амосов — «Алгоритм здоровья» и «Алгоритмы разума». А это означает, что слово живёт, обогащаясь всё новыми значениями и смысловыми оттенками.
4. Виды алгоритмов
Особую роль выполняют прикладные алгоритмы, предназначенные для решения определённых прикладных задач. Алгоритм считается правильным, если он отвечает требованиям задачи (например, даёт физически правдоподобный результат). Алгоритм (программа) содержит ошибки, если для некоторых исходных данных он даёт неправильные результаты, сбои, отказы или не даёт никаких результатов вообще. Последний тезис используется в олимпиадах по алгоритмическому программированию, чтобы оценить составленные участниками программы.
Важную роль играют рекурсивные алгоритмы (алгоритмы, вызывающие сами себя до тех пор, пока не будет достигнуто некоторое условие возвращения). Начиная с конца XX — начала XXI века активно разрабатываются параллельные алгоритмы, предназначенные для вычислительных машин, способных выполнять несколько операций одновременно.
5. Наличие исходных данных и некоторого результата
Алгоритм — это точно определённая инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так, алгоритм сложения применим к любой паре натуральных чисел. В этом выражается его свойство массовости, то есть возможности применять многократно один и тот же алгоритм для любой задачи одного класса.
Для разработки алгоритмов и программ используется алгоритмизация — процесс систематического составления алгоритмов для решения поставленных прикладных задач. Алгоритмизация считается обязательным этапом в процессе разработки программ и решении задач на ЭВМ. Именно для прикладных алгоритмов и программ принципиально важны детерминированность, результативность и массовость, а также правильность результатов решения поставленных задач.
Алгоритм — это понятное и точное предписание, исполнительно совершить последовательность действий, направленных на достижение цели.
6. Форма алгоритмов
Алгоритм может быть записан словами и изображён схематически. Обычно сначала (на уровне идеи) алгоритм описывается словами, но по мере приближения к реализации он обретает всё более формальные очертания и формулировку на языке, понятном исполнителю (например, машинный код). Например, для описания алгоритма применяются блок-схемы. Другим вариантом описания, не зависимым от языка программирования, является псевдокод.
7. Эффективность алгоритмов
Хотя в определении алгоритма требуется лишь конечность числа шагов, требуемых для достижения результата, на практике выполнение даже хотя бы миллиарда шагов является слишком медленным. Также обычно есть другие ограничения (на размер программы, на допустимые действия). В связи с этим вводят такие понятия как сложность алгоритма (временна́я, по размеру программы, вычислительная и др.).
Для каждой задачи может существовать множество алгоритмов, приводящих к цели. Увеличение эффективности алгоритмов составляет одну из задач современной информатики. В 50-х гг. XX века появилась даже отдельная её область — быстрые алгоритмы. В частности, в известной всем с детства задаче об умножении десятичных чисел обнаружился ряд алгоритмов, позволяющих существенно (в асимптотическом смысле) ускорить нахождение произведения. См. быстрое умножение
Ярким примером является алгоритм Чудновского для вычисления числа π.
Литература
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
- Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Порублев Илья Николаевич, Ставровский Андрей Борисович Алгоритмы и программы. Решение олимпиадных задач. — М.: «Вильямс», 2007. — С. 480. — ISBN 978-5-8459-1244-2
wreferat.baza-referat.ru
Понятие алгоритма, его свойства. Описание алгоритмов с помощью блок схем на языке Turbo Pascal
ИНСТИТУТ
КАЛИНИНГРАДСКАЯ ВЫСШАЯ ШКОЛА УПРАВЛЕНИЯ
РЕФЕРАТ
по теме
Понятие алгоритма, его свойства. Описание алгоритмов с помощью блок схем на языке Turbo Pascal
студент: Чижов Н. А.
группа: 02-СА9(2)
Калининград
2003
Содержание:
| Введение……………………………………………………………… Алгоритм. Свойства алгоритма…………………………………….. Описание алгоритмов на естественном языке…………………….. Описание алгоритмов с помощью блок-схем……………………... Заключение…………………………………………………………... Список литературы………………………………………………….. | 3 4 5 8 13 14 |
Введение.
Процессор электронно-вычислительной машины, это чудо техники, умеет, тем не менее, выполнять лишь простейшие команды. Каким же образом компьютер решает сложнейшие задачи обработки информации? Для решения этих задач программист должен составить подробное описание последовательности действий, которые необходимо выполнить центральному процессору компьютера. Составление такого пошагового описания процесса решения задачи называется алгоритмизацией, а алгоритмом называется конечный набор правил, расположенных в определённом логическом порядке, позволяющий исполнителю решать любую конкретную задачу из некоторого класса однотипных задач. В разных ситуациях в роли исполнителя может выступать электронное или какое-либо иное устройство или человек (например, военнослужащий, охраняющий склад боеприпасов и действующий согласно алгоритмам, записанным в устав караульной службы).
Алгоритм. Свойства алгоритма.
Само слово «алгоритм» возникло из названия латинского перевода книги арабского математика IX века Аль-Хорезми «Algoritmi de numero Indoru», что можно перевести как «Трактат Аль-Хорезми об арифметическом искусстве индусов». Составление алгоритмов и вопросы их существования являются предметом серьёзных математических исследований.
Свойства алгоритма. При составлении и записи алгоритма необходимо обеспечить, чтобы он обладал рядом свойств.
Однозначность алгоритма, под которой понимается единственность толкования исполнителем правила построения действий и порядок их выполнения. Чтобы алгоритм обладал этим свойством, он должен быть записан командами из системы команд исполнителя.
Конечность алгоритма – обязательность завершения каждого из действий, составляющих алгоритм, и завершимость выполнения алгоритма в целом.
Результативность алгоритма, предполагающая, что выполнение алгоритма должно завершиться получением определённых результатов.
Массовость, т. е. возможность применения данного алгоритма для решения целого класса задач, отвечающих общей постановке задачи. Для того чтобы алгоритм обладал свойством массовости, следует составлять алгоритм, используя обозначения величин и избегая конкретных значений.
Правильность алгоритма, под которой понимается способность алгоритма давать правильные результаты решения поставленных задач.
Эффективность – для решения задачи должны использоваться ограниченные ресурсы компьютера (процессорное время, объём оперативной памяти и т. д.).
Описание алгоритмов на естественном языке.
Если речь идёт о составлении алгоритмов для процессора ЭВМ (электронно-вычислительной машины), исполнителем является процессор. Упрощённая модель процессора содержит устройство считывания данных, стёк (специальную оперативную память небольшого объёма, предназначенную для временного хранения данных) и арифметическое устройство, которое может выполнять арифметические действия.
Предположим, что программа, составленная для такого процессора, содержит числовые данные и символы арифметических действий над этими данными. Вот пример такой программы, предназначенной для вычисления сумм двух чисел 2 и 3:
2, 3, +
Проследим выполнение этой программы. Первая операция - считывание в стёк значения 2. Затем в стёк считывается второе значение (3). Первое значение при этом сдвигается во вторую ячейку памяти. Третий шаг выполнения программы – вычисление суммы двух считанных значений (они называются операндами). Результат этой операции – значение 5 – записывается в первую ячейку стёка.
Был рассмотрен пример простейшей программы. Она является записью алгоритма решения некоторого класса задач – задач вычисления суммы двух чисел. Обозначим эти числа a и b. Тогда алгоритм можно записать следующим образом:
Считать число a.
Считать число b.
Выполнить суммирование c := a + b.
Вывести число c.
Это пример записи алгоритма на естественном языке, то есть на языке человеческого общения. Видно, что формулировка алгоритма не зависит от конкретных значений переменных a и b, поэтому его можно применять для решения достаточно большого числа сходных задач, вместе составляющих целый класс задач суммирования. Алгоритм описывает действия не над конкретными значениями, а над абстрактными объектами.
Основными объектами программирования являются переменные. Переменные в программе отличаются от переменных, используемых в записи математических формул. Несмотря на сходство терминов, правила использования переменных в программах для компьютера отличаются от правил работы с математическими переменными. Это различие необходимо уяснить. В программировании переменную можно трактовать как одну или несколько ячеек оперативной памяти компьютера, которым присвоено определённое имя. Содержимое этих ячеек может меняться, но имя переменной остаётся неизменным. В математике значение переменной в рамках определённой задачи неизменно, но меняется в других задачах из данного класса. Именно поэтому конструкция
а := а + 1
воспринимается программистом совершенно естественно, а уравнение
a = a + 1
математик сочтёт неверным. В первом случае имеется в виду вычисление суммы содержимого ячейки а и числовой константы 1 и занесение полученного результата в ту же ячейку а. Второй случай равносилен неверному тождеству 0 = 1.
Оставим алгоритм решения следующей задачи. Пусть заданы два значения x и y. Необходимо сравнить эти значения и напечатать имя большей переменной. Для этой задачи достаточно сравнить оба значения и в зависимости от результата сравнения вывести на печать символ «х» и символ «у»:
Ввести значение x.
Ввести значение y.
Если x < y, то напечатать «у», иначе напечатать «х».
В этом алгоритме используются алгоритмические структуры - линейная последовательность операций и ветвление (шаг 3, условный оператор). Последняя структура называется так потому, что после передачи в неё управления выполнение алгоритма может пойти по одному из двух возможных ветвлений. То, какая ветвь будет выбрана, зависит от выполнения условия. Линейная последовательность в данном примере состоит из блоков ввода/вывода данных.
Для записи алгоритмов использовался естественный язык. Иногда используют полуформальный язык с ограниченным словарём (часто на основе английского языка), промежуточный между естественным языком и языком программирования. Такой язык называется псевдокодом. Запись алгоритма на псевдокоде называется структурным планом. Псевдокод удобен тем, что позволяет программисту сосредоточиться на формулировке алгоритма, не задумываясь над синтаксическими особенностями конкретного языка программирования.
Описание алгоритмов с помощью блок-схем.
Для разработки структуры программы удобнее пользоваться записью алгоритма в виде блок-схемы (в англоязычной литературе используется термин flow-chart). Для изображения основных алгоритмических структур и блоков на блок-схемах используют специальные графические символы. Они приведены на рисунке
Начало/конец алгоритма
Передача управления
Ввод данных
Блок вычислений
Начало (заголовок) цикла
Конец цикла
Ветвление
Вывод данных
Составим алгоритм вычисления квадратного корня из произвольного положительного вещественного числа х методом Герона и запишем его на естественном языке, а также в виде блок-схемы. Метод основан на многократном применении формулы:
при
.
Числовая последовательность в пределе при сходится к искомому значению. Выполним только 5 итераций метода, считая, что при этом будет достигнута достаточно хорошая точность. Обычно десяти итераций метода Герона более чем достаточно для достижения хорошей точность расчёта. Оба варианта записи алгоритма:
| | Ввести х. Присвоить . Присвоить . Присвоить . Присвоить . Если , то перейти к шагу 4, иначе напечатать значение .
|
А теперь займёмся самым любимым занятием школьников всех времён и народов – решением квадратного уравнения:
.
Будем полагать, что коэффициенты этого уравнения , и представляют собой вещественные числа. Простейший случай предполагает, что все коэффициенты отличны от нуля. В зависимости от знака дискриминанта квадратного уравнения
возможны три случая:
Если , то имеются два различных вещественных корня, которые можно вычислить по следующим формулам:
, .
Если , то имеется единственный корень (точнее, двукратный корень):
.
Если , то вещественных корней нет.
Блок схема алгоритма приведена на рисунке:

Следует заметить, что приведённый алгоритм предназначен для решения узкого класса задач – квадратных уравнений с «хорошими» коэффициентами. Если допустить, что коэффициенты могут принимать произвольные вещественные значения, есть опасность, что при определённых значениях коэффициента (например, ) возникает аварийная ситуация (деление на ноль). Качественный алгоритм и качественная программа должны быть устойчивыми, то есть при любых входных параметрах завершение работы программы должно быть нормальным, хотя, возможно, и сопровождаться предупреждающим сообщением о некорректности входных данных. Свойством устойчивости обладает алгоритм решения квадратного уравнения, приведённый на рисунке:
Р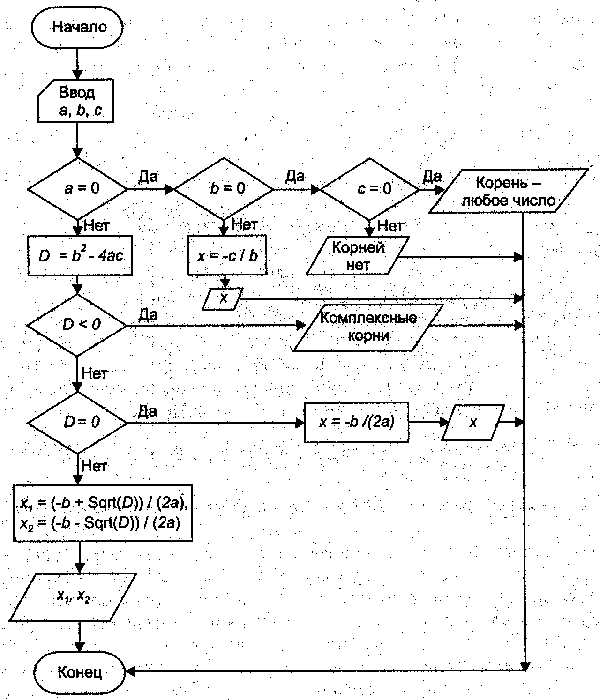 азработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнения трассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
азработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнения трассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
| i | z |
| 0 | 1,00000 |
| 1 | 1,50000 |
| 2 | 1,41666 |
| 3 | 1,41421 |
| 4 | 1,41421 |
| 5 | 1,41421 |
Как видно из таблицы, уже после третьей итерации приближенное значение квадратного корня отличается от точного 1,414213 лишь в шестом знаке после запятой.
Заключение.
Создание алгоритма для решения задач какого-либо типа, его представление исполнителю в удобной для него форме – это творческий акт. Алгоритм может быть представлен различными способами: на разговорном естественном язык; на языке блок-схем; на языке программирования. Выбор и разработка алгоритма и численного метода решения задачи имеют важнейшее значение для успешной работы над программой. Тщательно проработанный алгоритм решения задачи – необходимое условие эффективной работы по составлению алгоритму.
Список литературы.
Коляда М. Г. Окно в удивительный мир информатики. – Д.: Сталкер, 1997.
Немнюгин С. А. Turbo Pascal: практикум. – СПб: Питер, 2003.
Попов В. Б. Turbo Pascal для школьников: Учеб. пособие. – М.: Финансы и статистика, 2000.
Турбо Паскаль 7.0. Самоучитель. – СПб.: Питер; К.: Издательская группа BHV, 2002.
topref.ru
Алгоритмы — реферат
Министерство образования и науки РФ
ФГОУ СПО КСК
Реферат
на тему:
«Алгоритмы»
Выполнили: студентки гр. ГК-9-11 Сучевич Е., Марага О., Нигметзянова А.
Проверил: Азизов Р.Х.
Казань, 2012.
Содержание:
1. Алгоритм | 3 |
2. Виды алгоритмов | 4 |
3. Способы записи алгоритмов | 7 |
4. Список литературы | 10 |
Что такое алгоритм в информатике?
Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге "Об индийском счете" он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных. Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, - процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.
Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата». Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.
Такими свойствами являются:
• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
На основании этих свойств иногда дается определение алгоритма, например: “Алгоритм – это последовательность математических, логических или вместе взятых операций, отличающихся детерменированностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов”. [1]
Виды алгоритмов:
- Линейные - алгоритмы, в которых команды должны быть выполнены одна за другой. Программа имеет линейную структуру, если все операторы (команды) выполняются последовательно друг за другом.
[2]
- С ветвлением – это алгоритмическая конструкция, в которой в зависимости от условия выполняется та или иная последовательность действий. Если ветвление определяет действия для верного и неверного условия (содержит две ветки), то это полная форма ветвления. Если ветвление описывает действия только для верного условия, то это неполная форма. Полную форму ветвления используют в предложениях типа: если <условие> то .. иначе .. Неполную форму ветвления можно распознать в предложениях типа: если <условие> то …
Условный оператор
Условный оператор (оператор ветвления) описывается следующим образом: if условие then операторы else операторы это полная форма ветвления, а также существует неполная форма: if условие then операторы Для описания алгоритмов ветвления в графической форме используется специальный графический символ, имеющий одну входную вершину и две выходных, по одной из которых идет дальнейшее выполнение алгоритма:
Блок схема полной формы ветвления имеет следующий вид:
где Q - условие ветвления D1,D2 - действия неполная форма:
где Q - условие ветвления D – действия. [3]
3. Циклические - описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. Циклические алгоритмы бывают двух типов:
Циклы со счетчиком, в которых какие-то действия выполняются определенное число раз;
Циклы с условием, в которых тело цикла выполняется, в зависимости от какого-либо условия. Различают циклы с предусловием и постусловием.
Для счетчика от нач. значения до кон. значения выполнить действие.
Часто бывает так, что необходимо повторить тело цикла, но заранее неизвестно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия. Такие циклы называются циклы с условием. Циклы, в которых сначала проверяется условие, а затем, возможно, выполняется тело цикла, называют циклы с предусловием. Если условие проверяется после первого выполнения тела цикла, то циклы называются циклы с постусловием.
[4]
Способы записи.
Для записи алгоритмов используют самые разнообразные средства. Выбор средства определяется типом исполняемого алгоритма. Выделяют следующие основные способы записи алгоритмов:
- вербальный, когда алгоритм описывается на человеческом языке;
- символьный, когда алгоритм описывается с помощью набора символов;
- графический, когда алгоритм описывается с помощью набора графических изображений.
Общепринятыми способами записи являются графическая запись с помощью блок-схем и символьная запись с помощью какого-либо алгоритмического языка.
Описание алгоритма с помощью блок схем осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Написание алгоритмов с помощью блок-схем регламентируется ГОСТом. Внешний вид основных блоков, применяемых при написании блок схем, приведен на рисунке:
В зависимости от последовательности выполнения действий в алгоритме выделяют алгоритмы линейной, разветвленной и циклической структуры.
В алгоритмах линейной структуры действия выполняются последовательно одно за другим:
В алгоритмах разветвленной структуры в зависимости от выполнения или невыполнения какого-либо условия производятся различные последовательности действий. Каждая такая последовательность действий называется ветвью алгоритма.
В алгоритмах циклической структуры в зависимости от выполнения или невыполнения какого-либо условия выполняется повторяющаяся последовательность действий, называющаяся телом цикла. Вложенным называется цикл, находящийся внутри тела другого цикла. Различают циклы с предусловием и послеусловием:
Итерационным называется цикл, число повторений которого не задается, а определяется в ходе выполнения цикла. В этом случае одно повторение цикла называется итерацией. [5]
Список литературы:
- http://www.algoritmy.info/
- http://www.about.sch2451.edusite.ru/p19aa1.html
- http://pascalsupport.ucoz.ru/publ/linejnye_algoritmja_algoritmy_vetvlenija_ciklicheskie_algoritmy/1-1-0-2
- http://www.klyaksa.net/htm/exam/exam2007/exam_9_2007/bilet07.htm
- http://inf.e-alekseev.ru/text/Block_schem.html
myunivercity.ru
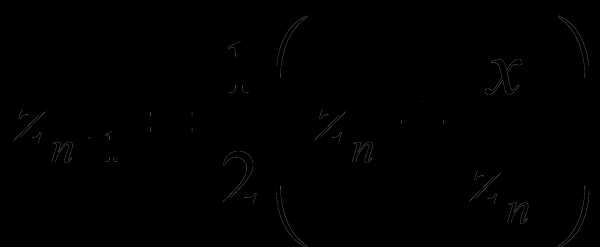 при
при 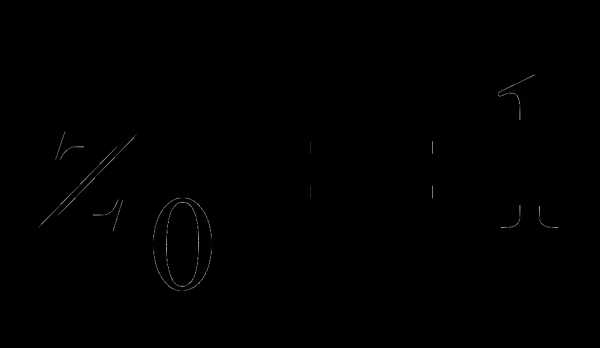 . Числовая последовательность
. Числовая последовательность  в пределе при сходится к искомому значению. Выполним только 5 итераций метода, считая, что при этом будет достигнута достаточно хорошая точность. Обычно десяти итераций метода Герона более чем достаточно для достижения хорошей точность расчёта. Оба варианта записи алгоритма:
в пределе при сходится к искомому значению. Выполним только 5 итераций метода, считая, что при этом будет достигнута достаточно хорошая точность. Обычно десяти итераций метода Герона более чем достаточно для достижения хорошей точность расчёта. Оба варианта записи алгоритма: .
. .
. .
. , то перейти к шагу 4, иначе напечатать значение
, то перейти к шагу 4, иначе напечатать значение  .
. ,
,  и
и  представляют собой вещественные числа. Простейший случай предполагает, что все коэффициенты отличны от нуля. В зависимости от знака дискриминанта квадратного уравнения возможны три случая:
представляют собой вещественные числа. Простейший случай предполагает, что все коэффициенты отличны от нуля. В зависимости от знака дискриминанта квадратного уравнения возможны три случая:  , то имеются два различных вещественных корня, которые можно вычислить по следующим формулам:
, то имеются два различных вещественных корня, которые можно вычислить по следующим формулам: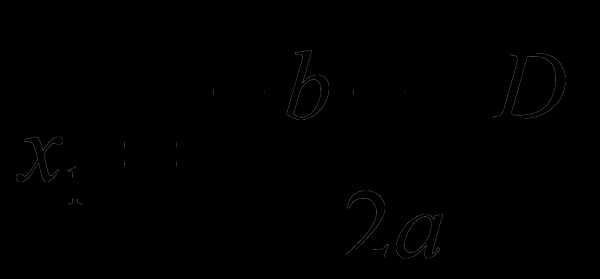 ,
, 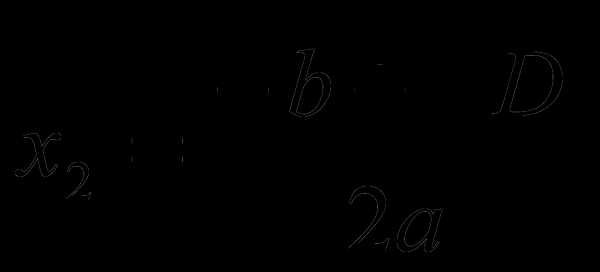 .
.  .
.  , то вещественных корней нет.
, то вещественных корней нет. Следует заметить, что приведённый алгоритм предназначен для решения узкого класса задач – квадратных уравнений с «хорошими» коэффициентами. Если допустить, что коэффициенты могут принимать произвольные вещественные значения, есть опасность, что при определённых значениях коэффициента (например,
Следует заметить, что приведённый алгоритм предназначен для решения узкого класса задач – квадратных уравнений с «хорошими» коэффициентами. Если допустить, что коэффициенты могут принимать произвольные вещественные значения, есть опасность, что при определённых значениях коэффициента (например,  ) возникает аварийная ситуация (деление на ноль). Качественный алгоритм и качественная программа должны быть устойчивыми, то есть при любых входных параметрах завершение работы программы должно быть нормальным, хотя, возможно, и сопровождаться предупреждающим сообщением о некорректности входных данных. Свойством устойчивости обладает алгоритм решения квадратного уравнения, приведённый на рисунке: Ра
) возникает аварийная ситуация (деление на ноль). Качественный алгоритм и качественная программа должны быть устойчивыми, то есть при любых входных параметрах завершение работы программы должно быть нормальным, хотя, возможно, и сопровождаться предупреждающим сообщением о некорректности входных данных. Свойством устойчивости обладает алгоритм решения квадратного уравнения, приведённый на рисунке: Ра зработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнениятрассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
зработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнениятрассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
 азработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнения трассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
азработанный программистом алгоритм должен давать правильный ответ. Проверка алгоритма может оказаться непростым делом. В простых случаях такая проверка может быть выполнена с помощью заполнения трассировочной таблицы. Каждый столбец такой таблицы соответствует определённой переменной, а каждая строка – одному шагу алгоритма. Для заполнения таблицы необходимо шаг за шагом проследить выполнение алгоритма, записывая в таблицу текущие значения выбранных для трассировки переменных. Такой метод позволяет выявить логические ошибки, допущенные при составлении или записи алгоритма, и определить, верен ли окончательный ответ. Составим в качестве примера трассировочную таблицу для алгоритма Герона вычисления квадратного корня из числа 2.
