P* — множество слов над алфавитом Р, и называется правилом подстановки. Смысл этогоправила состоит в том, что обрабатываемое слово w просматривается слеванаправо и ищется вхождение в него слова a.

Определение.3.1. Слово aназывается вхождением в слово w, если существуют такие слова b и n надтем же алфавитом, что и a и w, для которых верно: w=ban.

Если вхождение a в wнайдено, то слово a заменяется на слово g.

Все правила постановки упорядочиваются.Сначала ищется вхождение для первого правила подстановки. Если оно найдено, топроисходит подстановка и преобразуемое слово опять просматривается слеванаправо в поисках вхождения. Если вхождение для первого правила не найдено, тоищется вхождение для второго правила и т.д. Если вхождение найдено для i-го правила подстановки, то происходит подстановка, и просмотрправил начинается с первого, а слово просматривается сначала и слева направо.

Вся совокупность правил подстановкиназывается схемой алгоритма.

Правило начала — просмотр правил всегданачинается с первого.

Правило окончания — выполнение алгоритмазаканчивается, если:

было применено правило подстановки вида a a g,

не применимо ни одно правило подстановкииз схемы алгоритма.

7. Правило размещения результата — слово, полученное после окончания выполнения алгоритма.

Рассмотрим пример 1 из лекции 2:

построить алгоритм для вычисления

U(n)=n+1;

S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.

Cхемаэтого НАМ показана на рисунке 3.1.

Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов.

Увеличиваем на единицу, начиная с цифр младших разрядов.

Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове.

Рис.3.1. Схема НАМ для вычисления U1(n)=n+1

Нетрудно сообразить, что сложностьэтого алгоритма, выраженная в количестве выполненных правил подстановки, будетравна:

(k+1)+(l+1),

где k — количество цифр в n, l — количество 9, которые были увеличены на 1.

Но в любом случае сложность НАМ для U1(n) больше сложности Машины Тьюринга для этой же функции, котораяравнялась k+1.

Обратите внимание, что у НАМ порядокследования правил подстановки в схеме алгоритма существенно влияет нарезультат, в то время как для МТ он не существеннен.

Построим НАМ для примера 2 из лекции 2:

построить алгоритм для вычисления

U2((n)1)=(n-1)1

Итак,S={|}; W=S; V=Æ, т.е. пусто.

| a

Cложностьэтого алгоритма равна 1, в то время как сложность алгоритма для Машины Тьюрингаравнялась n.

Теперь построим НАМ для примера 3 излекции 2:

построить алгоритм для вычисления

U3((n)1)=(n)10

S={|}; W={0,1,2,3,4,5,6,7,8,9}; V=Æ

Схема этого алгоритма приведена нарисунке 3.2.

1|®2

2|®3

3|®4

4|®5

5|®6

6|®7

7|®8

8|®9

9|®|0

|0®10

0|®1

|®0|

Рис. 3.2. Схема НАМ для вычисления U3((n)1)=(n)10.

Сложность этого НАМ будет n+[log10n], что существенно меньше сложности для Машины Тьюринга,вычисляющей эту функцию, которая равнялась n2+[log10n(log10n+1)].

Реализацию функции U4 сравнения двух целых чисел оставляем читателю в качествеупражнения.

Замечание: исходное слово надо задать вформе /> * />

Для нормальных алгоритмов Марковасправедлив тезис, аналогичный тезису Тьюринга.

Тезис Маркова: Для любой интуитивновычислимой функции существует алгоритм, ее вычисляющий.

Построение алгоритмов из алгоритмов.

До сих пор, строя ту или иную МТ, илиНАМ мы каждый раз все делали заново. Естественно задать вопрос, а нельзя ли припостроении, например, новой МТ пользоваться уже построенной ранее МТ.

Например, МТ3 из примера 3

U3((n)1)=(n)10

по существу есть надлежащим образомобъединенные МТ для U1(n)=n+1 и U2((n)1)=(n-1)1.

Аналогичный вопрос можно сформулироватьдля НАМ. Другими словами можно ли аккумулировать знания в форме алгоритмов так,чтобы из них можно было строить другие алгоритмы.

Мы рассмотрим эту проблемуприменительно к МТ. Однако все сформулированные нами утверждения будутсправедливы и для НАМ и для других эквивалентных уточнений понятия алгоритма.Эквивалентость уточнений понятия алгоритма мы рассмотрим позже.

Определение.3.2.Будем говорить, что МТ1 можно эффективно построить изМТ2 и МТ3 если существует алгоритм, который позволяет,имея программу для МТ2 и МТ3, построитьпрограмму для МТ3.

Определение.3.3.Последовательнойкомпозицией МТ А и В называется такая МТ С, что

область применимости МТ А и С совпадают;

C(a)=B(A(a)).

Другими словами, применение С к слову aдает такой же результат, как последовательное применение к этому же словусначала А, а потом к результату применения А — В.

Последовательную композицию МТАи МТВ будем обозначать АoВ.

Теорема 3.1. Пусть даны МТ А и В, такие,что В применима к результатам работы А и QA/>QB=Æ.

Тогда можно эффективно построить МТ Стакую, что С= АoВ.

Доказательство.

В качестве алфавита данных и множествасостояний для МТС возьмем объединение алфавитов данных и множествсостояний для А и В, т.е.

DC=DA/>DВ, QC= QA/>QB

В программе для А все правила ap®b!w, где a,bÎDA*, wÎ{Л,П, Н} заменим на ap®bqoBw, где qoBÎ QB — начальное состояние для В. Этообеспечит включение В в тот момент, когда А свою работу закончила и не раньше,т.к. QA/>QB=Æ.

Что и т.д.

Табличная запись программы для Споказана на рисунке 3.3.

Рис 3.3 Структура табличной записипрограмм для Машины С.

Определение3.4. Параллельнойкомпозицией Машин Тьюринга А и В назовем такую МашинуС, для которой:

DC=DA/>DB

QC=QA/>QB

C(a||b)=A(a||b)°B=B(a||b)°A=A(a)||B(b).

Из этого определения видно, что порядокприменения МТА и МТВ не влияет на результат. Он будет такой же как если бы мынезависимо применили А к слову a, а В к слову b.

Теорема 3.2 Для любых МТ А и МТ Вможно эффективно построить МТ С такую, что С=А||В

Обоснование. Мы не будем давать здесьстрого доказательства в виду его технической сложности. Покажем лишьобоснование правильности утверждения теоремы. Обозначим DC=DA/>DB; QC=QA/>QB.

Основная проблема: какгарантировать чтобы А не затронула слово b, а В — слово a. Для этого введем в алфавит DС символ||. Добавим для всех состояний qiÎQC<sub/>таких,что qiÎQA<sub/> правила вида ||qi®||qiЛ, т.е. каретка машины Абудет, натыкаясь на символ ||, уходить влево.Соответственно для всех qjÎQC таких,что qjÎQB добавим правила вида ||qj®||qjП, т.е. каретка машины В будет уходитьвправо. Тем самым мы как бы ограничиваем ленту для Асправа, а для В слева.

Существенным здесь является вопрос: неокажутся ли вычислительные возможности Машины Тьюринга с полулентой слабее, чемвычислительные возможности Машины Тьюринга с полной лентой?

Оказывается справедливо следующееутверждение: множество алгоритмов, реализуемых МТ с полулентой, эквивалентномножеству алгоритмов, реализуемых МТ с полной лентой.Обозначим Ф(Р) Машину Тьюринга, реализующую распознающий алгоритм:

Теорема 3.3. Для любых МашинТьюринга А, В и Ф, имеющих один и тот же алфавит S,может быть эффективно построена машина С над тем же алфавитом S, такая что

Доказательство.

Обозначим: E(Р)тождественную машину, т.е. Е(Р)=Р

СOPY(Р)копирующую машину, т.е. СOPY(Р)=Р||Р,

где ||ÏS.

BRANCH(P) — эта машина переходит либо в состояние р1, либо всостоянии ро. Ее программа состоит из 4-х команд:

1qo®1р1П

||р1®||р1П

0qo®0роП

||ро®||роП

Построим машину

Эта машина строится по следующейформуле:

Согласно теоремам 3.1 и 3.2., мы можемпостроить машину />, зная Е, Ф и COPY. Теперь, имея />, BRNCH, A и В, можно построить машину С следующим образом:

Машина />o BRANCH заканчивает свою работу либо в состоянии р1, если слово P обладает нужным свойством, либо в состоянии ро,находясь в начале слова P.Поэтому, если принять у машины А состояние р1, как начальное, а умашины В состояние ро, как начальное, то машина А будет включена приусловии, что Ф(Р)=1, а машина В будет включена, если Ф(Р)=0.

Правило композиции, определяемое этойтеоремой будем записывать, если Ф то А иначе В.

Теорема 3.4. Для любых машин А и Фможно эффективно построить машину Lтакую, что

L(P)={ Пока Ф(Р)=1, применяй А }

Доказательство: Заменим в доказательстветеоремы 3.3. машину В машиной Е, а заключительное состояние в машине В заменимна начальное состояние в машине />. В итоге получим нужный результат.

Теорема 3.5. (Бомм, Джакопини, 1962)

Любая Машина Тьюринга может бытьпостроена с помощью операции композиций o, ||, если Ф, то А иначе В,пока Ф применяй А.

Эту теорему мы даем здесь бездоказательства.

Следствие 3.1. В силу Тезиса Тьюринга,любая интуитивно вычислимая функция может быть запрограммирована в терминахэтих операций.

Следствие 3.2 Мы получили что-то вродеязыка, на котором можно описывать новую Машину Тьюринга, используя описания ужесуществующих, а затем, используя теоремы 3.1 — 3.4, построить её функциональнуюсхему.

Следствие 3.3 Алгоритм — этоконструктивный объект. В случае Машины Тьюринга атомарными объектами являютсякоманды, а теорема 3.5 определяет правила композиции.

Выводы:

Алгоритм — конструктивный объект;

Алгоритм можно строить из другихалгоритмов;

o, ||, if_then_else, while_do — универсальный набор действий поуправлению вычислительным процессом.

Вопросы :

Что такое правило подстановки?

Зависит ли результат от порядкаследования правил в НАМ?

Что происходит когда не применимо ни одно правило подстановки?

Что утверждает тезис Маркова?

Можно ли доказать тезис Маркова?

Семантика операции o?

Семантика операции ||?

Семантика операции if_then_else?

Семантика операции while_do?

Что такое конструктивный объект?

Алгоритм — это конструктивный объект?

Списоклитературы

Для подготовки данной работы былииспользованы материалы с сайта www.ergeal.ru/

www.ronl.ru

Реферат Алгоритм Маркова

скачать

Реферат на тему:

План:

1 Описание
2 Примеры
- 2.1 Пример 1
- 2.2 Пример 2

Примечания

Введение

Норма́льный алгори́тм Ма́ркова (НАМ) — один из стандартных способов формального определения понятия алгоритма, так же как и машина Тьюринга. Понятие нормального алгоритма введено А.А. Марковым в конце 1940-х годов. Традиционно, когда говорят об алгоритмах Маркова, используют слово "алгорифм".

Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ является Тьюринг-полным языком, что делает его по выразительной силе эквивалентным машине Тьюринга и следовательно современным языкам программирования. На основе НАМ был создан функциональный язык программирования Рефал.

1. Описание

Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах. Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам в котором алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида $L\to D$ , где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида $L\to\cdot D$ , где L и D — два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы $\to$ и $\to\cdot$ не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгоритма в пятибуквенном алфавите | * abc может служить схема

$\left\{\begin{matrix} |b&\to& ba|\\ ab&\to& ba\\ b&\to&\\ {*}|&\to& b*& \\ {*}&\to& c& \\ |c&\to& c\\ ac&\to& c|\\ c&\to\cdot\end{matrix}\right.$

Процесс применения нормального алгоритма к произвольному слову V в алфавите этого алгорифма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем. Пусть V' — слово, полученное на предыдущем шаге работы алгорифма (или исходное слово V, если текущий шаг является первым). Если среди формул подстановки нет такой, левая часть которой входила бы в V', то работа алгоритма считается завершённой, и результатом этой работы считается слово V'. Иначе среди формул подстановки, левая часть которых входит в V', выбирается самая верхняя. Если эта формула подстановки имеет вид $L\to\cdot D$ , то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего работа алгоритма считается завершённой с результатом RDS. Если же эта формула подстановки имеет вид $L\to D$ , то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего слово RDS считается результатом текущего шага, подлежащим дальнейшей переработке на следующем шаге.

Например, в ходе процесса применения алгорифма с указанной выше схемой к слову | * | | последовательно возникают слова | b * | , ba | * | , a | * | , a | b * , aba | * , baa | * , aa | * , aa | c, aac, ac | и c | | , после чего алгорифм завершает работу с результатом | | . Другие примеры смотрите ниже.

Любой нормальный алгорифм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгорифму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгорифмам, принято называть «принципом нормализации».

Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.

2. Примеры

2.1. Пример 1

Использование алгоритма Маркова для преобразований над строками:

Правила:

«А» → «апельсин»
«кг» → «килограмм»
«М» → «магазинчике»
«Т» → «том»
«магазинчике» →• «ларьке» (заключительная формула)
«в том ларьке» → «на том рынке»

Исходная строка:

«Я купил кг Аов в Т М.»

При выполнении алгоритма строка претерпевает следующие изменения:

«Я купил кг апельсинов в Т М.»
«Я купил килограмм апельсинов в Т М.»
«Я купил килограмм апельсинов в Т магазинчике.»
«Я купил килограмм апельсинов в том магазинчике.»
«Я купил килограмм апельсинов в том ларьке.»

На этом выполнение алгоритма завершится (так как будет достигнута формула № 5, которую мы сделали заключительной).

2.2. Пример 2

Данный алгоритм преобразует двоичные числа в «единичные», то есть на выходе получается строка из N единичек, если на входе у нас было N в двоичной системе. Например, 101 преобразуется в 5 единиц:

Правила:

«|0» → "0||"
«1» → "0|"
«0» → ""

Исходная строка:

«101»

Выполнение:

«0|01»
«00||1»
"00||0|"
"00|0|||"
"000|||||"
"00|||||"
"0|||||"
"|||||"

Примечания

wreferat.baza-referat.ru

Алгоритмы Маркова — реферат

Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.

Нормальные алгоритмы Маркова.

Для формализации понятия алгоритма российский математик А.А. Марков предложил использовать ассоциативные исчисления.

Рассмотрим некоторые понятия ассоциативного исчисления. Пусть имеется алфавит (конечный набор различных символов). Составляющие его символы будем называть буквами. Любая конечная последовательность букв алфавита (линейный их ряд) называется словом в этом алфавите.

Рассмотрим два слова N и М в некотором алфавите А. Если N является частью М, то говорят, что N входит в М.

Зададим в некотором алфавите конечную систему подстановок N - М, S - Т,..., где N, М, S, Т,... - слова в этом алфавите. Любую подстановку N-M можно применить к некоторому слову К следующим способом: если в К имеется одно или несколько вхождений слова N, то любое из них может быть заменено словом М, и, наоборот, если имеется вхождение М, то его можно заменить словом N.

Например, в алфавите А = {а, b, с} имеются слова N = ab, М = bcb, К = abcbcbab, Заменив в слове К слово N на М, получим bcbcbcbab или abcbcbbcb, и, наоборот, заменив М на N, получим aabcbab или аbсаbаb.

Подстановка ab - bcb недопустима к слову bacb, так как ни ab, ни bcb не входит в это слово. К полученным с помощью допустимых подстановок словам можно снова применить допустимые подстановки и т.д. Совокупность всех слов в данном алфавите вместе с системой допустимых подстановок называют ассоциативным исчислением. Чтобы задать ассоциативное исчисление, достаточно задать алфавит и систему подстановок.

Слова P1 и Р2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.

Последовательность слов Р, P1, Р2,..., М называется дедуктивной цепочкой, ведущей от слова Р к слову М, если каждое из двух рядом стоящих слов этой цепочки - смежное.

Слова Р и М называют эквивалентными, если существует цепочка от Р к М и обратно.

Пример:

Алфавит Подстановки

{а, b, с, d, е} ас - сa,

ad - da; eca - ae

bc - cb; eda - be

bd - db; edb - be

Слова abcde и acbde - смежные (подстановка bc - cb). Слова abcde - cadbe эквивалентны.

Может быть рассмотрен специальный вид ассоциативного исчисления, в котором подстановки являются ориентированными: N > М (стрелка означает, что подстановку разрешается производить лишь слева направо). Для каждого ассоциативного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.

Любой процесс вывода формул, математические выкладки и преобразования также являются дедуктивными цепочками в некотором ассоциативном исчислении. Построение ассоциативных исчислений является универсальным методом детерминированной переработки информации и позволяет формализовать понятие алгоритма.

Введем понятие алгоритма на основе ассоциативного исчисления: алгоритмом в алфавите А называется понятное точное предписание, определяющее процесс над словами из А и допускающее любое слово в качестве исходного. Алгоритм в алфавите А задается в виде системы допустимых подстановок, дополненной точным предписанием о том, в каком порядке нужно применять допустимые подстановки и когда наступает остановка.

Пример:

Алфавит: Система подстановок В:

А = {а, b, с} cb - cc

сса - аb

ab - bса

Предписание о применении подстановок: в произвольном слове Р надо сделать возможные подстановки, заменив левую часть подстановок на правую; повторить процесс с вновь полученным словом.

Так, применяя систему подстановок В из рассмотренного примера к словам babaac и bсaсаbс получаем:

babaac > bbcaaac > остановка

bcacabc > bcacbcac > bcacccac > bсасаbс > бесконечные процесс (остановки нет), так как мы получили исходное слово.

Предложенный А.А. Марковым способ уточнения понятия алгоритма основан на понятии нормального алгоритма, который определяется следующим образом. Пусть задан алфавит А и система подстановок В. Для произвольного слова Р подстановки из В подбираются в том же порядке, в каком они следуют в В..Если подходящей подстановки нет, то процесс останавливается. В противном случае берется первая из подходящих подстановок и производится замена ее правой частью первого вхождения ее левой части в Р. Затем все действия повторяются для получившегося слова P1. Если применяется последняя подстановка из системы В, процесс останавливается.

Такой набор предписаний вместе с алфавитом А и набором подстановок В определяют нормальный алгоритм. Процесс останавливается только в двух случаях: 1) когда подходящая подстановка не найдена; 2) когда применена последняя подстановка из их набора. Различные нормальные алгоритмы отличаются друг от друга алфавитами и системами подстановок.

Приведем пример нормального алгоритма, описывающего сложение -натуральных чисел (представленных наборами единиц).

Пример:

Алфавит: Система подстановок В:

А = (+, 1) 1 + > + 1

+ 1 > 1

1 > 1

Слово Р: 11+11+111

Последовательная переработка слова Р с помощью нормального алгоритма Маркова проходит через следующие этапы:

Р = 11 + 11 + 111 Р5 = + 1 + 111111

Р1 = 1 + 111 + 111 Р6 = ++ 1111111

Р2 = + 1111 + 111 Р7 = + 1111111

Р3 = + 111 + 1111 Р8 = 1111111

Р4 = + 11 + 11111 Р9 = 1111111

Нормальный алгоритм Маркова можно рассматривать как универсальную форму задания любого алгоритма. Универсальность нормальных алгоритмов декларируется принципом нормализации: для любого алгоритма в произвольном конечном алфавите А можно построить эквивалентный ему нормальный алгоритм над алфавитом А,

Разъясним последнее утверждение. В некоторых случаях не удается построить нормальный алгоритм, эквивалентный данному в алфавите А, если использовать в подстановках алгоритма только буквы этого алфавита. Однако, можно построить требуемый нормальный алгоритм, производя расширение алфавита А (добавляя к нему некоторое число новых букв). В этом случае говорят, что построенный алгоритм является алгоритмом над алфавитом А, хотя он будет применяться лишь к словам в исходном алфавите A.

Если алгоритм N задан в некотором расширении алфавита А, то говорят, что N есть нормальный алгоритм над алфавитом А.

Условимся называть тот или иной алгоритм нормализуемым, если можно построить эквивалентный ему нормальный алгоритм, и ненормализуемым в противном случае. Принцип нормализации теперь может быть высказан в видоизмененной форме: все алгоритмы нормализуемы.

Данный принцип не может быть строго доказан, поскольку понятие произвольного алгоритма не является строго определенным и основывается на том, что все Известные в настоящее время алгоритмы являются нормализуемыми, а способы композиции алгоритмов, позволяющие строить новые алгоритмы из уже известных, не выводят за пределы класса нормализуемых алгоритмов. Ниже перечислены способы композиции нормальных алгоритмов.

I. Суперпозиция алгоритмов. При суперпозиции двух алгоритмов А и В выходное слово первого алгоритма рассматривается как входное слово второго алгоритма В. Результат суперпозиции С может быть представлен в виде С(р) = В(А(р)),

II. Объединение алгоритмов. Объединением алгоритмов А и В в одном и том же алфавите называется алгоритм С в том же алфавите, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В, в записанные рядом слова А(р) и В(р).

III. Разветвление алгоритмов. Разветвление алгоритмов представляет собой композицию D трех алгоритмов А, В и С, причем область определения алгоритма D является пересечением областей определения всех трех алгоритмов А, В и С, а для любого слова р из этого пересечения D(p) = А(р), если С(р) = е, D(p) = B(p), если С(р) = е, где е - пустая строка.

IV. Итерация алгоритмов. Итерация (повторение) представляет собой такую композицию С двух алгоритмов А и В, что для любого входного слова р соответствующее слово С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.

Нормальные алгоритмы Маркова являются не только средством теоретических построений, но и основой специализированного языка программирования, применяемого как язык символьных преобразований при разработке систем искусственного интеллекта. Это один из немногих языков, разработанных в России и получивших известность во всем мире.

Существует строгое доказательство того, что по возможностям преобразования нормальные алгоритмы Маркова эквивалентны машинам Тьюринга.

В 1956 году отечественным математиком А.А. Марковым было предложено новое уточнение понятия алгоритма, которое позднее было названо его именем.

В этом уточнении выделенные нами 7 параметров были определены следующим образом:

Совокупность исходных данных - слова в алфавите S;

Совокупность возможных результатов - слова в алфавите W;

Совокупность возможных промежуточных результатов - слова в алфавите

Р=SWV, где V - алфавит служебных вспомогательных символов.

Действия:

Действия имеют вид либо a®g, либо a a g, где a, g ÎP*, где

P* - множество слов над алфавитом Р, и называется правилом подстановки. Смысл этого правила состоит в том, что обрабатываемое слово w просматривается слева направо и ищется вхождение в него слова a.

Определение 1. Слово a называется вхождением в слово w, если существуют такие слова b и n над тем же алфавитом, что и a и w, для которых верно: w=ban.

Если вхождение a в w найдено, то слово a заменяется на слово g.

Все правила постановки упорядочиваются. Сначала ищется вхождение для первого правила подстановки. Если оно найдено, то происходит подстановка и преобразуемое слово опять просматривается слева направо в поисках вхождения. Если вхождение для первого правила не найдено, то ищется вхождение для второго правила и т.д. Если вхождение найдено для i-го правила подстановки, то происходит подстановка, и просмотр правил начинается с первого, а слово просматривается сначала и слева направо.

Вся совокупность правил подстановки называется схемой алгоритма.

Правило начала - просмотр правил всегда начинается с первого.

Правило окончания - выполнение алгоритма заканчивается, если:

было применено правило подстановки вида a a g,

не применимо ни одно правило подстановки из схемы алгоритма.

Правило размещения результата - слово, полученное после окончания выполнения алгоритма.

Рассмотрим пример 1:

построить алгоритм для вычисления

U(n)=n+1;

S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.

Cхема этого НАМ показана на рисунке 1.1.

Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов.

Увеличиваем на единицу, начиная с цифр младших разрядов.

Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове.

Рис.1.1. Схема НАМ для вычисления U1(n)=n+1

Нетрудно сообразить, что сложность этого алгоритма, выраженная в количестве выполненных правил подстановки, будет равна:

(k+1)+(l+1),

где k - количество цифр в n, l - количество 9, которые были увеличены на1.

Обратите внимание, что у НАМ порядок следования правил подстановки в схеме алгоритма существенно влияет на результат, в то время как для МТ он не существеннен.

turboreferat.ru

Доклад - Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.

НормальныеАлгоритмы Маркова.Построение алгоритмов из алгоритмов.

В этом уточнении выделенные нами 7параметров были определены следующим образом:

Совокупность исходных данных — слова валфавите S;

Совокупность возможных результатов — слова в алфавите W;

Совокупность возможных промежуточныхрезультатов — слова в алфавите

Р=S/>W/>V,где V — алфавит служебных вспомогательных символов.

Действия:

Действия имеют вид либо a®g,либо a a g,где a, g ÎP*, где

Если вхождение a в wнайдено, то слово a заменяется на слово g.

Вся совокупность правил подстановкиназывается схемой алгоритма.

Правило начала — просмотр правил всегданачинается с первого.

Правило окончания — выполнение алгоритмазаканчивается, если:

было применено правило подстановки вида a a g,

не применимо ни одно правило подстановкииз схемы алгоритма.

7. Правило размещения результата — слово, полученное после окончания выполнения алгоритма.

Рассмотрим пример 1 из лекции 2:

построить алгоритм для вычисления

U(n)=n+1;

S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.

Cхемаэтого НАМ показана на рисунке 3.1.

Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов.

Увеличиваем на единицу, начиная с цифр младших разрядов.

Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове.

Рис.3.1. Схема НАМ для вычисления U1(n)=n+1

(k+1)+(l+1),

где k — количество цифр в n, l — количество 9, которые были увеличены на 1.

Построим НАМ для примера 2 из лекции 2:

построить алгоритм для вычисления

U2((n)1)=(n-1)1

Итак,S={|}; W=S; V=Æ, т.е. пусто.

| a

Cложностьэтого алгоритма равна 1, в то время как сложность алгоритма для Машины Тьюрингаравнялась n.

Теперь построим НАМ для примера 3 излекции 2:

построить алгоритм для вычисления

U3((n)1)=(n)10

S={|}; W={0,1,2,3,4,5,6,7,8,9}; V=Æ

Схема этого алгоритма приведена нарисунке 3.2.

1|®2

2|®3

3|®4

4|®5

5|®6

6|®7

7|®8

8|®9

9|®|0

|0®10

0|®1

|®0|

Рис. 3.2. Схема НАМ для вычисления U3((n)1)=(n)10.

Реализацию функции U4 сравнения двух целых чисел оставляем читателю в качествеупражнения.

Замечание: исходное слово надо задать вформе /> * />

Для нормальных алгоритмов Марковасправедлив тезис, аналогичный тезису Тьюринга.

Тезис Маркова: Для любой интуитивновычислимой функции существует алгоритм, ее вычисляющий.

Построение алгоритмов из алгоритмов.

Например, МТ3 из примера 3

U3((n)1)=(n)10

по существу есть надлежащим образомобъединенные МТ для U1(n)=n+1 и U2((n)1)=(n-1)1.

Определение.3.3.Последовательнойкомпозицией МТ А и В называется такая МТ С, что

область применимости МТ А и С совпадают;

C(a)=B(A(a)).

Последовательную композицию МТАи МТВ будем обозначать АoВ.

Теорема 3.1. Пусть даны МТ А и В, такие,что В применима к результатам работы А и QA/>QB=Æ.

Тогда можно эффективно построить МТ Стакую, что С= АoВ.

Доказательство.

DC=DA/>DВ, QC= QA/>QB

Что и т.д.

Табличная запись программы для Споказана на рисунке 3.3.

Рис 3.3 Структура табличной записипрограмм для Машины С.

Определение3.4. Параллельнойкомпозицией Машин Тьюринга А и В назовем такую МашинуС, для которой:

DC=DA/>DB

QC=QA/>QB

C(a||b)=A(a||b)°B=B(a||b)°A=A(a)||B(b).

Теорема 3.2 Для любых МТ А и МТ Вможно эффективно построить МТ С такую, что С=А||В

Доказательство.

Обозначим: E(Р)тождественную машину, т.е. Е(Р)=Р

СOPY(Р)копирующую машину, т.е. СOPY(Р)=Р||Р,

где ||ÏS.

BRANCH(P) — эта машина переходит либо в состояние р1, либо всостоянии ро. Ее программа состоит из 4-х команд:

1qo®1р1П

||р1®||р1П

0qo®0роП

||ро®||роП

Построим машину

Эта машина строится по следующейформуле:

Правило композиции, определяемое этойтеоремой будем записывать, если Ф то А иначе В.

Теорема 3.4. Для любых машин А и Фможно эффективно построить машину Lтакую, что

L(P)={ Пока Ф(Р)=1, применяй А }

Теорема 3.5. (Бомм, Джакопини, 1962)

Эту теорему мы даем здесь бездоказательства.

Выводы:

Алгоритм — конструктивный объект;

Алгоритм можно строить из другихалгоритмов;

o, ||, if_then_else, while_do — универсальный набор действий поуправлению вычислительным процессом.

Вопросы :

Что такое правило подстановки?

Зависит ли результат от порядкаследования правил в НАМ?

Что происходит когда не применимо ни одно правило подстановки?

Что утверждает тезис Маркова?

Можно ли доказать тезис Маркова?

Семантика операции o?

Семантика операции ||?

Семантика операции if_then_else?

Семантика операции while_do?

Что такое конструктивный объект?

Алгоритм — это конструктивный объект?

Списоклитературы

Для подготовки данной работы былииспользованы материалы с сайта www.ergeal.ru/

www.ronl.ru

Курсовая работа - Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.

НормальныеАлгоритмы Маркова.Построение алгоритмов из алгоритмов.

В этом уточнении выделенные нами 7параметров были определены следующим образом:

Совокупность исходных данных — слова валфавите S;

Совокупность возможных результатов — слова в алфавите W;

Совокупность возможных промежуточныхрезультатов — слова в алфавите

Р=S/>W/>V,где V — алфавит служебных вспомогательных символов.

Действия:

Действия имеют вид либо a®g,либо a a g,где a, g ÎP*, где

Если вхождение a в wнайдено, то слово a заменяется на слово g.

Вся совокупность правил подстановкиназывается схемой алгоритма.

Правило начала — просмотр правил всегданачинается с первого.

Правило окончания — выполнение алгоритмазаканчивается, если:

было применено правило подстановки вида a a g,

не применимо ни одно правило подстановкииз схемы алгоритма.

7. Правило размещения результата — слово, полученное после окончания выполнения алгоритма.

Рассмотрим пример 1 из лекции 2:

построить алгоритм для вычисления

U(n)=n+1;

S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.

Cхемаэтого НАМ показана на рисунке 3.1.

Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов.

Увеличиваем на единицу, начиная с цифр младших разрядов.

Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове.

Рис.3.1. Схема НАМ для вычисления U1(n)=n+1

(k+1)+(l+1),

где k — количество цифр в n, l — количество 9, которые были увеличены на 1.

Построим НАМ для примера 2 из лекции 2:

построить алгоритм для вычисления

U2((n)1)=(n-1)1

Итак,S={|}; W=S; V=Æ, т.е. пусто.

| a

Cложностьэтого алгоритма равна 1, в то время как сложность алгоритма для Машины Тьюрингаравнялась n.

Теперь построим НАМ для примера 3 излекции 2:

построить алгоритм для вычисления

U3((n)1)=(n)10

S={|}; W={0,1,2,3,4,5,6,7,8,9}; V=Æ

Схема этого алгоритма приведена нарисунке 3.2.

1|®2

2|®3

3|®4

4|®5

5|®6

6|®7

7|®8

8|®9

9|®|0

|0®10

0|®1

|®0|

Рис. 3.2. Схема НАМ для вычисления U3((n)1)=(n)10.

Реализацию функции U4 сравнения двух целых чисел оставляем читателю в качествеупражнения.

Замечание: исходное слово надо задать вформе /> * />

Для нормальных алгоритмов Марковасправедлив тезис, аналогичный тезису Тьюринга.

Тезис Маркова: Для любой интуитивновычислимой функции существует алгоритм, ее вычисляющий.

Построение алгоритмов из алгоритмов.

Например, МТ3 из примера 3

U3((n)1)=(n)10

по существу есть надлежащим образомобъединенные МТ для U1(n)=n+1 и U2((n)1)=(n-1)1.

Определение.3.3.Последовательнойкомпозицией МТ А и В называется такая МТ С, что

область применимости МТ А и С совпадают;

C(a)=B(A(a)).

Последовательную композицию МТАи МТВ будем обозначать АoВ.

Теорема 3.1. Пусть даны МТ А и В, такие,что В применима к результатам работы А и QA/>QB=Æ.

Тогда можно эффективно построить МТ Стакую, что С= АoВ.

Доказательство.

DC=DA/>DВ, QC= QA/>QB

Что и т.д.

Табличная запись программы для Споказана на рисунке 3.3.

Рис 3.3 Структура табличной записипрограмм для Машины С.

Определение3.4. Параллельнойкомпозицией Машин Тьюринга А и В назовем такую МашинуС, для которой:

DC=DA/>DB

QC=QA/>QB

C(a||b)=A(a||b)°B=B(a||b)°A=A(a)||B(b).

Теорема 3.2 Для любых МТ А и МТ Вможно эффективно построить МТ С такую, что С=А||В

Доказательство.

Обозначим: E(Р)тождественную машину, т.е. Е(Р)=Р

СOPY(Р)копирующую машину, т.е. СOPY(Р)=Р||Р,

где ||ÏS.

BRANCH(P) — эта машина переходит либо в состояние р1, либо всостоянии ро. Ее программа состоит из 4-х команд:

1qo®1р1П

||р1®||р1П

0qo®0роП

||ро®||роП

Построим машину

Эта машина строится по следующейформуле:

Правило композиции, определяемое этойтеоремой будем записывать, если Ф то А иначе В.

Теорема 3.4. Для любых машин А и Фможно эффективно построить машину Lтакую, что

L(P)={ Пока Ф(Р)=1, применяй А }

Теорема 3.5. (Бомм, Джакопини, 1962)

Эту теорему мы даем здесь бездоказательства.

Выводы:

Алгоритм — конструктивный объект;

Алгоритм можно строить из другихалгоритмов;

o, ||, if_then_else, while_do — универсальный набор действий поуправлению вычислительным процессом.

Вопросы :

Что такое правило подстановки?

Зависит ли результат от порядкаследования правил в НАМ?

Что происходит когда не применимо ни одно правило подстановки?

Что утверждает тезис Маркова?

Можно ли доказать тезис Маркова?

Семантика операции o?

Семантика операции ||?

Семантика операции if_then_else?

Семантика операции while_do?

Что такое конструктивный объект?

Алгоритм — это конструктивный объект?

Списоклитературы

Для подготовки данной работы былииспользованы материалы с сайта www.ergeal.ru/

www.ronl.ru

Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.

В 1956 году отечественным математиком А.А. Марковым было предложено новое уточнение понятия алгоритма, которое позднее было названо его именем.

В этом уточнении выделенные нами 7 параметров были определены следующим образом:

Совокупность исходных данных - слова в алфавите S;

Совокупность возможных результатов - слова в алфавите W;

Совокупность возможных промежуточных результатов - слова в алфавите

Р=S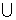W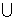V, где V - алфавит служебных вспомогательных символов.

Действия:

Действия имеют вид либо a®g, либо a a g, где a, g ÎP*, где

Определение.3.1. Слово a называется вхождением в слово w, если существуют такие слова b и n над тем же алфавитом, что и a и w, для которых верно: w=ban.

Если вхождение a в w найдено, то слово a заменяется на слово g.

Все правила постановки упорядочиваются. Сначала ищется вхождение для первого правила подстановки. Если оно найдено, то происходит подстановка и преобразуемое слово опять просматривается слева направо в поисках вхождения. Если вхождение для первого правила не найдено, то ищется вхождение для второго правила и т.д. Если вхождение найдено для i-го правила подстановки, то происходит подстановка, и просмотр правил начинается с первого, а слово просматривается сначала и слева направо.

Вся совокупность правил подстановки называется схемой алгоритма.

Правило начала - просмотр правил всегда начинается с первого.

Правило окончания - выполнение алгоритма заканчивается, если:

было применено правило подстановки вида a a g,

не применимо ни одно правило подстановки из схемы алгоритма.

7. Правило размещения результата - слово, полученное после окончания выполнения алгоритма.

Рассмотрим пример 1 из лекции 2:

построить алгоритм для вычисления

U(n)=n+1;

S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.

Cхема этого НАМ показана на рисунке 3.1.

Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов.

Увеличиваем на единицу, начиная с цифр младших разрядов.

Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове.

Рис.3.1. Схема НАМ для вычисления U1(n)=n+1

Нетрудно сообразить, что сложность этого алгоритма, выраженная в количестве выполненных правил подстановки, будет равна:

(k+1)+(l+1),

где k - количество цифр в n, l - количество 9, которые были увеличены на 1.

Обратите внимание, что у НАМ порядок следования правил подстановки в схеме алгоритма существенно влияет на результат, в то время как для МТ он не существеннен.

Построим НАМ для примера 2 из лекции 2:

построить алгоритм для вычисления

U2((n)1)=(n-1)1

Итак, S={|}; W=S; V=Æ, т.е. пусто.

| a

Cложность этого алгоритма равна 1, в то время как сложность алгоритма для Машины Тьюринга равнялась n.

Теперь построим НАМ для примера 3 из лекции 2:

построить алгоритм для вычисления

U3((n)1)=(n)10

S={|}; W={0,1,2,3,4,5,6,7,8,9}; V=Æ

Схема этого алгоритма приведена на рисунке 3.2.

1|®2

2|®3

3|®4

4|®5

5|®6

6|®7

7|®8

8|®9

9|®|0

|0®10

0|®1

|®0|

Рис. 3.2. Схема НАМ для вычисления U3((n)1)=(n)10.

Сложность этого НАМ будет n+[log10n], что существенно меньше сложности для Машины Тьюринга, вычисляющей эту функцию, которая равнялась n2+[log10n(log10n+1)].

Реализацию функции U4 сравнения двух целых чисел оставляем читателю в качестве упражнения.

Замечание: исходное слово надо задать в форме *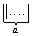

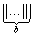
Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга.

Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий.

Построение алгоритмов из алгоритмов.

До сих пор, строя ту или иную МТ, или НАМ мы каждый раз все делали заново. Естественно задать вопрос, а нельзя ли при построении, например, новой МТ пользоваться уже построенной ранее МТ.

Например, МТ3 из примера 3

U3((n)1)=(n)10

по существу есть надлежащим образом объединенные МТ для U1(n)=n+1 и U2((n)1)=(n-1)1.

Аналогичный вопрос можно сформулировать для НАМ. Другими словами можно ли аккумулировать знания в форме алгоритмов так, чтобы из них можно было строить другие алгоритмы.

Мы рассмотрим эту проблему применительно к МТ. Однако все сформулированные нами утверждения будут справедливы и для НАМ и для других эквивалентных уточнений понятия алгоритма. Эквивалентость уточнений понятия алгоритма мы рассмотрим позже.

Определение.3.2. Будем говорить, что МТ1 можно эффективно построить из МТ2 и МТ3 если существует алгоритм, который позволяет, имея программу для МТ2 и МТ3, построить программу для МТ3.

Определение.3.3.Последовательной композицией МТ А и В называется такая МТ С, что

область применимости МТ А и С совпадают;

C(a)=B(A(a)).

Другими словами, применение С к слову a дает такой же результат, как последовательное применение к этому же слову сначала А, а потом к результату применения А - В.

Последовательную композицию МТА и МТВ будем обозначать АoВ.

Теорема 3.1. Пусть даны МТ А и В, такие, что В применима к результатам работы А и QAQB=Æ.

Тогда можно эффективно построить МТ С такую, что С= АoВ.

Доказательство.

В качестве алфавита данных и множества состояний для МТС возьмем объединение алфавитов данных и множеств состояний для А и В, т.е.

DC=DA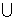DВ, QC= QA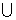QB

В программе для А все правила ap®b!w, где a,bÎDA*, wÎ{Л, П, Н} заменим на ap®bqoBw, где qoBÎ QB - начальное состояние для В. Это обеспечит включение В в тот момент, когда А свою работу закончила и не раньше, т.к. QAQB=Æ.

Что и т.д.

Табличная запись программы для С показана на рисунке 3.3.

Рис 3.3 Структура табличной записи программ для Машины С.

Определение3.4. Параллельной композицией Машин Тьюринга А и В назовем такую Машину С, для которой:

DC=DA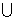DB

QC=QAQB

C(a||b)=A(a||b)°B=B(a||b)°A=A(a)||B(b).

Из этого определения видно, что порядок применения МТА и МТВ не влияет на результат. Он будет такой же как если бы мы независимо применили А к слову a, а В к слову b.

Теорема 3.2 Для любых МТ А и МТ В можно эффективно построить МТ С такую, что С=А||В

Обоснование. Мы не будем давать здесь строго доказательства в виду его технической сложности. Покажем лишь обоснование правильности утверждения теоремы. Обозначим DC=DA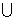DB; QC=QAQB.

Основная проблема: как гарантировать чтобы А не затронула слово b , а В - слово a . Для этого введем в алфавит DС символ ||. Добавим для всех состояний qiÎQC таких, что qiÎQA правила вида ||qi®||qiЛ, т.е. каретка машины А будет, натыкаясь на символ ||, уходить влево. Соответственно для всех qjÎQC таких, что qjÎQB добавим правила вида ||qj®||qjП, т.е. каретка машины В будет уходить вправо. Тем самым мы как бы ограничиваем ленту для А справа, а для В слева.

Существенным здесь является вопрос: не окажутся ли вычислительные возможности Машины Тьюринга с полулентой слабее, чем вычислительные возможности Машины Тьюринга с полной лентой?

Оказывается справедливо следующее утверждение: множество алгоритмов, реализуемых МТ с полулентой, эквивалентно множеству алгоритмов, реализуемых МТ с полной лентой. Обозначим Ф(Р) Машину Тьюринга, реализующую распознающий алгоритм:

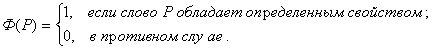
Теорема 3.3. Для любых Машин Тьюринга А, В и Ф, имеющих один и тот же алфавит S, может быть эффективно построена машина С над тем же алфавитом S, такая что

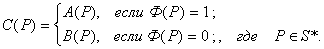
Доказательство.

Обозначим: E(Р) тождественную машину, т.е. Е(Р)=Р

СOPY(Р) копирующую машину, т.е. СOPY(Р)=Р||Р,

где ||ÏS.

BRANCH(P) - эта машина переходит либо в состояние р1, либо в состоянии ро. Ее программа состоит из 4-х команд:

1qo®1р1П

||р1®||р1П

0qo®0роП

||ро®||роП

Построим машину

Эта машина строится по следующей формуле:

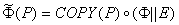
Согласно теоремам 3.1 и 3.2., мы можем построить машину , зная Е, Ф и COPY. Теперь, имея , BRNCH, A и В, можно построить машину С следующим образом:

Машина 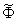o BRANCH заканчивает свою работу либо в состоянии р1, если слово P обладает нужным свойством, либо в состоянии ро, находясь в начале слова P. Поэтому, если принять у машины А состояние р1, как начальное, а у машины В состояние ро, как начальное, то машина А будет включена при условии, что Ф(Р)=1, а машина В будет включена, если Ф(Р)=0.

Правило композиции, определяемое этой теоремой будем записывать, если Ф то А иначе В.

Теорема 3.4. Для любых машин А и Ф можно эффективно построить машину L такую, что

L(P)={ Пока Ф(Р)=1, применяй А }

Доказательство: Заменим в доказательстве теоремы 3.3. машину В машиной Е, а заключительное состояние в машине В заменим на начальное состояние в машине 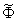. В итоге получим нужный результат.

Теорема 3.5. (Бомм, Джакопини, 1962)

Любая Машина Тьюринга может быть построена с помощью операции композиций o, || , если Ф, то А иначе В, пока Ф применяй А.

Эту теорему мы даем здесь без доказательства.

Следствие 3.1. В силу Тезиса Тьюринга, любая интуитивно вычислимая функция может быть запрограммирована в терминах этих операций.

Следствие 3.2 Мы получили что-то вроде языка, на котором можно описывать новую Машину Тьюринга, используя описания уже существующих, а затем, используя теоремы 3.1 - 3.4, построить её функциональную схему.

Следствие 3.3 Алгоритм - это конструктивный объект. В случае Машины Тьюринга атомарными объектами являются команды, а теорема 3.5 определяет правила композиции.

Выводы:

Алгоритм - конструктивный объект;

Алгоритм можно строить из других алгоритмов;

o, ||, if_then_else, while_do - универсальный набор действий по управлению вычислительным процессом.

Вопросы :

Что такое правило подстановки?

Зависит ли результат от порядка следования правил в НАМ?

Что происходит когда не применимо ни одно правило подстановки?

Что утверждает тезис Маркова?

Можно ли доказать тезис Маркова?

Семантика операции o?

Семантика операции ||?

Семантика операции if_then_else?

Семантика операции while_do?

Что такое конструктивный объект?

Алгоритм - это конструктивный объект?

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.ergeal.ru/

Дата добавления: 29.02.2004

www.km.ru

Нормальные Алгоритмы Маркова Построение алгоритмов из алгоритмов

В 1956 году отечественным математиком А.А. Марковым было предложено новое уточнение понятия алгоритма, которое позднее было названо его именем.

В этом уточнении выделенные нами 7 параметров были определены следующим образом:

Совокупность исходных данных - слова в алфавите S;

Совокупность возможных результатов - слова в алфавите W;

Совокупность возможных промежуточных результатов - слова в алфавите

Возможно вы искали - Реферат: Космическая программа Китая

Р=SWV, где V - алфавит служебных вспомогательных символов.

Действия:

Действия имеют вид либо a®g, либо aag, где a, gÎP* , где

Определение.3.1. Слово a называется вхождением в слово w, если существуют такие слова b и n над тем же алфавитом, что и a и w, для которых верно: w=ban.

Похожий материал - Реферат: Структуры данных

Если вхождение a в w найдено, то слово a заменяется на слово g.

Все правила постановки упорядочиваются. Сначала ищется вхождение для первого правила подстановки. Если оно найдено, то происходит подстановка и преобразуемое слово опять просматривается слева направо в поисках вхождения. Если вхождение для первого правила не найдено, то ищется вхождение для второго правила и т.д. Если вхождение найдено для i-го правила подстановки, то происходит подстановка, и просмотр правил начинается с первого, а слово просматривается сначала и слева направо.

Вся совокупность правил подстановки называется схемой алгоритма.

Правило начала - просмотр правил всегда начинается с первого.

Правило окончания - выполнение алгоритма заканчивается, если:

Очень интересно - Реферат: Ссылочный тип данных. Динамические объекты.

было применено правило подстановки вида aag,

не применимо ни одно правило подстановки из схемы алгоритма.

7. Правило размещения результата - слово, полученное после окончания выполнения алгоритма.

Рассмотрим пример 1 из лекции 2:

построить алгоритм для вычисления

Вам будет интересно - Реферат: Применение рекурсии в алгоритмах с возвратом. Файловый тип. Ввод/вывод

U(n)=n+1;

S={0,1,2,3,4,5,6,7,8,9}; S=W; V={*,+}.

Cхема этого НАМ показана на рисунке 3.1.

Перегоняем служебный символ * в конец слова n, чтобы отметить последнюю цифру младших разрядов.

Увеличиваем на единицу, начиная с цифр младших разрядов.

Похожий материал - Реферат: Познание природы и логика

Вводим служебный символ * в слово, чтобы им отметить последнюю цифру в слове.

Рис.3.1. Схема НАМ для вычисления U1 (n)=n+1

Нетрудно сообразить, что сложность этого алгоритма, выраженная в количестве выполненных правил подстановки, будет равна:

(k+1)+(l+1),

К-во Просмотров: 92

Бесплатно скачать Реферат: Нормальные Алгоритмы Маркова Построение алгоритмов из алгоритмов

cwetochki.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..