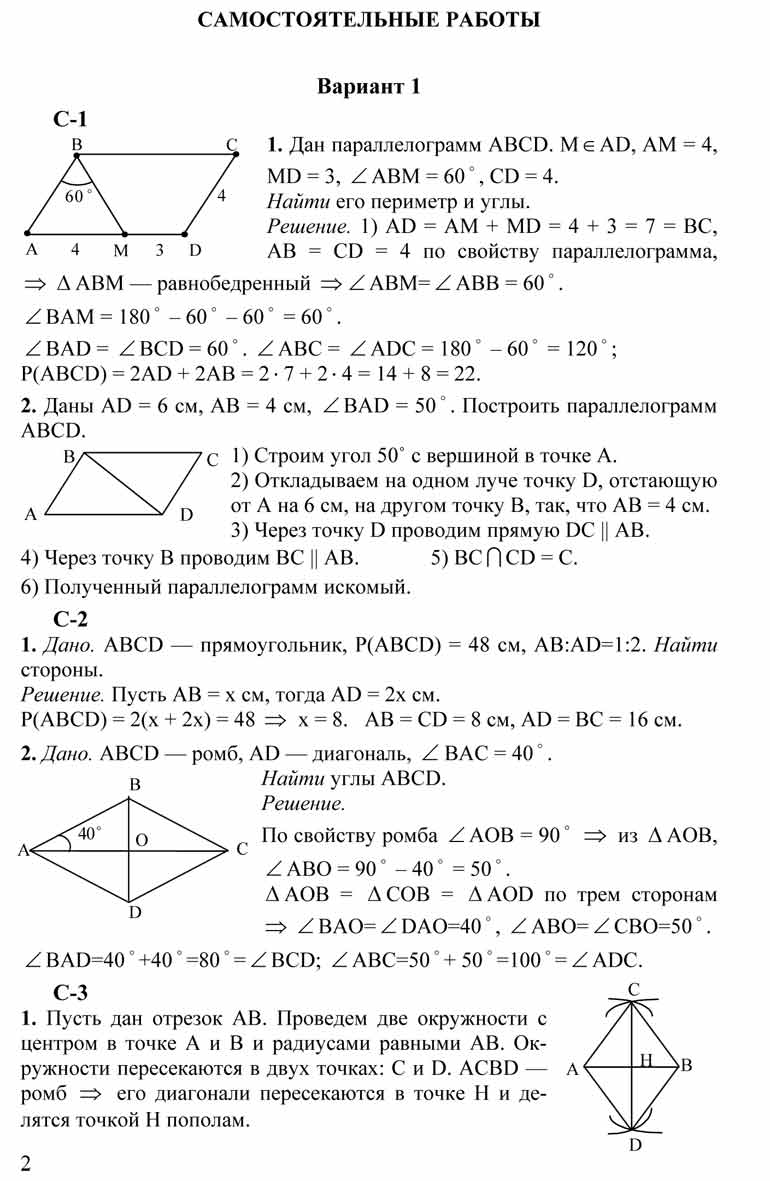
Вводная контрольная по геометрии 8 класс: Входная контрольная работа по геометрии 8 класс

Содержание

Геометрия 8 класс. Контрольная работа № 2 с ответами

Контрольная работа № 2 по геометрии в 8 классе «Площадь» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. Урок 30. Геометрия 8 класс. Контрольная работа по теме «Площадь».

Смотреть Список всех контрольных по геометрии в 8 классе по УМК Атанасян.

 

Контрольная работа № 2 
«Площадь» (8 класс)

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

1. Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

2. Выполнение контрольной работы

Контрольная работа по геометрии.
I уровень сложности
  1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
  2. Катеты прямоугольного треугольника равны 6 см и 8 см. Найдите гипотенузу и площадь треугольника.
  3. Найдите площадь и периметр ромба, если его диагонали равны 8 см и 10 см.
  4. * В прямоугольной трапеции АВСК большая боковая сторона равна З√2 см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.

Вариант 2

  1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника.
  2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника.
  3. Диагонали ромба равны 10 см и 12 см. Найдите его площадь и периметр.
  4. * В прямоугольной трапеции ABCD большая боковая сторона равна 8 см, угол А равен 60°, а высота ВН делит основание AD пополам. Найдите площадь трапеции.
Контрольная работа по геометрии.
II уровень сложности

Вариант 1

  1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 30°. Найдите площадь параллелограмма.
  2. Вычислите площадь трапеции ABCD с основаниями AD и ВС, если AD = 24 см, ВС = 16 см, ∠A = 45°, ∠D = 90°.
  3. Дан треугольник АВС. На стороне АС отмечена точка С так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см.
  4. * Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон.

Вариант 2

  1. Высота ВК, проведенная к стороне AD параллелограмма ABCD, делит эту сторону на два отрезка АК = 7 см, KD = 15 см. Найдите площадь параллелограмма, если ∠A = 45°.
  2. Вычислите площадь трапеции ABCD с основаниями AD и ВС, если ВС = 13 см, AD = 27 см, CD = 10 см, ∠D = 30°.
  3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ = 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см.
  4. * В равностороннем треугольнике большая сторона составляет 75% суммы двух других.
    Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Контрольная работа по геометрии.
III уровень сложности

Вариант 1

  1. На стороне AD параллелограмма ABCD взята точка Е так, что АЕ — 4 см, ED = 5 см, BE = 12 см, BD = 13 см. Найдите площадь параллелограмма.
  2. В остроугольном треугольнике АВС проведены высоты АК и СЕ, СЕ = 12 см, BE = 9 см, АК = 10 см. Найдите АС.
  3. В равнобедренной трапеции ABCD AD||ВС, ∠A = 30°, высота ВК = 1 см, ВС = 2√3 см. Найдите площадь треугольника KMD, если М — середина отрезка BD.
  4. * В выпуклом четырехугольнике ABCD проведены диагонали. Известно, что площади треугольников ABD, ACD, BCD равны. Докажите, что данный четырехугольник является параллелограммом.

Вариант 2

  1. В трапеции ABCD AD — большее основание, СК — высота, АВ = 5 см. На отрезке АК взята точка Е так, что АЕ = 3 см, ЕК = 6 см, KD = 1 см, BE = 4 см. Найдите площадь трапеции.
  2. В треугольнике АВС угол А тупой, ВК и CD — высоты, ВК = 12 см, АК = 9 см, CD = 10 см. Найдите AD.
  3. В параллелограмме ABCD ∠A = 60°, диагональ BD перпендикулярна к стороне АВ. Прямая, проходящая через середину отрезка BD — точку М — параллельно AD, пересекает сторону АВ в точке К, МК = 4 см. Найдите площадь треугольника AMD.
  4. * В выпуклом четырехугольнике ABCD проведены диагонали. Известно, что площади треугольников ABD и ACD равны, а площади треугольников ACD и BCD не равны. Докажите, что данный четырехугольник является трапецией.

3. Рефлексия учебной деятельности

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.

Решения и ответы на контрольную работу
I уровня сложности

 

Решения и ответы на контрольную работу
II уровня сложности

Годовая контрольная работа по геометрии 8 класс, 3 варианта

Годовая контрольная работа по геометрии 8 класс. Вариант 1.

  1. За­да­ние № 323159. Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 28 и 100.

  2. За­да­ние № 39. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

  3. За­да­ние № 169875. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

  4. За­да­ние  № 341044.

     От­ре­зок AB = 48 ка­са­ет­ся окруж­но­сти ра­ди­у­са 14 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

  5. За­да­ние  № 314811. Точка О — центр окруж­но­сти, ∠AOB = 84° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла ACB (в гра­ду­сах).

  6. За­да­ние  № 92. Най­ди­те тан­генс угла B тре­уголь­ни­каABC, изоб­ражённого на ри­сун­ке.

  7. За­да­ние  № 311321.

     На ри­сун­ке изоб­ра­же­на тра­пе­ция  . Ис­поль­зуя ри­су­нок, най­ди­те  .

  8. За­да­ние № 118. В тре­уголь­ни­ке ABC угол C пря­мой, BC = 8 , sin A = 0,4.   Най­ди­те AB.

  9. За­да­ние № 314914. Че­ло­век, рост ко­то­ро­го равен 1,8 м, стоит на рас­сто­я­нии 16 м от улич­но­го фо­на­ря. При этом длина тени че­ло­ве­ка равна 9 м. Опре­де­ли­те вы­со­ту фо­на­ря (в мет­рах). 

  1. Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 7.

Годовая контрольная работа по геометрии 8 класс. Вариант 2

1. За­да­ние № 323160.

Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 40 и 85.

2.За­да­ние  № 311682. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

3. За­да­ние № 195803. Одна из сто­рон па­рал­ле­ло­грам­ма равна 20, а опу­щен­ная на нее вы­со­та равна 23. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

4.За­да­ние № 339975. От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром 

O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

5. За­да­ние 10 № 314873. Точка О — центр окруж­но­сти, ∠ACB = 24° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла AOB (в гра­ду­сах).

6. За­да­ние № 196. Най­ди­те тан­генс угла С тре­уголь­ни­ка ABC , изоб­ражённого на ри­сун­ке.

7. За­да­ние № 311344. На ри­сун­ке изоб­ра­же­на тра­пе­ция  . Ис­поль­зуя ри­су­нок, най­ди­те  .

8. За­да­ние  № 315026.

 В тре­уголь­ни­ке ABC угол C пря­мой, BC = 3 , cosB = 0,6. Най­ди­те AB.

9. За­да­ние № 314820. На каком рас­сто­я­нии от фонаря находится человек?

10. Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 8.

Годовая контрольная работа по геометрии 8 класс. Вариант 3.

  1. За­да­ние № 323163.

Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 3 и 5.

  1. За­да­ние № 324162.

Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

3. За­да­ние № 195833. Одна из сто­рон па­рал­ле­ло­грам­ма равна 16, а опу­щен­ная на нее вы­со­та равна 25. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

4. За­да­ние № 311681. К окруж­но­сти с цен­тром в точке Опро­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см, AO = 13 см.

5. За­да­ние № 314896. Точка О — центр окруж­но­сти, ∠ACB = 32° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла AOB (в гра­ду­сах).

6. За­да­ние № 66. Най­ди­те тан­генс угла А тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

7. За­да­ние № 311356. На ри­сун­ке изоб­ра­жен па­рал­ле­ло­грамм  . Ис­поль­зуя ри­су­нок, най­ди­те  .

8. За­да­ние  № 340890. В тре­уголь­ни­ке OAB угол B равен 90°, AB = 6, sinO = 0,3. Най­ди­те OA.

(в мет­рах) от фо­на­ря стоит че­ло­век ро­стом 2 м, если длина его тени равна 1 м, вы­со­та фо­на­ря 9 м?

9. За­да­ние № 340961. На каком рас­сто­я­нии (в мет­рах) от фо­на­ря стоит че­ло­век ро­стом 1,8 м, если длина его тени равна 9 м, вы­со­та фо­на­ря 4 м?

10. Най­ди­те пло­щадь квад­ра­та, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 6.

Входная контрольная работа по геометрии 8 класс ФГОС Школа России |

Контрольная работа по геометрии

по теме: «Окружность».

1 вариант

AB и AC – отрезки касательных, проведенных к окружности с центром в точке O и радиусом 9 см. Найдите длины отрезков AC и AO,если AB=12 см.
Дано: AB: BC=11:12,

AOC=130°.

Найти: BCA, BAC

3). Хорды AB и CD пересекаются в точке E так, что AE= 3см, BE=36 см, CE : DE = 3:4. Найдите CD.

4). Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см.Найдите площадь этого треугольника и его боковую сторону.

Контрольная работа по геометрии

по теме: «Окружность».

2 вариант

MN и MK – отрезки касательных, проведенных к окружности с центром в точке O и радиусом 5 см. Найдите MN и MK,если MO=13 см.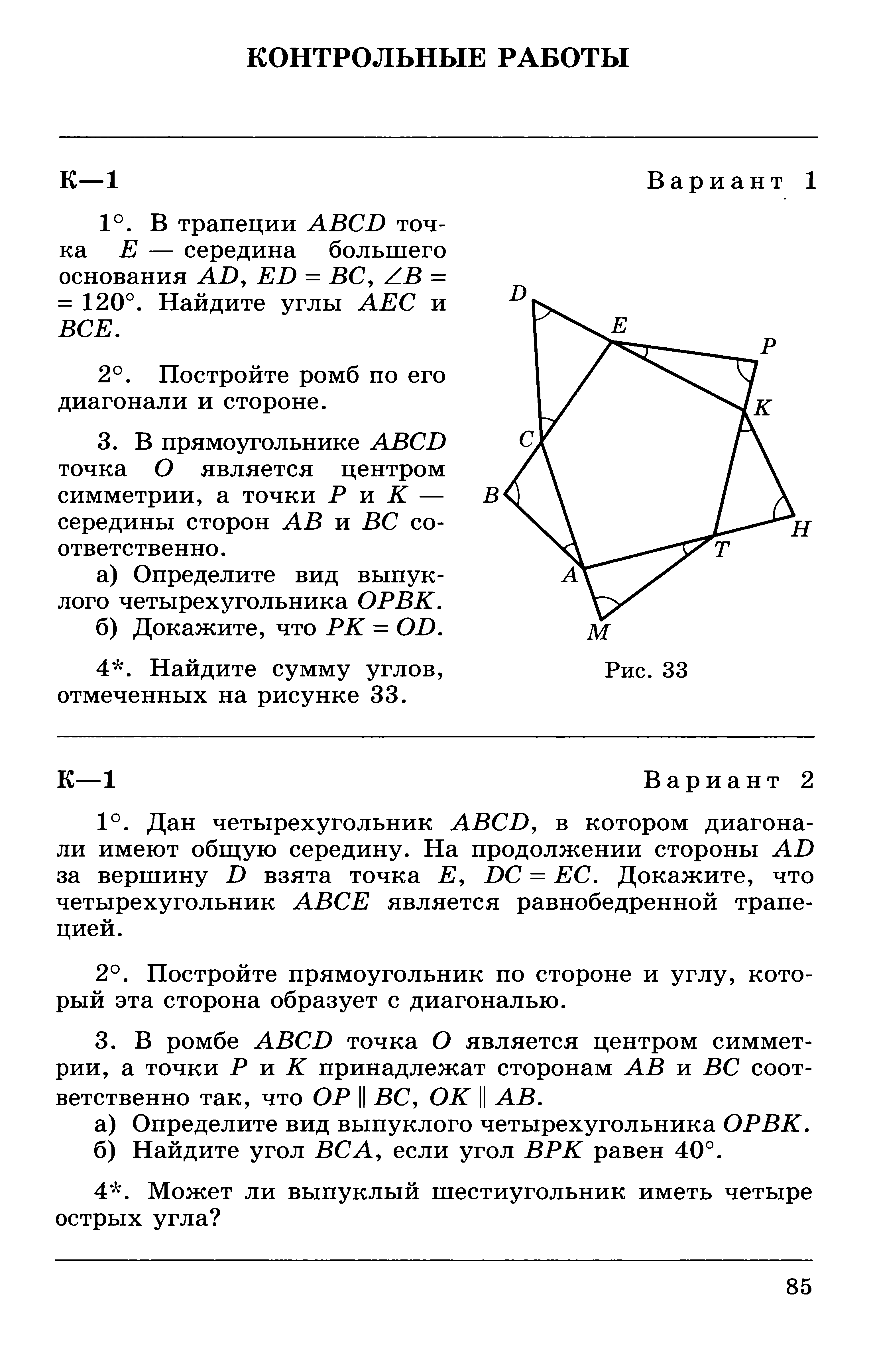
Дано: AB: AC=5:3,

BAC=60°.

Найти: BOC, ABC

3). Хорды MN и PK пересекаются в точке A так, что MA= 3см, NA=16 см, PA : KA = 1:3. Найдите PK.

4). Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см вписан в окружность радиуса 10 см.Найдите площадь этого треугольника и его боковую сторону.

Контрольная работа по геометрии

по теме: «Окружность».

1 вариант

AB и AC – отрезки касательных, проведенных к окружности с центром в точке O и радиусом 9 см. Найдите длины отрезков AC и AO,если AB=12 см.
Дано: AB: BC=11:12,

AOC=130°.

Найти: BCA, BAC

3). Хорды AB и CD пересекаются в точке E так, что AE= 3см, BE=36 см, CE : DE = 3:4. Найдите CD.

4). Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см.Найдите площадь этого треугольника и его боковую сторону.

Контрольная работа по геометрии

по теме: «Окружность».

2 вариант

MN и MK – отрезки касательных, проведенных к окружности с центром в точке O и радиусом 5 см. Найдите MN и MK,если MO=13 см.
Дано: AB: AC=5:3,

BAC=60°.

Найти: BOC, ABC

3). Хорды MN и PK пересекаются в точке A так, что MA= 3см, NA=16 см, PA : KA = 1:3. Найдите PK.

4). Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см вписан в окружность радиуса 10 см.Найдите площадь этого треугольника и его боковую сторону.

Контрольная работа по геометрии

по теме: «Окружность».

1 вариант

AB и AC – отрезки касательных, проведенных к окружности с центром в точке O и радиусом 9 см. Найдите длины отрезков AC и AO,если AB=12 см.
Дано: AB: BC=11:12,

AOC=130°.

Найти: BCA, BAC

3). Хорды AB и CD пересекаются в точке E так, что AE= 3см, BE=36 см, CE : DE = 3:4. Найдите CD.

4). Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см. Найдите площадь этого треугольника и его боковую сторону.

Контрольная работа по геометрии

по теме: «Окружность».

2 вариант

MN и MK – отрезки касательных, проведенных к окружности с центром в точке O и радиусом 5 см. Найдите MN и MK,если MO=13 см.
Дано: AB: AC=5:3,

BAC=60°.

Найти: BOC, ABC

3). Хорды MN и PK пересекаются в точке A так, что MA= 3см, NA=16 см, PA : KA = 1:3. Найдите PK.

4). Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см вписан в окружность радиуса 10 см.Найдите площадь этого треугольника и его боковую сторону.

Вводный семинар: Производная алгебраическая геометрия и

  • Создать учетную запись ИИГС
  • Войти в учетную запись ИИГС
  • Забыл пароль?
  • Дом
  • О нас
    • Наша миссия
    • Наша история
    • Разнообразие
    • Комитеты по управлению
      • Комитет по аудиту
      • Попечительский совет
      • Комитет академических спонсоров
      • Исполнительный подкомитет CAS
      • Подкомитет CAS по Дню академического спонсора
      • Подкомитет CAS по летним аспирантам
      • Попечительский комитет
      • Комитет по делам женщин в математике
      • Дирекция
      • Консультативный комитет по вопросам образования
      • Emeriti Trustees
      • Финансовый комитет
      • Консультативный комитет по кадрам
      • Инвестиционный комитет
      • Научно-консультативный комитет
      • Руководящий комитет
      • Математическая премия
      • Комиссия по приему пожертвований
    • Новости
      • ИИГС в СМИ
      • Информационный бюллетень эмиссара
      • Пресс-релизы
    • Справочник участников
    • Справочник персонала
    • Развитие
    • Удобства
    • Фото галерея
    • Вакансии
      • Работа
      • Заявка участника
      • Поиск директоров ИИГС (2022 г. )
    • Проезд
    • Свяжитесь с нами
    • Политика конфиденциальности
    • Женщины по математике
    • О персонале ИИГС
      • Дэвид Эйзенбуд
      • Элен Барсело
      • Артур Боссе
      • Кристин Маршалл
      • Ризалин Майодонг
      • Меган Нгуен
      • Линда Рив
      • Стефани Юрус
    • Заявление о коллегиальности
    • Политика противодействия дискриминации и преследованию
    • Омбудсмены
    • Кодекс поведения для виртуального участия
    • Жилье для инвалидов
  • Деятельность
    • Научные программы
    • Предложить сейчас
    • Подать заявку сейчас
    • Семинары
    • Мастерские
    • Летние исследования по математике
    • Летние аспирантуры
    • ИИГС УП
      • Объявления
    • Образование
    • Математические круги
    • Общественные мероприятия и инициативы
    • Премия CME Group-ИИГС
  • Научный
    • Программы
      • Программы на главную
      • Текущие программы
      • Предстоящие программы
      • Прошлые программы
    • Мастерские
      • Мастерские Дом
      • Все мастерские
        • Текущий
        • Предстоящий
        • Прошлые
      • Программные семинары
        • Текущий
        • Предстоящий
        • Прошлые
      • Горячие темы Мастерские
        • Текущий
        • Предстоящий
        • Прошлые
      • Летние аспирантуры
        • Текущий
        • Предстоящий
        • Прошлые
        • Объявления
      • ИИГС УП — РЭУ
      • Прочие мастерские
        • Текущий
        • Предстоящий
        • Прошлые
        • Лекции по программе Ленглендса
    • Летние исследования по математике
    • СОЕДИНЕНИЕ
      • ADJOINT 2021 Руководители и темы исследований
      • ADJOINT 2020 Мастерская
    • Коллоквиумы и семинары
      • Коллоквиумы и семинары Главная
      • Все коллоквиумы и семинары
        • Текущий
        • Предстоящий
        • Прошлые
      • ИИГС Эванс / Серия лекций
      • Семинары постдока
      • Семинары для выпускников
      • Другие коллоквиумы и семинары
      • Семинары осень 2020
        • RAS: Five Minute Talks
        • РАН: Научный семинар
        • РАН: Программный ассоциированный семинар
        • РАН: семинар постдоков
        • DDC: Five Minute Talks
        • ДДК: Диофантовы проблемы
        • DDC: Детский семинар
        • DDC: Теория оценки
        • DDC: Семинар по определению
        • DDC: Оценки на dp-конечных полях
        • DDC: онлайн-семинар
        • Теория вычислимости DDC
        • DDC: Семинар по теории моделей
        • DDC: Вводный семинар
    • Запрос предложений
      • Предложить программу
      • Предложить летнюю аспирантуру
      • Предложить семинар Горячие темы
      • Предложить CIME
    • Заявление участника
      • Профессора-исследователи
      • Участник исследования
      • Постдокторант
    • Ресурсы для участников
      • Заказать обед онлайн
      • Справочник участника
      • Руководство постдока-наставника
      • Справочник по вычислениям
      • Визовая информация
      • Жилье на короткий срок
      • Выписка
      • Информация для семьи
      • Рестораны и магазины
      • Отдых
      • Справочник участников
    • Библиотека
    • Календарь для ученых
    • Текущий
    • Прошлые
    • Предстоящий
  • Образование
    • Для постдока
    • Для аспирантов
      • Летняя аспирантура
        • Текущий
        • Предстоящий
        • Прошлые
        • Объявления
    • Для магистрантов
      • ИИГС-УП
    • Для учителей K-12
      • Критические проблемы
        • CIME 2020, серия семинаров
      • Математические круги
      • БАМО
      • Математический фестиваль Джулии Робинсон
      • Профессиональное развитие
      • Иллюстративные вебинары по математике
    • Библиотека
    • Текущий
    • Прошлые
    • Предстоящий
  • Связь
    • ИИГС в новостях
    • Пресс-релизы
    • Математические видео
    • Другие фильмы и видео
    • Книги / брошюры
    • Эмиссар
    • Подписка на информационный бюллетень
    • Библиотека
    • Открытки
    • Celebratio Mathematica
    • Обновления расписания на 2020 год (COVID-19)
    • Заявление об открытии ИИГС (август 2020 г. )
  • Общественный
    • Национальный математический фестиваль
    • Премия за книгу по математике
    • Фильмы и видео
    • Игрушки Тадаши
    • Прошлые
    • Предстоящий
  • В гостях
    • Маршруты и транспорт
    • Общественный транспорт
    • Расписание маршрутного автобуса
    • Парковка
    • Туристическая информация и политика
      • Встречи руководителей: политика и процедуры в отношении поездок
      • Исследователи: Политика и процедуры в отношении путешествий
      • Ограничения на возмещение командировок авиакомпаний
    • Справочник по вычислениям
    • Визовая информация
    • Информация о жилье
      • Жилье на короткий срок
      • Долгосрочное жилье
    • Ресурсы для участников
      • Заказать обед онлайн
      • Справочник участника
      • Руководство постдока-наставника
      • Справочник по вычислениям
      • Визовая информация
      • Жилье на короткий срок
      • Выписка
      • Информация для семьи
      • Рестораны и магазины
      • Отдых
      • Справочник участников
    • Семейные услуги
    • Рестораны и магазины
    • Отдых
      • Информация о здравоохранении
    • Поддержка
      • Сделать пожертвование
      • Способы поддержки ИИГС
        • Ежегодные подарки
        • Планируемые подарки
        • Подарки от пожертвований
        • Как отдать
          • Подарки наличными
          • Подарки ценных бумаг
          • Подарки недвижимости
          • Планируемые подарки
          • Завещания
        • Общество Гильберта
      • Академические спонсоры
        • Текущие академические спонсоры
        • Стать академическим спонсором
      • Спонсор издателя
      • Фонд поддержки
      • Федеральная поддержка
      • Корпоративные партнеры
      • Именованные должности
        • Стипендии с докторской степенью
        • Черн Профессорс
        • Simons Professors
        • Профессора Айзенбуда
        • Клей старший научный сотрудник
        • Канцлерская профессура
      • Доноры поддержки семьи
      • Марьям Мирзахани получил звание профессора
    • Календарь
      • Все события
      • Научные мероприятия
      • K-12 Education
      • Для широкой публики
      • Административный

    Магистр математики, 6 класс: вводная геометрия — Walmart. com

    «,» tooltipToggleOffText «:» Нажмите на переключатель, чтобы получить

    БЕСПЛАТНОЙ доставки на следующий день!

    «,» tooltipDuration «:» 5 «,» tempUnavailableMessage «:» Скоро вернусь! «,» TempUnavailableTooltipText «:»

    Мы прилагаем все усилия, чтобы снова начать работу.

    • Временно приостановлено в связи с высоким спросом.
    • Продолжайте проверять наличие.
    «,» hightlightTwoDayDelivery «:» false «,» locationAlwaysElposed «:» false «,» implicitOptin «:» false «,» highlightTwoDayDelivery «:» false «,» isTwoDayDeliveryTextEnabled «:» true «,» useTesting » «,» ndCookieExpirationTime «:» 30 «},» typeahead «: {» debounceTime «:» 100 «,» isHighlightTypeahead «:» true «,» shouldApplyBiggerFontSizeAndCursorWithPadding «:» true «,» isBackgroundGreyoutEnabled} «:» false » locationApi «: {» locationUrl «:» https: // www.walmart.com/account/api/location»,»hubStorePages»:»home,search,browse»,»enableHubStore»:»false»},»oneApp»:{«drop2″:»true»,»hfdrop2 «:» true «,» heartingCacheDuration «:» 60000 «,» hearting «:» false «},» feedback «: {» showFeedbackSuccessSnackbar «:» true «,» feedbackSnackbarDuration «:» 3000 «},» webWorker «: {» enableGetAll » : «false», «getAllTtl»: «

    0″}, «search»: {«searchUrl»: «/ search /», «enabled»: «false», «tooltipText»: «

    Скажите нам, что вам нужно

    » , «tooltipDuration»: 5000, «nudgeTimePeriod»: 10000}}}, «uiConfig»: {«webappPrefix»: «», «artifactId»: «header-footer-app», «applicationVersion»: «20. 0,40 «,» applicationSha «:» 41ed8468826085770503056bd2c9bc8be5b55386 «,» applicationName «:» верхний колонтитул «,» узел «:» 01d7dcaf-453b-4649-a0a2-6c13b7391551 «,» облако «:» eus9 «prod oneOpsEnv «:» prod-a «,» profile «:» PROD «,» basePath «:» / globalnav «,» origin «:» https://www.walmart.com «,» apiPath «:» / header- нижний колонтитул / электрод / api «,» loggerUrl «:» / заголовок-нижний колонтитул / электрод / api / logger «,» storeFinderApi «: {» storeFinderUrl «:» / store / ajax / primary-flyout «},» searchTypeAheadApi «: { «searchTypeAheadUrl»: «/ search / autocomplete / v1 /», «enableUpdate»: false, «typeaheadApiUrl»: «/ typeahead / v2 / complete», «taSkipProxy»: false}, «emailSignupApi»: {«emailSignupUrl»: » / account / electro / account / api / subscribe «},» feedbackApi «: {» fixedFeedbackSubmitUrl «:» / customer-survey / submit «},» logging «: {» logInterval «: 1000,» isLoggingAPIEnabled «: true,» isQuimbyLoggingFetchEnabled «: true,» isLoggingFetchEnabled «: true,» isLoggingCacheStatsEnabled «: true},» env «:» production «},» envInfo «: {» APP_SHA «:» 41ed8468826085770503056ERSbe2c9b «,» APP38 «,» APP «:0. 40-41ed84 «},» expoCookies «: {}}

    ГЕОМЕТРИЯ — Тематические тексты

    Главная → ГЕОМЕТРИЯ — Тематические тексты

    Текст 1

    Геометрия позволяет нам исследовать свойства пространства в терминах плоских (двухмерных) фигур и твердых (трехмерных) фигур. Мы можем использовать геометрические методы, чтобы нарисовать линию точной длины, разрезать линию пополам, разделить пополам угол, построить треугольник и вычислить площадь сферы. Принципы геометрии заложил греческий математик Евклид (К.330 г. до н.э. — 275 г. до н.э.) и с тех пор почти не изменились. Картографирование; Геодезия, проектирование, архитектура и компьютерные схемы — все зависит от геометрии в точном использовании углов, фигур и объема.

    Текст 2

    Треугольники, квадраты и пятиугольники — все это примеры многоугольников. У правильного многоугольника стороны равной длины и внутренние углы равны. Чем больше сторон у правильного многоугольника, тем больше он будет напоминать круг. Есть два вида многоугольников: выпуклые и входящие. У выпуклого многоугольника все углы направлены внутрь. У входящего многоугольника один или несколько углов направлены внутрь.

    Текст 3

    Углы образуются на стыке двух прямых линий. Их можно измерить с помощью транспортира или указателя угла. Углы измеряются в единицах, называемых градусами. Градус получается делением окружности круга на 360 частей равного размера. Математики используют маленький кружок как символ для обозначения градусов. Угол, который образует углы квадратов и других прямоугольников, составляет 90 градусов и называется прямым углом.Углы меньше 90 называются острыми углами. Углы от 90 до 180 называются тупыми углами. Углы от 180 до 360 называются углами отражения.

    Текст 4

    Преобразование — это изменение положения, размера или формы геометрической фигуры (например, треугольника). Основные преобразования — это отражение, увеличение, перемещение и вращение. Другие формы трансформации включают растяжение и сдвиг. Отражение, перемещение и вращение изменяют положение фигуры.

    No related posts.

Leave a Reply

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *