входная контрольная работа по математике 9 класс с ответами мордкович — JSFiddle
Editor layout
Classic Columns Bottom results Right results Tabs (columns) Tabs (rows)
Console
Console in the editor (beta)
Clear console on run
General
Line numbers
Wrap lines
Indent with tabs
Code hinting (autocomplete) (beta)
2 spaces3 spaces4 spaces
Key map:DefaultSublime TextEMACS
Font size:DefaultBigBiggerJabba
Behavior
Auto-run code
Only auto-run code that validates
Auto-save code (bumps the version)
Auto-close HTML tags
Auto-close brackets
Live code validation
Highlight matching tags
Boilerplates
Show boilerplates bar less often
Контрольна робота ман математика 9 клас
Скачать контрольна робота ман математика 9 клас PDF
Главная → Математика → 9 класс → Итоговая контрольная работа за 1 полугодие по алгебре для 9 класса.
Геометрическая прогрессия. Контрольные работы по алгебре 9 класс. Разбор контрольной работы по алгебре 9 класс. Контрольная работа №4 по алгебре в 9 классе по теме «Уравнения и неравенства с двумя переменными» Вариант 1 • 1.
Решите систему уравнений: 2x + y = 7, х2 — у = 1. • 2. Периметр прямоугольника равен Читать еще. 89169775797.ru doc. Посмотреть. Входная контрольная работа по алгебре 9 класс Часть Характеристика структуры и содержания работы. Работа по алгебре состоит из 2-х частей и включает в себя 15 заданий, различающихся формой и уровнем сложности: Часть 1 содержит 12 заданий: с выбором от.
Контрольные работы по предмету «Математика» для обучающихся с легкой степенью умственной отсталости 9 класса методическая разработка по математике (9 класс) по теме. Опубликовано — — Филиппова Наталья Анатольевна. К онтрольные работы разработаны для обучающихся 9 класса с легкой степенью умственной отсталости для выявления уровня усвоения программного материала по математике (программа под ред.
Опубликовано — — Филиппова Наталья Анатольевна. К онтрольные работы разработаны для обучающихся 9 класса с легкой степенью умственной отсталости для выявления уровня усвоения программного материала по математике (программа под ред.
В.В. Воронковой. – М.: «Просвещение», г.). В их содержание включены основные вопросы курса математики 9-го класса. Представлены в нескольких вариантах для обучающихся с ра. Название: Алгебра. Тесты. 9 класс. Формат: PDF (в zip-архиве).
Размер: 28,9 Мб. Объём: 64 стр. Аннотация Тесты имеют перед обычными контрольными работами ряд преимуществ, главное из которых — оперативность: его можно провести и проверить быстрее, чем обычную контрольную работу, а оценки можно объявить сразу по окончании.
Пособие содержит 20 тестов, из них 5 — обобщающего характера. Каждый тест рассчитан на 15 — 20 минут, однако, в зависимости от степени подготовленности класса, учитель может изменять как количество заданий, так и время их выполнения.
Каждый тест состоит из 5 заданий, снабженных вариантами ответов, из которых только один является верным. Контрольная работа по алгебре №1. 9 класс. Тема: Уравнение с двумя переменными и их системы.
Контрольная работа по алгебре №1. 9 класс. Тема: Уравнение с двумя переменными и их системы.
Цель: Проверить уровень усвоения ГОСО: умение решать систему уравнений способом подстановки, графическим способом. — знание нестандартных приемов решения систем уравнений. — умение решать текстовые задачи на составление систем уравнений. Вариант 1. Контрольная работа №3. 9 класс. Тема: «Арифметическая прогрессия». Цель: проверить уровень усвоения ГОСО: определение арифметической прогрессии.
— знание и применение свойств арифметической прогрессии для решения задач. — умение применять формулу суммы членов арифметической прогрессии при решении задач. I вариант.
В срезовой работе 14 заданий. Она рассчитана на 1 урок. Нормы оценок: оценка «3» ставится за верно выполненных заданий, оценка «4» — за заданий Скачиваний: Ефименко Татьяна Геннадьевна. Математика, 9 класс, Тесты. Скачать материал. Вам будет интересно. Справочник по подготовке к ОГЭ по математике. Есептерді шешуде векторларды қолдану.
Похожие материалы. Презентация к уроку математики в 9 классе «Формула суммы n первых членов геометрической прогрессии». Презентация «Построение математической модели задач на движение или работу».
• Вся математика • Математика 5 класс • Математика 6 класс • Математика 7 класс • Математика 8 класс • Математика 9 класс • Математика 10 класс • Математика 11 класс • ГИА по математике • ЕГЭ по математике • Игры и викторины • Олимпиады по матема.
• Методика преподавания. Неограниченная бесплатная загрука материала «Полный пакет тематических контрольных работ (алгебра + геометрия 9 класс)» доступна всем пользователям. Разработка находится в разделе «Математика 9 класс» и представляет собой: «повторение, систематизация».
Скачать материал Mb. Загрузка началась. Учебник к решебнику «Алгебра 9 класс Дидактические материалы» авторов Макарычева, Миндюка и Крайневой, изданный «Просвещением», содержит упражнения для самостоятельных работ, а также предлагает тексты для контрольных работ и задания для проведения школьных олимпиад по математике.
Математическое наполнение книги на высшем уровне. Достаточно открыть «ГДЗ по алгебре за 9 класс Макарычев» и детально разобраться в решении непонятого номера. Теперь проверить или улучшить знания в математике можно онлайн, находясь дома, в школе или в любом другом месте. Благодаря этому решебнику, успеваемость ребёнка только улучшиться.
Похожее:
Входная контрольная работа по информатике 9 класс
Входная контрольная работа по информатике
9 класс
Для передачи сообщения использовалась кодировка Unicode(N=65 536). Сообщение заняло 5 страниц, на каждой из которых 64 строки по 32 символа.
 Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём сообщения? Ответ дайте в килобайтах.Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1280×1024 и палитрой из 256 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы. Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
11001000
11000010
11010100
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Пользователь сначала работал с файлом C:\Work\9class\documents\anketa.doc. Потом он переместился на 1 уровень вверх, создал каталог otchet и перенес файл в новый каталог. Укажите новое полное имя данного файла?
1) C:\Work\9class\documents\otchet\anketa.doc
2) C:\Work\9class\otchet\anketa.doc
3) Work\9class\otchet\anketa.doc
4) C:\Work\otchet\anketa.doc
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв».
 Найдите значение логического выражения не X или Y и Z для слова клавиатура.
Найдите значение логического выражения не X или Y и Z для слова клавиатура.9 класс
Вариант 2.
Для передачи сообщения использовалась кодировка Unicode(N=65 536). Сообщение заняло 15 страниц, на каждой из которых 64 строки по 32 символа. Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1280×1024 и палитрой из 65 536 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы. Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
11001101
11011100
11011001
11011101
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Пользователь работал с каталогом D:\Фотографии\Дом\Кошка. Сначала он поднялся на два уровня вверх, потом спустился в каталог Экзамен и после этого спустился в каталог Сочинение.
 Укажите полный путь того каталога, в котором оказался пользователь.
Укажите полный путь того каталога, в котором оказался пользователь.1) D:\ Сочинение\Экзамен
2) D:\ Экзамен\Сочинение
3) D:\Фотографии\Экзамен\Сочинение
4) D:\Фотографии\Сочинение\Экзамен
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв». Найдите значение логического выражения не X или Y и Z для слова монитор.
Входная контрольная работа по информатике
9 класс
Вариант 3.
Для передачи сообщения использовалась кодировка ASCII (N=256). Сообщение заняло 10 страниц, на каждой из которых 64 строки по 32 символа. Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1024×768 и палитрой из 512 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы.
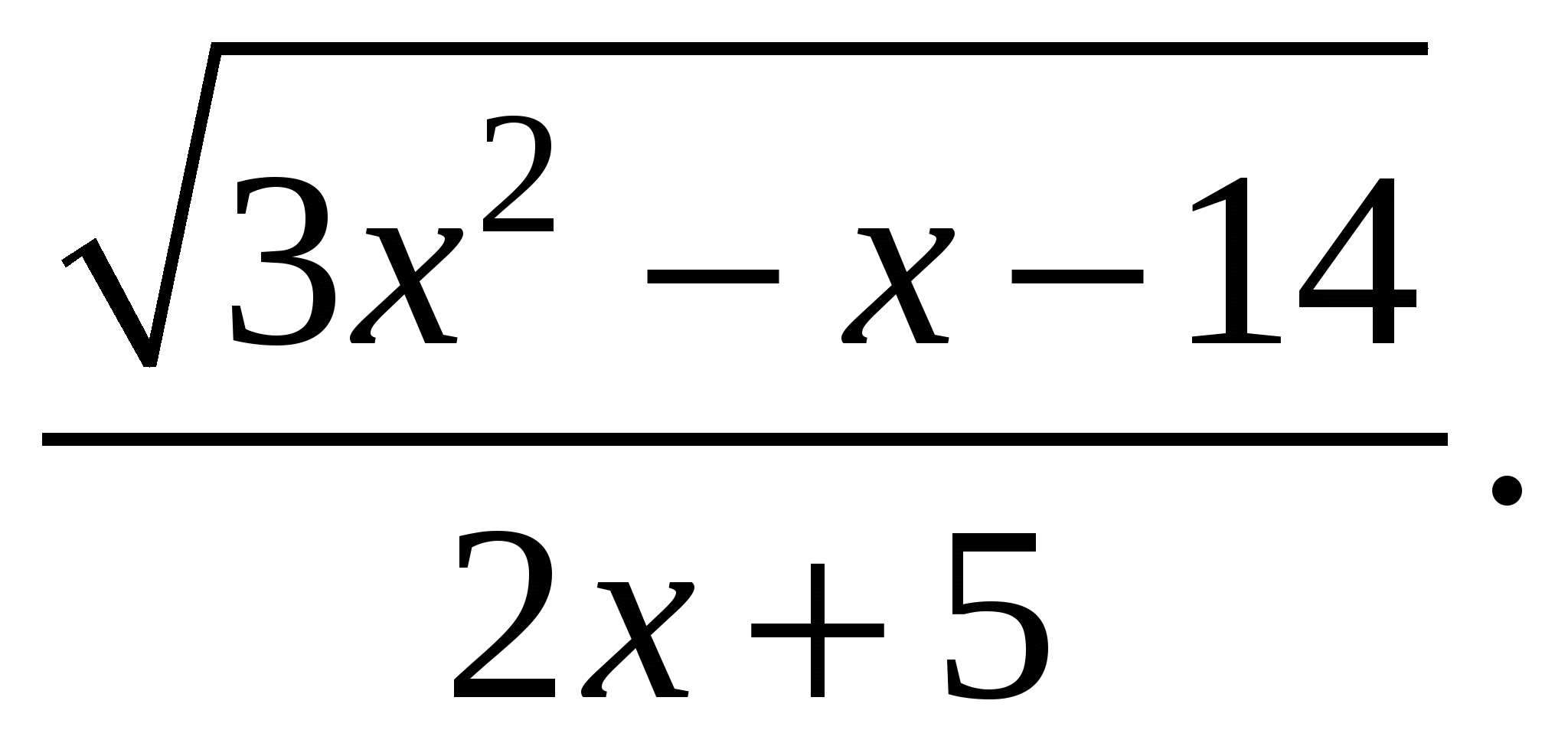 Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.11011001
11001001
11001110
11000000
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Пользователь работал с каталогом C:\2011\Избранное\Видео. Он поднялся на два уровня вверх, затем спустился на один уровень вниз. В результате он оказался в папке Фото. Запишите полный путь к этой папке.
1) C:\2011\Избранное\Фото
2) C:\2011\Фото
3) C:\Фото
4) C:\2011\Байкал\Фото
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв». Найдите значение логического выражения не X или Y и Z для слова мышь.
Входная контрольная работа по информатике
9 класс
Вариант 4.
Для передачи сообщения использовалась кодировка Unicode(N=65 536). Сообщение заняло 20 страниц, на каждой из которых 64 строки по 16 символа. Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1280×1024 и палитрой из 1024 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы. Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
11001011
11000000
11010001
11010011
11000000
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Директор работал с каталогом D:\Школа\Ученики\Адреса. Сначала он поднялся на один уровень вверх, затем спустился на один уровень вниз в каталог Успеваемость, потом ещё раз поднялся на один уровень вверх и после спустился в каталог Нарушения. Укажите полный путь каталога, в котором оказался директор.
1) D:\Школа\Ученики\Успеваемость
2) D:\Школа\Ученики\Нарушения
3) D:\Школа\Нарушения
4) D:\Школа\Ученики\Успеваемость\Нарушения
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв». Найдите значение логического выражения не X или Y и Z для слова принтер.
Найдите значение логического выражения не X или Y и Z для слова принтер.
Входная контрольная работа по информатике
9 класс
Вариант 5.
Для передачи сообщения использовалась кодировка Unicode(N=65 536). Сообщение заняло 50 страниц, на каждой из которых 32 строки по 16 символов. Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1024×768 и палитрой из 32 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы. Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
11001000
11001110
11000000
11001011
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Пользователь работал с каталогом Пушкин. Сначала он поднялся на один уровень вверх, потом спустился в каталог Лермонтов и после этого спустился в каталог Стихи. В результате он оказался в каталоге D:\Учеба\Литература\Лермонтов\Стихи.Укажите полный путь того каталога, в котором пользователь работал вначале.
В результате он оказался в каталоге D:\Учеба\Литература\Лермонтов\Стихи.Укажите полный путь того каталога, в котором пользователь работал вначале.
1) D:\Учеба\Литература\Пушкин
2) D:\Учеба\Литература\Пушкин\Стихи
3) D:\Учеба\Литература\Стихи\Пушкин
4) D:\Учеба\Пушкин
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв». Найдите значение логического выражения не X или Y и Z для слова пользователь.
Входная контрольная работа по информатике
9 класс
Вариант 6.
Для передачи сообщения использовалась кодировка Unicode(N=65 536). Сообщение заняло 2 страницы, на каждой из которых 64 строки по 64 символа. Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1280×1024 и палитрой из 16 384 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы. Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
11000100
11001001
11010010
11001011
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Пользователь работал с каталогом Задачи. Сначала он поднялся на один уровень вверх, потом ещё раз поднялся на один уровень вверх, затем спустился на один уровень вниз.
В результате он оказался в каталоге C:\Документы\Физика
Укажите возможный полный путь каталога, с которым пользователь начинал работу.
1) C:\Документы\Задачи
2) C:\Документы\Математика\Задачи
3) C:\Документы\Математика\Алгебра\Задачи
4) C:\Физика\Задачи
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв». Найдите значение логического выражения не X или Y и Z для слова сканер.
Входная контрольная работа по информатике
9 класс
Вариант 7.
Для передачи сообщения использовалась кодировка Unicode(N=65 536). Сообщение заняло 8 страниц, на каждой из которых 64 строки по 16 символов. Каков информационный объём сообщения? Ответ дайте в килобайтах.
Каков информационный объём картинки, занимающей весь экран компьютера с разрешением 1024×1024 и палитрой из 32 768 цветов?
Каждая буква русского алфавита закодирована трехзначным десятичным числом, причем код каждой последующей буквы на 1 больше предыдущей буквы. Известно, что буква «А» кодируется как 192. Расшифруйте слово, закодированное в двоичной системе счисления.
11000000
11010011
11010011
11000000
11011000
Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
Пользователь работал с каталогом Участники. После окончания работы с этим каталогом, он поднялся на два уровня вверх, затем спустился на один уровень вниз, потом ещё раз спустился на один уровень вниз.
В результате он оказался в каталоге C:\Конференция\Секции\Информатика
Укажите возможный полный путь каталога, с которым пользователь начинал работу.
1) C:\Конференция\Регионы\Списки\Участники
2) C:\Конференция\Участники
3) C:\Конференция\Регионы\Участники
4) C:\Участники
Пусть X = «Вторая буква слова согласная», Y = «Последняя буква слова гласная», Z = «В слове пять букв». Найдите значение логического выражения не X или Y и Z для слова информатика.
ОТВЕТЫ
В-1 В-2
20 Кб
1280 Кб=1,25 Мб
з в у к
200 194 212 203
2
ложь 60 Кб
2560 Кб=2,5 Мб
м ы ш ь
205 220 217 221
3
истина
В-3 В-4
20 Кб
864 Кб
ш и н а
217 201 206 192
2
истина 40 Кб
1600 Кб
к а рт а
203 192 209 211 192
2
ложь
В-5 В-6
50 Кб
480 Кб
з н а к
200 206 192 203
1
истина
16 Кб
2240 Кб
д и с к
196 201 210 203
2
ложь
В-7 16 Кб
1920 Кб
а т т а ч
192 211 211 192 216
3
ложь
Приложенные файлы
- 124683
Размер файла: 31 kB Загрузок: 0
входная контрольная работа по алгебре 9 класс макарычев
алгебра 7 класс макарычев контрольные — КОНТРОЛЬНАЯ РАБОТА ПО АЛГЕБРЕ. ПО АЛГЕБРЕ В 7 КЛАССАХ МАКАРЫЧЕВ — КЛАСС: КОНТРОЛЬНЫЕ 9 КЛАСС входная контрольная работа по алгебре 9 класс макарычев
Контрольная работа! Зарабатывай в интернете от 140$ в день! Россия и СНГ!
Рабочая программа по алгебре (9 — Входная контрольная работа: 21-22. График — по алгебре: 9 класс к учебнику Ю.Н. Макарычев и др. входная контрольная работа по алгебре 9 класс макарычев
АН Ваш Риэлтор набирает агентов Приглашаем на работу агентов по недвижимости Сменный график Хорошие условия
Контрольные работы по алгебре для 9 — входная контрольная работа по алгебре 9 класс макарычев . входная контрольная работа по — входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы по алгебре для 9. Контрольные работы по алгебре для 9 класса (Макарычев 2008 г). На сегодняшний день …
Рабочая программа по алгебре (9 — Макарычев «Дидактические материалы по алгебре для 9 класса — входная контрольная работа …
Заработок на дому Зарабатывай не выходя из дома в сети интернет
Контрольные работы от 120 руб/стр Любой предмет и сложность.
ПО АЛГЕБРЕ В 7 КЛАССАХ МАКАРЫЧЕВ — КЛАСС: КОНТРОЛЬНЫЕ 9 КЛАСС входная контрольная работа по алгебре 9 класс макарычев
Контрольная работа! Зарабатывай в интернете от 140$ в день! Россия и СНГ!
Рабочая программа по алгебре (9 — Входная контрольная работа: 21-22. График — по алгебре: 9 класс к учебнику Ю.Н. Макарычев и др. входная контрольная работа по алгебре 9 класс макарычев
АН Ваш Риэлтор набирает агентов Приглашаем на работу агентов по недвижимости Сменный график Хорошие условия
Контрольные работы по алгебре для 9 — входная контрольная работа по алгебре 9 класс макарычев . входная контрольная работа по — входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы по алгебре для 9. Контрольные работы по алгебре для 9 класса (Макарычев 2008 г). На сегодняшний день …
Рабочая программа по алгебре (9 — Макарычев «Дидактические материалы по алгебре для 9 класса — входная контрольная работа …
Заработок на дому Зарабатывай не выходя из дома в сети интернет
Контрольные работы от 120 руб/стр Любой предмет и сложность. Высокое качество. Доступно и точно в срок!
Контрольные работы по алгебре для 9 — входная контрольная работа по алгебре 9 класс макарычев . Контрольные работы по алгебре для 9 — входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы по алгебре по — Контрольные работы по алгебре по учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н …
Контрольные на заказ. СПБ Сделаем для Вас контрольную по любому предмету.Мин.сроки и цены.Офис центр входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы в СПб! Контрольные на заказ от 1 дня, готовые от 15 минут. В офисе и online! входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы по алгебре 7 — Контрольные работы по алгебре 7 класс по учебнику Ю.Н. Макарычев, Н. Г. Миндюк. — точка М (9; -25)?
Работа всем! Зарабатывай в интернете от 200$ в день! Начни прямо сейчас! входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы! СПб! Выполнение контрольных работ. Все предметы.
Высокое качество. Доступно и точно в срок!
Контрольные работы по алгебре для 9 — входная контрольная работа по алгебре 9 класс макарычев . Контрольные работы по алгебре для 9 — входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы по алгебре по — Контрольные работы по алгебре по учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н …
Контрольные на заказ. СПБ Сделаем для Вас контрольную по любому предмету.Мин.сроки и цены.Офис центр входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы в СПб! Контрольные на заказ от 1 дня, готовые от 15 минут. В офисе и online! входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы по алгебре 7 — Контрольные работы по алгебре 7 класс по учебнику Ю.Н. Макарычев, Н. Г. Миндюк. — точка М (9; -25)?
Работа всем! Зарабатывай в интернете от 200$ в день! Начни прямо сейчас! входная контрольная работа по алгебре 9 класс макарычев
Контрольные работы! СПб! Выполнение контрольных работ. Все предметы. Опыт. Срочное исполнение.
Дидактические материалы по алгебре — Дидактические материалы по алгебре для 9 класса — Макарычев Ю.Н., контрольные работы входная контрольная работа по алгебре 9 класс макарычев
входная контрольная работа по. … договор, гарантируем сдачу. входная контрольная работа по алгебре 9 класс макарычев ответы …
Кредиты от 3.000 до 30.000.000 р. Быстрый поиск по всем банкам. Уже через 9 минут Ваша проблема будет решена. входная контрольная работа по алгебре 9 класс макарычев
Опыт. Срочное исполнение.
Дидактические материалы по алгебре — Дидактические материалы по алгебре для 9 класса — Макарычев Ю.Н., контрольные работы входная контрольная работа по алгебре 9 класс макарычев
входная контрольная работа по. … договор, гарантируем сдачу. входная контрольная работа по алгебре 9 класс макарычев ответы …
Кредиты от 3.000 до 30.000.000 р. Быстрый поиск по всем банкам. Уже через 9 минут Ваша проблема будет решена. входная контрольная работа по алгебре 9 класс макарычев
Контрольна на 12 математика 9 класс
Скачать контрольна на 12 математика 9 класс PDF
Контрольные работы по алгебре 9 класс. Разбор контрольной работы по алгебре 9 класс. Контрольная работа №4 по алгебре в 9 классе по теме «Уравнения и неравенства с двумя переменными» Вариант 1 • 1.
Решите систему уравнений: 2x + y = 7, х2 — у = 1. • 2. Периметр прямоугольника равен Читать еще. dom-v-teple.ru doc. Посмотреть. Входная контрольная работа по алгебре 9 класс Часть Характеристика структуры и содержания работы. Работа по алгебре состоит из 2-х частей и включает в себя 15 заданий, различающихся формой и уровнем сложности: Часть 1 содержит 12 заданий: с выбором от Читать еще. dom-v-teple.ru Девятый класс — один из самых сложных.
Работа по алгебре состоит из 2-х частей и включает в себя 15 заданий, различающихся формой и уровнем сложности: Часть 1 содержит 12 заданий: с выбором от Читать еще. dom-v-teple.ru Девятый класс — один из самых сложных.
Перед вчерашним учеником маячит ответственный экзамен, первый за все годы обучения. Требования учителей растут: на каждом уроке дают новые знания, регулярно проводятся самостоятельные, а на дом задают десятки тяжелых упражнений. Все это нужно, чтобы ребенок мог успешно сдать ОГЭ и пойти в 10 или колледж.
Однако алгебра — не такой простой предмет, его нельзя понять обычной зубрежкой. Тогда на помощь и приходит эта книга. Решебник по математике пригодится: детям. Тут представлены тесты, решения на контрольные и проверочные работы, олимпиадные задания. Верные ответы подойдут для самоконтроля. родителям. 1 класс. Математика. Английский язык. Русский язык. Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева. Издательство: Просвещение Тип книги: Дидактические материалы.
Гдз и решебник Алгебра 9 класс Макарычев, Миндюк, Крайнева — Дидактические материалы. Алгебра 9 класс. Тип пособия: Дидактические материалы. Авторы: Макарычев, Миндюк, Крайнева. Что включено в Дидактические материалы. Решебник охватывает весь курс алгебры девятого класса и позволяет повторить ранее изученный материал.
Содержание пособия: Тридцать две самостоятельных работы, каждая из которых представлена в двух вариантах. Девять контрольных работ, составленных в четырех вариантах.
Задачи по всем разделам основного учебника для закрепления пройденного материала. Дополнительно в решебник включены задания для математических олимпиад и экзаменационный итоговый тест. На сайте dom-v-teple.ru вы можете получить ответы и методические рекомендации по экзамену для самостоятельной подготовки к « Контрольная работа по математике 9 класс» по направлению 56 регион (Оренбургская область) по предмету Математика.
Ответы на « Контрольная работа по математике 9 класс» доступны для 9 класса, но также вы всегда можете следить за актуальными обновлениями на сайте. Обучающие материалы от dom-v-teple.ru помогут вам: Подготовиться к будущему экзамену; Получить хорошую оценку после экзаменов; Проверить свои знания и быть уверенными в своих силах. Получая ответы к «
Обучающие материалы от dom-v-teple.ru помогут вам: Подготовиться к будущему экзамену; Получить хорошую оценку после экзаменов; Проверить свои знания и быть уверенными в своих силах. Получая ответы к «
членов арифметической прогрессии 5; 12; 3. Найдите первый член арифметической. прогрессии (а. Входной контроль по алгебре в 8 и 9 классах. Контрольная работа по алгебре «Показательная функция» 11 класс. Контрольная работа по алгебре «Корень n-ой степени» 11 класс. Контрольные работы по алгебре 7 класс (Ю.М. Колягин, М.В.
Ткачева, Н.Е. Федорова, М.И. Шабунин). Предметы. Алгебра. Математика. Музыка. МХК. Тест по математике. 9 класс. В тесте 5 вопросов. В каждом вопросе только один правильный вариант ответа. Контрольная работа состоит из 5 заданий. Работа позволит проанализировать ошибки учащихся, выработать умения, навыки исследования функции и построения графика.Умение анализировать, обобщать свои знания, применять свои знания при решении заданий; 0.
ГДЗ контрольные работы по алгебре 9 класс Мордкович Мнемозина. Авторы: Мордкович. Издательство: Мнемозина. Для девятого класса повышенное внимание к предметам нормальное явление.
Авторы: Мордкович. Издательство: Мнемозина. Для девятого класса повышенное внимание к предметам нормальное явление.
Все ученики стараются свои знания по выученному материалу закрепить всеми доступными методами. Алгебра – тот предмет, точное понимание правил, разбора математических функций и алгоритма решения необходимые перед сдачей ЭГЕ. Кому помогают готовые ответы для тетради авторства Мордкович для заданий контрольных проверок.
• Учителям – иногда молодые начинающие специалисты ночи напролет проводят в решении уравнений, которые.
PDF, fb2, fb2, txtПохожее:
Дети-вундеркинды и синдром саванта: почему люди с высоким IQ сходят с ума и не умеют дружить
Гениальность считается и даром, и проклятием. Известно достаточно много случаев, когда дети-вундеркинды страдали психическими заболеваниями и не умели налаживать дружеские связи. Но есть ли на самом деле связь между высоким IQ и проблемами в жизни?
Известно достаточно много случаев, когда дети-вундеркинды страдали психическими заболеваниями и не умели налаживать дружеские связи. Но есть ли на самом деле связь между высоким IQ и проблемами в жизни?
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
Винсент Ван Гог был склонен к депрессии и эпилептическим припадкам, а гениальный математик Джон Нэш страдал от параноидальной шизофрении и галлюцинаций. Мы привыкли слышать о том, что гениальность — тяжелое бремя. Но есть немало примеров, которые опровергают этот стереотип. Лев Ландау поступил в университет в 13 лет, а Бобби Фишер в 15 стал самым молодым гроссмейстером в истории. Оба они прожили долгую и яркую жизнь. Так можно ли говорить о связи гениальности и душевных расстройств?
Кто такие гении и вундеркинды
Слово «вундеркинд» в переводе с немецкого значит «чудесное дитя». Несколько этимологических словарей указывают, что раньше так называли Иисуса Христа, но достоверных данных о происхождении термина нет. Так или иначе, сейчас вундеркиндами называют детей, которые с юных лет опережают в развитии сверстников. Они могут обладать феноменальными способностями к математике, музыке, иностранным языкам, творчеству и спорту и быть гениальными как в одной сфере, так и сразу в нескольких. Есть и дети, которые невероятно успешны в какой-то одной дисциплине, а по другим отстают от сверстников, — это называют синдромом саванта, от французского idiot savant («ученый идиот»). Генетики считают, что гениальность — это не присутствие каких-то особых генов (например, гена гениальности), а их уникальное сочетание, случайная комбинация.
Так или иначе, сейчас вундеркиндами называют детей, которые с юных лет опережают в развитии сверстников. Они могут обладать феноменальными способностями к математике, музыке, иностранным языкам, творчеству и спорту и быть гениальными как в одной сфере, так и сразу в нескольких. Есть и дети, которые невероятно успешны в какой-то одной дисциплине, а по другим отстают от сверстников, — это называют синдромом саванта, от французского idiot savant («ученый идиот»). Генетики считают, что гениальность — это не присутствие каких-то особых генов (например, гена гениальности), а их уникальное сочетание, случайная комбинация.
Таким образом, гениальность не наследуется и не повторяется в поколениях
Феномен гениальности изучается давно, но остается одной из самых больших загадок науки. Понятие «гений» встречается в трудах Демокрита, Платона, Аристотеля (правда, древнегреческий «гений» считался чем-то вроде чувства вдохновения), его изучали философы Гегель, Кант, Фрейд, Шеллинг и Юнг. Считать гениальность высшей степенью одаренности начали с подачи математика Альфреда Уайтхеда, который назвал XVII век «веком гениев»: тогда жили Шекспир, Фрэнсис Бэкон, Гарвей, Кеплер, Галилей, Декарт, Паскаль, Ньютон, Локк, Спиноза, Лейбниц и другие выдающиеся деятели.
Одни ученые, как древние греки, считали гениальность божественным подарком, неким иррациональным озарением, которое снисходит на человека. Другие заявляли, что это врожденное качество человека, особенность ума.
Гениальный — значит сумасшедший?
Систематизировать знания о гениях первым попытался английский писатель Исаак Дизраэли. В 1795 году он выпустил книгу «Литературный характер, или История гения», в которой проанализировал характеры известных писателей. Среди прочих признаков гениальности он выделил меланхолию, внутреннее беспокойство и даже помешательство. Благодаря ему научное сообщество заметило, что между гениальным человеком и патологически сумасшедшим есть немало точек соприкосновения.
В 1863 году итальянский психиатр Чезаре Ломброзо издал книгу «Гениальность и помешательство», в которой заявил, что гениальность порой может зависеть от психопатологии, но считать всех гениальных людей помешанными, а всех помешанных гениальными неверно.
Современные психологии и педагоги к признакам гениальности (одаренности) относят:
- Раннее развитие речи;
- Точность выполнения умственных операций;
- Высокую познавательную активность;
- Отличную память;
- Способность к классификации;
- Раннюю увлеченность, любознательность;
- Стремление к творчеству, нестандартное мышление;
- Отставание моторной координации от познавательных способностей.
Пока одни размышляли о природе гениальности, другие подходили к вопросу с прикладной точки зрения. Долгое время педагоги и психологи составляли рекомендации и инструкции о том, как вырастить из ребенка гения. По их представлениям, нужно было лишь создать правильную внешнюю среду. На волне популярности этой темы для измерения гениальности было разработано множество тестов: тесты Айзенка, Векслера, Гилфорда, Равена и другие.
Прорыв в изучении одаренности сделал известный психолог Льюис Термен из Стэнфордского университета. В 1921 году Термен решил исследовать одаренных детей. Он провел собственные тесты на IQ в нескольких школах Калифорнии и отобрал полторы тысячи учеников, которые набрали выше 140–170 баллов (средний IQ детей находится в диапазоне от 90 до 110). На протяжении 30 лет он следил за судьбой «термитов» (так прозвали участников исследования): их успехами на работе, в семейной жизни и других сферах.
В 1921 году Термен решил исследовать одаренных детей. Он провел собственные тесты на IQ в нескольких школах Калифорнии и отобрал полторы тысячи учеников, которые набрали выше 140–170 баллов (средний IQ детей находится в диапазоне от 90 до 110). На протяжении 30 лет он следил за судьбой «термитов» (так прозвали участников исследования): их успехами на работе, в семейной жизни и других сферах.
Но определение гения по высокому показателю интеллекта не оправдало себя: выяснилось, что многие люди с высоким IQ не совершают никаких особенных открытий. Даже среди наиболее успешных «термитов» никто не показал достижений, сравнимых с Шекспиром, Ньютоном или Паскалем. Зато исследование Термена развенчало миф о том, что у вундеркиндов есть проблемы в социализации: повзрослев, дети не превращались в болезненных одиноких неудачников, а, наоборот, становились хорошо приспособленными, здоровыми и очень успешными взрослыми. В целом уровень разводов, алкоголизма и самоубийств в группе Термена был равен среднему по стране.
Брин, Цукерберг и Леди Гага
В 1955 году лонгитюдное исследование Льюиса Термена завершилось. Стало ясно, что тесты на IQ, возможно, не лучший показатель одаренности. Тогда к 1972 году профессор Джулиан Стэнли из Университета Джонса Хопкинса решил взять за основу результаты математической части теста SAT (тест для приема в высшие учебные заведения в США).
Он отобрал 450 подростков в возрасте 12–14 лет, которые набрали больше всего баллов, и стал следить за их судьбой. Через пять лет после тестирования первых детей профессор начал расширять выборку: к 1992 году общее количество «испытуемых» достигло пяти тысяч человек. На протяжении жизни эти дети проходили опросы в возрасте 18, 23, 33, 50 и 65 лет. Стэнли пришел к тому же выводу, что и Термен: в большинстве своем одаренные дети были успешны в жизни, вероятность получить докторскую степень, опубликовать научную работу, получить патент или высокий денежный доход у них оказалась выше, чем у их среднестатистических ровесников.
Джулиан Стэнли основал Центр талантливой молодежи, через который прошло много детей. В том числе Марк Цукерберг (основатель компании Facebook), Сергей Брин (основатель Google), певица Стефани Джерманотта (выступает под псевдонимом Lady Gaga), а также выдающиеся математики Теренс Тао и Ленард Ын. Все они — живые примеры одаренных детей, которые стали успешными взрослыми.
Дети Центра талантливой молодежиУмные дети чаще носят очки
Параллельно с исследованием Джулиана Стэнли в Великобритании начала работу Джоан Фримен, профессор психологии из Лондона. В 1974 году она отобрала 70 детей в возрасте от 5 до 14 лет. У нее было две контрольные группы: экспериментальная (с детьми, у которых был высокий результат по тесту Равена) и контрольная (одноклассники такого же возраста, пола, социального происхождения, что и испытуемые).
В 2001 году, спустя 27 лет, Фримен подвела итоги. Она сообщила, что интеллект никак не связан с эмоциональными проблемами, адаптацией и числом друзей в школе. Также она не выявила связи умственной одаренности с физическим развитием.
Также она не выявила связи умственной одаренности с физическим развитием.
Впрочем, один стереотип все же подтвердился — о том, что умные дети чаще носят очки
Публикация результатов вызвала недовольство: оказалось, что многим людям нравится считать, что одаренные дети обречены на трудную жизнь. «Мне казалось странным, что мои результаты о нормальном эмоциональном развитии одаренных были столь неблагожелательно встречены», — писала Фримен.
Последующие исследования других ученых тоже не обнаружили статистически значимой разницы между количеством проблем у обычных и гениальных детей. Они, наоборот, подтвердили, что высокий интеллект помогает людям адаптироваться к разным жизненным обстоятельствам. Научное сообщество пришло к выводу о том, что чувство одиночества и ментальные расстройства, которые порой сопутствуют гениальности, — это следствие не одаренности, а воспитания.
Родители маленьких гениев фокусируются на их профессиональной реализации, а не на социализации. Они радуются академическим достижениям ребенка и забывают о том, что ему нужно развиваться и в других областях жизни. Кроме того, частой проблемой становятся завышенные ожидания родителей: одаренные дети бывают особенно чувствительны к одобрениям и критике, и во взрослом возрасте они могут испытывать недостаток внимания, разочарование и тревогу.
Они радуются академическим достижениям ребенка и забывают о том, что ему нужно развиваться и в других областях жизни. Кроме того, частой проблемой становятся завышенные ожидания родителей: одаренные дети бывают особенно чувствительны к одобрениям и критике, и во взрослом возрасте они могут испытывать недостаток внимания, разочарование и тревогу.
Действительно ли существует «проклятие гениальности»?
Представление о том, что вундеркинды не способны жить полной жизнью и обречены на страдания, оказалось ложным. Почему же люди до сих пор верят в «проклятие гениальности»?
У ученых на этот счет есть несколько гипотез. Одна из них объясняет эту демонизацию гениальности завистью. Одаренность — особо ценное качество, но большинство людей не может отнести себя и своих детей к числу одаренных, поэтому им проще наделить гениев негативными характеристиками (чтобы было не так обидно). По этой же аналогии живет стереотип о том, что красивые девушки глупы.
По другой версии, людям проще принимать собственные недостатки, если даже у гениев бывают проблемы в жизни
Поэтому, например, так популярны истории об успешных людях, которые бросили школу, но стали богатыми и знаменитыми. Кроме того, многие считают, что гении и вундеркинды — это пассионарии, которые развивают мир, и их доля должна быть тяжела (есть тенденция считать, что за любой дар приходится платить).
Кроме того, многие считают, что гении и вундеркинды — это пассионарии, которые развивают мир, и их доля должна быть тяжела (есть тенденция считать, что за любой дар приходится платить).
Причины гениальности остаются неизученными. Одна из последних гипотез связывает одаренность с особенностями развития мозга. В 2006 году Филип Шоу и его коллеги из Национального института психического здоровья (штат Мэриленд, США) исследовали более 300 детей в возрасте от 6 до 19 лет.
Раз в два года дети проходили магнитно-резонансную интроскопию, с помощью которой измерялся размер внутренних частей мозга. Так, оказалось, что кора головного мозга у вундеркиндов начинала сокращаться позже, чем у всех остальных детей: не в 9 лет, а в 11. Самые большие различия при этом наблюдались в предлобных участках коры, которые отвечают за составление планов и выработку суждений. К 19 годам все различия нивелировались и кора мозга у всех выглядела одинаково.
Эта задержка может предполагать высокие умственные способности, ведь одаренный ребенок обрабатывает более сложные операции, хотя кора мозга продолжает формироваться. Однако эксперимент ученых поставил вопрос о том, с чем связана эта задержка. По одной из версий, c формированием и устранением связей между клетками головного мозга.
Однако эксперимент ученых поставил вопрос о том, с чем связана эта задержка. По одной из версий, c формированием и устранением связей между клетками головного мозга.
«Вундеркинд — это человек, чье будущее остается в прошлом»
Виктория Юркевич, профессор кафедры «Возрастная психология имени профессора Л. Ф. Обуховой» факультета «Психология образования» МГППУ: Вундеркинд — это ребенок, значительно опережающий своих сверстников по какой-либо характеристике. Чаще всего этим словом обозначается уровень умственного развития, превышающий уровень ровесников.
Но иногда весьма значительное опережение у вундеркинда связано не столько с подлинной одаренностью (то есть с умственным развитием), сколько, скажем, с исключительной памятью. С точки зрения усвоения знаний блестящая память — это неплохо, но знания сами по себе, без критического мышления, без яркой познавательной мотивации сейчас уже мало что значат.
Именно поэтому будущее таких детей бывает крайне неопределенным, а чаще всего — весьма драматичным
Одаренность раньше рассматривалась главным образом как высокий интеллект. Сейчас большинство специалистов считает, что в одаренность обязательно входит ярко выраженная познавательная мотивация — страсть к познанию, яркая увлеченность какой-либо областью знания или практики.
Сейчас большинство специалистов считает, что в одаренность обязательно входит ярко выраженная познавательная мотивация — страсть к познанию, яркая увлеченность какой-либо областью знания или практики.
Впрочем, в большинстве случаев высокого интеллекта без познавательной мотивации и не бывает, но вот страсти, поглощенности конкретной познавательной деятельностью может и не быть. Кроме того, некоторые специалисты в понятие одаренности вкладывают и наличие нестандартного мышления. И это логично: высокий интеллект даже с высокой познавательной мотивацией сам по себе в наше время мало что значит. Для высоких достижений в любой области науки и практики необходимо нестандартное (творческое) и еще критическое мышление. Если этого нет, то все достоинства такого одаренного человека пригодятся разве что для составления энциклопедий или успешного участия в конкурсе знатоков («синдром Анатолия Вассермана»).
И наконец, самый «дорогой» термин: «гениальность». Гениальность — это прежде всего высочайшая реализация одаренности в социально ценных достижениях. Гений — это тот, кто много сделал для человечества. Надо понимать: если взять всех одаренных людей, то гениев среди них будет меньше одного процента. А вундеркиндов — исчезающая доля процента. Иначе говоря, вундеркинды гениями бывают, но достаточно редко. Для большинства из них актуально замечательное определение «Вундеркинд — это человек, чье будущее остается в прошлом».
Гений — это тот, кто много сделал для человечества. Надо понимать: если взять всех одаренных людей, то гениев среди них будет меньше одного процента. А вундеркиндов — исчезающая доля процента. Иначе говоря, вундеркинды гениями бывают, но достаточно редко. Для большинства из них актуально замечательное определение «Вундеркинд — это человек, чье будущее остается в прошлом».
Конечно, вундеркиндов Гаусса, Моцарта или великого психолога Жана Пиаже из списка гениев не выкинешь
Но при этом, например, Ньютон никаким вундеркиндом категорически не был, даже сначала несколько отставал от других одноклассников. А уж что касается Эйнштейна или, скажем, Дарвина, то там ситуация еще отчетливей: учителя считали их слабыми учениками, а Дарвина даже безнадежно отстающим.
Альберт Эйнштейн в 14 лет, 1894 годИнтересно, что в России было два великих поэта по имени Александр Сергеевич. Один из них, Пушкин, относился явно к антивундеркиндному типу развития: он только в 15 лет начал активно писать стихи, но они были очевидно слабыми (найдите в интернете и убедитесь сами). Неуспешен он был и в обучении (исключая, конечно, французский). Настолько неуспешен, что директор Лицея Егор Антонович Энгельгардт при его выпуске дал ему уничтожающую характеристику, предсказывая ему незавидное будущее. И это «солнцу русской поэзии»!
Неуспешен он был и в обучении (исключая, конечно, французский). Настолько неуспешен, что директор Лицея Егор Антонович Энгельгардт при его выпуске дал ему уничтожающую характеристику, предсказывая ему незавидное будущее. И это «солнцу русской поэзии»!
Другой, тоже великий русский поэт Александр Сергеевич, был именно вундеркиндом. Он в 11 лет (был немножко старше Алисы Тепляковой) поступил в Московский университет, блестяще его окончил, стал потом знаменитым поэтом, драматургом, композитором, дипломатом. Да, это Грибоедов Александр Сергеевич.
«Бродский умудрился стать второгодником в 7-м классе»
Для того чтобы разобраться в этом вопросе, надо ввести новое понятие — «высокая интеллектуальная норма». Для одаренности, как уже говорилось выше, мало высокого интеллекта: нужна познавательная страсть, глубокая поглощенность каким-либо занятием. Если этого нет, то это все-таки не совсем одаренность — это именно «высокая норма». Для хорошей адаптации и высокой социальной успешности совсем неплохо, но для ярких достижений, особенно в науке и технике, всё-таки маловато.
Подлинно одаренные школьники редко бывают во всем обычными. Они меньше времени проводят со сверстниками, меньше интересуются разного рода молодежными направлениями и модами, меньше подчиняются социуму. Для хорошей адаптации это, как правило, не очень хорошо. Кроме того, эти дети не всегда ровно и не всегда хорошо учатся в школе, да и потом их путь сильно отличается от обычного успешного представителя «высокой нормы».
Посмотрите биографию, скажем, Иосифа Бродского. Он умудрился стать второгодником в 7-м классе. В 15 лет он уходит из школы и потом никогда и нигде больше не учится. Он успел поработать и сторожем, и санитаром в морге, потом несколько лет был в ссылке, а через 25 лет стал лауреатом Нобелевской премии.
Это что, нормальное развитие? И такие «экстримы» — почти со всеми одаренными людьми
Что уж говорить о вундеркиндах. Сам факт резкого опережения ровесников уже не позволяет говорить о нормальности развития. У этих детей по понятным причинам хуже социализация, часто бывают проблемы с саморегуляцией, с эмоциональным интеллектом, с критическим мышлением и так далее. По этим причинам чаще всего академической успешностью все и ограничивается, а собственно серьезные достижения, важные для общества, отмечаются редко.
По этим причинам чаще всего академической успешностью все и ограничивается, а собственно серьезные достижения, важные для общества, отмечаются редко.
Что касается описанных в статье лонгитюдов, то у Термена в его знаменитом исследовании 1921 года участники были главным образом из числа «высокой интеллектуальной нормы» и даже в исследовании Джоан Фримен была примерно та же ситуация. Дело в том, что в исследовании Термена входной порог включения в группу испытуемых был именно и только интеллект — 140 единиц IQ и ни одной единицей меньше. Всё, и никаких других характеристик уже не требовалось.
Еще важная деталь: так называемых одаренных детей в тот эксперимент «поставляли» учителя
А учителя и тогда, и даже сейчас любят прежде всего академически успешных учеников. Работая в самых престижных школах, я довольно часто (слава богу, не всегда) встречалась со следующим заявлением: «Да какой же он одаренный: у него по трём предметам сплошь тройки» (особенно любят одаренные дети получать тройки по географии и литературе — при врожденной грамотности, кстати говоря). А во времена Термена, в 1921 году, это было еще очевидней.
А во времена Термена, в 1921 году, это было еще очевидней.
Некоторым подтверждением того, что набиралась в этот эксперимент именно «высокая норма», служит обстоятельство, которое далеко не всегда упоминается: ни один из подростков, принявших участие в лонгитюде, потом не стал выдающимся человеком (хотя, действительно, практически все были очень успешными). При этом два подростка, которых не взяли в этот эксперимент, так как им не хватило нескольких баллов до заветных 140, стали лауреатами Нобелевской премии.
Большинство фактов, особенно в таких науках, как психология, при ближайшем рассмотрении перестают быть фактами и становятся материалом для серьезного и критического анализа. К сожалению, не только в психологии.
Фото на обложке: Shutterstock / frantic00
VDOE :: Математика
Ваш браузер не поддерживает джаваскрипт! Этот сайт использует JavaScript, но полностью работает без него. ИнструкцияНовости и объявления
НОВИНКА! Стандартные документы по математике
Стандартные документы по математике (K-8) были созданы как часть ресурсов Virginia LEARNS, чтобы помочь в выявлении контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися. Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.
Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.
журналов отслеживания учебных стандартов по математике (с 2020-2021 учебного года по 2021-2022 учебный год)!
Журналы отслеживания для оценок от детского сада до алгебры II были разработаны, чтобы помочь учителям определить, какие стандарты учащиеся имели достаточно знаний и опыта в течение 2020-2021 учебного года.Эти журналы могут помочь в принятии решений относительно того, когда и как можно будет познакомиться с новыми стандартами в 2021-2022 учебном году.
Инициатива по математике в Вирджинии
Инициатива Вирджиния по математическим путям (VMPI) — это совместная инициатива Департамента образования Вирджинии (VDOE), Государственного совета высшего образования Вирджинии (SCHEV) и системы общественных колледжей Вирджинии (VCCS). Инициатива поддерживает Профиль выпускника Вирджинии, переопределяя математические пути для студентов в Содружестве, чтобы охватить знания, навыки, опыт и атрибуты, которые студенты должны достичь, чтобы добиться успеха в колледже и / или на работе и быть «готовыми к жизни».”
Инициатива поддерживает Профиль выпускника Вирджинии, переопределяя математические пути для студентов в Содружестве, чтобы охватить знания, навыки, опыт и атрибуты, которые студенты должны достичь, чтобы добиться успеха в колледже и / или на работе и быть «готовыми к жизни».”
Содержание страницы
Стандарты обучения Математика K-12Включает:
- Стандарты обучения и рамки учебных программ
- Планы обучения математике (MIP)
- Тестовые чертежи
- Практические задания
Обзор
Стандарты обучения математике определяют основной учебный контент на каждом уровне обучения для последовательного обучения.Содержание стандартов по математике поддерживает следующие пять целей для студентов: научиться решать математические задачи, общаться математически, рассуждать математически, устанавливать математические связи и использовать математические представления для моделирования и интерпретации практических ситуаций.
Ресурсы по математике для поддержки перехода к новому обучению 2021-2022 гг.
Стандарты обучения Вирджинии — журналы отслеживания математики (с 2020-2021 учебного года по 2021-2022 учебный год)
Журналы отслеживания учебных стандартов по математике для классов от детского сада до алгебры II были разработаны, чтобы помочь учителям определить, с какими стандартами учащиеся знакомы и имеют достаточный опыт в течение 2020-2021 учебного года.Они могут поддержать решения относительно того, когда и как можно будет познакомиться с новыми стандартами в 2021-2022 учебном году. Документы по математическим стандартам — это документ в формате PDF. (PDF) можно использовать вместе с журналами отслеживания в качестве поддержки при идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися.
Переходная математика
Стандартные документы по математике — это документ в формате PDF.(PDF) можно использовать вместе с журналами отслеживания в качестве поддержки при идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися. Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.
Обучение на месте — Интернет-ресурсы Обучение на месте — Интернет-ресурсы содержат некоторые из множества общих онлайн-ресурсов, которые всегда бесплатны для учителей, родителей и учащихся.
Ресурсы для профессионального развития
VDOE продолжает обеспечивать профессиональное развитие школьных подразделений и учителей, чтобы поддержать внедрение стандартов обучения математике. Школьным подразделениям и учителям рекомендуется использовать ресурсы профессионального развития для повышения успеваемости учащихся за счет качественного обучения.
- 2019 Развитие более глубокого обучения с помощью разнообразных математических задач — Институт математики — Институты 2019 года предоставили учителям и руководителям математики возможность повышения квалификации, направленную на выполнение разнообразных математических задач, чтобы поддержать более глубокие возможности обучения для студентов и укрепить учебные программы, разработанные на местном уровне. Материалы институтов были включены для использования учителями и педагогическими коллективами.
- Институты по стандартам обучения по математике (SOL) 2018 — Институты по стандартам обучения по математике 2018 года обеспечили обучение, направленное на внедрение стандартов обучения по математике 2016 года; усиление преподавания и изучения математики посредством содействия содержательному математическому дискурсу; и поддержка равных возможностей обучения математике для всех учащихся.Продукт Математических институтов 2018 года представляет собой набор онлайн-модулей профессионального развития, предназначенных для использования группой учителей определенного уровня или курса при содействии одного из членов команды.
- Институт стандартов обучения математике (SOL) 2017 г. — VDOE обеспечил повышение квалификации школьных подразделений и их учителей в поддержку внедрения Стандартов обучения по математике и структуры учебной программы 2016 года. Ресурсы профессионального развития VDOE поддерживают использование эффективных методов преподавания математики.
- Институты по стандартизации обучения математике (SOL) на 2009-2014 гг. — VDOE обеспечивает целевое профессиональное развитие через институты математики с 2009 года. Эти институты сосредоточились на стандартах обучения по математике 2009 года и были сформулированы пятью целями процесса для студентов, которые становятся математиками. решатели проблем, математически общаются, рассуждают математически, устанавливают математические связи и используют математические представления для моделирования и интерпретации практических ситуаций.
Учебные ресурсы по математике
В дополнение к стандартам, рамкам учебных программ, планам тестов и выпущенным тестам, другие учебные ресурсы включают:
- Algeblocks Training — онлайн-тренинг для учителей, которым либо необходимо введение в использование алгебр, либо необходимо заново познакомиться с манипулятивным
- Инициатива готовности к алгебре — информация для подготовки студентов к успеху в алгебре
- Корреляция между VASOL и CCSS. Это таблица в формате Excel.(XLS) — Эта электронная таблица содержит черновик корреляций между детским садом и алгеброй II — 2016 Стандарты обучения Вирджинии (VASOL) для математики с Общими государственными стандартами (CCSS) для математики. Эта корреляция была создана для поддержки преподавателей по всему Содружеству, поскольку они пытаются использовать материалы, которые могут указывать только на соответствие CCSS. Все VASOL и CCSS, а также цели процесса Вирджинии и математические практики CCSS связаны по всей таблице, чтобы упростить перекрестные ссылки.
- Планы совместного преподавания математики — В этих планах используются шесть общих подходов к совместному обучению и содержатся предложения о том, как другие преподаватели могут эффективно использовать опыт каждого учителя для улучшения уроков и занятий в классе с совместным преподаванием. Эти планы совместного обучения были созданы и изменены избранной группой учителей Вирджинии, участвующих в Инициативе «Совершенство для совместного обучения». Эти планы согласовывают обучение с требованиями стандартов обучения по математике 2016 года и были проверены специалистами VDOE и специалистами по специальному образованию.
- Нарушения обучаемости по математике — Эта страница содержит информацию и ресурсы, а также два новых сопутствующих руководства VDOE:
- Учебные видеоролики для учителей — видеоролики, предоставленные в качестве поддержки для внедрения Стандартов обучения математике штата Вирджиния
- Just in Time Mathematics Quick Checks — Эти формирующие экзамены соответствуют Стандартам обучения математике 2016 года (SOL). Эти ресурсы, разработанные учителями Вирджинии и руководителями математики, предназначены для того, чтобы помочь учителям выявлять учащихся с незавершенным обучением и помогать в планировании обучения, чтобы «вовремя» заполнить потенциальные пробелы.По мере того, как в течение учебного года вводится новый контент, учителя могут использовать эти быстрые проверки для выявления и диагностики незавершенного обучения на уровне класса и / или для оценки понимания необходимых знаний, которые могут потребоваться для доступа к контенту на уровне класса. Пробелы в понимании математики учащимися существуют по разным причинам, и эти ресурсы можно использовать, чтобы помочь вернуть учащимся математическое обучение в нужное русло.
- K-3 Образцы результатов успеваемости по математике — школы ведут учет достижений по математике для каждого ученика K-3, чтобы отслеживать его успеваемость и способствовать успеваемости на экзаменах SOL в третьем классе.Эта запись сопровождает ученика, который переходит в новую школу
- Математика Capstone Информация о курсе — Руководящие документы и ссылки на учебные ресурсы Учебные планы по математике
- — ранее известные как Уроки с расширенным объемом и последовательностью , теперь доступны для классов K-8, алгебры I, геометрии, алгебры II и алгебры, функций и анализа данных. Эти учебные планы включают обновленные документы 2009 года, а также недавно разработанные учебные планы, соответствующие Стандартам обучения по математике 2016 года .Учебные планы по математике помогают учителям привести обучение в соответствие со Стандартами обучения по математике 2016 года , предоставляя примеры того, как знания, навыки и процессы, содержащиеся в SOL и структуре учебной программы, могут быть представлены учащимся в классе. Инструмент для вертикальной артикуляции математики
- (MVAT) — этот инструмент обеспечивает поддержку в определении концепций, соответствующих Стандартам обучения по математике (SOL) 2016 года, которые формулируются на разных уровнях обучения математике или на разных курсах.
- Математические настенные карточки словарного запаса (K-8, Алгебра I, Геометрия, AFDA и Алгебра II) — обеспечивают отображение слов математического содержания и связанных визуальных подсказок, помогающих в развитии словарного запаса.
- Расширенные математические задачи — (K-8, Алгебра I, Геометрия, Алгебра II) Эти ресурсы предназначены для поддержки учителей во внедрении Стандартов обучения по математике 2016 года в своих классах. Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.
- Программа подготовки к детскому саду штата Вирджиния — многомерная оценка готовности к детскому саду, которая дополняет существующую оценку навыков грамотности учащихся с использованием скрининга грамотности фонологической осведомленности (PALS) с оценками ранней математики учащихся, саморегуляции и навыки общения.
- Цель ВКРП состоит в том, чтобы школьные подразделения и Содружество имели более полное представление о критических навыках готовности учащихся к школе при поступлении в детский сад.Школы, подразделения и руководители штатов могут использовать данные о готовности для определения приоритетов индивидуальных потребностей учащихся и целевых программ, ресурсов и возможностей профессионального развития учителей.
- В 2018 году Генеральная ассамблея Вирджинии приняла закон, который требует, чтобы все учащиеся детских садов проходили аттестацию с использованием VKRP до конца 2019-2020 учебного года, а затем ежегодно (HB5002, пункт 128, H.).
Технологические и математические ресурсы
Профессиональные организации
Премиальные программы
- Президентские награды за выдающиеся достижения в преподавании математики и естествознания — Президентская награда за выдающиеся достижения в преподавании математики и естествознания (PAEMST) — это высшее признание, которое учитель математики или естествознания с детского сада по 12-й класс может получить за выдающееся преподавание в Соединенных Штатах.
- Учитель года по математике Уильяма К. Лоури — Каждый год Совет учителей математики Вирджинии признает классного учителя начального, среднего, среднего, университетского уровня, а также специалиста / тренера по математике за его или ее выдающуюся работу и достижения в области математики. обучение математике.
Начало страницы
Математика | Texas Education Agency
На этой странице представлена информация по таким темам, как учебная программа, оценка и правила.Мы приветствуем любые предложения по улучшению этой страницы для лиц, работающих над обеспечением студентов высококачественными математическими программами. Присоединяйтесь к списку рассылки по математике и получайте обновления по мере поступления информации.
Команда математиков Отдела учебных программ обеспечивает руководство и руководство программами математики от детского сада до 12 класса.
Сотрудники отдела математики делают следующее:
- Оказывает помощь округам штата во внедрении Техасского курса основных знаний и навыков (TEKS) по математике
- Курирует разработку и управление финансируемыми государством программами повышения квалификации
- Сотрудничает с отделом оценки успеваемости учащихся в разработке государственных оценок по математике
- Оказывает помощь отделу учебных материалов и образовательных технологий (IMET) в надзоре за процессом принятия учебников для учебных материалов по математике для K-12
- Проверяет государственные сертификаты по математике Государственным советом по сертификации педагогов (SBEC)
Команда математиков обеспечивает постоянную связь с областью, связанной с учебной программой по математике и требованиями к выпускным экзаменам в главе 74.
Объявления
Ресурсы по математике Веб-страница ТЕКС
Ресурсы на веб-странице TEKS по математике предоставляют ресурсы для помощи родителям и учителям в переходе на новую версию TEKS по математике для K-8, которая была внедрена в 2014–2015 годах.
Президентские награды за выдающиеся достижения в области преподавания математики и естественных наук (PAEMST)
Президентские награды за выдающиеся достижения в области преподавания математики и естествознания (PAEMST) — это высшие награды, присуждаемые правительством США специально за преподавание естественных наук, технологий, инженерии, математики и / или информатики в школах до 12 лет.Награды были учреждены Конгрессом в 1983 году. Национальный научный фонд под руководством Белого дома утверждает кандидатов Техаса на получение национальной премии. Если кандидат будет выбран в качестве лауреата, он получит 10 000 долларов и оплаченную поездку в Вашингтон, округ Колумбия, для проведения церемоний, включающих признание со стороны президента Соединенных Штатов. Для получения дополнительной информации посетите www.paemst.org .
В Техасе учителя, отвечающие критериям, которые подадут заполненное заявление до 1 апреля 2021 года, получат 25 часов CPE.С вопросами обращайтесь к координаторам PAEMST штата Техас по адресу [email protected].
Открыто окно подачи заявок на участие в конкурсе PAEMST 2021
TEA ищет экспертов в области математического образования для рассмотрения и оценки заявок на участие в конкурсе PAEMST 2021 года. В этом году в конкурсе участвуют учителя с 7 по 12 классы. Подача заявок до четверга, 25 марта 2021 г. или до этой даты.
Заявление рецензента PAEMST 2021 г. (PDF, 238 КБ)
PAEMST Mentors
TEA ищет экспертов в области математического образования в качестве наставников PAEMST для абитуриентов.Учителя заполняют онлайн-заявку, которая включает письменное описание и видео урока. Чтобы узнать больше о процессе подачи заявки или просмотреть пакет заявки, посетите веб-сайт PAEMST по адресу www.paemst.org.
Наставников могут попросить обучить до трех претендентов на получение награды. Это может включать в себя помощь кандидатам в видеосъемке, ответах на вопросы или просмотре / редактировании описательной части заявки. Наставничество может осуществляться лично, по телефону, по электронной почте или другим способом, определенным наставником и кандидатом.
Будет предоставлено обучение и материалы, чтобы помочь наставникам, а также помочь обеспечить последовательность в каждом наставничестве. Педагоги, желающие принять участие, должны написать координатору штата Техас по адресу [email protected].
Объявлен национальный лауреат PAEMST по математике
Бриджит Матаморос-Мота была выбрана в качестве победителя национальной премии PAEMST по математике 2019 года. Г-жа Матаморос-Мота преподает статистику AP в средней школе Джона Х. Гайера в Дентоне, штат Техас.Дополнительная информация об объявлении для г-жи Матаморос-Мота доступна на веб-сайте PAEMST (внешний источник).
PAEMST Финалист штата Техас на 2020 год
В конкурсе 2020 отмечаются учителя математики и естествознания от детских садов до 6 классов, чьи инновационные методы воплощают в жизнь обучение в классе. Финалисты штата Техас были признаны в январе 2021 года на заседании Совета по образованию штата Техас. Финалисты штата Техас по средней математике перечислены ниже:
- Кэссиди Вагнер преподает математику в 6 классе в средней школе Lorene Rogers в Prosper ISD в Проспере, штат Техас.
- Кристи Батлер преподает компактную математику для 6-7 классов в средней школе Медлин на северо-западе ISD в Трофи-клубе, штат Техас.
- Дезира Хэркроу преподает в детском саду начальной школы Тимбер-Крик в Томбалле, штат Техас.
Профессиональное развитие
Несколько общегосударственных курсов повышения квалификации по математике в настоящее время доступны очно в вашем ESC и онлайн через Центр поддержки математики Техаса. Скоро будут доступны новые курсы.Для получения подробной информации о доступных курсах и о том, как получить к ним доступ, обратитесь в свой ESC, посетите веб-сайт Texas Algebra Ready или посетите http://texasmathsupportcenter.org.
Ссылки по теме
Ресурсы, представленные ниже, посвящены различным темам, связанным с заданиями учителей, стандартами и учебными материалами.
Техас: основные знания и навыки математики 19 Глава 111 TAC
Texas Essential Knowledge and Skills Глава 111. Математика (Matemáticas) — детский сад — 5 класс, принята в 2012 г.(PDF, 783 КБ)
Texas Essential Knowledge and Skills Глава 111. Математика (Matemáticas) -Grade 6, Adopted 2012. (PDF, 622KB)
Прокламация 2014 г. (утвержденные классы учебных материалов K-8)
Прокламация 2015 г. (Принятые учебные материалы для средних школ)
Материалы с открытым исходным кодом
Таблица назначений для аттестации учителей
Texas Gateway (внешний источник)
Стандарты карьеры и готовности к колледжу (внешний источник)
Академия математики и чтения
Награды
Президентская награда за выдающиеся достижения в области преподавания математики и естественных наук (PAEMST) является высшей национальной наградой для учителей математики и естественных наук.
Президентские награды за выдающиеся достижения в области преподавания математики и естественных наук (внешний источник)
Оценочные ссылки
Следующие ссылки предоставляют поддержку со стороны отдела оценки знаний учащихся.
Ресурсы STAAR
Политика калькулятора
Отдел оценки успеваемости учащихся
Тесты для учащихся с ограниченными возможностями
Ответ на материалы вмешательства (RtI)
Следующие ссылки предоставляют бесплатные ресурсы для учителей Техаса, которые могут помочь студентам на всех уровнях структуры RtI.
ESTAR / MSTAR (внешний источник)
Инициатива Texas Algebra Ready (TXAR) (внешний источник)
Texas Regional Collaboratives (внешний источник): Texas Regional Collaboratives for Excellence in Science and Mathematics Teaching (TRC) поддерживает сеть партнерств K-16, чтобы обеспечить высококачественное, устойчивое и интенсивное наставничество учителей, ориентированное на укрепление материалов по естествознанию и математике. и педагогика. Эта инфраструктура, состоящая из более чем 56 высших учебных заведений, сотрудничает с Агентством образования Техаса, центрами образовательных услуг, школьными округами и деловыми партнерами.TRC имеет 18-летний опыт разработки и реализации образцовых профессиональных разработок с использованием основанных на исследованиях учебных моделей, материалов и передового опыта. Посетите TRC, чтобы получить самую свежую информацию о профессиональном развитии науки.
Прочие ресурсы
Следующие документы предназначены для помощи учителям математики в процессе планирования.
Дополнительная информация (внешний источник)
Teacher2Teacher Math Videos (внешний источник)
Глоссарий по интерактивной математике (внешний источник)
Revised Mathematics TEKS: параллельное сравнение TEKS (внешний источник)
Ответ штата Техас на координаторов учебной программы, пересмотренный в 2013 г. (внешний источник)
Карты вертикального выравнивания (внешний источник)
Математика / Финансовый анализ и управление рисками | Программы бакалавриата
Хрустящие числа.Рассчитайте шансы. Создавайте карьерный успех.
Мир финансов требует профессионалов с сильными математическими и аналитическими навыками. Вы отточите их обоих в этой сложной программе — одной из немногих по всей стране, признанных Институтом CFA.
Выбираете ли вы специализацию в области дипломированного финансового аналитика или профессионального управления рисками, вы будете изучать сочетание математики, финансов, бухгалтерского учета и экономики, что даст вам идеальную основу для карьеры в банковском деле, управлении инвестициями или управлении рисками.
Между тем, если вы выберете программу совместной работы, вы закончите учебу, имея в своем резюме два года оплачиваемого опыта работы.
Основные моменты программы
- Социальная и академическая поддержка. Через Ассоциацию студентов финансового анализа и управления рисками (FARMSA) вы найдете знания, инструменты и сети, необходимые для процветания в индустрии финансовых услуг.
- Получите CFA или PRM. Когда вы закончите учебу, вы будете готовы к сдаче экзаменов дипломированного финансового аналитика (CFA) или к получению других профессиональных назначений, таких как профессиональный риск-менеджер (PRM) или член Канадского института ценных бумаг.
Многие из наиболее востребованных должностей в сфере бизнеса требуют математических навыков и навыков управления рисками, которые сочетает в себе эта программа.
Чему вы научитесь?
Первокурсники
В течение первого года вы пройдете несколько базовых курсов по математике, информатике и коммуникациям.
В старшие классы вы будете изучать курсы статистики, финансов, бухгалтерского учета и бизнеса.
Узнайте больше о курсах, которые вы пройдете для получения степени.
Настройте степень
На третьем курсе вы сможете выбрать специализацию дипломированного финансового аналитика или специализацию профессионального управления рисками.
Когда вы станете студентом, консультанты помогут выяснить, какие несовершеннолетние или специальности могут вписаться в ваши планы.
Получите советы от студентов Ватерлоо
Подпишитесь на нашу ежемесячную новостную рассылку, чтобы получать такие советы, как выбор университетской программы, жизнь в Ватерлоо и финансы.
Связаться со студенческим послом
Спросите студента математического факультета об их программе, классах, участии в кампусе и многом другом!
Co-op = соответствующий оплачиваемый опыт работы
Чередуя условия обучения в школе и условия оплачиваемой совместной работы на протяжении всей вашей степени, вы можете исследовать новые области карьеры и типы работодателей по мере развития ваших карьерных интересов.
Образцы должностей в кооперативном режиме
- Помощник по информационным системам
- Младший бизнес-аналитик
- Эффективность инвестиций стажер
- Младший игровой аналитик
- Аналитик данных
- Специалист по хеджированию и активам
- Количественный аналитик по торговым продуктам
Примеры работодателей кооперативов
- Финансовая группа ТД Банк
- Банк Монреаля
- Белл Канада
- SS&C Technologies
- Лотерея и игровая корпорация Онтарио
- Пенсионный план учителей Онтарио
- Инвестиционный совет CPP
Что вы можете делать со степенью в области финансового анализа и управления рисками?
Наши выпускники часто делают карьеру в области анализа рисков, консалтинга, развития бизнеса и смежных областях.Они часто работают в страховых компаниях и финансовых учреждениях.
Недавние выпускники
- Управление портфелем, оценщик — Foresea Life Insurance Company
- Наблюдательный аналитик рисков — CIBC
- Аналитик по поддержке данных — Sustainanalytics
- Сотрудник по управлению рисками рынков капитала — TD Securities
- Планировщик развития бизнеса, Nissan Finance — Nissan Canada
- Консультант — Capgemini Canada
- Управляющий казначейством — TD Canada Trust
Узнайте о будущем карьеры в бизнесе.
Студенческая жизнь, включая женщин по математике
Математическое общество (MathSoc)
MathSoc управляется студентами для студентов и предоставляет широкий спектр клубов и услуг, а также общественные и академические мероприятия, чтобы сделать ваш опыт в качестве студента математики Ватерлоо как можно лучше. Есть много способов принять участие и познакомиться со студентами других программ факультета математики.
Женщины-математики
Сообщество «Женщины в математике» (WiM) поощряет и защищает женщин всех возрастов, которые заинтересованы в изучении математики и карьере в смежной области.WiM стремится к тому, чтобы представители всех полов были хорошо представлены в математике, и приветствует людей с недопредставленной гендерной идентичностью.
Женщины в информатике
«Женщины в компьютерных науках» (WiCS) продвигает гендерное равенство для студентов, заинтересованных в изучении информатики и продолжающих карьеру в области вычислительной техники. WiCS имеет очень активный комитет, управляемый студентами, и предлагает такие мероприятия, как программа наставничества Big CSters, семинары, серии выступлений и панели о разнообразии в компьютерных науках и STEM.
Также существует клуб «Женщины в науке, технологиях, инженерии и математике» (WiSTEM), управляемый студентами, который приветствует всех студентов (независимо от пола) для продвижения равенства в STEM. Возможности включают практические семинары, обсуждения, помощь в выполнении домашних заданий и приглашенных докладчиков.
Требования для зачисления
студентов Онтарио: шесть курсов 12 классов U и / или M, включая
- Расширенные функции
- Исчисление и векторы
- Любые классы 12 U Английский язык
- Еще один курс 4U
- 11 класс Рекомендуется введение в информатику
Средние показатели приема: индивидуальный выбор из высоких 80-х
Не учишься в Онтарио? Найдите наши требования к зачислению.
Мы настоятельно рекомендуем вам принять участие в олимпиаде по математике для старших классов в Канаде и / или в олимпиаде по математике Евклида, чтобы повысить свой статус зачисления. Кроме того, чтобы получить стипендию для поступления на математический факультет, вы должны написать один или оба конкурса. Если вы выполните оба варианта, мы воспользуемся вашей более высокой оценкой.
Дистанционное обучение | Manitoba Education
The Independent Study Option предлагает следующие курсы по математике.Пожалуйста, укажите Код темы, Обозначение темы, и обозначение ISO на заявке для идентификации требуется курс (ы).
За каждым списком имени субъекта следует уникальный 10-значный код, состоящий из трех частей:
Выберите желаемый вариант, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1668 Репетитор / маркер: Д. Брэдфорд
Класс № 1703 Репетитор / Маркер: Д.Неметчек
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Этот курс развивает базовые навыки и идеи, которые вам понадобятся для продолжения изучения математики в будущем. Решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые вы откроете для себя в каждом модуле.Вы будете изучать четыре основных области: числа, отношения и закономерности, геометрию, статистику и вероятность. По окончании этого курса вы приобретете важные навыки и знания, которые понадобятся вам для дальнейшего изучения математики, а также уверенность в своих математических способностях. Он имеет следующую структуру:
- Модуль 1: Статистика
- Модуль 2: Чувство числа
- Модуль 3: Полномочия
- Модуль 4: Многочлены
- Модуль 5: Линейные отношения
- Модуль 6: Геометрия окружности
- Модуль 7: 2D и 3D объекты
- Модуль 8: Симметрия
Оценка основана на:
| Назначения | 60% |
| Промежуточный экзамен (модули 1-4) * | 15% |
| Заключительный экзамен (модули 1-8) * | 25% |
| Итого | 100% |
* Когда студенты напишут свои промежуточные и заключительные экзамены, им будет разрешено принести лист материалов по экзаменам в экзаменационную комнату.Более подробная информация представлена во введении к курсу в предварительном обзоре курса .
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS).Зарегистрированные студенты получат имя пользователя и пароль.
Практические экзамены и ключи для ответов
Вариант 2 — Mathématiques, 9e année (10F)
10 класс по основам математики (20S) 1 кредит (2012)
Код курса 3000 20S 001
Предварительный просмотр курса (981 КБ)
Варианты регистрации (Выберите 1)
Выберите желаемую опцию, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1651
Репетитор / маркер: J. Voth
Класс № 1700
Репетитор / маркер: S. De Ruyck
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Примечание: Учащиеся не могут иметь зачетные единицы ни по одному из бывших курсов «Потребительская математика 25G, часть I и часть II (код 3911/3912)» и / или курса «Потребительская математика 20S (код 3904)», и — по новому курсу «Основы математики 10 класса». (код 3000).
Этот курс развивает математические навыки, идеи и уверенность, которые позволят студентам продолжить изучение математики в будущем. Студенты будут использовать многие из уже приобретенных навыков для решения задач и выполнения основных арифметических операций. В этом курсе будут изучены четыре основные области: личные финансы, формы и пространство, числа и принятие решений. Решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые вы откроете для себя в каждом модуле.Он имеет следующую структуру:
- Модуль 1: Валовая заработная плата, табели учета рабочего времени и проценты
- Модуль 2: Чистая оплата
- Модуль 3: Измерение
- Модуль 4: Геометрия
- Модуль 5: Работа с углами
- Модуль 6: Решения потребителей
- Модуль 7: Тригонометрия
- Модуль 8: Преобразования
Оценка основана на:
| Назначения | 75% |
| Промежуточный экзамен (модули 1–4) * | 12.5% |
| Заключительный экзамен (модули 5-8) * | 12,5% |
| Итого | 100% |
* Когда студенты напишут свои промежуточные и заключительные экзамены, им будет разрешено принести лист материалов по экзаменам в экзаменационную комнату. Более подробная информация представлена во введении к курсу, которое находится в предварительном обзоре курса (981 КБ).
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Доступ в Интернете
Практические экзамены и ключи ответов (также доступны в Blackboard)
См. Предварительный просмотр курса (981 КБ) для получения информации о необходимых / рекомендуемых ресурсах.
Вариант 2 — Mathématiques au quotidien, 10e année (20S)
10 класс Введение в прикладную и предварительную математику (20S) 1 кредит (2011)
Код курса 3905 20S 000
Предварительный просмотр курса (1,0 МБ)
Варианты регистрации (Выберите 1)
Выберите желаемую опцию, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1663
Репетитор / Маркер: Олексук И.
Класс № 1699
Репетитор / маркер: Д. Классен
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Примечание : Учащиеся не могут иметь зачетные баллы ни за один из предыдущих курсов Pre-Calculus для 10 класса (код 3939) и / или Grade 10 Applied 20S (код 3903) курс , и за новый Grade 10 Introduction по математике перед исчислением (код 3905) .
Этот курс является продолжением концепций, которые были изучены в 9 классе по математике, и вводит новые темы. Это основа для курсов прикладной и предварительной математики для 11 и 12 классов. В этом курсе будут рассмотрены четыре основные области: числа, закономерности и отношения, форма и пространство, а также статистика и вероятность. Решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые исследуются в каждом модуле.Он имеет следующую структуру:
- Модуль 1: Графики и отношения
- Модуль 2: Чувство числа
- Модуль 3: Измерение
- Модуль 4: Тригонометрия
- Модуль 5: Взаимосвязи и функции
- Модуль 6: Многочлены
- Модуль 7: Координатная геометрия
- Модуль 8: Системы и уравнения
Оценка основана на:
| Назначения | 55% |
| Промежуточный экзамен (модули 1–4) * | 20% |
| Заключительный экзамен (модули 1-8) * | 25% |
| Итого | 100% |
* Когда студенты напишут свои промежуточные и заключительные экзамены, им будет разрешено принести лист материалов по экзаменам в экзаменационную комнату.Дополнительная информация будет предоставлена во введении к курсу, которое находится в предварительном обзоре курса (1,0 МБ).
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS).Зарегистрированные студенты получат имя пользователя и пароль.
Практические экзамены и ключи для ответов
Вариант 2 — Введение в математические аппликации и предварительный расчет, 10e année (20S)
11 класс Прикладная математика (30S) 1 кредит (2016)
Код курса 3903 30S 002
Класс № 1620
Репетитор / маркер: L Isaak
Класс № 1696
Репетитор / маркер: J.Майерс
Предварительный просмотр курса (1,07 КБ)
Рекомендуемое предварительное условие — 10 класс «Введение в прикладную математику и математику перед исчислением» (20S).
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
11 класс «Прикладная математика» — это продолжение концепций, которые вы изучали в предыдущие годы, а также введение в новые темы.В этом курсе решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые вы откроете для себя в каждом модуле. В этом курсе вы изучите несколько областей, включая линейные и квадратичные функции, логику и рассуждения, геометрию, тригонометрию, статистику и математические модели.
Этот курс разделен на восемь модулей, организованных следующим образом:
- Модуль 1. Квадратичные функции
- Модуль 2: Исследовательский проект по математике
- Модуль 3: Обоснование решения проблем
- Модуль 4: Геометрия углов и треугольников
- Модуль 5: Тригонометрия
- Модуль 6: Статистика
- Модуль 7: Математические модели
- Модуль 8: Коэффициенты масштабирования для двумерных и трехмерных фигур
Оценка основана на:
| Назначения | 55% |
| Промежуточный экзамен (модули 1-4) | 20% |
| Заключительный экзамен (модули 5-8) | 25% |
| Итого | 100% |
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамен), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы пройти модуль дистанционного обучения выставить окончательную оценку.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS). Зарегистрированные студенты получат имя пользователя и пароль.
Обязательно
Для завершения этого курса вам потребуется графический калькулятор или доступ к компьютерным программным приложениям для работы с графиками и финансовой математики. Для написания экзаменов вам понадобится доступ к тем же ресурсам, которые вы использовали для модулей.
Экзамены
При планировании промежуточного экзамена вас попросят указать одно приложение для построения графиков или технологию построения графиков, а при планировании заключительного экзамена вам будет предложено указать одно приложение для построения графиков или технологию построения графиков и одно приложение для статистики или статистическую технологию. Убедитесь, что ваш наставник / маркер одобрил ваш выбор до того, как писать экзамен, и что инспектор на экзамене знает о приложении или технологии, которые вы будете использовать.Организация этого при планировании обследования должна дать достаточно времени, чтобы убедиться, что приложение или технология одобрены и могут быть установлены при необходимости. Когда вы напишете свои промежуточные и выпускные экзамены, вам будет разрешено взять с собой на экзамен лист материалов по экзаменам. Этот лист будет размером в одну букву, 8 1/2 «на 11», и может быть написан от руки или на машинке. Обе стороны страницы могут быть заполнены. Его нужно отправить вместе с экзаменом. Лист материалов по экзамену не выставляет никаких оценок.
Каждый экзамен длится 2,5 часа.
Практические экзамены и ключи для ответов
11 класс по основам математики (30S) 1 кредит (2014)
Код курса 3000 30S 001
Предварительный просмотр курса (1,0 МБ)
Варианты регистрации (Выберите 1)
Выберите желаемую опцию, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1652
Репетитор / маркер: J. Voth
Класс № 1698
Репетитор / маркер: П. Маршалл
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Примечание: Студенты не могут иметь зачетные единицы ни по одному из бывших курсов Consumer Mathematics 35G Part III и Part IV (код 3913/3914), и / или Consumer Math 30S (code 3904), курса , и по новому 11 класс Основы математики (код 3000) .
Курс «Основы математики» для 11 класса основан на знаниях и навыках, приобретенных учащимися при изучении основ математики для 10-го класса. В целом учебная программа Essential Math делает упор на потребительские приложения, решение проблем, принятие решений и пространственное восприятие. Конкретные темы, изучаемые в 11 классе, перечислены ниже. После завершения этого курса учащиеся будут хорошо подготовлены к изучению основ математики в 12 классе. Он имеет следующую структуру:
- Модуль 1: Проценты и кредит
- Модуль 2: Трехмерная статистика
- Модуль 3: Статистика
- Модуль 4: Управление деньгами
- Модуль 5: Отношения и закономерности
- Модуль 6: Тригонометрия
- Модуль 7: Моделирование конструкции
Оценка основана на:
| Назначения | 75% |
| Промежуточный экзамен (модули 1-3) * | 12.5% |
| Заключительный экзамен (модули 4-7) * | 12,5% |
| Итого | 100% |
* Когда студенты напишут свои промежуточные и заключительные экзамены, им будет разрешено принести лист материалов по экзаменам в экзаменационную комнату. Более подробная информация представлена во введении к курсу, которое можно найти в предварительном обзоре курса (1.0 МБ)
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Доступ в Интернете
* Если требуется бумажная копия, обратитесь в DLU.
Практические экзамены и ключи ответов (также доступны в Blackboard)
См. Предварительный просмотр курса (1.0 МБ) для требуемых / предлагаемых ресурсов.
Вариант 2 — Mathématiques au quotidien, 11e année (30S)
Предисчисление по математике в 11 классе (30S) 1 кредит (2013)
Код курса 3939 30S 002
Предварительный просмотр курса (1,01 МБ) Рекомендуемое предварительное условие — 10-й класс по математике перед исчислением (20S) ИЛИ 10-й класс «Введение в прикладную математику» и
Предварительная математика (20S)
Выберите желаемую опцию, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1682
Репетитор / Маркер: Олексук И.
Класс № 1702
Репетитор: Ящишин С.
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Курс предисчислительной математики для 11 класса основан на предисчислительных темах, с которыми учащиеся были ознакомлены во введении 10-го класса в прикладную и предисчислительную математику.Студенты будут изучать три основных области: число, шаблоны и отношения и форма и пространство. Решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые студенты откроют для себя в каждом модуле. После завершения этого курса учащиеся будут хорошо подготовлены к выполнению предисчислительной математики в 12 классе. Он имеет следующую структуру:
- Модуль 1: Последовательности и серии
- Модуль 2: Факторинг и реляционные выражения
- Модуль 3: Квадратичные функции
- Модуль 4: Решение квадратичных функций
- Модуль 5: радикалы
- Модуль 6: Системы уравнений и неравенств
- Модуль 7: Тригонометрия
- Модуль 8: Абсолютное значение и взаимные функции
Оценка основана на:
| Назначения | 55% |
| Промежуточный экзамен (модули 1–4) * | 20% |
| Заключительный экзамен (модули 1-8) * | 25% |
| Итого | 100% |
* 80% заключительного экзамена покрывает содержание модулей 5-8
* Когда учащиеся напишут свои промежуточные и заключительные экзамены, им будет разрешено взять лист материалов по экзаменам в экзаменационную комнату.
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS). Зарегистрированные студенты получат имя пользователя и пароль.
Практические экзамены и ключи для ответов
См. Предварительный просмотр курса (1,01 МБ) для получения информации о необходимых / рекомендуемых ресурсах.
Вариант 2 — Предварительный расчет Mathématiques, 11e année (30S)
12 класс Прикладная математика (40S) 1 кредит (2018)
Код курса 3903 40S 004
Класс № 1621
Репетитор / маркер: J.Майерс
Класс № 1622
Репетитор / маркер: Исаак Л.
Предварительный просмотр курса (1,16 МБ)
Рекомендуемое предварительное условие — 11 класс Прикладная математика (30S)
Вариант 1
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Вариант 2 — аппликации Mathématiques, 12e année (40S)
12 класс «Прикладная математика» — это продолжение концепций, которые вы изучали в предыдущие годы, а также введение в новые темы.В этом курсе решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые вы откроете для себя в каждом модуле. В этом курсе вы изучите несколько областей, включая линейные и нелинейные функции, вероятность, методы подсчета, финансы, а также проектирование и измерения.
Этот курс разделен на восемь модулей, организованных следующим образом:
- Модуль 1: Функции
- Модуль 2: Исследовательский проект по математике
- Модуль 3: Логические рассуждения
- Модуль 4: Вероятность
- Модуль 5: Финансовая математика
- Модуль 6: Методы счета
- Модуль 7: Синусоидальные функции
- Модуль 8: Проектирование и измерение
Оценка основана на:
| Назначения | 55% |
| Промежуточный экзамен (модули 1-4) | 20% |
| Заключительный экзамен (модули 5-8) | 25% |
| Итого | 100% |
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамен), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы пройти модуль дистанционного обучения выставить окончательную оценку.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS). Зарегистрированные студенты получат имя пользователя и пароль.
Для завершения этого курса вам потребуется графический калькулятор или доступ к компьютерным программным приложениям для работы с графиками и финансовой математики. Для написания экзаменов вам понадобится доступ к тем же ресурсам, которые вы использовали для модулей.
Экзамены
В день промежуточного экзамена вас попросят указать одно графическое приложение или графическую технологию, а в день заключительного экзамена вас попросят указать одно графическое приложение или графическую технологию и одно финансовое приложение или финансовую технологию. Перед тем, как писать экзамены, убедитесь, что ваш наставник / маркер одобрил ваш выбор. Когда вы напишете свои промежуточные и выпускные экзамены, вам будет разрешено взять с собой на экзамен лист материалов по экзаменам.Этот лист будет размером в одну букву, 8½ «x 11», и может быть написан от руки или на машинке. Обе стороны страницы могут быть заполнены. Его нужно отправить вместе с экзаменом. Ресурсный лист экзамена не стоит никаких оценок. Каждый экзамен длится 3 часа.
Практические экзамены и ключи для ответов
12 класс Введение в исчисление (45S) 1/2 кредита (2015)
Код курса 3940 45S 001
Класс № 1665
Репетитор / маркер: C.Билык
Предварительный просмотр курса (409 КБ)
Рекомендуемое предварительное условие — математика перед математикой в 12 классе (40S)
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Этот курс является факультативным.Он основан на темах, которые были введены в предисчислительную математику 12-го класса. Основная цель этого курса — познакомить учащихся с областями математики, которые будут углубленно изучаться в программах послесреднего образования. Студенты знакомятся с концепциями пределов, деривативов, приложений деривативов и интеграции. В этом курсе решение проблем, общение, рассуждение и мысленная математика являются одними из тем каждого модуля. Он имеет следующую структуру:
- Блок 1: Пределы
- Блок 2: Производная
- Раздел 3: Применение производных инструментов
- Раздел 4: Интеграция
Оценка основана на:
| Назначения | 55% |
| Заключительный экзамен (модули 1-4) | 45% |
| Итого | 100% |
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамен), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы пройти модуль дистанционного обучения выставить окончательную оценку.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS). Зарегистрированные студенты получат имя пользователя и пароль.
Практические экзамены и ключи для ответов
12 класс по основам математики (40S) 1 кредит (2014)
Код курса 3000 40S 001
Предварительный просмотр курса (1.19 МБ)
Варианты регистрации (Выберите 1)
Выберите желаемую опцию, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1653
Репетитор / маркер: Д. Брэдфорд
Класс № 1654
Репетитор / маркер: Исаак Л.
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Вариант 2 — Mathématiques au quotidien, 12e année (40S)
Примечание: Студенты не могут иметь зачетные единицы ни по одному из бывших курсов Consumer Mathematics 45S, Часть V и Часть VI (код 3915/3916), и / или Consumer Math 40S (код 3904), курс , и , новый 12 класс Основы математики (код 3000) .
Курс «Основы математики» для 12 класса основан на знаниях и навыках, приобретенных учащимися при изучении основ математики для 11-го класса. В этом курсе студенты будут исследовать новые идеи и концепции, укрепляя уверенность, необходимую для принятия решений и решения проблем, связанных с потребительскими приложениями математики. Он имеет следующую структуру:
- Модуль 1: Домашние финансы
- Модуль 2: Геометрия и тригонометрия
- Модуль 3: Бизнес и финансы
- Модуль 4: Вероятность
- Модуль 5: Финансирование транспортных средств
- Модуль 6: Карьерная жизнь
- Модуль 7: Статистика
- Модуль 8: Прецизионные измерения
Оценка основана на:
| Назначения | 75% |
| Промежуточный экзамен (модули 1–4) * | 12.5% |
| Заключительный экзамен (модули 5-8) * | 12,5% |
| Итого | 100% |
* Когда студенты напишут свои промежуточные и заключительные экзамены, им будет разрешено принести лист материалов по экзаменам в экзаменационную комнату. Более подробная информация будет предоставлена во введении к курсу в предварительном просмотре курса. (1,14 МБ)
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS). Зарегистрированные студенты получат имя пользователя и пароль.
Практические экзамены и ключи для ответов
12 класс Предисчисление по математике (40S) 1 кредит (2016)
Код курса 3939 40S 003
Предварительный просмотр курса (996 КБ)
Рекомендуемое предварительное условие — математика перед математикой в 11 классе (30S)
Варианты регистрации (Выберите 1)
Выберите желаемую опцию, чтобы получить доступ к кнопке запроса курса.
Вариант 1
Класс № 1683
Репетитор / маркер: К. Билык
Класс № 1684
Репетитор / маркер: J. Voth
Класс № 1697
Репетитор / маркер: П. Маршалл
Добавить запрос на курс в корзину — включает печатные материалы курса и LMS Access
Добавить запрос рекомендации в корзину — Учителя / школы / подразделения Манитобы ИЛИ Родители / студенты Манитобы — не для целей зачета (аудит)
Вариант 2 — Предварительный расчет Mathématiques, 12e année (40S)
Курс предисчислительной математики для 12-х классов основан на темах, с которыми учащиеся были ознакомлены в предисчислительной математике для 11-х классов.Студенты будут изучать три основных области: число, шаблоны и отношения и форма и пространство. Решение проблем, общение, рассуждение и мысленная математика — вот некоторые из тем, которые студенты откроют для себя в каждом модуле. Этот курс помогает студентам развить навыки, идеи и уверенность, чтобы продолжить изучение математики в будущем. Он имеет следующую структуру:
- Модуль 1. Перестановки, комбинации и биномиальная теорема
- Модуль 2: Преобразования функций
- Модуль 3: Размышления
- Модуль 4: Многочлены
- Модуль 5: Тригонометрические функции и единичная окружность
- Модуль 6: Тригонометрические уравнения и тождества
- Модуль 7: Показатели и логарифмы
- Модуль 8: Радикальные и рациональные функции
Оценка основана на:
| Назначения | 55% |
| Промежуточный экзамен (модули 1–4) * | 20% |
| Заключительный экзамен (модули 1-8) * | 25% |
| Итого | 100% |
* 80% заключительного экзамена охватывает содержание модулей 5–8.
* Когда учащиеся напишут свои промежуточные и заключительные экзамены, им будет разрешено взять лист материалов по экзаменам в экзаменационную комнату.
Все задания должны быть выполнены, минимальная оценка 40% требуется по всем контролируемым частям оценивания (промежуточный и заключительный экзамены), а общая итоговая оценка 50% или выше должна быть получена для того, чтобы модуль дистанционного обучения выдал последняя отметка.
РЕСУРСЫ
Обязательные и дополнительные ресурсы доступны в системе управления обучением (LMS).Зарегистрированные студенты получат имя пользователя и пароль.
Практические экзамены и ключи для ответов
Как стать учителем математики: информация о карьере и заработной плате
Учитель математики обучает студентов широкому кругу вопросов математики. Это может включать общую математику и / или любые области математики, такие как алгебра, геометрия, статистика и исчисление. Учителя математики считаются учителями STEM (естественных наук, технологий, инженерии и математики).В последние годы в сфере STEM-образования наблюдается всплеск, поскольку эти предметы считаются важными для развития будущих лидеров, способных конкурировать во все более сложном мире. В этом руководстве представлена дополнительная информация о том, чем занимаются учителя математики, как им им стать, а также о зарплате и перспективах работы будущих учителей математики.
Описание работы учителя математики
Учителя математики составляют планы уроков, чтобы обучать своих учеников общим или специальным предметам математики. Они готовят задания по математике, домашние задания и тесты, чтобы передать знания и понимание своим ученикам.Они также оценивают успеваемость и способности учащихся в течение учебного года. Поскольку математика является частью основной учебной программы в государственных школах K-12, учителя математики должны идти в ногу с изменениями в правилах и задачах штата в отношении обучения математике, чтобы помочь учащимся соответствовать установленным критериям. Учителя математики обычно проводят несколько занятий в течение дня, при этом учащиеся изучают разные предметы на уровне способностей от начального до продвинутого. Учителя математики обычно работают в государственных или частных средних или средних школах, а также в высших учебных заведениях (колледжах и университетах).На более низких уровнях математику обычно преподают учителя начальных классов, которые преподают все предметы.
Требования к учителю математики и общие задачи
Чтобы стать учителем математики, обычно требуется степень бакалавра математики или среднее образование и завершение программы подготовки учителей. Инструкторы также должны получить государственный сертификат учителя традиционным или альтернативным путем. От учителей математики может потребоваться наблюдение за учебными залами, классными комнатами, внешкольными мероприятиями или производственными поездками.Они также могут давать студентам советы по учебе и карьере. Большинство учителей математики будут участвовать в семинарах и конференциях, чтобы поддерживать свои передовые навыки математики и математического образования в актуальном состоянии. Учителя обычно также проводят уроки в нерабочее время с учениками, которые с трудом изучают свой предмет.
Учителя математики должны обладать сильными математическими навыками и знаниями и уметь эффективно передавать математические принципы своим ученикам. Учителям математики необходимо терпение и понимание, чтобы развивать у учащихся навыки критического мышления и способность использовать математику в повседневной жизни.Работа учителей математики может быть очень полезной, поскольку они играют жизненно важную роль в поощрении интеллектуального развития.
Как стать учителем математики
Самым распространенным способом стать учителем математики является получение степени бакалавра математики, которая включает утвержденную государством программу подготовки учителей. Студенты обычно проходят двухгодичные общеобразовательные курсы, а также курсы математики более низкого уровня, прежде чем подавать заявление на программу подготовки учителей на младшем году обучения.Затем они пройдут углубленные курсы математики вместе с курсами подготовки учителей. Имейте в виду, что от учителей математики в частных школах может не требоваться сертификация, поэтому уточните в своих школах, что вы отвечаете уникальным требованиям этих школ. Обычные шаги к тому, чтобы стать учителем математики в государственной школе K-12, следующие:
- Получите степень бакалавра по математике или подполе математики, которая включает утвержденную государством программу подготовки учителей.
- Пройдите стажировку по математике на том уровне (-ах), на котором вы хотите получить сертификат.
- Пройдите необходимые в вашем штате тесты для учителей.
- Подайте заявление на получение диплома преподавателя.
- Подать заявку на вакансию учителя математики.
Люди, которые хотели бы стать учителями и уже получили степень бакалавра по математике, но не завершили программу подготовки учителей, могут иметь право на сертификацию по альтернативному пути к лицензированию учителей, который также может включать программу получения степени магистра. Потенциальные преподаватели, желающие преподавать высшую математику, такую как исчисление или математику, на уровне высшего образования, как правило, должны получить как минимум степень магистра (иногда докторскую степень по математике.Учителя математики на всех уровнях должны предусмотреть курсы повышения квалификации, в том числе курсы математики, чтобы сохранить высокие рабочие знания математической теории.
Заработная плата учителя математики и перспективы трудоустройства
Даже в школьных округах, где учителя должны преподавать более одного предмета, математические специальности пользуются большим спросом — по данным Министерства образования США, в 2016-2017 учебном году 45 штатов по всему штату нехватка учителей математики хотя бы в одном классе.По всей стране учителя начальной школы получают среднюю годовую зарплату в размере 57 980 долларов. 1 Учителя средних школ получают среднюю годовую зарплату в размере 58 600 долларов США. 2 Учителя средней школы получают среднюю годовую зарплату в размере 60 320 долларов США. 3 Ожидается, что к 2028 году количество рабочих мест для учителей всех уровней возрастет на 3-4%. 1,2,3 Рабочие места учителей математики доступны для общих и специализированных преподавателей как в государственных, так и в частных школах. Учителя математики средних и старших классов обычно могут увеличить свой годовой потенциал заработной платы за счет накопления опыта и / или дополнительного образования.Учителя высших учебных заведений по математике получают среднюю зарплату 73 230 долларов в год. 4
Карьерные интервью учителя математики
Цитата учителя: «Чтобы математика была увлекательной, нужно внести как можно больше ясности в концепции и процедуры. Во многом это связано с пониманием того, что приведет учащихся к мысли, что да, они могут ошибаться, но если они будут настаивать и продолжать попытки, мы сможем прийти к правильным решениям, независимо от того, сколько решений существует.”-Хосе Вилсон, преподаватель математики из Нью-Йорка и спикер TEDx
Полезные навыки и опыт
Учителя математики, которые получают ученую степень, обычно считаются более высококвалифицированными и поэтому более востребованы на текущем рынке труда. Получение степени магистра или доктора или других свидетельств о высшем образовании может помочь учителям математики отточить свои навыки в математике и педагогике и найти дополнительные возможности для карьерного роста. В дополнение к сильным математическим знаниям учителя математики должны обладать способностью передавать иногда обширные математические знания учащимся на всех уровнях понимания.
Дополнительные ресурсы
Часто задаваемые вопросы
Вопрос : Каковы требования к учителю математики в средней школе?
Ответ : Требования к преподаванию зависят от штата. Как общее требование, чтобы быть учителем математики в средней школе в системе государственных школ, вы должны иметь четырехлетнее образование в колледже с основным или второстепенным предметом в математике или подполе математики. Вы также должны пройти программу подготовки учителей и пройти тест на получение сертификата.В большинстве штатов вам также придется продемонстрировать свои способности в математике, пройдя тест по предметной области. Учителя математики в частных школах могут не иметь таких требований, поскольку они различаются в зависимости от школы.
Вопрос : Могу ли я получить диплом магистра учителя математики?
Ответ : Сертификация магистра или профессионального учителя предлагается не во всех штатах. В штатах, где это предлагается, учителя математики являются кандидатами, если они могут продемонстрировать передовые знания в своей предметной области, способность вести учащихся к успешному обучению и от трех до пяти лет опыта преподавания.Получение этого сертификата может привести к повышению заработной платы и расширению возможностей карьерного роста учителей математики.
Вопрос : Каковы перспективы карьерного роста учителей математики?
Ответ : Учителя математики востребованы на всех уровнях обучения, особенно высококвалифицированные учителя математики, получившие степень магистра математики. 5 Во многих районах США наблюдается нехватка квалифицированных учителей математики, что дает возможность карьерного роста будущим учителям, желающим переехать. 5 Учителя математики, желающие преподавать в городских или сельских школьных округах, могут найти дополнительные возможности. 1-3
Вопрос : Сколько зарабатывают учителя математики?
Ответ : Сумма денег, которую зарабатывает учитель математики, зависит от множества факторов, в том числе от уровня обучения, уровня образования, многолетнего опыта, местоположения и типа школы, суммы денег, которую зарабатывает учитель математики. По данным BLS, средняя годовая зарплата учителей средних и старших классов всех предметов составляет от 58 600 до 60 320 долларов. 2,3
Вопрос : Что такое STEM-образование и почему оно важно?
Ответ : Учителя STEM обучают студентов широким предметам науки, техники, инженерии и математики. Таким образом, учителя математики являются неотъемлемой частью образования в области STEM. Согласно Министерству образования США, STEM важна для образования, потому что концепции, преподаваемые в рамках этих предметов, готовят учащихся к решению проблем, оценке информации и использованию фактов для принятия решений, помогая развить их в будущих лидеров.
Ссылки:
1. Справочник профессионального обзора Бюро статистики труда, учителя детских садов и начальных школ: https://www.bls.gov/ooh/education-training-and-library/kindergarten-and-elementary-school- Teachers.htm
2. Справочник по профессиональным прогнозам Бюро статистики труда, учителя средних школ: https://www.bls.gov/ooh/education-training-and-library/middle-school-teachers.htm
3. Бюро Справочник по статистике труда по профессиональным прогнозам, учителя старших классов https: // www.bls.gov/ooh/education-training-and-library/high-school-teachers.htm
4. Справочник по профессиональным прогнозам Бюро статистики труда, учителя среднего образования https://www.bls.gov/ooh/education-training- and-library / postsecondary-Teacher.htm
5. Министерство образования США, общенациональный список зон нехватки учителей с 1990–1991 по 2017–2018 годы: https://www2.ed.gov/about/offices/list/ope/pol/ tsa.pdf
Серия научных обзоров: математика — GOV.UK
Введение
Математика, универсальный язык, позволяющий понимать мир, является неотъемлемой частью учебной программы.Помимо изучения чисел, форм и узоров, он также предоставляет важные инструменты для работы в таких областях, как инженерия, физика, архитектура, медицина и бизнес. Это способствует развитию логического и методичного мышления, а также помогает привить сосредоточенность и способность решать всевозможные проблемы. Достижения в предмете также являются ключом к открытию новых дверей для дальнейшего обучения и трудоустройства. Однако, несмотря на свою важность, для многих этот предмет остается загадочным и трудным, прерогативой тех, кто кажется «естественным».В системе инспекции образования ( EIF ) четко указано, что школы должны обеспечивать, чтобы учебная программа по математике «помогала ученикам получать удовольствие через растущую уверенность в своих силах». [сноска 1]
В этом обзоре исследуется литература, относящаяся к области математического образования. Его цель — выявить факторы, которые могут способствовать созданию высококачественных школьных программ по математике, оцениванию, педагогике и системам. Мы будем использовать это понимание качества предмета, чтобы изучить, как математика преподается в английских школах, начиная с приемной.Затем мы опубликуем тематический отчет, чтобы поделиться тем, что мы узнали.
Цель настоящего обзора исследования и его предполагаемая аудитория более подробно изложены в «Принципах, лежащих в основе обзоров исследований и тематических отчетов Ofsted». [сноска 2]
Поскольку существует множество способов, с помощью которых школы могут составить и преподавать высококачественную математическую программу, важно понимать, что не существует единственного способа добиться высококачественного математического образования.
В этом обзоре нас:
описал национальный контекст в связи с математикой
обобщил наш обзор исследований факторов, которые могут повлиять на качество образования по математике
рассматривается прогресс в учебной программе по математике, педагогике, оцениванию и влияние решений руководителей школ на положения
Обзор основан на ряде источников, в том числе на нашей «Рамке проверки образования: обзор исследований» и на трех этапах исследования учебной программы. [сноска 3]
Мы надеемся, что эта работа внесет свой вклад в повышение качества математического образования для всей молодежи.
Амбиции для всех
Сводка
Этот обзор показывает, что, несмотря на то, что ученики-англичане в среднем достигают более высоких результатов, чем ученики во многих других странах, разрыв в успеваемости между учениками с низкой и высокой успеваемостью в Англии велик. Таким образом, помимо освещения подходов, которые могут еще больше повысить успеваемость всех учащихся, основной темой этого обзора является то, как мы можем предотвратить дальнейшее отставание учащихся, испытывающих трудности, от своих сверстников.
Контекст
Англия показывает хорошие результаты по математике по сравнению с другими странами. [сноска 4] и математика продолжает оставаться самым популярным предметом для изучения на уровне A. [сноска 5] В 2004 году правительство провело расследование в области математики после 14 лет. [сноска 6] Вмешательства, последовавшие за этим расследованием, способствовали положительным изменениям. Эти действия включали:
изменений к спецификациям по математике A-level
переработка спецификаций по математике GCSE для повышения их строгости и сложности
создание Национального центра передового опыта в области преподавания математики
установление более высоких целей по набору учителей и создание программ повышения квалификации учителей
Еще многое можно сделать для улучшения математического образования, например, сократить нехватку учителей-специалистов по математике. [сноска 7] Кроме того, разрыв между самыми низкими и самыми успешными в Англии больше, чем в среднем по Организации экономического сотрудничества и развития ( ОЭСР, ). [сноска 8] Средний разрыв в успеваемости учащихся из неблагополучных и благополучных семей также велик. [сноска 9] Учащиеся из неблагополучных семей в Англии гораздо реже, чем их сверстники из более благополучных семей, достигают 4-го класса на экзамене GCSE [сноска 10] или соответствуют ожидаемым стандартам на ключевых этапах 1 и 2 или в конце раннего лет стадия основания ( EYFS ). [сноска 11] Факторы, объясняющие различия в качестве математического образования в Англии, поэтому, вероятно, будут способствовать долгому хвосту неуспеваемости и широкому разбросу уровней успеваемости, а также общему успеху.
Последние влияния на математическое образование включают:
Педагогические подходы «мастерства», которые повлияли на английское математическое образование, как правило, требуют от учеников продемонстрировать высокий уровень успеваемости, прежде чем они перейдут к новому содержанию.Некоторые подходы к овладению навыками делают больший упор на решение проблем и углубление понимания учащимися. [сноска 15]
Культурные факторы, такие как стремление к успеху на экзамене и преклонение перед ним, а также упор на усилия, а не на способности, могут, тем не менее, оказывать значительное влияние на расположение учеников. [сноска 16] Это, например, может быть причиной того, что 75% китайских учеников в английских школах, получающих бесплатное школьное питание, достигли ожидаемого стандарта по математике на ключевом этапе 2 в 2019 году по сравнению с 44% их белых британских сверстников. [сноска 17]
Также важно учитывать, что высокая успеваемость и квалификация старшеклассников могут быть связаны с историческими учебными и педагогическими подходами, а не с образовательными подходами того времени. Финляндия является хорошим примером системы образования, где успех программы OECD по международной оценке учащихся ( PISA ) считается результатом исторического подхода. [сноска 18] Для изменения подходов, с которыми знакомы учителя и ученики, может потребоваться время.Таким образом, они могут влиять на образовательный опыт учеников даже после официального изменения учебной программы или педагогического подхода. [сноска 19]
Принципы, лежащие в основе процесса проверки
Это исследование основано на доказательствах и принципах, лежащих в основе EIF , которые включают:
Объем, содержание и последовательность учебной программы
спецификация и заказ комплектующих, составляющих композитные навыки
ценность предметных знаний учителей
содействие качественному общению с учениками
качество и скорость обучения
как избежать перегрузки рабочей памяти
ценность осознанной практики, чередования и регулярного тестирования с низкими ставками [сноска 20]
Они стали полезной линзой для тщательного изучения тематических тем.
В этом обзоре делается попытка провести четкое различие между учебной программой по математике и педагогикой. Мы также классифицировали содержание учебных программ по математике. Мы использовали эти классификации в нашем обзоре доступной литературы. Мы взяли формы или категории содержания из дисциплин, в которых применяется математика. [сноска 21] Эти категории основаны на том, как работает наш разум [сноска 22] , и предназначены для облегчения понимания.
В математических исследованиях часто встречается множество совпадающих терминов.«Свободное владение языком» — хороший пример. В литературе это слово имеет несколько значений:
иногда относится к простоте отзыва и вычислений (что в обзоре называется «автоматизмом»).
иногда относится к концептуальным знаниям
Условия также меняются со временем. Например, значение слова «таблицы» изменилось: оно использовалось для обозначения числовых фактов во всех операциях, которые младшие и младшие школьники должны были выучить [сноска 23] , но теперь это сокращение для фактов умножения в наши дни. [сноска 24] Примеры терминов (и связанных с ними понятий), которые использовались все реже и реже с течением времени, включают «механическое сверло», «учебный план» и «отзыв».
Как в обзоре классифицируется содержание учебной программы по математике
Для этого обзора мы разделили содержание учебной программы по математике на декларативные, процедурные и условные знания.
Декларативные знания статичны по своей природе и состоят из фактов, формул, концепций, принципов и правил.
Все материалы в этой категории могут начинаться с предложения «Я знаю это».
Процедурные знания вызываются как последовательность шагов. В эту категорию входят методы, алгоритмы и процедуры: все, от деления в столбик, способов изложения вычислений в рабочих тетрадях до знакомых пошаговых подходов к решению квадратных уравнений.
Все материалы в этой категории могут начинаться с предложения «Я знаю как».
Условные знания дают ученикам способность рассуждать и решать проблемы.Полезные комбинации декларативных и процедурных знаний превращаются в стратегии, когда ученики учатся подбирать типы задач, для решения которых они могут быть использованы.
Все материалы в этой категории могут начинаться с предложения «Я знаю когда».
Когда ученики изучают и используют декларативные, процедурные и условные знания, их знания о взаимосвязях между концепциями со временем развиваются. [сноска 25] Эти знания относятся к подкатегории контента «тип 2» (см. Таблицу ниже).Например, распознавание глубокой математической структуры проблем и их связи с основными стратегиями — это форма условного знания второго типа.
Сводная таблица категорий контента, рассмотренных в обзоре:
| Категория | Тип 1 | Тип 2 |
|---|---|---|
| Декларативная «Я знаю это» | Факты и формулы | Связь между фактами (концептуальное понимание) |
| Процедурная «Я знаю как» | Методы | Связь между фактами, процедурами и недостающими фактами (принципы / механизмы) |
| Условное «Я знаю когда» | Стратегии | Связь между информацией, стратегиями и недостающей информацией (рассуждения) |
Развитие учебной программы: запланированный и целенаправленный путь к опыту
Сводка
Представленные здесь данные подтверждают тщательное рассмотрение последовательности и содержания, которые делают учебную программу по математике гарантией долгосрочного обучения.Полезные факты и эффективные и точные методы идеально сочетаются в рамках тематической последовательности. Стратегии решения типов задач лучше всего преподавать и усваивать, когда ученики могут быстро и точно вспомнить и применить факты и методы. При планировании содержания учебной программы учителя также должны уделять приоритетное внимание «перспективным» знаниям. Это выходит за рамки важных цифр. Он включает математические методы, которые ученики возьмут с собой в путешествие. Идеальная цель для учеников — достичь профессиональных навыков, а не просто коллективных моментов понимания, знакомства или опыта.Это поможет ученикам развить мотивацию в предмете.
Выбор и упорядочение основных декларативных, процедурных и условных знаний
Учебная программа по математике является продуктом тщательного отбора, упорядочивания и увязки декларативных, процедурных и условных знаний. Ученикам необходимо систематически усваивать основные математические факты, концепции, методы и стратегии, чтобы иметь возможность добиться успеха при решении задач и стать хорошими математиками. [сноска 26] Возможности развития так называемых общих навыков решения проблем, таких как анализ и оценка, не должны обходить этот процесс. [сноска 27] Тщательная последовательность содержания, обучения и репетиции также может показать ученикам новые и последовательные образцы полезной информации. Затем они образуют основу для дальнейших концепций, правил и принципов, которые ученики могут сохранить в своей долговременной памяти. [сноска 28]
Решение проблем требует от учеников твердого мышления.Нелегко выучить, репетировать или испытать на практике, если факты и методы, которые составляют часть стратегии решения типа проблемы, незнакомы и занимают слишком много рабочей памяти. Например, учащиеся вряд ли смогут решить задачу с квадратным словом, которая требует от них умножить 2 длины с разными единицами измерения, если они не осознают, что в вопросе им предлагается использовать стратегию для поиска области. Они также вряд ли добьются успеха, если они не знают многих числовых связей, фактов измерения единиц измерения, формулы преобразования или эффективного метода автоматического умножения.Следовательно, первоначальный акцент в любой последовательности обучения должен заключаться в том, чтобы ученики были знакомы с фактами и методами, которые сформируют стратегии, которым они будут обучаться и которые будут применяться позже в последовательности тем. [сноска 29]
Связь между основными математическими фактами и мощными методами
Связанные декларативные и процедурные знания идеально упорядочены вместе, чтобы отразить взаимные отношения обучения между ними. Это потому, что:
В качестве простого примера, ученик может лучше понять связи числа, а также концепции сложения и количества, если у них есть декларативные знания о числовых связях и процедурные знания о сложении столбцов, которые усиливают друг друга.Что касается последовательности учебной программы, ученики могут сохранять знания и способность использовать основные методы, когда учителя применяют итеративный подход к обучению и повторению концепций и основных методов. [сноска 30]
Долгосрочное влияние раннего и тщательного акцента на основном содержании
Приобретение новых фундаментальных знаний требует времени и усилий. Однако вознаграждение выходит за рамки непосредственной выгоды от возможности вспомнить и применить полезные факты и методы.
Базовые знания, особенно умение работать с числами, в дальнейшем дают ученикам возможность продвигаться по учебной программе с возрастающей скоростью. [сноска 31] Таким образом, путь обучения, который начинается с пристального внимания к основным декларативным и процедурным знаниям, представляет собой не прямую линию, а кривую. Это результат продуманного дизайна учебной программы. Например, в странах, где ученики успевают хорошо, ученики могут попробовать более сложные аспекты умножения и деления в 4 классе, если им было уделено больше времени по основам арифметики в 1 классе. [сноска 32] Это может объяснить, почему успешно В подходах к учебной программе, как правило, на ранних этапах делается упор на основные знания. [сноска 33]
Кроме того, если это основное содержание было хорошо упорядочено и ученики выучили его досконально, они с меньшей вероятностью забудут и, следовательно, им не придется «заново выучивать» его позже. [сноска 34] Сосредоточение внимания на основных знаниях в младших школьных группах может быть достигнуто, если сосредоточить внимание на глубине, а не на широте, охватить меньше основных тем, но более подробно.
Расширение учебной программы за счет инструкций, репетиций и планов оценки
Успешные учебные программы демонстрируют важность детализации, последовательности и согласования содержания, инструкций, репетиций, оценивания и механизмов, которые необходимо постоянно совершенствовать. [сноска 35]
Учебники, планы уроков и ресурсы — общие черты успешных подходов. [сноска 36] Они гарантируют, что усвоение учащимися содержания отражает последовательность учебной программы. Это превращает предложение учебной программы в нечто большее, чем гарантия. Учителя в этих системах также имеют больше времени, чтобы сосредоточиться на том, как воплотить в жизнь содержание математики, вместо того, чтобы изменять последовательность содержания, инструкций и репетиций с нуля. [сноска 37] В системах образования, где содержание и последовательность содержания решаются централизованно, ученики могут перемещаться между школами с минимальным нарушением их обучения. [сноска 38]
Подход, описанный выше, сильно отличается от предложения по учебной программе, в котором отсутствуют системы документирования качественных последовательностей обучения и репетиций, что может привести к более изменчивым темпам обучения и результатам. Например, младшие ученики могут достичь профессионального уровня за счет более неформальных возможностей для обучения и того, где учителя отвечают их интересам, но лидерам следует отметить, что находящиеся в неблагоприятном положении начинающие математики извлекают выгоду из проактивных подходов, которые могут быть столь же простыми, как выделение им времени на учебу и обучение. репетировать математику каждый день. [сноска 39]
Преимущества этого и других систематических подходов применимы ко всем возрастным группам, включая год приема. [сноска 40] Однако слишком часто ученики отстают, и ученики из неблагополучных семей с меньшей вероятностью добьются успехов по сравнению с их более обеспеченными сверстниками. Если лидеры предоставляют согласованные ресурсы для планирования, обучения и репетиции содержания, то этот риск снижается, но при этом учителям предоставляется свобода выбора того, как преподавать.Систематические подходы под руководством учителя, особенно на начальных этапах обучения, приводят к лучшему усвоению знаний. [сноска 41] Это дает ученикам больше возможностей для успешной учебы в средней школе.
Положительное отношение к математике — результат успеха в предмете
Учащиеся с большей вероятностью разовьют положительное отношение к математике, если они будут в ней успешны, [сноска 42] особенно, если они осознают свои успехи. [сноска 43] Однако учителям следует опасаться соблазна изменить этот причинный путь, например, заменив уроки забавными играми как способом получения удовольствия и мотивации.Это потому, что использование игр в качестве учебной деятельности может привести к меньшему обучению, чем к большему. [сноска 44]
Некоторые ученики заболевают математикой. В основе пути беспокойства лежит не природа субъекта, а неспособность получить знания. [сноска 45] Истоки этого беспокойства могли быть даже присутствовать в начале академического пути ученика. [сноска 46] Однако, если учителя позаботятся о том, чтобы обеспокоенные ученики приобрели основные математические знания и начали добиваться успеха, эти ученики начнут связывать предмет с удовольствием и мотивацией.
Это также влияет на восприятие ошибок учениками и учителями. В идеале учителя и ученики должны осознавать разницу между редкими ошибками, на которых можно научиться, и постоянными ошибками, которые приводят начинающих математиков на путь беспокойства. Ошибки такого рода происходят из-за слабых фундаментальных знаний, которые с большей вероятностью приводят к ошибкам и неправильным представлениям. [сноска 47] Учителя должны попытаться направить учеников на путь причинно-следственной связи, ведущий от успеха к мотивации, сосредоточив внимание на раннем овладении навыками, а не на ожидании, что ученики будут учиться, совершая ошибки.Такой подход, ориентированный на умение, может предотвратить развитие тревожности у учеников. Для учителей учеников, которые испытали неудачи, разочарование и развитие тревожности, вместо того, чтобы устранять опыт, когда ученики могут столкнуться с неудачей (например, тесты), данные свидетельствуют о том, что решение заключается в устранении пробелов, чтобы тревожные ученики могли испытать больше понимания , точность и успех. [сноска 48]
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Успешное продвижение по учебной программе планируется с самого начала обучения ученика за счет сосредоточения внимания на основном содержании, для развития мотивации учеников и обеспечения большей широты и глубины позже.
В запланированной учебной программе подробно излагаются основные факты, концепции, методы и стратегии, которые дают учащимся наилучшие шансы развить знания по этому предмету.
Изучение связанных фактов и методов организовано так, чтобы использовать преимущества того, как знание фактов помогает ученикам изучать методы, и наоборот.
Последовательности обучения позволяют ученикам получить доступ к фактам и методам, которые им нужны, чтобы изучить стратегии решения типов задач.
Последовательность учебных программ: декларативные знания
Математические факты, словарный запас и символы в начале школьного пути
Многие ученики начинают школу с некоторыми математическими знаниями. [сноска 49] Это не обязательно результат естественных способностей или другого пути развития. Скорее, это может быть признаком родительского вклада и раннего ознакомления с основами математики дома. [сноска 50]
Исследования показывают, что раннее приобретение знаний в значительной степени предсказывает успех в будущем. [сноска 51] Они также предполагают, что большая часть этого успеха зависит от учеников, знающих код числа (например, арабских цифр), а не от общего чувства количества. [сноска 52] Ранняя нехватка знаний также предсказывает более позднюю борьбу [сноска 53] и более поздний диагноз инвалидности. [сноска 54] Ученики, которые не могут быстро и легко вспомнить математические факты, испытывают трудности с вычислениями из-за перегрузки рабочей памяти. [сноска 55] Например, ребенок, который не знает числовых связей, будет застрять, используя различные формы «подсчета» при выполнении простого сложения. Даже на ключевой ступени 3 незнание учеником основ числа будет отрицательно сказаться на его изучении алгебры. [сноска 56] В совокупности эта информация указывает на приоритетность основных декларативных знаний в математике с раннего возраста, чтобы уравнять правила игры, особенно для учеников с особыми образовательными потребностями. [сноска 57]
Учитывая, что многие ученики, у которых есть ранние знания, получили знания дома, решение школы полагаться на создание «богатой математикой» среды должно быть сбалансировано с потребностями учеников, которые не имели этого преимущества и которые с меньшей вероятностью выберут предлагаемые математические задания. Многие молодые ученики нуждаются в систематическом предоставлении упорядоченного основного контента, который становится строительным блоком их дальнейшего успеха, и извлекает из него пользу. [сноска 58] Например, «более 100 дополнительных фактов должны стать автоматическими, прежде чем дети смогут играть и размышлять над [различными] типами задач». [сноска 59] Учащиеся из групп риска, которым систематически преподают составные части декларативных знаний, не только получают выгоду, [сноска 60] , но и имеют потенциал для выбора различных траекторий обучения. Тогда они часто могут соответствовать или даже превосходить достижения своих более обеспеченных сверстников. [сноска 61]
Особенно важно, чтобы дети овладели навыками работы с целыми числами и дробями, а также для работы с двумерными и трехмерными фигурами на начальном этапе, так как они используются в более поздних темах и на ключевых этапах.Это включает, например, автоматический вызов числовых фактов и знакомство с основными понятиями, такими как ассоциативные, распределительные и коммутативные свойства. [сноска 62] Ученикам также полезно указывать на фундаментальные особенности математики, такие как закономерности и структуры, даже если они, вероятно, со временем интуитивно усвоят эту информацию. [сноска 63]
Проактивный подход к помощи детям в овладении повседневным языком, используемым для описания количества, формы и времени, также принесет пользу ученикам из неблагополучных семей, которые с большей вероятностью неправильно поймут инструкции и действия. [сноска 64] Школам необходимо сбалансировать этот подход со знанием того, что ученики, которые уже хорошо знакомы с начальной математикой, могут пострадать, если от них ожидается, что они будут повторять старый контент, такой как счет и базовые знания форм. [сноска 65]
Математические факты, словарь и символы в начале последовательности
Ученикам также необходимо знать основные концепции, формулы и правила, которые можно использовать в таких темах, как алгебра, геометрия, статистика и математические вычисления.Ученики, которым не хватает знаний о концепциях, которые они обычно усвоили бы на предыдущих ключевых этапах, могут извлечь пользу из дополнительных инструкций по конкретной теме. [сноска 66] Это также имеет значение, когда мы делаем предположения об общих знаниях учеников. Например, концепция «случайных явлений», которая возникнет в результате воздействия учеников на игры с бросанием игральных костей, может легко отсутствовать в схеме для учеников, которые изучают вероятность. [сноска 67] Основные концепции должны полностью основываться на знаниях, полученных на предыдущих этапах.Например, знание младшим учеником концепции «баланса» и того, как это понятие связано со знаком равенства, поможет им, когда они столкнутся с линейными уравнениями на ключевом этапе 3. [сноска 68]
Тематические исследования учебных программ для преподавания алгебры в странах, где учащиеся преуспевают, также показывают, что концептуальные строительные блоки алгебраического мышления систематически планируются на самых ранних этапах учебной программы. «Переменные, уравнения, решение уравнений и смысл функций пронизывают арифметический анализ количественных соотношений». [сноска 69] Этот подход позволяет ученикам выучить понятие переменных, а также стандартное соглашение об использовании символа «x» для обозначения неизвестной переменной, когда им около 10 лет. Затем их можно обучить и вскоре после этого применять дополнительные коды, правила и принципы простых уравнений. Этот подход показывает, что переход от арифметики к алгебре следует тщательно продумывать, обеспечивая учащимся наличие кодов для чисел (математические факты, символы, словарный запас) в качестве предварительного условия для перехода к новой теме или предметной области. [сноска 70]
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Учителя создают для учеников наилучший возможный старт, устраняя пробелы в знаниях начального математического кода: факты, концепции, лексику и символы.
Ученикам преподаются основные факты, формулы и концепции, которые могут быть полезны сейчас и на следующем этапе обучения.
Учителя помогают ученикам развивать автоматическое восприятие основных декларативных знаний, вместо того, чтобы полагаться на вывод, догадки или поиск подсказок.
Последовательность учебных программ: процедурные знания
Запланированное устаревание ранних методов
В идеале ученики постепенно перестают зависеть от некоторых методов подсчета и подсчета и связанных с ними ресурсов, которым их учили ранее. Это связано с тем, что использование некоторых ранних методов подсчета и вычислений при отсутствии изучения ценных числовых фактов может помешать дальнейшему прогрессу. [сноска 71]
Ученикам можно помочь с простыми повседневными предметами и полубетонными представлениями, такими как Нумикон, но цель должна состоять в том, чтобы ученики переходили к работе с символами и абстрактными представлениями. [сноска 72] Использование манипуляторов, например, не всегда гарантирует, что ученик поймет [сноска 73] , и их использование может отвлекать учеников от размышлений о содержании, которое нужно изучить. [сноска 74] Метод вычислений, основанный на выводе, может быть полезен в краткосрочной перспективе и в качестве моста к формальным методам письменных вычислений, которые требуют от учеников точного запоминания числовых связей. [сноска 75] В отсутствие усвоения этих основных знаний ученики могут слишком полагаться на оценку и поиски подсказок, или же они могут развить привычки угадывать и копировать. [сноска 76]
Напротив, визуально простая система подсчета (такая как соробан, обычно используемая в странах, где учащиеся добиваются первых успехов) является ресурсом, который представляет собой эффективный и мощный метод начальных расчетов. Метод, связанный с этим ресурсом, после того, как ученик научился его использовать, последовательно представляет точные связи чисел, которые можно выучить, а затем вспомнить в виде числовых последовательностей, правил и связей. Предоставление молодым ученикам эффективного, менее отвлекающего метода расчета, который не связан с другими привычными занятиями (например, с игрушками, используемыми для социальной игры), помогает им увидеть прошлые методы и любые связанные с ними ресурсы к новым связям числа. [сноска 77] В случае простой рамки подсчета детям она больше не нужна, как только они научатся автоматически вспоминать числовые связи, последовательности, шаблоны и правила. [сноска 78] Математические факты, которые они приобрели благодаря знакомству с мощным методом и его использованию, могут помочь им в умственной арифметике. [сноска 79] Не сам ресурс, а тот факт, что его использование связано с эффективностью, точностью и визуальной простотой, является наиболее важной характеристикой эффективных ранних методов.
Методы более сложных измерений и расчетов
Идеальные методы рисования ручкой и бумагой для 4 операций и для работы с дробями — эффективные, точные и ясные. В результате аккуратность и логичный подход помогают минимизировать риск случайных ошибок учеников. [сноска 80] Приложения к национальной учебной программе в Англии по математике [сноска 81] дают примеры формальных методов, которые ученики могли бы использовать для наибольшей вероятности успеха в вычислениях по мере прохождения учебной программы.
Неформальные методы, некоторые из которых могут включать физические ресурсы, могут быть полезны для раскрытия основных принципов и концепций. [сноска 82] Однако учителям следует проявлять осторожность при рассмотрении подходов к учебной программе, которые в значительной степени ориентированы на поощрение неформальных и самопроизвольных методов. Эти подходы могут иметь целью развитие у учеников понимания, но факты показывают, что когда ученики используют различные неформальные процедуры, это может препятствовать пониманию позже. [сноска 83]
Дополнительные риски возникают из-за смешения и согласования набора неформальных и самогенерируемых методов для работы с большими числами и более сложными вычислениями по мере того, как ученики продвигаются по учебной программе. Это увеличивает вероятность того, что ученики будут делать ошибки и плохо структурировать письменные записи, что может привести к путанице. [сноска 84]
Учителя должны стремиться сбалансировать развитие понимания учащимися и связанное с ним использование неформальных и схематических методов с обучением эффективным методам, которые точно и последовательно раскрывают новые модели и связи чисел.Это потому, что два аспекта понимания и навыков вычислений усиливают и дополняют друг друга. [сноска 85] Один из способов добиться этого — спланировать использование неформальных методов в течение короткого промежутка времени в качестве моста к формальным письменным методам. Это обеспечит ученикам адекватные возможности учиться, репетировать, а затем использовать формальные методы. Более раннее обучение и, следовательно, более широкое использование основных математических методов [сноска 86] также дает учителям большую уверенность в том, что их ученики будут готовы использовать эти методы в последовательности вычислений и решать более сложные задачи на следующем этапе обучения.
Методы алгебраической работы
Идея качества важнее количества процедурных знаний также применяется на ключевых этапах 3 и 4.
В алгебре учащиеся извлекают пользу из меньшего числа, но мощных представлений и итеративного подхода к упорядочиванию фактов и процедур для алгебраической работы. [сноска 87] Абстрактные представления могут быть столь же эффективными, как и контекстуализированные представления. [сноска 88] Метод стержневого моделирования можно использовать как мост от арифметики к ранней алгебре.Это полезный промежуточный метод абстрагирования арифметических и алгебраических выражений от текстовых задач. [сноска 89] Учителя могут даже научить методам оценки алгебраических выражений и способам изложения их в виде серии шагов, которые ученики должны выучить наизусть. [сноска 90] Это контрастирует с подходом, поощряющим учеников к более неформальным, самопроизвольным способам решения линейных уравнений. Это может быть самоограничением, когда ученики сталкиваются с нетрадиционными представлениями линейных уравнений.
Если учащиеся приобретут качественные, полезные и эффективные процедурные знания, они смогут затем применить их для определения и использования формул, от вычисления площадей и периметров различных классов многоугольников на ключевом этапе 2 до использования тригонометрических формул, таких как косинус. Правило на ключевой стадии 4.
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Учителя обучают младших школьников не отвлекающим и точным математическим методам, которые побуждают их использовать воспоминание, а не вывод.
Учителя планируют обучать старших школьников эффективным, систематическим и точным математическим методам, которые они могут использовать для более сложных вычислений и на следующем этапе обучения.
Учителя помогают ученикам использовать эти методы, чтобы увидеть новые связи числа, геометрии и времени.
Учителя поощряют учеников использовать основные математические методы, а не прибегать к догадкам, поискам подсказок или неструктурированным методам проб и ошибок.
Последовательность учебных программ: условные знания
Важность учебного подхода
Анализ решения проблем опытными математиками показывает, что их мышление высокоорганизовано. Он основан на хорошо связанной базе знаний фактов, методов и стратегий, которые ранее использовались для решения проблем с подобной глубокой структурой. [сноска 91] Таким образом, успешное решение проблем — это не просто деятельность, а результат успешного изучения фактов и методов, а также их полезных комбинаций в качестве стратегий.И наоборот, если решатель проблем не обладает условными знаниями, он с большей вероятностью будет отвлекаться на поверхностные особенности проблем. [сноска 92]
Это имеет значение для того, как решение проблем как деятельность реализуется в классах, где учителя ожидают, что ученики научатся решать проблемы путем решения проблем.
Учителя могут использовать учебный подход, который поможет инженерам лучше решать проблемы путем обучения:
полезных комбинаций фактов и методов
как распознать типы проблем
глубокие структуры, которые эти стратегии объединяют с [сноска 93]
Ученики должны свободно владеть соответствующими фактами и методами, прежде чем они научатся применять их в условиях решения проблем. [сноска 94]
Обучение младших школьников понимать текстовые задачи
На начальных этапах школьный опыт решения проблем часто включает решение словесных задач. Первое, что нужно преодолеть, — это язык. Поэтому учащиеся должны хорошо читать на необходимом уровне. [сноска 95]
Однако, даже когда ученики могут читать и понимать контекст, они должны смотреть за пределы поверхностных особенностей проблемы в сторону глубокой структуры, которая сигнализирует о стратегии, которую следует использовать.Некоторым ученикам, которые быстро усваивают новые процедурные знания, например, как находить эквивалентные дроби, может быть предложено связанное решение проблем посредством дифференциации. Затем эти ученики могут интуитивно понять связи между недавно изученными методами и некоторыми типами (словесных) задач. Когда они изучают условия более широкого использования метода, с течением времени создается банк стратегий. Затем они могут использовать этот банк стратегий для классификации и решения различных задач, представленных в тестовых документах.Однако ученикам, у которых не было такого опыта, будет сложно установить правильные связи, когда им будут предложены контрольные работы для решения проблем и рассуждений.
Таким образом, учителя должны обеспечить, чтобы больше учеников добились успеха в решении словесных задач, путем упорядочивания обучения стратегиям «преобразования» глубинной структуры текстовых задач в простые уравнения. [сноска 96]
Стратегии решения классов задач
Учитывая, что опыт в значительной степени зависит от предметной области, [сноска 97] стратегии решения проблем привязаны к конкретной теме и, следовательно, могут быть запланированы в последовательности содержания для этой темы. [сноска 98] Это помогает предотвратить появление пробелов в стратегиях решения проблем и означает, что запланированная учебная программа становится более инклюзивной.
Это контрастирует с взглядом на решение проблем как на общий навык, который ученики могут передать нескольким темам и поддоменам. [сноска 99] Применение общих стратегий для поиска примеров, поиска взаимосвязей или взвешивания характеристик может дать точную и неточную информацию. Однако учащиеся, испытывающие трудности, могут не знать, какую информацию выбрать для использования.
Учащиеся, которые уже владеют знаниями, могут добиться успеха, используя общий процесс, который включает в себя более тщательное взвешивание, просеивание и обработку информации методом проб и ошибок. С другой стороны, ученики, которым не хватает навыков, испытывают разочарование и меньше учатся в этих условиях. [сноска 100] Новичкам выгодна возможность распознавать глубинную структуру проблемы и быстро внедрять подходящую стратегию. [сноска 101] Затем ученики могут развить дальнейшее концептуальное понимание, применяя процедуры к классам проблем. [сноска 102]
Планирование учебной программы должно быть направлено на выявление и упорядочение наиболее полезных комбинаций фактов и методов для решения подклассов проблем, а также характеристик условий, при которых эти стратегии были бы полезны.
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Учителя обучают учеников полезным стратегиям, ориентированным на конкретные темы, а также способам подбора их соответствия типам задач.
Ученики уверенно используют связанные факты и методы, которые являются строительными блоками стратегий, до того, как они будут изучены.
Учителя поощряют учеников использовать основные систематические стратегии, а не прибегать к догадкам или неструктурированным пробам и ошибкам.
Последовательность учебных программ: удовлетворение потребностей учеников
Планирование того, о чем будут думать ученики
Тщательное изучение планирования уроков и мыслей учителей о планировании уроков в системах образования, где учащиеся преуспевают, выявляет повышенное внимание к базовым структурам знаний и связям, а не к поверхностной согласованности действий и преподавания.Это означает, что учителя планируют, о чем ученики будут думать или о чем, а не о том, что они будут «делать».
Учителя создают эти возможности для подробного, ориентированного на содержание планирования на основе знаний о предыдущем обучении учеников. [сноска 103] В год приема мероприятия могут иметь похожее ощущение. Но намеренный, а не развивающий подход все же с большей вероятностью приведет к тому, что дети станут умелыми. [сноска 104] Учителям следует с осторожностью относиться к тому, чтобы дать ученикам право собственности на их собственный путь продвижения по учебной программе.Это происходит не только из-за влияния предшествующих знаний на продвижение по учебной программе, но и из-за того, что ученики могут не знать достаточно о будущем прогрессе в математике, чтобы сделать лучший выбор сейчас. [сноска 105] Например, решение о том, когда и сколько репетировать базовые вычисления, может непреднамеренно сократить шансы на успех в будущем, если ученики почувствуют, что немедленный успех и точность являются лучшими сигналами, чтобы двигаться дальше.
Кроме того, возможность решения проблем как часть дифференциации задач не гарантирует, что все ученики изучат стратегии решения проблем.Руководители и учителя должны в идеале рассматривать изучение всего основного содержания, включая связи между содержанием, как право и, следовательно, заранее запланированный путь для всех учеников.
Уравновешивание нового обучения и репетиции обучения
Момент понимания не гарантирует долгосрочного обучения. Ученикам полезно изучать рабочие примеры, а не только практиковаться в решении аналогичных задач. [сноска 106]
Таким образом, учителям необходимо найти баланс между введением нового содержания и потребностью учеников тратить время на повторное изучение содержания. [сноска 107] В учебной программе должно быть место для запланированной консолидации. Учащиеся не должны спешить с содержанием.
Это будет проще, если учебная программа по математике на раннем этапе сосредоточена на основном содержании, а лидеры расставляют приоритеты и объединяют ценности. Сведение к минимуму поведения вне задачи также может помочь максимизировать количество времени, доступного для извлечения, репетиции и закрепления обучения. Учащиеся с хорошей успеваемостью, как правило, уделяют этому предмету больше времени. [сноска 108]
Собственный капитал
Учителя и руководители должны попытаться найти баланс между учебными подходами, которые позволяют ученикам не отставать от своих сверстников, и реактивными подходами, которые выявляют, помогают и поддерживают учеников после того, как они отстают.Эти реактивные подходы, скорее всего, будут полагаться на оценку, диагноз, персонализацию и вмешательство.
В английской системе математического образования акцент на реактивных подходах связан с широким разбросом достижений и длинным хвостом недостаточных достижений. В 2019 году почти 180000 студентов были вынуждены повторно сдавать экзамен по математике на GCSE. Из них только 22,3% получили стандартный балл (4 класс) или выше. [сноска 109]
В классах стран Восточной Азии, похоже, мало различий. [сноска 110] Можно предположить, что это результат педагогического решения держать учеников в учебе и делать то же самое. Учителя могут беспокоиться о том, что успевающие сдерживаются или что ученикам с особыми образовательными потребностями и / или ограниченными возможностями ( ОТПРАВИТЬ ) не оказывается достаточная поддержка. Однако в таких странах, как Сингапур, все группы учеников успевают. 51% сингапурских учеников соответствовали продвинутому международному стандарту по сравнению с 11% английских учеников.По промежуточному критерию, описываемому как способность «применять базовые математические знания в различных ситуациях», только 8% сингапурских детей не соответствовали этому стандарту по сравнению с 31% английских детей. [сноска 111] Причина этого успеха заключается в том, что эффективная учебная программа и множество возможностей для целенаправленной и разумной практики приводят к лучшим результатам для учеников. [сноска 112]
Лидеры могут рассматривать эту стратегию как способ повышения уровня владения предметом, при котором ученики остаются вместе не потому, что ученики с более высоким уровнем успеваемости сдерживаются, а потому, что ученики с более низким уровнем успеваемости могут «не отставать».
Инклюзивность
Ученики с SEND извлекают огромную пользу из четкого, систематического обучения и систематического повторения декларативных и процедурных знаний. [сноска 113] Преимущества этих подходов выходят за рамки повышения академической успеваемости и профессиональных навыков. Взаимосвязь между когнитивными способностями и академическими достижениями, в том числе по математике, на самом деле двунаправленная. [сноска 114] Следовательно, образовательные результаты для учеников с SEND , вероятно, улучшатся, если учителя будут использовать систематическое обучение и репетиции, чтобы помочь ученикам усвоить запланированный контент. [сноска 115]
Этот подход особенно полезен для учеников с умеренными трудностями в обучении, у которых скорость когнитивной обработки ниже. [сноска 116] Систематические подходы увеличивают количество контента, рассматриваемого в единицу времени. Эти подходы также очень полезны для улучшения успеваемости, успеваемости и самооценки учащихся из неблагополучных семей. [сноска 117] Систематические подходы к учебной программе дают учащимся с SEND и учащимся из неблагополучных семей больше шансов на успех, успеваемость и, следовательно, чувство вовлеченности.
Игра на сильных сторонах учеников: мощные системы декларативной памяти учеников с аутизмом
Многие учащиеся с аутизмом обладают «способностью алгоритмического мышления от нормального до выше среднего», но могут испытывать трудности с рассуждением и решением проблем из-за:
дефицит языковой обработки
трудности классификации задач по типу
незнание стратегий
использование «неэффективных и слишком сложных процедур» для расчета [сноска 118]
Учителя могут заполнить эти пробелы в знаниях с помощью систематических учебных программ, подходов к обучению и репетиций.Например, обучение эффективным алгоритмам учеников с аутизмом ускоряет их вычисления. Тогда у них будет больше времени, чтобы изучить стратегии решения классов проблем.
Однако исследования также показывают, что уникальная организация и мощные системы декларативной памяти многих людей с аутизмом помогают им изучать этот предмет и развивать в нем навыки. [сноска 119] Потенциально мощная декларативная система памяти может взять на себя компенсирующую роль; таким образом, многим ученикам с аутизмом может быть полезно сосредоточиться на запоминании основных фактов и методов.
Таким образом, руководителям следует подумать о том, как дать аутичным ученикам больше времени для изучения основного содержания, чтобы они могли закрыть пробелы в обучении путем преднамеренного запоминания. Руководители также должны следить за тем, чтобы учебное время учеников использовалось рационально и эффективно.
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Новое содержание основано на содержании, которое ученики усвоили ранее, и устанавливает связи с ним.
Прогресс по учебной программе осуществляется по разумному плану, а не по выбору или случайности.
Репетиционные последовательности совпадают с последовательностями учебной программы.
Ученикам, которые с большей вероятностью будут бороться или которые рискуют отстать, дается больше времени на выполнение заданий, а не на выполнение других заданий или учебных программ, чтобы они могли закрепить основные факты и методы в долговременной памяти.
Педагогика: новое обучение
Сводка
В этом разделе мы обсуждаем учебные потребности учеников по мере их прохождения по учебной программе.Когда ученики только начинают учебу или начинают новую последовательность обучения, им нужно больше инструкций, чем ученикам, которые уже компетентны в этой области. На протяжении всего обучения ученики извлекают пользу из систематического и ясного обучения. Ученики могут также развить дальнейшее понимание, когда наборы упражнений составлены таким образом, чтобы представить новые и полезные числовые связи, когда ученики репетируют недавно изученный контент.
Новичку нужно больше обучения, не менее
«Начинающим ученикам» нового материала по математике необходимы систематические учебные подходы, аналогичные тем, которые используются для обучения чтению и письму в раннем возрасте.Учителям необходимо ежедневно выделять время для обучения и отработки составных частей. [сноска 120] Подобно «коду» языка, полезно думать о раннем математическом содержании как о «коде». Не все ученики будут «взламывать», открывать или изобретать этот код для себя. Подход, который ближе всего подходит к обеспечению фундаментального успеха в математике, — это тот, который признает, что:
Для наиболее эффективного развития более всеобъемлющего и абстрактного мышления о математике детям часто требуется нечто большее, чем их естественное, спонтанное обучение. [сноска 121]
Такой подход должен включать дополнительные элементы четкого систематического обучения. Это поможет восполнить пробел в знаниях при поступлении в школу. Это также даст большему количеству учеников основы математического успеха, [сноска 122] , а также повысит самооценку. [сноска 123]
Использование интеллектуальных вариаций в комплексах упражнений
Существует разница между содержанием, которое ученики недавно изучали, и содержанием, которое развивается в их сознании в процессе практики.Оба могут быть запланированы. Разнообразие комплексов упражнений может помочь ученикам в обучении:
диапазоны и границы применимости стратегии
важных закономерностей и правил
связей между различными проблемами [сноска 124]
привычек поиска шаблонов
как сфокусироваться
логический и системный подходы к решению задач [сноска 125]
Лидеры должны убедиться, что они курируют и контролируют этот подход.Это проявляется в систематическом использовании вариаций в сборниках заданий, которые даются ученикам в Китае, Гонконге и Тайване. [сноска 126]
Систематические подходы к обучению также подходят для всех возрастов и стадий
Опытные математики способны продемонстрировать успехи в уроках решения задач. [сноска 127] Однако тогда легко предположить, что деятельность, демонстрирующая способность опытного математика решать задачи, является идеальным средством приобретения профессиональных навыков. [сноска 128] Обучение посредством участия в подобных открытых мероприятиях по решению проблем может быть приятным как для учителей, так и для учеников, [сноска 129] , но это не обязательно приводит к улучшению результатов. [сноска 130] Взрослый в комнате — важный посредник в успехах учеников.
Без взрослого, даже если содержание и последовательность содержания могут быть идеальными, обучение учащихся из групп риска оказывается под угрозой. [сноска 131] Свидетельства показывают, что ученики могут учиться на отработанных примерах, [сноска 132] особенно, если учителя помогают ученикам разобраться в отработанных примерах. [сноска 133] Опрос, если учителя заботятся о языке и времени, также может помочь в обучении. [сноска 134] Обучение учеников построению и использованию визуальных представлений может помочь ученикам преобразовать информацию, представленную в задаче, в символические уравнения. [сноска 135]
Систематическое обучение может также принести пользу, помимо углубленного изучения фактов, методов и стратегий, поскольку более успешные ученики развивают лучшее учебное поведение. [сноска 136]
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Учителя помнят, что ученики не могут развивать свои навыки, подражая опыту, но имитируя путь к опыту.
Систематические учебные подходы к успеху инженера в обучении включены во все этапы и фазы.
Учителя стремятся передать основное содержание в соответствии с деталями и последовательностью запланированной учебной программы.
Учителя помогают ученикам не полагаться на догадки или неструктурированные методы проб и ошибок.
Педагогика: закрепление знаний
Сводка
По мере того, как ученики продвигаются по учебной программе, им нужны регулярные возможности для репетиций и применения важных фактов, концепций, методов и стратегий, которые они усвоили. При разработке последовательностей репетиций учителя должны учитывать как качество, так и количество практики, необходимой ученикам для развития их понимания и для того, чтобы основное содержание было прочным и точным в уме.Практика должна выходить за рамки непосредственной точности и понимания. Последовательность репетиций должна помочь не допустить, чтобы ученики со временем забывали содержание.
Категории репетиций / закрепления обучения
| Категория содержимого | Практика 1-го типа | Практика 2-го типа |
|---|---|---|
| Декларативная | Извлечение фактов (отзыв) | Объяснение взаимосвязи между фактами (вывод и анализ числа) |
| Процедурные | Репетиция метода (упражнения) | Объяснение принципов, доказательство концептуального понимания (например, использование неформальных методов, создание барных моделей и интерпретация контекста) |
| Условный | Репетиция стратегий (сборники задач одинаковой глубинной структуры) | Описание взаимосвязей между проблемой и выбором стратегии (доказательство / рассуждение) |
Кол. Акций
Некоторые ученики быстро усваивают новое содержание, в то время как другим может потребоваться больше времени, чтобы подумать, попрактиковаться, вспомнить и применить.Учитывая, что знание математики требует от учеников свободного владения процедурами, [сноска 137] учителей должны обеспечить ученикам адекватные возможности для практики. Это с большей вероятностью повысит уровень владения учащимися процедурами.
Консолидация обучения превращает первые моменты успеха, осознания и понимания учеников в долговременные воспоминания. [сноска 138] Чем моложе ученик и чем ниже общий уровень математических навыков, тем больше времени и больше повторений требуется для достижения автоматизма в фактах и методах. [сноска 139] Следовательно, если ученик не может вспомнить, возможно, ему нужно больше практики [сноска 140] , а не просто повторное обучение. [сноска 141]
В наиболее успешных системах математического образования систематическим репетициям уделяется больше времени и внимания, чем в Англии. Эффективное преподавание и обучение в классах, где ученики хорошо успевают, подкрепляются регулярными домашними заданиями, которые требуют от учеников систематического повторения содержания дома. [сноска 142] Учителя в этих системах могут планировать будущие последовательности обучения, будучи уверенными в надежности базовых знаний учеников. В этих условиях закрепление обучения персонализировано по времени, затраченному на выполнение заданий, где:
каждому ребенку нужно будет уделить внимание каждому слову, каждой задаче и каждому упражнению, включенному в каждый учебник. [сноска 143]
Напротив, ученики в Англии тратят меньше времени на домашние задания по математике, чем ученики в странах с высокими показателями. [сноска 144] Тот факт, что дополнительные репетиции, особенно по основному содержанию, помогают ученикам достичь автоматического запоминания и использования фактов и методов [сноска 145] может объяснить некоторые улучшения в успеваемости после введения «математики» час в английских начальных школах. [сноска 146] И наоборот, когда уроки и, следовательно, возможности для репетиций сокращаются, уровень успеваемости снижается. [сноска 147]
Сравнение учебников также показывает, что ожидаемый объем вычислений, упражнений и сборников задач, которые необходимо выполнить, выше в странах, где ученики, как правило, преуспевают. [сноска 148] Свидетельства указывают на необходимость для учителей предоставлять достаточно возможностей для практического применения изучаемых фактов, методов и стратегий, а также дополнительных возможностей для повторного изучения. [сноска 149] Эффективные педагогические приемы, такие как хоровой отклик, четкое определение времени и постановка целей, могут помочь повысить «скорость» практики на уроках, если трудно предоставить дополнительные возможности для повторного изучения. [сноска 150]
Качество
Анализ учебника может дать полезную информацию о качестве репетиции.В отличие от идеала систематических репетиций, согласованных с последовательностью обучения:
Вместо этогоучебников английского языка для начальной школы имеют тенденцию к быстрому перемещению и постоянному перепросмотру. [сноска 151]
Отсутствие согласованности и фактических данных в учебниках, выдаваемых самым младшим ученикам, может потенциально повлиять на вероятность более позднего ОТПРАВИТЬ . [сноска 152] Это может усугубляться тем фактом, что учителя в Англии обычно рассматривают учебники как дополнительный ресурс, а не как потенциальную и ценную систему репетиций. [сноска 153] Это отличается от того, как учебники используются в странах, где учащиеся справляются лучше всего, не только с точки зрения количества вопросов, но и с точки зрения последовательности и соответствия учебной программе. [сноска 154]
Учебники особенно важны для людей с низким уровнем успеваемости [сноска 155] , и они также могут быть полезны для поддержки учеников и родителей. Ученики знают, что им нужно сконцентрироваться на уроке, чтобы иметь возможность выполнить домашнее задание, и они знают, что им нужно выполнить домашнее задание, чтобы понять следующий урок. [сноска 156] Родители также могут легко следить за успеваемостью своего ребенка. [сноска 157]
Для систематических репетиций не всегда нужны учебники, карандаш и бумага. Для младших школьников репетиция чисел и последовательностей может опираться на канон игр и песен с играми в кости, домино и счетными последовательностями. [сноска 158] Вычислительные технологии также могут помочь ученикам усвоить числовые данные, предоставляя им достаточное количество повторений и прямую обратную связь таким образом, который им нравится. [сноска 159] Ученики также получают больший прогресс и получают удовольствие от компьютерных математических игр, когда основной контент вводится в виде отдельных обучающих компонентов, за которыми систематически следуют «мини-игры», чем если бы контент полностью учитывался в условиях игры. [сноска 160] Этот подход также может быть полезным для учеников с ОТПРАВИТЬ . [сноска 161] Однако учителя должны проявлять осторожность, применяя такой подход, потому что не все дети достигают одинакового прогресса в обучении на компьютерах. [сноска 162]
Задачи, ориентированные на содержание и выполнимые
По математике, исследования показывают, что долгосрочное извлечение основного содержания должно быть в центре внимания при планировании учителей и руководителей. [сноска 163] Это означает, что учителя должны ставить перед учениками задачи, в которых основное внимание уделяется повторению фактов, методов и стратегий в дополнение к задачам, развивающим понимание учениками.
Наблюдение за активностью может показать, что ученики заняты и получают удовольствие от занятия, но если ученики тратят много времени, делая выбор, решая, что делать или что делать, например, когда задействован физический аппарат, их внимание и обучение могут быть скомпрометирован. [сноска 164] Например, рисование, измерение и сравнение углов в многоугольнике, чтобы узнать, а затем выучить формулу для суммы углов, означает, что ученики думают над этой формулой в последние несколько минут урока. Даже образы могут отвлекать: в учебниках в странах, где учащиеся хорошо учатся, меньше не относящихся к содержанию и отвлекающих иллюстраций, картинок и мультфильмов. [сноска 165]
Учащиеся с большей вероятностью будут проявлять деструктивное поведение, если от них ожидается выполнение задач, составные части которых они еще не освоили.Они с большей вероятностью будут продолжать выполнять задачу и будут мотивированы, если задачи выполнимы. [сноска 166] В свою очередь, постоянное выполнение заданий помогает ученикам улучшить их способность сосредотачиваться. [сноска 167] Ученикам лучше сначала изучить и отрепетировать содержание как составные части, прежде чем изучать условия его использования в рамках составного навыка. [сноска 168] Это имеет значение для «задачи», потому что ученики, сталкиваясь с незнакомыми или сложными задачами, склонны прибегать к использованию тех методов, с которыми у них есть больше всего возможностей, а не тех, которые наиболее действенны и которым недавно научили.Например, учащиеся, решающие сложные арифметические задачи, по умолчанию будут прибегать к сложению, [сноска 169] учеников, которые плохо знакомы с алгеброй, по умолчанию будут использовать арифметические методы или метод проб и ошибок, [сноска 170] и новые ученики, изучающие математику, упадут вернуться к знакомым концепциям, которые визуально похожи, но не имеют отношения к вопросу. [сноска 171]
Когда ученики готовы решать задачи, им необходимо уметь удерживать линию мысли и концентрироваться. [сноска 172] Было показано, что фоновый шум и общая болтовня негативно влияют на способность учеников понимать, что говорит учитель, поддерживать соответствующее поведение и концентрироваться. Больше всего страдают дети младше 13 лет и дети с . ОТПРАВИТЬ . [сноска 173] Исследования также показали, что идеальная среда для периодов самостоятельной работы — это не только тихая, но и почти тихая среда. [сноска 174] Это не означает, что все репетиции должны проходить без звука.Групповая работа может помочь ученикам в развитии объяснений, если ею строго управлять. [сноска 175] Однако есть пределы его воздействия на обучение, поскольку оно не всегда улучшает успеваемость и его трудно реализовать. [сноска 176] Учителя должны находить баланс между возможностями для обсуждения и потребностями учеников в спокойных периодах времени для размышлений.
Строительные леса как вспомогательные средства, а не костыли
Учителям необходимо тщательно продумать, как они используют строительные леса, каркасы, физические приспособления и альтернативные источники информации для учеников, которым требуется дополнительная поддержка.Следует различать использование физического устройства для раскрытия полезной информации [сноска 177] и его обычное использование в качестве внешнего запоминающего устройства.
Опора и последующая зависимость от манипуляторов и связанных с ними средств может помешать продвижению по учебной программе. [сноска 178] Значит, учителям нужно дать ученикам достаточно времени, чтобы закрепить обучение, и им нужно спланировать, как ученики уйдут от использования манипуляторов.Это поможет избежать того, чтобы ученики полагались на манипуляторы для устранения пробелов в основных знаниях, которые в дальнейшем могут стать препятствием для обучения.
Уравновешивание репетиции доказательства и объяснения с репетицией фактов, методов и стратегий
Есть 2 «типа» практики:
«тип 1» включает в себя репетицию основных фактов, методов и стратегий, которые можно использовать для выполнения упражнений и решения проблем сейчас и на следующем этапе обучения.
«тип 2» включает объяснение, обоснование и доказательство концепций с использованием неформальных и схематических методов, анализ и вывод числа
Учителям необходимо найти баланс между этими двумя.Ученикам полезно воспроизводить объяснения и доказательства как способ улучшить свое собственное концептуальное понимание того, «почему», но когда дело доходит до обучения тому, как находить решения проблем, практикуйте сами методы расчета, чтобы их можно было понять. напоминание в долгосрочной перспективе, вероятно, будет ключом к профессиональному мастерству, [сноска 179] , особенно для учеников, которые определены как более склонные к трудностям. [сноска 180] Это дает большую уверенность в том, что ученики могут использовать базовые знания фактов, эффективные методы и полезные стратегии на следующем этапе своего образования.Тщательное изучение учебных программ в странах, где учащиеся преуспевают, показывает, что систематические репетиции делают упор на изучение и применение основных фактов и методов одновременно с развитием концептуального понимания, а не после него. [сноска 181]
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Педагоги планируют дать ученикам возможность закрепить знания, которые:
выходите за рамки немедленных правильных ответов на вопросы
предполагает повторное обучение
в соответствии с деталями и последовательностью учебной программы
не отвлекают и не отвлекают
найти баланс между практиками типа 1 и типа 2
Избегайте использования внешних вспомогательных средств памяти или физических ресурсов
помогает ученикам не полагаться на догадки, искать подсказки или использовать неструктурированный метод проб и ошибок
Оценка
Сводка
Оценка в процессе обучения наиболее полезна, когда она фокусируется на компонентах знаний, которые усвоили ученики.Такой подход помогает ученикам обрести уверенность в себе и упрощает анализ и устранение пробелов в обучении. В математике ученики извлекают пользу из практики знания, которое должно быть легко запомнено, например, математических фактов. Элемент времени дает уверенность в том, что ученики не полагаются на вывод.
Частое тестирование с низкими ставками помогает подготовить учеников к итоговой успеваемости
Суммарные оценки обучения должны регулярно предоставлять легко сопоставимую информацию всем заинтересованным сторонам, включая родителей и самих учеников. [сноска 182] Модульные экзамены обеспечивают краткосрочные цели и чувство достижения, но они могут способствовать развитию подхода к обучению «как раз вовремя», что означает, что знания отбрасываются вскоре после сдачи тестов. Экзамены по окончании курса дают большую уверенность в том, что изучение содержания будет долгосрочным. [сноска 183] Это говорит о том, что лучше всего подходит сочетание подходов: регулярные тесты по недавно изученному и изученному содержанию и объективная, справедливая и точная итоговая оценка в конце года или курса.
Руководителям, однако, следует избегать смешивания двух концепций с частым использованием суммативных тестов, таких как прошлые статьи. Это может привести к тому, что ученики с более низким уровнем успеваемости и ученики с SEND будут регулярно получать напоминания о том, чего они не знают и не могут делать (что может побуждать к догадкам, повторению неправильных представлений или тактике избегания). Со временем ученики, которые не добились успеха, могут потерять мотивацию, что может негативно повлиять на их шансы получить проходной балл при повторном прохождении курсов между 16 и 18 годами. [сноска 184]
Однако это беспокойство по поводу производительности вызывают не тесты, а отсутствие навыков. Недостаток знаний может также усугубляться использованием «реалистичных» постановок сюжетных задач, которые создают языковой барьер для детей из неблагополучных семей. [сноска 185] Учителя могут сделать так, чтобы ученики пришли к тестам и тестам как к удачным моментам, приняв принципы, лежащие в основе причинного пути к мотивации и получению удовольствия от изучения предмета.Этого можно достичь, стремясь к повышению квалификации и начальному успеху в предмете.
Когда ученики достигают уровня владения языком, они с нетерпением ждут тестов. [сноска 186] Соревновательные математические игры, например, более эффективны для обучения и удержания, чем несоревновательные игры. [сноска 187] Цели попытки достичь личного лучшего и преуспевания по сравнению со средним опосредуются более поздним достижением. [сноска 188] Таким образом, помимо обеспечения хорошей подготовки учеников к тестам, руководители должны следить за тем, чтобы критерии успеха были понятны.
Частое тестирование преподаваемого контента с низкими ставками может помочь подготовить учеников к итоговым тестам, предоставляя улучшающие память возможности вспоминать и применять преподаваемый контент. [сноска 189] Тестирование с низкими ставками также хорошо работает, когда тесты составных частей, таких как математические факты, рассчитаны по времени. [сноска 190] Если учителя дают честную обратную связь, интерес учеников и чувство собственной эффективности также возрастают. [сноска 191] Учителя также могут устанавливать критерии для усвоения фактов и методов, чтобы они могли быть уверены, что ученики припоминают, а не догадываются или выводят. [сноска 192] Таким образом, тесты должны быть тесно согласованы с последовательностью учебных программ, поскольку общие тесты не могут дать такую обратную связь. [сноска 193]
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Ученики хорошо подготовлены к оцениванию, поскольку они усвоили все факты, методы и стратегии, которые могут быть проверены.
Учителя планируют частое тестирование с низкими ставками, чтобы помочь ученикам запоминать содержание.
Уроки включают в себя тестирование по времени, чтобы помочь ученикам усвоить математические факты в автоматическом режиме.
Системы на школьном уровне
Сводка
Руководители могут поддерживать успеваемость учеников по программе математики, обеспечивая высокое качество учебной работы учеников. Это важно, потому что, когда ученики проводят систематические и упорядоченные вычисления, они лучше видят взаимосвязь между числами и выявляют ошибки, которые можно исправить.Руководители также могут планировать развитие предметных и предметно-педагогических знаний учителей, давая учителям возможность работать и учиться друг у друга. Это, например, помогает новым учителям увидеть и принять полезные способы объяснения основных концепций, методов и стратегий ученикам, которых они обучают.
Расчет и представление
Точные вычисления и внимательное изложение дают ученикам возможность замечать важные и интересные схемы чисел, а также ошибки, которые необходимо исправить.Методы вычислений и правила представления — это процедурные знания, которые необходимо обучать и репетировать в автоматическом режиме. Некоторые ученики могут естественным образом развить «аккуратность» и последующую аккуратность, но обучение и повторение этих процедурных знаний дает большую уверенность в том, что большее количество учеников сможет видеть ошибки и определять числовые шаблоны, а также испытывать чувство выполненного долга.
Это не означает, что нельзя допускать более «грязных» экспериментальных работ. Однако учителя могут помочь добиться успеха в расчетах и презентациях, уравновешивая экспериментальные подходы с возможностями научиться быть систематизированными, логичными и точными при применении изученных фактов, методов и стратегий.
Проактивное профессиональное развитие: запланированный и целенаправленный путь к профессиональному опыту
Потребность в прочном фундаменте относится ко всем новичкам, включая начинающих учителей математики. Регулярные наблюдения часто рассматриваются как главный двигатель профессионального развития, когда учителям дают обратную связь по аспектам, которые необходимо улучшить. Использование стандартов учителей для этих реактивных подходов ставит во главу угла развитие педагогических и предметно-педагогических знаний на местах, выделяя особенности, которые отсутствуют или нуждаются в корректировке на этом пути.
У лидеров может возникнуть соблазн сосредоточиться на отношениях между учителем и учеником как на показателе высокого качества преподавания и обучения. Однако анализ успеваемости и отношения учеников показывает, что сосредоточение внимания на усилиях учеников и их интерес к предмету может иметь большее значение. [сноска 194] Учитывая, что начальная подготовка учителей может варьироваться с точки зрения педагогических, предметно-педагогических и конкретных предметных знаний, [сноска 195] мы не можем предполагать, что все начинающие учителя математики будут обладать всеми необходимыми инструментами для сделать самый успешный старт.
Руководители могли бы рассмотреть возможность включения более активных подходов, которые ликвидируют пробелы и позволяют начинающим учителям применять и улучшать экспертные методы обучения, а не разрабатывать свои собственные аспекты эффективного преподавания математики с нуля. [сноска 196] Такие подходы могут включать:
регулярных возможностей для наблюдения и наставничества со стороны опытных и успешных учителей математики
обеспечение последовательных схем обучения, соответствие учебников и заметок учителя, чтобы помочь объяснениям и помочь начинающему учителю воплотить предмет в жизнь [сноска 197]
систематических планов по построению этих моделей обучения и репетиций с течением времени, чтобы будущие поколения учителей могли принести пользу
совместное планирование с более опытными и успешными учителями математики
Уроки японского языка являются примером систематического подхода к обмену предметно-педагогическими знаниями, который формирует и распространяет предметно-педагогические знания в организационном, местном и национальном масштабах. [сноска 198] Тот факт, что изучение уроков — это система, должен также предупреждать учителей и руководителей об опасностях использования «поверхностных элементов», а не систем. Это также может объяснить, почему попытки установить (поверхностные особенности) «изучения урока» в качестве учебной программы или педагогического вмешательства приводят к несколько менее убедительным результатам. [сноска 199]
Учителя также должны стремиться обновлять и улучшать свои знания по предметам, даже если они преподают основополагающие концепции. [сноска 200] Например, учителя начальных возрастных групп получают больше, если они знают основные принципы, которым ученики могут научиться, чтобы помочь им на последующих уроках алгебры. [сноска 201]
Исходя из вышесказанного, качественное математическое образование может иметь следующие особенности
Общешкольные подходы к расчету и оформлению в школьных учебниках.
Общешкольные подходы к выделению времени и ресурсов учителям для развития предметных знаний и изучения ценных способов обучения друг у друга.
Заключение
На протяжении всего обзора преобладает тема инженерного успеха, подкрепленного системным мышлением. Эти подходы направлены на то, чтобы превратить предложение контента в большую гарантию того, что контент может и будет изучен. Результатом этого системного мышления являются наблюдаемые особенности и подходы успешного математического образования:
подробная кодификация и последовательность фактов, методов и стратегий, которые ученики усвоят
согласованность обучения и согласованные репетиции, которые увеличивают шансы понимания и запоминания, сводя к минимуму необходимость в догадках или пробах и ошибках
В рамках этих мощных систем математического образования учебники, руководства для учителей и рабочие тетради рассматриваются как жизненно важная часть инфраструктуры для эффективной передачи предметных знаний и предметно-педагогических знаний новым поколениям учеников и учителей.Это сигнализирует о необходимости для учителей и руководителей избегать установки функций и подходов в отсутствие «инфраструктуры», лежащей в основе их эффективности. Также вероятно, что черты, которые обычно не наблюдаются или не выбираются, такие как менее привлекательное качество и количество занятий, также являются неотъемлемой частью общего успеха начинающих математиков.
Качество и количество практики — жизненно важный ключ, открывающий путь к развитию двойного пути концептуального понимания и беглости процедур.Кроме того, при наблюдении за относительной квалификацией и умением учеников, например, на уроке решения проблем, учителя и руководители должны помнить о пути, который прошли ученики, чтобы достичь умения решать проблемы. Это путешествие будет включать в себя не только особенности и упражнения уроков, в которых в то время принимают участие опытные математики. Различия в качестве математического образования в Англии, вероятно, являются результатом отсутствия системного и системного мышления, а также возможных пробелов в содержании, обучении, репетициях, оценках и планах их развития с течением времени.
Распечатать или сохранить в PDF
Для печати содержания вы можете:
- используйте кнопку «Распечатать эту страницу» в меню «Содержание».
- Щелкните правой кнопкой мыши в любом месте страницы с помощью мыши и выберите «Печать» в меню.
- нажмите Ctrl + P на клавиатуре Windows или Command + P на Mac
Вы также можете использовать эти параметры и изменить место назначения принтера, чтобы сохранить содержимое в формате PDF.
Инструкции могут различаться в зависимости от того, какой интернет-браузер вы используете, например Internet Explorer или Google Chrome, а также от типа используемого вами устройства, например телефона или ноутбука.Вы можете найти параметры печати и сохранения в меню браузера.
.