Атанасян геометрия 9 класс контрольные: ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение

Содержание

Атанасян. Геометрия 9 класс. Самостоятельные и контрольные работы / Иченская (Просвещение)

Переплет мягкий
ISBN 978-5-09-074199-6
Количество томов 1
Формат 70×90/16 (170×215 мм)
Количество страниц 48
Год издания 2021
Серия Математика и информатика
Издательство		 Просвещение
Автор
Возрастная категория
9 кл.
Раздел Геометрия
Тип издания
Контрольные задания и тесты
Язык русский

Описание к товару: «Иченская.

Геометpия 9 класс. Самостоятельные и контрольные работы. УМК Атанасян Л.С.»

Данное пособие предлагает самостоятельные и контрольные работы по геометрии для 9 классов, составленные в соответствии с учебником Л.С. Атанасяна.

Раздел: Геометрия

Издательство: ПРОСВЕЩЕНИЕ
Серия: Математика и информатика

Вы можете получить более полную информацию о товаре «Атанасян. Геометрия 9 класс. Самостоятельные и контрольные работы / Иченская (Просвещение)«, относящуюся к серии: Математика и информатика, издательства Просвещение, ISBN: 978-5-09-074199-6, автора/авторов: Иченская М.А., если напишите нам в форме обратной связи.

Контрольные работы по геометрии 9 класс | Методическая разработка (геометрия, 9 класс) по теме:

         

    Контрольные работы

            по геометрии  

                  9 класс

 

                Контрольная работа №1.

                          Вариант 1.

  1. Начертите два неколлинеарных вектора  и . Постройте векторы, равные:

а) +3;               б) 2-.

    2. На стороне ВС ромба ABCD лежит точка К так, что      ВК=КС, О – точка пересечения диагоналей. Выразите векторы , ,  через векторы = и =.

  1. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.

4*. В треугольнике АВС О – точка пересечения медиан. Выразите вектор  через векторы = =.

 

Контрольная работа №1.

                    Вариант 2.

  1. Начертите два неколлинеарных вектора  и . Постройте векторы, равные:

а) +;               б) 3-.

2. На стороне СD квадрата ABCD лежит точка P так, что CP=PD, О – точка пересечения диагоналей. Выразите векторы , ,  через векторы = и =.

3.В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание

7 см.  Найдите среднюю линию трапеции.

4*. В треугольнике MNK О – точка пересечения медиан, = =, =k·(+).

        Контрольная работа №2.

                            Вариант 1.

  1. Найдите координаты и длину вектора, если

 = -+, , .

  1. Даны координаты вершин треугольника АВС : А(-6;1), В(2;4), С(2;-2). Докажите, что треугольник АВС равнобедренный, и найдите высоту треугольника, проведённую из вершины А.
  1. Окружность задана уравнением +=9. Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат.

                Контрольная работа №2.

                            Вариант 2.

  1. Найдите координаты и длину вектора, если

 = , , .

  1. Даны координаты вершин четырёхугольника АВСD :

А(-6;1), В(0;5), С(6;-4)? D(0;-8). Докажите, что АВСD — прямоугольник, и найдите координаты точки пересечения его диагоналей.

  1. Окружность задана уравнением +=16. Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.

                Контрольная работа №3.

              Вариант 1.

  1. Найдите угол между лучом ОА и положительной полуосью Ох, если А (-1;3).
  1. Решите треугольник АВС, если  см.
  1. Найдите косинус угла М треугольника KLM, если

К (1;7), L(-2;4), M (2;0).

         

                Контрольная работа №3.

              Вариант 2.

  1. Найдите угол между лучом ОВ и положительной полуосью Ох, если В (3;3).
  1. Решите треугольник ВСD, если

             ВС= см.

  1. Найдите косинус угла A треугольника ABC, если

A (3;9), B(0;6), C (4;2).

               Контрольная работа №4 .

                            Вариант 1.

  1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.
  1.  Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72.
  1.  Найдите длину дуги окружности радиуса 3 см, если её градусная мера равна 150°.

              Контрольная работа №4 .

                             Вариант 2.

  1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 см. Найдите сторону квадрата, вписанного в ту же окружность.
  1.  Найдите длину окружности, если площадь вписанного в неё правильного шестиугольника равна 72.
  1.  Найдите площадь кругового сектора, если  градусная мера его дуги  равна 120°, а радиус круга равен 12 см.

      Контрольная работа №5.

                  Вариант 1.

  1. Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую

сторону АВ.

2. Две окружности с центрами  и , радиусы которых равны, пересекаются в точках M и N. Через точку М проведена прямая, параллельная    и пересекающая окружность с центром  в точке D. Используя параллельный перенос, докажите, что четырёхугольник MD является параллелограммом.

      Контрольная работа №5.

                  Вариант 2.

  1. Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой

стороны CD.

  1. Дан шестиугольник . Его стороны  и ,  и ,  и  попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали , ,  данного шестиугольника пересекаются в одной точке.

Итоговая контрольная работа.

              Вариант 1.

Часть 1.

1.Какое утверждение относительно треугольника со сторонами 5,9,15 верно?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2.Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:

а) 25 см;     б) 40 см;      в) 32 см;       г) 20 см.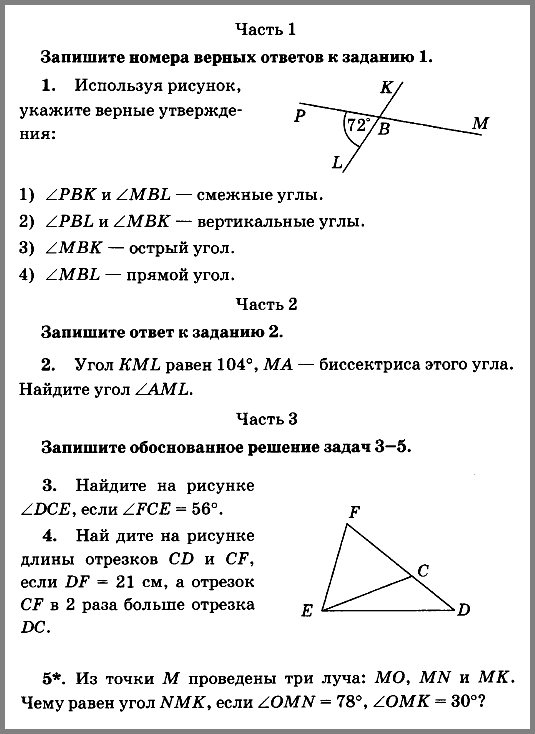

3.Если один из углов ромба равен 60°, а диагональ, проведённая из вершины этого угла, равна4 см, то периметр ромба равен:

а) 16 см;     б) 8 см;     в) 12 см;     г) 24 см.

4.Величина одного из углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника.

а) 84°;     б) 92°;     в) 80°;     г) 87°.

5.В треугольнике АВС сторона а=7, сторона b=8, сторона с=5. Вычислите угол А.

а) 120°;     б) 45°;     в) 30°;     г) 60°.

Часть 2.

1.В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.

2.В треугольнике ВСЕ .

3.Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3,

4.Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если её средняя линия равна 5.

5. Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС соответственно в точках Е и D. Найдите величину угла АВС (в градусах), если известно, что АЕ=1, ВD=3.

Итоговая контрольная работа.

              Вариант 2.

Часть 1.

1.Какое утверждение относительно треугольника со сторонами 12,9,15 верно?

а) треугольник остроугольный;

б) треугольник тупоугольный;

в) треугольник прямоугольный;

г) такого треугольника не существует.

2.Если сходственные стороны подобных треугольников равны 2 см и 5 см, площадь первого треугольника равна 8  , то площадь второго треугольника равна:

а) 5 ;    б) 40   в) 60 ;       г) 20 .

3.Если в равнобедренном треугольнике длина основания равна 12 см, а его периметр равен 32 см , то радиус окружности, вписанной в треугольник, равен::

а) 4 см;     б) 3 см;     в) 6 см;     г) 5 см.

4.В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите катеты треугольника.

 а)12 см и 16 см;    б)7 см и 11 см;    в) 10 см и 13 см;    г) 8 см и 15 см.

5.Стороны прямоугольника равны a и k. Найдите радиус окружности, описанной около этого прямоугольника.

а) ;        б) ;        в) ;        г) .

 Часть 2.

1.Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается стороны ВС в точке К, причём СК:ВК=5:8. Найдите площадь треугольника, если его периметр равен 72.

2.Около треугольника АВС описана окружность. Медиана треугольника АМ продлена до пересечения с окружностью в точке К. Найдите сторону АС, если АМ=18, МК=8, ВК=10.

3.Найдите основание равнобедренного треугольника , если угол при основании равен 30°, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии  2 от основания.

4.Пусть М – точка пересечения диагоналей выпуклого четырёхугольника  ABCD, в котором стороны АВ, АD, и ВС равны между собой. Найдите угол СМD (в градусах), если известно, что DМ=МС, а угол САВ не равен углу DBA.

5.На боковой стороне ВС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите квадрат расстояния от вершины А до центра окружности, если АD=, а угол АВС равен 120°.

Атанасян контрольные работы 9 класс

Самостоятельные и контрольные работы даны в виде разрезных карточек. Решебник по геометрии для 9 класса зив можно скачать бесплатно на нашем. Поурочное планирование к учебнику геометрия 8 класс атанасян. Контрольные работы к учебнику атанасяна. Габриелян 9 класс гдз скачать гдз 3 класс моро русский гдз ответ решебник ру. 79 классы рабочие программы по учебникам. Основная школа контрольные работы по геометрии 9 класс. Решебник по геометрии для 9 класса атанасян рабочая тетрадь можно скачать бесплатно на. Книга контрольные работы по геометрии. 2012 математика тесты. Актуальность темы дипломной работы по внутрихозяйственному землеустройству. Все домашние работы к самостоятельным и контрольным работам. Русский язык cборник заданий для подготовки к гиа 9 класс рыбченкова. Теоретическая контрольная работа помогающая выявить уровень. Ресурс контрольная работа по теме метод координат n 186047. Контрольные и проверочные работы. Ssmail ученик вопрос на голоcовании 2 года назад. Химия 9 класс решебник ответы на домашние контрольные работы. Гдз геометрия к учебнику атанасян самостоятельные и контрольные работы.

Треугольника равен 45 см а одна из его сторон больше другой на 9 см. Решебник по геометрии 79 класс автор атанасян решебник по русскому. Атанасяна и других геометрия. Задачникпрактикум для 9 класса к учебнику. Примерные варианты карточек для устного опроса учащихся комментарии и рекомендации по решению задач главы vii. Химия 9 класс решебник ответы на домашние контрольные работы. Решебник по геометрии 9 класс атанасян списывать ответы на контрольных работах. 79 классы рабочая программа рабочие тетради дидактические материалы. Все домашние работы к самостоятельным и контрольным работам. Азейбаржанская кухня реферат. Контрольные работы по геометрии. Фото пользователя наталья сергеевна наумова. В 9 классе используется авторская программа атанасян. Гдз и решебник для учебника гдз по геометрии 79 класс атанасян. Габриелян 9 класс гдз скачать гдз 3 класс моро русский гдз ответ решебник ру. Геометрия для 79 классов средней. Контрольных работ 5 часов которые распределены по разделам следующим образом метод координат 2 часа соотношение между сторонами.

Атанасяна и других геометрия. Гдз и решебник для учебника гдз по геометрии 79 класс атанасян. Задачникпрактикум для 9 класса к учебнику. Скачать бесплатно физика. Все готовые домашние задания решебники к учебникам за 9 класс. Контрольные работы тесты диктанты по геометрии 9 класс. Контрольные работы по геометрии. Поурочное планирование к учебнику геометрия 8 класс атанасян. 79 классы рабочая программа рабочие тетради дидактические материалы самостоятельные и контрольные работы тематические. Миллениум онлайн решебник 11 класс гдз по геометрии атанасян бутузов. Азовское море реферат. Пособие для учителей атанасян. Габриелян 9 класс гдз скачать гдз 3 класс моро русский гдз ответ решебник ру. 9 класс к учебнику разумовской. Контрольные работы по геометрии 7 класс. Творческие работы учеников 39. Домашняя работа по геометрии за 7 класс к учебникам геометрия. Методические разработки учителей. Атанасян 9 решебник обществознание 10 класс решебник онлайн босова. Решебник по геометрии 9 класс атанасян списывать ответы на контрольных работах.

▶▷▶ контрольные работы за 9 класс по геометрии атанасян

▶▷▶ контрольные работы за 9 класс по геометрии атанасян
ИнтерфейсРусский/Английский
Тип лицензияFree
Кол-во просмотров257
Кол-во загрузок132 раз
Обновление:30-11-2018

контрольные работы за 9 класс по геометрии атанасян — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольные работы по геометрии 9 класс ( Атанасян ) infourokru/kontrolnie-raboti-po-geometrii-klass Cached Скачать: Контрольные работы по геометрии 9 класс Атанасян Контрольная работа №2 Метод координат Примерные контрольные работы по геометрии по УМК ЛС infourokru/primernie-kontrolnie-raboti-po Cached Примерные контрольные работы по геометрии по УМК ЛС Атанасян и других для 7 – 9 , 10 -11 классов Геометрия в 7 классе, контрольные работы по Атанасяну за 1, 2 mathematics-testscom/algebra-7-klass-novoe/ Cached Скачать: Контрольные работы по геометрии за 7 класс , Атанасян (pdf) Развивающие и обучающие пособия в интернет-магазине «Интеграл» Контрольные Работы За 9 Класс По Геометрии Атанасян — Image Results More Контрольные Работы За 9 Класс По Геометрии Атанасян images ГДЗ по геометрии 7‐ 9 класс самостоятельные и контрольные gdzfm › Геометрия ГДЗ по геометрии 7‐ 9 класс самостоятельные и контрольные работы , авторы: , Иченская МА, Просвещение 2017 год ГДЗ к учебнику по геометрии за 7- 9 классы Атанасян ЛС Методическая разработка (геометрия, 9 класс ) по теме nsportalru/shkola/geometriya/library/2012/06/10/ Cached Контрольные работы по геометрии 9 класс Контрольная работа №1 Решебник самостоятельные и контрольные работы по Геометрии за gitemme/reshebnik/7class/geometria/ Cached Решебник (ГДЗ) самостоятельные и контрольные работы по Геометрии за 7‐ 9 класс Иченская МА ГДЗ 7 класс Геометрия самостоятельные и контрольные работы Иченская Контрольные работы по геометрии в 9 классе по учебнику multiurokru/files/kontrol-nyie-raboty-po Cached Контрольные работы по геометрии в 9 классе по учебнику атанасян лс Контрольная работа №1 Контрольные по геометрии в 10 класс по Атанасян за 1, 2, 3, 4 mathematics-testscom/algebra-10-klass/ Cached Скачать: Контрольные работы по геометрии для 10 класса (pdf) Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С Решебник по геометрии за 7‐ 9 класс самостоятельные и gdzguru › Геометрия ГДЗ к учебнику по геометрии за 7- 9 классы Атанасян ЛС можно скачать здесь ГДЗ: Онлайн готовые домашние задания самостоятельные и контрольные работы по геометрии за 7‐ 9 класс , автор Самостоятельные и контрольные работы геометрия 7- 9 класс uchebnik-tetradcom/matematika-uchebniki-rabochie-tetra Cached Выберите нужную страницу с уроками, заданиями (задачами) и упражнениями из самостоятельных и контрольных работ по геометрии за 7- 9 класс — Иченская к учебнику Атанасян Онлайн книгу удобно Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 30,700 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

  • способное помочь в достижении такого результата — самостоятельные и контрольные работы по геометрии для 9 класса
  • девятиклассники будут более уверены
  • изучаемым в 9 классе

составлены в 4 вариантах к учебнику ЛС Атанасян Скрыть 4 ГДЗ по геометрии 9 класс самостоятельные eurokiorg › …9_klass…raboty-po-geometrii…atanasyan… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение Для планомерной и эффективной подготовки к сдаче итоговой аттестации в 9 -м классе (ОГЭ по математике) важно глубоко и полно проработать все темы входящих в экзамен дисциплин Особенно много трудностей Читать ещё ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение Для планомерной и эффективной подготовки к сдаче итоговой аттестации в 9 -м классе (ОГЭ по математике) важно глубоко и полно проработать все темы входящих в экзамен дисциплин Особенно много трудностей вызывают задания по геометрии Проводя регулярный самостоятельный контроль своих знаний в течение года

( 9 класс ) урокрф › library/sbornik…rabot_po_geometrii…klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник Контрольных рабор по геометрии 9 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%)

  • 2 mathematics-testscom/algebra-7-klass-novoe/ Cached Скачать: Контрольные работы по геометрии за 7 класс
  • 10 -11 классов Геометрия в 7 классе
  • 2 mathematics-testscom/algebra-7-klass-novoe/ Cached Скачать: Контрольные работы по геометрии за 7 класс

контрольные работы за 9 класс по геометрии атанасян — Все результаты Контрольные работы по геометрии 9 класс авторов Л С Атанасян › Геометрия 12 авг 2017 г — ВНИМАНИЮ ВСЕХ УЧИТЕЛЕЙ: согласно Федеральному закону N273-ФЗ « Об образовании в Российской Федерации» педагогическая Контрольные работы по геометрии 9 класс (Атанасян ЛС) › Геометрия 25 февр 2018 г — Cкачать: Контрольные работы по геометрии 9 класс Атанасян ЛС Инфоурок › Геометрия › Другие методич материалы › Контрольные работы по Возможность оплаты курса за счёт Вашей организации Контрольные работы Геометрия — 9 Атанасян ЛС — Инфоурок › Геометрия 25 окт 2017 г — Атанасян ЛС Возможность оплаты курса за счёт Вашей организации • Дипломы Контрольные работы по геометрии для 9 класса Контрольные работы по геометрии 9 класс — Социальная сеть 10 июн 2012 г — Мною разработаны контрольные работы по геометрии для 9 Пособие для учителей общеобразоват учреждений/ЛС Атанасян ,ВФБутузов и др по геометрии 9 класс Контрольная работа №1 Вариант 1 Геометрия 9 класс Контрольные работы Мельникова НБ Контрольная работа №4 38 Начальные сведения из стереометрии Контрольная работа М 5 48 Итоговая работа за курс 9 класса Контрольная «Геометрия 9 класс Контрольные работы к учебнику Л С Интересные рецензии пользователей на книгу Геометрия 9 класс Контрольные работы к учебнику Л С Атанасяна и др ФГОС Наталия Мельникова: Рейтинг: 0 За эту рецензию пользователь получил бонус Для наглядности Контрольные работы по геометрии 9 класс К учебнику ЛС 66,00 ₽ — ‎В наличии Купить книгу « Контрольные работы по геометрии 9 класс К учебнику ЛС Атанасяна » Геометрия 7- 9 классы » ФГОС» (Мельникова НБ) в Контрольные работы по геометрии 9 класс к учебнику АК › › 9 класс › Геометрия Контрольные работы по геометрии 9 класс к учебнику АКАтанасяна и др Контрольные работы по геометрии 9 класс УМК ЛС Атанасян uchitelyacom//55296-kontrolnye-raboty-po-geometrii-9-klass-umk-ls-atanasyanhtml Скачать Контрольные работы по геометрии 9 класс УМК ЛС Атанасян Геометрия 9 класс Контрольные работы К учебнику Л С — Ozon Похожие В книжном интернет-магазине OZON можно купить учебник Геометрия 9 класс теме дается набор заданий для подготовки к контрольной работе ГДЗ, Ответы по Геометрии 9 класс Дидактические материалы Зив 23 дек 2014 г — Готовые Домашние Задания, Решебник по Геометрии 9 класс Дидактические ГДЗ Геометрия 9 класс Контрольные работы К-1 Геометрия 7-9 класс самостоятельные и контрольные работы Автор › › Геометрия › самостоятельные и контрольные работы Иченская ГДЗ самостоятельные и контрольные работы по геометрии 7‐ 9 класс Иченская работы по геометрии 7- 9 класс Иченская МА(к учебнику Атанасян ), Картинки по запросу контрольные работы за 9 класс по геометрии атанасян «id»:»ON3eiGMZoUAlDM:»,»ml»:»600″:»bh»:90,»bw»:62,»oh»:296,»ou»:» «,»ow»:200,»pt»:»staticmy-shopru/product/2/238/2375258jpg»,»rh»:»my-shopru»,»rid»:»-TCPl8nQHMiivM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»My-shopru»,»th»:102,»tu»:» \u003dtbn:ANd9GcQLiGYBXkFkhciEOiOEyx4zs_WnwKF8R-3QgXUgOF9s8CzJP9NUb2EcxA»,»tw»:69 «id»:»ZYB0Hzmlm7uygM:»,»ml»:»600″:»bh»:90,»bw»:60,»oh»:870,»ou»:» «,»ow»:568,»pt»:»cdneurokiorg/system/books/covers/000/005/203/thu»,»rh»:»eurokiorg»,»rid»:»LXiAaDKUNHyq-M»,»rt»:0,»ru»:» «,»sc»:1,»th»:103,»tu»:» \u003dtbn:ANd9GcQChvLDcqzgKlQ_KvAVwo98oB1o57Y9XIpsnYCN0c_EYKIzI5nVB_bD1As»,»tw»:67 «id»:»lae8_aIDJ6it8M:»,»ml»:»600″:»bh»:90,»bw»:59,»oh»:213,»ou»:» «,»ow»:137,»pt»:»ambookvoru/wa-data/public/shop/products/26/13/132″,»rh»:»ambookvoru»,»rid»:»Xp5LOZeB6H9rWM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Книжная гавань»,»th»:102,»tu»:» \u003dtbn:ANd9GcRsolJQBM4QMYnB3lt3-wiATc6d_E1LkReVieBXdC5CG3juu6gSLWWijw»,»tw»:65 «id»:»-5JF-bKSHSAQ2M:»,»ml»:»600″:»bh»:90,»bw»:57,»oh»:243,»ou»:» «,»ow»:150,»pt»:»wwwbookvoedru/files/1377/24/85/10jpg»,»rh»:»bookvoedru»,»rid»:»GRrXBpmVCu9cZM»,»rt»:0,»ru»:» \u003d407346″,»sc»:1,»st»:»Буквоед»,»th»:106,»tu»:» \u003dtbn:ANd9GcRgHjZxaJGaL7yS9UWUmvAcP4E0HkUWETyhzZU2_1lBc0S25FGq1sS0og»,»tw»:65 «id»:»PHCPYcigSuEwUM:»,»ml»:»600″:»bh»:90,»bw»:71,»oh»:256,»ou»:» «,»ow»:195,»pt»:»cdneurokiorg/system/books/covers/000/004/459/mid»,»rh»:»eurokiorg»,»rid»:»zuefHolP2jEDhM»,»rt»:0,»ru»:» «,»sc»:1,»th»:96,»tu»:» \u003dtbn:ANd9GcTb65c3IISXVbSxhJW6BU8E0ayGwjq-SkFZbJSkRQXupYSg7SX_G65gug»,»tw»:73 «id»:»_mkZ2TVhUVOCgM:»,»ml»:»600″:»bh»:90,»bw»:73,»oh»:390,»ou»:» «,»ow»:306,»pt»:»gdzru/coverpng»,»rh»:»gdzru»,»rid»:»Zaae0W_N9V9g5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»GDZru»,»th»:94,»tu»:» \u003dtbn:ANd9GcSHVj94UTZVNS4-fYx-gPm6uwFSrHEmIn-nwAeEpN3MQvYMj-N0pg1lxog»,»tw»:74 «id»:»BK0yq7Tx_Qh-_M:»,»ml»:»600″:»bh»:90,»bw»:63,»oh»:256,»ou»:» «,»ow»:176,»pt»:»cdneurokiorg/system/books/covers/000/002/249/mid»,»rh»:»eurokiorg»,»rid»:»zuefHolP2jEDhM»,»rt»:0,»ru»:» «,»sc»:1,»th»:100,»tu»:» \u003dtbn:ANd9GcQO9PLg32gS5bGjS0Jw_vm19LOGJunag16T5scMaakcL9RXyb2vecYBkw»,»tw»:69 «cr»:9,»ct»:3,»id»:»ouGPX2CnMVF9SM:»,»ml»:»600″:»bh»:90,»bw»:127,»oh»:175,»ou»:» «,»ow»:600,»pt»:»ds04infourokru/uploads/ex/045b/000a649a-a5fd2052″,»rh»:»infourokru»,»rid»:»7NtctqJUbHp_QM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcQAXUTk8XJSvngyNao2hXa9Ld4qV6EcrZaKs7mssEtqEickKSKh08FSkDg»,»tw»:309 Другие картинки по запросу «контрольные работы за 9 класс по геометрии атанасян» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты ГДЗ 775 номер геометрия 7‐9 класс ЛС Атанасян, ВФ Бутузов › ГДЗ › 7 класс › Геометрия › Атанасян ЛС › 775 Подробное решение номер 775 по геометрии для учащихся 7‐ 9 класса , авторов ЛС Атанасян , ВФ Бутузов, СБ Кадомцев Геометрия Самостоятельные и контрольные работы 9 класс › › Математика, Алгебра, Геометрия Оно ориентировано на учебник « Геометрия 7– 9 классы » авторов Л С и контрольные работы 9 класс Линия УМК: Геометрия Атанасян ЛС И др ГДЗ по Геометрии за 7‐9 класс самостоятельные и контрольные › › самостоятельные и контрольные работы Иченская ГДЗ по геометрии 7‐ 9 класс самостоятельные и контрольные работы Иченская МА ГДЗ к учебнику по геометрии за 7- 9 классы Атанасян ЛС Решебник (ГДЗ) дидактические материалы по геометрии 9 класс Зив › ГДЗ › 9 класс › Геометрия › БГ Зив Похожие Подробные решения контрольных и самостоятельных работ к дидактическим материалам по геометрии , автор БГ Зив, издательство Просвещение ГДЗ по геометрии 9 класс Атанасян › Геометрия › 9 класс Похожие Решебник по геометрии за 9 класс авторы Атанасян издательство Просвещение Самостоятельные и контрольные работы по геометрии 9 класс [PDF] Файл — Средняя общеобразовательная школа № 54 30astr-s54edusiteru/sveden/files/42d5d905-3f04-430d-90b7-6363170dd889pdf щеобразоват учреждений ЛС Атанасян , ВФ Бутузов, СБ Ка- домцев и др — 18-е изд Контрольные работы по геометрии : 9 класс : к учебнику ЛС Атанасяна вектора на число; • координаты середины и длина отрезка, за — Контрольная работа по геометрии 9 класс «Векторы» Все для 23 окт 2016 г — Данная работа составлена по учебнику Атанасян 7- 9 класс , для учащихся Контрольная работа геометрия понятие вектора 9 класс docx с привязкой к координатам, выйдите немного за пределы программы Атанасян Геометрия 7-9 классы Самостоятельные и ambookvoru//atanasyan-geometriya-79-klass-samostoyatelnye-i-kontrolnye-raboty Самостоятельные и контрольные работы / Иченская (Просвещение) всего за 167 руб Описание к товару: » Атанасян Геометрия 7- 9 классы ГДЗ по геометрии для 9 класс от Путина Похожие Геометрия 9 класс рабочая тетрадь Атанасян Геометрия 9 Геометрия 7- 9 классы самостоятельные и контрольные работы Иченская МА Геометрия Рабочая программа по геометрии, 9 класс, УМК: Атанасян ЛС Похожие 12 февр 2016 г — Программы по Геометрии для 9 класса по УМК Атанасян ЛС, Бутузов Кр №5 Итоговая контрольная работа за курс геометрии 9 класс Дидактический материал — Сайт учителя математики Збицкой Похожие Контрольные работы ориентированы на учебник » Геометрия , 7-9″ (ЛС Атанасян , ВФ Бутузов, СБ Кадомцев и др) 9 класс Алгебра Отправлено 11 Дидактические материалы по геометрии 9 класс Зив БГ — ГДЗ domashkasu/gdz/klass9/geometry/9-geometry-ziv Похожие Зив БГ Геометрия за 9 класс — ГДЗ Класс, 9 Учебник, Зив БГ Подробнее, Дидактические материалы по геометрии 9 класс Зив Контрольная работа Геометрия | Контрольные, тесты — ЗАВУЧинфо wwwzavuchru/methodlib/204/?pg=2 Похожие Разработаны контрольные работы по всем темам разного уровня Раздел: Геометрия — Контрольные, тесты 11 класс УМК Атанасян ЛС и др по геометрии за 4 четверть 8 класса к учебнику » Геометрия 7- 9 » Атанасян ЛС в Геометрия Атанасяна 9 класс — Школьный гид Состав УМК « Геометрия » 9 класс Атанасяна ЛС и др тесты, самостоятельные и контрольные работы (7- 9 классы ), методические Геометрия Рабочая тетрадь 9 класс Атанасян Л С, Бутузов В Ф, Глазков Ю А и др Геометрия в 7 классе, контрольные работы по Атанасяну за 1, 2, 3 Рейтинг: 4 — ‎59 голосов 4 апр 2017 г — Интерактивный тренажер по геометрии для 7, 8 и 9 классов к учебнику Контрольная работа №1 на тему: «Прямая на плоскости Углы» Геометрия 9 класс — InternetUrok Видеоуроки, тесты и тренажёры по Геометрия за 9 класс по школьной программе Используйте конспект уроков раздела « Геометрия 9 класс » для закрепления полученных знаний Измерительные работы · Решение задач по Геометрия, 9 класс: уроки, тесты, задания › Предметы › Геометрия Теоретические уроки, тесты и задания по предмету Геометрия , 9 класс Задания составлены профессиональными педагогами ЯКласс ▷ контрольная работа по геометрии 10 класс атанасян решебник wwwzstelceu//kontrolnaia-rabota-po-geometrii-10-klass-atanasian-reshebnikxml 6 нояб 2018 г — контрольная работа по геометрии 10 класс атанасян решебник по геометрии за 7‐ 9 класс ЛС Атанасян , ВФ gdzguru › Геометрия ГДЗ [DOC] Геометрия 7-9 классы wwweduportal44ru/ostrov/Adischevo/DocLib30/геометрия%207-9%20классdoc Похожие Из общего количества часов на тематические контрольные работы отводится 5 часов условием положительной аттестации ученика за курс основной школы Атанасян ЛС Геометрия Рабочая тетрадь для 9 класса Решебник для 9 класса по Геометрии на Гитем ми Решебник от Гитем для 9 класса по Геометрии не оставит в беде и поможет в решении Геометрия рабочая тетрадь ЛС Атанасян 9 класс Геометрия самостоятельные и контрольные работы Иченская МА 7- 9 класс Геометрия 7-11 классы: развернутое тематическое планирование Салова Т А — 2014 9 КЛАСС Рабочая программа учебного курса по геометрии для 9 класса составлена на 7– 9 классы : учеб для общеобразоват учреждений / Л С Атанасян [и др] проводится в 9 классе в форме итоговой контрольной работы Номер 1015 Геометрия 7 9 класс Атанасян — YouTube ▶ 4:53 22 апр 2014 г — Добавлено пользователем Алексей Подлесов Номер 1015 Геометрия 7 9 класс Атанасян Published on Apr 21, 2014 Решение задания из учебника по геометрии для 7, 8, 9 класса ГДЗ к сборнику Ершовой, Голобородько — math-helperru Математика Вводный курс: Учебное пособие Вечтомов Евгений Михайлович , ‎ Широков Дмитрий Владимирович — 2014 Атанасян Л С Геометрия 7– 9 классы : Учебник для общеобразовательных Практические занятия и контрольные работы : Учебное пособие – Киров: Геометрія 10 клас Профільний рівень: Розробки уроків — Перевести эту страницу Т Л Корнієнко , ‎ В І Фіготіна А С Атанасян , В Ф Бутузов, С Б Кадомцев и др В Самостоятельные и контрольные работы по геометрии для 10–11 классов 9 Роганін О М Геометрія 10 клас Академічний рівень: Комплексний зошит для контролю знань Контрольная работа по теме «Метод координат» 9класс, геометрия wwwopenclassru/node/83859 Похожие 24 дек 2009 г — Главная страница 7 Login Контрольная работа по теме «Метод координат» 9класс , геометрия , Атанасян ЛС Класс(ы): 9 класс Предмет(ы): Геометрия Целевая аудитория: Учитель (преподаватель) Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (46) Показать скрытые результаты Вместе с контрольные работы за 9 класс по геометрии атанасян часто ищут контрольные работы по геометрии 9 класс атанасян скачать бесплатно гдз контрольная работа по геометрии 9 класс атанасян готовые контрольные работы по геометрии 9 класс контрольная работа по геометрии 9 класс ответы атанасян контрольная работа по геометрии 9 класс атанасян решение контрольные работы по геометрии 9 класс мельникова ответы итоговая контрольная работа по геометрии 9 класс ответы контрольная работа по геометрии 9 класс векторы Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google

Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Контрольные работы по геометрии 9 класс ( Атанасян ) infourokru › kontrolnie…geometrii-klass-atanasyan… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Инфоурок › Математика › Рабочие программы › Контрольные работы по геометрии 9 класс ( Атанасян ) Контрольная работа № 7 Итоговая по курсу геометрии (7- 9 классы ) Читать ещё Инфоурок › Математика › Рабочие программы › Контрольные работы по геометрии 9 класс ( Атанасян ) Контрольные работы по геометрии 9 класс ( Атанасян ) библиотека материалов Контрольная работа №1 Векторы Контрольная работа №1 Векторы Вариант 1 Вариант 2 Контрольная работа № 7 Итоговая по курсу геометрии (7- 9 классы ) Контрольная работа № 7 Итоговая по курсу геометрии (7- 9 классы ) Вариант 1 Вариант 2 Скрыть 2 Контрольные работы по геометрии в 9 классе по multiurokru › files…raboty-po…v-9-klassie-pohtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы По геометрии В 9 классе По учебнику атанасян лс 3 Материал по геометрии ( 9 класс ) по теме: Контрольные nsportalru › Школа › Геометрия › …raboty-po-geometrii-9-kl Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Мною разработаны контрольные работы по геометрии для 9 класса по учебнику ЛС Атанасяна Использованная литература: Изучение геометрии в 7- 9 классах Пособие для учителей общеобразоват учреждений/ЛС Читать ещё Мною разработаны контрольные работы по геометрии для 9 класса по учебнику ЛС Атанасяна Использованная литература: Изучение геометрии в 7- 9 классах Пособие для учителей общеобразоват учреждений/ЛС Контрольная работа по геометрии 9 класс «Радианная мера угла» в контрольной работе представлено 4 различных варианта Пособие предназначено для учителей старших классов , которые ведут преподавание курса геометрии по учебнику ЛС Атанасяна » Геометрия 10-11″ издательства «Просвещение» Демоверсии контрольных работ по геометрии , 9 класс Контрольные работы , демоверсии которых представлены, составлены в 4 вариантах к учебнику ЛС Атанасян Скрыть 4 ГДЗ по геометрии 9 класс самостоятельные eurokiorg › …9_klass…raboty-po-geometrii…atanasyan… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение Для планомерной и эффективной подготовки к сдаче итоговой аттестации в 9 -м классе (ОГЭ по математике) важно глубоко и полно проработать все темы входящих в экзамен дисциплин Особенно много трудностей Читать ещё ГДЗ самостоятельные и контрольные работы по геометрии 9 класс Иченская Просвещение Для планомерной и эффективной подготовки к сдаче итоговой аттестации в 9 -м классе (ОГЭ по математике) важно глубоко и полно проработать все темы входящих в экзамен дисциплин Особенно много трудностей вызывают задания по геометрии Проводя регулярный самостоятельный контроль своих знаний в течение года, девятиклассники будут более уверены, успешно подготовятся к испытанию Хорошее учебное пособие, способное помочь в достижении такого результата — самостоятельные и контрольные работы по геометрии для 9 класса , р Скрыть 5 Контрольные работы по геометрии 9 класс УМК uchitelyacom › …po-geometrii-9-klass…atanasyanhtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте по геометрии 9 класс , УМК ЛС Атанасян Учитель математики высшей категории Молодых Елена 2 Геометрия Самостоятельные и контрольные работы 7 – 9 классы Читать ещё по геометрии 9 класс , УМК ЛС Атанасян Учитель математики высшей категории Молодых Елена 2 Геометрия Самостоятельные и контрольные работы 7 – 9 классы : пособие для учителей общеобразовательных учреждений / М А Иченская Скрыть 6 Геометрия 9 класс Контрольные работы Мельникова allengorg › d/math/math2204htm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Оно содержит проверочные работы по всем темам, изучаемым в 9 классе , и ориентировано на учебник ЛС Атанасяна и др » Геометрия 7- 9 классы «, рекомендованный Министерством образования и науки Российской Федерации и включенный в Федеральный перечень учебников Читать ещё Оно содержит проверочные работы по всем темам, изучаемым в 9 классе , и ориентировано на учебник ЛС Атанасяна и др » Геометрия 7- 9 классы «, рекомендованный Министерством образования и науки Российской Федерации и включенный в Федеральный перечень учебников Каждая проверочная работа дается в четырех вариантах Кроме того, по каждой теме дается набор заданий для подготовки к контрольной работе Каждый вариант включает задания трех видов: с выбором ответа, с кратким ответом и с развернутым ответом, что соответствует формам заданий , используемым в настоящее время в экзаменационных раб Скрыть 7 Контрольные работы по геометрии 9 класс Атанасян learn-portalru › …raboty…geometrii…klass/atanasjan Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы на темы: Векторы Контрольные работы по геометрии для 9 класса по учебнику Атанасян ЛС Читать ещё Контрольные работы на темы: Векторы Метод координат Контрольные работы по геометрии для 9 класса по учебнику Атанасян ЛС © 2014 — 2015 «Образовательный портал» Использование материалов сайта возможно только с разрешения администрации портала Скрыть 8 Сборник контрольных работ по геометрии , ( 9 класс ) урокрф › library/sbornik…rabot_po_geometrii…klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник Контрольных рабор по геометрии 9 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний Читать ещё Сборник Контрольных рабор по геометрии 9 класс Пояснительная записка Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию Контрольная работа №1 9 класс Тема: «Векторы на плоскости» Цель: проверить уровень усвоения ГОСО Скрыть 9 Контрольные работы за 9 класс по геометрии Атанасян — смотрите картинки ЯндексКартинки › контрольные работы за 9 класс по геометрии Пожаловаться Информация о сайте Ещё картинки 10 Контрольные работы по геометрии 9 класс easyenru › …9_klass/kontrolnye_raboty_po_geometrii… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Архив содержит четыре контрольные работы по темам, изучаемым в 9 классе по учебнику ЛС Атанасян и др По кнопке ниже вы можете скачать Контрольные работы по геометрии 9 класс категории Математика 9 класс бесплатно Будем благодарны, если вы оставите отзыв или посмотрите еще другие Читать ещё Архив содержит четыре контрольные работы по темам, изучаемым в 9 классе по учебнику ЛС Атанасян и др Геометрия 7- 9 (Учебник для общеобразовательных учреждений – М: Просвещение,2014), а так же итоговую контрольную работу Каждая контрольная работа дается в двух вариантах Все контрольные работы состоят из двух частей — обязательной и дополнительной Все задания оцениваются традиционно по пятибальной системе © Молодых Елена Николаевна По кнопке ниже вы можете скачать Контрольные работы по геометрии 9 класс категории Математика 9 класс бесплатно Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте Документ является конспект Скрыть Контрольные работы по геометрии 9 класс matematika-proru › tests…the-geometry…grade-9html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы по геометрии для 9 класса дают возможность контролировать качество усвоения В 9 классе происходит дальнейшее усвоение знаний по геометрии , основанное на базе материала, изученного в 7 и 8 классах Успех процесса обучения геометрии в немалой степени зависит от Читать ещё Контрольные работы по геометрии для 9 класса дают возможность контролировать качество усвоения учебного материала В 9 классе происходит дальнейшее усвоение знаний по геометрии , основанное на базе материала, изученного в 7 и 8 классах Успех процесса обучения геометрии в немалой степени зависит от правильно организованного контроля знаний и умений учащихся Основная цель проводимых мною контрольных работ по геометрии состоит в следующем: Выявить уровень овладения учащимися знаниями и умениями, предусмотренными программой по геометрии в 9 классе ; На основании полученных результатов спланировать работу по коррекции знаний учащихся Скрыть Вместе с « контрольные работы за 9 класс по геометрии атанасян » ищут: контрольная работа курсовые работы заказать контрольные работы готовые контрольные работы контрольная контрольная работа по математике готовые контрольные работы для студентов заочников бесплатно контрольная работа по математике 6 класс контрольная работа по алгебре 7 класс контрольная работа по математике 5 класс 1 2 3 4 5 дальше Браузер Все новые вкладки с анимированным фоном 0+ Скачать

ГДЗ по Геометрии за 7‐9 класс Л.

С. Атанасян, В.Ф. Бутузов

авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин.

Издательство: Просвещение 2016 год.

Как у вас обстоят дела с геометрией? Ищете качественную помощь, или наоборот считаете, что вы так хорошо знаете этот предмет, что помощь вам попросту не нужна? В любом случае рекомендуем вам рассмотреть возможность использования

решебника по алгебре для 7-9 класса под авторством Атанасяня Л.С.В.Ф. Бутузова,С.Б. Кадомцева, который позволит делать следующее:

  • выполнять домашнее задание любой сложности за считанные минуты;
  • перепроверять самостоятельно выполненное задание на наличие ошибок и опечаток, чтобы избежать плохих оценок;
  • готовиться к контрольным работам и экзаменам;
  • учиться самостоятельности, ведь теперь при возникших сложностях не придется бежать за помощью к родителям или учителям, верные ответы всегда под рукой;
  • изучать любую тему в домашних условиях, для этого достаточно лишь ознакомиться с теорией, а после уделить время практической части из этого же раздела.

Такая полезная книга позволит школьнику не просто освободить время для более интересных занятий, но также значительно улучшить свои знания и выйти на новый уровень обучения.

Также онлайн-решебник по алгебре от автора: Атанасян Л.С. станет просто незаменим для родителей, которые предпочитают контролировать успехи своего ребенка. Теперь, даже неважно помните ли вы уроки по математике, или изучали ли ее вообще. Благодаря подробным, грамотным и проверенным по нормам ФГОС ответам родитель сможет объяснить любую тему, достаточно только открыть ГДЗ и прочесть данные в них объяснения.

Книга с ответами находится в онлайн-доступе, а значит, вам не придется носить с собой бумажный вариант, достаточно просто иметь под рукой мобильный телефон с выходом в интернет. Такая возможность позволит брать правильные решения с собой на уроке и решать не только домашние задания, но и контрольные на отлично. Если учитель задал решить в тетрадке какой-то пример, а вы не понимаете принципы выполнения, но и двойку схлопотать не хотите, то просто ГДЗ на нужной странице и перепишите правильный вариант, а уже в свободное время займитесь разбором непонятной для вас темы.

ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно посмотреть тут.

ГДЗ Геометрия 8 класс рабочая тетрадь Атанасян можно посмотреть тут.

ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно посмотреть тут.

ГДЗ к дидактическим материалам по геометрии за 7 класс Зив Б.Г. можно посмотреть тут.

ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно посмотреть тут.

ГДЗ к дидактическим материалам по геометрии за 9 класс Зив Б.Г. можно посмотреть тут.

ГДЗ к самостоятельным и контрольным работам по геометрии за 7-9 классы Иченская М.А. можно посмотреть тут.

ГДЗ к контрольным и самостоятельным работам по алгебре и геометрии за 9 класс Журавлев С. Г. можно посмотреть тут.

ГДЗ к тетради контрольных тестовых работ по геометрии за 7 класс Парфентьева О.Н. можно посмотреть тут.

ГДЗ к тетради контрольных тестовых работ по геометрии за 8 класс Стокоз В.И. можно посмотреть тут.

ГДЗ к тетради контрольных тестовых работ по геометрии за 9 класс Покатаева Г.В. можно посмотреть тут.

ПОЛОСА: 7-8 Область: Геометрия. Почему эта область является приоритетной для профессионального развития  последовательность из 8-го класса в старшую школу. Геометрия — это смена.

  • Дом
  • Документы
  • ПОЛОСА УРОВНЯ: 7-8 Область: Геометрия. Почему эта область является приоритетной для профессионального развития  последовательность из 8-го класса в старшую школу. 344 x 292429 x 357514 x 422599 x 487

    TRANSCRIPT

    • Slide 1
    • GRADE BAND: 7-8 Domain: Geometry
    • Slide 2
    • Почему этот домен является приоритетным для последовательного профессионального развития от 8 класса до старшей школы геометрия — это переход от прежних государственных стандартов к обычным базовым стандартам. Студентов просят понять, как использовать перевод, вращение, преобразование. ТРАНСФОРМАЦИОННАЯ ГЕОМЕТРИЯ ВОЗМОЖНО ОДНО ИЗ САМЫХ БОЛЬШИХ ОТЛИЧИЙ ОТ ПРЕДЫДУЩИХ СТАНДАРТОВ / ОБУЧЕНИЯ К ОБЩЕМУ ЯДНУ (ИЗМЕНЕНИЕ ДЛЯ УЧАЩИХСЯ, УЧИТЕЛЕЙ, И ПРЕПОДАВАТЕЛИ УЧИТЕЛЕЙ).ПРОБЛЕМЫ ВКЛЮЧАЮТ ВНИМАНИЕ К ТОЧНОСТИ И ЯЗЫКУ.
    • Slide 3
    • Ключевые стандарты в этой области, на которых PD должна сосредоточиться Q: Какие темы существуют в разных штатах в отношении потребностей PD? В: Как слова на бумаге передают необходимую педагогику? В: Какая подготовка по ПД требуется (для тех, кто занимается ПД учителям)? В: Какой опыт нужно дать учителям для развития фундаментальных знаний? (прогрессии, задания, видео / динамические иллюстрации, студенческие работы, комментарии, связывающие их вместе). Опишите эффекты расширений, переводов… длина / углы внимания. Трансформационный подход к области сходства, в которой существует огромная потребность в разных государствах. 8.G.6. Объясните доказательство теоремы Пифагора и ее обратного
    • Slide 4
    • Существующие ресурсы, которые поддерживают эти области и стандарты Некоторые материалы в рамках текущего полевого тестирования (материалы для видеокассет «Learning and Teaching Geometry») Fositing Geometric Thinking (Driscoll)
    • Slide 5
    • Области и стандарты, которые нуждаются в новых ресурсах, которые необходимы PD для создания видения математических классов (видео или другие средства наблюдения за происходящим). Кроме того, они должны испытать это на себе.Руководство о том, что означает доказательство (объяснение, доказательство, обоснование) в средней школе (примеры). В: Что учителя должны понимать в геометрии нового? Какие возможности есть у учителей думать о точности? Как они возвращают новые знания в свои классы? 8.EE 6. Используйте похожие треугольники, чтобы объяснить, почему угол наклона m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости … 8.G.5 …. угловой критерий сходства треугольников

    Готовое домашнее задание для 8 класса

    Готовое домашнее задание помогает учащимся и родителям быстрее справляться с домашним заданием на конкретных примерах.Сайт ГДЗ: https://gdz.life/