Входная контрольная алгебра 8 класс: Входная контрольная работа по алгебре 8 класс

Входная контрольная работа по алгебре 8 класс

Входная контрольная работа по алгебре

Вариант 1

1. Упростите выражение:

а) ; б) ; в) .

2. Разложите на множители:

а); б) ; в) 3 — 3 — а + в.

3. Постройте график функции и укажите координаты точек его пересечения с осями координат.

4. Решите систему уравнений .

5. Решите уравнение: а) ; б) 3х – 5(2х + 1) = 3(3 – 2х)

6. Из деревни в город, расстояние между которыми 120 км, выехал мотоциклист. Через 1,5 ч из города ему на встречу выехала машина и встретила мотоциклиста через 0,5 ч после своего выезда. Найдите скорость мотоциклиста и скорость машины, если скорость машины на 10 км/ч больше скорости мотоцикла.

7*. Докажите, что верно равенство

(а +с)(а – с) – в(2а –в) – (а – в + с)(а – в – с) = 0.

____________________________________________________________________________

Входная контрольная работа по алгебре

Вариант 2

1. Упростите выражение:

а) ; б) ; в) .

2. Разложите на множители:

а); б) , в) х – у -2 + 2.

3. Постройте график функции и укажите координаты точек его пересечения с осями координат.

4. Решите систему уравнений .

5. Решите уравнение; а) ; б) 4(1 – 5х) = 9 – 3(6х – 5).

6. Из пункта А в пункт В, расстояние между которыми 14 км, вышел пешеход. Через 1,5 ч из пункта В в пункт А выехал велосипедист со скоростью на 8 км/ч больше, чем скорость пешехода. Найдите скорость пешехода и велосипедиста, если велосипедист встретил пешехода через 0,5 ч после своего выезда.

7*. Докажите, что верно равенство

(х – у)(х + у) – (а – х + у)(а – х – у) – а( 2х – а) = 0.

Входная контрольная работа по алгебре 8 класса

Входная контрольная работа по алгебре

Вариант 1.

Часть А. (по 1 баллу)

1. Сколько процентов составляет число 16 от 200.
2. Найдите значение выражения: .
3. Упростите выражение и найдите его значение: .
4. Найдите корень уравнения:
5. Найдите среднее арифметическое, размах и моду ряда чисел: 32, 26, 18, 26, 15, 21, 26 .
6. Найдите медиану ряда чисел: 30, 32, 37, 40, 41, 42, 45, 49, 59 .
7. Найдите область определения функции, заданной формулой:
8. Вычислите:        а) ,           б) 
9. Найдите наибольший общий делитель чисел:  765 и 315 .
10. Найдите наименьшее общее кратное чисел:   60 и 75 .
11. Выполните преобразование по соответствующей формуле:  а) ,  б)
12. Разложите многочлен на множители:

 

Часть B. (по 2 балла)

1. В одной кассе кинотеатра продали на 36 билетов больше, чем в другой. Сколько билетов продали в каждой кассе, если всего было продано 392 билета?
2. Постройте график функции, заданной формулой: .
3. Найдите значение выражения:   .
4. Найдите координаты точки пересечения графиков линейных функций:

  и  .

5. Разложите на множители: 
6. Решите систему уравнений: 

 

Меньше 7 баллов – 2    

7-12 б   — 3

13- 16 б – 4

17 – 20б  —  5

 

 

 

Входная контрольная работа по алгебре

Вариант 2.

Часть А. (по 1 баллу)

1. Сколько процентов составляет число 32 от 400.
2. Найдите значение выражения: 8 .
3. Упростите выражение и найдите его значение: .
4. Найдите корень уравнения:
5. Найдите среднее арифметическое, размах и моду ряда чисел: 0.6, 0.8, 0.5, 0.9, 0.6, 1.1 .
6. Найдите медиану ряда чисел: 16, 18, 20, 22, 24, 26 .
7. Найдите область определения функции, заданной формулой:
8. Выполните действие:       
9. Найдите наибольший общий делитель чисел:  864 и 648 .
10. Найдите наименьшее общее кратное чисел:   72, 80 и 96 .
11. Выполните преобразование по соответствующей формуле:  а) ,  б)
12. Разложите многочлен на множители: 

 

Часть B. (

по 2 балла)

1. В трёх седьмых классах 103 ученика. В 7 «Б» на 4 ученика больше, чем в 7 «А», и на 2 ученика меньше, чем в 7 «В». Сколько учеников в каждом классе?
2. Постройте график функции, заданной формулой: .
3. Найдите значение выражения:   .
4. Найдите координаты точки пересечения графиков линейных функций:   и  .
5. Замените знак * одночленом так, чтобы получившееся равенство было тождеством:

6. Решите систему уравнений:  

 

Меньше 6 б – 2

7-12 б   — 3

13- 16 – 4

17 – 20 —  5

Входная контрольная работа по алгебре 8 класс

Входная контрольная работа

Цель: проверить уровень остаточных знаний за курс 7 класса.

Предметные: проверить остаточные знания.

Личностные: формирование навыков самооценки результатов своей работы, умение признавать собственные ошибки.

Познавательные: ориентироваться в своей системе знаний: самостоятельно предполагать, какая информация нужна для решения учебной задачи, делать выводы. Перерабатывать полученную информацию: делать выводы на основе обобщения знаний.

Коммуникативные: правильно оформлять работу.

Регулятивные: работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки.

Работа состоит из 8 заданий и направлена на проверку достижений уровня базовой подготовки. С помощью анализа результатов выполнения предложенных заданий проверяется знание и понимание важных элементов содержания (вычислительных навыков, алгоритм решения систем уравнений, знание формул сокращенного умножения, знание правил выполнения действий с алгебраическими выражениями, способов разложения многочленов на множители) и применение знания к решению математических задач, применение знаний в простейших практических ситуациях.

При выполнении заданий учащиеся должны продемонстрировать системность знаний, узнавать стандартные задачи в разнообразных формулировках.

Работа включает в себя 8 заданий. Каждое задание с 1 по 7 оценивается в 1 балл, задание 8 оценивается 2 баллами. На выполнение работы дается 1 урок (40 – 45 минут).

Баллы	Критерии оценки выполнения задания 8
2	Правильно выполнен и оформлен чертеж, верно найдены координаты точек пересечения графика с осями координат
1	Правильно выполнен и оформлен чертеж, неверно найдены координаты точек пересечения графика с осями координат
0	Все случаи решения, не соответствующие указанным выше критериям выставления оценок в 1 или 2 балла.

Таблица перевода баллов в отметки по пятибалльной шкале

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Баллы	0 – 3 баллов	4 – 5 баллов	6– 7 баллов	8 – 9 баллов

Вариант 1.

Найдите значение выражения: 8 ∙ х3 – ∙ у2, при х = – , у = – 5.

2. Решите систему уравнений:

3. Упростите выражение: (2∙а + b) ∙ (3∙a – 4∙b) – 6 (a – b)2.

4. Упростите выражение: (–2∙х2 ∙у)3 ∙ ( –4∙х3 ∙у)2.

5. Разложите на множители: x∙y + x∙z – x.

6. Разложите на множители: 9∙a2 – b2 + 3∙a – b.

7. Велосипедист ехал 2 ч по проселочной дороге и 1ч по шоссе. Всего он проехал 28 км. С какой скоростью велосипедист ехал по проселочной дороге и с какой по шоссе, если известно, что его скорость по шоссе была на 4 км/ч больше, чем скорость по проселочной дороге?

8. Постройте график функции, заданной формулой у = 0,5х – 2. С помощью графика найдите координаты точек пересечения графика с осями координат.

Вариант 2.

Найдите значение выражения: 4 ∙ х2 – ∙ у3, при х = – , у = – 4.

Решите систему уравнений:

3. Упростите выражение: (3∙а – 2∙b) ∙ (2∙а + b) – 6 ∙ (a + b)2.

4. Упростите выражение: (–4∙х3 ∙ у2)3 ∙ (2∙х4 ∙ у)2.

5. Разложите на множители: a + ab – ac.

6. Разложите на множители: 4∙х + у + 16∙х2 – у2.

7. Пешеход прошел расстояние от станции до поселка за 5 ч, а велосипедист проехал это же расстояние за 2 ч. Скорость велосипедиста на 6 км/ч больше скорости пешехода. Найдите скорость пешехода и скорость велосипедиста?

8. Постройте график функции, заданной формулой у = – х + 1. С помощью графика найдите координаты точек пересечения графика с осями координат.

Входная контрольная работа по алгебре 8 класс

Входной контроль по алгебре 8 класс

ВАРИАНТ 1   ЧАСТЬ А

1.    Найдите значение выражения  при а= -1,5; b=1

2.    Упростите выражение 3ху-3х-(х+3ху).

3.    Представьте выражение (5a-2)² в виде многочлена.

4.    Выполните умножение: (5b-3а)(5b+3а)

5.    Вынесите за скобки общий множитель 15a³-3a²b

ЧАСТЬ В

6.    Решить уравнение 2х-7=10-3(х+2)

7.    Упростить выражение  х⁵(х²)⁴

8.    Упростить выражение (а-4)²-а(2а-8)

9.    Разложить на множители 2ху+6у-хс-3с

10.              Изобразите на координатной плоскости множество точек, удовлетворяющих условию: у=2х-3

ЧАСТЬ С

11.              Решить уравнение  –  

12.              В 15 одинаковых пакетов и 5 одинаковых коробок расфасовали 2400 г конфет. В каждую коробку уместилось на 20 г конфет больше, чем в каждый пакет. Сколько граммов конфет было в каждом пакете и каждой коробке?

 

Входной контроль по алгебре 8 класс ВАРИАНТ 2    ЧАСТЬ А

1.    Найдите значение выражения  при а= 1,5; с= -3,5

2.    Упростите выражение:  -6х+5ху-2(х+2ху).

3.    Представьте выражение (3a-2)² в виде многочлена.

4.    Выполните умножение: (7-9b)(7+9b)

5.    Вынесите за скобки общий множитель 15ab²-6b

ЧАСТЬ В

6.    Решить уравнение 5x+12-3(x+16)= -20

7.    Упростить выражение  (у³)⁵у²

8.    Упростить выражение (2b+c)²-b(4b-3c)

9.    Разложить на множители  ab+3ac-2b-6c

10. Изобразите на координатной плоскости множество точек, удовлетворяющих условию: у=3х+1

ЧАСТЬ С

11. Решить уравнение  +  

12. Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил свою работу за 5 ч, а второй за 4 ч, так как изготовлял на 12 деталей в час больше второго. Сколько деталей изготовил каждый рабочий?

 

 

 

Входной контроль по алгебре 8 класс

ВАРИАНТ 1   ЧАСТЬ А

1.    Найдите значение выражения  при а= -1,5; b=1

2.    Упростите выражение 3ху-3х-(х+3ху).

3.    Представьте выражение (5a-2)² в виде многочлена.

4.    Выполните умножение: (5b-3а)(5b+3а)

5.    Вынесите за скобки общий множитель 15a³-3a²b

ЧАСТЬ В

6.    Решить уравнение 2х-7=10-3(х+2)

7.    Упростить выражение  х⁵(х²)⁴

8.    Упростить выражение (а-4)²-а(2а-8)

9.    Разложить на множители 2ху+6у-хс-3с

10.              Изобразите на координатной плоскости множество точек, удовлетворяющих условию: у=2х-3

ЧАСТЬ С

11.              Решить уравнение  –  

12.               В 15 одинаковых пакетов и 5 одинаковых коробок расфасовали 2400 г конфет. В каждую коробку уместилось на 20 г конфет больше, чем в каждый пакет. Сколько граммов конфет было в каждом пакете и каждой коробке?

Входной контроль по алгебре 8 класс ВАРИАНТ 2    ЧАСТЬ А

1.    Найдите значение выражения  при а= 1,5; с= -3,5

2.    Упростите выражение:  -6х+5ху-2(х+2ху).

3.    Представьте выражение (3a-2)² в виде многочлена.

4.    Выполните умножение: (7-9b)(7+9b)

5.    Вынесите за скобки общий множитель 15ab²-6b

ЧАСТЬ В

6.    Решить уравнение 5x+12-3(x+16)= -20

7.    Упростить выражение  (у³)⁵у²

8.    Упростить выражение (2b+c)²-b(4b-3c)

9.    Разложить на множители  ab+3ac-2b-6c

10. Изобразите на координатной плоскости множество точек, удовлетворяющих условию: у=3х+1

ЧАСТЬ С

11. Решить уравнение  +  

12. Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил свою работу за 5 ч, а второй за 4 ч, так как изготовлял на 12 деталей в час больше второго. Сколько деталей изготовил каждый рабочий?

 

ГДЗ контрольные работы по алгебре 8 класс Александрова Мнемозина

Заблаговременно готовясь к контрольным по ведущим предметам, восьмиклассники смогут рассчитывать на более высокий балл и уверенные знания по изучаемым параграфам и темам. В числе эффективных помощников в такой практике – гдз по алгебре за 8 класс контрольные работы Александрова, работу с которыми следует проводить системно и качественно. Желательно приступать к разбору каждого задания по вынесенной на проверку тематике не позднее, чем за две-три недели до намеченной даты контроля. Также в числе важных факторов успеха – ежедневные занятия, минимум по часу в день.

Кому пригодится решебник в первую очередь?

Среди тех, кто часто или на постоянной основе применяет онлайн ответы по алгебре 8 класс к контрольным работам Александрова в своей практике, такие пользователи:

• восьмиклассники, часто пропускающие уроки по причине болезни, посещения спортивных или творческих мероприятий и конкурсов. Чтобы систематизировать свои теоретические знания, эти подростки применяют данный решебник;
• переведенные на дистанционную форму обучения школьники или те, кто учится в формате домашнего/семейного образования. Для них материал станет источником дополнительных знаний в условиях ограниченного доступа к объяснению тем и разделов, порядка выполнения заданий учителем;
• школьные педагоги, которым необходимо в течение короткого времени проверить значительное количество сданных учениками контрольных работ. Учитывая, что сегодня учителя загружены дополнительной срочной работой (отчетной, плановой и пр.), им крайне важно выполнить проверку в кратчайший срок, не теряя в качестве. И этот источник информации для них актуален и необходим;
• родители восьмиклассников, которые желают проверить степень готовности своего ребенка к контрольным и проверочным, не вникая глубоко в тематику вынесенных на контроль заданий.

Доводы в защиту онлайн справочников

Хотя некоторые родители и учителя крайне негативно относятся к еуроки ГДЗ, утверждая, что дети списывают чужие решения, не вникая в их суть, этот взгляд является достаточно поверхностным и неубедительным. В числе аргументов в пользу этого источника:

• его доступность для всех пользователей, круглосуточно, каждый день;
• возможность заменить им дорогостоящую помощь репетиторов, кружки и курсы;
• соответствие данных, представленных в решебнике, требованиям образовательных Стандартов, в том числе – к порядку оформления работ;
• удобный формат поиска, позволяющий оперативно отыскать нужный ответ и воспользоваться им в условиях ограниченного времени.

Внедряя правильные решения контрольных работ по алгебре за 8 класс Александрова в свою практику, восьмиклассники учатся самостоятельно работать с информацией: находить её, выбирать, сравнивать, анализировать и использовать по назначению. Это пригодится школьникам в настоящем и будущем.

ГДЗ по алгебре 8 класс контрольные Александрова (Мордкович) Базовый

Готовое домашнее задание авторы разной классификации, составляют по различным предмету от начальных до старших классов. Оно даёт возможность ученикам закрепить полученные знания в школе и самостоятельно изучить дополнительный материалы для себя. Довольно часто ГДЗ по алгебре 8 класс, контрольные работы, базовый уровень от Александровой Л.А., используют как помощь с верными ответами, перепроверяют свою работу и получить хорошие оценки.

Но главное правило решебника по Алгебре за 8 класс, созданный Александровой Л.А усвоить, развить и закрепить материал учащимися 8 класса.

Описание учебно-методического пособия контрольные работы по алгебре за 8 класс Александрова ФГОС Базовый уровень

Рабочая программа, составленная по всем требованиям ФГОС по алгебре, состоит из разносторонних заданий для успешного преодоления пробелов в знаниях и развитию способностей в решении сложного уровня решения. В целом в него входит упражнений порядка 1600. Тесты – вопрос с одним или несколькими вариантами верного (правильного) ответа, включены в одно задание, требующее решения, согласно правилам. Контрольные работы – систематическая пошаговая задача по ФГОС, разделенная на несколько вариантов и имеющая несколько номеров для тщательного решения. Решение заданий – в данном пункте расписаны всевозможные задачи простой, средней и высокой сложности, решение которых, даёт возможность каждому школьнику в силу своих знаний, попрактиковаться и сформировать новые знания, умения и навыки, они станут хорошей платформой для успешной учебы в школе.

Сборник по алгебре для 8 класса (автор: Александрова Л.А.) , помимо всего поможет родителям быстро проверить работу сына или дочери, даже не имея математический склад ума. Преимущества решебника:

1. В рабочую программу за 8 класс, встроена система изучения в онлайн-режиме.
2. Учителям, упрощается работа, при проверке домашних работ учащихся, на это уходит меньшее количество времени.
3. Хитрость и продуманность учеников, позволила активно использовать её в своих интересах. Выполняя уроки дома намного быстрее, и за это получая поощрительные хорошие отметки и похвалы от родителей.
4. Так же для проверки выполненной работы при помощи ГДЗ по алгебре за 8 класс контрольные работы Александрова Л.А. Базовый уровень подходит и для родителей пригласив ребёнка, разобрать проблемные моменты.

Входная контрольная работа по алгебре (8 класс)

Входная контрольная работа по алгебре

Вариант 1

1. Упростите выражение:

а) ; б) ; в) .

1. Разложите на множители:

а) ; б) ; в) 3 — 3 — а + в.

1. Постройте график функции и укажите координаты точек его пересечения с осями координат.

2. Решите систему уравнений .

3. Решите уравнение: а) ; б) 3х – 5(2х + 1) = 3(3 – 2х)

4. Из деревни в город, расстояние между которыми 120 км, выехал мотоциклист.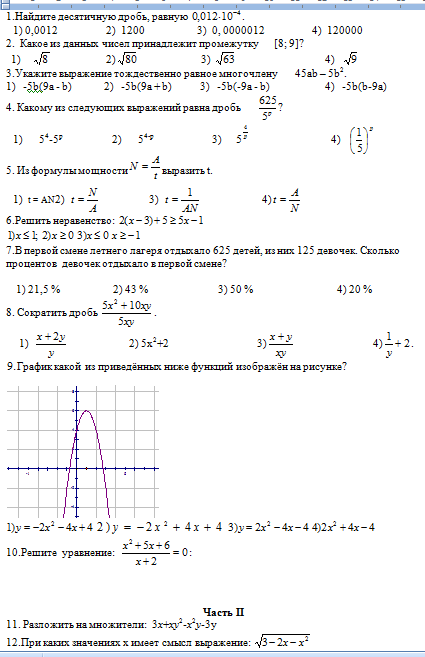 Через 1,5 ч из города ему на встречу выехала машина и встретила мотоциклиста через 0,5 ч после своего выезда. Найдите скорость мотоциклиста и скорость машины, если скорость машины на 10 км/ч больше скорости мотоцикла.

7*. Докажите, что верно равенство

(а +с)(а – с) – в(2а –в) – (а – в + с)(а – в – с) = 0.

____________________________________________________________________________

Входная контрольная работа по алгебре

Вариант 2

1. Упростите выражение:

а) ; б) ; в) .

1. Разложите на множители:

а) ; б) , в) х – у -2 + 2 .

1. Постройте график функции и укажите координаты точек его пересечения с осями координат.

2. Решите систему уравнений .

3. Решите уравнение; а) ; б) 4(1 – 5х) = 9 – 3(6х – 5).

4. Из пункта А в пункт В, расстояние между которыми 14 км, вышел пешеход. Через 1,5 ч из пункта В в пункт А выехал велосипедист со скоростью на 8 км/ч больше, чем скорость пешехода. Найдите скорость пешехода и велосипедиста, если велосипедист встретил пешехода через 0,5 ч после своего выезда.

7*. Докажите, что верно равенство

(х – у)(х + у) – (а – х + у)(а – х – у) – а( 2х – а) = 0.

____________________________________________________________________________

Определение входов и выходов функций — видео и стенограмма урока

Табличные функции

В алгебре таблица обычно имеет столбец цифр, слов или символов, которые представляют входы функции, и еще один столбец вещей, которые представляют выходы. Набор значений — это та группа, которая включает в себя все подходящие значения, но не имеет дополнительных элементов, которые не принадлежат. Посмотрите на пример здесь:

. Вы можете видеть, что набор входных значений, показанный в левом столбце, будет состоять из букв A, B и C.Набор выходных значений будет состоять из чисел 1, 2 и 3.

В алгебре функции часто имеют имя и переменную, которые предназначены для воздействия. Например, в таблице здесь входным параметрам присваивается переменная x , а имя функции — f (x) или «функция f , которая действует на переменную x. »

Графики

График — это изображение, которое представляет математическую взаимосвязь. Например, этот первый график, показанный здесь, использует две линии для сравнения расстояния, пройденного между двумя разными кораблями за определенный период времени.

График 1

На подобном графике шкала и единицы для входных значений будут отмечены в нижней части графика, а шкала и единицы для выходных значений будут отмечены слева. Если вы посмотрите на любую точку на графике, вы можете определить ее входное и выходное значение, сравнив ее положение со шкалами входных и выходных данных. Например, если вы посмотрите на синюю линию для Serendipity, вы увидите, что, когда она достигает входного значения 10 часов пути, она пересекает выходное значение 30 миль пройденного пути.Введенные 10 часов в пути дали результат в 30 миль.

Какие входные данные возможны для нашего графика? Вы можете видеть, что обе линии начинаются с 0 и тянутся до края графика. Это означает, что пройденное время будет не менее 0. Расстояние также начинается с 0 и увеличивается со временем, что говорит о том, что возможные выходные значения также являются любыми значениями, большими или равными 0.

Алгебраические выражения

Алгебраические функции — это алгебраические выражения, комбинации букв и чисел, которые представляют вычисления.Эти функции могут ограничивать соответствующие входные данные, например, указывать, что входные данные должны быть больше 0 или что входные данные должны быть целыми числами, но часто вы можете использовать любое значение для ввода, которое хотите. Например, если вы знаете, что f (x) = x + 1, вы можете поставить «1» для x , а затем посмотреть, что произойдет. Эта конкретная функция требует, чтобы вы добавляли 1 к любому входному значению, которое вы ей даете, поэтому ваше входное значение 1 даст выход 2. Поскольку это выражение позволяет вам вводить любое значение, которое вы хотите, как набор входных данных, так и набор выходов бесконечны.Возможна любая стоимость.

Некоторые примеры из реальной жизни

Функции, с которыми вы сталкиваетесь в реальной жизни, часто можно оформить в виде вопросов и ответов. Например, если вы купите пачку DVD по 10 долларов каждый, сколько это будет стоить? Количество DVD, которые вы покупаете (ввод), определяет, сколько денег он стоит (вывод). Если вы пробежите определенное расстояние, сколько времени это у вас займет? Если вы знаете, что в среднем вы бежите пять миль в час, то время, которое потребуется (вывод), будет зависеть от пройденного вами расстояния (ввод). Выход всегда зависит от входа, а вход управляет выходом.

Функции также могут отображаться как отношения. Например, в каждом штате Соединенных Штатов Америки есть столица. Если вы хотите узнать название столицы штата Северная Дакота (ввод), вы можете посмотреть таблицу, которая показывает, что Бисмарк (вывод) является столицей. Обратите внимание, что в этой функции набор возможных входов — это 50 штатов Америки, а набор возможных выходов — это 50 столиц.

Резюме урока

Хорошо, давайте на минутку вспомним, что мы узнали. В математике функция — это виртуальная «машина», которая дает ровно один ответ на любое число или выражение, которое вы ей даете. Мы также узнали, что информация, которую вы предоставляете, — это ввод , а информация, которую производит «машина», — это вывод . Любое выражение, которое дает ровно один ответ для любого заданного ввода, можно рассматривать как функцию.

Затем мы узнали, что таблица даст вам столбец входных значений и соответствующий столбец выходных значений, а график — это изображение числовой связи. На графике входные значения — это причины, а выходные — следствия. В алгебраической функции входными значениями являются все числа, которые не были исключены выражением и имеют смысл для выражения. Выходы — это то, что вы получаете, когда применяете выражение к входам. Наконец, набор значений включает все значения, которые верны для ситуации, исключая все остальные.

Математика Стандарты учебных ресурсов

Ваш браузер не поддерживает джаваскрипт! Этот сайт использует JavaScript, но полностью работает без него.Стандарты обучения (SOL) и тестирования

Новости и объявления

НОВИНКА! Virtual Just in Time Mathematics Quick Checks

Virtual Just in Time Mathematics Quick Checks (Virtual JIT QCs) предоставляются Департаментом образования Вирджинии (VDOE) для облегчения использования Just in Time Mathematics Quick Checks при преподавании и обучении в виртуальной среде. Педагоги штата Вирджиния со всего штата создали виртуальную версию для каждой быстрой проверки по математике. В марте / апреле 2021 года группа руководителей учителей из Вирджинии помогла VDOE провести проверку виртуальных JIT QC, связанных в этой виртуальной оперативной математической быстрой проверке — это таблица Excel. (XLSX) таблица. Эти виртуальные JIT QC в максимально возможной степени отражают оригинальные своевременные математические быстрые проверки, с изменениями, которые вносятся только в случае необходимости для использования в виртуальной среде.В настоящее время виртуальные JIT QC доступны для детского сада через алгебру I, а ссылки для геометрии и алгебры II будут добавлены в электронную таблицу, как только будет завершен процесс проверки этих ресурсов. Вопросы о виртуальных быстрых проверках по математике точно в срок следует направлять по адресу [email protected].

НОВИНКА! Стандартные документы по математике

Стандартные документы по математике (K-8) были созданы как часть ресурсов Virginia LEARNS, чтобы помочь в выявлении контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися. Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.

Теперь доступны

журналов отслеживания учебных стандартов по математике (с 2020-2021 учебного года по 2021-2022 учебный год)!

Журналы отслеживания для оценок от детского сада до алгебры II были разработаны, чтобы помочь учителям определить, какие стандарты учащиеся имели достаточный уровень знаний и опыта в течение 2020-2021 учебного года.Эти журналы могут помочь в принятии решений относительно того, когда и как можно будет познакомиться с новыми стандартами в 2021-2022 учебном году.

Информационные сессии сообщества Инициативы по математике в Вирджинии

В течение следующих нескольких месяцев будет проведена серия одночасовых информационных сессий сообщества VMPI, чтобы предоставить родителям и членам сообщества возможность узнать больше об Инициативе Вирджиния по математике. Заседания пройдут в следующие даты:

.

• Вторник, 23 марта 2021 г. — Зачем менять инструкции по математике?
• Вторник, 13 апреля 2021 г. — Как VMPI влияет на будущее детей Вирджинии?
• Вторник, 27 апреля 2021 г. — Основные понятия для 8-10 классов
• Вторник, 25 мая 2021 г. — Программа повышения квалификации в 11–12 классах

Все занятия будут транслироваться в прямом эфире на канале VDOE на YouTube, начало в 18:30 с 20-минутной презентацией членов комитетов по планированию VMPI, а затем координаторы смогут ответить на вопросы сообщества.Вопросы, которые участники хотели бы задать во время занятий, можно задать через форму «Инициатива по математике в Вирджинии». Посетите Инициативу подготовки к математике в Вирджинии (VMPI): отзывы о записях каждого занятия.

Инициатива по математике в Вирджинии

Инициатива подготовки к математике в Вирджинии (VMPI) — это совместная инициатива Департамента образования Вирджинии (VDOE), Государственного совета высшего образования Вирджинии (SCHEV) и системы общественных колледжей Вирджинии (VCCS). Инициатива поддерживает Профиль выпускника Вирджинии, переопределяя математические пути для студентов в Содружестве, чтобы обратиться к знаниям, навыкам, опыту и характеристикам, которые студенты должны достичь, чтобы добиться успеха в колледже и / или на рабочем месте и быть «готовыми к жизни». ”

Содержание страницы

Записки суперинтенданта относительно реализации

Ожидаемые результаты по математике в Вирджинии, готовые к поступлению в колледж и карьеру

Ожидаемые результаты по математике определяют уровень успеваемости, которого должны достичь учащиеся, чтобы быть академически подготовленными к успешной прохождению начальных зачетных курсов колледжа.Эти ожидания были разработаны в рамках Инициативы готовности к колледжам и карьере — процесса, в котором участвовали преподаватели двух- и четырехлетних колледжей и университетов Вирджинии, представители бизнес-сообщества и преподаватели средних школ.

Ресурсы для инструкций

• Стандарты математики для журналов отслеживания обучения (с 2020-2021 учебного года по 2021-2022 учебный год) — были разработаны журналы отслеживания для оценок от детского сада до алгебры II, чтобы помочь учителям определить, какие стандарты учащиеся имели достаточно знаний и опыта в течение 2020 года. -2021 учебный год.Они могут поддержать решения относительно того, когда и как можно будет познакомиться с новыми стандартами в 2021-2022 учебном году. Документы стандартов по математике — это документ в формате PDF. (PDF) можно использовать вместе с журналами отслеживания в качестве поддержки при идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися.
• Стандартные документы по математике — это документ в формате PDF. (PDF) (K-8) были созданы, чтобы помочь в идентификации контента, который можно связать при планировании обучения и содействия более глубокому пониманию учащимися. Стандарты считаются мостом, когда они: функционируют как мост, к которому подключается другой контент в рамках уровня обучения / курса; служат в качестве предварительных знаний для содержания, которое будет рассматриваться в будущих классах / курсах; или обладать выносливостью, превышающей одну единицу обучения в рамках учебного уровня / курса.
• Just in Time Mathematics Quick Checks — Эти формирующие экзамены соответствуют Стандартам обучения математике 2016 года (SOL). Эти ресурсы, разработанные учителями Вирджинии и руководителями математики, предназначены для того, чтобы помочь учителям выявлять учащихся с незавершенным обучением и помогать в планировании обучения, чтобы «вовремя» заполнить потенциальные пробелы.По мере того, как в течение учебного года вводится новый контент, учителя могут использовать эти быстрые проверки для выявления и диагностики незавершенного обучения на уровне класса и / или для оценки понимания необходимых знаний, которые могут потребоваться для доступа к контенту на уровне класса. Пробелы в понимании математики учащимися существуют по разным причинам, и эти ресурсы можно использовать, чтобы помочь вернуть учащимся математическое обучение в нужное русло.
• Инструмент вертикального сочленения по математике (MVAT) — этот инструмент обеспечивает поддержку в определении концепций, соответствующих Стандартам обучения по математике (SOL) 2016 года, которые формулируются на разных уровнях обучения математике или на разных курсах.
Учебные планы по математике
• — включают учебные планы, соответствующие Стандартам обучения по математике от 2016 г. , чтобы помочь учителям привести обучение в соответствие с основными знаниями и навыками.
• Корреляция между VASOL и CCSS. Это таблица в формате Excel. (XLS) — Эта электронная таблица содержит черновик корреляций между детским садом и алгеброй II — 2016 Стандарты обучения Вирджинии (VASOL) для математики с Общими основными государственными стандартами (CCSS) для математики. Эта корреляция была создана для поддержки преподавателей по всему Содружеству, поскольку они пытаются использовать материалы, которые могут указывать только на соответствие CCSS. Все VASOL и CCSS, а также цели процесса Вирджинии и математические практики CCSS связаны по всей таблице, чтобы упростить перекрестные ссылки.
• Совместные учебные планы по математике — включает учебные планы, соответствующие Стандартам обучения по математике от 2016 г. , разработанным учителями, участвующими в инициативе «Совершенство в совместном обучении».Эти планы включают предложения по улучшению уроков и занятий в классе с совместным преподаванием.
• Настенные карточки с словарным запасом математики (K-8, Алгебра I, Геометрия, AFDA и Алгебра II) — обеспечивают отображение слов математического содержания и связанных визуальных подсказок, помогающих в развитии словарного запаса.
• Нарушение обучаемости по математике — Эта страница содержит информацию и ресурсы, а также два новых сопутствующих руководства VDOE:
• Rich Mathematical Tasks — (K-8, Algebra I, Geometry, Algebra II) Эти ресурсы предназначены для поддержки учителей во внедрении в их классах «Стандартов обучения по математике » 2016 года . 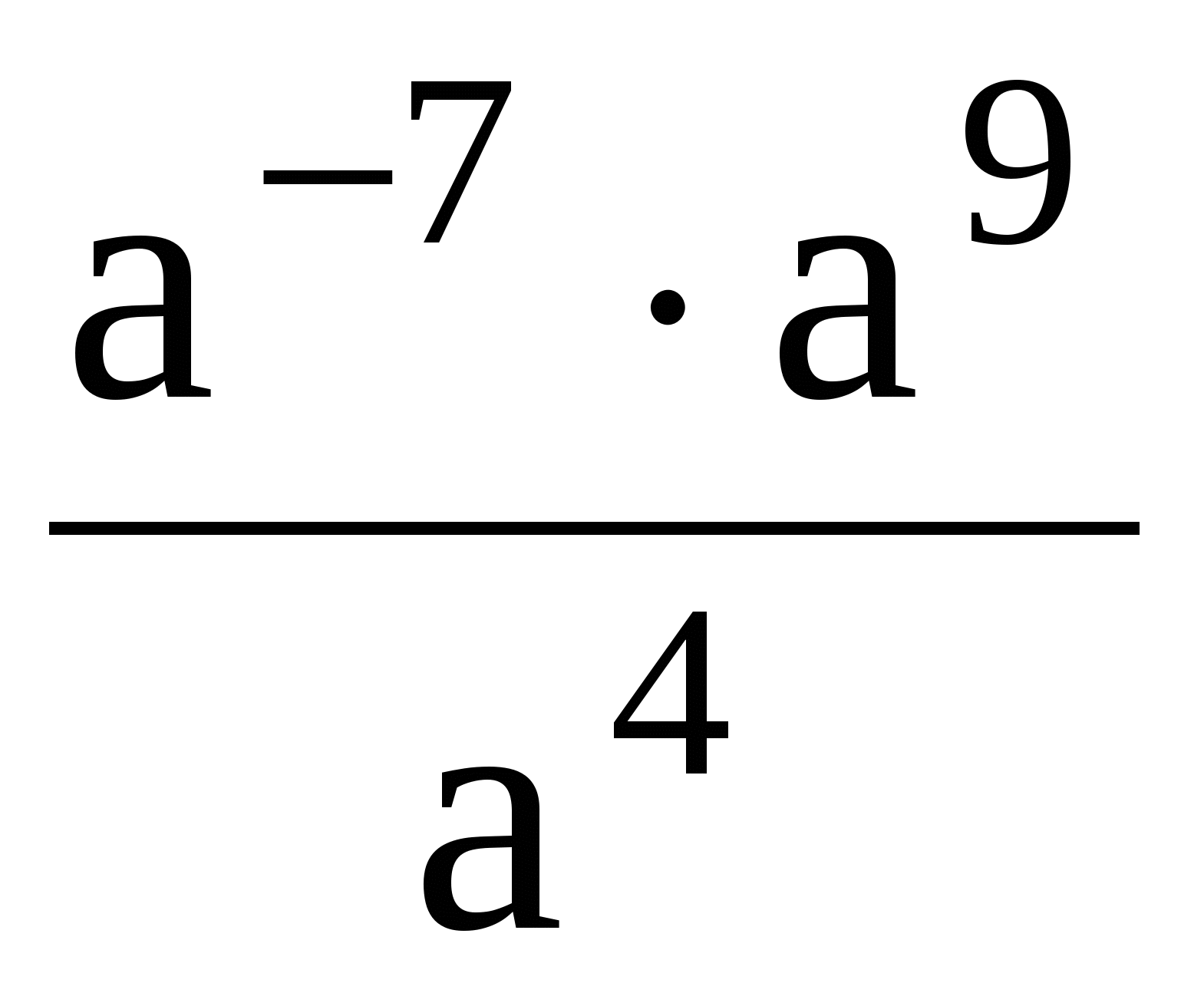Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.

• Математические стандарты обучения (SOL) 2018 институты — Математические стандарты обучения 2018 институты обеспечили обучение, направленное на внедрение математических стандартов обучения 2016 года; усиление преподавания и изучения математики посредством содействия содержательному математическому дискурсу; и поддержка равных возможностей обучения математике для всех учащихся.Продукт Математических институтов 2018 года представляет собой набор онлайн-модулей профессионального развития, предназначенных для использования группой учителей определенного уровня или курса при содействии одного из членов команды.
• Математические стандарты учебных заведений 2017 — предоставлены ресурсы для профессионального развития, направленные на углубление понимания участниками Стандартов обучения по математике от 2016 года и использования эффективных методов преподавания математики, как указано в NCTM Принципы действий: обеспечение успеха в математике для всех резюме.
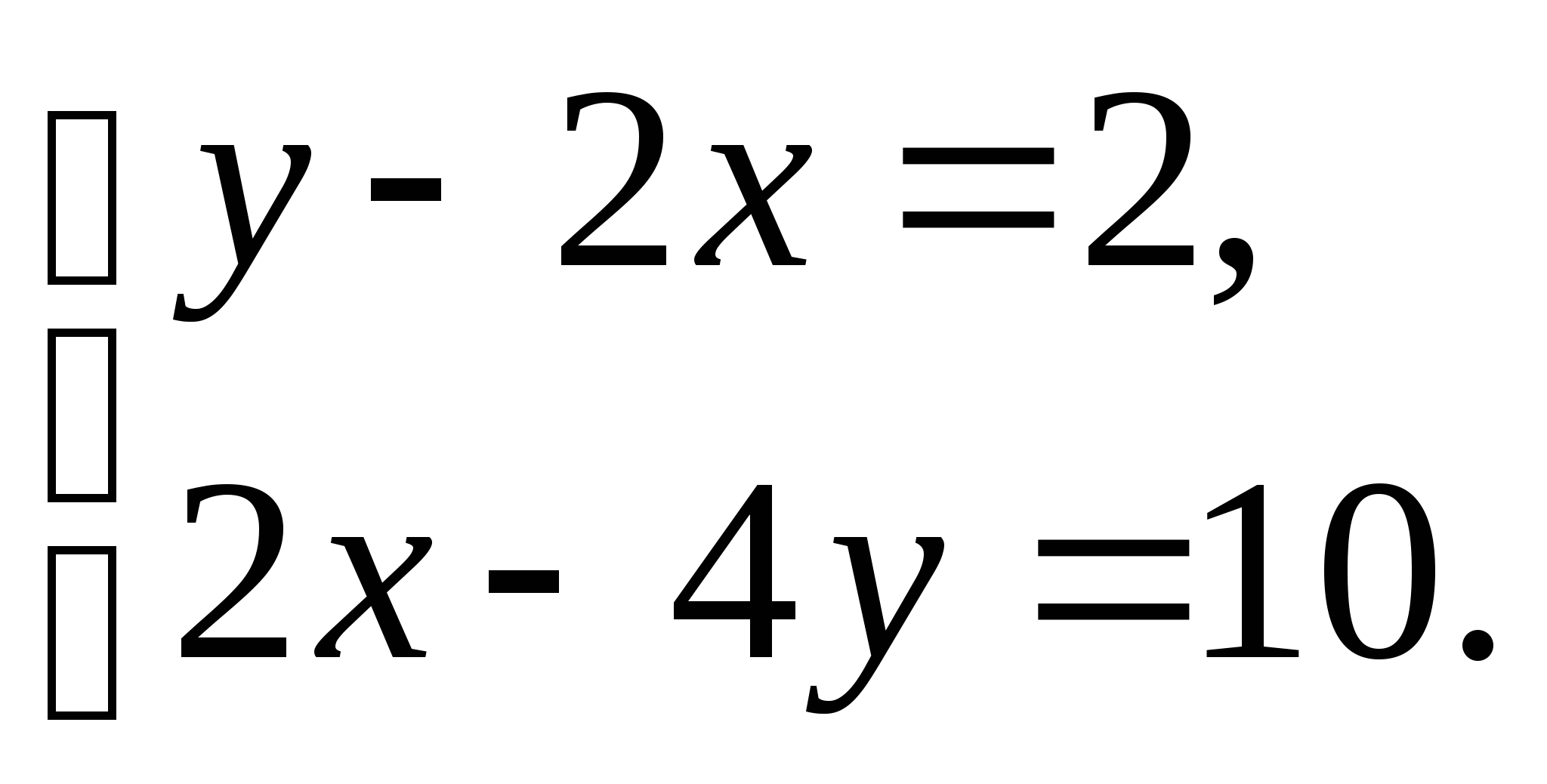
• Computer Adaptive Testing (CAT) — включает информационные видеоролики и ресурсы CAT
• Обучающие видеоролики для учителей — обучающие видеоролики, предназначенные для учителей в поддержку внедрения Стандартов обучения по математике от 2016 г.
Практические элементы
• SOL в TestNav 8 — предоставьте примеры контента, соответствующего Стандартам обучения Mathematics of Learning 2016 года, и возможности попрактиковаться с онлайн-инструментами и функциями, которые доступны в TestNav 8 во время онлайн-тестирования SOL.

Ресурсы для оценки

Начало страницы

Функции и взаимосвязи — стало проще

Введение

Упорядоченная пара представляет собой набор входов и выходов и представляет отношение между двумя значениями. Отношение , — это набор входов и выходов, а функция , — это отношение с одним выходом для каждого входа.

Что такое функция?

Некоторые отношения имеют смысл, а другие — нет.Функции — это отношения, которые имеют смысл. Все функции являются отношениями , но не все отношения являются функциями.

Функция — это отношение, в котором для каждого входа существует только один выход.

Вот отображение функций. Домен — это вход или x-значение , а диапазон — это выход или y-значение .

Каждое значение x связано только с одним значением y.

Хотя входы, равные -1 и 1, имеют одинаковый выход, это отношение по-прежнему является функцией, потому что каждый вход имеет только один выход.

Это отображение не является функцией. Вход для -2 имеет более одного выхода.

Графические функции

Использование входов и выходов, перечисленных в таблицах, картах и ​​списках, упрощает нанесение точек на координатную сетку . Используя график точек данных, вы можете определить, является ли отношение функцией, с помощью теста с вертикальной линией . Если вы можете провести вертикальную линию через график и коснуться только одной точки, отношение является функцией.

Взгляните на график этой карты отношений. Если бы вы провели вертикальную линию через каждую точку на графике, каждая линия касалась бы только одной точки, так что это отношение является функцией.

Специальные функции

Специальные функции и их уравнения имеют узнаваемые характеристики.

Постоянная функция

$ f (x) = c $

Значение c может быть любым числом, поэтому график постоянной функции представляет собой горизонтальную линию.Вот график $ f (x) = 4 $

.

Функция идентификации

долл. США f (x) = x

долл. США

Для функции идентичности значение x совпадает с значением y. График представляет собой диагональную линию, проходящую через начало координат.

Линейная функция

долл. США f (x) = mx + b

долл. США

Уравнение, записанное в форме пересечения наклона , является уравнением линейной функции , а график функции представляет собой прямую линию.

Вот график $ f (x) = 3x + 4 $

Функция абсолютного значения

долл. США f (x) = | x |

долл. США

Функцию абсолютного значения легко распознать по V-образному графику. График состоит из двух частей и представляет собой одну из кусочных функций.

Это лишь некоторые из наиболее часто используемых специальных функций.

Обратные функции

Инверсная функция меняет местами входы и выходы.{-1} (x) = \ frac {x + 4} {3} $.

Не каждая инверсия функции является функцией, поэтому для проверки используйте тест вертикальной линии.

Функциональные операции

Вы можете складывать, вычитать, умножать и делить функции .

• $ f (x) + g (x) = (f + g) (x) $
• $ f (x) — g (x) = (f — g) (x) $
• $ f (x) \ times g (x) = (f \ times g) (x) $
• $ \ frac {f (x)} {g (x)} = \ frac {f} {g} (x) $

Посмотрите на два примера операций функции:

Какова сумма этих двух функций? Просто добавьте выражения.{2} + 11x + 28 \ end {align}

долларов США Домен

и диапазон

В домен из функция ж ( Икс ) — это набор всех значений, для которых определена функция, а диапазон функции — это набор всех значений, которые ж берет.

(В гимназии вы, вероятно, называли домен набором замены, а диапазон — набором решений. Их также можно было назвать входом и выходом функции.)

Пример 1:

Рассмотрим функцию, показанную на диаграмме.

Здесь домен — это множество { А , B , C , E } . D не входит в домен, так как функция не определена для D .

Диапазон — это набор { 1 , 3 , 4 } .2 не входит в диапазон, так как в домене нет буквы, которая сопоставляется с 2 .

Вы также можете поговорить о домене связь , где один элемент в домене может быть сопоставлен более чем с одним элементом в диапазоне.

Пример 2:

Рассмотрим соотношение { ( 0 , 7 ) , ( 0 , 8 ) , ( 1 , 7 ) , ( 1 , 8 ) , ( 1 , 9 ) , ( 2 , 10 ) } .

Здесь отношение задано как набор упорядоченных пар. Домен — это набор Икс -координаты, { 0 , 1 , 2 } , а диапазон — это набор у -координаты, { 7 , 8 , 9 , 10 } . Обратите внимание, что элементы домена 1 а также 2 связаны с более чем одним элементом диапазона, поэтому это нет функция.

Но чаще, особенно при работе с графиками на координатной плоскости, мы имеем дело с функциями, в которых каждый элемент области связан с одним элементом диапазона. (См. Тест вертикальной линии .)

Пример 3:

Область определения функции

ж ( Икс ) знак равно 1 Икс

все действительные числа, кроме нуля (так как at Икс знак равно 0 , функция не определена: деление на ноль недопустимо!).

Диапазон также состоит из действительных чисел, кроме нуля. Вы можете видеть, что на кривой есть точка для каждого у -значение кроме у знак равно 0 .

Домены также могут быть указаны явно, если есть значения, для которых функция может быть определена, но которые мы не хотим рассматривать по какой-то причине.

Пример 4:

Следующие обозначения показывают, что область определения функции ограничена интервалом ( — 1 , 1 ) .

ж ( Икс ) знак равно Икс 2 , — 1 < Икс < 1

График этой функции показан на рисунке. Обратите внимание на белые кружки, которые показывают, что функция не определена в Икс знак равно — 1 а также Икс знак равно 1 . В у -значения варьируются от 0 вплоть до 1 (в том числе 0 , но не включая 1 ).Таким образом, диапазон функции

0 ≤ у < 1 .

уроков в классе | Математические решения

Черил начала урок с чтения Спагетти и фрикадельки для всех! вслух классу. По сюжету мистер и миссис Комфорт приглашают 32 члена семьи и друзей на встречу и устанавливают восемь квадратных столов, чтобы разместить по четыре человека за каждым, по одному сбоку. По мере того, как приходят гости, у всех есть свои идеи о том, как переставить столы, чтобы группы разного размера могли сидеть вместе.Миссис Комфорт протестует, зная, что позже возникнут проблемы с сиденьем, но ее протесты игнорируются. Вечеринка превращается в веселую смесь переставленных столов, стульев, тарелок, стаканов и еды. Однако, в конце концов, все работает, когда миссис Комфорт оказалась права.

Когда Шерил закончила читать рассказ, она спросила класс: «О чем беспокоилась миссис Комфорт?»

Николь сначала ответила: «Здесь не будет достаточно места, потому что, когда вы складываете столы вместе, вы теряете стулья», — сказала она.

«Что ты имеешь в виду?» — спросила Черил.

«Это как если вы сложите два стола вместе, вы потеряете места там, где они соприкасаются. Это трудно объяснить.» Николь нарисовала в воздухе два стола, указывая на стороны, где они встретились. Черил нарисовала на доске два квадрата, нарисовав стрелку там, где стороны касались друг друга. «Вы имеете в виду потерять стулья здесь?» она спросила. Николь кивнула. (См. Рисунок 1).

Выслушав идеи других студентов о проблеме миссис Комфорт, Шерил сказала: «Давайте использовать цветные плитки, чтобы изучить различные способы расстановки всего четырех столов.Начнем всего с четырех столов ».

Черил дала классным указаниям по расстановке квадратных «столов». «Когда плитки соприкасаются, — сказала она, — они должны касаться всей стороны. Прикосновение к частям сторон или только к углам недопустимо ». Она продемонстрировала на диапроекторе. (См. Рисунок 2.)

Шерил также расположила плитки так, чтобы не следовать ее правилу, и попросила учеников объяснить, почему. (См. Рисунок 3.)

Затем она выполнила инструкции.«В своей группе поделитесь плитками, которые я положил на ваш стол, и найдите разные способы расставить четыре плитки. Обязательно следуй моему правилу ». Черил разложила около 70 плиток для каждой группы из четырех учеников.

Пока ученики работали, Шерил ходила по классу, наблюдая за учениками и отвечая на вопросы по мере необходимости. Когда у всех была возможность поработать над проблемой, она прервала студентов и попросила их внимания.

«Что вы сделали?» — спросила Черил.«Кто бы хотел описать расположение, чтобы я мог построить его из плитки наверху?»

«Вы можете провести прямую линию», — сообщил Брэндон.

«Как это?» — спросила Черил, складывая четыре плитки в прямоугольник 1 на 4. Брэндон кивнул.

«Сделайте квадрат со всеми четырьмя из них», — сказала Рахиль. Черил построила квадрат из четырех плиток.

«Я сделала тройку и одну», — сказала Николь.

«Что ты имеешь в виду?» — спросила Черил.

«Один маленький столик, как у Натана, — объяснила Николь, — а затем столик 1 на 3.”

«Вы можете сделать четыре отдельных стола», — сказал Натан.

«Ты мог бы поставить Т», — сказал Зак. «Положите три в ряд и один под средним».

«Я тоже сделал это, но мой перевернут», — сказал Эрик.

Шерил построила аранжировку Эрика под руководством Зака ​​и указала классу, что когда вы можете перевернуть, повернуть или сдвинуть фигуру, чтобы она точно соответствовала другой фигуре, формы совпадают. «Мы будем считать конгруэнтные формы одинаковыми», — пояснила она.

Когда расположение студентов заполнило накладные расходы, Черил спросила: «Что, если бы мы использовали только отдельные прямоугольные столы, сделанные из четырех плиток? Какие формы мы должны удалить? »

«Я предложил четыре отдельные таблицы, — сказал Натан.

Рифка добавила: «И та, которая похожа на букву Т».

«Вы также должны снять мою», — сказала Николь. «Это не один прямоугольник».

Когда Малкия предложила убрать квадрат, разговор разгорелся. Некоторые ученики помнили, что квадрат — это прямоугольник, а другие — нет. Черил пояснила: «Квадрат — это особый вид прямоугольника, потому что все его стороны имеют одинаковую длину. Но, как и прямоугольник, квадрат по-прежнему имеет четыре угла в 90 градусов, а противоположные стороны параллельны.”

Шерил хотела убедиться, что ученики умеют маркировать построенные ими прямоугольники. Она нарисовала на доске прямоугольник размером 1 на 4. «Я могу записать это двумя способами», — сказала она и записала под прямоугольником:

Затем Шерил нарисовала квадрат 2 на 2 и пометила его.

Шерил указала на квадратный стол 2 на 2 и спросила: «Если один человек сидит сбоку от небольшого квадратного стола, и никто не сидит в углах или в щелях между столами, сколько людей может сидеть здесь? ”

«Легко, восемь», — ответила Николь. «Просто сосчитайте по два человека с каждой стороны, умноженные на четыре стороны».

«Когда вы подсчитываете количество людей, которые могут сесть за стол, вы фактически находите его периметр», — объяснила Шерил. «Это потому, что каждый человек сидит по одну сторону от меньшего квадрата и занимает одну единицу длины. Таким образом, периметр прямоугольника 2 на 2 составляет 8 единиц ».

«Периметр стола размером 1 на 4 равен 10», — заметил Эрик.

Шерил попросила остальных проверить показания Эрика, а также изобразить периметр нескольких других прямоугольников.Затем она представила другую проблему.

— Давайте вспомним вечеринку мистера и миссис Комфорт, — начала Черил. «Предположим, миссис Комфорт решила, что все 32 человека должны сесть за один большой массивный прямоугольный стол, и она хотела выяснить, сколько маленьких квадратных столов можно арендовать. Посмотрите, сможете ли вы найти все возможные прямоугольные столы разных размеров и форм, на которых могут разместиться 32 человека ».

«Должен ли каждый стол вмещаться ровно 32?» JT хотел знать.

«Да», — ответила Черил.

«Сколько плиток мы используем?» — спросила Малкия.

«Это будет зависеть от столов, которые вы построите», — ответила Черил.

«Можем ли мы работать с партнером?» — спросила Николь.

«Да, — ответила Черил, — но веди свои записи».

Больше вопросов не было. Черил дала последнее указание. «Используйте плитки, но нарисуйте свои решения на листе бумаги. Обязательно запишите размеры каждого стола и количество людей, за которыми он может разместиться ».

Наблюдая за детьми

Остаток урока Черил наблюдала за учениками за работой и при необходимости оказывала помощь.

Она смотрела, как Кэтлин составляла прямоугольник 16 на 2. «Хм, — громко сказала Кэтлин, работая, — давайте посмотрим, 32 человека. Это должно сработать, потому что 16 умножить на 2 будет 32 ». Кэтлин сосредоточенно нахмурилась, считая стороны квадратов. Затем она с удивлением посмотрела на Шерил.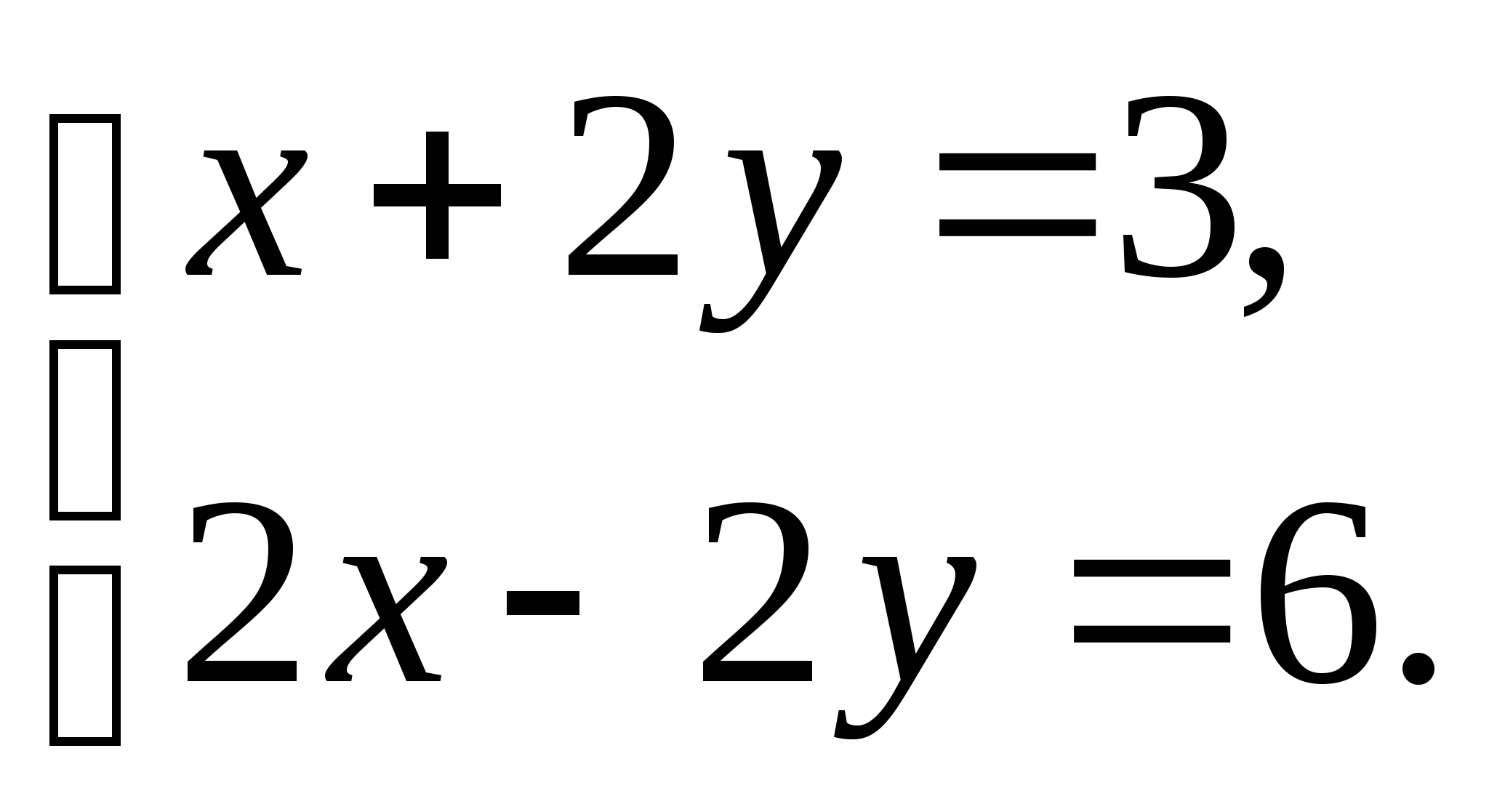

«Я не понимаю», — сказала она. «Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны.

«Еще 36. Ага». Кэтлин пожала плечами, перемешала 16 плиток обратно в стопку в центре стола и начала строить еще один прямоугольник.

«Что ты делаешь?» — спросила ее Шерил.

«Что ж, я, должно быть, напортачила, потому что первая, которую я сделал, не сработала, поэтому я попробую что-нибудь еще», — ответила Кэтлин.

«Что ты собираешься попробовать?» — спросила Черил.

«Не знаю. Я просто собираюсь повозиться и посмотреть, что будет », — сказала она.

Черил наблюдала, как Кэтлин начала складывать плитки в длинный ряд шириной в один квадрат. Она продолжала считать стороны одну за другой каждый раз, когда добавляла новую плитку.Наконец она улыбнулась.

«Работает! Этот вмещает 32 человека. Это 1 на 15. А теперь записать это ». Кэтлин начала рисовать прямоугольник на бумаге.

Алекс сидел напротив Кэтлин. «Я тоже нашел это», — сказал он. «Теперь я пробую что-то вдвое».

«О», — ответила Кэтлин и начала строить прямоугольник шириной в четыре квадрата.

Натан подошел к Шерил. «Я не рисую на бумаге прямоугольники, как все, — сказал он. «Вместо этого я решил использовать Xs.Но Люк сказал мне, что это неправильно. Разве я не могу нарисовать крестики, если захочу? » Натан показал Шерил свою газету.

Черил попросила Натана объяснить, что он сделал. Удовлетворенная тем, что он понимает, что делает, Шерил сказала: «То, что вы сделали, имеет для меня смысл».

Натан вернулся к Люку. «Я сказал вам, что она скажет, что все в порядке», — сказал он.

Черил продолжила движение по классной комнате. К концу периода она увидела, что все студенты нашли некоторые прямоугольники, а некоторые нашли их все.Она попросила детей убрать плитку и собрала их бумаги. Шерил планировала продолжить урок на следующий день.

На следующий день

На следующее утро Черил дала классу возможность подумать над расширением. «Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас нужно будет найти дополнительные расстановки столов ».

Примерно через 10 минут Черил прервала учеников, чтобы начать обсуждение в классе.«Какие варианты есть у Comforts, чтобы посадить всех 32 человека за один стол?» — спросила Черил. Руки студентов вскинулись.

«У них будет группа, точнее восемь», — сказала Рэйчел. Большинство студентов кивнули или пробормотали свое согласие.

«Может ли кто-нибудь описать размеры таблиц, которые подойдут?» — спросила Черил. «Я запишу их на доске».

Эрик сообщил: «Один раз-15, 2-раз-14, 3-раз-13, 4-раз-12, 5-раз-11, 6-раз-10, 7-раз-9 и-8-раз-8. . » После того, как Шерил записала размеры, она вернулась и зарисовала каждый соответствующий прямоугольник.

«О, я вижу закономерность!» — сказала Анферни. «Могу я показать это?» Черил кивнула, и Анферни подошла к доске. Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».

«А другая сторона идет вниз», — добавила Анн Мария.

«О да, я этого не видела», — сказал Анферни. «Ага, 15, 14, 13 и так далее». Он снова сел.

«Разве список не должен продолжаться?» — спросила Черил. «Разве не следует прямоугольник 9 на 7?» (См. Рисунок 6.)

«Этот у тебя уже есть», — сказала Малкия.

«Да, 9 на 7 и 7 на 9 — это одно и то же, — добавила Николь.

«Все числа после 8-умножить на 8 — это повторения, — сказала Кирстен, — так что вы не можете их сосчитать».

«Давайте подумаем, сколько квадратных столов придется арендовать мистеру и миссис Комфорт для каждого большого прямоугольника», — сказала Шерил. «Сколько им придется арендовать за стол размером 15 на 1?»

«Пятнадцать. Легко, — ответили несколько студентов.

«А как насчет 2х14?» Черил продолжила.«Сколько столов придется арендовать Comforts для такой договоренности?»

«Двадцать восемь», — звали многие дети.

«А как насчет расположения 3 на 13?» — спросила Черил. Класс быстро понял, чем занимается Шерил.

«Вы просто размножаетесь», — сказала Рифка. «Просто сделай это для всех — 28, 39, 48, 55, 60, 63 и 64».

«Что вы заметили в форме столов?» Затем спросила Черил.

Малкия сказал: «Размер 8 на 8 — квадрат, а все остальные — прямоугольники.”

«Но ведь размер 8 на 8 тоже прямоугольник, помнишь?» Эрин напомнила Малкию.

«Смотрите, — сказал Брэндон. «Если они устроят длинный тонкий прямоугольник для 32 человек, то они смогут сделать это всего с 15 столами. Так дешевле всего.

«И они также сэкономили бы место, поскольку 1-умноженный на 15 занимает меньше всего места», — добавил Шарнет.

«Но вам понадобится длинная комната, — добавила Николь, — как для королевского банкета».

Затем Шерил прервала беседу и дала письменное задание оценить мышление каждого ученика.Она написала на доске три вопроса, чтобы дети могли ответить:

1. Какие шаблоны вам пригодились в работе?
2. Какие расстановки столов наиболее и наименее экономичны?
3. Что вы замечаете в областях и периметрах выполненных вами аранжировок?

Учащиеся работали над заданием на оставшуюся часть класса.

Бесплатные рабочие листы по математике

Вы здесь: Главная → Рабочие листы Здесь вы можете создавать распечатываемые математические рабочие листы по множеству тем: все основные операции, часы, деньги, измерения, дроби, десятичные дроби, проценты, пропорции, отношения, разложение на множители, уравнения, выражения, геометрия, квадратные корни и многое другое.Мы также предлагаем страницы со списком рабочих листов по классам (1, 2, 3, 4, 5, 6 и 7). Рабочие листы доступны как в формате PDF, так и в формате HTML. Они также очень настраиваемые : вы можете контролировать количество задач, размер шрифта, интервал, диапазон чисел и так далее. Рабочие листы генерируются случайным образом, поэтому каждый раз вы получаете разные. Все рабочие листы имеют ключ ответа на 2-й странице файла. НОВИНКА! Страница рабочих листов с квадратным корнем была обновлена ​​с большим количеством опций, включая рабочие листы в форматах PDF и html. Разрешение на копирование : вы можете свободно печатать и копировать неограниченное количество копий рабочих листов для использования в классе, дома, в учебном центре — где бы вы ни учились. Если вы хотите разместить ссылки или рабочие листы на веб-сайте или в публикации, свяжитесь с нами. Ниже вы можете увидеть примеры разнообразия рабочих листов: По классам ГОТОВЫЕ рабочие листы по различным математическим темам для 4 класса.По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. ПРЕДВАРИТЕЛЬНЫХ рабочих листов по различным математическим темам для 5-го класса. По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. готовых рабочих листа по различным математическим темам для 6 класса. По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. ПРЕДВАРИТЕЛЬНЫХ рабочих листов по различным математическим темам для 7-го класса.По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. Элементарная математика Сложение целых чисел и целых чисел по горизонтали или по столбцу. Может иметь до 6 слагаемых. Отсутствуют проблемы с аддендом, вариант без переноски. Числовые связи — это пары чисел, которые в сумме дают заданное число. Найдите готовые рабочие листы для числовых связей от 8 до 15 и генератор, который вы можете использовать для других чисел.Доступен как в формате html, так и в формате PDF. Таблицы с числами для счета, пропуска, кратного. Выберите список или диаграмму с числами в квадратах. Выберите шаг подсчета и сколько заполняет студент. Основные операции с целыми числами и целыми числами, включая операции с столбцами, деление в столбцы и деление с остатком, проблемы с отсутствующим сложением / множителем. Легко контролировать диапазоны номеров. Для классов 3, 4 и 5.Включает подсчет пропусков, таблицы умножения, недостающие факторы, алгоритм умножения (длинное умножение) и факторинг. Заменить обычные числа на римские или наоборот. Или решите задачи на сложение и вычитание с римскими цифрами. Назовите время по аналоговым часам или начертите стрелки на часах, когда указано цифровое время. Вы можете выбрать размер изображения часов. Доступен как в формате PDF, так и в формате html.На странице есть как генератор, так и готовые рабочие листы для 1-3 классов. Практикуйтесь в преобразовании общепринятых единиц измерения. Доступен как в формате PDF, так и в формате html. На странице есть как генератор, так и готовые рабочие листы для 2-7 классов. Практикуйтесь в переводе метрических единиц измерения. Доступен как в формате PDF, так и в формате html. На странице есть как генератор, так и готовые рабочие листы для 2-7 классов. Особый … и образцы страниц из книг Math Mammoth, совершенно бесплатно! Они не созданы по сценариям, но содержат очень разные проблемы по множеству тем. Подсчет объектов, чет / нечет, сложение, вычитание, умножение, деление, валюта, сравнения, значения разряда, последовательности, игры. Деньги (разные валюты) Подсчитайте обычные монеты или банкноты США. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные канадские монеты или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные австралийские монеты и / или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Подсчитайте обычные южноафриканские монеты и / или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные британские монеты и / или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные монеты и / или банкноты евро. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Дроби Генератор рабочих листов для сложения, вычитания, умножения и деления дробей и смешанных числа. Упрощение (сокращение) дробей, эквивалентных дробей, преобразование дробей в смешанные числа или наоборот. Вы можете контролировать диапазоны числителя, знаменателя и целой числовой части. Рабочие листы для сложения фракций, разделенные на разделы для классов 4, 5 и 6-7. Доступен как в формате PDF, так и в формате html. Рабочие листы для умножения дробей и смешанных чисел, сгруппированные по разделам для классов 4, 5 и 6-7.Доступен как в формате PDF, так и в формате html. Сравните или упорядочите дроби. Множество вариантов; вы даже можете добавить изображения пирогов, чтобы студенты раскрасили их! Пять различных типов задач, четыре из которых включают визуальные модели (круговые изображения). Доступен как в формате PDF, так и в формате html. На странице есть как генератор, так и готовые рабочие листы для 4-5 классов. Сложите, вычитайте, умножайте или делите дроби с помощью этого удобного калькулятора. Десятичные Теория чисел Рабочие листы для округления целых чисел с различными вариантами. Рабочие листы для записи чисел в развернутой или нормальной форме или записи чисел в экспоненциальном представлении. Рабочие листы для экспонентов с множеством вариантов. Доступен в форматах PDF и html. Опции включают диапазон подкоренных выражений, ограничение подкоренных выражений до точных квадратов, использование целых или десятичных чисел, предоставление ответа в упрощенной форме или в виде десятичной дроби, а также другие операции (сложение, вычитание, умножение, деление и возведение в квадрат), помимо взятия квадрата. корень.Доступен в форматах PDF и html. Рабочие листы для разложения на простые множители. Легкий, средний или сложный уровни. Рабочие листы для наибольшего общего множителя и / или наименьшего общего кратного чисел. Соотношение, пропорции и проценты Создавайте рабочие листы пропорций либо с числовыми задачами, либо с простыми задачами со словами (например, проблемы скорости / расстояния или стоимости / количества).Варианты использования только целых чисел или чисел с определенным диапазоном или определенным количеством десятичных цифр. Простые словесные задачи с коэффициентами для 6–8 классов. Рабочие листы для изменения процентов на десятичные числа или десятичных чисел на проценты. Или выберите смешанный лист с обоими типами. Таблицы для определения процента от заданного числа в форматах PDF и html. Вы можете управлять диапазоном процентов и основного числа, а также десятичных цифр, чтобы создавать процентные задачи, которые вы можете решить в уме, или более сложные. Три различных основных типа задач: найти процент от заданного числа, найти фактический процент, когда даны число и часть, или найти базовое число, когда даны процент и часть. Вы можете выбрать формулировку задач и контролировать количество десятичных знаков, диапазон, размер шрифта и многое другое. Геометрия Определите различные типы треугольников.Классифицируйте треугольники по сторонам, углам или по обоим направлениям. Определите семь различных типов четырехугольников (квадрат, прямоугольник, ромб, параллелограмм, трапеция, воздушный змей и разносторонний четырехугольник). Задачи для площади и периметра прямоугольников / квадратов с изображениями, задачи со словами, напишите выражение для площади, используя свойство распределения, неправильные прямоугольные области и многое другое. Вычислить радиус, диаметр, длину окружности или площадь, если указан один из них. Найдите площадь треугольников, параллелограммов, других четырехугольников и многоугольников (пятиугольников / шестиугольников) в координатной сетке. Найдите объем и / или площадь поверхности прямоугольной призмы, в том числе с дробной длиной ребер. Вы также можете создать задачи, где указан объем или площадь поверхности вместе с некоторыми размерами, а затем вам нужно вычислить либо объем, либо площадь поверхности. Учащиеся наносят точки, сообщают координаты точек, строят фигуры из точек, отражают фигуры по оси x или y или перемещают (переводят) их вверх, вниз, влево или вправо. Предалгебра Рабочие листы для написания простых выражений с переменными, когда выражения заданы словами. Для 6-8 классов, предалгебра и алгебра 1. Рабочие листы для оценки простых выражений с переменными, когда задано значение переменной (ей). Для 6-8 классов, предалгебра и алгебра 1. Для преалгебры и алгебры 1.Вы можете контролировать количество задач, уровень сложности, тип выражений, рабочее пространство и многое другое. Рабочие листы для линейных уравнений. Включает одношаговые, двухшаговые, многоступенчатые уравнения, переменные с обеих сторон и многое другое. Для 6-9 классов, предалгебра и алгебра 1. Для предалгебры и алгебры 1. Постройте линейные уравнения и определите наклон или уравнение прямой. Вы можете контролировать тип проблем, количество проблем, разрешен ли дробный уклон, рабочее пространство и многое другое. Для предалгебры и алгебры 1. Постройте заданное неравенство, запишите неравенство из графика или решите различные типы линейных неравенств с построением набора решений или без него. Задачи со словами, связанные с постоянной (или средней) скоростью, временем и расстоянием. Выберите одну из пяти операций и скобок. Вы можете выбрать используемый диапазон номеров, количество задач и т. Д. Решайте уравнения, неравенства и системы уравнений, упрощайте или множите выражения и многое другое с помощью этого онлайн-решателя алгебры. Бесплатный онлайн-редактор формул для учителей. Создает изображение, которое вы можете сохранить. Рабочие листы для отработки отрицательных и нулевых показателей степени, доступные в форматах PDF и html. Список других веб-сайтов, предлагающих бесплатные рабочие листы по алгебре. Другие веб-сайты с математическими листами DadsWorksheets.com — тысячи бесплатных заданий по математике На этом сайте есть более 5000 различных заданий по математике от детского сада до предварительной алгебры и обучения. Math Maze Создайте лабиринт, выполняющий любую из четырех операций. Вы можете выбрать уровень сложности и размер лабиринта. 10 рабочих листов Quickies Интересные рабочие листы по математике … с 10 вопросами на страницу, но на каждой странице есть декорации, которые дети могут потом раскрасить. Доступно несколько бесплатных образцов.

Развитие навыков с помощью практических манипуляторов

Этот глоссарий практических манипуляторов был создан, чтобы помочь учителям узнать о манипуляторах и использовать их в обычных условиях класса.Хотя существуют десятки различных манипуляторов, которые можно использовать для обучения студентов, педагогическая основа для использования одного и того же: непосредственное взаимодействие с манипуляторами помогает учащимся понять математику. Манипуляторы предоставляют учащимся конкретные способы придать смысл абстрактным математическим идеям. Они помогают студентам изучать новые концепции и соотносить новые концепции с тем, что они уже узнали. Они помогают студентам решать проблемы. Когда учащиеся исследуют с помощью манипуляторов, у них есть возможность увидеть математические взаимосвязи.У них есть тактильные и визуальные модели, которые помогают развить их понимание. Без этих конкретных ссылок студенты слишком часто теряются в болоте абстрактных символов, к которым у них нет конкретной связи или понимания. Учителям необходимо научиться использовать конкретные манипуляторы, чтобы учащиеся узнали, как и почему используются математические концепции. Мышление и рассуждение учащихся должны быть главными приоритетами, когда они учатся с помощью манипуляторов. Конкретные манипуляторы и виды деятельности, для которых они используются, имеют такую ​​же ценность, как и размышления студентов над математическими концепциями.

Блоки атрибутов AngLegs® Базовые десять блоков Счетчики ошибок Сантиметровые кубики Цветные кубики Сортировочный лоток CountTEN® Стержни Cuisenaire® DecaDots® Fraction Circle Rings Fraction Circles Часы с редуктором Geoboards Inchworms ™ Inchworms ™ Ruler Link ‘N’ Learn® Links Reflect-Itational ™ HingoSolids ® Spinners Tangrams Three Bear Family® Счетчики Часы записи / стирания Координатные доски XY Плитки AlgebraБаланс ведраЦветовые плиткиDeluxe Rainbow Fraction® КругиDeluxe Rainbow Fraction® SquaresFraction TilesFraction Tower® Equivalence CubesGeolyReflector ™ MirroratCubesGraphing® .