МАСТЕР-КЛАСС ГЕОМЕТРИЯ 9 КЛАСС КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «ВЕКТОРЫ» Предмет
МАСТЕР-КЛАСС
ГЕОМЕТРИЯ, 9 КЛАСС, КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ: «ВЕКТОРЫ»
Предмет: Геометрия
Тема: Контрольная работа по теме ”Векторы”
Класс: 9 класс
Педагог: Аширбекова Лариса
Александровна, заместитель директора
по воспитательной работе, учитель
математики и информатики.
Учреждение
образования: МОУ Шуринская средняя
общеобразовательная школа Кемеровской
области
Город: Кемеровская область
Цель урока: контроль знаний учащихся
Ход урока.
Организационный момент: объяснить цель урока.
Контрольная работа (тестирование)
Вариант 1
1. Вектором называется направленный …. (отрезок)
2. Векторы называются равными, если они
сонаправлены и .
3. Дан треугольник АВС.
Выразите через векторы = и = вектор
А) — ; б) -; в) +
ABCD — трапеция. Найдите сумму векторов ++; разность векторов —
А) ++=, -=
Б) ++=, -=
В) ++=, —=
4. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина ВС, =, = . Выразите через векторы и следующие векторы:
А) , б) , в) , г)
Б) А) = -, б) = , в) = -, г) =-
В) А) = +, б) = , в) = +, г) =-
5. Одно основание трапеции на 4 см больше
другого, а средняя линия равна 8 см.
Найдите основания трапеции
Одно основание трапеции на 4 см больше
другого, а средняя линия равна 8 см.
Найдите основания трапеции
а)
б) 6 см и 8 см
в) 8 см и 10 см
Вариант 2
1. Закончи предложение.
От любой точки М можно отложить вектор, равный данному вектору, и притом только… (один)
2. Вставь пропущенное слово.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на … прямых
3. Дан треугольник АВС. Выразите через векторы = и = вектор .
А) —
Б) +
В) —
4. ABCD — трапеция. Найдите сумму векторов +; разность векторов —
а) +=, -=
б) +=, -=
в) +=, -=
5. ABCD — параллелограмм, О — точка пересечения диагоналей, М — середина АВ, =, =. Выразите через векторы и следующие векторы: А) , б) , в) , г)
А) ABCD — параллелограмм, О — точка пересечения
диагоналей, М — середина АВ, =, =. Выразите через векторы и следующие векторы: А) ,
б) ,
в) ,
г)
Выразите через векторы и следующие векторы: А) ,
б) ,
в) ,
г)
Б) а)=-, б) =, в) =-, г) =-
В) а)=+, б) =, в) =+, г) =-
Глава X. §1 Координаты вектора ( 2 часа)
Урок 7. Разложение вектора по двум неколлинеарным векторам.
Учащиеся должны:
Знать формулировку и доказательство леммы о коллинеарных векторах, и теорему о разложении по двум неколлинеарным векторам;
Уметь решать задачи, применяя полученные знания.
Ход урока
Организационный момент: назвать цели урока.
Анализ контрольной работы.
Объяснение нового материала:
План объяснения:
1. Разложение вектора по двум
неколлинеарным векторам.
Разложение вектора по двум
неколлинеарным векторам.
При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.
2. Лемма о коллинеарных векторах.
Лемма — это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.
Теорема:Если векторы и коллинеарны и 0, то существует такое число k, что = k.
Так как рассматриваемые векторы, по условию коллинеарны, то они могут иметь одинаковые направления. Рассмотрим два случая, когда векторы и сонаправлены и противоположно направлены.
Доказательство:
1) . Возьмем число . Так как k 0, то векторы k и сонаправлены (рисунок 1). Кроме того, их длины равны: k= k = =. Поэтому = k
2) .
Возьмем число
.
Так как k<0,
то векторы k
и снова сонаправлены (рисунок2). Их длины
также равны: k=
k
=
=.
Поэтому
=
k
Их длины
также равны: k=
k
=
=.
Поэтому
=
k
рисунок2
3. Теорема о разложении вектора по двум неколлинеарным векторам.
Теорема: Любой вектор можно разложить по двум данным неколлинеарным вект
Пусть и — данные неколлинеарные векторы, вектор представлен в виде
= х+у, где х и у — некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.
Доказательство:
Возможны два случая:
1) Вектор коллинеарен одному из векторов и , например, вектору (рисунок1). В этом случае по лемме о неколлинеарных векторах вектор можно представить в виде =
и
.
2) Вектор не коллинеарен ни вектору , ни вектору . Отметим какую-нибудь точку О и отложим от нее векторы = , =, = (рисунок2).
Через точку Р проведем прямую, параллельную прямой ОВ, и обозначим через А1 точку пересечения этой прямой с прямой ОА. По правилу треугольника = + . Но векторы и коллинеарны соответственно векторам и , поэтому существует числа х и у, такие, что = х, = у
Докажем теперь,
что коэффициенты х и у разложения
определяются единственным образом.
Допустим, что наряду с разложением
= х+у имеет место другое разложение
= х1+у1.
Вычитая второе равенство из первого и
используя правила действий над векторами,
получаем
=(х-х1) + (у-у1) . Это равенство может выполняться только
в том случае, когда коэффициенты
Это равенство может выполняться только
в том случае, когда коэффициенты
Выводу по теме:
1.Лемма — это вспомогательное утверждение, употребляемое при доказательстве одной или нескольких теорем.
2. Лемма (о коллинеарных векторах). Если векторы и коллинеарны и вектор 0, то существует такое число k, при котором = k
3. Пусть и — данные неколлинеарные векторы, вектор представлен
в виде
Пусть и — данные неколлинеарные векторы, вектор представлен
в виде
= х+у, где х и у — некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.
4. Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом
IV. Закрепление полученных знаний:
Тестирование:
1. Диагонали параллелограмма АВСD пересекаются в точке О. Выразите вектор через векторы и .
а) = —
б) = —
в) =+
2. №911 (а)
Найдите такое число k,
чтобы выполнялось равенство = k,
если известно, что векторы и противоположно направлены и =0,5 см, = 2см.
а) -4
б) 4
в) 0,4
3. №911(б). Найдите такое число k, чтобы выполнялось равенство = k, если известно, что векторы и сонаправлены и =12 см, = 24 дм.
А) -20
Б) 20
В) 0,2
4. №912(а,г). Диагонали параллелограмма пересекаются в точке О, М — середина отрезка АО. Найдите, если это возможно, такое число k, чтобы выполнялось равенство: = k, = k
а) -2,
б) 2, 1
в) 2,
5. Дан произвольный треугольник АВС с медианой АD. Найдите , как вектор выражается через векторы и .
А) = +
Б) = +
В) = +
V. Подведение итогов.
Подведение итогов.
VI. Задание на дом: п. 86, №№ 911 (в,г), 912 2,3 столбик), 916 (в,г)
Контрольная работа по теме: «Метод координат в пространстве» Вариант 1 1 . Если А (4;-2) , В(-8;0) – координаты концов отрезка АВ, то его середина имеет координаты…. 2. Вектор а =-5i +12j. Длина вектора равна…… 3 . Вектор а имеет координаты а{-3;3} .Его разложение по координатным векторам равно… 4. А ( -3;5), В( 3;-2). Координаты вектора АВ равны…… 5. Даны точки А(0;1) и В ( 5;-3) . В – середина отрезка СA. Координаты точки С равны… 6. Найдите координаты и длину вектора n, если n= c – d, c{6; -2} d{1;-2} 7.Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 8. Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что ΔCDE- равнобедренный; б ) Найдите биссектрису, проведённую из вершины С. 9 . Даны векторы а{3; -2}, b{-2; 3} c{-3; 2}. Найти длину ветора р и q, если р=2а+3с и q =2 b — 3с | Контрольная работа по теме: «Метод координат в пространстве» Вариант 2 1. Если А(5;0) , В(3;-6) – координаты концов отрезка АВ, то его середина имеет координаты…. 2. Вектор а = 6 i –8 j. Длина вектора равна…… 3 Вектор а имеет координаты а(-3;1) .Его разложение по координатным векторам равно… 4 А ( 2;7), В( -2;1). Координаты вектора АВ равны…… 5. Даны точки А(0;3) и В ( 5;-3) . А – середина отрезка СВ. Координаты точки С равны….. 6 . Даны векторы а{3; -2}, b{-2; 1} c{ 2;1}. Найти р и q, если р = 2а+ 3с и q= 2 b — 3с; 7. Найдите координаты и длину вектора d, если d = m – n, m{-3, 6} n {2; -2} 8. Напишите уравнение окружности с центром в точке А (- 3;2), проходящей через точку В (0; — 2). 9. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что ΔMNK- равнобедренный; б) Найдите высоту, проведённую из вершины М. | Контрольная работа по теме: «Метод координат в пространстве» Вариант 1 1 . Если А (4;-2) , В(-8;0) – координаты концов отрезка АВ, то его середина имеет координаты…. 2. Вектор а =-5i +12j. Длина вектора равна…… 3 . Вектор а имеет координаты а{-3;3} .Его разложение по координатным векторам равно… 4. А ( -3;5), В( 3;-2). Координаты вектора АВ равны…… 5. Даны точки А(0;1) и В ( 5;-3) . В – середина отрезка СA. Координаты точки С равны… 6. Найдите координаты и длину вектора n, если n= c – d, c{6; -2} d{1;-2} 7.Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 8. Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что ΔCDE- равнобедренный; б ) Найдите биссектрису, проведённую из вершины С. 9 . Даны векторы а{3; -2}, b{-2; 3} c{-3; 2}. Найти длину ветора р и q, если р=2а+3с и q =2 b — 3с | Контрольная работа по теме: «Метод координат в пространстве» Вариант 2 1. 2. Вектор а = 6 i –8 j. Длина вектора равна…… 3 Вектор а имеет координаты а(-3;1) .Его разложение по координатным векторам равно… 4 А ( 2;7), В( -2;1). Координаты вектора АВ равны…… 5. Даны точки А(0;3) и В ( 5;-3) . А – середина отрезка СВ. Координаты точки С равны….. 6 . Даны векторы а{3; -2}, b{-2; 1} c{ 2;1}. Найти р и q, если р = 2а+ 3с и q= 2 b — 3с; 7. Найдите координаты и длину вектора d, если d = m – n, m{-3, 6} n {2; -2} 8. Напишите уравнение окружности с центром в точке А (- 3;2), проходящей через точку В (0; — 2). 9. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что ΔMNK- равнобедренный; б) Найдите высоту, проведённую из вершины М. |
Контрольные и самостоятельные работы по алгебре и геометрии 9 класс
АЛГЕБРА
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
KBАДРАТИЧНАЯ ФУНКЦИЯ
C1. Функции и их свойства
C2. Квадратный трехчлен
C3. График квадратичной функции
C4. Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа)
C5. Решение квадратичных неравенств
C6. Решение неравенств методом интервалов
УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
C7. Решение целых уравнений
C8. Уравнения высших степеней: методы решения, задачи с параметрами (домашняя самостоятельная работа)
C9. Решение систем уравнений второй степени
C10. Решение задач с помощью систем уравнений. Графическое решение систем
C11. Системы рациональных уравнений, (домашняя самостоятельная работа)
АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
C12. Арифметическая прогрессия. Формула n-го члена
C13. Формула суммы n первых членов арифметической прогрессии
C14. Геометрическая прогрессия. Формула n-го члена
C15. Формула суммы первых n членов геометрической прогрессии. Бесконечная геометрическая прогрессия
C16. Комбинированные задачи на прогрессии (домашняя самостоятельная работа)
Комбинированные задачи на прогрессии (домашняя самостоятельная работа)
СТЕПЕНЬ ЧИСЛА
C17. Четные и нечетные функции. Функция у = xn
C18. Корень n-й степени и его свойства
C19. Определение и свойства степени с дробным показателем
C20. Преобразование степенных выражений с рациональными показателями
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
C21. Элементы комбинаторики
C22. Начальные сведения из теории вероятностей
C23. Элементы статистики и теории вероятностей
ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ
C24. Определение тригонометрических функций
C25. Свойства тригонометрических функций. Радианная мера угла
C26. Тригонометрические тождества и их применение
C27. Формулы приведения
C28. Формулы сложения
C29. Формулы двойного угла
C30. Формулы суммы и разности тригонометрических функций
C31. Дополнительные тригонометрические задачи (домашняя самостоятельная работа)
КОНТРОЛЬНЫЕ РАБОТЫ
К1. Квадратичная функция
Квадратичная функция
К2. Решение неравенств
К3. Целые уравнения и системы уравнений
К4. Арифметическая прогрессия
К5. Геометрическая прогрессия
К6. Степень с рациональным показателем
К7. Элементы комбинаторики и теории вероятностей
К8. Свойства тригонометрических функций. Тригонометрические тождества. Формулы приведения
К9. Формулы сложения и их следствия
К10. Итоговая контрольная работа
ГЕОМЕТРИЯ
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику Л.C. Атанасяна и др.)
МЕТОД КООРДИНАТ
C1. Координаты вектора
C2. Простейшие задачи в координатах
C3. Уравнение окружности
C4. Уравнение прямой
C5. Применение векторов и координат к решению задач (домашняя самостоятельная работа)
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
C6. Синус, косинус, тангенс угла
C7. Теорема о площади треугольника. Теорема синусов
C8. Теорема косинусов. Решение треугольников
Решение треугольников
C9. Скалярное произведение векторов
C10. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа)
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
C11. Правильные многоугольники
C12. Длина окружности, площадь круга, площадь кругового сектора
ДВИЖЕНИЯ
C13. Понятие движения
C14. Параллельный перенос и поворот
КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)
K1. Метод координат
K2. Соотношение между сторонами и углами треугольника
K3. Длина окружности й площадь круга
K4. Движение
K5. Итоговая контрольная работа
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)
ПОДОБИЕ ФИГУР
C1. Преобразование подобия и его свойства
C2. Признаки подобия треугольников
C3. Подобие прямоугольных треугольников. Свойство биссектрисы угла треугольника
C4. Подобие треугольников (домашняя самостоятельная работа)
C5. Теорема о вписанных углах и ее следствия
C6. Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)
Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)
РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
C7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма
C8. Теорема синусов и ее следствия
C9. Теоремы косинусов и синусов (домашняя самостоятельная работа)
МНОГОУГОЛЬНИКИ
C10. Выпуклый многоугольник
C11. Правильные многоугольники. Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
C12. Длина окружности. Радианная мера угла
ПЛОЩАДИ ФИГУР
C13. Площадь прямоугольника, квадрата, параллелограмма
C14. Площадь треугольника
C15. Площадь трапеции, площадь четырехугольника
C16. Окружность и многоугольники (домашняя самостоятельная работа)
C17. Площади подобных фигур. Площадь круга и его частей
C18. Площади фигур (домашняя самостоятельная работа)
КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)
K1. Подобие фигур
K2. Решение треугольников
Решение треугольников
K3. Многоугольники
K4. Площади фигур
K5. Итоговая контрольная работа
ОТВЕТЫ
АЛГЕБРА
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
КОНТРОЛЬНЫЕ РАБОТЫ
ГЕОМЕТРИЯ
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)
КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)
КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)
Конспект урока «Контрольная работа по теме «Векторы»
Конспект урока
Тема урока: Контрольная работа № 1 по теме «Векторы».
Предмет: геометрия
Контингент: 9 класс
Цель урока:
Проверить знания, умения и навыки учащихся по теме «Векторы».
Тип урока:
контроль, оценка и коррекция знаний.
Форма организации совзаимодействия на уроке:
индивидуальная
Планируемые образовательные результаты:
Учащиеся демонстрируют: знания о векторах, действиях с векторами, средней линии трапеции.
Учащиеся могут свободно пользоваться этими понятиями при решении задач.
Учащиеся могут оформлять решения, выполнять перенос ранее усвоенных способов действий.
Приобретенная компетентность:
предметная
Ход урока
Организационный момент.
Выполнение контрольной работы
Контрольная работа по теме «Векторы»
9 класс, 1 четверть
1 вариант
1. Начертите два неколлинеарных вектора и . Постройте векторы, равные
Постройте векторы, равные
а) б)
2. На стороне ВС ромба АВСD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы , .
3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
Дополнительное задание
4. Дана трапеция АВСD с основаниями AD=20 и BC=8, О – точка пересечения диагоналей. Разложите вектор по векторам , .
2 вариант
1. Начертите два неколлинеарных вектора и . Постройте векторы, равные
а) б)
2. На стороне CD квадрата ABCD лежит точка Р так, что CP=PD, O- точка пересечения диагоналей. Выразите векторы , , через векторы , .
Выразите векторы , , через векторы , .
3. В равнобедренной трапеции один из углов равен 60о, боковая сторона равна 8 см, а меньшее основание 7см. Найдите среднюю линию трапеции.
Дополнительное задание
4. Дана трапеция АВСD с основаниями AD=20 и BC=8, О – точка пересечения диагоналей. Разложите вектор по векторам , .
Примерно в середине урока проводится зарядка для снятия зрительного напряжения
Подведение итогов урока
Домашнее задание
Решить задачи, с которыми ученик не справился во время контрольной работы (условия задач контрольной работы прикрепляются в электронном дневнике индивидуально каждому ученику).
Контрольная Работа 1 Векторы 9 Класс Ответы – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
Контрольная Работа 1 Векторы 9 Класс Ответы
Опубликовано 08. 01.2018 — 5:03 — Пак Светлана Валентиновна
01.2018 — 5:03 — Пак Светлана Валентиновна
9 класс. Контрольная работа № 1. «Векторы».
Контрольная работа № 1 по геометрии для 9 класса
1. Вектором называется направленный …. (закончить предложение)
2. Начертите два неколлинеарных вектора и . Постройте векторы, равные
3. На стороне ВС ромба АВСD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы .
4. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
5. Расстояния от концов диаметра окружности до некоторой касательной равны a и b . Найдите радиус окружности.
Контрольная работа № 1 по геометрии для 9 класса
1. От любой точки М можно отложить вектор, равный данному вектору, и притом только… (закончить предложение).
2. Начертите два неколлинеарных вектора . Постройте векторы, равные
3. На стороне CD квадрата ABCD лежит точка Р так, что CP=PD, O- точка пересечения диагоналей. Выразите векторы через векторы .
Выразите векторы через векторы .
4. В равнобедренной трапеции один из углов равен 60 о , боковая сторона равна 8см, а меньшее основание 7см. Найдите среднюю линию трапеции.
5. Найдите площадь трапеции ABCD с боковой стороной BC = 5, если расстояния от вершин A и D до прямой BC равны 3 и 7 соответственно.
Контрольная работа № 1 по геометрии для 9 класса
1. Вектором называется направленный …. (закончить предложение)
2. Начертите два неколлинеарных вектора и . Постройте векторы, равные
3. На стороне ВС ромба АВСD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы .
4. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
5. Расстояния от концов диаметра окружности до некоторой касательной равны a и b . Найдите радиус окружности.
Контрольная работа № 1 по геометрии для 9 класса
1. От любой точки М можно отложить вектор, равный данному вектору, и притом только. .. (закончить предложение).
.. (закончить предложение).
2. Начертите два неколлинеарных вектора . Постройте векторы, равные
3. На стороне CD квадрата ABCD лежит точка Р так, что CP=PD, O- точка пересечения диагоналей. Выразите векторы через векторы .
4. В равнобедренной трапеции один из углов равен 60 о , боковая сторона равна 8см, а меньшее основание 7см. Найдите среднюю линию трапеции.
5. Найдите площадь трапеции ABCD с боковой стороной BC = 5, если расстояния от вершин A и D до прямой BC равны 3 и 7 соответственно.
Контрольные работы составлены с учётом материалов учебников «Природоведение 5 класс» авторы: Т.С. Сухова, В.И.Строганов и «Землеведение 6 класс» авторы :В.П.Дронов,Л.Е.Савельева.Данные работы ап…
Контрольная работа по теме «Наречие», контрольная работа по теме «Частицы»…
9 класс. Контрольная работа № 3. Соотношение между сторонами и углами треугольника. Скалярное произведение векторов….
9 класс. Контрольная работа № 3. «Скалярное произведение векторов». Дидактические материалы Б.Г. Зив…
Дидактические материалы Б.Г. Зив…
11 класс. Контрольная работа № 1 по теме: «Координаты точки. Координаты вектора»…
11 класс. Контрольная работа № 2 по теме: «Скалярное произведение векторов в пространстве. Движения»…
Контрольная работа состоит из 10 заданий различного уровня сложности и включает в себя задания с краткой записью ответа, задания с развернутым ответом, задание на выбор двух верных утверждений из пяти…
9 класс . Контрольная работа № 1 . » Векторы «
Контрольная работа по геометрии на тему Векторы ( 9 класс )
К- 1 Геометрия 9 Атанасян Ответы | КОНТРОЛЬНАЯ РАБОТА
Геометрия. 9 класс . Контрольная работа № 1 по теме: « Векторы »
ГДЗ: Геометрия 9 класс Мельникова — Тетрадь для контрольных …
Сочинение На Тему Золотая Осень Класс
Проблема Актуальности Произведений Толстого Сочинение Егэ
Сочинение Рассуждение На Тему Учение
Как Писать Сочинение По Русскому 5 Класс
Курсовая Влияние Скандинавской Ходьбы На Здоровье Человека
|
№ урока Дата |
Тема урока |
Основные понятия |
Виды деятельности ученика |
Виды контроля |
Учебно-методическое и материально-техническое обеспечение |
Домашнее задание |
|
Вводное повторение(2 часа)
|
||||||
|
1. |
Вводное повторение |
Теоретические основы геометрии за курс 8 класса |
Уметь решать задачи на применение знаний из курса 8 класса
|
|
Таблицы |
№ 10-15 по карточке |
|
2. |
Вводное повторение |
Теоретические основы геометрии за курс 8 класса |
Тест |
ИКТ(компьютер, проектор)(демонстрационный материал для решения задач по готовым чертежам) |
Задачи по карточке |
|
|
Глава IX.
|
||||||
|
3. |
Понятие вектора. Равенство векторов |
Вектор, равенство векторов |
Формулировать определения и иллюстрировать понятия вектора, его длины, коллинеарных и равных векторов; мотивировать введение понятий и действий, связанных с векторами, соответствующими примерами, относящимися к физическим векторным величинам; применять векторы и действия над ними, теорему о средней линии трапеции при решении геометрических задач. |
|
ИКТ(компьютер, проектор)презентация Таблицы |
П. |
|
4. |
Откладывание вектора от данной точки |
Вектор, равенство векторов, коллинеарные и неколлинеарные векторы |
Индивидуальная работа по карточкам, самостоятельная работа обучающего характера |
Раздаточный диф-ференцированный материал |
П.-76-78, вопросы 1-6, №748, 749,752 |
|
|
5. |
Сумма двух векторов |
Сумма двух векторов, правило параллелограмма, законы сложения векторов |
|
ИКТ(компьютер, проектор) презентация
|
П. |
|
|
6. |
Сложение нескольких векторов |
законы сложения векторов, сумма нескольких векторов |
индивидуальная работа по карточкам |
Раздаточный материал |
П.81, №755, 760, 761 |
|
|
7. |
Вычитание векторов. |
Теорема о разности двух векторов |
|
|
П. |
|
|
8 |
Умножение вектора на число |
Свойства умножения вектора на число |
индивидуальные карточки, самостоятельная работа |
Раздаточный материал |
№782, 784(б), 787 |
|
|
9 |
Применение векторов к решению задач |
коллинеарные и неколлинеарные векторы, законы сложения векторов, теорема о разности двух векторов, свойства умножения вектора на число |
индивидуальные карточки |
ИКТ(компьютер, проектор) видео фрагмент |
П. |
|
|
10 |
Средняя линия трапеции |
Средняя линия трапеции, свойства средней линии трапеции |
Теоретический тест, самостоятельное решение задач |
Раздаточный диф-ференцированный материал |
Решить оставшиеся задачи с карточки для самостоятельного решения |
|
|
Глава X. Метод координат(10 часов)
|
||||||
|
11. |
Разложение вектора по двум неколлинеарным векторам |
Лемма о коллинеарных векторах, теорема о разложении вектора |
Объяснять и иллюстрировать понятия прямоугольной системы координат, координат точки и координат вектора; выводить и использовать при решении задач формулы координат середины отрезка, длины вектора, расстояния между двумя точками, уравнения окружности и прямой. |
|
ИКТ(компьютер, проектор) презентация
|
П.86, вопросы 1-3, №911 |
|
12 |
Координаты вектора. |
Координаты вектора, правила нахождения координат суммы, разности и произведения вектора на число
|
Теоретический опрос, самостоятельное решение задач |
|
П.87, вопросы 7-8, №919, 918, 926(б,в) |
|
|
13. |
Простейшие задачи в координатах |
Правило определения координат вектора |
самостоятельная работа проверочного характера |
ИКТ(компьютер, проектор) презентация Раздаточный диф-ференцированный материал |
П. |
|
|
14 |
Простейшие задачи в координатах |
Координаты середины отрезка, длина вектора, расстояние между точками |
индивидуальная работа по карточкам |
Раздаточный материал |
№944, 949(а) |
|
|
15 |
Уравнение линии на плоскости. Уравнение окружности |
Уравнение окружности (х-х0)2 +(у-у0)2=r2 |
математический диктант |
|
П. |
|
|
16 |
Уравнение прямой. Использование уравнений окружности и прямой при решении задач |
Уравнение окружности (х-х0)2 +(у-у0)2=r2, Уравнение прямой ах+bу+с=0 |
Теоретический опрос, индивидуальная работа по карточкам, математический диктант |
Раздаточный диф-ференцированный материал |
П.92, вопросы 18-20, №972(в), 974, 976 |
|
|
17 |
Использование уравнений окружности и прямой при решении задач |
Уравнение окружности (х-х0)2 +(у-у0)2=r2, Уравнение прямой ах+bу+с=0 |
самостоятельная работа |
ИКТ(компьютер, проектор) презентация
|
№978, 979,969(б) |
|
|
18 |
Решение задач по теме «Уравнения прямой и окружности» |
Уравнение окружности (х-х0)2 +(у-у0)2=r2, уравнение прямой ах+bу+с=0 |
|
|
№990,992, 993, 996 |
|
|
19 |
Решение задач по теме «Метод координат» |
правила нахождения координат суммы, разности и произведения вектора на число, уравнение окружности (х-х0)2 +(у-у0)2=r2, уравнение прямой ах+bу+с=0 |
|
Тестирование, самостоятельное решение задач |
Раздаточный материал |
Задачи по карточке |
|
20 |
Контрольная работа №1 по теме « Векторы. |
Уметь решать простейшие задачи методом координат Уметь применять уравнения прямой и окружности при решении задач |
Контрольная работа №1 |
Дифференцирован-ные контрольно-измерительные материалы |
Повторить п.76-92 |
|
|
Глава XI. Соотношение между сторонами и углами треугольника. Скалярное произведение векторов(11 часов) |
||||||
|
21/1. |
Синус, косинус и тангенс угла |
Синус, косинус, тангенс |
Формулировать и иллюстрировать определения синуса, косинуса и тангенса углов от 0° до 180°; выводить основное тригонометрическое тождество и формулы приведения; формулировать и доказывать теоремы синусов и косинусов, применять их при решении треугольников; объяснять, как используются тригонометрические формулы в измерительных работах на местности; формулировать определение угла между векторами и скалярного произведения векторов; выводить формулу скалярного произведения через координаты векторов; формулировать и обосновывать утверждение о свойствах скалярного произведения; использовать скалярное произведение при решении задач. |
тестирование |
ИКТ(компьютер, проектор) презентация Таблицы |
П.93-95, вопросы 1-6, 1011 |
|
22/2 |
Основное тригонометрическое тождество. Формулы приведения |
Основное тригонометрическое тождество, правила применения формул приведения |
Теоретический опрос; индивидуальные карточки |
Раздаточный материал |
№1017,1018(б,г),1019(а,в) |
|
|
23/3 |
Формулы для вычисления координат точки. Теорема о площади треугольника |
Формулы для вычисления координат точки х=ОАcosа; у=ОАsinа |
самостоятельная работа |
Раздаточный диф-ференцированный материал |
задачи 2 или 3 уровня на карточках |
|
|
25/4 |
Теорема синусов. Теорема косинусов |
Теорема синусов. Теорема косинусов |
индивидуальная работа по карточкам, решение задач на готовых чертежах |
ИКТ(компьютер, проектор) презентация Таблицы Раздаточный материал |
П. |
|
|
25/5 |
Соотношение между сторонами и углами треугольника |
Теорема синусов, теорема косинусов, синус, косинус, тангенс |
Теоретический опрос, индивидуальные карточки |
Раздаточный материал |
№1034 |
|
|
26/6 |
Теоремы синусов и косинусов. Решение треугольников |
Теорема синусов, теорема косинусов |
Решение задач на готовых чертежах, самостоятельное решение задач |
Раздаточный материал |
№1060(а,в), 1061 (а,в), 1038 |
|
|
27/7 |
Угол между векторами |
Угол между векторами |
|
ИКТ(компьютер, проектор) презентация Таблицы |
П. |
|
|
28/8 |
Скалярное произведение векторов. Свойства скалярного произведения векторов. |
Свойства скалярного произведения. |
Тестирование |
Раздаточный материал |
П.103,104, в.17-20, №1044(б), 1047(б),
|
|
|
29/9 |
Скалярное произведение векторов в координатах |
Теорема о вычислении скалярного произведения двух векторов, зная координаты этих векторов. |
|
|
П.103,104, в.17-20, №1048, 1049, 1051
|
|
|
30/10 |
Решение задач по теме «Соотношение между сторонами и углами треугольника» |
Теорема синусов, теорема косинусов, угол между векторами, свойства скалярного произведения |
математический диктант, самостоятельное решение задач |
|
Задание по карточке |
|
|
31/11 |
Контрольная работа №2 по теме «Соотношения между сторонами и углами треугольника» |
Теорема синусов, теорема косинусов, угол между векторами, свойства скалярного произведения |
Уметь решать задачи на применение скалярного произведения векторов, теорем синусов и косинусов, о площади треугольника |
Контрольная работа №2 |
Дифференцирован-ные контрольно-измерительные материалы |
Повторить п. |
|
Глава XII. Длина окружности и площадь круга(12 часов) |
||||||
|
32/1 |
Правильный многоугольник. |
Правильный много-угольник, формула для вычисления угла пра-вильного n-угольника |
Формулировать определение правильного многоугольника; формулировать и доказывать теоремы об окружностях, описанной около правильного многоугольника и вписанной в него; выводить и использовать формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности; решать задачи на построение правильных многоугольников; объяснять понятия длины окружности и площади круга; выводить формулы для вычисления длины окружности и длины дуги, площади круга и площади кругового сектора; применять эти формулы при решении задач. |
самостоятельной решение задач с целью подготовки к восприятию материала |
ИКТ(компьютер, проектор) презентация Таблицы |
П.105,1081(в) |
|
33/2 |
Окружность, описанная и вписанная в правильный многоугольник |
Теоремы и следствия о вписанных и описа-нных окружностях в правильные многоугольники |
индивидуальные карточки |
|
П.106,107, вопросы 3,4, №1084,1086 |
|
|
34/3 |
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности |
Формулы для вычис-ления площади прави-льного многоугольни-ка, его стороны и радиуса вписанной окружности |
Теоретический опрос, индивидуальные карточки |
Таблицы |
П.108, вопросы 5-7, № 1087(3,5), 1093 |
|
|
35/4 |
Построение правильных многоугольников |
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности |
Теоретический опрос |
ИКТ(компьютер, проектор) видео фрагмент Таблицы |
П.109, вопросы 6,7, №1094(а,г), 1095 |
|
|
36/5 |
Решение задач по теме «Правильные многоугольники» |
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности |
Самостоятельная работа |
Раздаточный диф-ференцированный материал |
индивидуальные карточки |
|
|
37/6 |
Длина окружности |
Формула вычисления длины окружности |
математический диктант |
Таблицы |
П.110,№ 1104(а) |
|
|
38/7 |
Длина окружности. Решение задач |
Формула вычисления длины окружности |
самостоятельная работа |
Раздаточный диф-ференцированный материал |
№1106 |
|
|
39/8 |
Площадь круга. Площадь кругового сектора |
Формула для вычисления площади круга, формула для вычисления площади кругового сектора |
индивидуальные карточки |
ИКТ(компьютер, проектор) презентация Таблицы Раздаточный материал |
П.111,112, №1114, 1116(а,в), 1117(б,в) |
|
|
40/9 |
Площадь круга. Решение задач |
Формула для вычисления площади круга, формула для вычисления площади кругового сектора |
Теоретический опрос, решение задач на готовых чертежах |
Таблицы |
№1121,1123, 1124 |
|
|
42/11 |
Решение задач по теме «Длина окружности и площадь круга» |
Правильные многоугольники. Формулы для вычисления длины окружности, площади круга, площади кругового сектора |
Тестирование, самостоятельное решение разноуровневых задач |
Таблицы. Раздаточный диф-ференцированный материал |
№1129(а,в),1130,1131, 1135 |
|
|
42/1 |
Решение задач по темам «Правильные многоугольники» и «Длина окружности и площадь круга» |
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Формулы для вычисления длины окружности, площади круга, площади кругового сектора |
Тестирование |
Таблицы. Раздаточный материал |
№1137, 1138,1139 |
|
|
43/12 |
Контрольная работа №3 по теме «Длина окружности и площадь круга» |
Уметь решать задачи на применение этих формул |
Контрольная работа №3 |
Дифференцирован-ные контрольно-измерительные материалы |
Повторить понятия центральная и осевая симметрия |
|
|
Глава XIII. Движения(8 часов) |
||||||
|
44/1 |
Понятие движения |
Осевая симметрия, центральная симметрия, движение |
Объяснять, что такое отображение плоскости на себя и в каком случае оно называется движением плоскости; объяснять, что такое осевая симметрия, центральная симметрия, параллельный перенос и поворот; обосновывать, что эти отображения плоскости на себя являются движениями; объяснять, какова связь между движениями и наложениями; иллюстрировать основные виды движений, в том числе с помощью компьютерных программ. |
|
ИКТ(компьютер, проектор) видео фрагмент
|
П.113,114, №1148(а) |
|
45/2 |
Наложения и движения. Свойства движений |
Осевая симметрия, центральная симметрия, движение, свойства движений |
индивидуальные карточки |
Раздаточный материал |
П.114,115, №1150(устно)1153,1152(а), 1159 |
|
|
46/3 |
Решение задач по теме «Понятие движения. Осевая и центральная симметрия» |
Осевая симметрия, центральная симметрия, движение, свойства движений |
Творческая работа |
|
№1155, 1156, 1160,1161 |
|
|
47/4 |
Параллельный перенос |
Параллельный перенос |
|
ИКТ(компьютер, проектор) презентация |
П.116,вопросы 14, 15, № 1162,1163,1165 |
|
|
48/5 |
Поворот |
Поворот |
Творческая работа, индивидуальные карточки |
ИКТ(компьютер, проектор) видео фрагмент Раздаточный материал |
П.117, вопросы 16,17,№1166(б)1167 |
|
|
49/6 |
Решение задач по теме «Параллельный перенос. Поворот» |
Поворот, параллельный перенос |
Самостоятельная работа |
Раздаточный диф-ференцированный материал |
Вопросы 1-17, №1170,1171, карточка |
|
|
50/7 |
Подготовка к контрольной работа по теме «Движение» |
Осевая симметрия, центральная симметрия, поворот, параллельный перенос |
самостоятельное решение задач подготовительного варианта |
Раздаточный диф-ференцированный материал |
разноуровне-вые карточки |
|
|
51/8 |
Контрольная работа №4 по теме «Движение» |
Осевая симметрия, центральная симметрия, поворот, параллельный перенос |
Уметь решать задачи с движением |
Контрольная работа №4 |
Дифференцирован-ные контрольно-измерительные материалы |
С. 344 читать приложение 1 |
|
Глава XIV. Начальные сведения из стереометрии(8 часов) |
||||||
|
52/1 |
Предмет стереометрии. Многогранник. |
Куб, параллелепипед, призма, пирамида, шар, конус, сфера, шар, цилиндр. Развёртки некоторых многогранников. Построение простейших сечений многогранников.
|
Объяснять, что такое многогранник и его элементы, виды многогранников, приводить формулы объёмов; объяснять, что такое тела вращения, их виды, какими формулами выражаются объём и площадь боковой поверхности цилиндра, конуса и шара, что такое радиус и диаметр сферы (шара), какой формулой выражается площадь сферы; изображать и распознавать на рисунках призму, параллелепипед, пирамиду, цилиндр, конус, шар. |
|
Таблицы ИКТ(компьютер, проектор) презентация |
П.124,119 |
|
53/2 |
Призма. Параллелепипед. Объём тела. |
|
Таблицы ИКТ(компьютер, проектор) презентация
|
П.120-122 |
||
|
54/3 |
Свойства прямоугольного параллелепипеда. |
|
Таблицы |
П.123, |
||
|
55/4 |
Пирамида |
|
Таблицы |
П.124 |
||
|
56/5 |
Цилиндр. |
|
Таблицы ИКТ(компьютер, проектор) презентация
|
П.125 |
||
|
57/6 |
Конус. |
|
Таблицы |
П.126 |
||
|
58/7 |
Сфера и шар. |
|
Таблицы |
П.127 |
||
|
59/8 |
Обобщающий урок по теме: «Начальные сведения из стереометрии» |
Тестирование |
Таблицы Раздаточный материал |
П. П.118-127 |
||
|
Об аксиомах планиметрии(2часа) |
||||||
|
60/1 61/2 |
Об аксиомах планиметрии |
Аксиомы планиметрии |
Иметь представление об основных этапах развития геометрии Знать аксиомы планиметрии |
|
|
Повторить главы 1, 3. Приложение п.1. |
|
Повторение. Решение задач(7 часов) |
||||||
|
62/1 |
Повторение. «Начальные геометрические сведения. Параллельные прямые». Решение задач |
Свойства углов при параллельных прямых |
Знать свойства углов при параллельных прямых уметь решать задачи
|
Тестирование |
Таблицы. |
Повторить главы 2,4,7,9 |
|
63/2 |
Повторение. «Треугольники» Решение задач |
признаки равенства и подобия треугольников, формулы площади треугольника |
уметь решать задачи на нахождение элементов треугольника |
Математический диктант |
Таблицы |
Карточки |
|
64/3 |
Повторение. «Треугольники». Решение задач |
признаки равенства и подобия треугольников, формулы площади треугольника
|
уметь решать задачи на нахождение элементов треугольника |
самостоятельное решение задач |
Таблицы. |
повторить главы 8,12, карточки |
|
65/4 |
Повторение. «Окружность». Решение задач |
касательная к окружности, центральные и вписанные углы, правильные многоугольники, длина окружности, площадь круга |
уметь решать задачи |
|
Таблицы. |
повторить главу5, карточки |
|
66/5 |
Повторение. «Четырехугольники. Многоугольники». Решение задач |
четырехугольник, выпуклый многоугольник, параллелограмм, трапеция, прямоугольник, ромб, квадрат |
уметь решать задачи |
тестирование |
Таблицы. Раздаточный диф-ференцированный материал |
повторить главы, 9,10,13; карточки |
|
67/6 |
Повторение. «Векторы. Метод координат. Движения» Решение задач |
коллинеарные и неколлинеарные векторы, законы сложения векторов, теорема о разности двух векторов, свойства умножения вектора на число, правила нахождения координат суммы, разности и произведения вектора на число, уравнение окружности (х-х0)2 +(у-у0)2=r2, уравнение прямой ах+bу+с=0 |
Уметь решать задачи на применение теории векторов Уметь решать простейшие задачи методом координат Уметь применять уравнения прямой и окружности при решении задач |
|
Таблицы |
подготовить ся к контрольной работе |
|
68/7 |
Контрольная работа №5 (итоговая) |
|
уметь применять полученные знания при решении задач |
Контрольная работа№6 |
Контрольно-измерительные материалы |
|
Геометрия 9 Атанасян (Мельникова) | КОНТРОЛЬНЫЕ РАБОТЫ
Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных работ по геометрии в 9 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 9 класс. Дидактические материалы к учебнику Л.С. Атанасяна и др. ФГОС, в которой контрольные работы представлены в 4-х вариантах, а также есть набор заданий по каждой теме для подготовки к контрольным работам. Структура контрольных работ и форма заданий соответствуют структуре и форме заданий Основного государственного экзамена (ОГЭ).
Контрольные работы по геометрии в 9 классе:
Контрольная работа 1 К-1. Векторы. Метод координат
Контрольная работа 2 К-2. Соотношения в треугольнике
Контрольная работа 3 К-3. Длина окружности и площадь круга
Контрольная работа 4 К-4. Движения
Контрольная работа 5 К-5. Начальные сведения из стереометрии
Контрольная работа 6 К-6. ИТОГОВАЯ за 9 класс
Контрольная работа 7 К-7. ИТОГОВАЯ за 7-9 классы
Структура контрольной работы
Каждая контрольная работа рассчитана на один урок. Все работы составлены в четырех вариантах одинакового уровня сложности (только в пособии). Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.
В часть А включаются задания с выбором ответа. Учащимся нужно выбрать из предложенных вариантов либо верное утверждение, либо нужный рисунок. При этом верных ответов может быть несколько, и учащимся необходимо записать номера ответов, которые, по их мнению, верны. Заметим, что, вообще говоря, в заданиях с выбором ответа применяются два подхода. При первом подходе среди предлагаемых вариантов ответа имеется только один правильный. При втором — верных ответов может быть несколько, и результатом решения задачи является не один номер, а все номера верных ответов. При этом задание считается выполненным верно, если указаны номера всех верных ответов.
В часть В входят вычислительные задачи, которые необходимо решить и записать число, которое получилось в результате вычислений.
При выполнении частей А и В контрольной работы учащиеся не записывают ни обоснования, ни вычисления, нужные для решения задач. Все записи или рисунки учащиеся, в случае необходимости, могут делать в черновике. Черновик не сдается учителю и не влияет на оценку за выполнение работы.
В части С имеются и задачи на доказательство, и задачи на вычисление геометрических величин. Решение этих задач должно быть оформлено письменно, как в традиционной контрольной работе. Следует иметь в виду, что при записи решения вычислительных задач, так же как и при решении задач на доказательство, необходимо приводить обоснования с использованием изученных геометрических фактов.
Последняя задача, в каждом варианте отмеченная звездочкой, предназначена для наиболее подготовленных учащихся, успевающих достаточно быстро выполнить все предыдущие задания. В зависимости от уровня подготовленности класса эту задачу можно считать дополнительной и оценивать ее решение отдельно.
Перед проведением первой контрольной работы необходимо проинструктировать учащихся о том, как они должны оформить решение задач. Полезно привести пример, показывающий, как должны выглядеть ответы на задачи частей А и В.
Следует напомнить эти инструкции и при проведении каждой последующей контрольной работы.
Дифференцированный подход к учащимся осуществляется за счет того, что в работах представлены задания разного уровня, которые, как правило, расположены по мере возрастания уровня сложности. Стереометрический материал может изучаться в ознакомительном плане без обязательной проверки его усвоения. Поэтому контрольную № 5 по усмотрению учителя можно не проводить или полученные за нее оценки выставлять в журнал по желанию учащегося.
Номера заданий обязательного уровня, посильных для менее подготовленных учащихся, отмечены кружком. Такие задания представлены во всех трех частях работы.
Следует заметить, что при традиционном письменном оформлении решения задач предлагаемое в контрольных работах количество задач было бы нереально решить за один урок. Однако нужно иметь в виду, что задания с выбором ответа и с кратким ответом не требуют времени на оформление решения и очень часто ответы на них могут быть получены устно. Поэтому основные затраты времени будут связаны с решением задач части С.
Тематика контрольных работ
Каждая тематическая контрольная работа направлена на проверку усвоения материала главы учебника. Одна из итоговых контрольных работ проверяет усвоение материала, изучавшегося в 9 классе, другая составлена по материалу всего курса планиметрии. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах.
Контрольная работа № 1. Векторы. Метод координат
• равенство векторов, координаты и модуль вектора, сложение векторов и умножение вектора на число;
• координаты середины и длина отрезка, заданного координатами концов;
• уравнение окружности;
• средняя линия трапеции.
Контрольная работа № 2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
• теорема синусов, теорема косинусов;
• формула площади треугольника;
• скалярное произведение векторов.
Контрольная работа № 3. Длина окружности и площадь круга
• правильные многоугольники;
• длина окружности и длина дуги окружности;
• площадь круга и кругового сектора.
Контрольная работа № 4. Движения
• понятие движения;
• симметрия относительно прямой, симметрия относительно точки, параллельный перенос; поворот.
Контрольная работа № 5. Начальные сведения из стереометрии
• геометрические тела: призма, параллелепипед, пирамида, цилиндр, конус;
• свойства правильной призмы и правильной пирамиды;
• объемы тел, боковая поверхность цилиндра и конуса;
• сечение прямоугольного параллелепипеда плоскостью.
Итоговая контрольная работа за курс 9 класса
• координаты середины отрезка, заданного координатами концов;
• равенство векторов, модуль вектора;
• скалярное произведение векторов;
• теорема синусов, теорема косинусов;
• длина окружности и площадь круга;
• площадь правильного многоугольника.
Итоговая контрольная работа за курс 7-9 классов
• свойства параллелограмма, прямоугольника и ромба;
• признаки подобия треугольников;
• средняя линия треугольника;
• формулы площади треугольника;
• теорема Пифагора и определения синуса, косинуса и тангенса острого угла прямоугольного треугольника;
• теорема синусов, теорема косинусов.
Геометрия 9 Атанасян (Мельникова) — контрольные работы с ответами, цитаты из пособия «Геометрия 9 класс. Дидактические материалы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова). Цитаты из пособия указаны в учебных целях.
BestMaths
Вектор — это способ представления величины, имеющей размер и направление. например Полет самолета или траектория мяча для крикета
Векторы также используются, чтобы показать, куда перемещается фигура при переводе.
Обозначение
Векторы иногда помечены как или.
Можно представить вектор:
Длина вектора
Длину вектора (называемую его величиной) можно найти с помощью теоремы Пифагора.
Свойства векторов
Умножение на число.
Вектор можно умножить на обычное число (называемое константой или скаляром).
Оба компонента умножаются на число.
например
Умножение вектора на число дает параллельный вектор.
Умножение на отрицательного числа изменяет направление стрелки вектора.
Добавление векторов
Векторов можно сложить вместе.
По матрицам. Добавьте соответствующие элементы.
например
По чертежу . Сформируйте треугольник. Второй вектор добавляется в конец первого вектора. Результирующий вектор (помеченный c) может быть отмечен двумя стрелками. Стрелки на результирующем элементе имеют направление, противоположное добавляемым векторам.
например
показан на схеме. Примечание Стрелки на a и b идут по часовой стрелке. Стрелка на результат c идет против часовой стрелки. |
Решение задач с использованием векторов
Многие типы задач, от физики до навигации, можно решить, нарисовав векторную диаграмму, а затем используя тригонометрию или даже масштабную диаграмму.
Пример
Катер должен переплыть реку Вайкато в Гамильтоне. Он может двигаться со скоростью 10 км / ч в стоячей воде, но река течет со скоростью 6 км / ч. а. Нарисуйте векторный треугольник, чтобы показать это. г. В каком направлении должна идти лодка? | |
а. Векторная диаграмма b. Используйте чертеж в масштабе 1 см: 1 км / ч С помощью транспортира на масштабном чертеже x = 37 ° (с точностью до градуса) | |
Захватывающая и увлекательная практика с подшипниками —
9 класс Физика Векторы
Темы, затронутые в этой небольшой главе:
Векторное количество
Примеры
- Ускорение, скорость, сила, смещение и т. Д.
Скалярная величина
- Примеры включают скорость, время и расстояние.
Графическое представление
Величина и угол представления векторов
Шаг 1:
Шаг 2:
Шаг 3:
или
Пример:
и
Решение
Некоторые свойства сложения векторов
, г.
Где — нулевой вектор.
Пример
и
Решение:
упражнений | Векторы в двух измерениях
Чтобы определить ответ, нам нужно найти величину и направление полученного результата.Тогда это направление, в котором будет толкаться полюс.
Отметим, что у нас более двух векторов, поэтому мы должны сначала найти результирующую в направлении \ (x \) и результирующую в направлении \ (y \).
В направлении \ (x \) у нас есть только один вектор, поэтому он является результирующим.
В направлении \ (y \) у нас есть три вектора. Мы можем сложить их алгебраически, чтобы найти \ (\ vec {R} _ {y} \):
\ begin {align *} \ vec {F} _ {1} & = — \ text {11,7} \ text {N} \\ \ vec {F} _ {2} & = — \ text {6,9} \ text {N} \\ \ vec {F} _ {3} & = — \ text {1,9} \ text {N} \ end {выровнять *}Таким образом, равнодействующая сила:
\ begin {align *} \ vec {F} _ {1} + \ vec {F} _ {2} + \ vec {F} _ {3} & = (- \ text {11,7}) + (- \ text {6,9 }) + (- \ text {1,9}) \\ & = — \ text {20,5} \ end {выровнять *}Теперь мы используем \ (\ vec {R} _ {x} \) и \ (\ vec {R} _ {y} \), чтобы найти результат.{2} \\ R & = \ text {20,63} \ text {N} \ end {align *}
Ориентировочный эскиз поможет определить направление.
Чтобы определить направление результирующей силы, мы вычисляем угол α между вектором результирующей силы и положительной осью \ (x \), используя простую тригонометрию: \ begin {align *} \ tan \ alpha & = \ frac {\ text {противоположная сторона}} {\ text {смежная сторона}} \\ \ tan \ alpha & = \ frac {\ text {2,3}} {\ text {20,5}} \\ \ alpha & = \ tan ^ {- 1} (\ text {0,112}) \\ \ альфа & = \ текст {6,40} \ текст {°} \ end {align *}
Результирующая сила действует в направлении \ (\ text {6,40} \) \ (\ text {°} \) к оси \ (x \).Однако на самом деле мы обозначаем это как \ (\ text {186,4} \) \ (\ text {°} \), чтобы сохранить определенное нами соглашение об указании векторных направлений.
Сложение и вычитание векторов — Практика — Гипертекст по физике
Практика
практическая задача 1
Два человека толкают инвалидную машину. Один прикладывает силу 200 N на восток, другой — 150 N на восток. Какая чистая сила действует на машину? (Предположим, трение незначительно.)
раствор
Силы направлены в одном направлении, поэтому они складываются.
| ∑ F = F 1 + F 2 ∑ F = 200 Н + 150 Н ∑ F = 350 Н |
Две исходные силы — восток, поэтому результирующая — восток.
∑ F = 350 с.ш. восток
Никаких уловок. Некоторые проблемы решаются просто.
практическая задача 2
Два футболиста одновременно бьют по мячу с противоположных сторон.Красный № 3 бьет с силой 50 Н, а синий № 5 бьет с силой 63 Н. Какая чистая сила действует на мяч?
раствор
Силы направлены в противоположные стороны, поэтому они вычитаются. Подумайте об этом по-другому: одна из сил положительна, а другая — отрицательна. Знаки — это способ указать основные направления. Думаю, я сделаю первый положительным, а второй отрицательным, потому что почему бы и нет?
| ∑ F = F красный — F синий ∑ F = 50 Н — 63 Н ∑ F = −13 Н |
Как описать это направление? Никаких сторон света, таких как север, юг, восток или запад, не было.Ничего не было сказано о левом или правом (или даже о верхних или нижних позициях). Мы произвольно присвоили отрицательное значение направлению, в котором пинал Синий № 5. Ответ был отрицательным, поэтому чистая сила указывает в том направлении, в котором пинал Синий № 5. Назовем это подальше от Blue # 5.
∑ F = 13 N от синего # 5
Можно также написать…
∑ F = 13 N в сторону красного # 3
Это тоже был бы хороший ответ. Ни один из них не является более правильным, чем другой.
практическая задача 3
Самолет движется строго на север со скоростью 100 м / с из-за поперечного ветра 30 м / с, дующего с востока на запад. Определите результирующую скорость самолета (относительно севера).
раствор
Север (направление, в котором работают двигатели) перпендикулярно западу (направление, в котором толкает ветер). Результирующая этих двух векторов — гипотенеза прямоугольного треугольника. Воспользуемся теоремой Пифагора, чтобы найти его величину…
| v 2 = | v 2 плоскость + v 2 ветер | |
| v 2 = | (100 м / с) 2 + (30 м / с) 2 | |
| v = | 104 м / с | |
и касательная, чтобы найти его направление…
| тангенс угла θ = | напротив | = | v ветер |
| смежные | v плоскость | ||
| тангенс угла θ = | 30 м / с | ||
| 100 м / с | |||
| θ = | 17 ° | ||
Эти 17 ° находятся на западной стороне севера, поэтому окончательный ответ…
v = 104 м / с, 17 ° к западу от севера
практическая задача 4
Альпинистская экспедиция устанавливает базовый лагерь и два промежуточных лагеря, A и B.Лагерь А находится в 11 200 м к востоку от базового лагеря и на 3 200 м над ним. Лагерь B находится на 8400 м к востоку от лагеря A и на 1700 м выше него. Определите смещение между базовым лагерем и лагерем B.
раствор
Складываем векторы в одном направлении «обычным» сложением.
| x = 11 200 м + 8 400 м x = 19 600 м y = 3200 м + 1700 м y = 4900 м |
Сложите вектора под прямым углом с помощью комбинации теоремы Пифагора для величины…
| r = √ ( x 2 + y 2 ) r = √ [(19600 м) 2 + (4900 м) 2 ] 3 r r = 20 200 м |
и касательная для направления.
| тангенс угла θ = | y | = | 4900 м | |
| x | 19 600 м | |||
| θ = | 14,0 ° | |||
Не забудьте ответить на вопрос.
Лагерь B находится на расстоянии 20 200 м от базового лагеря под углом возвышения 14.0 ° .
Да, и не забудьте нарисовать рисунок. Я, наверное, должен был сказать тебе об этом раньше.
Прочтите вопросы и ответы по физике 9-го класса с несколькими вариантами ответов (MCQ): викторины и практические тесты с ключом ответа (рабочие листы по физике для 9-го класса и краткое руководство) Онлайн, Аршад Икбал
-й класс Вопросы и ответы по физике с несколькими вариантами ответов (MCQ): викторины & Практические тесты с ключом ответа (Рабочие листы по физике для 9-х классов и Краткое руководство) включают в себя рабочие листы оценочных тестов для конкурсного экзамена для решения 800 MCQ.»MCQ 9 Grade 9 Physics MCQ» с ответами охватывает базовые концепции с теоретическими и аналитическими оценочными тестами. Книга в формате PDF «Викторина по физике для 9 класса» помогает отработать контрольные вопросы для онлайн-сертификационного экзамена.
Книга в формате PDF «Физика 9 классов с множественным выбором вопросов и ответов», которую можно загрузить, включает решенные вопросы викторины и ответы на следующие темы: динамика, гравитация, кинематика, свойства материи, физические величины и измерения, тепловые свойства материи, перенос тепла, эффект поворота рабочая тетрадь сил, работы и энергии для школьных и экзаменационных работ в колледже.Загрузка PDF-файла «Викторина по физике для 9 класса» включает вопросы для начинающих, рабочую тетрадь к экзамену и подготовку к сертификационному экзамену с ключом ответа.
Рабочие листы «MCQ по физике 9-го класса» с ответами охватывают базовую терминологию и определения в рабочей тетради самооценки с тестами по физике в главах:
Глава 1: MCQ по динамике
Глава 2: MCQ по гравитации
Глава 3: MCQ по кинематике
Глава 4 : MCQ свойств вещества
Глава 5: MCQ физических величин и измерений
Глава 6: MCQ тепловых свойств вещества
Глава 7: MCQ передачи тепла
Глава 8: Поворачивающий эффект сил MCQs
Глава 9: MCQ работы и энергии
» Dynamics MCQ »PDF с ответами на вопросы теста MCQ: динамика и трение, сила инерции и импульс, сила, инерция и импульс, законы движения Ньютона, трение, типы трения и равномерное круговое движение.
PDF «Gravitation MCQ» с ответами на вопросы теста MCQ: сила тяжести, искусственные спутники, значение g и высота, масса земли, изменение g с высотой.
PDF «Kinematics MCQ» с ответами на вопросы теста MCQ: анализ движения, уравнения движения, графический анализ движения, движение свободно падающих тел, покой и движение, скаляры и векторы, термины, связанные с движением, типы движения .
PDF-файл «Matter Properties MCQ» с ответами на вопросы теста MCQ: кинетическая молекулярная модель вещества, принцип Архимеда, атмосферное давление, упругость, закон Гука, кинетическая молекулярная теория, давление жидкостей, плотность вещества, законы физики, плотность, давление в жидкости, принцип плавучести и давление.
PDF-файл «Physical Quantities and Measurement MCQ» PDF с ответами на вопросы теста MCQ: физические величины, измерительные устройства, измерительные приборы, основные измерительные устройства, введение в физику, основы физики, международная система единиц, наименьший счет, значащие цифры, префиксы , научные обозначения и значащие цифры.
PDF «Тепловые свойства вещества MCQ» с ответами на вопросы теста MCQ: изменение тепловых свойств вещества, тепловое расширение, состояние, равновесие, испарение, скрытая теплота плавления, скрытая теплота испарения, удельная теплоемкость, температура и тепло, преобразование температуры и термометр.
PDF «Передача тепла MCQ» с ответами на вопросы теста MCQ: Тепло, теплопередача и излучение, применение и последствия излучения, теплопроводности, конвекции и теплофизики.
PDF «Эффект поворота сил MCQ» с ответами на вопросы теста MCQ: крутящий момент или момент силы, сложение сил, угловой момент, центр тяжести, центр масс, пара, равновесие, общая физика, принцип моментов, разрешение сил, разрешение векторов, крутящий момент и момент силы.
PDF «Работа и энергия MCQ» с ответами на вопросы теста MCQ: работа и энергия, формы энергии, взаимное преобразование энергии, кинетическая энергия, источники энергии, потенциальная энергия, мощность, основные источники энергии и эффективность .
Исчисление 2, Глава 4 — Векторное исчисление
Обзор
Исчисление — это математика изменения и движения. Исчисление было независимо разработано в конце 17 века Исааком Ньютоном и Готфридом Вильгельмом Лейбницем.Исчисление II — это интегральное исчисление.
В основном в этом курсе мы изучаем множество методов для решения множества различных проблем с приложениями. Пройдя этот курс, вы сможете настраивать и оценивать интегралы, чтобы находить площади и объемы и решать реальные проблемы, вычислять интегралы вручную, используя различные методы, включая подстановки, части, частичные дроби и гиперболическую тригонометрию, анализировать Сходимость последовательностей, рядов,
и степенных рядов, решение элементарных задач векторного анализа
Этот курс состоит из четырех основных глав:
1.Применение интегралов: использование интегралов для поиска площадей и объемов и решения реальных задач
2. Вычисление интегралов вручную: вычисление интегралов вручную с использованием различных методов, включая подстановки, части, частичные дроби и гиперболическую тригонометрию
3. Анализ сходимости последовательностей, рядов и степенных рядов
4. Векторный анализ: решение элементарных задач векторного анализа
Инструктор
Я доктор Миуран Денсил, профессиональный математик, в настоящее время работаю доцентом.Я получил степень магистра и доктора математики в 2016 и 2020 годах в Техасском техническом университете, Техас, США. Во время учебы в колледже я выиграл очень престижную президентскую стипендию для аспирантов на 5 лет, которую получают самые лучшие аспиранты в школе. Я был приглашенным докладчиком на многие признанные конференции и выиграл много грантов на свои исследования. Моя диссертация была посвящена геометрическим свойствам специальных функций и связанных с ними квадратичных дифференциалов. Мои исследовательские интересы включают дифференциальные уравнения с частными производными и теорию чисел.Я окончила Университет Келании, Шри-Ланка, в 2011 году со степенью бакалавра, то есть специальной степенью по математике с отличием первого класса.
Преподавание — моя страсть и призвание! Кроме того, математика — это весело и интерактивно! Я начал преподавать математику в очень молодом возрасте. У меня более 16 лет опыта преподавания и преподавания математики в детском саду для старшеклассников, на уровне колледжа и на уровне выпускников.
После того, как я получил степень бакалавра, я работал инструктором в Университете Келания с 2011 по 2013 год, а затем работал преподавателем в университете Моратува с 2013 по 2015 год.Затем я поступил в аспирантуру Техасского технологического университета, работая ассистентом GPTI / исследователем в 2015-2020 годах.
Я преподавал: исчисление I, II, III + Pre-Cal, AP Cal AB / AP Cal BC, тригонометрия, линейная алгебра, геометрия, ODE / PDE, алгебра 1,2, численные методы, действительный / расширенный анализ, комплексные числа , Дискретная математика, Теория групп / Теория колец / Теория чисел, Интегрирование / Уравнения Лапласа / Преобразование рядов Фурье, Математика для степеней, Механика / Движение частицы / Силовое равновесие / Гармоническое движение, Тренажер для экзаменов, таких как разделы по математике SAT, GRE .
За 16 лет опыта преподавания и долгой академической жизни я нашел методы, которые помогли мне понять и решить любую проблему быстрее и точнее. Теперь я готов преподавать их вам, так как считаю, что нет ничего слишком сложного, если ученик желает учиться.
Поскольку математика является интерактивным и увлекательным предметом, она позволяет студентам получить дополнительную практику и обеспечивает индивидуальную учебную атмосферу для студентов, чтобы отточить их аналитическое мышление и технику решения проблем.
Посмотреть полный профиль
Отличные новости! Миюран хочет помочь тебе раскрыть свой потенциал.
Виртуальное обучение теперь доступно в несколько кликов.
Параллельные векторы — объяснение и примеры
Скалярное умножение дает параллельных векторов. Это векторы, которые:
«Имеют одинаковое или противоположное направление и скалярно кратны друг другу».
В этой теме мы обсудим следующие важные аспекты параллельных векторов:
- Что такое параллельные векторы?
- Как определить, параллельны ли два вектора.
Что такое параллельные векторы?
Обычно два параллельных вектора являются скалярными, кратными друг другу. Предположим, что два вектора a и b, определены как:
b = c * a
Где c — некоторое скалярное действительное число. В приведенном выше уравнении вектор b выражается как скалярное кратное векторам a, , и два вектора называются параллельными. Знак скаляра c будет определять направление вектора b.Если значение c положительное, c> 0, оба вектора будут иметь одинаковое направление. Если значение c отрицательное, то есть c <0, вектор b будет указывать в направлении, противоположном вектору a.
Аналогично, из приведенного выше уравнения вектор a может быть выражен как:
a = 1 / c * b
Таким образом, ясно, что они должны быть скалярными кратными друг другу, чтобы любые два вектора были параллельны. Рассмотрим случай, когда значение c равно нулю.Тогда мы можем написать:
b = 0 * a
b = 0
Вектор b становится в этом случае нулевым вектором, и нулевой вектор считается параллельным каждому вектору.
Как определить, параллельны ли два вектора
Чтобы определить, параллельны ли два вектора или нет, мы проверяем, могут ли данные векторы быть выражены как скалярные кратные друг другу. Например, два вектора U и V параллельны, если существует действительное число t, такое, что:
U = t * V
Это число t может быть положительным, отрицательным или нулевым.
Примеры
В этом разделе мы обсудим примеры, связанные с параллельными векторами и их пошаговые решения. Это поможет глубже понять параллельные векторы.
Пример 1
Автомобиль движется с вектором скорости V1 = 30 м / с на север, а другой автомобиль движется на север с вектором скорости V2 = 60 м / с. Определите, параллельны два вектора скорости или нет.
Решение
У нас есть следующая информация:
V1 = 30 м / с, север
V2 = 60 м / с, север
Чтобы определить, параллельны ли заданные векторы или нет, мы проверяем, могут ли они быть выражены как кратные друг другу или нет.Мы можем связать два вектора как:
V2 = 2 * (30 м / с)
V2 = 2 * V1
V2 = 2 * (30 м / с)
Или,
V1 = 1/2 * V1
V1 = 1/2 * (60 м / с)
V1 = 30 м / с.
Поскольку данные векторы могут быть связаны друг с другом скалярным множителем 2 или 1/2, мы можем заключить, что два вектора скорости V1, и V2, параллельны друг другу.
Пример 2
Для двух векторов S1 = (2, 3) и S2 = (10, 15) определите, параллельны два вектора или нет. 2
| S2 | = √100 + 225
| S2 | = √325
| S2 | = √25 * 13
| S2 | = 5 * √13
Величины двух векторов также связаны коэффициентами масштабирования.
Пример 3
Учитывая два вектора, P = (4, 6) и Q = (-2, -3), определите, параллельны два вектора или нет.
Решение
Данные векторы P и Q выражены в виде столбцов. Чтобы определить, являются ли они параллельными или они, мы можем проверить, могут ли их соответствующие компоненты быть выражены как скалярные кратные друг другу или нет.
P = (4, 6)
Q = (-2, -3)
P = -2 (-2, -3)
P = -2 * Q
Поскольку вектор P в 2 раза больше вектора Q , два вектора параллельны друг другу, а направление вектора Q противоположно направлению вектора P .
Пример 4
Обратитесь к изображению, приведенному ниже, и определите параллельные векторы.
Решение
Все четыре вектора, показанные на изображении, параллельны друг другу, потому что они могут быть выражены как скалярное кратное другим.
Чтобы проверить это, выразите векторы в их формах столбцов как:
A = (10,10) , вектор B = (-10, -10), C = (-5, -5) и D = (5, 5)
Сначала мы проверяем, параллельны ли векторы A и B или нет.
Ясно, что вектор B можно выразить как:
В = (-10, -10)
B = -1 * (10,10)
Или,
B = -1 * A
Таким образом, векторы A, и B, параллельны друг другу.
Затем мы проверяем векторы C и D как:
D = (5, 5)
С = -1 * (5,5)
C = -1 * D
Векторы C и D также являются скалярными, кратными друг другу.
Аналогично проверяем отношения между оставшимися векторами:
B = 2 * C
B = — 2 * D
C = — 2 * A
D = 2 * A
Таким образом, из приведенных выше уравнений и данного изображения ясно, что все четыре вектора, A, , B, , C, и D, параллельны друг другу.
Пример 5
Учитывая, что векторы A = (-4, 6) и B = (x, 12) являются параллельными векторами, определите значение x.
Решение
Поскольку векторы параллельны, мы знаем, что:
B = c * A
Где c — некоторая скалярная величина. Подстановка значений векторов дает нам:
(х, 12) = с * (-4, 6)
(х, 12) = (-4c, 6c)
Устанавливая значения отдельных компонентов равными друг другу, получаем:
х = -4c
12 = 6c
Упрощение приведенных выше уравнений дает:
с = 2
Если мы поместим значение c в другое уравнение и упростим, мы получим:
х = -4 * 2
х = -8
Таким образом, вектор B принимает вид:
B = (-8, 12).
Пример 6
Учитывая вектор m = 5i + 6j +3 в ортогональной системе, определите вектор, параллельный этому вектору, и укажите в противоположном направлении.
Решение
Рассмотрим вектор n , который параллелен данному вектору m. Вектор n можно выразить как:
n = k * м
n = k * (5i + 6j +3)
Где k — скалярное кратное вектору m. Кроме того, k может быть положительным, отрицательным или нулевым. Поскольку было указано, что данный вектор должен указывать в направлении, противоположном направлению м , k не должно быть положительным. То есть k <0. Если k = -3 и получаем:
n = -3 * (5i + 6j +3)
n = ((-3 * 5i + (-3 * 6j) + (-3 * 3))
n = -15i -18j -9
Результирующий вектор n параллелен данному вектору и противоположен по направлению, хотя существует бесконечно много векторов, удовлетворяющих этому критерию.
Практические вопросы- Дан вектор M = 10 м, восток и второй вектор, 3 M, запад . Определите, параллельны два вектора или нет.
- Учитывая вектор N = 15 м северной широты, определите результирующий вектор, полученный умножением данного вектора на -4. Затем проверьте, параллельны ли два вектора друг другу или нет.
- Пусть u = (-1, 4) и v = (n, 20) — два параллельных вектора.Определите значение n.
- Пусть v = (3, 9). Найдите 1/3 v и проверьте, параллельны ли два вектора или нет.
- Дан вектор b = -3i + 2j +2 в ортогональной системе, найдите параллельный вектор.
- Пусть a = (1, 2), b = (2, 3) и c = (2,4). Определите, параллельны ли данные векторы друг другу или нет.
Ответы
- 3 M = 30 м, направление — запад.Ясно, что новый вектор параллелен вектору M , но его направление противоположно направлению вектора M .
- -4 N = -60 м. Направление — юг. Два вектора действительно параллельны друг другу.
- u = k * v , где k = 1/5 и n = -5, v = (-5, 20). Направление u и v остается прежним.
- 1/3 v = (1, 3), | v | = 3 * √10, | 1/3 v | = √10.Направление вектора 1/3 v такое же, как направление вектора v, , и два вектора параллельны друг другу.
- 5 b = -15i + 10j + 10 — один из бесконечного множества векторов, параллельных b .
- Векторы a, и c, параллельны друг другу, но вектор b не параллелен ни одному из двух других.

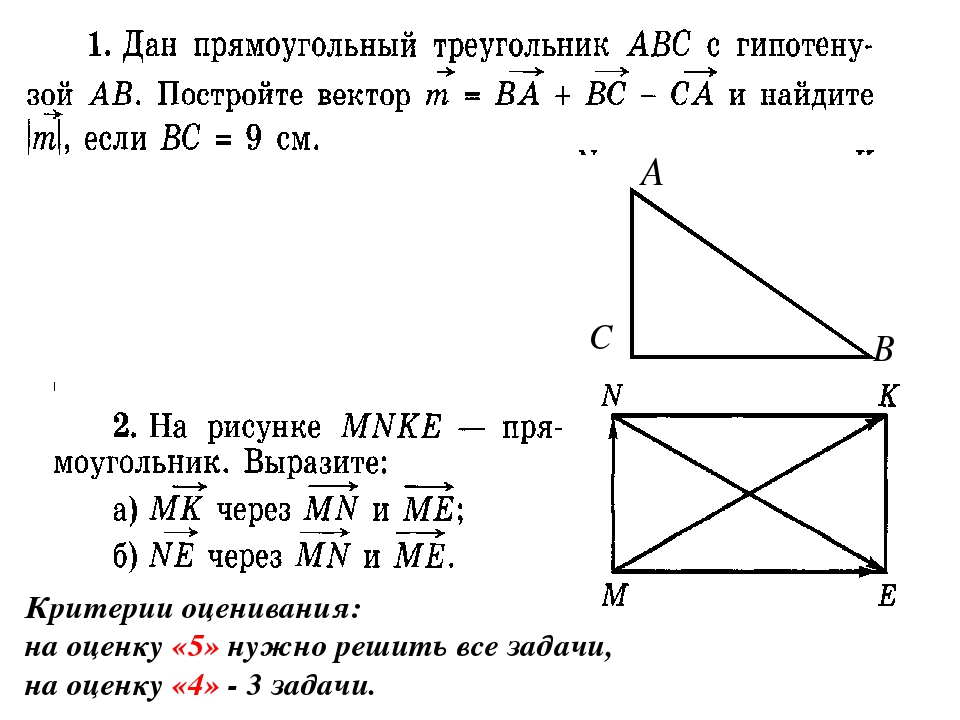

 Если А(5;0) , В(3;-6) – координаты концов отрезка АВ, то его середина имеет координаты….
Если А(5;0) , В(3;-6) – координаты концов отрезка АВ, то его середина имеет координаты….
 Векторы(8 часов)
Векторы(8 часов)
 76,77, вопросы 1-5, №739, 741
76,77, вопросы 1-5, №739, 741
 82, № 757, 763(а,г), 767(устно)
82, № 757, 763(а,г), 767(устно)
 84, №789,790, 788(устно)
84, №789,790, 788(устно)

 Связь между координатами вектора и координатами его начала и конца
Связь между координатами вектора и координатами его начала и конца
 88,89, вопросы 9-13, №930,932
88,89, вопросы 9-13, №930,932
 90, 91, вопросы 15-17, №959(б,г), 966(б,г)
90, 91, вопросы 15-17, №959(б,г), 966(б,г)
 Метод координат»
Метод координат»


 97-99, вопросы 8-11, №1025(б,д,ж,и)
97-99, вопросы 8-11, №1025(б,д,ж,и)
 101,102, вопросы 13-16, №1040
101,102, вопросы 13-16, №1040

 93-104
93-104