Контрольная работа по геометрии «Центральные и вписанные углы окружности» (9 класс)
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 1
Углы MNK и MPN вписаны в одну окружность. Найдите градусную меру угла MKN, если угол MPN равен 400 и точки К и Р лежат:
а) в одной полуплоскости относительно прямой MN;
б) в разных полуплоскостях относительно прямой MN.
По данным рисунка определите градусную меру угла α.
Хорды АВ и CD пересекаются в точке Е. Найдите величину CD, если АЕ = 4см, ВЕ = 9см, а длина СЕ в четыре раза больше длины DE.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 2:4:6 соответственно.

Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 2
Углы АВС и ADC вписаны в одну окружность. Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
а) в одной полуплоскости относительно прямой АС;
б) в разных полуплоскостях относительно прямой АС.
По данным рисунка определите градусную меру угла α
Хорды АВ и CD пересекаются в точке М. АМ = 9см, МВ = 4см, СМ=MD. Вычислите длину хорды CD.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 3:7:8 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 1
Углы MNK и MPN вписаны в одну окружность.
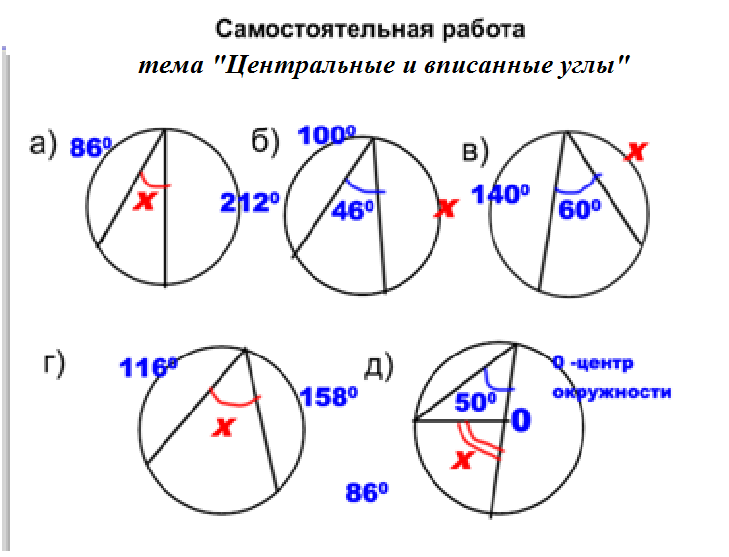 Найдите градусную меру угла MKN, если угол MPN равен 40
Найдите градусную меру угла MKN, если угол MPN равен 40
а) в одной полуплоскости относительно прямой MN;
б) в разных полуплоскостях относительно прямой MN.
По данным рисунка определите градусную меру угла α.
Хорды АВ и CD пересекаются в точке Е. Найдите величину CD, если АЕ = 4см, ВЕ = 9см, а длина СЕ в четыре раза больше длины DE.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 2:4:6 соответственно. Найдите градусную меру большего угла треугольника АВС.
Контрольная работа №3
«Центральные и вписанные углы окружности»
Вариант 2
Углы АВС и ADC вписаны в одну окружность.
 Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
Найдите градусную меру угла АВС, если угол ADC равен 1200 и точки В и D лежат:
а) в одной полуплоскости относительно прямой АС;
б) в разных полуплоскостях относительно прямой АС.
Хорды АВ и CD пересекаются в точке М. АМ = 9см, МВ = 4см, СМ=MD. Вычислите длину хорды CD.
Точки А, В, С делят окружность на три части так, что градусные меры дуг АВ, ВС, АС относятся как 3:7:8 соответственно. Найдите градусную меру большего угла треугольника АВС.
Тест по теме «Вписанные и центральные углы»
Проверочная работа в форме теста по теме «Вписанные и центральные углы». В данной работе выбраны задания с сайта ФИПИ, которые позволяют закрепить понятия центрального, вписанного углов. В работе два варианта. В каждом варианте по семь заданий, систематизированные от простейшего до более сложного.
Просмотр содержимого документа
«тест по теме «Вписанные и центральные углы» »
Вариант 1.
Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
4. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
5.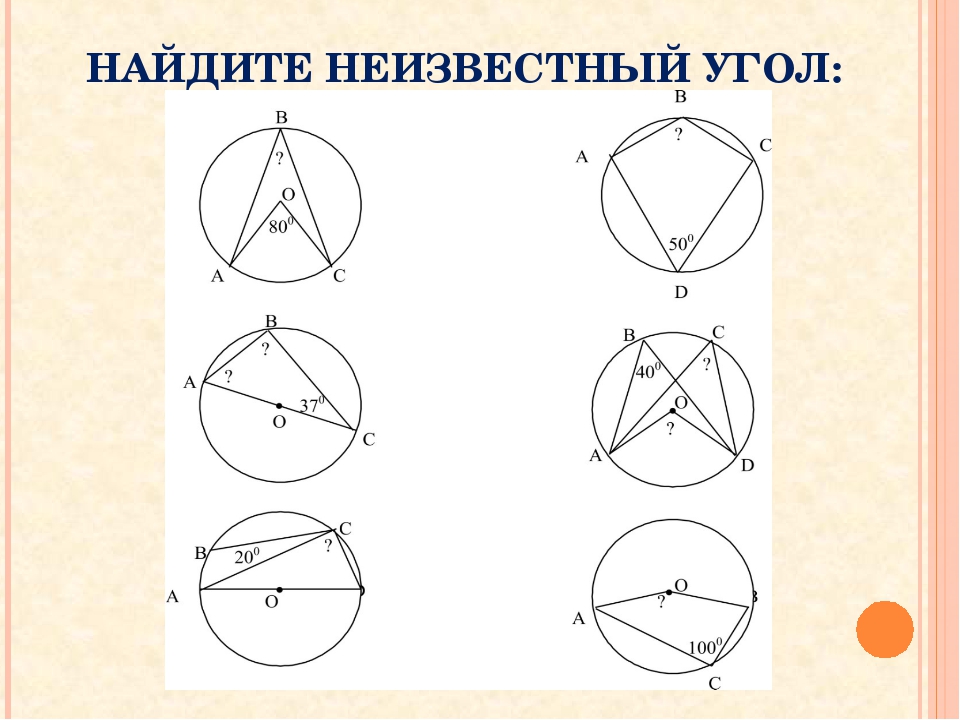 Найдите ∠KOM, если известно, что градусная мера дуги MNравна 124°, а градусная мера дуги KN равна 180°.
Найдите ∠KOM, если известно, что градусная мера дуги MNравна 124°, а градусная мера дуги KN равна 180°.
6. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.
7. На окружности по разные стороны от диаметра AB взяты точки Mи N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.
Вариант 2 1.Точка О — центр окружности, ∠ACB = 65° (см. рисунок). Найдите величину угла AOB (градусах).
|
3.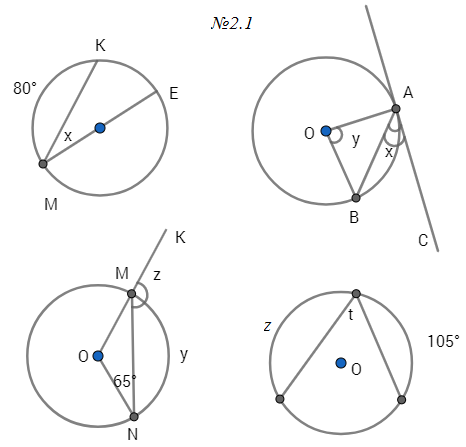 Центральный угол AOB равен 60° . Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
Центральный угол AOB равен 60° . Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
4. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
5. Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера ∠AOC равна 96°.
6. В окружности с центром
7. На окружности по разные стороны от диаметра AB взяты точкиM и N. Известно, что ∠NBA = 70°. Найдите угол NMB. Ответ дайте в градусах.
Учебно-методический материал по геометрии (8, 9 класс) на тему: Работа по теме «Центральные и вписанные углы» по геометрии 8 класса (4 варианта)
- Точка О — центр окружности, ∠AOB =54° (см.
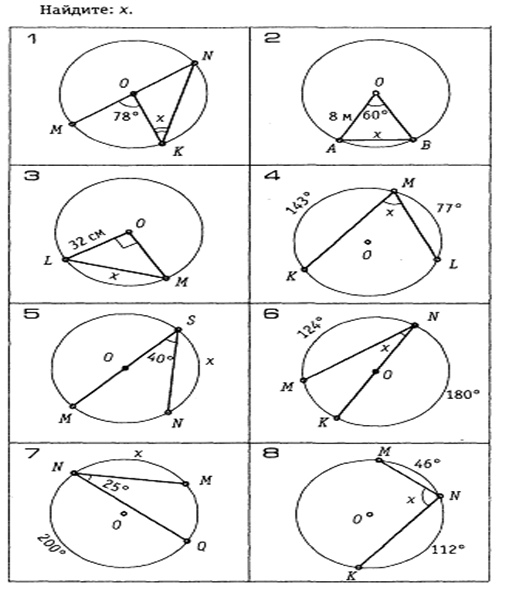 рисунок). Найдите угол ACB .
рисунок). Найдите угол ACB . - Хорда AB = 2,5 см стягивает дугу в 300°. Найдите радиус окружности.
3. Из точки Е, находящейся на окружности, проведены две хорды ЕF и ЕD, лежащие по одну сторону от центра окружности. Найдите ∠DEF, если градусные меры дуг ЕD и EF равны 68° и 150° соответственно.
4. Известно, что КN является диаметром окружности с центром в точке О, точка М лежит на окружности. Найдите ∠KMО, если известно, что градусная мера дуги MN равна 124°.
5. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB.
1.Точка О — центр окружности (см. рисунок),, ∠ACB = 63° . Найдите величину
угла AOB.
2. Дуга AB равна 270°. Найдите длину хорды AB, если радиус окружности см.
3. Из точки Р, находящейся на окружности, проведены хорды РК и РМ, лежащие по разные
стороны от центра окружности. Найдите ∠KРM, если градусные меры дуг KР и РM равны
112° и 170° соответственно.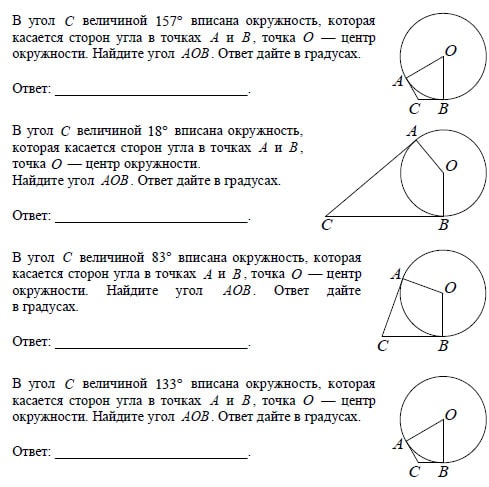
4. Отрезок BC является диаметром окружности с центром в точке О. Точка А лежит на окружности так, что дуга AC= 96°. Найдите градусную меру ∠ОAB.
5. На окружности по одну сторону от диаметра AB взяты точки D и С. Известно, что ∠СBA = 74°. Найдите угол СDB.
- Точка О — центр окружности, ∠AOB = 48° (см. рисунок). Найдите угол ACB .
- Хорда AB = 1,5 см стягивает дугу в 300°. Найдите радиус окружности.
3. Из точки М, находящейся на окружности, проведены две хорды МF и МD, лежащие по одну сторону от центра окружности. Найдите ∠DМF, если градусные меры дуг МF и МD равны 50° и 168° соответственно.
4. Известно, что КА является диаметром окружности с центром в точке О, точка В лежит на окружности. Найдите ∠KВО, если известно, что градусная мера дуги АВ равна 83°.
5. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 26°. Найдите угол NMB.
1.Точка О — центр окружности (см. рисунок), ∠ACB = 56° . Найдите величину
Найдите величину
угла AOB.
2. Дуга AB равна 270°. Найдите радиус окружности, если длина хорды AB= см.
3. Из точки Р, находящейся на окружности, проведены хорды РК и РМ, лежащие по разные стороны от центра окружности. Найдите ∠KРM, если градусные меры дуг KР и РM равны 112° и 140° соответственно.
4.Отрезок BC является диаметром окружности с центром в точке О. Точка А лежит на окружности так, что дуга AC= 86°. Найдите градусную меру ∠ОAB.
5. На окружности по одну сторону от диаметра AB взяты точки D и W. Известно, что ∠WBA = 62°. Найдите угол WDB.
Тест по геометрии по теме «Центральные и вписанные углы», (8 класс)
Проверочный тест по теме
«Центральные и вписанные углы» (8 класс)
I вариант:
Обязательная часть.
А1. Вершины треугольника АВС лежат на окружности. < С = 60, < А = 50.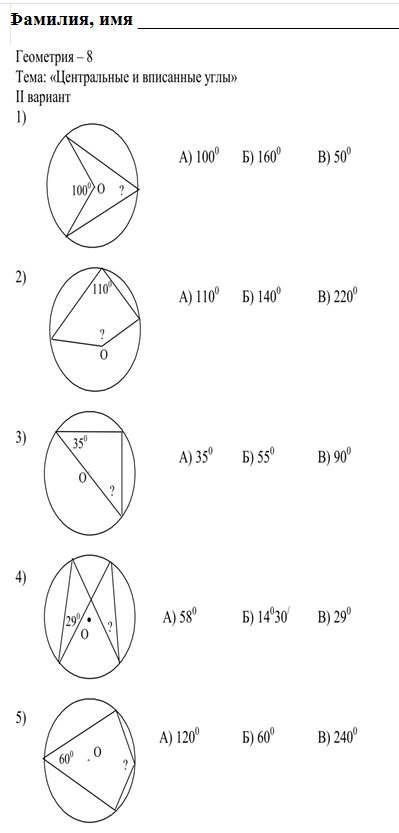 Найдите градусную меру наименьшей из дуг АС.
Найдите градусную меру наименьшей из дуг АС.
Варианты ответов:
1) 140
2) 70
3) 160
4) 120
Ответ: ___
А2. Хорды МК и СР пересекаются в точке Н, причем МН =5см, НК = 8см, СН = 10см. Найдите НР.
1) 4
2) 5
3) 12
4) 2
Ответ: ___
А3. Точки А, В, и С лежат на окружности с центром в точке О. Найдите угол ВСО, если <АВС = 62, < ОАВ = 53.
Варианты ответов:
1) 18
2) 9
3) 6
4) 10
Ответ: ___
А4. Точки А и В лежат на окружности с центром в точке О так, что <АОВ = 20, а длина меньшей дуги АВ равна 88.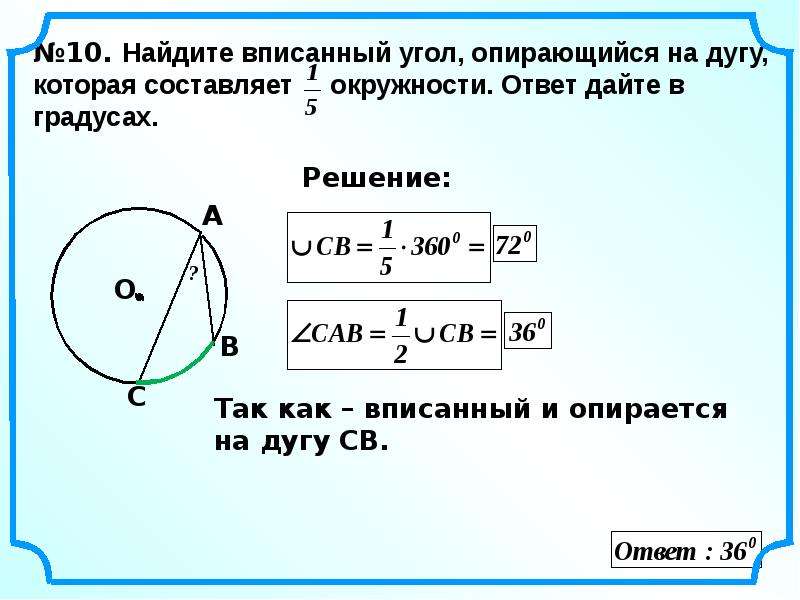 Найдите длину большей дуги АВ.
Найдите длину большей дуги АВ.
Варианты ответов:
1) 748
2) 1496
3) 800
4) 1500
Ответ: ___
Дополнительная часть.
В1. Дана окружность с центром в точке О. Хорды МР и СК пересекаются в точке В так, что МВ = 4, ВР = 15, КВ на 7 больше ВС. Найдите КС.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
II вариант:
Обязательная часть.
А1. Вершины треугольника АВС лежат на окружности. < В = 45, < А = 65.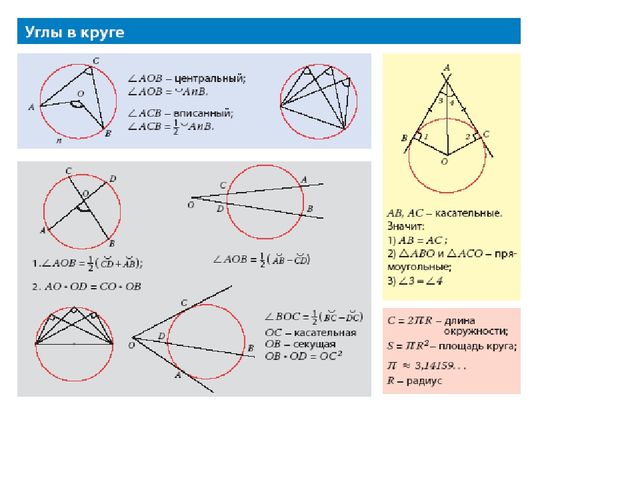 Найдите градусную меру наименьшей из дуг АВ.
Найдите градусную меру наименьшей из дуг АВ.
Варианты ответов:
1) 160
2) 80
3) 110
4) 120
Ответ: ___
А2. Хорды МС и КД пересекаются в точке Р, причем МР =3см, РК = 2см, РС = 8см. Найдите ДР.
1) 6
2) 10
3) 12
4) 24
Ответ: ___
А3. Точки А, В, и С лежат на окружности с центром в точке О. Найдите угол ВСО, если <АВС = 22, < ОАВ = 71.
Варианты ответов:
1) 98
2) 49
3) 28
4) 70
Ответ: ___
А4. Точки А и В лежат на окружности с центром в точке О так, что <АОВ = 18, а длина меньшей дуги АВ равна 5. Найдите длину большей дуги АВ.
Найдите длину большей дуги АВ.
Варианты ответов:
1) 95
2) 190
3) 100
4) 105
Ответ: ___
Дополнительная часть.
В1. Дана окружность с центром в точке О. Хорды МР и СК пересекаются в точке В так, что СВ = 8, ВК = 9, РВ в 2 раза больше ВМ. Найдите МР.
Решение:
______________________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ: ________
ОТВЕТЫ на КР-5 Геометрия 8 (Зив)
ОТВЕТЫ на КР-5 Геометрия 8 (Зив)
Контрольная работа по геометрии «Окружность» (8 класс)
ОТВЕТЫ на КР-5 Геометрия 8 (Зив) — это решения и ответы на контрольную работу № 5 «Окружность» (в 4-х вариантах) из пособия для учащихся «Геометрия.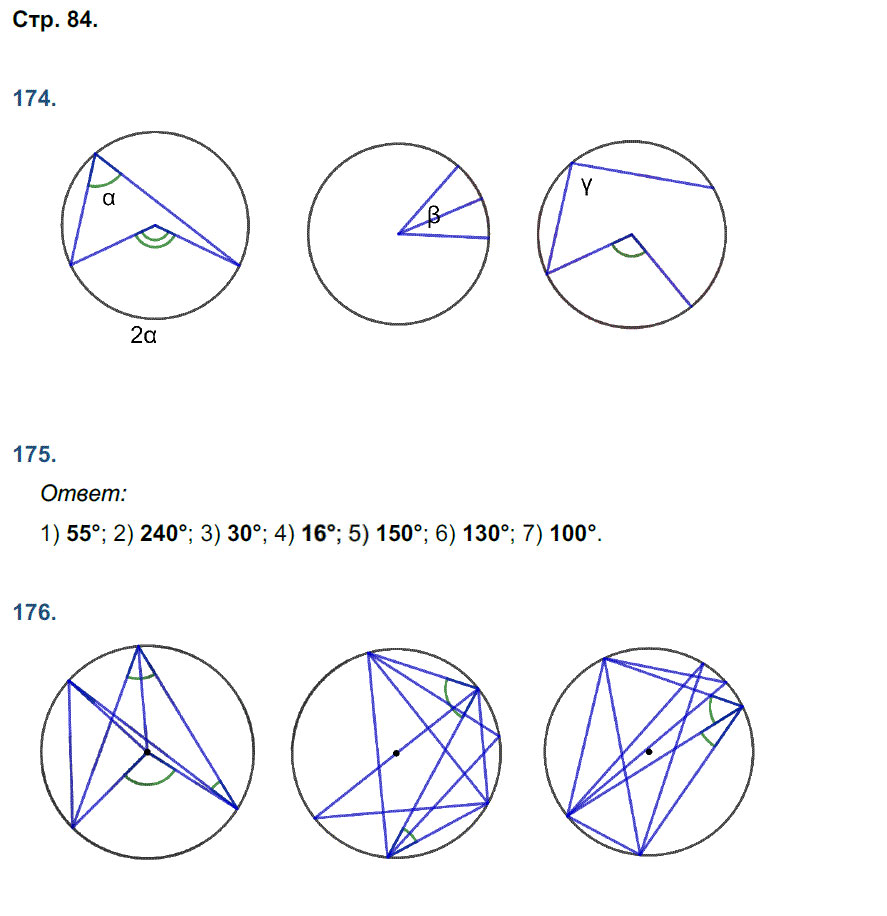 Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной.
Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной.
Геометрия 8 класс (УМК Атанасян и др.)
Контрольная работа № 5 «Окружность».
К–5 Вариант 1
1. В равностороннем треугольнике сторона равна 2√3 см. Найдите радиус вписанной в него окружности.
2. Около остроугольного треугольника АВС описана окружность. Точка О пересечения серединных перпендикуляров удалена от прямой АВ на 6 см. Найдите ∠OBA и радиус окружности, если ∠AOC = 90°, ∠OBC = 15°.
3. В параллелограмм ABCD с углом А, равным 45°, и стороной AD, равной 10√2 дм, вписана окружность.
а) Найдите радиус окружности.
б) Найдите с помощью микрокалькулятора сумму расстояний от вершины D до точек касания окружности с прямыми AD и DC.
4*. Даны окружность диаметра АВ и точка О внутри нее. Используя только линейку без делений, опустите перпендикуляр из точки О на прямую АВ.
Используя только линейку без делений, опустите перпендикуляр из точки О на прямую АВ.
К–5 Вариант 2
1. В равнобедренном треугольнике ABC ∠B = 120°. Радиус окружности, описанной около треугольника, равен 2 см. Найдите сторону АВ.
2. В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон треугольника АВ, ВС, АС в точках М, Т, Р соответственно. Расстояние от точки пересечения биссектрис треугольника АВС до вершины С равно √8 см. Найдите радиус окружности, угол ТОР и угол ТМР.
угол ТОР и угол ТМР.
3. Стороны АВ и CD четырехугольника ABCD, вписанного в окружность радиуса 4 см, параллельны и имеют равные длины, ∠ADB = 60°.
а) Найдите АВ.
б) Какие значения может принимать угол МВС, если М – точка окружности – равноудалена от концов отрезка ВС?
4*. Даны два отрезка PQ и ЕТ (ЕТ > PQ). Постройте четырехугольник ABCD, в котором АВ = ВС = PQ, BD = ЕТ, диагонали пересекаются в точке О и АО • ОС = ВО • OD.
К–5 Вариант 3
1. В треугольнике ABC ∠A = 60°. Радиус окружности, вписанной в этот треугольник, равен 1 см. Найдите расстояние от точки касания окружности и прямой АС до вершины А.
В треугольнике ABC ∠A = 60°. Радиус окружности, вписанной в этот треугольник, равен 1 см. Найдите расстояние от точки касания окружности и прямой АС до вершины А.
2. В треугольнике АВС с тупым углом В О – точка пересечения серединных перпендикуляров, АС = 4√2 дм, ∠AOC = 90°. Найдите радиус окружности, описанной около треугольника, и ∠ABC.
3. В трапецию ABCD вписана окружность с центром О и радиуса 6 см, ∠CAD = 45°, ∠ACD = 90°.
а) Найдите сумму ВС + AD, если АВ = 10√2 см.
б) Найдите произведение ОС • OD.
4*. Даны окружность диаметра АВ и точка О вне ее. Используя только линейку без делений, опустите перпендикуляр из точки О на прямую АВ.
К–5 Вариант 4
1. Радиус окружности, описанной около треугольника АВС, √8 см, а два угла треугольника равны по 45°. Найдите стороны треугольника АВС.
2. В равнобедренном треугольнике ABC ∠B = 120°, О – точка пересечения биссектрис. Окружность радиуса 2√3 см вписана в этот треугольник и касается прямых ВС и АС в точках D и Е соответственно. Найдите ВО и ∠BED.
Найдите ВО и ∠BED.
3. Трапеция ABCD вписана в окружность, ∠A = 60°, ∠ABD = 90°, CD = 4 см.
а) Найдите радиус окружности.
б) Какие значения может принимать угол ВМС, если М – произвольная точка окружности?
4*. Даны два отрезка PQ, ЕТ и угол Н. Постройте четырехугольник ABCD, в котором О – точка пересечения диагоналей, ВО = PQ, DO = ET, ∠DOC = ∠H и АО • ОС = = DO • ОB.
Геометрия 8 класс (УМК Атанасян и др.)
ОТВЕТЫ на КР-5 Геометрия 8 (Зив)
Контрольная работа по геометрии 8 класс. Окружность (Атанасян). Ответы и решения.
ОТВЕТЫ на КР-5 Геометрия 8 (Зив) — это решения и ответы на контрольную работу № 5 «Окружность» (в 4-х вариантах) из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И. И. Юдиной.
И. Юдиной.
Геометрия 8 класс Контрольная № 5 с ответами
Контрольная работа по геометрии в 8 классе «Окружность» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. ГЛАВА VIII. ОКРУЖНОСТЬ. Урок 66. Геометрия 8 класс Контрольная № 5 по теме «Окружность».
Смотреть Список всех контрольных по геометрии в 8 классе УМК Атанасян.
Контрольная работа № 5
«Окружность»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Выполнение контрольной работы
Контрольная работа по геометрии 8 класс.
I уровень сложности
Вариант 1
- АВ и АС — отрезки касательных, проведенные к окружности радиусом 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см.
- Дано: ∪АВ : ∪BC = 11 : 12 (рис. 8.178). Найти: ∠BCA, ∠BAC.
- * Окружность с центром О и радиусом 16 см описана около треугольника АВС так, что ∠OAB = 30°, ∠OCB = 45°. Найдите стороны АВ и ВС треугольника.
Вариант 2
- MN и МК — отрезки касательных, проведенные к окружности радиусом 5 см. Найдите MN и МК, если МО = 13 см.
- Дано: ∪АВ : ∪АС = 5 : 3 (рис. 8.179). Найти: ∠BOC, ∠ABC.
- Хорды АВ и CD пересекаются в точке F так, что АF = 4 см, BF = 16 см, CF = DF. Найдите CD.
- * Окружность с центром О и радиусом 12 см описана около треугольника MNK так, что ∠MON = 120°, ∠NOK= 90°. Найдите стороны MN и NK треугольника.
Контрольная работа по геометрии.
II уровень сложности
Вариант 1
- В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см, 4 см, 5 см. Определите вид треугольника.
- Точки А и В делят окружность с центром О на дуги AMВ и АСВ так, что дуга АСВ на 60° меньше дуги AMВ. AM — диаметр окружности. Найдите углы АМВ, АВМ, АСВ.
- Хорды АВ и CD пересекаются в точке Е так, что АЕ = 3 см, BE = 36 см, СЕ : DE = 3 : 4. Найдите CD и наименьшее значение радиуса этой окружности.
- * В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию, — 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
Вариант 2
- В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см.
 Найдите стороны треугольника, если его периметр равен 24 см.
Найдите стороны треугольника, если его периметр равен 24 см. - Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 90° меньше дуги ЕАН, ЕА — диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН.
- Хорды MN и РК пересекаются в точке А так, что МА = 3 см, NA = 16 см, РА : КА = 1 : 3. Найдите РК и наименьшее значение радиуса этой окружности.
- * В равнобедренном треугольнике основание равно 10 см, а высота, проведенная к ней, — 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
Контрольная работа по геометрии.
III уровень сложности
Вариант 1
- Найдите радиус окружности, вписанной в треугольник, и радиус окружности, описанной около треугольника, стороны которого равны 20 см, 26 см и 26 см.
- Расстояния от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны равны 6 см и 8 см.
 Найдите площадь трапеции.
Найдите площадь трапеции. - Точка М лежит на хорде АВ так, что AM : ВМ = 4 : 3, АВ = 14 см. Расстояние от центра окружности до точки М равно 4 см. Найдите радиус окружности.
- * Точка О равноудалена от сторон треугольника АВС, ∠АСО = 34°. Найдите ∠АОВ.
Вариант 2
- Найдите радиус окружности, вписанной в треугольник, и радиус окружности, описанной около треугольника, стороны которого равны 16 см, 17 см и 17 см.
- Расстояния от центра вписанной в равнобедренную трапецию окружности до концов боковой стороны равны 9 см и 12 см. Найдите площадь трапеции.
- Точка Е делит хорду АВ так, что BE на 1 см меньше АЕ. Радиус окружности равен 9 см, АВ = 15 см. Найдите расстояние от центра окружности до точки Е.
- * Точка О равноудалена от вершин треугольника АВС, ∠АВО = 48°. Найдите ∠АСВ.
3. Рефлексия учебной деятельности
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.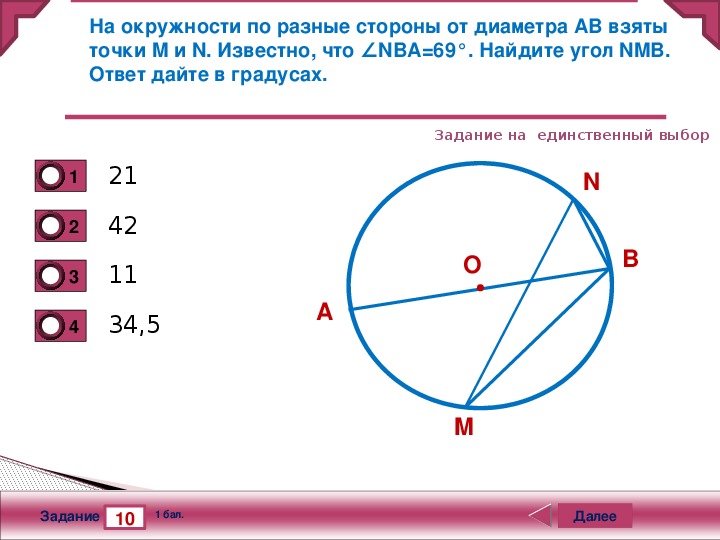
Домашнее задание: решить задачи, с которыми ученик не справился.
Решения и ответы на контрольную работу
I уровня сложности
Решения и ответы на контрольную работу
II уровня сложности
Решения и ответы на контрольную работу
III уровня сложности
Критерии оценивания результатов контрольной работы
- оценка «5» — правильно решены четыре задачи;
- оценка «4» — правильно решены три задачи или правильно решены две задачи, а при решении двух других задач допущены ошибки;
- оценка «3» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
- оценка «2» — правильно решено менее двух задач.
За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.
Вы смотрели: Геометрия 8 класс Контрольная № 5. Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 66. Контрольная работа № 5 по теме «Окружность» + ОТВЕТЫ и РЕШЕНИЯ.
Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 66. Контрольная работа № 5 по теме «Окружность» + ОТВЕТЫ и РЕШЕНИЯ.
Смотреть Список всех контрольных по геометрии в 8 классе по УМК Атанасян.
Вернуться к Списку уроков Тематического планирования в 8 классе.
вписанных углов в круг
Именной
угол — это угол, вершина которого находится на окружности, а стороны содержат
хорды круга. Дуга, которая лежит
внутри вписанного угла и имеет концы на углу, называется
перехваченная дуга угла.
Теорема (мера вписанного угла)
Если в круг вписан угол, то его
мера — половина меры его перехваченной дуги.
Это показано ниже.
На диаграмме, показанной выше, мы имеем
м ADB = 1/2 ⋅ м∠ дуга AB
Теорема о двух вписанных углах
Если два вписанных угла окружности пересекают одну и ту же дугу, то эти углы совпадают.
Это показано ниже.
На схеме, показанной выше, мы имеем
м∠C ≅ м∠D
Определение мер дуг и вписанных углов
Пример 1:
Найдите меру синего дуга.
Решение:
m∠arc QTS = 2 ⋅ m∠QRS = 2 ⋅ 90 ° = 180 °
Пример 2:
Найдите размер синей дуги.
Решение:
m∠arc ZWX = 2 ⋅ m∠ZYX = 2 ⋅ 115 ° = 230 °
Пример 3:
Найдите величину синего угла.
Раствор:
м∠NMP = 1/2 ⋅ m∠arc NP = 1/2 ⋅ 100 ° = 50 °
Сравнение размеров вписанных углов
Пример:
Найдите m∠ACB, m∠ADB и m∠AEB на схеме, показанной ниже.
Решение:
На диаграмме, показанной выше, вписанные углы m∠ACB, m∠ADB и m∠AEB пересекают ту же дугу AB.
Итак, размер каждого угла равен половина меры дуги AB.
То есть
м∠дуги AB = 60 °
Таким образом, размер каждого угла равен 30 °.
То есть
m∠ACB = m∠ADB = m∠AEB = 60 °
Определение меры угла
Пример:
На диаграмме ниже указано, что mE =
75 °.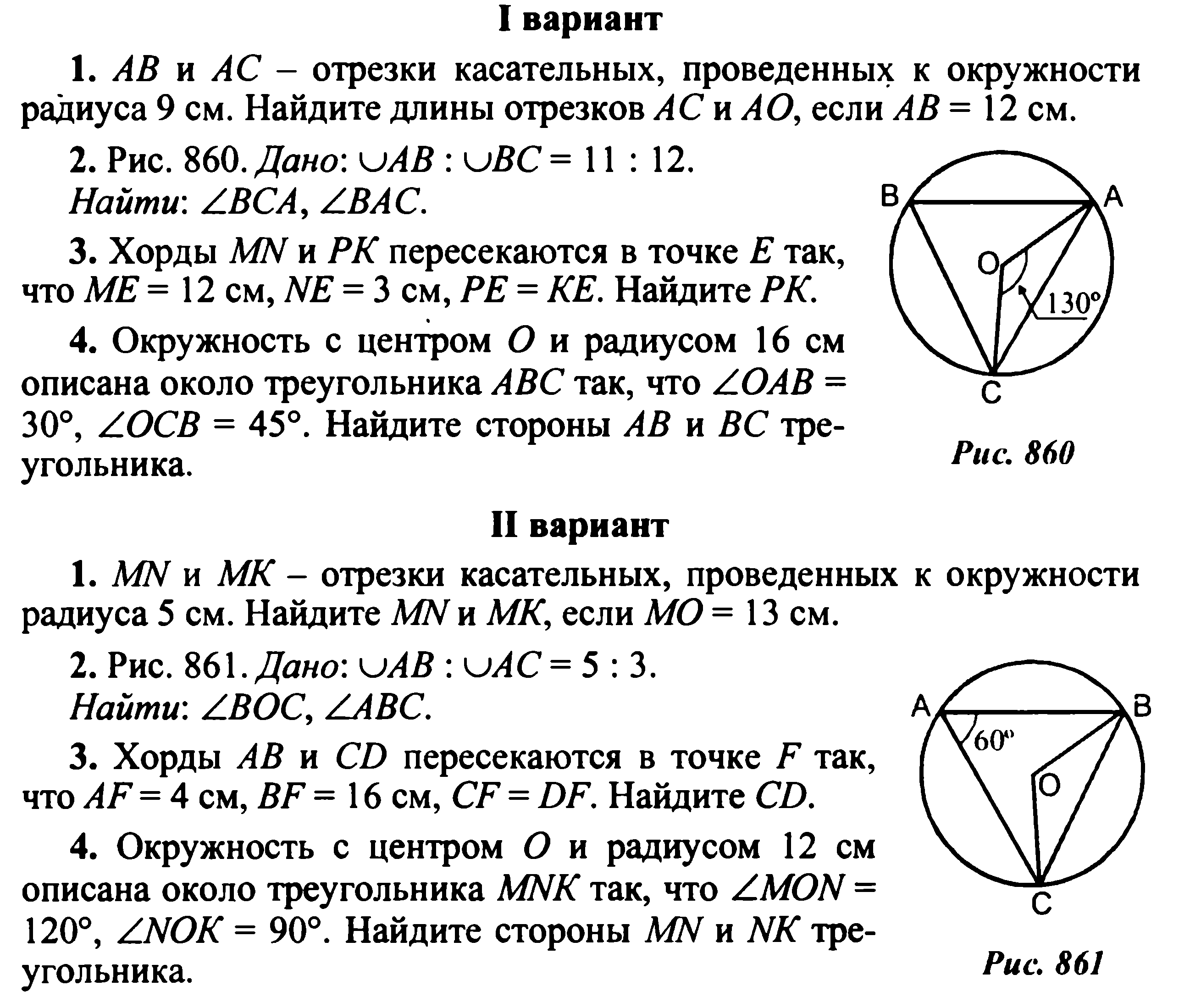 Что такое m∠F?
Что такое m∠F?
Решение:
m∠E и m∠F оба пересекают дугу GH, поэтому ∠E ≅ ∠F.
Итак, имеем
m∠F = m∠E = 75 °
Измерение вписанного угла
Пример:
Когда мы идем в кино, мы можем захотеть быть ближе к экрану фильма, но мы не хотим, чтобы глаза слишком много, чтобы видеть края картинки.
На схеме, показанной ниже, если E и G являются концами экран и мы находимся на F, m∠EFG называется нашим просмотром угол.
Решаем, что у середины шестого ряда лучший угол обзора. Если кто-то сидит там, где еще мы можем сесть, чтобы иметь такой же угол обзора?
Решение:
Нарисуйте круг, определяется конечными точками экрана и центральным сиденьем шестого ряда. В любом другом месте круга будет такой же угол обзора, как показано ниже.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
v4formath@gmail. com
com
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебра 4 задачи на слова 9000
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
Word по типам ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных дробях
Одношаговые задачи о словах с уравнениями
Проблемы с линейными неравенствами
Слово соотношения и пропорции задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами в теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Домен и диапазон рациональных функций
Область и диапазон рациональных функций функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью long di видение
L. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Урок Равнобедренную трапецию можно вписать в круг
Равнобедренную трапецию можно вписать в круг
Задача 1
Если трапеция равнобедренная, ее можно вписать в круг. Докажи.
Докажи.
Задача 1
Если трапеция равнобедренная, ее можно вписать в круг. Докажи.
Докажи. Проба
| Пусть ABCD будет равнобедренной трапецией с основаниями AB и CD и боковые стороны AD и BC ( Рисунок 1a ). Нам нужно доказать, что существует круг, который проходит через все вершины Нарисуем диагонали трапеции AC и BD ( Рисунок 1b ) и Эти треугольники имеют общую сторону AB и конгруэнтные стороны BC и | Рисунок 1а .К проблеме 1 | Рисунок 1b . К решению задачи 1 |
Углы L BAD и L ABC , заключенные между этими конгруэнтными сторонами, совпадают как базовые углы равнобедренной трапеции (см.
 Урок
Урок Трапеции и их базовые углы в теме Многоугольники раздела Геометрия на этом сайте).
Следовательно, треугольники ABC и ABD конгруэнтны в соответствии с тестом SAS на конгруэнтность треугольников.
Это означает, что углы L ACB и L ADB совпадают как соответствующие углы конгруэнтных треугольников.
Таким образом, углы L ACB и L ADB совпадают и опираются на один и тот же сегмент AB .Значит, эти углы вписываются в круг в соответствии с уроком.
Обратная теорема о вписанных углах в теме Окружности и их свойства раздела Геометрия на этом сайте.
Доказательство завершено.
Обратное утверждение доказано в уроке Две параллельные секущие окружности, отсекающие конгруэнтные дуги в теме Окружности и их свойства раздела Геометрия на этом сайте: если трапеция вписана в круг, то трапеция равнобедренная.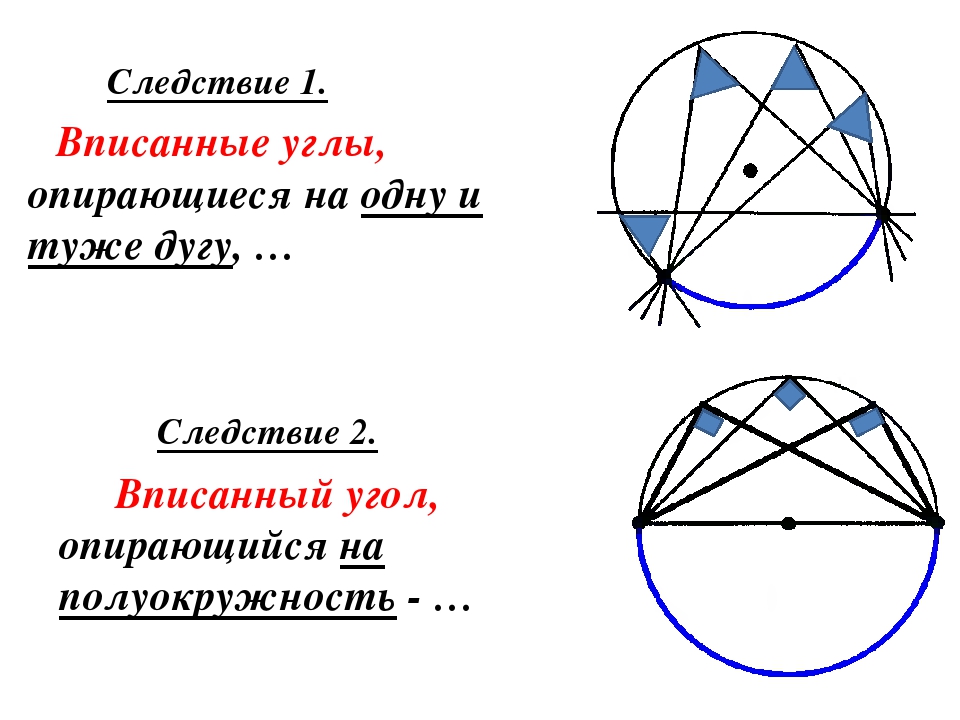
Комбинируя прямое и обратное утверждения, вы можете заключить, что трапеция может быть вписана в круг тогда и только тогда, когда трапеция равнобедренная .
Другие мои уроки по кругам на этом сайте в логическом порядке
— Окружность, ее хорды, касательные и секущие линии — основные определения,
— Чем длиннее хорда, тем больше ее центральный угол,
— Хорды окружности и радиусы, перпендикулярные хордам,
— Касательная линия к окружности перпендикулярна радиусу, проведенному к точке касания,
— Угол, вписанный в круг,
— Две параллельные секущие окружности, отсекающие конгруэнтные дуги,
— Угол между двумя хордами, пересекающимися внутри круга,
— Угол между двумя секущими, пересекающимися вне круга,
— Угол между хордой и касательной к окружности,
— Касательные сегменты к окружности от точки вне окружности,
— Обратная теорема о вписанных углах,
— Части хорд, пересекающиеся внутри круга,
— Метрические соотношения для секущих, пересекающихся вне круга и
— Метрические соотношения для касательной и секущей линий, выпущенных из точки за пределами круга
в разделе Окружности и их свойства раздела Геометрия и
— КАК РАЗДЕЛАТЬ дугу в окружности с помощью циркуля и линейки,
— КАК найти центр круга, заданного двумя аккордами,
— Решенные задачи по радиусу и касательной к окружности,
— Решенные задачи по вписанным углам,
— Свойство углов четырехугольника, вписанного в круг,
— КАК построить касательную линию к окружности в заданной точке окружности,
— КАК построить касательную линию к окружности через заданную точку вне окружности,
— КАК построить общую внешнюю касательную к двум окружностям,
— КАК построить общую внутреннюю касательную к двум окружностям,
— Решенные задачи на хордах, которые пересекаются внутри круга,
— Решенные задачи на секущих, которые пересекаются вне круга,
— Решенные задачи касательной и секущей линии, выпущенной из точки за пределами круга
— Радиус круга, вписанного в прямоугольный треугольник
— Решенные проблемы касательных линий, выпущенных из точки за пределами круга
под текущую тему.
Обзор уроков по Свойствам Кругов находится в этом файле СВОЙСТВА КРУГОВ, ИХ ХОРДЫ, СЕКАНТЫ И ТАНГЕНТЫ.
Вы можете использовать файл обзора или список ссылок выше для навигации по этим урокам.
Для навигации по всем темам / урокам онлайн-учебника по геометрии используйте этот файл / ссылку ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.
Углы в круге — манекены
- Образование
- Математика
- Тригонометрия
- Углы в круге
Мэри Джейн Стерлинг
Есть несколько способов нарисовать угол в круге, и каждый из них имеет особый способ вычисления размера этого угла.Четыре различных типа углов: центральный, вписанный, внутренний и внешний. Здесь вы видите примеры этих различных типов углов.
Центральный угол
Центральный угол имеет вершину в центре окружности, а стороны угла лежат на двух радиусах окружности. Мера центрального угла такая же, как мера дуги, которую две стороны вырезают из круга.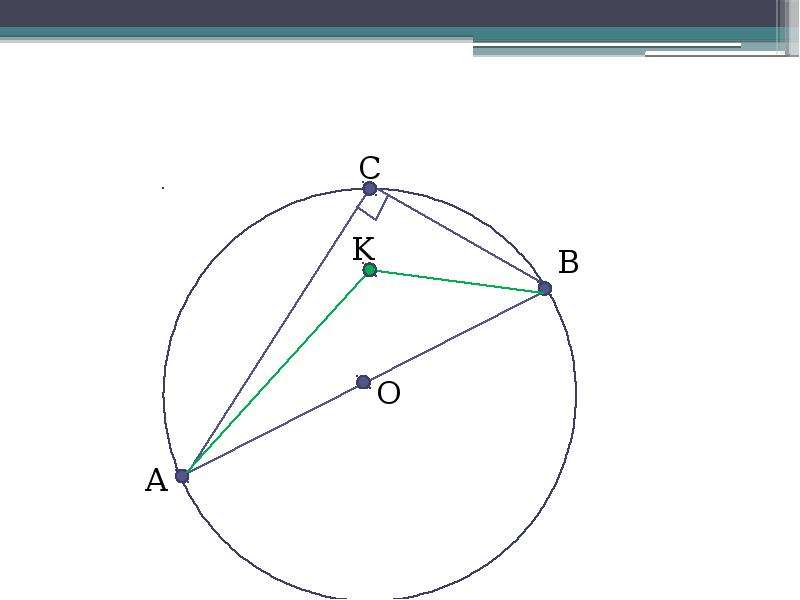
Уголок вписанный
Вписанный угол имеет вершину на окружности, а стороны угла лежат на двух хордах окружности.Размер вписанного угла составляет половину дуги, которую две стороны вырезают из круга.
Уголок внутренний
Внутренний угол имеет вершину на пересечении двух прямых, пересекающихся внутри круга. Стороны угла лежат на пересекающихся линиях. Мера внутреннего угла — это среднее значение мер двух дуг, которые вырезаны из круга этими пересекающимися линиями.
Внешний угол
Внешний угол имеет вершину, в которой два луча имеют общую конечную точку вне круга.Стороны угла — это два луча. Мера внешнего угла находится путем деления разницы между размерами пересеченных дуг на два.
Пример: Найдите угол EXT , учитывая, что внешний угол отсекает дуги в 20 градусов и 108 градусов.
Найдите разницу между размерами двух пересеченных дуг и разделите на 2:
Угол EXT составляет 44 градуса./918870b1bc4a305.s.siteapi.org/img/8aa195e2cfb8b8b18f3ad80023d4eae977f22c8f.jpg)
Сектора
Сектор круга — это сечение круга между двумя радиусами (во множественном числе). Вы можете рассматривать эту часть как кусок пирога, вырезанный из круглой тарелки.
Вы можете найти площадь сектора круга, если знаете угол между двумя радиусами. Круг имеет в общей сложности 360 градусов вокруг центра, поэтому, если этот центральный угол, определяющий сектор, имеет угловую меру 60 градусов, тогда сектор занимает 60/360 или 1/6 градусов на всем пути. около.В этом случае сектор составляет 1/6 площади всего круга.
Пример: Найдите площадь сектора круга, если угол между двумя радиусами, образующими сектор, составляет 80 градусов, а диаметр круга равен 9 дюймам.
Найдите площадь круга.
Площадь всего круга
или около 63,6 квадратных дюймов.
Найдите часть круга, которую представляет сектор.
Сектор занимает всего 80 градусов окружности.
. Разделите 80 на 360, чтобы получить
Разделите 80 на 360, чтобы получитьВычислить площадь сектора.
Умножьте дробную или десятичную дробь из шага 2 на общую площадь, чтобы получить площадь сектора:
Весь круг имеет площадь почти 64 квадратных дюйма, а сектор — чуть более 14 квадратных дюймов.
Об авторе книги
Мэри Джейн Стерлинг является автором книги Алгебра I для чайников и многих других книг Для чайников .Она преподавала математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет и любила работать с будущими руководителями бизнеса, физиотерапевтами, учителями и многими другими.
Площадь прямоугольника, вписанного в круг
Беннет, у нас есть для вас два ответа.
Привет, Беннет.
Я нарисовал произвольный прямоугольник, вписанный в круг, радиус которого равен R ниже:
Как видите, радиус окружности равен длине гипотенузы прямоугольного треугольника, который 8 раз дублируется в прямоугольнике:
Это означает, что площадь прямоугольника в 8 раз больше площади одного из прямоугольных треугольников.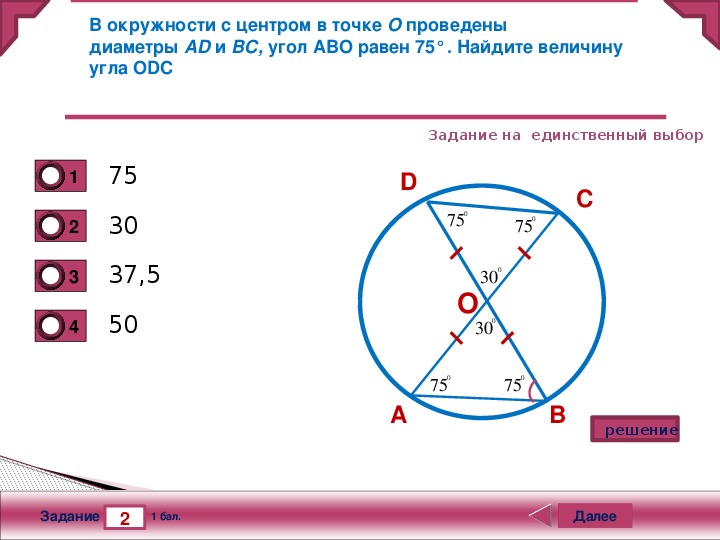 И, конечно же, площадь каждого прямоугольного треугольника — это просто ½bh , где этими переменными являются основание и высота.
И, конечно же, площадь каждого прямоугольного треугольника — это просто ½bh , где этими переменными являются основание и высота.
Пропорциональные величины треугольника, конечно, зависят от формы прямоугольника, с предельными размерами от бесконечно короткого до бесконечно тонкого, при этом середина диапазона — квадрат. Вот набросок нескольких из них, наложенных на круг:
Итак, наименьшая область прямоугольника, несомненно, является бесконечно тонкой или короткой, поскольку ее другое измерение в основном равно R.Это означает, что наименьшая возможная область — 8 (½) (0) (R) , что равно нулю. Настоящий вопрос в том, какова максимально возможная площадь.
Интуиция должна сказать вам, что квадрат — это самая большая площадь, и ваша интуиция будет правильной, но это не удовлетворительный ответ на вопрос математики. Давайте еще раз посмотрим на эти треугольники:
Вот несколько возможных форм. Гипотенуза всегда имеет длину R единицы, так что это означает, что мы можем использовать тригонометрию, чтобы найти площадь треугольника.Назовем угол в углу треугольника, который находится в центре окружности, A . Это нижний левый угол в этих треугольниках.
Гипотенуза всегда имеет длину R единицы, так что это означает, что мы можем использовать тригонометрию, чтобы найти площадь треугольника.Назовем угол в углу треугольника, который находится в центре окружности, A . Это нижний левый угол в этих треугольниках.
Это означает, что длина основания составляет RcosA единиц, а высота — RsinA единиц. Таким образом, площадь треугольника ½R 2 cosA sinA . Таким образом, площадь всего прямоугольника в восемь раз больше: 4R 2 cosA sinA .Какое значение A дает нам наибольшую общую площадь?
Для этого мы можем использовать несколько методов, но самый простой — это расчет. Критические точки этой функции могут сказать нам, какой угол A должен быть максимальным.
Производная 4R 2 cosA sinA равна 4R 2 (cos 2 A — sin 2 A) ; Я использовал правило продукта, чтобы получить это. Когда он равен нулю, у нас есть критическая точка, которая является значением A, для которого мы получаем максимальную площадь.
Когда он равен нулю, у нас есть критическая точка, которая является значением A, для которого мы получаем максимальную площадь.
Таким образом, cos 2 A = sin 2 A и, следовательно, cosA = sinA . Поскольку косинус — это основание над гипотенузой R , а синус — это высота над гипотенузой R , это означает, что основание = высота . А это означает равнобедренный прямоугольный треугольник, поэтому прямоугольник и есть квадрат. Мы давно доказали то, что подсказывала нам интуиция.
Таким образом, площадь прямоугольника ограничена от 0 до площади квадрата, длина диагонали которого составляет 2R .
Надеюсь, это поможет,
Стивен Ла Рок.
Беннет,
На самом деле — каждый прямоугольник можно вписать в (уникальный круг), поэтому ключевым моментом является то, что радиус круга равен R (я думаю).
Одно из свойств прямоугольника состоит в том, что диагонали делят пополам «центр» прямоугольника, который также будет центром описывающего круга.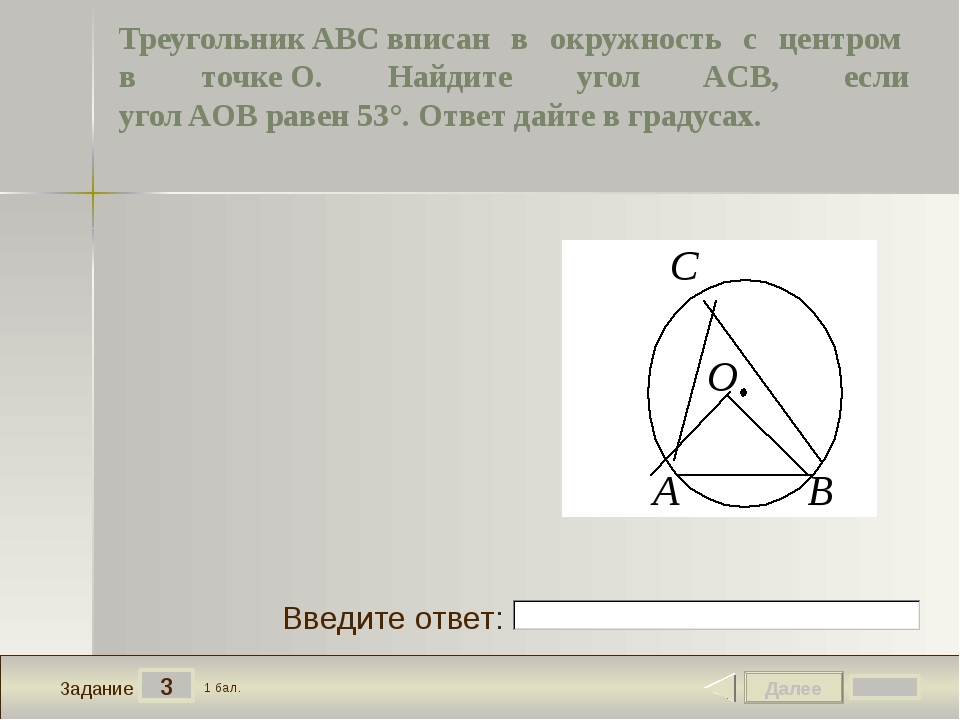 Теперь «максимум» и «минимум» лучше всего представить (и отобразить) с помощью такой программы, как Geometer’s Sketchpad, где вы можете поиграть с параметрами.
Теперь «максимум» и «минимум» лучше всего представить (и отобразить) с помощью такой программы, как Geometer’s Sketchpad, где вы можете поиграть с параметрами.
Вместо того, чтобы давать ответ, позвольте мне пройти пару примеров из программы, чтобы стимулировать ваше воображение:
Вы можете видеть, что область становится больше, а затем меньше по мере того, как угол перемещается по четверти круга.
Думаю, отсюда можно определить наименьшую площадь. Самая большая область — это большая сложность, но, опять же, я думаю, вы можете ее «увидеть». Если вы не уверены, можете подумать о максимальной площади треугольника ABC (все диагонали имеют одинаковую длину — 2R).
Целый прямоугольник — это всего лишь два из этих треугольников. Опять же, если вы не совсем уверены, визуально будет немного легче, если вы «наклоните голову» и сделаете диагональ переменного тока горизонтальной, и подумайте о том, чтобы сделать «высоту» треугольника как можно большей над этим основанием!
Уолтер
вписанных и ограниченных кругов и многоугольников GMAT
Вписанные и ограниченные
Еще один сложный тип геометрической диаграммы включает в себя многоугольники «внутри» окружностей или окружности «внутри» многоугольников. Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на окружности:
Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на окружности:
На этой диаграмме неправильный пятиугольник ABCDE — это , вписанный в круг на , а круг — это , описанный вокруг пятиугольника . Можно также сказать: окружность ограничивает пятиугольник. Слово «вписанный» описывает внутреннюю форму, а слово «описанный» описывает внешнюю форму. Вот еще одна диаграмма с многоугольником снаружи.
Обратите внимание на то, что каждая сторона этого неправильного пятиугольника составляет касательную к окружности.Теперь пятиугольник — это , описанный по окружности , и круг — это , вписанный в пятиугольника . В обоих случаях внешняя форма описывается, а внутренняя форма вписывается.
Треугольники
Как это часто бывает при обсуждении многоугольников, треугольники — это особый случай при обсуждении вписанного и описанного. Каждый возможный треугольник можно вписать в одну окружность и описать другую окружность. .Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.
Каждый возможный треугольник можно вписать в одну окружность и описать другую окружность. .Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.
Обратите внимание, что когда один угол является особенно тупым, близким к 180 °, разница в размерах между описанной окружностью и вписанной окружностью становится довольно большой. Также обратите внимание: в случае прямоугольного треугольника, второго изображения, гипотенуза треугольника равна диаметру описанной окружности.Мы вернемся к этому моменту.
Четырехугольники
Многие четырехугольники нельзя ни вписать в круг, ни описать кругом: то есть невозможно построить круг, проходящий через все четыре вершины, а также невозможно построить круг, к которому все четыре стороны обращены. касательная.
Некоторые четырехугольники, например продолговатый прямоугольник, можно вписать в круг, но нельзя описать круг.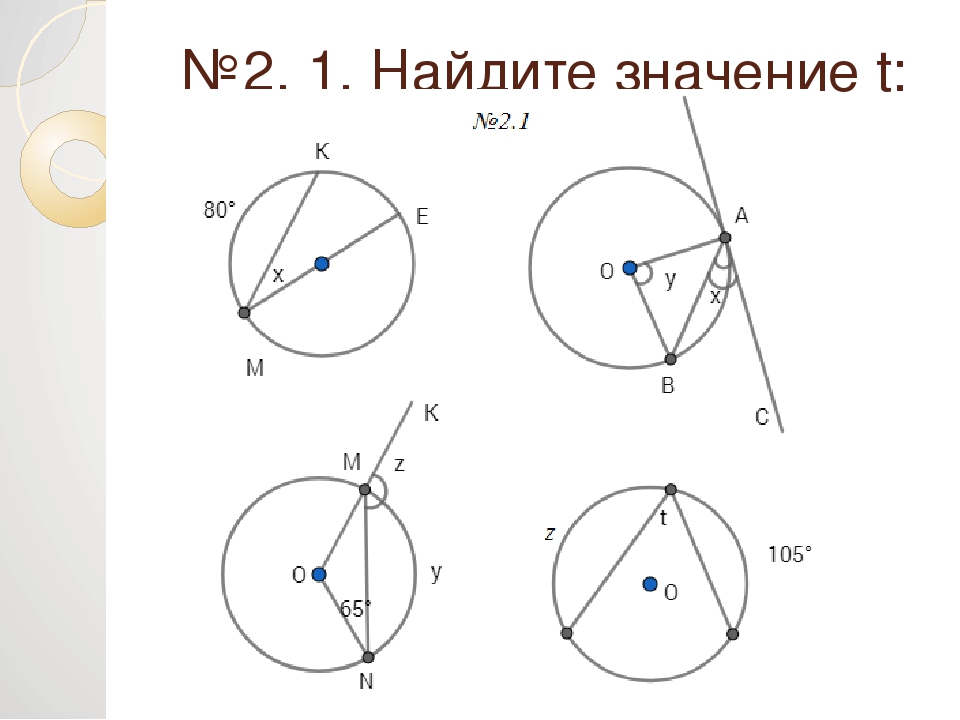 Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в него.
Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в него.
Несколько элитных четырехугольников могут описывать один круг и вписываться в другой круг. Конечно, квадрат (внизу слева), самый элитный из четырехугольников, обладает этим свойством. Другой пример — «правый змей» (внизу справа), змей с парой противоположных прямых углов:
Хотя это «двойное членство» верно для всех треугольников, оно ограничено некоторыми частными случаями с четырехугольниками.
Высшие полигоны
То, что было верно для четырехугольников, верно и для всех высших многоугольников.
а. Большинство, подавляющее большинство, не могут ни описать круг, ни вписать круг.
г. Некоторые можно вписать в круг, но нельзя описать круг.
г. Некоторые могут описать круг, но не могут быть вписаны в круг.
г. Некоторые избранные могут как описать круг, так и вписаться в него.
Последняя категория, элитные члены, всегда включает правильный многоугольник.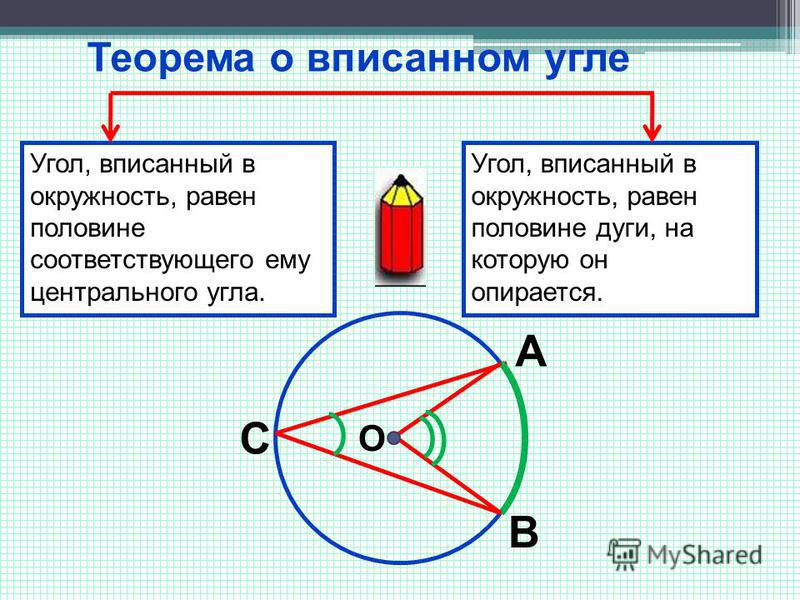 Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники.Вот галерея правильных многоугольников, как с вписанными, так и с описанными кругами.
Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники.Вот галерея правильных многоугольников, как с вписанными, так и с описанными кругами.
Очевидно, что по мере увеличения количества сторон размеры двух окружностей становятся все ближе и ближе.
вопросов GMAT о вписанных и описанных многоугольниках встречается редко, и они могут проверить как ваше понимание терминологии, так и ваши навыки визуализации, описывая геометрическую ситуацию (например, «прямоугольник JKLM вписан в круг») и , а не , дающий вам диаграмму .
Частный случай: треугольник, вписанный в полукруг
Это особый случай, который нравится GMAT. Он появляется в OG13 (DS # 118) и может легко появиться где-нибудь в разделе Quant вашего настоящего GMAT.
Если все, что вам известно, это то, что KL — это диаметр окружности, этого достаточно, чтобы установить, что ∠J = 90 ° и что треугольник JKL является прямоугольным треугольником с KL в качестве гипотенузы. С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром.Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.
С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром.Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.
Кстати, этот пост — четвертый в серии из пяти статей. Вот вся серия.
1) Введение в круги на GMAT
2) GMAT Geometry: круги и углы
3) Круговые и линейные диаграммы на GMAT
4) Вписанные и ограниченные круги и многоугольники в GMAT
5) Разбиение кругов GMAT: длины арок, секторы и числа Пи
Практический вопрос
1) На диаграмме выше S — центр круга.Если QS = 5 и QR = 6, что такое PQ?
А. 7
Б. 8
C. 9
Д. 10
E. 11
Разъяснение практических вопросов
1) Прежде всего, QS — это радиус, поэтому, если QS = 5, это означает PS = SR = 5 и диаметр PR = 10.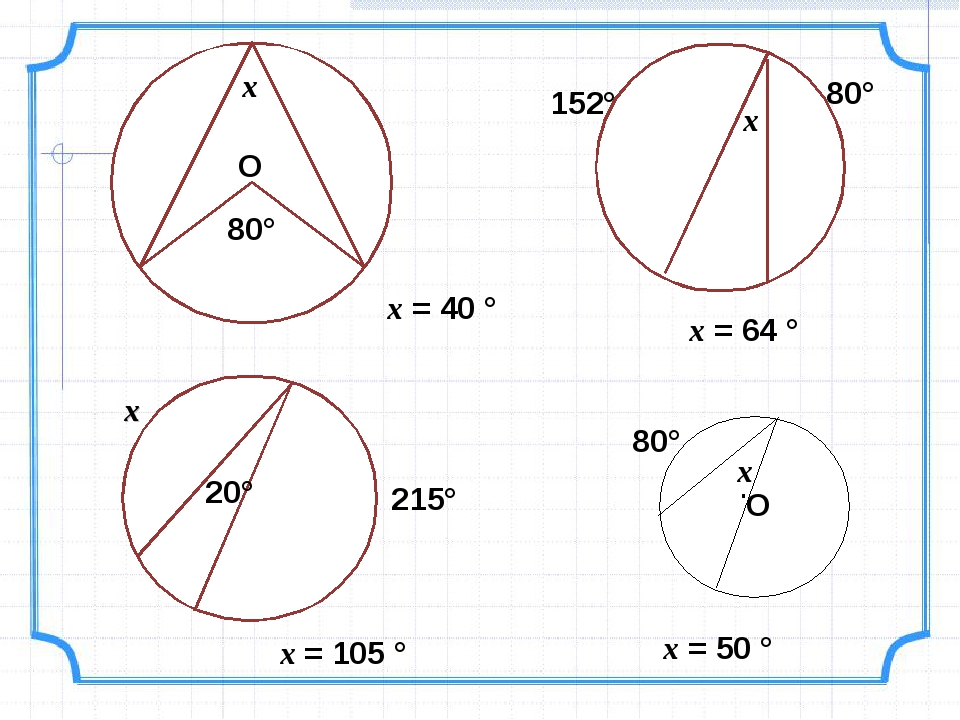 Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным треугольником с ∠PQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64
Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным треугольником с ∠PQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64
PQ = sqrt {64} = 8
Ответ = B
Самые популярные ресурсы
О Майке MᶜGarry
Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидных черепных дефектов, он настаивает на том, чтобы поддержать Нью-Йорк Метс.SAT Math: круги, вписанные в квадраты
В этой серии мы рассмотрим множество типов геометрических сценариев, встречающихся в тесте SAT Math. Базовые знания простых формул (площадь, периметр и т. Д.) Очень важны, но есть множество ярлыков для вопросов о геометрии, которые сэкономят ваше время. Сегодня мы исследуем круги, вписанные в квадраты.
Некоторые вещи, о которых следует помнить
- Центр квадрата совпадает с центром круга
- Нарисуйте линии! В зависимости от того, чего требует стимул, нарисуйте линии, образующие простые формы.(Квадраты можно, например, превратить в треугольники.)
- Общие углы обычно не указываются явно, за исключением случаев необходимости.
- Доверяйте картинкам, но не слишком. Выводы следует делать из фактов. То, что оно похоже на 90 градусов, еще не значит, что это так! (Многие из этих общих выводов будут подробно описаны в этой серии статей.)
- Длины не могут быть отрицательными. Будьте осторожны с вопросами DS, которые ставят уравнения в контексте квадратных уравнений с двумя решениями.
 Если одно решение отрицательное, а другое положительное, остается только положительное решение и информации достаточно.
Если одно решение отрицательное, а другое положительное, остается только положительное решение и информации достаточно.
Для кругов:
- d = 2r и все прямые от центра к внешней стороне равны r.
- С = 2πr = πd
- A = πr²
- НИКОГДА не используйте 2πr², если вы не добавляете области одинаковых кругов!
- Касательные линии образуют прямые углы с радиусом, который пересекает эту касательную.
- Если вы знаете r, вы знаете о круге все!
- С осторожностью используйте π = 22/7. Помните 22/7> π.
Для квадратов:
- Диагональ равна s√2, так как она образует углы в 45 градусов.
- Пересечение диагоналей создает прямой угол.
- Когда круг вписан в квадрат, сторона равна диаметру.
Обычно вам будет предоставлен один бит информации, который говорит вам многое, если не все. Если задана длина стороны квадрата на изображении выше, мы действительно можем найти длину гипотенузы внутреннего треугольника (s = d = 2r, поэтому гипотенуза = (s√2) / 2).
Затененные области
Найдите большую область и вычтите из нее маленькую.Имея дело с кругами вместе с другими фигурами, исключите варианты ответов, в которых ТОЛЬКО есть числа π или которых нет вообще. Обычно ваш ответ будет иметь вид x + yπ.
На рисунке выше изображен круг, идеально вписанный в квадрат. Заштрихованная область> 4?
(1) Площадь большого прямоугольника равна 64.
(2) Периметр заштрихованной области равен 8 + 2π.
Заявление 1: Зная площадь большого квадрата, мы также знаем длины его сторон.(Обратите внимание, что 64 — это идеальный квадрат, который должен быть подсказкой.) Если сторона равна 8, значит, диаметр равен 4, что означает, что радиус равен 4. На изображении мы видим, что «большая фигура» — это верхний правый квадрат, ограниченный двумя радиусами и внешней границей. Откуда мы знаем, что это квадрат? Две части информации: все стороны равны 4, а радиус пересекает большой квадрат под прямым углом, потому что это касательная. В этом случае площадь меньшего квадрата равна 16. Поскольку внутренний угол равен 90 градусам (360/4), площадь сектора круга может быть представлена как A = πr² / 4.Итак, A = 16π / 4 = 4π.
В этом случае площадь меньшего квадрата равна 16. Поскольку внутренний угол равен 90 градусам (360/4), площадь сектора круга может быть представлена как A = πr² / 4.Итак, A = 16π / 4 = 4π.
A (закрашенный) = A (маленький квадрат) — A (сектор) = 16 — 4π <4, потому что 4π> 12. Достаточно.
Утверждение 2: Первое, что должно выскочить, — это комбинация π-члена и не-π-члена. Мы можем разумно предположить, что 8 представляет две прямые стороны периметра, а 2π — длину дуги четверти окружности, которая известна из-за внутреннего прямого угла. Если 2π = C / 4, то C = 8π. Если C = 8π, то r = 4. Отсюда мы возвращаемся к тем же рассуждениям, что и выше:
A (закрашенный) = A (маленький квадрат) — A (сектор) = 16 — 4π <4, потому что 4π> 12.Достаточно.
Каждого утверждения достаточно, , поэтому ответ — выбор D .
Два важных вывода:
- Никогда не предполагайте без доказательств.
- Следуйте по следу.
