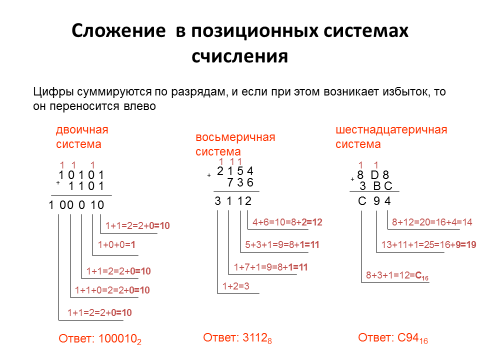
Системы счисления контрольная работа 9 класс: Контрольная работа по информатике на тему «Системы счисления»

Содержание

Проверочная работа по теме «Системы счисления»

Проверочная работа по теме «Системы счисления», 8 класс

Автор: Кордина Нина Евгеньевна, учитель информатики.

Место работы: МБОУ СШ №2 г. Демидова Смоленской области

Учебный предмет: информатика.

Класс: 8.

УМК Босовой Л.Л

Темы: Системы счисления(§1.1), представление чисел в компьютере (§1.2)

Цель: проверка уровня усвоения знаний по данным темам

Время выполнения работы: 20-25 минут.

Вариант 1.

1. Запишите определение позиционной системы счисления. Приведите пример.

2. Он был первым, кто предсказал наступление цифровой информационной эры — в 1489 году, проиллюстрировав пример первичного бинарного машинного кода, состоящего из нулей и единиц. Кто он?

Фамилия состоит из 9 букв. Числа, соответствующие этим буквам согласно алфавиту, удовлетворяют следующим условиям:

 

задание

 

3. Внимательно прочитайте текст и ответьте на вопросы.

    Родившийся в 1444 году в Парме, этот средневековый гений до двенадцати лет обучался у монахов, где приобрел известность как талантливый ученик, художник и скульптор. В восемнадцать лет он поступил на службу к кардиналу Римской католической церкви и выполнял обязанности архитектора, консультанта и пророка. Его научные работы настолько опережали время, что напугали священнослужителей и, несмотря на благосклонное к нему отношение кардинала, большинство его изобретений были уничтожены и не дошли до наших дней. В 1492 году мастерская ученого была разгромлена, а его самого приговорили к сожжению на костре.

    Вопросы:

    В каком году он закончил обучение у монахов? Ответ дайте в шестнадцатеричной системе счисления.

    Сколько лет он состоял на службе у кардинала? Ответ дайте в восьмеричной системе счисления.

      4. С кем сравнивают нашего героя?

      Подсказка. Если 4810 =11 00002 , то -48 в дополнительном 8-разрядном коде записывается как…  

      Выберите ответ:

      А) 11001111 — Микеланджело Б) 1100 1110 — Эйнштейн В) 1101 0000 — Леонардо да Винчи

       

       

      Домашнее задание:

      1) Существовал ли этот гений на самом деле? Найдите информацию об этом человеке и попробуйте обосновать свой ответ.

      2) Составьте и решите свое занимательное задание о нашем герое по теме «Системы счисления»

      Вариант 2.

      1. Запишите определение непозиционной системы счисления. Приведите пример

       

      2. Начиная с XVII века, математиков стали привлекать различные системы счисления с основаниями, отличными от 10. Около 1600 г. двоичную систему счисления предложил английский ученый Томас … (правда, об этом не было известно вплоть до появления в 1951 г статьи в американском журнале для физиков).

      Запишите его фамилию, состоящую из 7 букв. Числа, соответствующие этим буквам согласно алфавиту, удовлетворяют следующим условиям:

       

      задание 1

       

       

        3. Внимательно прочитайте текст и ответьте на вопросы

         

        Паскаль

         

        В 1654 г. Паскаль высказывал мнение, что основанием системы счисления может быть любое положительное число. 

         

        Через 16 лет испанский епископ Хуан Карамюэль опубликовал работу “Два лика математики – новой и старой”, где рассмотрел системы счисления с основаниями 2, 3, 4, 5, 6, 7, 8, 9, 10, 12 и 60.  

         

         

        Лейбниц

        Начиная с 1697 г. в письмах к разным адресатам выработанные им принципы двоичной арифметики неоднократно излагал великий немецкий учёный Готфрид Вильгельм Лейбниц. После появления в 1703 г. статьи Лейбница, в которой объяснялись правила двоичной арифметики, именно двоичная система приобрела наибольшую известность. 

         

        Ответьте на вопросы:

        В каком году опубликована работа «Два лика математики – новой и старой»? Увеличьте год в 2 раза и дайте ответ дайте в шестнадцатеричной системе счисления.

        Какое наибольшее основание системы счисления рассмотрел Карамюэль? Ответ дайте в восьмеричной системы счисления.

          4. Кому принадлежат слова: « десятичная система построена не слишком разумно, поскольку следует людским обычаям, а не требованиям естественной необходимости»?

          Подсказка. Если 6510=100 0001  , то число -65 в обратном 8-разрядном коде записывается как…

          Выберите ответ:

          А) 0011 1110 — Лейбниц, Б)1011 1110 — Паскаль, В) 1011 1111 – Карамюэль.

          Домашнее задание:

          1) Кто из ученых нашел в начертаниях китайского царя Фуси арифметическое счисление с двумя цифрами. Какое двоичное число соответствовало триграмме озеро?

          2) Составьте и решите занимательное задание об этом ученом по теме «Двоичная система счисления»

          Приложение

          Алфавит

          1  2  3  4  5  6  7  8   9  10  11 12  13 14  15

          А  Б  В  Г  Д  Е  

          Ë Ж  З   И   Й   К    Л   М   Н

          16 17 18 19 20 21 22 23 24 25 26 27 28 29

          О   П   Р   С   Т   У   Ф  Х    Ц  Ч   Ш  Щ Ъ  Ы

          30 31 32 33

          Ь  Э    Ю  Я


           

          Критерии оценивания:

          № задания

          Максимальное количество баллов

          1

          1

          2

          6

          3

          2

          4

          1


           

          оценка

          Количество баллов

          5

          10

          4

          8-9

          3

          6-7

          2

          Менее 6


           

          Ответы:

          № задания

          I вариант

          II вариант

          2

          18,1,14,2,13,30,5,10

          Рамбальди

          4,1,18,10,16,20

          Гарриот

          3

          5B0, 36

          D0C , 74

          4

          Леонардо да Винчи

          Паскаль


           

          Домашнее задание для каждого варианта предлагается свое.

          На следующем уроке проходит его обсуждение. Нашел в начертаниях Фуси двоичную систему счисления Лейбниц. Триграмме Озеро соответствует 610=1102 (http://px-pict.com/10/4/2/2.html)

          Большинство пользователей интернета считает информацию о Майло Джакомо Рамбальди плодом фантазии авторов телесериала «Шпионка», кто-то верит в его существование, но согласитесь, история захватывающая. Можно обсудить с учащимися все «за» и «против», достоверность информации в интернете, необходимость критического подхода к ней.

          Контрольная работа по теме «Системы счисления»

          Контрольная работа по теме

          «Системы счисления» 8 класс

          1 ВАРИАНТ

          Переведите число в десятичную с.с

          10011012=X10

          100112=X10

          123018=X10

          121108=X10

          10А616=X10

          А0F816=X10

          Переведите число из десятичной с.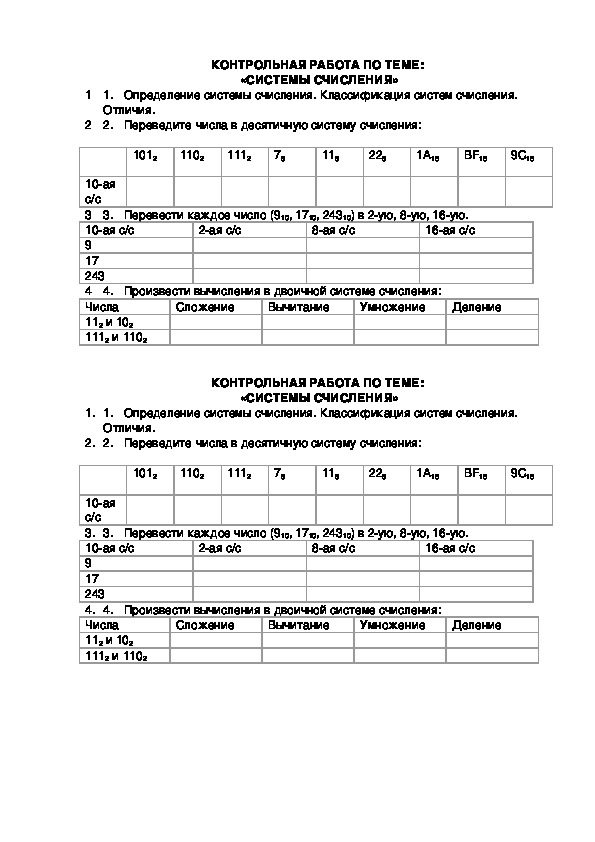 с в двоичную, восьмеричную и шестнадцатеричную

          10110=X2=X8=X16

          3710=X2=X8=X16

          73510=X2=X8=X16

          ***Решите уравнение 11012+Х16=С016

          Контрольная работа по теме

          «Системы счисления» 8 класс

          2 ВАРИАНТ

          Переведите число в десятичную с.с

          10111002=X10

          101012=X10

          123078=X10

          127708=X10

          17А616=X10

          АВF016=X10

          Переведите число из десятичной с.с в двоичную, восьмеричную и шестнадцатеричную

          20210=X2=X8=X16

          7310=X2=X8=X16

          56210=X2=X8=X16

          ***Решите уравнение Х8-2В16=1011102

          Контрольная работа по теме

          «Системы счисления» 8 класс

          3 ВАРИАНТ

          Переведите число в десятичную с. с

          1001102=X10

          101002=X10

          1245128=X10

          1270208=X10

          А65016=X10

          АВ2F16=X10

          Переведите число из десятичной с.с в двоичную, восьмеричную и шестнадцатеричную

          30310=X2=X8=X16

          8910=X2=X8=X16

          88010=X2=X8=X16

          ***Решите уравнение Х2+3F16=1068

          Контрольная работа по теме

          «Системы счисления» 8 класс

          1 ВАРИАНТ

          Переведите число в десятичную с.с

          10011012=X10

          100112=X10

          123018=X10

          121108=X10

          10А616=X10

          А0F816=X10

          Переведите число из десятичной с. с в двоичную, восьмеричную и шестнадцатеричную

          10110=X2=X8=X16

          3710=X2=X8=X16

          73510=X2=X8=X16

          ***Решите уравнение 11012+Х16=С016

          Контрольная работа по теме

          «Системы счисления» 8 класс

          2 ВАРИАНТ

          Переведите число в десятичную с.с

          10111002=X10

          101012=X10

          123078=X10

          127708=X10

          17А616=X10

          АВF016=X10

          Переведите число из десятичной с.с в двоичную, восьмеричную и шестнадцатеричную

          20210=X2=X8=X16

          7310=X2=X8=X16

          56210=X2=X8=X16

          ***Решите уравнение Х8-2В16=1011102

          Контрольная работа по теме

          «Системы счисления» 8 класс

          3 ВАРИАНТ

          Переведите число в десятичную с. с

          1001102=X10

          101002=X10

          1245128=X10

          1270208=X10

          А65016=X10

          АВ2F16=X10

          Переведите число из десятичной с.с в двоичную, восьмеричную и шестнадцатеричную

          30310=X2=X8=X16

          8910=X2=X8=X16

          88010=X2=X8=X16

          ***Решите уравнение Х2+3F16=1068

          Проверочная работа по информатике Системы счисления 8 класс

          Проверочная работа по информатике Системы счисления с ответами для учащихся 8 класса. Проверочная работа включает 6 вариантов в каждом по 4 задания.

          1 вариант

          1. Выполните действие:

          А) 11000112 — 101112;
          Б) 1000012 + 1111002;
          В) 1038 + 1478;
          Г) A216 + 1F16 .

          2. Переведите числа в восьмеричную и шестнадцатеричную системы счисления:

          А) 100001111012;
          Б) 10101010102;
          В) 2910;
          Г) 9910.

          3. Переведите числа из десятичной системы счисления в двоичную:

          А) 4710;
          Б) 11110;
          В) 9510;
          Г) 7310

          .

          4. Сравните числа:

          А) 2510 и 110012;
          Б) 1D16 и 358;
          В) 1000012 и 428.

          2 вариант

          1. Выполните действие:

          А) 10110012 — 101012;
          Б) 1010012 + 1001002;
          В) 1208 — 1138;
          Г) 1816 + A316.

          2. Переведите числа в восьмеричную и шестнадцатеричную системы счисления:

          А) 101101111012;
          Б) 101011010102;
          В) 2410;
          Г) 8910.

          3. Переведите числа из десятичной системы счисления в двоичную:

          А) 4910;
          Б) 2110;
          В) 8510;
          Г) 9910.

          4. Сравните числа:

          А) 2910 и 111012;
          Б) 2С16 и 428;
          В) 1001012 и 778.

          3 вариант

          1. Выполните действие:

          А) 11010112 — 10012;
          Б) 11111012 + 1111002;
          В) 2018 — 1178;
          Г) 1A16 + A116.

          2. Переведите числа в восьмеричную и шестнадцатеричную системы счисления:

          А) 1001100110012;
          Б) 1011110000002;
          В) 5510;
          Г) 11110.

          3. Переведите числа из десятичной системы счисления в двоичную:

          А) 6410;
          Б) 10010;
          В) 8410;
          Г) 9310.

          4. Сравните числа:
          А) 3310 и 110112;
          Б) 2E16 и 558;
          В) 1001012 и 458.

          4 вариант

          1. Выполните действие:

          А) 11010112 — 111112;
          Б) 1000012 + 111002;
          В) 338 + 1178;
          Г) 2F16 + D116.

          2. Переведите числа в восьмеричную и шестнадцатеричную системы счисления:

          А) 10111110012;
          Б) 10110001102;
          В) 8710;
          Г) 17710.

          3. Переведите числа из десятичной системы счисления в двоичную:

          А) 4710;
          Б) 11010;
          В) 6510;
          Г) 7310.

          4. Сравните числа:

          А) 3510 и 11012;
          Б) FD16 и 25310;
          В) 100112 и 408.

          5 вариант

          1. Выполните действие:

          А) 11001112 — 1010012;
          Б) 1110012 + 1011002;
          В) 1238 + 1748;
          Г) AA16 + 2B16.

          2. Переведите числа в восьмеричную и шестнадцатеричную системы счисления:

          А) 100001001012;
          Б) 101010101002;
          В) 7910;
          Г) 18510.

          3. Переведите числа из десятичной системы счисления в двоичную:

          А) 3310;
          Б) 11310;
          В) 6710;
          Г) 7310.

          4. Сравните числа:
          А) 2810 и 111002;
          Б) 1C16 и 338;
          В) 100112 и 428.

          6 вариант

          1. Выполните действие:

          А) 1101112 — 101102;
          Б) 1010012 + 101102;
          В) 778 + 748;
          Г) 2A16 + A216.

          2. Переведите числа в восьмеричную и шестнадцатеричную системы счисления:

          А) 1000011112;
          Б) 101011110102;
          В) 12310;
          Г) 10510.

          3. Переведите числа из десятичной системы счисления в двоичную:

          А) 3710;
          Б) 9110;
          В) 10510;
          Г) 8410.

          4. Сравните числа:

          А) 9510 и 111112;
          Б) AA16 и 2528;
          В) 1000112 и 458.

          Ответы на проверочную работу по информатике Системы счисления
          1 вариант
          1
          А) 10011002
          Б) 10111012
          В) 2528
          Г) C116
          2
          А) 20758; 43D16
          Б) 12528; 2AA16
          В) 358; 1D16
          Г) 1438; 6316
          3
          А) 1011112
          Б) 11011112
          В) 10111112
          Г) 10010012
          4
          А) =
          Б) =
          В) 2 вариант
          1
          А) 10001002
          Б) 10011012
          В) 58
          Г) BB16
          2
          А) 26758; 5BD16
          Б) 25528; 56A16
          В) 308; 1816
          Г) 1318; 5916
          3
          А) 1100012
          Б) 101012
          В) 10101012
          Г) 11000112
          4
          А) =
          Б) >
          В) 3 вариант
          1
          А) 11000102
          Б) 101110012
          В) 628
          Г) BB16
          2
          А) 46318; 99916
          Б) 57008; BC016
          В) 678; 3716
          Г) 1578; 6F16
          3
          А) 10000002
          Б) 11001002
          В) 10101002
          Г) 10111012
          4
          А) >
          Б) >
          В) =
          4 вариант
          1
          А) 10011002
          Б) 1111012
          В) 1528
          Г) 10016
          2
          А) 13718; 2F916
          Б) 13068; 2C616
          В) 1278; 5716
          Г) 2618; B116
          3
          А) 1011112
          Б) 11011102
          В) 10000012
          Г) 10010012
          4
          А) >
          Б) =
          В) 5 вариант
          1
          А) 1111102
          Б) 11001012
          В) 3178
          Г) D516
          2
          А) 20458; 42516
          Б) 25248; 55416
          В) 1178; 4F16
          Г) 2718; B916
          3
          А) 1000012
          Б) 11100012
          В) 10000112
          Г) 10010012
          4
          А) =
          Б) >
          В) 6 вариант
          1
          А) 10110002
          Б) 1111112
          В) 1738
          Г) CC16
          2
          А) 4178; 10F16
          Б) 25728; 57A16
          В) 1738; 7B16
          Г) 1518; 6916
          3
          А) 1001012
          Б) 10110112
          В) 11010012
          Г) 10101002
          4
          А) >
          Б) =
          В)

          Информатика 9 класс. Тесты презентации контрольные работы

          № урока Содержание (тема) урока
          Обработка графической информации (6 ч.)
          1. ПТБ. Растровые и векторные графические изображения.
          В качестве векторного графического редактора используется Inkscape. Программа совершенно бесплатная — можно скачать здесь.
          Практические работы отобраны с обучающих материалов сайта Inkscape и адаптированы для школьников.
          В качестве растрового графического редактора используется PaintNet. Программа совершенно бесплатная — можно скачать здесь.
          Практические работы отобраны с обучающих материалов сайта PaintNet и адаптированы для школьников. Работы подобраны таким образом, что для их выполнения не требуется дополнительных плагинов.
          2. Векторный редактор Inkscape: графические примитивы и контуры &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Рисуем стрелку»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Рисуем звездочку»
          3. Работа с текстом в программе Inkscape &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Простой векторный текст»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Рисуем сердечко»
          4. Растровый редактор PaintNet: основные инструменты. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Как нарисовать каплю»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Прозрачный шар»
          5. Работа с цветом  и эффекты в программе PaintNet. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Стилизованный медвежонок»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрактическая работа «Игрушечная собачка»
          6. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspТест «Обработка графической информации» (контрольный)
          Мультимедийные технологии (8 ч.)
          7. Компьютерные презентации – основы эргономики и дизайна.
          8. Макеты слайдов, запись показа.
          9. Демонстрация презентации. Презентационное оборудование.
          10. Работа со звуком. Композиция и монтаж. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspУпражнение «Форматы звуковых файлов»
          11. Цифровое фото и видео.
          12. Технические приемы записи звука и видео.
          13. Вставка звука и видео в презентацию. Запись показа слайдов.
          14. Практическая контрольная работа по теме «Мультимедийные технологии»
          Моделирование и формализация (3 ч.)
          15. Моделирование как метод познания, материальные и информационные модели. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspМоделирование и формализация &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПример физической модели из презентации (Excel) &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspЗадание «Деревья и графы»
          16. Математическое моделирование. Основные этапы разработки и исследования моделей на компьютере. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspОсновные этапы моделирования
          17. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspТест «Моделирование и формализация» (контрольный)
          Представление информации (6 ч.)
          18. Язык — как форма представления информации. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspЯзыки естественные и формальные
          19. Компьютерное представление текста.
          20. Системы счисления &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspУпражнение «Степени числа 2»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspУпражнение «Перевод чисел — двоичная, восмеричная, шестнадцатиричные системы счисления»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspУпражнение «Соответствие шестнадцатеричной цифры двоичной тетраде»
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspУпражнение «Соответствие восьмеричной цифры двоичной триаде»
          21. Перевод из десятичной системы в q-ичную и обратно: практическая работа
          22. Перевод из десятичной системы в q-ичную и обратно: практическая работа
          23. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspДомашнее задание «Переводчисел в системах счисления» Контрольная работа по теме «Системы счисления»
          Обработка числовой информации в электронных таблицах (8 ч.)
          24. Электронная таблица. Типы и формат данных. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspПрезентация «Ввод, редактирование и обработка данных в Excel. Построение диаграмм.» &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspЗадание «Базовые функции Excel»
          25. Относительные и абсолютные ссылки, работа с диапазоном ячеек
          26. Использование формул. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspМатематические функции в Excel.
          &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspЗадание по теме «Математические функции Excel».
          27. Встроенные функции для обработки данных.
          28. Построение диаграмм и графиков. &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbspЗадание по теме «Построение графиков в Excel» (17 вариантов).
          29. Логические функции.
          30.

          Тест по информатике Системы счисления 8 класс

          Тест по информатике Системы счисления 8 класс с ответами. Тест включает в себя 2 варианта. В каждом варианте по 7 заданий.

          Вариант 1

          1. Алфавит позиционной системы счисления:

          1) 1, V, Х, L
          2) 0, 1, 2
          3) 1, 2, 3
          4) £, ¥, ¢

          2. Десятичный эквивалент числа 11008:

          1) 576
          2) 240
          3) 10 000
          4) 88

          3. Двоичное значение выражения 1016 + 108 + 102 · 1016:

          1) 1110002
          2) 1010002
          3) 1100002
          4) 1111002

          4. Для выражения 14х = 1010 основание системы счислениях:

          1) 8
          2) 6
          3) 16
          4) 5

          5. Неравенство 14616 > С > 5048 верно для числа:

          1) 1010001102
          2) 1010001012
          3) 1110001112
          4) 1010001112

          6. Результат операции сложения 1100112 + 111012:

          1) 10100002
          2) 11100002
          3) 1000002
          4) 10000002

          7. Результат операции умножения 1112 · 1012:

          1) 1001112
          2) 1000112
          3) 1001012
          4) 1101112

          Вариант 2

          1. Алфавит непозиционной системы счисления:

          1) I, V, X, L
          2) 0, 1, 2
          3) 0, 1, 2, 3, 4, 5
          4) 0, 1, 2, 3, А, В

          2. Десятичный эквивалент числа 1000112:

          1) 35
          2) 43
          3) 25
          4) 23

          3. Двоичное значение выражения 10112 + 328:

          1) 1001012
          2) 1011012
          3) 1100012
          4) 1110002

          4. Для выражения 12х = 810 основание системы счислениях:

          1) 8
          2) 6
          3) 16
          4) 5

          5. Неравенство 11001012 = С < 6616 верно для числа:

          1) 1458
          2) 1558
          3) 1448
          4) 1348

          6. Результат операции сложения 1018 + 1178:

          1) 2208
          2) 2108
          3) 2188
          4) 3008

          7. Результат операции умножения 118 · 118:

          1) 10018
          2) 1218
          3) 1208
          4) 2218

          Ответы на тест по информатике Системы счисления 8 класс
          Вариант 1
          1-2
          2-1
          3-1
          4-2
          5-2
          6-1
          7-2
          Вариант 2
          1-1
          2-1
          3-1
          4-2
          5-1
          6-1
          7-2

          Контрольная работа по информатике «Системы счисления. Двоичная арифметика», 10 класс

          1 вариант

          Данные числа из различных систем счислений перевести в двоичную систему:

           

          a)      3248 (11010100)

          b)      AF116(101011110001)

          c)      8710 (1010111)

           

          1. Данные числа из различных систем счисления перевести в шестнадцатеричную систему:

           

          a)      110110112 (DB16)

          b)      2238 (9316)

          c)      19910 (C716)

           

          1. Даны пары чисел. Перевести числа в двоичную систему счисления и проделать над ними операции сложения, вычитания, умножения и деления

           

          a)      23410 и 910 (11101010 и 1001) сум: 11110011 раз. 11100001 прз. 100000111010 частн. 1101

           

          1. Даны дробные числа. Перевести числа в двоичную систему счисления.

           

          a)      76,08710 (1001100,0001011)

          b)      34, 9910 (100010,111111)

           

          2 вариант 

          1       Данные числа из различных систем счислений перевести в двоичную систему:

           

          d)      3258 (11010101)

          e)      FA116(111110100001)

          f)      8910 (1011001)

           

          2       Данные числа из различных систем счисления перевести в шестнадцатеричную систему:

           

          d)      110111112 (DF16)

          e)      2328 (9A16)

          f)      20110 (C916)

           

          3       Даны пары чисел. Перевести числа в двоичную систему счисления и проделать над ними операции сложения, вычитания, умножения и деления

           

          57610 и 1210 (1001000000 и 1100) (1001001100)    (1000110100)  (1101100000000)    (110000)

           

          4       Даны дробные числа. Перевести числа в двоичную систему счисления.

           

          a)      76,8710 (1001100,110111)

          b)      34, 09910 (100010,000110) 

          Онлайн-имитационные тесты CBSE Class 9 Number System

          Вышеупомянутые ссылки на главы Online Mock Tests для CBSE Class 9 Number System помогут вам провести тесты на основе MCQ и проверить ваше понимание всех важных концепций, которые были подготовлены на основе последней учебной программы CBSE Class 9 2020. Бесплатные пробные онлайн-тесты для CBSE Class 9 должны использоваться студентами, чтобы проверить их понимание своих концепций системы счисления CBSE Class 9. На сайте StudiesToday.com представлена ​​самая большая коллекция онлайн-тестов на основе MCQ класса 9 для экзаменов CBSE Class 9 Number System 2020, которые помогут вам правильно подготовиться и получить наивысший рейтинг на экзаменах. Учащиеся могут проходить пробные тесты для CBSE Class 9 столько раз, сколько захотят, а также загружать проходной сертификат после прохождения онлайн-теста. Эти имитация онлайн-тестов для системы счисления для 9 классов, которые были разработаны преподавателями StudiesToday.com после тщательного изучения последней книги и основаны на шаблонах вопросов на предстоящих экзаменах для учащихся класса CBSE.

          Преимущества пробных онлайн-тестов для стандартной 9-ти системной системы

          a) -онлайн-пробных онлайн-тестов для нумерационной системы класса 9 CBSE были разработаны опытными преподавателями после серьезного исследования всех тем.

          b) Онлайн-тесты CBSE Class 9 с ответами были созданы таким образом, чтобы обеспечить полные и всесторонние знания по каждой теме на легком и понятном языке.

          c) Вы также обнаружите, что некоторые из вопросов, которые задаются в наших онлайн-тестах, могут появиться и на предстоящих экзаменах CBSE Class 9 Number System .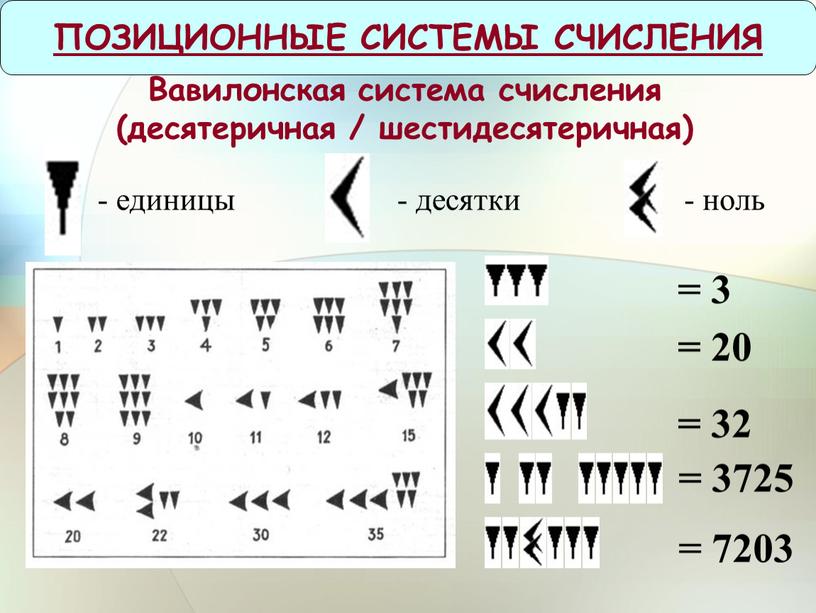

          d) Тысячи учеников класса 9 CBSE прошли эти онлайн-тесты и получили отличные результаты и высокие оценки на экзаменах по системе счисления 9 класса CBSE.

          Пробные онлайн-тесты для системы нумерации CBSE Class 9 доступны бесплатно всем студентам, которые хотят участвовать в предстоящих экзаменах. Studytoday.com предлагает самую эксклюзивную и самую большую базу данных бесплатных онлайн-пробных тестов для всех студентов. Повторение вопросов снова и снова в тестах даст дополнительное преимущество учащимся класса CBSE. Большинство вопросов взяты из предыдущих экзаменов по системе счисления NCERT класса 9, поэтому их практика в условиях экзамена определенно поможет вам получить более высокий рейтинг.

          Для получения дополнительных бесплатных учебных материалов щелкните по ссылкам ниже для Система счисления , чтобы загрузить решенные образцы работ, вопросы за прошлый год с решениями, рабочие листы в формате pdf, CBSE Class 9 Книги и решения для Системы счисления 9 на основе учебная программа и руководства, выпущенные CBSE и NCERT . Учебный материал и решенные образцы работ для CBSE Class 9 для системы счисления были подготовлены опытными преподавателями ведущих институтов Индии и доступны для бесплатного скачивания.

          Назначения для системы счисления класса 9 PDF Скачать

          Вышеупомянутые назначения NCERT CBSE и KVS для системы счисления класса 9 помогут вам повысить свои баллы, очистив концепции системы счисления и улучшив навыки решения данных и решения ситуаций. Эти рабочие листы системы нумерации CBSE NCERT для класса 9 и буклеты с вопросами были разработаны опытными преподавателями сайта StudiesToday.com для учащихся 9 класса.

          Преимущества Назначения CBSE NCERT для системы номеров класса 9

          a) Задания NCERT CBSE KVS по системе номеров класса 9 помогут детям укрепить свои представления и улучшить оценки на тестах и ​​экзаменах.

          b) Эти распечатываемые задания для Класса Системы счисления 9 помогут улучшить аналитические навыки и навыки декодирования сложных задач.

          c) Ежедневная практика различных тестовых заданий по различным предметам поможет развить четкое понимание каждой темы, которую вы будете помнить до даты экзамена

          d) Вы также сможете правильно пересмотреть все главы системы счисления и сэкономить время во время ваших классных тестов и экзаменов.

          Бесплатные задания для печати в формате PDF системы счисления 9 класса CBSE, разработанные школьными учителями в StudiesToday.com. Мы предоставляем самые эксклюзивные базы данных бесплатных печатных заданий в соответствии со стандартами CBSE NCERT и KVS. Все рабочие листы были тщательно разработаны для всех типов студентов, вы можете загрузить в формате PDF CBSE Class 9 Number System Chapter (Банк вопросов ) и использовать их для дальнейшего изучения. Внимательно ознакомьтесь с программой для системы счисления 9 класса и загрузите задания по каждой изучаемых вами темах. Это очень поможет в выявлении всех ошибок в вашем понимании темы.Выполняйте хотя бы одно задание по системе счисления CBSE для класса 9 в день, чтобы вы могли получить более высокие баллы на экзамене.

          Не забудьте щелкнуть поля ниже, чтобы загрузить систему номеров класса 9, решенную последними образцами документов CBSE, заданиями за прошлый год (предыдущий год / 10 лет), задания для печати в формате pdf, последние бесплатные книги NCERT и решения NCERT для системы номеров класса 9 на основе учебной программы CBSE и книг, выпущенных NCERT. Учебный материал для 9 класса по системе счисления был подготовлен опытными учителями ведущих школ Индии и доступен для бесплатного скачивания в формате pdf

          Решения NCERT для класса 9 по математике Глава 1

          Страница № 5:
          Вопрос 1:

          Является ли ноль рациональным числом? Можете ли вы записать это в виде, где p и q — целые числа, а q ≠ 0?

          Ответ:

          Да.Ноль — это рациональное число, так как его можно представить как setc.

          Видео решение для систем счисления (Страница: 5, Q. No .: 1)

          Решение NCERT для математики класса 9 — системы счисления 5, вопрос 1

          Страница № 5:
          Вопрос 2:

          Найдите шесть рациональных чисел от 3 до 4.

          Ответ:

          Между 3 и 4 есть бесконечные рациональные числа.

          3 и 4 можно представить соответственно.

          Следовательно, рациональные числа от 3 до 4 равны

          .


          Видео решение для систем счисления (Страница: 5, Q.No .: 2)

          Решение NCERT для математики класса 9 — системы счисления 5, вопрос 2

          Страница № 5:
          Вопрос 3:

          Найдите пять рациональных чисел между ними.

          Ответ:

          Между ними бесконечные рациональные числа.

          Следовательно, рациональные числа между


          Видео решение для систем счисления (Страница: 5, Q.No .: 3)

          Решение NCERT для математики класса 9 — системы счисления 5, вопрос 3

          Страница № 5:
          Вопрос 4:

          Укажите, верны ли следующие утверждения.Обоснуйте свои ответы.

          (i) Каждое натуральное число является целым числом.

          (ii) Каждое целое число является целым числом.

          (iii) Каждое рациональное число является целым числом.

          Ответ:

          (i) Верно; так как набор целых чисел содержит все натуральные числа.

          (ii) Неверно; поскольку целые числа могут быть отрицательными, но целые числа положительны. Например: −3 — целое, но не целое число.

          (iii) Неверно; поскольку рациональные числа могут быть дробными, а целые — нет. Например: рациональное число, а не целое число.

          Видео решение для систем счисления (Страница: 5, Q.No .: 4)

          Решение NCERT для математики класса 9 — системы счисления 5, вопрос 4

          Страница № 8:
          Вопрос 1:

          Укажите, верны ли следующие утверждения.Обоснуйте свои ответы.

          (i) Каждое иррациональное число является действительным числом.

          (ii) Каждая точка на числовой прямой имеет форму, где м — натуральное число.

          (iii) Каждое действительное число является иррациональным числом.

          Ответ:

          (i) Верно; поскольку набор действительных чисел состоит из рациональных и иррациональных чисел.

          (ii) Неверно; поскольку отрицательные числа не могут быть выражены как квадратный корень из любого другого числа.

          (iii) Неверно; поскольку действительные числа включают как рациональные, так и иррациональные числа. Следовательно, каждое действительное число не может быть иррациональным числом.

          Видео решение для систем счисления (Страница: 8, Q.No .: 1)

          Решение NCERT для математики класса 9 — системы счисления 8, вопрос 1

          Страница № 8:
          Вопрос 2:

          Являются ли квадратные корни из всех натуральных чисел иррациональными? Если нет, приведите пример квадратного корня из числа, которое является рациональным числом.

          Ответ:

          Если рассматриваются такие числа, как,

          Тогда здесь 2 и 3 — рациональные числа. Таким образом, квадратные корни из всех натуральных чисел не являются иррациональными.

          Видео решение для систем счисления (Страница: 8, Q.No .: 2)

          Решение NCERT для математики класса 9 — системы счисления 8, вопрос 2

          Страница № 8:
          Вопрос 3:

          Покажите, как можно представить в числовой строке.

          Ответ:

          Мы знаем это,

          А,

          Отметьте точку «A», представляющую 2 на числовой прямой. Теперь построим AB единичной длины перпендикулярно OA. Затем, взяв O за центр и OB за радиус, нарисуйте

          дуга, пересекающая числовую прямую в точке C.

          C представляет.

          Видео решение для систем счисления (Страница: 8, Q.No .: 3)

          Решение NCERT для математики класса 9 — системы счисления 8, вопрос 3

          Страница № 14:
          Ответ:

          (я)

          Завершение

          (ii)

          Непрерывное повторение

          (iii)

          Завершение

          (iv)

          Непрерывное повторение

          (в)

          Непрерывное повторение

          (vi)

          Завершение

          Видео решение для систем счисления (Страница: 14, В.№: 1)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 1

          Страница № 14:
          Вопрос 2:

          Вы это знаете. Можете ли вы предсказать, что такое десятичное разложение, не делая на самом деле длинного деления? Если да, то как?

          [ Подсказка: Изучите остатки, внимательно находя значение.]

          Ответ:

          Да.Это можно сделать следующим образом.


          Видео решение для систем счисления (Страница: 14, Q.No .: 2)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 2

          Страница № 14:
          Вопрос 3:

          Выразите следующее в форме, где p и q — целые числа, а q ≠ 0.

          (i) (ii) (iii)

          Ответ:

          (i)

          Пусть x = 0,666…

          10 x = 6,666…

          10 x = 6 + x

          9 x = 6

          (ii)

          Пусть x = 0,777…

          10 x = 7,777…

          10 x = 7 + x

          (iii)

          Пусть x = 0.001001…

          1000 x = 1,001001…

          1000 x = 1 + x

          999 x = 1

          Видео решение для систем счисления (Страница: 14, Q.No .: 3)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 3

          Страница № 14:
          Вопрос 4:

          Экспресс 0.99999… в форме. Вас удивил ваш ответ? Обсудите с учителем и одноклассниками, почему ответ имеет смысл.

          Ответ:

          Пусть x = 0,9999…

          10 x = 9,9999…

          10 x = 9 + x

          9 x = 9

          x = 1

          Видео решение для систем счисления (Страница: 14, В.№: 4)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 4

          Страница № 14:
          Вопрос 5:

          Какое максимальное количество цифр может быть в повторяющемся блоке цифр в десятичном расширении? Выполните деление, чтобы проверить свой ответ.

          Ответ:

          Можно заметить, что,

          В повторяющемся блоке десятичной дроби содержится 16 цифр.

          Видео решение для систем счисления (Страница: 14, Q.No .: 5)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 5

          Страница № 14:
          Вопрос 6:

          Посмотрите несколько примеров рациональных чисел в форме ( q 0), где p и q — целые числа без общих факторов, кроме 1, и имеющие завершающие десятичные представления (расширения).Сможете догадаться, какое свойство q должно удовлетворять?

          Ответ:

          Завершающее десятичное разложение произойдет, когда знаменатель q рационального числа будет равен 2, 4, 5, 8, 10 и так далее…

          Можно заметить, что завершающая десятичная дробь может быть получена в ситуации, когда разложение на простые множители знаменателя данных дробей имеет степень только 2 или только 5, или и то, и другое.

          Видео решение для систем счисления (Страница: 14, Q.No .: 6)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 6

          Страница № 14:
          Вопрос 7:

          Запишите три числа, десятичные разложения которых не завершаются и не повторяются.

          Ответ:

          3 числа, десятичные разложения которых не завершаются и не повторяются, следующие.

          0,505005000500005000005…

          0,7207200720007200007200000…

          0,080080008000080000080000008…

          Видео решение для систем счисления (Страница: 14, Q.No .: 7)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 7

          Страница № 14:
          Вопрос 8:

          Найдите три разных иррациональных числа между рациональными числами и.

          Ответ:

          3 иррациональные числа следующие.

          0,73073007300073000073…

          0,75075007500075000075…

          0,7

          07

          79…

          Видео решение для систем счисления (Страница: 14, Q.No .: 8)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 8

          Страница № 14:
          Вопрос 9:

          Классифицируйте следующие числа как рациональные или иррациональные:

          (i) (ii) (iii) 0.3796

          (iv) 7,478478 (v) 1,101001000100001…

          Ответ:

          (я)

          Поскольку десятичное разложение этого числа является неповторяющимся неповторяющимся числом, это иррациональное число.

          (ii)

          Это рациональное число, поскольку оно может быть представлено в форме.

          (iii) 0,3796

          Поскольку десятичное раскрытие этого числа заканчивается, это рациональное число.

          (iv) 7,478478…

          Поскольку десятичное раскрытие этого числа является непрерывным, повторяющимся, следовательно, это рациональное число.

          (в) 1.10100100010000…

          Поскольку десятичное разложение этого числа является неповторяющимся, неповторяющимся, следовательно, это иррациональное число.

          Видео решение для систем счисления (Страница: 14, Q.No .: 9)

          Решение NCERT для математики класса 9 — системы счисления 14, вопрос 9

          Страница № 18:
          Вопрос 1:

          Визуализировать 3.765 на числовой прямой при последовательном увеличении.

          Ответ:

          3,765 можно визуализировать, как в следующих шагах.


          Видео решение для систем счисления (Страница: 18, Q.No .: 1)

          Решение NCERT для математики класса 9 — системы счисления 18, вопрос 1

          Страница № 18:
          Вопрос 2:

          Визуализируйте числовую строку до 4 знаков после запятой.

          Ответ:

          = 4,2626…

          4,2626 можно визуализировать, как в следующих шагах.


          Видео решение для систем счисления (Страница: 18, Q.No .: 2)

          Решение NCERT для математики класса 9 — системы счисления 18, вопрос 2

          Страница № 24:
          Вопрос 1:

          Классифицируйте следующие числа как рациональные или иррациональные:

          (i) (ii) (iii)

          (iv) (v) 2π

          Ответ:

          (i) = 2 — 2.2360679…

          = — 0,2360679…

          Поскольку десятичное разложение этого выражения является непрерывным, неповторяющимся, следовательно, это иррациональное число.

          (ii)

          Следовательно, это рациональное число, которое можно представить по форме.

          (iii)

          Следовательно, это рациональное число, которое можно представить по форме.

          (iv)

          Поскольку десятичное разложение этого выражения является непрерывным, неповторяющимся, следовательно, это иррациональное число.

          (в) 2π = 2 (3,1415…)

          = 6,2830…

          Поскольку десятичное разложение этого выражения является непрерывным, неповторяющимся, следовательно, это иррациональное число.

          Видео решение для систем счисления (Страница: 24, Q.No .: 1)

          Решение NCERT для математики класса 9 — системы счисления 24, вопрос 1

          Страница № 24:
          Вопрос 2:

          Упростите каждое из следующих выражений:

          (i) (ii)

          (iii) (iv)

          Ответ:

          (я)

          (ii)

          = 9 — 3 = 6

          (iii)

          (iv)

          = 5 — 2 = 3

          Видео решение для систем счисления (Страница: 24, В.№: 2)

          Решение NCERT для математики класса 9 — системы счисления 24, вопрос 2

          Страница № 24:
          Вопрос 3:

          Напомним, π определяется как отношение длины окружности (скажем, c ) к ее диаметру (скажем, d ). То есть, . Похоже, это противоречит тому факту, что π иррационально. Как вы разрешите это противоречие?

          Ответ:

          Нет противоречия.Когда мы измеряем длину с помощью шкалы или любого другого инструмента, мы получаем только приблизительное рациональное значение. Мы никогда не получаем точного значения. По этой причине мы можем не осознавать, что либо c , либо d иррационально. Следовательно, дробь иррациональна. Следовательно, π иррационально.

          Видео решение для систем счисления (Страница: 24, Q.No .: 3)

          Решение NCERT для математики класса 9 — системы счисления 24, вопрос 3

          Страница № 24:
          Вопрос 4:

          Обозначьте на числовой строке.

          Ответ:

          Отметьте на числовой прямой отрезок OB = 9,3. Далее берем БК 1 шт. Найдите среднюю точку D OC и нарисуйте полукруг на OC, взяв D за его центр. Нарисуйте перпендикуляр к линии OC, проходящей через точку B. Пусть он пересекает полукруг в точке E. Взяв B за центр и BE за радиус, нарисуйте дугу, пересекающую числовую линию в точке F. BF.

          Видео решение для систем счисления (Страница: 24, В.№: 4)

          Решение NCERT для математики класса 9 — системы счисления 24, вопрос 4

          Страница № 24:
          Вопрос 5:

          Рационализируйте следующие знаменатели:

          (i) (ii)

          (iii) (iv)

          Ответ:

          (я)

          (ii)

          (iii)

          (iv)


          Видео решение для систем счисления (Страница: 24, В.№: 5)

          Решение NCERT для математики класса 9 — системы счисления 24, вопрос 5

          Страница № 26:
          Вопрос 1:

          Находят:

          (i) (ii) (iii)

          Ответ:

          (я)

          (ii)

          (iii)


          Видео решение для систем счисления (Стр .: 26, В.№: 1)

          Решение NCERT для математики класса 9 — системы счисления 26, вопрос 1

          Страница № 26:
          Вопрос 2:

          2 кв. Находка:

          (i) (ii) (iii)

          (iv)

          Ответ:

          (я)

          (ii)

          (iii)

          (iv)

          Видео решение для систем счисления (Стр .: 26, В.№: 2)

          Решение NCERT для математики класса 9 — системы счисления 26, вопрос 2

          Страница № 26:
          Вопрос 3:

          Упростить:

          (i) (ii) (iii)

          (iv)

          Ответ:

          (я)

          (ii)

          (iii)

          (iv)

          Видео решение для систем счисления (Стр .: 26, В.№: 3)

          Решение NCERT для математики класса 9 — системы счисления 26, вопрос 3

          Посмотреть решения NCERT для всех глав класса 9

          .

          No related posts.

          Leave a Reply

          Добавить комментарий

          Ваш адрес email не будет опубликован. Обязательные поля помечены *