ГДЗ по Алгебре за 10 класс контрольные работы Глизбург В.И. Базовый и углубленный уровень ФГОС 2014
Решебники, ГДЗ
- 11 Класс
- Русский язык
- Английский язык
- Немецкий язык
- Математика
- Геометрия
- Физика
- Химия
- Биология
- История
- География
- Обществознание
- Литература
- ОБЖ
- Информатика
- Белорусский язык
- Астрономия
ГДЗ Алгебра за 10 класс Глизбург В. И. контрольные работы
И. контрольные работы
Показать решебникиКлассы
1 2 3 4 5 6 7 8 9 10 11Математика
1 2 3 4 5 6 7 8 9 10 11
1
2
3
4
5
6
7
8
9
10
11 Русский язык
1
2Алгебра и начала анализа. 10 класс. Контрольные работы (профильный уровень). Глизбург В.И. 2007 г
10 класс. Контрольные работы (профильный уровень). Глизбург В.И. 2007 г
АЛГЕБРА И НАЧАЛА АНАЛИЗА
10 КЛАСС
КОНТРОЛЬНЫЕ РАБОТЫ (ПРОФИЛЬНЫЙ УРОВЕНЬ).
ГЛИЗБУРГ В.И.
2007 г.
Скачать бесплатно пособие в формате DjVu можно по ссылке ниже (кнопка).
Пособие доступно для скачивания в формате
Если на Вашем компьютере не установлена программа для просмотра файлов DjVu,
то можно скачать программу здесь:
Пособие содержит примерное тематическое планирование курса в трех вариантах — из расчета 4,5,6 часов в неделю на изучение курса алгебры и начал анализа в 10 классе профильной школы. Каждая из девяти контрольных работ составлена в шести вариантах.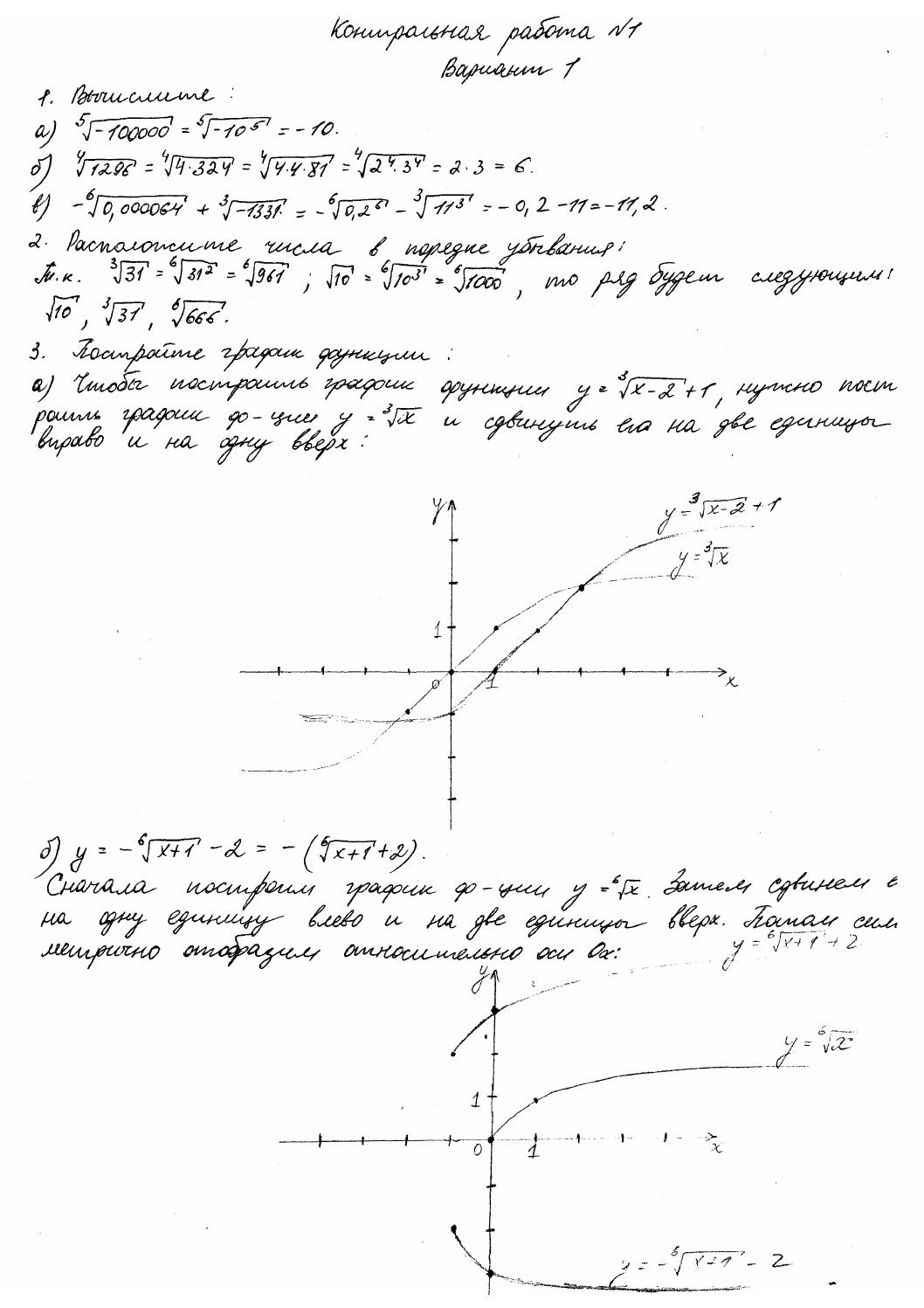 Задумка автора состояла в следующем: первый и второй варианты ориентированы на классы с недельной нагрузкой 4 ч, третий и четвертый варианты — 5ч, пятый и шестой варианты — 6ч. Выбор вариантов для проведения контрольной работы, равно как и количество выбранных вариантов, — дело учителя. Этот выбор зависит и от того количества часов в неделю, которыми располагает педагог, и от уровня подготовленности класса.
Задумка автора состояла в следующем: первый и второй варианты ориентированы на классы с недельной нагрузкой 4 ч, третий и четвертый варианты — 5ч, пятый и шестой варианты — 6ч. Выбор вариантов для проведения контрольной работы, равно как и количество выбранных вариантов, — дело учителя. Этот выбор зависит и от того количества часов в неделю, которыми располагает педагог, и от уровня подготовленности класса.
Каждый вариант контрольной работы выстроен по одной схеме: задания базового (обязательного) уровня — до первой черты, задания уровня выше среднего — между первой и второй чертой, задания повышенной сложности — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий до первой черты — оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) — оценка 4; за успешное выполнение заданий трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Если какая-либо контрольная работа представляется вам чересчур сложной или, напротив, чересчур простой для вашего класса, внесите соответствующие коррективы, но при этом постарайтесь сохранить саму концепцию контрольной работы.
| < Предыдущая | Следующая > |
|---|
ГДЗ ЛОЛ за 10 класс по Алгебре Глизбург В.И. контрольные работы ФГОС
☰
- ГДЗ
- 1 КЛАСС
- Английский язык
- Русский язык
- Математика
- Окружающий мир
- Литература
- Информатика
- Музыка
- Человек и мир
- Технология
- 2 КЛАСС
- Английский язык
- Русский язык
- Немецкий язык
- Математика
- Окружающий мир
- Литература
- Белорусский язык
- Информатика
- Музыка
- Человек и мир
ГДЗ ЛОЛ за 10 класс по Алгебре Глизбург В. И. контрольные работы ФГОС
И. контрольные работы ФГОС
☰
- ГДЗ
- 1 КЛАСС
- Английский язык
- Русский язык
- Математика
- Окружающий мир
- Литература
- Информатика
- Музыка
- Человек и мир
- Технология
- 2 КЛАСС
- Английский язык
- Русский язык
- Немецкий язык
- Математика
- Окружающий мир
- Литература
- Белорусский язык
- Информатика
- Музыка
- Человек и мир
- Французский язык
ГДЗ по Алгебре для 10 класса Глизбург В. И. контрольные работы Базовый уровень
И. контрольные работы Базовый уровень
автор: Глизбург В.И..
ГДЗ к учебнику по алгебре 10-11 класса Мордкович, Базовый уровень можно скачать здесь.
ГДЗ к задачнику по алгебре 10-11 класса Мордкович, Базовый уровень можно скачать здесь.
ГДЗ к самостоятельным работам по алгебре за 10 класс Александрова, Базовый уровень можно скачать здесь.
ГДЗ к учебнику по алгебре за 10 класс Мордкович, Базовый и углубленный уровень можно скачать
здесь.
ГДЗ к задачнику по алгебре за 10 класс Мордкович, Базовый и углубленный уровень можно скачать здесь.
ГДЗ к контрольным работам по алгебре за 10 класс Глизбург, Базовый и углубленный уровень можно скачать здесь.
ГДЗ к самостоятельным работам по алгебре за 10 класс Александрова, Базовый и углубленный уровень можно скачать здесь.
Test (algebra) — Wikipédia
Az algebrában a test egy olyan F = (T; +, ⋅) {\ displaystyle F = (T; +, \ cdot)} kétműveletes algebrai Struktúrát jelöl, ahol T {\ displaystyle jelöl, ahol T {\ displaystyle F = (T; +, \ cdot)} T} kommutatív csoportot alkot a + {\ displaystyle +} («összeadás») műveletre nézve, a ⋅ {\ displaystyle \ cdot} («szorzás») kommutatív, asszociatív, minden nem null \ cdot \ vancé elemnek { } műveletre nézve, továbbá a ⋅ {\ displaystyle \ cdot} művelet disztributív a + {\ displaystyle +} műveletre.
Egyes szerzők testnek nevezik az olyan algebrai Struktúrákat is, amelyekben a szorzás nem feelétlenül kommutatív, де a fenti tulajdonságok egyébként teljesülnek. E cikkben аз ilyenstruktúrákat ferdetestnek nevezzük, és testen mindig kommutatív ferdetestet értünk.
A test nagyon fontos fogalom az algebrán belül, nem utolsósorban amiatt, mivel rendkívül sok, az elemi matematikából is ismert számcsoport közös általánosítújtását ny. racionális, valós — это komplex számokét.Тест на математику над соком más területén — это felhasználhatóak (ld. «A testelmélet alkalmazásai»).
TestSzerkesztés
- R (x) знак равно {p (x) q (x) | p (x), q (x) ∈R [x], q (x) ≢0} {\ displaystyle \ mathbb {R} ( x) = {\ biggl \ {} {\ frac {p (x)} {q (x)}} \, {\ biggl |} \, p (x), q (x) \ in \ mathbb {R} [x], \ q (x) \ not \ Equiv 0 {\ biggl \}}}
- a racionális számok kibővítve t {\ displaystyle {\ sqrt {t}}} -vel (t∈Q { \ displaystyle t \ in \ mathbb {Q}})
- Q (t) = {a + bt | a, b∈Q} {\ displaystyle \ mathbb {Q} ({\ sqrt {t}} ) = {\ big \ {} a + b {\ sqrt {t}} \, {\ big |} \, a, b \ in \ mathbb {Q} {\ big \}}}
FerdetestSzerkesztés
- {a + bi + cj + dk | a, b, c, d∈R} {\ displaystyle \ {a + bi + cj + dk \, | \, a, b, c, d \ in \ mathbb {R} \}}
A testaxiómák és egyszerű következményeikSzerkesztés
A testaxiómák:
- ∀a, b, c∈F: a + (b + c) = (a + b) + c, a ∗ (b ∗ c) = (a ∗ b) ∗ c {\ displaystyle \ forall a, b, c \ in F: \ quad a + (b + c) = (a + b) + c, a * (b * c) = (a * b) * c}
- ∀a , b∈F: a + b = b + a, a ∗ b = b ∗ a {\ displaystyle \ forall a, b \ in F: \ quad a + b = b + a, a * b = b * a}
- ∀a, b∈F: a ∗ (b + c) = (a ∗ b) + (a ∗ c) {\ displaystyle \ forall a, b \ in F: \ quad a * (b + c) = (a * b) + (a * c)}
- Létezik nullelem (additív semleges elem), azaz olyan 0-val jelölt elem, hogy
- ∃ 0∈F: ∀a∈F: a + 0 знак равно a {\ displaystyle \ exists 0 \ in F: \ quad \ forall a \ in F: \ quad a + 0 = a}
- Létezik egységelem (multiplikatív semleges elem), azaz olyan 1-gyel jelölt elem, hogy
- ∃1 (≠ 0) ∈F: ∀a∈F: a ∗ 1 = a {\ displaystyle \ exists 1 (\ neq 0) \ in F: \ quad \ forall a \ in F: \ quad a * 1 = a}
- ∀a∈ F: ∃ − a∈F: a + (- a) = 0 {\ displaystyle \ forall a \ in F: \ quad \ exists -a \ in F: \ quad a + (- a) = 0}
- Léteznek multiplikatív Inverz Elemek vagy reciprokok (0-hoz pedig az előbbiekből bizonyíthatóan biztosan nincs):
- ∀a ≠ 0∈F: ∃a − 1 − 1∈F: a ∗ {a ∗ \ displaystyle \ forall a \ neq 0 \ in F: \ quad \ exists a ^ {- 1} \ in F: \ quad a * a ^ {- 1} = 1}
Általában ki szokták kötni, hogy испытание legalább két elemet tartalmazzon, ezt a fentiekben az 1 ≠ 0 követelmény biztosítja. {- 1}}
{- 1}}
га a és b nem nulla;
- −a = (- 1) ∗ a {\ displaystyle -a = (- 1) * a}
- sőt — (a ∗ b) = (- a) ∗ b = a ∗ (- b) {\ displaystyle — (a * b) = (- a) * b = a * (- b)}
- továbbá a * 0 = 0 {\ displaystyle a * 0 = 0};
Testben érvényesek Az alapműveletekkel kapcsolatban a racionális vagy a valós számok között megszokott azonosságok (például a törtekkel való műveletegysek elvállás), когда вы + 1 тестируете, когда хотите ответить.
Karakterisztika
Что такое алгебра? | История алгебры
Алгебра — это раздел математики, имеющий дело с символами и правилами манипулирования этими символами. В элементарной алгебре эти символы (сегодня они пишутся латинскими и греческими буквами) представляют величины без фиксированных значений, известные как переменные. Подобно тому, как предложения описывают отношения между конкретными словами, в алгебре уравнения описывают отношения между переменными. Возьмем следующий пример:
Возьмем следующий пример:
У меня есть два поля общей площадью 1800 квадратных ярдов.Урожайность для каждого поля составляет галлона зерна с квадратного ярда и ½ галлона с квадратного ярда. Первое поле дало на 500 галлонов больше, чем второе. Каковы площади каждого поля?
Распространено мнение, что подобные задачи были придуманы, чтобы мучить студентов, и это может быть недалеко от истины. Эта задача почти наверняка была написана, чтобы помочь учащимся понять математику, но что особенного в ней, так это то, что ей почти 4000 лет! Согласно Жаку Сезиано в «Введение в историю алгебры» (AMS, 2009), эта проблема основана на вавилонской глиняной табличке около 1800 г. до н. Э.C. (НДС 8389, Музей Древнего Ближнего Востока). Начиная с древней Месопотамии, алгебра играла центральную роль во многих достижениях науки, техники и цивилизации в целом. Язык алгебры значительно изменился на протяжении истории всех цивилизаций, чтобы унаследовать его (включая нашу собственную). Сегодня мы запишем задачу так:
x + y = 1,800
⅔ ∙ x — ½ ∙ y = 500
Буквы x и y обозначают площади полей. Первое уравнение понимается просто как «сложение двух областей дает общую площадь 1800 квадратных ярдов.«Второе уравнение более тонкое. Поскольку x — это площадь первого поля, а урожайность первого поля составляла две трети галлона на квадратный ярд», ⅔ ∙ x — означает «две трети, умноженные на x» — представляет собой общее количество зерна, произведенное на первом поле. Точно так же «½ ∙ y» представляет общее количество зерна, произведенное на втором поле. Поскольку первое поле дало на 500 галлонов зерна больше, чем второе, разница (следовательно, вычитание) между зерном первого поля (⅔ ∙ x) и зерном второго поля (½ ∙ y) составляет (=) 500 галлонов.
Первое уравнение понимается просто как «сложение двух областей дает общую площадь 1800 квадратных ярдов.«Второе уравнение более тонкое. Поскольку x — это площадь первого поля, а урожайность первого поля составляла две трети галлона на квадратный ярд», ⅔ ∙ x — означает «две трети, умноженные на x» — представляет собой общее количество зерна, произведенное на первом поле. Точно так же «½ ∙ y» представляет общее количество зерна, произведенное на втором поле. Поскольку первое поле дало на 500 галлонов зерна больше, чем второе, разница (следовательно, вычитание) между зерном первого поля (⅔ ∙ x) и зерном второго поля (½ ∙ y) составляет (=) 500 галлонов.
Выскакивает ответ
Конечно, сила алгебры не в кодировании утверждений о физическом мире. Компьютерный ученый и писатель Марк Джейсон Доминус пишет в своем блоге «Вселенная дискурса»: «На первом этапе вы переводите проблему в алгебру, а затем на втором этапе вы почти механически манипулируете символами, пока не появится ответ, как если бы по волшебству «. Хотя эти правила манипуляции основаны на математических принципах, новизна и непоследовательность «поворота рукоятки» или «затыкания и пыхтения» была замечена многими студентами и профессионалами.
Хотя эти правила манипуляции основаны на математических принципах, новизна и непоследовательность «поворота рукоятки» или «затыкания и пыхтения» была замечена многими студентами и профессионалами.
Здесь мы решим эту проблему, используя методы, которым их учат сегодня. И как отказ от ответственности, читателю не нужно понимать каждый конкретный шаг, чтобы понять важность этой общей техники. Я намерен сделать так, чтобы историческое значение и тот факт, что мы можем решить проблему без каких-либо предположений, вдохновят неопытных читателей узнать об этих шагах более подробно. Вот снова первое уравнение:
x + y = 1,800
Мы решаем это уравнение относительно y, вычитая x из с каждой стороны уравнения :
y = 1,800 — x
Теперь мы вводим второе уравнение:
⅔ ∙ x — ½ ∙ y = 500
Поскольку мы обнаружили, что «1,800 — x» равно y, оно может быть заменено во второе уравнение:
⅔ ∙ x — ½ ∙ (1,800 — x) = 500
Затем распределяет отрицательную половину (–½) по выражению «1,800 — x»:
⅔ ∙ x + (–½ ∙ 1,800) + (–½ ∙ –x) = 500
Этот упрощает до:
⅔ ∙ x — 900 + ½ ∙ x = 500
Сложите две доли x вместе и прибавьте 900 к с каждой стороны уравнения :
(7/6) ∙ x = 1,400
Теперь разделите с каждой стороны уравнения на 7/6:
x = 1,200
Таким образом, первое поле имеет площадь 1200 квадратных ярдов. Это значение может быть заменено на в первом уравнении для определения y:
Это значение может быть заменено на в первом уравнении для определения y:
(1,200) + y = 1,800
Вычтем 1,200 из с каждой стороны уравнения , чтобы найти y:
y = 600
Таким образом, второе поле имеет площадь 600 квадратных ярдов.
Обратите внимание, как часто мы используем технику выполнения операций с каждой стороной уравнения . Эту практику лучше всего понимать как визуализацию уравнения в виде шкалы с известным весом с одной стороны и неизвестным весом с другой.Если мы добавляем или вычитаем одинаковое количество веса с каждой стороны, весы остаются сбалансированными. Точно так же шкала остается сбалансированной, если мы умножаем или
Pre-Algebra Test (10
- Ресурс исследования
- Исследовать
- Искусство и гуманитарные науки
- Бизнес
- Инженерная технология
- Иностранный язык
- История
- Математика
- Наука
- Социальная наука
Лучшие подкатегории
- Продвинутая математика
- Алгебра
- Базовая математика
- Исчисление
- Геометрия
- Линейная алгебра
- Предалгебра
- Предварительное исчисление
- Статистика и вероятность
- Тригонометрия
- Другое →
Лучшие подкатегории
- Астрономия
- Астрофизика
- Биология
- Химия
- Науки о Земле
- Наука об окружающей среде
- Здравоохранение
- Физика
- Другое →
Лучшие подкатегории
- Антропология
- Закон
- Политология
- Психология
- Социология
- Другое →
Концепции алгебры, протестированные на GRE: Обзор
Добро пожаловать в нашу серию статей о специфике раздела GRE Quantitative Reasoning. (Звучит пугающе, правда? Назовем это просто «математикой».)
(Звучит пугающе, правда? Назовем это просто «математикой».)
В прошлый раз мы подробно рассказали о том, какие задачи вы можете ожидать увидеть в день тестирования, и сосредоточились на арифметической части. На этой неделе мы рассмотрим раздел теста по алгебре. Однако прежде чем мы начнем, напомним:
В разделе математики GRE нет ничего, что вы не изучали бы в средней школе (или иногда в средней школе)!
Вопросы могут показаться сложными, но это только потому, что тестировщики пытаются вас обмануть.Однако основные концепции — это просто базовая алгебра. Вам не потребуется придумывать какие-либо доказательства, и вам не понадобится какой-либо словарь алгебры (например, распределительное свойство, коммутативность и т. Д.). Вам не нужно ничего изучать; скорее, ваша подготовка к этому разделу будет в основном запоминанием и практикой.
Итак, по какой алгебре тестируется GRE?
Вот и все!
Вроде много?
Честно говоря, нет. Возьмем наугад: уравнения с показателями.Вопрос может задать вам разницу между (y⁵) • (y⁵) и (y⁵) ⁵. Как вы помните, это не одно и то же выражение. Умножение переменных (одной базы!) Требует сложения показателей вместе. Хороший способ визуализировать это — представить (y⁵) как (y • y • y • y • y).
Возьмем наугад: уравнения с показателями.Вопрос может задать вам разницу между (y⁵) • (y⁵) и (y⁵) ⁵. Как вы помните, это не одно и то же выражение. Умножение переменных (одной базы!) Требует сложения показателей вместе. Хороший способ визуализировать это — представить (y⁵) как (y • y • y • y • y).
В первом выражении просто удалите скобки и получите y 10 . Во втором случае вы возьмете показатель степени на показатель и умножите их, что даст вам y 25 .
Не так уж и плохо, правда?
Верно! Как я уже сказал: в GRE нет математики, которую вы еще не выучили. Но это не похоже на ваши уроки математики в старшей школе; GRE пытается заставить вас выбрать неправильный ответ.
К счастью, наша программа подготовки к экзаменам научит вас двум методам, которые помогут вам получить как правильный ответ, так и получить заслуженный балл. Они называются подключением и обратным подключением (работа в обратном направлении), и прежде чем мы перейдем к нашему обзору геометрии, мы рассмотрим эти простые методы.
