Геометрия 7 Атанасян К-2 В-3
Контрольная работа № 2 «Треугольники» по геометрии в 7 классе с ответами для УМК Атанасян. Вариант 3. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей. Геометрия 7 Атанасян К-2 В-3.
Геометрия 7 класс (Атанасян)
Контрольная работа № 2. Вариант 3.
К-2 «Треугольники» (транскрипт заданий)
Часть А. Запишите номера верных ответов к заданию 1.
№ 1. Используя рисунок, укажите верные утверждения: 1) PN — биссектриса треугольника МРК. 2) PN — высота треугольника МРК. 3) ЕК — биссектриса треугольника DEC. 4) ВМ — медиана треугольника CBD. 5) ВМ — биссектриса треугольника CBD.
Часть В. Запишите ответ к заданию 2.
№ 2. Треугольник РОВ — равнобедренный с основанием PR. Чему равен ∠1, если ∠2 = 42°?
Часть С. Запишите обоснованное решение задач 3-5.
№ 3. Луч КС — биссектриса угла DKB, а отрезок DK равен отрезку ВК. Докажите, что ΔKDC = ΔКВС.
Докажите, что ΔKDC = ΔКВС.
№ 4. На основании NK равнобедренного треугольника NBK отложены отрезки NA = КС. Докажите, что ∠NBA= ∠KBC.
№ 5*. В окружности с центром О проведены диаметр АС и хорда BD, пересекающиеся в точке М, причем ВМ = DM. ∠BAC = 35°. Найдите ∠BAD.
Геометрия 7 Атанасян К-2 В-3
ОТВЕТЫ на контрольную работу:
№ 1. 1, 4.
№ 2. 42°.
№ 3. См.решения.
№ 4. См.решения.
№ 5. 70°.
Смотреть РЕШЕНИЯ заданий Варианта 3 в тетради
Вы смотрели: Контрольная работа № 2 «Треугольники» по геометрии в 7 классе с ответами для УМК Атанасян. Дидактические материалы (упражнения) для учителей, учащихся и родителей.
К-2. Вариант 0 К-2. Вариант 1 К-2. Вариант 2 К-2. Вариант 3 К-2. Вариант 4
Вернуться на страницу: Контрольные работы по геометрии в 7 классе УМК Атанасян.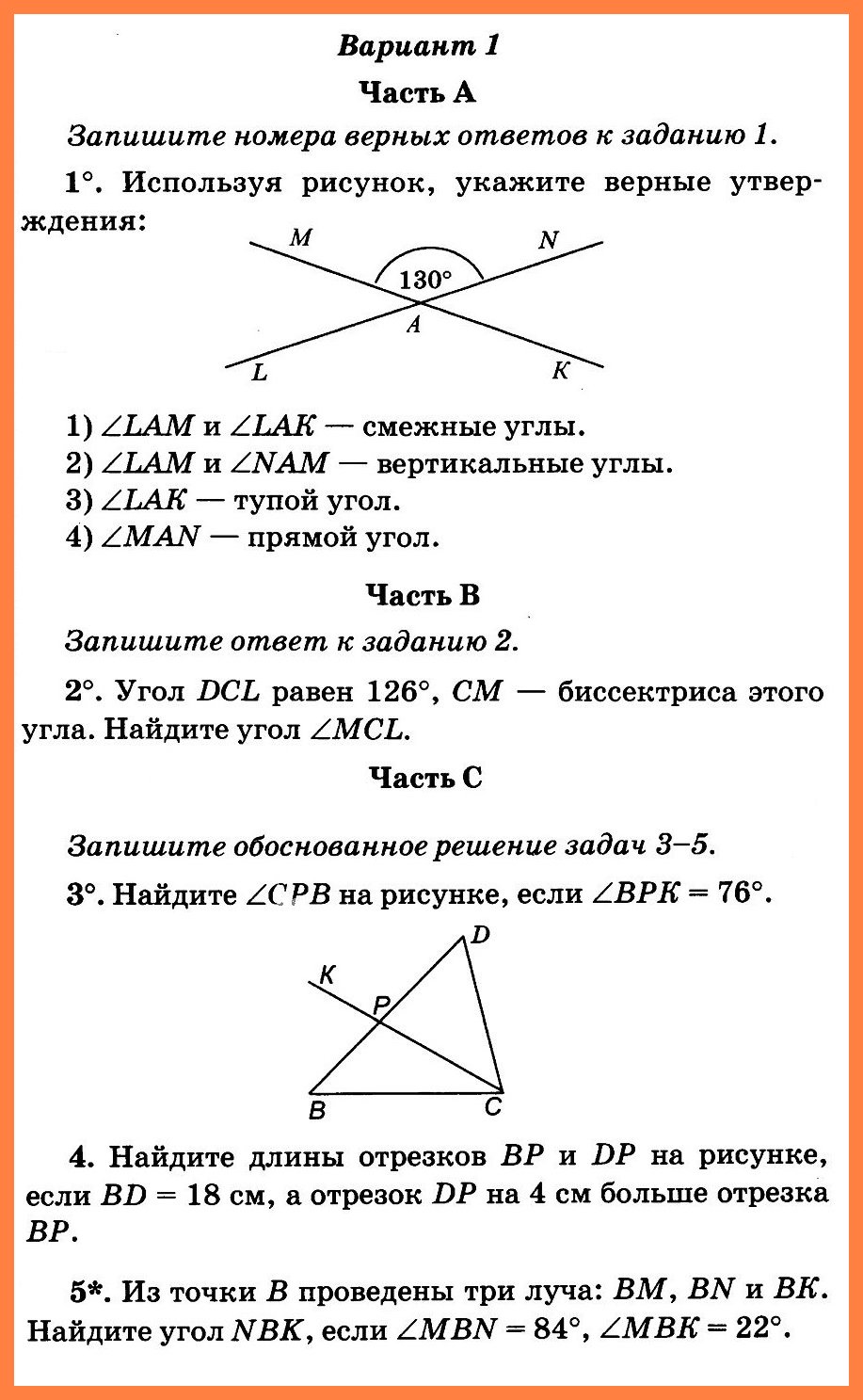
Перейти на страницу: Контрольные работы по геометрии в 7 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова) использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.
ГДЗ 7 класс / контрольные работы / К-1. вариант 2 геометрия 7‐9 класс самостоятельные и контрольные работы Иченская
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- 5 класс
- Математика
Решебник по геометрии за 7 класс контрольные работы Мельникова Н. Б. ФГОС
Б. ФГОС
gdzguru.com
Видеорешения
решебники- 1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Французский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Человек и мир
ГДЗ за 7‐9 класс по Геометрии Иченская М. А. самостоятельные и контрольные работы
А. самостоятельные и контрольные работы
gdz-bot.ru
НайтиНавигация по гдз
1 класс Русский язык Математика Английский язык Окружающий мир Литература Информатика Музыка Человек и мир 2 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка Технология Человек и мир 3 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка 4 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка Белорусский язык 5 класс Русский язык Математика Английский язык Немецкий язык История География Биология Обществознание Физика Литература ИнформатикаКонтрольные работы по геометрии для 7 класса
Контрольные работы по геометрии для 7 класса.
К учебнику «Геометрия 7-9», автор Атанасян Л.С, Бутузов В.Ф,Кодомцев С.Б. и др.Москва, Просвещение, 2010г .
Составитель: Котова Лилия Анатольевна.
МБОУ СОШ №1 г. Сальск.
Контрольная работа №1.
Вариант 1.
1)Три точки В,С и Д лежат на одной прямой. Известно, что ВД=17см,ДС=25см.Какой может быть длина отрезка ВС?
2)Сумма вертикальных углов МОЕ и ДОС, образованных при пересечении прямых МС и ДЕ, равна 204°.Найдите угол МОД.
3)С помощью транспортира начертите угол, равный 78° ,и проведите биссектрису смежного с ним угла.
Контрольная работа №1.
Вариант 2.
1)Три точки М,N и К лежат на одной прямой. Известно, что MN=15см,NК=18см.Каким может быть расстояние МК?
2)Сумма вертикальных углов АОВ и СОД, образованных при пересечении прямых АД и ВС, равна 108°. Найдите угол ВОД.
3) С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов. Контрольная работа №2.
Вариант 1.
1)На рис.1 отрезки АВ и СД имеют общую середину О.Докажите, что
2)Луч АД — биссектриса угла А.На сторонах угла А отмечены точки В и С так, что
3)Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
Вариант 2.
1)На рис. 2 отрезки МЕ и РК точкой Д делятся пополам. Докажите, что
2)На сторонах угла Д отмечены точки М и К так, что ДМ=ДК. Точка Р лежит внутри угла Д и РК=РМ. Докажите, что луч ДР- биссектриса угла МДК.
3) Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Контрольная работа №3.
Вариант 1.
1)Отрезки ЕF и РД пересекаются в их середине М.Докажите, что РЕ II ДF.
2)Отрезок ДМ- биссектриса треугольника СДЕ. Через точку М проведена прямая, параллельная стороне СД и пересекающая сторону ДЕ в точке N.Найдите углы треугольника ДМN, если
Контрольная работа №3.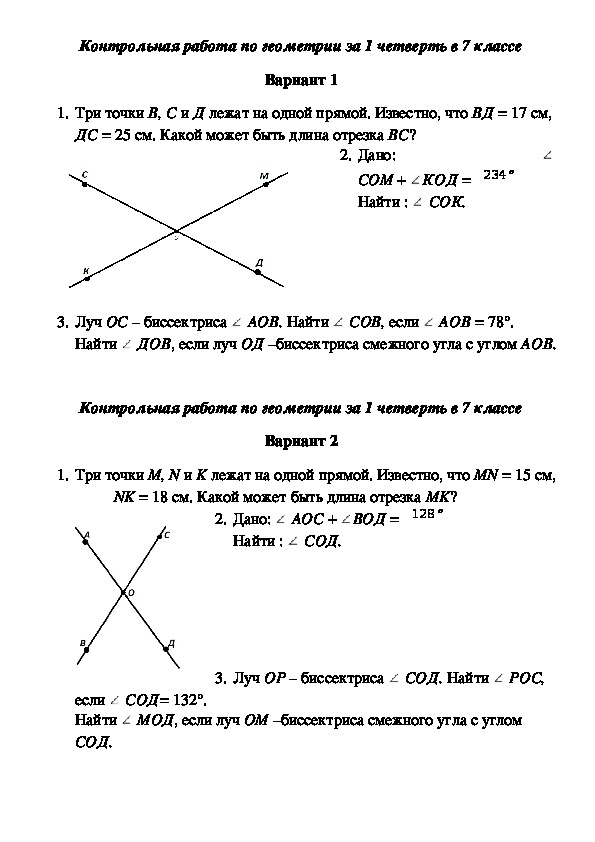
Вариант 2.
Отрезки MN и EF пересекаются в их середине Р. Докажите, что EN II MF.
Отрезок АД-биссектриса треугольника АВС. Через точку Д проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F.Найдите углы треугольника АДF, если
Контрольная работа №4.
Вариант 1.
1)На рис.1 угол АВЕ равен 104°, угол ДСF равен 76°,АС=12 см.Найдите сторону АВ треугольника АВС.
2)В треугольнике СДЕ точка М лежит на стороне СЕ, причём угол СМД острый. Докажите, что ДЕ> ДМ.
3)Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант 2.
1)На рис.2 угол ВАЕ равен 112 °, угол ДВF равен 68° , ВС=9см.Найдите сторону АС треугольника АВС.
2)В треугольнике MNP точка К лежит на стороне МN, причём угол NКР острый. Докажите, что КР
3)Одна из сторон равнобедренного тупоугольного треугольника на 17см меньше другой.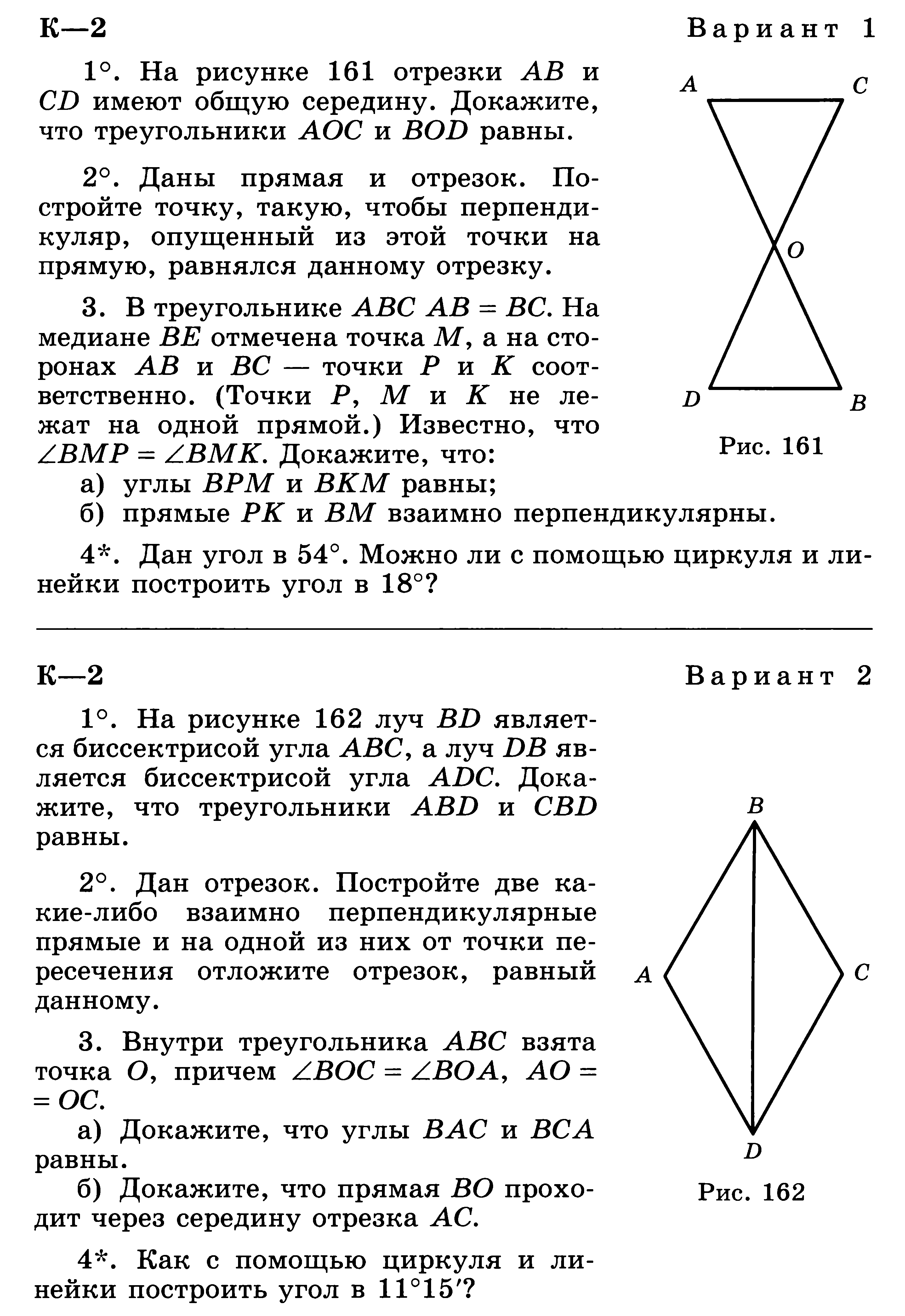 Найдите стороны этого треугольника, если его периметр равен 77см.
Найдите стороны этого треугольника, если его периметр равен 77см.
Контрольная работа №5.
Вариант 1.
1)В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NК в точке О, причём ОК=9см.Найдите расстояние от точки О до прямой МN.
2)Постойте прямоугольный треугольник по гипотенузе и острому углу.
Дополнительное задание.
С помощью циркуля и линейки постройте угол равный 150°.
Контрольная работа №5.
Вариант 2.
1)В прямоугольном треугольнике ДСЕ с прямым углом С проведена биссектриса ЕF, причём FC=13cм.Найдите расстояние от точки F до прямой ДЕ.
2) Постойте прямоугольный треугольник по катету и прилежащему к нему острому углу.
Дополнительное задание.
С помощью циркуля и линейки постройте угол равный 105°.
контрольные работы геометрия 7 класс
Контрольные работы по геометрии 7 класс
Сакуновой И.В. учителя математики МКОУ ДСОШ №1
Контрольная работа №1
Начальные геометрические сведения
Вариант 1
Три точки В, С и К лежат на одной прямой. Известно, что ВК = 17 см, КС = 25 см. Какой может быть длина отрезка ВС?
Известно, что ВК = 17 см, КС = 25 см. Какой может быть длина отрезка ВС?
Сумма вертикальных углов МОЕ, РОК, образованных при пересечении прямых МК и РЕ равна 198о. Найдите угол МОР.
С помощью транспортира начертите угол, равный 56о и проведите биссектрису смежного с ним угла.
__________________________________________________________________
Контрольная работа №1
Начальные геометрические сведения
Вариант 2
Три точки М, N и К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК?
Сумма вертикальных углов АОВ и СОК, образованных при пересечении прямых АК и ВС равна 108о. Найдите угол ВОК.
С помощью транспортира начертите угол, равный 132о и проведите биссектрису смежного с ним угла.
Контрольная работа №2
Треугольники
Вариант 1
1.Каждый из отрезков АВ и CD на рисунке точкой О делится пополам. Докажите, что DAO = CBO.
Докажите, что DAO = CBO.
2.Луч АК – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что АКВ = АКС. Докажите, что АВ = АС.
3.Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВМ к боковой стороне АС.
__________________________________________________________________
К онтрольная работа №2
Треугольники
Вариант 2
Каждый из отрезков АВ и CD на рисунке точкой О делится пополам. Докажите, что СAO = DBO.
2. На сторонах угла А отмечены точки М и К так, что АМ = АК. Известно, что точка Р лежит внутри угла А и РК = РМ. Докажите, что АВ = АС.
3.Начертите треугольник АВС с основанием АС. С помощью циркуля и линейки проведите высоту АН.
Контрольная работа №3
Параллельные прямые
Вариант 1
1 .Отрезки АВ и CD пересекаются в их середине О. Докажите, что
АС || BD.
2.На рисунке 1 = 63о,2 = 77о, 4 = 117о.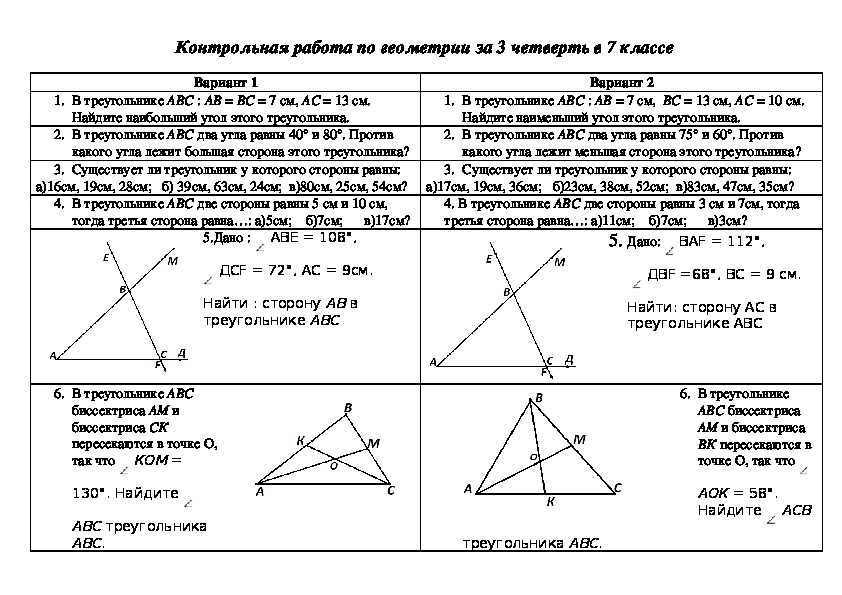 Найдите 3.
Найдите 3.
3.ОтрезокDМ – биссектриса треугольника СDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N.
Найдите углы треугольника DMN, если CDE = 68о.
__________________________________________________________________
Контрольная работа №3
Параллельные прямые
Вариант 2
О трезки PN и ED пересекаются в их середине M. Докажите, что EN || PD.
На рисунке 1 = 47о,2 = 118о, 3 = 62о. Найдите 4.
ОтрезокDМ – биссектриса треугольника ADC. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DA в точке N.
Найдите углы треугольника DMN, если ADC = 72о.
Контрольная работа №4
Соотношения между сторонами и углами треугольника
Вариант 1
1. В треугольникеCDE точка К лежит на отрезке СЕ, причем СКD – острый угол. Докажите, что DE > DK.
2. Основание равнобедренного треугольника равно 29,9 см. Могут ли боковые стороны быть равными 15 см каждая?
3.Заданы отрезки РК, РМ и угол Р. Постройте треугольник АВС так, чтобы АВ = РМ, АС = РК, А =Р.
С помощью циркуля и линейки постройте угол, равный 150о.
__________________________________________________________________
Контрольная работа №4
Соотношения между сторонами и углами треугольника
Вариант 2
В треугольникеMNP точка К лежит на отрезке MN, причем NKP – острый угол. Докажите, что KP < MP.
Боковые стороны равнобедренного треугольника равны 10 см. Может ли основание быть равным 20,01 см?
Заданы отрезки КЕ, угол К и угол Е. Постройте треугольник АВС так, чтобы АВ = КЕ, А =К, В =Е.
С помощью циркуля и линейки постройте угол, равный 105о.
Контрольная работа №5
Итоговое повторение курса геометрии 7 класса
Вариант 1
1.Сумма двух углов, которые получаются при пересечении двух прямых, равна 50о. Найдите эти углы.
Найдите эти углы.
2. В равнобедренном треугольнике АВС с основанием АС проведена медиана ВМ. На ней взята точка О. Докажите равенство треугольников АВО и СВО.
3. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса СК. Найдите углы треугольника АВС, если угол АКС = 60о.
4. В прямоугольном треугольнике АВС катет АВ равен 3 см, угол С равен 15о. На катете АС отмечена точка D так, что угол СBD равен 15о.
а) найдите длину отрезка BD.
б) Докажите, что ВС < 12 см.
__________________________________________________________________
Контрольная работа №5
Итоговое повторение курса геометрии 7 класса
Вариант 2
Один из углов, которые получаются при пересечении двух прямых, равен 30о. Чему равны остальные углы ?
В равнобедренном треугольнике АВС с основанием АС и углом при вершине В, равным 36о, проведена биссектриса АК.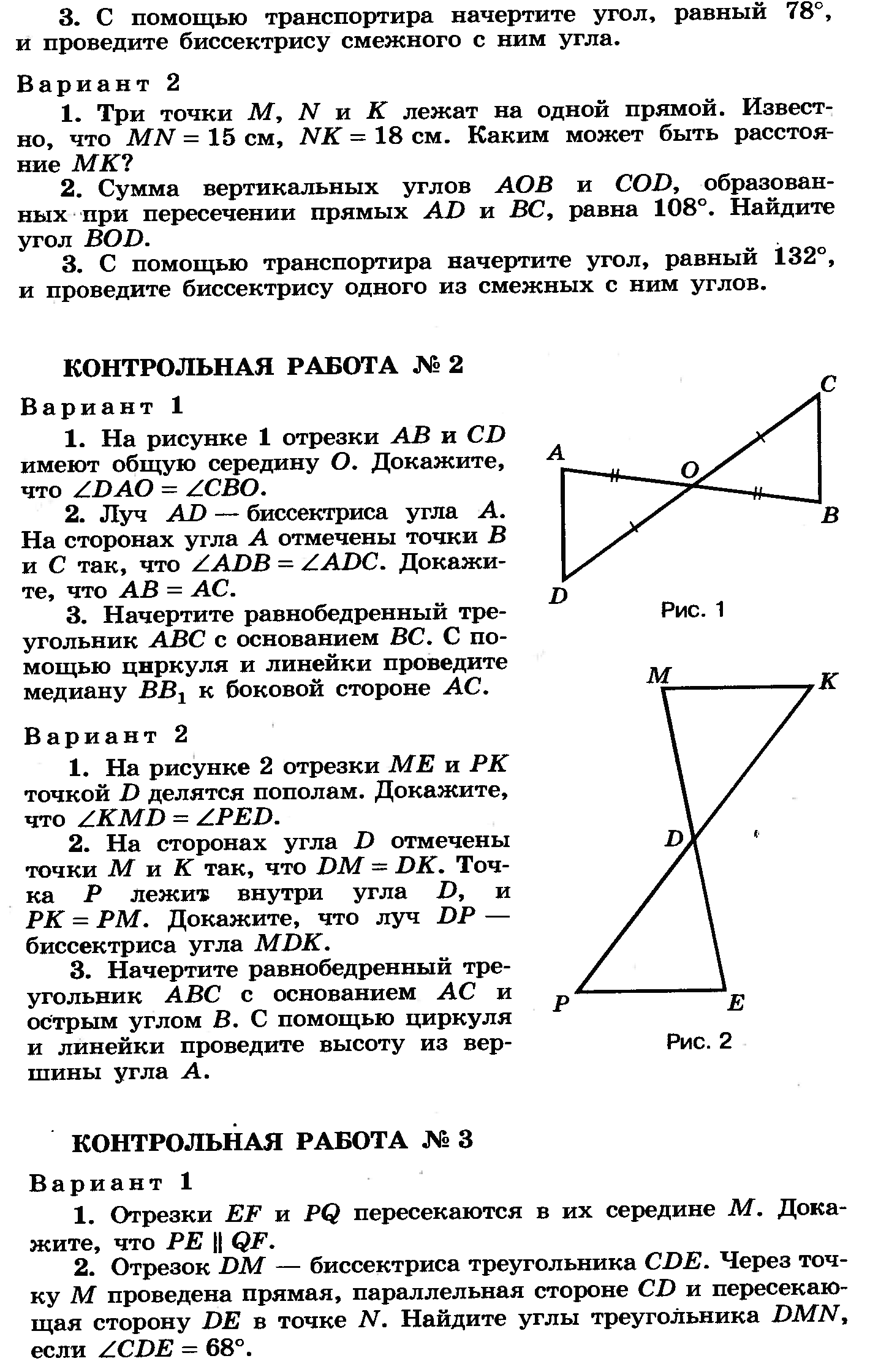 Докажите, что треугольники СКА и АКВ равнобедренные..
Докажите, что треугольники СКА и АКВ равнобедренные..
В равнобедренном треугольнике АВС с основанием АС проведена медиана ВМ. На ней взята точка О. Докажите равенство треугольников АМО и СМО.
4. В треугольнике АВС В = 90о,С = 60о, ВС = 2 см. На стороне АС отмечена точка D так, что угол АBD равен 30о.
а) найдите длину отрезка АD.
б) Докажите, что периметр треугольника АВС меньше 10 см.
РешенияNCERT для математики класса 10 Глава 7
Страница № 161:
Вопрос 1:
Найдите расстояние между следующими парами точек:
(i) (2, 3), (4, 1) (ii) (−5, 7), (−1, 3) (iii) ( a , b ), (- a , — б )
Ответ:
(i) Расстояние между двумя точками равно
.(ii) Расстояние между дается
(iii) Расстояние между дается
Видео решение для координатной геометрии (Страница: 161, Q. №: 1)
№: 1)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 1
Страница № 161:
Вопрос 2:
Найдите расстояние между точками (0, 0) и (36, 15). Можете ли вы теперь найти расстояние между двумя городами A и B, обсуждаемыми в разделе 7.2.
Ответ:
Расстояние между точками
Да, мы можем найти расстояние между заданными городами A и B.
Предположим, что город A находится в исходной точке (0, 0).
Следовательно, город B будет в точке (36, 15) относительно города A.
Таким образом, согласно расчетам выше, расстояние между городами A и B будет
. 39 км.
Видео решение для координатной геометрии (Страница: 161, Q.No .: 2)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 2
Страница № 161:
Вопрос 3:
Определите, лежат ли точки (1, 5), (2, 3) и (- 2, — 11) на одной прямой.
Ответ:
Пусть точки (1, 5), (2, 3) и (−2, −11) представляют вершины A, B и C данного треугольника соответственно.
Пусть
Следовательно, точки (1, 5), (2, 3) и (−2, −11) не лежат на одной прямой.
Видео решение для координатной геометрии (Страница: 161, Q.No .: 3)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 3
Страница № 161:
Вопрос 4:
Проверить, являются ли (5, — 2), (6, 4) и (7, — 2) вершинами равнобедренного треугольника.
Ответ:
Пусть точки (5, −2), (6, 4) и (7, −2) представляют вершины A, B и C данного треугольника соответственно.
Так как две стороны равны, значит, ABC — равнобедренный треугольник.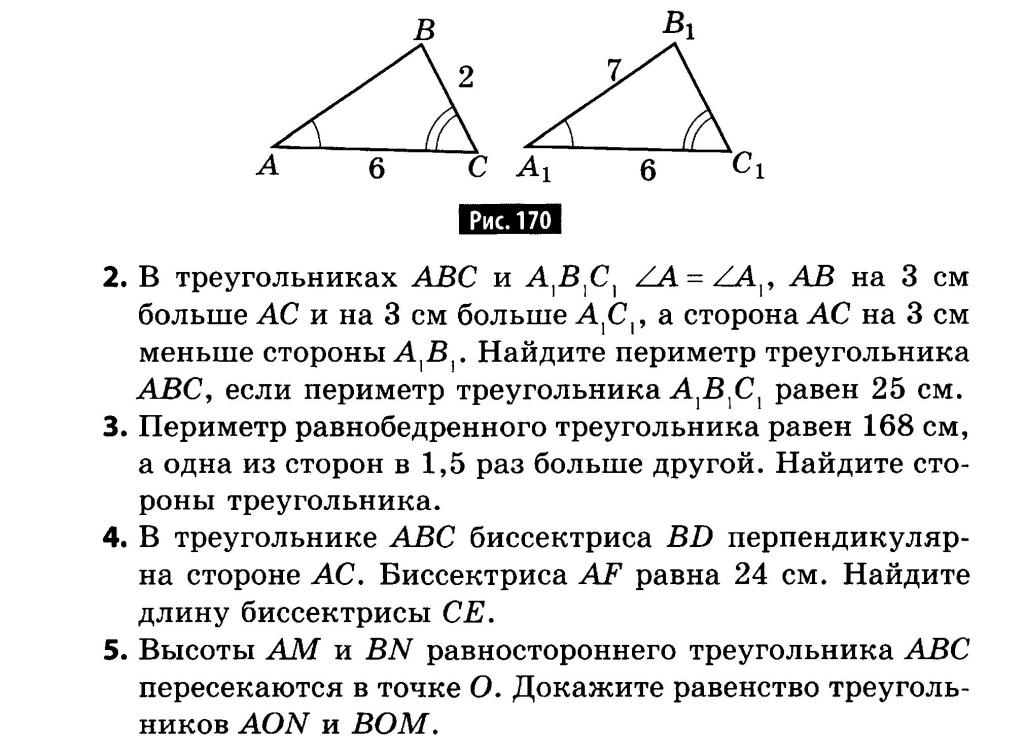
Видео решение для координатной геометрии (Страница: 161, Q.No .: 4)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 4
Страница № 161:
Вопрос 5:
В классе 4 друга сидят в точках A, B, C и D, как показано на следующем рисунке.Чампа и Чамели входят в класс и, понаблюдав в течение нескольких минут, спрашивает Чамели: «Вам не кажется, что ABCD — квадрат?» Чамели не согласен.
Используя формулу расстояния, найдите, какое из них правильное.
Ответ:
Можно заметить, что A (3, 4), B (6, 7), C (9, 4) и D (6, 1) являются позициями этих четырех друзей.
CD = 9-62 + 4-12 = 32 + 32 = 9 + 9 = 18 = 32
Можно заметить, что все стороны этого четырехугольника ABCD имеют одинаковую длину, а также диагонали одинаковой длины.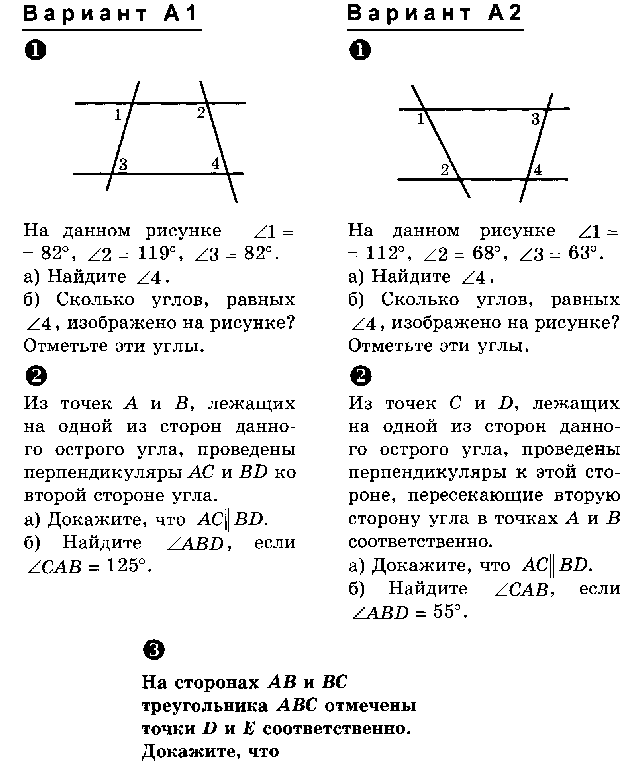
Следовательно, ABCD — квадрат и, следовательно, Чампа был прав
Видео решение для координатной геометрии (Страница: 161, Q.No .: 5)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 5
Страница № 161:
Вопрос 6:
Назовите тип четырехугольника, образованного, если таковой имеется, следующими точками, и объясните причины своего ответа:
(i) (- 1, — 2), (1, 0), (- 1, 2), (- 3, 0)
(ii) (- 3, 5), (3, 1), (0, 3), (- 1, — 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Ответ:
(i) Пусть точки (−1, −2), (1, 0), (−1, 2) и (−3, 0) представляют вершины A, B, C и D данного четырехугольник соответственно.
Можно заметить, что все стороны этого четырехугольника имеют одинаковую длину, а также диагонали одинаковой длины. Следовательно, данные точки являются вершинами квадрата.
Следовательно, данные точки являются вершинами квадрата.
(ii) Пусть точки (- 3, 5), (3, 1), (0, 3) и (−1, −4) представляют вершины A, B, C и D данного четырехугольника соответственно.
Видно, что все стороны этого четырехугольника имеют разную длину. Следовательно, можно сказать, что это только общий четырехугольник, а не конкретный, такой как квадрат, прямоугольник и т. Д.
(iii) Пусть точки (4, 5), (7, 6), (4, 3) и (1, 2) представляют вершины A, B, C и D данного четырехугольника соответственно.
Можно заметить, что противоположные стороны этого четырехугольника имеют одинаковую длину. Однако диагонали бывают разной длины. Следовательно, данные точки являются вершинами параллелограмма.
Видео решение для координатной геометрии (Страница: 161, Q. No.: 6)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 6
Страница № 161:
Вопрос 7:
Найдите точку на оси x , которая равноудалена от (2, — 5) и (- 2, 9).
Ответ:
Нам нужно найти точку на оси x . Следовательно, его координата y будет равна 0.
Пусть точка на оси x будет.
По заданному условию эти расстояния равны по мере.
Следовательно, точка (- 7, 0).
Видео решение для координатной геометрии (Страница: 161, Q.No .: 7)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 7
Страница № 161:
Вопрос 8:
Найдите значения y , для которых расстояние между точками P (2, — 3) и Q (10, y ) равно 10 единицам.
Ответ:
Принято, что расстояние между (2, −3) и (10, y ) равно 10.
Видео решение для координатной геометрии (Страница: 161, Q.No .: 8)
Решение NCERT для математики класса 10 — координатная геометрия 161, вопрос 8
Страница № 162:
Вопрос 9:
Если Q (0, 1) равноудалено от P (5, — 3) и R ( x , 6), найдите значения x .Также найдите расстояние QR и PR.
Ответ:
Следовательно, точка R равна (4, 6) или (−4, 6).
Когда точка R равна (4, 6),
Когда точка R равна (−4, 6),
Видео решение для координатной геометрии (Страница: 162, Q.No .: 9)
Решение NCERT для математики класса 10 — координатная геометрия 162, вопрос 9
Страница № 162:
Вопрос 10:
Найдите соотношение между x и y , при котором точка ( x , y ) находится на равном расстоянии от точки (3, 6) и (- 3, 4).
Ответ:
Точка( x , y ) равноудалена от (3, 6) и (−3, 4).
Видео решение для координатной геометрии (Страница: 162, Q.No .: 10)
Решение NCERT для математики класса 10 — координатная геометрия 162, вопрос 10
Страница № 167:
Вопрос 1:
Найдите координаты точки, которая делит соединение (- 1, 7) и (4, — 3) в соотношении 2: 3.
Ответ:
Пусть P ( x , y ) будет требуемой точкой. Используя формулу сечения, получаем
Следовательно, точка (1, 3).
Видео решение для координатной геометрии (Страница: 167, Q.No .: 1)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 1
Страница № 167:
Вопрос 2:
Найдите координаты точек тройного пересечения отрезка прямой, соединяющего (4, — 1) и (- 2, — 3).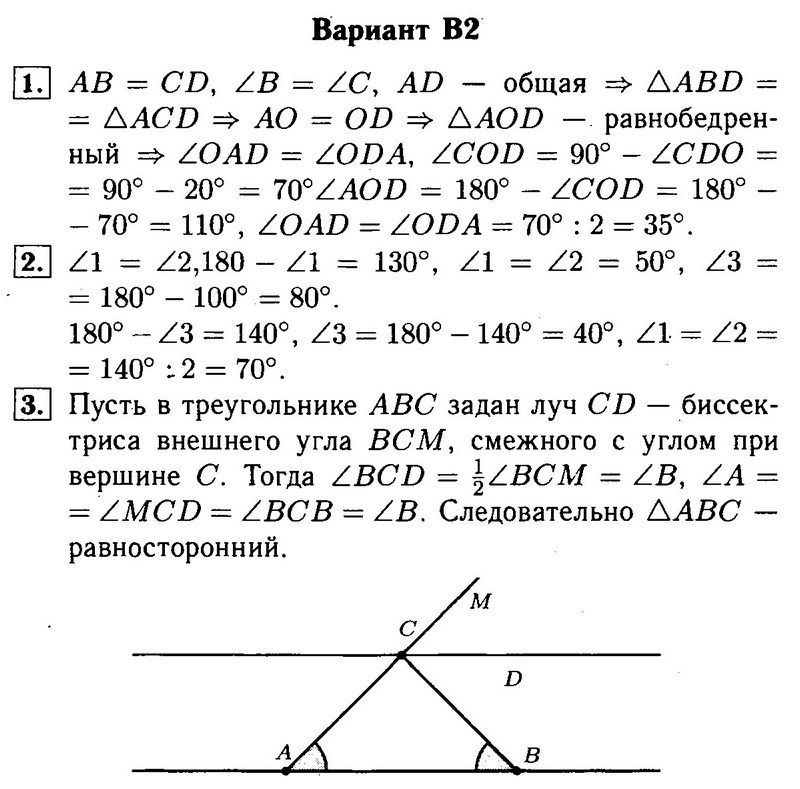
Ответ:
Пусть P ( x 1 , y 1 ) и Q ( x 2 , y 2 ) являются точками трисечения отрезка прямой, соединяющего данные точки, т. Е. AP = PQ = QB
Следовательно, точка P делит AB внутри в соотношении 1: 2.
Точка Q делит AB внутри в соотношении 2: 1.
Видео решение для координатной геометрии (Страница: 167, Q.№: 2)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 2
Страница № 167:
Вопрос 3:
Для проведения Дня спорта на школьной площадке ABCD прямоугольной формы были нарисованы линии мелом на расстоянии 1 м каждая. 100 цветочных горшков были размещены на расстоянии 1 м друг от друга по AD, как показано на следующем рисунке. Нихарика пробегает дистанцию AD по линии 2 и и вывешивает зеленый флаг. Прит пробегает дистанцию AD на восьмой строчке и ставит красный флаг. Какое расстояние между обоими флажками? Если Рашми нужно вывесить синий флаг ровно посередине между отрезком линии, соединяющим два флага, где она должна разместить свой флаг?
Нихарика пробегает дистанцию AD по линии 2 и и вывешивает зеленый флаг. Прит пробегает дистанцию AD на восьмой строчке и ставит красный флаг. Какое расстояние между обоими флажками? Если Рашми нужно вывесить синий флаг ровно посередине между отрезком линии, соединяющим два флага, где она должна разместить свой флаг?
Ответ:
Видно, что Нихарика вывесил зеленый флаг на расстоянии AD i.е., м от начальной точки 2 линии -й . Следовательно, координаты этой точки G равны (2, 25).
Точно так же Прит вывесил красный флаг на расстоянии AD, то есть в метрах от начальной точки линии 8 -й . Следовательно, координаты этой точки R равны (8, 20).
Расстояние между этими флажками по формуле расстояния = GR
=
Точка, в которой Рашми должна вывесить свой синий флаг, — это середина линии, соединяющей эти точки.Пусть эта точка будет A ( x , y ).
Следовательно, Рашми следует вывесить свой синий флаг на высоте 22,5 м на линии 5 .
Видео решение для координатной геометрии (Страница: 167, Q.No .: 3)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 3
Страница № 167:
Вопрос 4:
Найдите отношение, в котором отрезок прямой, соединяющий точки (- 3, 10) и (6, — 8), делится на (- 1, 6).
Ответ:
Пусть соотношение, в котором отрезок линии, соединяющий (−3, 10) и (6, −8), делится на точку (−1, 6), составляет k : 1.
Видео решение для координатной геометрии (Страница: 167, Q.No .: 4)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 4
Страница № 167:
Вопрос 5:
Найдите отношение, в котором отрезок линии, соединяющий A (1, — 5) и B (- 4, 5), делится на ось x . Также найдите координаты точки разделения.
Также найдите координаты точки разделения.
Ответ:
Пусть отношение, в котором отрезок линии, соединяющий A (1, −5) и B (−4, 5), делится на x — осей be.
Следовательно, координаты точки разделения есть.
Мы знаем, что координата y любой точки на оси x равна 0.
Следовательно, ось x делит его в соотношении 1: 1.
Балл деления =
Видео решение для координатной геометрии (Страница: 167, Q.No .: 5)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 5
Страница № 167:
Вопрос 6:
Если (1, 2), (4, y ), ( x , 6) и (3, 5) — вершины параллелограмма, взятые по порядку, найдите x и y .
Ответ:
Пусть (1, 2), (4, y ), ( x , 6) и (3, 5) — координаты вершин A, B, C, D параллелограмма ABCD. Точка пересечения O диагоналей AC и BD также делит эти диагонали.
Точка пересечения O диагоналей AC и BD также делит эти диагонали.
Следовательно, O — это средняя точка AC и BD.
Если O — средняя точка AC, то координаты O равны
.Если O — средняя точка BD, то координаты O равны
.Поскольку обе координаты относятся к одной и той же точке O,
Видео решение для координатной геометрии (Страница: 167, Q.№: 6)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 6
Страница № 167:
Вопрос 7:
Найдите координаты точки A, где AB — диаметр окружности с центром (2, — 3), а B — (1, 4)
Ответ:
Пусть координаты точки A будут ( x , y ).
Средняя точка AB — (2, −3), которая является центром круга.
Видео решение для координатной геометрии (Страница: 167, Q.No .: 7)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 7
Страница № 167:
Вопрос 8:
Если A и B равны (- 2, — 2) и (2, — 4) соответственно, найдите координаты P такие, что и P лежит на отрезке AB.
Ответ:
Координаты точек A и B равны (−2, −2) и (2, −4) соответственно.
С,
Следовательно, AP: PB = 3: 4
Точка P делит отрезок AB в соотношении 3: 4.
Видео решение для координатной геометрии (Страница: 167, Q.No .: 8)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 8
Страница № 167:
Вопрос 9:
Найдите координаты точек, разделяющих отрезок прямой, соединяющий точки A (- 2, 2) и B (2, 8), на четыре равные части.
Ответ:
Из рисунка видно, что точки P, Q, R разделяют отрезок прямой в соотношении 1: 3, 1: 1, 3: 1 соответственно.
Видео решение для координатной геометрии (Страница: 167, Q.No .: 9)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 9
Страница № 167:
Вопрос 10:
Найдите площадь ромба, если его вершины (3, 0), (4, 5), (- 1, 4) и (- 2, −1) взяты по порядку.[ Подсказка: Площадь ромба = (произведение его диагоналей)]
Ответ:
Пусть (3, 0), (4, 5), (−1, 4) и (−2, −1) — вершины A, B, C, D ромба ABCD.
Видео решение для координатной геометрии (Страница: 167, Q. No .: 10)
No .: 10)
Решение NCERT для математики класса 10 — координатная геометрия 167, вопрос 10
Страница № 170:
Вопрос 1:
Найдите площадь треугольника с вершинами:
(i) (2, 3), (- 1, 0), (2, — 4) (ii) (- 5, — 1), (3, — 5), (5, 2)
Ответ:
(i) Площадь треугольника равна
.(ii)
Видео решение для координатной геометрии (Страница: 170, Q.№: 1)
Решение NCERT для математики класса 10 — координатная геометрия 170, вопрос 1
Страница № 170:
Вопрос 2:
В каждом из следующих значений найдите значение « k », для которого точки лежат на одной прямой.
(i) (7, — 2), (5, 1), (3, — k ) (ii) (8, 1), ( k , — 4), (2, — 5)
Ответ:
(i) Для коллинеарных точек площадь образованного ими треугольника равна нулю.
Следовательно, для точек (7, −2) (5, 1) и (3, k ) площадь = 0
(ii) Для коллинеарных точек площадь образованного ими треугольника равна нулю.
Следовательно, для точек (8, 1), ( k , −4) и (2, −5) площадь = 0
Видео решение для координатной геометрии (Страница: 170, Q.No .: 2)
Решение NCERT для математики класса 10 — координатная геометрия 170, вопрос 2
Страница № 170:
Вопрос 3:
Найдите площадь треугольника, образованного соединением середин сторон треугольника с вершинами (0, — 1), (2, 1) и (0, 3). Найдите отношение этой площади к площади данного треугольника.
Найдите отношение этой площади к площади данного треугольника.
Ответ:
Пусть вершины треугольника равны A (0, −1), B (2, 1), C (0, 3).
Пусть D, E, F — середины сторон этого треугольника. Координаты D, E и F даются
.Видео решение для координатной геометрии (Страница: 170, Q.No .: 3)
Решение NCERT для математики класса 10 — координатная геометрия 170, вопрос 3
Страница № 170:
Вопрос 4:
Найдите площадь четырехугольника, вершины которого, взятые по порядку, равны (- 4, — 2), (- 3, — 5), (3, — 2) и (2, 3)
Ответ:
Пусть вершины четырехугольника равны A (−4, −2), B (−3, −5), C (3, −2) и D (2, 3).Соедините AC, чтобы образовать два треугольника ΔABC и ΔACD.
Видео решение для координатной геометрии (Страница: 170, Q.No .: 4)
Решение NCERT для математики класса 10 — координатная геометрия 170, вопрос 4
Страница № 170:
Вопрос 5:
В классе IX вы изучали, что середина треугольника делит его на два треугольника равной площади.Проверьте этот результат для ΔABC, вершинами которого являются A (4, — 6), B (3, — 2) и C (5, 2)
.Ответ:
Пусть вершины треугольника равны A (4, −6), B (3, −2) и C (5, 2).
Пусть D — середина стороны BC отрезка ΔABC. Следовательно, AD — это медиана в ΔABC.
Однако площадь не может быть отрицательной. Следовательно, площадь ΔABD составляет 3 квадратных единицы.
Однако площадь не может быть отрицательной. Следовательно, площадь ΔADC составляет 3 квадратных единицы.
Следовательно, площадь ΔADC составляет 3 квадратных единицы.
Очевидно, что медиана AD разделила ΔABC на два треугольника равной площади.
Видео решение для координатной геометрии (Страница: 170, Q.No .: 5)
Решение NCERT для математики класса 10 — координатная геометрия 170, вопрос 5
Лист № 171:
Вопрос 1:
Определите соотношение, в котором прямая 2 x + y -4 = 0 делит отрезок прямой, соединяющий точки A (2, — 2) и B (3, 7)
Ответ:
Пусть данная прямая делит отрезок, соединяющий точки A (2, −2) и B (3, 7), в соотношении k : 1.
Координаты точки деления
Эта точка также лежит на 2 x + y — 4 = 0
Следовательно, соотношение, при котором линия 2 x + y -4 = 0 делит отрезок прямой, соединяющий точки A (2, −2) и B (3, 7), составляет 2: 9.
Видео решение для координатной геометрии (Страница: 171, Q.No .: 1)
Решение NCERT для математики класса 10 — координатная геометрия 171, вопрос 1
Лист № 171:
Вопрос 2:
Найдите соотношение между x и y , если точки ( x , y ), (1, 2) и (7, 0) коллинеарны.
Ответ:
Если данные точки лежат на одной прямой, то площадь треугольника, образованного этими точками, будет равна 0.
Это необходимое соотношение между x и y .
Видео решение для координатной геометрии (Страница: 171, Q.No .: 2)
Решение NCERT для математики класса 10 — координатная геометрия 171, вопрос 2
Лист № 171:
Вопрос 3:
Найдите центр окружности, проходящей через точки (6, — 6), (3, — 7) и (3, 3).
Ответ:
Пусть O ( x , y ) будет центром круга. И пусть точки (6, −6), (3, −7) и (3, 3) представляют точки A, B и C на окружности круга.
Складывая уравнения (1) и (2), получаем
10 y = −20
y = −2
Из уравнения (1) получаем
3 x — 2 = 7
3 x = 9
х = 3
Следовательно, центр круга равен (3, −2).
Видео решение для координатной геометрии (Страница: 171, Q.No .: 3)
Решение NCERT для математики класса 10 — координатная геометрия 171, вопрос 3
Лист № 171:
Вопрос 4:
Две противоположные вершины квадрата — это (- 1, 2) и (3, 2). Найдите координаты двух других вершин.
Ответ:
Пусть ABCD — квадрат, имеющий (−1, 2) и (3, 2) как вершины A и C соответственно. Пусть ( x , y ), ( x 1 , y 1 ) будет координатой вершины B и D соответственно.
Пусть ( x , y ), ( x 1 , y 1 ) будет координатой вершины B и D соответственно.
Мы знаем, что стороны квадрата равны друг другу.
∴ AB = BC
Мы знаем, что в квадрате все внутренние углы равны 90 °.
В ΔABC,
AB 2 + BC 2 = AC 2
⇒ 4 + y 2 + 4-4 y + 4 + y 2 -4 y + 4 = 16
⇒ 2 y 2 + 16-8 y = 16
⇒ 2 y 2 -8 y = 0
⇒ y ( y -4) = 0
⇒ y = 0 или 4
Мы знаем, что в квадрате диагонали равны по длине и делят друг друга пополам под углом 90 °.Пусть O — середина AC. Следовательно, это также будет средняя точка BD.
⇒ y + y 1 = 4
Если y = 0,
y 1 = 4
Если y = 4,
y 1 = 0
Следовательно, требуются координаты (1, 0) и (1, 4).
Видео решение для координатной геометрии (Страница: 171, Q.№: 4)
Решение NCERT для математики класса 10 — координатная геометрия 171, вопрос 4
Лист № 171:
Вопрос 5:
Учащимся X класса средней школы в Кришинагаре выделен прямоугольный участок земли для их садоводства. Саженцы Гульмохара высаживают на границе на расстоянии 1 м друг от друга. На участке есть треугольный газон, покрытый травой, как показано на следующем рисунке.На оставшейся площади делянки ученики высевают семена цветущих растений.
(i) Взяв за начало координат A, найдите координаты вершин треугольника.
(ii) Каковы будут координаты вершин Δ PQR, если C — начало координат?
Также рассчитайте площади треугольников в этих случаях. Что вы наблюдаете?
Ответ:
(i) Взяв за точку отсчета A, мы возьмем AD за ось x и AB за ось y . Можно заметить, что координаты точек P, Q и R равны (4, 6), (3, 2) и (6, 5) соответственно.
Можно заметить, что координаты точек P, Q и R равны (4, 6), (3, 2) и (6, 5) соответственно.
(ii) Если взять C за начало координат, CB как ось x и CD как ось y , координаты вершин P, Q и R равны (12, 2), (13, 6) и (10, 3) соответственно.
Видно, что площадь треугольника одинакова в обоих случаях.
Видео решение для координатной геометрии (Страница: 171, Q.№: 5)
Решение NCERT для математики класса 10 — координатная геометрия 171, вопрос 5
Лист № 171:
Вопрос 6:
Вершины ΔABC — это A (4, 6), B (1, 5) и C (7, 2). Проводится линия, пересекающая стороны AB и AC в точках D и E соответственно, так что. Вычислите площадь ΔADE и сравните ее с площадью ΔABC. (Напомним, обратное основной теореме о пропорциональности и теореме 6.6 относится к
соотношение площадей двух одинаковых треугольников)
Ответ:
Учитывая это,
Следовательно, D и E — две точки на сторонах AB и AC соответственно, так что они делят стороны AB и AC в соотношении 1: 3.
Очевидно, что соотношение площадей ΔADE и ΔABC равно 1:16.
Или
Мы знаем, что если отрезок прямой в треугольнике делит две стороны в одинаковом соотношении, то отрезок параллелен третьей стороне треугольника.Эти два образованных таким образом треугольника (здесь ΔADE и ΔABC) будут похожи друг на друга.
Следовательно, отношение площадей этих двух треугольников будет квадратом отношения сторон этих двух треугольников.
Следовательно, соотношение площадей ΔADE и ΔABC =
Видео решение для координатной геометрии (Страница: 171, Q.No .: 6)
Решения NCERT для математики 7 класса в формате PDF на сессию 2020-2021 гг.
Решения NCERT для математики класса 7
Решения CBSE NCERT для математики класса 7 на хинди и английском
Решения по главам для математики класса 7 на хинди
4
3
- 33
Математические решения класса 7 на хинди, английском языке и видео
Класс: 7 Математика (Ганит) Средний: Решения на английском и хинди Средний Класс
на хинди и английском Medium Решения NCERT для математики класса 7 теперь доступны для бесплатной загрузки как на английском, так и на хинди.
 Эти решения обновлены для текущей сессии 2020-21.
Эти решения обновлены для текущей сессии 2020-21.Математические решения класса 7 и основные положения всех глав
Глава 1: Целые числа
Мы закончили с числовой строкой, когда добавили положительное целое число, и мы переместились вправо. Чтобы добавить отрицательное целое число, мы перемещаемся влево. Аналогично, вычитая положительное целое число, мы перемещаемся влево, а чтобы вычесть отрицательное целое число, мы перемещаемся вправо. В главе 1 по математике класса 7 мы должны использовать эти факты в повседневной жизни.
Математика класса 7 Глава 1 Упражнение 1.1 Решение Математика класса 7 Глава 1 Упражнение 1. 2 Решение
2 РешениеГлава 2: Дроби и десятичные числа
В главе 2 по математике класса 7 мы узнаем о дробях и десятичных дробях, а также о сложении и вычитание по ним. Мы также узнали, как умножать два десятичных числа. При умножении двух десятичных чисел сначала умножьте их на целые числа. Подсчитайте количество цифр справа от десятичной точки в обоих десятичных числах.Добавьте количество подсчитанных цифр. Поместите десятичную точку в продукте, считая цифры от крайнего правого места. Подсчетом должна быть сумма, полученная ранее. Мы также изучим операции умножения и деления на дроби и десятичные дроби. Существуют методы умножения двух дробей путем раздельного умножения их числителей и знаменателей и записи произведения. Как получить величину, обратную дроби, получается, перевернув ее вверх дном. Эта концепция также используется в главе 4 «Простые уравнения».
Математика класса 7 Глава 2 Упражнение 2. 1 Решение Математика класса 7 Глава 2 Упражнение 2.2 Решение
1 Решение Математика класса 7 Глава 2 Упражнение 2.2 РешениеГлава 3: Обработка данных
В главе 3 математики класса 7 мы узнаем о сборе, записи и представлении данных. Перед сбором данных мы должны знать, что собранные данные должны быть организованы в надлежащую таблицу, чтобы их было легко понять и интерпретировать. Мы обсудим среднее значение, которое представляет собой число, которое представляет или показывает центральную тенденцию группы наблюдений или данных вместе со средним арифметическим, Mode, которое является другой формой центральной тенденции или символического значения, и Medium.Медиана также является формой символического значения. Он относится к значению, которое находится в середине данных, причем половина наблюдений находится над ним, а другая половина — под ним.
Математика класса 7 Глава 3 Упражнение 3.1 Решение Математика класса 7 Глава 3 Упражнение 3.2 Решение Гистограмма и использование полосок одинаковой ширины и двойных гистограмм для быстрого сравнения двух наборов данных также описаны в главе 3 «Обработка данных» 7th Maths. В конце концов, есть вопросы, основанные на вероятности, которые описывают ситуации в нашей повседневной жизни, которые обязательно произойдут, некоторые из них невозможны, а некоторые могут произойти или не произойти.
Гистограмма и использование полосок одинаковой ширины и двойных гистограмм для быстрого сравнения двух наборов данных также описаны в главе 3 «Обработка данных» 7th Maths. В конце концов, есть вопросы, основанные на вероятности, которые описывают ситуации в нашей повседневной жизни, которые обязательно произойдут, некоторые из них невозможны, а некоторые могут произойти или не произойти.Глава 4: Простые уравнения
Глава 4 Математики класса 7 описывает уравнение, которое является условием для переменной, так что два выражения в переменная должна иметь равное значение.
Математика класса 7 Глава 4 Упражнение 4.1 Решение Математика класса 7 Глава 4 Упражнение 4.2 Решение Он также сообщает о значении переменной, для которой выполняется уравнение, которое называется решением уравнения. Мы знаем, что уравнение остается прежним, если местами LHS и RHS поменять местами.Сложение или вычитание с обеих сторон в равной степени в уравнении остается неизменным. Это свойство, которое используется для решения уравнения. Транспонирование числа имеет тот же эффект, что и добавление или вычитание одного и того же числа к обеим сторонам уравнения. Класс 7 Глава 4 Простые уравнения описывает здесь, как построить простые алгебраические выражения, соответствующие практическим ситуациям, и используя технику выполнения одинаковых математических операций с обеих сторон, мы можем построить уравнение, исходя из его решения.
Он также сообщает о значении переменной, для которой выполняется уравнение, которое называется решением уравнения. Мы знаем, что уравнение остается прежним, если местами LHS и RHS поменять местами.Сложение или вычитание с обеих сторон в равной степени в уравнении остается неизменным. Это свойство, которое используется для решения уравнения. Транспонирование числа имеет тот же эффект, что и добавление или вычитание одного и того же числа к обеим сторонам уравнения. Класс 7 Глава 4 Простые уравнения описывает здесь, как построить простые алгебраические выражения, соответствующие практическим ситуациям, и используя технику выполнения одинаковых математических операций с обеих сторон, мы можем построить уравнение, исходя из его решения.Глава 5: Линии и углы
Мы уже знаем, что сегмент линии имеет две конечные точки, а луч — только одну конечную точку. В классе 6 по математике мы выяснили, что линия не имеет оконечных точек с обеих сторон. Теперь в главе 5 математики класса 7 мы должны обсудить условия пар углов, такие как два дополнительных угла (сумма мер составляет 90 °), два дополнительных угла (сумма мер составляет 180 °), два смежных угла (имеют общую вершину и общий), линейная пара, смежные и дополнительные углы.Ты знаешь? Когда две линии пересекаются, точка встречи называется точкой пересечения, а когда линии, нарисованные на листе бумаги, не пересекаются, как бы далеко они ни производились, мы называем их параллельными линиями. В главе 5 урока 7 по математике мы должны изучить две пары противоположных углов, называемых вертикально противоположными углами.
Математика класса 7 Глава 5 Упражнение 5.1 Решение Математика класса 7 Глава 5 Упражнение 5.2 Решение Мы также рассмотрим трансверсаль — это линия, которая пересекает две или более прямых в разных точках. Глава 5 также будет полезна в главе 6 «Треугольники и их свойства».
Мы также рассмотрим трансверсаль — это линия, которая пересекает две или более прямых в разных точках. Глава 5 также будет полезна в главе 6 «Треугольники и их свойства».Глава 6: Треугольники и их свойства
Глава 6 Математики класса 7 описывает шесть элементов треугольника: его три угла и с трех сторон. Он также сообщает о трех срединных значениях и трех высотах треугольника. Мы знаем, что внешний угол треугольника образуется, когда получается сторона треугольника.
Математика класса 7 Глава 6 Упражнение 6.1 Решение Математика класса 7 Глава 6 Упражнение 6. Итак, у нас может быть два способа формирования внешнего угла.Мы должны выучить наизусть, что мера любого внешнего угла треугольника равна сумме мер его внутренних противоположных углов и свойству суммы углов треугольника, которое говорит о том, что общая мера трех углов треугольника треугольник равен 180 °. В главе 6 «Математики 7 класса» мы должны прочитать о равностороннем треугольнике, в котором каждый угол имеет меру 60 °, и о равнобедренном, если хотя бы две его стороны имеют одинаковую длину. Мы будем использовать свойство длин сторон треугольника, чтобы быстро решать различные суммы.Также введено свойство Pythagoras, которое также может быть полезно в других классах.
Итак, у нас может быть два способа формирования внешнего угла.Мы должны выучить наизусть, что мера любого внешнего угла треугольника равна сумме мер его внутренних противоположных углов и свойству суммы углов треугольника, которое говорит о том, что общая мера трех углов треугольника треугольник равен 180 °. В главе 6 «Математики 7 класса» мы должны прочитать о равностороннем треугольнике, в котором каждый угол имеет меру 60 °, и о равнобедренном, если хотя бы две его стороны имеют одинаковую длину. Мы будем использовать свойство длин сторон треугольника, чтобы быстро решать различные суммы.Также введено свойство Pythagoras, которое также может быть полезно в других классах. 2 Решение
2 РешениеГлава 7: Конгруэнтность треугольников
Знаете ли вы, что конгруэнтные объекты являются точными копиями друг друга? В 7-м классе по математике, глава 7, мы также будем изучать конгруэнтность треугольников и их теоремы. В этой главе объясняется, как метод суперпозиции исследует соответствие плоских фигур.Есть четыре основных правила сравнения двух треугольников. Правила согласования SSS, SAS, ASA и RHS. Здесь S обозначает сторону, а A обозначает угол треугольника. Не существует такой вещи, как AAA-конгруэнтность двух треугольников. Эта глава очень полезна для решения геометрических вопросов даже в старших классах.
Математика класса 7 Глава 7 Упражнение 7.1 Решение Математика класса 7 Глава 7 Упражнение 7. 2 Решение
2 РешениеГлава 8: Сравнение величин
Сравнение величин означает нахождение относительного отношения между двумя или более величинами.В повседневной жизни нам часто приходится сравнивать две величины. Итак, книги NCERT по математике 7 класса, глава 8 «Сравнение количеств» помогут найти эти сравнения. Величины могут быть ростом, весом, окладами, отметками и т. Д. Два соотношения можно сравнить, преобразовав их в одинаковые дроби. Если две дроби равны, мы говорим, что эти два соотношения эквивалентны. Если два соотношения эквивалентны, то говорят, что четыре величины пропорциональны. Мы также можем использовать процент для сравнения количеств.Проценты — это числители дробей со знаменателем 100. Проценты широко используются в нашей повседневной жизни.
Математика класса 7 Глава 8 Упражнение 8. 1 Решение Математика класса 7 Глава 8 Упражнение 8.2 Решение
1 Решение Математика класса 7 Глава 8 Упражнение 8.2 РешениеГлава 9: Рациональные числа
Рациональные числа очень распространены для нас, поскольку они уже использовались в предыдущих классах. Мы знаем, что число, которое может быть выражено в форме p / q, где p и q — целые числа, а q не равно 0, называется рациональным числом.Числа ½, 2/5, 7/2 и т. Д. Являются примером рациональных чисел. Все числа и дроби — рациональные числа. Книга по математике в главе 9 «Рациональные числа» представляет собой идеальный способ вычисления суммы на основе рациональных чисел. Когда числитель и знаменатель являются целыми положительными числами, это положительное рациональное число. Когда числитель или знаменатель являются отрицательным целым числом, это отрицательное рациональное число.
Математика класса 7 Глава 9 Упражнение 9.1 Решение Математика класса 7 Глава 9 Упражнение 9.2 Решение Число 0 не является ни положительным, ни отрицательным рациональным числом. Здесь мы также узнаем о стандартной форме рационального числа и о том, как найти сумму, произведение, деление и разность двух рациональных чисел, используя числитель и корректировку знаменателя.
Число 0 не является ни положительным, ни отрицательным рациональным числом. Здесь мы также узнаем о стандартной форме рационального числа и о том, как найти сумму, произведение, деление и разность двух рациональных чисел, используя числитель и корректировку знаменателя.Глава 10: Практическая геометрия
В главе 10 математики класса 7 мы рассмотрели методы построения фигур с помощью линейки и циркуля. Математика класса 7 Глава 7 Конгруэнтность Трингла используется в этой главе для рисования треугольных фигур.
Математика класса 7 Глава 10 Упражнение 10.1 Решение Математика класса 7 Глава 10 Упражнение 10.2 Решение Во время построения, если дана линия, а на ней нет точки, мы использовали идею «равных чередующихся углов» на поперечной диаграмме, чтобы провести линию, параллельную данной линии.Мы также могли бы использовать идею «равных соответствующих углов» для построения конструкции. Свойства треугольников конгруэнтности, такие как SSS, ASA, SAS и RHS, также могут быть полезны при изучении главы 10 7-го раздела математики.
Во время построения, если дана линия, а на ней нет точки, мы использовали идею «равных чередующихся углов» на поперечной диаграмме, чтобы провести линию, параллельную данной линии.Мы также могли бы использовать идею «равных соответствующих углов» для построения конструкции. Свойства треугольников конгруэнтности, такие как SSS, ASA, SAS и RHS, также могут быть полезны при изучении главы 10 7-го раздела математики.Глава 11: Периметр и площадь
Математика класса 7 Глава 11 включает измерение двумерных фигур.
Математика класса 7 Глава 11 Упражнение 11. Мы знаем, что периметр — это расстояние вокруг замкнутой фигуры, а площадь — это часть плоскости, занимаемая замкнутой фигурой.Здесь мы должны найти периметр различных предметов, используемых в повседневной жизни. Чтобы найти периметр или площадь, мы можем использовать различные формулы, такие как периметр квадрата = 4 × стороны, периметр прямоугольника = 2 × (длина + ширина), площадь квадрата = сторона × сторона, площадь прямоугольника = длина. × ширина и т. Д. Для достижения окончательных результатов. Основываясь на преобразовании единиц длины в изученных ранее классах, единицы площади можно также использовать, например, 1 квадратный см = 100 квадратных мм, 1 квадратный метр = 10000 квадратных см и 1 гектар = 10000 квадратных метров.
Мы знаем, что периметр — это расстояние вокруг замкнутой фигуры, а площадь — это часть плоскости, занимаемая замкнутой фигурой.Здесь мы должны найти периметр различных предметов, используемых в повседневной жизни. Чтобы найти периметр или площадь, мы можем использовать различные формулы, такие как периметр квадрата = 4 × стороны, периметр прямоугольника = 2 × (длина + ширина), площадь квадрата = сторона × сторона, площадь прямоугольника = длина. × ширина и т. Д. Для достижения окончательных результатов. Основываясь на преобразовании единиц длины в изученных ранее классах, единицы площади можно также использовать, например, 1 квадратный см = 100 квадратных мм, 1 квадратный метр = 10000 квадратных см и 1 гектар = 10000 квадратных метров. 1 Решение Математика класса 7 Глава 11 Упражнение 11.2 Решение
1 Решение Математика класса 7 Глава 11 Упражнение 11.2 РешениеГлава 12: Алгебраические выражения
В главе 12 математики класса 7 мы узнаем, как алгебраические выражения формируются из переменных и констант. Мы также будем использовать операции сложения, вычитания, умножения и деления переменных и констант для формирования выражений. Мы должны знать, что выражения состоят из терминов, а термины добавляются, чтобы составить выражение.Обычно термин представляет собой произведение факторов, а факторы, содержащие переменные, называются алгебраическими факторами. Коэффициент — это числовой коэффициент в члене, и любое выражение с одним или несколькими членами называется полиномом. Многочлены могут быть в форме двучлена или трехчлена. Термины, которые имеют одинаковые алгебраические факторы, подобны терминам, тогда как термины с разными алгебраическими факторами отличаются от терминов.
Математика для класса 7 Глава 12 Упражнение 12.1 Решение Математика для класса 7 Глава 12 Упражнение 12.2 Решение
Глава 13: Показатели и степени
Мы знаем, что огромные числа трудно читать, понимать, сравнивать и оперировать. В главе 13 «Математика 7-го класса» описан способ сделать все это проще. Мы используем экспоненты, преобразуя многие большие числа в более короткую форму. Показатели и степени также полезны для последующих классов. Числа в экспоненциальной форме подчиняются определенным законам, которые уникальны. Единственная практика дает хорошее понимание главы 13 математики 7 класса.
Математика 7-й класс Глава 13 Упражнение 13.1 Решение Математика для класса 7 Глава 13 Упражнение 13.2 Решение
Глава 14: Симметрия
Глава 14 математики для 7-го класса основана на симметрии. Фигура имеет линейную симметрию, если есть линия, вокруг которой фигура может быть сложена так, чтобы две части фигуры совпадали. Мы знаем, что у правильных многоугольников равные стороны и равные углы, поэтому у них есть несколько линий симметрии. У каждого правильного многоугольника столько линий симметрии, сколько сторон. Зеркальное отражение приводит к симметрии, при которой необходимо позаботиться об ориентации влево-вправо.
Математика для класса 7 Глава 14 Упражнение 14.1 Решение Математика для класса 7 Глава 14 Упражнение 14.2 Решение Его можно получить, повернув объект вокруг фиксированной точки, где фиксированная точка является центром вращения. Точно так же мы можем найти угол поворота, левый или правый поворот. Если после поворота объект выглядит точно так же, мы говорим, что он обладает симметрией вращения. Изучение симметрии важно из-за ее частого использования в повседневной жизни и еще больше из-за прекрасного дизайна, который она может предоставить нам.
Его можно получить, повернув объект вокруг фиксированной точки, где фиксированная точка является центром вращения. Точно так же мы можем найти угол поворота, левый или правый поворот. Если после поворота объект выглядит точно так же, мы говорим, что он обладает симметрией вращения. Изучение симметрии важно из-за ее частого использования в повседневной жизни и еще больше из-за прекрасного дизайна, который она может предоставить нам.Глава 15: Визуализация твердых форм
Мы знаем, что круг, квадрат, прямоугольник, четырехугольник и треугольник являются примерами плоских фигур.
Математика класса 7 Глава 15 Упражнение 15.1 Решение Математика класса 7 Глава 15 Упражнение 15. Точно так же куб, кубоид, сфера, цилиндр, конус и пирамида являются примерами твердых форм. В главе 15 «Стандартной 7 математики» рассказывается о формах и эскизах этих фигур. Если дана плоская фигура, она будет считаться двумерной или двухмерной, и аналогично трехмерной для сплошных фигур. Углы твердого тела называются его вершинами, отрезки скелета — его ребрами, а плоские поверхности — его гранями.Математика в классе 7 Глава 15 Визуализация твердых форм — очень полезный навык. Различные участки твердого тела можно рассматривать разными способами.
Точно так же куб, кубоид, сфера, цилиндр, конус и пирамида являются примерами твердых форм. В главе 15 «Стандартной 7 математики» рассказывается о формах и эскизах этих фигур. Если дана плоская фигура, она будет считаться двумерной или двухмерной, и аналогично трехмерной для сплошных фигур. Углы твердого тела называются его вершинами, отрезки скелета — его ребрами, а плоские поверхности — его гранями.Математика в классе 7 Глава 15 Визуализация твердых форм — очень полезный навык. Различные участки твердого тела можно рассматривать разными способами. 2 Решение
2 РешениеМудрое решение по математике класса 7 на английском и хинди Средний
Отзывы и предложения
по-прежнему сталкиваются с проблемой понимания решения любого вопроса, сообщите нам об этом через раздел «Форум обсуждения».Все упражнения NCERT Solutions 2020-21 представлены в виде отдельных файлов PDF. Очень скоро будут загружены важные вопросы от U-like, Р. С. Аггарвала, П. К. Гарга, Р. Д. Шармы, Задания, Заметки, Образцы статей, Тесты по главам и другие учебные материалы.
Загрузите 7 офлайн-приложений по математике на английском языке и 7 офлайн-приложений на. Вопросы взяты из последней программы CBSE Syllabus на 2020-2021 годы. Пожалуйста, дайте отзывы и предложения по улучшению содержания и качества, если это возможно.Решения на хинди для среднего и английского для среднего
На хинди для среднего уровня Решения NCERT для класса 7 по математике теперь доступны в текущем 2020-21 учебном году.
 यदि विद्यार्थियों या अभिभावकों की तरफ से कोई सलाह वेबसाइट को लिए हो तो अवश्य दे। आपका योगदान अन्य विद्यार्थिओं के लिए मददगार होगा। इस वर्ष 2020-2021 में लगभग सभी विषयों के हिंदी और अंग्रेजी माध्यम के हल उपलब्ध होंगे।
यदि विद्यार्थियों या अभिभावकों की तरफ से कोई सलाह वेबसाइट को लिए हो तो अवश्य दे। आपका योगदान अन्य विद्यार्थिओं के लिए मददगार होगा। इस वर्ष 2020-2021 में लगभग सभी विषयों के हिंदी और अंग्रेजी माध्यम के हल उपलब्ध होंगे।
Ваше предложение всегда полезно для нас при улучшении веб-сайта, а также его содержимого. Мы также работаем с UP Board и Bihar Board. Его содержание будет доступно в апреле. NCERT Books 2020-2021 для всех предметов доступны в формате PDF и ZIP. Загрузите автономное приложение 7 Maths на английском языке и 7 गणित Offline приложение на मीडियम.Важные вопросы по математике класса 7 (FAQ)
Самолет летит на высоте 5000 м над уровнем моря. В определенной точке он находится точно над подводной лодкой, плавающей на 1200 м ниже уровня моря. Какое расстояние между ними по вертикали?
Высота места над уровнем моря = 5000 м
Плавание подводной лодки ниже уровня моря = 1200 м
Расстояние по вертикали между самолетом и подводной лодкой = 5000 + 1200 = 6200 м
Таким образом, расстояние по вертикали между самолетом а подводная лодка 6200 м.
Автомобиль проезжает 16 км на 1 литре бензина. Какое расстояние он преодолеет на 2 и 3/4 литрах бензина?
За 1 литр пертрола автомобиль преодолевает расстояние = 16 км
В литрах бензина автомобиль преодолевает расстояние = 2 и 3/4 из 16 км = 11/4 x 16 = 44 км
Таким образом, автомобиль преодолевает расстояние Расстояние 44 км.Найдите режим и медианное значение данных: 13, 16, 12, 14, 19, 12, 14, 13, 14.
Упорядочивание данных в порядке возрастания,
12, 12, 13, 13, 14, 14, 14, 16, 19
Режим — наибольшее количество наблюдений = 14
Медиана — среднее наблюдение = 14लक्ष्मी के पिता की आयु 49 वर्ष है। उनकी आयु लक्ष्मी की आयु के तीन गुने से 4 वर्ष अधिक है। लक्ष्मी की आयु क्या है?
माना, लक्ष्मी की आयु = y वर्ष
इसलिए, पिता की आयु = 3 y + 4 वर्ष
प्रश्न के अनुसार,
3 y + 4 = 49
Итак, 3y = 49 — 4 = 45
и y = 45 / 3 = 15
अतः, लक्ष्मी की आयु 15 वर्ष है।क्या दो ऐसे कोण संपूरक हो सकते हैं यदि दोनों अधिक कोण हैं?
नहीं, क्योंकि दो अधिक कोणों का योग सदैव 180 से अधिक होता है।
त्रिभुज PQR के अभ्यंतर में कोई बिंदु O लीजिए। क्या यह सही है कि OP + OQ> PQ?
हाँ, क्योंकि POQ एक त्रिभुज है और त्रिभुज कोई दो भुजाओं के मापों का योग, तीसरी भुजा की माप से अधिक होती है।
Приведите любые два примера конгруэнтных форм в реальном времени.

Два футбольных мяча одинакового размера и разного цвета.
Я покупаю телевизор за 10 000 фунтов стерлингов и продаю его с прибылью 20%. Сколько денег я получу за это?
Себестоимость T.V. = 10 000 ₹
Процент прибыли = 20%
Теперь прибыль =% прибыли C.P.
= 20/100 x 1000 = 2000 ₹
Цена продажи = C.P. + Прибыль = 10 000 ₹ + 2 000 = 12 000
Следовательно, он получает 12 000 при продаже своего телевизораКак можно сложить два различных рациональных числа?
Два рациональных числа с разными знаменателями складываются, сначала беря НОК двух знаменателей, а затем преобразовывая оба рациональных числа в их эквивалентные формы, используя НОК в качестве знаменателя, и складывая их, как указано выше.
Постройте DEF так, чтобы DE = 5 см, DF = 3 см и EDF = 90.
Построить: DEF, где DE = 5 см, DF = 3 см и EDF = 90
Шаги построения:
(a) Нарисуйте отрезок прямой DF = 3 см.
(b) В точке D начертите с помощью циркуля угол 90, т. Е. XDF = 90.
Е. XDF = 90.
(c) Взяв D за центр, нарисуйте дугу радиуса 5 см, которая разрезает DX в точке E.
(d) Присоединяйтесь к EF.
(e) Это необходимый прямоугольный треугольник DEF.एक वृत्ताकार फूलों के बगीचे का क्षेत्रफल 314 м2 है। बगीचे के केंद्र में एक घूमने वाला फव्वारा (спринклер) लगाया जाता है, जो अपने चारों ओर 12 м त्रिज्या के क्षेत्रफल में पानी का छिड़काव करता है। क्या फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा? (π = 3.2
वृत्ताकार फूलों के बगीचे का क्षेत्रफल = 314 м2
यहाँ, वृत्ताकार फूलों के बगीचे का क्षेत्रफल, फव्वारे द्वारा छिड़काव किए गए क्षेत्रफल से कम है।
अतः, फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा।Как математические операции выполняются в алгебраических выражениях?
Когда мы складываем (или вычитаем) два алгебраических выражения, одинаковые термины складываются (или вычитаются), а разные термины записываются как есть.
Что такое стандартная форма или научное обозначение?
Любое число может быть выражено десятичным числом от 1.
 0 и 10,0 (включая 1,0), умноженные на степень 10. Такая форма числа называется его стандартной формой или научным представлением.
0 и 10,0 (включая 1,0), умноженные на степень 10. Такая форма числа называется его стандартной формой или научным представлением.Какое еще название вы можете дать линии симметрии равнобедренного треугольника?
Линия симметрии равнобедренного треугольника — это медиана или высота.
जाँच कीजिए कि क्या ये कथन सत्य हैं। एक घन एक षट्भुज के आकार की छाया दे सकता है।
ВЫПУЩЕННАЯ ФОРМА ВЫПУЩЕНА. Выпускные экзамены в Северной Каролине 7 класс. Математический калькулятор Активный математический калькулятор неактивен (стр. 15)
Математический тест общего керна
Математический тест Common Core Sampler Сэмплер 6-го класса охватывает наиболее частые вопросы, которые мы видим в тестах Common Core и тестовых выборках.
Подробнее Мы просмотрели более 40 различных прошлых экзаменов и образцов, чтобы создать
Мы просмотрели более 40 различных прошлых экзаменов и образцов, чтобы создатьГеометрия и измерения
Учащийся сможет: Геометрия и измерение 1. Продемонстрировать понимание принципов геометрии, измерения и операций с использованием измерений. Использовать американскую систему измерения для
. ПодробнееXII.Математика, 6 класс
XII. Математика, 6-й класс Тест по математике для 6-го класса Весной 2013 г. тест по математике в 6-м классе был основан на стандартах по пяти предметам для 6-го класса в Программе обучения математике штата Массачусетс
ПодробнееМатематический тест общего керна
Математический тест Common Core Sampler В этом образце теста рассматриваются 20 основных вопросов, которые мы видели в 37 тестах, написанных непосредственно для Common Core Curriculum.
. Подробнее Этот тест будет обновляться по мере появления новых вопросов
Этот тест будет обновляться по мере появления новых вопросовПримеры проблем NMC: уровень 5
Примеры задач NMC: степень 5 1. Какое значение имеет 5 6 3 4 + 2 3 1 2? 1 3 (a) (b) (c) (d) 1 5 1 4 4 4 12 12 2. Каково значение 23, 456 + 15, 743 3, 894, выраженное с точностью до тысячи? (а) 34,
ПодробнееПрактический тест по алгебре EOC # 4
Класс: Дата: Алгебра Практический тест EOC № 4 Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос.1. Для f (x) = 3x + 4 найдите f (2) и найдите x такое, что f (x) = 17.
ПодробнееМатематические вопросы и ответы
Какие пять монет составляют никель? пять пенни (1 + 1 + 1 + 1 + 1 = 5) Что больше всего: фут, ярд или дюйм? ярд (3 фута = 1 ярд; 12 дюймов = 1 фут) Как вы называете ответ на умножение
ПодробнееОбъем пирамид и конусов
Объем пирамид и конусов.
Подробнее Цель: предоставить опыт исследования взаимосвязей между объемами геометрических тел.www.everydaymathonline.com презентации etoolkit Algorithms
Цель: предоставить опыт исследования взаимосвязей между объемами геометрических тел.www.everydaymathonline.com презентации etoolkit AlgorithmsПриложения для треугольников
Не в масштабе Приложения для треугольников 1. 36 дюймов 40 дюймов 33 дюймов 1188 дюймов 2 69 дюймов 2 138 дюймов 2 1440 дюймов 2 2. 188 дюймов 2 278 дюймов 2 322 дюйма 2 ни один из Находят площадь параллелограмма с заданными
ПодробнееXI.Математика, 5 класс
XI. Математика, 5-й класс Тест по математике для 5-го класса Весной 2012 г. тест по математике в 5-м классе был основан на стандартах обучения по пяти основным направлениям учебной программы по математике штата Массачусетс
. ПодробнееXII. Математика, 6 класс
XII. Математика, 6 класс Тест 6 класса по математике Весенний тест 1 класса по математике в 6 классе был основан на стандартах обучения по пяти основным направлениям учебной программы по математике штата Массачусетс
ПодробнееПервый квартал: август-октябрь
Первый квартал: август-октябрь (Главы 13, 5-6, 10) Август — декабрь Ежеквартальное сложение фактов с суммами по 20 Общим математическим материалам 1.
Подробнее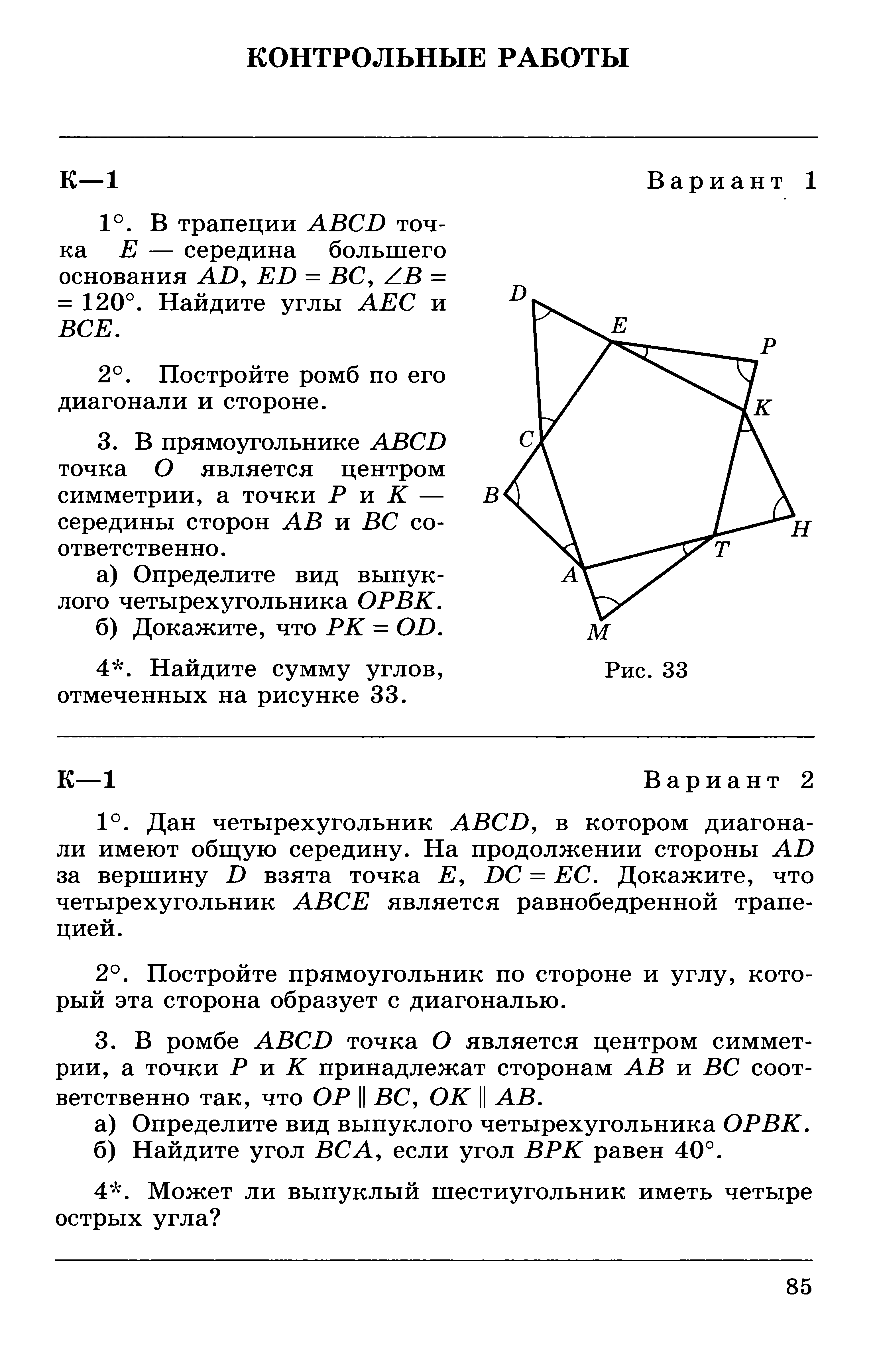 Напишите суммы до 20. 1. Выберите и введите соответствующий ответ.
Напишите суммы до 20. 1. Выберите и введите соответствующий ответ.Среднее значение, медиана и мода
ИНИЦИАТИВА ПАРТНЕРСТВА DELTA MATH SCIENCE M 3 Летние институты (математика, средняя школа, MS Common Core) Среднее значение, медиана и мода Проблема с крючком: для сравнения двух отправлений, пять пакетов из каждой партии были
ПодробнееТЕСТ ПО МАТЕМАТИКЕ ДЛЯ ВХОДА
ТЕСТ ПО МАТЕМАТИЧЕСКОМУ УРОВНЮ ВХОДА Copyright 0 Попечительского совета Калифорнийского государственного университета.Все права защищены. C Формулы для справки по геометрии Прямоугольник w Площадь = w Периметр = + w l Треугольник h Площадь =
ПодробнееФормулы и решение проблем
2.4 Формулы и решение задач 2.4 ЗАДАЧИ. Решите буквальное уравнение для одной из его переменных 2.
Подробнее Преобразуйте словесное выражение в уравнение 3. Используйте уравнение для решения приложения. Формулы чрезвычайно велики
Преобразуйте словесное выражение в уравнение 3. Используйте уравнение для решения приложения. Формулы чрезвычайно велики10-3 Площадь параллелограммов
0-3 Площадь параллелограммов ОСНОВНАЯ ИДЕЯ Найдите площади параллелограммов.Основная учебная программа штата Нью-Йорк 6.A.6 Оценить формулы для заданных входных значений (окружность, площадь, объем, расстояние, температура, процент,
ПодробнееТестовая тетрадь по математике 1
Математический тест 1 класс 7 9 марта 13, 2009 г. 21317 разработан и опубликован по контракту с Департаментом образования штата Нью-Йорк компанией T / McGraw-Hill LL, дочерней компанией McGraw-Hill ompanies, Inc.,
ПодробнееЕжедневная математика ЦЕЛИ
Copyright Wright Group / McGraw-Hill ЦЕЛИ В следующих таблицах перечислены цели уровня обучения, организованные по направлениям содержания и целям программы.
Подробнее Контентная цепочка: НОМЕР И НОМЕР Цель программы: понимание
Контентная цепочка: НОМЕР И НОМЕР Цель программы: пониманиеXV. Математика, 10 класс
XV. Математика, 10-й класс Тест 10-го класса по математике Весной 2011 года тест MCAS по математике для 10-го класса был основан на учебных стандартах, изложенных в Программе обучения математике штата Массачусетс (2000). Фреймворк
ПодробнееXII.Математика, 6 класс
XII. Математика, 6-й класс Тест по математике 6-го класса Весной 04-й класс 6-й класс по математике был основан на стандартах по пяти предметам для 6-го класса в Программе обучения математике штата Массачусетс
Подробнееповерхности, 569-571, 576-577, 578-581 треугольника, 548 Ассоциативное свойство сложения, 12, 331 умножения, 18, 433
Абсолютное значение и арифметика, 730-733 определены, 730 Острый угол, 477 Острый треугольник, 497 Дополнение, 12 Дополнительное ассоциативное свойство, (см.
Подробнее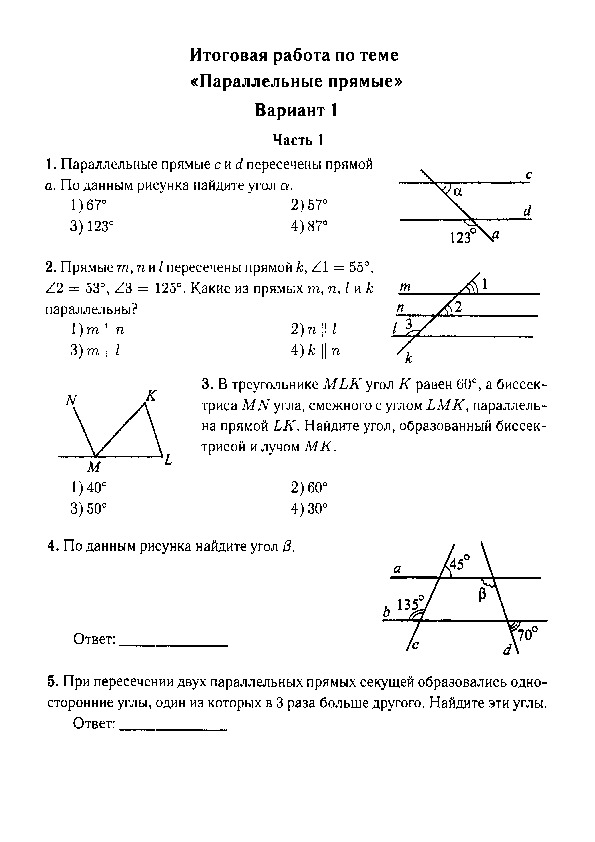 Коммутативное свойство), переносящее, 11, 92 коммутативное свойство
Коммутативное свойство), переносящее, 11, 92 коммутативное свойствоПериметр, площадь и объем
Периметр, площадь и объем Периметр обычных геометрических фигур Периметр геометрической фигуры определяется как расстояние вокруг внешней стороны фигуры.Периметр рассчитывается путем сложения всех
ПодробнееГлоссарий по алгебре и геометрии. Угол 90
lgebra Геометрия Глоссарий 1) острый угол угол меньше 90 острый угол 90 угол 2) острый треугольник треугольник, все углы которого меньше 90 3) смежные углы, углы, имеющие общий отрезок Пример:
ПодробнееИМЯ УЧАЩЕГОСЯ: 9 КЛАСС ПО МАТЕМАТИКЕ
ИМЯ УЧАЩЕГОСЯ: 9 КЛАСС ПО МАТЕМАТИКЕ Дата регистрации: январь 2010 г. Имя: Класс: Дата: 9-й класс Тест TAKS по математике 1.Ольга планирует съездить из своего дома в Сан-Маркос, штат Техас, в дом друга в Сапате,
. Leave a Reply
Leave a Reply

