Контрольная работа «Прямолинейное равномерное и равноускоренное движения»
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 1
Задача 1.
Один автомобиль, двигаясь со скоростью 72 км/ч, проехал за 10 с такой же путь, какой преодолел другой автомобиль за 15 с. Чему равна скорость второго автомобиля? Считать движение автомобилей равномерным.
Задача 2.
Какую скорость приобретает троллейбус за 5 с, если он трогается с места с ускорением 1,2 м/с 2?
Задача 3.
Определите ускорение автомобиля, если при разгоне за 15 с он приобретает скорость 54 км/ч. Какой путь он за это время проходит?
Задача 4.
Уравнение движения тела дано в виде x=3+5t+t2. Определите начальную скорость и ускорение движения тела, а также координату и скорость через 3 с после начала движения.
Задача 5.
Автомобиль, остановившись перед светофором, набирает затем скорость 54км/ч на пути 50 м. С каким ускорением он должен двигаться? Сколько времени будет длиться этот разбег?
Задача 6.
С каким ускорение движется тело, если за восьмую секунду оно прошло 30 м? Определите перемещение тела за пятую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 2
Задача 1.
Тело, двигаясь равномерно в начальный момент времени находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Задача 2.
Поезд подходит к станции со скоростью 36 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?
С каким ускорением двигался поезд?
Задача 3.
Автомобиль увеличил свою скорость с 36 км/ч до 54 км/ч за 4с. Определите ускорение автомобиля. Какой путь прошел автомобиль за это время?
Задача 4.
Прямолинейное движение тела описывается уравнением движения x=12t+0,5t2. Найдите ускорение тела. Напишите уравнение скорости данного движения. Найдите координату и скорость через 4 с после начала движения.
Задача 5.
Тормоз легкового автомобиля считается исправен, если при скорости
движения 8 м/с его тормозной путь равен 7,2 м. Каково время движения и ускорение автомобиля?
Задача 6.
За вторую секунду после начала движения автомобиль прошел 1,2 м. С каким ускорением двигался автомобиль? Определите перемещение автомобиля за седьмую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 3
Задача 1.
Тело, двигаясь равномерно в начальный момент времени находилось в точке с координатой 10 м, а через 1 мин от начала движения — в точке с координатой 130 м. Определите скорость тела и его перемещение.
Задача 2.
С каким ускорением должен затормозить автомобиль, движущийся со скоростью 72 км/ч, чтобы через 10 с остановиться?
Задача 3.
За 5 с до финиша скорость велосипедиста равнялась 18 км/ч, а на финише 36 км/ч. Определите ускорение, с которым двигался велосипедист. Какой путь он прошел за это время?
Задача 4.
Прямолинейное движение тела описывается уравнением движения x=10+8t+t2. Найдите ускорение тела. Напишите уравнение скорости данного движения. Найдите координату и скорость через 2 с после начала движения.
Задача 5.
В момент падения на сетку акробат имел скорость 9 м/с. С каким ускорением происходило торможение, если до полной остановки акробата сетка прогнулась на 1,5 м? Каково время торможения?
Задача 6.
За седьмую секунду после начала движения автомобиль прошел 5,2 м. С каким ускорением двигался автомобиль? Определите перемещение автомобиля за вторую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 4
Задача 1.
Автомобиль, двигаясь равномерно со скоростью 90 км/ч, проехал за 15 с такой же путь, какой преодолел мотоциклист за 20 с. Чему равна скорость мотоциклиста? Считать движение мотоциклиста так же равномерным.
Определите, какую скорость развивает мотоциклист за 15 с, двигаясь из состояния покоя с ускорением 1,3 м/с2?
Задача 3.
Определите ускорение автомобиля, если он увеличивает скорость с 54 км/ч до 72 км/ч за 5 с. Какой путь он за это время проходит?
Задача 4.
Уравнение движения тела дано в виде x=15t+0. 4t2. Определите начальную скорость и ускорение движения тела, а также координату и скорость через 5 с после начала движения. Напишите уравнение скорости данного движения.
4t2. Определите начальную скорость и ускорение движения тела, а также координату и скорость через 5 с после начала движения. Напишите уравнение скорости данного движения.
Задача 5.
Пуля, летящая со скоростью 400 м/с, ударяется в земляной вал и проникает в него на глубину 40 см. С каким ускорением и сколько времени двигалась пул внутри вала?
Задача 6.
С каким ускорение движется тело, если за пятую секунду оно прошло 18 м? Определите перемещение тела за восьмую секунду после начала движения.
Контрольная работа «Прямолинейное равномерное и равноускоренное движения»
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 3
Задача 1.
Тело, двигаясь равномерно в начальный момент времени находилось
в точке с координатой 10 м, а через 1 мин от начала движения — в
точке с координатой 130 м. Определите скорость тела и его
перемещение.
Задача 2.
С каким ускорением должен затормозить автомобиль, движущийся
со скоростью 72 км/ч, чтобы через 10 с остановиться?
Задача 3.
За 5 с до финиша скорость велосипедиста равнялась 18 км/ч, а на
финише 36 км/ч. Определите ускорение, с которым двигался
велосипедист. Какой путь он прошел за это время?
Задача 4.
Прямолинейное движение тела описывается уравнением движения
x=10+8t+t
2
. Найдите ускорение тела. Напишите уравнение скорости
данного движения. Найдите координату и скорость через 2 с после
начала движения.
Задача 5.
В момент падения на сетку акробат имел скорость 9 м/с. С каким
ускорением происходило торможение, если до полной остановки
акробата сетка прогнулась на 1,5 м? Каково время торможения?
Задача 6.
За седьмую секунду после начала движения автомобиль прошел 5,2
м. С каким ускорением двигался автомобиль? Определите
С каким ускорением двигался автомобиль? Определите
перемещение автомобиля за вторую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 4
Задача 1.
Автомобиль, двигаясь равномерно со скоростью 90 км/ч, проехал за
15 с такой же путь, какой преодолел мотоциклист за 20 с. Чему равна
скорость мотоциклиста? Считать движение мотоциклиста так же
равномерным.
Задача 2.
Определите, какую скорость развивает мотоциклист за 15 с, двигаясь
из состояния покоя с ускорением 1,3 м/с2?
Задача 3.
Определите ускорение автомобиля, если он увеличивает скорость с
54 км/ч до 72 км/ч за 5 с. Какой путь он за это время проходит?
Задача 4.
Уравнение движения тела дано в виде x=15t+0.4t
. Определите
начальную скорость и ускорение движения тела, а также координату
и скорость через 5 с после начала движения. Напишите уравнение
Напишите уравнение
скорости данного движения.
Задача 5.
Пуля, летящая со скоростью 400 м/с, ударяется в земляной вал и
проникает в него на глубину 40 см. С каким ускорением и сколько
времени двигалась пул внутри вала?
Задача 6.
С каким ускорение движется тело, если за пятую секунду оно прошло
18 м? Определите перемещение тела за восьмую секунду после
начала движения.
контрольная работа по физике 7 класс «Прямолинейное равномерное движение» | План-конспект урока по физике (7 класс) на тему:
Контрольная работа №1 «Прямолинейное равномерное движение»
Вариант 1.
1. Даны законы движения двух точечных тел:
а) х = 3+5t;
б) х = 7-t, где х – координата в м, t – время в с.
Определите координаты тел в моменты времени t = 1 с.
Определите моменты времени, когда координата тел х = 4 м.
2. На рисунке приведены графики движения пешехода (1), собаки (2) и велосипедиста (3).
Заполните в соответствии с рисунком таблицу.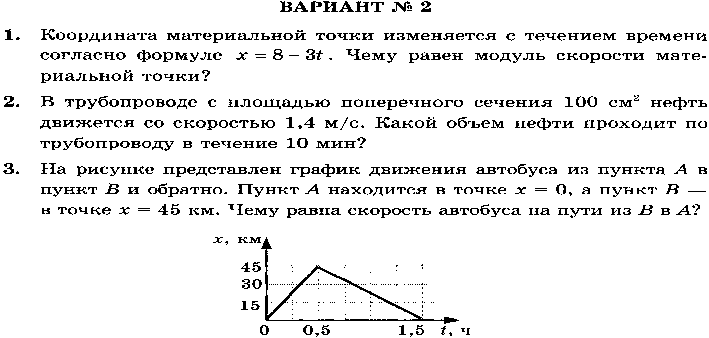
тело | Начальная координата, м | Координата (м) в момент t=4с | Скорость м/с | Закон движения |
Пешеход | ||||
Собака | ||||
Велосипедист |
3. Автобус за 3 часа проехал в положительном направлении оси Х (на восток) 100 км. После этого он развернулся и проехал в обратном направлении 20 км за 1 час. Найдите:
Найдите:
а) путь S, пройденный автобусом за все время движения;
б) модуль | ∆x| и направление вектора перемещения за все время движения. Выполните соответствующий рисунок.
Контрольная работа №1 «Прямолинейное равномерное движение»
Вариант 2.
1. Даны законы движения двух точечных тел:
а) х = 4+2t;
б) х = 10-2t, где х – координата в м, t – время в с.
Определите координаты тел в моменты времени t = 3 с.
Определите моменты времени, когда координата тел х = 5 м.
2. На рисунке приведены графики движения стрекозы (1), червяка (2) и мухи (3).
Заполните в соответствии с рисунком таблицу.
тело | Начальная координата, м | Координата (м) в момент t=4с | Скорость м/с | Закон движения |
Стрекоза | ||||
Червяк | ||||
Муха |
3. Автомобильс за 3 часа проехал в положительном направлении оси Х (на север) 90 км. После этого он развернулся и проехал в обратном направлении 30 км за 1 час. Найдите:
Автомобильс за 3 часа проехал в положительном направлении оси Х (на север) 90 км. После этого он развернулся и проехал в обратном направлении 30 км за 1 час. Найдите:
а) путь S, пройденный автомобилем за все время движения;
б) модуль | ∆x| и направление вектора перемещения за все время движения. Выполните соответствующий рисунок.
Задачи на прямолинейное равномерное движение
Контрольная работа содержит 3 расчетные задачи по теме «Прямолинейное равномерное движение. Скорость равномерного прямолинейного движения» с возможностью их автоматизированной проверки. Модуль относится к III уровню интерактивности
Категория пользователей
Обучаемый, Преподаватель
Дисциплины
Физика
/ Прямолинейное равномерное движение
Уровень образования
Профессионально-техническая подготовка, повышение квалификации
Статус
Завершенный вариант (готовый, окончательный)
Тип ИР сферы образования
информационный модуль
Издатель
ООО «Физикон»
Физикон
Россия, 141700, г. Долгопрудный, Московской обл., оф. 406, д. 7, ул. Первомайская,
Долгопрудный, Московской обл., оф. 406, д. 7, ул. Первомайская,
Тел. — +7-495-408-7772, +7-495-408-7772
Сайт —
http://www.physicon.ru
Правообладатель
Федеральное агентство по образованию
Федеральное агентство по образованию
Внимание! Для воспроизведения модуля необходимо установить на компьютере проигрыватель ресурсов.
Характеристики информационного ресурса
Тип используемых данных:
text/plain, text/html
Объем цифрового ИР
474 669 байт
Проигрыватель
Категория модифицируемости компьютерного ИР
Признак платности
бесплатный
Наличие ограничений по использованию
нет ограничений
Рубрикация
Ступени образования
Основное общее образование
Целевое назначение
Учебное
Тип ресурса
Открытая образовательная модульная мультимедийная система (ОМС)
Классы общеобразовательной школы
7, 8, 9
Уровень образовательного стандарта
Федеральный
Характер обучения
Базовое
Контрольна работа по физике 9 класс
Скачать контрольна работа по физике 9 класс doc
Контрольная работа № 1. «Прямолинейное равномерное и равноускоренное движение» 9 класс. 2 вариант. 1. Автомобиль, двигаясь равномерно, проехал 50 м за 2 с. Какой путь он проедет за 20 с, двигаясь с той же скоростью? 2. С каким ускорением должен затормозить автомобиль, движущийся со скоростью 36 км/ч, чтобы через 10 с остановиться? 3. Автомобиль, остановившись перед светофором, набирает затем скорость 54км/ч на пути. Контрольная работа №2 «Законы динамики» 9 класс 2 вариант.
«Прямолинейное равномерное и равноускоренное движение» 9 класс. 2 вариант. 1. Автомобиль, двигаясь равномерно, проехал 50 м за 2 с. Какой путь он проедет за 20 с, двигаясь с той же скоростью? 2. С каким ускорением должен затормозить автомобиль, движущийся со скоростью 36 км/ч, чтобы через 10 с остановиться? 3. Автомобиль, остановившись перед светофором, набирает затем скорость 54км/ч на пути. Контрольная работа №2 «Законы динамики» 9 класс 2 вариант.
1. Вагонетка массой кг движется с ускорением 0,2 м/с. Определите силу, сообщающую. вагонетке это ускорение. 2. Чему равно ускорение, с которым движется тело массой 3 кг, если на него действует сила. 12 Н?. Дифференцированная контрольная работа по физике 11 класс к теме «Фотоны» по учебнику Тихомировой С.А.
В настоящее время в связи с сокращением часов на изучение физики в старших классах некоторые школы перешли на учебник Тихомировой С.А.
Учебник в целом не плохой, красочный, хорошо иллюстрирован, «Плотность» дифференцированная контрольная работа по физике 7 класс (по учебнику Перышкина). Данная работа по теме «Плотность» составлена в трех вариантах.
Данная работа по теме «Плотность» составлена в трех вариантах.
Возрастание сложности от 1-го к 3-му. Работа оформлена в виде карточек, которые удобно распечатывать. Контрольн. Контрольные по физике для девятиклассников и решебники к ним.
Основные темы и разделы, по которым представлены задания в сборнике контрольных и самостоятельных работ по физике за 9 класс Громцевой О. И., таковы: перемещение; — понятие и определение движущихся тел; — прямолинейное движение, ускорение и перемещение при движении различных типов — равноускоренном, прямолинейном; — относительность движения и понятия пути в установленную единицу времени; — инерциальные системы отсчета; — физические законы Ньютона; — движение тела, брошенного вверх вертикально; — закон всемирного тяготения.
Контрольная работа № 1. «Прямолинейное равномерное и равноускоренное движение» 9 класс. 1 вариант. 1. Велосипедист, двигаясь равномерно, проезжает 20 м за 2 с.
Какой путь он проедет при движении с той же скоростью за 10 с? 2. Через 25 с после начала движения спидометр автомобиля показал скорость движения.
Через 25 с после начала движения спидометр автомобиля показал скорость движения.
36 км/ч. С каким ускорением двигался автомобиль? 3.Самолет для взлета должен приобрести скорость км/ч. Какой должна быть длина взлетной полосы, если известно, что время разгона самолета равно 30 с?
4.Пуля, летящая со скоростью м/с, ударяет в земляной вал и проникает в него на глубину. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия. Каждая цитата представлена в форме удобной для проверки знаний (на одной странице). Затем представлены ответы на оба варианта контрольной. При постоянном использовании данных контрольных работ лучше всего КУПИТЬ книгу: Марон, Марон: Физика. Другие варианты контрольных работ по физике в 9 классе: УМК Перышкин — Громцева.
Контрольные и самостоятельные работы по физике. К любому УМК — Годова. Физика 9. Контрольные работы в новом формате (годовая).
Контрольные работы в новом формате (годовая).
Контрольная работа № 1. «Прямолинейное равномерное и равноускоренное движение» 9 класс. 1 вариант. 1. Велосипедист, двигаясь равномерно, проезжает 20 м за 2 с. Какой путь он проедет при движении с той же скоростью за 10 с? 2. Через 25 с после начала движения спидометр автомобиля показал скорость движения. 36 км/ч. С каким ускорением двигался автомобиль? 3.Самолет для взлета должен приобрести скорость км/ч. Какой должна быть длина взлетной полосы, если известно, что время разгона самолета равно 30 с?
4.Пуля, летящая со скоростью м/с, ударяет в земляной вал и проникает в него на глубину. Контрольные по физике для девятиклассников и решебники к ним. Основные темы и разделы, по которым представлены задания в сборнике контрольных и самостоятельных работ по физике за 9 класс Громцевой О. И., таковы: перемещение; — понятие и определение движущихся тел; — прямолинейное движение, ускорение и перемещение при движении различных типов — равноускоренном, прямолинейном; — относительность движения и понятия пути в установленную единицу времени; — инерциальные системы отсчета; — физические законы Ньютона; — движение тела, брошенного вверх вертикально; — закон всемирного тяготения.
Физика 9 Контрольные Перышкин + ОТВЕТЫ на 4 варианта. Контрольные работы (цитаты) из пособия для учащихся «Контрольные и самостоятельные работы к учебнику А.В.
Перышкина Физика 9 класс ФГОС» (авт. О.И. Громцева, изд-во «Экзамен»). Работы представлены в формате удобном для копирования и распечатывания на принтере. При постоянном использовании контрольных работ по физике в 9 классе рекомендуем купить книгу: Ольга Громцева: Физика. 9 класс. Контрольные и самостоятельные работы к учебнику А.В.
Перышкина, Е.М. Гутник, в которой кроме контрольных работ в 4-х вариантах есть еще самостоятельные работы и ответы на них.
doc, rtf, doc, txtПохожее:
Контрольная работа «Прямолинейное равномерное и равноускоренное движения» (9 класс)
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 1
Задача 1.
Один автомобиль, двигаясь со скоростью 72 км/ч, проехал за 10 с такой же путь, какой преодолел другой автомобиль за 15 с. Чему равна скорость второго автомобиля? Считать движение автомобилей равномерным.
Задача 2.
Какую скорость приобретает троллейбус за 5 с, если он трогается с места с ускорением 1,2 м/с 2?
Задача 3.
Определите ускорение автомобиля, если при разгоне за 15 с он приобретает скорость 54 км/ч. Какой путь он за это время проходит?
Задача 4.
Уравнение движения тела дано в виде x=3+5t+t2. Определите начальную скорость и ускорение движения тела, а также координату и скорость через 3 с после начала движения. Напишите уравнение скорости данного движения.
Задача 5.
Автомобиль, остановившись перед светофором, набирает затем скорость 54км/ч на пути 50 м. С каким ускорением он должен двигаться? Сколько времени будет длиться этот разбег?
С каким ускорением он должен двигаться? Сколько времени будет длиться этот разбег?
Задача 6.
С каким ускорение движется тело, если за восьмую секунду оно прошло 30 м? Определите перемещение тела за пятую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 2
Задача 1.
Тело, двигаясь равномерно в начальный момент времени находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Задача 2.
Поезд подходит к станции со скоростью 36 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?
Задача 3.
Автомобиль увеличил свою скорость с 36 км/ч до 54 км/ч за 4с. Определите ускорение автомобиля. Какой путь прошел автомобиль за это время?
Какой путь прошел автомобиль за это время?
Задача 4.
Прямолинейное движение тела описывается уравнением движения x=12t+0,5t2. Найдите ускорение тела. Напишите уравнение скорости данного движения. Найдите координату и скорость через 4 с после начала движения.
Задача 5.
Тормоз легкового автомобиля считается исправен, если при скорости
движения 8 м/с его тормозной путь равен 7,2 м. Каково время движения и ускорение автомобиля?
Задача 6.
За вторую секунду после начала движения автомобиль прошел 1,2 м. С каким ускорением двигался автомобиль? Определите перемещение автомобиля за седьмую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 3
Задача 1.
Тело, двигаясь равномерно в начальный момент времени находилось в точке с координатой 10 м, а через 1 мин от начала движения — в точке с координатой 130 м. Определите скорость тела и его перемещение.
Определите скорость тела и его перемещение.
Задача 2.
С каким ускорением должен затормозить автомобиль, движущийся со скоростью 72 км/ч, чтобы через 10 с остановиться?
Задача 3.
За 5 с до финиша скорость велосипедиста равнялась 18 км/ч, а на финише 36 км/ч. Определите ускорение, с которым двигался велосипедист. Какой путь он прошел за это время?
Задача 4.
Прямолинейное движение тела описывается уравнением движения x=10+8t+t2. Найдите ускорение тела. Напишите уравнение скорости данного движения. Найдите координату и скорость через 2 с после начала движения.
Задача 5.
В момент падения на сетку акробат имел скорость 9 м/с. С каким ускорением происходило торможение, если до полной остановки акробата сетка прогнулась на 1,5 м? Каково время торможения?
Задача 6.
За седьмую секунду после начала движения автомобиль прошел 5,2 м.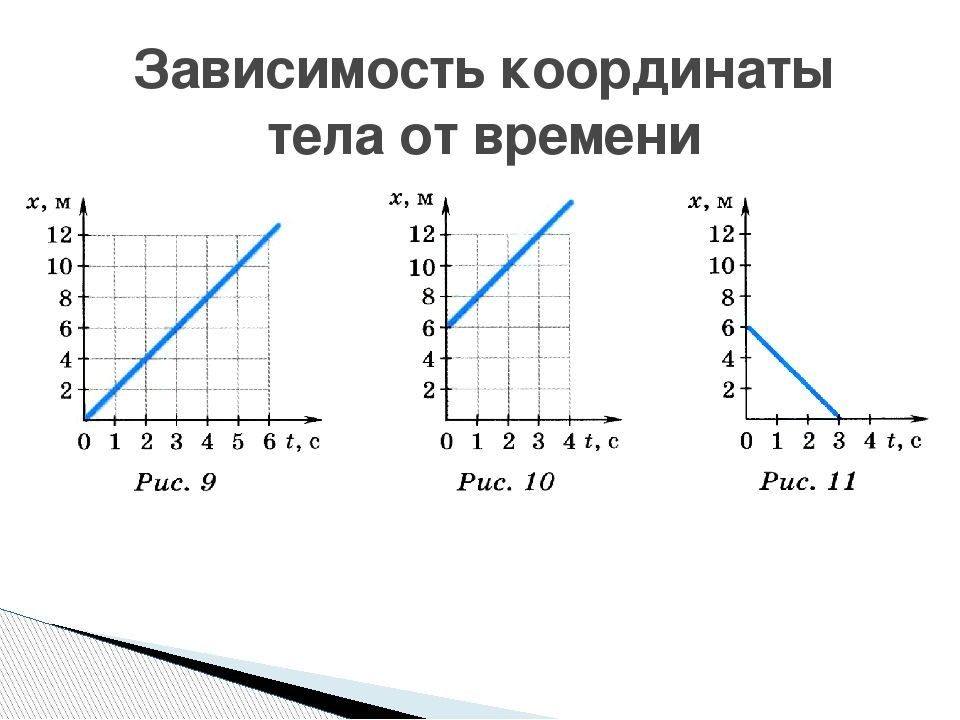 С каким ускорением двигался автомобиль? Определите перемещение автомобиля за вторую секунду после начала движения.
С каким ускорением двигался автомобиль? Определите перемещение автомобиля за вторую секунду после начала движения.
Контрольная работа №1.
«Прямолинейное равномерное и равноускоренное движения»
Вариант 4
Задача 1.
Автомобиль, двигаясь равномерно со скоростью 90 км/ч, проехал за 15 с такой же путь, какой преодолел мотоциклист за 20 с. Чему равна скорость мотоциклиста? Считать движение мотоциклиста так же равномерным.
Задача 2.
Определите, какую скорость развивает мотоциклист за 15 с, двигаясь из состояния покоя с ускорением 1,3 м/с2?
Задача 3.
Определите ускорение автомобиля, если он увеличивает скорость с 54 км/ч до 72 км/ч за 5 с. Какой путь он за это время проходит?
Задача 4.
Уравнение движения тела дано в виде x=15t+0.4t2. Определите начальную скорость и ускорение движения тела, а также координату и скорость через 5 с после начала движения. Напишите уравнение скорости данного движения.
Напишите уравнение скорости данного движения.
Задача 5.
Пуля, летящая со скоростью 400 м/с, ударяется в земляной вал и проникает в него на глубину 40 см. С каким ускорением и сколько времени двигалась пул внутри вала?
Задача 6.
С каким ускорение движется тело, если за пятую секунду оно прошло 18 м? Определите перемещение тела за восьмую секунду после начала движения.
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории.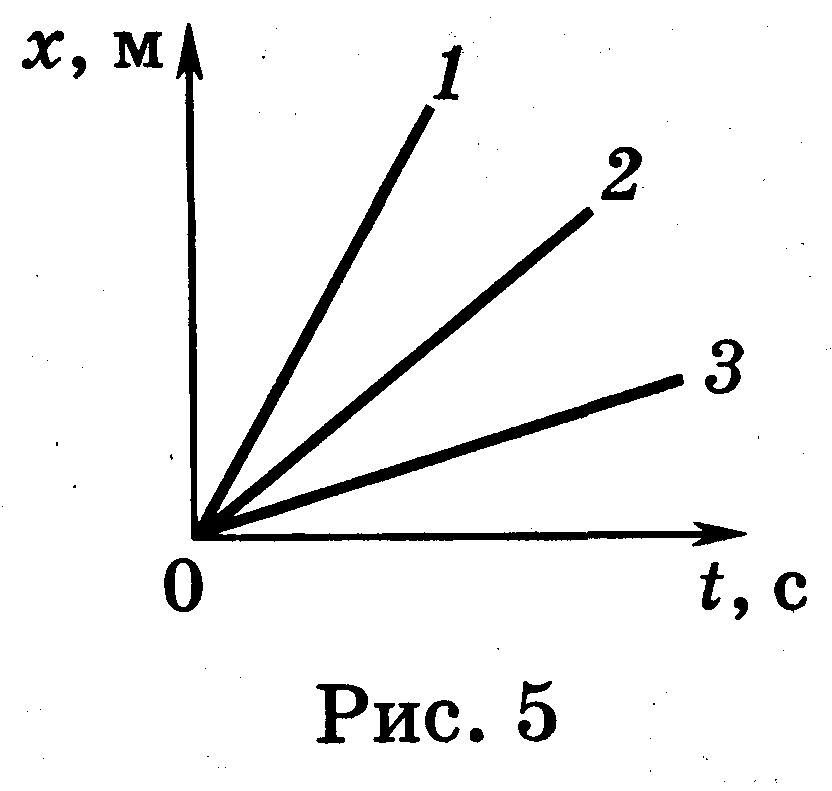 Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t0 принять равным нулю, то скорость равна:
Выразим отсюда радиус-вектор :
Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т. е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с.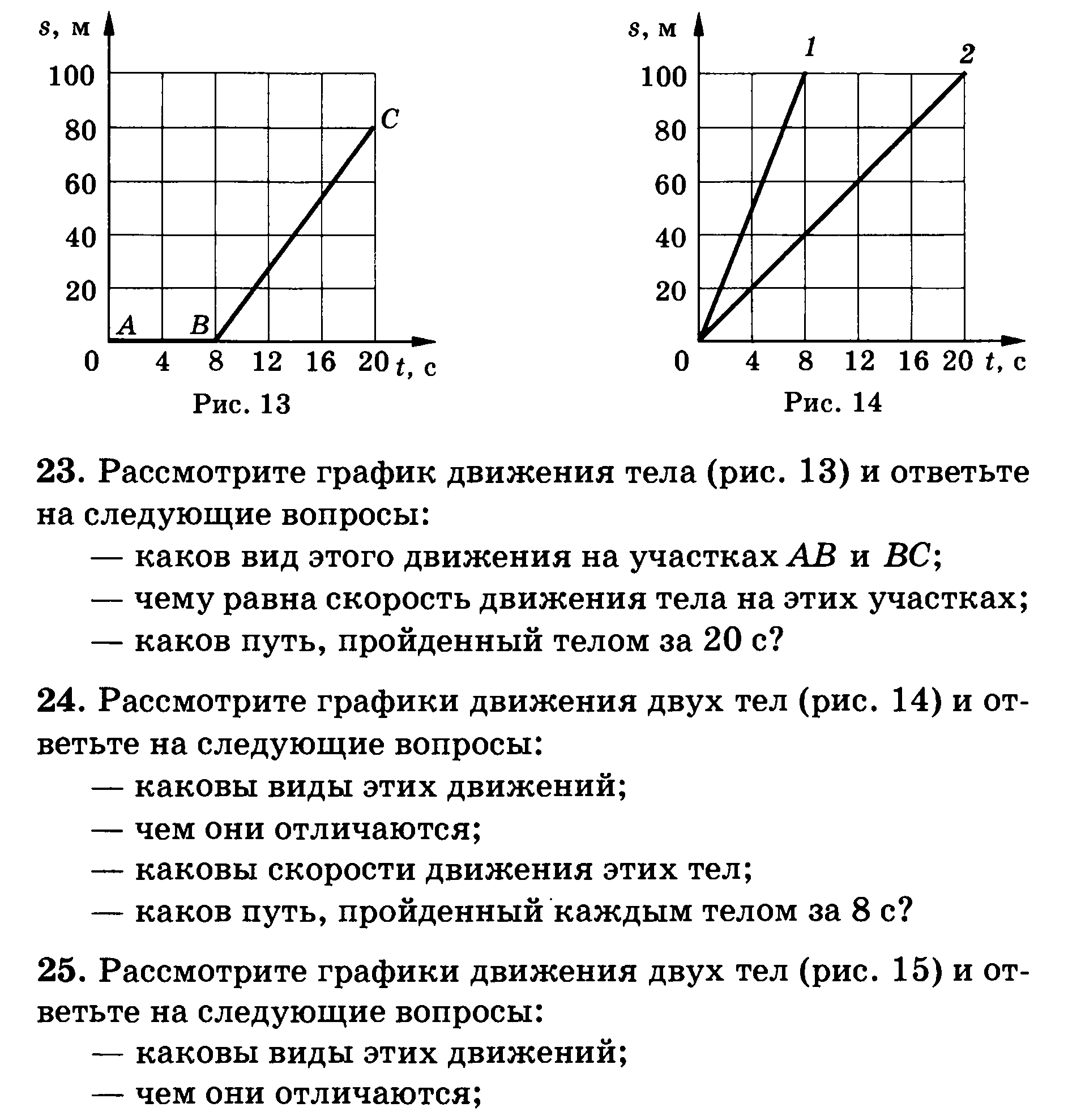 Найти s, х.
Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:
Найти .
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
,
где — искомая величина.
Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины
Ответ: .
Системы линейного перемещения Подробное исследование и информация для будущих отраслей
]]> Что такое линейное движение? Системы линейного перемещения помогают ускорить движение определенного механического инструмента в определенном направлении, которое более или менее задано заранее. Фактически, эти системы компактны по размеру для обеспечения высоких характеристик, связанных с кинетическими системами для различных отраслей промышленности, таких как производство.
Фактически, эти системы компактны по размеру для обеспечения высоких характеристик, связанных с кинетическими системами для различных отраслей промышленности, таких как производство.
Многие, кто даже проявляет незначительный интерес к управлению движением, знают о прецизионных линейных приводах — устройствах позиционирования, которые создают движение с одной степенью свободы и обычно не включают в себя систему управления для полезной нагрузки.
Обычно устройства с электрическим приводом являются наиболее точными, а некоторые приводные технологии, такие как электромеханические, пьезоэлектрические и линейные двигатели, способны производить линейное движение.
Читайте также: Hexapod robot
Содержание
Такие прецизионные линейные приводы разработаны для обеспечения высокой производительности в ситуациях, требующих непрерывной работы, и часто используются в таких приложениях, как управление стоимостью в транспортных средствах, а также в обрабатывающей промышленности и упаковочной промышленности, прессование и зажим, управление направляющими кромок, регулировка обратного хода, загрузка и разгрузка, а также сверление, сварка, склеивание или термоформование.
ALIO не имеет себе равных для 6-D Nano Precision®. Благодаря нанометровой прямолинейности и плоскостности вы можете быть уверены, что точность вашей точки соответствует True Nano®. Это сценическое семейство доступно от 25 мм до 450 мм. Стандартная двунаправленная повторяемость по оси составляет менее 50 нанометров с дополнительной двунаправленной повторяемостью 10 нанометров для требовательных метрологических или производственных нужд.
Читайте также: Линейный привод
Ступени могут поставляться с данными, отслеживаемыми в соответствии с NIST, что гарантирует наноточность, а не только оптимизм маркетинговых данных.
- Ход: 30 мм — 440 мм
- Скорость: до 1 м / сек
- Разрешение: <5 нм
- Двунаправленная повторяемость: <± 30 нм
- Точность смещения: <1 мкм
- Стандартный и высокодинамичный сплав
Чтобы узнать больше об этих системах, давайте читать дальше:
Читайте также: Нанопозиционирование
Что такое системы линейного движения?
Эти подшипники предназначены для обеспечения движения без шарнира в одном конкретном направлении. Он сочетается с современными технологиями, такими как линейные приводы, подшипники качения, линейные двигатели и т. Д.
Он сочетается с современными технологиями, такими как линейные приводы, подшипники качения, линейные двигатели и т. Д.
Чаще всего системы линейного перемещения помогают инженерам успешно работать на сборочных линиях и станках. Это может потребовать критических расчетов, связанных с размерами роботов и транспортных средств, используемых для linear motion .
Таким образом, их конструкции иногда бывают очень дорогими и сложными. Но такие факторы, как нагрузка, ориентация, точность, перемещение и скорость, помогают разделить сложности систем линейного перемещения и собрать точные и точные инженерные модули.
В конце концов, вся совокупность систем линейного перемещения способствует ускорению и / или замедлению при постоянных скоростях, которые можно дополнительно настроить в соответствии с требованиями производственного процесса.
Читайте также: Система воздушных подшипников
Как рассчитать линейное движение?
Основные принципы линейного движения включают вычисление скорости и ускорения для начинающих.
Формула расчета движущегося объекта:
V = с / т
Где «V» обозначается как Скорость, «s» — это линейное расстояние, которое машина должна преодолеть или преодолела до сих пор, «t» — это время, затраченное на то же расстояние.
Чтобы глубже понять смысл, мы можем сказать, что «Расстояние» — это длина пути, который тело или машина преодолели от точки A до точки B.
Итак, когда объект меняет свое положение с одного конца на другой, на профессиональном языке это называется «смещение». С другой стороны, когда необходимо зафиксировать измененное положение или смещение объекта с учетом фактора времени, это называется «скорость».
В случае, если ускорение постоянное, мы рассчитываем скорость по:
В = v0 + а т
Здесь «v0» определяется как начальная линейная скорость, «a» — это ускорение, «t» — это, очевидно, затраченное время.
Теперь линейное расстояние при статическом ускорении:
S = v0 t + ½ a t2
Теперь общая скорость здесь:
.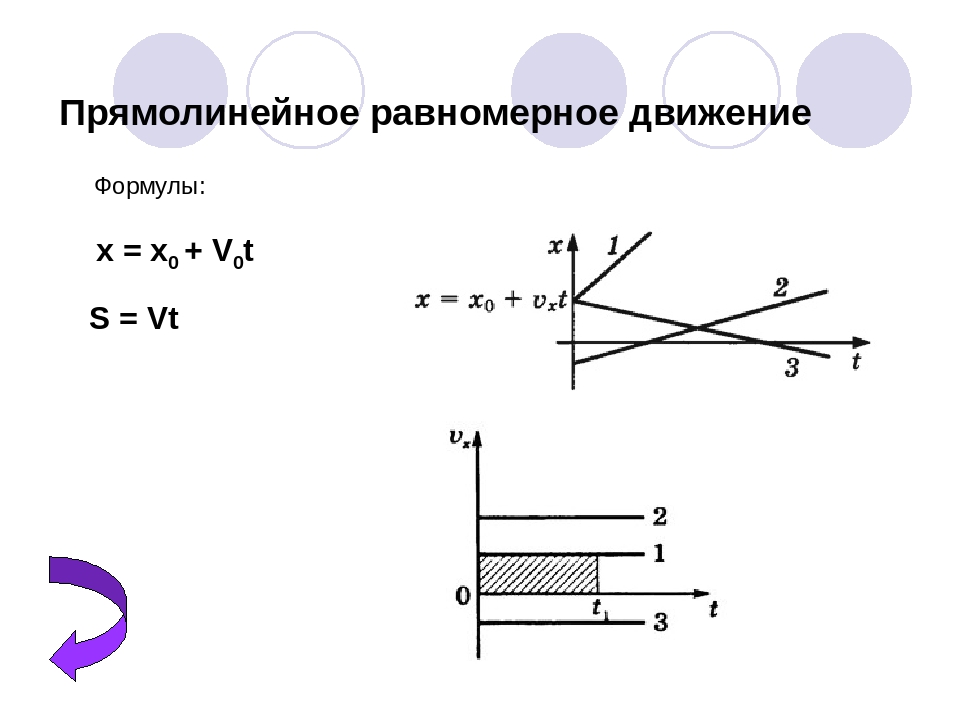 V = (v02 + 2 а с) 1/2
V = (v02 + 2 а с) 1/2
Когда скорость постоянно меняется или меняется:
V = ds / dt
Здесь «ds» представляет изменение расстояния, а «dt» — изменение времени.
Соответственно, рассчитываемое ускорение будет:
а = дв / дт
Здесь «dv» — это изменение скорости.
Читайте также: Ступень вращения
Что такое линейное движение объекта?
Линейное движение объекта будет определяться одномерным движением, совмещенным с прямой линией. И поскольку формулы упомянуты выше, ускорение и скорость объекта при различных обстоятельствах заставят его двигаться линейным движением .
Ведущие отрасли, такие как ALIO Industries, преуспели в использовании этих формул на базовом уровне для проверки направления, в котором движется объект, по сравнению с эталонами.
Эти эталонные тесты для объекта могут быть требуемым набором скорости с точностью, воспроизводимостью и точностью, который клиент должен предоставить на рынке другим поставщикам или конечному конечному потребителю.
Короче говоря, существует два типа линейных движений объекта:
- Равномерное поступательное движение при постоянной скорости или нулевом ускорении.
- Неравномерное линейное движение при переменной скорости или ненулевом ускорении.
Для тех, кто не осведомлен, линейное движение на самом деле является основной формой движения объекта.
Даже первый закон движения Ньютона гласит, что объект будет продолжать двигаться по прямой со скоростью постоянного градуса, то есть до тех пор, пока внешняя или чистая сила не будет приложена в значительной степени.
Под внешними силами следует понимать, что о гравитации и трении говорят на общем уровне, если и пока не указано иное.
Другой способ сравнить траекторию линейного движения — с общим движением. Во время общего движения скорость объекта, добавленная к положению, называется векторами, ограниченными пределами направления и величины.
Другими словами, векторы линейного движения систем постоянны и равны. Проще говоря, это означает, что определенный объект не движется в другом направлении. Его траектория идет по оси.
Проще говоря, это означает, что определенный объект не движется в другом направлении. Его траектория идет по оси.
Читайте также: Ступень оси Z
Как работает слайд с линейным движением?Одним из наиболее важных компонентов во всем пакете систем линейного перемещения является линейный ползун или подшипник линейного перемещения .Он разработан и используется ведущими игроками, такими как ALIO Industries , чтобы свободно направлять объекты в одном направлении.
В этих подшипниках обычно используются такие компоненты, как колодка, роликовые системы, рельс, втулка и т. Д. Рельс размещается на основании и не обязательно должен иметь прямую линию. Каретка — это еще одна часть, которая вместе работает с подвижными частями линейного слайдера .
Шариковые или светодиодные винты поддерживают поворотный механизм в линейном слайдере, чтобы ускорить движение каретки.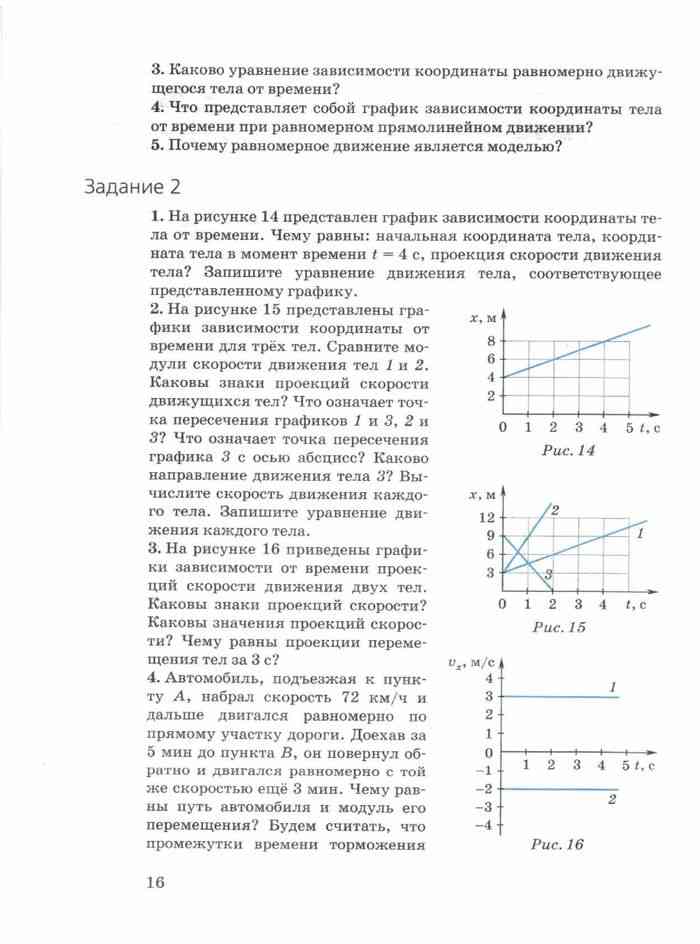 Эти винты прикреплены к неподвижному основанию, пока гайка в сборе работает с кареткой, когда она начинает двигаться.
Эти винты прикреплены к неподвижному основанию, пока гайка в сборе работает с кареткой, когда она начинает двигаться.
При перемещении винтов гайка и каретка перемещаются в одинаковом направлении. Этим винтом можно управлять с помощью маховика. Принимая во внимание, что когда мы говорим о других системах линейного перемещения , таких как приводы, пневматические цилиндры, гидроцилиндры и т. Д., Они могут не требовать шарико-винтовой передачи или ходового винта.
Преимущества и недостатки
| Преимущества : | Недостатки: |
|---|---|
|
|
| |
Разгон
Как упоминалось ранее в Уроке 1, объект, движущийся равномерно по кругу, движется по кругу с постоянной или постоянной скоростью. Вектор скорости постоянен по величине, но меняется по направлению.Поскольку скорость такого движения постоянна, многие ученики ошибочно полагают, что ускорения нет. «В конце концов, — могут сказать они, — если бы я вел машину по кругу с постоянной скоростью 20 миль / ч, тогда скорость не уменьшалась и не увеличивалась; следовательно, не должно быть ускорения». В основе этого распространенного заблуждения студентов лежит неправильное представление о том, что ускорение связано со скоростью, а не со скоростью. Но дело в том, что ускоряющийся объект — это объект, который меняет свою скорость.А поскольку скорость — это вектор, который имеет как величину, так и направление, изменение либо величины, либо направления составляет изменение скорости. По этой причине можно с уверенностью заключить, что объект, движущийся по кругу с постоянной скоростью, действительно ускоряется. Он ускоряется, потому что направление вектора скорости меняется.
В основе этого распространенного заблуждения студентов лежит неправильное представление о том, что ускорение связано со скоростью, а не со скоростью. Но дело в том, что ускоряющийся объект — это объект, который меняет свою скорость.А поскольку скорость — это вектор, который имеет как величину, так и направление, изменение либо величины, либо направления составляет изменение скорости. По этой причине можно с уверенностью заключить, что объект, движущийся по кругу с постоянной скоростью, действительно ускоряется. Он ускоряется, потому что направление вектора скорости меняется.
Геометрический
Доказательство внутреннего ускоренияЧтобы понять это на более глубоком уровне, нам придется объединить определение ускорения с обзором некоторых основных векторных принципов.Напомним, из раздела 1 в классе физики, что ускорение как величина определялось как скорость, с которой изменяется скорость объекта. Таким образом, он рассчитывается с использованием следующего уравнения:
, где v i представляет начальную скорость, а v f представляет конечную скорость через некоторое время t . Числитель уравнения находится путем вычитания одного вектора ( v i ) из второго вектора ( v f ).Но сложение и вычитание векторов друг из друга происходит иначе, чем сложение и вычитание скалярных величин. Рассмотрим случай, когда объект движется по окружности вокруг точки C, как показано на диаграмме ниже. За время t секунд объект переместился из точки A в точку B. За это время скорость изменилась с v i на v f . Процесс вычитания v i из v f показан на векторной диаграмме; этот процесс приводит к изменению скорости.
Числитель уравнения находится путем вычитания одного вектора ( v i ) из второго вектора ( v f ).Но сложение и вычитание векторов друг из друга происходит иначе, чем сложение и вычитание скалярных величин. Рассмотрим случай, когда объект движется по окружности вокруг точки C, как показано на диаграмме ниже. За время t секунд объект переместился из точки A в точку B. За это время скорость изменилась с v i на v f . Процесс вычитания v i из v f показан на векторной диаграмме; этот процесс приводит к изменению скорости.
Направление вектора ускорения
Обратите внимание на диаграмму выше, что есть изменение скорости для объекта, движущегося по кругу с постоянной скоростью. Тщательный осмотр вектора изменения скорости на приведенной выше диаграмме показывает, что он указывает вниз и влево. В средней точке дуги, соединяющей точки A и B, изменение скорости направлено в сторону точки C — центра окружности.Ускорение объекта зависит от этого изменения скорости и находится в том же направлении, что и это изменение скорости. Ускорение объекта совпадает с направлением вектора изменения скорости; ускорение также направлено в сторону точки C — центра окружности. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются к центру круга.
В средней точке дуги, соединяющей точки A и B, изменение скорости направлено в сторону точки C — центра окружности.Ускорение объекта зависит от этого изменения скорости и находится в том же направлении, что и это изменение скорости. Ускорение объекта совпадает с направлением вектора изменения скорости; ускорение также направлено в сторону точки C — центра окружности. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются к центру круга.
Ускорение объекта часто измеряется с помощью устройства, известного как акселерометр. Простой акселерометр состоит из объекта, погруженного в жидкость, например воду.Рассмотрим герметичную банку, наполненную водой. Пробка, прикрепленная к крышке шнурком, может служить акселерометром. Чтобы проверить направление ускорения объекта, движущегося по кругу, банку можно перевернуть и прикрепить к концу короткой секции деревянного 2х4. Второй акселерометр, сконструированный таким же образом, может быть прикреплен к противоположному концу 2×4. Если 2х4 и акселерометры закреплены на вращающейся платформе и вращаются по кругу, направление ускорения можно четко определить по направлению наклона пробок.Когда смесь пробки и воды вращается по кругу, пробка наклоняется к центру круга. Наименее массивный из двух объектов всегда наклоняется в направлении ускорения. В случае пробки и воды пробка менее массивна (в пересчете на мл) и, следовательно, испытывает большее ускорение. Имея меньшую инерцию (из-за своей меньшей массы на мл), пробка меньше всего сопротивляется ускорению, и, таким образом, наклоняется на внутрь банки к центру круга.Это очевидное свидетельство того, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение, направленное к центру круга.
Если 2х4 и акселерометры закреплены на вращающейся платформе и вращаются по кругу, направление ускорения можно четко определить по направлению наклона пробок.Когда смесь пробки и воды вращается по кругу, пробка наклоняется к центру круга. Наименее массивный из двух объектов всегда наклоняется в направлении ускорения. В случае пробки и воды пробка менее массивна (в пересчете на мл) и, следовательно, испытывает большее ускорение. Имея меньшую инерцию (из-за своей меньшей массы на мл), пробка меньше всего сопротивляется ускорению, и, таким образом, наклоняется на внутрь банки к центру круга.Это очевидное свидетельство того, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение, направленное к центру круга.
Еще один простой самодельный акселерометр — это зажженная свеча, расположенная вертикально по центру открытого стакана. Если стакан держать ровно и неподвижно (так, чтобы не было ускорения), то пламя свечи распространяется вверх. Однако, если вы держите систему стекло-свеча вытянутой рукой и вращаете по кругу с постоянной скоростью (так, чтобы пламя испытывало ускорение), то пламя свечи больше не будет распространяться вертикально вверх.Вместо этого пламя отклоняется от вертикального положения. Это означает, что существует ускорение, когда пламя движется по круговой траектории с постоянной скоростью. Отклонение пламени будет в сторону ускорения. Это можно объяснить, утверждая, что горячие газы пламени менее массивны (в расчете на миллилитр) и, следовательно, имеют меньшую инерцию, чем более холодные газы, которые его окружают. Впоследствии более горячие и легкие газы пламени испытывают большее ускорение и наклоняются в направлении ускорения.Тщательное изучение пламени показывает, что пламя направлено к центру круга, указывая, таким образом, на то, что не только ускорение; но есть внутреннее ускорение. Это еще одно наблюдаемое свидетельство того, что объекты, движущиеся по кругу с постоянной скоростью, испытывают ускорение, направленное к центру круга.
Однако, если вы держите систему стекло-свеча вытянутой рукой и вращаете по кругу с постоянной скоростью (так, чтобы пламя испытывало ускорение), то пламя свечи больше не будет распространяться вертикально вверх.Вместо этого пламя отклоняется от вертикального положения. Это означает, что существует ускорение, когда пламя движется по круговой траектории с постоянной скоростью. Отклонение пламени будет в сторону ускорения. Это можно объяснить, утверждая, что горячие газы пламени менее массивны (в расчете на миллилитр) и, следовательно, имеют меньшую инерцию, чем более холодные газы, которые его окружают. Впоследствии более горячие и легкие газы пламени испытывают большее ускорение и наклоняются в направлении ускорения.Тщательное изучение пламени показывает, что пламя направлено к центру круга, указывая, таким образом, на то, что не только ускорение; но есть внутреннее ускорение. Это еще одно наблюдаемое свидетельство того, что объекты, движущиеся по кругу с постоянной скоростью, испытывают ускорение, направленное к центру круга.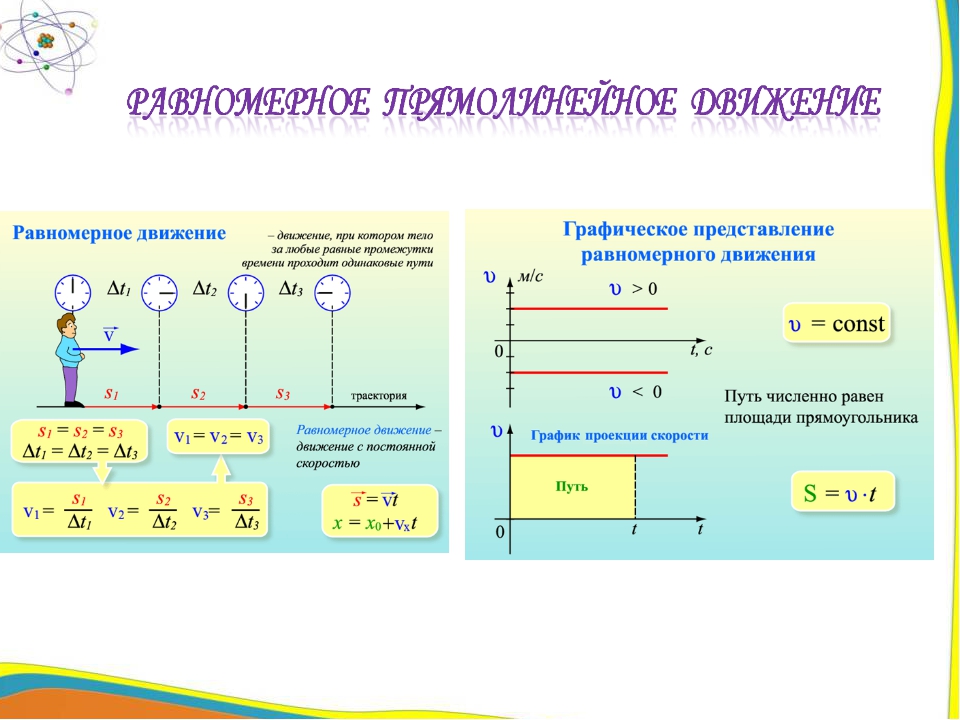
Итак, мы видели геометрическое доказательство и две реальных демонстрации этого внутреннего ускорения.На этом этапе ученик принимает решение верить или не верить. Разве разумно, что объект, движущийся по кругу, испытывает ускорение, направленное к центру круга? Можете ли вы придумать логическую причину, чтобы верить в отсутствие ускорения или даже внешнего ускорения, испытываемого объектом, движущимся в равномерном круговом движении? В следующей части Урока 1 будут представлены дополнительные логические доказательства в поддержку идеи внутренней силы для объекта, движущегося по кругу.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства Uniform Circular Motion Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.
Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.
1. Начальная и конечная скорости мяча в два разных момента времени показаны ниже. Направление мяча указано стрелкой. Для каждого случая укажите, есть ли ускорение. Объясните, почему да или почему нет. Укажите направление ускорения.
| а. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
| б. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
c. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
| d. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
| е. | |
| Ускорение: да или нет? Объяснять. | Если есть ускорение, то в каком оно направлении? |
2.Объясните связь между вашими ответами на вышеуказанные вопросы и аргументацией, использованной для объяснения того, почему можно сказать, что объект, движущийся по кругу с постоянной скоростью, испытывает ускорение.
3. Диззи Смит и Гектор Вектор все еще обсуждают № 1e. Диззи говорит, что мяч не ускоряется, потому что его скорость не меняется. Гектор говорит, что, поскольку мяч изменил свое направление, происходит ускорение.С кем ты согласен? Обсудите свою позицию, объяснив несоответствие в аргументах другого ученика.
4. Найдите на автомобиле три элемента управления, которые позволяют автомобилю ускоряться.
Для вопросов № 5- № 8: Объект движется в направлении по часовой стрелке по окружности с постоянной скоростью.Используйте свое понимание концепций скорости и ускорения, чтобы ответить на следующие четыре вопроса. Используйте диаграмму, показанную справа.
5. Какой вектор ниже представляет направление вектора скорости, когда объект находится в точке B на окружности?
6. Какой из приведенных ниже векторов представляет направление вектора ускорения, когда объект расположен в точке C на окружности?
7. Какой из приведенных ниже векторов представляет направление вектора скорости, когда объект находится в точке C на окружности?
Какой из приведенных ниже векторов представляет направление вектора скорости, когда объект находится в точке C на окружности?
8. Какой из приведенных ниже векторов представляет направление вектора ускорения, когда объект находится в точке A на окружности?
2.3 Графики положения в зависимости от времени — Физика
Графическое представление положения в зависимости от времени
График, как и картинка, стоит тысячи слов. Графики содержат не только числовую информацию, они также показывают взаимосвязь между физическими величинами. В этом разделе мы исследуем кинематику, анализируя графики положения во времени.
Графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная. Когда две физические величины наносятся друг на друга, горизонтальная ось обычно считается независимой переменной, а вертикальная ось — зависимой переменной. В алгебре вы бы назвали горизонтальную ось осью x , а вертикальную ось — осью y . Как и на рис. 2.10, прямолинейный граф имеет общий вид y = mx + by = mx + b.
В алгебре вы бы назвали горизонтальную ось осью x , а вертикальную ось — осью y . Как и на рис. 2.10, прямолинейный граф имеет общий вид y = mx + by = mx + b.
Здесь м. — это уклон, определяемый как подъем, деленный на пробег (как показано на рисунке) прямой линии. Буква b представляет собой точку пересечения y , которая является точкой, в которой линия пересекает вертикальную ось y . С точки зрения физической ситуации в реальном мире эти величины приобретают особое значение, как мы увидим ниже.(Рисунок 2.10.)
Рисунок 2.10 На диаграмме показан прямолинейный график. Уравнение прямой: y равно mx + b .
В физике время обычно является независимой переменной. Говорят, что от него зависят другие величины, такие как смещение. График положения в зависимости от времени, таким образом, будет иметь положение на вертикальной оси (зависимая переменная) и время на горизонтальной оси (независимая переменная). В этом случае, к чему бы относились наклон и интервал y ? Давайте вернемся к нашему первоначальному примеру при изучении расстояния и смещения.
График положения в зависимости от времени, таким образом, будет иметь положение на вертикальной оси (зависимая переменная) и время на горизонтальной оси (независимая переменная). В этом случае, к чему бы относились наклон и интервал y ? Давайте вернемся к нашему первоначальному примеру при изучении расстояния и смещения.
Дорога в школу находилась в 5 км от дома. Предположим, поездка заняла 10 минут, и ваш родитель все это время вел машину с постоянной скоростью. График положения в зависимости от времени для этого участка пути будет выглядеть так, как показано на рисунке 2.11.
Рисунок 2.11 Показан график зависимости положения от времени на дорогу в школу. Как бы выглядел график, если бы мы добавили обратный путь?
Как мы уже говорили, d 0 = 0, потому что мы называем домой наш O и начинаем отсчет.На рисунке 2.11 линия также начинается с d = 0. Это b в нашем уравнении для прямой. Наше начальное положение на графике зависимости положения от времени — это всегда место, где график пересекает ось x при t = 0. Каков наклон? Подъем на , — это изменение положения (т. Е. Смещение), а пробег — — это изменение во времени. Это отношение также можно записать
Это b в нашем уравнении для прямой. Наше начальное положение на графике зависимости положения от времени — это всегда место, где график пересекает ось x при t = 0. Каков наклон? Подъем на , — это изменение положения (т. Е. Смещение), а пробег — — это изменение во времени. Это отношение также можно записать
Это соотношение было тем, как мы определили среднюю скорость.Следовательно, наклон на графике d по сравнению с t — это средняя скорость.
Советы для успеха
Иногда, как в случае, когда мы строим график как поездки в школу, так и обратного пути, поведение графика выглядит по-разному в разные промежутки времени. Если график выглядит как серия прямых линий, то вы можете рассчитать среднюю скорость для каждого временного интервала, посмотрев на наклон. Если затем вы хотите рассчитать среднюю скорость для всей поездки, вы можете сделать средневзвешенное значение.
Если затем вы хотите рассчитать среднюю скорость для всей поездки, вы можете сделать средневзвешенное значение.
Давайте посмотрим на другой пример. На рис. 2.12 показан график положения в зависимости от времени для реактивного автомобиля на очень плоском высохшем дне озера в Неваде.
Рис. 2.12 На диаграмме показан график положения в зависимости от времени для автомобиля с реактивным двигателем на солончаках Бонневиль.
Используя соотношение между зависимыми и независимыми переменными, мы видим, что наклон на графике на рисунке 2.12 — это средняя скорость, v avg , а точка пересечения — смещение в нулевой момент времени, то есть d 0 .Подставляя эти символы в y = mx + b , получаем
или
Таким образом, график положения в зависимости от времени дает общую взаимосвязь между перемещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации. Из рисунка видно, что автомобиль имеет позицию 400 м при т = 0 с, 650 м при т = 1,0 с и так далее. И мы также можем узнать о скорости объекта.
Из рисунка видно, что автомобиль имеет позицию 400 м при т = 0 с, 650 м при т = 1,0 с и так далее. И мы также можем узнать о скорости объекта.
Поддержка учителей
Поддержка учителей
Демонстрация учителей
Помогите ученикам узнать, чем отличаются графики смещения отвремя похоже.
[Визуальный] Установите измерительную ручку.
- Если вы можете найти машину с дистанционным управлением, попросите одного ученика записать время, когда вы отправляете машину вперед вдоль ручки, затем назад, затем снова вперед с постоянной скоростью.
- Возьмите записанное время и изменение положения и сложите их.
- Попросите студентов научить вас рисовать график зависимости положения от времени.
Каждый отрезок пути должен представлять собой прямую линию с разным уклоном.Части, по которым машина двигалась вперед, должны иметь положительный наклон. Та часть, где он движется назад, будет иметь отрицательный наклон.
Та часть, где он движется назад, будет иметь отрицательный наклон.
[OL] Спросите, влияет ли на график место, которое они принимают за ноль .
[AL] Реально ли нарисовать любой график положения, который начинается в состоянии покоя, без какой-либо кривой? Почему мы можем пренебречь кривой в некоторых сценариях?
[Все] Обсудите, что можно обнаружить на этом графике. Учащиеся должны уметь считывать чистое смещение, но они также могут использовать график для определения общего пройденного расстояния.Затем спросите, как скорость или скорость отражаются на этом графике. Посоветуйте учащимся увидеть, что крутизна линии (уклона) является мерой скорости, а направление уклона — направлением движения.
[AL] Некоторые студенты могут заметить, что кривая на линии представляет собой своего рода наклон наклона, предварительный просмотр ускорения, о котором они узнают в следующей главе.
Snap Lab
Построение графика движения
В этом упражнении вы отпустите мяч по наклонной плоскости и построите график зависимости смещения мяча от смещения. время.
время.
- Выберите открытое место с большим количеством свободного пространства, чтобы было меньше шансов споткнуться или упасть из-за катящихся шаров.
- 1 мяч
- 1 доска
- 2 или 3 книги
- 1 секундомер
- 1 рулетка
- 6 штук малярной ленты
- 1 миллиметровая бумага
- 1 карандаш
Процедура
- Постройте пандус, поместив один конец доски поверх стопки книг.При необходимости отрегулируйте местоположение, пока не будет препятствий на прямой линии от нижней части пандуса до следующих 3 м.
- Отметьте расстояния 0,5 м, 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части пандуса. Напишите расстояния на ленте.
- Попросите одного человека взять на себя роль экспериментатора. Этот человек выпустит мяч с вершины рампы. Если мяч не достигает отметки 3,0 м, то увеличьте наклон пандуса, добавив еще одну книгу.При необходимости повторите этот шаг.
- Попросите экспериментатора выпустить мяч.
 Попросите второго человека, таймера, начать отсчет времени испытания, как только мяч достигнет нижней части рампы, и остановить отсчет, когда мяч достигнет 0,5 м. Попросите третьего человека, записывающего устройства, записать время в таблицу данных.
Попросите второго человека, таймера, начать отсчет времени испытания, как только мяч достигнет нижней части рампы, и остановить отсчет, когда мяч достигнет 0,5 м. Попросите третьего человека, записывающего устройства, записать время в таблицу данных. - Повторите шаг 4, остановив раз на расстоянии 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части пандуса.
- Используйте свои измерения времени и смещения, чтобы составить позицию vs.временной график движения мяча.
- Повторите шаги с 4 по 6 с разными людьми, которые берут на себя роли экспериментатора, таймера и записывающего устройства. Получаете ли вы одинаковые значения измерений независимо от того, кто выпускает мяч, измеряет время или записывает результат? Обсудите возможные причины расхождений, если таковые имеются.
Захват
Верно или неверно: средняя скорость мяча будет меньше средней скорости мяча.
- Истинно
- Ложь
Поддержка учителя
Поддержка учителя
[BL] [OL] Подчеркните, что движение в этой лабораторной работе — это движение мяча, когда он катится по полу. Спросите студентов, где должен быть ноль.
Спросите студентов, где должен быть ноль.
[AL] Спросите учащихся, как бы выглядел график, если бы они начали отсчет времени вверху по сравнению с основанием пандуса. Почему график должен выглядеть иначе? Что может объяснить разницу?
[BL] [OL] Попросите учащихся сравнить графики, построенные с разными людьми, выполняющими разные роли. Попросите их определить и сравнить среднюю скорость для каждого интервала. Каковы были абсолютные различия в скоростях и каковы были различия в процентах? Оказываются ли различия случайными или есть систематические различия? Почему могут существовать систематические различия между двумя наборами измерений с разными людьми в каждой роли?
[BL] [OL] Попросите учащихся сравнить графики, построенные с разными людьми, выполняющими разные роли.Попросите их определить и сравнить среднюю скорость для каждого интервала. Каковы были абсолютные различия в скоростях и каковы были различия в процентах? Оказываются ли различия случайными или есть систематические различия? Почему могут существовать систематические различия между двумя наборами измерений с разными людьми в каждой роли?
Решение задач с использованием графиков положения и времени
Итак, как мы можем использовать графики для решения таких задач, как скорость?
Рабочий пример
Использование графика положения и времени для расчета средней скорости: Jet Car
Найдите среднюю скорость автомобиля, положение которого показано на рисунке 1.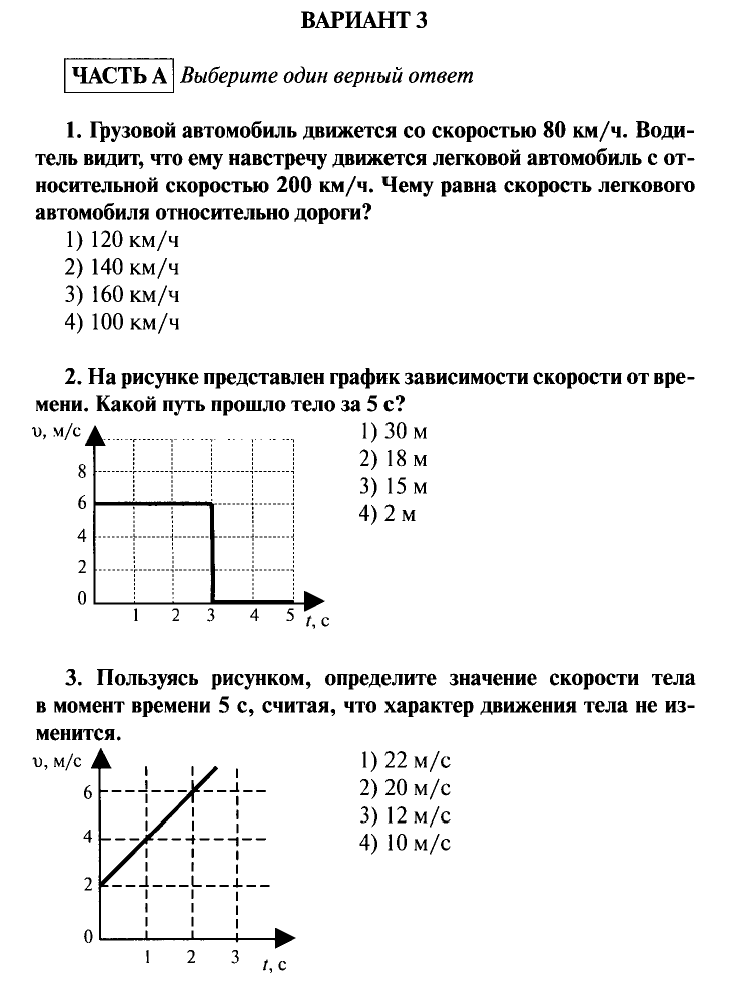 13.
13.
Стратегия
Наклон графика d против t — это средняя скорость, поскольку наклон равен подъему за пробег.
наклон = ΔdΔt = vsсклон = ΔdΔt = v2,7
Поскольку наклон здесь постоянный, любые две точки на графике можно использовать для определения наклона.
Решение
- Выберите две точки на линии. В этом случае мы выбираем точки, обозначенные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Обратите внимание, однако, что вы можете выбрать любые две точки.)
- Подставьте значения d и t выбранных точек в уравнение. Помните, что при вычислении изменения (Δ) мы всегда используем конечное значение минус начальное значение.
v = ΔdΔt = 2000 м − 525 м6,4 с − 0,50 с = 250 м / с, v = ΔdΔt = 2000 м − 525 м6,4 с − 0,50 с = 250 м / с,
2,8
Обсуждение
Это впечатляюще высокая сухопутная скорость (900 км / ч или около 560 миль / ч): намного больше, чем типичное ограничение скорости на шоссе, равное 27 м / с или 96 км / ч, но значительно ниже рекордных 343 м. / с или 1234 км / ч, установленный в 1997 году.
/ с или 1234 км / ч, установленный в 1997 году.
Поддержка учителей
Поддержка учителей
Если график положения представляет собой прямую линию, то единственное, что ученикам нужно знать для расчета средней скорости, — это наклон линии, подъем / бег. Они могут использовать любые наиболее удобные точки на линии.
А что, если график позиции сложнее прямой линии? Что, если объект ускоряется или поворачивается и движется назад? Можем ли мы выяснить что-нибудь о его скорости из графика такого движения? Давайте еще раз посмотрим на реактивный автомобиль.График на рис. 2.13 показывает его движение по мере набора скорости после запуска в состоянии покоя. Время для этого движения начинается с нуля (как если бы оно измерялось секундомером), а смещение и скорость изначально равны 200 м и 15 м / с соответственно.
Рис. 2.13 На схеме показан график положения автомобиля с реактивным двигателем в течение периода времени, когда он набирает скорость. Наклон графика зависимости расстояния от времени — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке — это наклон касательной в этой точке.
Наклон графика зависимости расстояния от времени — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке — это наклон касательной в этой точке.
Рис. 2.14 Реактивный автомобиль ВВС США едет по рельсовому пути. (Мэтт Тростле, Flickr)
График положения в зависимости от времени на рис. 2.13 представляет собой кривую, а не прямую линию. Наклон кривой с течением времени становится более крутым, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости положения от времени — это мгновенная скорость в этой точке. Его можно найти, проведя прямую, касательную к кривой в интересующей точке, и взяв наклон этой прямой.Касательные линии показаны для двух точек на рисунке 2.13. Средняя скорость — это чистое смещение, деленное на пройденное время.
Рабочий пример
Использование графика положения и времени для расчета средней скорости: реактивный автомобиль, дубль
Рассчитайте мгновенную скорость реактивного автомобиля за время 25 с, определив наклон касательной в точке Q на рисунке 2. 13.
13.
Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке.
Решение
- Найдите касательную к кривой при t = 25 st = 25 с.
- Определите конечные точки касательной. Это соответствует положению 1300 м за 19 с и положению 3120 м за 32 с.
- Подставьте эти конечные точки в уравнение, чтобы найти наклон, v .
уклон = vQ = ΔdQΔtQ = (3120−1300) м (32−19) s = 1820 м13 s = 140 м / с уклон = vQ = ΔdQΔtQ = (3120−1300) м (32−19) s = 1820 м13 s = 140 м / с
2.9
Обсуждение
Таким образом можно получить весь график v и t .
Поддержка учителя
Поддержка учителя
Изогнутая линия — более сложный пример. Определите касательную как линию, которая касается кривой только в одной точке. Покажите, что, когда прямая линия меняет свой угол рядом с кривой, она на самом деле несколько раз ударяет по кривой в основании, но только одна линия никогда не соприкасается. Эта линия образует прямой угол с радиусом кривизны, но на этом уровне они могут просто смотреть на нее.Наклон этой линии дает мгновенную скорость. Самая полезная часть этой строки состоит в том, что учащиеся могут определить, когда скорость увеличивается, уменьшается, положительная, отрицательная и нулевая.
Покажите, что, когда прямая линия меняет свой угол рядом с кривой, она на самом деле несколько раз ударяет по кривой в основании, но только одна линия никогда не соприкасается. Эта линия образует прямой угол с радиусом кривизны, но на этом уровне они могут просто смотреть на нее.Наклон этой линии дает мгновенную скорость. Самая полезная часть этой строки состоит в том, что учащиеся могут определить, когда скорость увеличивается, уменьшается, положительная, отрицательная и нулевая.
[AL] Вы можете найти мгновенную скорость в каждой точке на графике, и если вы изобразите каждую из этих точек, у вас будет график скорости.
3.4 Движение с постоянным ускорением
Цели обучения
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени. Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения.Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемых задачами преследования двух тел .
Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения.Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемых задачами преследования двух тел .
Обозначение
Сначала сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно [латекс] \ text {Δ} t = {t} _ {\ text {f}} — {t} _ {0} [/ latex], беря [латекс] {t} _ {0} = 0 [/ latex] означает, что [latex] \ text {Δ} t = {t} _ {\ text {f}} [/ latex], последнее время на секундомере.Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть [latex] {x} _ {0} [/ latex] — это начальная позиция , а [latex] {v} _ {0} [/ latex] — начальная скорость . Мы не ставим индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для истекшего времени, [latex] \ text {Δ} t = t [/ latex].Он также упрощает выражение для смещения x , которое теперь имеет вид [latex] \ text {Δ} x = x- {x} _ {0} [/ latex]. Кроме того, он упрощает выражение для изменения скорости, которое теперь имеет вид [latex] \ text {Δ} v = v- {v} _ {0} [/ latex]. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Мы не ставим индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для истекшего времени, [latex] \ text {Δ} t = t [/ latex].Он также упрощает выражение для смещения x , которое теперь имеет вид [latex] \ text {Δ} x = x- {x} _ {0} [/ latex]. Кроме того, он упрощает выражение для изменения скорости, которое теперь имеет вид [latex] \ text {Δ} v = v- {v} _ {0} [/ latex]. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
[латекс] \ begin {array} {c} \ text {Δ} t = t \ hfill \\ \ text {Δ} x = x- {x} _ {0} \ hfill \\ \ text {Δ} v = v- {v} _ {0}, \ hfill \ end {array} [/ latex]
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
[латекс] \ overset {\ text {-}} {a} = a = \ text {constant} \ text {.} [/ Latex]
Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучать, и не ухудшает точность нашего лечения.Во-первых, ускорение является постоянным в большом количестве ситуаций. Более того, во многих других ситуациях мы можем точно описать движение, предполагая постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко изменяется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до полной остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.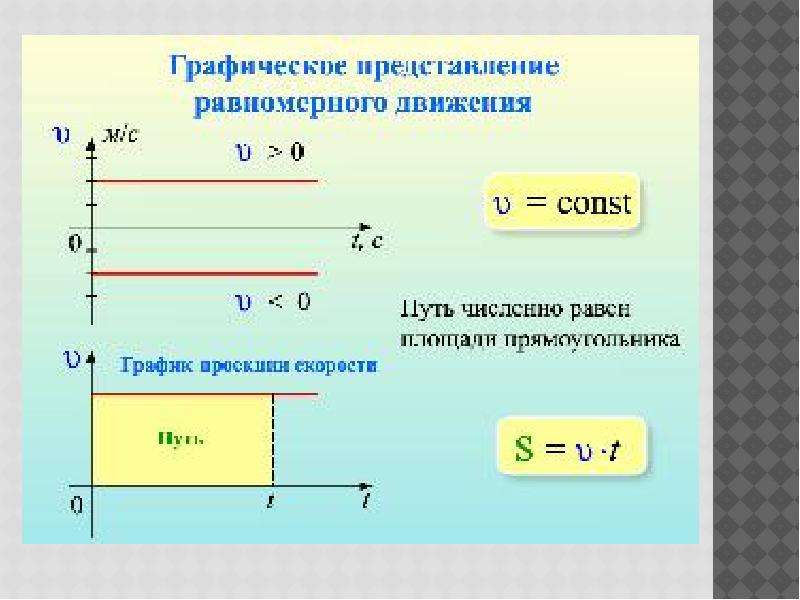
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
[латекс] \ overset {\ text {-}} {v} = \ frac {\ text {Δ} x} {\ text {Δ} t}.[/ латекс]
Замена упрощенного обозначения для [латекс] \ text {Δ} x [/ latex] и [latex] \ text {Δ} t [/ latex] дает
[латекс] \ overset {\ text {-}} {v} = \ frac {x- {x} _ {0}} {t}. [/ латекс]
Решение для x дает нам
[латекс] x = {x} _ {0} + \ overset {\ text {-}} {v} t, [/ latex], где средняя скорость
[латекс] \ overset {\ text {-}} {v} = \ frac {{v} _ {0} + v} {2}. [/ латекс]
Уравнение [латекс] \ overset {\ text {-}} {v} = \ frac {{v} _ {0} + v} {2} [/ latex] отражает тот факт, что при постоянном ускорении v — это просто среднее значение начальной и конечной скоростей.(Рисунок) графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью.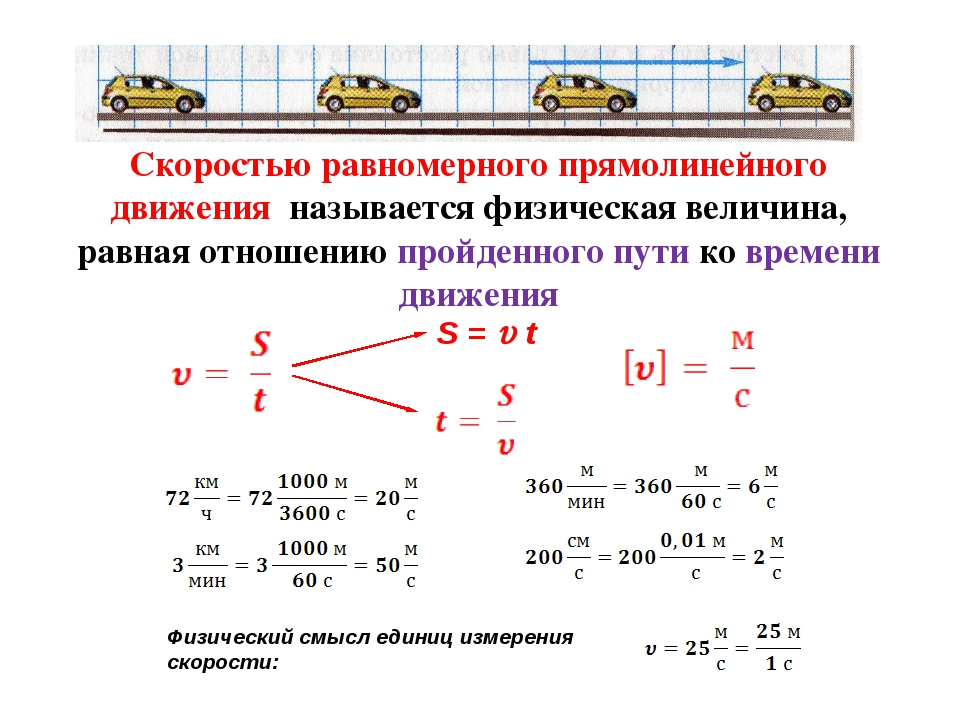 Средняя скорость на 1-часовом интервале от 40 км / ч до 80 км / ч составляет 60 км / ч:
Средняя скорость на 1-часовом интервале от 40 км / ч до 80 км / ч составляет 60 км / ч:
[латекс] \ overset {\ text {-}} {v} = \ frac {{v} _ {0} + v} {2} = \ frac {40 \, \ text {км / ч} +80 \ , \ text {км / ч}} {2} = 60 \, \ text {км / ч} \ text {.} [/ latex]
В части (b) ускорение непостоянно. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рис. 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости [латекс] {v} _ {0} \, \ text {и} \, v [/ latex]. Средняя скорость [latex] \ frac {1} {2} ({v} _ {0} + v) = 60 \, \ text {km} \ text {/} \ text {h} [/ latex]. (b) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не дается [латекс] \ frac {1} {2} ({v} _ {0} + v) [/ latex], но превышает 60 км / ч.
Решение для окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
[латекс] a = \ frac {\ text {Δ} v} {\ text {Δ} t}.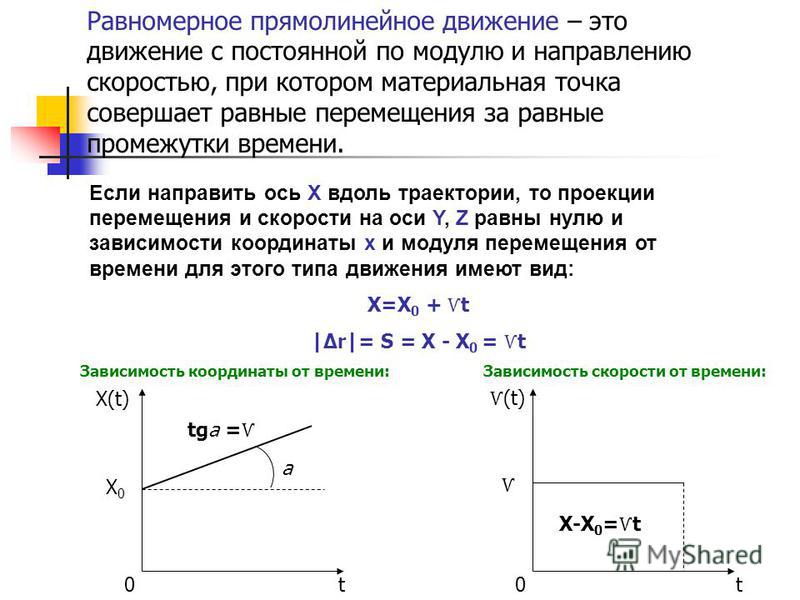 [/ латекс]
[/ латекс]
Подстановка упрощенных обозначений для [латекс] \ text {Δ} v [/ latex] и [latex] \ text {Δ} t [/ latex] дает нам
[латекс] a = \ frac {v- {v} _ {0}} {t} \ enspace (\ text {constant} \, a). [/ латекс]
Решение для v дает
[латекс] v = {v} _ {0} + at \ enspace (\ text {constant} \, a). [/латекс]Пример
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется со скоростью 1,50 м / с 2 на 40.{2}, t = 40 \, \ text {s} [/ latex].
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость [латекс] {v} _ {\ text {f}} [/ latex].
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя (Рисунок), [latex] v = {v} _ {0} + at [/ latex].
Решение
Показать ответ Подставьте известные значения и решите: [латекс] v = {v} _ {0} + at = 70,0 \, \ text {м / с} + (- 1. {2}) (40,0 с) = 10,0 м / с. [/ latex] (Рисунок) — это эскиз, на котором показаны векторы ускорения и скорости.
{2}) (40,0 с) = 10,0 м / с. [/ latex] (Рисунок) — это эскиз, на котором показаны векторы ускорения и скорости.
Рисунок 3.19 Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок).В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.
Уравнение [латекс] v = {v} _ {0} + at [/ latex] не только помогает при решении проблем, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции.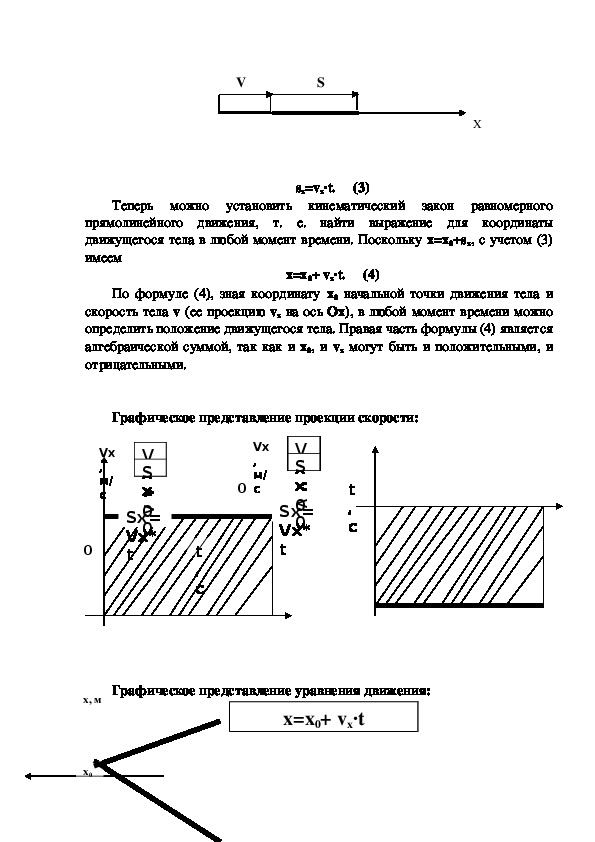 Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
[латекс] v = {v} _ {0} + at. [/ латекс]
Добавление [latex] {v} _ {0} [/ latex] к каждой стороне этого уравнения и деление на 2 дает
[латекс] \ frac {{v} _ {0} + v} {2} = {v} _ {0} + \ frac {1} {2} at.{2} \ enspace (\ text {constant} \, а). [/латекс]
Пример
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью за 5,56 с (рисунок). Как далеко он пролетит за это время?
Рисунок 3. {2}.{2} = 402 \, \ text {m} \ text {.} [/ Latex]
{2}.{2} = 402 \, \ text {m} \ text {.} [/ Latex]
Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут проехать четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.{2} \, \ text {становится} \, x = {x} _ {0} + {v} _ {0} t. [/ латекс]
Решение окончательной скорости на основе расстояния и ускорения
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим [latex] v = {v} _ {0} + at [/ latex] для t , мы получим
[латекс] t = \ frac {v- {v} _ {0}} {a}. [/ латекс]
Подставив это и [латекс] \ overset {\ text {-}} {v} = \ frac {{v} _ {0} + v} {2} [/ latex] в [латекс] x = {x} _ {0} + \ overset {\ text {-}} {v} t [/ latex], получаем
[латекс] {v} ^ {2} = {v} _ {0} ^ {2} + 2a (x- {x} _ {0}) \ enspace (\ text {constant} \, a).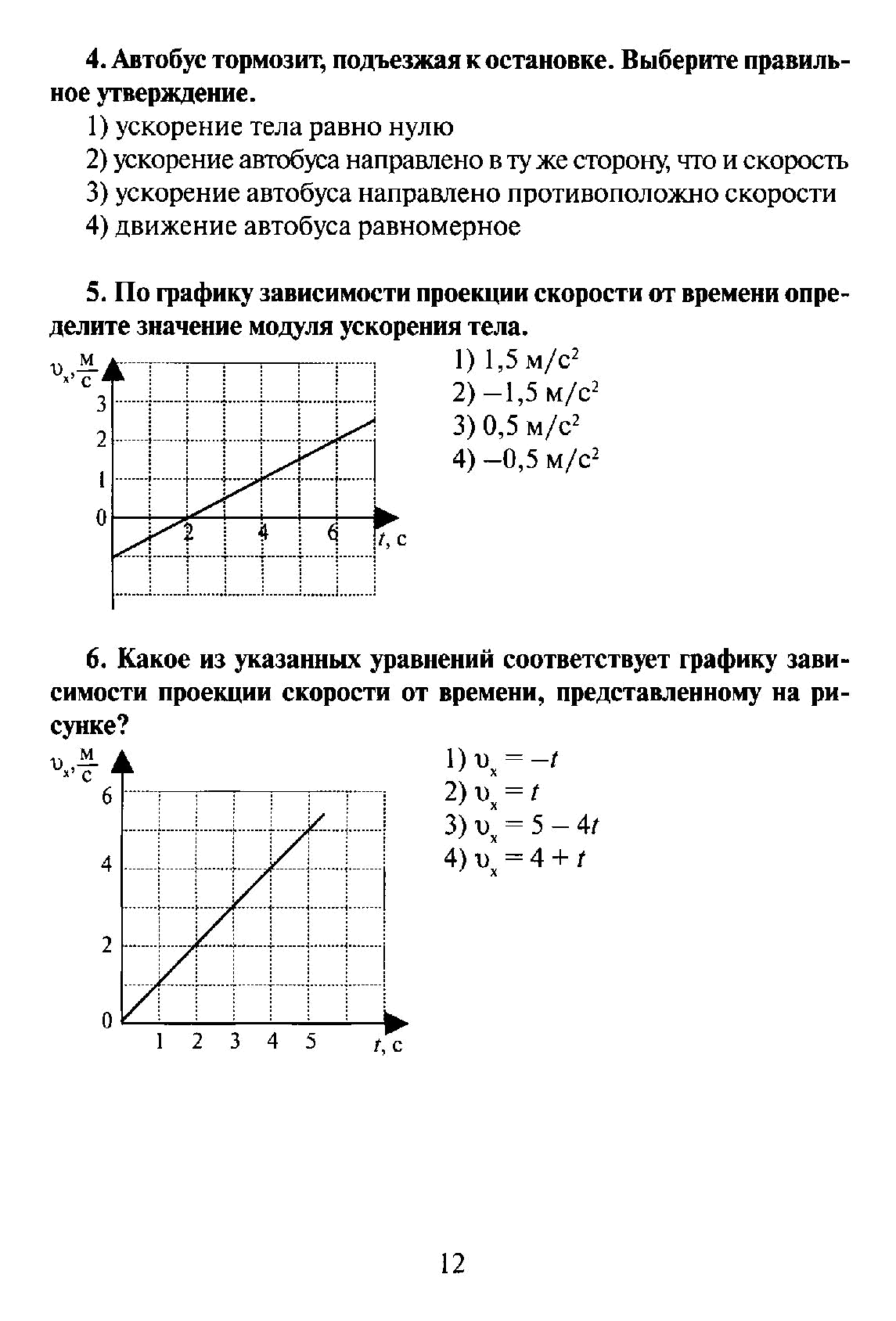 {2} + 2a (x- {x} _ {0}) [/ latex] может дать дополнительную информацию об общих отношениях между физическими величинами:
{2} + 2a (x- {x} _ {0}) [/ latex] может дать дополнительную информацию об общих отношениях между физическими величинами:- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, просто не останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Собираем уравнения
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных. {2}} {2 (x- {x} _ {0})}.[/ латекс]
{2}} {2 (x- {x} _ {0})}.[/ латекс]
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример
Как далеко уезжает машина?
На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может замедляться только со скоростью 5.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, в которой водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.
Стратегия
Сначала нам нужно нарисовать эскиз (рисунок). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рисунок 3.22 Пример эскиза для визуализации замедления и тормозного пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение [латекс] \ text {Δ} x [/ latex], или x — x 0 .{2} + 2a (x- {x} _ {0}). [/ латекс]
Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.
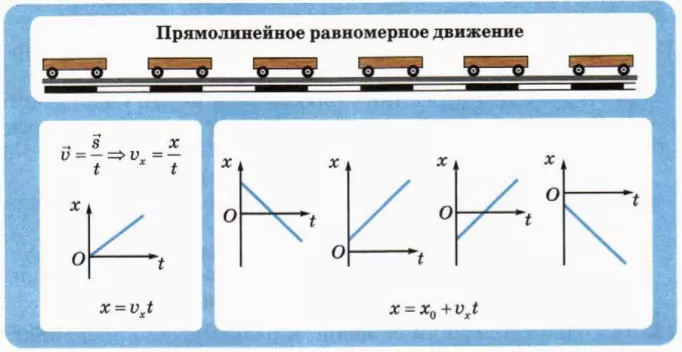 {2} — {(30.{2})}. [/ латекс]
{2} — {(30.{2})}. [/ латекс]Таким образом,
[латекс] x = 64,3 \, \ text {м на сухом бетоне} \ text {.} [/ Латекс]
- Эта часть может быть решена точно так же, как (a). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат
[латекс] {x} _ {\ text {wet}} = 90,0 \, \ text {м на мокром бетоне.} [/ Latex]
- Показать ответ
Когда водитель реагирует, тормозной путь такой же, как в пунктах (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время к времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя. Для этого мы, опять же, определяем известные факторы и то, что мы хотим решить. Мы знаем, что [латекс] \ overset {\ text {-}} {v} = 30.0 \, \ text {m / s} [/ latex], [latex] {t} _ {\ text {response}} = 0.500 \, \ text {s} [/ latex] и [latex] {a} _ {\ text {response}} = 0 [/ latex].
 Считаем [latex] {x} _ {\ text {0-response}} [/ latex] равным нулю. Мы ищем [латекс] {x} _ {\ text {response}} [/latex]. Во-вторых, как и раньше, мы определяем лучшее уравнение для использования.В этом случае [latex] x = {x} _ {0} + \ overset {\ text {-}} {v} t [/ latex] работает хорошо, потому что единственное неизвестное значение — это x, что мы и хотим решите для. В-третьих, мы подставляем известные для решения уравнения: [latex] x = 0 + (30.0 \, \ text {m / s}) (0.500 \, \ text {s}) = 15.0 \, \ text { м}. [/ latex] Это означает, что автомобиль движется на 15,0 м, пока водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции. Наконец, мы затем добавляем смещение во время реакции к смещению при торможении ((Рисунок)), [latex] {x} _ {\ text {braking}} + {x} _ {\ text {response}} = { x} _ {\ text {total}}, [/ latex] и найдите (a) равным 64.3 м + 15,0 м = 79,3 м в сухом состоянии и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Считаем [latex] {x} _ {\ text {0-response}} [/ latex] равным нулю. Мы ищем [латекс] {x} _ {\ text {response}} [/latex]. Во-вторых, как и раньше, мы определяем лучшее уравнение для использования.В этом случае [latex] x = {x} _ {0} + \ overset {\ text {-}} {v} t [/ latex] работает хорошо, потому что единственное неизвестное значение — это x, что мы и хотим решите для. В-третьих, мы подставляем известные для решения уравнения: [latex] x = 0 + (30.0 \, \ text {m / s}) (0.500 \, \ text {s}) = 15.0 \, \ text { м}. [/ latex] Это означает, что автомобиль движется на 15,0 м, пока водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции. Наконец, мы затем добавляем смещение во время реакции к смещению при торможении ((Рисунок)), [latex] {x} _ {\ text {braking}} + {x} _ {\ text {response}} = { x} _ {\ text {total}}, [/ latex] и найдите (a) равным 64.3 м + 15,0 м = 79,3 м в сухом состоянии и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рисунок 3.23 Расстояние, необходимое для остановки автомобиля, сильно варьируется в зависимости от дорожных условий и времени реакции водителя. Здесь показан тормозной путь для сухой и мокрой дороги, рассчитанный в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля. Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важным является общий подход к решению проблем. Мы определяем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример
Время расчета
Предположим, автомобиль выезжает на шоссе на съезде длиной 200 м. Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)
Стратегия
Сначала мы рисуем эскиз (рисунок). Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t .)
Рисунок 3.24 Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Показать ответ Опять же, мы определяем известные и то, что мы хотим решить.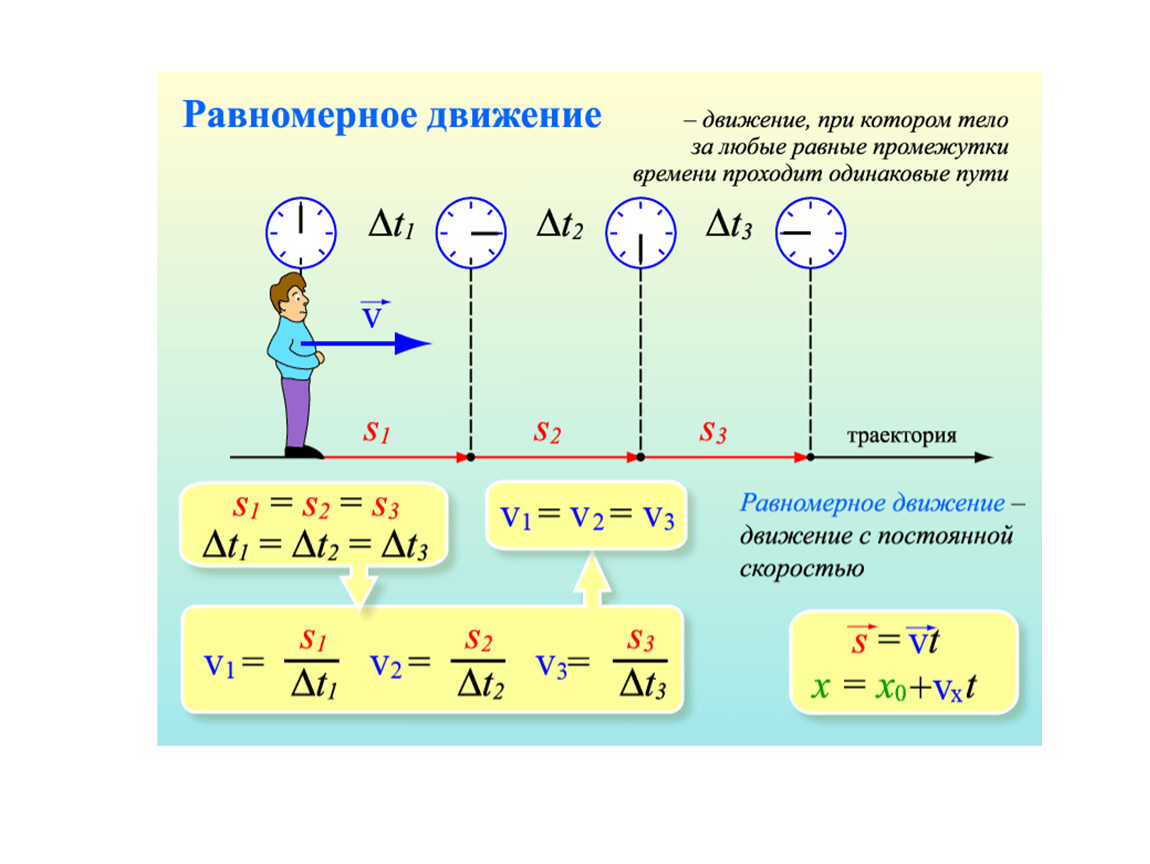 Мы знаем, что [латекс] {x} _ {0} = 0, [/ latex]
Мы знаем, что [латекс] {x} _ {0} = 0, [/ latex][латекс] {v} _ {0} = 10 \, \ text {m / s}, a = 2.{2} -4ac}} {2a}, \ end {array} [/ latex], что дает два решения: t = 10,0 и t = -20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
[латекс] t = 10,0 \, \ text {s} \ text {.} [/ Латекс]
Значение
Каждый раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. 10.Ответ 0 кажется разумным для типичной автострады на съезде.
Проверьте свое понимание
Пилотируемая ракета ускоряется со скоростью 20 м / с 2 во время пуска. Сколько времени требуется ракете, чтобы достичь скорости 400 м / с?
Показать решениеЧтобы ответить на этот вопрос, выберите уравнение, которое позволяет нам решить для времени t , учитывая только a , v 0 и v :
[латекс] v = {v} _ {0} + at. {2}} = 20 \, \ text {s} \ text {.} [/ latex]
{2}} = 20 \, \ text {s} \ text {.} [/ latex]
Пример
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа. Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость.{2}) (120.0 \, \ text {s}) = 9533.3 \, \ text {m / s.} [/ Latex]
Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть нелегкими, например простой заменой одного из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.
Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.
Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики включает движение двух взаимосвязанных тел, называемых задачами преследования двух тел .
Проблемы с преследованием двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче о преследовании двух тел движения объектов связаны — это означает, что искомая неизвестная зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на (Рисунок).
Это показано на (Рисунок).
Рисунок 3.25 Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с. В тот момент, когда газель проезжает мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?
Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно рассмотрим проблему, становится ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку оба они начинаются с [latex] {x} _ {0} = 0 [/ latex], их смещения будут такими же в более позднее время t , когда гепард догонит газель.Если мы выберем уравнение движения, которое решает проблему смещения для каждого животного, мы сможем приравнять уравнения друг к другу и решить неизвестное, то есть время.
Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно рассмотрим проблему, становится ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку оба они начинаются с [latex] {x} _ {0} = 0 [/ latex], их смещения будут такими же в более позднее время t , когда гепард догонит газель.Если мы выберем уравнение движения, которое решает проблему смещения для каждого животного, мы сможем приравнять уравнения друг к другу и решить неизвестное, то есть время.
Решение
- Показать ответ
Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется. Поэтому мы используем (Рисунок) с [latex] {x} _ {0} = 0 [/ latex]: [latex] x = {x} _ {0} + \ overset {\ text {-}} {v} t = \ overset {\ text {-}} {v} t.
 {2}.{2} \ hfill \\ t = \ frac {2 \ overset {\ text {-}} {v}} {a}. \ Hfill \ end {array} [/ latex] Газель имеет постоянную скорость 10 м. / с — его средняя скорость. Ускорение гепарда составляет 4 м / с2. Оценивая t, время, за которое гепард достигает газели, мы имеем [latex] t = \ frac {2 \ overset {\ text {-}} {v}} {a} = \ frac {2 (10)} { 4} = 5 \, \ text {s} \ text {.} [/ Latex]
{2}.{2} \ hfill \\ t = \ frac {2 \ overset {\ text {-}} {v}} {a}. \ Hfill \ end {array} [/ latex] Газель имеет постоянную скорость 10 м. / с — его средняя скорость. Ускорение гепарда составляет 4 м / с2. Оценивая t, время, за которое гепард достигает газели, мы имеем [latex] t = \ frac {2 \ overset {\ text {-}} {v}} {a} = \ frac {2 (10)} { 4} = 5 \, \ text {s} \ text {.} [/ Latex] - Показать ответ
Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны давать одинаковый ответ.{2} = 50 \, \ text {m} \ text {.} [/ Latex] Смещение газели: [латекс] x = \ overset {\ text {-}} {v} t = 10 (5) = 50 \, \ text {m} \ text {.} [/ Latex] Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов. {2} [/ латекс].
{2} [/ латекс].
Сводка
- При анализе одномерного движения с постоянным ускорением определите известные величины и выберите соответствующие уравнения для решения неизвестных. Для решения неизвестных необходимы одно или два кинематических уравнения, в зависимости от известных и неизвестных величин.
- Задачи двухчастичного преследования всегда требуют одновременного решения двух уравнений относительно неизвестных.
Концептуальные вопросы
При анализе движения отдельного объекта, какое количество известных физических переменных необходимо для решения неизвестных величин с использованием кинематических уравнений?
Укажите два сценария кинематики отдельного объекта, в которых три известные величины требуют решения двух кинематических уравнений для неизвестных.
Показать решение Если ускорение, время и перемещение являются известными, а начальная и конечная скорости являются неизвестными, то два кинематических уравнения должны решаться одновременно. Также, если конечная скорость, время и смещение являются известными, тогда необходимо решить два кинематических уравнения для начальной скорости и ускорения.
Также, если конечная скорость, время и смещение являются известными, тогда необходимо решить два кинематических уравнения для начальной скорости и ускорения.
Проблемы
Частица движется по прямой с постоянной скоростью 30 м / с. Каково его смещение между t = 0 и t = 5.0 с?
Частица движется по прямой с начальной скоростью 30 м / с и постоянным ускорением 30 м / с 2 . Если при [latex] t = 0, x = 0 [/ latex] и [latex] v = 0 [/ latex], каково положение частицы при t = 5 с?
Частица движется по прямой с начальной скоростью 30 м / с и постоянным ускорением 30 м / с 2 . (а) Какое у него водоизмещение при т = 5 с? б) Какова его скорость в это же время?
Показать решениеа.525 м;
г. [латекс] v = 180 \, \ text {м / с} [/ латекс]
(a) Постройте график зависимости скорости от времени, соответствующий графику перемещения от времени, представленному на следующем рисунке. (b) Определите время или моменты времени ( t a , t b , t c и т. д.), в которые мгновенная скорость имеет наибольшее положительное значение. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
Показать ответ(a) Постройте график зависимости ускорения от времени, соответствующий графику зависимости скорости от времени, представленному на следующем рисунке.(b) Определите время или моменты времени ( t a , t b , t c и т. д.), в которые ускорение имеет наибольшее положительное значение. (c) В какое время он равен нулю? (г) В какое время он отрицательный?
а.
г. Ускорение имеет наибольшее положительное значение в [latex] {t} _ {a} [/ latex]
г. Ускорение равно нулю на [latex] {t} _ {e} \, \ text {and} \, {t} _ {h} [/ latex]
г.Ускорение отрицательное при [латексе] {t} _ {i} \ text {,} {t} _ {j} \ text {,} {t} _ {k} \ text {,} {t} _ {l } [/ latex]
Частица имеет постоянное ускорение 6,0 м / с 2 . (а) Если его начальная скорость составляет 2,0 м / с, в какое время его смещение составляет 5,0 м? б) Какова его скорость в то время?
При t = 10 с частица движется слева направо со скоростью 5,0 м / с. При t = 20 с частица движется справа налево со скоростью 8.{\ text {-} 4} \, \ text {s} [/ latex]. Какова его начальная скорость (то есть конечная скорость)?
Показать решение[латекс] v = 502.20 \, \ text {m / s} [/ latex]
(a) Пригородный легкорельсовый поезд ускоряется со скоростью 1,35 м / с 2 . Сколько времени нужно, чтобы достичь максимальной скорости 80,0 км / ч, начиная с состояния покоя? (b) Этот же поезд обычно замедляется со скоростью 1,65 м / с 2 . Сколько времени нужно, чтобы остановиться с максимальной скорости? (c) В аварийных ситуациях поезд может замедляться быстрее, останавливаясь после 80.0 км / ч за 8,30 с. Каково его аварийное ускорение в метрах на секунду в квадрате?
При выезде на автостраду автомобиль ускоряется из состояния покоя со скоростью 2,04 м / с 2 за 12,0 с. (а) Нарисуйте набросок ситуации. (б) Перечислите известных в этой проблеме. (c) Как далеко проехала машина за эти 12,0 с? Чтобы решить эту часть, сначала определите неизвестное, а затем укажите, как вы выбрали соответствующее уравнение для его решения. После выбора уравнения покажите свои шаги в решении неизвестного, проверьте свои единицы и обсудите, является ли ответ разумным.{2} = 172.80 \, \ text {m} [/ latex], ответ кажется разумным примерно на 172,8 м; d. [латекс] v = 28,8 \, \ text {м / с} [/ латекс]
Необоснованные результаты В конце забега бегун замедляется со скорости 9,00 м / с со скоростью 2,00 м / с 2 . а) Как далеко она продвинется в следующие 5,00 с? б) Какова ее конечная скорость? (c) Оцените результат. Имеет ли это смысл?
Кровь ускоряется из состояния покоя до 30,0 см / с на расстоянии 1,80 см от левого желудочка сердца.(а) Сделайте набросок ситуации. (б) Перечислите известных в этой проблеме. (c) Как долго длится ускорение? Чтобы решить эту часть, сначала определите неизвестное, затем обсудите, как вы выбрали соответствующее уравнение для его решения. После выбора уравнения покажите свои шаги в решении неизвестного, проверяя свои единицы. (г) Является ли ответ разумным по сравнению со временем биения сердца?
Показать решениеа.
г. Знает: [латекс] v = 30.0 \, \ text {cm} \ text {/} \ text {s,} \, x = 1.{\ text {-} 2} \, \ text {s} [/ latex], на каком расстоянии разгоняется шайба?
Мощный мотоцикл может разогнаться с места до 26,8 м / с (100 км / ч) всего за 3,90 с. а) Какое у него среднее ускорение? б) Как далеко он уйдет за это время?
Показать решениеа. 6,87 с 2 ; б. [латекс] x = 52,26 \, \ text {m} [/ latex]
Грузовые поезда могут развивать только относительно небольшие ускорения. (a) Какова конечная скорость грузового поезда, который ускоряется со скоростью [латекс] 0.{2} [/ latex], как далеко он пролетит, прежде чем взлетит? б) Сколько времени это займет?
Мозг дятла особенно защищен от сильных ускорений связками внутри черепа, похожими на сухожилия. Во время клевания дерева голова дятла останавливается с начальной скорости 0,600 м / с на расстоянии всего 2,00 мм. (a) Найдите ускорение в метрах в секунду в квадрате и кратно g , где g = 9,80 м / с 2 . (b) Рассчитайте время остановки.{2} \ hfill \\ a = 4.08 \, g \ hfill \ end {array} [/ latex]
Неосторожный футболист сталкивается со стойкой ворот с мягкой подкладкой при беге со скоростью 7,50 м / с и полностью останавливается, сжав подушку и свое тело на 0,350 м. а) Каково его ускорение? б) Как долго длится столкновение?
Посылка выпадает из грузового самолета и приземляется в лесу. Если предположить, что скорость посылки при ударе составляет 54 м / с (123 мили в час), то каково ее ускорение? Предположим, деревья и снег останавливают его на расстоянии 3.{2} [/ latex] как проходит. Длина станции 210,0 м. а) Как быстро он движется, когда нос покидает станцию? б) Какова длина носа поезда на станции? (c) Если длина поезда 130 м, какова скорость конца поезда, когда он уходит? (d) Когда поезд отправляется со станции?
Неоправданные результаты Драгстеры могут развить максимальную скорость 145,0 м / с всего за 4,45 с. (а) Рассчитайте среднее ускорение для такого драгстера.(b) Найдите конечную скорость этого драгстера, начиная с состояния покоя и ускоряясь со скоростью, указанной в (a) для 402,0 м (четверть мили), без использования какой-либо информации о времени. (c) Почему конечная скорость больше той, которая использовалась для определения среднего ускорения? ( Подсказка : подумайте, справедливо ли предположение о постоянном ускорении для драгстера. Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.{2} [/ latex] в течение последних нескольких метров, но существенно меньше, и конечная скорость будет меньше, чем [latex] 162 \, \ text {m / s} [/ latex].
Глоссарий
- задача преследования двух тел
- задача кинематики, в которой неизвестные вычисляются путем одновременного решения кинематических уравнений для двух движущихся объектов.
Равномерное круговое движение | MIT OpenCourseWare
Равномерное круговое движение
Материалы курса, относящиеся к этой теме:
Динамика равномерного кругового движения; движение по вертикальному кругу, с примером; конический маятник, с примерами.
Центростремительное ускорение шайбы, движущейся по кругу.
Материалы курса, относящиеся к этой теме:
Скорость и ускорение объекта, движущегося по кругу постоянного радиуса.
Материалы курса, относящиеся к этой теме:
Натяжение веревки, удерживающей камень, движущийся по вертикальной круговой траектории.
Материалы курса, относящиеся к этой теме:
Период вращающегося диска, прикрепленного к пружине.
В начало
Круговое движение
Материалы курса, относящиеся к этой теме:
Равномерное круговое движение; центростремительное ускорение; неравномерное круговое движение; системы отсчета; относительность движения; стратегия решения задач для относительных скоростей с примерами.
Скорость объекта с постоянно меняющимся вектором скорости.
Материалы курса, относящиеся к этой теме:
Положение и перемещение объекта по круговой орбите; величина смещения; величина скорости и угловая скорость; направление скорости; определено тангенциальное ускорение; равномерное круговое движение; период и частота обращения.
Резюме кругового движения с уравнениями; описание вектора кругового движения с помощью уравнений; задачи моделирования кругового движения; анализ ускорения при круговом движении.
Угловая скорость двух жуков на карусели.
Линейное ускорение жука на карусели.
Тангенциальное ускорение жука на карусели.
Ускорение скольжения льда в чаше.
В начало
Угловой момент
Теорема о параллельных осях, с примером; теорема о перпендикулярной оси с примерами; определение момента количества движения частицы; определение центральных сил; угловой момент частицы, движущейся по прямой; угловой момент частицы при равномерном круговом движении; момент количества движения конического маятника.
Материалы курса, относящиеся к этой теме:
В начало
Снаряд и круговое движение
Уравнения движения снаряда; уравнения кругового движения; центростремительное ускорение с уравнением; метод размерного анализа.
Материалы курса, относящиеся к этой теме:
В начало
Обзор круговой динамики
Вектор положения круговой орбиты; угловая скорость и тангенциальная скорость; радиальное ускорение; равномерное круговое движение; неравномерное круговое движение; сравнение линейного и кругового движения при постоянном ускорении; стратегия решения задач с использованием кругового движения.
Материалы курса, относящиеся к этой теме:
В начало
Обзор вращательной кинематики
Кинематика вращения с фиксированной осью, с определениями угловой скорости, углового ускорения, тангенциальной скорости, тангенциального ускорения и радиального ускорения.
Материалы курса, относящиеся к этой теме:
В начало
Модель самолета на проводе
Задача из 3 частей; расчет натяжения проволоки, критического угла и безопасной скорости полета.
Материалы курса, относящиеся к этой теме:
В начало
Бусина скользящая на проволоке
Задача из 3 частей; определение нормальной силы проволоки и высоты борта на обратном пути.
Материалы курса, относящиеся к этой теме:
В начало
Круговое движение с гравитацией
Силы и ускорение объектов, движущихся по вертикальным круговым траекториям.
Материалы курса, относящиеся к этой теме:
В начало
Угловая скорость
Относительная угловая скорость двух объектов в разных точках карусели.
Материалы курса, относящиеся к этой теме:
В начало
Вихревые объекты
Силы, действующие на два тела, вращающихся вокруг вала с постоянной угловой скоростью.
Материалы курса, относящиеся к этой теме:
В начало
Круговое движение внутри конуса
Движение объекта по круговой орбите внутри конуса.
Материалы курса, относящиеся к этой теме:
В начало
Автомобиль на повороте
Определение скорости, необходимой для предотвращения скольжения автомобиля на крутом повороте.
Материалы курса, относящиеся к этой теме:
В начало
Модель самолета U-Control
Движение самолета, привязанного к фиксированной точке.
Материалы курса, относящиеся к этой теме:
В начало
Круговое движение и сохранение механической энергии
Движение объекта по петлеобразной траектории без трения.
Материалы курса, относящиеся к этой теме:
В начало
Бусины скользящие по кольцу
Силы, действующие на подвесное кольцо со скользящими бортами.
Материалы курса, относящиеся к этой теме:
В начало
Система кругового движения и системы отсчета
Движение мяча, брошенного из карусели.
Материалы курса, относящиеся к этой теме:
В начало
Центростремительная сила и трение
Минимальная угловая скорость, необходимая для «бочки веселья».
Материалы курса, относящиеся к этой теме:
В начало
Неравномерное круговое движение
Скорость объекта, движущегося по круговой траектории с неравномерным ускорением.
Материалы курса, относящиеся к этой теме:
В начало
Ускорение кругового движения
Направление вектора ускорения объекта, движущегося по кругу с возрастающей скоростью.
Материалы курса, относящиеся к этой теме:
В начало
Центростремительная сила
Материалы курса, относящиеся к этой теме:
Силы, действующие на пассажира автомобиля, совершающего круговой поворот.
Источник центростремительной силы шара, движущегося на поворотной платформе тележки.
В начало
Центростремительное ускорение
Материалы курса, относящиеся к этой теме:
Силы, способные вызывать центростремительное ускорение.
Ускорение движения шайбы по равномерному кругу на столе.
Ускорение движения шайбы по равномерному кругу на столе с более коротким плечом рычага.
В начало
Автокатастрофа
Определение вращательного движения разбитой машины.
Материалы курса, относящиеся к этой теме:
В начало
Вертикальное круговое движение
Натяжение тетивы, удерживающей шар, качаясь по вертикальному кругу.
Материалы курса, относящиеся к этой теме:
В начало
Велосипедная шина
Материалы курса, относящиеся к этой теме:
Скорость точки на внешней стороне шины по отношению к скорости центра масс.
Относительные скорости точек на внешней стороне катящейся шины.
Направление движения точек на внешней стороне катящейся шины.
В начало
Поворотный стол
Силы, действующие на куб, лежащий на вращающейся платформе.
Материалы курса, относящиеся к этой теме:
В начало
Вращающийся шар
Натяжение струн при подвешивании шара к вращающемуся вертикальному стержню.
Материалы курса, относящиеся к этой теме:
В начало
Прокатка и работа
Работа, проделанная с шариком, катящимся по спирали по внутренней части полого цилиндра.
Материалы курса, относящиеся к этой теме:
В начало
Эксперимент 4 Предварительная лаборатория
Определение жесткости пружины; определение радиуса объекта при равномерном круговом движении.
Материалы курса, относящиеся к этой теме:
В начало
Кинематика вращения
Скорость и центростремительное ускорение человека на поверхности Земли.
Материалы курса, относящиеся к этой теме:
В начало
Поворот с наклоном
Движение автомобиля, пересекающего крутой поворот.
Материалы курса, относящиеся к этой теме:
В начало
Тетербол
Движение мяча, подвешенного на веревке и движущегося по вертикальной окружности.
Материалы курса, относящиеся к этой теме:
В начало
Круговая гоночная трасса
Максимальная скорость перед заносом автомобиля по фрикциону для двух разных масс; Угловая скорость.
Материалы курса, относящиеся к этой теме:
В начало
Круговое движение автомобиля
Движение автомобиля по внутренней части полого конуса.
Материалы курса, относящиеся к этой теме:
В начало
Удочка и масса
Динамика системы массы, подвешенной к вертикальному спиннингу на струне и шкиве.
Материалы курса, относящиеся к этой теме:
В начало
Равновесие бегуна
Силы и моменты, действующие на бегунок, огибающий круговую дорожку.
Материалы курса, относящиеся к этой теме:
В начало
Круговое движение в конусе
Задача из 4 частей; построение диаграммы свободного тела и нахождение v, T объекта; максимальная скорость с трением.
Материалы курса, относящиеся к этой теме:
В начало
Экспериментальная центростремительная сила
Нахождение ω, T, f для гайки, вращающейся вокруг оси на конце резинки.
Материалы курса, относящиеся к этой теме:
В начало
Мяч в вертикальном круге
Скорость и напряжение в верхней части круга для качания мяча.
Материалы курса, относящиеся к этой теме:
В начало
Остался на астероиде
Задача из 4 частей; нахождение сжатия, необходимого для вывода пера на орбиту; скорость и радиус на орбите.
Материалы курса, относящиеся к этой теме:
В начало
Ведро для воды
Движение ведра с водой по вертикальному кругу.
Материалы курса, относящиеся к этой теме:
В начало
Сохранение энергии
Кинематика и динамика привязанного шара, движущегося по вертикальной окружности.
Материалы курса, относящиеся к этой теме:
В начало
Равномерное движение — определение равномерного движения в The Free Dictionary
Мотивация, лежащая в основе этой статьи, заключалась в том, чтобы реализовать метод слепого удаления размытия, который полагается только на естественные предположения: PSF присутствует на всем изображении (ограничивая подход к равномерному размытию движения), и изображение содержит достаточную неповторяющуюся информацию (небольшой узор, который присутствует на всем изображении, может быть ошибочно принят за ядро).Закон гласит, что «объект будет оставаться в покое или в равномерном движении по прямой, если на него не действует внешняя сила». По словам самого великого человека, они следующие: (1) Каждый объект остается в своем состоянии покоя или однородности. движение по прямой, если только оно не вынуждено изменить это состояние под действием приложенных к нему сил; (2) Сила равна изменению количества движения за изменение во времени. Наиболее распространенными движениями летательного аппарата являются равномерное и ускоренное движение, в этой статье в основном анализируется влияние ошибок акселерометра на погрешность положения и погрешность скорости в этих двух типах. движения.Самый простой случай — это равномерное движение из заданных начальных положений (раздел 2.2). Его регулируемые клапаны уменьшили потери тепла и позволили двигателю работать с более равномерным движением, одновременно снижая затраты на топливо … каждый объект будет оставаться в покое или в неподвижном состоянии. равномерное движение по прямой, если только его не заставляют изменить свое состояние под действием внешней силы. Чанг и Ву предложили новый метод деконволюции для устранения размытости изображения с равномерным размытием движения с использованием априорных гиперлапласовских параметров [13].Сделано простое приближение к распределению времен пересечения (индуцированного диффузией), однако предполагается равномерное движение поперек интерференционного поля. Условие поддержания равномерного движения без эффекта вращения сосуда может быть реализовано из условия равенства моментов и сил по обе стороны от базовой тележки (центр масс). Исследователи использовали две разные области физики: специальную теорию относительности Эйнштейна, которая интерпретирует равномерное движение между двумя объектами, движущимися с относительной скоростью, в сочетании с силой квантовой теории, новой физикой субатомный мир, который Эйнштейн назвал «жутким».Бесконечный эллиптический радиус двойной поверхности обеспечивает равномерное движение электрона по орбите атома.Первый закон Ньютона, примененный к воздушному змею
| Эта страница предназначена для учащихся колледжей, старших и средних школ. Для младших школьников более простое объяснение информации на этой странице: доступно на Детская страница. |
Сэр Исаак Ньютон впервые представил свои три закона движения в «Principia Mathematica Philosophiae Naturalis» 1686 г. Его первый закон заявляет, что каждый объект будет оставаться в покое или в равномерном движении по прямой линия, если она не вынуждена изменить свое состояние под действием внешней силы. Обычно это определение инерции . Ключевой момент здесь состоит в том, что при отсутствии чистой силы в результате несбалансированного силы, действующие на объект (если все внешние силы нейтрализуют друг друга), тогда объект будет поддерживать постоянную скорость .Если эта скорость равна нулю, тогда объект остается в покое. А если приложить дополнительную внешнюю силу, скорость изменится из-за силы. Величина изменения скорости определяется вторым законом движения Ньютона.
А воздушный змей, летящий через воздух — хороший пример этого принципа. В силы действующие на воздушном змее в полете включают масса, аэродинамический лифт и тащить, и напряжение в линия управления.В стабильном полете все эти силы уравновешены, и кайт удерживает фиксированную высота. Вертикальная скорость воздушного змея равна нулю. Если ветер немного усиливается, подъемная сила и сопротивление увеличиваются, потому что аэродинамические силы зависят от квадрата скорость. Силы на кайте больше не сбалансирован, и на кайте действует чистая вертикальная сила . Кайт движется вертикально, потому что подъемная сила теперь превышает вес и вертикальная составляющая натяжения в контрольной линии.Когда кайт набирает высоту, сила натяжения увеличивается из-за увеличения подъемной силы и тащить. Сила натяжения — это векторная величина и мы можем разрешить усилие на горизонтальное и вертикальное натяжение . По мере увеличения силы натяжения вертикальная тяга увеличивается.

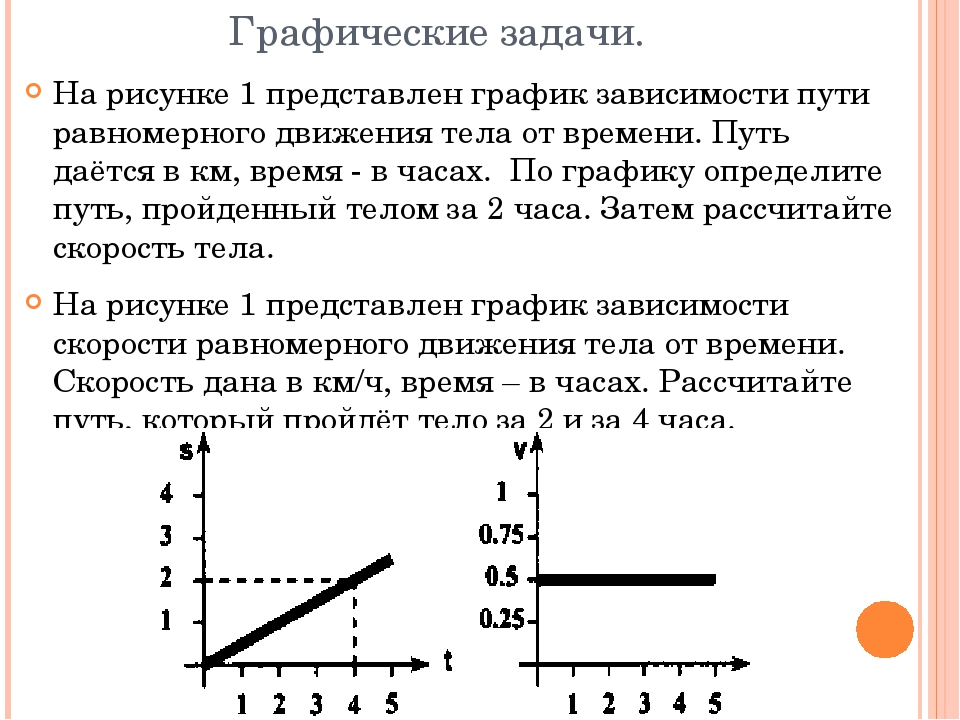 Когда один из компонентов линейной направляющей не соединен должным образом ни с основанием, ни с кареткой, движение не будет ускорено.
Когда один из компонентов линейной направляющей не соединен должным образом ни с основанием, ни с кареткой, движение не будет ускорено.