Производная 10 класс контрольная работа: Контрольная работа по теме «Вычисление производных «10 класс (разноуровневые)

Содержание

Контрольная работа по теме «Вычисление производных «10 класс (разноуровневые)

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 1.

1.Найдите производные функций f(x), если

a) f(x) =6х¹⁰-1; б) f(x) = 12 х⁷+ 17х³; в) f(x) =11х⁶ +5 х ^-24 – 2х³;

г) f(x) =(3x-14)∙(3х² +5)

д) f(x)= -3 sin(5х-6) + 12х²; e); ж) ; з)

2.Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 3х -2)⁷ ; б) f(x)=( 6-4х)¹¹; в).

3. Тело, масса которого 63 кг, движется прямолинейно по закону S(x) = 25х-2х². Рассчитайте силу, действующую на тело и кинетическую энергию через 3 секунды.

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 2.

1.Найдите производные функций f(x), если

a) f(x) =4х⁷-13; б) f(x) = 5 х¹²+ 12х⁶; в) f(x) =14х³ +5 х ^-12 – 2х⁸;

г) f(x) =(9x-4)∙(8х² +3)

д) f(x)= -2 cos(7х-1) + 9х²; e); ж) ; з)

2.Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 4х -5)⁶ ; б) f(x)=( 3-2х)²¹; в).

3. Тело, масса которого 35 кг, движется прямолинейно по закону S(x) = 12х+5х². Рассчитайте силу, действующую на тело и кинетическую энергию через 3 секунды.

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 3.

1.Найдите производные функций f(x), если

a) f(x) =15х⁸-7; б) f(x) = 45 х⁹+ 17х³; в) f(x) =4х⁶ +7 х ^-12 – х³;

г) f(x) =(4x-11)∙(х² -5)

д) f(x)= 5 sin(5х-8) + 13х²; e); ж) ; з)

2. Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 7х -5)³ ; б) f(x)=( 9+4х)¹⁵; в).

3. Тело, масса которого 12 кг, движется прямолинейно по закону S(x) = 49х+2х

2. Рассчитайте силу, действующую на тело и кинетическую энергию через 3 секунды.

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 4.

1.Найдите производные функций f(x), если

a) f(x)=х⁷-13х⁵+24х²+102; б) f(x) = 4х⁷+ 9х³; в) f(x) =19х³ +6 х ^-9 – 4х¹⁵;

г) f(x) =(18x-1)∙(х² +2)

д) f(x)= 5cos( 2X+1) + 4X²; e); ж) ; з)

2.Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 5-6х)⁶ ; б) f(x)=( 1-х)²¹; в).

3. Тело, масса которого 72 кг, движется прямолинейно по закону S(x) = 56х-4х². Рассчитайте силу, действующую на тело и кинетическую энергию через 3 секунды.

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 1.

1.Найдите производные функций f(x), если

a) f(x) =6х¹⁰-1; б) f(x) = 12 х⁷+ 17х³; в) f(x) =11х⁶ +5 х ^-24 – 2х

г) f(x) =(3x-14)∙(3х² +5)

д) f(x)= -3 sin(5х-6) + 12х²; e); ж) ; з)

2.Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 3х -2)⁷ ; б) f(x)=( 6-4х)¹¹; в).

4. Составить уравнение касательных к графикам функций

а) в точке х₀=2

б) в точке х₀= -1

5. Определить, какой угол (тупой или острый) образует с положительным направлением оси

х касательная к графику функции у=f(х), проведенная в точке с абсциссой х₀

а)у=-х²-7х+8 в точке х₀=1

б) в точке х₀=2

в) в точке х₀= -1

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 2.

1.Найдите производные функций f(x), если

a) f(x) =4х⁷-13; б) f(x) = 5 х¹²+ 12х⁶; в) f(x) =14х³ +5 х ^-12 – 2х⁸;

г) f(x) =(9x-4)∙(8х² +3)

д) f(x)= -2 cos(7х-1) + 9х²; e); ж) ; з)

2.Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 4х -5)⁶ ; б) f(x)=( 3-2х)²¹; в).

4. Составить уравнение касательных к графикам функций

а) в точке х₀=2

б) в точке х₀= -1

5. Определить, какой угол (тупой или острый) образует с положительным направлением оси х касательная к графику функции у=f(х), проведенная в точке с абсциссой х

а)у=-х²-6х+4 в точке х₀=-1

б) в точке х₀=8

в) в точке х₀= 1

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 3.

1.Найдите производные функций f(x), если

a) f(x) =15х⁸-7; б) f(x) = 45 х⁹+ 17х³; в) f(x) =4х⁶ +7 х ^-12 – х³;

г) f(x) =(4x-11)∙(х² -5)

д) f(x)= 5 sin(5х-8) + 13х²; e); ж) ; з)

2.Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 7х -5)³ ; б) f(x)=( 9+4х)¹⁵; в).

3. Тело, масса которого 12 кг, движется прямолинейно по закону S(x) = 49х+2х². Рассчитайте силу, действующую на тело и кинетическую энергию через 3 секунды.

4. Составить уравнение касательных к графикам функций

а) в точке х₀=4

б) в точке х₀= -1

5. Определить, какой угол (тупой или острый) образует с положительным направлением оси х касательная к графику функции у=f(х), проведенная в точке с абсциссой х₀

а)у=-3х

2-5х+7 в точке х₀=1

б) в точке х₀=2

в) в точке х₀= 0

Алгебра 10 класс.

Контрольная работа №2. по теме « Вычисление производных»

Вариант 4.

1.Найдите производные функций f(x), если

a) f(x)=х⁷-13х⁵+24х²+102; б) f(x) = 4х⁷+ 9х³; в) f(x) =19х³ +6 х ^-9 – 4х¹⁵;

г) f(x) =(18x-1)∙(х² +2)

д) f(x)= 5cos( 2X+1) + 4X²; e); ж) ; з)

2. Найдите производные функции f(x) и вычислите их значения при х = 1 и х =0

a) f(x)=( 5-6х)⁶ ; б) f(x)=( 1-х)²¹; в).

4. Составить уравнение касательных к графикам функций

а) в точке х₀=2

б) в точке х₀= -1

а)у=-3х²-5х+4 в точке х₀=-1

б) в точке х₀=5

в) в точке х

0= 1

Контрольная работа «Производная. Геометрический и механический смысл производной» 10 класс

5 вариант

1. Найдите производные функций:

а) f(x) = 5х

+ 3х

– 8х – 9; б) g(x) = ;

в) q(x) = ; г) u(x) = sin 5x

2. Точка движется по закону х(t)=t3-1 Найдите

ускорение точки в момент времени 2сек.

3. Найдите угол наклона касательной к графику

функции f(x)= в точке х

4. напишите уравнение касательной к графику

функции f(x) = x

-1 в точке х

=-1. Сделайте рисунок

5. На рисунке изображены

график функции и

касательная к нему в точке

с абсциссой . Найдите

значение производной

функции в точке

6.Решите

неравенство:(х

+х-6) < 0

6 вариант

1. Найдите производные функций:

а) f(x) = 3х

+ 2х

– 4х – 3; б)g(x) = ;

в) q(x) = ; г) u(x) = cos 4x 2. Точка движется

по закону х(t)= t

+5t Найдите, в какой момент

времени скорость была равна 32м/с

3. Найдите угол наклона касательной к графику

функции f(x)=sinx-7 в точке х

=2π

4. напишите уравнение касательной к графику

функции f(x) = x

+2x в точке х

=1. Сделайте рисунок

5. На рисунке

изображены график

функции и

касательная к нему в

точке с абсциссой .

Найдите значение

производной функции

в точке

6. Решите неравенство: (х

-1) ≥ 0

7 вариант

1. Найдите производные функций:

а) f(x) = х

+ 3х

– х – 4; б) g(x) = ;

в) q(x) = ; г) u(x) = sin 5x

2. Точка движется по закону х(t)= t

+1 Найдите

скорость точки в момент времени 1сек.

3. Найдите угол наклона касательной к графику

функции f(x)= в точке х

4. напишите уравнение касательной к графику

функции f(x) = x

+3 в точке х

=1. Сделайте рисунок

5. На рисунке

изображены

график

функции

касательная к

нему в точке с

абсциссой .

Найдите

значение производной функции в точке

6. Решите неравенство: (х+1) < 0

8 вариант

1. Найдите производные функций:

а) f(x) = — 2х

+ х

– 3; б)g(x) = ;

в) q(x) = ; г) u(x) = cos 4x

2. Точка движется по закону х(t)=2t

+1 Найдите в

какой момент времени ускорение было 48м/с

3. Найдите угол наклона касательной к графику

функции f(x)= в точке х

4. напишите уравнение касательной к графику

функции f(x) = 0,5x

-2x в точке х

=1. Сделайте

рисунок

5. На рисунке

изображены

график функции

касательная к

нему в точке с

абсциссой .

Найдите значение

производной функции в точке

6. Решите неравенство: (х+1) ≤ 0

«Производная. Механический и геометрический смысл производной».

Всероссийский дистанционный конкурс для учителей математики «Контрольная работа в формате теста»

11 класс

Алгебра и начала математического анализа

Разработала: учитель математики

ГБОУ РО НШИ с ПЛП М.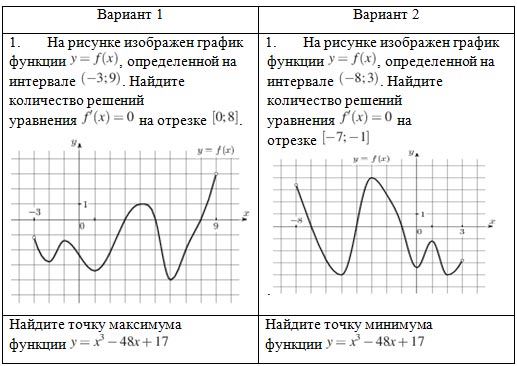 В. Франк

Контрольная работа в формате теста по теме:

«Производная. Геометрический и механический смысл производной».

КИМ

Инструкция по выполнению работы

Время выполнения работы 40 мин. Задания выполняются в КИМе.

Работа состоит из двух частей и содержит 10 заданий.

Часть I содержит 7 заданий базового уровня. Задания части I считаются выполненными, если учащийся правильно заполнил пропуски (в заданиях I-II) и записал верный ответ в виде числа или полное решение (в заданиях III — V), а в заданиях VI – VII — верно установил соответствие.

Часть II содержит 3 задания, соответствующих уровню возможностей и доступных учащимся, хорошо успевающим по математике. При выполнении задания VIII надо установить соответствие между элементами четырёх множеств, а в заданиях IX — X записать полное решение и ответ.

При этом реализуется основной принцип итоговой аттестации: успешное выполнение заданий второй части работы не компенсирует отсутствие результата выполнения заданий первой части. Оценивание осуществляется способом «сложения». Система оценивания 5 – балльная.

Оценочная таблица:

№ задания I II III IV V VI VII VIII IX X Итого Балл 4 4 1 2 1 5 2 5 2 4 30

Таблица перевода тестовых баллов в оценку:

Тестовый балл Оценка

1-10 «2»

11- 15	«3»
16-21	«4»
22-30	«5»

Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Удачи!

* С данной инструкцией необходимо ознакомить школьников до проведения контрольной работы. Инструкция и текст работы выдаются каждому учащемуся.

Ф. И учащегося

Класс

Дата

Часть 1.

I. Продолжите утверждения так, чтобы получились верные высказывания:

1) Процесс нахождения производной называется …

2) Значение производной функции в точке х₀показывает …

3) Мгновенной скоростью называется …

4) Геометрический смысл производной состоит в том, что производная функции в точке

есть …

Итого: 4 балла

II. Вставьте пропущенные выражения так, чтобы получились верные правила дифференцирования:

1) … = С f^/(х)

2) (f(x)+g(x))^/ = …

3) … = f^/(х)g(x) + f(x)g^/(х)

4) ….

Итого: 4 балла

III. Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Средняя скорость движения точки в (м/с) равна …

Ответ: 1,6 м/с

Итого: 1 балл

IV. Материальная точка движется прямолинейно по закону x(t) = — t⁴ + 6t³ + 5t + 23, её скорость в (м/с) в момент времени t = 1 c, равна:

Решение:

Ответ:

Итого: 2 балла

V. Укажите, для какой функции:

1) = ; 2) = ;

3) = ; 4) =

функция = является производной.

Ответ:

Итого: 1 балл

VI. Установите соответствие между функцией и её производной: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

f ( x) (функция)	f ^/( x) (производная функции)
1. 2х² + 5 х — 47	1.
2. х ^{– 5}— 7х	2. — 60(2 – 5 х)¹¹
3. +	3.
4. х⁵+1/х	4. 4х + 5
5.	5. (х²+8) + 2х (х-2)
6. (х-2)(х²+8)	6.
7.	7. -5х ^{– 6}— 7
8. —	8.
9. (2 – 5 х)¹²	9.
10. 2^х + tgx — lnx	10. 5х⁴— 1\x²

В таблице под каждой цифрой, соответствующей функции, укажите номер её производной

Ответ:

Итого: 5 баллов

VII. Установите соответствия между графиками функций и значениями производных в точке х₀.

Графики функций.

A. B. C.

Значения производных:

1) 0,25; 2) -1; 3) 0,5; 4) — 0,25.

В таблице под каждой буквой, соответствующей графику, укажите номер её значения

Ответ:

Итого: 2 балла

Часть 2.

VIII. Установите соответствие между функцией ⇒ графиком функции ⇒ производной ⇒ графиком производной функции.

Функция: 1. у = х³; 2. у = — 3; 3. у = х² – 2; 4. у = — 2х + 5; 5. у = — 1\х

График функции:

1. 2. 3. 4.

Производная функции: 1. у^/ = 2х; 2. у^/ = 3х²; 3. у^/ = 1\х² ;

4. у^/ = 0; 5. у^/ = — 2.

График производной функции:

1.23.

4. 5.

В таблице под каждой цифрой, соответствующей функции, укажите номер её графика, затем укажите номер производной этой функции и номер графика, соответствующий графику производной.

Ответ:

Итого: 5 баллов

IX. Прямая f(x) = — 4х — 11 является касательной к графику функции . Абсцисса точки касания равна

Решение:

Ответ:

Итого: 2 балла

X. Прямая у = 6х – 5 является касательной к графику функции

f(x) = 9х2 + bх + 76 . Найдите b, учитывая, что абсцисса точки касания меньше 0.

Решение:

Ответ:

Итого: 4 балла

Задания контрольной работы в формате теста предназначены для проверки уровня знаний, умений и навыков по теме: «Производная. Механический и геометрический смысл производной» и соответствуют теории в пределах учебного материала.

Тест позволяют оценить достигнутый уровень усвоения материала учеником и зону его ближайшего развития.

Данная работа может помочь выпускникам и при подготовке к ЕГЭ. Задания по этой теме включены как в КИМы профильного уровня, так и в КИМы базового уровня.

В тесте использованы задания из открытого банк заданий ЕГЭ (базовый и профильный уровень) и сайта «Решу ЕГЭ».

http://os.fipi.ru/tasks/2/a

Ключи к контрольной работе в формате теста

Часть 1.

I. Продолжите утверждения так, чтобы получились верные высказывания:

1) Процесс нахождения производной называется … дифференцированием

2) Значение производной функции в точке х₀показывает … скорость изменения функции

3) Мгновенной скоростью называется … производная от пути по времени

4) Геометрический смысл производной состоит в том, что производная функции в точке

есть …угловой коэффициент касательной к графику функции в этой точке

II. Вставьте пропущенные выражения так, чтобы получились верные правила дифференцирования:

1) = С f^/(х)

2) (f(x) + g(x))^/ = f^/(x) + g^/(x)

3) (f(x)g(x))^/ = f^/(x)g(x) + f(x)g^/(x)

III. Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Средняя скорость движения точки в (м/с) равна 1,6 м\с.

Решение.

Чтобы найти среднюю скорость движения точки, необходимо пройденное расстояние поделить на время прохождения: 8:5 = 1,6 м/с

Ответ: 1,6 м\с.

IV. Материальная точка движется прямолинейно по закону

x(t) = — t⁴ + 6t3 + 5t + 23, её скорость в (м/с) в момент времени t = 1 c, равна:

Решение: x^/(t) = — 4t³ + 18t² + 5, x^/(1) = -4 + 18 +5 = 19

Ответ: 19 м/с.

V. Укажите, для какой функции:

1) = ; 2) = ;

3) = ; 4) =

функция = является производной.

Ответ: 4

f ( x) (функция)	f ^/( x) (производная функции)
1. 2х² + 5 х — 47	1.
2. х^{– 5}— 7х	2. — 60(2 – 5 х)¹¹
3. +	3.
4. х⁵+1/х	4. 4х + 5
5.	5. (х²+8) + 2х (х-2)
6. (х-2)(х²+8)	6.
7.	7. -5х ^{– 6}— 7
8. —	8.
9. (2 – 5 х)¹²	9.
10. 2^х+ tgx — lnx	10. 5х⁴— 1\x²

В таблице под каждой цифрой, соответствующей функции, укажите номер её производной

Ответ:

1	2	3	4	5	6	7	8	9	10
4	7	8	10	1	5	3	6	2	9

VII. Установите соответствия между графиками функций и значениями производных в точке х₀.

Графики функций.

A. B. C.

Значения производных:

1) 0,25; 2) -1; 3) 0,5; 4) — 0,25.

В таблице под каждой буквой, соответствующей графику, укажите номер её значения

Ответ:

Часть 2.

Функция: 1. у = х³; 2. у = — 3; 3. у = х² – 2; 4. у = — 2х + 5; 5. у = — 1\х

График функции:

1. 2. 3. 4.

Производная функции:

1. у^/ = 2х; 2. у^/ = 3х²; 3. у^/ = 1\х² ; 4. у^/ = 0; 5. у^/ = — 2

График производной функции:

1.23.

4. 5.

Ответ:

1	2	3	4	5
5	1	3	2	4
2	4	1	5	3
3	5	4	1	2

IX. Прямая f(x) = — 4х — 11 является касательной к графику функции . Абсцисса точки касания равна

Решение: f^/(x) = -4; у^/ = 3х² + 14х +7, f^/(x)= у^/,

3х² + 14х +7 = — 4, 3х² + 14х +11 = 0, D = 196 – 132 = 64, х₁= — 1, х₂ = — 11\3 .

Ответ: — 1; — 11\3 .

X. Прямая у = 6х – 5 является касательной к графику функции f(x) = 9х² + bх + 76 . Найдите b, учитывая, что абсцисса точки касания меньше 0.

Решение: f^/(x)= у^/

18х + b = 6, b = 6 — 18х,

у = f(x), 9х² + х (6 — 18х) + 76 = 6х – 5, 9х² + 6х – 18 х² – 6х + 81 = 0,

— 9х² + 81 = 0,

х²= 9,

х₁ = + 3, х₂= -3

Ответ: — 3

▶▷▶ контрольная работа по математике за 10 класс по теме производная

контрольная работа по математике за 10 класс по теме производная — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа по теме » Производная » ( 10 класс ) infourokru/kontrolnaya_rabota_po_teme Cached Контрольная работа по теме : » Производная » 10 класс № i вариант ii вариант 1 Найдите значение производной функции в точке Контрольная работа по теме :» Производная » (11 класс ) infourokru/kontrolnaya-rabota-po Cached Контрольная работа №3 по теме : « Производная » Вариант №1 b 1 Функция определена на промежутке Контрольная работа по Алгебре » Производная функции и её globuss24ru/doc/kontrolynaya-rabota-po-algebre Cached Контрольная работа по теме « Производная функции и её применение» ориентирована на учебник ШААлимова и др «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и Контрольные работы по алгебре 10 класс , контрольные по mathematics-testscom/algebra- 10 -klass/ Cached Дополнительные материалы по алгебре Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Контрольная работа по теме » Производная » в формате ЕГЭ pedportalnet/starshie-klassy/algebra/ Cached Контрольная работа по алгебре 10 класса по теме » Производная и её применение» Работа составлена в 2 вариантах в формате ЕГЭ Производная , введение и определение в 10 классе по алгебре mathematics-testscom/algebra- 10 -klass-urok Cached Производная , введение и определение урок и презентация в 10 классе по по математике Контрольная работа по алгебре на тему производная 10 класс с dankonoycom/ege2016/kontrolnaya-rabota-po Cached Контрольная работа по алгебре на тему производная 10 класс с ответами скачать 08122016 Алгебра 10 класс , Без рубрики Комментарии: 0 Конспект урока по теме » Производная » по алгебре 10 класс urokimatematikiru/konspekt-uroka-po-teme Cached Контрольная работа по теме «Применение производной», 10 кл 21052017 1922 0 Туынды тақырыбын қайталау ( 10 сынып) Контрольная работа по математике 11 класс первообразная krysadclijadfileswordpresscom/2015/05/ контрольная работа11клdocx 11 класс контрольная работа по математике производная Производная и первообразная логарифмической функцииУчебник по Алгебре за 10 класс Контрольная работа по алгебре 11 класс колмогоров docplayerru/64559499-Kontrolnaya-rabota-po Cached Входная контрольная работа по математике 10 класс мордкович Итоговая контрольная работа по алгебре и началам анализа в 10 классе итоговая работа по математике за 8 класс к учебникам АГ Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 12,000 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

контрольная работа по математике за 10 класс по теме производная — Все результаты Контрольная работа по алгебре и началам анализа по теме › Математика 13 июн 2017 г — материалов Контрольная работа « Производная » вариант 1 1 Исследовать функцию на монотонность : а) у= х 3 + 4х 2 -3х б) у = 0,5х 4 – 4х 2 в) у = Контрольная 5)у= 6) у= 7) у=(9х– 7) 10 8) у= cos5x + 9) у=(х 4 — 1)(3х 2 + 2) 2 Найти указав свой предмет (категорию), класс , учебник и тему : Контрольная работа по алгебре на тему: «Производная» 10 класс › Математика 10 апр 2017 г — Контрольная работа по теме : “ Производная ” 10 класс Вариант 1 Часть 1 А1 Найдите производную функции А2 Найдите значение Контрольная работа по алгебре 10 класс «Производная › Математика Похожие Cкачать: Контрольная работа по алгебре 10 класс » Производная Презентация по математике на тему «Умножение рациональных чисел» 05012016 Зачет по теме «Производная», 10 класс — Урокрф Похожие 2 сент 2016 г — Контрольная / проверочная работа для учителя-предметника для 11 класса обл, Донецк Материал размещён в группе « Математика — наука великая» Зачет по теме « Производная », 10 класс На рисунке изображен график производной функции , определенной на интервале текст контрольной работы 10 класс по теме ПРОИЗВОДНАЯ Похожие 6 янв 2015 г — текст контрольной работы 10 класс по теме ПРОИЗВОДНАЯ на промежутке hello_html_404e62egif При каком Математика Контрольная работа по теме: “Производная ” 10 класс — Документ Документ — Найдите среднее арифметическое корней уравнения , принадлежащих отрезку , если известно, что Контрольная работа по теме : Методическая разработка по алгебре (10 класс) на тему 14 сент 2014 г — Контрольная работа 10класс Тема » Производная » Контрольная работа по математике по теме «Производная» Похожие 2 февр 2015 г — На рисунке изображён график функции и касательная к нему в точке с Контрольная работа по теме : » Производная » 10 класс АиНА 10 класс, КР , Производнаяdocx — Контрольная работа по Файл АиНА 10 класс , КР , Производная docx для материала по дисциплинам за внедрение творческих и прогрессивных педаг идей Контрольная работа по алгебре и началам анализа в 10 классе по теме » Производная » Картинки по запросу контрольная работа по математике за 10 класс по теме производная «cb»:9,»cl»:12,»cr»:18,»ct»:6,»id»:»bGiBKB1wQt6z7M:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:230,»ou»:» «,»ow»:163,»pt»:»znanioru/static/files/cache/43/2f/432f4ef3cc4cb02″,»rh»:»znanioru»,»rid»:»xHcz7jickOFe5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Знанио»,»th»:99,»tu»:» \u003dtbn:ANd9GcQGLVKm5XUHn-yLyBDbdI-DG-Al9N7vnrzN1Yg7DpNxErDhyhcV5QLC3Q»,»tw»:70 «id»:»1iQDfphWHF5QUM:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:969,»ou»:» «,»ow»:1529,»pt»:»mpglaganedusiteru/DswMedia/zadanielist110klassj»,»rh»:»mpglaganedusiteru»,»rid»:»VD99NKtqy29IDM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Наш коллектив»,»th»:90,»tu»:» \u003dtbn:ANd9GcSNj1K3vtDqP2w7I085ettQn6LIWxR9Fu85Qjs-zIHiIE6l08hYGSY8tUg»,»tw»:142 «cb»:21,»cr»:3,»id»:»e6yFMuzRoKKz7M:»,»ml»:»600″:»bh»:90,»bw»:119,»oh»:450,»ou»:» «,»ow»:600,»pt»:»otvetimgsmailru/download/1e409993eec4ac8e47ae928″,»rh»:»otvetmailru»,»rid»:»BKrXo7rd6MOAFM»,»rt»:0,»ru»:» «,»st»:»Ответы@MailRu»,»th»:90,»tu»:» \u003dtbn:ANd9GcT3b80UerjIQNAENvpKayyxU01kV6F-e7D12umhhVlHPpjK8m1N2z-Ezg»,»tw»:120 «id»:»HyaJL2qcWNalQM:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:904,»ou»:» «,»ow»:1468,»pt»:»mpglaganedusiteru/DswMedia/zadanielist210klassj»,»rh»:»mpglaganedusiteru»,»rid»:»VD99NKtqy29IDM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Наш коллектив»,»th»:90,»tu»:» \u003dtbn:ANd9GcQGPdMlZmjY3yPA6uXM6dQ3yc3Hk5-ne6a7m0v3iNo0P889aFggxDRyLktK»,»tw»:146 «cb»:6,»cl»:12,»cr»:18,»ct»:6,»id»:»kWPesDJ2o4HfJM:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:708,»ou»:» «,»ow»:500,»pt»:»znanioru/static/files/cache/37/84/378412d47dc62f2″,»rh»:»znanioru»,»rid»:»m743aHQBDa3UeM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Знанио»,»th»:99,»tu»:» \u003dtbn:ANd9GcRj9OkWvphiy3_pMF2cQPkkRTdSGzj86zkfxif0cZCeVjzFZ5fkVt3Whg»,»tw»:70 «cb»:6,»cl»:3,»cr»:6,»ct»:15,»id»:»GksXXmFpUGw9EM:»,»ml»:»600″:»bh»:90,»bw»:105,»oh»:533,»ou»:» «,»ow»:654,»pt»:»arhivurokovru/videouroki/html/2015/02/02/98701900″,»rh»:»videourokinet»,»rid»:»jgwj_b5XFAQGoM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Видеоуроки»,»th»:90,»tu»:» \u003dtbn:ANd9GcTDgcP7KscufHyUxCc5FAKQE1KkP2a6OKO4jHgtYIxRKVQVNb8JTubyY68″,»tw»:110 Другие картинки по запросу «контрольная работа по математике за 10 класс по теме производная» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты контрольные и самостоятельные работы по алгебре 10 класс Похожие контрольные и самостоятельные работы по алгебре 10 класс Данный файл по алгебре для учащихся 10 класса содержит 2 варианта базовых работ по теме В зачет входят задание на нахождение значения производной в Контрольная работа по теме «Производная», алгебра 10 класс 31 мар 2017 г — Контрольная работа по теме « Производная », алгебра 10 класс 10 класс Автор: учитель математики Губкина Светлана Павловна Место На рисунке изображены график функции и касательная к нему в точке с Курс: АЛГЕБРА И НАЧАЛА АНАЛИЗА 10, : Контрольная работа Похожие Контрольная работа № 5 по теме » Производные тригонометрических функций AlContrItog10_v1 AlContrItog10_v2 AlContrItog10_v3 AlContrItog10_v4 Урок 92 Контрольная работа №4 — поурочные планы unimathru › › Глава 4 Производная Похожие Алгебра 10 класс по учебнику АГ Мордковича и др Глава 4 Производная Урок 92 Контрольная работа №4 Приветствие, сообщение темы и задач урока значение площади квадрата, построенного на гипотенузе треугольника 4 задание: Сделать краткий конспект теории по теме « Производная » Конспект урока по теме «Производная» по алгебре 10 класс › Конспект урока 13 сент 2017 г — Контрольная работа по теме «Применение производной «, 10 кл Конспект урока по теме » Производная » по алгебре 10 класс SMART цель урока: к концу урока учащиеся смогут за 10 минут решить 4 ошибки, делать выводы и планировать работу по их ликвидации, умения осуществлять Модуль по теме: «Производная» (алгебра и начала анализа) 10-й открытыйурокрф/статьи/411417/ Предлагаемый вашему вниманию модуль по теме » Производная » обеспечивает в процессе работы над составлением и решением задач на карточке Демиденко Лидия Васильевна, учитель математики Контрольная работа № 4 или тест материалы по алгебре и началам анализа для 10 класса ” [PDF] Демонстрационный вариант по математике для учащихся 10 sarschool76narodru/demo_math_10pdf Похожие по математике за курс 10 класса (УМК Мордкович АГ) Базовый уровень Годовая контрольная работа составлена в соответствии с программным Задания данной работы отражают следующие основные темы курса алгебры: Нахождение значения производной рациональной функции в точке 6 Годовая контрольная работа по математике (профильный уровень 4 июн 2016 г — Задания данной работы отражают следующие основные темы курса алгебры: Тригонометрические выражения, Тригонометрические уравнения, Производная , Применение произв работа по математике (профильный уровень, 10 класс ) На выполнение работы отводится 2 урока ЗАВУЧинфо — 10 класс Контрольная работа по теме «Применение wwwzavuchru/methodlib/359/66823/ Похожие 10 класс Контрольная работа по теме «Применение производной к Контрольная работа для базовой группы по алгебре и началам анализа 10 класс составленной на основе федерального государственного стандарта Домашняя работа по алгебре за 11 класс — PDF — DocPlayerru docplayerru/45685459-Domashnyaya-rabota-po-algebre-za-11-klasshtml Домашняя работа по алгебре за класс к учебнику «Алгебра и начала 00 г учебно-практическое пособие Содержание VIII Глава Производная и ее Контрольные работы по алгебре и началам математического анализа в Алгебра 10 класс Тема 1 Тригонометрические функции и преобразования Ответы@MailRu: Помогите с решением контрольной по алгебре 10 › Наука, Техника, Языки › Естественные науки Похожие 3 ответа Вот фото вариантов контрольных [PDF] Рабочая программа по алгебре и началам анализа 10 класс (4 wwwschool49tomskru/files/img/file/rpa10%204chpdf Рабочая программа по алгебре для 10 класса рассчитана на это же коли Применение производной для доказательства тождеств и неравенств тельная работа 52 Контрольная работа по теме : «Т ригонометрические [DOC] алгебра и начала анализа school4kotucozru/docs1/11_klassdocx Изучение алгебры в 11 классе направлено на достижение следующих целей : познакомить с основными идеями и методами математического анализа Контрольные работы составляются с учетом обязательных результатов обучения, они Повторение курса алгебры и начал анализа 10 класса ( 1 ч ) [PDF] Untitled — Школа №18 г Сыктывкара we18ru/wp-content/uploads/Математика-ФК-ГОС-СООpdf Рабочая программа по математике для 10 -11 классов составлена на основе В рабочую учебную программу по математике включена тема «Элементы комбинаторики, проверочные работы, решение задач, контрольные работы , Понятие о производной функции, физический и геометрический смысл [DOC] по алгебре и началам анализа — Официальный сайт МАОУ СОШ 43tyumenschoolru/file/download/1168 Задачник «Алгебра и начала математического анализа 10 -11 классы Применение производной для исследования функций на монотонность и экстремумы 11102017, Числовые функции, Контрольная работа № 1 по теме : для 10 класса — Наш коллектив mpglaganedusiteru/p19aa1html Похожие 29042016 ссылка на участие в вебинаре по математике от Калмыцкого государственного задания по алгебре для 10 класса Контрольная работа » формулы задания для 10 класса по теме производная скачать лист1 Определение производной функции — урок Алгебра, 10 класс › › 10 класс › Производная › Определение производной Урок по теме Определение производной функции Теоретические материалы и задания Алгебра, 10 класс ЯКласс — онлайн-школа нового поколения [DOC] Математика, 10-11 классы, базовый уровень (10г, 11г) — Лицей № 9 лицей9рф/filephp/id/f7563-file-originaldoc Учебники: АГ Мордкович Алгебра и начала анализа, 10 -11 класс Часть 1 Изучение математики на базовом уровне среднего (полного) общего образования направлено на Понятие о производной функции, физический и геометрический смысл производной тема урока Контрольная работа №1 1 Контрольная работа по теме: «Производная функции» (10-11 класс) metodistyru/m/files/view/kontrolnaya_rabota_po_teme_-proizvodnaya_2013_01_29 Похожие 1 февр 2013 г — Контрольная работа по теме : » Производная функции» ( 10 -11 класс ) без перехода через десяток в пределах 100 ( математика , 2 класс ) 2 Задания по развитию самообразовательной компетентности на уроках Видеоуроки Алгебра 10 класс Производная — Учительский портал 9 мая 2018 г — Решение 8 заданий на вычисление производных сложных функций Видеоурок по математике » Производная сложной функции» Алгебра (математика) 10 класс — InternetUrok Видеоуроки, тесты и тренажёры по Алгебра за 10 класс по школьной программе Решение задач по теме «Числовая окружность на координатной плоскости» Производная в задачах на прямоугольный параллелепипед [PDF] Рабочая программа по математике среднего общего образования leonidovoschoolru/storage/app/media/Rabochie_programmy/math_10-11pdf и «Геометрия 10 -11 классы » Атанасян ЛС,Бутузов ВФ,Кадомцев СБ и др 2004г Выбран В результате изучения математики на базовом уровне ученик должен знать/ Контрольная работа №9 по теме « Производная » 10 [PDF] Контрольная работа № 2 по теме ,,ПРОИЗВОДНАЯ” wwwschool195orgru/public/files/page/59/a-11_kr__2_proizvodnaja_pdf?21120 Похожие Контрольная работа № 2 по теме ,, ПРОИЗВОДНАЯ ” 11 класс ( 10 – 11) Вариант 1 1 Найдите в точке хо = 0 5 На рисунке изображён график функ- 2828 ГДЗ Алгебра 10-11 класс Мордкович Найдите производную Ответы на вопрос – № 2828 ГДЗ Алгебра 10 -11 класс Мордкович Найдите производную функции Домашняя контрольная работа № 3 Вариант 2 10 [PDF] 10 класс (профильный уровень) — МОУ «СОШ № 25 при МаГК» г sch35mgnru/docum/obrazov/rp_po_matematike_10-profilpdf Похожие автор: СВ Абхаликова — ‎ Похожие статьи Рабочая программа по учебному предмету « Математика 10 класс ( Контрольная работа за первое полугодие 1 Тема № урока Вид контроля Тематические Контрольные работы по Понятие производной n-го порядка [PDF] Рабочая программа по алгебре (базовый уровень) 10 класс egorggymnasiaedumskoru/uploads/2000/1078/section/52289//10/algebra_10pdf 10 класс Рабочая программа составлена на основе Фундаментального ядра 5 Производная 31 28 3 Контрольная работа №1по теме « Числовые [PDF] Итоговая контрольная работа 10 класс I вариант Часть В 1 internat23ru/files/attest/kr_alg10bpdf Похожие Итоговая контрольная работа 10 класс I вариант Часть В Найдите значение производной функции в точке: у = -3 + 2 , х0 = 7 у = х + на отрезке [PDF] Рабочая программа учебного предмета «Математика» art-lyceumru/Docs/rab_prog/rab_prog_sred_obch/matem10-17PDF При изучении курса математики на базовом уровне продолжаются и алгебра и начала анализа и геометрия в 10 классе объединены в один Понятие о производной функции, физический и геометрический смысл производной обобщающий урок 1 Контрольная работа по геометрии № 3 по теме [DOC] Контрольные работы по математике (алгебра) 10 класс Похожие Контрольные работы по математике (алгебра) 10 класс Контрольная работа №1 по теме «Применение производной к исследованию функций» Я иду на урок — УчПортфолио Презентация по алгебре для 10 класса по теме « Производная функции» На данном уроке Контрольная работа по алгебре за I полугодие, 11 класс [PDF] Промежуточная аттестация по математике 10 класс (профиль) 1 уровня за 10 класс Выполнение и стереометрия), алгебра, начала математического анализа, теория вероятностей и статистика Вид: контрольная работа (промежуточная аттестация) 2 Производная 25 35 П 8 билете школьнику не достанется вопроса по теме «Страны Африки» 5Решите [DOC] Рабочая учебная программа по алгебре и началам ou166omskobr55ru/doc/Matem(10-11)doc Похожие Контрольные работы формируются на основании примерных Алгебра и начала анализа»: дидактические материалы для 10 , 11 класса / СМ Понятие о производной функции, физический и геометрический смысл производной При изучении первой темы проводится повторение изученного [PDF] Untitled Похожие автор: АП Ершова — ‎ Похожие статьи АП Ершова, ЕП Нелин |f(x)dx = F(b) — Fa) Самостоятельные и контрольные работы по алгебре и началам математического анализа Класс иеге [DOC] Оценка устных ответов обучающихся по математике — СОШ №19 -Программа по алгебре и началам математического анализа 10 класс Изучение математики в старшей школе на базовом уровне направлено на достижение Контрольная работа № 9 по теме : «Применение производной к [PDF] Алгебра и начала анализа 10 класс ecolecousteauru/indexphp?option=com_docmantask=doc_download Похожие Календарно-тематическое планирование по алгебре 10 класс (см Изучение математики в старшей школе на базовом уровне направлено на овладение умением исследования функции с помощью производной , При выполнении практической работы и контрольной работы : Наименование темы 10 класс Алгебра Проверка знаний Тематическая контрольная Похожие Алгебра 10 класс Алгебра Проверка знаний Тематическая контрольная работа Производная Числовая последовательность Длительность: 10 минут Каталог сочинений Сочинения на любую тему Учитель, стаж 21 год, имеется опыт преподавания математики , физики, химии, биологии, географии [PDF] 1 РАБОЧАЯ ПРОГРАММА по алгебре 11 класс Составители lomonru/lomonintek/ofitsialnye-dokumenty/10klass//algebra-11-klasspdf Контрольные работы по алгебре и началам анализа для 10 – 11 классов На подготовку дается две недели (сообщается тема , основные вопросы теории, вычислять производные и первообразные элементарных функций, Алгебра – 10 класс Производная — Контрольные работы Рейтинг: 3 — ‎7 голосов 9 апр 2017 г — Урок на тему : «Что такое производная ? Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса Пробные работы ЕГЭ по математике — 4ЕГЭ 4egeru/trening-matematika/ Похожие Задачи на движение по прямой Проверочная работа по теме «Теория вероятности» Входная контрольная работа по математике для 10 класса Алгебра и начала анализа 10 класс — Поурочные планы wwwcompendiumsu/mathematics/algebra10/indexhtml Урок 58 Итоги контрольной работы · Уроки 59-60 Зачетная работа по теме «Преобразование тригонометрических выражений» Глава 5 Производная Вместе с контрольная работа по математике за 10 класс по теме производная часто ищут контрольная работа по теме производная 10 класс мордкович контрольная работа по теме производная 10 класс (1 час) ответы контрольная работа по алгебре 10 класс производная ответы контрольная работа по теме производная 10 класс ответы контрольная работа по теме производная ответы контрольная работа по теме производная 10 класс с ответами контрольная работа по теме производная с ответами контрольная работа по алгебре 10 класс применение производной Навигация по страницам 1 2 3 4 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google

Проверочная работа по алгебре и началам анализа по теме: «Производная функции и ее применение» 10 класс.

| Методическая разработка по алгебре (10 класс):

МОУ СШ № 61 Тракторозаводский район г. Волгоград

Проверочная работа по алгебре и началам анализа, 10 класс по теме: «Производная функции и ее применение»

к учебно-методическому комплексу А.Г. Мордковича.

Подготовила: учитель математики

Прокудина Ирина Юрьевна

2018-2019 год

Цель: Проверка усвоения учащимися темы «Производная функции», умение применять полученные знания на конкретных примерах и задачам физики и геометрии.

Уровень сложности: базовый

Время на выполнение работы: 40 мин.

Инструкция по выполнению работы

Работа содержит 12 заданий с кратким ответом. Содержание, проверяемое заданиями, включает: геометрический смысл производной, физический смысл производной, таблица производных, исследование функции с помощью производной.

В бланке теста отмечать правильный ответ запрещено. Выбранный ответ необходимо отметить на отдельном бланке ответов.

Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднения, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.

За выполнение заданий дается один балл. Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Инструкция по проверке тестового задания.

За каждое верно выполненное задание учащийся получает 1 балл. Максимальное количество баллов – 12. Оценка определяется исходя из следующих показателей:

11 — 12 баллов – оценка «5»

9 -10 баллов – оценка «4»

6 -8 баллов – оценка «3»

5 и менее баллов – оценка «2»

№	I вариант
1	Найдите значение производной функции в точке .	5	Укажите промежуток, на котором функция убывает.	9	Прямая является касательной к графику функции . Найдите абсциссы точек касания.
2	На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .	6	На рисунке изображен график производной функции, определенной на интервале(-12;4). Найдите промежутки возрастания функции, в ответе укажите длину наибольшего из них.	10	На рисунке изображен график производной функции, определенной на интервале (-4;16). Найдите количество точек максимума функции на отрезке .
3	Найдите угловой коэффициент касательной к графику функции в точке с абсциссой .	7	Найдите точки экстремума функции .	11	Два тела движутся по законам и . В какой момент времени их скорости будут равны?
4	На рисунке изображен график функции , определенной на интервале (-3;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой .	8	На рисунке изображен график функции, определенной на интервале (-4;7). Найдите сумму точек экстремума функции.	12	На рисунке изображен график производной функции, определенной на интервале (-8; 4). В какой точке отрезка функция принимает наименьшее значение.

№	II вариант
1	Найдите значение производной функции в точке .	5	Укажите промежуток, на котором функция возрастает.	9	Прямая является касательной к графику функции. Найдите абсциссы точек касания.
2	На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .	6	На рисунке изображен график производной функции, определенной на интервале(-1;17). Найдите промежутки убывания функции, в ответе укажите длину наибольшего из них.	10	На рисунке изображен график производной функции, определенной на интервале (-17;2). Найдите количество точек максимума функции на отрезке .
3	Найдите угловой коэффициент касательной к графику функции в точке с абсциссой .	7	Найдите точки экстремума функции .	11	Тело движется по закону S(t)=2t³-12t²+7 . Через сколько секунд после начала движения ускорение тела будет равно 36 м/с²?
4	На рисунке изображен график функции , определенной на интервале (-3;11). Найдите количество точек, в которых касательная к графику функции параллельна прямой .	8	На рисунке изображен график функции, определенной на интервале (-7;5). Найдите сумму точек экстремума функции.	12	На рисунке изображен график производной функции, определенной на интервале (-8; 3). В какой точке отрезка функция принимает наибольшее значение.

Подготовительный вариант

1. Найдите значение производной функции в точке .

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .

3. Найдите угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой х=1.

4. На рисунке изображен график производной функции, определенной на интервале (-4; 8). Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

5. На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых производная функции равна 0 .

6. На рисунке изображен график производной функции, определенной на интервале (-9; 2). Найдите промежутки убывания функции. В ответе укажите сумму целых точек, входящих в эти промежутки.

7. При движении тела по прямой расстояние s (в км) от начальной точки меняется по закону

s(t)= + 2 (t – время движения в часах). Найдите скорость (в км/ч) тела через 1 час после начала движения.

8. На рисунке изображен график производной функции , определенной на интервале(-7; 5). Найдите точку экстремума функции на отрезке[-6; 4].

9. В какой точке графика функции у = х2 – 3х + 5 тангенс угла наклона касательной равен 1?

10. На рисунке изображен график производной функции, определенной на интервале (-8; 4). В какой точке отрезка[-7; -3] функция принимает наименьшее значение.

11.Найдите промежутки убывания функции

у = -6х – 0,5х+ х

12. Составьте уравнение касательной к графику функции у = в точке х=3.

ПР
В-	Дата ФИ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

ПР
В-	Дата ФИ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

ПР
В-	Дата ФИ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

ПР
В-	Дата ФИ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Проверочная работа по теме:

«Производная функции и ее применение»

10-А

Ответы

	В-1	В-2	Подг. вар
1	-3	4	0
2	1	-0,5	-0,25
3	0	-4	0
4	5	7	3
5	x	x > -1	6
6	6	7	-17
7	хmax= -3, хmin=1	хmax= -1, хmin =3	0,5
8	7	-2	-3
9	-1; -3 2/3	0; -2 2/3	2
10	2	1	-7
11	2	5	[ -2;3]
12	-7	-4	-2/3 х+4

Контрольная работа по алгебре на тему «Производная» 10 кл.

Контрольная работа №5 по алгебре. Тема «Производная».

Вариант №7. ( знак / означает операцию деления.)

Найти производную и вычислить ее значение при заданном Х в каждом задании.

1. f(x) = 8√x + x³ — (2 / x) +5 при x = 4.

2. g(x) = (1 / x⁴)— 5x ^{– 3}+ 8x – 18 при x = — 1.

3. h (x) = ( 4x⁵ +2)·Sin x при x = 0.

4. f(x) = ( 7x³ -3x) / (2x²) при x = — 2.

5. V(x) = ( 3x² – 7x) ⁵ при x = 1.

6. g(x) = Cos (10x ⁵ -3) при x = 0.

7. f(x) = tg ( x⁶ + 4x²) при x = 0.

Образцы решения заданий №4 — №7.

Найти производную и вычислить ее значение при заданном Х в каждом задании. (Значек / означает операцию деления, он отделяет числитель дроби от знаменателя. В заданиях №1 и №2 дроби взяты в скобки, в зад.№4 — числитель и знаменатель ).

Пример 1. На производную частного ( U / V ). f(x) = (15x⁵– 4x²) / (2x³) при x=2.

Решение.

f ´ (x) = ((15x⁵– 4x²) / (2x³))´ = ((15x⁵– 4x²)´· (2x³) — (15x⁵– 4x²)· (2x³) ´) / (2x³)² =((75x⁴– 8x)· (2x³) — (15x⁵– 4x²)·(6x²)) / (4x⁶)= (150x⁷ – 16x⁴ – 90x⁷ +24x⁴)/ (4x⁶) =

(60 x⁷ + 8x⁴)/ (4x⁶) =(4x⁴(15x³ +2))/4x⁶= (15x³ +2) / x²

Вычисляем при х=2: ( 15·2³+2) / 2² = (15·8 +2) / 4 =122 / 4 = 30,5

Ответ: 30,5

1. На производную сложной функции (f(g(x)) <Правило: Сначала берется производная от внешней функции f(x) и умножается на производную от внутренней функции g(x)>

Пример 2. g(x) =(7x²+3x⁵)³ при х = 1. Решение.

g´(x) = ((7x²+3x⁵)³ )´ = 3·(7x²+3x⁵)²·(7x²+3x⁵)´ =3·(7x²+3x⁵)²·(14x + 15x⁴)

Вычисляем при х=1: 3·( 7·1² +3·1⁵)²·(14·1 +15·1⁴) =3·10²·29 = 300·29 =8700.

Ответ: 8700.

Пример 3. h(x) = Ctg (5x⁴ – 3x² +2) при х = 0 Решение.

h´(x) = (Ctg (5x⁴ – 3x² +2))´ = (- 1 / ( Sin²(5x⁴ – 3x² +2))· (5x⁴ – 3x² +2)´ = — (20x³ -6x +0) /

( Sin²(5x⁴ – 3x² +2) )= (6x – 20x³) / ( Sin²(5x⁴ – 3x² +2)).

Вычисляем при х = 0: (6·0 — 20·0³) / ( Sin²(5·0⁴ – 3·0² +2)) = 0 / Sin²(2) =0. Ответ: 0.

Ответы на примеры.

№1. 4/√x + 3x²+ 2/x² = 50,125

№2. – 4/x⁵ +15/x⁴ +8 = 27

№3. 20х⁴Sin x + 4x⁵Cos x + 2 Cos x= 2

№4. ( 7х² +3)/ (2x²) = 3,875

№5. 5(3х² – 7х)⁴ (6х – 7)= — 1280

№6. –Sin (10x⁵ — 3) 50x⁴ =0

№7. (6х⁵ +8х) / (Cos²(x⁶ +4x²)) = 0

Контрольная работа по теме Производная и её применение

Контрольная работа по алгебре и началам математического анализа

Тема «Производная функции и её применение»

2 курс системы НПО и 1 курс СПО

на базе основного образования

Контрольная работа по теме «Производная функции и её применение» ориентирована на учебник Ш. А.Алимова и др. «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и естественно-математического профилей.

Контрольная работа предназначена для самостоятельного выполнения вне аудитории.

Работа включает в себя 10 вариантов заданий одинакового уровня сложности. Вариант определяется последними цифрами номера зачетной книжки студента.

Работа выполняется студентом в отдельной тетради с соответствующим оформлением титульного листа. Оформление работы должно соответствовать «Единым требованиям оформления письменных работ по математике».

Правильное выполнение каждого задания оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 12. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.

Задание 1. Вычислить пределы

1 вариант	а)	б)
2 вариант	a)	б)
3вариант	а)	б)
4 вариант	а)	б)
5 вариант	а)	б)
6 вариант	а)	б)
7 вариант	а)	б)
8 вариант	а)	б)
9 вариант	а)	б)
10 вариант	а)	б)

Задание 2. Найти точки разрыва графика функции:

1 вариант 2 вариант

3 вариант 4 вариант

5 вариант 6 вариант

7 вариант 8 вариант

9 вариант 10 вариант

Задание 3. Найти главное приращение функцииdy

1 вариант у = х² + cos 3x – 5 2 вариант y = cos (1- x²)

3 вариант у = (1 – х²)⁵ 4 вариант у = (2х² – 5)³

5 вариант у = 6 вариант у =

7 вариант у = 8 вариант у =

9 вариант 10 вариант

Задание 4. Найти вторую производную функции

1 вариант у = 2 вариант

3 вариант 4 вариант

5 вариант 6 вариант

7 вариант 8 вариант

9 вариант 10 вариант

Задание 5. Найти производную по её определению (через предел)

1 вариант у = 2х² – 3х 2 вариант у = 2х³

3 вариант у = х³ + х 4 вариант у = 5х² — х

5 вариант у = 6 вариант у = 6 – х – х²

7 вариант у = 2 – х² 8 вариант у = х² + 4х

9 вариант у = х² – х 10 вариант у = х² + 2х

Задание 6. Найти скорость и ускорение материальной точки в момент времени t

1 вариант
2 вариант
3 вариант
4 вариант
5 вариант
6 вариант
7 вариант
8 вариант
9 вариант
10 вариант

Задание 7. Найти производные, используя таблицу и правила дифференцирования

1 вариант а) y = б) y =

6.7 Приложения дифференциального исчисления | Дифференциальное исчисление

Сумма двух положительных чисел равна \ (\ text {20} \). Один из числа умножается на квадрат другого. Находить числа, которые делают этот продукт максимальным.

Пусть первое число будет \ (x \), а второе число будет \ (y \) и пусть произведение будет \ (P \).{2} — 80х + 400 \\ & = (3x-20) (x-20) \ end {выровнять *}

Следовательно, \ (x = 20 \) или \ (x = \ frac {20} {3} \).

Если \ (x = 20 \), то \ (y = 0 \) и произведение является минимумом, а не максимум.

Следовательно, \ (x = \ frac {20} {3} \) и \ (y = 20- \ frac {20} {3} = \ frac {40} {3} \). {2} — 2 (2) — 3 \\ & = 4 + 4-4-3 \\ & = \ текст {1} \ текст {блок} \ end {выровнять *}

На схеме изображен план веранды, которая будет построен на углу коттеджа.Перила \ (ABCDE \) — это должны быть построены по четырем краям веранды.

Если \ (AB = DE = x \) и \ (BC = CD = y \), а длина перил должно быть \ (\ text {30} \ text {m} \), найдите значения \ (x \) и \ (y \) для которых на веранде будет максимум площадь.

Нам нужно определить выражение для площади через только одна переменная.

Периметр:

\ begin {align *} Р & = 2х + 2у \\ 30 & = 2х + 2у \\ 15 & = х + у \\ у & = 15-х \ end {выровнять *}

Площадь:

\ begin {align *} A & = y ^ {2} — (y-x) ^ {2} \\ & = y ^ {2} — (y ^ {2} — 2xy + x ^ {2}) \\ & = y ^ {2} — y ^ {2} + 2xy — x ^ {2} \\ & = 2xy — x ^ {2} \ end {выровнять *}

Мы используем выражение для периметра, чтобы исключить \ (y \) переменная, чтобы у нас было выражение для площади в терминах только из \ (x \):

\ begin {align *} A (x) & = 2x (15-x) — x ^ {2} \\ & = 30x — 2x ^ {2} — x ^ {2} \\ & = 30x — 3x ^ {2} \ end {выровнять *}

Чтобы найти максимум, нам нужно взять производную и положить он равен \ (\ text {0} \):

\ begin {align *} А ‘(х) & = 30 — 6х \\ 0 & = 30 — 6x \\ 6x & = 30 \\ х & = 5 \ end {выровнять *}

Следовательно, \ (x = \ text {5} \ text {m} \) и подставляя это значение обратно в формулу для периметра дает \ (y = \ text {10} \ text {m} \). 2 \ end {выровнять *}

Определите размеры контейнера так, чтобы площадь используемого картона сведена к минимуму.2} \\ & \ приблизительно \ текст {12,0} \ текст {см} \ end {выровнять *}

3.2 Производная как функция — Объем исчисления 1

Цели обучения

Определите производную функцию заданной функции.
Постройте производную функцию от графика заданной функции.
Укажите связь между производными финансовыми инструментами и непрерывностью.
Опишите три условия, когда функция не имеет производной.
Объясните значение производной высшего порядка.

Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент.Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.

Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная.Мы можем формально определить производную функцию следующим образом.

Определение

Позвольте быть функцией. Функция производной , обозначенная как, — это функция, область определения которой состоит из таких значений, что существует следующий предел:

Говорят, что функция дифференцируема на , если
существует. В более общем смысле, функция называется дифференцируемой на , если она дифференцируема в каждой точке открытого набора, а дифференцируемая функция — это функция, в которой существует в своей области.

В следующих нескольких примерах мы используем (рисунок), чтобы найти производную функции.

Нахождение производной функции квадратного корня

Найдите производную от.

Решение

Начните непосредственно с определения производной функции. Используйте (рисунок).

Нахождение производной квадратичной функции

Найдите производную функции.

Решение

Выполните здесь ту же процедуру, но без умножения на конъюгат.

Найдите производную от.

Решение

Мы используем множество различных обозначений для выражения производной функции. На (Рисунок) мы показали, что если, то. Если бы мы выразили эту функцию в форме, мы могли бы выразить производную как или. Мы могли бы передать ту же информацию письменно. Таким образом, для функции каждое из следующих обозначений представляет собой производную от:

Вместо мы также можем использовать. Использование обозначений (так называемых обозначений Лейбница) довольно распространено в инженерии и физике.Чтобы лучше понять это обозначение, напомним, что производная функции в точке — это предел наклона секущих линий, когда секущие линии приближаются к касательной. Наклоны этих секущих линий часто выражаются в виде где — разница значений, соответствующая разнице значений, которые выражаются как ((Рисунок)). Таким образом, производная, которую можно представить как мгновенную скорость изменения относительно, выражается как

. Рисунок 1.Производная выражается как.

Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку дает скорость изменения функции (или наклон касательной к).

На (рис.) Мы обнаружили, что для. Если мы построим график этих функций на тех же осях, что и на (Рисунок), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями.Во-первых, мы замечаем, что он увеличивается по всей своей области, что означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем для всех значений в его области. Кроме того, по мере увеличения наклон касательных к уменьшается, и мы ожидаем увидеть соответствующее уменьшение. Мы также замечаем, что это не определено и соответствует вертикальной касательной к точке 0.

Рис. 2. Производная везде положительна, потому что функция возрастает.

На (рис.) Мы обнаружили, что для. Графики этих функций показаны на (Рисунок). Обратите внимание, что для. Для этих же значений. Для значений увеличивается и. Кроме того, имеет горизонтальную касательную в точках и.

Построение производной с помощью функции

Используйте следующий график, чтобы нарисовать график.

Нарисуйте график. На каком интервале находится график выше оси?

Решение

Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков.Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть непрерывной там; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин.

Проба

Если дифференцируем в, то существует и

Мы хотим показать, что это непрерывно, показав это.Таким образом,

Следовательно, поскольку определено и, заключаем, что непрерывна в точке.

Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию. Эта функция всюду непрерывна; однако не определено. Это наблюдение приводит нас к мысли, что непрерывность не предполагает дифференцируемости. Давайте изучим дальше. Для,

Этот предел не существует, потому что

См. (Рисунок).

Рисунок 4. Функция непрерывна в 0, но не дифференцируема в 0.

Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не дифференцируема. Рассмотрим функцию:

Таким образом не существует. Беглый взгляд на график проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((рисунок)).

Рисунок 5. Функция имеет вертикальную касательную в точке. Он непрерывен в 0, но не дифференцируем в 0.

У функции также есть производная, которая демонстрирует интересное поведение при 0. Мы видим, что

Этот предел не существует, главным образом потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю ((Рисунок)).

Рисунок 6. Функция не дифференцируема в 0.

Итого:

Заметим, что если функция не является непрерывной, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она все равно не может быть дифференцируемой.
Мы видели, что это невозможно дифференцировать в 0, потому что предел наклона касательных линий слева и справа не был одинаковым. Визуально это привело к появлению острого угла на графике функции в 0. Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
Как мы видели в примере, функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
Как мы видели, функция может быть не дифференцируемой в точке и более сложными способами.

Непрерывная и дифференцируемая кусочная функция

Производная функции сама по себе является функцией, поэтому мы можем найти производную от производной. Например, производная функции положения — это скорость изменения положения или скорости. Производная скорости — это скорость изменения скорости, которая является ускорением. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать использовать производные для получения третьей производной, четвертой производной и так далее.В совокупности они называются производными более высокого порядка . Обозначения для производных высшего порядка от могут быть выражены в любой из следующих форм:

Интересно отметить, что обозначение для можно рассматривать как попытку выразить более компактно. Аналогично.

Поиск второй производной

Для, найдите.

В поисках ускорения

Положение частицы вдоль оси координат в момент времени (в секундах) определяется выражением (в метрах).Найдите функцию, описывающую его ускорение во времени.

Производная функция

В следующих упражнениях используйте определение производной для поиска.

Решение

10.

Решение

Для следующих упражнений используйте график, чтобы нарисовать график его производной.

11. 12.

Решение

13, 14.

Решение

Для следующих упражнений данный предел представляет собой производную функции в.Найти и .

15.

16.

Решение

17.

18.

Решение

19.

20.

Решение

Для следующих функций

набросок графика и
использует определение производной, чтобы показать, что функция не дифференцируема в.

21.

23.

Для следующих графиков

определяет, для каких значений существует, но не является непрерывным, и
определяет, для каких значений функция является непрерывной, но не дифференцируемой в.

25.

Для следующих функций используйте, чтобы найти.

28.

29.

30.

Решение

Для следующих упражнений используйте калькулятор для построения графиков. Определите функцию, затем используйте калькулятор для построения графика.

31. [Т]

33. [Т]

35. [Т]

Для следующих упражнений опишите, что представляют собой эти два выражения в терминах каждой из данных ситуаций. Обязательно укажите единицы измерения.

37. обозначает население города во время в годах.

38. обозначает общую сумму денег (в тысячах долларов), потраченную клиентами на концессии в парке развлечений.

Решение

а. Средняя ставка, с которой клиенты потратили на уступки, в тысячах на одного покупателя.
г. Скорость (в тысячах на одного покупателя), по которой покупатели тратили деньги на уступки, в тысячах на одного покупателя.

39. обозначает общую стоимость (в тысячах долларов) производства радиочасов.

40. обозначает оценку (в процентных пунктах), полученную по тесту за количество часов обучения.

Решение

а. Средняя оценка, полученная за тест, при среднем времени обучения между двумя суммами.
г. Скорость (в процентных пунктах в час), с которой оценка по тесту повышалась или понижалась за данное среднее время обучения в часах.

41. обозначает стоимость (в долларах) учебника социологии в университетских книжных магазинах США с 1990 года.

42. обозначает атмосферное давление на высоте футов.

Решение

а. Среднее изменение атмосферного давления между двумя разными высотами.
г. Скорость (торр на фут), с которой атмосферное давление увеличивается или уменьшается на высоте.

Решение

а. Скорость (в градусах на фут), с которой температура повышается или понижается для данной высоты.
г. Скорость изменения температуры при изменении высоты на высоте 1000 футов составляет -0.1 градус на фут.

Решение

а. Скорость, с которой число людей, заболевших гриппом, меняется через несколько недель после первоначальной вспышки.
г. Скорость резко увеличивается до третьей недели, после чего она замедляется, а затем становится постоянной.

Для следующих упражнений используйте следующую таблицу, которая показывает высоту ракеты Saturn V для миссии Apollo 11 через несколько секунд после запуска.

Время (секунды)	Высота (метры)
0	0
1	2
2	4
3	13
4	25
5	32

47. В чем физический смысл? Какие единицы?

48. [T] Создайте таблицу значений и график для обоих и на том же графике. ( Подсказка: для внутренних точек, оцените как левый предел, так и правый предел и усредните их.)

Решение

Время (секунды)

(м / с)

5.{2} + 3h} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {h (-4x — 2h + 3)} {h} \\ & = \ lim_ {h \ to 0} (- 4x-2h + 3) \\ f ‘(x) & = — 4x + 3 \ end {align *}

Определите производную \ (f \ left (x \ right) = \ frac {1} {x-2} \), используя первые принципы.

\ begin {align *} f (x) & = \ frac {1} {x-2} \\ f (x + h) & = \ frac {1} {x + h-2} \\ f ‘(x) & = \ lim_ {h \ to 0} \ dfrac {f (x + h) -f (x)} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ frac {1} {x + h-2} — \ frac {1} {x-2}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ frac {(x-2) — (x + h-2)} {(x + h-2) (x-2)}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ frac {x-2-x-h + 2} {(x + h-2) (x-2)}} {h} \\ & = \ lim_ {h \ to 0} \ left (\ dfrac {-h} {(x + h-2) (x-2)} \ right) \ раз \ frac {1} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {-1} {(x + h-2) (x-2)} \\ f ‘(x) & = \ frac {-1} {(x-2) ^ {2}} \ end {align *}

Определите \ ({g} ‘\ left (3 \ right) \) из первых принципов, если \ (g \ left (x \ right) = — 5 {x} ^ {2} \).{2}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {h (-10x-5h)} {h} \\ & = \ lim_ {h \ to 0} (- 10x-5h) \\ & = — 10x \ end {align *}

Следовательно: \ begin {align *} g ‘(3) & = -10 (3) \\ & = -30 \ end {align *}

Если \ (p \ left (x \ right) = 4x (x-1) \), определите \ ({p} ‘\ left (x \ right) \) используя первые принципы. 4 \ qquad & & & & 1 & & 4 & & 6 & & 4 & & 1 & \\ .{n-1} \ end {выровнять *}

Это очень ценное общее правило для нахождения производной функция.

Математика 105 (Исчисление I): старые экзамены | Математика

Семестр	Дата	Инструктор	Темы	Текстовые разделы	Решения
W16	29.01.16	Боатенг	функции, графики, функции суммы, функции скорости, геометрия производных и производных высшего порядка	(O / Z) 1.1-1,4, 1,6-1,7	нет
W16	12.02.16	Боатенг	все от 29.01 оценка плюс оценка производных, определение производных, производных и первообразных степенных функций, пределы	(O / Z) 1,1–1,4, 1,6–1,7, 2,1–2,4	нет
W16	04.03.16	Боатенг	все из оценки 02/12 плюс дифференциальные уравнения, производные от экспоненциальной, логарифмической и тригонометрической функций, производные от произведений, частных и композитов	(O / Z) 1.1-1,4, 1,6-1,7, 2,1-2,7, 3,1-3,2	нет
W16	18.03.16	Боатенг	все оценки от 03/04 (кроме 1.1-1.4, 1.6-1.7) плюс производные композитов, неявное дифференцирование, обратные функции, оптимизация	(O / Z) 2,1–2,7, 3,1–3,5, 4,3	нет
W16	01.04.16	Боатенг	все из оценки 18 марта (кроме 2.1–2.4) плюс правило L’Hospital, соответствующие ставки, теорема о промежуточном значении, теорема об экстремальном значении, теорема о среднем значении, площади и интегралы	(O / Z) 2.5-2.7, 3.1-3.5, 4.2-4.3, 4.5, 4.8-4.9, 5.1-5.2	нет
W16	12.02.16	Салерно	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	нет
W16	18.03.16	Салерно	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	нет
W16	10.02.16	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
W16	16.03.16	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
W16	10.04.16	Таун	Задачи обзора для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
W16	11.04.16	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F15	25.09.15	Боатенг	функции суммы, функции курса, геометрия производных и производных высшего порядка	(O / Z) 1,4, 1,6-1,7	нет
F15	10.09.15	Боатенг	все из оценки 25.09 плюс определение производных, производных и первообразных степенных функций, пределы	(O / Z) 1.4, 1,6–1,7, 2,1–2,4	нет
F15	30.10.15	Боатенг	все оценки от 10/09 плюс производные от экспоненциальной, логарифмической и тригонометрической функций, производные от произведений, частных и композитов, неявное дифференцирование	(O / Z) 1,4, 1,6-1,7, 2,1-2,4, 2,6-2,7, 3,1-3,3	нет
F15	13.11.15	Боатенг	все из оценки 10/30 (кроме 1.4, 1.6–1.7) плюс производные обратных функций, правило Л’Опиталя, оптимизация	(O / Z) 2,1–2,4, 2,6–2,7, 3,1–3,5, 4,2–4,3	нет
F15	12.04.15	Боатенг	все из оценки 11/13 (кроме 2.1–2.4) плюс теорема о промежуточном значении, теорема о крайнем значении, теорема о среднем значении, площади и интегралы	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3, 4,8–4,9, 5,1	нет
F15	15.12.15	Боатенг	все из оценок 11/13 и 12/04 плюс функция площади, Фундаментальная теорема исчисления, аппроксимирующие суммы	(O / Z) 2.1-2.4, 2.6-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6	нет
F15	10.09.15	Салерно	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	нет
F15	13.11.15	Салерно	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	нет
F15	15.12.15	Салерно	Финал: все экзамены 10.09 и 13.11 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
F15	10.07.15	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
F15	11.11.15	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F15	13.12.15	Таун	Задачи на повторение для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
F15	14.12.15	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W15	13.02.15	Грир	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	да
W15	20.03.15	Грир	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	да
W15	14.04.15	Грир	Финал: все экзамены 13.02 и 20.03 (кроме оптимизации) плюс соответствующие оценки , теорема о промежуточном значении, теорема об экстремальном значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W15	11.02.15	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
W15	18.03.15	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
W15	12.04.15	Таун	Задачи на повторение для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
W15	13.04.15	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F14	03.10.14	Балкомб	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	нет
F14	07.11.14	Балкомб	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	нет
F14	12.09.14	Балкомб	Финал: все экзамены 10/03 и 11/07 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
F14	03.10.14	Салерно	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1.1-1,7, 2,1-2,5	нет
F14	07.11.14	Салерно	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	нет
F14	12.09.14	Салерно	Финал: все экзамены 10/03 и 11/07 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
F14	01.10.14	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
F14	11.05.14	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F14	07.12.14	Таун	Задачи обзора для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
F14	08.12.14	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W14	07.02.14	Buell	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1.1-1,7, 2,1-2,5	да
W14	14.03.14	Buell	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
W14	08.04.14	Buell	Финал: все экзамены 02/07 и 14 марта плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
W14	05.02.14	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
W14	12.03.14	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
W14	06.04.14	Таун	Задачи обзора для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
W14	07.04.14	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F13	10/04/13 A	Нельсон	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1.1-1.7, 2.1-2,4	да
F13	10/04/13B	Нельсон	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1,1–1,7, 2,1–2,4	да
F13	11.08.13	Нельсон	дифференциальные уравнения, производные правила (произведение, частное, цепочка, экспонента, тригонометрические, обратные), неявное дифференцирование, логарифмическое дифференцирование, оптимизация	(O / Z) 2.5-2.7, 3.1-3.5, 4.3	да
F13	10.12.13	Нельсон	Финал: все экзамены 10/04 и 11/08 плюс правило Л’Опиталя, соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
F13	10.04.13	Росс	(экзамен 1) функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1.1-1,7, 2,1-2,4	да
F13	11.08.13	Росс	(экзамен 2) производные правила (произведение, частное, цепочка, экспонента, тригонометрический, обратный), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F13	10.12.13	Росс	(Заключительный экзамен) все экзамены 10/04 и 11/08 плюс соответствующие оценки , теорема о промежуточном значении, теорема об экстремальном значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F13	10.04.13	Салерно	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1,1–1,7, 2,1–2,4	нет
F13	11.08.13	Салерно	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, логарифмическое дифференцирование, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	нет
F13	10.12.13	Салерно	Финал: все экзамены 10/04 и 11/08 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
F13	02.10.13	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,4	да
F13	06.11.13	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F13	08.12.13	Таун	Задачи на повторение для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
F13	12.09.13	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W13	08.02.13	Нельсон	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1,1–1,7, 2,1–2,4	да
W13	15.03.13	Нельсон	дифференциальные уравнения, производные правила (произведение, частное, цепочка, экспонента, тригонометрические, обратные), неявное дифференцирование, первообразные, оптимизация	(O / Z) 2.5-2,7, 3,1-3,5, 4,2	да
W13	09.04.13	Нельсон	Финал: все экзамены 02/08 и 03/15 плюс теорема о промежуточном значении, теорема об экстремальном значении, теорема о среднем значении, соответствующие оценки , правило Л’Опиталя, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W13	08.02.13	Вайс	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1.1-1,7, 2,1-2,4	нет
W13	15.03.13	Вайс	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2	да
W13	06.02.13	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,4	да
W13	13.03.13	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6-2,7, 3,1-3,5, 4,2-4,3, 4,8 (только IVT)	да
W13	07.04.13	Таун	Задачи на повторение для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
W13	08.04.13	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F12	05.10.12	Buell	функции, графики, первая и вторая производные (графические, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1.1-1,4, 1,6-1,7, 2,1-2,5	да
F12	09.11.12	Buell	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F12	11.12.12	Buell	Финал: все экзамены 10/05 и 11/09 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F12	05.10.12	Куломб	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	да
F12	09.11.12	Куломб	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	да
F12	11.12.12	Куломб	Финал: все экзамены 10/05 и 11/09 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F12	05.10.12	Хейнс	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1.1-1,7, 2,1-2,5	нет
F12	09.11.12	Хейнс	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	нет
F12	11.12.12	Хейнс	Финал: все экзамены 10/05 и 11/09 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
F12	10/05/12 A	Нельсон	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1,1–1,7, 2,1–2,4	да
F12	10/05/12B	Нельсон	функции, графики, первые и вторые производные (графические, числовые, аналитические), пределы, первообразные	(O / Z) 1.1-1,7, 2,1-2,4	да
F12	09.11.12	Нельсон	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F12	11.12.12	Нельсон	Финал: все экзамены 10/05 и 11/09 плюс соответствующие оценки , теорема о промежуточном значении, теорема о крайнем значении, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F12	03.10.12	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
F12	07.11.12	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F12	09.12.12	Таун	Задачи обзора для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
F12	10.12.12	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W12	10.02.12	Buell	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1.1-1,7, 2,1-2,5	да
W12	16.03.12	Buell	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация, теорема о промежуточном значении	(O / Z) 2,6-2,7, 3,1-3,5, 4,2-4,3, 4,8 (только IVT)	да
W12	10.04.12	Buell	Финал: все экзамены 02/10 и 03/16 плюс теорема об экстремальном значении, теорема о среднем значении, соответствующие оценки , правило Л’Опиталя, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	нет
W12	10.02.12	Грир	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	да
W12	16.03.12	Грир	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация, теорема о промежуточном значении	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3, 4.8 (только IVT)	да
W12	10.04.12	Грир	Финал: все экзамены 02/10 и 03/16 (кроме оптимизации) плюс теорема об экстремальном значении, теорема о среднем значении, соответствующие оценки , правило Л’Опитала, площади, интегралы, основная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
W12	08.02.12	Таун	Просмотрите задачи к экзамену 1.	(O / Z) 1,1–1,7, 2,1–2,5	да
W12	14.03.12	Таун	Просмотрите задачи к экзамену 2.	(O / Z) 2,6-2,7, 3,1-3,5, 4,2-4,3, 4,8 (только IVT)	да
W12	08.04.12	Таун	Задачи на повторение для финала, часть I.	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2	да
W12	09.04.12	Таун	Задачи обзора для финала, часть II.	(O / Z) 4.3, 4.5, 4.8-4.9, 5.1-5.3, 5.6-5.7	да
F11	10.07.11A	Куломб	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1,1–1,7, 2,1–2,5	да
F11	10/07/11B	Куломб	функции, графики, первая и вторая производные (графические, числовые, аналитические), пределы, первообразные, дифференциальные уравнения	(O / Z) 1.1-1,7, 2,1-2,5	да
F11	11/11/11 A	Куломб	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2,6–2,7, 3,1–3,5, 4,2–4,3	да
F11	11/11 / 11B	Куломб	производных правил (произведение, частное, цепочка, экспонента, тригонометрических, обратных), неявное дифференцирование, первообразные, ограничения, включая правило L’Hopital , оптимизация	(O / Z) 2.6-2.7, 3.1-3.5, 4.2-4.3	да
F11	13.12.11	Куломб	Финал: все экзамены 10.07 и 11.11 плюс метод Ньютона, соответствующие оценки , теорема о промежуточном значении, теорема об экстремальном значении, площади, интегралы, фундаментальная теорема , суммы	(O / Z) 1.1-1.7, 2.1-2.7, 3.1-3.5, 4.2-4.3, 4.5-4.6, 4.8, 5.1-5.3, 5.6-5.7	да

Тест второй производной — условия, полезность, удобство использования и примеры

Что такое тест второй производной

В математике значение второй производной обозначает функцию, которая является производной производной этой функции.Хотели бы вы знать, как записать вторую производную в математическом выражении? Запишите это как: — f 00 (x) или как d 2 f dx2. Теперь вы знаете, насколько полезна первая производная по отношению ко второй производной? В то время как первая производная может дать нам понять, увеличивается или уменьшается функция, вторая производная показывает, увеличивается или уменьшается первая производная.

Условия вогнутости для теста второй производной

Всегда имейте в виду, что если вторая производная положительна, это означает, что первая производная увеличивается, так что наклон касательной к функции увеличивается с увеличением x .Мы воспринимаем это явление графически, как изогнутая вверх кривая графика, то есть имеющая форму параболы, направленной вверх.

Теперь, аналогично, если вторая производная оказывается отрицательной, тогда первая производная уменьшается, так как наклон касательной к функции уменьшается по мере увеличения «x». В качестве иллюстрации в Graphs мы замечаем это как кривую графика, которая вогнута вниз, то есть смоделирована как парабола, открывающаяся вниз. В точках, где вторая производная равна 0, мы ничего не узнаем о форме графика: он может быть либо вогнутым вверх, либо вогнутым вниз, либо он может меняться от полного вогнутого вверх к вогнутому вниз или наоборот.Следовательно, подведем итог:

Если d 2 f dx ² (p) больше 0 при x = p, то f (x) вогнутая вверх при x = p.

Если d 2 f dx ² (p) меньше 0 при x = p, то f (x) вогнута вниз при x = p.

Если d 2 f dx ² (p) равно 0 при x = p, то мы не знаем ничего нового об отношении f (x) при x = p.

[Изображение будет загружено в ближайшее время]

Утилита второго производного теста

Второй производный тест фактически менее доминирующий, чем первый производный тест.Это явно вызвало у вас любопытство относительно того, почему тогда оно вообще используется? Основная причина заключается в том, что в условиях, когда он является окончательным, второй производный тест обычно и сравнительно легче применять. Это, в свою очередь, связано с тем, что проверка второй производной требует только вычисления формальных выражений для производных. Кроме того, это требует оценки символов этих выражений предпочтительно в точке, а не в интервале. Для оценки в точке обычно требуется меньше арифметических / алгебраических маневров или обработки.

Кроме того, тест 2-й производной может помочь определить, является ли стационарная точка Локальным максимумом или Локальным минимумом, или это глобальный максимум / глобальный минимум. Это определяется путем сравнения значений локальных максимумов / минимумов с другими глобальными максимумами / глобальными минимумами.

Проверка пригодности второй производной

Проверка второй производной часто наиболее полезна при вычислении относительного максимума или минимума, если функция имеет первую производную, равную (0) в определенной точке.Поскольку в этой точке было обнаружено, что тест первой производной не работает или не проходит, эта точка является точкой перегиба. Тест второй производной фиксируется на символе второй производной в этой точке. Если он отрицательный, точка является относительным максимумом, тогда как если он положительный, точка является относительным минимумом.

Решенные примеры

Найдите и используйте вторую производную функции

Возьмите f (x) = 3x 3 — 6x 2 + 2x — 1.

Теперь

f 0 (x) = 9x 2 — 12x + 2, а f 00 (x) = 18x — 12.

Таким образом, при x = 0,

2-я производная f (x) равна −12,

Итак, мы понимаем, что график f (x) вогнут вниз при x = 0.

Аналогично, при x = 1 2-я производная f (x) равна f 00 (1) = 18 1 — 12 = 18 — 12 = 6,

Таким образом, график f (x) опирается на вогнутый вверх в точке x = 1

[Изображение будет загружено в ближайшее время]

Знаете ли вы,

Существует также односторонняя версия 2-го производного теста
, односторонняя версия работает как альтернатива или, скажем, исправительный вариант для случаев, чтобы не возвращаться к первому производному тесту.
Если односторонние производные f ‘доступны в c, то мы можем проверить, что обе односторонние производные f’ имеют знак для f », указанный в реальном анализе

— Почему мы учить студентов математике использовать производную как предел?

Я согласен с приведенными выше комментариями.

Суть моего комментария-вопроса «Какое конкурирующее определение вы имеете в виду?» должен был подчеркнуть то, что кажется недооцененным в самом вопросе: причина, по которой мы говорим о производных как о пределах, заключается в том, что это определение производной, и мы хотим дать определение концепции, которая будет обсуждается большую часть семестра.

[Можно дать другие определения производной, но все они являются вариациями на одну и ту же тему и, в частности, все используют либо понятие предела, либо (эквивалентное!) Понятие непрерывности. Например, у Каратеодори есть хорошее определение производной в терминах функций, исчезающих до первого порядка, но это не будет более приемлемым для первокурсника, изучающего математику.]

[ Добавлено : Признаюсь, что забыл о нестандартном анализе, когда писал вышеупомянутый абзац.Это действительно несколько отличается от обычных ограничений и непрерывности. С одной стороны, хотя я никогда не учил математическому анализу таким образом, я весьма сомневаюсь, что это внезапно заставит легко перейти на сложные концепции непрерывности и дифференцируемости. С другой стороны, я, конечно, не мог решить преподавать нестандартный подход к исчислению, потому что это было бы … нестандартным. Учебная программа для разных разделов, разных классов и разных факультетов должна иметь определенный минимальный уровень согласованности, и в настоящее время большинство аспирантов и преподавателей на всех математических факультетах, которые я когда-либо видел, недостаточно знакомы с нестандартным анализом, чтобы проводить практические занятия. вопросы от студентов, которые изучили математический анализ с помощью этого подхода.]

Если мы не дадим определение наиболее важному понятию в курсе, то мы потеряем всякую претензию развивать вещи в логической последовательности. В частности, трудно понять, как обсуждать вывод какого-либо из основных правил, которые студенты будут фактически использовать для вычисления производных, и поэтому мы были бы вынуждены сократить исчисление до (длинного!) Списка алгоритмов, основанных на некоторых необъяснимых правила.

Тем не менее, я серьезно отношусь к вашему вопросу, так как за последние годы я изучил довольно много математики для первокурсников.Абсолютно правильно, что многие студенты становятся нетерпеливыми, сердитыми и / или сбиваются с толку из-за предельного определения производной (или, на самом деле, из-за чего-либо, имеющего отношение к ограничениям и / или непрерывности). Я довольно быстро делаю вывод таких вещей, как правило продукта и правило мощности в классе, потому что я знаю, что что-то вроде половины класса не следует и не хочет следовать. И тем не менее, я все равно выполняю их (не все, а больше половины), потому что для меня отказ от них делает курс тем, чему я не могу заставить себя преподавать (и, кстати, поставил бы его намного ниже уровень класса AP по математике, который у меня был в старшей школе: я чувствую себя обязанным дать своим ученикам по математике не намного меньше, чем было дано мне).Таким образом, существует настоящий разрыв между классом математического анализа, который я хочу преподавать, и классом математического анализа, который хочет посещать примерно половина студентов. Это обескураживает.

Я был бы счастлив услышать, что я делаю ложную дихотомию между предоставлением предельного определения производной и просто предоставлением алгоритмов для решения проблем. Я определенно экспериментирую с различными видами объяснений помимо (и вместо!) Простого доказательства. Вот несколько вещей, которые я пробовал:

1) Возьмите определение непрерывности как первичное и определите предел функции в точке как значение, при котором можно (пере) определить функцию, чтобы сделать ее непрерывной.Я думаю, что это должно быть полезно, поскольку я думаю, что у большинства людей есть интуитивное представление о «непрерывной, непрерывной кривой» и гораздо меньше о пределе функции в точке.

2) Подчеркните физическое мышление. В последний раз, когда я преподавал математику первокурсникам, я весь первый день говорил о скоростях: сначала средняя скорость, затем мгновенная скорость. Если у правила дифференциации есть правдоподобная физическая интерпретация — например, правило цепочки гласит, что темпы изменения должны умножаться — тогда я часто его и даю.

3) Подчеркните «химическое рассуждение», то есть размерный анализ :. Я часто даю единицы независимой переменной и зависимой переменной и подчеркиваю, что единицы производной отличается от единиц исходной функции. Таким образом, можно увидеть, что правило предполагаемого произведения $ (fg) ‘= f’g’ $ размерно неверно и, следовательно, бессмысленно. (И снова цепное правило «очевидно» с точки зрения преобразования единиц.) Подобным образом анализ размеров должен остановить вас от утверждения, что объем цилиндра равен $ \ pi rh $.

К сожалению, ни одна из этих вещей не сработала с частью класса, которая не хочет слышать ничего , кроме того, как решить проблемы.

Добавлено : Чтобы более точно ответить на ваш конкретный вопрос: да, есть проблемы, которые можно задать первокурсникам, изучающим математику, которые требуют от них использования предельного определения производной, а не (просто) правил дифференциации, но я не рекомендую задавая многие из этих вопросов, так как студенты находят их очень трудными .2}) $ для $ x \ neq 0 $ и $ f (0) = 0 $. Какое наименьшее целое значение $ a $ такое, что $ f $ (i) непрерывно, (ii) дифференцируемо, (iii) дважды дифференцируемо?

Мне посчастливилось оценить эту проблему. Из примерно 200 долларов за экзамены средний балл составлял 0,5 доллара из 12 долларов. Около трех студентов записали правильный числовой ответ для части (iii), но это не было подтверждено какой-либо работой или какими-либо рассуждениями.

Добавлено : кстати, это не значит, что вышеупомянутый вопрос «плохой» в том смысле, что он не проверяет математическую компетентность и глубину понимания математического анализа.Я думаю, что это действительно так, просто на уровне, намного превышающем тот, который следует тестировать в классе первокурсников для не математических специальностей. В течение следующих нескольких лет, когда эта история всплывала в социальной среде с участием математиков, после ее рассказа я сразу же требовал от них ответа на часть c). Большинство людей, которых я спрашивал, не понимали. (Обратите внимание, что я бы, конечно, не дал им ручку и бумагу и не дал бы им какое-то время подумать о проблеме. Обычно мне требовался ответ примерно через минуту.В конце концов, давайте заставим математиков с докторской степенью соответствовать более высоким стандартам, чем новички, не имеющие специальности!) Например, я наблюдал, как облако пролетело над лицом одного медалиста Филдса, когда он был очень сбит с толку. Однако через некоторое время я перестал использовать это как популярную викторину в дополнение к рассказу: я не могу точно вспомнить, почему, но я хотел бы думать, что меня осенило, насколько неприятно было ставить людей в такое положение …

Wolfram | Примеры альфа: производные

Производные

Дифференцировать выражение по заданной переменной.

Вычислить производную функции:

Другие примеры

Производные высшего порядка

Вычислить производные высшего порядка.

Вычислить производные высшего порядка:

Другие примеры

Неявная дифференциация

Дифференцируйте функции, неявно определяемые уравнениями.

Продифференцируйте уравнение:

Вычислить производную, используя неявное дифференцирование:

Другие примеры

Частные производные

Найдите частную производную по одной переменной или вычислите смешанные частные производные.

Вычислить частные производные:

Вычислить частные производные высшего порядка:

Другие примеры

Направленные производные

Вычислить производную многомерной функции в заданном направлении.

Вычислить производную по направлению:

Другие примеры

Производные абстрактных функций

Найдите производную произвольной функции.

Вычислить производные с использованием абстрактных функций:

Вычислить частные производные абстрактных функций:

Другие примеры

Дифференцируемость

Проверить, дифференцируемы ли функции над полем действительных чисел.

Проверить дифференцируемость функции:

Другие примеры

Производные приложения

Изучите множество приложений деривативов.

Найдите интервалы монотонности:

Изучите примечательные точки кривых:

Вычислить экстремальные значения одномерных и многомерных функций:

Вычислить касательную к уравнению в заданной точке:

Другие примеры

Производная 10 класс контрольная работа: Контрольная работа по теме «Вычисление производных «10 класс (разноуровневые)

Контрольная работа по теме «Вычисление производных «10 класс (разноуровневые)

Контрольная работа «Производная. Геометрический и механический смысл производной» 10 класс

«Производная. Механический и геометрический смысл производной».

▶▷▶ контрольная работа по математике за 10 класс по теме производная

Проверочная работа по алгебре и началам анализа по теме: «Производная функции и ее применение» 10 класс.

Контрольная работа по алгебре на тему «Производная» 10 кл.

Контрольная работа по теме Производная и её применение

6.7 Приложения дифференциального исчисления | Дифференциальное исчисление

3.2 Производная как функция — Объем исчисления 1

Цели обучения

Определение

Нахождение производной функции квадратного корня

Решение

Нахождение производной квадратичной функции

Решение

Решение

Построение производной с помощью функции

Решение

Проба

Непрерывная и дифференцируемая кусочная функция

Поиск второй производной

В поисках ускорения

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Математика 105 (Исчисление I): старые экзамены | Математика

Тест второй производной — условия, полезность, удобство использования и примеры

— Почему мы учить студентов математике использовать производную как предел?

Wolfram | Примеры альфа: производные

Добавить комментарий Отменить ответ