Пример построение контрольных карт шухарта: Пример построения контрольной карты Шухарта в Excel

Пример построения контрольной карты Шухарта в Excel

В настоящей заметке представлены удобные шаблоны в Excel для построения контрольных карт Шухарта. Если эта тема для вас новая, предлагаю начать с книги Д. Уилер, Д. Чамберс. Статистическое управление процессами. Существует много видов контрольных карт (см., например, ГОСТ Р 50779.42-99. Статистические методы. Контрольные карты Шухарта). Но основных – два: карта средних и индивидуальных значений. Если контролируемый процесс устроен так, что некоторые значения образуют естественные группы, то рекомендуется использовать контрольную карту средних. Исходные данные следует собрать в группы, рассчитав для каждой из них среднее значение и размах (размах – разность между максимальным и минимальным значением в группе; рис. 1).

Рис. 1. Исходные данные для построения карты среднего и размаха

Скачать заметку в формате Word или pdf, примеры в формате Excel

Рекомендуется накопить 20–30 средних значений, и уже по ним строить карту. Карта среднего и размаха содержит два графика (рис. 2), на верхнем – карта среднего, на нижнем – карта размаха. На карте среднего отображают средние значения отдельных групп, а также три линии: центральную (среднее средних) и две контрольные границы – верхнюю и нижнюю. Если расчетное значение для нижней границы меньше нуля, эту границу, либо не наносят на карту, либо проводят на отметке ноль. На карте размаха, присутствуют аналогичные данные. Нижняя контрольная граница, как правило отсутствует.

Границы рассчитывают по следующим формулам:
UCL_X̅ = X̿ + A₂R̅ – верхняя граница карты средних;
CL_X̅ = X̿ – центральная линия карты средних;
LCL_X̅ = X̿ – A₂R̅ – нижняя граница карты средних;

UCL_R = D₄R̅ – верхняя граница карты размахов;
CL_R = R̅ – центральная линия карты размахов;
LCL_R = D₃R̅ – нижняя граница карты размахов.

Здесь Х̅ – среднее значение в одной выборке, X̿ – среднее по нескольким значениям средних Х̅, R̅ – среднее по размахам в нескольких выборках, A₂, D₃, D₄ – коэффициенты, зависящие от размера выборок n (рис. 3). При построении карты на рис. 2 использованы 30 первых значений.

Рис. 2. Карта среднего и размаха; значение D₃ для n = 4 отсутствует, поэтому нижней границы на карте размаха нет

Рис. 3. Константы для контрольных карт среднего и размаха (A₂, D₃, D₄) и индивидуальных значений (d₂)

Если данные образуют некий ряд, не подлежащий группировке, применяются карты индивидуальных значений и скользящего размаха. Они получили название XmR-карт. Скользящий размах есть модуль разности последовательных значений (рис. 4; использованы данные из столбца В на рис. 1).

Рис. 4. Исходные данные для построения XmR-карты

Для XmR-карты границы рассчитывают по следующим формулам:

нижняя граница карты размахов отсутствует.

Здесь  – средний скользящий размах, а значения коэффициентов d

2 и D₄ берутся для n = 2 (см рис. 3). Почему так? Потому что карта скользящего размаха фактически использует группы из двух последовательных измерений для вычисления размаха. Для расчета всех линий использованы первые 30 значений.

Рис. 5. XmR-карта индивидуальных значений и скользящего размаха

Если сравнить карту средних (рис. 2) и индивидуальных значений (рис. 5), видно, что последняя обладает большей волатильностью, и диапазон между нижней и верхней контрольными границами шире. Это не удивительно, так как на карте средних используется усреднение по четырем значениям. Если выполнить усреднение по еще большему числу значений, границы станут еще ближе.

Важным моментом при построении контрольных карт является использование двух статистик: средних и размахов. Часто используемый неверный способ расчета контрольных границ заключается в том, что используется лишь одна статистика. Например, при построении карты как на рис. 5, использовались бы только индивидуальные значения и их дисперсия. В этом случаев границы рассчитывались бы по следующим формулам:

Поскольку при таком подходе используется единая статистика рассеяния, карты размахов в данном случае нет. Вычисление контрольных пределов, основанное на использовании единой статистики рассеяния, приведет к неправильному результату. Подобные вычисления приводят к расширению полосы между контрольными пределами. Правильный путь вычисления контрольных пределов для карты индивидуальных значений всегда должен использовать двухточечные скользящие размахи.

Эта заметка была полностью переработана в октябре 2016 г. Оказалось, что в первоначальном варианте я предлагал неверное решение. С первоначальным вариантом, представляющим лишь исторический интерес, можно ознакомиться здесь.

Возможно вас также заинтересует:
Контрольные карты Шухарта. Правила определения отсутствия управляемости
Рациональная группировка данных при построении контрольной карты Шухарта

Практикум использования контрольных карт Шухарта / Хабр

Недавно я публиковал здесь свой слайдкаст с рассказом о 6-сигмах, контрольных картах Шухарта и людях снежинках, где достаточно простым языком, местами злоупотребляя сквернословием, под 20-ти минутный хохот слушателей рассказывал о том, как отделить системные вариации от вариаций, вызванных особыми причинами.

Теперь хочу подробно разобрать пример построения контрольной карты Шухарта на основе реальных данных. В качестве реальных данных я взял историческую информацию о завершенных личных задачах. Эта информация у меня есть благодаря адаптации под себя модели личной эффективности Дэвида Аллена Getting Things (про это у меня тоже есть старый слайдкаст в трех частях: Часть 1, Часть 2, Часть 3 + Excel-табличка с макросами для анализа задач из Outlook ).

Постановка задачи выглядит так. У меня имеется распределение среднего числа завершенных задач в зависимости от дня недели (ниже на графике) и нужно ответить на вопрос: «есть ли что-то особенное в понедельниках или это всего лишь погрешность системы?»

Ответим на этот вопрос при помощи контрольной карты Шухарта – основного инструмента статистического управления процессами.

Итак, критерий Шухарта наличия особой причины вариации достаточно прост: если какая-то точка выходит за контрольные пределы, рассчитанные особым образом, то она свидетельствует об особой причине.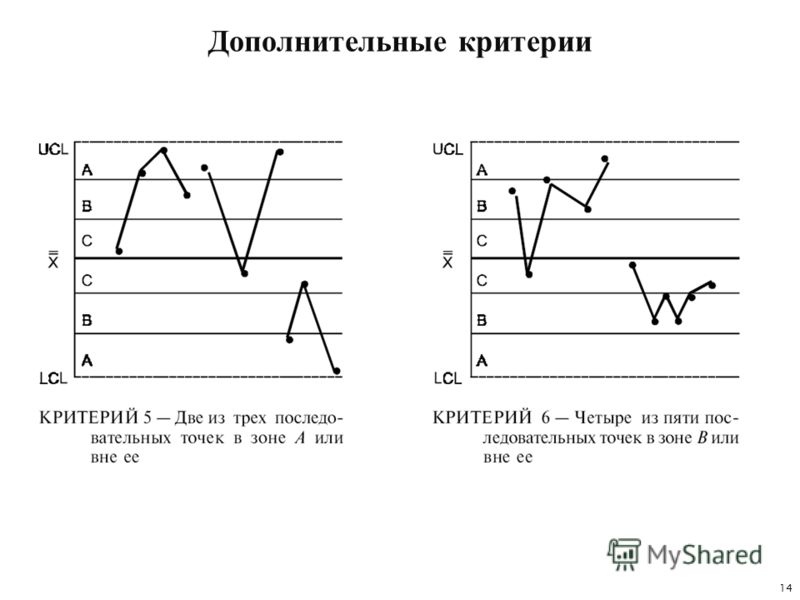

Если точка лежит внутри этих пределов, то отклонение обусловлено общими свойствами самой системы. Грубо говоря, является погрешностью измерений.
Формула для вычисления контрольных пределов выглядит так:

Где
— среднее значение средних значений по подгруппе,
— средний размах,
— некоторый инженерный коэффициент, зависящий от размера подгруппы.

Все формулы и табличные коэффициенты можно найти, например, в ГОСТ 50779.42-99, где кратко и понятно изложен подход к статистическому управлению (честно, сам не ожидал, что есть такой ГОСТ. Более подробно тема статистического управления и его места в оптимизации бизнеса раскрыта в книге Д. Уилера).

В нашем случае мы группируем количество выполненных задач по дням недели – это и будет подгруппами нашей выборки. Я взял данные о числе завершенных задач за 5 недель работы, то есть, размер подгруппы равен 5. При помощи таблицы 2 из ГОСТа находим значение инженерного коэффициента:

Вычисление среднего значения и размаха (разницы между минимальным и максимальным значениями) по подгруппе (в нашем случае по дню недели) задача достаточно простая, в моем случае результаты такие:

День недели	Групповое среднее	Размах
Понедельник	10.2	8
Вторник	6.7	10
Среда	7.2	11
Четверг	4.2	9
Пятница	5.0	10
Суббота	0.5	2
Воскресенье	0.5	3

Центральной линией контрольной карты будет являться среднее групповых средних, то есть:

Так же вычисляем средний размах:

Теперь мы знаем, что нижний контрольный предел для числа выполненных задач будет равен:

То есть, те дни, в которые я в среднем завершаю меньшее число задач, с точки зрения системы являются особенными.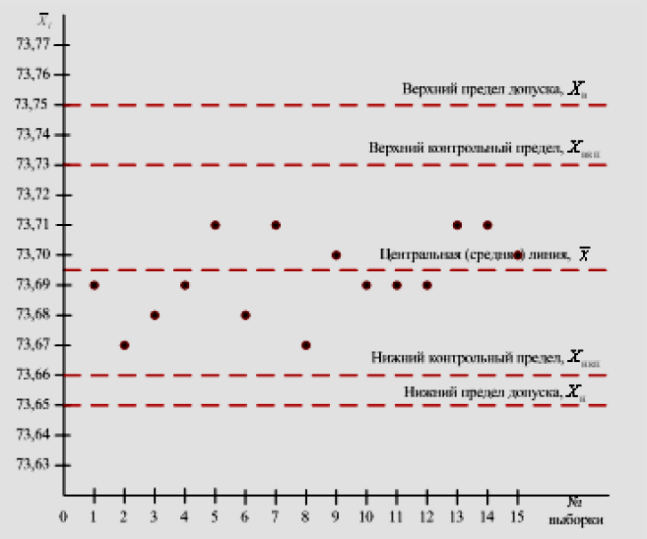

Аналогично получаем верхний контрольный предел:

Теперь нанесем на график центральную линию (красная), верхний контрольный предел (зеленая) и нижний контрольный предел (фиолетовая):

И, о, чудо! Мы видим три явно особенные группы, выходящие за контрольные пределы, в которых присутствуют явно не системные причины вариаций!

По субботам и воскресеньям я не работаю. Факт. А понедельник оказался действительно особенным днем. И теперь можно думать и искать что же такого реально особенного в понедельниках.

Однако если бы среднее число выполненных в понедельник задач находилось внутри контрольных пределов и пусть даже сильно выделялось на фоне остальных точек, то с точки зрения Шухарта и Деминга искать какие-то особенности в понедельниках было бы бессмысленным занятием, так как подобное поведение обуславливается исключительно общими причинами. Например, я построил контрольную карту для других 5-ти недель в конце прошлого года:

И вроде как есть какое-то ощущение того, что понедельник как-то выделяется, но согласно критерию Шухарта — это всего-лишь флуктуация или погрешность самой системы. Согласно Шухарту, в данном случае можно сколь угодно долго исследовать особые причины понедельников — их просто нет. С точки зрения статистического управления, на этих данных понедельник ничем не отличается от любого другого рабочего дня (даже воскресенья).

Контрольные карты Шухарта для Excel (Shewhart control charts for Excel) от DEMING.PRO

Программное обеспечение

Shewhart control charts for Excel

​ Mac OS & Windows

Контрольные карты Шухарта самый эффективный инструмент статистического управления процессами (Statistical Process Control, SPC) и незаменим для совершенствования качества продукции и услуг, лучшего управления человеческими ресурсами, закупками, продажами, планированием, обслуживанием оборудования.

Основной принцип нашего ПО: Установи и сразу используй. Лучшее решение для оперативного ведения контрольных карт Шухарта на цеховом уровне и для последующей аналитической работы с контрольными картами.

​

​

 

Контрольные карты Шухарта самый эффективный инструмент статистического управления процессами (Statistical Process Control, SPC) и незаменим для совершенствования качества продукции и услуг, лучшего управления человеческими ресурсами, закупками, продажами, планированием, обслуживанием оборудования. Контрольные карты Шухарта с успехом применяются в промышленности, торговле, сфере обслуживания, здравоохранении, спорте, образовании, страховании, сферах безопасности, государственном управлении и даже в космосе.

 

Назначение программного продукта — запуск цепной реакции Деминга

 

 

Улучшайте качество

​

За счет меньшего количества ошибок, переделок и задержек, а также лучшего использования машинного времени и материалов уменьшатся затраты

​

Повысится производительность

​

Займете рынок, предлагая лучшее качество по более низкой цене

​

Останетесь в деле

​

Сохраните и умножите количество рабочих мест

 

 

Для оперативного диагностирования процесса и принятия необходимых мер к нему, избегая совершения ошибок первого и второго рода, могут быть использованы данные «голоса» любого процесса, собираемые автоматизировано или вручную.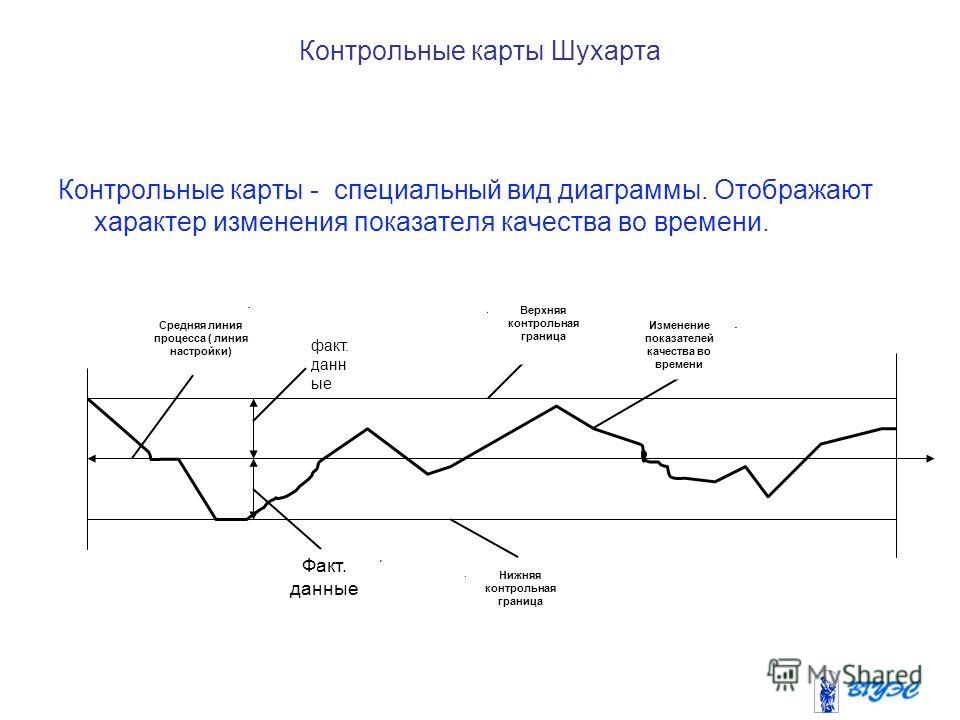 Для анализа подойдут показатели декомпозированные в разрезе любого фактора (источника вариабельности), например:

• любые ключевые показатели эффективности закупок, продажах, проектирования, технического обслуживания оборудования и т. д.;
• данные входного контроля СиМ, управления качеством поставщиков, качества собственных полуфабрикатов и продукции;
• частота событий, происшествий, любые данные подсчётов;
• данные размера, производительности, вибрации (вибродиагностика), зазора, расхода, уровня жидкости, давления, температуры, влажности, газового анализа, положения, скорости, силы, вязкости, плотности, твердости, радиоактивности, освещенности, запыленности, концентрации, наличия и количества примесей,  трибодиагностики, кислотности, загрязненности, акустических измерений, электрических измерений и др. измерения.

 

 

 

Онлайн-демонстрация на ваших данных

 

Вы можете заказать бесплатную онлайн-демонстрацию работы программного обеспечения для решения ваших задач. В демонстрации могут быть использованы предоставленные вами данные, например, самый проблемный размер самой проблемной детали по всем переделам. Скачать форму предоставления данных для онлайн-демонстрации.

 

При необходимости засекретить реальные данные, вы можете произвести их предварительное шифрование, которое не окажет влияния на выводы.

 

 

​

 

 

 

 

Отличительные особенности

 

Аналитический инструментарий нашего программного обеспечения может уверенно конкурировать с лучшими и дорогими мировыми аналогами ПО для статистического управления процессами (Statistical Process Control, SPC) и обладает востребованным практиками в области качества и повышения операционной эффективности функционалом, которого нет у конкурентов.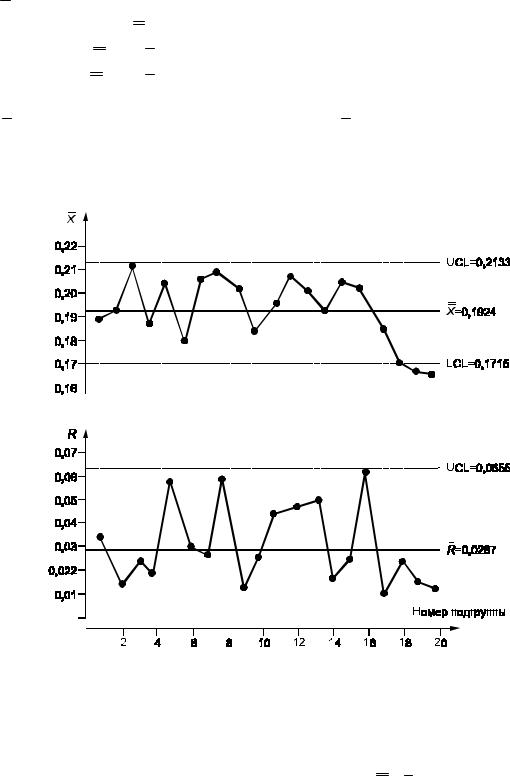 Вместо того чтобы наполнять наше ПО различными заумными инструментами теоретической статистики, мы акцентируем внимание на полноценном практическом использовании самых эффективных методологий статистического управления процессами и постоянно наращиваем их аналитическую функциональность. Поддержка пользователей осуществляется профессионалами нашего Центра на русском языке. Особое достоинство — интерфейс программы для лёгкого использования имеющихся функций вашим персоналом, ничего запоминать не надо — все кнопки находятся в зонах элементов, которыми они управляют, имеют понятные подписи и контекстную справочную информацию.

 

 

ПО Контрольные карты Шухарта для Excel за 2 минуты

 

​

 

 

К программному обеспечению прилагаются бланки контрольных карт Шухарта с программным калькулятором в Excel для ведения на цеховом уровне:

​

 

Вырабатывайте с помощью нашего программного обеспечения решения направленные на существенное повышение эффективности процессов и бизнеса в целом, ранее недоступные вашей команде.

 

Вы можете делиться подготовленными с помощью нашего программного обеспечения контрольными картами с любыми пользователями. Такие файлы могут открываться на любом компьютере с установленным Excel, но без возможности применения функций ПО.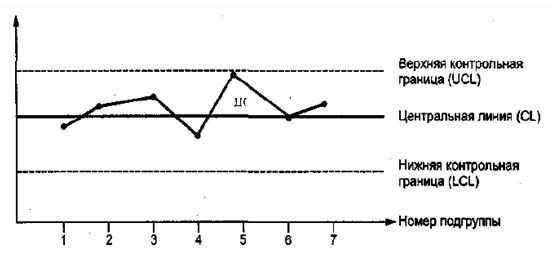

 

 

​

 

В PQ Systems мы используем контрольные карты Шухарта в наших системах продаж, поддержки, бухгалтерского учета и других системах. Отслеживая количество исходящих и входящих звонков, продолжительность времени на звонки, количество контактов в каждом периоде, а также другие входные данные, благодаря контрольным картам Шухарта мы можем отслеживать тенденции и устанавливать реалистичные ожидания для отдельных лиц и отдела в целом.

 

Вы не найдёте ни одного бухгалтера в нашей компании, представляющего чистую прибыль в этом месяце по сравнению с прошлым месяцем. Вместо этого, чистая прибыль отчётного месяца отображается на контрольной карте Шухарта вместе с предыдущими 24 или 36 месяцами.

 

Одно из самых больших преимуществ контрольных карт заключается в том, что субъективность сводится к минимуму, а решения принимаются на основе полученных данных. Голос процесса говорит вам, что происходит. Когда в систему вносятся изменения с целью улучшения, Контрольная карта Шухарта покажет вам, как процесс ведёт себя после изменения, чтобы вы могли определить результирующий эффект.

 

— Мэтт Сэвидж, вице-президент PQ Systems,
Источник: www.forbes.com

 

​

 

 

Описание методологии использования

 

[4] — Дональд Уилер, Дэвид Чамберс, Статистическое управление процессами.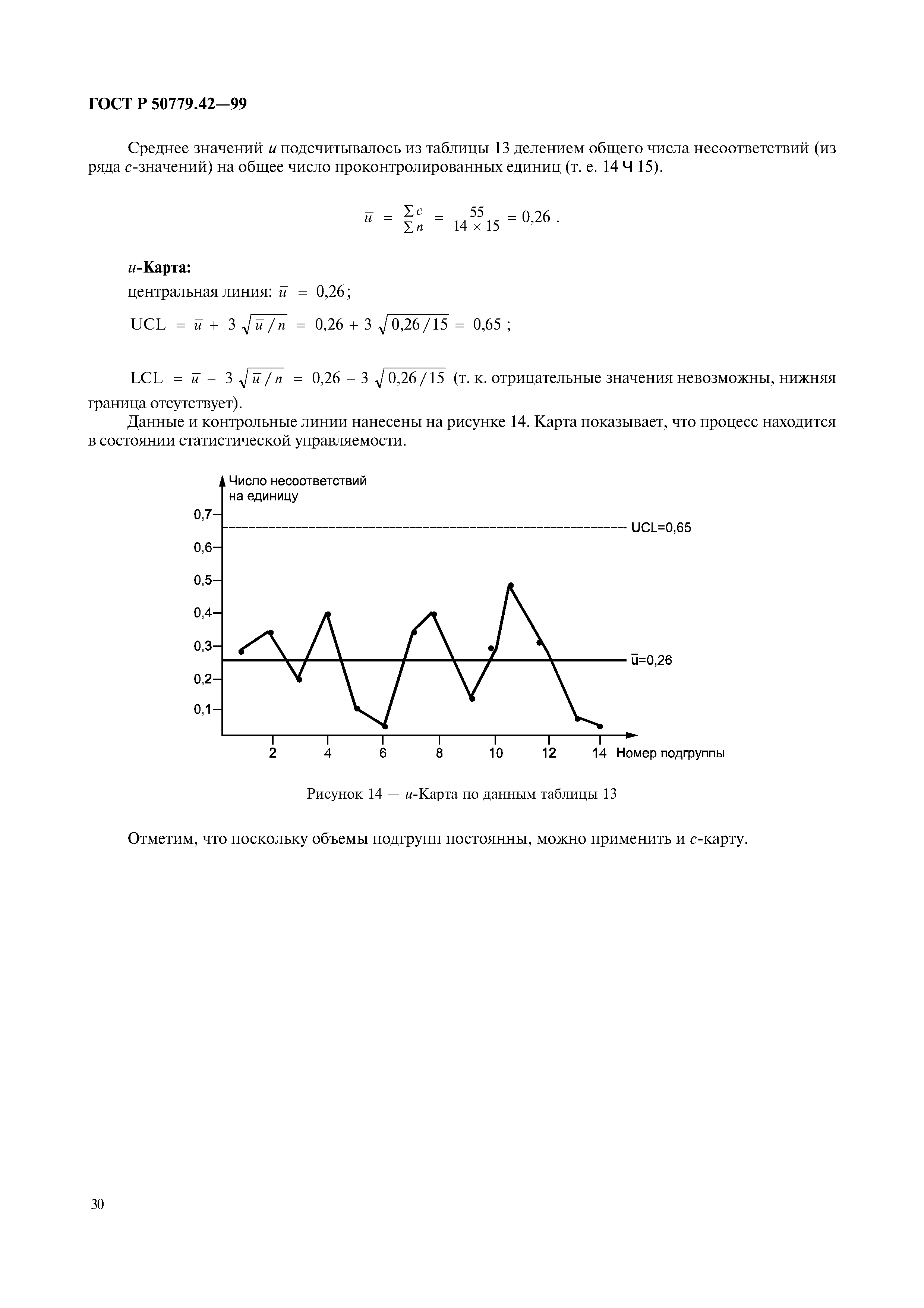 Оптимизация бизнеса с использованием контрольных карт Шухарта / Understanding Statistical Process Control, Donald J. Wheeler.

[9], [19], [20], [21], [25], [26], [29], [31], [33], [34] — Дональд Уилер. Статьи в научных изданиях о применении контрольных карт Шухарта в промышленности.

[2] — У. Эдвардс Деминг, «Выход из кризиса: Новая парадигма управления людьми, системами и процессами» / «Out of the Crisis», W. Edwards Deming.

[11] ГОСТ Р ИСО 7870-1-2011 (ISO 7870-1:2007), ГОСТ Р ИСО 7870-2-2015 (ISO 7870-2:2013) — Статистические методы. Контрольные карты Шухарта.

[12] ГОСТ 51814.3-2001 – Системы качества в автомобилестроении. Методы статистического управления процессами.

[22] The Boeing Company «Advanced Quality System Tools» (Передовые инструменты системы качества), 1998г.

 

 

 

​

 

Статистический контроль открывает дорогу к улучшениям и инженерным инновациям, дает возможность измерить результаты любых попыток улучшений, делает процесс по-настоящему прозрачным и измеримым.

— [2] Э. Деминг

 

​

 

 

Предложение

 

Приобретая наш программный продукт, вы получаете возможность автоматизации статистического управления процессами (Statistical Process Control, SPC) и доступ к уникальным компетенциям применения контрольных карт Шухарта для совершенствования бизнеса в целом.

 

Разработанная и поддерживаемая нами программа служит для глубокого анализа ваших данных с использованием простых графических методов и включает следующие инструменты:

 

• Контрольная XmR-карта индивидуальных значений и скользящих размахов, также используемая для категоризированных данных (подсчётов, атрибутивных данных) вместо часто ошибочно применяемых p-, np-, c- и u-карт;
• Контрольная XbarR-карта для средних и размахов подгрупп, с выбором размера подгруппы от 2 до 100, при том что в [11] ГОСТ Р ИСО 7870-2-2015 имеются коэффициенты для построения контрольных XbarR-карт только до 25 подгрупп;
• Гистограмма распределения индивидуальных значений с границами поля допуска (спецификации) с возможностью модификации границ допусков по данным об ошибке и смещении стабильной системы измерения;
• Оценка измерительных систем;
• Диаграммы Парето по частоте и весу событий,

 

соответствует требованиям российских ГОСТ, зарубежных стандартов ISO и самым последним методологиям в области статистических методов управления процессами (Statistical Process Control, SPC).

 

 

 

​

 

Статистическое управление процессами — это в первую очередь целое мировоззрение, подкрепленное определенными методами. Это способ мышления, и в этом вся суть. Без такого мышления методы совершенно бесполезны! Обозначить важность контрольных карт для непрерывного совершенствования может только высшее руководство. Если высшее руководство оказывает этому активную поддержку, потенциальный эффект от внедрения контрольных карт превзойдет все ожидания!

— [4] Дональд Уилер

 

​

 

 

 

 

Функции нашего программного обеспечения SPC для Excel

 

​

— 1 —

 

Зональные критерии Western Electric

 

Построение отчёта с контрольными картами Шухарта и гистограммой распределения строится в один клик после вставки ваших данных. Вы можете выбирать любые правила, применяемые к точкам на контрольной карте, для выделения красным цветом и формой в соответствии с зональными критериями Western Electric.

​

Контрольные границы процесса (красные верхняя и нижняя линии) на рисунке выше демонстрируют минимально достижимый потенциал процесса в случае идентификации и ликвидации влияния особых причин вариабельности, которые явно проявились в красных точках.

​

— 2 —

Подписи к точкам

 

Вы можете дополнительно вывести/удалить подписи из поля «Дата время» и/или по данным из полей «Факторов» для которых мы предусмотрели 18 столбцов для неограниченного количества позиций из ваших 18 справочников факторов, воспользовавшись панелью управления подписями точек.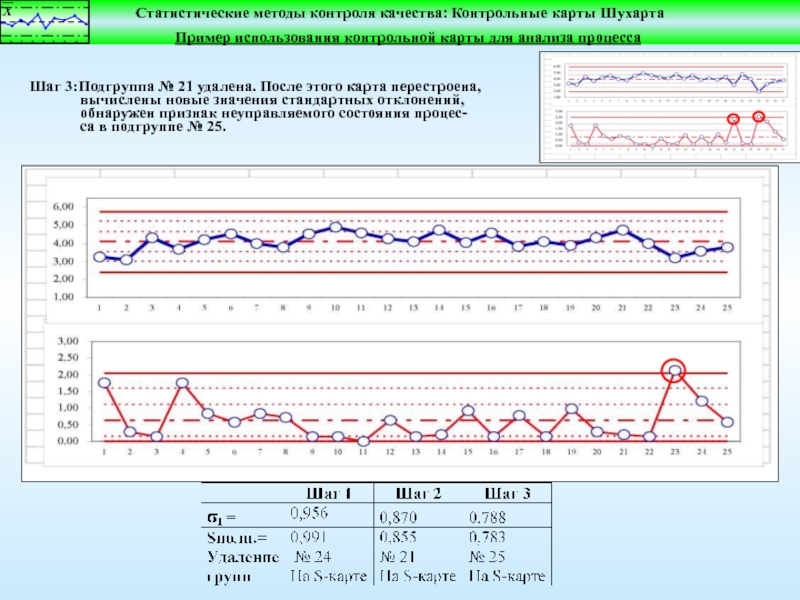 Изменение размера шрифта подписей к точкам осуществляется кнопкой со стрелками.

​

Поле «Дата и время» предназначено для записи информации о времени создания измеряемой характеристики. Порядок точек графиках на контрольных картах слева направо строится в соответствии с их расположением сверху вниз в исходных данных.

 

Поля «Факторов» позволяют фиксировать любые изменения, вносимые в процесс, например, смена инструмента, новая партия сырья, новый источник сырья, новый измерительный инструмент, оператор, корректировка станка, корректировка измерительного оборудования, изменений внешних условий и т. д., — всё, что поможет идентифицировать выявленные контрольной картой особые причины изменений процесса или, наоборот, отнести такие «Факторы» к общим причинам вариабельности (системным причинам). Переключение по записям (столбцам) факторов производится с помощью кнопок со стрелками с панели управления.

​

— 3 —

Разделители серий точек

 

Вы можете дополнительно вывести/удалить вертикальные пунктирные линии разделяющие серии точек по данным из полей «Факторов» для которых мы предусмотрели 18 столбцов  для неограниченного количества позиций из ваших 18 справочников факторов, воспользовавшись панелью управления манипуляциями с графиком.

 

Эту функцию особенно удобно использовать для визуализации условий протекания процесса, когда целые серии точек (от двух и более) находятся под действием одного фактора и для выбора необходимого поля фактора для вывода подписей к «красным» или всем точкам, см. П. 2. Используя эту функцию и функцию, описанную в П. 2, вы можете получить 18х18-18=306 перекрёстных уникальных вариантов подписей к точкам на контрольной карте и это только по количеству справочников, записанных в исходных данных факторов.

 

Использование в исходных данных полей «Факторов» при построении контрольных карт Шухарта поможет отследить значимость факторов на течение процесса. Например, вы провели мозговой штурм по причинно-следственной диаграмме Исикавы и решили, что основная причина проблемы — изменившееся сырье. Вы указываете в исходных данных с повторениями в соответствующем столбце факторов тип фактора «Сырьё» со значениями этого сырья до изменения и после, а контрольные XmR-карта индивидуальных значений или XbarR-карта (XR-карта) средних и размахов подгрупп покажут правомочность ваших предположений демонстрируя или нет изменение процесса на границе смены сырья.

​

Имеется возможность изменения высоты вертикальных пунктирных линий и подписей факторов. Эта функция может потребоваться, когда подписи факторов закрывают собой важные элементы контрольной карты.

— 4 —

Масштабирование по оси X

 

Вы можете подробно рассмотреть на экране и отправить на печать любой интересующий участок серии точек, воспользовавшись инструментом масштабирования графика контрольной карты по оси X. Дополнительно это помогает избежать наложения подписей к точкам, когда на контрольной карте их более ста.

​

​

Масштабирование по оси Y

 

Для лучшего заполнения рабочего пространства контрольной карты вы можете установить минимум по оси Y на своё усмотрение.

​

 

​

— 5 —

Практически без ограничений

 

Для любопытных мы реализовали возможность отображения на контрольных картах Шухарта до 10000 точек.

​

​

— 6 —

Закрепление контрольных пределов (прогнозирование и оперативный контроль стабильности)

 

Предусмотрена функция закрепления контрольных границ на картах Шухарта, рассчитанных до указанной точки статистически устойчивого состояния процесса и продление их пунктирной линией для прогнозирования его поведения в будущем (для нового ряда точек).

 

Функция позволяет, упростить понимание цеховым персоналом сути контрольных карт Шухарта для отслеживания изменений в процессе требующих внимания (происходящих под действием особых причин вариабельности) и оперативного реагирования для идентификации особых причин и их ликвидации. И наоборот, если наблюдаемые вариации будут вписываться в интервал между закрепленными границами, это сообщит, что корректировки процесса в этом случае лишь увеличит вариабельность (разброс данных вверх и вниз от центральной линии).

 

Другой пример использования этой функции цеховым персоналом и сотрудниками ОТК для периодического контроля используемых систем измерения в межповерочный интервал. Операторы станков используют свою измерительную систему для оценки результатов своей работы и осуществления корректировок технологического процесса, а сотрудники ОТК для контроля качества произведенной продукции. Ведите периодический ввод полученных значений повторных измерений эталона (тест-ретест) для отслеживания стабильности и смещения измерительной системы относительно закреплённых границ, например, одни раз в начале каждого рабочего дня или каждого понедельника.

 

На картинке ниже, закрепление контрольных границ произведено на шестой подгруппе (точке данных).

​

Обратите внимание на значительное упрощение интерпретации контрольной карты, а именно идентификацию сдвига процесса на рисунке выше в сравнении с контрольной картой на рисунке ниже для тех же данных, но без закрепления контрольных границ.

​

Смотрите пример использования этой функции в открытом решении: «Анализ количества исходящих контактов отдела продаж и произвольных норм, предъявляемых руководителем к продавцам».

​

​

— 7 —

 

Контрольные пределы для отдельных серий точек

 

Для нестабильных процессов предусмотрена возможность построения контрольных границ, рассчитанных для отдельных серий до указанных пользователем последних подгрупп в выбранной им серии точек (подгрупп). Это позволяет выделять области кратковременных стабильных состояний процесса. Далее вы можете заняться поиском причин, повлёкших изменения от серии к серии. Выделить кратковременный период лучшего стабильного состояния, в общем, нестабильного процесса для углублённого исследования этого периода и приведения будущего поведения всего процесса в статистически устойчивое состояние, как минимум с такими же показателями. Интерпретация такой контрольной карты даёт новое представление о процессе и позволяет произвести мероприятия для его существенного совершенствования в кратчайший период.

 

Для примера на рисунке ниже построена контрольная XmR-карта индивидуальный значений и выбраны отдельные серии первая до подгруппы 24, вторая по оставшимся точкам.

​

​

Для наглядности представляем ниже рисунок с построенной контрольной XmR-картой индивидуальный значений по тем же данным, что и на рисунке выше, но без закрепления контрольных границ для отдельных серий.

​

​

Конечно, выбор точек конца серий должен быть связан с контекстом. Например, вы знаете о каких-либо изменениях в начале следующих за ними сериях, а иногда достаточно обоснованного предположения.

 

Но контрольная карта Шухарта позволяет искать и обратную связь. Видимые различия в сериях данных позволяют задавать правильные вопросы и искать связь с контекстом. Например, контрольная карта зафиксировала изменения, и наблюдатели начинают искать связь отображённого на контрольной карте с произошедшими или происходящими событиями. Многие факторы могут даже не дифференцироваться наблюдателями, пока наблюдатели не получат от контрольной карты указания (координаты) на время начала и продолжительность их действия.

 

О таком подходе к поиску причинно-следственных связей в наблюдательных исследованиях читайте в статье [25] Дональда Уилера (ENG): «Но эти границы слишком широки! Когда диаграмма XmR, кажется, не работает».

 

Смотрите пример использования функции построения контрольных границ для отдельных серий XbarR-карты средних и размахов подгрупп в управлении продажами: «Ошибочное использование KPI в системе мотивации персонала. Или как руководство лишает себя важнейшей для управления компанией информации и разрушает командную работу».

​

​

 

 

​

— 8 —

 

Эффект объединения функций

 

При совмещении на контрольной карте двух функций описанных выше, а именно вертикальных пунктирных линий с указанием длительно действующих факторов (П. 3) и установки контрольных границ для отдельных серий точек (П. 7) — объем полезной для совершенствования информации передаваемой такой картой трудно переоценить. Смотрите рисунок ниже.

 

Вы можете легко отследить, с каким из известных и зафиксированных в данных факторов совпадают изменения процесса. Часто, когда вы только начинаете использовать контрольные карты для совершенствования процессов, изменения процесса не совпадают ни с одним зафиксированным в данных фактором. Одна из причин — влияющий на изменения процесса фактор не зафиксирован вами или он даже не определён. Ищите новые причины. Самый лучший способ отследить такие причины, вести контрольные карты на цеховом уровне операторами и контролёрами и как только процесс продемонстрирует изменения, по горячим следам произвести определение причины (фактора), характеристики которого придётся обязательно фиксировать в данных.

 

На рисунке ниже выбраны отдельные серии до подгрупп 6, 9, 12 и оставшиеся. Рисунок с некоторой степенью вероятности свидетельствует об отсутствии видимой зависимости нестабильного поведения процесса от типа фактора Операторы (верхний график) и демонстрирует вероятную зависимость нестабильности процесса с типом факторов — Партия сырья (нижний график).

​

​

​

​

Эта функция позволяет провести аналитическое исследование и в обратном порядке. Когда вы выбираете подгруппы (точки) конца серий совпадающие с границами действия фактора. Если в сериях, ограниченных действием одного типа фактора, процесс будет находиться в кратковременных стабильных состояниях, скорее всего, этот тип фактора и является особой причиной изменения процесса. Но если, наоборот, процесс даже в отдельных сериях зон действия факторов выбранного типа нестабилен — скорее всего, этот тип фактора не та причина, которую следует обвинять в нестабильности исследуемого процесса, смотрите рисунок ниже. Либо сам фактор ведёт себя непредсказуемо по особым причинам под действием другого типа фактора, с которыми вам придётся разобраться, что опять же свидетельствует о неверном предположении зависимости поведения процесса от факторов выбранного типа.

 

 

​

 

Руководящим принципом организации контрольных карт должно быть раскрытие неизвестных сторон процесса, а не демонстрация того, что и так понятно.

— [4] Дональд Уилер

 

​

 

 

При разделении процесса на отдельные серии с соответствующими  контрольными пределами вы можете использовать все четыре правила зональных критериев Western Electric.

 

На рисунке ниже выбраны отдельные серии границам зон действия выбранного типа факторов до подгрупп 6, 13 и оставшиеся.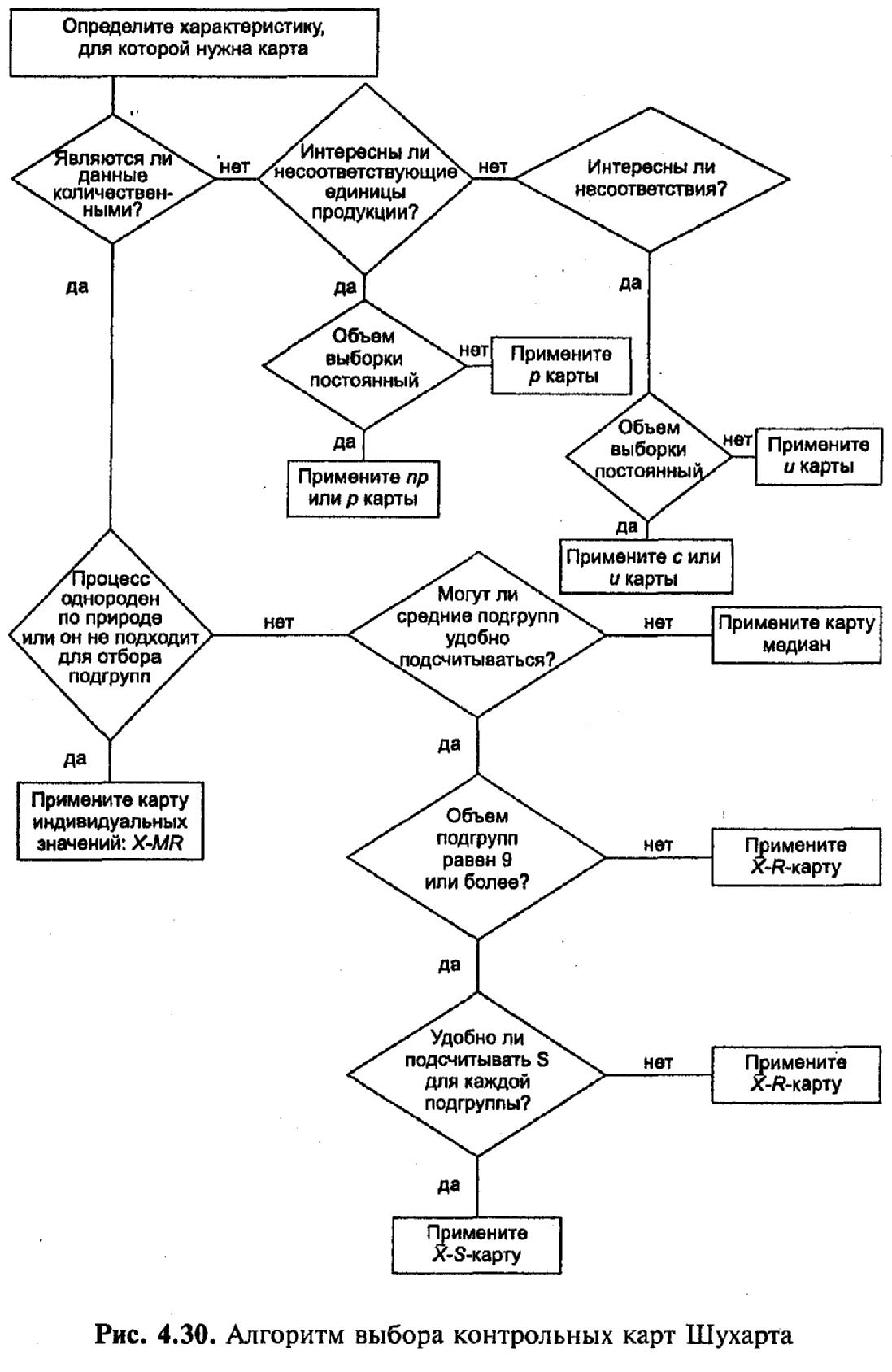

​

​

 

​

— 9 —

Разрыв соединительной линии для визуального отделения серий точек

 

Функция разрыва соединительной линии для визуального отделения серий точек в соответствии с зонами действия факторов, выведенных в виде вертикальных пунктирных линий, позволяет существенно облегчить интерпретацию контрольных карт Шухарта и особенно полезна при анализе функционирования различных объектов относительно возможностей системы, для определения тех кто работает в пределах системы или вне её с худшими или лучшими результатами. Эта функция незаменима при проведении оценки процесса измерений (Evaluating the Measurement Process, EMP), смотрите пример использования для этой цели в п. 17.

​

​

Смотрите открытое решение «Ошибочное использование KPI в системе мотивации персонала. Или как руководство лишает себя важнейшей для управления компанией информации и разрушает командную работу».

— 10 —

Гистограмма, контрольные пределы, допуски, Cp, Cpk

 

На графике гистограммы индивидуальных значений отображаются контрольные границы процесса, полученные в результате автоматизированного расчёта по вашим данным и установленные границы допуска (спецификации).

​Автоматически рассчитываются индексы воспроизводимости Cp (жизненное пространство процесса относительно поля допуска), Cpk (центрированность процесса в поле допуска), минимальные и максимальные индивидуальные значения, количество точек выше или ниже контрольных границ и границ допусков.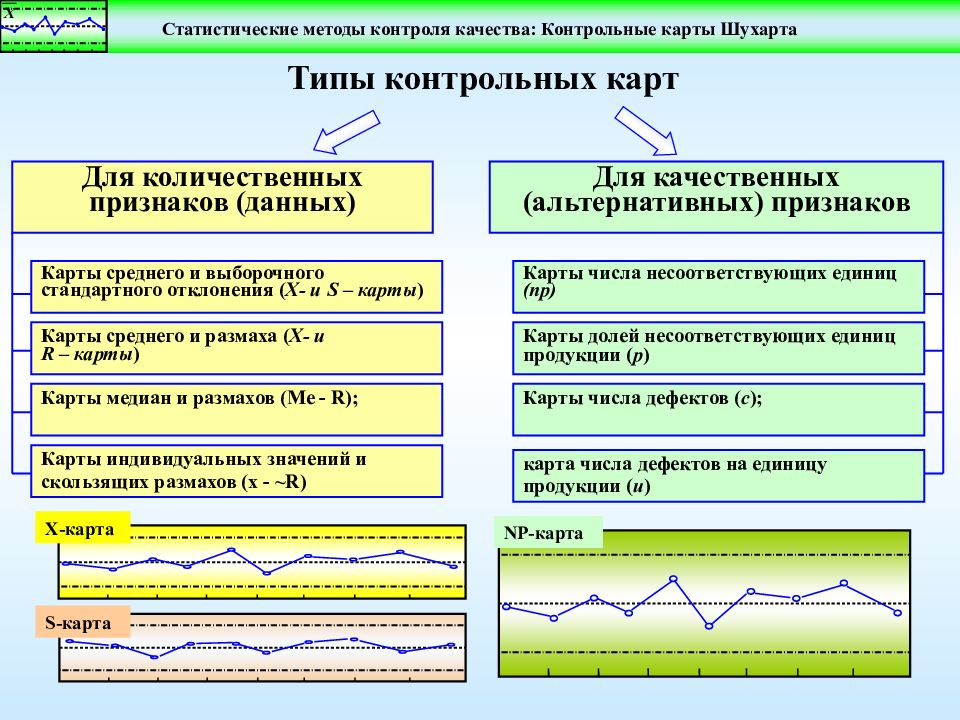

 

Внимание! Если процесс находится в статистически неуправляемом состоянии, индексы Cp, Cpk не имеют смысла, такой процесс по определению невоспроизводим. Мы делаем напоминание об этом красным шрифтом, когда контрольная карта демонстрирует нестабильное состояние процесса.

​

— 11 —

Производственные суженые допуски

 

Уникальная востребованная практиками в области качества функция, которой нет ни у одного из поставщиков ПО класса Quality Management.

 

Если ваша система измерений находится в статистически устойчивом состоянии (оценивается с помощью XmR-карты 25-30 измерений тест-ретест одного и того же стандарта), то на графике гистограммы индивидуальных значений вместе с контрольными границами процесса, могут быть отображены границы производственного допуска (спецификации), полученные с учётом ошибки и смещения измерительной системы для выбранных пользователем минимальных вероятностей (85%, 96%, 99% и 99,9%) соответствия допускам продукции. Эта функция используется при разделении продукции на годную и негодную с учётом соответственного сужения установленных границ клиентских допусков от одной до четырёх вероятностных ошибок системы измерений с каждой стороны соответственно.

 

Подробно о методе установки производственных допусков смотрите статью: «Соответствующая спецификации продукция действительно соответствующая?».

​

​

​

— 12 —

Ручной ввод данных в онлайн

 

Просто установите компьютер с нашим программным обеспечением у рабочего места оператора в цехе и начните работу с качеством производства на новом уровне.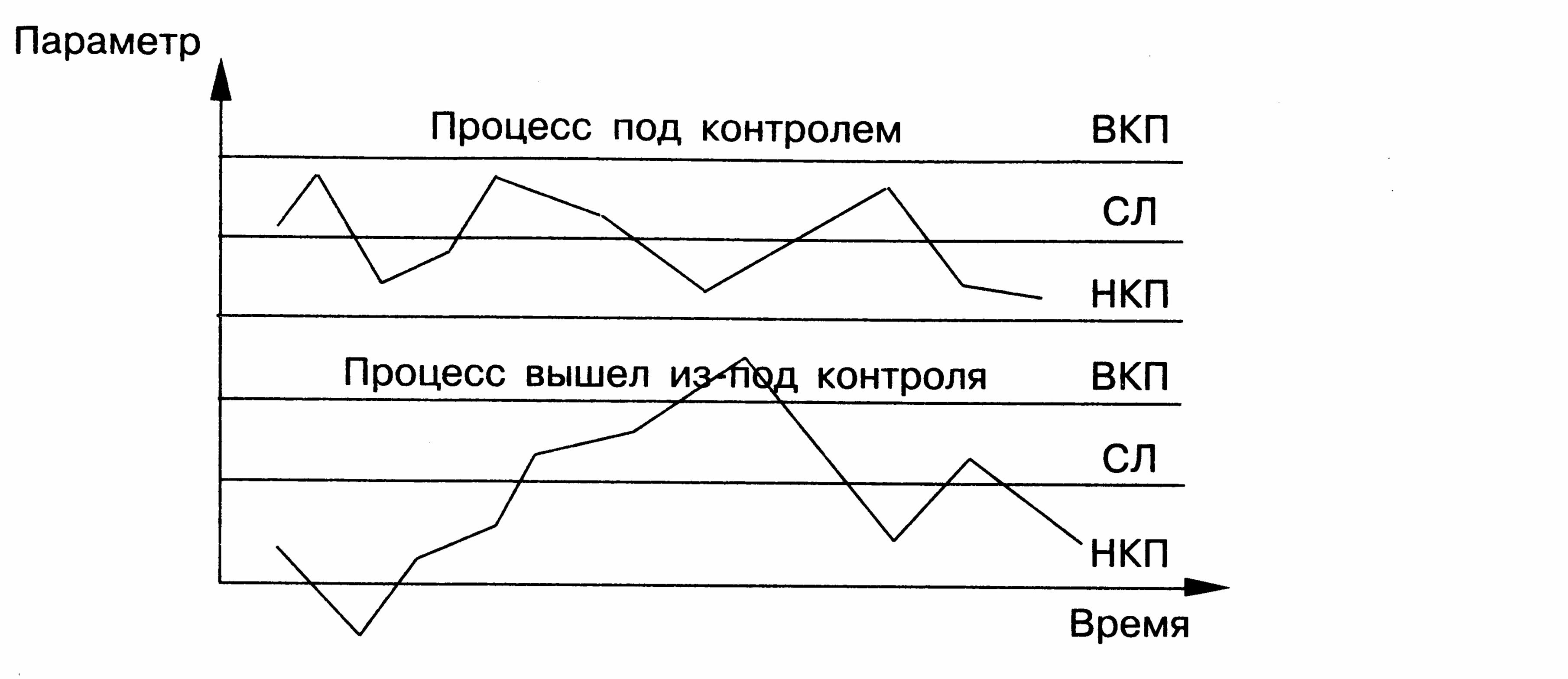 Это лучшее место установки нашего ПО для контроля своих процессов операторами, операторы всегда производят 100%-й контроль производимой ими продукции, в отличии от выборочного контроля сотрудниками ОТК.

 

В оперативном режиме оператор может продолжать вести контрольную карту и отслеживать положение каждой новой точки относительно автоматически пересчитываемых или закрепленных контрольных границ, см. пункт 6 и 7 выше. Анализ контрольных карт Шухарта в реальном времени это лучший способ их применения на практике. Наше программное обеспечение позволяет пользователю достоверно интерпретировать контрольную карту по мере её заполнения, чтобы она смогла своевременно пролить свет на природу различных источников вариабельности наблюдаемого процесса. Более того, индивидуальное использование контрольных карт операторами станков естественным образом защищает компанию от проблем, возникающих из-за смешивания продукта из разных источников.

 

 

​

 

Эксперименты на смеси продуктов могут ухудшать шансы на улучшение.

— [2] Э. Деминг

 

​

 

 

​

 

Функция ручного ввода новых данных позволяет строить новую контрольную карту с первой точки или продолжить ввод новых данных для предварительно построенной по историческим данным контрольной карты и гистограммы с сохранением всех настроек, произведённых в отчёте до введения значения новой точки, в том числе допуски, отдельные зоны контрольной карты, подписи к точкам и т. д.

 

Поле «Фактор» позволяет фиксировать любые изменения, вносимые в процесс, например, смена инструмента, новая партия сырья, новый источник сырья, новый измерительный инструмент, оператор и т. д., — всё, что поможет идентифицировать выявленные контрольной картой особые причины изменений процесса или, наоборот, отнести такие «Факторы» к общим причинам вариабельности (системным причинам). Такие факторы могут быть выведены на контрольную карту в виде подписей к точкам, смотрите описание функций в пунктах 2 или в виде вертикальных пунктирных линий зон действия факторов, см. пункт 3 выше.

 

Для упрощения работы с ручным вводом поле «Дата и время» заполняется  автоматически текущим временем с возможностью изменения пользователем. Поле ввода факторов с контекстно-зависимым выпадающим списком служит для записи зафиксированных наблюдателем связанных факторов. Если в выпадающем списке соответствующего типа факторов не окажется необходимого значения оператор может ввести новое обозначение, которое появится в списке при вводе им следующих точек. Впоследствии аналитик сможет переименовать или добавить столбцы новых типов и значений факторов в исходную таблицу на основании информации зафиксированной наблюдателем в поле «Прочее» или при выявлении новых типов факторов. Способ выбора типа фактора в форме ручного ввода данных напоминает наблюдателю о необходимости указать фактор на каждом последовательном шаге обхода всех типов факторов.

 

​

​

 

Более того, на листе с исходными данными в поле «Отметка ручного ввода» автоматически вписывается время внесения новой строки через ручной ввод.

— 13 —

 

Печать отчетов

 

Печать отчёта в альбомной форме на двух листах А4 позволяет работать с распечатанными контрольными картами и гистограммой распределения индивидуальных значений с границами допуска (спецификации), смотрите пример.

​

 

​

— 14 —

 

Контекстная помощь (подсказки)

 

Все функции ПО Контрольные карты Шухарта имеют кнопки вызова окна информации с кратким описанием и ссылками на статьи на нашем сайте с подробными пояснениями и примерами. Эта контекстная помощь позволяет начать полезное использование нашего программного обеспечения с первого запуска и не требует изучения многостраничных инструкций.

​

​

​

— 15 —

 

Система измерений

 

Система измерения, это результат взаимодействия используемого измерительного инструмента, метода измерения, окружающей среды и оператора. Каждый оператор станка, который производит измерения детали в ходе её изготовления является частью своей измерительной системы, имеющей свою неопределённость (вариабельность, ошибку), смещение и может находиться в статистически управляемом (стабильном) или неуправляемом (непредсказуемом) состоянии. Система измерений, находящаяся в статистически неуправляемом состоянии — бесполезна. Измерительная система контролёров — это другая измерительная система. Когда оператор передаёт произведённую им продукцию на контроль, он определяет её соответствие допускам посредством своей уникальной системы измерений. Оценку измерительных систем необходимо производить до начала мониторинга рабочих процессов.

 

Программа имеет функцию определения эффективного приращения (инкремента) измерительной системы.

​

​

​

 

Эффективный шаг записи значений измерений (минимальное приращение, инкремент), находится в диапазоне значений от 0,2 до 2 вероятностных ошибок системы измерений. Вероятностная ошибка системы измерений, в свою очередь, определяется как 0,675*сигма стабильной измерительной системы. Иначе, при использовании шага измерений меньше 0,2 вероятностной ошибки мы будем записывать шум, а при записях с шагом боле чем две вероятностной ошибки мы потеряем важную для анализа информацию, получив неадекватные единицы измерения.

— [20] Дональд Уилер

 

​

 

 

Для подробного пояснения смотрите статью: «Построение контрольных карт по неадекватным единицам измерения ведет к ошибочным выводам».

— 16 —

 

Проверка обнаруживаемого смещения измерительной системы

 

Функция проверки обнаруживаемого контрольной картой смещения измерительной системы, находящейся в статистически управляемом состоянии, сообщает, когда действительно стоит задуматься о её настройке. На рисунке ниже проверка обнаружила смещение измерительной системы.

 

Если же вам приходится сортировать продукцию относительно границ допуска на годную и негодную вы можете воспользоваться функцией, описанной в п. 11 «Производственные суженые допуски» для получения компенсирующего смещения допуска на величину смещения измерительной системы, находящейся в статистически устойчивом состоянии.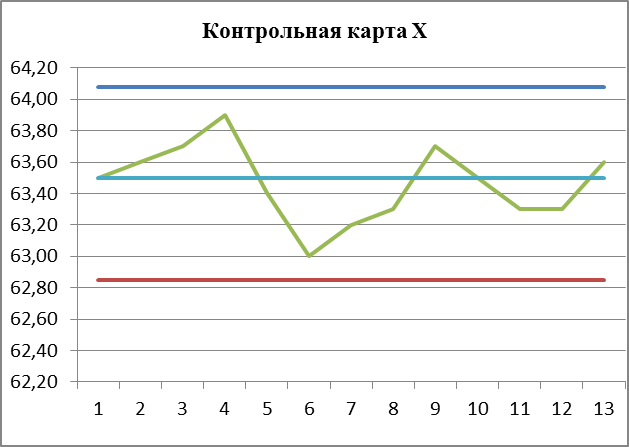

​

​

 

​

 

Простой способ графически проверить значимость смещения измерительной системы состоит в том, чтобы сдвинуть центральную линию и контрольные пределы для диаграммы X (XmR-карты), так чтобы центральная линия оказалась на значении стандарта, используемого в испытаниях тест-ретест (многократные измерения одного и того же эталона).

Если сдвиг Центральной линии и пределов относительно ряда данных не приводит к появлению сигналов (красных точек) за границами этих пределов и каких-либо длинных серий выше или ниже центральной линии, или каких-либо других сигналов, то в измерительной системе не наблюдается обнаруживаемого смещения.

  — [33] Дональд Уилер, статья «Диаграммы Согласованности»

 

​

​

— 17 —

 

Оценка процесса измерений (Evaluating the Measurement Process, EMP)

 

С помощью нашего ПО вы можете провести оценку процесса измерений (Evaluating the Measurement Process, EMP), которая будет понятна всем, кому вы решите показать результаты, от операторов производящих измерения до высшего менеджмента.

​

​

О чем же говорит контрольная XbarR-карта средних и размахов подгрупп построенная по данным исследования измерительного процесса, см. рисунок выше?

 

Оператор 5 имеет большие размахи подгрупп, плохой параллелизм и неправильное среднее значение для этих четырех частей. Что бы вы ни говорили о нем, он явно не знает, как пользоваться измерительным оборудованием. Он должен быть перемещен на другую работу до тех пор, пока он не сможет обучиться тому, как использовать это устройство, и не сможет показать уровень квалификации, сопоставимый с тем, который отображается другими операторами.

В то время как операторы 3 и 4 могут нуждаться в повторном обучении при использовании измерительного оборудования.

 

 

 

​

 

В исследовании EMP мы пытаемся определить, можем ли мы обнаружить различия между деталями из потока процесса, несмотря на неопределенность, вызванную ошибкой измерения. Этот сдвиг как в характере данных, так и в характере наших вопросов изменит способ интерпретации диаграммы средних и размахов подгрупп для исследования EMP.

 

Хотя подход EMP может быть адаптирован ко многим различным структурам данных и схемам сбора данных, мы проиллюстрируем базовое исследование EMP с использованием той же стратегии сбора данных, которая используется в исследовании калибровочных исследования (gauge R&R). Простой, полностью скрещенный эксперимент выполняется, когда два или более операторов измеряют каждую из трех-десяти деталей три или четыре раза каждый.

 

  — [34] Дональд Уилер, статья «Лучший способ сделать исследования R&R. Оценка процесса измерений». (A Better Way to Do R&R Studies. The Evaluating the Measurement Process Approach)

 

​

 

 

В представленной выше цитате Д.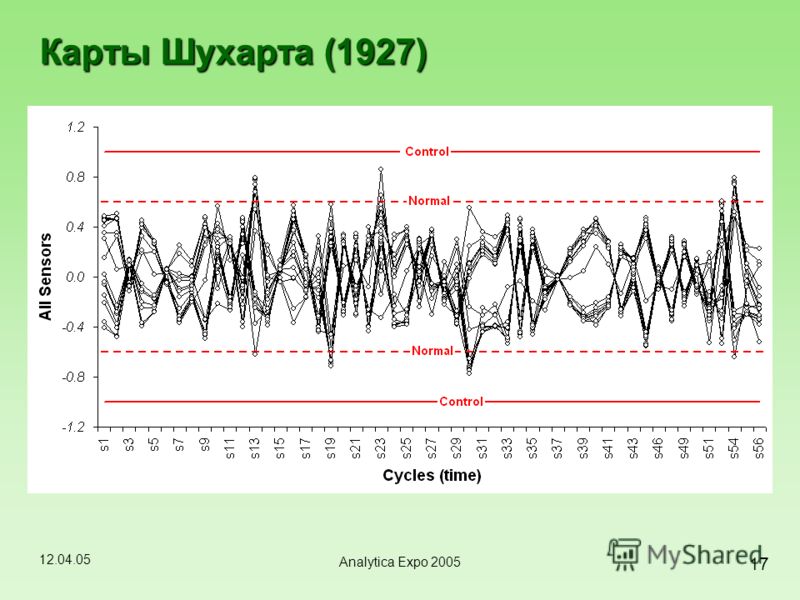 Уилера говорится об отличительной особенности XbarR-карты в возможности локализации информации об ошибке повторных измерений деталей (тест-ретест) в подгруппах на R-карте размахов, при этом различия между деталями из потока процесса (ширина зоны, заполняемой точками) и операторами (параллелизм и положение) будут представлены средними подгрупп на X-карте. Более того, ширина контрольных пределов на X-карте позволит оценить относительную полезность (пригодность) измерительной системы для отслеживания поведения процесса, производящего анализируемые детали — чем больше точек окажется вне контрольных пределов, тем лучше ваша измерительная система: «Это сдвиг как в характере данных, так и в характере наших вопросов изменит способ интерпретации диаграммы средних и размахов подгрупп».

 

В наших обучающих семинарах мы простым языком объясняем суть методов оценки измерительных систем с применением нашего программного обеспечения. В ближайшее время мы подготовим статью по этой теме.

— 18 —

 

Векторная графика обеспечивает высочайшее качество картинок

 

Вы можете скопировать графики контрольных карт Шухарта и гистограмм распределения индивидуальных значений со всей выведенной на них информацией в буфер обмена в высоком разрешении и вставить в любые собственные формы отчётов и презентации.

​

 

 

 

Дополнительные инструменты

 

​

— 1 —

 

Диаграммы Парето

 

Построение диаграммы Парето с графиком кумулятивного процента осуществляется на двух диаграммах. Одна без учёта веса событий, другая с учётом их веса. Весом единицы события (значимость) может быть любая измеримая величина потерь, например, время или стоимость. Даже если события не имеют численного измерения, вы можете разработать собственное операциональное определение и использовать присвоенный им численный эквивалент размерности, подобно тому, как это реализовано в методологии FMEA. Вы можете строить диаграммы Парето вставив заранее подготовленные данные в таблицу исходных данных программы или производить ручной ввод через форму с возможность продолжения ввода или построения диаграмм Парето «с нуля».

 

Вы можете строить гистограммы по типам дефектов, типам жалоб клиентов, видам травм на предприятии, причинам возврата товара, причинам простоя, причинам просроченных заказов, причинам недовольства персонала и т. д. А при накоплении достаточного объема данных подсчётов событий (альтернативных данных) можно будет оценить стабильность их появления с помощью контрольной XmR-карты Шухарта, что даст возможность определить один из двух противоположных методов улучшения этого показателя. О правиле определения достаточности данных можно узнать из статьи: Контрольные карты для альтернативных данных (подсчётов) p-карта, np-карта, C-карта и u-карта или XmR-карта индивидуальных значений?

​

​

 

Диаграммы Парето служат лучшим графическим дополнением к инструментам Анализа видов и последствий отказов FMEA (Failure Mode and Effects Analysis), используемого, как основы риск-ориентированного мышления и менеджмента рисков.

 

Например, в FMEA:

• значимость (вес, тяжесть) последствий отказа устанавливается в диапазоне от 1 до 10, где 1 – определяет незначительные последствия, 10 – катастрофические последствия;
• шанс возникновения причины отказа устанавливается в диапазоне от 1 до 10, где 1 – маловероятно, 10 – неизбежно;
• шанс обнаружения возникших причин отказов, или их последствий устанавливается в диапазоне от 1 до 10, где 1 – абсолютно точно проблема будет обнаружена, 10 – проблему обнаружить невозможно или контроль отсутствует вообще.

 

 

 

 

 

СЕРТИФИКАТ БЕЗОПАСНОСТИ КОДА

 

​

 

Мы получили международный сертификат безопасности кода (Code Signing Certificate) нашего программного обеспечения от аккредитованного Microsoft центра сертификации Sectigo.

 

 

 

Цены

 

​

НДС не облагается.

 

 

Скидки

 

От двух до трёх лицензий — скидка 10%.

От четырёх до десяти лицензий — скидка 20%.

От одиннадцати и более — скидка 30%.

 

 

 

​

 

Статистическое управление процессами — это в первую очередь целое мировоззрение, подкрепленное определенными методами. Это способ мышления, и в этом вся суть. Без такого мышления методы совершенно бесполезны! Обозначить важность контрольных карт для непрерывного совершенствования может только высшее руководство. Если высшее руководство оказывает этому активную поддержку, потенциальный эффект от внедрения контрольных карт превзойдет все ожидания!

— [4] Дональд Уилер

 

​

 

 

 

Качество исходных данных

 

В абсолютном большинстве случаев в компаниях в качестве исходных данных используются имеющиеся данные, которые собирались для других целей (акты браковки, рекламации, количественный анализ и т.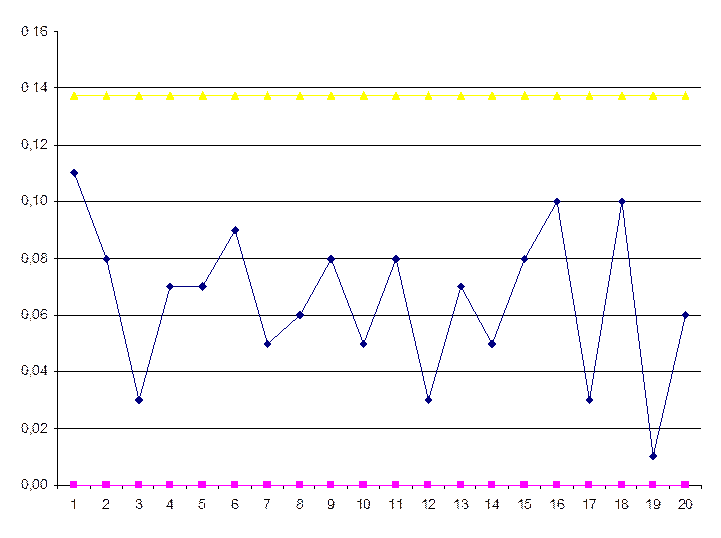 п.) и не подходят для эффективного использования контрольных карт Шухарта.

 

«Мусор на входе — мусор на выходе» (GIGO, Garbage In, Garbage Out)

 

В 99% случаев данные различных производственных процессов, предоставляемые нам для анализа, вообще не содержат информации о причинных факторах, в то время как наше ПО позволяет вести учёт одновременно до 18 таких факторов.

 

По нашему мнению, именно этот фактор не позволяет этим компаниям достигать даже малой части пользы, которую несут в себе контрольные карты Шухарта. Мы готовы оказать помощь в разработке плана сбора данных для эффективного применения контрольных карт Шухарта в каждом конкретном случае.

12 Примеры контрольных карт для количественных данных

12.1 — и-карты. Стандартные значения заданы

Менеджер по качеству импортера чая на основании подобных процессов предъявляет требования к процессу упаковки такие, чтобы средний вес упаковки был 100,6 г и предполагаемое стандартное отклонение процесса равно 1,4 г — получено на основе аналогичных упаковочных процессов.

Поскольку стандартные значения даны (= 100,6;= 1,4), контрольную карту средних и карту размахов можно построить с использованием формул, приведенных в таблице 1 и коэффициентов,,и, приведенных в таблице 2 для= 5.

-КАРТА:

центральная линия: = 100,6 г

= 100,6 + (1,342 х 1,4) = 102,5 г

= 100,6 — (1,342 x 1,4) = 98,7 г

-КАРТА:

центральная линия: = 2,326 х 1,4 = 3,3 г

= 4,918 х 1,4 = 6,9 г

= 0 х 1,4 = 0

(т.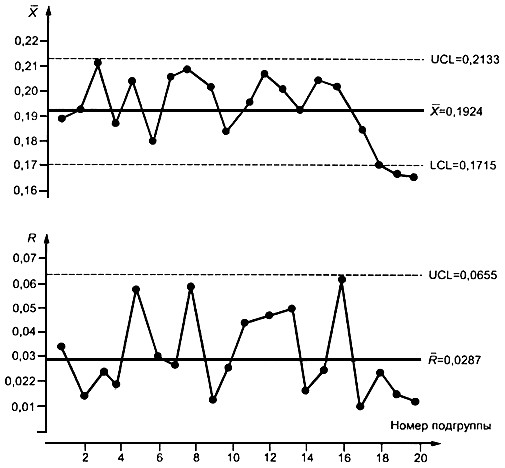 к. < 7, то LCL отсутствует)

Для контроля следует взять 25 выборок объема 5. Значения их средних и размахов приведены в таблице 6. На рисунке 5 они нанесены вместе с контрольными границами.

Таблица 6 — Процесс упаковки чая

Номер подгруппы	Среднее подгруппы	Размах подгруппы
1	100,6	3,4
2	101,3	4,0
3	99,6	2,2
4	100,5	4,5
5	99,9	4,8
6	99,5	3,8
7	100,4	4,1
8	100,5	1,7
9	101,1	2,2
10	100,3	4,6
11	100,1	5,0
12	99,6	6,1
13	99,2	3,5
14	99,4	5,1
15	99,4	4,5
16	99,6	4,1
17	99,3	4,7
18	99,9	5,0
19	100,5	3,9
20	99,5	4,7
21	100,1	4,6
22	100,4	4,4
23	101,1	4,9
24	99,9	4,7
25	99,7	3,4

Рисунок 5 — Карты средних и размахов по данным таблицы 6

Карты, изображенные на рисунке 5, показывают, что процесс не находится в статистически управляемом состоянии на требуемом уровне, так как есть последовательность из 20 точек, лежащих ниже центральной линии на -карте и последовательность из 21 точек выше центральной линии на-карте.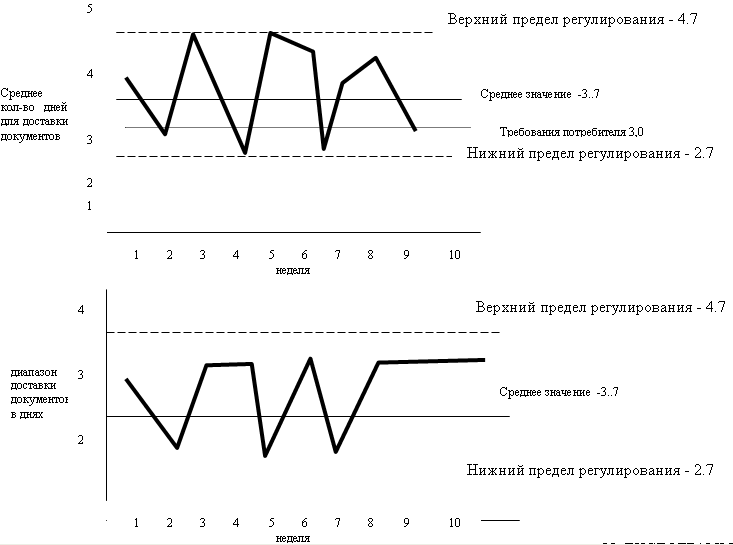 Причина столь длинной последовательности низких значений среднего должна быть исследована и устранена.

12.2 — и -карты. Стандартные значения не заданы

В таблице 7 приведены результаты измерений внешнего радиуса втулки. Каждые полчаса делалось четыре измерения, всего взято 20 выборок. Средние и размахи подгрупп также приведены в таблице 7. Установлены предельно допустимые значения внешнего радиуса: 0,219 и 0,125 дм. Цель — определение показателей процесса и управление им по настройке и разбросу так, чтобы он соответствовал установленным требованиям.

Таблица 7 — Производственные данные для внешнего радиуса втулки

Номер подгруппы	Радиус				Среднее	Размах
1	0,1898	0,1729	0,2067	0,1898	0,1898	0,0338
2	0,2012	0,1913	0,1878	0,1921	0,1931	0,0134
3	0,2217	0,2192	0,2078	0,1980	0,2117	0,0237
4	0,1832	0,1812	0,1963	0,1800	0,1852	0,0163
5	0,1692	0,2263	0,2066	0,2091	0,2033	0,0571
6	0,1621	0,1832	0,1914	0,1783	0,1788	0,0293
7	0,2001	0,1937	0,2169	0,2082	0,2045	0,0242
8	0,2401	0,1825	0,1910	0,2264	0,2100	0,0576
9	0,1996	0,1980	0,2076	0,2023	0,2019	0,0096
10	0,1783	0,1715	0,1829	0,1961	0,1822	0,0246
11	0,2166	0,1748	0,1960	0,1923	0,1949	0,0418
12	0,1924	0,1984	0,2377	0,2003	0,2072	0,0453
13	0,1768	0,1986	0,2241	0,2022	0,2004	0,0473
14	0,1923	0,1876	0,1903	0,1986	0,1922	0,0110
15	0,1924	0,1996	0,2120	0,2160	0,2050	0,0236
16	0,1720	0,1940	0,2116	0,2320	0,2049	0,0600
17	0,1824	0,1790	0,1876	0,1821	0,1828	0,0086
18	0,1812	0,1585	0,1699	0,1680	0,1694	0,0227
19	0,1700	0,1567	0,1694	0,1702	0,1666	0,0135
20	0,1698	0,1664	0,1700	0,1600	0,1655	0,0100

= 0,1924, = 0,0287,

где — число подгрупп, = 20.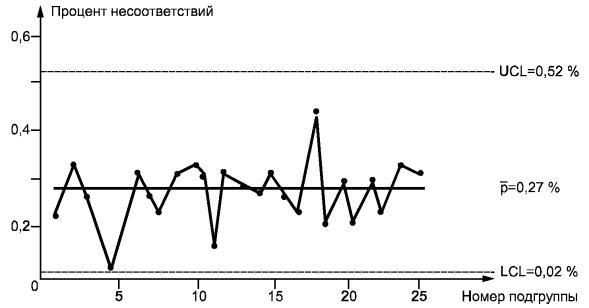

Первый шаг: построение -карты и определение по ней состояния процесса.

-КАРТА:

центральная линия: = 0,0287;

= 2,282 х 0,0287 = 0,0655;

= 0 х 0,0287 = 0 (т.к. < 7, то LCL отсутствует).

Значения множителей ивзяты из таблицы 2 для= 4. Поскольку значенияв таблице 7 находятся внутри контрольных границ,-карта указывает на статистически управляемое состояние. Значениетеперь может быть использовано для вычисления контрольных границ-карты.

—КАРТА.

Центральная линия: = 0,1924;

= 0,1924 + (0,729 x 0,0287) = 0,2133;

= 0,1924 — (0,729 x 0,0287) = 0,1715.

Значение множителя берется из таблицы 2 для= 4.

и -карты представлены на рисунке 6. Анализ-карты показывает, что последние три точки вышли за границы. Это указывает на возможность действия некоторых особых причин вариаций. Если пределы были вычислены на основе предыдущих данных, то должно быть предпринято действие в точке, соответствующей 18-й подгруппе.

Рисунок 6 — Карты средних и размахов по данным таблицы 7

В этой точке процесса следует произвести соответствующее корректирующее действие, чтобы устранить особые причины и предотвратить их повторение. Работа с картами продолжается после установления пересмотренных контрольных границ без исключенных точек, которые вышли за старые границы, т.е. значений для выборок N 18, 19 и 20. Значения ,и линии контрольной карты пересчитывают следующим образом:

пересмотренное значение = 0,1968,

пересмотренное значение = 0,0310,

пересмотренная -карта имеет следующие параметры:

центральная линия: = 0,1968;

= 0,1968 + (0,729 x 0,0310) = 0,2194;

= 0,1966 — (0,729 x 0,0310) = 0,1742.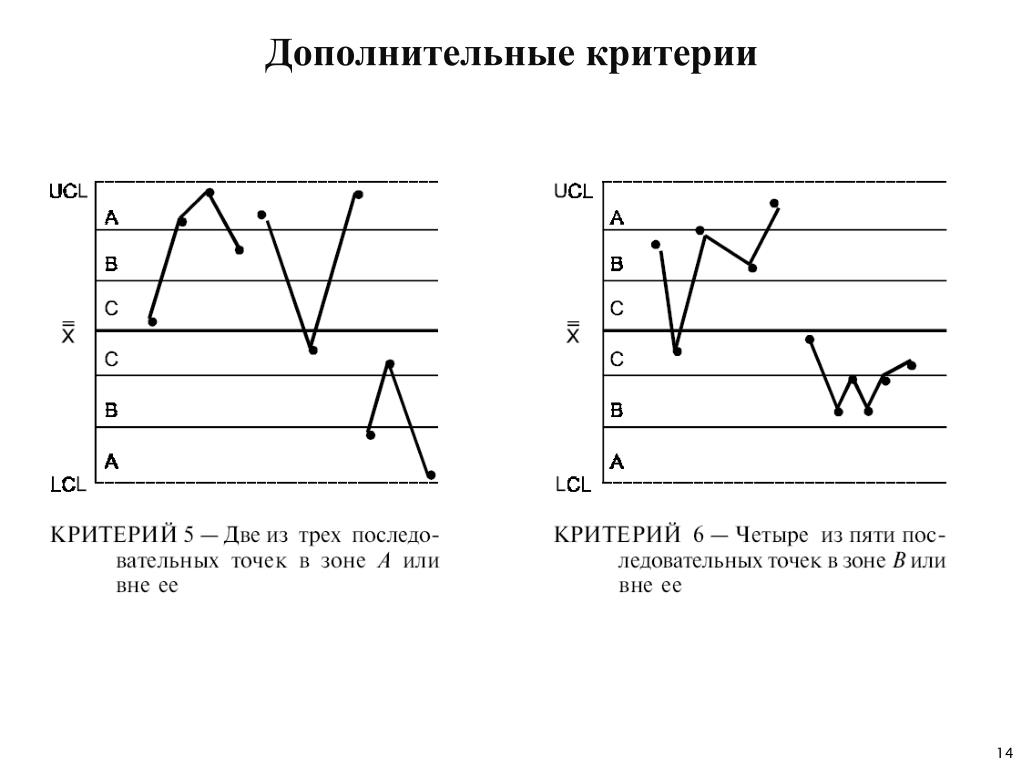

пересмотренная -карта:

центральная линия: = 0,0310;

= 2,282 x 0,0310 = 0,0707;

= 0 x 0,0310 = (т.к. < 7, LCL отсутствует).

Рисунок 7 — Пересмотренные — и -карты по данным таблицы 7

Для стабильного процесса с пересмотренными контрольными границами можно оценить возможности. Вычисляем индекс возможностей:

,

где оценивается как= 0,0310/2,059 = 0,0151;

значение постоянной берется из таблицы 2 для= 4.

Таким образом,

Поскольку больше 1, возможности процесса можно считать приемлемыми. Однако при тщательном изучении можно увидеть, что процесс не настроен правильно относительно допуска и поэтому около 11,8% единиц будут выходить за установленное верхнее предельно допустимое значение. Поэтому, прежде чем установить постоянные параметры контрольных карт, надо попытаться правильно настроить процесс, поддерживая его при этом в статистически управляемом состоянии.

Контрольные карты

При организации любого производственного процесса возникает задача установки пределов характеристик изделия, в рамках которых произведенная продукция удовлетворяет своему предназначению. Вообще говоря, существует два «врага» качества продукции: (1) отклонения от плановых спецификаций и (2) слишком большой разброс реальных характеристик изделий (относительно плановых спецификаций). На ранних стадиях отладки производственного процесса для оптимизации этих двух показателей качества часто используются методы планирования.

Общий подход к текущему контролю качества достаточно прост. В процессе производства проводятся выборки изделий заданного объема. После этого на специально разлинованной бумаге строятся диаграммы изменчивости выборочных значений плановых спецификаций в этих выборках и рассматривается степень их близости к заданным значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или оказывается, что выборочные значения находятся вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки. Иногда такие специально разлинованные бумаги называют контрольными картами Шухарта (в честь W. A. Shewhart, который общепризнанно считается первым, применившим на практике описываемые здесь методы анализа в 1924 г).

Виды контрольный карт

по шкале измерения

§     качественные

§     количественные

По выборочному параметру

§     среднего

§     среднеквадратического отклонения

§     медиана

§     размах

Контрольные карты по количественным признакам

Контрольные карты используются для статистического контроля и регулирования технологического процесса. На контрольную карту наносят значения некоторой статистической характеристики (точки), рассчитываемые по данным выборок в порядке их получения, верхнюю и нижнюю контрольные границы К_в (или UCL) и К_н (или LCL), верхнюю и нижнюю границы технических допусков Т_в и Т_н (при их наличии), а также среднюю линию (CL). Иногда используют также предупредительные границы К_п. Для расчёта границ и построения контрольной карты используют обычно 20…30 точек. Пример контрольной карты представлен на рисунке 6.1.

Рис.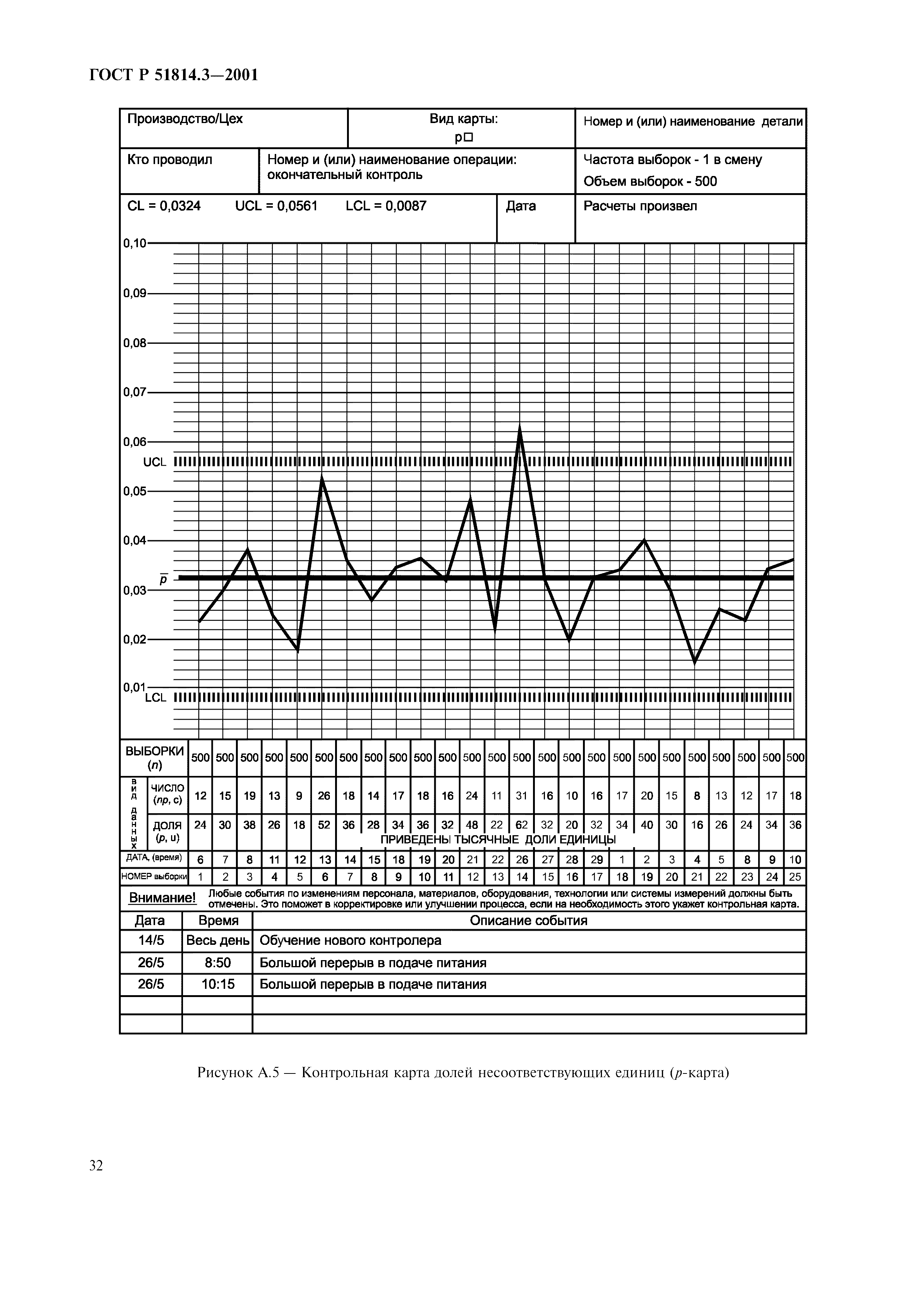 6.1. Пример контрольной карты.

По положению точек относительно границ судят о налаженности или разлаженности технологического процесса. Обычно процесс считают разлаженным в следующих случаях:

1 Некоторые точки выходят за контрольные пределы.

2 Серия из семи точек оказывается по одну сторону от средней линии. Кроме того, если по одну сторону от средней линии находятся:

а) десять из серии в одиннадцать точек

б) двенадцать из четырнадцати точек

в) шестнадцать из двадцати точек

3  Имеется тренд (дрейф), т.е. точки образуют непрерывно повышающуюся или непрерывно понижающуюся кривую.

4 Две – три точки оказываются за предупредительными двухсигмовыми границами

5 Приближение к центральной линии. Если большинство точек находится внутри полуторасигмовых линий, это значит, что в подгруппах смешиваются данные из различных распределений

6 Имеет место периодичность, т.е. то подъём, то спад с примерно одинаковыми интервалами времени

7 Контрольные границы шире поля допуска. В идеальном случае достаточно, чтобы контрольные границы составляли ¾ величины поля допуска.

Если процесс налажен (достигнута необходимая точность и стабильность), на контрольную карту продолжают наносить точки, но через 20…30 точек пересчитывают контрольные границы. Они должны совпадать с исходными границами. Если контрольная карта показывает, что процесс разлажен, находят причины разладки и производят наладку.

Бывают контрольные карты по количественным признакам (для непрерывных значений) и по качественным признакам (для дискретных значений). По количественным признакам используют в основном следующие контрольные карты:

-карта средних арифметических значений (-карта)

-карта медиан (-карта)

-карта средних квадратичных отклонений (s-карта)

-карта размахов (R-карта)

-карта индивидуальных значений (x-карта)

Карта средних значений используется для контроля отклонения параметра от нормы и настройки на норму. Точки на контрольной карте – это средние значения небольших выборок, обычно одинакового объёма, из 3…10 элементов:

 , где n – объём выборки (подгруппы).

Для получения выборок можно также использовать результаты измерений, проводившихся через одинаковые промежутки времени, путём разбиения их на группы.

Средние значения выборок находят с одним лишним знаком по сравнению с исходными данными. Среднюю линию рассчитывают как среднее из средних значений выборок:

 , где k – число подгрупп (число точек). Обычно k = 20…30.

Контрольные границы рассчитывают по формуле

 , где  — среднее квадратичное отклонение всей совокупности данных. В этом выражении (как и при расчёте контрольных границ для других видов контрольных  карт) коэффициент 3 используется, исходя из правила трёх сигм.

Карта медиан используется вместо карты средних значений, когда хотят упростить расчёты. Точки на карте – это медианы выборок одинакового объёма из 3…10 элементов. Медиана – это при нечётном объёме выборки середина вариационного ряда, при чётном объёме выборки – среднее из двух значений середины вариационного ряда.

Средняя линия — это среднее из медиан выборок. Контрольные границы находят по формуле

 

Карта медиан менее точна, чем карта средних значений. При использовании для расчётов компьютера применение карты медиан вместо карты средних значений вряд ли оправдано.

Карта средних квадратичных отклонений используется для контроля рассеяния показателя. Точки на карте – средние квадратичные отклонения выборок одинакового объёма из 3…10 элементов. Средняя линия  — это среднее из СКО выборок. Контрольные границы:

         , где c² – критерий Пирсона, n – объём выборки, a — уровень значимости. Обычно принимают a = 0,0027, что соответствует доверительной вероятности 0,9973. Часто на s-карте используют только верхнюю границу.

Карта размахов используется вместо карты средних квадратичных отклонений, когда хотят упростить расчёты. При этом карта размахов менее точна.

При построении R-карты берут 20…30 выборок одинакового объёма из 2…10 элементов. Точки ан карте – размахи выборок. Размах выборки R – это разность между максимальным x_max и минимальным x_min значениями выборки. Средняя линия  — это среднее размахов выборок. Контрольные границы рассчитывают по формулам:

                 

При уровне значимости 0,0027 коэффициенты D₃ и D₄ можно найти из табл. 6.1. При n<7 нижняя контрольная граница не используется.

Таблица 6.1.

n	2	3	4	5	6	7	8	9	10
D3	—	—	—	—	—	0,076	0,136	0,184	0,223
D4	3,267	2,575	2,282	2,115	2,004	1,924	1,864	1,816	1,777

Часто при статистическом регулировании технологических процессов используют двойные карты, отражающие как отклонение параметра от нормы, так и его рассеяние. Это могут быть, например, -карты или другие.

Контрольные карты по качественным признакам

По качественным признакам (или по альтернативному признаку) различают следующие контрольные карты:

—        карта доли дефектной продукции (p-карта)

—        карта числа дефектных единиц продукции (pn-карта)

—        карта числа дефектов (c-карта)

—        карта числа дефектов на единицу продукции (u-карта)

Карта доли дефектной продукции. Применяется для контроля и регулирования технологического процесса по доле дефектных изделий в выборке. Точки на контрольной карте ставят по значениям доли дефектной продукции в выборках:

, где n_i – объём i-й выборки, x – количество бракованных изделий в выборке. Выборка берётся за смену, сутки или более.

Среднюю линию рассчитывают по уравнению

, где k – число выборок. Обычно k = 20…30.

Контрольные границы находят по уравнению

Объём выборки подбирают так, чтобы в ней было в основном от 1 до 5 дефектных изделий. Если объём выборки неодинаков при каждом отборе, то контрольные границы вычисляют при каждом отборе (для каждой точки), т.е. границы в этом случае непостоянны.

Карта числа дефектных единиц продукции. Используется для контроля и регулирования технологического процесса по числу дефектных изделий в выборке. Используют выборки постоянного объёма. Объём выборки подбирают так, чтобы в ней было в основном от 1 до 5 дефектных изделий. Точки наносят на карту по количеству дефектных изделий в выборке p_in. Среднюю линию рассчитывают как значение

Контрольные границы находят по уравнению , где . Если К_н<0, его не рассматривают.

Карта числа дефектов. В этих картах регистрируется число дефектов c, выявленных в установленной единице контролируемой продукции, например, в рулоне ткани или бумаги, на определённой площади пластика, стекла и т.п. Предусматривают такую единицу контролируемой продукции, чтобы она содержала в основном 1…5 дефектов.

Среднюю линию находят по уравнению

Контрольные границы 

Карта числа дефектов на единицу продукции. Используется вместо с-карты, когда параметр единицы продукции (например, площадь, длина) не является постоянной величиной, т.е объём выборки непостоянен. Точки на u-карте – это значения u_i=c_i/n_i, где c_i – число дефектов в i-й выборке. Средняя линия

Контрольные границы: . Поскольку объём выборки непостоянен, границы тоже непостоянны, и их вычисляют для каждой точки.

Разладка процесса: критерии серий

Когда точка на контрольной карте, соответствующая выборочному значению контролируемой характеристики (например, среднему значению в X-карте) оказывается вне ограниченной контрольными переделами области, это дает основания предполагать, что производственный процесс разладился. Далее, при этом необходимо отслеживать появление систематической тенденции в расположении точек (например, выборочных средних) на контрольной карте, так как наличие такой тенденции может служить свидетельством тренда среднего значения контролируемого процесса.  Эти критерии иногда называют критериями серий типа AT&T или критериями против альтернатив специального вид. Термин специальные альтернативы, как альтернатива случайным или общим причинам, был использован в работе Шухарта (Shewhart) для того, чтобы сделать разграничение между нормальным производственным процессом, вариации в котором появляются только в силу действия случайных причин, и вышедшим из-под контроля процессом , в котором вариации характеристик обусловлены некоторыми неслучайными, то есть специальными факторами (см. Montgomery, 1991, стр. 102).

Как и обсуждавшиеся ранее контрольные пределы, выраженные в единицах сигмы, критерии серий имеют в своей основе «статистическое» обоснование. Так, например, вероятность того, что любое выборочное среднее значение для X-карты окажется выше центральной линии, равна 0.5 при следующих условиях: (1) производственный процесс находится в нормальном состоянии (т.е. центральная линия проведена через значение, равное среднему контролируемой характеристики генеральной совокупности изделий), (2) средние значения следующих друг за другом выборок независимы (т.е. отсутствует автокорреляция) и (3) выборочные средние значения контролируемой характеристики распределены по нормальному закону. Проще говоря, при таких условиях для выборочного среднего значения шансы попасть выше или ниже центральной линии составляют 50 на 50. Поэтому вероятность того, что два следующих друг за другом выборочных средних окажутся выше центральной линии, будет равна 0.5, умноженному на 0.5 , т.е. 0.25.

Соответственно, вероятность того, что выборочные средние девяти последующих выборок (или серия из 9 точек контрольной карты) окажется с одной стороны от центральной линии, составит 0.59 = .00195. Заметим, что это значение приблизительно равно вероятности того, что отдельное выборочное среднее значение не попадет в интервал, ограниченный контрольными пределами в 3 сигма (при условии нормального распределения выборочных средних и нормальности производственного процесса). Поэтому, в качестве еще одного индикатора разладки производственного процесса можно рассматривать ситуацию, когда девять последовательных выборочных средних находятся с одной стороны от центральной линии.

Зоны A, B, C. Обычно для задания критериев поиска серий область контрольной карты над центральной линией и под ней делится на три «зоны».

По умолчанию, зона А определяется как область, расположенная на расстоянии от 2 до 3 сигма по обе стороны от центральной линии. Зона В определяется как область, отстоящая от центральной линии на расстояние от 1 до 2 сигма, а зона С — как область, расположенная между центральной линией по обе ее стороны и ограниченная прямой, проведенной на расстоянии одной сигма от центральной линии.

9 точек в зоне С или за ее пределами (с одной стороны от центральной линии). Если этот критерий выполняется (т.е. если на контрольной карте обнаружено такое расположение точек), то делается вывод о возможном изменении среднего значения процесса в целом. Заметим, что здесь делается предположение о симметричности распределения исследуемых характеристик качества вокруг среднего значения процесса на графике. Но это условие не выполняется, например, для R-карт, S-карт и большинства карт по альтернативному признаку. Тем не менее, данный критерий полезен для того, чтобы указать занимающемуся контролем качества инженеру на присутствие потенциальных трендов процесса. Например, здесь стоит обратить внимание на последовательные выборочные значения с изменчивостью ниже среднего, так как с их помощью можно догадаться, каким образом снизить вариацию процесса.

6 точек монотонного роста или снижения, расположенные подряд. Выполнение этого критерия сигнализирует о сдвиге среднего значения процесса. Часто такой сдвиг обусловлен изнашиванием инструмента, ухудшением технического обслуживания оборудования, повышением квалификации рабочего и т.п.

14 точек подряд в «шахматном» порядке (через одну над и под центральной линией). Если этот критерий выполняется, то это указывает на действие двух систематически изменяющихся причин, которое приводит к получению различных результатов. Например, в данном случае может иметь место использование двух альтернативных поставщиков продукции или отслеживание двух различных альтернативных воздействий.

2 из 3-х расположенных подряд точек попадают в зону A или выходят за ее пределы. Этот критерий служит «ранним предупреждением» о начинающейся разладке процесса. Заметим, что для данного критерия вероятность получения ошибочного решения (критерий выполняется, однако процесс находится в нормальном режиме) в случае Х-карт составляет приблизительно 2 %.

4 из 5-ти расположенных подряд точек попадают в зону B или за ее пределы. Как и предыдущий, этот критерий может рассматриваться в качестве индикатора — «раннего предупреждения» о возможной разладке процесса. Процент принятия ошибочного решения о наличии разладки процесса для этого критерия также находится на уровне около 2%.

15 точек подряд попадают в зону C (по обе стороны от центральной линии). Выполнение этого критерия указывает на более низкую изменчивость по сравнению с ожидаемой (на основании выбранных контрольных пределов).

8 точек подряд попадают в зоны B, A или выходят за контрольные пределы, по обе стороны от центральной линии (без попадания в зону C). Выполнение этого критерия служит свидетельством того, что различные выборки подвержены влиянию различных факторов, в результате чего выборочные средние значения оказываются распределенными по бимодальному закону. Такая ситуация может сложиться, например, когда отмечаемые на Х-карте выборки изделий были произведены двумя различными станками, один из которых производит изделия со значением контролируемой характеристики выше среднего, а другой — ниже.

Контрольные карты

Контроль качества по непрерывному признаку

Контроль качества по атрибутивному признаку

Резюме

Проблема текущего мониторинга качества продукции в процессе ее производства всегда остро стояла перед производителями. Если под мониторингом качества понимать не только непосредственную проверку пригодности выпускаемого изделия, но и наблюдение за тенденциями изменения качества, то поставленная задача представляется достаточно трудоемкой.

Для решения подобных вопросов в условиях современного производства менеджеры по контролю качества используют методики и процедуры, основанные на статистическом анализе характеристик изделий.

Одним из таких инструментов являются незаменимые при поточном мониторинге качества контрольные карты (или контрольные карты Шухарта), визуализирующие статистические характеристики исследуемого производственного процесса.

В данном материале рассматриваются модельные примеры контрольных карт и на их основе демонстрируются способы выявления нарушений качества.

Общий подход к текущему контролю качества достаточно прост. В процессе производства проводятся выборочные измерения изделий. После этого на графике (карте) строятся диаграммы изменчивости выборочных значений плановых спецификаций в выборках, и рассматривается степень их близости к заданным значениям. Если диаграммы обнаруживают наличие тренда выборочных значений или оказывается, что выборочные значения находятся вне заданных пределов, то считается, что процесс вышел из-под контроля, и предпринимаются необходимые действия для того, чтобы найти причину его разладки.

Критерии серий служит для выделения систематических тенденций в расположении точек контрольной карты, которые могут указать на разладку контролируемого процесса.

Далее мы рассмотрим основные виды контрольных карт.

Контроль по непрерывному признаку

Для контроля качества по непрерывному признаку (анализа изменчивости параметров) обычно применяются X-bar, R или S карты.

На X-bar карту наносятся значения выборочных средних для того, чтобы контролировать отклонение непрерывной переменной от среднего значения.

На контрольную R-карту наносятся значения размахов выборок для контроля за степенью изменчивости непрерывного параметра, на S и S2 картах строятся соответственно графики выборочных стандартных отклонений и дисперсий.

Далее приводится несколько примеров контроля качества на основе X-bar и R-карт.

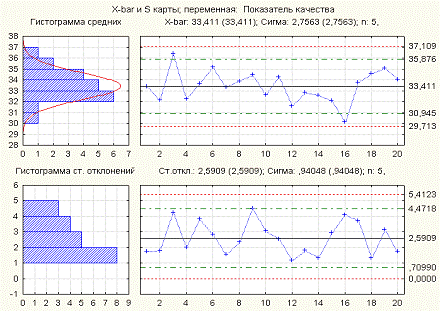
Рисунок 1

Данный пример (см. Рисунок 1) демонстрирует контрольные карты «хорошего» процесса. Точки на обеих контрольных картах находятся внутри контрольных пределов. При этом не наблюдается ни систематических смещений (трендов), ни каких-либо других признаков выхода процесса из-под контроля: точки обеих карт равномерно (во всяком случае, на основе визуального анализа) колеблются относительно соответствующих средних линий.

Среднее значение шестой выборки находится достаточно близко к нижнему контрольному пределу, однако на фоне общей положительной картины, это не является тревожным событием. Управляемость процесса также подтверждается хорошей подгонкой гистограмм наблюдаемых выборочных средних и размахов теоретическим нормальным распределением (гистограммы в левой части рисунка).

Рисунок 2

В следующем примере, на рисунке выше приводятся «плохие» контрольные карты. Явно видно, что процесс плохо управляем: выборочные средние 1-й и 4-й выборок находится вне контрольных пределов. Также настораживает то, что шесть из семи выборочных средних находятся по одну сторону средней линии.

Дополнительно на разладку производственного процесса указывает гистограмма распределения выборочных средних (левый верхний график), показывающая явное отличие распределения средних от нормального.

Стоит также отметить, что при явных выбросах на X-bar карте, значения выборочных размахов (R-карта) лежат в рамках контрольных пределов.

Рисунок 3

В данном примере контрольных карт (см. Рисунок 3) демонстрируется обратная ситуация. Средние значения по выборкам (точки на X-bar карте) находятся в контрольных пределах, при этом на R-карте размахов имеется выброс (размах второй выборки выше верхнего контрольного предела). Большие значения в выборке с критическим размахом сокращаются с малыми значениями, в результате чего, выборочное среднее значение находится в пределах нормы. Также стоит отметить небольшое систематическое смещение на карте средних, но его при малом количестве выборок и критическом размахе значений такое смещение можно считать не существенным на данном этапе исследования.

В итоге в такой ситуации требуется проведение мероприятий по снижению разброса значений исследуемого параметра, после чего перейти к более глубокому анализу выборочных средних.

Рисунок 4

В следующем примере (см. Рисунок 4) снова можно наблюдать наличие выбросов на X-bar карте и их отсутствие на карте размахов. Однако наиболее показательным результатом в данном примере является наличие заметного тренда на обеих картах: положительного на карте средних и отрицательного на карте размахов. Систематическое снижение значений выборочных размахов означает сходимость процесса (уменьшение разброса значений). Казалось бы, это – положительное явление. Но, при положительном тренде значений средних, процесс, скорее всего, сходится к значению, лежащему вне контрольных пределов. В итоге, в скором времени, все измерения исследуемого параметра могут оказаться вне значений спецификаций.

Контроль качества по атрибуту

Другим типом контрольных карт являются карты по атрибутивному признаку (атрибуту) – например, по числу дефектных деталей в партии, по числу отклонений характеристик изделия от стандарта в расчете на выборку.

Преимущество контрольных карт по атрибутивному признаку состоит в возможности быстро получить общее представление о различных аспектах качества анализируемого изделия; то есть, на основании различных критериев качества инженер может сразу принять или забраковать продукцию.

Контрольные карты по атрибутивному признаку иногда позволяют обойтись без применения дорогих точных приборов и требующих значительных затрат времени для измерительных процедур. Кроме того, этот тип контрольных карт более понятен менеджерам, которые не разбираются в тонкостях методов контроля качества. Таким образом, с помощью этих карт можно более убедительно продемонстрировать руководству наличие проблем с качеством изделий.

Однако, по сравнению с контрольными картами по атрибутивному признаку, карты для непрерывных переменных обладают большей чувствительностью. Благодаря этому, контрольные карты для непрерывных переменных могут указать на существование проблемы ухудшения качества, прежде чем в потоке продукции появятся настоящие бракованные изделия, выделяемые с помощью контрольной карты по атрибутивному признаку.

Контрольные карты для непрерывных переменных можно считать предвестниками проблем ухудшения качества, которые предупреждают об их наличии задолго до того, как в процессе производства резко возрастет доля бракованных изделий.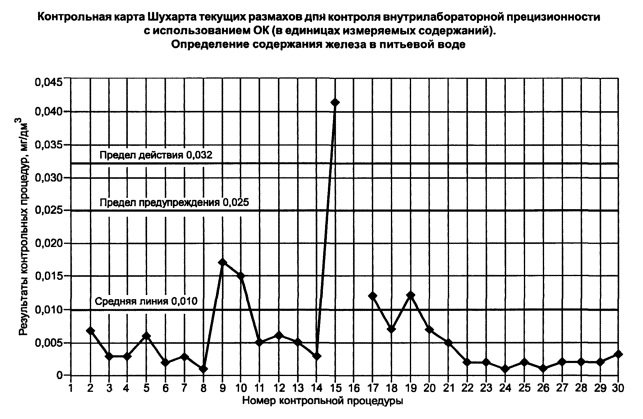

Для контроля качества продукции по атрибутивному признаку обычно используются следующие типы карт:

• С-карта
• U-карта
• Np-карта
• P-карта

При использовании С- и U-карт принимается предположение о том, что дефекты контролируемой характеристики продукции встречаются сравнительно редко и контрольные пределы для данных типов карт рассчитываются на основе свойств распределения Пуассона (распределения редких событий).

В свою очередь контрольные пределы для Np- и P-карт рассчитываются на основе биномиального распределения, а не распределения редких событий. Поэтому данный тип карт должен использоваться в том случае, когда обнаружение дефекта не является редким событием (например, происходит более чем у 5% проверенных единиц продукции).

При этом на С- и Np-картах отображается число дефектов (в партии, в день, на один станок), а на U- и P-картах отображается относительная частота дефектов, то есть отношение числа обнаруженных дефектов к числу проверенных единиц продукции.

Рисунок 5

На рисунке выше представлен пример P-карты по атрибуту. На основе визуального анализа графика можно заключить, что данный процесс является управляемым: не наблюдается значений вне контрольных пределов (выбросов), нет заметного тренда, а также не наблюдаются систематические тенденции в расположении точек на карте.

Рисунок 6

В противовес предыдущему графику на данной P-карте (см. Рисунок 6) демонстрируется «плохой» процесс. В шестой и седьмой выборках встречается более 80% бракованных изделий, что выше предопределенных контрольных пределов. Естественно такой высокий процент отбраковки продукции свидетельствует о наличии серьезных проблем качества данного производственного процесса.

Рисунок 7

На следующей P-карте (см. Рисунок 7) также представлен пример «плохого» процесса. Причем, помимо выброса в последней выборке (80% брака), можно наблюдать систематическое увеличение процента бракованных изделий.

Аналогично продемонстрированным методам проводится визуальный анализ качества на основе других карт по атрибуту. Далее приводятся некоторые примеры текущего контроля качества на основе C-карты.

Рисунок 8

На этой С-карте показан хорошо управляемый технологический процесс: количество бракованной продукции в каждой выборке находится в рамках контрольных пределов.

Рисунок 9

А в этом примере (см. Рисунок 9) на C-карте наблюдается выброс (первая выборка). Однако соответствующие статистики по остальным выборкам находятся в рамках контрольных пределов. Таким образом, на основании этой карты, исключив первую выборку, можно считать процесс управляемым. Если проблемная выборка отражает начало реального технологического процесса, то, скорее всего, ее неудовлетворительное качество связано с первоначальной настройкой процесса. В этом случае рекомендуется провести дополнительный анализ качества продукции, выпущенной на начальном этапе и, исключив имеющийся выброс, признать процесс управляемым.

Резюме

В заключение еще раз хочется подчеркнуть высокую эффективность применения контрольных карт в управлении качеством. Используя подходящие средства графического отображения, человеческий глаз способен отлавливать признаки ухудшения качества и тревожные тенденции в режиме поточного конвейерного производства.

При этом мощный аналитический пакет, такой как STATISTICA, способен взять на себе практически всю работу по обнаружению признаков разладки технологического процесса в online режиме, оставив оператору лишь анализ наиболее изощренных критериев визуальной проверки качества (малых трендов).

В начало

Содержание портала

Контрольные карты Шухарта — Описание программы

 

Описание программы

___Контрольные карты Шухарта (ГОСТ Р 50779.40 — 96) предназначены для статистического анализа и управления качеством процесса. Контрольные карты используют для оценки того, находится или не находится исследуемый процесс в статистически управляемом состоянии.
___На одной карте может быть отображен только один показатель, изменяющийся во времени. Для одновременного анализа нескольких показателей их необходимо привести к одному параметру.
___Для достаточно надежного статистического анализа, количество точек должно быть достаточно большим, от 30 и выше. Однако на практике для ориентировки используют и меньшие выборки, но не менее 12-15 значений.

___Чем статистически стабильнее процесс, тем выше его качество и тем меньше различного рода издержек на исправление ошибок, брака, аварий, потерь времени и т.д. Например, сильные колебания давления воды в трубопроводе могут привести к его разрушению.

___КК составляются с помощью программы “Контрольные карты” следующим образом. Берется некоторая временная выборка значений контролируемого процесса (это может быть и количество бракованных деталей в партии, и дебеторская задолженность, и т.д.). В таблицу заносятся по оси X — время (часы, дни, или месяцы) или последовательный порядок измерения данного параметра (формат произвольный), а по оси Y — откладываются значения контролируемого процесса (формат числовой). Нельзя вводить для неизвестных точек ноль! Если значение на данный момент не известно, то такие точки не вводятся вообще.

___Программа автоматически строит на графике среднее значение и две контрольных границы: верхняя контрольная граница (ВКГ), равная среднему значению, плюс 3 среднеквадратичных отклонения (+ 3 Sigma), и нижняя контрольная граница (НКГ), равная среднему значению, минус 3 среднеквадратичных отклонения (— 3 Sigma). В том случае, если значения графика не выходят за рамки этих контрольных границ, то с вероятностью 99,73% можно считать контролируемый процесс статистически стабильным и управляемым.

___Для более жесткого контроля иногда используют контрольные границы в 2 среднеквадратичных отклонения, вверх и вниз от среднего значения по всей выборке. Эти контрольные границы называют предупреждающими. Если график укладывается и в эти границы, то с вероятностью 95,46% можно говорить о еще более статистически стабильном и более управляемом процессе, иначе — о его более высоком качестве.

___Необходимый коэффициент среднеквадратичных отклонений в программе можно задать, всё зависит от решаемых задач, по умолчанию предлагается равным 3.

___Все отклонения показателя качества разделены на 2 класса: случайные и неслучайные. Случайные отклонения, являясь итогом действия большого числа несущественных дестабилизирующих причин, имеют место при нормальном ходе технологического процесса, как, например, колебания любых параметров механической обработки заготовки (размеров, твердости и т.д.). Такие причины называют обычными. На КК показатели такого статистически устойчивого процесса не выходят за рамки контрольных границ. Неслучайные отклонения являются итогом действия значительных дестабилизирующих причин, называемых особыми причинами. Действие особых причин отразится на графике выходом за контрольные границы. При этом теряется качество и процесс характеризуется как нестабильный и неуправляемый. Особыми причинами могут быть наше собственное вмешательство в процесс, например, перенастройка станка. Причины могут быть и неизвестны заранее. Тогда они становятся объектом специального наблюдения. В период такого наблюдения никакие вмешательства в процесс со стороны его контролеров не допустимы.

___Качество процесса можно дополнительно оценить (визуально) по форме кривой нормального распределения значений, в частности, по ее симметричности относительно среднего значения.

___Описанный вариант анализа статистических данных — стандартный, предложенный Шухартом. При этом среднее значение вычисляется как «кривая» 0-порядка, т.е. прямая параллельная оси Х. Функция имеет вид:

              Y = C, где С = (Х₁ + Х₂ + … + Х_n) / n.

Среднеквадратичное отклонение от среднего вычисляется по формуле
                            _________________________
           Sigma = V (Х₁² + Х₂² + … + Х_n²) / (n-1)  

 

___Можно использовать карту, как приемочную (ГОСТ Р 50779.40 — 96). Для этого необходимо на графике указать верхний и нижний допуски для исследуемого процесса. Допуски являются либо технологическими границами (если они известны), выход за которые нежелателен (технологически, экономически, экологически и т.п.) или даже опасен (например, допустимые нормы концентрации вредных веществ), либо границами плана (например, освоенных денег на капитальный ремонт), выход за которые чреват рядом экономически нежелательных последствий.

___Программа “Контрольные карты” позволяет интерпретировать введенные данные, как контрольную карту трендов (тренд — тенденция изменения процесса с течением времени). Такая карта предназначена для оценки уровня процесса по отклонениям от ожидаемого тренда, что позволяет иначе взглянуть на контролируемый процесс и выявить скрытые закономерности. В программе реализовано два вида трендов для среднего и один для контрольных границ. ___Среднее значение, как линейный тренд. ___Среднее значение рассматривается, как «кривая» 1-порядка, т.е. прямая, имеющая наклон относительно оси Х. Функция имеет вид:

              Y = A * X + C

На рисунке приведен пример такого графика. Этот график позволяет легко оценить тенденцию процесса.

Важным моментом является то, что в этом случае контрольные границы строются относительно меняющегося среднего, поэтому они проходят параллельно средней линии! Действительно, предположим мы оцениваем себестоимость выпускаемого продукта (по месяцам) и она объективно снижается. Что же мы должны считать процесс нестабильным? Нет, но мы  в этом случае должны оценивать колебания значений вокруг среднего значения для оценки качества процесса!  

___Среднее значение, как периодический тренд.

___Среднее значение рассматривается, как «кривая» 1-порядка, т.е. прямая, имеющая наклон относительно оси Х плюс гармонические составляющие (ряд Фурье). Функция имеет вид:

           Y = A * X + C +
                 A₁ * Sin(w * X) + B₁ * Cos(w * X) +
                 A₂ * Sin(2 * w * X) + B₂ * Cos(2 * w * X) + … +
                 A_n * Sin(n * w * X) + B_n * Cos(n * w * X)

На рисунке приведен пример такого графика. Этот график позволяет легко оценить периодичность процесса.

В этом случае программа также строит контрольные границы относительно меняющегося среднего.
На этом графике изображен процесс потребления тепла (пара) предприятием на хозяйственные нужды и отопление за три года по месяцам. На графике отчетливо видно, что максимумы приходятся на 1 месяц года (январь), а минимумы — на 7 (июль). Почему так получается, думаю понятно всем жителям северного полушария.

___Контрольные границы, как линейный тренд.

___Каждая контрольная граница рассматривается, как  «кривая» 1-порядка, т.е. прямая, имеющая наклон относительно оси Х. Функция имеет вид:

              Y = A * X + C

На рисунке приведен пример такого графика. Этот график позволяет легко оценить тенденцию изменения качества процесса.

На таком графике отчетливо видно, что качество процесса ухудшается, т.к. контрольные границы расходятся.

___Отображение относительно средней линии в процентах.

___Позволяет исключить колебания средней линии (т.е. как бы «вытянуть» среднюю в горизонтальную прямую) и рассматривать относительные изменения для оценки качества. В этом случае, график будет выглядеть как стандартная контрольная карта, но отклонения указываются в процентах относительно среднего значения, а среднее значение принимается за ноль.

___Программа «Контрольные карты Шухарта” позволяет экспортировать любой вариант графика в Excel для дальнейшего анализа, а также импортировать данные из Excel.

___Предусмотрена возможность вводить комментарии по конкретной карте. Введенный комментарий хранится в теле основного документа (это файл с расширением .SHU) и имеет формат MS Word, т.е. комментарий может быть очень сложным (с таблицами, картинками и т.д.)

___Печать графиков осуществляется через MS Word, что дает некоторые преимущества. Можно, например, добавить какой-то поясняющий текст перед печатью.

___Для нормальной работы программы в системе должен быть установлен MS Office 97 (или более новая версия). В противном случае не будут работать режимы «Комментарий», «Печать», «Импорт из Excel» и «Экспорт в Excel».

 

Разработчик:  Лебский Геннадий Николаевич

 

3,4. Диаграммы Шухарта — Улучшение процессов с использованием данных

Диаграмма Шухарта, названная в честь Уолтера Шухарта из Bell Telephone и Western Electric, отслеживает, чтобы переменная процесса оставалась на заданном уровне и в заданных верхних и нижних пределах. Это диаграмма мониторинга для локации . Он отвечает на вопрос, стабильно ли положение переменной с течением времени. Он не отслеживает ничего другого, связанного с измерением, например, его стандартное отклонение. Забегая вперед: позже мы покажем, что чистая диаграмма Шухарта нуждается в дополнительных правилах, чтобы помочь эффективно отслеживать местоположение переменной.

Определяющими характеристиками диаграммы Шухарта являются: целевой, верхний и нижний контрольные пределы (UCL и LCL). Эти пределы действия определены таким образом, что никаких действий не требуется, пока отображаемая на графике переменная остается в пределах. Другими словами, особая причина маловероятна, если точки остаются в пределах UCL и LCL.

3.4.1. Вывод с использованием теоретических параметров

Определите интересующую переменную как \ (x \) и предположите, что у нас есть образцы \ (x \), доступные в порядке следования.2 / n \), где \ (\ mu \) и \ (\ sigma \) относятся к распределению, из которого взяты образцы \ (x \). На рисунке показан случай для \ (n = 5 \).

Итак, взяв подгруппы значений размера \ (n \), теперь у нас есть для каждой подгруппы вновь вычисленная переменная, \ (\ overline {x} \), и мы определим сокращенный символ для ее стандартного отклонения: \ (\ sigma_ {\ overline {X}} = \ sigma / \ sqrt {n} \). Записать \ (z \) — значение для \ (\ overline {x} \) и связанный с ним доверительный интервал для \ (\ mu \) теперь легко после изучения раздела о доверительных интервалах:

\ [z = \ frac {\ displaystyle \ overline {x} — \ mu} {\ displaystyle \ sigma _ {\ overline {X}}} \]

Предполагая, что мы знаем \ (\ sigma _ {\ overline {X}} \), чего мы обычно не знаем на практике, мы можем вызвать нормальное распределение и вычислить вероятность нахождения значения \ (z \) между \ (c_n = -3 \) до \ (c_n = +3 \):

(1) \ [\ begin {split} \ begin {array} {rcccl} — c_n & \ leq & \ dfrac {\ overline {x} — \ mu} {\ sigma _ {\ overline {X}}} & \ leq & + c_n \\ \\ \ overline {x} — c_n \ sigma _ {\ overline {X}} & \ leq & \ mu & \ leq & \ overline {x} + c_n \ sigma _ {\ overline {X}} \\ \\ \ text {LCL} & \ leq & \ mu & \ leq & \ text {UCL} \ end {массив} \ end {split} \]

Причина \ (c_n = \ pm 3 \) в том, что общая площадь между этой нижней и верхней границей составляет 99. {K} {\ overline {x} _k} \ ), где \ (K \) — количество \ (\ overline {x} \) выборок, доступных для построения диаграммы мониторинга, называемых данными фазы 1.{K} {s_k} \) — это просто среднее стандартное отклонение, рассчитанное по подгруппам \ (K \). Значения для \ (a_n \) ищутся из таблицы или с использованием приведенной ниже формулы и зависят от количества образцов, которые мы используем в каждой подгруппе.

\ (п \)	2	3	4	5	6	7	8	10	15
\ (а_н \)	0.7979	0,8862	0,9213	0,9400	0,9515	0,9594	0,9650	0,9727	0,9823

В более общем смысле, используя функцию \ (\ Gamma (…) \), например gamma (...) в R или MATLAB, или math.gamma (...) в Python , вы можете воспроизвести указанные выше значения \ (a_n \).

\ [a_n = \ frac {\ sqrt {2} \, \, \ Gamma (n / 2)} {\ sqrt {n-1} \, \, \ Gamma (n / 2 — 0,5)} \]

Обратите внимание, как значения \ (a_n \) стремятся к 1,0, чем больше размер подгруппы, что указывает на то, что нам нужно меньше коррекции, чтобы сделать стандартное отклонение менее смещенным. Когда у нас есть эта беспристрастная оценка стандартного отклонения от этих \ (K \) подгрупп, мы можем записать подходящие нижний и верхний контрольные пределы для диаграммы Шухарта:

(2) \ [\ begin {array} {rcccl} \ text {LCL} = \ overline {\ overline {x}} — 3 \ cdot \ frac {\ displaystyle \ overline {S}} {\ displaystyle a_n \ sqrt {n}} && && \ text {UCL} = \ overline {\ overline {x}} + 3 \ cdot \ frac {\ displaystyle \ overline {S}} {\ displaystyle a_n \ sqrt {n}} \ конец {массив} \]

Маловероятно, что все данные, выбранные для расчета пределов фазы 1, действительно лежат в этих рассчитанных LCL и UCL.Части данных, не относящиеся к стабильной работе и выходящие за установленные пределы, не должны использоваться для расчета этих пределов. Эти нестабильные данные приводят к тому, что пределы становятся шире, чем требуется.

Исключите эти точки данных с выбросами и повторно вычислите LCL и UCL. Обычно этот процесс повторяется 2–3 раза. Целесообразно исследовать исключаемые данные, чтобы убедиться, что они действительно происходят из-за нестабильной работы. Если они из стабильной работы, то исключать их не стоит. Эти данные могут противоречить предположению о независимости.Можно рассмотреть возможность использования более широких лимитов или использовать контрольную диаграмму EWMA.

Пример

Производится

тюков резины, каждый десятый тюк автоматически снимается с линии для тестирования. Измерения интенсивности цвета производятся на 5 сторонах тюка с помощью откалиброванных цифровых камер в контролируемых условиях освещения. Резиновая смесь используется для медицинских устройств, поэтому она должна иметь правильный цвет, измеряемый по шкале от 0 до 255. Среднее значение 5 цветовых измерений должно быть нанесено на диаграмму Шухарта.Таким образом, у нас появляется новая точка данных, появляющаяся на диаграмме мониторинга после каждого 10-го тюка.

В приведенном выше примере исходными данными является цвет тюка. В каждой подгруппе есть \ (n = 5 \) значений. Соберите, скажем, \ (K = 20 \) образцов тюков хорошего качества, которые считаются стабильными. Во время изготовления этих тюков не происходило никаких особых событий технологического процесса.

Данные ниже представляют собой среднее значение \ (n = 5 \) образцов из каждого тюка, есть \ (K = 20 \) этих подгрупп.

\ [\ overline {x} = [245, 239, 239, 241, 241, 241, 238, 238, 236, 248, 233, 236, 246, 253, 227, 231, 237, 228, 239, 240] \ ]

Общее среднее значение \ (\ overline {\ overline {x}} = 238.8 \) и \ (\ overline {S} = 9.28 \). Необработанные данные доступны на этом веб-сайте, и вы можете убедиться, что значения \ (\ overline {\ overline {x}} \) и \ (\ overline {S} \) были правильно рассчитаны.

В исходном коде:

# Информация дана (но посчитай сам # с https://openmv.net/info/rubber-colour) xbar = c (245, 239, 239, 241, 241, 241, 238, 238, 236, 248, 233, 236, 246, 253, 227, 231, 237, 228, 239, 240) # Количество измерений в подгруппе N.sub = 5 # Среднее из 20 стандартных отклонений # из 20 подгрупп S = 9.28 год # xdb = x двойная полоса = общее среднее значение = # среднее из средств xdb = среднее значение (xbar) num.an = sqrt (2) * гамма (N.sub / 2) den.an = sqrt (N.sub-1) * гамма ((N.sub-1) / 2) an = num.an / den.an LCL = xdb - (3 * S / (an * sqrt (N.sub))) UCL = xdb + (3 * S / (an * sqrt (N.sub))) paste0 ('Контрольные пределы: [', round (LCL, 2), '; ', раунд (UCL, 2),'] ') paste0 ('Число> UCL:', сумма (xbar> UCL)) paste0 ('Number UCL] = NA # Вычислить среднее значение, удалив недостающие # значения (игнорировать). xdb = среднее (xbar, na.rm = TRUE) # 'S' также изменится.Если вы загрузите # необработанные данные (ссылка выше), вы можете доказать # что новая буква S будет: S = 9,68 # Значения «an» и «Nsub» не изменятся. LCL = xdb - (3 * S / (an * sqrt (N.sub))) UCL = xdb + (3 * S / (an * sqrt (N.sub))) paste0 ('Контрольные пределы: [', round (LCL, 0), '; ', раунд (UCL, 0),'] ')

3.4.3. Судя по графику

Есть два способа оценить эффективность диаграммы мониторинга. В частности, здесь мы обсуждаем график Шухарта:

1.Вероятность ошибки.

Мы определяем два типа ошибок, Тип I и Тип II, которые являются функцией нижнего и верхнего контрольных пределов (LCL и UCL).

Вы делаете ошибку типа I , когда ваш образец типичен для нормальной работы, но не выходит за пределы UCL или LCL. В теоретическом выводе мы показали, что площадь, охватываемая верхним и нижним контрольными пределами, составляет 99,73%. Вероятность совершения ошибки типа I, обычно обозначаемой как \ (\ alpha \), тогда равна \ (100-99.73 = 0,27 \% \).

Синонимы для ошибки типа I : ложная тревога, ложное срабатывание (используется в основном для тестирования заболеваний), риск производителя (используется для приемочной выборки, потому что здесь, как производитель, вы будете отклонять приемлемый образец), ложное отклонение ставка или альфа.

Вы делаете ошибку типа II , когда ваш образец действительно ненормальный, но попадает в пределы UCL и LCL и поэтому не обнаруживается. Этот коэффициент ошибок обозначается как \ (\ beta \), и он является функцией степени отклонения от нормы, которую мы выведем далее.

Синонимы для ошибки типа II : ложноотрицательный (используется в основном для тестирования заболеваний), риск потребителя (используется для приемочной выборки, потому что ваш потребитель будет получать доступный продукт, который является дефектным), уровень ложного принятия или бета .

Чтобы количественно оценить вероятность \ (\ beta \), напомним, что диаграмма Шухарта предназначена для мониторинга местоположения, поэтому мы делаем предположение, что новая, ненормальная выборка происходит из распределения, которое сместило свое местоположение с \ (\ mu \) на \ (\ mu + \ Delta \ sigma \) (напр.грамм. \ (\ Delta \) может быть положительным или отрицательным). Теперь, какова вероятность того, что эта новая выборка, полученная в результате смещенного распределения, попадет в существующие LCL и UCL? На этом рисунке показана вероятность \ (\ beta = (1 - \ text {заштрихованная область}) \).

\ [\ begin {split} \ alpha & = Pr \ left (\ overline {x} \, \, \ text {находится под контролем, но выходит за установленные пределы} \ right) = \ text {частота ошибок типа I} \ \ \ beta & = Pr \ left (\ overline {x} \, \, \ text {не контролируется, но находится в допустимых пределах} \ right) = \ text {частота ошибок типа II} \ end {split} \]

В таблице подчеркивается, что \ (\ beta \) является функцией величины, на которую процесс сдвигается = \ (\ Delta \), где \ (\ Delta = 1 \) означает, что процесс сдвинулся вверх на \ (1 \ сигма\).Таблица была рассчитана для \ (n = 4 \) и использовала критические пределы \ (\ pm 3 \ sigma _ {\ overline {X}} \). Вы можете рассчитать свои собственные значения \ (\ beta \), используя эту строку кода R: beta <- pnorm (3 - delta * sqrt (n)) - pnorm (-3 - delta * sqrt (n))

\ (\ Delta \)	0,25	0,50	0,75	1,00	1.50	2,00
\ (\ beta \) когда \ (n = 4 \)	0,9936	0,9772	0,9332	0,8413	0,5000	0,1587

дельта

Ключевым моментом, который вы должны отметить из таблицы, является то, что диаграмма Шухарта плохо (это медленно) при обнаружении изменения местоположения (уровня) переменной.Это удивительно, учитывая, что цель сюжета - отслеживать местоположение переменной. Даже умеренный сдвиг на \ (0,75 \ сигма \) единиц \ ((\ Delta = 0,75) \) будет обнаружен только в 6,7% случаев (\ (100-93,3 \% \)), когда \ (n = 4 \). Далее мы обсудим графики CUSUM и правила Western Electric как способ решения этой проблемы.

Несложно увидеть, как можно отрегулировать частоту ошибок типа I, \ (\ alpha \) - просто перемещайте LCL и UCL вверх и вниз по мере необходимости, чтобы достичь желаемой частоты ошибок.Нет ничего плохого в произвольном изменении этих пределов - подробнее об этом позже в разделе о регулировке пределов.

Однако что происходит с частотой ошибок типа II, когда границы LCL и UCL смещаются от цели? Представьте себе случай, когда вы хотите иметь \ (\ alpha \ rightarrow 0 \). По мере того, как вы делаете UCL все выше и выше, значение для \ (\ alpha \) падает, но значение для \ (\ beta \) также будет увеличиваться, поскольку пределы управления стали шире! Вы не можете одновременно иметь ошибку типа I и типа II , или, как говорится в более разговорной речи, «бесплатного обеда нет».

2. Использование средней длины пробега (ARL)

Средняя длина серии (ARL) определяется как среднее количество последовательных выборок, которые мы ожидаем, прежде чем увидим выход за пределы или неконтролируемый сигнал. Это дается обратной величиной \ (\ alpha \), как ARL = \ (\ frac {1} {\ alpha} \). Напомним, что для теоретического распределения у нас было \ (\ alpha = 0,0027 \), поэтому ARL = 370. Таким образом, мы ожидаем, что прогон будет 370 выборок, прежде чем мы получим неконтролируемый сигнал.

3.4.4. Расширения к основной диаграмме Шухарта для контроля стабильности местоположения

Правила Western Electric: выше мы видели, насколько медленно диаграмма Шухарта обнаруживает небольшой сдвиг в среднем процессе с \ (\ mu \) на \ (\ mu + \ Delta \ sigma \).Правила Western Electric представляют собой попытку более быстрого обнаружения сдвига процесса, путем подачи сигнала тревоги, когда происходят эти невероятных событий:

1. Две из 3 точек лежат за \ (2 \ sigma \) на одной стороне от центральной линии

2. Четыре из 5 точек лежат за \ (1 \ sigma \) по одну сторону от центральной линии

3. Восемь следующих друг за другом точек лежат по одну сторону от центральной линии

Однако альтернативная диаграмма, диаграмма CUSUM, более эффективна при обнаружении сдвига в среднем.Также обратите внимание, что теоретический ARL, \ (1 / \ alpha \), уменьшается за счет использования этих правил в дополнение к границам LCL и UCL.

Повышение устойчивости : этап I построения диаграммы мониторинга является итеративным. Если вы обнаружите точку, которая нарушает пределы LCL и UCL, то подход состоит в том, чтобы удалить эту точку и пересчитать значения LCL и UCL. Это потому, что пределы LCL и UCL были смещены вверх или вниз из-за этих необычных точек \ (\ overline {x} _k \) точек.

Этот итеративный подход может быть утомительным при работе с данными, имеющими всплески, пропущенные значения, выбросы и другие проблемы, типичные для данных, извлеченных из базы данных процессов (архиватор).Надежные диаграммы мониторинга - это процедуры для расчета пределов, чтобы LCL и UCL были устойчивы к влиянию выбросов. Например, надежная процедура может использовать медианы и MAD вместо среднего и стандартного отклонения. Изучение различных робастных процедур, особенно межквартильного размаха, дается в статье Д. М. Рокка, Робастные контрольные диаграммы, Technometrics , 31 (2), стр. 173 - 184, 1989.

Примечание : не используйте надежные методы для расчета значений, нанесенных на диаграммы во время фазы 2, используйте только надежные методы для расчета пределов диаграммы в фазе 1!

Пределы предупреждений : обычно пределы предупреждений можно увидеть на диаграмме мониторинга в \ (\ pm 2 \ sigma \), в то время как пределы \ (\ pm 3 \ sigma \) называются пределами действия.Компьютерные системы реального времени обычно используют цветовую схему, чтобы различать состояние предупреждения и состояние действия. Например, фон диаграммы меняется с зеленого на оранжевый и затем на красный, когда отклонения от цели становятся более серьезными.

Регулировка пределов : Пределы \ (\ pm 3 \ sigma \) не высечены из камня. В зависимости от степени, в которой исходные данные подчиняются предположениям, и частоты, с которой пики и выбросы загрязняют ваши данные, вам может потребоваться отрегулировать свои пределы, обычно более широкие, чтобы избежать частых ложных тревог.Ничто не делает карту мониторинга более бесполезной для операторов, чем частые ложные срабатывания («плачущий волк»). Однако помните, что бесплатного обеда не бывает: нельзя одновременно иметь ошибку I и II типа.

Изменение размера подгруппы : Возможно, это противоречит здравому смыслу, что увеличение размера подгруппы \ (n \) приводит к более чувствительной системе обнаружения сдвигов в среднем, поскольку контрольные пределы ужесточены. Однако большее значение \ (n \) также означает, что для просмотра сигнала обнаружения потребуется больше времени, поскольку среднее значение подгруппы усредняется по большему количеству точек необработанных данных.Таким образом, существует компромисс между размером подгруппы и длиной серии (время до обнаружения сигнала).

3.4.5. Ошибки, которых следует избегать

1. Представьте, что вы отслеживаете какой-то аспект качества конечного продукта, например вязкость, и у вас есть спецификация продукта, которая требует, чтобы эта вязкость находилась в пределах, скажем, от 40 до 60 сП. Было бы ошибкой помещать эти пределы спецификации на диаграмму мониторинга в качестве руководства, когда действовать. Также ошибочно использовать требуемые пределы спецификации вместо LCL и UCL.Диаграмма мониторинга предназначена для выявления ненормальных изменений в процессе и дает сигнал о том, когда действовать, а не проверять спецификации качества. У вас, конечно, может быть другая диаграмма для этого, но пределы диаграммы мониторинга процесса предназначены для мониторинга стабильности процесса, и эти пределы стабильности Шухарта рассчитываются по-другому. В идеале пределы спецификации лежат за пределами действия LCL и UCL.

2. Пределы диаграммы Шухарта были рассчитаны с допущением, что независимая подгруппа (например.грамм. подгруппа \ (i \) не влияет на подгруппу \ (i + 1 \)). Для процесса с умеренной автокорреляцией действие по созданию подгрупп с \ (n \) выборками в каждой группе удаляет большую часть, если не все, взаимосвязи между подгруппами. Однако для процессов с сильной автокорреляцией (например, для медленных процессов с высокой частотой дискретизации) LCL и UCL будут вычисляться по уравнению (2), что будет вызывать ложные тревоги слишком часто. В этих случаях вы можете расширить пределы или удалить автокорреляцию из сигнала.Подробнее об этом в следующем разделе, посвященном графикам экспоненциально взвешенной скользящей средней (EWMA).

3. Использование диаграмм Шухарта для двух или более высококоррелированных переменных качества , обычно при измерении конечного продукта, может значительно увеличить ваш тип II (потребительский риск). Мы вернемся к этой очень важной теме в разделе, посвященном моделям со скрытыми переменными, где мы нелогично докажем, что даже наличие отдельных диаграмм, каждая в своих соответствующих пределах, может привести к тому, что она выйдет за общие пределы.

Контрольная диаграмма

: ключевой инструмент для обеспечения качества и минимизации отклонений

Изобретенная Уолтером А. Шухартом, когда он работал в Bell Labs в 20-х годах, контрольные диаграммы использовались в различных отраслях как часть методологии улучшения процессов . Шухарт понимал, что независимо от того, насколько хорошо был спроектирован процесс, всегда будут вариации внутри этого процесса - и эффект может стать отрицательным, если вариации мешают вам уложиться в сроки или квоты.

Вам нужно будет принять меры для исправления отклонений, которые негативно влияют на ваш бизнес, и именно здесь контрольная диаграмма может быть полезной для вашей компании. Узнайте больше о контрольных диаграммах и начните работу с шаблоном прямо сейчас.

Пример контрольной диаграммы (Щелкните изображение, чтобы изменить онлайн)

Что такое контрольная диаграмма?

Контрольная диаграмма - иногда называемая диаграммой Шухарта, статистической контрольной диаграммой процесса или диаграммой SPC - является одним из нескольких графических инструментов, которые обычно используются в анализе контроля качества, чтобы понять, как процесс изменяется с течением времени.

К основным элементам контрольной диаграммы относятся:

• Визуальный график временных рядов, иллюстрирующий точки данных, собранные в определенные промежутки времени.
• Горизонтальная контрольная линия для более удобной визуализации изменений и тенденций.
• Горизонтальные линии, представляющие верхний и нижний контрольные пределы, размещенные на равных расстояниях выше и ниже контрольной линии. Эти верхний и нижний пределы рассчитываются на основе данных, записанных на графике временных рядов за определенный период времени.

Преимущества использования контрольной диаграммы

Контрольные карты могут вам помочь:

• Поймите вариации, которые всегда присутствуют в процессах. Вариации в пределах ваших контрольных пределов указывают на то, что процесс работает. Вариации, которые выходят за пределы ваших контрольных пределов, указывают на проблемы, которые необходимо исправить.
• Смотрите, когда что-то идет не так или может пойти не так. Эти индикаторы проблемы сообщают вам, что необходимо предпринять корректирующие действия.
• Обратите внимание на закономерности в нанесенных точках. Шаблоны указывают на возможные причины, которые могут помочь вам найти возможные решения.
• Прогнозируйте будущую производительность.
• Генерируйте новые идеи для улучшения качества на основе вашего анализа.

Разновидности процесса

Прежде чем вы сможете построить свою контрольную диаграмму, вам необходимо понять различные типы вариаций процесса, чтобы вы могли контролировать, является ли ваш процесс стабильным. Вариации могут быть вызваны как общими, так и особыми причинами.

Варианты общей причины

Вариации по общей причине предсказуемы и всегда присутствуют в ваших процессах.

В качестве простого примера рассмотрим, сколько времени у вас уходит на работу каждое утро. Вы можете ездить по одному и тому же маршруту каждое утро, но поездка никогда не будет прежней. Возможно, с момента выхода из дома до парковки у вас проходит в среднем 20 минут. Из-за вариаций по общей причине, таких как стоп-сигналы и заторы на дорогах, в некоторые дни на это уходит меньше времени, а в другие - больше.

Даже если вы не знаете точно, когда вы придете на работу завтра, вы знаете, что это произойдет в приемлемые сроки, и вы приедете вовремя.

Когда вариации остаются в пределах ваших верхних и нижних пределов, нет необходимости срочно изменять процесс, потому что все работает в пределах предсказуемых параметров.

Варианты особой причины

Вариации по особой причине обычно бывают спорадическими и непредсказуемыми. Например, из-за того, что закончился бензин, отказ двигателя или спущенная шина, время в пути может продлиться на час или больше, но такие особые причины не будут происходить каждый день.

Когда возникают вариации по особой причине, все же неплохо проанализировать, что пошло не так, чтобы увидеть, можно ли предотвратить эти аномалии в будущем. В нашем примере с поездками вы могли бы остановиться на заправке, когда у вас заканчивается бензин, и убедиться, что ваш автомобиль находится в хорошем состоянии, чтобы обеспечить правильную работу.

Как сделать контрольную карту

Контрольные диаграммы - отличный способ отделить вариации по общей причине от вариаций по особой причине. С помощью контрольной диаграммы вы можете отслеживать переменную процесса во времени.

Чтобы начать работу, выполните следующие действия:

1. Выберите период времени, обычно отмечаемый на оси X контрольной диаграммы, для сбора необходимых данных и установления ваших контрольных пределов.
2. Соберите свои данные и нанесите их на контрольную диаграмму.
3. Рассчитайте среднее значение ваших данных и добавьте контрольную линию.
4. Рассчитайте верхний и нижний контрольные пределы и добавьте эти линии в диаграмму, в идеале - другого цвета или стиля.
5. Отметьте любые «неконтролируемые сигналы» или места, где ваши данные выходят за пределы ваших контрольных пределов.Выясните причину и скорректируйте процесс, чтобы минимизировать риск этих отклонений.
6. Помня о ваших пределах контроля, продолжайте отслеживать свой процесс.

Не волнуйтесь - мы пройдем через все эти шаги на нашем примере поездки на работу.

Например, предположим, вы хотите записать количество времени, которое требуется, чтобы добираться до работы каждый день в течение определенного количества дней. Каждый день вы измеряете количество времени, которое проходит с момента выхода из дома до въезда на парковку.После того, как данные нанесены на контрольную диаграмму, вы можете рассчитать среднее время, необходимое для завершения поездки.

Контрольная диаграмма, представленная ниже, представляет собой простое наглядное пособие для определения количества времени, затрачиваемого на поездку на работу более 25 дней.

В нашем примере данные собирались в течение 25 дней подряд. Расчетное среднее значение показывает, что в среднем поездка занимает 24,9 минуты каждый день. Это среднее значение становится вашей контрольной линией (CL), показанной зеленым цветом.

Как рассчитать верхний и нижний контрольные пределы

После того, как вы вычислили среднее значение, вы можете рассчитать свои контрольные пределы.Верхний контрольный предел (UCL) - это наибольшее количество времени, которое вы ожидаете от поездки на работу при наличии общих причин. Нижний контрольный предел (LCL) - это наименьшее значение, которое вы ожидаете от поездки на работу с общими причинами отклонений.

Для расчета контрольных пределов выполните следующие действия:

1. Вычтите среднее число из числа, записанного вами для каждого дня, и возведите результат в квадрат. (Например, наш расчет дня 1 будет 23 - 24,9 = -1,9 x -1,9 = 3.61.)
2. Найдите среднее значение всех результатов, возведенных в квадрат.
3. Найдите квадратный корень из этого результата. Квадратный корень - это стандартное отклонение.
4. Определите, на сколько стандартных отклонений вы хотите допустить в рамках контролируемого вами процесса. Верхний и нижний пределы в хорошо контролируемом процессе равны +3 и -3 стандартных отклонения от среднего.

В этом примере стандартное отклонение составляет 6,9. Наш верхний контрольный предел составляет 45,6 минут (24.9 + 6,9 + 6,9 + 6,9), а нижний контрольный предел составляет 4,2 минуты (24,9 - 6,9 - 6,9 - 6,9), что показано красным на примере контрольной диаграммы.

Пока все точки на графике находятся в контрольных пределах, процесс считается находящимся под статистическим контролем. Это отличная новость для вашего бизнеса - срочных изменений нет. Вы всегда можете внести улучшения, но работа в установленных пределах - замечательная цель.

Точки, выходящие за пределы вашего контроля, указывают на моменты, когда процесс выходил из-под контроля.Если эти неконтролируемые точки случаются редко, вам нужно посмотреть на них, чтобы проанализировать, что пошло не так, и спланировать их исправление в будущем. Если вы обнаружите, что процесс часто выходит из-под контроля, это может указывать на закономерность и требует решения.

Контрольная диаграмма с примером плана действий (Нажмите на изображение, чтобы изменить в Интернете)

Теперь вы готовы оптимизировать процессы, повысить качество и остановить вариации в его следах. Начните с нашего шаблона контрольной диаграммы.

Теперь, когда вы знаете о контрольных диаграммах, ознакомьтесь с 6 другими базовыми инструментами качества , которые помогут вам улучшить ваши процессы.

Узнать больше

Как построить индивидуальные контрольные карты

Октябрь 2006 г.

В этом выпуске:

Предположим, ваш процесс генерирует данные с очень ограниченной частотой. Может быть, вы получаете данные только раз в день, раз в неделю или раз в две недели. Как мы можем применить контрольные диаграммы к этим типам данных? Если мы дождемся получения нескольких точек данных для формирования подгруппы, мы не сможем построить точку очень часто. Возможно, метод тестирования, используемый для анализа процесса, очень дорог в использовании или занимает много времени.Как мы можем справиться с такой ситуацией? В этих случаях полезны индивидуальные контрольные диаграммы. Этот тип диаграммы полезен, когда у вас есть только одна точка данных одновременно, чтобы представить данную ситуацию. Контрольная карта отдельных лиц представлена ​​в этой публикации.

Введение

Индивидуальная контрольная диаграмма - это тип контрольной диаграммы, которую можно использовать с данными переменных. Как и большинство других диаграмм управления переменными, на самом деле это две диаграммы. Одна диаграмма предназначена для результатов индивидуального образца (X).Другая диаграмма предназначена для скользящего диапазона (R) между последовательными отдельными выборками. Диаграмма отдельных лиц очень полезна для мониторинга процессов, когда данные часто недоступны. Диаграмма индивидуального контроля исследует изменение результатов отдельных выборок с течением времени. Хотя рациональное разделение на подгруппы неприменимо, необходимо подумать о том, когда будут измеряться результаты. Если процесс находится под статистическим контролем, среднее значение на индивидуальной диаграмме является нашей оценкой среднего населения.Средний диапазон будет использоваться для оценки стандартного отклонения совокупности.

Контрольная карта отдельных лиц - это метод анализа вариаций. Одним из источников вариаций является вариация результатов отдельных выборок. Это представляет собой «долгосрочное» изменение в процессе. Второй источник вариаций - это вариации в диапазонах между последовательными выборками. Это представляет собой «краткосрочное» изменение.

X Диаграмма

Рисунок в этом разделе является примером X-диаграммы для отдельных результатов.В этом примере образец отбирается один раз в день из заданного технологического потока и проверяется на наличие определенного загрязнителя. Поскольку данные собираются не очень часто, была выбрана контрольная карта отдельных лиц. В первый день метод испытания показал, что в потоке продукта было 105 частей на миллион загрязняющих веществ. На второй день результат пробы составил 93 ppm. Общее среднее значение процесса было рассчитано и нанесено на график в виде сплошной линии. Верхний и нижний контрольные пределы также были рассчитаны и нанесены пунктирными линиями.

График подвижного диапазона

Рисунок в этом разделе представляет собой график скользящего диапазона, который соответствует графику X. Эта диаграмма представляет собой диапазон между последовательными точками данных. Этот диапазон часто называют скользящим диапазоном. Значение диапазона для второго дня - это просто диапазон между днем ​​1 и днем ​​2 (наибольший минус наименьший). Этот диапазон составляет 105 - 93 = 12. Средний диапазон был рассчитан и нанесен на график в виде сплошной линии. Верхний контрольный предел также был рассчитан и нанесен пунктирной линией.На диаграмме диапазона для индивидуальной диаграммы нет нижнего контрольного предела.

Статистический контроль

Графики выше находятся под статистическим контролем. Что это значит, когда контрольная диаграмма отдельных лиц находится под статистическим контролем? Это означает, что результаты отдельных образцов согласованы во времени, то есть существенно не отличаются от среднего по процессу. Это также означает, что разница между результатами последовательных проб остается неизменной во времени. Мы можем предсказать, что будет происходить в ближайшем будущем.Дополнительную информацию об интерпретации контрольных диаграмм см. В нашей публикации за апрель 2004 г. на нашем веб-сайте.

Когда использовать

Индивидуальные контрольные диаграммы следует использовать, когда есть только одна точка данных для представления ситуации в данный момент времени. Контрольная диаграмма отдельных лиц позволяет наносить точки на диаграмме для каждой взятой пробы. Это позволяет определить, находится ли процесс под статистическим контролем для каждой взятой пробы. Может показаться, что это означает, что вы всегда должны использовать индивидуальные диаграммы.Это не обязательно верно, как обсуждается ниже.

Чтобы использовать индивидуальную контрольную карту, результаты индивидуальной выборки должны иметь «отчасти» нормальное распределение. В противном случае индивидуальная контрольная диаграмма будет давать больше ложных сигналов для тестов, таких как зонные тесты, то есть будет чаще указывать на то, что процесс выходит из-под контроля, хотя на самом деле это не так.

Индивидуальные контрольные диаграммы не так чувствительны к изменениям, как диаграммы Xbar-R. Кроме того, значения X и R могут значительно варьироваться (даже если процесс находится под контролем), пока количество отдельных точек данных не достигнет 100.

Шаги построения

Шаги по построению индивидуальной контрольной карты приведены ниже.

1. Соберите данные.

а. Выберите частоту, с которой будут собираться данные. Данные следует собирать в порядке их создания.

b. Выберите количество точек данных (k), которые необходимо собрать до расчета контрольных пределов (не менее двадцати). Это будут предварительные ограничения. Пределы контроля следует пересчитать после того, как вы соберете 100 точек данных.

г. Запишите результаты отдельных проб.

г. Рассчитайте диапазон перемещения (Ri + 1) между последовательными результатами выборки:

Ri + 1 = | Xi + 1 - Xi |

, где Xi + 1 - результат выборки i + 1, а Xi - результат выборки i. Значение диапазона всегда положительное.

2. Постройте данные.

а. Выберите масштабы для осей x и y для диаграмм X и R.

г. Нанесите диапазоны на диаграмму R и соедините последовательные точки прямой линией.

г. Нанесите результаты отдельных образцов на диаграмму X и соедините последовательные точки прямой линией.

3. Рассчитайте общие средние значения процесса и контрольные пределы.

а. Рассчитаем средний скользящий диапазон (Rbar):

Обратите внимание, что всегда на одно значение диапазона меньше, чем у результатов индивидуальной выборки для индивидуальной контрольной диаграммы.

г. Нанесите Rbar на диаграмму диапазонов в виде сплошной линии и метки.

г. Рассчитайте общее среднее значение процесса (X):

г. Нанесите X на диаграмму X в виде сплошной линии и метки.

e. Рассчитайте контрольные пределы для диаграммы R. Верхний предел управления задается UCLr. Нижний предел управления задается LCLr.

ф. Нанесите верхний контрольный предел на диаграмму R в виде пунктирной линии и метки.

г. Рассчитайте контрольные пределы для диаграммы X. Верхний предел управления задается UCLx. Нижний предел управления задается LCLx.

ч. Нанесите контрольные пределы на диаграмму X в виде пунктирных линий и метки.

4. Интерпретируйте обе диаграммы для статистического контроля.

а. Всегда сначала учитывайте вариации. Если диаграмма R выходит из-под контроля, контрольные пределы на диаграмме X могут быть недействительными, поскольку у вас нет точной оценки Rbar.

г. Все тесты для статистического контроля применимы к X-диаграмме. Однако данные на диаграмме диапазона не являются независимыми. Каждая точка данных используется дважды.Единственный тест, который действителен для диаграммы диапазона, - это точки за контрольными пределами.

5. При необходимости вычислите стандартное отклонение процесса.

а. Если диаграмма R находится в статистическом контроле, стандартное отклонение процесса,

с, можно рассчитать как:

Пример: ожидание в строке

Ожидание в очереди в банке может быть очень неприятным. Ваш банк только что выполнил обещание, что ваше ожидание в очереди никогда не будет дольше пяти минут.Вы решаете выяснить, правда ли это. Поскольку вы ходите в банк примерно раз в неделю, данные у вас нечастые. Вы чувствуете, что отдельные измерения (время ожидания в очереди), вероятно, являются нормальным распределением (ожидание в очереди обычно не распределяется нормально, но мы предполагаем для этого примера). Вы решаете использовать график отдельных лиц / скользящего диапазона, чтобы определить, выполняет ли банк свое обещание. Каждый раз, когда вы идете в банк, вы измеряете, сколько времени вы ждете в очереди, до ближайшего нуля.1 минута. Результаты для 24 поездок в банк приведены ниже.

Поездка	Ожидание на линии
1	3,5
2	2,4
3	4,1
4	2,8
5	3
6	4,7
7	1,2
8	0.9
9	2,5
10	3,1
11	3,6
12	4,1
13	3,8
14	2,5
15	2,8
16	4,3
17	4,1
18	3,6
19	2.4
20	4,8
21	3,5
22	2,5
23	1,3
24	4,5

Первым шагом после сбора данных является расчет диапазона движения между поездками в банк. Например, диапазон перемещения - это диапазон между поездками 1 и 2:

.

Ri + 1 знак равно | Xi + 1 - Xi | = 3.5 - 2,4 = 1,1

Это делается для каждой последующей поездки. Диапазон перемещения между поездками 2 и 3 составляет | 2,4 - 4,1 | = 1,7. Помните, диапазон всегда положительный.

Следующим шагом является вычисление общего среднего значения процесса и среднего диапазона. Общее среднее значение процесса определяется путем сложения индивидуальных результатов для каждой поездки и деления на количество проб (поездок). В этом случае количество поездок (k) равно 24. Средний диапазон определяется путем сложения значений скользящего диапазона и деления на k-1, поскольку на одно значение диапазона меньше, чем в отдельных выборках.

Xbar = 76/24 = 3,17

Rбар = 27,4 / 23 = 1,19

Следующим шагом является расчет контрольных пределов. Пределы контроля:

UCLr = 3,27 Rбар = 3,27 (1,19) = 3,89

LCLr = Нет

UCLx = Xbar + 2,66Rbar = 3,17 + 2,66 (1,19) = 6,34

LCLx = Xbar - 2,66Rbar = 3,17 - 2,66 (1,19) = 0,005

Если график скользящего диапазона находится под контролем, можно определить стандартное отклонение отдельных результатов.График скользящего диапазона (как показано ниже) находится под контролем. Стандартное отклонение тогда определяется как:

s '= Rbar / 1,128 = 1,19 / 1,128 = 1,05

X Диаграмма - Пример

В этом примере показан график X для ожидания в очереди. График скользящего диапазона показан ниже. Все под контролем. Это означает, что, пока процесс остается неизменным, вы можете в определенном диапазоне предсказать, как долго вы будете ждать в очереди, когда пойдете в банк.

Это означает, что когда вы пойдете в банк, вы будете ждать в очереди от 0 до 6.34 мин. Что это означает в отношении обязательства вашего банка о том, что вы не будете ждать в очереди более 5 минут? Это означает, что банк не в состоянии выполнить эту гарантию. Судя по данным, вы еще не ждали более 5 минут. Но прежде чем вы это сделаете, это лишь вопрос времени.

График подвижного диапазона

- пример

Резюме

В этой публикации представлены контрольные карты физических лиц. Этот тип диаграммы следует использовать, когда данные нечасто доступны.Отдельные измерения должны быть «в некоторой степени» нормально распределены, чтобы использовать индивидуальную диаграмму. X-диаграмма исследует долгосрочные вариации результатов отдельных выборок. Диаграмма диапазона исследует краткосрочные вариации между последовательными результатами выборки. Как и все контрольные диаграммы, индивидуальная диаграмма используется для определения того, находится ли процесс под статистическим контролем.

О контрольных диаграммах | SQC Online

Что такое контрольные диаграммы?

Контрольная диаграмма - популярный статистический инструмент для контроля и повышения качества.Созданная Уолтером Шухартом в 1924 году для производственной среды, позже У. Эдвард Деминг расширил ее до улучшения качества во всех областях организации (философия, известная как Total Quality Management, или TQM).
Попробуйте наш калькулятор контрольной диаграммы для атрибутов (дискретные данные) и калькулятор контрольной диаграммы для переменных (непрерывные данные).

Назначение контрольных карт

Успех подхода Шухарта основан на идее, что независимо от того, насколько хорошо спроектирован процесс, в выходных измерениях существует определенная вариативность природы.

Когда изменение качества процесса происходит только из-за случайных причин, говорят, что процесс находится под контролем. Если отклонение процесса включает как случайные, так и особые причины отклонения, процесс считается неконтролируемым.

Контрольная карта предназначена для выявления особых причин отклонений.

В своей базовой форме контрольная диаграмма представляет собой график зависимости некоторой функции измерения процесса от времени. Точки, нанесенные на график, сравниваются с парой контрольных пределов.Точка, превышающая контрольные пределы, сигнализирует о тревоге.

Аварийный сигнал, сигнализируемый контрольной диаграммой, может указывать на наличие особых причин отклонений, и необходимо предпринять некоторые действия, начиная от взятия пробы для повторной проверки и заканчивая остановкой производственной линии, чтобы отследить и устранить эти причины. С другой стороны, тревога может быть ложной, если на практике в процессе не произошло никаких изменений. Дизайн контрольных диаграмм - это компромисс между рисками не обнаружения реальных изменений и ложных тревог.

Допущения, лежащие в основе контрольных диаграмм

Два важных допущения:

1. Функция измерения (например, среднее значение), которая используется для отслеживания параметра процесса, распределяется согласно нормальному распределению. На практике, если кажется, что ваши данные очень далеки от этого предположения, попробуйте их преобразовать.
2. Измерения независимы друг от друга.

Построение контрольной карты 3-сигм ("типа Шухарта")

Во время стабильной стадии процесса:

1. Определите параметр процесса, который вы хотите отслеживать (например, среднее значение процесса или разброс).
2. Создайте осевую линию графика в соответствии с целевым значением отслеживаемого параметра.
3. Сгруппируйте измерения процесса в подгруппы (выборки) по периоду времени. Точки, которые должны быть нанесены на график, являются некоторой функцией измерений процесса в каждой подгруппе, которые оценивают целевое значение.
   Например, если вы отслеживаете среднее значение процесса, то точки на графике должны быть средними выборками, вычисляемыми через равные промежутки времени. Обозначим момент времени t как Xt.
4. Создайте верхний и нижний контрольные пределы (UCL, LCL) в соответствии со следующей формулой:

   UCL = CL + 3 с
   LCL = CL - 3 с
    

   , где s - стандартное отклонение X _t .
   В приведенном выше примере Xt может быть ежедневным средством измерения процесса. Если каждая ежедневная выборка состоит из n измерений, то стандартное отклонение Xt равно стандартному отклонению процесса, деленному на корень из n.
   
   После установки контрольных пределов продолжайте рисовать точки на графике как функцию времени.Когда точка превышает контрольные пределы, это указывает на то, что процесс вышел из-под контроля и необходимо принять меры (конечно, есть небольшая вероятность, что это ложная тревога).

Пример

Чтобы вы почувствовали эту статистическую терминологию, представьте себе процесс, в котором производятся бруски мыла. Начальник производства хочет контролировать средний вес кусков мыла, производимых на линии. Целевое значение веса одного куска мыла составляет 100 г. Также известно, что оценка стандартного отклонения веса для одного куска мыла составляет 5 г.

Ежедневно берутся образцы из 10 баров в течение стабильного периода процесса. Для каждого образца записываются веса и вычисляется их среднее / среднее значение. Средние значения выборки представляют собой оценки среднего значения процесса.

1. Контролируемый параметр - это среднее значение процесса.
2. Средняя линия в этом случае будет равна 100 г (мишень).
3. Точки на графике будут средними значениями выборки (где каждая выборка состоит из 10 измерений).
4. Контрольные пределы даются как 100 ± 3 Â · 5 / корень (10).

Правила сенсибилизации для контрольных карт

Американский стандарт основан на контрольных пределах «трех сигм» (соответствует 0,27% ложных срабатываний), в то время как Британский стандарт использует пределы «3,09 сигма» (соответствует 0,2% ложных срабатываний). В обоих случаях предполагается, что в основе соответствующих оценок лежит нормальное распределение.

Было показано, что диаграммы типа Шухарта эффективны при обнаружении средних и больших сдвигов, но нечувствительны к небольшим сдвигам.Одна из попыток повысить эффективность диаграмм типа Шухарта заключается в добавлении дополнительных правил остановки, основанных на прогонах. Наиболее популярные правила остановки были предложены компанией «Western Electric Company» («WECO»). Эти правила дополняют обычное правило: «Один балл превышает контрольные пределы». Вот самые популярные правила Western Electric:

• 2 из 3 последовательных точек выходят за пределы предупреждений (2-сигма), но в пределах контроля (3-сигма).
• 4 из 5 последовательных точек выходят за пределы 1 сигмы, но в пределах контроля.
• 8 последовательных точек приходятся на одну сторону от средней линии.

Онлайн-калькулятор правил Western Electric доступен здесь.

Дополнительная информация о контрольных диаграммах

контрольные диаграммы Шухарта - контрольная диаграмма MATLAB

синтаксис

контрольная диаграмма (X)
контрольная диаграмма (x, группа)
контрольная диаграмма (X, группа)
[статистика, данные графика] = контрольная диаграмма (x, [группа])
контрольная диаграмма (x , группа, ' имя ', значение )


Описание

controlchart (X) создает диаграмму xbar измерений в матрице X .Каждая строка X - это считается подгруппой измерений, содержащей повторяющиеся наблюдения взяты одновременно. Строки должны быть в порядке времени. Если X - это объект временного ряда, временные образцы должны содержать повторяющиеся наблюдения.

Диаграмма отображает средние значения подгрупп во временном порядке, центральная линия ( CL ) в среднем от средних значений, и верхний и нижний контрольные пределы ( UCL , LCL ) при трех стандартных ошибках от центральной линии.Стандартная ошибка - расчетное стандартное отклонение процесса, деленное на квадрат корень размера подгруппы. Стандартное отклонение процесса оценивается от среднего стандартного отклонения подгруппы. Вне контроля измерения отмечены как нарушения и обведены красным кружком. Включен режим курсора данных, поэтому при нажатии любой точки данных отображается информация об этом.

controlchart (x, group) принимает переменную группировки группа для вектора измерений x . группа - категориальная переменная, числовой вектор, символьный вектор, строка array или массив ячеек из символьных векторов той же длины, что и x . Последовательный измерения x (n) с одинаковым значением группы (n) для 1 ≤ n ≤ длина (x) определены как подгруппа. Подгруппы могут имеют разное количество наблюдений.

контрольная диаграмма (X, группа) принимает группирующая переменная группа для матрица измерений в X .В этом случае группа используется только для обозначения оси времени; не меняет группировку по умолчанию по строкам.

[stats, plotdata] = controlchart (x, [group]) возвращает структура статистика статистики и параметра подгруппы оценок, а структура plotdata построенных значения. plotdata содержит по одной записи для каждой диаграммы.

Поля в stats и plotdata зависят на тип диаграммы.

Поля в статистике выбираются из следующие:

• среднее значение - подгруппа означает

• стандартное - стандартное значение подгруппы отклонения

• диапазон - диапазоны подгруппы

• n - размер подгруппы или всего размер или область контроля

• i - Индивидуальные значения данных

• ma - Скользящие средние

• mr - Диапазон перемещения

• count - Количество дефектов или дефектные изделия

• mu - Расчетное среднее значение процесса

• сигма - Расчетное значение процесса стандартное отклонение

• p - Расчетная доля дефектный

• м - Оценка среднего дефекта на единицу

Поля в plotdata следующие:

• pts - Значения точек на графике

• cl - Центральная линия

• lcl 903 - Нижний предел контроля

• ucl - Верхний контрольный предел

• se - Стандартная ошибка построения point

• n - Размер подгруппы

• ooc - Логично, что верно для точек, которые находятся вне контроля

controlchart (x, group, ' name ', value ) указывает одна или несколько из следующих пар необязательных параметров имя / значение, с именем в одинарных кавычках:

• charttype - Имя тип диаграммы, выбранный из следующего:

  • 'xbar' - X бар или среднее значение

  • 's' - Стандартное отклонение

  • 'r' - Диапазон

  • 'ewma' - Экспоненциально взвешенное скользящее среднее

  • 'i' - Индивидуальное наблюдение

  • 'mr' - Диапазон перемещения индивидуума наблюдений

  • 'ma' - Скользящее среднее индивидуальные наблюдения

  • 'p' - Дефектная доля

  • 'np' - Количество дефектных

  • 'u' - Дефектов на единицу

  • 'c' Количество дефектов

  В качестве альтернативы параметр может быть массивом строк или массивом ячеек, перечисляющим несколько совместимых типы диаграмм.Есть четыре набора совместимых типов:

  • 'xbar' , 's' , 'r' , и 'ewma'

  • 'i' , 'mr' и 'ma'

  • 'p' и 'np'

  • 'u ' и ' c '

• дисплей - Либо ' на ' (по умолчанию) для отображения контрольной диаграммы или «выкл.» для исключения дисплей

• метка - вектор символов, массив строк или массив ячеек векторы символов, по одному на подгруппу.Эта метка отображается как часть курсора данных для точка на сюжете.

• лямбда - параметр между 0 и 1 контролируют степень влияния текущего прогноза по прошлым наблюдениям на графике EWMA. Более высокие значения 'лямбда' дают меньший вес для прошлых наблюдений и больший вес для текущего наблюдения. По умолчанию 0,4.

• пределы - Трехэлементный вектор, определяющий значения нижний контрольный предел, центральная линия и верхние контрольные пределы.По умолчанию оценивается центр линии и вычислить контрольные пределы на основе оценочного значения сигмы. Не допускается, если есть несколько типов диаграмм.

• среднее значение - Значение для процесса среднее или пустое значение (по умолчанию), чтобы оценить среднее значение от X . Это параметр p для диаграмм p и np , средние дефекты на единицу для карт u и c , и нормальный параметр mu для других диаграмм.

• nsigma - Количество сигм кратно от центральной линии до контрольного предела. По умолчанию 3.

• родительский - дескриптор по осям для получения графика контрольной диаграммы. По умолчанию создаются оси. в новой фигуре. Не разрешено, если существует несколько типов диаграмм.

• правила - Имя правила управления, строкового массива или ячейки массив, содержащий несколько имен правил управления. Эти правила вместе с контрольными пределами, определить, помечена ли точка как неконтролируемая.По умолчанию правила контроля не применяются, и использовать только контрольные пределы, чтобы решить, выходит ли точка из-под контроля. См. Правила управления для получения дополнительной информации. Правила управления применяются к диаграммам, которые измерить уровень процесса ( xbar , i , c , u , p и np ), а не изменчивость ( r , s ), и они не применяются к графикам на основе статистики движения ( ma , mr , ewma ).

• сигма - Либо значение для сигма, или метод оценки сигмы, выбранный из 'std' ( по умолчанию), чтобы использовать среднее стандартное отклонение внутри подгруппы, 'диапазон' от до используйте средний диапазон подгруппы и «отклонение» от до используйте квадратный корень из объединенной дисперсии. При создании i , mr , или ma диаграммы для данных не в подгруппах, оценка всегда основывается на диапазоне перемещения.

• specs - вектор, определяющий пределы спецификации.Обычно это двухэлементный вектор нижнего и верхние пределы спецификации. Поскольку пределы спецификации обычно применяются к отдельным измерениям, этот параметр подходит в первую очередь для диаграмм и . Эти пределы не нанесены на r , s , или MR графиков.

• шт. - Общее количество проверенных позиций для карт p и np , и размер проверяемой единицы для карт u и c .В обоих случаях X должно быть подсчетом числа. обнаруженных дефектов или дефектов. По умолчанию 1 для диаграмм u и c . Этот аргумент является обязательным (по умолчанию) для диаграмм p и np .

• ширина - ширина окно, используемое для вычисления скользящих диапазонов и средних значений на графиках mr и ma , и для вычисления сигма-оценки в i , mr , и ma карт.По умолчанию 5.

Согласован ли ваш процесс? Предсказуемо? Контрольная диаграмма Шухарта (диаграмма SPC) может вам сказать.

Каждый процесс индивидуален. Если вы напишете свое имя десять раз, ваше подписи все будут похожи, но никакие две подписи не будут точно так же. Есть внутренняя вариация, но она бывает разной. между предсказуемыми пределами. Если, когда вы подписываете свое имя, кто-то толкает вас локтем, получается необычная вариация из-за то, что называется «особой причиной».Если вы режете бриллианты, и кто-то ударил вас локтем, особая причина может быть дорогостоящей. Для многих, многих процессов важно отметить особые причины изменения, как только они возникают.

Также существует вариация по «общей причине». Рассмотрим бейсбол кувшин. Если у него хороший контроль, большинство его передач будет быть там, где он хочет. Будут какие-то вариации, но не слишком много. Если он «дикий», его передачи идут не туда, куда он хочет. их; есть еще варианты.Особых причин быть не может - ни ветра, ни изменения мяча - просто более «общее дело» вариация. Результат: выдается больше прогулок, и есть непреднамеренный жир просачивается по тарелке, где может ударить тесто их. В бейсболе контроль побеждает в играх с мячом. Точно так же в большинстве процессы, уменьшающие вариации по общей причине, экономят деньги.

К счастью, есть простые в использовании диаграммы, которые позволяют легко увидеть вариации процесса как по особой, так и по общей причине. Они есть называемые контрольными диаграммами, а иногда и диаграммами Шухарта, после их изобретатель Уолтер Шухарт из Bell Labs.Есть много разных подвиды контрольных карт, которые могут быть применены к различные типы данных процесса, которые обычно доступный.

Все контрольные карты состоят из трех основных компонентов:

• средняя линия, обычно математическое среднее всех образцы построены.
• верхние и нижние пределы статистического контроля, определяющие ограничения вариаций по общей причине.
• данные о производительности в динамике.

На что обратить внимание для:

Смысл создания контрольных диаграмм - посмотреть на вариации, поиск особых причин и отслеживание общих причин. Особые причины можно определить с помощью нескольких тестов:

• 1 точка данных выходит за пределы контроля
• 6 и более очков подряд постоянно увеличивается или убывающая
• 8 или более точек подряд по одну сторону от средней линии
• 14 или более точек, чередующихся вверх и вниз

В тех диаграммах, которые объединяют две диаграммы вместе, вам понадобится искать эти аномалии на обоих графиках.

Самая простая интерпретация контрольной диаграммы - использовать только первый из перечисленных тестов. Остальные действительно могут быть полезны (и есть и другие, не перечисленные здесь), но имейте в виду, что, поскольку вы примените больше тестов, ваши шансы на ошибку типа I, т. е. получение ложных срабатываний значительно возрастает.

Типы ошибок:

Контрольные пределы на контрольной диаграмме обычно отображаются через 3 секунды. от центральной линии, потому что пределы 3-сигма - хороший баланс точка между двумя типами ошибок:

• Ошибки типа I или альфа возникают, когда точка выходит за пределы контрольные пределы, даже если нет особой причины.В результат - охота на ведьм по особым причинам и корректировка вещи здесь и там. Фальсификация обычно искажает стабильную процесс, а также трата времени и энергии.
• Ошибки типа II или бета-версии возникают, когда вы пропускаете особую причину. потому что диаграмма недостаточно чувствительна, чтобы ее обнаружить. В этом случае, вы не подозреваете, что проблема существует, и, таким образом, невозможно искоренить это.

Управление всеми процессами уязвимо для этих двух типов ошибки.Причина, по которой лимиты контроля 3-сигма уравновешивают риск ошибки заключается в том, что для нормально распределенных данных точки данных будут попадают в пределы 3-сигма 99,7% времени, когда процесс находится в контроль. Это делает охоту на ведьм нечастой, но все же делает ее вероятно, что будут обнаружены необычные причины отклонений.

Если ваш процесс под контролем, хорошо ли это? довольно? Нет. Вы должны начать с устранения особых причин, чтобы у вас есть стабильный процесс, с которым можно работать.Но потом приходит настоящая удовольствие, а зачастую и самые существенные преимущества: пришло время улучшить процесс, чтобы даже вариации по общей причине уменьшенный.

Создавайте контрольные диаграммы с помощью инструмента Data Analyst PathMaker.

---

Рекомендуемая литература:

Учебные заметки для практикующих врачей

Примечания

Предположения в c-диаграмме заключаются в том, что события: (а) происходят по одному

за один раз без одновременного возникновения нескольких событий или

в одном месте; и (b) являются независимыми в том смысле, что

наступления события в одном временном периоде или регионе не влияют на вероятность наступления любого другого события.

Несмотря на то, что все эти предположения не могут быть выполнены точно на практике

, опыт показывает, что c-диаграмма

полезна в практических обстоятельствах, даже если имеется значительное отклонение

от идеальных условий. Важно отметить

, что u-диаграмма предпочтительнее c-диаграммы, когда доступны размеры выборки или области возможностей

, которые значительно различаются. Когда

такая область информации о возможностях недоступна, тогда

c-диаграмма является единственным реальным вариантом при условии, что

разумно предположить, что основные области возможностей

относительно большие и довольно постоянные, поскольку это случай в нашем примере

для неотложной помощи.

Контрольные пределы для c-диаграммы получены из

.

Когда

.10

10

, как здесь, распределение Пуассона

примерно симметрично, и поэтому концепция трех сигм Шухарта

работает хорошо. Однако, когда

.10 не удовлетворяет, тогда требуется другой подход

. Один из методов заключается в вычислении точных пределов

с использованием функции распределения вероятностей распределения Пуассона

с помощью компьютерного программного обеспечения или статистических таблиц

.

10

Также были предложены другие подходы, использующие преобразования как

, а также ограничения на основе регрессии.

29

Когда вычисление нижнего контрольного предела дает

значение ниже 0,

10

, которое обычно сбрасывается на 0, потому что процесс

не может производить отрицательный счет. Однако отрицательный нижний контрольный предел

также указывает на то, что распределение Пуассона

не является симметричным, и тогда рекомендуется вычисление точных пределов

.Кроме того, согласно

Уиллеру,

17

, c-диаграмма сломается, когда среднее число

событий упадет ниже 1, и в этот момент может быть полезным построение графика времени

между событиями.

20

В этом рабочем примере мы построили график количества госпитализаций

в экстренных случаях по понедельникам подряд, а не по дням подряд.

Причина этого связана с рациональным разделением на подгруппы. Некоторые процессы

состоят из различных основных причинно-следственных связей

подпроцессов, и один из примеров

- это неотложная госпитализация.Так, например, мы не ожидаем, что вероятность экстренной госпитализации

в больницу будет одинаковой для выходных

(суббота / воскресенье) и будних дней, а также мы не ожидаем, что пятница будет

такой же, как и в другие будние дни. Другими словами, процесс демонстрирует

сезонности. Чтобы не нарушать требования рационального разбиения на подгруппы

, мы разбили данные о приеме в экстренных случаях по дням недели

и использовали понедельники в качестве иллюстративного примера. Если требуется контрольный график

для неотложных госпитализаций в течение последовательных дней

, тогда должны использоваться методы, которые сначала десезонизируют данные.

20

Другие типы контрольных карт

Мы рассмотрели четыре типа контрольных карт, которые будут

часто применяться в здравоохранении. Многие другие типы контроля

диаграмм и связанных графиков задокументированы в литературе.

10 17

Эти

включают контрольные диаграммы EWMA, графики CUSUM, Q-диаграммы

22

и

графики числа между событиями,

21

, чтобы упомянуть лишь некоторые из них.Хотя

некоторые из этих диаграмм имеют явно более высокую производительность

по сравнению с описанными здесь базовыми диаграммами, важно отметить, что

, вообще говоря, они часто не предназначены для полной замены

контрольных диаграмм Шухарта; скорее они считаются полезными дополнениями

.

12

Интересной особенностью

применения контрольных карт в здравоохранении является включение

корректировки состава пациентов, которая была описана

в другом месте.

52532–34

Корректировка набора случаев часто требуется для проведения значимых сравнений

между поставщиками медицинских услуг.

35

ВЫБОР ТРЕХСИГМОВЫХ ПРЕДЕЛОВ

Шухарт утверждал - на основе математической теории

(теорема Чебышева)

36

, а также на основе опыта

и прагматизма - что устойчивые процессы порождают вариативность.

в пределах, и что в поисках экономического контроля вариации

эти пределы могут быть с успехом установлены на трех сигмах.Несколько десятилетий

опыта работы в целом ряде областей приложений,

включая здравоохранение, показали, что пределы трех сигм действительно полезны. Тем не менее, это не означает, что пределы

не могут быть изменены. По словам Нельсона,

13

обоснованием для

расширения или сужения пределов является вынесение суждения, в котором

затраты на поиск отклонений по особой причине, когда их нет

, необходимо уравновесить с затратами. пропустить такой сигнал

, когда он действительно существует.Однако мы должны подчеркнуть, что

везде, где контрольные пределы установлены на конечном положительном расстоянии

от центральной линии, мы рискуем ошибиться одним из двух типов

24

:

c тип I: обработать результат, являющийся результатом общая причина

, как если бы это была особая причина;

c тип II: для обработки результата, возникшего по особой причине, как

, если это была общая причина.

Невозможно уменьшить частоту обеих ошибок до 0, но

мы можем минимизировать экономические потери из-за ошибок типа

.Тем не менее, несмотря на некоторые разногласия

относительно теоретической основы контрольных диаграмм,

12

, имеется достаточно доказательств

, которые все чаще поступают от здравоохранения, чтобы показать, что в контексте постоянного улучшения

контрольные карты предлагают основные

.

преимущества, которые стоит затраченных усилий.

Благодарности: Мы благодарим г-на А. М. Ибрагима за предоставленное нам разрешение на использование его данных измерений артериального давления

и г-жу М. Нараян-Ли для перелома шейки бедренной кости

и наборы данных для неотложной госпитализации, использованные в этой статье.Также выражаем благодарность

StatIt.com (www.statit.com) за любезное разрешение на использование данных о водопадах.

Конкурирующие интересы: не заявлены.

СПРАВОЧНАЯ ИНФОРМАЦИЯ

1. Mohammed MA. Использование статистического контроля процессов для повышения качества медицинской помощи

. Qual Saf Health Care 2004; 13: 243–5.

2. Беннеян Дж. К., Ллойд Р. К., Плсек ЧП. Статистический контроль процессов как инструмент исследования

и улучшения здравоохранения. Qual Saf Health Care 2003; 12: 458–64.

3. Адаб П., Роуз А., Мохаммед М.А. и др. Таблицы результатов: NHS

заслуживает лучшего. BMJ 2002; 324: 95–8.

4. Диаз М., Нойхаузер Д. Пастер и парашюты: при статистическом контроле процесса на

лучше, чем рандомизированное контролируемое исследование. Qual Saf Health Care 2005; 14: 140–3.

5. Woodall WH. Использование контрольных карт в здравоохранении и надзоре за общественным здоровьем

(с обсуждением). Журнал технологий качества 2006; 38: 104–5.

6. Мохаммед М.А., Ченг К.К., Роуз А. и др. Бристоль, Шипман и клиническое управление

: забытые уроки Шухарта. Ланцет 2001; 357: 463–7.

7. Dettmer HW. Теория ограничений Голдратта: системный подход к постоянному совершенствованию

. Висконсин, США: ASQ Press Milwaukee, 1997.

8. Kelly DL. Как пользоваться контрольными картами в здравоохранении. Висконсин, США: Quality Press,

1999.

9. Кэри Р.Г. Улучшение здравоохранения с помощью контрольных карт: базовые и расширенные методы SPC

и тематические исследования.Висконсин, США: Quality Press, 2003.

10. Райан Т.П. Статистические методы повышения качества, 2-е изд. Нью-Йорк: Джон

Wiley & Sons, 2000.

11. Уилер Д.Д., Чемберс Д.С. Понимание статистического управления процессами, 2-е изд.

No related posts.