Пределы контрольная работа с ответами: Контрольная работа по теме «Вычисление пределов»

Контрольная работа на тему: теория пределов, непрерывность

Теория пределов. Непрерывность

Задание: Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей.

Целы формирование умения вычислять пределы функций, раскрывая неопределенности и используя замечательные пределы.

Задание для самостоятельной внеаудиторной работы:

10.1. Выучите определение предела функции в точке. Выясните, когда при вычислении пределов функции в точке возникает неопределенность вида и в чем заключается техника ее раскрытия.

10.2. Вычислите предел функции в точке:

10.3. Выучите определение предела функции на бесконечности. Выясните, когда при вычислении пределов функции возникает неопределенность вида и в чем заключается техника ее раскрытия.

10.4. Вычислите предел функции на бесконечности:

10.5. Запомните, какие пределы называются замечательными и проанализируйте, как они используются для вычисления пределов.

10.6. Вычислите предел функции с помощью замечательных пределов:

10. 7. Вычислите предел функции:

10.8. Выясните, при каком значении параметра будет равен -1; 0.

Методические указания по выполнению работы:

При решении задач необходимо знание следующего теоретического материала:

1. Предел функции в точке. Вычисление пределов путем раскрытия неопределенности вида .

Число называется пределом функции при , стремящемся к (или в точке ), если для любого наперед заданного существует такое , что для всех , удовлетворяющих условиям , имеет место неравенство: .

Если есть предел функции при , то пишут: .

При вычислении предела функции в точке удобно использовать следующую технику:

1. Если под знаком предела стоит многочлен, то предел вычисляется простой подстановкой.

Вычислите: .

Решение:

Подставим в многочлен вместо значение -1, тогда

Ответ: .

2. Если под знаком предела стоит отношение двух многочленов , то проверяем, обращается ли при подстановке знаменатель в ноль. Если не обращается, то предел вычисляется простой подстановкой.

Если при подстановке знаменатель обращается в ноль, то необходимо использовать дополнительные приемы.

Если , то имеем неопределенность вида . В этом случае предел можно вычислить разложением многочленов и на множители, используя формулы сокращенного умножения и формулу разложения квадратного трехчлена на множители:

, где и — корни уравнения .

Если разложение выполнено верно, то в числителе и знаменателе дроби должны получиться одинаковые множители, которые следует сократить. После сокращения предел вычисляется простой подстановкой.

Вычислите .

Решение:

Проверим, какие значения будут принимать числитель и знаменатель при подстановке вместо значения 3: . Получили неопределенность вида .

Разложим числитель на множители по формуле разложения квадратного трехчлена. Составим уравнение и найдем его корни:

или .

Тогда числитель можно представить в виде произведения двух множителей:

Знаменатель разложим по формуле разности квадратов: .

Вернемся к исходному пределу:

Ответ: .

3. Если под знаком предела стоит дробь вида , включающая иррациональную функцию (функцию, содержащую корень), то домножаем числитель и знаменатель дроби на выражение, сопряженное иррациональному.

Вычислите .

Решение:

Поскольку при подстановке в числитель и знаменатель вместо значение 0, получаем неопределенность вида , домножим числитель и знаменатель дроби на выражение , сопряженное знаменателю. Получим:

В знаменателе дроби воспользуемся формулой разности квадратов:

Вынесем в знаменателе за скобки и сократим дробь на : .

Видим, что при подстановке числитель и знаменатель не обращаются в 0, следовательно, теперь предел вычисляется простой подстановкой:

Ответ: .

2. Предел функции на бесконечности. Вычисление пределов путем раскрытия неопределенности вида .

Число называется пределом функции при , если для любого наперед заданного существует такое , что для всех имеет место неравенство: .

Если есть предел функции при , то пишут: .

Для нахождения пределов функций на бесконечности часто используют два основных предела: и , где — константа.

При вычислении предела дроби при возникает неопределенность вида . Техника ее раскрытия заключается в том, что каждое слагаемое числителя и знаменателя нужно разделить на в наивысшей степени. Возможны три случая:

1) наивысшая степень числителя совпадает с наивысшей степенью знаменателя:

Вычислите .

Решение:

Разделим каждое слагаемое числителя и знаменателя на . Получим:

Каждое слагаемое стремится к 0 при , тогда

Ответ: .

Итак, если наивысшая степень числителя совпадает с наивысшей степенью знаменателя, то в пределе получается число, отличное от нуля.

Вычислите .

Решение:

Разделим каждое слагаемое числителя и знаменателя на . Получим:

Ответ: .

Таким образом, если наивысшая степень числителя больше наивысшей степени знаменателя, то в пределе получается бесконечность.

3) наивысшая степень числителя меньше наивысшей степени знаменателя:

Вычислите .

Решение:

Разделим каждое слагаемое числителя и знаменателя на Получим:

Ответ:

Таким образом, если наивысшая степень числителя меньше наивысшей степени знаменателя, то в пределе получается ноль.

3. Замечательные пределы. Вычисление пределов с помощью замечательных.

Вычисление пределов функции можно осуществлять с помощью замечательных пределов:

— первый замечательный предел;

— второй замечательный предел.

Вычислите .

Решение:

Поскольку под знаком синуса стоит угол , домножим числитель и знаменатель дроби на 3, чтобы выражение под знаком синуса и выражение в знаменателе стали равны: .

Вынесем число 3 за знак предела: .

Применив первый замечательный предел, получим, что .

Ответ: .

Вычислите .

Решение:

Постараемся преобразовать выражение под знаком предела таким образом, чтобы прийти ко второму замечательному пределу. Необходимо, чтобы числитель дроби был равен 1. Для этого разделим числитель и знаменатель данной дроби на 3; получим дробь вида: . Теперь постараемся преобразовать показатель степени таким образом, чтобы в нем можно было выделить множитель . Для этого домножаем на 2 и 3 и делим на 2 и 3:

Применив к выражению в скобках второй замечательный предел, получим, что

Ответ: .

На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:

Готовые контрольные работы по высшей математике

Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

как понять, вычислить, подробное объяснение с решением

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim — от английского limit — предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача — найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Все онлайн калькуляторы для решения задач · Контрольная Работа РУ · Теперь вы можете задать любой вопрос!

Кусочно-заданная функция

Укажите кусочно-заданную функцию и перейдите к нужному вам сервису, например, к одному из: нахождению интеграла, производной, исследованию и построение графика и др.

Решение уравнений

Это сервис позволяет решать уравнения, в том числе получить подробное решение, а также увидеть решение уравнения на графике.

Решение пределов

Этот сервис позволяет найти предел функции. Также рассматривается подробное решение правилом Лопиталя.

Производная функции

Это сервис, где можно вычислить производную функции, частную производную функции, а также производную неявно заданной функции.

Разложение в ряд

Здесь можно выполнить разложение в ряд Тейлора, Фурье, найти сумму ряда.

Системы уравнений

Позволяет решать системы линейных уравнений методом Крамера, методом Гаусса, а также вообще любые системы уравнений.

Решение неравенств

Решает неравенство, а также изображает решённое неравенство на графике.

Решение интегралов

Это сервис, где можно вычислить определённые, неопредёленные интегралы, а также двойные, несобственные, кратные.

График функции

Это сервис построения графиков на плоскости и в пространстве. Приводится подробное решение на исследование функции.

Решение систем неравенств

Вы можете попробовать решить любую систему неравенств с помощью данного калькулятора систем неравенств.

Первый замечательный предел

Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.

Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:

Приведённое выше равенство основано на эквивалентности бесконечно малых . Следовательно, верно равенство и следующего отношения:

.

Это разновидность первого замечательного предела.

Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.

Пример 1. Найти предел .

Решение. Подстановка вместо x нуля приводит к неопределённости:

.

В знаменателе — синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:

.

В знаменателе — синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .

И приходим к разновидности первого замечательного предела:

,

потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.

Умножаем икс на три и тут же делим:

.

В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:

.

Теперь можем окончательно решить данный предел:

.

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 2. Найти предел .

Решение. Непосредственная подстановка вновь приводит к неопределённости «нуль делить на нуль»:

.

Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:

.

Пример 3. Найти предел .

Решение. При подстановке вновь получаем неопределённость «нуль делить на нуль»:

.

Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:

.

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 4. Найти предел .

Решение. Вновь получаем неопределённость «нуль делить на нуль»:

.

Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:

Пример 5. Найти предел .

Решение. И вновь неопределённость «нуль делить на нуль»:

.

Помним из тригонометрии, что тангенс — это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:

.

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 6. Найти предел .

Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.

.

Так как , то и

Пример 7. Найти предел .

Решение. И вновь неопределённость «ноль делить на ноль» и синус под знаком предела. Значит надо приводить к первому замечательному пределу. Умножим числитель и знаменатель на выражение сопряжённое числителю и получим

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 8. Найти предел .

Решение. Бороться с неопределённостью «ноль делить на ноль» будем приведением к первому замечательному пределу. Вспоминаем формулу тригонометрической единицы и подставляем её. Потом вспоминаем, что косинус в квадрате нуля и просто косинус нуля равны единице, а они у нас с противоположными знаками, значит взаимно уничтожаются. Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю. И дальнейшие преобразования. Всё вышеописанное выглядит так:

Начало темы «Предел»

Продолжение темы «Предел»

Site1

САЙТ 

ШЕРШНЕВА  ВЛАДИМИРА ГРИГОРЬЕВИЧА

         Данный сайт рассчитан, прежде всего, на студентов дистанционного и финансового факультетов и преподавателей, ведущих занятия на этих факультетах

ПРОГРАММЫ КУРСОВ

для факультетов финансового и дистанционного обучения

1.     Программа «Математический анализ»

2.     Программа «Линейная алгебра»

3.     Программа «Теория вероятностей и математическая статистика»

4.     Программа «Финансовая математика»

5.     Программа «Финансовые инвестиции»

6.   Программа «Финансовые вычисления»

КОНТРОЛЬНЫЕ РАБОТЫ ПО ФИНАНСОВОЙ МАТЕМАТИКЕ

Разовые платежи 10 вариантов

Потоки платежей 10 вариантов

УЧЕБНИК ФИНАНСОВАЯ МАТЕМАТИКА (из 3-х частей)

М., Изд-во РЭУ им. Г.В. Плеханова. – 2010.

1. Учебник Финансовая математика Часть 1 Простые и сложные проценты, инфляция

2. Учебник Финансовая математика Часть 2 Потоки платежей

3. Учебник Финансовая математика Часть 3 Потоки (продолжение), Ответы

МАТЕМАТИЧЕСКИЙ АНАЛИЗ. КОНТРОЛЬНЫЕ РАБОТЫ

1. Контрольная работа №1 Пределы (без правила Лопиталя)

2. Контрольная работа №2 Пределы (по правилу Лопиталя)

3. Контрольная работа №3 Графики

4 Контрольная работа №4 Функции нескольких переменных

5. Контрольная работа №5 Неопределенные интегралы

6. Контрольная работа №6 Определенные интегралы

7. Контрольная работа №7 Диф. уравнения

8. Контрольная работа №8 Ряды

ТЕСТЫ  ПРЕДЕЛЫ И ИНТЕГРАЛЫ

Тесты пределы с ответами

Тесты интегралы с ответами

ЛИНЕЙНАЯ АЛГЕБРА. КОНТРОЛЬНЫЕ РАБОТЫ

Линейная алгебра Часть I

Линейная алгебра Часть II

Вопросы и ответы о правах человека

Что такое «права человека»?

Права человека – это то, чем, согласно нормам морали, наделен каждый живущий в мире просто в силу того, что он — человек. Добиваясь реализации наших прав, мы обращаемся, как правило, к собственному правительству с позиций морали: так поступать нельзя, потому что это – вторжение в сферу моей морали и оскорбление моего личного достоинства. Никто,  ни человек, ни правительство, никогда не может отобрать у нас наших прав человека.

Откуда они взялись?

Они возникли потому, что человек помимо физической, имеет также моральную и духовную сущность. Права человека нужны для того, чтобы защитить и сохранить человеческую сущность каждого, чтобы обеспечить каждому человеку достойную жизнь – жизнь, которую человек заслуживает.

Почему кто-то «должен» их уважать? 

Прежде всего потому, что человеческая сущность включает и нравственную составляющую. Большинство людей, если им указать на то, что они ущемляют чье-то личное достоинство, постараются этого не делать. Как правило, люди не хотят причинять зла другим. Однако теперь помимо моральных санкций собственной или чужой совести в большинстве стран мира существуют законы, которые обязывают правительства уважать основные права своих граждан, даже если им этого, может быть, и не хочется. 

Кто обладает правами человека? 

Абсолютно все. Преступники, главы государств, дети, мужчины, женщины, африканцы, американцы, европейцы, беженцы, лица без гражданства, безработные, работающие, банкиры, лица, обвиняемые в совершении террористических актов, работники благотворительных учреждений, учителя, танцоры балета, астронавты. .. 

Даже преступники и главы государств? 

Абсолютно все. Преступники и главы государств — тоже люди. Сила прав человека заключается  в том, что они признают всех равными с точки зрения обладания человеческим достоинства. Кто-то порой может нарушить чьи-либо права или стать угрозой для общества, и поэтому может возникнуть необходимость тем или иным образом ограничить права таких людей, чтобы защитить права других,  но только в определенных пределах. Эти пределы определяются как минимум, необходимый  для сохранения человеческого достоинства.

Почему некоторым группам требуются особые права человека? Означает ли это, что у них больше прав, чем у других людей?

Нет, не означает, но некоторые группы, такие как цыгане-рома в Европе, далиты и определенные касты в Индии так долго подвергались дискриминации в том или ином обществе, что потребовались специальные меры, чтобы обеспечить им равный с другими людьми стандарт прав человека. Было бы смешно полагать, что после долгих лет укоренившейся дискриминации и стереотипов, откровенной ненависти и социальных барьеров будет достаточно просто предоставить им общеприменимые права, полагая, что этого будет достаточно для соблюдения равенства.

Почему речь идет о правах людей, а не об их ответственности? 

Несмотря на то, что некоторые философы и НПО выдвинули веские аргументы в пользу необходимости определить меру ответственности людей и даже представили в защиту этого довода свои «кодексы» и «декларации», сообщество правозащитников в целом хранит молчание по поводу этого спора. Причина в том, что многие правительства ставят «дарование» прав в зависимость от определенных обязанностей, налагаемых на людей правительством или правителем, отчего сама идея прав человека изначально теряет смысл. И все же, разумеется, все мы ‒ отдельные люди и группы людей ‒ должны со всей ответственностью относиться к правам других, не злоупотреблять ими, но уважать, как свои собственные права. И в этом свете статья 29 Всеобщей Декларации прав человека признает, что: «1. Каждый человек имеет обязанности перед обществом, в котором только и возможно свободное и полное развитие его личности. 2. При осуществлении своих прав и свобод каждый человек должен подвергаться только таким ограничениям, какие установлены законом исключительно с целью обеспечения должного признания и уважения прав и свобод других и удовлетворения справедливых требований морали, общественного порядка и общего благосостояния в демократическом обществе».

Кто следит за соблюдением прав человека? 

Все мы должны за этим следить. Существуют законы, как национальные, так и международные, которые ограничивают свободу действий правительств в отношении своих граждан, но если никто им не укажет на то, что своими действиями они нарушают международные нормы, правительства могут безнаказанно продолжать нарушения. Каждый из нас, как личность, должен в повседневной жизни не только уважать права других, но и внимательно следить за действиями наших и не наших правительств. Системы защиты прав существуют для того, чтобы все мы могли ими воспользоваться. 

Как я могу защитить свои права? 

Постарайтесь обратить внимание других на то, что ваши права были нарушены; потребуйте их соблюдения. Дайте противоположной стороне понять: вам известно, что она не имеет права обращаться с вами подобным образом. Выделить соответствующие статьи во Всеобщей декларации прав человека, Конвенции о правах человека или других международных документах. Если соответствующие законы есть в вашей собственной стране, сошлитесь и на них. Сообщите другим о случившемся: дайте сообщение в печать, напишите вашему депутату парламента и главе государства, проинформируйте об этом неправительственные организации, занимающиеся правами человека. Спросите у них совета. Если есть возможность, поговорите с адвокатом. Постарайтесь, чтобы правительству стало известно о ваших действиях.  Дайте ему понять, что вы не собираетесь отступать. Продемонстрируйте поддержку, на которую вы можете рассчитывать. Наконец, если все остальное не помогло, вы можете обратиться в суд. 

Как мне обратиться в Европейский Суд?

Европейская Конвенция о защите прав человека и основных свобод определяет процедуры рассмотрения индивидуальных жалоб. Однако принятие дел к  рассмотрению регламентируется строгими требованиями. Например, до подачи дела в Европейский суд вы должны подтвердить, что ваша жалоба уже подавалась в национальные суды вашей страны (вплоть до самой высшей инстанции!). Если вы хотите попытаться, и полагаете, что ваша жалоба отвечает установленным требованиям, ее можно представить на официальном бланке, который можно получить в Секретариате. Однако вам настоятельно рекомендуется обратиться за советом к юристу или неправительственным организациям, действующим в этой области, и убедиться, действительно ли у вас есть реальный шанс на успех. Имейте в виду, что вынесению окончательного решения может предшествовать длительный и сложный процесс. 

У кого мне требовать соблюдения моих прав?

Соблюдения почти всех основных прав человека, перечисленных в международных соглашениях,  вы должны требовать от правительства вашей страны, или от официальных должностных лиц государства. Права человека защищают ваши интересы от посягательств государства, поэтому вы должны требовать их соблюдения от государства или от его представителей. Если вы считаете, что ваши права нарушаются, например, вашим работодателем или соседом, вы не можете напрямую ссылаться на международные законы о правах человека, за исключением тех случаев, когда правительство вашей страны было обязано принять меры, чтобы не допустить таких действий работодателей или соседей. 

А лежит ли на ком-нибудь обязанность защищать мои права? 

Да. Право не имеет смысла, если на кого-то не возложена соответствующая ответственность и обязанность. Моральная обязанность не посягать на ваше личное достоинство возложена на каждого человека, но правительство вашей страны, подписав международные соглашения, несет не только моральную, но и юридическую ответственность.

Права человека – это проблема только недемократических стран?

Даже сегодня в мире нет такой страны, где бы полностью были соблюдены все права человека. В одних странах нарушения могут происходить чаще, чем в других, затрагивать бóльшую или меньшую часть населения, но всякое, даже единичное нарушение представляет проблему, которая не должна возникать и которой надо заниматься. Человеку, чьи права были нарушены в стране с устоявшейся демократией, вряд ли будет легче от того, что в целом в его стране положение с соблюдением прав человека лучше, чем в других странах мира. 

Добились ли мы прогресса в борьбе с нарушениями прав человека? 

Большого прогресса — даже если порой он и кажется каплей в море. Вспомните об уничтожении рабства, о предоставлении женщинам права голоса, о странах, которые отменили смертную казнь, об освобождении узников совести в результате международного нажима, о крахе режима апартеида в Южной Африке, о делах, рассмотренных в Европейском суде и законах, измененных в результате этого. Задумайтесь над тем, что постепенное развитие культуры международного общения означает, что даже наиболее авторитарным режимам приходится сегодня считаться с правами человека, если они хотят быть принятыми на международной арене. Положительных результатов было достигнуто много, особенно за последние 50 лет, но гораздо больше еще предстоит сделать.

Исчисление I — бесконечные пределы (практические задачи)

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-6: Бесконечные пределы

Для задач 1–6 оцените указанные пределы, если они существуют. {\, +}}} R \ left (y \ right) \)

Для задач 7 и 8 найдите все вертикальные асимптоты заданной функции.4}}} \) Решение

Исчисление I — Пределы вычислений (задачи назначения)

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Пожалуйста, не пишите мне, чтобы получить решения и / или ответы на эти проблемы. Я не буду раздавать их ни при каких обстоятельствах и не отвечу на любые запросы об этом.4} — 1}} {h} \)

Учитывая функцию \ [f \ left (x \ right) = \ left \ {{\ begin {align *} {15} & {\ hspace {0. 2}} & {\ hspace {0,25 дюйма} w \ le 6} \\ {w — 8} & {\ hspace {0,25 дюйма} w> 6} \ end {align *}} \ right. \]

Оцените следующие пределы, если они существуют.

1. \ (\ mathop {\ lim} \ limits_ {w \ to 6} h \ left (w \ right) \)
2. \ (\ mathop {\ lim} \ limits_ {w \ to 2} h \ left (w \ right) \)

Для задач 25 — 30 оцените предел, если он существует.

1. \ (\ mathop {\ lim} \ limits_ {z \ to \, — 10} \ left ({\ left | {t + 10} \ right | + 3} \ right) \)
2. \ (\ mathop {\ lim} \ limits_ {x \ to 4} \ left ({9 + \ left | {8 — 2x} \ right |} \ right) \)
3. \ (\ displaystyle \ mathop {\ lim} \ limits_ {h \ to 0} \ frac {{\ left | h \ right |}} {h} \)
4. \ (\ displaystyle \ mathop {\ lim} \ limits_ {t \ to 2} \ frac {{2 — t}} {{\ left | {t — 2} \ right |}} \)
5. \ (\ displaystyle \ mathop {\ lim} \ limits_ {w \ to \, — 5} \ frac {{\ left | {2w + 10} \ right |}} {{w + 5}} \)
6. \ (\ displaystyle \ mathop {\ lim} \ limits_ {x \ to 4} \ frac {{\ left | {x — 4} \ right |}} {{{x ^ 2} — 16}} \)
7. Учитывая, что \ (3 + 2x \ le f \ left (x \ right) \ le x — 1 \) для всех x определяет значение \ (\ mathop {\ lim} \ limits_ {x \ to — 4} f \ влево (х \ вправо) \). 2} \ cos \ left ({\ frac {1} {{x — 1}}} \ right) \).

Вопросы и ответы о пределах в исчислении

Набор вопросов о понятиях предела функции в исчисления представлены вместе с их ответами. Эти вопросы были разработаны, чтобы помочь вам, , глубоко понять концепцию пределов , которая имеет большое значение для понимания таких концепций исчисления, как производная и интегралы функции. Эти вопросы также помогут вам узнать о концепциях, которые необходимо пересмотреть.

Вопросы с решениями Вопрос 1 Верно или неверно . Если функция f не определена при x = a, то предел lim f (x), когда x приближается к никогда не существует. Ответ: Неверно. lim f (x), когда x приближается к a, может существовать, даже если функция f не определена при x = a. Концепция пределов связана с поведением функции при близком к x = a, а не к x = a. Вопрос 2 Верно или неверно .Если f и g — две функции такие, что lim f (x) при x -> a = + infinity и lim g (x) as x -> a = + infinity тогда lim [f (x) — g (x)] as x -> a всегда равно 0. Ответ: Неверно. Бесконечность — это не число, а бесконечность — бесконечность не равна 0. + Бесконечность — это символ, обозначающий большие, но неопределенные числа. -infinity — небольшое, но неопределенное число. Вопрос 3 Верно или неверно . График рациональной функции может пересекать свою вертикальную асимптоту. Ответ: Неверно. 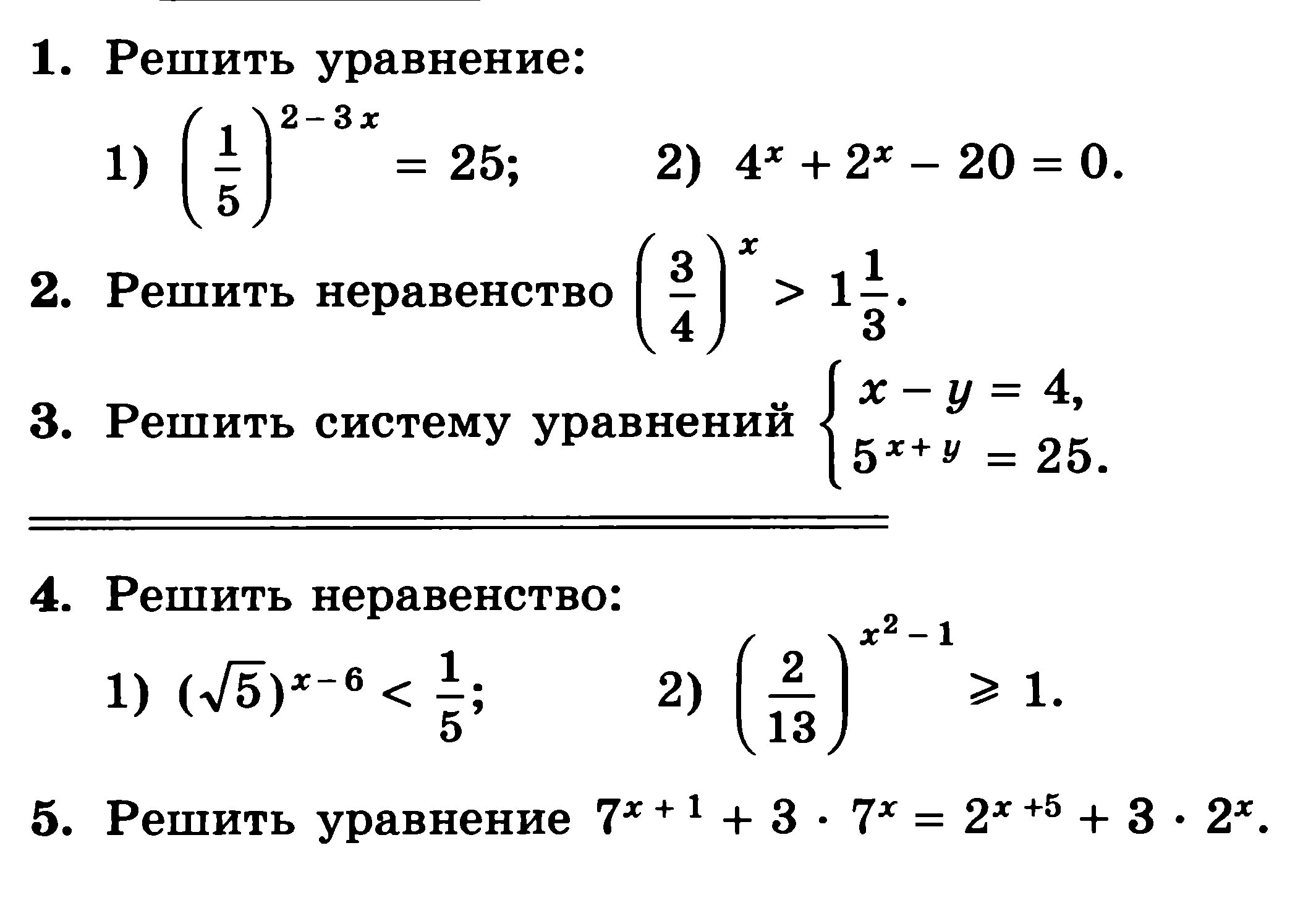Вертикальные асимптоты определены при значениях x, которые делают знаменатель рациональной функции равным 0, и поэтому функция не определена при этих значениях. Вопрос 4 Верно или неверно . График функции может пересекать свою горизонтальную асимптоту. Ответ: Верно. Вот пример. f (x) = (x — 2) / [(x — 1) (x + 3)] Степень знаменателя (2) выше, чем степень числителя (1), поэтому график имеет горизонтальную асимптоту y = 0, которая является осью x.Но график f имеет точку пересечения x в точке x = 2, что означает, что он отсекает ось x, которая является горизонтальной асимптотой в точке x = 2. Вопрос 5 Если f (x) и g (x) таковы, что lim f (x) при x -> a = + infinity и lim g (x) при x -> a = 0 , тогда (А) lim [f (x). g (x)], поскольку x -> a всегда равно 0 (B) lim [f (x). g (x)], поскольку x -> a никогда не равно 0 (C) lim [f (x). g (x)] как x -> a может быть + бесконечность или-бесконечность (D) lim [f (x).g (x)] при x -> a может быть конечным значением. Ответ: (С) и (D). Попробуйте следующие функции: f (x) = 1 / x и g (x) = 2x, когда x приближается к 0. f (x) = 1 / x 2 и g (x) = x, когда x приближается к 0. Вопрос 6 Верно или неверно . Если lim f (x) и lim g (x) существуют, когда x приближается к a, то lim [f (x) / g (x)] = lim f (x) / lim g (x), когда x приближается к a. Ответ: Неверно. Только если lim g (x) не равно 0. Вопрос 7 Верно или неверно . Для любой полиномиальной функции p (x) lim p (x) при приближении x к a всегда равно p (a). Ответ: Верно. Все полиномиальные функции являются непрерывными функциями и, следовательно, lim p (x), когда x приближается к a = p (a). Вопрос 8 Верно или неверно . Если lim f (x) = L1, когда x приближается к a от слева , и lim f (x) = L2, когда x приближается к a от справа . lim f (x) при приближении x к a существует, только если L1 = L2. Ответ: Верно. Это важное свойство пределов. Вопрос 9 Верно или неверно . lim sin x, когда x приближается к очень большим значениям (+ бесконечность), составляет + 1 или — 1. Ответ: Неверно. sin x является осциллирующей функцией и не имеет ограничений, так как x становится очень большим (+ бесконечность) или очень маленьким (-infinity). То же можно сказать и о cos x. Дополнительные ссылки по исчислению вопросы с ответами и руководствами и проблемами.

Ограничения скорости — практическое испытание на получение разрешения

и ответы на ограничения скорости во Флориде

В данном разрешительном практическом испытании рассматриваются ограничения скорости во Флориде. Чтобы подготовиться к этому практическому тесту, вам следует ознакомиться с видео и учебными пособиями по ограничению скорости.

Ниже приведены вопросы об ограничениях скорости во Флориде в форме множественного выбора, как и в тесте на разрешение во Флориде. По мере того, как вы отвечаете на каждый вопрос, вы узнаете правильный ответ, чтобы вы могли узнать его, пройдя тест.

1. Какое обычно ограничение скорости при проезде по району?

Вам необходимо:

Неправильно: Повторите попытку.

Правильно: Ограничение скорости в жилых помещениях составляет 30 миль в час, если не указано иное. 30 миль в час применяется к жилым, муниципальным и деловым улицам, но всегда ищите вывешенный знак ограничения скорости, если он отличается.

2. Какое ограничение скорости обычно действует при движении по шоссе или улице?

Неправильно: Повторите попытку.

Правильно: Ограничение скорости на улице и шоссе составляет 55 миль в час, если не указано иное. Обязательно всегда регулируйте скорость в плохих условиях (плохая погода или плохие дороги).

3. Вам нужно проехать по сельской (а не городской) автомагистрали, но вы не можете запомнить ограничение скорости. что это такое?

Неправильно: Повторите попытку.

Правильно: Ограничение скорости между штатами в сельской местности составляет 70 миль в час, если не указано иное.

4. Если вы видите ограничение скорости на уровне 50 миль в час, но идет дождь, нужно ли вам изменить скорость?

Неправильно: Повторите попытку.

Правильно: Да, регулировать скорость в плохую погоду. Ограничение скорости Знаки указывают на максимальную скорость, с которой вы должны двигаться в хороших условиях. В плохих условиях, таких как плохая погода или плохое движение, вам необходимо отрегулировать скорость (снизить скорость), чтобы полностью контролировать свой автомобиль и избегать столкновений.

5. Что такое ограничение скорости в школьной зоне?

Неправильно: Повторите попытку.

Правильно: Ограничение скорости в школьной зоне составляет 20 миль в час, если не указано иное, а штрафы за нарушение правил дорожного движения в школьных зонах удваиваются.

6. Если вас поймают на превышении скорости только на 5 миль в час, установленной в школьной зоне, получите ли вы меньший штраф в размере?

Неправильно: Повторите попытку.

Правильно: Нет, если вы превысите ограничение скорости в школьной зоне, ваш штраф удваивается.Вы также можете получить гражданский штраф в размере до 1000 долларов США и, возможно, должны пройти школу дорожного движения.

7. При приближении к Зоне строительства вы должны:

Неправильно: Повторите попытку.

Правильно: Найдите ограничение скорости в зоне строительства и отрегулируйте скорость. Штраф за превышение скорости удваивается, если вы превышаете скорость в зоне строительства.

8. Если вы находитесь на красном светофоре, а машина рядом с вами заводит двигатель и ускоряется, пытаясь заставить вас участвовать в гонке, вам следует:

Неправильно: Повторите попытку.

Правильно: Игнорируйте их и не участвуйте в гонках. Вместо этого ускоряйтесь с нормальной скоростью, чтобы вы соблюдали ограничение скорости, а не участвовали в гонках. Гонки чрезвычайно опасны и могут привести к аннулированию ваших прав (прекращению водительских прав).

Начните с начала и пройдите все практические тесты DMV

Создание викторины с ограничениями по времени

Домой | Справочные руководства : Добавление ограничений по времени

Добавление ограничения по времени к вашему тесту означает, что тестируемый должен будет ответить и отправить все вопросы в течение отведенного времени.Временные ограничения популярны для создания тестов на пригодность, вступительных экзаменов в колледж или проверки знаний сотрудников. Ограничения по времени могут держать участников сосредоточенными, могут быть трудными или могут свести к минимуму вероятность несправедливого поиска ответов учащимися.

FlexiQuiz предлагает всем участникам возможность установить ограничение по времени для каждой страницы, всей викторины или того и другого.

Время начинается, когда участники нажимают Начать тест со страницы приветствия, страницы регистрации или прямо с URL-адреса викторины. По истечении времени участники опроса автоматически перейдут на следующую страницу (если для каждой страницы викторины установлено ограничение по времени).Или тест будет отправлен на оценку, если для всей викторины установлен временной предел.

Как добавить ограничение по времени

1. Создайте свою викторину

2. Перейдите на вкладку Configure вверху и выберите General в левом меню

3. Прокрутите вниз на странице

4. Отметьте поле, чтобы показать, что вы хотите сделать:

• Ограничение времени всего викторины — отметьте Ограничение времени
• Ограничение времени по странице — отметьте Ограничение времени страницы

5.Введите количество времени, которое вы хотите разрешить.

• Полный лимит времени викторины. Введите время в часах и минутах. Например: 20 минут = 00:20
• Ограничение времени на страницу . Нажмите Установите ограничения по времени. Рядом с номером каждой страницы введите время в часах: минутах: секундах.

Например, 2 минуты и 2 секунды = 00:02:02

Примечание: при создании теста вам необходимо создавать новую страницу для каждого необходимого ограничения времени страницы.

Невозможно использовать функцию «Вопросы на страницу», доступную в меню конфигурации.

6. Завершите настройку теста и опубликуйте его.

Пример всплывающего окна, которое вы увидите при установке ограничения по времени по страницам. В этом примере ограничение по времени на странице 2 составляет 40 секунд.

Часто задаваемые вопросы

Может ли участник приостановить ограничение по времени?

№Как только участники нажмут «Старт», им будет предоставлено время, которое вы позволили пройти тест или страницу.

Если участники не завершат и не отправят тест в течение установленного времени, тест будет отправлен автоматически. Участникам будет показана страница результатов (если настроена), а результаты викторины будут добавлены на вашу панель анализа.

Если участники не заполняют страницу в установленный срок, они автоматически переходят на следующую страницу.

Может ли участник пройти тест или просмотреть страницу еще раз, если он не ответит на все вопросы в отведенное время?

Это зависит от того, как вы настроили викторину.

Если вы установили максимальное количество попыток викторины равным 1, участники не смогут пройти тест повторно.

Если я настроил мгновенную пометку и обратную связь во время викторины, будет ли таймер приостанавливаться во время просмотра участниками?

Нет. Время будет продолжать идти.

Как работает подсчет баллов, если тест отправляется автоматически по истечении срока?

Все вопросы, на которые были даны ответы, будут отмечены, и участникам будут выставлены баллы по всем вопросам теста.Например. Участнику дается 10 вопросов, и он отвечает только на 5 вопросов в отведенное время. Если все ответы верны, участники получат 5 баллов из 10 или 50%.

Как изменить шрифт и положение таймера? Участники

Premium или Enterprise могут изменить шрифт и положение таймера, показываемого участникам, выполнив следующие действия:

1. Создайте викторину

2. На вкладке «Настроить» выберите Тема в левом меню.

3.Рядом с параметром Таймер вам будут показаны раскрывающиеся параметры для изменения шрифта, размера шрифта, цвета шрифта и его расположения. Вы можете установить таймер вверху или внизу страницы.

Как я могу исправить положение таймера, чтобы при прокрутке страницы вверх или вниз тестируемый таймер был виден?

Членам Premium или Enterprise нужно будет установить таймер внизу страницы.

Нижнюю панель навигации можно исправить, перейдя на вкладку Configure и выбрав General в левом меню.

Прокрутите страницу вниз до Положение панели навигации

Из раскрывающегося меню измените наклон на Фиксированный

Соответствующие справочные руководства:

Как создать викторину

Создание учетной записи FlexiQuiz

Главная | Справочные руководства

Есть отзывы, предложения или идеи? Пожалуйста дай нам знать.

Комментарии:

Calc Ch 1.3 — Аналитическая оценка пределов

вопросов для проверки ваших возможностей: Эвелин МакФарлейн, Джеймс Сэйвелл: 9780375502422: Amazon.com: Книги

Какого вы придерживаетесь самого твердого мнения? Какая самая большая ложь, которую вы когда-либо говорили? Что вы больше всего хотели бы изменить в мире? Кого вы больше всего боялись в своей жизни? Какое у вас самое сильное желание? Что вы потеряли и что больше всего хотели бы вернуть? Где и когда вы чувствовали себя наиболее неудобно в обнаженном виде?
В, авторы бестселлеров «Если.. . серии запускают свой фирменный формат в новом направлении: какие и где ограничения, которые делают каждого из нас личностями, которые мы есть?
Пятьсот наводящих на размышления вопросов, проиллюстрированных убедительными черно-белыми фотографиями, помогут вам исследовать мир вокруг вас и пережить самые смешные, самые страшные, самые странные, величайшие и самые незабываемые моменты. Наши ответы на эти вопросы отражают наши приоритеты, определяют наши пределы и исследуют границы того, кем мы являемся на самом деле. Эти вопросы могут помочь нам узнать больше о себе, своих друзьях и членах семьи.

Джеймс Сэйвелл родился в Канаде и в детстве жил в Азии. Помимо вопросов, он проектирует здания и мебель. Он делит свое время между США, Италией и Гонконгом.

Выдержка. © Печатается с разрешения автора. Все права защищены.

Что вы больше всего хотели бы изменить в мире?

Чего вы хотите сейчас больше всего?

За что вы больше всего благодарны?

Какой самый теплый прием вы когда-либо встречали?

Что было самым лучшим в вашей молодости?

Что было худшим?

Когда и где вы чувствовали себя наиболее неудобно в обнаженном виде?

Кто самый интересный человек, которого вы когда-либо встречали?

Что самое интересное из того, что вы когда-либо делали во взрослом возрасте?

Что вы меньше всего надевали на публике?