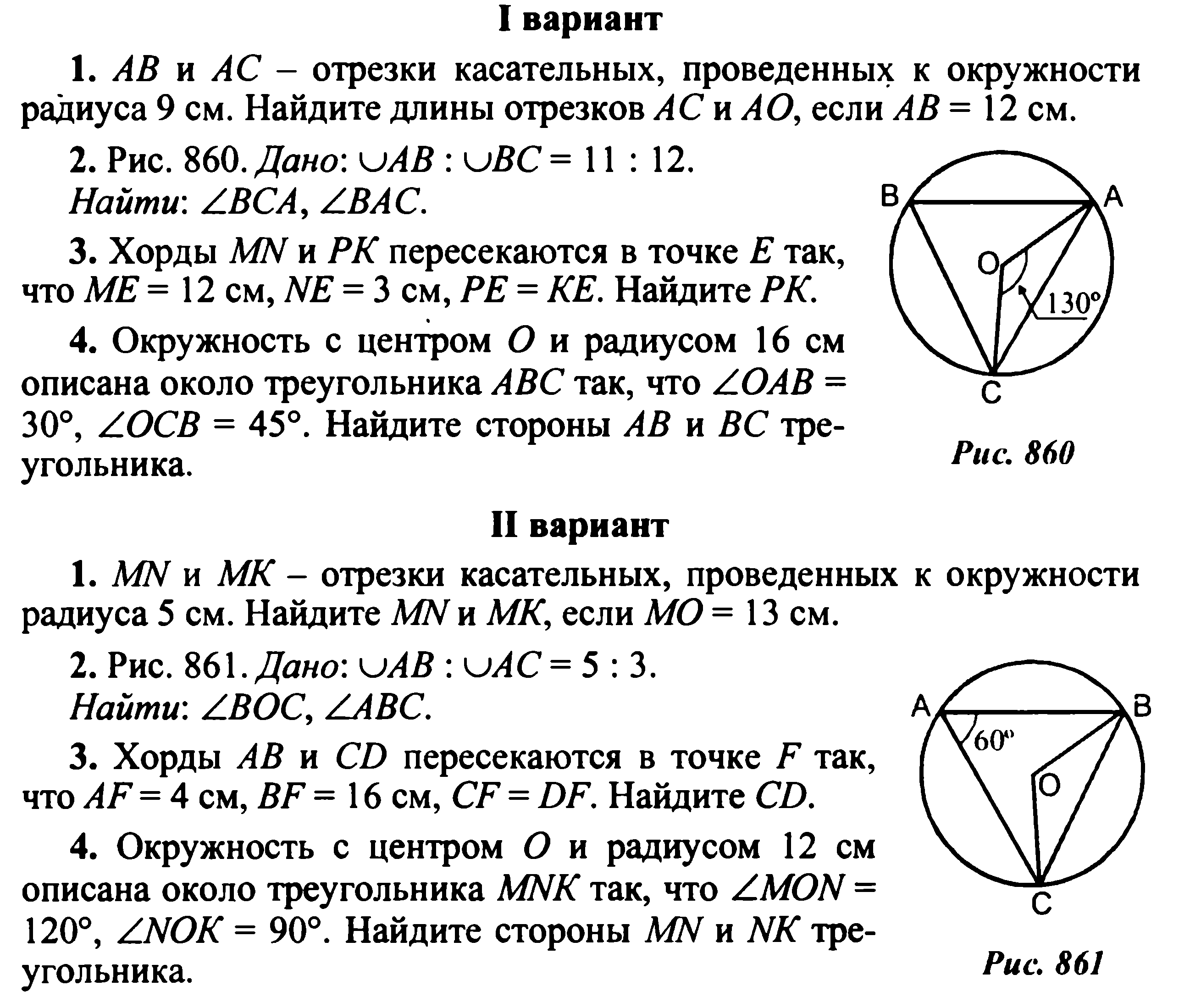
ГДЗ самостоятельные и контрольные работы по геометрии 7 класс Иченская, Атанасян Просвещение
С началом изучения геометрии у семиклассников возникают сложности, так как предмет довольно объемный и сложный. Часто проблема возникает с пониманием геометрических терминов, теорем и аксиом. Но тяжелее всего детям выполнять геометрические задачи. Благодаря хорошему учебнику эта проблема не возникнет. Практическое пособие Иченской М.А. получило хороший отклик у преподавателей и экспертов. А с помощью гдз по геометрии самостоятельные и контрольные работы за 7 класс Иченская освоить материалы пособия станет еще легче. Ребенок сможет понять не только принцип решения упражнения, но и правильность оформления ответа.
Для кого онлайн справочник является незаменимым помощником?
Больше всего к помощи онлайн решений к самостоятельным и контрольным работам по геометрии 7 класс Иченской, Атанасяна прибегают такие группы людей:
- ученики, которые испытывают трудности в изучении точных наук.
- дети, которые вынуждены часто пропускать занятия, так как часто болеют или выезжают на различные внешкольные мероприятия. После систематических пропусков возникает пробел в знаниях, а это влечет за собой риск получения плохих оценок. Геометрия сложный предмет, для изучения которого важная регулярность. С помощью решебника ребенок без труда наверстает упущенное и не будет чувствовать себя неуверенно во время написания итоговых работ;
- преподаватели, которые обучают детей геометрии в седьмом класса. На них лежит большая нагрузка в виде большого количества письменных заданий и упражнений школьников, которые нужно регулярно проверять. Очень часто после проведенных занятий не хватает времени на оперативную проверку и контроль. Использование ГДЗ поможет решить эту проблему, быстрая и качественная проверка гарантирована;
- родители, которым нужно постоянно следить за уровнем полученных знаний ребенка. Важно всегда быть на чеку и регулярно проверять, как ребенок осваивает курс школьной программы по ГДЗ. С применением решебника не потребуется много времени и сил, чтобы дать оперативную оценку ситуации.
Важно всегда быть на чеку и регулярно проверять, как ребенок осваивает курс школьной программы по ГДЗ. С применением решебника не потребуется много времени и сил, чтобы дать оперативную оценку ситуации.Доводы в защиту сборников готовых заданий
Среди значительных плюсов сборника ответов к самостоятельным и контрольным работам по геометрии 7 класс авторы Иченская, Атанасян можно выделить:
- быстрый и доступный поиск нужных заданий и решений;
- отсутствие материальных затрат на дополнительные занятия с репетитором;
- оформление всех ответов в полном соответствии с действующими образовательными стандартами;
- возможность прибегнуть к помощи пособия в любой день и любое время;
- постоянный самоконтроль выполненных домашних заданий, перед тем как сдать работу на проверку.
Ребенок, который занимается с решебником на еуроки ГДЗ, научится понимать материал, грамотно записывать условия и решения, научиться строить геометрические чертежи и выделять основную информацию из справочного пособия.
Контрольная работа по математике в 6 классе на тему «Окружность»
К/р № 5 Вариант 1 ( «3» — 3-4 б. «4» — 5-6 б. «5» — 7-8 б. «5» и «5» — 9 б.)
1. Выберите верные утверждения: (1 б.)
1. Если прямая и окружность не пересекаются, то расстояние от центра окружности до прямой меньше радиуса этой окружности.
3. Касательная перпендикулярна радиусу окружности, проведённому в точку касания.
2. Постройте окружность радиусом 4 см. Проведите касательную к этой окружности.
(1 б.
)
3. Выясните, можно ли построить треугольник по трём данным сторонам:
а) ; б) . (1 б.)
4. Постройте треугольник со сторонами 30 мм, 25 мм и 40 мм. (1 б.)
5. Изобразите конус, высота которого равна 4 см. (1 б.)
6. Постройте равнобедренный треугольник с вершиной в точке А, основанием ВК, лежащим на прямой
(2б.
)
7. Радиус одной окружности равен 5 см, радиус другой – 3 см, расстояние между их центрами – 3,5 см. Каково взаимное расположение окружностей?
1) Касаются внешним образом
2) Касаются внутренним образом
3) Пересекаются
4) Меньшая целиком лежит внутри большей
Сделайте чертёж. (2б.)
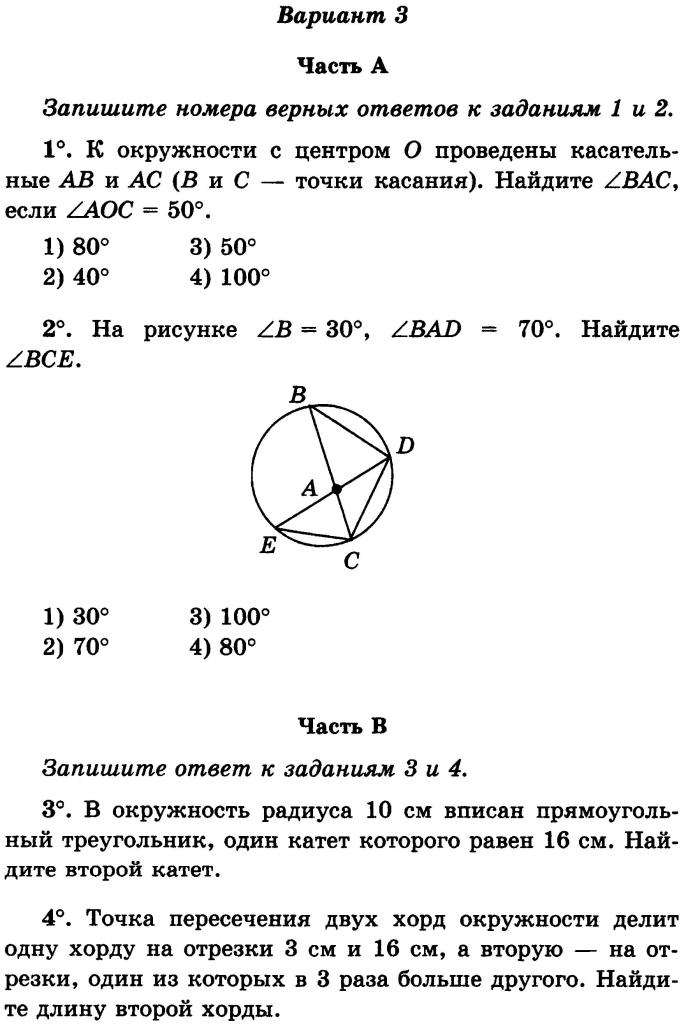
К/р № 5 Вариант 2 ( «3» — 3-4 б.
«4» — 5-6 б. «5» —
7-8 б. «5» и «5» — 9 б.)
1. Выберите верные
1. Если прямая и окружность пересекаются, то расстояние от центра окружности до прямой больше радиуса этой окружности.
2. Если расстояние между центрами окружностей больше суммы их радиусов, то окружности не пересекаются.
3. Любая сторона треугольника меньше суммы двух других сторон.
2. Постройте окружность радиусом 5 см. Проведите касательную к этой окружности
3.
Выясните,
можно ли построить треугольник по трём данным сторонам: а)
; б) .
(1б.)
4. Постройте треугольник со сторонами 35 мм, 20 мм и 30 мм. (1б.)
5. Изобразите цилиндр, радиус основания которого равен 2 см. (1б.)
6. Постройте равнобедренный треугольник с вершиной в точке С, основанием АВ, лежащим на прямой с, и боковыми сторонами равными 2 см.
(2б.
)
7. Радиус одной окружности равен 4 см, радиус другой – 2,5 см, расстояние между их центрами – 1 см. Каково взаимное расположение окружностей?
1) Касаются внешним образом
2) Касаются внутренним образом
3) Пересекаются
4) Меньшая целиком лежит внутри большей
Сделайте чертёж. (2б.)
|
№ урока |
Тема урока, тип урока |
Дата проведения
|
Домашнее задание
|
|
|
|
|
план |
факт |
|
|
Глава 1.
|
||||
|
1 |
Простейшие геометрические фигуры. Точки и прямые.
Урок изучения нового материала |
01.09 |
|
§1,вопр.1-7, №2,4.7
|
|
2 |
Точки и прямые. Решение задач. Урок закрепления знаний. |
03.09 |
|
§1 №13,15
|
|
3 |
Отрезок и его длина. Урок изучения нового материала |
08.09 |
|
§2,вопр.1-10, №21,25,29 |
|
4. |
Основное свойство длины отрезка. Урок закрепления знаний. |
10.09 |
|
§2, №31,33,35,37 |
|
5 |
Отрезок и его длина. Решение задач. Урок закрепления знаний. |
15.09 |
|
§2, №43,45,47 |
|
6 |
Луч. Урок изучения нового материала |
17.09 |
|
§3,вопр.1-9, №50, 52,57 |
|
7 |
Измерение углов. Урок изучения нового материала |
22.09 |
|
§3,вопр.10-17, №61 ,64, 66,70 |
|
8 |
Луч и угол. Урок закрепления знаний |
24.09 |
|
§3, №72, 74,76 |
|
9. |
Смежные углы. Урок изучения нового материала |
29.09 |
|
§4,вопр.1,2 №90, 95,98 |
|
10. |
Вертикальные углы. Урок изучения нового материала |
01.10 |
|
§4,вопр.3,4, №102, 104,107 |
|
11. |
Смежные и вертикальные углы. Урок закрепления знаний |
06.10 |
|
§4, №109, 111 |
|
12 |
Перпендикулярные прямые. Урок изучения нового материала. |
08.10 |
|
§5,вопр.1-8, №115, 124, 127, 130 |
|
13 |
Аксиомы. Комбинированный урок. |
13.10 |
|
§6,№80, 90,91 |
|
14. |
Повторение и систематизация учебного материала по теме «Простейшие геометрические фигуры и их свойства». Комбинированный урок. |
15.10 |
|
Повт. §§1-6, тест «Проверь себя», итоги гл.1 |
|
15 |
Контрольная работа №1 «Простейшие геометрические фигуры и их свойства». Урок – практикум. |
20.10 |
|
Повт. §§1-6 |
|
Глава 2.
|
||||
|
16. |
Равные треугольники. Урок изучения нового материала.
|
22.10 |
|
§7,вопр.1-7, №138, 141,144 |
|
17. |
Высота, медиана, биссектриса треугольника. Урок изучения нового материала. |
27. |
10.11 |
§7,вопр.8-12, №134, 148,150 |
|
18 |
Первый признак равенства треугольников. Комбинированный урок. |
29.10 |
12.11 |
§8,вопр.1-3, №155, 161,163 |
|
19 |
Первый признак равенства треугольников. Урок закрепления знаний |
10. |
17.11 |
§8,№167, 176 |
|
20 |
Второй признак равенства треугольников. Урок изучения нового материала. |
12.11 |
19.11 |
§8,вопр.4,№169, 171,173 |
|
21 |
Первый и второй признаки равенства треугольников. Урок закрепления знаний. |
17. |
24.11 |
§7, №179, 184 |
|
22 |
Первый и второй признаки равенства треугольников. Решение задач. Урок закрепления знаний. |
19.11 |
§7, №187, 189 |
|
|
23 |
Равнобедренный, равносторонний и разносторонний треугольники. Урок изучения нового материала. |
24. |
26.11 |
§9,вопр.1-4, №197, 198,200 |
|
24 |
Свойства равнобедренного и равностороннего треугольников. Урок изучения нового материала. |
26.11 |
01.12 |
§9,вопр.5-9, №205, 208,210 |
|
25 |
Применение свойств равнобедренного и равностороннего треугольников.
Урок закрепления знаний. |
01.12 |
03.12 |
§9, №215, 221 |
|
26 |
Свойства равнобедренного и равностороннего треугольников. Урок обобщения и систематизации знаний. |
03.12 |
§9, №219, 224 |
|
|
27 |
Признаки равнобедренного треугольника. Урок – лекция
|
08. |
08.12 |
§10,вопр.1-2, №236, 237 |
|
28 |
Применение признаков равнобедренного треугольника при решении задач. Урок закрепления знаний. |
10.12 |
|
§10, №241, 243 |
|
29 |
Третий признак равенства треугольников.
Урок изучения нового материала. |
15.12 |
|
§11,вопр.1-2, №253, 255 |
|
30 |
Применение третьего признака равенства треугольников при решении задач. Урок закрепления знаний. |
17.12 |
|
§11 №257, 260 |
|
31 |
Теоремы. Урок изучения нового материала |
22.12 |
|
§12,вопр.1-7, №272, 274,276 |
|
32 |
Контрольная работа №2 по теме«Треугольники». |
24.12 |
|
Повт. §§7-12, тест «Проверь себя», итоги гл. |
|
Глава 3. Параллельные прямые.Сумма углов треугольника, 16 часов.
|
||||
|
33 |
Параллельные прямые. Урок изучения нового материала |
12.01 |
|
§13,вопр.1-8, №289,292,294 |
|
34 |
Признаки параллельности прямых. Урок изучения нового материала |
14.01 |
|
§14,вопр.1-3, №303, 306,308 |
|
35 |
Применение признаков параллельности прямых при решении задач. Урок закрепления знаний. |
19.01 |
|
§14, №311, 314,319 |
|
36 |
Свойства параллельных прямых. Комбинированный урок. |
21.01 |
|
§15,вопр.1-5, №327, 329,331 |
|
37 |
Применение свойства параллельности прямых при решении задач. Урок закрепления знаний. |
26.01 |
|
§15, №336, 339,342 |
|
38 |
Свойства параллельных прямых. Урок обобщения и систематизации знаний. |
28.01 |
|
§15, №347, 349,352 |
|
39 |
Сумма углов треугольника. Урок изучения нового материала |
02.02 |
|
§16,вопр.1-2, №359, 361,365 |
|
40 |
Сумма углов треугольника. Внешний угол треугольника. Урок изучения нового материала |
04.02 |
|
§16,вопр.3-5, №382, 389 |
|
41 |
Сумма углов треугольника. Неравенство треугольника. Урок изучения нового материала |
09.02 |
|
§16,вопр. |
|
42 |
Сумма углов треугольника. Урок обобщения и систематизации знаний. |
11.02 |
|
§16, №396, 397,404 |
|
43 |
Прямоугольный треугольник. Урок изучения нового материала |
16.02 |
|
§17,вопр. |
|
44. |
Применение признаков равенства прямоугольных треугольников при решении задач. Урок закрепления знаний. |
18.02 |
|
§17, №435, 437,446 |
|
45 |
Свойства прямоугольного треугольника. Урок изучения нового материала |
25.02 |
|
§18,вопр. |
|
46 |
Применение свойств прямоугольных треугольников при решении задач. Урок закрепления знаний. |
02.03 |
|
§18, №467,471 |
|
47 |
Повторение и систематизация учебного материала по теме «Параллельные прямые. Сумма углов треугольника. Прямоугольный треугольник». Комбинированный урок. |
04. |
|
Повт. §§13-18, тест «Проверь себя», итоги гл.3 |
|
48 |
Контрольная работа №3 «Параллельныепрямые. Сумма углов треугольника. Прямоугольный треугольник». |
09.03 |
|
Повт. §§13-18 |
|
Глава 4. Окружность и круг.Геометрические построения, 16 часов |
||||
|
49 |
Геометрическое место точек. Урок изучения нового материала |
11.03 |
|
§19,вопр.1-14, №482, 484,488 |
|
50 |
Геометрическое место точек. Окружность и круг. Решение задач. Урок закрепления знаний. |
16.03 |
|
§19, №492,494, 496 |
|
51 |
Некоторые свойства окружности. Урок — лекция |
18.03 |
|
§20,вопр.1-7, №508,513,516 |
|
52 |
Некоторые свойства окружности. Касательная к окружности. Решение задач. Урок закрепления знаний. |
23.03 |
|
§20, №522, 524,526 |
|
53 |
Некоторые свойства окружности. Урок обобщения и систематизации знаний. |
25.03 |
|
§20, №530,534 |
|
54 |
Описанная и вписанная окружности треугольника. Урок – лекция
|
06.04 |
|
§21,вопр.1-8, №541,544, 547 |
|
55 |
Применение свойств описанной и вписанной окружности треугольника при решении задач. Урок закрепления знаний. |
08.04 |
|
§21, №553,555 |
|
56 |
Описанная и вписанная окружности треугольника. Решение задач. Урок обобщения и систематизации знаний. |
13.04 |
|
§21, №558,563 |
|
57 |
Задачи на построение. Урок изучения нового материала. |
15.04 |
|
§22,вопр.1-2, №575, 577,579 |
|
58 |
Задачи на построение. Построение треугольника по заданным элементам. Комбинированный урок. |
20.04 |
|
§22, №591,593,594 |
|
59 |
Задачи на построение. Урок обобщения и систематизации знаний. |
22.04 |
|
§22, №601,603,605 |
|
60 |
Метод геометрических мест точек в задачах на построение.Урок изучения нового материала. |
27.04 |
|
§23, №623,625,628 |
|
61 |
Метод геометрических мест точек в задачах на построение. Урок закрепления знаний. |
29.04 |
|
§23, №632,635,637 |
|
62 |
Метод геометрических мест точек в задачах на построение. Урок обобщения и систематизации знаний. |
04.05 |
|
§23, №640,649,656 |
|
63 |
Повторение и систематизация учебного материала по теме «Окружность и круг. Комбинированный урок. |
06.05 |
|
Повт. §§19-23, тест «Проверь себя», итоги гл.4 |
|
64 |
Контрольная работа №4 «Окружность и круг.Геометрические построения». |
11.05 |
|
Повт. §§19-23, тест |
|
Обобщения и систематизации знаний учащихся,4часа.
|
||||
|
65-67 |
Повторение курса геометрии 7 класса.
|
13.05 18.05 20.05 |
|
|
|
68 |
Итоговая контрольная работа №5. |
25.05 27.05 |
|
|
Простейшие геометрические фигуры и их свойства, 15 часов
Угол.
Измерение углов.
Треугольники, 18 часов
10
11
11
11
12
2
6-7, №389,391,409
1-8, №425, 427,430
1-3, №459,461,463
03
Окружность и круг.
Касательная к окружности.
Касательная к окружности. Решение задач.
Геометрические построения».
7-Геометрия . Итоговая контрольная работа
Геометрия 7 класс. Итоговая контрольная работа Вариант 1Часть А. Запишите номера верных ответов к заданиям 1 и 2.
1. Используя данные, приведенные на рисунках, укажите номера рисунков, на которых изображены равнобедренные треугольники:
1) 13 EMBED Unknown 14152) 13 EMBED Unknown 14153) 13 EMBED Unknown 1415 4)
2. Начертите треугольник BCD и проведите медиану ВК, биссектрису DN и высоту СН.
Укажите номера верных утверждений:
1) ВH = DH. 3) (BKC = (BKD. 5) (CHD = 90°.
2) DК = CК. 4) (CDN = (BDN. 6) (BND = 90°.
Часть В.
Выполните чертежи и запишите ответы к заданиям 3 и 4.
3. МК хорда окружности с центром в точке О, причем хорда МК равна радиусу
окружности. Найдите периметр
· OMK, если радиус окружности равен 7 см.
4. На рисунке 5 (1 = 115о, (2 = 65о, (3 = 100о. Найдите (4.
Часть С. Запишите обоснованное решение задач 5-6.
5. На рисунке 6 точка К является серединой отрезка AD, (ВАK = (CDK.
Докажите, что точка К является серединой отрезка ВС.
б*. В треугольнике МКР сторона МР равна 20 см. Расстояние от точки К до прямой МР равно 13 EMBED Equation.3 1415КР.
Через точку М проведена прямая т, параллельная КР. Найдите: а) (МРK;
б) расстояние между прямыми т и КР.
Геометрия 7 класс. Итоговая контрольная работа Вариант 2
Часть А. Запишите номера верных ответов к заданиям 1 и 2.
1. Используя данные, приведенные на рисунках, укажите номера рисунков, на которых изображены равнобедренные треугольники:
1) 13 EMBED Unknown 14152) 13 EMBED Unknown 1415 3) 4)
2.
Начертите треугольник ABC, в котором проведите медиану AD, биссектрису BE и высоту СК.
Укажите номера верных утверждений:
1) AE = СE. 3) (BAD = (CAD. 5) (CKB = 90°.
2) BD = CD. 4) (ABE = (CBE. 6) (BEC = 90°.
Часть В. Запишите ответы к заданиям 3-4.
3. ВС хорда окружности с центром в точке О, причем BC = 6 см. Рис. 5
Найдите периметр
·BOC, если радиус окружности равен 5см.
4. На рисунке 5 (1 = 125о, (2 = 125о, (3 = 110о. Найдите (4.
Часть С. Запишите обоснованное решение задач 5-6.
5. На рисунке 6 отрезки АВ и CD параллельны и равны. Рис. 6
Докажите, что точка К является серединой отрезка ВС.
·
6*. В треугольнике ABC АС = 10 см, ВС = 8 см. Расстояние от вершины В до стороны АС равно 4 см.
Через вершину А проведена прямая а, параллельная ВС.
Найдите: а) (ACB;
б) расстояние между прямыми а и ВС.
Пояснительная записка
Административная работа по геометрии за курс 7 класса согласно программе Атанасяна Л. С. применительно к учебнику Геометрия 7, 8, 9 классов (авторы Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.) М.: Просвещение, 2012 г.
Время проведения 45 минут.
Основные темы курса:
Начальные геометрические сведения (середина отрезка, биссектриса угла, вертикальные и смежные углы).
Треугольники (равнобедренный треугольник и его свойства, периметр треугольника, медиана, биссектриса, высота треугольника, признаки равенства треугольников, окружность, построение с помощью циркуля).
Параллельные прямые (признаки и свойства параллельных прямых).
Соотношение между сторонами и углами треугольника (сумма внутренних углов треугольника, внешний угол треугольника, прямоугольный треугольник и его свойства, расстояние от точки до прямой, расстояние между двумя параллельными прямыми)
Структура работы:
№ задания
Тема курса
Количество баллов
Часть А
№ 1
№ 2
Признак равнобедренного треугольника
Сумма острых углов прямоугольного треугольника
Внешний угол треугольника (Смежные углы)
Построение медианы, высоты и биссектрисы треугольника
Определение медианы
Определение высоты
Определение биссектрисы
1
1
1
1
1
1
1
Часть В
№ 3
№ 4
Окружность (понятие хорды, радиуса окружности)
Вычисление периметра треугольника
Свойства параллельных прямых
Признаки параллельности прямых
1
1
1
1
Часть С
№ 5
№ 6
Понятие середины отрезка
Признаки равенства треугольников
Свойство вертикальных углов/Свойство параллельных прямых
Расстояние от точки до прямой
Расстояние между двумя параллельными прямыми
Свойство катета, равного половине гипотенузы, для прямоугольного треугольника
Свойство угла в 30о для прямоугольного треугольника
1
1
1
1
1
1
1
Критерии оценивания:
Количество баллов
(рейтинг работы)
Процент выполнения
Отметка
Менее 9 баллов
менее 50 %
2
9 – 12 баллов
50% — 69%
3
13 – 15 баллов
70% — 84%
4
16 – 18 баллов
85% — 100%
5
62o
118o
118o
3
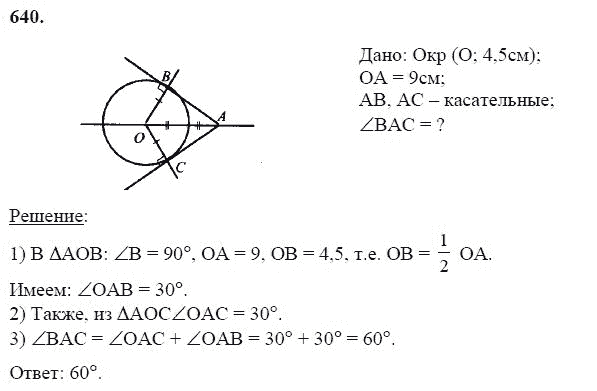
Рис.
5
1
2
4
Рис. 6
82o
98o
60o
90o
1
3
2
4
Root Entry
ГДЗ Геометрия 7 класс Зив, Мейлер
Геометрия 7 класс
Дидактические материалы
Зив, Мейлер
Просвещение
Давно известно, что невозможно качественно подготовиться к проверочным работам, пока нет понимания сути самого предмета. Можно конечно заучить готовые ответы по всем контрольным заданиям, но так как нет знания тематики, то соответственно не будет и необходимых ассоциаций, которые помогают лучше запомнить информацию. В случае возникновения каких-либо затруднений учащиеся всегда могут обратиться за помощью к решебнику к учебнику «Геометрия. Дидактические материалы 7 класс» Зив, Мейлер, где даны тщательные ответы по всем параметрам.
Что имеется в сборнике
Двадцать шесть самостоятельных работ содержат задания, рассчитанные на восемь вариантов. Так же сюда включены пять контрольных работ по четыре варианта каждая и четыре математических диктанта.
Помимо этого представлены приблизительные задачи к экзамену, распределенные по различным тематическим главам. ГДЗ по геометрии 7 класс Зив предоставляет детальные ответы по всем номерам и доступно онлайн.
В чем смысл его использования
Семиклассникам предстоит познакомиться и начать изучать новые предметы, что значительно увеличит общую учебную нагрузку. То, что эти дисциплины относятся к разряду сложных, еще больше усложняет ребятам жизнь. Быстрые темпы, по которым идет программа, любви к ним тоже не прибавляет. Сама затейливость упражнений вынуждает школьников обращаться за помощью к взрослым. Но так как учителя предпочитают не замечать проблем и не портить себе статистику, а многие родители просто не помнят всех нюансов данной науки, то подросткам приходится искать другие варианты решения своих проблем. Нередко им становится решебник к учебнику «Геометрия. Дидактические материалы 7 класс» Зив, где нашли свое отражение подробные выкладки по всему материалу этого года.
«Просвещение», 2015 г.
Название
Условие
Решение
Домашняя контрольная работа Окружность
Домашняя контрольная работа по теме «Окружность»
Вариант 1
АС и ВD – диаметры окружности с центром О. Угол АСВ равен 54°. Найдите угол АОD.
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Найдите угол АВС, если угол ВАС равен 25°.
В треугольнике АВС известно, что АС = 12, ВС = 5, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Стороны угла С касаются окружности в точках А и В, точка О – центр окружности. Найдите угол АОВ, если угол С равен 79°.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 15, СР = 6, DP = 10. Найдите АР.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 82°. Найдите угол С этой трапеции.
Трапеция АВСD с основаниями АD и ВС описана около окружности, АВ = 14, ВС = 13, СD = 22. Найдите АD.
Из точки А проведены две касательные к окружности с центром в точке О.
Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Четырехугольник АВСD вписан в окружность. Угол АВС равен 80°, угол САD равен 34°. Найдите угол АВD.
Сторона квадрата равна . Найдите радиус окружности, описанной около этого квадрата.
Домашняя контрольная работа по теме «Окружность»
Вариант 2
АС и ВD – диаметры окружности с центром О. Угол АСВ равен 34°. Найдите угол АОD.
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Найдите угол АВС, если угол ВАС равен 54°.
В треугольнике АВС известно, что АС = 3, ВС = 4, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Стороны угла С касаются окружности в точках А и В, точка О – центр окружности. Найдите угол АОВ, если угол С равен 55°.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 15, СР = 9, DP = 12. Найдите АР.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 76°.
Найдите угол С этой трапеции.
Трапеция АВСD с основаниями АD и ВС описана около окружности, АВ = 7, ВС = 10, СD = 15. Найдите АD.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 9.
Четырехугольник АВСD вписан в окружность. Угол АВС равен 88°, угол САD равен 30°. Найдите угол АВD.
Сторона квадрата равна . Найдите радиус окружности, описанной около этого квадрата.
Домашняя контрольная работа по теме «Окружность»
Вариант 3
АС и ВD – диаметры окружности с центром О. Угол АСВ равен 48°. Найдите угол АОD.
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Найдите угол АВС, если угол ВАС равен 41°.
В треугольнике АВС известно, что АС = 6, ВС = 8, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Стороны угла С касаются окружности в точках А и В, точка О – центр окружности.
Найдите угол АОВ, если угол С равен 64°.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 12, СР = 14, DP = 21. Найдите АР.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 55°. Найдите угол С этой трапеции.
Трапеция АВСD с основаниями АD и ВС описана около окружности, АВ = 8, ВС = 11, СD = 13. Найдите АD.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 7.
Четырехугольник АВСD вписан в окружность. Угол АВС равен 70°, угол САD равен 22°. Найдите угол АВD.
Сторона квадрата равна . Найдите радиус окружности, описанной около этого квадрата.
Домашняя контрольная работа по теме «Окружность»
Вариант 4
АС и ВD – диаметры окружности с центром О. Угол АСВ равен 16°. Найдите угол АОD.
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Найдите угол АВС, если угол ВАС равен 46°.
В треугольнике АВС известно, что АС = 9, ВС = 12, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Стороны угла С касаются окружности в точках А и В, точка О – центр окружности. Найдите угол АОВ, если угол С равен 39°.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 14, СР = 10, DP = 15. Найдите АР.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 63°. Найдите угол С этой трапеции.
Трапеция АВСD с основаниями АD и ВС описана около окружности, АВ = 11, ВС = 8, СD = 14. Найдите АD.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 10.
Четырехугольник АВСD вписан в окружность. Угол АВС равен 76°, угол САD равен 30°. Найдите угол АВD.
Сторона квадрата равна . Найдите радиус окружности, описанной около этого квадрата.
Домашняя контрольная работа по теме «Окружность»
Вариант 5
АС и ВD – диаметры окружности с центром О.
Угол АСВ равен 66°. Найдите угол АОD.
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Найдите угол АВС, если угол ВАС равен 22°.
В треугольнике АВС известно, что АС = 12, ВС = 16, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Стороны угла С касаются окружности в точках А и В, точка О – центр окружности. Найдите угол АОВ, если угол С равен 41°.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 18, СР = 12, DP = 16. Найдите АР.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 34°. Найдите угол С этой трапеции.
Трапеция АВСD с основаниями АD и ВС описана около окружности, АВ = 12, ВС = 10, СD = 11. Найдите АD.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 11.
Четырехугольник АВСD вписан в окружность. Угол АВС равен 60°, угол САD равен 28°.
Найдите угол АВD.
Сторона квадрата равна . Найдите радиус окружности, описанной около этого квадрата.
Домашняя контрольная работа по теме «Окружность»
Вариант 6
АС и ВD – диаметры окружности с центром О. Угол АСВ равен 25°. Найдите угол АОD.
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Найдите угол АВС, если угол ВАС равен 58°.
В треугольнике АВС известно, что АС = 24, ВС = 10, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Стороны угла С касаются окружности в точках А и В, точка О – центр окружности. Найдите угол АОВ, если угол С равен 82°.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 18, СР = 15, DP = 10. Найдите АР.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 48°. Найдите угол С этой трапеции.
Трапеция АВСD с основаниями АD и ВС описана около окружности, АВ = 9, ВС = 12, СD = 20. Найдите АD.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 13.
Четырехугольник АВСD вписан в окружность. Угол АВС равен 64°, угол САD равен 20°. Найдите угол АВD.
Сторона квадрата равна . Найдите радиус окружности, описанной около этого квадрата.
Домашняя контрольная работа по теме «Окружность»
Вариант 7
Сторона квадрата равна 16. Найдите радиус окружности, вписанной в этот квадрат.
Точка О – центр окружности, угол АОВ равен 118°. Найдите величину угла АСВ.
В окружности с центром в точке О проведены диаметры АD и ВС, угол ОСD равен 30°. Найдите величину угла ОАВ.
К окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите радиус окружности, если АВ = 4, АО = 5.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 5.
Ответы
В1 | В2 | В3 | В4 | В5 | В6 | В7 | |
72 | 112 | 84 | 148 | 48 | 130 | ||
65 | 36 | 49 | 44 | 68 | 32 | ||
6,5 | 2,5 | 5 | 7,5 | 10 | 13 |
101 | 125 | 116 | 141 | 139 | 98 | ||
25 | 20 | 18 | 21 | 24 | 12 | ||
98 | 104 | 125 | 117 | 146 | 132 | ||
23 | 12 | 10 | 17 | 13 | 17 | ||
16 | 18 | 14 | 20 | 22 | 26 | ||
46 | 58 | 48 | 46 | 32 | 44 | ||
12 | 14 | 16 | 10 | 8 | 9 |
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/424027-domashnjaja-kontrolnaja-rabota-okruzhnost
| |
|
|
7 класс Математика Модуль 3, Тема C, Обзор
В теме C учащиеся продолжают работать с геометрией, используя уравнения и выражения для изучения площади, периметра, площади поверхности и объема. Эта последняя тема начинается с моделирования круга с помощью велосипедной шины и сравнения его периметра (один оборот шины) с длиной в поперечнике (измеренной с помощью веревки), чтобы позволить учащимся найти самое известное соотношение из всех, пи. Действия по сравнению окружности с диаметром организованы именно для того, чтобы учащиеся осознали, что этот символ имеет определенное значение и может быть приблизительно равен 22/7 или 3.14, чтобы дать учащимся интуитивное представление о существующих отношениях. В дополнение к представлению этого значения символом пи, дробное и десятичное приближение позволяют студентам продолжать практиковать свою работу с операциями с рациональными числами. Все задачи созданы таким образом, чтобы позволить учащимся отработать навыки сокращения в рамках задачи, например, использовать 22/7 для нахождения окружности с заданной длиной диаметра 14 см, и понять, какое значение лучше всего подходит для аппроксимации решения.Такое понимание позволяет студентам точно оценивать работу на предмет разумности ответов. После открытия и понимания значения этого особого соотношения учащиеся продолжат использовать число «Пи» при решении задач площади и окружности (7.G.B.4).
В этой теме учащиеся выводят формулу площади круга, разделив круг радиусом r на части пи и переставив части таким образом, чтобы они выстраивались в линию, меняя направление и образовывая форму, напоминающую прямоугольник.Этот «прямоугольник» имеет длину, равную 1/2 окружности, и ширину r . Учащиеся определяют, что площадь этого прямоугольника (реконфигурированного из круга той же площади) является произведением его длины и ширины: 1/2 ( C ) ( r ) = 1/2 2 (pi) ( r ) ( r ) = pi ( r ) 2 ( 7.GB4 ). Точные определения диаметра, окружности, пи и круговой области или диска будут разработаны в рамках этой темы, при этом значительное время будет уделено пониманию учащимися каждого термина.
Учащиеся, опираясь на свою работу в 6 классе по площади поверхности и сеткам, понимают, что площадь поверхности — это просто сумма площади боковых сторон и основания (я) (6.G.A.4). В 7 классе они продолжают решать реальные и математические задачи, касающиеся площади двумерных форм, площади поверхности и объема призм, например прямоугольной, треугольной, уделяя особое внимание задачам, которые включают дробные значения длины ( 7.GB6 ). Дополнительная работа (примеры) с площадью поверхности будет произведена в Модуле 6 после того, как будет дано формальное определение прямоугольной пирамиды.
% PDF-1.4 % 399 0 объект > / Metadata 204 0 R / Outlines 191 0 R / PageLabels 194 0 R / Pages 197 0 R / StructTreeRoot 206 0 R / Type / Catalog / ViewerPreferences >>> эндобдж 204 0 объект > поток 2019-08-28T17: 04: 05-05: 002019-08-28T17: 08: 11-05: 002019-08-28T17: 08: 11-05: 00Adobe InDesign CS6 (Macintosh) uuid: ea25b744-645a-aa48- 9009-decf54653089adobe: docid: indd: a570f4a9-bfe8-11de-8db5-92712aaa0f73xmp.id: B8225685232068118A6DE00193EED20C proof: pdfxmp.iid: B6225685232068118AED2068118.сделал: DCB7F8AC092068118C14C640FFA3D008adobe: docid: indd: a570f4a9-bfe8-11de-8db5-92712aaa0f73default
Четыре основных математических понятия, которые дети изучают в 7-8 классах | Scholastic
Учащиеся 6 -го класса закладывают фундамент для математики, над которой они будут работать в 7-м -м классе и 8-м -м классах. Многие из концепций являются продолжением работы 6 th и позволяют глубже погрузиться в понимание и развитие, ведущее к алгебре. Учащиеся классов 7 th и 8 th готовятся к работе, которую они будут выполнять в средней школе как по алгебре, так и по геометрии.Эти строительные блоки будут иметь решающее значение для их общего понимания и успеха на уровне старшей школы.
1. Система счисления. В 7 -м классе учащиеся полностью поймут, как интерпретировать и вычислять все рациональные числа. Они могут складывать, вычитать, умножать и делить все десятичные дроби и дроби, а также представлять проценты. Они вычисляют как положительные, так и отрицательные числа, используя все четыре основные операции, и интерпретируют значение абсолютного значения. В 8 -м классе ученики переходят от рациональных чисел к иррациональным числам.Они понимают концепцию десятичного разложения и могут интерпретировать и находить как рациональные, так и иррациональные числа на числовой прямой.
Поощряйте своего ребенка:
- Используйте числовые линии при расчетах как с положительными, так и с отрицательными числами. Наличие вертикальной и / или горизонтальной числовой линии при выполнении домашнего задания может быть очень полезным.
- Мысленно оцените и рассчитайте чаевые, налог с продаж и проценты продаж при покупках и еде вне дома.
- Интерпретируйте положительные и отрицательные числа в реальной жизни, например, с температурой, долгом / задолженностью, отрицательными и положительными расходами, выигрышем / проигрышем и т. Д.
- Узнавайте рациональные и иррациональные числа.
2. Выражения и уравнения. Ожидания учащихся сильно возрастают в 7 -м и 8 -м классах при изучении выражений и уравнений. Они начинают использовать переменные и решать многоступенчатые задачи реального мира. Учащиеся интерпретируют неравенства и рисуют их соответствующим образом. Они готовятся к алгебре, рассматривая и понимая линейные уравнения и находя наклон таблицы, графика и уравнения.
Поощряйте своего ребенка:
- Различайте равенство и неравенство (>, <, > , <) с помощью переменных:
- равенство: 4s + 20 = 46
- неравенство: 4s + 20 <46
- Рассматривайте и решайте многоступенчатые реальные задачи, используя переменные. Например, Как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата составляла не менее 100 долларов.Напишите неравенство для количества продаж, которые вам нужно совершить, и опишите решения .
- Изучите и изучите различные типы графиков и таблиц в Интернете или в газете.
- Разберитесь в значении наклона и как его найти с помощью графика, таблицы или уравнения:
3. Геометрия. Студенты уделяют большое внимание лексике по геометрии и точно используют свой словарный запас при письме. Они расширяют свое понимание объема и площади для расчета площади поверхности двух- и трехмерных объектов.Они также изучают формулы площади и окружности круга. В 8 -м классе они изучают теорему Пифагора и применяют ее к реальным и математическим задачам. Студенты также должны знать формулы для определения объема конусов, сфер и цилиндров.
Поощряйте своего ребенка:
- Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств. Например: дополнительных углов: два угла, которые в сумме дают 180 °.
- Создавайте словарные карточки для всего их математического словаря и еженедельно практикуйте их.
- Найдите разные двухмерные и трехмерные объекты в реальном мире и обсудите разницу между нахождением площади поверхности и объема каждого объекта.
- Понять теорему Пифагора и как использовать ее в реальном мире:
Источник изображения: FreeLearningChannel.com
4. Функции. В 8 -м классе ученики начнут знакомиться с функциями.Студенты будут определять, сравнивать и оценивать функции. Они будут использовать функции для моделирования отношений между различными величинами. Они будут сравнивать функции алгебраически, графически, численно в таблицах или с помощью словесных описаний.
Поощряйте своего ребенка:
Источник изображения: Slideshare.net
У вас есть вопросы об этих концепциях или другие вопросы по математике? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге.Или поделитесь ими с нами на странице Scholastic Parents в Facebook.
Автор фотографии: © DragonImages / Thinkstock
ch07.indd
% PDF-1.6 % 699 0 объект / M (D: 20110125145506-06’00 ‘) / Имя (ARE Acrobat Product v8.0 P23 0002337) / ByteRange [0 116 9650 2583256] / Ссылка [> / Data 699 0 R / TransformMethod / UR3 / Type / SigRef> >] / Prop_Build> / App> / PubSec >>> / Type / Sig >>>> / Metadata 778 0 R / AcroForm 774 0 R / Pages 689 0 R / Type / Catalog / PageLabels 687 0 R >> эндобдж 700 0 объект > эндобдж 778 0 объект > поток PScript5.dll Версия 5.2.22011-01-25T14: 55: 06-06: 002011-01-25T08: 23: 13-08: 002011-01-25T14: 55: 06-06: 00application / pdf
IJ [uƭ # — ɋ! X8pxMQ3 .XμL9Π9DЮyhWCpcj> T 猈 uH (܇` X72KA.Vş> 4 ~ $ BKilsy ه (gM @ TT8dOe> Ś2Drs ~ vL_m [> {ԝp! B: + w5: WÉz’u \>; iSwTR5 ‘) T2 S’Otevq W _ :! ԕ5 # U! FjuUVX [jmЧ% 9Dyo06) q`fjZ
7 способов поддерживать отношения во время закрытия школы
Но как преподаватели должны воспитывать это чувство принадлежности к этому новому децентрализованному миру — с учителями и студенты, свободно связанные друг с другом через Wi-Fi и сотовые сети?
«Прямо сейчас все дело в технологии — механике дистанционного обучения.Но когда я говорю со своими коллегами, учителями средней школы, я спрашиваю себя: «Как мы собираемся удержать сердца наших учеников?» — говорит Мэйс Имад, профессор патофизиологии и биомедицинской этики в Общественном колледже Пима.
Итак, мы попросили десятки учителей и заглянули в ветки Instagram и Twitter, чтобы найти одни из лучших идей, с которыми учителя экспериментируют, чтобы поддерживать отношения, которые стимулируют вовлеченность и обучение.
1. Попытайтесь поздороваться почаще, если можете
Постарайтесь, чтобы ваши дети знали, что вы о них думаете, заботитесь о них и скучаете по ним.Для детей, имеющих доступ к технологиям, простые ежедневные приветствия через видео могут быть единственным случаем, когда ученик видит учителя в некоторые дни, и это чувство связи важно поддерживать.
Прекрасный тому пример — мастерское, веселое видео-приветствие учителя первого и второго классов Джона Томаса своим ученикам.
Студентам, не имеющим доступа к Интернету, попробуйте позвонить по телефону; подумайте о чередовании небольших групп студентов каждый день, чтобы сделать эту задачу более управляемой. «На то, чтобы протянуть руку и позвонить каждому ребенку, уходит вечность», — говорит учительница английского в шестом и восьмом классах Кэтлин Бичборд, но она видит большое влияние: «В первые несколько дней у меня было всего несколько детей, которые входили в систему, но сейчас у меня почти 98 процентов посещаемости », — говорит она.
2. Как проводить утренние встречи
Процедуры, которые способствуют установлению связи, являются основной частью классной жизни, и поиск способов испытать их дома будет иметь большое значение для облегчения перехода учащихся к домашнему обучению. «Если вы проводите утреннее собрание, подумайте об элементах, которые у вас есть на собрании, и о том, что можно выполнить виртуально дома», — пишет Томас. «Если позволяют технологии, записывайте и публикуйте ежедневные видеообъявления и объявления для чтения».
Маргарет Шафер, учительница третьего класса, заставляет детей отвечать на ежедневные подсказки во время ее утренних встреч.Дети могут видеть ответы друг друга и реагировать, если хотят. «Мои отношения с моими учениками являются частью моего обучения, и их отношения друг с другом имеют решающее значение для получения ими удовольствия от учебы», — говорит она, подчеркивая тот факт, что поддержание отношений не является второстепенным. «Поэтому, когда я планировал (очень быстро!) Начать дистанционное обучение, первое, что я хотел начать каждый день, — это утешить детей и дать им понять, что я по-прежнему забочусь о них, а их друзья все еще рядом.”
3. Новый взгляд на проверку температуры
Обычные ежедневные проверки — например, розы и шипы или выбор смайликов в соответствии с вашим настроением — не должны остаться незамеченными. Делайте это быстро и просто: «Я писал на Schoology, чтобы показать мне большой палец вверх, большой палец в сторону (м-м-м) или большой палец вниз, чтобы описать свой день…». Я призываю их делать селфи своими большими пальцами », — говорит учитель средней школы Хавьер Ривера в Twitter.
Наряду с самим общением со своими учениками, Имад делает общение со сверстниками частью домашней работы своих учеников: каждому ученику поручается установить связь с одним одноклассником.«Затем я прошу их написать мне и рассказать, как, скажем, у Джеки сегодня дела. Они могут решить, как они хотят регистрироваться — электронная почта, текстовые сообщения, Skype », — говорит она, добавляя, что сначала устанавливает руководящие принципы и моделирует практику для своих учеников. «Это упражнение могло бы работать даже лучше с K-12 -« Моя домашняя работа — проверить, как там Элли »».
Наконец, некоторые учителя используют формы, подобные этой, созданной Ассоциацией среднего образования, как быстрый и асинхронный способ побудить детей рассказать вам, как они себя чувствуют в этот день.
4. Попробуйте Snail-Mail Pen Pals, Phone Pals или Virtual Turn and Talk
Мы лучше учимся в социальном контексте. Для многих студентов переход к обучению из дома затруднен из-за того, что они оторваны от сверстников, даже несмотря на то, что многие старшие ученики могут общаться с друзьями через социальные сети и текстовые сообщения.
«Если технологии не позволяют, создавайте друзей по переписке или выполняйте другие действия с бумагой и ручкой, отправляя домой конверты, бумагу и марки, если ваша школа может», — говорит Томас.«Или имитируйте« повернуться и поговорить », установив друзей по телефону, когда студенты звонят друг другу по телефону несколько раз в неделю, чтобы обсудить определенные темы или подсказки».
Учитель третьего класса Майкл Данли следует своим инструкциям в группе через Zoom с комнатами для обсуждения, чтобы сверстники могли вместе размышлять над изученным материалом. Затем он ищет более глубокие связи со студентами индивидуально: «Я приглашаю одного студента на личную конференцию и прошу их читать вслух несколько минут. Это время также дает возможность проверить их эмоциональное благополучие и понять, нужны ли им разъяснения по заданиям.”
5. Создавайте виртуальные столы (но не только с друзьями в группе)
Для детей старшего возраста, говорит Кейси Шорт, учительница английского в восьмом классе дневной школы Charlotte Country Day School в Шарлотте, Северная Каролина, учителя могут создавать виртуальные столовые группы. Шорт использует для этого Google Classroom, потому что ее ученики уже знакомы с платформой. «Я создам темы для обсуждения с четырьмя-пятью студентами, чтобы они могли обсуждать задания, задавать друг другу вопросы и оставаться на связи», — говорит она.
Хотя многие дети будут поддерживать связь со своим кругом друзей, она говорит, что важно думать о том, чтобы объединить детей со сверстниками, которые не входят в их непосредственный круг общения, а затем еженедельно смешивать группы. «Также будут места для обсуждения в классе, но я знаю, что многим ученикам будет удобнее делиться идеями в небольшой группе», — говорит она.
6. Рассмотрите возможность включения родителей
Данлеа, учитель третьего класса, просит учеников пригласить родителей через Интернет, давая взрослым возможность задать вопросы, выразить озабоченность или попросить совета.
Beachboard, учительница английского в шестом и восьмом классах, ежедневно общается с родителями — она использует платформу обмена сообщениями Remind или выделенную телефонную линию Google Voice для родителей, у которых нет текстовых сообщений. Она также общается с семьями по электронной почте. «Я проверяю их раз в день, спрашивая« Как дела? »И« Вам что-нибудь нужно? », — говорит она. «В настоящее время важно, как никогда раньше, заботиться о психическом здоровье наших семей и учащихся».
7.Заставьте детей называть и обрабатывать собственные эмоции
Письменные задания, говорит Шорт, учитель английского языка, предлагают учащимся ценные возможности для обработки сложной смеси эмоций, которые они могут испытывать в результате перевернутого распорядка и расписания, социальной изоляции и проблем, связанных с пребыванием взаперти дома.
«Я собираюсь использовать некоторые возможности написания для студентов, чтобы выразить свои мысли, чувства, страхи и вопросы в творческом формате по их выбору», — говорит она.«Я дам им возможность поделиться с классом или поделиться только со мной. Это не только позволит им поделиться своими чувствами, но и даст мне возможность проверить их и принять меры, если я увижу, что кто-то из них выражает печаль, страх и т. Д., О которых, возможно, нужно знать их родителям ».
Самое важное, — говорит Шорт, — «Я буду честен и с максимальным пониманием сообщу студентам, что мы все вместе и всем, вероятно, потребуется немного благодати».
Оценка, исследования и оценка программы / Кредит за экзамен
Часто задаваемые вопросы для зачета зачетных единиц (CBE)
1.Когда студент может пройти тестирование на CBE?
Учащиеся 1–12 классов могут сдавать экзамены CBE четыре раза в год. Администрации тестирования перечислены на веб-сайте и разделены по классам. Учащиеся детского сада могут сдавать экзамены CBE два раза в год. * Обратитесь к консультанту, чтобы определить, на какую администрацию студент имеет право.
2. Может ли студент сдавать экзамен CBE более одного раза?
Да. Студенты могут попытаться пройти ускорение только два раза для одного и того же курса / уровня обучения.
3.Может ли студент пройти следующий курс по порядку до завершения обязательного курса?
Нет, студенты должны пройти и получить кредиты за все обязательные курсы, прежде чем пытаться зачислить за экзамен для следующего курса в последовательности.
4. От чего зависит, будет ли студент предварительно обучаться на экзамене CBE?
* Только школьный консультант принимает предварительные решения по обучению. *
Чтобы принять участие в зачетном экзамене с предварительным инструктажем, студент должен быть зарегистрирован на формальном курсе, что подтверждается:
- Выписка из аккредитованного или неаккредитованного учреждения или
- Другая документация, подтверждающая прохождение официального курса
- Программа с ежедневными заданиями
- Разъяснение временных параметров курса
- Документация об успеваемости студента на протяжении всего курса
- Документация по соответствию базовым знаниям и навыкам Техаса
5.Записываются ли оценки за экзамен CBE в стенограмме?
Если студент сдает экзамен CBE и получает зачетные баллы, результат будет указан в транскрипте. Баллы не будут записаны в транскрипт, если студент не сдает экзамен CBE и не получает зачет.
6. Включаются ли экзамены CBE в средний балл студента?
№
7. Есть ли экзамен CBE для курсов EOC?
Да. Студенты могут пройти CBE по алгебре I, биологии, английскому языку I, английскому языку II и истории США.
8. Если студент сдает CBE в середине года, когда он / она может быть переведен на следующий курс / уровень обучения?
Размещение на новый курс / уровень обучения будет происходить только в начале учебного года (или семестра для семестровых курсов), независимо от того, когда будет сдан CBE для ускоренного обучения.
9. Будут ли уведомлены учащиеся, сдающие тесты в средней или старшей школе, перед тестированием?
Да. Студенты получат письмо-подтверждение через мобильное приложение PISD за две-три недели до тестирования с информацией об экзамене.